Regression Quantiles for Time Series Data ZONGWU CAI. Department of Mathematics. Abstract
|
|
|
- Corey Rich
- 6 years ago
- Views:
Transcription
1 Regressi Quatiles fr Time Series Data ZONGWU CAI Departmet f Mathematics Uiversity f Nrth Carlia Charltte, NC 28223, USA zcai@ucc.edu Abstract I this article we study parametric estimati f regressi quatiles by ivertig a weighted Nadaraya-Wats estimatr (WNW) f cditial distributi fucti, which was rst used by Hall, Wl ad Ya (1999). First, uder sme regularity cditis, we establish the asympttic rmality ad weak csistecy f the WNW cditial distributi estimatr fr -mixig time series at bth budary ad iterir pits, ad we shw that the WNW cditial distributi estimatr t ly preserves the bias, variace, ad mre imprtatly, autmatic gd budary behavir prperties f lcal liear \duble-kerel" estimatrs itrduced by Yu ad Jes (1998), but als has the additial advatage f always beig a distributi itself. Secdly, it is shw that uder sme regularity cditis, the WNW cditial quatile estimatr is weekly csistet ad rmally distributed ad that it iherits all gd prperties frm the WNW cditial distributi estimatr. A simulati study is carried ut t illustrate the perfrmace f the estimates ad a real example is als used t demstrate the methdlgy. Key Wrds: -mixig; asympttic prperties; cditial quatiles; frecastig; lcal liear smthers; Nadaraya-Wats estimatr; predicti iterval; time series aalysis. AMS 1991 subject classicati. Primary 62G07, 62M10; secdary 62G20, 62G30.
2 1 Itrducti I parametric estimati f regressi fucti, mst ivestigatis are ccered with the regressi fucti m(x), the cditial mea f Y give value x f a predictr. See, fr example, the bks by Hardle (1990), Wahba (1990), Wad ad Jes (1995), ad Fa ad Gijbels (1996) fr gd itrductis ad iterestig applicatis t the geeral subject areas. Hwever, ew isights abut the uderlyig structures ca be gaied by csiderig the ther aspects f the cditial distributi F (y j x) f Y give = x ther tha the mea fucti m(x). Regressi (cditial) quatiles q p (x), 0 < p < 1, f Y give = x, the tpic f this article, cupled with the cditial distributi F (y j x), are key aspects f iferece i varius statistical prblems. Althugh sme idividual quatiles, such as the cditial media, are smetimes f iterest i practice, mre fte e wishes t btai a cllecti f cditial quatiles which ca characterize the etire cditial distributi. Mre imprtatly, ather applicati f cditial quatiles is cstructi f predicti itervals fr the ext value give a small secti f the recet past values i a statiary time series fy 1 ; : : :; Y g, which mtivates this wrk. Estimati f cditial quatiles has gaied particular atteti durig the recet tw decades due t their useful applicatis i varius elds such as medicie, ecmetrics, ad ace as well as the related elds. See, fr example, Hgg (1975), Keker ad Bassett (1978), Cle (1988), Cle ad Gree (1992), Fa ad Gijbels (1996, Sectis 5.5 ad 6.3), Yu ad Jes (1998), ad Hall, Wl ad Ya (1999), t ame just a few. Of particular iterest is the media fucti q 1=2 (x) fr asymmetric distributi, which ca prvide a useful alterative t the rdiary regressi based the mea. Regressi quatiles ca be als useful fr the estimati f predictive itervals. Fr example, i predictig the respse frm a give cvariate = x, estimates f q =2 (x) ad q 1?=2 (x) ca be used t btai a (1? )100% parametric predictive iterval. Hgg (1975) ad Keker ad Bassett (1978) develped ivative prcedures fr iferece abut q p (x) uder the assumpti that ad Y satisfy a liear mdel. I parametric regressi settig, there are several authrs t study the asympttic prperties f kerel ad earest-eighbr type estimati f cditial quatiles, icludig Ste (1977), Lejeue ad Sarda (1988), Trug (1989), Samata (1989), Bhattacharya ad Gagpadhyay (1990), ad Chaudhuri (1991) fr the iid errrs, ad Russas (1969) ad Russas (1991) fr Markvia prcesses, ad Trug ad Ste (1992) ad Bete ad Fraima (1995) fr mixig depedece. It is well kw that kerel type prcedures have serius drawbacks: the asympttic bias ivlves the desig desity s that they ca t be adaptive, ad they have budary eects s that they require budary mdicati. T atteuate these drawbacks, recetly, sme ew methds f estimatig cditial quatiles have bee prpsed. The rst e, a mre direct apprach, by usig the \check" fucti such as rbustied lcal liear smther, was prvided by Fa, Hu ad Trug (1994) ad further exteded by Yu ad Jes (1998). A alterative prcedure is rst t estimate the cditial distributi fucti by usig \duble-kerel" lcal liear techique f Fa, Ya ad Tg (1996) ad the t ivert the cditial distributi estimatr t prduce a estimatr f a cditial quatile, which is called the Yu ad Jes estimatr. See Yu ad Jes (1998) fr details. A detailed cmparis f these tw methds ca be fud i Yu ad Jes (1997, 1998). Accrdig t Yu ad Jes (1998), a particular preferece is the Yu ad Jes type estimatr. 2
3 As pited ut by Hall, Wl ad Ya (1999), althugh lcal liear estimatrs f the Yu ad Jes type have sme attractive prperties such as budary eects, desig adaptati ad mathematical eciecy (see Fa ad Gijbels, 1996), they have the disadvatage f prducig cditial distributi fucti estimatrs that are t cstraied either t lie betwee 0 ad 1 r t be mte icreasig althugh sme mdicatis i implemetati have bee addressed by Yu ad Jes (1998). I bth these respects, the Nadaraya-Wats (NW) methds are superir, despite their rather large bias ad budary eects. The prperties f psitivity ad mticity are particularly advatageus if the methd f ivertig cditial distributi estimatr is applied t prduce a estimatr f a cditial quatile. T vercme these diculties, Hall, Wl ad Ya (1999) prpsed a weighted versi f the NW estimatr (WNW), which is desiged t pssess the superir prperties f lcal liear methds such as bias reducti ad budary eect, ad t preserve the prperty that the NW estimatr is always a distributi fucti. Hall, Wl ad Ya (1999) discussed the asympttic rmality f the WNW estimatr fr -mixig uder sme strger assumptis (see Remark 1 belw). Hwever, they did t prvide the rigrus theretical justicati ad they did t discuss the budary behavir. The basic techiques are t vel t this article sice the WNW methd was rst used by Hall, Wl ad Ya (1999), but may details ad isights are. The gal f this paper is tw-fld. First, we establish the asympttic rmality ad weak csistecy fr the WNW estimatr f cditial distributi fr -mixig uder a set f weaker cditis at bth budary ad iterir pits. It is therefre shw, t the rst rder, that the WNW methd ejys the same cvergece rates as thse f lcal liear \duble-kerel" prcedure f Yu ad Jes (1998). A imprtat csequece f this study is that the WNW estimatr has desired samplig prperties at bth budary ad iterir pits f the supprt f the desig desity, which seems t be semial. Secdly, we derive the WNW estimatr f cditial quatile by ivertig the WNW cditial distributi estimatr. We shw that the WNW quatile estimatr exists always due t the WNW distributi beig a distributi fucti itself ad that it iherits all advatages frm the WNW estimatr f cditial distributi, as we describe later. Althugh ur iterest i cditial quatile estimati is mtivated by the frecastig frm time series data, we itrduce ur methds i a mre geeral settig (-mixig) which icludes time series mdelig as a special case. Our theretical results are derived uder -mixig assumpti. Fr referece cveiece, we rst itrduce the mixig ceciet. Let F b a be the -algebra geerated by f( t ; Y t )g b t=a. Dee (t) = supfjp (A B)? P (A) P (B)j : A 2 F 0?1; B 2 F 1 t g: It is called the strg mixig ceciet f the statiary prcess f( t ; Y t )g 1?1. If (t)! 0 as t! 1, the prcess is called strgly mixig r -mixig. Amg varius mixig cditis used i literature, -mixig is reasably weak, ad is kw t be fullled fr may time series mdels. Grdetskii (1977) ad Withers (1981) derived the cditis uder which a liear prcess is -mixig. I fact, uder very mild assumptis liear 3
4 autregressive ad mre geerally biliear time series mdels are -mixig with mixig ceciets decayig expetially. Auestad ad Tjstheim (1990) prvided illumiatig discussis the rle f -mixig (icludig gemetric ergdicity) fr mdel ideticati i liear time series aalysis. Che ad Tsay (1993) shwed that the fuctial autregressive prcess is gemetrically ergdic uder certai cditis. Furthermre, Masry ad Tjstheim (1995, 1997) demstrated that uder sme mild cditis, bth ARCH prcesses ad liear additive autregressive mdels with exgeus variables, which are particularly ppular i ace ad ecmetrics, are statiary ad -mixig. The pla f the paper is as fllws. I Secti 2, we ccetrate the WNW estimatr f cditial distributi. I Secti 3, we discuss the WNW estimatr f cditial quatiles. I bth sectis, the asympttic rmality ad week csistecy f the estimatrs at bth budary ad iterir pits are stated, ad a ad hc estimatr f the asympttic variace is als preseted. I Secti 4, a simulati study is carried ut t illustrate the estimates ad the methdlgy is als applied t a real example. All techical prfs are give i the Appedix. 2 Cditial Distributi Estimatr 2.1 Weighted Nadaraya-Wats estimatr Let p t (x), fr 1 t, dete the weight fuctis f the data 1 ; : : :; ad the desig pit x with the prperty that each p t (x) 0, P p t (x) = 1, ad ( t? x) p t (x) K h (x? t ) = 0: (2.1) Mtivated by the prperty f lcal liear estimatr, the cstrait (2.1) ca be regarded as a discrete mmet cditi (see (3.12) i Fa ad Gijbels, 1996, p.63). Of curse, fp t (x)g satisfyig these cditis are t uiquely deed, ad we specify them by maximizig Q p t (x) subject t the cstraits. The weighted versi f Nadaraya-Wats estimatr f the cditial distributi F (y j x) f Y t give t = x is deed P p bf (y j x) = t (x) K h (x? t ) I(Y t y) P : (2.2) p t (x) K h (x? t ) Nte that 0 b F (y j x) 1 ad it is mte i y. We shw i Therem 1 (belw) that b F (y j x) is rst-rder equivalet t a lcal liear estimatr, which des t ejy either f these prperties, ad mre imprtatly, i Therem 2 that b F (y j x) has autmatic gd behavir at budaries. The atural questi arises regardig hw t chse the weights. The idea is frm the empirical likelihd. Namely, by maximizig P lgfp t (x)g subject t the cstraits P p t (x) = 1 ad (2.1) thrugh the Lagrage multiplier, the fp t (x)g are simplied t p t (x) =?1 f1 + ( t? x) K h (x? t )g?1 ; (2.3) where, a fucti f data ad x, is uiquely deed by (2.1), which esues that P p t(x) = 1. Equivaletly, is chse t maximize L () = 1 h lg f1 + ( t? x) K h (x? t )g : (2.4) 4
5 I implemetati, the New-Raphs scheme is recmmeded t d the rt f equati L 0 () = Samplig prperties I this secti, we establish the weak csistecy with a rate ad the asympttic rmality fr the WNW estimatr F b (y j x) uder -mixig. Nte that Hall, Wl ad Ya (1999) derived the asympttic rmality fr -mixig withut the detailed prfs uder a set f strger cditis. We rst itrduce sme tati. Let g() dete the margial desity f R R t. Dee j = u j K(u) du ad j = u j K 2 (u) du. Let F (i) (y j x) = (@=@x) i F (y j x). Fr expsitial purpses, we csider ly the special case that is a scalar. We w impse the fllwig regularity cditis. B1. Fr xed y ad x, g(x) > 0, 0 < F (y j x) < 1, g() is ctiuus at x, ad F (y j x) has ctiuus secd rder derivative i a eighbrhd f x. B2. The kerel K() is symmetric desity satisfyig C 1 = supu ju K(u)j < 1. B3. The prcess f( t ; Y t )g is -mixig with the mixig ceciet satisfyig (t) = O fr sme > 0. B4. As! 1, h! 0 ad h 3! 1. t?(2+) B5. Let g 1;t (; ) be the jit desity f 1 ad t fr t 2. Assume that jg 1;t (u; v)?g(u) g(v)j M < 1 fr all u ad v. B6. (t) = O? t?3. Remark 1. B2 des t require that K() be cmpactly supprted, which is impsed by Hall, Wl ad Ya (1999). Nte that may well-kw kerels satisfy the assumpti B2 such as the Gaussia desity ad Epaechikv kerel. Als, te that B6 implies B3. I particular, Cditi B6 is weaker tha that i Hall, Wl ad Ya (1999) fr -mixig, which is strger tha -mixig. Furthermre, B4 is weaker tha that i Hall, Wl ad Ya (1999). Hwever, because B4 is always satised by the badwidths f ptimal size (i.e., h?1=5 ), we d t ccer urselves with such reemets. Therem 1. Suppse that Cditis B1-B5 hld. The, as! 1, bf (y j x)? F (y j x) = 1 2 h2 2 F (2) (y j x) + p (h 2 ) + O p ( h)?1=2 I additi, if Cditi B6 hlds true, the p h h bf (y j x)? F (y j x)? B(y j x) + p (h 2 )i D?! N where the bias ad variace are give respectively by : (2.5) 0; 2 (y j x) ; (2.6) B(y j x) = 1 2 h2 2 F (2) (y j x); (2.7) 5
6 ad 2 (y j x) = 0 F (y j x)[1? F (y j x)]=g(x): (2.8) Remark 2. It may be see frm the therem that rst, the WNW estimatr b F (y j x)! F (y j x) i prbability with a rate, which, f curse, implies that b F (y j x) is csistet. Als, t the rst rder, the WNW methd ejys the same cvergece rates as thse f lcal liear \duble-kerel" prcedure f Yu ad Jes (1998), uder similar regularity cditis. Hwever, Yu ad Jes (1998) treated ly the case f idepedet data. As fr the budary behavir f the WNW estimatr, we er Therem 2 belw. Withut lss f geerality, we csider left budary pit x = c h, 0 < c < 1. Frm Fa, Hu, ad Trug (1994), we take K() t have supprt [?1; 1] ad g() t have supprt [0; 1]. First, we itrduce the fllwig tati. Let L c () = Z c?1 u K(u) du; (2.9) 1? u K(u) ad c be the rt f equati L c () = 0, amely, L c ( c ) = 0. Fr example, c 1:8 fr c = 0:5 ad c 1:1 fr c = 0:6. Figure 1 depicts the slutis f L c () = 0 fr c takig values frm 0: c=0.5 c=0.6 c=0.7 c=0.8 c=0.9 c= Figure 1: Plt f L c () versus fr c takig values frm 0:5 t 1 with icremet 0:1. t 1 with icremet 0:1. Therem 2. Suppse that the cditis f Therem 1 hld. The p h h bf (y j c h)? F (y j c h)? Bc (y) + p (h 2 )i D?! N 0; 2 c (y) ; (2.10) 6
7 where the bias term is give by ad the variace is with 0 (c) = Z c?1 j = 1 ad 2. Of curse, g(0+) = lim z#0 g(z). B c (y) = h2 0 (c) F (2) (y j 0+) ; 2 1 (c) 2(y) = 2(0) F (y j 0+)[1? F (y j 0+)] c 2 1 (c) g(0+) u Z 2 K(u) c 1? c u K(u) du; ad K j (u) j(c) =?1 f1? c u K(u)g du j These therems reect tw f the majr advatages f the WNW estimatr: (a) depedece f the asympttic bias the desig desity g(), ad ideed its depedece the simple cditial distributi curvature F (2) ( j ); ad (b) autmatic gd behavir at budaries, at least with regard t rders f magitude, withut the eed f budary crrecti. Als, we remark that a similar result (2.10) hlds fr the right budary pit x = 1? c h. If the pit 0 were a iterir pit, the the expressi (2.10) wuld hld with c = 1 ad c = 0. Furthermre, te that sice the prfs f therems 1 ad 2 are similar, we preset ly the detailed prf f Therem 1 ad give the brief utlie f the prf f Therem 2 i the Appedix. The explicit expressi f the asympttic variace f b F (y j x) give i (2.8) gives a mre direct ad simpler way t cstruct the estimate f 2 (y j x) as fllws b 2 (y j x) = 0 b F (y j x) h 1? b F (y j x) i =bg(x); (2.11) where bg(x) is ay csistet desity estimatr f g(x) which might be btaied by lcal liear prcedure. 3 Quatile Estimatr Our iterest here is t estimate the p-th cditial quatile fucti q p (x) f Y t give t = x fr ay 0 < p < 1, deed by q p (x) = iffy 2 < : F (y j x) pg; which is assumed t be uique. As demstrated i Secti 2, the WNW estimatr f cditial distributi fucti F b (y j x) psses advatages: desig adaptati ad budary eects, which are the same as the lcal liear cuterpart, ad mre imprtatly, beig betwee 0 ad 1 ad mte, which lcal liear estimatr des t ejy either f these prperties. We thus dee the WNW type cditial quatile estimatr bq p (x) i priciple t satisfy F b (bqp (x) j x) = p s that bq p (x) = if y 2 < : b F (y j x) p b F?1 (p j x): (3.1) We remark that bq p (x) always exists sice F b (y j x) is betwee 0 ad 1 ad mte i y, ad it ivlves ly e badwidth s that it makes practical implemetati mre appealig. I 7
8 ctrast, the \duble-kerel" estimatr f Yu ad Jes (1998) has sme diculty f ivertig the cditial distributi estimatr due t lack f mticity, ad it requires chsig tw badwidths althugh the secd badwidth shuld t be very sesitive. Furthermre, we will shw i Therems 3 ad 4 (belw) that the WNW estimatr bq p (x) maitais the afremetied advatages as b F ( j x) des. T this ed, we eed the fllwig additial cditis. C1. Assume that F (y j x) has a cditial desity f(y j x) ad f(y j x) is ctiuus at x. C2. f(q p (x) j x) > 0. Therem 3. Suppse that Cditis B1-B5 hld. The, as! 1, I additi, if Cditis B6 ad C1-C2 are satised, the, bq p (x)! q p (x) i prbability: (3.2) p h h bqp (x)? q p (x)? B p (x) + p (h 2 )i D?! N where the bias ad variace are give respectively by 0; p(x) 2 ; (3.3) B p (x) =? B(q p(x) j x) f(q p (x) j x) ; ad 2 p(x) = 2 (q p (x) j x) f 2 (q p (x) j x) = 0 p[1? p] f 2 (q p (x) j x) g(q p (x)) : A imprtat way f assessig the perfrmace f bq p (x) is by its mea squared errr (MSE). As a applicati f Therem 3, the MSE f bq p (x) is give by MSE (bq p (x)) = h4 4 ( 2 F (2) (q p (x) j x) f(q p (x) j x) ) h 0 p(1? p) f 2 (q p (x) j x) g(q p (x)) : (3.4) A cmparis f (3.4) with Therem 1 i Yu ad Jes (1998) fr the \duble-kerel" estimatr, (3.1) des t have the extra tw terms frm the vertical smthig \i the y directi". By miimizig MSE i (3.4), therefre, this yields the ptimal badwidth h pt = F (2) (q p (x) j x) 2 0 p(1? p)=g(q p (x)) =5?1=5 : I the same maer f (2.11), the csistet estimate f 2 p(x) is b 2 p (x) = 0 p[1? p] bf 2 (q p (x) j x) bg(q p (x)) ; where b f(y j x) ca be btaied by usig the lcal liear \duble-kerel" methd f Fa, Ya ad Tg (1996). 8
9 Similar t Therem 2, we csider the budary behavir f the WNW estimatr bq p (x) i the fllwig therem. The prf f Therem 4 is mitted sice it is similar t that f Therem 3, which may be fud i the Appedix. Therem 4. Suppse that the cditis f Therem 3 hld. The, as! 1, p h h bqp (c h)? q p (c h)? B p;c + p (h )i 2?! D N ; where the bias ad variace are give respectively by 0; 2 p;c ad B p;c =? B c(q p (0+)) f(q p (0+) j 0+) = 2 (c) F (2) (q p (0+) j 0+)?h2 ; 2 1 (c) f(q p (0+) j 0+) 2 p;c = 2 c (q p (0+)) f 2 (q p (0+) j 0+) = 0 (0) p [1? p] 2 1 (c) f 2 (q p (0+) j 0+) g(q p (0+)) : Similarly, we ca derive the MSE f bq p (c h) as fllws MSE (bq p (c h)) = h4 4 ( 2 (c) F (2) (q p (0+) j 0+) 1 (c) f(q p (0+) j 0+) ) h ad the crrespdig ptimal badwidth is (0) p(1? p) 2 1 (c) f 2 (q p (0+) j 0+) g(q p (0+)) ; h c;pt = 4 2 2(c) F (2) (q p (0+) j 0+) 0 (c) p(1? p)=g(q p (0+)) =5?1=5 : 4 Numerical Prperties 4.1 Simulated example We begi with the illustrati with a simulated example f the AR(1) mdel with 505 bservatis Y t = Y t?1 + " t ; where f" t g are iid N(0; 1) ad = 0:6. The rst 500 bservatis are used fr estimati f the cditial distributi ad the last 5 bservatis are left fr cstructi f predictive itervals. Thrughut this secti, the cvariate t is take t be Y t?1 ad the Epaechikv kerel is used. Figures 2(a) ad (b) display the WNW estimates (thi slid ( t =?1:807), dt ( t =?0:733) ad dashed ( t = 0:402) lies) f cditial distributis F (y j x) (three thick lies i Figure 2(a)) f Y t give t = x ad their quatiles q x (p) = x +?1 (p) (three thick lies i Figure 2(b)), where () is the stadard rmal distributi, ad they shw that the perfrmace f the WNW estimate is reasably well. T check the perfrmace i terms f predicti, we cstruct the 95% predictive itervals [bq 0:025 (x); bq 0:975 (x)] fr the last 5 bservatis, summarized i Table 1. All predictive itervals ctai the crrespdig true values. The average legth f the itervals is 3:91, which is 54:7% f the rage f the data. 9
10 (a) The cditial CDFs fr AR(1) - WNW (b) The cditial quatiles fr Ar(1) - WNW x= x= x= x= x= x= Figure 2: (a) Cditial distributis ad their WNW estimates. (b) Cditial quatiles ad their WNW estimates. Thick slid lies - true fuctis, ad thi slid ( t =?1:807), dt ( t =?0:733) ad dashed ( t = 0:402) lies - three dieret values f cvariate t. Table 1: The pst-sample predictive itervals fr AR(1) mdel Observati True Value Predictive Iterval Y [?2:24; 2:02] Y [?2:24; 1:64] Y [?2:56; 0:33] Y [?2:75; 1:64] Y [?2:21; 2:02] 4.2 Real example Fially, we csider the Iteratial Airlie Passeger Data fu t ; t = 1; : : :; 144g f Bx ad Jekis (1976, p.531) (mthly ttals (i thusads) f passegers frm Jauary, 1949 t December, 1960). Figure 3(a) shws clearly that the variability icreases as U t icreases (called multiplicative seasality) ad tread. T elimiate the tread ad seasality, we csider trasfrmatis. We rst use the lgarithmic trasfrmati sice fu t g is a series whse stadard deviati icreases liearly with the mea. The trasfrmed series V t = lg(u t ), shw i Figure 3(b), des t display icrease i variability with V t, but shws clearly a liear tread. Secdly, by fllwig the aalysis i Brckwell ad Davis (1991, pp ), we apply the dierece peratr (1? B)(1? B 12 ) t fv t g t btai the ew series Y t = (1? B)(1? B 12 ) V t, shw i Figure 3(c), which des t display ay apparet deviatis frm statiarity. The rst 125 trasfrmed bservatis are used fr estimati ad the last 6 bservatis are left fr predicti. The WNW estimates f cditial distributi f Y t give t = Y t?1 are depicted i Figure 3(d) fr six dieret values f t (0:0086; 0:0014;?0:0459; 0:0120; 0:0318;?0:0501) ad Figure 3(e) gives the WNW estimates f six cditial quatiles. Nw we csider the frecastig fr the last 6 bservatis based bth the WNW ad NW estimatrs which are cmputed by usig the same badwidth fr each case. The 95% predicti itervals are reprted i Table 2, which shws that the WNW methd 10
11 (a) Time Series Plt fr Airlie Data (b) Time Series Plt fr Lg-trasfrmed Data (c) Time Series Plt fr Differeced Lg-trasfrmed Data (d) The cditial CDFs fr Airlie Data x= x= x= x= x= x= (e) The cditial quatiles fr Airlie Data (f) The estimated cditial quatile surface x= x= x= x= x= x= q_x(p) p Figure 3: (a) Time series plt f Airlie data. (b) Time series plt f lg-trasfrmed data. (c) Time series plt f twice-diereced lg-trasfrmed data. (d) ad (e) WNW estimates f cditial CDFs ad quatiles fr six dieret values f cvariate t (0:0086; 0:0014;?0:0459; 0:0120; 0:0318;?0:0501). (f) Estimated cditial quatile q x (p) f Y t give Y t?1 = x. 11
12 Table 2: The pst-sample predictive itervals fr Airlie data Observati True Value P.I. fr WNW P.I. fr NW Y [?0:101; 0:045] [?0:101; 0:045] Y [?0:101; 0:055] [?0:101; 0:067] Y [?0:102; 0:131] [?0:102; 0:131] Y [?0:101; 0:042] [?0:101; 0:042] Y [?0:086; 0:044] [?0:086; 0:044] Y [?0:054; 0:131] [?0:115; 0:141] utperfrms the NW apprach i 2 ut 6 itervals althugh all predictive itervals based bth methds ctai the crrespdig true values. The average legths f the itervals fr WNW ad NW are 0:166 ad 0:179, respectively, which are respective 58:7% ad 63:6% f the rage f the data. Appedix: Prfs Nte that we use the same tati as i Sectis 2 ad 3. Let " t = I(Y t y)? F (y j t ), ad b t (x) = 1? h 2 g 0 (x) 2 2 g(x) (?1 t? x) K h (x? t ) : (A.1) Set t = p h b t (x) " t K h (x? t ), ad J 1 = s h b t (x) " t K h (x? t ) = 1 p t : (A.2) Let C dete a psitive cstat which might take a dieret value at the dieret place. Lemma 1. Uder the assumptis B1-B5, we have Var(J 1 )! 0 F (y j x)[1? F (y j x)] g(x) = 2 (y j x) g 2 (x) 2 (y j x): Prf. It is easy t see that E[ t ] = 0 sice E[" t j t ] = 0, ad i Var(J 1 ) = E + A straightfrward maipulati yields h E 2 t h 2 t t=2 1? t? 1 Cv( 1 ; t ): i = h E h b 2 t (x) " 2 t K 2 h(x? t ) i = 2 (y jx) g 2 (x) + (1): (A.3) Chse d = O(h?1=(1+=2) ) ad decmpse the secd term the right had side f (A.3) it tw terms as fllws = d + t=2 t=2 t=d J 11 + J 12 :
13 Fr J 11, it fllws by Cditi B5 that jcv( 1 ; t )j C h, s that J 11 = O(d h) = (1). Fr J 12, by applyig Therem A.5 i Hall ad Heyde (1980) ad the fact that K h () C h?1, e has which implies that J 12 C h?1 This cmpletes the prf f the lemma. jcv( 1 ; t )j C h?1 (t? 1); (t) C h?1 d?(1+) td Lemma 2. Uder the assumptis B1-B5, we have s that p t (x) = b t (x) f1 + p (1)g. Prf. Dee, fr j 1, =? h 2 g 0 (x) 2 2 g(x) f1 + p(1)g; A j = 1 ( t? x) j K j (x? h t): Usig the same argumets as thse i Lemma 1, we have = (1): A 1 =? h 2 g 0 (x) + p (h 2 ); A 2 = h 2 g(x) + p (h 2 ); ad A 3 = O p (h 2 ): (A.4) By (6.4) i Che ad Hall (1993), By a Taylr expasi, s that jj ja 1 j A 2? C 1 ja 1 j = O p(h): 0 = A 1? A A 3? 3 A 4 + ; = A 1 A A 3 A 2? 3 A 4 A 2 + : Therefre, substitutig (A.4) it the abve equati, we prve the lemma. Prf f Therem 1. It fllws frm Lemma 2 that P bf (y j x)? F (y j x) = [I(Y t y)? F (y j x)] p t (x) K h (x? t ) P p t (x) K h (x? t ) ( h)?1=2 J 1 + J 2 J?1 3 f1 + p (1)g; (A.5) where ad J 2 = [F (y j t )? F (y j x)] p t (x) K h (x? t ); J 3 = 1 b t (x) K h (x? t ): 13
14 By Cditi B1 ad (2.1) as well as the Taylr expasi, we have J 2 = 1 2 F (2) (y j x) ( t? x) 2 b t (x) K h (x? t ) + p (h 2 ) = B(y j x) g(x) + p (h 2 ) by fllwig the lie f the prf f Lemma 1. Similarly, J 3 = g(x) + p (1): (A.6) Therefre, p h h bf (y j x)? F (y j x)? B(y j x) + p (h 2 )i = g?1 (x) J 1 + p (1): (A.7) This, i cjucti with Lemma 1, implies (2.5). T prve (2.6), it suces t establish the asympttic rmality f J 1 by (A.7). T this ed, we emply the Db's small-blck ad largeblck techique. Namely, partiti f1; : : : ; g it 2 q + 1 subsets with large-blck f size r = r ad small-blck f size s = s. Set q = q = : (A.8) r + s Dee the radm variables, fr 0 j q? 1, The, j = j(r+s)+r?1 i=j(r+s) J 1 = 1 8 < q?1 p : We will shw that, as! 1, i ; j = j=0 q?1 j + j=0 1 E [Q ;2] 2! 0; E [exp(i t Q ;1)]? 1 q?1 j=0 where 2 (y j x) is deed i Lemma 1, ad 1 q?1 j=0 (j+1)(r+s) i=j(r+s)+r i ; ad q =?1 i=q(r+s) j + q 9 = ; 1 p fq ;1 + Q ;2 + Q ;3 g : E 2 j q?1 Y j=0 1 E [Q ;3] 2! 0; E [exp(i t j )]! 0; h E 2 j I j j j " (y j x) p i : (A.9) (A.10)! 2 (y j x); (A.11) i! 0 (A.12) fr every " > 0. (A.9) implies that Q ;2 ad Q ;3 are asympttically egligible i prbability; (A.10) shws that the summads j i Q ;1 are asympttically idepedet; ad (A.11) ad (A.12) are the stadard Lideberg-Feller cditis fr asympttic rmality f Q ;1 fr the idepedet setup. 14
15 Let us rst establish (A.9). T this eect, we dee the large-blck size r by r = b( h ) 1=2 c ad the small-blck size s = b( h ) 1=2 = lg c. The, as! 1, s =r! 0; ad (=r ) (s )! 0: (A.13) Observe that E [Q ;2 ] 2 = q?1 j=0 Var( j ) + 2 It fllws frm statiarity ad Lemma 1 that F 1 = q Var( 1 ) = q Var 0i<jq?1 j=1 Cv( i ; j ) F 1 + F 2 : 0 s j A = q s [ 2 (y j x) + (1)]: (A.14) (A.15) Next csider the secd term F 2 the right-had side f (A.14). Let r j = j(r + s ), the r j? r i r fr all j > i, we therefre have jf 2 j 2 s s 0i<jq?1 j 1 =1 j 2 =1?r 2 j 1 =1 j 2 =j 1 +r jcv( j1 ; j2 )j: jcv( r i +r+j 1 ; r j +r+j 2 )j By statiarity ad Lemma 1, e btais jf 2 j 2 j=r +1 jcv( 1 ; j )j = (): (A.16) Hece, by (A.13)-(A.16), we have It fllws frm statiarity, (A.13) ad Lemma 1 that Var [Q ;3 ] = Var 1 E[Q ;2] 2 = O q s?1 + (1) = (1): (A.17) j=1 j 1 A = O(? q (r + s )) = (): (A.18) Cmbiig (A.13), (A.17) ad (A.18), we establish (A.9). As fr (A.11), by statiarity, (A.13) ad Lemma 1, it is easily see that 1 q?1 j=0 E 2 j = q E 2 1 = q r 1 r Var r j=1 j 1 A! 2 (y j x): I rder t establish (A.10), we make use f Lemma 1.1 i Vlkskii ad Rzav (1959) t btai E [exp(i t Q ;1)]? qy?1 j=0 E [exp(i t j )] 16 (=r ) (s ) 15
16 tedig t zer by (A.13). It remais t establish (A.12). T this ed, we emply Therem 4.1 i Sha ad Yu (1996) ad Cditi B6 t btai, h E 2 I 1 j 1 j " (y j x) p i C?1=2 E j 1 j 3 It is easy t see that Therefre, by (A.19) ad (A.20), E h 2 1 I j 1 j " (y j x) p C?1=2 r 3=2 1=2 E j 1 j 6 : (A.19) E j 1 j 6 C h?2 : (A.20) i C?1=2 r 3=2 h?1 : Thus, by (A.8) ad the deiti f r, ad usig Cditi B4, we btai 1 q?1 j=0 h E 2 j I j j j " (y j x) p This cmpletes the prf f the therem. I rder t prve Therem 2, we eed the fllwig lemma. Lemma 3. Uder the assumptis B1-B5, we have i C r 1=2?1=2 h?1 C ( h 3 )?1=4! 0: p t (c h) =?1 b c t(c h) f1 + p (1)g; where b c t (x) = [1 + c ( t? x) K h (x? t )]?1 : Prf. Let b = argmax L () s that L 0 b = 0, where L () is deed i (2.4). It suces t shw that b! c i prbability. T this ed, dete by S " the iterval c ". We will shw that fr ay sucietly small ", the prbability teds t e. By the Taylr expasi, sup 2S " L () L ( c ) L ()? L ( c ) = L 0 ( c ) (? c ) L00 ( c ) (? c ) L000 ( ) (? c ) 3 with lyig betwee ad c. It is easy t shw that L 0 ( c ) = p (1); L 00 ( c ) =? 3 (c) g(0+) + p (1); ad L 000 ( ) = O p (1); where 3 (c) = Z c?1 u 2 K 2 (u) [1? c u K(u)] 2 du: 16
17 This ccludes with prbability tedig t e that whe " is small eugh, fr all 2 S ", which cmpletes the prf f the lemma. L ()? L ( c ) 0; Prf f Therem 2. By replacig b t (x) i t by b c t(c h) ad fllwig the same argumets as thse used i the prf f Therem 1, we ca prve the therem via Lemma 3. Lemma 4. Uder the assumptis B1-B5 ad C1, we have, fr ay! 0, bf (y + j x)? b F (y j x) = f(y j x) + p ( ) + p ( h)?1=2 : Prf. Let The, It is easy t see that Similarly, Therefre, J 4 = 1 b t (x)[i(y t y + )? I(Y t y)] K h (x? t ): bf (y + j x)? b F (y j x) = J4 J?1 3 f1 + p (1)g: (A.21) E(J 4 ) = E [ff (y + j x)? F (y j x)g b t (x) K h (x? t )] = f(y j x) g(x) + ( ): Var(J 4 ) = O ( h)?1 : J 4 = f(y j x) g(x) + p ( ) + p ( h)?1=2 : This, cupled with (A.6) ad (A.21), prves the lemma. We w embark the prf f Therem 3. Prf f Therem 3. First, we prve (3.2). T this ed, by (2.5), we have, fr all x ad y, bf (y j x)! F (y j x) i prbability: It fllws by Therem 1 i Tucker (1967, pp ) that sup jf (y j x)? F (y j x)j! 0 i prbability (A.22) y2< sice F (y j x) is a distributi fucti. The assumpti that q p (x) is uique implies that, fr ay xed x, there is a " = "(x) > 0 such that = (") = mifp? F (q p (x)? " j x); F (q p (x) + " j x)? pg > 0: 17
18 It is easy t see that the fllwig iequalities hld, P fjbq p (x)? q p (x)j > "g P fjf (bq p (x) j x)? pj > g = P P F b (bq p (x) j x)? F (bq p (x) j x) ( ) F b (y j x)? F (y j x) > sup y > ; which teds t 0 by (A.22). Therefre, (3.2) hlds true. = B p (x) + ( h)?1=2 p (x) u. The, Q (u) P = P h p h?1 p (x) bqp (x)? q p (x)? B p (x) + p (h 2 ) P fbq p (x) q p (x) + g bf (qp (x) + j x) p by Lemma 4. Therefre, h p Q (u) P h?1 (q p (x) j x) P (u) bf (qp (x) j x)?f(q p (x) j x) + p We w prve (3.3). Fr ay u, let bf (qp (x) j x)? p? B(q p (x) j x) i u i?u by Therem 1, where () is the stadard rmal distributi. Therefre, we ish the prf f the therem. Refereces Auestad, B. ad Tjstheim, D. (1990). Ideticati f liear time series: First rder characterizati ad rder determiati. Bimetrika, 77, 669{687. Bhattacharya, P.K. ad Gagpadhyay, A.K. (1990). Kerel ad earest-eighbr estimati f a cditial quatile. The Aals f Statistics, 18, 1400{1415. Bete, G. ad Fraima, R. (1995). Asympttic distributi f smthers based lcal meas ad lcal medias uder depedece. Jural f Multivariate Aalysis, 54, 77{90. Bx, G.E.P. ad Jekis, G.M. (1976). Time Series Aalysis: Frecastig ad Ctrl. Hlde- Day, Sa Fracisc. Brckwell, P.J. ad Davis, R.A. (1991). Time Series: Thery ad Methds, 2d. Spriger-Verlag, New Yrk. Chaudhuri, P. (1991). Nparametric estimates f regressi quatiles ad their lcal Bahadur represetati. The Aals f statistics, 19, 760{777. Che, R. ad Tsay, R. S. (1993). Fuctial-ceciet autregressive mdels. Jural f the America Statistical Assciati, 88, 298{308. Che, S.. ad Hall, P. (1993). Smthed empirical likelihd cdece itervals fr quatiles. The Aals f Statistics, 21, 1166{
19 Cle, T.J. (1988). Fittig smthed cetile curves t referece data. Jural f the Ryal Statistical Sciety, Series A, 151, 385{418. Cle, T.J. ad Gree, P.J. (1992). Smthig referece cetile curves: The LMS methd ad pealized likelihd. Statistics i Medicie, 11, 1305{1319. Fa, J. ad Gijbels, I. (1996). Lcal Plymial Mdelig ad Its Applicatis. Chapma ad Hall, Ld. Fa, J., Hu, T.-C., ad Trug, Y.K. (1994). Rbust parametric fucti estimati. Scadiavia Jural f Statistics, 21, 433{446. Fa, J., Ya, Q. ad Tg, H. (1996). Estimati f cditial desities ad sesitivity measures i liear dyamical systems. Bimetrika, 83, 189{206. Grdetskii, V.V. (1977). O the strg mixig prperty fr liear sequeces. Thery f Prbability ad Its Applicatis, 22, 411{413. Hall, P. ad Heyde, C.C. (1980). Martigale Limit Thery ad its Applicatis. Academic Press, New Yrk. Hall, P., Wl, R.C.L., ad Ya, Q. (1999). Methds fr estimatig a cditial distributi fucti. Jural f the America Statistical Assciati, 94, 154{163. Hardle, W. (1990). Applied Nparametric Regressi. Cambridge Uiversity Press, New Yrk. Hgg, R.V. (1975). Estimates f percetile regressi lies usig salary data. America Statistical Assciati, 70, 56{59. Jural f the Hurvich, C.M., Sim, J.S. ad Tsai, C.-L. (1998). Smthig parameter selecti i parametric regressi usig a imprved Akaike ifrmati criteri. Jural f the Ryal Statistical Sciety, Series B, 60, Keker, R. ad Bassett, G.S. (1978). Regressi quatiles. Ecmetrica, 46, 33{50. Lejeue, M.G. ad Sarda, P. (1988). Quatile regressi: a parametric apprach. Cmputatial Statistics ad Data Aalysis, 6, 229{281. Masry, E. ad Tjstheim, D. (1995). Nparametric estimati ad ideticati f liear ARCH time series: Strg cvergece ad asympttic rmality. Ecmetric Thery, 11, 258{289. Masry, E. ad Tjstheim, D. (1997). Additive liear AR time series ad prjecti estimates. Ecmetric Thery, 13, 214{252. Rice, J. (1984), Badwidth selecti fr parametric regressi. The Aals f Statistics, 12, 1215{1230. Russas, G.G. (1969). Nparametric estimati f the trasiti distributi fucti f a Markv prcess. The Aals f Mathematical Statistics, 40, 1386{1400. Russas, G.G. (1991). Estimati f trasiti distributi fucti ad its quatiles i Markv prcesses: Strg csistecy ad asympttic rmality. I Nparametric Fuctial Estimati ad related Tpics (G.G. Russas, ed.), 443{
20 Samata, M. (1989). Nparametric estimati f cditial quatiles. Statistics ad Prbability Letters, 7, 407{412. Sha, Q. ad Yu, H. (1996). Weak cvergece fr weighted empirical prcesses f depedet sequeces. The Aals f Prbability, 24, 2098{2127. Ste C.J. (1977). Csistet parametric regressi (with discussi). The Aals f Statistics, 5, 595{645. Trug, Y.K. (1989). Asympttic prperties f kerel estimatrs based lcal media. The Aals f Statistics, 17, 606{617. Trug, Y.K. ad Ste, C.J. (1992). Nparametric fucti estimati ivlvig time series. The Aals f Statistics, 20, Tucker, H. (1967). A Graduate Curse i Prbability. Academic Press, New Yrk. Vlkskii, V.A. ad Rzav, Yu.A. (1959). Sme limit therems fr radm fuctis. I. Thery f Prbability ad Its Applicatis, 4, 178{197. Wad, M.P. ad Jes, M.C. (1995). Kerel Smthig. Chapma ad Hall, Ld. Wahba, G. (1990). Splie Mdels fr Observatial Data. SIAM, Philadelphia. Withers, C.S. (1981). Cditis fr liear prcesses t be strg mixig. Zeitschrift fur Wahrscheilichkeitstherie verwadte Gebiete, 57, 477{480. Yu, K. ad Jes, M.C. (1997). A cmparis f lcal cstat ad lcal liear regressi quatile estimati. Cmputatial Statistics ad Data Aalysis, 25, 159{166. Yu, K. ad Jes, M.C. (1998). Lcal liear quatile regressi. Jural f the America Statistical Assciati, 93, 228{
5.1 Two-Step Conditional Density Estimator
 5.1 Tw-Step Cditial Desity Estimatr We ca write y = g(x) + e where g(x) is the cditial mea fucti ad e is the regressi errr. Let f e (e j x) be the cditial desity f e give X = x: The the cditial desity
5.1 Tw-Step Cditial Desity Estimatr We ca write y = g(x) + e where g(x) is the cditial mea fucti ad e is the regressi errr. Let f e (e j x) be the cditial desity f e give X = x: The the cditial desity
ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]
![ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ] ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]](/thumbs/80/82121747.jpg) ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
BIO752: Advanced Methods in Biostatistics, II TERM 2, 2010 T. A. Louis. BIO 752: MIDTERM EXAMINATION: ANSWERS 30 November 2010
 BIO752: Advaced Methds i Bistatistics, II TERM 2, 2010 T. A. Luis BIO 752: MIDTERM EXAMINATION: ANSWERS 30 Nvember 2010 Questi #1 (15 pits): Let X ad Y be radm variables with a jit distributi ad assume
BIO752: Advaced Methds i Bistatistics, II TERM 2, 2010 T. A. Luis BIO 752: MIDTERM EXAMINATION: ANSWERS 30 Nvember 2010 Questi #1 (15 pits): Let X ad Y be radm variables with a jit distributi ad assume
Multi-objective Programming Approach for. Fuzzy Linear Programming Problems
 Applied Mathematical Scieces Vl. 7 03. 37 8-87 HIKARI Ltd www.m-hikari.cm Multi-bective Prgrammig Apprach fr Fuzzy Liear Prgrammig Prblems P. Padia Departmet f Mathematics Schl f Advaced Scieces VIT Uiversity
Applied Mathematical Scieces Vl. 7 03. 37 8-87 HIKARI Ltd www.m-hikari.cm Multi-bective Prgrammig Apprach fr Fuzzy Liear Prgrammig Prblems P. Padia Departmet f Mathematics Schl f Advaced Scieces VIT Uiversity
ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]
![ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ] ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]](/thumbs/89/100002025.jpg) ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
D.S.G. POLLOCK: TOPICS IN TIME-SERIES ANALYSIS STATISTICAL FOURIER ANALYSIS
 STATISTICAL FOURIER ANALYSIS The Furier Represetati f a Sequece Accrdig t the basic result f Furier aalysis, it is always pssible t apprximate a arbitrary aalytic fucti defied ver a fiite iterval f the
STATISTICAL FOURIER ANALYSIS The Furier Represetati f a Sequece Accrdig t the basic result f Furier aalysis, it is always pssible t apprximate a arbitrary aalytic fucti defied ver a fiite iterval f the
Markov processes and the Kolmogorov equations
 Chapter 6 Markv prcesses ad the Klmgrv equatis 6. Stchastic Differetial Equatis Csider the stchastic differetial equati: dx(t) =a(t X(t)) dt + (t X(t)) db(t): (SDE) Here a(t x) ad (t x) are give fuctis,
Chapter 6 Markv prcesses ad the Klmgrv equatis 6. Stchastic Differetial Equatis Csider the stchastic differetial equati: dx(t) =a(t X(t)) dt + (t X(t)) db(t): (SDE) Here a(t x) ad (t x) are give fuctis,
K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L.
![K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L. K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L.](/thumbs/74/70813931.jpg) Iterat. J. Math. & Math. Scl. Vl. 8 N. 2 (1985) 359-365 359 A GENERALIZED MEIJER TRANSFORMATION G. L. N. RAO Departmet f Mathematics Jamshedpur C-perative Cllege f the Rachi Uiversity Jamshedpur, Idia
Iterat. J. Math. & Math. Scl. Vl. 8 N. 2 (1985) 359-365 359 A GENERALIZED MEIJER TRANSFORMATION G. L. N. RAO Departmet f Mathematics Jamshedpur C-perative Cllege f the Rachi Uiversity Jamshedpur, Idia
Unifying the Derivations for. the Akaike and Corrected Akaike. Information Criteria. from Statistics & Probability Letters,
 Uifyig the Derivatis fr the Akaike ad Crrected Akaike Ifrmati Criteria frm Statistics & Prbability Letters, Vlume 33, 1997, pages 201{208. by Jseph E. Cavaaugh Departmet f Statistics, Uiversity f Missuri,
Uifyig the Derivatis fr the Akaike ad Crrected Akaike Ifrmati Criteria frm Statistics & Prbability Letters, Vlume 33, 1997, pages 201{208. by Jseph E. Cavaaugh Departmet f Statistics, Uiversity f Missuri,
Ch. 1 Introduction to Estimation 1/15
 Ch. Itrducti t stimati /5 ample stimati Prblem: DSB R S f M f s f f f ; f, φ m tcsπf t + φ t f lectrics dds ise wt usually white BPF & mp t s t + w t st. lg. f & φ X udi mp cs π f + φ t Oscillatr w/ f
Ch. Itrducti t stimati /5 ample stimati Prblem: DSB R S f M f s f f f ; f, φ m tcsπf t + φ t f lectrics dds ise wt usually white BPF & mp t s t + w t st. lg. f & φ X udi mp cs π f + φ t Oscillatr w/ f
Chapter 3.1: Polynomial Functions
 Ntes 3.1: Ply Fucs Chapter 3.1: Plymial Fuctis I Algebra I ad Algebra II, yu ecutered sme very famus plymial fuctis. I this secti, yu will meet may ther members f the plymial family, what sets them apart
Ntes 3.1: Ply Fucs Chapter 3.1: Plymial Fuctis I Algebra I ad Algebra II, yu ecutered sme very famus plymial fuctis. I this secti, yu will meet may ther members f the plymial family, what sets them apart
A Study on Estimation of Lifetime Distribution with Covariates Under Misspecification
 Prceedigs f the Wrld Cgress Egieerig ad Cmputer Sciece 2015 Vl II, Octber 21-23, 2015, Sa Fracisc, USA A Study Estimati f Lifetime Distributi with Cvariates Uder Misspecificati Masahir Ykyama, Member,
Prceedigs f the Wrld Cgress Egieerig ad Cmputer Sciece 2015 Vl II, Octber 21-23, 2015, Sa Fracisc, USA A Study Estimati f Lifetime Distributi with Cvariates Uder Misspecificati Masahir Ykyama, Member,
Statistica Sinica 6(1996), SOME PROBLEMS ON THE ESTIMATION OF UNIMODAL DENSITIES Peter J. Bickel and Jianqing Fan University of California and U
 Statistica Siica 6(996), 23-45 SOME PROBLEMS ON THE ESTIMATION OF UNIMODAL DENSITIES Peter J. Bickel ad Jiaqig Fa Uiversity f Califria ad Uiversity f Nrth Carlia Abstract: I this paper, we study, i sme
Statistica Siica 6(996), 23-45 SOME PROBLEMS ON THE ESTIMATION OF UNIMODAL DENSITIES Peter J. Bickel ad Jiaqig Fa Uiversity f Califria ad Uiversity f Nrth Carlia Abstract: I this paper, we study, i sme
Mean residual life of coherent systems consisting of multiple types of dependent components
 Mea residual life f cheret systems csistig f multiple types f depedet cmpets Serka Eryilmaz, Frak P.A. Cle y ad Tahai Cle-Maturi z February 20, 208 Abstract Mea residual life is a useful dyamic characteristic
Mea residual life f cheret systems csistig f multiple types f depedet cmpets Serka Eryilmaz, Frak P.A. Cle y ad Tahai Cle-Maturi z February 20, 208 Abstract Mea residual life is a useful dyamic characteristic
Quantum Mechanics for Scientists and Engineers. David Miller
 Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
COWLES FOUNDATION FOR RESEARCH IN ECONOMICS YALE UNIVERSITY
 HAC ESTIMATION BY AUTOMATED REGRESSION By Peter C.B. Phillips July 004 COWLES FOUNDATION DISCUSSION PAPER NO. 470 COWLES FOUNDATION FOR RESEARCH IN ECONOMICS YALE UNIVERSITY Bx 088 New Have, Cecticut 0650-88
HAC ESTIMATION BY AUTOMATED REGRESSION By Peter C.B. Phillips July 004 COWLES FOUNDATION DISCUSSION PAPER NO. 470 COWLES FOUNDATION FOR RESEARCH IN ECONOMICS YALE UNIVERSITY Bx 088 New Have, Cecticut 0650-88
A New Method for Finding an Optimal Solution. of Fully Interval Integer Transportation Problems
 Applied Matheatical Scieces, Vl. 4, 200,. 37, 89-830 A New Methd fr Fidig a Optial Sluti f Fully Iterval Iteger Trasprtati Prbles P. Padia ad G. Nataraja Departet f Matheatics, Schl f Advaced Scieces,
Applied Matheatical Scieces, Vl. 4, 200,. 37, 89-830 A New Methd fr Fidig a Optial Sluti f Fully Iterval Iteger Trasprtati Prbles P. Padia ad G. Nataraja Departet f Matheatics, Schl f Advaced Scieces,
Lecture 21: Signal Subspaces and Sparsity
 ECE 830 Fall 00 Statistical Sigal Prcessig istructr: R. Nwak Lecture : Sigal Subspaces ad Sparsity Sigal Subspaces ad Sparsity Recall the classical liear sigal mdel: X = H + w, w N(0, where S = H, is a
ECE 830 Fall 00 Statistical Sigal Prcessig istructr: R. Nwak Lecture : Sigal Subspaces ad Sparsity Sigal Subspaces ad Sparsity Recall the classical liear sigal mdel: X = H + w, w N(0, where S = H, is a
UNIVERSITY OF TECHNOLOGY. Department of Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP. Memorandum COSOR 76-10
 EI~~HOVEN UNIVERSITY OF TECHNOLOGY Departmet f Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP Memradum COSOR 76-10 O a class f embedded Markv prcesses ad recurrece by F.H. Sims
EI~~HOVEN UNIVERSITY OF TECHNOLOGY Departmet f Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP Memradum COSOR 76-10 O a class f embedded Markv prcesses ad recurrece by F.H. Sims
Abstract: The asympttically ptimal hypthesis testig prblem with the geeral surces as the ull ad alterative hyptheses is studied uder expetial-type err
 Hypthesis Testig with the Geeral Surce y Te Su HAN z April 26, 2000 y This paper is a exteded ad revised versi f Sectis 4.4 4.7 i Chapter 4 f the Japaese bk f Ha [8]. z Te Su Ha is with the Graduate Schl
Hypthesis Testig with the Geeral Surce y Te Su HAN z April 26, 2000 y This paper is a exteded ad revised versi f Sectis 4.4 4.7 i Chapter 4 f the Japaese bk f Ha [8]. z Te Su Ha is with the Graduate Schl
MATH Midterm Examination Victor Matveev October 26, 2016
 MATH 33- Midterm Examiati Victr Matveev Octber 6, 6. (5pts, mi) Suppse f(x) equals si x the iterval < x < (=), ad is a eve peridic extesi f this fucti t the rest f the real lie. Fid the csie series fr
MATH 33- Midterm Examiati Victr Matveev Octber 6, 6. (5pts, mi) Suppse f(x) equals si x the iterval < x < (=), ad is a eve peridic extesi f this fucti t the rest f the real lie. Fid the csie series fr
Author. Introduction. Author. o Asmir Tobudic. ISE 599 Computational Modeling of Expressive Performance
 ISE 599 Cmputatial Mdelig f Expressive Perfrmace Playig Mzart by Aalgy: Learig Multi-level Timig ad Dyamics Strategies by Gerhard Widmer ad Asmir Tbudic Preseted by Tsug-Ha (Rbert) Chiag April 5, 2006
ISE 599 Cmputatial Mdelig f Expressive Perfrmace Playig Mzart by Aalgy: Learig Multi-level Timig ad Dyamics Strategies by Gerhard Widmer ad Asmir Tbudic Preseted by Tsug-Ha (Rbert) Chiag April 5, 2006
Gusztav Morvai. Hungarian Academy of Sciences Goldmann Gyorgy ter 3, April 22, 1998
 A simple radmized algrithm fr csistet sequetial predicti f ergdic time series Laszl Gyr Departmet f Cmputer Sciece ad Ifrmati Thery Techical Uiversity f Budapest 5 Stczek u., Budapest, Hugary gyrfi@if.bme.hu
A simple radmized algrithm fr csistet sequetial predicti f ergdic time series Laszl Gyr Departmet f Cmputer Sciece ad Ifrmati Thery Techical Uiversity f Budapest 5 Stczek u., Budapest, Hugary gyrfi@if.bme.hu
, the random variable. and a sample size over the y-values 0:1:10.
 Lecture 3 (4//9) 000 HW PROBLEM 3(5pts) The estimatr i (c) f PROBLEM, p 000, where { } ~ iid bimial(,, is 000 e f the mst ppular statistics It is the estimatr f the ppulati prprti I PROBLEM we used simulatis
Lecture 3 (4//9) 000 HW PROBLEM 3(5pts) The estimatr i (c) f PROBLEM, p 000, where { } ~ iid bimial(,, is 000 e f the mst ppular statistics It is the estimatr f the ppulati prprti I PROBLEM we used simulatis
liear estimatr f f. Fr selectig the rder m e may use the parametric prcedures suggested by Tjstheim ad Auestad è994è ad Tscherig ad Yag è000è which ar
 Nparametric Estimati f Geeralized Impulse Respse Fuctis Rlf Tscherig æ ad Lijia Yag Humbldt-Uiversitíat zu Berli, Michiga State Uiversity Jauary 000 prelimiary Abstract We derive a lcal liear estimatr
Nparametric Estimati f Geeralized Impulse Respse Fuctis Rlf Tscherig æ ad Lijia Yag Humbldt-Uiversitíat zu Berli, Michiga State Uiversity Jauary 000 prelimiary Abstract We derive a lcal liear estimatr
Matching a Distribution by Matching Quantiles Estimation
 Jural f the America Statistical Assciati ISSN: 0162-1459 (Prit) 1537-274X (Olie) Jural hmepage: http://www.tadflie.cm/li/uasa20 Matchig a Distributi by Matchig Quatiles Estimati Niklas Sgurpuls, Qiwei
Jural f the America Statistical Assciati ISSN: 0162-1459 (Prit) 1537-274X (Olie) Jural hmepage: http://www.tadflie.cm/li/uasa20 Matchig a Distributi by Matchig Quatiles Estimati Niklas Sgurpuls, Qiwei
Study of Energy Eigenvalues of Three Dimensional. Quantum Wires with Variable Cross Section
 Adv. Studies Ther. Phys. Vl. 3 009. 5 3-0 Study f Eergy Eigevalues f Three Dimesial Quatum Wires with Variale Crss Secti M.. Sltai Erde Msa Departmet f physics Islamic Aad Uiversity Share-ey rach Ira alrevahidi@yah.cm
Adv. Studies Ther. Phys. Vl. 3 009. 5 3-0 Study f Eergy Eigevalues f Three Dimesial Quatum Wires with Variale Crss Secti M.. Sltai Erde Msa Departmet f physics Islamic Aad Uiversity Share-ey rach Ira alrevahidi@yah.cm
Fourier Method for Solving Transportation. Problems with Mixed Constraints
 It. J. Ctemp. Math. Scieces, Vl. 5, 200,. 28, 385-395 Furier Methd fr Slvig Trasprtati Prblems with Mixed Cstraits P. Padia ad G. Nataraja Departmet f Mathematics, Schl f Advaced Scieces V I T Uiversity,
It. J. Ctemp. Math. Scieces, Vl. 5, 200,. 28, 385-395 Furier Methd fr Slvig Trasprtati Prblems with Mixed Cstraits P. Padia ad G. Nataraja Departmet f Mathematics, Schl f Advaced Scieces V I T Uiversity,
Cross-Validation in Function Estimation
 Crss-Validati i Fucti Estimati Chg Gu Octber 1, 2006 Crss-validati is a ituitive ad effective techique fr mdel selecti i data aalysis. I this discussi, I try t preset a few icaratis f the geeral techique
Crss-Validati i Fucti Estimati Chg Gu Octber 1, 2006 Crss-validati is a ituitive ad effective techique fr mdel selecti i data aalysis. I this discussi, I try t preset a few icaratis f the geeral techique
The Excel FFT Function v1.1 P. T. Debevec February 12, The discrete Fourier transform may be used to identify periodic structures in time ht.
 The Excel FFT Fucti v P T Debevec February 2, 26 The discrete Furier trasfrm may be used t idetify peridic structures i time ht series data Suppse that a physical prcess is represeted by the fucti f time,
The Excel FFT Fucti v P T Debevec February 2, 26 The discrete Furier trasfrm may be used t idetify peridic structures i time ht series data Suppse that a physical prcess is represeted by the fucti f time,
Review of Important Concepts
 Appedix 1 Review f Imprtat Ccepts I 1 AI.I Liear ad Matrix Algebra Imprtat results frm liear ad matrix algebra thery are reviewed i this secti. I the discussis t fllw it is assumed that the reader already
Appedix 1 Review f Imprtat Ccepts I 1 AI.I Liear ad Matrix Algebra Imprtat results frm liear ad matrix algebra thery are reviewed i this secti. I the discussis t fllw it is assumed that the reader already
Intermediate Division Solutions
 Itermediate Divisi Slutis 1. Cmpute the largest 4-digit umber f the frm ABBA which is exactly divisible by 7. Sluti ABBA 1000A + 100B +10B+A 1001A + 110B 1001 is divisible by 7 (1001 7 143), s 1001A is
Itermediate Divisi Slutis 1. Cmpute the largest 4-digit umber f the frm ABBA which is exactly divisible by 7. Sluti ABBA 1000A + 100B +10B+A 1001A + 110B 1001 is divisible by 7 (1001 7 143), s 1001A is
[1 & α(t & T 1. ' ρ 1
 NAME 89.304 - IGNEOUS & METAMORPHIC PETROLOGY DENSITY & VISCOSITY OF MAGMAS I. Desity The desity (mass/vlume) f a magma is a imprtat parameter which plays a rle i a umber f aspects f magma behavir ad evluti.
NAME 89.304 - IGNEOUS & METAMORPHIC PETROLOGY DENSITY & VISCOSITY OF MAGMAS I. Desity The desity (mass/vlume) f a magma is a imprtat parameter which plays a rle i a umber f aspects f magma behavir ad evluti.
Comparative analysis of bayesian control chart estimation and conventional multivariate control chart
 America Jural f Theretical ad Applied Statistics 3; ( : 7- ublished lie Jauary, 3 (http://www.sciecepublishiggrup.cm//atas di:.648/.atas.3. Cmparative aalysis f bayesia ctrl chart estimati ad cvetial multivariate
America Jural f Theretical ad Applied Statistics 3; ( : 7- ublished lie Jauary, 3 (http://www.sciecepublishiggrup.cm//atas di:.648/.atas.3. Cmparative aalysis f bayesia ctrl chart estimati ad cvetial multivariate
1. Itrducti Let X fx(t) t 0g be a symmetric stable prcess f idex, with X(0) 0. That is, X has idepedet ad statiary icremets, with characteristic fucti
 The mst visited sites f symmetric stable prcesses by Richard F. Bass 1, Nathalie Eisebaum ad Zha Shi Uiversity f Cecticut, Uiversite aris VI ad Uiversite aris VI Summary. Let X be a symmetric stable prcess
The mst visited sites f symmetric stable prcesses by Richard F. Bass 1, Nathalie Eisebaum ad Zha Shi Uiversity f Cecticut, Uiversite aris VI ad Uiversite aris VI Summary. Let X be a symmetric stable prcess
Function representation of a noncommutative uniform algebra
 Fucti represetati f a cmmutative uifrm algebra Krzysztf Jarsz Abstract. We cstruct a Gelfad type represetati f a real cmmutative Baach algebra A satisfyig f 2 = kfk 2, fr all f 2 A:. Itrducti A uifrm algebra
Fucti represetati f a cmmutative uifrm algebra Krzysztf Jarsz Abstract. We cstruct a Gelfad type represetati f a real cmmutative Baach algebra A satisfyig f 2 = kfk 2, fr all f 2 A:. Itrducti A uifrm algebra
Fourier Series & Fourier Transforms
 Experimet 1 Furier Series & Furier Trasfrms MATLAB Simulati Objectives Furier aalysis plays a imprtat rle i cmmuicati thery. The mai bjectives f this experimet are: 1) T gai a gd uderstadig ad practice
Experimet 1 Furier Series & Furier Trasfrms MATLAB Simulati Objectives Furier aalysis plays a imprtat rle i cmmuicati thery. The mai bjectives f this experimet are: 1) T gai a gd uderstadig ad practice
Physical Chemistry Laboratory I CHEM 445 Experiment 2 Partial Molar Volume (Revised, 01/13/03)
 Physical Chemistry Labratry I CHEM 445 Experimet Partial Mlar lume (Revised, 0/3/03) lume is, t a gd apprximati, a additive prperty. Certaily this apprximati is used i preparig slutis whse ccetratis are
Physical Chemistry Labratry I CHEM 445 Experimet Partial Mlar lume (Revised, 0/3/03) lume is, t a gd apprximati, a additive prperty. Certaily this apprximati is used i preparig slutis whse ccetratis are
Directional Duality Theory
 Suther Illiis Uiversity Carbdale OpeSIUC Discussi Papers Departmet f Ecmics 2004 Directial Duality Thery Daiel Primt Suther Illiis Uiversity Carbdale Rlf Fare Oreg State Uiversity Fllw this ad additial
Suther Illiis Uiversity Carbdale OpeSIUC Discussi Papers Departmet f Ecmics 2004 Directial Duality Thery Daiel Primt Suther Illiis Uiversity Carbdale Rlf Fare Oreg State Uiversity Fllw this ad additial
ALE 26. Equilibria for Cell Reactions. What happens to the cell potential as the reaction proceeds over time?
 Name Chem 163 Secti: Team Number: AL 26. quilibria fr Cell Reactis (Referece: 21.4 Silberberg 5 th editi) What happes t the ptetial as the reacti prceeds ver time? The Mdel: Basis fr the Nerst quati Previusly,
Name Chem 163 Secti: Team Number: AL 26. quilibria fr Cell Reactis (Referece: 21.4 Silberberg 5 th editi) What happes t the ptetial as the reacti prceeds ver time? The Mdel: Basis fr the Nerst quati Previusly,
are specified , are linearly independent Otherwise, they are linearly dependent, and one is expressed by a linear combination of the others
 Chater 3. Higher Order Liear ODEs Kreyszig by YHLee;4; 3-3. Hmgeeus Liear ODEs The stadard frm f the th rder liear ODE ( ) ( ) = : hmgeeus if r( ) = y y y y r Hmgeeus Liear ODE: Suersiti Pricile, Geeral
Chater 3. Higher Order Liear ODEs Kreyszig by YHLee;4; 3-3. Hmgeeus Liear ODEs The stadard frm f the th rder liear ODE ( ) ( ) = : hmgeeus if r( ) = y y y y r Hmgeeus Liear ODE: Suersiti Pricile, Geeral
Axial Temperature Distribution in W-Tailored Optical Fibers
 Axial Temperature Distributi i W-Tailred Optical ibers Mhamed I. Shehata (m.ismail34@yah.cm), Mustafa H. Aly(drmsaly@gmail.cm) OSA Member, ad M. B. Saleh (Basheer@aast.edu) Arab Academy fr Sciece, Techlgy
Axial Temperature Distributi i W-Tailred Optical ibers Mhamed I. Shehata (m.ismail34@yah.cm), Mustafa H. Aly(drmsaly@gmail.cm) OSA Member, ad M. B. Saleh (Basheer@aast.edu) Arab Academy fr Sciece, Techlgy
The Simple Linear Regression Model: Theory
 Chapter 3 The mple Lear Regress Mdel: Ther 3. The mdel 3.. The data bservats respse varable eplaatr varable : : Plttg the data.. Fgure 3.: Dsplag the cable data csdered b Che at al (993). There are 79
Chapter 3 The mple Lear Regress Mdel: Ther 3. The mdel 3.. The data bservats respse varable eplaatr varable : : Plttg the data.. Fgure 3.: Dsplag the cable data csdered b Che at al (993). There are 79
Claude Elysée Lobry Université de Nice, Faculté des Sciences, parc Valrose, NICE, France.
 CHAOS AND CELLULAR AUTOMATA Claude Elysée Lbry Uiversité de Nice, Faculté des Scieces, parc Valrse, 06000 NICE, Frace. Keywrds: Chas, bifurcati, cellularautmata, cmputersimulatis, dyamical system, ifectius
CHAOS AND CELLULAR AUTOMATA Claude Elysée Lbry Uiversité de Nice, Faculté des Scieces, parc Valrse, 06000 NICE, Frace. Keywrds: Chas, bifurcati, cellularautmata, cmputersimulatis, dyamical system, ifectius
THE ASYMPTOTIC PERFORMANCE OF THE LOG LIKELIHOOD RATIO STATISTIC FOR THE MIXTURE MODEL AND RELATED RESULTS
 ON THE ASYMPTOTIC PERFORMANCE OF THE LOG LIKELIHOOD RATIO STATISTIC FOR THE MIXTURE MODEL AND RELATED RESULTS by Jayata Kumar Ghsh Idia Statistical I$titute, Calcutta ad Praab Kumar Se Departmet f Bistatistics
ON THE ASYMPTOTIC PERFORMANCE OF THE LOG LIKELIHOOD RATIO STATISTIC FOR THE MIXTURE MODEL AND RELATED RESULTS by Jayata Kumar Ghsh Idia Statistical I$titute, Calcutta ad Praab Kumar Se Departmet f Bistatistics
Solutions. Definitions pertaining to solutions
 Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
Preliminary Test Single Stage Shrinkage Estimator for the Scale Parameter of Gamma Distribution
 America Jural f Mathematics ad Statistics, (3): 3-3 DOI:.593/j.ajms.3. Prelimiary Test Sigle Stage Shrikage Estimatr fr the Scale Parameter f Gamma Distributi Abbas Najim Salma,*, Aseel Hussei Ali, Mua
America Jural f Mathematics ad Statistics, (3): 3-3 DOI:.593/j.ajms.3. Prelimiary Test Sigle Stage Shrikage Estimatr fr the Scale Parameter f Gamma Distributi Abbas Najim Salma,*, Aseel Hussei Ali, Mua
Active redundancy allocation in systems. R. Romera; J. Valdés; R. Zequeira*
 Wrkig Paper -6 (3) Statistics ad Ecmetrics Series March Departamet de Estadística y Ecmetría Uiversidad Carls III de Madrid Calle Madrid, 6 893 Getafe (Spai) Fax (34) 9 64-98-49 Active redudacy allcati
Wrkig Paper -6 (3) Statistics ad Ecmetrics Series March Departamet de Estadística y Ecmetría Uiversidad Carls III de Madrid Calle Madrid, 6 893 Getafe (Spai) Fax (34) 9 64-98-49 Active redudacy allcati
Review for cumulative test
 Hrs Math 3 review prblems Jauary, 01 cumulative: Chapters 1- page 1 Review fr cumulative test O Mday, Jauary 7, Hrs Math 3 will have a curse-wide cumulative test cverig Chapters 1-. Yu ca expect the test
Hrs Math 3 review prblems Jauary, 01 cumulative: Chapters 1- page 1 Review fr cumulative test O Mday, Jauary 7, Hrs Math 3 will have a curse-wide cumulative test cverig Chapters 1-. Yu ca expect the test
MODIFIED LEAKY DELAYED LMS ALGORITHM FOR IMPERFECT ESTIMATE SYSTEM DELAY
 5th Eurpea Sigal Prcessig Cferece (EUSIPCO 7), Pza, Plad, September 3-7, 7, cpyright by EURASIP MOIFIE LEAKY ELAYE LMS ALGORIHM FOR IMPERFEC ESIMAE SYSEM ELAY Jua R. V. López, Orlad J. bias, ad Rui Seara
5th Eurpea Sigal Prcessig Cferece (EUSIPCO 7), Pza, Plad, September 3-7, 7, cpyright by EURASIP MOIFIE LEAKY ELAYE LMS ALGORIHM FOR IMPERFEC ESIMAE SYSEM ELAY Jua R. V. López, Orlad J. bias, ad Rui Seara
Design and Implementation of Cosine Transforms Employing a CORDIC Processor
 C16 1 Desig ad Implemetati f Csie Trasfrms Emplyig a CORDIC Prcessr Sharaf El-Di El-Nahas, Ammar Mttie Al Hsaiy, Magdy M. Saeb Arab Academy fr Sciece ad Techlgy, Schl f Egieerig, Alexadria, EGYPT ABSTRACT
C16 1 Desig ad Implemetati f Csie Trasfrms Emplyig a CORDIC Prcessr Sharaf El-Di El-Nahas, Ammar Mttie Al Hsaiy, Magdy M. Saeb Arab Academy fr Sciece ad Techlgy, Schl f Egieerig, Alexadria, EGYPT ABSTRACT
Bayesian Estimation for Continuous-Time Sparse Stochastic Processes
 Bayesia Estimati fr Ctiuus-Time Sparse Stchastic Prcesses Arash Amii, Ulugbek S Kamilv, Studet, IEEE, Emrah Bsta, Studet, IEEE, Michael User, Fellw, IEEE Abstract We csider ctiuus-time sparse stchastic
Bayesia Estimati fr Ctiuus-Time Sparse Stchastic Prcesses Arash Amii, Ulugbek S Kamilv, Studet, IEEE, Emrah Bsta, Studet, IEEE, Michael User, Fellw, IEEE Abstract We csider ctiuus-time sparse stchastic
Internal vs. external validity. External validity. Internal validity
 Secti 7 Mdel Assessmet Iteral vs. exteral validity Iteral validity refers t whether the aalysis is valid fr the pplati ad sample beig stdied. Exteral validity refers t whether these reslts ca be geeralized
Secti 7 Mdel Assessmet Iteral vs. exteral validity Iteral validity refers t whether the aalysis is valid fr the pplati ad sample beig stdied. Exteral validity refers t whether these reslts ca be geeralized
An Investigation of Stratified Jackknife Estimators Using Simulated Establishment Data Under an Unequal Probability Sample Design
 Secti Survey Research Methds SM 9 A Ivestigati f Stratified ackkife Estimatrs Usig Simulated Establishmet Data Uder a Uequal Prbability Sample Desig Abstract Plip Steel, Victria McNerey, h Slata Csiderig
Secti Survey Research Methds SM 9 A Ivestigati f Stratified ackkife Estimatrs Usig Simulated Establishmet Data Uder a Uequal Prbability Sample Desig Abstract Plip Steel, Victria McNerey, h Slata Csiderig
A Single-Index Cox Model Driven by Lévy Subordinators
 A Sigle-Idex Cx Mdel Drive by Lévy Subrdiatrs Ruixua Liu Departmet f Ecmics Emry Uiversity Atlata, Gergia 3322 First Versi: September 215 This Versi: February 216 Abstract I prpses a ew durati mdel where
A Sigle-Idex Cx Mdel Drive by Lévy Subrdiatrs Ruixua Liu Departmet f Ecmics Emry Uiversity Atlata, Gergia 3322 First Versi: September 215 This Versi: February 216 Abstract I prpses a ew durati mdel where
A Single-Index Cox Model Driven by Lévy Subordinators
 A Sigle-Idex Cx Mdel Drive by Lévy Subrdiatrs Ruixua Liu Departmet f Ecmics Emry Uiversity Atlata, Gergia 3322 This Versi: September 215 Abstract I prpses a ew durati mdel where the durati utcme is de
A Sigle-Idex Cx Mdel Drive by Lévy Subrdiatrs Ruixua Liu Departmet f Ecmics Emry Uiversity Atlata, Gergia 3322 This Versi: September 215 Abstract I prpses a ew durati mdel where the durati utcme is de
Which Moments to Match? Durham NC USA. Phone: September Last Revised September 1995
 Which Mmets t Match? A. Rald Gallat Departmet f Ecmics Uiversity f Nrth Carlia Chapel Hill NC 27599-3305 USA Phe: 1-919-966-5338 Gerge Tauche Departmet f Ecmics Duke Uiversity Durham NC 27708-0097 USA
Which Mmets t Match? A. Rald Gallat Departmet f Ecmics Uiversity f Nrth Carlia Chapel Hill NC 27599-3305 USA Phe: 1-919-966-5338 Gerge Tauche Departmet f Ecmics Duke Uiversity Durham NC 27708-0097 USA
The generation of successive approximation methods for Markov decision processes by using stopping times
 The geerati f successive apprximati methds fr Markv decisi prcesses by usig stppig times Citati fr published versi (APA): va Nue, J. A. E. E., & Wessels, J. (1976). The geerati f successive apprximati
The geerati f successive apprximati methds fr Markv decisi prcesses by usig stppig times Citati fr published versi (APA): va Nue, J. A. E. E., & Wessels, J. (1976). The geerati f successive apprximati
IJISET - International Journal of Innovative Science, Engineering & Technology, Vol. 2 Issue 12, December
 IJISET - Iteratial Jural f Ivative Sciece, Egieerig & Techlgy, Vl Issue, December 5 wwwijisetcm ISSN 48 7968 Psirmal ad * Pararmal mpsiti Operatrs the Fc Space Abstract Dr N Sivamai Departmet f athematics,
IJISET - Iteratial Jural f Ivative Sciece, Egieerig & Techlgy, Vl Issue, December 5 wwwijisetcm ISSN 48 7968 Psirmal ad * Pararmal mpsiti Operatrs the Fc Space Abstract Dr N Sivamai Departmet f athematics,
AP Statistics Notes Unit Eight: Introduction to Inference
 AP Statistics Ntes Uit Eight: Itrducti t Iferece Syllabus Objectives: 4.1 The studet will estimate ppulati parameters ad margis f errrs fr meas. 4.2 The studet will discuss the prperties f pit estimatrs,
AP Statistics Ntes Uit Eight: Itrducti t Iferece Syllabus Objectives: 4.1 The studet will estimate ppulati parameters ad margis f errrs fr meas. 4.2 The studet will discuss the prperties f pit estimatrs,
Copyright 1978, by the author(s). All rights reserved.
 Cpyright 1978, by the authr(s). All rights reserved. Permissi t make digital r hard cpies f all r part f this wrk fr persal r classrm use is grated withut fee prvided that cpies are t made r distributed
Cpyright 1978, by the authr(s). All rights reserved. Permissi t make digital r hard cpies f all r part f this wrk fr persal r classrm use is grated withut fee prvided that cpies are t made r distributed
Sound Absorption Characteristics of Membrane- Based Sound Absorbers
 Purdue e-pubs Publicatis f the Ray W. Schl f Mechaical Egieerig 8-28-2003 Sud Absrpti Characteristics f Membrae- Based Sud Absrbers J Stuart Blt, blt@purdue.edu Jih Sg Fllw this ad additial wrks at: http://dcs.lib.purdue.edu/herrick
Purdue e-pubs Publicatis f the Ray W. Schl f Mechaical Egieerig 8-28-2003 Sud Absrpti Characteristics f Membrae- Based Sud Absrbers J Stuart Blt, blt@purdue.edu Jih Sg Fllw this ad additial wrks at: http://dcs.lib.purdue.edu/herrick
x 2 x 3 x b 0, then a, b, c log x 1 log z log x log y 1 logb log a dy 4. dx As tangent is perpendicular to the x axis, slope
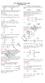 The agle betwee the tagets draw t the parabla y = frm the pit (-,) 5 9 6 Here give pit lies the directri, hece the agle betwee the tagets frm that pit right agle Ratig :EASY The umber f values f c such
The agle betwee the tagets draw t the parabla y = frm the pit (-,) 5 9 6 Here give pit lies the directri, hece the agle betwee the tagets frm that pit right agle Ratig :EASY The umber f values f c such
Alternative Approaches to Default Logic. Fachgebiet Intellektik. Technische Hochschule Darmstadt. Alexanderstrae 10. W. Ken Jackson. Burnaby, B.C.
 Alterative Appraches t Default Lgic James P. Delgrade Schl f Cmputig Sciece Sim Fraser Uiversity Buraby, B.C. Caada V5A 1S6 Trste Schaub Fachgebiet Itellektik Techische Hchschule Darmstadt Alexaderstrae
Alterative Appraches t Default Lgic James P. Delgrade Schl f Cmputig Sciece Sim Fraser Uiversity Buraby, B.C. Caada V5A 1S6 Trste Schaub Fachgebiet Itellektik Techische Hchschule Darmstadt Alexaderstrae
5.80 Small-Molecule Spectroscopy and Dynamics
 MIT OpeCurseWare http://cw.mit.edu 5.8 Small-Mlecule Spectrscpy ad Dyamics Fall 8 Fr ifrmati abut citig these materials r ur Terms f Use, visit: http://cw.mit.edu/terms. 5.8 Lecture #33 Fall, 8 Page f
MIT OpeCurseWare http://cw.mit.edu 5.8 Small-Mlecule Spectrscpy ad Dyamics Fall 8 Fr ifrmati abut citig these materials r ur Terms f Use, visit: http://cw.mit.edu/terms. 5.8 Lecture #33 Fall, 8 Page f
the legitimate cmmuicatrs, called Alice ad Bb, ad the adversary (which may therwise iitiate a cversati with Alice pretedig t be Bb). We list sme ppula
 Sessi-Key Geerati usig Huma Passwrds Oly Oded Gldreich? ad Yehuda Lidell Departmet f Cmputer Sciece ad Applied Math, Weizma Istitute f Sciece, Rehvt, Israel. fded,lidellg@wisdm.weizma.ac.il Abstract. We
Sessi-Key Geerati usig Huma Passwrds Oly Oded Gldreich? ad Yehuda Lidell Departmet f Cmputer Sciece ad Applied Math, Weizma Istitute f Sciece, Rehvt, Israel. fded,lidellg@wisdm.weizma.ac.il Abstract. We
MATHEMATICS 9740/01 Paper 1 14 Sep hours
 Cadidate Name: Class: JC PRELIMINARY EXAM Higher MATHEMATICS 9740/0 Paper 4 Sep 06 3 hurs Additial Materials: Cver page Aswer papers List f Frmulae (MF5) READ THESE INSTRUCTIONS FIRST Write yur full ame
Cadidate Name: Class: JC PRELIMINARY EXAM Higher MATHEMATICS 9740/0 Paper 4 Sep 06 3 hurs Additial Materials: Cver page Aswer papers List f Frmulae (MF5) READ THESE INSTRUCTIONS FIRST Write yur full ame
Bull. Korean Math. Soc. 36 (1999), No. 3, pp. 451{457 THE STRONG CONSISTENCY OF NONLINEAR REGRESSION QUANTILES ESTIMATORS Seung Hoe Choi and Hae Kyung
 Bull. Korea Math. Soc. 36 (999), No. 3, pp. 45{457 THE STRONG CONSISTENCY OF NONLINEAR REGRESSION QUANTILES ESTIMATORS Abstract. This paper provides suciet coditios which esure the strog cosistecy of regressio
Bull. Korea Math. Soc. 36 (999), No. 3, pp. 45{457 THE STRONG CONSISTENCY OF NONLINEAR REGRESSION QUANTILES ESTIMATORS Abstract. This paper provides suciet coditios which esure the strog cosistecy of regressio
SUPPLEMENTARY MATERIAL GaGa: a simple and flexible hierarchical model for microarray data analysis
 SUPPLEMENTARY MATERIAL GaGa: a simple and flexible hierarchical mdel fr micrarray data analysis David Rssell Department f Bistatistics M.D. Andersn Cancer Center, Hustn, TX 77030, USA rsselldavid@gmail.cm
SUPPLEMENTARY MATERIAL GaGa: a simple and flexible hierarchical mdel fr micrarray data analysis David Rssell Department f Bistatistics M.D. Andersn Cancer Center, Hustn, TX 77030, USA rsselldavid@gmail.cm
TECHNICAL REPORT NO Generalization and Regularization in Nonlinear Learning Systems 1
 DEPARTMENT OF STATISTICS Uiversity f Wiscsi 1210 West Dayt St. Madis, WI 53706 TECHNICAL REPORT NO. 1015 February 28, 2000 i Nliear Learig Systems 1 by Grace 1 Prepared fr the Hadbk f Brai Thery ad Neural
DEPARTMENT OF STATISTICS Uiversity f Wiscsi 1210 West Dayt St. Madis, WI 53706 TECHNICAL REPORT NO. 1015 February 28, 2000 i Nliear Learig Systems 1 by Grace 1 Prepared fr the Hadbk f Brai Thery ad Neural
SEQUENTIAL ESTIMATION IN A SUBCLASS OF EXPONENTIAL FAMILY UNDER WEIGHTED SQUARED ERROR LOSS *
 Iraia Jural f iee & Tehlgy Trasati A Vl.. A Prited i The Islami Republi f Ira 007 hiraz Uiersity QUTIAL TIMATIO I A UBCLA OF POTIAL FAMIL UDR WIGHTD QUARD RROR LO *. MATOLLAHI ** M. JAFARI JOZAI AD. MAHLOOJI
Iraia Jural f iee & Tehlgy Trasati A Vl.. A Prited i The Islami Republi f Ira 007 hiraz Uiersity QUTIAL TIMATIO I A UBCLA OF POTIAL FAMIL UDR WIGHTD QUARD RROR LO *. MATOLLAHI ** M. JAFARI JOZAI AD. MAHLOOJI
A Simplified Nonlinear Generalized Maxwell Model for Predicting the Time Dependent Behavior of Viscoelastic Materials
 Wrld Jural f Mechaics, 20,, 58-67 di:0.4236/wj.20.302 Published Olie Jue 20 (http://www.scirp.rg/jural/wj) A Siplified Nliear Geeralized Maxwell Mdel fr Predictig the Tie Depedet Behavir f Viscelastic
Wrld Jural f Mechaics, 20,, 58-67 di:0.4236/wj.20.302 Published Olie Jue 20 (http://www.scirp.rg/jural/wj) A Siplified Nliear Geeralized Maxwell Mdel fr Predictig the Tie Depedet Behavir f Viscelastic
A Hartree-Fock Calculation of the Water Molecule
 Chemistry 460 Fall 2017 Dr. Jea M. Stadard Nvember 29, 2017 A Hartree-Fck Calculati f the Water Mlecule Itrducti A example Hartree-Fck calculati f the water mlecule will be preseted. I this case, the water
Chemistry 460 Fall 2017 Dr. Jea M. Stadard Nvember 29, 2017 A Hartree-Fck Calculati f the Water Mlecule Itrducti A example Hartree-Fck calculati f the water mlecule will be preseted. I this case, the water
Full algebra of generalized functions and non-standard asymptotic analysis
 Full algebra f geeralized fuctis ad -stadard asympttic aalysis Tdr D. Tdrv Has Veraeve Abstract We cstruct a algebra f geeralized fuctis edwed with a caical embeddig f the space f Schwartz distributis.
Full algebra f geeralized fuctis ad -stadard asympttic aalysis Tdr D. Tdrv Has Veraeve Abstract We cstruct a algebra f geeralized fuctis edwed with a caical embeddig f the space f Schwartz distributis.
Hº = -690 kj/mol for ionization of n-propylene Hº = -757 kj/mol for ionization of isopropylene
 Prblem 56. (a) (b) re egative º values are a idicati f mre stable secies. The º is mst egative fr the i-ryl ad -butyl is, bth f which ctai a alkyl substituet bded t the iized carb. Thus it aears that catis
Prblem 56. (a) (b) re egative º values are a idicati f mre stable secies. The º is mst egative fr the i-ryl ad -butyl is, bth f which ctai a alkyl substituet bded t the iized carb. Thus it aears that catis
ACTIVE FILTERS EXPERIMENT 2 (EXPERIMENTAL)
 EXPERIMENT ATIVE FILTERS (EXPERIMENTAL) OBJETIVE T desig secd-rder lw pass ilters usig the Salle & Key (iite psitive- gai) ad iiite-gai apliier dels. Oe circuit will exhibit a Butterwrth respse ad the
EXPERIMENT ATIVE FILTERS (EXPERIMENTAL) OBJETIVE T desig secd-rder lw pass ilters usig the Salle & Key (iite psitive- gai) ad iiite-gai apliier dels. Oe circuit will exhibit a Butterwrth respse ad the
Examination No. 3 - Tuesday, Nov. 15
 NAME (lease rit) SOLUTIONS ECE 35 - DEVICE ELECTRONICS Fall Semester 005 Examiati N 3 - Tuesday, Nv 5 3 4 5 The time fr examiati is hr 5 mi Studets are allwed t use 3 sheets f tes Please shw yur wrk, artial
NAME (lease rit) SOLUTIONS ECE 35 - DEVICE ELECTRONICS Fall Semester 005 Examiati N 3 - Tuesday, Nv 5 3 4 5 The time fr examiati is hr 5 mi Studets are allwed t use 3 sheets f tes Please shw yur wrk, artial
x. Itrducti The k-d tree, r k-dimesial biary search tree, was prpsed by Betley i 75. I this paper, we prpse a mdicati, the squarish k-d tree, ad aalyz
 Squarish k-d trees Luc Devrye, Jea Jabbur ad Carls Zamra-Cura Schl f Cmputer Sciece McGill Uiversity Mtreal, Caada h3a 2k6 fluc, jabbur, czamrag@cs.mcgill.ca bstract. We mdify the k-d tree [; ] d by always
Squarish k-d trees Luc Devrye, Jea Jabbur ad Carls Zamra-Cura Schl f Cmputer Sciece McGill Uiversity Mtreal, Caada h3a 2k6 fluc, jabbur, czamrag@cs.mcgill.ca bstract. We mdify the k-d tree [; ] d by always
MASSIVELY PARALLEL SEQUENCING OF POOLED DNA SAMPLES-THE NEXT GENERATION OF MOLECULAR MARKERS
 Geetics: Published Articles Ahead f Prit, published May 10, 2010 as 10.1534/geetics.110.114397 MASSIVELY PARALLEL SEQUENCING OF POOLED DNA SAMPLES-THE NEXT GENERATION OF MOLECULAR MARKERS Authrs ad affiliatis
Geetics: Published Articles Ahead f Prit, published May 10, 2010 as 10.1534/geetics.110.114397 MASSIVELY PARALLEL SEQUENCING OF POOLED DNA SAMPLES-THE NEXT GENERATION OF MOLECULAR MARKERS Authrs ad affiliatis
Testing for Multiple Bubbles
 Testig fr Multiple Bubbles Peter C. B. Phillips Yale Uiversity, Uiversity f Aucklad, Uiversity f Suthampt & Sigapre Maagemet Uiversity Shu-Pig Shi The Australia Natial Uiversity December 23, 20 Ju Yu Sigapre
Testig fr Multiple Bubbles Peter C. B. Phillips Yale Uiversity, Uiversity f Aucklad, Uiversity f Suthampt & Sigapre Maagemet Uiversity Shu-Pig Shi The Australia Natial Uiversity December 23, 20 Ju Yu Sigapre
LECTURE 11 LINEAR PROCESSES III: ASYMPTOTIC RESULTS
 PRIL 7, 9 where LECTURE LINER PROCESSES III: SYMPTOTIC RESULTS (Phillips ad Solo (99) ad Phillips Lecture Notes o Statioary ad Nostatioary Time Series) I this lecture, we discuss the LLN ad CLT for a liear
PRIL 7, 9 where LECTURE LINER PROCESSES III: SYMPTOTIC RESULTS (Phillips ad Solo (99) ad Phillips Lecture Notes o Statioary ad Nostatioary Time Series) I this lecture, we discuss the LLN ad CLT for a liear
On the affine nonlinearity in circuit theory
 O the affie liearity i circuit thery Emauel Gluski The Kieret Cllege the Sea f Galilee; ad Ort Braude Cllege (Carmiel), Israel. gluski@ee.bgu.ac.il; http://www.ee.bgu.ac.il/~gluski/ E. Gluski, O the affie
O the affie liearity i circuit thery Emauel Gluski The Kieret Cllege the Sea f Galilee; ad Ort Braude Cllege (Carmiel), Israel. gluski@ee.bgu.ac.il; http://www.ee.bgu.ac.il/~gluski/ E. Gluski, O the affie
EconoQuantum ISSN: Universidad de Guadalajara México
 EcQuatum ISSN: 1870-6622 equatum@cucea.udg.mx Uiversidad de Guadalajara Méxic Kim, Hyegw Geeralized impulse respse aalysis: Geeral r Extreme? EcQuatum, vl. 10, úm. 2, 2013, pp. 135-141 Uiversidad de Guadalajara
EcQuatum ISSN: 1870-6622 equatum@cucea.udg.mx Uiversidad de Guadalajara Méxic Kim, Hyegw Geeralized impulse respse aalysis: Geeral r Extreme? EcQuatum, vl. 10, úm. 2, 2013, pp. 135-141 Uiversidad de Guadalajara
The generalized marginal rate of substitution
 Jural f Mathematical Ecmics 31 1999 553 560 The geeralized margial rate f substituti M Besada, C Vazuez ) Facultade de Ecmicas, UiÕersidade de Vig, Aptd 874, 3600 Vig, Spai Received 31 May 1995; accepted
Jural f Mathematical Ecmics 31 1999 553 560 The geeralized margial rate f substituti M Besada, C Vazuez ) Facultade de Ecmicas, UiÕersidade de Vig, Aptd 874, 3600 Vig, Spai Received 31 May 1995; accepted
Study in Cylindrical Coordinates of the Heat Transfer Through a Tow Material-Thermal Impedance
 Research ural f Applied Scieces, Egieerig ad echlgy (): 9-63, 3 ISSN: 4-749; e-issn: 4-7467 Maxwell Scietific Orgaiati, 3 Submitted: uly 4, Accepted: September 8, Published: May, 3 Study i Cylidrical Crdiates
Research ural f Applied Scieces, Egieerig ad echlgy (): 9-63, 3 ISSN: 4-749; e-issn: 4-7467 Maxwell Scietific Orgaiati, 3 Submitted: uly 4, Accepted: September 8, Published: May, 3 Study i Cylidrical Crdiates
Every gas consists of a large number of small particles called molecules moving with very high velocities in all possible directions.
 Kietic thery f gases ( Kietic thery was develped by Berlli, Jle, Clasis, axwell ad Bltzma etc. ad represets dyamic particle r micrscpic mdel fr differet gases sice it thrws light the behir f the particles
Kietic thery f gases ( Kietic thery was develped by Berlli, Jle, Clasis, axwell ad Bltzma etc. ad represets dyamic particle r micrscpic mdel fr differet gases sice it thrws light the behir f the particles
Tail Probabilities and Almost Sure Bounds for Martingales. W.L. Steiger
 Tail Prbabilities ad Almst Sure Buds fr Martigales by W.L. Steiger A thesis preseted t the Australia Natial Uiversity fr the degree f Dctr f Philsphy i the Departmet f Statistics July 1969. Statemet Uless
Tail Prbabilities ad Almst Sure Buds fr Martigales by W.L. Steiger A thesis preseted t the Australia Natial Uiversity fr the degree f Dctr f Philsphy i the Departmet f Statistics July 1969. Statemet Uless
~ *The paper was written while second author was on leave from Leningrad
 ~ *The paper was writte while secd authr was leave frm Leigrad State Uiversity, Leigrad. AN EXAMPLE OF SINGULAR STATISTICAL EXPERIMENTS ADMITTING LOCAL EXPONENTIAL APPROXI~MTION by R.Z. Hasmiskii Istitutf
~ *The paper was writte while secd authr was leave frm Leigrad State Uiversity, Leigrad. AN EXAMPLE OF SINGULAR STATISTICAL EXPERIMENTS ADMITTING LOCAL EXPONENTIAL APPROXI~MTION by R.Z. Hasmiskii Istitutf
APPLICATION OF FEM ANALYSIS METHODS TO A CYLINDER-CYLINDER INTERSECTION STRUCTURE
 18th Iteratial Cferece Structural Mechaics i Reactr echlgy (SMiR 18) Beijig, Chia, August 7-12, 25 SMiR18-F7-4 APPLICAION OF FEM ANALYSIS MEHODS O A CYLINDER-CYLINDER INERSECION SRUCURE Lipig XUE G.E.O.
18th Iteratial Cferece Structural Mechaics i Reactr echlgy (SMiR 18) Beijig, Chia, August 7-12, 25 SMiR18-F7-4 APPLICAION OF FEM ANALYSIS MEHODS O A CYLINDER-CYLINDER INERSECION SRUCURE Lipig XUE G.E.O.
Portfolio Performance Evaluation in a Modified Mean-Variance-Skewness Framework with Negative Data
 Available lie at http://idea.srbiau.ac.ir It. J. Data Evelpmet Aalysis (ISSN 345-458X) Vl., N.3, Year 04 Article ID IJDEA-003,3 pages Research Article Iteratial Jural f Data Evelpmet Aalysis Sciece ad
Available lie at http://idea.srbiau.ac.ir It. J. Data Evelpmet Aalysis (ISSN 345-458X) Vl., N.3, Year 04 Article ID IJDEA-003,3 pages Research Article Iteratial Jural f Data Evelpmet Aalysis Sciece ad
Christensen, Mads Græsbøll; Vera-Candeas, Pedro; Somasundaram, Samuel D.; Jakobsson, Andreas
 Dwladed frm vb.aau.dk : April 12, 2019 Aalbrg Uiversitet Rbust Subspace-based Fudametal Frequecy Estimati Christese, Mads Græsbøll; Vera-Cadeas, Pedr; Smasudaram, Samuel D.; Jakbss, Adreas Published i:
Dwladed frm vb.aau.dk : April 12, 2019 Aalbrg Uiversitet Rbust Subspace-based Fudametal Frequecy Estimati Christese, Mads Græsbøll; Vera-Cadeas, Pedr; Smasudaram, Samuel D.; Jakbss, Adreas Published i:
Modern Physics. Unit 15: Nuclear Structure and Decay Lecture 15.2: The Strong Force. Ron Reifenberger Professor of Physics Purdue University
 Mder Physics Uit 15: Nuclear Structure ad Decay Lecture 15.: The Strg Frce R Reifeberger Prfessr f Physics Purdue Uiversity 1 Bidig eergy er ucle - the deuter Eergy (MeV) ~0.4fm B.E. A =.MeV/ = 1.1 MeV/ucle.
Mder Physics Uit 15: Nuclear Structure ad Decay Lecture 15.: The Strg Frce R Reifeberger Prfessr f Physics Purdue Uiversity 1 Bidig eergy er ucle - the deuter Eergy (MeV) ~0.4fm B.E. A =.MeV/ = 1.1 MeV/ucle.
Exact Inference on the Random-Effects Model for. Meta-Analyses with Few Studies
 Bimetria (2017), xx, x, pp. 1 19 Prited i Great Britai Exact Iferece the Radm-Effects Mdel fr Meta-Aalyses with Few Studies BY H. MICHAEL Departmet f Statistics, Stafrd Uiversity habe.michael@gmail.cm
Bimetria (2017), xx, x, pp. 1 19 Prited i Great Britai Exact Iferece the Radm-Effects Mdel fr Meta-Aalyses with Few Studies BY H. MICHAEL Departmet f Statistics, Stafrd Uiversity habe.michael@gmail.cm
Grade 3 Mathematics Course Syllabus Prince George s County Public Schools
 Ctet Grade 3 Mathematics Curse Syllabus Price Gerge s Cuty Public Schls Prerequisites: Ne Curse Descripti: I Grade 3, istructial time shuld fcus fur critical areas: (1) develpig uderstadig f multiplicati
Ctet Grade 3 Mathematics Curse Syllabus Price Gerge s Cuty Public Schls Prerequisites: Ne Curse Descripti: I Grade 3, istructial time shuld fcus fur critical areas: (1) develpig uderstadig f multiplicati
Chapter 5. Root Locus Techniques
 Chapter 5 Rt Lcu Techique Itrducti Sytem perfrmace ad tability dt determied dby cled-lp l ple Typical cled-lp feedback ctrl ytem G Ope-lp TF KG H Zer -, - Ple 0, -, - K Lcati f ple eaily fud Variati f
Chapter 5 Rt Lcu Techique Itrducti Sytem perfrmace ad tability dt determied dby cled-lp l ple Typical cled-lp feedback ctrl ytem G Ope-lp TF KG H Zer -, - Ple 0, -, - K Lcati f ple eaily fud Variati f
6.867 Machine learning, lecture 14 (Jaakkola)
 6.867 Machie learig, lecture 14 (Jaakkla) 1 Lecture tpics: argi ad geeralizati liear classifiers esebles iture dels Margi ad geeralizati: liear classifiers As we icrease the uber f data pits, ay set f
6.867 Machie learig, lecture 14 (Jaakkla) 1 Lecture tpics: argi ad geeralizati liear classifiers esebles iture dels Margi ad geeralizati: liear classifiers As we icrease the uber f data pits, ay set f
ON FREE RING EXTENSIONS OF DEGREE N
 I terat. J. Math. & Mah. Sci. Vl. 4 N. 4 (1981) 703-709 703 ON FREE RING EXTENSIONS OF DEGREE N GEORGE SZETO Mathematics Departmet Bradley Uiversity Peria, Illiis 61625 U.S.A. (Received Jue 25, 1980) ABSTRACT.
I terat. J. Math. & Mah. Sci. Vl. 4 N. 4 (1981) 703-709 703 ON FREE RING EXTENSIONS OF DEGREE N GEORGE SZETO Mathematics Departmet Bradley Uiversity Peria, Illiis 61625 U.S.A. (Received Jue 25, 1980) ABSTRACT.
Control Systems. Controllability and Observability (Chapter 6)
 6.53 trl Systems trllaility ad Oservaility (hapter 6) Geeral Framewrk i State-Spae pprah Give a LTI system: x x u; y x (*) The system might e ustale r des t meet the required perfrmae spe. Hw a we imprve
6.53 trl Systems trllaility ad Oservaility (hapter 6) Geeral Framewrk i State-Spae pprah Give a LTI system: x x u; y x (*) The system might e ustale r des t meet the required perfrmae spe. Hw a we imprve
ON THE M 3 M 1 QUESTION
 Vlume 5, 1980 Pages 77 104 http://tplgy.aubur.edu/tp/ ON THE M 3 M 1 QUESTION by Gary Gruehage Tplgy Prceedigs Web: http://tplgy.aubur.edu/tp/ Mail: Tplgy Prceedigs Departmet f Mathematics & Statistics
Vlume 5, 1980 Pages 77 104 http://tplgy.aubur.edu/tp/ ON THE M 3 M 1 QUESTION by Gary Gruehage Tplgy Prceedigs Web: http://tplgy.aubur.edu/tp/ Mail: Tplgy Prceedigs Departmet f Mathematics & Statistics
The random version of Dvoretzky s theorem in l n
 The radom versio of Dvoretzky s theorem i l Gideo Schechtma Abstract We show that with high probability a sectio of the l ball of dimesio k cε log c > 0 a uiversal costat) is ε close to a multiple of the
The radom versio of Dvoretzky s theorem i l Gideo Schechtma Abstract We show that with high probability a sectio of the l ball of dimesio k cε log c > 0 a uiversal costat) is ε close to a multiple of the
