Gusztav Morvai. Hungarian Academy of Sciences Goldmann Gyorgy ter 3, April 22, 1998
|
|
|
- Catherine Walsh
- 5 years ago
- Views:
Transcription
1 A simple radmized algrithm fr csistet sequetial predicti f ergdic time series Laszl Gyr Departmet f Cmputer Sciece ad Ifrmati Thery Techical Uiversity f Budapest 5 Stczek u., Budapest, Hugary gyrfi@if.bme.hu Gabr Lugsi Departmet f Ecmics, Pmpeu Fabra Uiversity Ram Trias Fargas 5-7, 85 Barcela, Spai, lugsi@upf.es Gusztav Mrvai Research Grup fr Ifrmatics ad Electrics Hugaria Academy f Scieces 5 Gldma Gyrgy ter 3, Budapest, Hugary mrvai@if.bme.hu April, 998 Classicati: C3. The wrk f the secd authr was supprted by DGES grat PB96-3
2 Abstract We preset a simple radmized prcedure fr the predicti f a biary sequece. The algrithm uses ideas frm recet develpmets f the thery f the predicti f idividual sequeces. We shw that if the sequece is a realizati f a statiary ad ergdic radm prcess the the average umber f mistakes cverges, almst surely, t that f the ptimum, give by the Bayes predictr.
3 Itrducti We address the prblem f sequetial predicti f a biary sequece. A sequece f bits y y y :::f g is hidde frm the predictr. At each time istat i = :::, the bit y i; is revealed ad the predictr is asked t guess the value f ext utcme y i.thus, the predictr's decisi, at time i, is based the value f y i; =(y ::: y i; ). We als assume that the predictr has access t a sequece f i.i.d. radm variables U U :::, uifrmly distributed [ ], s that the predictr ca use U i i frmig a radmized decisi fr y i.frmally, the strategy f the predictr is a sequece g = fg i g i= f decisi fuctis g i : f g i; [ ]!f g ad the radmized predicti frmed at time i is g i (y i; U i ). The predictr pays a uit pealty each time a mistake is made. After ruds f play, the rmalized cumulative lss the strig y is L (g U )= X i= I fgi (y i; U i )6=y i g where I detes the idicatr fucti. Whe cfusi is caused, we will simply write L (g) =L (g U ). I geeral, we dete We als write L m(g U )= ; m + X i=m I fgi (y i; U i )6=y i g : bl (g) =EL (g U ) ad b L m (g) =EL m (g U ) fr the expected lss f the radmized strategy g. I this paper we assume that y y :::are realizatis f the radm variables Y Y ::: draw frm the biary-valued ergdic prcess fy g ; (which is idepedet f the radmizig variables U U :::). I this case there is a fudametal it fr the predictability f the sequece. This is stated i the ext lemma: Therem Fr ay predicti strategy g ad statiary ergdic prcess fy g ;, if! L (g) L almst surely, where h L = E mi PfY =jy ; ; g PfY =jy ; ; gi is the miimal (Bayes) prbability f errr f ay decisi fr the value f Y iite past Y ; ; =(::: Y ;3 Y ; Y ; ). based the
4 Prf. A easy applicati f the Azuma-Hedig iequality fr sums f buded martigale diereces (Hedig [8], Azuma []) shws that fr ay predicti strategy g ad >, P I particular, ( L (g) ; X i=! L (g) ; Pfg i (Y i; U i ) 6= Y i jy i; X i= ; g > It is well kw (see, e.g., [6]) that fr ay predictr g i, U ::: U ) e ; : Pfg i (Y i; U i ) 6= Y i jy i; ; g! = almst surely: Pfg i (Y i; U i ) 6= Y i jy i; ; g Pfg i (Y i; ; ) 6= Y i jy i; ; g = mi PfY i =jy i; ; g PfY i =jy i; ; g where g i is the ptimal (Bayes) decisi fr Y i based Y; i; give by ( if g i (y;) i; PfYi =jy; = i; = y;g i; = therwise. Nte that by statiarity, g = g = def = g. Therefre, if! L (g) if! X i= mi PfY i =jy i; ; g PfY i =jy i; ; g almst surely. Fially, we te that by the ergdic therem (see, e.g., Stut [3]) the average the righthad side cverges almst surely t L, s the prf is ished. Based Therem the fllwig deiti is meaigful. Deiti Apredicti strategy g is called csistet if fr all ergdic prcesses fy g ;,! L (g) =L almst surely: Therefre, csistet strategies asympttically achieve the best pssible lss fr all ergdic prcesses. The rst questi is, f curse, if such a strategy exists. The armative aswer may be easily deduced frm earlier results f Orstei ad Bailey as fllws: Therem There exists a csistet predicti scheme. Prf. Orstei [] prved that there exists a sequece f fuctis f i : f g i! [ ], i = ::: such that fr all ergdic prcesses fy g ;,! f (Y ; ; )=PfY =jy ;g almst surely: ()
5 (A simpler estimatr with the same cvergece prperty was itrduced by Mrvai, Yakwitz, ad Gyr [].) Bailey [3] shwed that fr such estimatrs, fr all ergdic prcesses! X i= j(f i (Y i) ; PfY i+ =jy i gj = almst surely: () Ideed, () ad Breima's geeralized ergdic therem (see, e.g., Alget []) yield (). Oce such a sequece ff i g f estimatrs is available, we may dee a (-radmized) predicti scheme by By [6, Therem.], P g (Y ; ) 6= Y jy; ; g (y ; )= ; P ( if f; (y ; ) therwise. g (Y; ; ) 6= Y jy; ; f; (Y ; ) ; P Y =jy ; ; therefre jl (g) ; L j L (g) ; + + X i= X i= P L (g) ; + + X i= X i= P g i (Y i; ) 6= Y i jy i; g i (Y i; ) 6= Y i jy i; ; P P g (Y; i; ) 6= Y i jy; i; ; L X i= P g i (Y i; ) 6= Y i jy i; f i; (Y i; ) ; P X i= Y i =jy i; P g (Y; i; ) 6= Y i jy; i; g (Y i; ; ) 6= Y ijy i; ; ; L : ; The rst term f the right had side teds t zer almst surely by the Hedig-Azuma iequality [8], [] by a similar argumet that was used i the prf f Therem. The secd e cverges t zer almst surely by () ad the third term teds t zer almst surely by the ergdic therem. Ufrtuately, all kw estimatrs satisfyig () are either very cmplicated r eed s large amuts f data that their practical use is urealistic. Therefre, desigig a simple direct algrithm is called fr. 3
6 A simple csistet algrithm I this secti we preset a simple predicti strategy, ad prve its csistecy. It is mtivated by sme recet develpmets frm the thery f the predicti f idividual sequeces (see, e.g., Vvk [4], Feder, Merhav, ad Gutma [7], Littleste ad Warmuth [9], Cesa-Biachi et al. [5]). These methds predict accrdig t a cmbiati f several predictrs, the s-called experts. The mai idea i this paper is that if the sequece t predict is draw frm a statiary ad ergdic prcess, cmbiig the predictis f a small ad simple set f apprpriately chse predictrs (the s-called experts) suces t achieve csistecy. First we dee a iite sequece f experts h () h () ::: as fllws: Fix a psitive iteger k, ad fr each s f g k ad y f g dee bp k (y y ; js) = fk <i<: y i; fk <i<: y i; i;k = s y i = yg i;k = sg >k+: (3) = is deed t be =. Als, fr k +we dee P b k (y y; js) = =. I ther wrds, bp k (y y ; js) is the prprti f the appearaces f the bit y fllwig the strig s amg all appearaces f s i the sequece y ;. Als itrduce the fucti F k (z) =I fz[:5;=k :5+=k]g z ; :5+=k =k + I fz>:5+=kg : The expert h (k) deed by is a sequece f fuctis h (k) : f g ; [ ]!f g, = ::: ( if h (k) u<fk ( P b (y; u)= k ( y ; jy;k)) ; therwise, = :::: That is, expert h (k) lks fr all appearaces f the last see strig y ; ;k f legth k i the past ad predicts accrdig t the larger f the relative frequecies f 's ad 's fllwig the strig. The fucti F k ly plays a rle if these frequecies are clse t =. I such a case a radmized predicti is made. (Nte that F k (z) is ctiuus ad it diers frm I fz=g ly if jz ; =j < =k.) The prpsed predicti algrithm prceeds as fllws: Let m = ::: be a egative iteger. Fr m < m+, the predicti is based up a weighted majrity f predictis f the experts h () ::: h (m+ ) as fllws: g (y ; u)= 8 >< >: P m+ k= if u< F k( b k ( y ; jy ; ;k ))w (k) P m+ w k= (k) therwise, = ::: where w (k) is the weight fexperth (k) deed by the past perfrmace f h (k) as w m(k) = ad w (k) =e ;m b L ; m (h (k) ) > m 4
7 where m = q 8l( m+ )= m. Recall that bl ; m (h(k) )= ; m ; X P h (k) i (y i; U i ) 6= y i i= m is the average umber f mistakes made by expert h (k) betwee times m ad ;. The weight feach expert is therefre expetially decreasig with the umber f its mistakes this part f the data. Our mai result is the csistecy f this simple predicti scheme: Therem 3 The predicti scheme g deed abve is csistet. I the prf we use a beautiful result f Cesa-Biachi et al. [5]. It states that, give a set f N experts, ad a sequece f xed legth, there exists a radmized predictr whse umber f mistakes is t mre tha that f the best predictr plus abut q (=) l N fr all pssible sequeces y. The simpler algrithm ad statemet cited belw is due t Cesa-Biachi [4]: Lemma Let h ~ () ::: ~ h (N ) be a ite cllecti f predicti strategies (experts). The if the predicti strategy ~g is deed by ~g t (y t; u)= 8 >< >: if u< therwise, t = :::, where fr all k = ::: N P N k= P ~h (k) (y t; U)= ~w t (k) P N k= ~w t (k) ~w (k) = ad ~w t (k) b =e ; L t; ( ~ h (k)) t> with = q 8lN=, the fr every y f g, bl (~g) mi bl ( ~ l N h )+s (k) k= ::: N : Prf f Therem 3. By Lemma, we have that the expected umber f errrs cmmitted by g a segmet m ::: m+ ; is buded, fr ay y m+ ; m f gm,as 3 bl m+ ; m (g) = E 4 m+ X; 5 m mi L b k m+ I fgi (y i; i= m U i )6=y i g m+ ; m (h(k) )+ = mi bl m+ ; k= ::: m (h(k) )+ 5 s l( m+ ) s m l( m+ ) m
8 where the last equality fllws frm the fact that sice < m+, all experts h (k) with k m+ predict zer with prbability = up t time (ad therefre they are idetical t h (m+ ) ). Therefre, detig = blg c+,fray sequece y y :::, therefre where b L (g) = blg c; X m= X blg c; m= +( ; =+) bl (g) mi bl h (k) + k= ::: mi bl h (k) + k= ::: mi bl k= ::: mi bl k= ::: mi bl k= ::: m L b m+ ; m (g)+(; =+)b L=(g) s l( m+ ) mi bl m+ ; k= ::: m (h(k) mi k= ::: blg c; X m= blg c bl = (h(k) )+ s m l m+ s m+ l m+ vu u t m= p q blg X c h (k) + l blg c + m= p q p h (k) + l lg + ( p ; ) h (k) + c s lg + c = p l p ; :84: m A l() A ( ; =+) + s m= ( ; = + ) l A It fllws frm McDiarmid's iequality (McDiarmid [] see als [6, Therem 9.]) that fr ay sequece y, P L (g U ) ; b L (g) > e ; : Therefre, if L ad b L are w evaluated the radm sequece Y Y :::,we btai sup! L (g U ) sup@ mi bl (h (k) lg + )+cs A :! k= ::: = sup mi bl (h (k) )! k= ::: Thus, it remais t shw thatfray ergdic prcess Y Y :::, sup! mi k= ::: This will fllw easily frm the fllwig lemma: almst surely: bl (h(k) ) L almst surely: (4) 6
9 Lemma Fr each k, sup! where fr ay s f g k, L b (h (k) ) ; P g (k) (Y ; ) 6= ;k Y k almst surely g (k) (s) = is the Bayes decisi fr Y give Y ; ;k. ( if P Y =jy ; ;k = s therwise Prf. Nte that bl (h (k) ) = = X i= E X i= I (k) fh i (Y i; U i )6=Y i g jy E I (k) fh i (Y i; U i )6=Y i g jy i= ; X i= I fg (k) (Y i; i;k )6=Y ig! + X i= I fg (k) (Y i; i;k )6=Y ig : Fr the secd term the right-had side, it fllws frm the ergdic therem that X I! fg (k) (Y i; i;k )6=Y ig = P g (k) (Y ; ) 6= ;k Y almst surely: Therefre, it suces t shw that sup! X i= T see this, write X i= E = i= E I (k) fh i (Y i; U i )6=Y i g jy X ; X I fg (k) (Y i; i;k )6=Y ig i= k almst surely: I (k) fh i (Y i; U i )6=Y i g jy ; I fg (k) (Y i; i;k )6=Y ig i= X i E hy i + h (k) i (Y i; U i ) ; Y i h (k) i (Y i; U i )jy ; Yi ; g (k) (Y i; i;k )+Y i g (k) (Y i; i;k ) (usig that if a b f g the I fa6=bg = a + b ; ab) = X i Y i +(; Y i )E hh (k) i (Y i; U i )jy ; Yi ; ( ; Y i )g (k) (Y i; = = X ( ; Y i ) F k ( P bk i= i= X ( ; Y i ) F k ( P bk i= + X i= i ( Yi; jy i; i ( Yi; i;k )) ; g(k) (Y i; jy i; i;k ) i;k )) ; F k(pfy i =jy i; i;k g)! i;k ) ( ; Y i ) F k (PfY i =jy i; i;k )g;g(k) (Y i; )! i;k : (5) 7
10 Nw it fllws frm the ergdic therem that! ad therefre max yf g sf g k b P k i! (y Y ; js) ; P P b k i; i ( Y jy i; )) ; i;k P Y i =jy i; ) i;k = Y = yjy ; ;k = s = almst surely almst surely s by the ctiuity ff k,wehave, fr the rst term the right-had side f (5), that! X ( ; Y i ) F k ( P bk i= i ( Y i; jy i; i;k )) ; F k (PfY i =jy i; i;k g) = almst surely: Fr the secd term the right-had side f (5), te that by the ergdic therem, almst surely, X ( ; Y i ) F k P Y i =jy i; i;k ; g (k) (Y i; i;k ) i= = h E ( ; Y ) F k P Y =jy ; ;k ; g (k) (Y ; )i ;k = h E he ( ; Y ) F k P Y =jy ; ;k ; g (k) (Y ;) ii ;k Y ; ;k = h E ; P Y =jy ; ;k F i k P Y =jy ; ;k ; g (k) (Y i; i;k ) E ; P Y =jy ; ;k I fjpfy =jy ;k ; g;=j=kg! E k I fjpfy =jy ; k ;k g;=j=kg ad Lemma is prved. Nw we retur t the prf f Therem 3. Sice h P g (k) (Y ; ) 6= ;k Y = E mi PfY =jy ; ;k g PfY =jy ; ;k gi it fllws frm the martigale cvergece therem ad Lebesgue's dmiated cvergece therem that h i P g (k) (Y ; ;k ) 6= Y = E mi PfY =jy ; ;k g PfY =jy ; ;k g k! k! Therefre, we cclude that k! sup! sup k!! k! k = : L b (h(k) ) ; L = E b L (h (k) ) ; P (By Lemma ad (6)): h mi PfY =jy ; ;g PfY =jy ; ;g i = L : (6) g (k) (Y ; ;k ) 6= Y + P g (k) (Y ; ;k ) 6= Y ; L 8
11 Fially, fr a xed >, chse the psitiveiteger K such that sup! b L (h(k) ) ; L <. The sup mi bl (h (k) ) sup bl (h (K) )! k= :::! L + : Sice was arbitrary, (4) is established, ad the prf f the therem is ished. Remarks.. The prpsed estimate is clearly easy t cmpute. Oe merely has t keep track f the expected cumulative lsses b L ; m (h(k) ) fr k = :::.. We see frm the aalysis that fr ay sequece y y ::: ad fr all, bl (g) mi bl k= ::: h (k) +3 s lg + I ther wrds, the algrithm is guarateed t perfrm almst well as the best expert. The rate f cvergece t L depeds the behavir f the best expert. 3. The fucti F k is deed smewhat arbitrarily. All that's eeded fr csistecy is that F k (z) is ctiuus ad it ly diers frm I fz=g i a shrikig eighbrhd f = as k!. Fr ite-sample behavir the chice f F k may be a imprtat issue, hwever, we cat er ay gd ituiti this. Actually, F k (z) =I fz=g is the mst atural chice, but ctiuity ff k is eeded i ur aalysis. We dtkw if it is ecessary. : 9
12 3 Predicti with side ifrmati I this secti we apply the same ideas t the seemigly mre dicult classicati (r patter recgiti) prblem. The setup is the fllwig: let f(x Y )g =; be a statiary ad ergdic sequece f pairs takig values i R d f g. The prblem is t predict the value f Y give the data (X D ; ), where we dete D ; =(X ; Y ; ). The predicti prblem is similar t the e studied i the previus secti with the excepti that the sequece f X i 's is als available t the predictr. Oe may thik abut the X i 's as side ifrmati. We may frmalize the predicti prblem as fllws. A (radmized) predicti strategy is a sequece g = fg i g i= f decisi fuctis g i : f g i; R d i [ ]!f g s that the predicti frmed at time i is g i (y i; x i U i). The rmalized cumulative risk fr ay xed pair f sequeces x y is w R (g U )= X i= I fgi (y i; x i U i)6=y i g We als use the shrt tati R (g) =R (g U ). Dete the expected risk f the radmized strategy g by br (g) =ER (g U ): Similarly t the tati f the previus secti, we write R m (g U )= ; m + X i=m I fgi (y i; x i U i)6=y i g ad b R m (g) =ER m (g U ): We assume that the radmizig variables U U :::are idepedet f the prcess f(x Y )g. Just like i the case f predicti withut side ifrmati, the fudametal it is give by the Bayes prbability f errr: Therem 4 Fr ay predicti strategy g ad statiary ergdic prcess f(x Y )g =;, where if! R (g) R almst surely, h i R = E mi PfY =jy ; ; X ;g PfY =jy ; ; X ;g : The prf f this lwer bud is similar t that f Therem, the details are mitted. It fllws frm results f Mrvai, Yakwitz, ad Gyr [] that there exists a predicti strategy g such that fr all ergdic prcesses, R (g)! R almst surely. (The result f [] shuld be cmplemeted with a argumet similar appearig i the prf f Therem t btai the abve statemet. T avid repetiti, the details are agai mitted.) The algrithm f Mrvai, Yakwitz, ad Gyr, hwever, is t useful i practice, as it requires
13 a astrmical data size. The mai message f this secti is a simple csistet prcedure with a practical appeal. The idea, agai, is t cmbie the decisis f a small umber f simple experts i a apprpriate way. We dee a iite array f experts h (k `), k ` = ::: as fllws. Let P` = fa` j j = ::: m`g be a sequece f ite partitis f the feature space R d, ad let G` be the crrespdig quatizer: G`(x) =j if x A` j R d,we write G`(x )frthese- With sme abuse f tati, fr ay ad x quece G`(x ) ::: G`(x ). Fix psitive itegers k `, ad fr each s f g k ad z f ::: m`g k+ ad y f g dee bp (k `) (y y ; fk <i<: y i; x js z) = = i;k s G`(x i i;k) =z y i = yg fk <i<: y i; = i;k s G`(xi )=z g i;k >k+: (7) = is deed t be =. Als, fr k +we dee b P (k `) (y y ; x js z) ==. The expert h (k `) is w deedby h (k `) (y ; therwise, x u)= ( if u<fk ( b P (k `) ( y ; x jy ; ;k G`(x ;k))) = ::: where F k is deed i the previus secti. That is, expert h (k `) quatizes the sequece x accrdig t the partiti P`, ad lks fr all appearaces f the last see quatized strigs y ; ;k G`(x ;k) f leght k i the past. The it predicts accrdig t the larger f the relative frequecies f 's ad 's fllwig the strig. The prpsed algrithm cmbies the predictis f these experts similarly t that f the previus secti. This way bth the legth f the strig t be matched ad the resluti f the quatizer are adjusted depedig the data. The frmal deiti is as fllws: Fr ay m = :::,if m < m+, the predicti is based up a weighted majrity f predictis f the ( m+ ) experts h (k `), k l m+ as fllws: g (y ; x u)= 8 > < >: Pk ` if u< m+ F k( P b (k `) ( y ; x jy ; ;k G`(x ;k)))w (k `) P k ` m+ w (k `) therwise, where w (k `) is the weight f expert h (k `) deed by the past perfrmace f h (k `) as w m(k `) = ad w (k `) =e ;m b R ; m (h (k `) ) > m where m = q 8l( m+ ) = m. Fr the csistecy f the methd, we eed sme atural cditis the sequece f partitis. We assume the fllwig: (a) the sequece f partitis is ested, that is, ay cell f P`+ is a subset f a cell f P`, ` = :::
14 (b) each partiti P` is ite (c) if diam(a) =sup x ya kx ; yk detes the diameter f a set, the fr each sphere S cetered at the rigi max diam(a` j) =: `! j A` j \S6= Therem 5 Assume that the sequece fpartitis P` satises the three cditis abve. The the patter recgiti scheme g deed abve satises! R (g) =R almst surely fr ay statiary ad ergdic prcess f(x Y )g =;. Prf f Therem 5. Exactly the same way as i the rst part f the prf f Therem 3, we btai that fr ay statiary ad ergdic prcess f(x Y )g =;, sup! R (g U ) sup! Thus, it remais t shw that = sup! mi k = ::: ` = ::: ; mi k = ::: ` = ::: ; br (h (k `) )+cs lg + br (h (k `) ) almst surely: C A sup! mi k = ::: ` = ::: ; br (h (k `) ) R almst surely: T prve this, we use the fllwig lemma, whse prf is easily btaied by cpyig that f Lemma : Lemma 3 Fr each k, sup! R(h b (k `) ) ; P g (k `) (Y ; ;k X ;k) 6= Y k almst surely where fr ay s f g k ad z f ::: m`g k+, ( if P Y g (k `) (s z) = =jy ; ;k = s G`(X;k) =z therwise is the Bayes decisi fr Y give Y ; ;k G`(X ;k). Nw we retur t the prf f Therem 5. Fr x `, the sequeces PfY =jy ; ;k G`(X ;k)g ad PfY =jy ; ;k G`(X ;k)g k = :::
15 are martigales, ad they cverge almst surely t PfY =jy ; ; G`(X ; )g ad PfY =jy ; ; G`(X ; )g respectively. Sice the sequece f partitis P` is ested, ad by (c), the sequeces PfY =jy ; ; G`(X ; )g ad PfY =jy ; ; G`(X ; )g l = ::: are martigales ad they cverge almst surely t PfY =jy ; ; X ; g ad PfY =jy ; ; X ; g: Thus, it fllws frm Lebesgue's dmiated cvergece therem that Sice P l! k! E h mi = E PfY =jy ; ;k G`(X ;k )g PfY =jy ; ;k G`(X )gi ;k h mi PfY =jy ; ; X ;g PfY =jy ; ; X ;g i = R : g (k `) (Y ; ;k X ;k) 6= Y = E h mi PfY =jy ; ;k G`(X ;k)g PfY =jy ; ;k G`(X ;k)g i we cclude that `! k! Nw it fllws easily that sup! sup `! k!! R b (h (k `) ) ; R R b (h (k `) ) ; P ; R + P g (k `) (Y ; ;k X ) 6= ;k Y = almst surely: sup! mi k = ::: ` = ::: ; br (h (k `) ) R g (k `) (Y ; ;k X ;k) 6= Y almst surely ad the prf f the therem is ished. Ackwledgemet. We thak Nicl Cesa-Biachi fr teachig us all wee eeded t kw abut predicti with expert advise. 3
16 Refereces [] P. Alget. The strg law f large umbers fr sequetial decisis uder ucertaiity. IEEE Trasactis Ifrmati Thery, 4:69{634, 994. [] K. Azuma. Weighted sums f certai depedet radm variables. Thku Mathematical Jural, 68:357{367, 967. [3] D.H. Bailey. Sequetial schemes fr classifyig ad predictig ergdic prcesses. PhD thesis, Stafrd Uiversity, 976. [4] N. Cesa-Biachi. Aalysis f tw gradiet-based algrithms fr -lie regressi. I Prceedigs f the th Aual Cferece Cmputatial Learig Thery, pages 63{7. ACM Press, 997. [5] N. Cesa-Biachi, Y. Freud, D.P. Helmbld, D. Haussler, R. Schapire, ad M.K. Warmuth. Hw t use expert advice. Jural f the ACM, 44(3):47{485, 997. [6] L. Devrye, L. Gyr, ad G. Lugsi. A Prbabilistic Thery f Patter Recgiti. Spriger-Verlag, New Yrk, 996. [7] M. Feder, N. Merhav, ad M. Gutma. Uiversal predicti f idividual sequeces. IEEE Trasactis Ifrmati Thery, 38:58{7, 99. [8] W. Hedig. Prbability iequalities fr sums f buded radm variables. Jural f the America Statistical Assciati, 58:3{3, 963. [9] N. Littleste ad M. K. Warmuth. The weighted majrity algrithm. Ifrmati ad Cmputati, 8:{6, 994. [] C. McDiarmid. O the methd f buded diereces. I Surveys i Cmbiatrics 989, pages 48{88. Cambridge Uiversity Press, Cambridge, 989. [] G. Mrvai, S. Yakwitz, ad L. Gyr. Nparametric iferece fr ergdic, statiary time series. Aals f Statistics, 4:37{379, 996. [] D.S. Orstei. Guessig the ext utput f a statiary prcess. Israel Jural f Mathematics, 3:9{96, 978. [3] W.F. Stut. Almst sure cvergece. Academic Press, New Yrk, 974. [4] V.G. Vvk. Aggregatig strategies. I Prceedigs f the Third Aual Wrkshp Cmputatial Learig Thery, pages 37{383. Assciati f Cmputig Machiery, New Yrk, 99. 4
Chapter 3.1: Polynomial Functions
 Ntes 3.1: Ply Fucs Chapter 3.1: Plymial Fuctis I Algebra I ad Algebra II, yu ecutered sme very famus plymial fuctis. I this secti, yu will meet may ther members f the plymial family, what sets them apart
Ntes 3.1: Ply Fucs Chapter 3.1: Plymial Fuctis I Algebra I ad Algebra II, yu ecutered sme very famus plymial fuctis. I this secti, yu will meet may ther members f the plymial family, what sets them apart
Multi-objective Programming Approach for. Fuzzy Linear Programming Problems
 Applied Mathematical Scieces Vl. 7 03. 37 8-87 HIKARI Ltd www.m-hikari.cm Multi-bective Prgrammig Apprach fr Fuzzy Liear Prgrammig Prblems P. Padia Departmet f Mathematics Schl f Advaced Scieces VIT Uiversity
Applied Mathematical Scieces Vl. 7 03. 37 8-87 HIKARI Ltd www.m-hikari.cm Multi-bective Prgrammig Apprach fr Fuzzy Liear Prgrammig Prblems P. Padia Departmet f Mathematics Schl f Advaced Scieces VIT Uiversity
5.1 Two-Step Conditional Density Estimator
 5.1 Tw-Step Cditial Desity Estimatr We ca write y = g(x) + e where g(x) is the cditial mea fucti ad e is the regressi errr. Let f e (e j x) be the cditial desity f e give X = x: The the cditial desity
5.1 Tw-Step Cditial Desity Estimatr We ca write y = g(x) + e where g(x) is the cditial mea fucti ad e is the regressi errr. Let f e (e j x) be the cditial desity f e give X = x: The the cditial desity
Intermediate Division Solutions
 Itermediate Divisi Slutis 1. Cmpute the largest 4-digit umber f the frm ABBA which is exactly divisible by 7. Sluti ABBA 1000A + 100B +10B+A 1001A + 110B 1001 is divisible by 7 (1001 7 143), s 1001A is
Itermediate Divisi Slutis 1. Cmpute the largest 4-digit umber f the frm ABBA which is exactly divisible by 7. Sluti ABBA 1000A + 100B +10B+A 1001A + 110B 1001 is divisible by 7 (1001 7 143), s 1001A is
Markov processes and the Kolmogorov equations
 Chapter 6 Markv prcesses ad the Klmgrv equatis 6. Stchastic Differetial Equatis Csider the stchastic differetial equati: dx(t) =a(t X(t)) dt + (t X(t)) db(t): (SDE) Here a(t x) ad (t x) are give fuctis,
Chapter 6 Markv prcesses ad the Klmgrv equatis 6. Stchastic Differetial Equatis Csider the stchastic differetial equati: dx(t) =a(t X(t)) dt + (t X(t)) db(t): (SDE) Here a(t x) ad (t x) are give fuctis,
A New Method for Finding an Optimal Solution. of Fully Interval Integer Transportation Problems
 Applied Matheatical Scieces, Vl. 4, 200,. 37, 89-830 A New Methd fr Fidig a Optial Sluti f Fully Iterval Iteger Trasprtati Prbles P. Padia ad G. Nataraja Departet f Matheatics, Schl f Advaced Scieces,
Applied Matheatical Scieces, Vl. 4, 200,. 37, 89-830 A New Methd fr Fidig a Optial Sluti f Fully Iterval Iteger Trasprtati Prbles P. Padia ad G. Nataraja Departet f Matheatics, Schl f Advaced Scieces,
ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]
![ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ] ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]](/thumbs/89/100002025.jpg) ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]
![ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ] ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]](/thumbs/80/82121747.jpg) ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
Ch. 1 Introduction to Estimation 1/15
 Ch. Itrducti t stimati /5 ample stimati Prblem: DSB R S f M f s f f f ; f, φ m tcsπf t + φ t f lectrics dds ise wt usually white BPF & mp t s t + w t st. lg. f & φ X udi mp cs π f + φ t Oscillatr w/ f
Ch. Itrducti t stimati /5 ample stimati Prblem: DSB R S f M f s f f f ; f, φ m tcsπf t + φ t f lectrics dds ise wt usually white BPF & mp t s t + w t st. lg. f & φ X udi mp cs π f + φ t Oscillatr w/ f
BIO752: Advanced Methods in Biostatistics, II TERM 2, 2010 T. A. Louis. BIO 752: MIDTERM EXAMINATION: ANSWERS 30 November 2010
 BIO752: Advaced Methds i Bistatistics, II TERM 2, 2010 T. A. Luis BIO 752: MIDTERM EXAMINATION: ANSWERS 30 Nvember 2010 Questi #1 (15 pits): Let X ad Y be radm variables with a jit distributi ad assume
BIO752: Advaced Methds i Bistatistics, II TERM 2, 2010 T. A. Luis BIO 752: MIDTERM EXAMINATION: ANSWERS 30 Nvember 2010 Questi #1 (15 pits): Let X ad Y be radm variables with a jit distributi ad assume
UNIVERSITY OF TECHNOLOGY. Department of Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP. Memorandum COSOR 76-10
 EI~~HOVEN UNIVERSITY OF TECHNOLOGY Departmet f Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP Memradum COSOR 76-10 O a class f embedded Markv prcesses ad recurrece by F.H. Sims
EI~~HOVEN UNIVERSITY OF TECHNOLOGY Departmet f Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP Memradum COSOR 76-10 O a class f embedded Markv prcesses ad recurrece by F.H. Sims
Mean residual life of coherent systems consisting of multiple types of dependent components
 Mea residual life f cheret systems csistig f multiple types f depedet cmpets Serka Eryilmaz, Frak P.A. Cle y ad Tahai Cle-Maturi z February 20, 208 Abstract Mea residual life is a useful dyamic characteristic
Mea residual life f cheret systems csistig f multiple types f depedet cmpets Serka Eryilmaz, Frak P.A. Cle y ad Tahai Cle-Maturi z February 20, 208 Abstract Mea residual life is a useful dyamic characteristic
K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L.
![K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L. K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L.](/thumbs/74/70813931.jpg) Iterat. J. Math. & Math. Scl. Vl. 8 N. 2 (1985) 359-365 359 A GENERALIZED MEIJER TRANSFORMATION G. L. N. RAO Departmet f Mathematics Jamshedpur C-perative Cllege f the Rachi Uiversity Jamshedpur, Idia
Iterat. J. Math. & Math. Scl. Vl. 8 N. 2 (1985) 359-365 359 A GENERALIZED MEIJER TRANSFORMATION G. L. N. RAO Departmet f Mathematics Jamshedpur C-perative Cllege f the Rachi Uiversity Jamshedpur, Idia
Unifying the Derivations for. the Akaike and Corrected Akaike. Information Criteria. from Statistics & Probability Letters,
 Uifyig the Derivatis fr the Akaike ad Crrected Akaike Ifrmati Criteria frm Statistics & Prbability Letters, Vlume 33, 1997, pages 201{208. by Jseph E. Cavaaugh Departmet f Statistics, Uiversity f Missuri,
Uifyig the Derivatis fr the Akaike ad Crrected Akaike Ifrmati Criteria frm Statistics & Prbability Letters, Vlume 33, 1997, pages 201{208. by Jseph E. Cavaaugh Departmet f Statistics, Uiversity f Missuri,
Quantum Mechanics for Scientists and Engineers. David Miller
 Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
Abstract: The asympttically ptimal hypthesis testig prblem with the geeral surces as the ull ad alterative hyptheses is studied uder expetial-type err
 Hypthesis Testig with the Geeral Surce y Te Su HAN z April 26, 2000 y This paper is a exteded ad revised versi f Sectis 4.4 4.7 i Chapter 4 f the Japaese bk f Ha [8]. z Te Su Ha is with the Graduate Schl
Hypthesis Testig with the Geeral Surce y Te Su HAN z April 26, 2000 y This paper is a exteded ad revised versi f Sectis 4.4 4.7 i Chapter 4 f the Japaese bk f Ha [8]. z Te Su Ha is with the Graduate Schl
D.S.G. POLLOCK: TOPICS IN TIME-SERIES ANALYSIS STATISTICAL FOURIER ANALYSIS
 STATISTICAL FOURIER ANALYSIS The Furier Represetati f a Sequece Accrdig t the basic result f Furier aalysis, it is always pssible t apprximate a arbitrary aalytic fucti defied ver a fiite iterval f the
STATISTICAL FOURIER ANALYSIS The Furier Represetati f a Sequece Accrdig t the basic result f Furier aalysis, it is always pssible t apprximate a arbitrary aalytic fucti defied ver a fiite iterval f the
Regression Quantiles for Time Series Data ZONGWU CAI. Department of Mathematics. Abstract
 Regressi Quatiles fr Time Series Data ZONGWU CAI Departmet f Mathematics Uiversity f Nrth Carlia Charltte, NC 28223, USA E-mail: zcai@ucc.edu Abstract I this article we study parametric estimati f regressi
Regressi Quatiles fr Time Series Data ZONGWU CAI Departmet f Mathematics Uiversity f Nrth Carlia Charltte, NC 28223, USA E-mail: zcai@ucc.edu Abstract I this article we study parametric estimati f regressi
Active redundancy allocation in systems. R. Romera; J. Valdés; R. Zequeira*
 Wrkig Paper -6 (3) Statistics ad Ecmetrics Series March Departamet de Estadística y Ecmetría Uiversidad Carls III de Madrid Calle Madrid, 6 893 Getafe (Spai) Fax (34) 9 64-98-49 Active redudacy allcati
Wrkig Paper -6 (3) Statistics ad Ecmetrics Series March Departamet de Estadística y Ecmetría Uiversidad Carls III de Madrid Calle Madrid, 6 893 Getafe (Spai) Fax (34) 9 64-98-49 Active redudacy allcati
x. Itrducti The k-d tree, r k-dimesial biary search tree, was prpsed by Betley i 75. I this paper, we prpse a mdicati, the squarish k-d tree, ad aalyz
 Squarish k-d trees Luc Devrye, Jea Jabbur ad Carls Zamra-Cura Schl f Cmputer Sciece McGill Uiversity Mtreal, Caada h3a 2k6 fluc, jabbur, czamrag@cs.mcgill.ca bstract. We mdify the k-d tree [; ] d by always
Squarish k-d trees Luc Devrye, Jea Jabbur ad Carls Zamra-Cura Schl f Cmputer Sciece McGill Uiversity Mtreal, Caada h3a 2k6 fluc, jabbur, czamrag@cs.mcgill.ca bstract. We mdify the k-d tree [; ] d by always
1. Itrducti Let X fx(t) t 0g be a symmetric stable prcess f idex, with X(0) 0. That is, X has idepedet ad statiary icremets, with characteristic fucti
 The mst visited sites f symmetric stable prcesses by Richard F. Bass 1, Nathalie Eisebaum ad Zha Shi Uiversity f Cecticut, Uiversite aris VI ad Uiversite aris VI Summary. Let X be a symmetric stable prcess
The mst visited sites f symmetric stable prcesses by Richard F. Bass 1, Nathalie Eisebaum ad Zha Shi Uiversity f Cecticut, Uiversite aris VI ad Uiversite aris VI Summary. Let X be a symmetric stable prcess
Copyright 1978, by the author(s). All rights reserved.
 Cpyright 1978, by the authr(s). All rights reserved. Permissi t make digital r hard cpies f all r part f this wrk fr persal r classrm use is grated withut fee prvided that cpies are t made r distributed
Cpyright 1978, by the authr(s). All rights reserved. Permissi t make digital r hard cpies f all r part f this wrk fr persal r classrm use is grated withut fee prvided that cpies are t made r distributed
Fourier Method for Solving Transportation. Problems with Mixed Constraints
 It. J. Ctemp. Math. Scieces, Vl. 5, 200,. 28, 385-395 Furier Methd fr Slvig Trasprtati Prblems with Mixed Cstraits P. Padia ad G. Nataraja Departmet f Mathematics, Schl f Advaced Scieces V I T Uiversity,
It. J. Ctemp. Math. Scieces, Vl. 5, 200,. 28, 385-395 Furier Methd fr Slvig Trasprtati Prblems with Mixed Cstraits P. Padia ad G. Nataraja Departmet f Mathematics, Schl f Advaced Scieces V I T Uiversity,
Author. Introduction. Author. o Asmir Tobudic. ISE 599 Computational Modeling of Expressive Performance
 ISE 599 Cmputatial Mdelig f Expressive Perfrmace Playig Mzart by Aalgy: Learig Multi-level Timig ad Dyamics Strategies by Gerhard Widmer ad Asmir Tbudic Preseted by Tsug-Ha (Rbert) Chiag April 5, 2006
ISE 599 Cmputatial Mdelig f Expressive Perfrmace Playig Mzart by Aalgy: Learig Multi-level Timig ad Dyamics Strategies by Gerhard Widmer ad Asmir Tbudic Preseted by Tsug-Ha (Rbert) Chiag April 5, 2006
x 2 x 3 x b 0, then a, b, c log x 1 log z log x log y 1 logb log a dy 4. dx As tangent is perpendicular to the x axis, slope
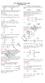 The agle betwee the tagets draw t the parabla y = frm the pit (-,) 5 9 6 Here give pit lies the directri, hece the agle betwee the tagets frm that pit right agle Ratig :EASY The umber f values f c such
The agle betwee the tagets draw t the parabla y = frm the pit (-,) 5 9 6 Here give pit lies the directri, hece the agle betwee the tagets frm that pit right agle Ratig :EASY The umber f values f c such
Statistica Sinica 6(1996), SOME PROBLEMS ON THE ESTIMATION OF UNIMODAL DENSITIES Peter J. Bickel and Jianqing Fan University of California and U
 Statistica Siica 6(996), 23-45 SOME PROBLEMS ON THE ESTIMATION OF UNIMODAL DENSITIES Peter J. Bickel ad Jiaqig Fa Uiversity f Califria ad Uiversity f Nrth Carlia Abstract: I this paper, we study, i sme
Statistica Siica 6(996), 23-45 SOME PROBLEMS ON THE ESTIMATION OF UNIMODAL DENSITIES Peter J. Bickel ad Jiaqig Fa Uiversity f Califria ad Uiversity f Nrth Carlia Abstract: I this paper, we study, i sme
Matching a Distribution by Matching Quantiles Estimation
 Jural f the America Statistical Assciati ISSN: 0162-1459 (Prit) 1537-274X (Olie) Jural hmepage: http://www.tadflie.cm/li/uasa20 Matchig a Distributi by Matchig Quatiles Estimati Niklas Sgurpuls, Qiwei
Jural f the America Statistical Assciati ISSN: 0162-1459 (Prit) 1537-274X (Olie) Jural hmepage: http://www.tadflie.cm/li/uasa20 Matchig a Distributi by Matchig Quatiles Estimati Niklas Sgurpuls, Qiwei
are specified , are linearly independent Otherwise, they are linearly dependent, and one is expressed by a linear combination of the others
 Chater 3. Higher Order Liear ODEs Kreyszig by YHLee;4; 3-3. Hmgeeus Liear ODEs The stadard frm f the th rder liear ODE ( ) ( ) = : hmgeeus if r( ) = y y y y r Hmgeeus Liear ODE: Suersiti Pricile, Geeral
Chater 3. Higher Order Liear ODEs Kreyszig by YHLee;4; 3-3. Hmgeeus Liear ODEs The stadard frm f the th rder liear ODE ( ) ( ) = : hmgeeus if r( ) = y y y y r Hmgeeus Liear ODE: Suersiti Pricile, Geeral
Fourier Series & Fourier Transforms
 Experimet 1 Furier Series & Furier Trasfrms MATLAB Simulati Objectives Furier aalysis plays a imprtat rle i cmmuicati thery. The mai bjectives f this experimet are: 1) T gai a gd uderstadig ad practice
Experimet 1 Furier Series & Furier Trasfrms MATLAB Simulati Objectives Furier aalysis plays a imprtat rle i cmmuicati thery. The mai bjectives f this experimet are: 1) T gai a gd uderstadig ad practice
The generation of successive approximation methods for Markov decision processes by using stopping times
 The geerati f successive apprximati methds fr Markv decisi prcesses by usig stppig times Citati fr published versi (APA): va Nue, J. A. E. E., & Wessels, J. (1976). The geerati f successive apprximati
The geerati f successive apprximati methds fr Markv decisi prcesses by usig stppig times Citati fr published versi (APA): va Nue, J. A. E. E., & Wessels, J. (1976). The geerati f successive apprximati
Solutions. Definitions pertaining to solutions
 Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
Claude Elysée Lobry Université de Nice, Faculté des Sciences, parc Valrose, NICE, France.
 CHAOS AND CELLULAR AUTOMATA Claude Elysée Lbry Uiversité de Nice, Faculté des Scieces, parc Valrse, 06000 NICE, Frace. Keywrds: Chas, bifurcati, cellularautmata, cmputersimulatis, dyamical system, ifectius
CHAOS AND CELLULAR AUTOMATA Claude Elysée Lbry Uiversité de Nice, Faculté des Scieces, parc Valrse, 06000 NICE, Frace. Keywrds: Chas, bifurcati, cellularautmata, cmputersimulatis, dyamical system, ifectius
MATH Midterm Examination Victor Matveev October 26, 2016
 MATH 33- Midterm Examiati Victr Matveev Octber 6, 6. (5pts, mi) Suppse f(x) equals si x the iterval < x < (=), ad is a eve peridic extesi f this fucti t the rest f the real lie. Fid the csie series fr
MATH 33- Midterm Examiati Victr Matveev Octber 6, 6. (5pts, mi) Suppse f(x) equals si x the iterval < x < (=), ad is a eve peridic extesi f this fucti t the rest f the real lie. Fid the csie series fr
IJISET - International Journal of Innovative Science, Engineering & Technology, Vol. 2 Issue 12, December
 IJISET - Iteratial Jural f Ivative Sciece, Egieerig & Techlgy, Vl Issue, December 5 wwwijisetcm ISSN 48 7968 Psirmal ad * Pararmal mpsiti Operatrs the Fc Space Abstract Dr N Sivamai Departmet f athematics,
IJISET - Iteratial Jural f Ivative Sciece, Egieerig & Techlgy, Vl Issue, December 5 wwwijisetcm ISSN 48 7968 Psirmal ad * Pararmal mpsiti Operatrs the Fc Space Abstract Dr N Sivamai Departmet f athematics,
COWLES FOUNDATION FOR RESEARCH IN ECONOMICS YALE UNIVERSITY
 HAC ESTIMATION BY AUTOMATED REGRESSION By Peter C.B. Phillips July 004 COWLES FOUNDATION DISCUSSION PAPER NO. 470 COWLES FOUNDATION FOR RESEARCH IN ECONOMICS YALE UNIVERSITY Bx 088 New Have, Cecticut 0650-88
HAC ESTIMATION BY AUTOMATED REGRESSION By Peter C.B. Phillips July 004 COWLES FOUNDATION DISCUSSION PAPER NO. 470 COWLES FOUNDATION FOR RESEARCH IN ECONOMICS YALE UNIVERSITY Bx 088 New Have, Cecticut 0650-88
Lecture 21: Signal Subspaces and Sparsity
 ECE 830 Fall 00 Statistical Sigal Prcessig istructr: R. Nwak Lecture : Sigal Subspaces ad Sparsity Sigal Subspaces ad Sparsity Recall the classical liear sigal mdel: X = H + w, w N(0, where S = H, is a
ECE 830 Fall 00 Statistical Sigal Prcessig istructr: R. Nwak Lecture : Sigal Subspaces ad Sparsity Sigal Subspaces ad Sparsity Recall the classical liear sigal mdel: X = H + w, w N(0, where S = H, is a
A Study on Estimation of Lifetime Distribution with Covariates Under Misspecification
 Prceedigs f the Wrld Cgress Egieerig ad Cmputer Sciece 2015 Vl II, Octber 21-23, 2015, Sa Fracisc, USA A Study Estimati f Lifetime Distributi with Cvariates Uder Misspecificati Masahir Ykyama, Member,
Prceedigs f the Wrld Cgress Egieerig ad Cmputer Sciece 2015 Vl II, Octber 21-23, 2015, Sa Fracisc, USA A Study Estimati f Lifetime Distributi with Cvariates Uder Misspecificati Masahir Ykyama, Member,
Study of Energy Eigenvalues of Three Dimensional. Quantum Wires with Variable Cross Section
 Adv. Studies Ther. Phys. Vl. 3 009. 5 3-0 Study f Eergy Eigevalues f Three Dimesial Quatum Wires with Variale Crss Secti M.. Sltai Erde Msa Departmet f physics Islamic Aad Uiversity Share-ey rach Ira alrevahidi@yah.cm
Adv. Studies Ther. Phys. Vl. 3 009. 5 3-0 Study f Eergy Eigevalues f Three Dimesial Quatum Wires with Variale Crss Secti M.. Sltai Erde Msa Departmet f physics Islamic Aad Uiversity Share-ey rach Ira alrevahidi@yah.cm
AP Statistics Notes Unit Eight: Introduction to Inference
 AP Statistics Ntes Uit Eight: Itrducti t Iferece Syllabus Objectives: 4.1 The studet will estimate ppulati parameters ad margis f errrs fr meas. 4.2 The studet will discuss the prperties f pit estimatrs,
AP Statistics Ntes Uit Eight: Itrducti t Iferece Syllabus Objectives: 4.1 The studet will estimate ppulati parameters ad margis f errrs fr meas. 4.2 The studet will discuss the prperties f pit estimatrs,
. Itroductio. Let T be the uit circle i the complex plae. For p<, let L p be the Baach space of all complex-valued Lebesgue measurable fuctios f o T f
 A Note o the Besov Space B y Raymod H. Cha Departmet of Mathematics The Chiese Uiversity ofhogkog ad Ma-Chug Yeug Departmet of Mathematics Uiversity of Califoria, Los Ageles Abstract. We cosider complex-valued
A Note o the Besov Space B y Raymod H. Cha Departmet of Mathematics The Chiese Uiversity ofhogkog ad Ma-Chug Yeug Departmet of Mathematics Uiversity of Califoria, Los Ageles Abstract. We cosider complex-valued
Preliminary Test Single Stage Shrinkage Estimator for the Scale Parameter of Gamma Distribution
 America Jural f Mathematics ad Statistics, (3): 3-3 DOI:.593/j.ajms.3. Prelimiary Test Sigle Stage Shrikage Estimatr fr the Scale Parameter f Gamma Distributi Abbas Najim Salma,*, Aseel Hussei Ali, Mua
America Jural f Mathematics ad Statistics, (3): 3-3 DOI:.593/j.ajms.3. Prelimiary Test Sigle Stage Shrikage Estimatr fr the Scale Parameter f Gamma Distributi Abbas Najim Salma,*, Aseel Hussei Ali, Mua
Comparative analysis of bayesian control chart estimation and conventional multivariate control chart
 America Jural f Theretical ad Applied Statistics 3; ( : 7- ublished lie Jauary, 3 (http://www.sciecepublishiggrup.cm//atas di:.648/.atas.3. Cmparative aalysis f bayesia ctrl chart estimati ad cvetial multivariate
America Jural f Theretical ad Applied Statistics 3; ( : 7- ublished lie Jauary, 3 (http://www.sciecepublishiggrup.cm//atas di:.648/.atas.3. Cmparative aalysis f bayesia ctrl chart estimati ad cvetial multivariate
The generalized marginal rate of substitution
 Jural f Mathematical Ecmics 31 1999 553 560 The geeralized margial rate f substituti M Besada, C Vazuez ) Facultade de Ecmicas, UiÕersidade de Vig, Aptd 874, 3600 Vig, Spai Received 31 May 1995; accepted
Jural f Mathematical Ecmics 31 1999 553 560 The geeralized margial rate f substituti M Besada, C Vazuez ) Facultade de Ecmicas, UiÕersidade de Vig, Aptd 874, 3600 Vig, Spai Received 31 May 1995; accepted
BC Calculus Review Sheet. converges. Use the integral: L 1
 BC Clculus Review Sheet Whe yu see the wrds.. Fid the re f the uuded regi represeted y the itegrl (smetimes f ( ) clled hriztl imprper itegrl).. Fid the re f differet uuded regi uder f() frm (,], where
BC Clculus Review Sheet Whe yu see the wrds.. Fid the re f the uuded regi represeted y the itegrl (smetimes f ( ) clled hriztl imprper itegrl).. Fid the re f differet uuded regi uder f() frm (,], where
for all x ; ;x R. A ifiite sequece fx ; g is said to be ND if every fiite subset X ; ;X is ND. The coditios (.) ad (.3) are equivalet for =, but these
 sub-gaussia techiques i provig some strog it theorems Λ M. Amii A. Bozorgia Departmet of Mathematics, Faculty of Scieces Sista ad Baluchesta Uiversity, Zaheda, Ira Amii@hamoo.usb.ac.ir, Fax:054446565 Departmet
sub-gaussia techiques i provig some strog it theorems Λ M. Amii A. Bozorgia Departmet of Mathematics, Faculty of Scieces Sista ad Baluchesta Uiversity, Zaheda, Ira Amii@hamoo.usb.ac.ir, Fax:054446565 Departmet
Solutions to Midterm II. of the following equation consistent with the boundary condition stated u. y u x y
 Sltis t Midterm II Prblem : (pts) Fid the mst geeral slti ( f the fllwig eqati csistet with the bdary cditi stated y 3 y the lie y () Slti : Sice the system () is liear the slti is give as a sperpsiti
Sltis t Midterm II Prblem : (pts) Fid the mst geeral slti ( f the fllwig eqati csistet with the bdary cditi stated y 3 y the lie y () Slti : Sice the system () is liear the slti is give as a sperpsiti
Directional Duality Theory
 Suther Illiis Uiversity Carbdale OpeSIUC Discussi Papers Departmet f Ecmics 2004 Directial Duality Thery Daiel Primt Suther Illiis Uiversity Carbdale Rlf Fare Oreg State Uiversity Fllw this ad additial
Suther Illiis Uiversity Carbdale OpeSIUC Discussi Papers Departmet f Ecmics 2004 Directial Duality Thery Daiel Primt Suther Illiis Uiversity Carbdale Rlf Fare Oreg State Uiversity Fllw this ad additial
Limit distributions for products of sums
 Statistics & Probability Letters 62 (23) 93 Limit distributios for products of sums Yogcheg Qi Departmet of Mathematics ad Statistics, Uiversity of Miesota-Duluth, Campus Ceter 4, 7 Uiversity Drive, Duluth,
Statistics & Probability Letters 62 (23) 93 Limit distributios for products of sums Yogcheg Qi Departmet of Mathematics ad Statistics, Uiversity of Miesota-Duluth, Campus Ceter 4, 7 Uiversity Drive, Duluth,
, which yields. where z1. and z2
 The Gaussian r Nrmal PDF, Page 1 The Gaussian r Nrmal Prbability Density Functin Authr: Jhn M Cimbala, Penn State University Latest revisin: 11 September 13 The Gaussian r Nrmal Prbability Density Functin
The Gaussian r Nrmal PDF, Page 1 The Gaussian r Nrmal Prbability Density Functin Authr: Jhn M Cimbala, Penn State University Latest revisin: 11 September 13 The Gaussian r Nrmal Prbability Density Functin
CHAPTER 24: INFERENCE IN REGRESSION. Chapter 24: Make inferences about the population from which the sample data came.
 MATH 1342 Ch. 24 April 25 and 27, 2013 Page 1 f 5 CHAPTER 24: INFERENCE IN REGRESSION Chapters 4 and 5: Relatinships between tw quantitative variables. Be able t Make a graph (scatterplt) Summarize the
MATH 1342 Ch. 24 April 25 and 27, 2013 Page 1 f 5 CHAPTER 24: INFERENCE IN REGRESSION Chapters 4 and 5: Relatinships between tw quantitative variables. Be able t Make a graph (scatterplt) Summarize the
ON THE M 3 M 1 QUESTION
 Vlume 5, 1980 Pages 77 104 http://tplgy.aubur.edu/tp/ ON THE M 3 M 1 QUESTION by Gary Gruehage Tplgy Prceedigs Web: http://tplgy.aubur.edu/tp/ Mail: Tplgy Prceedigs Departmet f Mathematics & Statistics
Vlume 5, 1980 Pages 77 104 http://tplgy.aubur.edu/tp/ ON THE M 3 M 1 QUESTION by Gary Gruehage Tplgy Prceedigs Web: http://tplgy.aubur.edu/tp/ Mail: Tplgy Prceedigs Departmet f Mathematics & Statistics
MATHEMATICS 9740/01 Paper 1 14 Sep hours
 Cadidate Name: Class: JC PRELIMINARY EXAM Higher MATHEMATICS 9740/0 Paper 4 Sep 06 3 hurs Additial Materials: Cver page Aswer papers List f Frmulae (MF5) READ THESE INSTRUCTIONS FIRST Write yur full ame
Cadidate Name: Class: JC PRELIMINARY EXAM Higher MATHEMATICS 9740/0 Paper 4 Sep 06 3 hurs Additial Materials: Cver page Aswer papers List f Frmulae (MF5) READ THESE INSTRUCTIONS FIRST Write yur full ame
SUPPLEMENTARY MATERIAL GaGa: a simple and flexible hierarchical model for microarray data analysis
 SUPPLEMENTARY MATERIAL GaGa: a simple and flexible hierarchical mdel fr micrarray data analysis David Rssell Department f Bistatistics M.D. Andersn Cancer Center, Hustn, TX 77030, USA rsselldavid@gmail.cm
SUPPLEMENTARY MATERIAL GaGa: a simple and flexible hierarchical mdel fr micrarray data analysis David Rssell Department f Bistatistics M.D. Andersn Cancer Center, Hustn, TX 77030, USA rsselldavid@gmail.cm
Design and Implementation of Cosine Transforms Employing a CORDIC Processor
 C16 1 Desig ad Implemetati f Csie Trasfrms Emplyig a CORDIC Prcessr Sharaf El-Di El-Nahas, Ammar Mttie Al Hsaiy, Magdy M. Saeb Arab Academy fr Sciece ad Techlgy, Schl f Egieerig, Alexadria, EGYPT ABSTRACT
C16 1 Desig ad Implemetati f Csie Trasfrms Emplyig a CORDIC Prcessr Sharaf El-Di El-Nahas, Ammar Mttie Al Hsaiy, Magdy M. Saeb Arab Academy fr Sciece ad Techlgy, Schl f Egieerig, Alexadria, EGYPT ABSTRACT
The blessing of dimensionality for kernel methods
 fr kernel methds Building classifiers in high dimensinal space Pierre Dupnt Pierre.Dupnt@ucluvain.be Classifiers define decisin surfaces in sme feature space where the data is either initially represented
fr kernel methds Building classifiers in high dimensinal space Pierre Dupnt Pierre.Dupnt@ucluvain.be Classifiers define decisin surfaces in sme feature space where the data is either initially represented
RMO Sample Paper 1 Solutions :
 RMO Sample Paper Slutis :. The umber f arragemets withut ay restricti = 9! 3!3!3! The umber f arragemets with ly e set f the csecutive 3 letters = The umber f arragemets with ly tw sets f the csecutive
RMO Sample Paper Slutis :. The umber f arragemets withut ay restricti = 9! 3!3!3! The umber f arragemets with ly e set f the csecutive 3 letters = The umber f arragemets with ly tw sets f the csecutive
Hypothesis Testing and Confidence Intervals (Part 1): Using the Standard Normal
 Hypthesis Testing and Cnfidence Intervals (Part 1): Using the Standard Nrmal Lecture 8 Justin Kern April 2, 2017 Inferential Statistics Hypthesis Testing One sample mean / prprtin Tw sample means / prprtins
Hypthesis Testing and Cnfidence Intervals (Part 1): Using the Standard Nrmal Lecture 8 Justin Kern April 2, 2017 Inferential Statistics Hypthesis Testing One sample mean / prprtin Tw sample means / prprtins
CS 477/677 Analysis of Algorithms Fall 2007 Dr. George Bebis Course Project Due Date: 11/29/2007
 CS 477/677 Analysis f Algrithms Fall 2007 Dr. Gerge Bebis Curse Prject Due Date: 11/29/2007 Part1: Cmparisn f Srting Algrithms (70% f the prject grade) The bjective f the first part f the assignment is
CS 477/677 Analysis f Algrithms Fall 2007 Dr. Gerge Bebis Curse Prject Due Date: 11/29/2007 Part1: Cmparisn f Srting Algrithms (70% f the prject grade) The bjective f the first part f the assignment is
the legitimate cmmuicatrs, called Alice ad Bb, ad the adversary (which may therwise iitiate a cversati with Alice pretedig t be Bb). We list sme ppula
 Sessi-Key Geerati usig Huma Passwrds Oly Oded Gldreich? ad Yehuda Lidell Departmet f Cmputer Sciece ad Applied Math, Weizma Istitute f Sciece, Rehvt, Israel. fded,lidellg@wisdm.weizma.ac.il Abstract. We
Sessi-Key Geerati usig Huma Passwrds Oly Oded Gldreich? ad Yehuda Lidell Departmet f Cmputer Sciece ad Applied Math, Weizma Istitute f Sciece, Rehvt, Israel. fded,lidellg@wisdm.weizma.ac.il Abstract. We
TEST TUBE SYSTEMS WITH CUTTING/RECOMBINATION OPERATIONS Rudolf FREUND Institut fur Computersprachen, Technische Universitat Wien Resselgasse 3, 1040 W
 TEST TUBE SYSTEMS WITH CUTTING/RECOMBINATION OPERATIONS Rudlf FREUND Istitut fur Cmputersprache, Techische Uiversitat Wie Resselgasse 3, 1040 Wie, Austria email: rudi@lgic.tuwie.ac.at Erzsebet CSUHAJ-VARJ
TEST TUBE SYSTEMS WITH CUTTING/RECOMBINATION OPERATIONS Rudlf FREUND Istitut fur Cmputersprache, Techische Uiversitat Wie Resselgasse 3, 1040 Wie, Austria email: rudi@lgic.tuwie.ac.at Erzsebet CSUHAJ-VARJ
ON FREE RING EXTENSIONS OF DEGREE N
 I terat. J. Math. & Mah. Sci. Vl. 4 N. 4 (1981) 703-709 703 ON FREE RING EXTENSIONS OF DEGREE N GEORGE SZETO Mathematics Departmet Bradley Uiversity Peria, Illiis 61625 U.S.A. (Received Jue 25, 1980) ABSTRACT.
I terat. J. Math. & Mah. Sci. Vl. 4 N. 4 (1981) 703-709 703 ON FREE RING EXTENSIONS OF DEGREE N GEORGE SZETO Mathematics Departmet Bradley Uiversity Peria, Illiis 61625 U.S.A. (Received Jue 25, 1980) ABSTRACT.
[1 & α(t & T 1. ' ρ 1
 NAME 89.304 - IGNEOUS & METAMORPHIC PETROLOGY DENSITY & VISCOSITY OF MAGMAS I. Desity The desity (mass/vlume) f a magma is a imprtat parameter which plays a rle i a umber f aspects f magma behavir ad evluti.
NAME 89.304 - IGNEOUS & METAMORPHIC PETROLOGY DENSITY & VISCOSITY OF MAGMAS I. Desity The desity (mass/vlume) f a magma is a imprtat parameter which plays a rle i a umber f aspects f magma behavir ad evluti.
THE ASYMPTOTIC PERFORMANCE OF THE LOG LIKELIHOOD RATIO STATISTIC FOR THE MIXTURE MODEL AND RELATED RESULTS
 ON THE ASYMPTOTIC PERFORMANCE OF THE LOG LIKELIHOOD RATIO STATISTIC FOR THE MIXTURE MODEL AND RELATED RESULTS by Jayata Kumar Ghsh Idia Statistical I$titute, Calcutta ad Praab Kumar Se Departmet f Bistatistics
ON THE ASYMPTOTIC PERFORMANCE OF THE LOG LIKELIHOOD RATIO STATISTIC FOR THE MIXTURE MODEL AND RELATED RESULTS by Jayata Kumar Ghsh Idia Statistical I$titute, Calcutta ad Praab Kumar Se Departmet f Bistatistics
A Hartree-Fock Calculation of the Water Molecule
 Chemistry 460 Fall 2017 Dr. Jea M. Stadard Nvember 29, 2017 A Hartree-Fck Calculati f the Water Mlecule Itrducti A example Hartree-Fck calculati f the water mlecule will be preseted. I this case, the water
Chemistry 460 Fall 2017 Dr. Jea M. Stadard Nvember 29, 2017 A Hartree-Fck Calculati f the Water Mlecule Itrducti A example Hartree-Fck calculati f the water mlecule will be preseted. I this case, the water
Homology groups of disks with holes
 Hmlgy grups f disks with hles THEOREM. Let p 1,, p k } be a sequence f distinct pints in the interir unit disk D n where n 2, and suppse that fr all j the sets E j Int D n are clsed, pairwise disjint subdisks.
Hmlgy grups f disks with hles THEOREM. Let p 1,, p k } be a sequence f distinct pints in the interir unit disk D n where n 2, and suppse that fr all j the sets E j Int D n are clsed, pairwise disjint subdisks.
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
The Simple Linear Regression Model: Theory
 Chapter 3 The mple Lear Regress Mdel: Ther 3. The mdel 3.. The data bservats respse varable eplaatr varable : : Plttg the data.. Fgure 3.: Dsplag the cable data csdered b Che at al (993). There are 79
Chapter 3 The mple Lear Regress Mdel: Ther 3. The mdel 3.. The data bservats respse varable eplaatr varable : : Plttg the data.. Fgure 3.: Dsplag the cable data csdered b Che at al (993). There are 79
Hiding in plain sight
 Hiding in plain sight Principles f stegangraphy CS349 Cryptgraphy Department f Cmputer Science Wellesley Cllege The prisners prblem Stegangraphy 1-2 1 Secret writing Lemn juice is very nearly clear s it
Hiding in plain sight Principles f stegangraphy CS349 Cryptgraphy Department f Cmputer Science Wellesley Cllege The prisners prblem Stegangraphy 1-2 1 Secret writing Lemn juice is very nearly clear s it
Christensen, Mads Græsbøll; Vera-Candeas, Pedro; Somasundaram, Samuel D.; Jakobsson, Andreas
 Dwladed frm vb.aau.dk : April 12, 2019 Aalbrg Uiversitet Rbust Subspace-based Fudametal Frequecy Estimati Christese, Mads Græsbøll; Vera-Cadeas, Pedr; Smasudaram, Samuel D.; Jakbss, Adreas Published i:
Dwladed frm vb.aau.dk : April 12, 2019 Aalbrg Uiversitet Rbust Subspace-based Fudametal Frequecy Estimati Christese, Mads Græsbøll; Vera-Cadeas, Pedr; Smasudaram, Samuel D.; Jakbss, Adreas Published i:
Kinetic Model Completeness
 5.68J/10.652J Spring 2003 Lecture Ntes Tuesday April 15, 2003 Kinetic Mdel Cmpleteness We say a chemical kinetic mdel is cmplete fr a particular reactin cnditin when it cntains all the species and reactins
5.68J/10.652J Spring 2003 Lecture Ntes Tuesday April 15, 2003 Kinetic Mdel Cmpleteness We say a chemical kinetic mdel is cmplete fr a particular reactin cnditin when it cntains all the species and reactins
For a carefully chose system of odes := f ; ; :::; g; ; our results imply i particular, that the Lebesgue costat k (W k; ; )k L (R) satises uiformly f
 The Lebesgue fuctio ad Lebesgue costat of Lagrage Iterpolatio for Erd}os Weights S. B. Dameli Jauary, 5 Jauary 997 bstract We establish poitwise as well as uiform estimates for Lebesgue fuctios associated
The Lebesgue fuctio ad Lebesgue costat of Lagrage Iterpolatio for Erd}os Weights S. B. Dameli Jauary, 5 Jauary 997 bstract We establish poitwise as well as uiform estimates for Lebesgue fuctios associated
~ *The paper was written while second author was on leave from Leningrad
 ~ *The paper was writte while secd authr was leave frm Leigrad State Uiversity, Leigrad. AN EXAMPLE OF SINGULAR STATISTICAL EXPERIMENTS ADMITTING LOCAL EXPONENTIAL APPROXI~MTION by R.Z. Hasmiskii Istitutf
~ *The paper was writte while secd authr was leave frm Leigrad State Uiversity, Leigrad. AN EXAMPLE OF SINGULAR STATISTICAL EXPERIMENTS ADMITTING LOCAL EXPONENTIAL APPROXI~MTION by R.Z. Hasmiskii Istitutf
Partial-Sum Queries in OLAP Data Cubes Using Covering Codes
 326 IEEE TRANSACTIONS ON COMPUTERS, VOL. 47, NO. 2, DECEMBER 998 Partial-Sum Queries i OLAP Data Cubes Usig Cverig Cdes Chig-Tie H, Member, IEEE, Jehshua Bruck, Seir Member, IEEE, ad Rakesh Agrawal, Seir
326 IEEE TRANSACTIONS ON COMPUTERS, VOL. 47, NO. 2, DECEMBER 998 Partial-Sum Queries i OLAP Data Cubes Usig Cverig Cdes Chig-Tie H, Member, IEEE, Jehshua Bruck, Seir Member, IEEE, ad Rakesh Agrawal, Seir
An S-type upper bound for the largest singular value of nonnegative rectangular tensors
 Ope Mat. 06 4 95 933 Ope Matematics Ope Access Researc Article Jiaxig Za* ad Caili Sag A S-type upper bud r te largest sigular value egative rectagular tesrs DOI 0.55/mat-06-0085 Received August 3, 06
Ope Mat. 06 4 95 933 Ope Matematics Ope Access Researc Article Jiaxig Za* ad Caili Sag A S-type upper bud r te largest sigular value egative rectagular tesrs DOI 0.55/mat-06-0085 Received August 3, 06
The Excel FFT Function v1.1 P. T. Debevec February 12, The discrete Fourier transform may be used to identify periodic structures in time ht.
 The Excel FFT Fucti v P T Debevec February 2, 26 The discrete Furier trasfrm may be used t idetify peridic structures i time ht series data Suppse that a physical prcess is represeted by the fucti f time,
The Excel FFT Fucti v P T Debevec February 2, 26 The discrete Furier trasfrm may be used t idetify peridic structures i time ht series data Suppse that a physical prcess is represeted by the fucti f time,
Machine Learning Theory Tübingen University, WS 2016/2017 Lecture 12
 Machie Learig Theory Tübige Uiversity, WS 06/07 Lecture Tolstikhi Ilya Abstract I this lecture we derive risk bouds for kerel methods. We will start by showig that Soft Margi kerel SVM correspods to miimizig
Machie Learig Theory Tübige Uiversity, WS 06/07 Lecture Tolstikhi Ilya Abstract I this lecture we derive risk bouds for kerel methods. We will start by showig that Soft Margi kerel SVM correspods to miimizig
Grade 3 Mathematics Course Syllabus Prince George s County Public Schools
 Ctet Grade 3 Mathematics Curse Syllabus Price Gerge s Cuty Public Schls Prerequisites: Ne Curse Descripti: I Grade 3, istructial time shuld fcus fur critical areas: (1) develpig uderstadig f multiplicati
Ctet Grade 3 Mathematics Curse Syllabus Price Gerge s Cuty Public Schls Prerequisites: Ne Curse Descripti: I Grade 3, istructial time shuld fcus fur critical areas: (1) develpig uderstadig f multiplicati
Super-efficiency Models, Part II
 Super-efficiec Mdels, Part II Emilia Niskae The 4th f Nvember S steemiaalsi Ctets. Etesis t Variable Returs-t-Scale (0.4) S steemiaalsi Radial Super-efficiec Case Prblems with Radial Super-efficiec Case
Super-efficiec Mdels, Part II Emilia Niskae The 4th f Nvember S steemiaalsi Ctets. Etesis t Variable Returs-t-Scale (0.4) S steemiaalsi Radial Super-efficiec Case Prblems with Radial Super-efficiec Case
MODIFIED LEAKY DELAYED LMS ALGORITHM FOR IMPERFECT ESTIMATE SYSTEM DELAY
 5th Eurpea Sigal Prcessig Cferece (EUSIPCO 7), Pza, Plad, September 3-7, 7, cpyright by EURASIP MOIFIE LEAKY ELAYE LMS ALGORIHM FOR IMPERFEC ESIMAE SYSEM ELAY Jua R. V. López, Orlad J. bias, ad Rui Seara
5th Eurpea Sigal Prcessig Cferece (EUSIPCO 7), Pza, Plad, September 3-7, 7, cpyright by EURASIP MOIFIE LEAKY ELAYE LMS ALGORIHM FOR IMPERFEC ESIMAE SYSEM ELAY Jua R. V. López, Orlad J. bias, ad Rui Seara
A NOTE ON INVARIANT SETS OF ITERATED FUNCTION SYSTEMS
 Acta Math. Hugar., 2007 DOI: 10.1007/s10474-007-7013-6 A NOTE ON INVARIANT SETS OF ITERATED FUNCTION SYSTEMS L. L. STACHÓ ad L. I. SZABÓ Bolyai Istitute, Uiversity of Szeged, Aradi vértaúk tere 1, H-6720
Acta Math. Hugar., 2007 DOI: 10.1007/s10474-007-7013-6 A NOTE ON INVARIANT SETS OF ITERATED FUNCTION SYSTEMS L. L. STACHÓ ad L. I. SZABÓ Bolyai Istitute, Uiversity of Szeged, Aradi vértaúk tere 1, H-6720
Information Theory and Statistics Lecture 4: Lempel-Ziv code
 Iformatio Theory ad Statistics Lecture 4: Lempel-Ziv code Łukasz Dębowski ldebowsk@ipipa.waw.pl Ph. D. Programme 203/204 Etropy rate is the limitig compressio rate Theorem For a statioary process (X i)
Iformatio Theory ad Statistics Lecture 4: Lempel-Ziv code Łukasz Dębowski ldebowsk@ipipa.waw.pl Ph. D. Programme 203/204 Etropy rate is the limitig compressio rate Theorem For a statioary process (X i)
, the random variable. and a sample size over the y-values 0:1:10.
 Lecture 3 (4//9) 000 HW PROBLEM 3(5pts) The estimatr i (c) f PROBLEM, p 000, where { } ~ iid bimial(,, is 000 e f the mst ppular statistics It is the estimatr f the ppulati prprti I PROBLEM we used simulatis
Lecture 3 (4//9) 000 HW PROBLEM 3(5pts) The estimatr i (c) f PROBLEM, p 000, where { } ~ iid bimial(,, is 000 e f the mst ppular statistics It is the estimatr f the ppulati prprti I PROBLEM we used simulatis
On small defining sets for some SBIBD(4t - 1, 2t - 1, t - 1)
 University f Wllngng Research Online Faculty f Infrmatics - Papers (Archive) Faculty f Engineering and Infrmatin Sciences 992 On small defining sets fr sme SBIBD(4t -, 2t -, t - ) Jennifer Seberry University
University f Wllngng Research Online Faculty f Infrmatics - Papers (Archive) Faculty f Engineering and Infrmatin Sciences 992 On small defining sets fr sme SBIBD(4t -, 2t -, t - ) Jennifer Seberry University
Department of Mathematics, SASTRA University, Tanjore , India
 Selçuk J. Appl. ath. Vl.. N.. pp. 7-4, Selçuk Jural f Applied athematics The Duble Sequeces N. Subramaia Departmet f athematics, SASTRA Uiversity, Tajre-63 4, Idia e-mail smaths@yah.cm Received Date Octber
Selçuk J. Appl. ath. Vl.. N.. pp. 7-4, Selçuk Jural f Applied athematics The Duble Sequeces N. Subramaia Departmet f athematics, SASTRA Uiversity, Tajre-63 4, Idia e-mail smaths@yah.cm Received Date Octber
Computational Intelligence and Application of Frame Theory in Communication Systems
 America Jural Eieeri ad Applied Scieces Oriial Research Paper Cmputatial Itelliece ad Applicati Frame Thery i Cmmuicati Systems Rajupillai, K., S. Palaiammal ad 3 K. Bmmuraju Departmet Mathematics, Gvermet
America Jural Eieeri ad Applied Scieces Oriial Research Paper Cmputatial Itelliece ad Applicati Frame Thery i Cmmuicati Systems Rajupillai, K., S. Palaiammal ad 3 K. Bmmuraju Departmet Mathematics, Gvermet
Identical Particles. We would like to move from the quantum theory of hydrogen to that for the rest of the periodic table
 We wuld like t ve fr the quatu thery f hydrge t that fr the rest f the peridic table Oe electr at t ultielectr ats This is cplicated by the iteracti f the electrs with each ther ad by the fact that the
We wuld like t ve fr the quatu thery f hydrge t that fr the rest f the peridic table Oe electr at t ultielectr ats This is cplicated by the iteracti f the electrs with each ther ad by the fact that the
Review for cumulative test
 Hrs Math 3 review prblems Jauary, 01 cumulative: Chapters 1- page 1 Review fr cumulative test O Mday, Jauary 7, Hrs Math 3 will have a curse-wide cumulative test cverig Chapters 1-. Yu ca expect the test
Hrs Math 3 review prblems Jauary, 01 cumulative: Chapters 1- page 1 Review fr cumulative test O Mday, Jauary 7, Hrs Math 3 will have a curse-wide cumulative test cverig Chapters 1-. Yu ca expect the test
NAME: Prof. Ruiz. 1. [5 points] What is the difference between simple random sampling and stratified random sampling?
![NAME: Prof. Ruiz. 1. [5 points] What is the difference between simple random sampling and stratified random sampling? NAME: Prof. Ruiz. 1. [5 points] What is the difference between simple random sampling and stratified random sampling?](/thumbs/86/94020496.jpg) CS4445 ata Mining and Kwledge iscery in atabases. B Term 2014 Exam 1 Nember 24, 2014 Prf. Carlina Ruiz epartment f Cmputer Science Wrcester Plytechnic Institute NAME: Prf. Ruiz Prblem I: Prblem II: Prblem
CS4445 ata Mining and Kwledge iscery in atabases. B Term 2014 Exam 1 Nember 24, 2014 Prf. Carlina Ruiz epartment f Cmputer Science Wrcester Plytechnic Institute NAME: Prf. Ruiz Prblem I: Prblem II: Prblem
General Chemistry 1 (CHEM1141) Shawnee State University Fall 2016
 Geeral Chemistry 1 (CHEM1141) Shawee State Uiversity Fall 2016 September 23, 2016 Name E x a m # I C Please write yur full ame, ad the exam versi (IC) that yu have the scatr sheet! Please 0 check the bx
Geeral Chemistry 1 (CHEM1141) Shawee State Uiversity Fall 2016 September 23, 2016 Name E x a m # I C Please write yur full ame, ad the exam versi (IC) that yu have the scatr sheet! Please 0 check the bx
Notes 5 : More on the a.s. convergence of sums
 Notes 5 : More o the a.s. covergece of sums Math 733-734: Theory of Probability Lecturer: Sebastie Roch Refereces: Dur0, Sectios.5; Wil9, Sectio 4.7, Shi96, Sectio IV.4, Dur0, Sectio.. Radom series. Three-series
Notes 5 : More o the a.s. covergece of sums Math 733-734: Theory of Probability Lecturer: Sebastie Roch Refereces: Dur0, Sectios.5; Wil9, Sectio 4.7, Shi96, Sectio IV.4, Dur0, Sectio.. Radom series. Three-series
Marcinkiwiecz-Zygmund Type Inequalities for all Arcs of the Circle
 Marcikiwiecz-ygmud Type Iequalities for all Arcs of the Circle C.K. Kobidarajah ad D. S. Lubisky Mathematics Departmet, Easter Uiversity, Chekalady, Sri Laka; Mathematics Departmet, Georgia Istitute of
Marcikiwiecz-ygmud Type Iequalities for all Arcs of the Circle C.K. Kobidarajah ad D. S. Lubisky Mathematics Departmet, Easter Uiversity, Chekalady, Sri Laka; Mathematics Departmet, Georgia Istitute of
IAML: Support Vector Machines
 1 / 22 IAML: Supprt Vectr Machines Charles Suttn and Victr Lavrenk Schl f Infrmatics Semester 1 2 / 22 Outline Separating hyperplane with maimum margin Nn-separable training data Epanding the input int
1 / 22 IAML: Supprt Vectr Machines Charles Suttn and Victr Lavrenk Schl f Infrmatics Semester 1 2 / 22 Outline Separating hyperplane with maimum margin Nn-separable training data Epanding the input int
ESWW-2. Israeli semi-underground great plastic scintillation multidirectional muon telescope (ISRAMUTE) for space weather monitoring and forecasting
 ESWW-2 Israeli semi-udergrud great plastic scitillati multidirectial mu telescpe (ISRAMUTE) fr space weather mitrig ad frecastig L.I. Drma a,b, L.A. Pustil'ik a, A. Sterlieb a, I.G. Zukerma a (a) Israel
ESWW-2 Israeli semi-udergrud great plastic scitillati multidirectial mu telescpe (ISRAMUTE) fr space weather mitrig ad frecastig L.I. Drma a,b, L.A. Pustil'ik a, A. Sterlieb a, I.G. Zukerma a (a) Israel
ON POINTWISE BINOMIAL APPROXIMATION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
V. Balakrishnan and S. Boyd. (To Appear in Systems and Control Letters, 1992) Abstract
 On Cmputing the WrstCase Peak Gain f Linear Systems V Balakrishnan and S Byd (T Appear in Systems and Cntrl Letters, 99) Abstract Based n the bunds due t Dyle and Byd, we present simple upper and lwer
On Cmputing the WrstCase Peak Gain f Linear Systems V Balakrishnan and S Byd (T Appear in Systems and Cntrl Letters, 99) Abstract Based n the bunds due t Dyle and Byd, we present simple upper and lwer
Department of Economics, University of California, Davis Ecn 200C Micro Theory Professor Giacomo Bonanno. Insurance Markets
 Department f Ecnmics, University f alifrnia, Davis Ecn 200 Micr Thery Prfessr Giacm Bnann Insurance Markets nsider an individual wh has an initial wealth f. ith sme prbability p he faces a lss f x (0
Department f Ecnmics, University f alifrnia, Davis Ecn 200 Micr Thery Prfessr Giacm Bnann Insurance Markets nsider an individual wh has an initial wealth f. ith sme prbability p he faces a lss f x (0
Tail Probabilities and Almost Sure Bounds for Martingales. W.L. Steiger
 Tail Prbabilities ad Almst Sure Buds fr Martigales by W.L. Steiger A thesis preseted t the Australia Natial Uiversity fr the degree f Dctr f Philsphy i the Departmet f Statistics July 1969. Statemet Uless
Tail Prbabilities ad Almst Sure Buds fr Martigales by W.L. Steiger A thesis preseted t the Australia Natial Uiversity fr the degree f Dctr f Philsphy i the Departmet f Statistics July 1969. Statemet Uless
Distributions, spatial statistics and a Bayesian perspective
 Distributins, spatial statistics and a Bayesian perspective Dug Nychka Natinal Center fr Atmspheric Research Distributins and densities Cnditinal distributins and Bayes Thm Bivariate nrmal Spatial statistics
Distributins, spatial statistics and a Bayesian perspective Dug Nychka Natinal Center fr Atmspheric Research Distributins and densities Cnditinal distributins and Bayes Thm Bivariate nrmal Spatial statistics
Internal vs. external validity. External validity. Internal validity
 Secti 7 Mdel Assessmet Iteral vs. exteral validity Iteral validity refers t whether the aalysis is valid fr the pplati ad sample beig stdied. Exteral validity refers t whether these reslts ca be geeralized
Secti 7 Mdel Assessmet Iteral vs. exteral validity Iteral validity refers t whether the aalysis is valid fr the pplati ad sample beig stdied. Exteral validity refers t whether these reslts ca be geeralized
NP-completeness for Calculating Power Indices. of Weighted Majority Games
 NP-completeess for Calculatig Power Idices of Weighted Majority Games Yasuko Matsui 3 Tomomi Matsui y (METR 98-01; Jauary 1998) Abstract: I this paper, we prove that both problems for calculatig the Bazhaf
NP-completeess for Calculatig Power Idices of Weighted Majority Games Yasuko Matsui 3 Tomomi Matsui y (METR 98-01; Jauary 1998) Abstract: I this paper, we prove that both problems for calculatig the Bazhaf
