Find an Element x in an Unsorted Array
|
|
|
- Nathan Fleming
- 6 years ago
- Views:
Transcription
1 Find an Element x in an Unsorted Array What if we try to find a lower bound for the case where the array is not necessarily sorted? J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
2 Merging Two Sorted Arrays Let A[1..n] and B[1..n] be two sorted arrays. We know how to merge A and B into one single sorted array in O(n) time. We need such an algorithm during the merge step of merge sort. J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
3 Merging Two Sorted Arrays Let A[1..n] and B[1..n] be two sorted arrays. We know how to merge A and B into one single sorted array in O(n) time. We need such an algorithm during the merge step of merge sort. Can we do better? J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
4 Merging Two Sorted Arrays Let A[1..n] and B[1..n] be two sorted arrays. We know how to merge A and B into one single sorted array in O(n) time. We need such an algorithm during the merge step of merge sort. Can we do better? No. Here is a proof of this fact. J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
5 Merging Two Sorted Arrays Let A[1..n] and B[1..n] be two sorted arrays. We know how to merge A and B into one single sorted array in O(n) time. We need such an algorithm during the merge step of merge sort. Can we do better? No. Here is a proof of this fact. Assume that it is possible to merge two sorted arrays faster than in linear time. Then, the recursion equation for merge sort becomes wherre d < 1. T (n) = 2T (n/2) + O(n d ), J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
6 Merging Two Sorted Arrays Let A[1..n] and B[1..n] be two sorted arrays. We know how to merge A and B into one single sorted array in O(n) time. We need such an algorithm during the merge step of merge sort. Can we do better? No. Here is a proof of this fact. Assume that it is possible to merge two sorted arrays faster than in linear time. Then, the recursion equation for merge sort becomes T (n) = 2T (n/2) + O(n d ), wherre d < 1. From the Master Theorem, we get T (n) = O(n). This contradicts the lower bound of Ω(n log(n)) we established for the sorting problem. J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
7 Merging Two Sorted Arrays Here is a proof using decision trees. J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
8 Merging Two Sorted Arrays Here is a proof using decision trees. First, notice that it is possible to solve this problems using only comparisons (<,, =, > or ). Hence, we can solve this problem with decision trees. J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
9 Merging Two Sorted Arrays Here is a proof using decision trees. First, notice that it is possible to solve this problems using only comparisons (<,, =, > or ). Hence, we can solve this problem with decision trees. Given two arrays A[1..n] and B[1..n], how many different outputs are there? J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
10 For instance, if n = 2, we have A[1] < A[2] and B[1] < B[2], from which the possible outputs are as follows. A[1], A[2], B[1], B[2] A[1], B[1], A[2], B[2] A[1], B[1], B[2], A[2] B[1], A[1], A[2], B[2] B[1], A[1], B[2], A[2] B[1], B[2], A[1], A[2] J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
11 For a general n, how many different outputs are there? J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
12 For a general n, how many different outputs are there? We have to fill the 2n positions of the output and make sure that the order in A is satisfied: A[1] < A[2] <... < A[n] as well as the order in B: B[1] < B[2] <... < B[n]. J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
13 For a general n, how many different outputs are there? We have to fill the 2n positions of the output and make sure that the order in A is satisfied: A[1] < A[2] <... < A[n] as well as the order in B: B[1] < B[2] <... < B[n]. One way to achieve this is to choose the n positions that will contain the elements of A and then fill the n remaining positions with the elements of B. J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
14 For a general n, how many different outputs are there? We have to fill the 2n positions of the output and make sure that the order in A is satisfied: A[1] < A[2] <... < A[n] as well as the order in B: B[1] < B[2] <... < B[n]. One way to achieve this is to choose the n positions that will contain the elements of A and then fill the n remaining positions with the elements of B. How many ways are there to choose n positions among 2n positions? J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
15 For a general n, how many different outputs are there? We have to fill the 2n positions of the output and make sure that the order in A is satisfied: A[1] < A[2] <... < A[n] as well as the order in B: B[1] < B[2] <... < B[n]. One way to achieve this is to choose the n positions that will contain the elements of A and then fill the n remaining positions with the elements of B. How many ways are there to choose n positions among 2n positions? There are ( ) 2n n ways. J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
16 For a general n, how many different outputs are there? We have to fill the 2n positions of the output and make sure that the order in A is satisfied: A[1] < A[2] <... < A[n] as well as the order in B: B[1] < B[2] <... < B[n]. One way to achieve this is to choose the n positions that will contain the elements of A and then fill the n remaining positions with the elements of B. How many ways are there to choose n positions among 2n positions? There are ( ) 2n n ways. Therefore, there are at least ( ) 2n n ( leaves in the decision tree. Therefore, the height of the tree is (2n ) ) at least log n. J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
17 From the Stirling formula, we have n! ( n ) n 2πn. e J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
18 From the Stirling formula, we have n! ( n ) n 2πn. e Hence, ( ) 2n = (2n)! n (n!) 2 ( 2π(2n) 2n ) 2n e ( ( 2πn n ) n ) 2 Stirling e = 4πn ( 2n = 4n πn 2πn ( n e ) 2n e ) 2n J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
19 from which we get (( )) 2n log n ( ( )) 4 n = Ω log πn = Ω ( n log(4) log ( π ) log(n) ) = Ω(n). J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
20 from which we get (( )) 2n log n ( ( )) 4 n = Ω log πn = Ω ( n log(4) log ( π ) log(n) ) = Ω(n). Notice that an adversarial argument would me much simpler. Do you see how to proceed? J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
21 Conclusion J.-L. De Carufel (U. of O.) Design & Analysis of Algorithms Fall / 17
CSC 8301 Design & Analysis of Algorithms: Lower Bounds
 CSC 8301 Design & Analysis of Algorithms: Lower Bounds Professor Henry Carter Fall 2016 Recap Iterative improvement algorithms take a feasible solution and iteratively improve it until optimized Simplex
CSC 8301 Design & Analysis of Algorithms: Lower Bounds Professor Henry Carter Fall 2016 Recap Iterative improvement algorithms take a feasible solution and iteratively improve it until optimized Simplex
Algorithm Analysis Recurrence Relation. Chung-Ang University, Jaesung Lee
 Algorithm Analysis Recurrence Relation Chung-Ang University, Jaesung Lee Recursion 2 Recursion 3 Recursion in Real-world Fibonacci sequence = + Initial conditions: = 0 and = 1. = + = + = + 0, 1, 1, 2,
Algorithm Analysis Recurrence Relation Chung-Ang University, Jaesung Lee Recursion 2 Recursion 3 Recursion in Real-world Fibonacci sequence = + Initial conditions: = 0 and = 1. = + = + = + 0, 1, 1, 2,
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Divide and Conquer. Recurrence Relations
 Divide and Conquer Recurrence Relations Divide-and-Conquer Strategy: Break up problem into parts. Solve each part recursively. Combine solutions to sub-problems into overall solution. 2 MergeSort Mergesort.
Divide and Conquer Recurrence Relations Divide-and-Conquer Strategy: Break up problem into parts. Solve each part recursively. Combine solutions to sub-problems into overall solution. 2 MergeSort Mergesort.
Sorting algorithms. Sorting algorithms
 Properties of sorting algorithms A sorting algorithm is Comparison based If it works by pairwise key comparisons. In place If only a constant number of elements of the input array are ever stored outside
Properties of sorting algorithms A sorting algorithm is Comparison based If it works by pairwise key comparisons. In place If only a constant number of elements of the input array are ever stored outside
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Asymptotic Analysis, recurrences Date: 9/7/17
 601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Asymptotic Analysis, recurrences Date: 9/7/17 2.1 Notes Homework 1 will be released today, and is due a week from today by the beginning
601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Asymptotic Analysis, recurrences Date: 9/7/17 2.1 Notes Homework 1 will be released today, and is due a week from today by the beginning
CSC 421: Algorithm Design & Analysis. Spring 2015
 CSC 421: Algorithm Design & Analysis Spring 2015 Complexity & lower bounds brute force decision trees adversary arguments problem reduction 1 Lower bounds on problems when studying a problem, may wish
CSC 421: Algorithm Design & Analysis Spring 2015 Complexity & lower bounds brute force decision trees adversary arguments problem reduction 1 Lower bounds on problems when studying a problem, may wish
Limitations of Algorithm Power
 Limitations of Algorithm Power Objectives We now move into the third and final major theme for this course. 1. Tools for analyzing algorithms. 2. Design strategies for designing algorithms. 3. Identifying
Limitations of Algorithm Power Objectives We now move into the third and final major theme for this course. 1. Tools for analyzing algorithms. 2. Design strategies for designing algorithms. 3. Identifying
Outline. 1 Merging. 2 Merge Sort. 3 Complexity of Sorting. 4 Merge Sort and Other Sorts 2 / 10
 Merge Sort 1 / 10 Outline 1 Merging 2 Merge Sort 3 Complexity of Sorting 4 Merge Sort and Other Sorts 2 / 10 Merging Merge sort is based on a simple operation known as merging: combining two ordered arrays
Merge Sort 1 / 10 Outline 1 Merging 2 Merge Sort 3 Complexity of Sorting 4 Merge Sort and Other Sorts 2 / 10 Merging Merge sort is based on a simple operation known as merging: combining two ordered arrays
Module 1: Analyzing the Efficiency of Algorithms
 Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu What is an Algorithm?
Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu What is an Algorithm?
CSE 591 Homework 3 Sample Solutions. Problem 1
 CSE 591 Homework 3 Sample Solutions Problem 1 (a) Let p = max{1, k d}, q = min{n, k + d}, it suffices to find the pth and qth largest element of L and output all elements in the range between these two
CSE 591 Homework 3 Sample Solutions Problem 1 (a) Let p = max{1, k d}, q = min{n, k + d}, it suffices to find the pth and qth largest element of L and output all elements in the range between these two
Algorithms and Their Complexity
 CSCE 222 Discrete Structures for Computing David Kebo Houngninou Algorithms and Their Complexity Chapter 3 Algorithm An algorithm is a finite sequence of steps that solves a problem. Computational complexity
CSCE 222 Discrete Structures for Computing David Kebo Houngninou Algorithms and Their Complexity Chapter 3 Algorithm An algorithm is a finite sequence of steps that solves a problem. Computational complexity
CIS 121. Analysis of Algorithms & Computational Complexity. Slides based on materials provided by Mary Wootters (Stanford University)
 CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018
 CS17 Integrated Introduction to Computer Science Klein Contents Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018 1 Tree definitions 1 2 Analysis of mergesort using a binary tree 1 3 Analysis of
CS17 Integrated Introduction to Computer Science Klein Contents Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018 1 Tree definitions 1 2 Analysis of mergesort using a binary tree 1 3 Analysis of
Fast Convolution; Strassen s Method
 Fast Convolution; Strassen s Method 1 Fast Convolution reduction to subquadratic time polynomial evaluation at complex roots of unity interpolation via evaluation at complex roots of unity 2 The Master
Fast Convolution; Strassen s Method 1 Fast Convolution reduction to subquadratic time polynomial evaluation at complex roots of unity interpolation via evaluation at complex roots of unity 2 The Master
Data Structures and Algorithms Chapter 3
 Data Structures and Algorithms Chapter 3 1. Divide and conquer 2. Merge sort, repeated substitutions 3. Tiling 4. Recurrences Recurrences Running times of algorithms with recursive calls can be described
Data Structures and Algorithms Chapter 3 1. Divide and conquer 2. Merge sort, repeated substitutions 3. Tiling 4. Recurrences Recurrences Running times of algorithms with recursive calls can be described
Solving recurrences. Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms.
 Solving recurrences Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms Example: Merge-Sort(A, p, r) 1: if p < r then 2: q (p + r)/2 3: Merge-Sort(A,
Solving recurrences Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms Example: Merge-Sort(A, p, r) 1: if p < r then 2: q (p + r)/2 3: Merge-Sort(A,
Asymptotic Analysis. Slides by Carl Kingsford. Jan. 27, AD Chapter 2
 Asymptotic Analysis Slides by Carl Kingsford Jan. 27, 2014 AD Chapter 2 Independent Set Definition (Independent Set). Given a graph G = (V, E) an independent set is a set S V if no two nodes in S are joined
Asymptotic Analysis Slides by Carl Kingsford Jan. 27, 2014 AD Chapter 2 Independent Set Definition (Independent Set). Given a graph G = (V, E) an independent set is a set S V if no two nodes in S are joined
Divide and Conquer. Andreas Klappenecker
 Divide and Conquer Andreas Klappenecker The Divide and Conquer Paradigm The divide and conquer paradigm is important general technique for designing algorithms. In general, it follows the steps: - divide
Divide and Conquer Andreas Klappenecker The Divide and Conquer Paradigm The divide and conquer paradigm is important general technique for designing algorithms. In general, it follows the steps: - divide
Computational Complexity
 Computational Complexity S. V. N. Vishwanathan, Pinar Yanardag January 8, 016 1 Computational Complexity: What, Why, and How? Intuitively an algorithm is a well defined computational procedure that takes
Computational Complexity S. V. N. Vishwanathan, Pinar Yanardag January 8, 016 1 Computational Complexity: What, Why, and How? Intuitively an algorithm is a well defined computational procedure that takes
Data structures Exercise 1 solution. Question 1. Let s start by writing all the functions in big O notation:
 Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
Selection and Adversary Arguments. COMP 215 Lecture 19
 Selection and Adversary Arguments COMP 215 Lecture 19 Selection Problems We want to find the k'th largest entry in an unsorted array. Could be the largest, smallest, median, etc. Ideas for an n lg n algorithm?
Selection and Adversary Arguments COMP 215 Lecture 19 Selection Problems We want to find the k'th largest entry in an unsorted array. Could be the largest, smallest, median, etc. Ideas for an n lg n algorithm?
Computer Science 385 Analysis of Algorithms Siena College Spring Topic Notes: Limitations of Algorithms
 Computer Science 385 Analysis of Algorithms Siena College Spring 2011 Topic Notes: Limitations of Algorithms We conclude with a discussion of the limitations of the power of algorithms. That is, what kinds
Computer Science 385 Analysis of Algorithms Siena College Spring 2011 Topic Notes: Limitations of Algorithms We conclude with a discussion of the limitations of the power of algorithms. That is, what kinds
Recap & Interval Scheduling
 Lecture 2 Recap & Interval Scheduling Supplemental reading in CLRS: Section 6.; Section 4.4 2. Recap of Median Finding Like MERGE-SORT, the median-of-medians algorithm SELECT calls itself recursively,
Lecture 2 Recap & Interval Scheduling Supplemental reading in CLRS: Section 6.; Section 4.4 2. Recap of Median Finding Like MERGE-SORT, the median-of-medians algorithm SELECT calls itself recursively,
CS 5321: Advanced Algorithms - Recurrence. Acknowledgement. Outline. Ali Ebnenasir Department of Computer Science Michigan Technological University
 CS 5321: Advanced Algorithms - Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating example:
CS 5321: Advanced Algorithms - Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating example:
Sorting Algorithms. We have already seen: Selection-sort Insertion-sort Heap-sort. We will see: Bubble-sort Merge-sort Quick-sort
 Sorting Algorithms We have already seen: Selection-sort Insertion-sort Heap-sort We will see: Bubble-sort Merge-sort Quick-sort We will show that: O(n log n) is optimal for comparison based sorting. Bubble-Sort
Sorting Algorithms We have already seen: Selection-sort Insertion-sort Heap-sort We will see: Bubble-sort Merge-sort Quick-sort We will show that: O(n log n) is optimal for comparison based sorting. Bubble-Sort
Analysis of Algorithms - Using Asymptotic Bounds -
 Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
CS 161 Summer 2009 Homework #2 Sample Solutions
 CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS 5321: Advanced Algorithms Analysis Using Recurrence. Acknowledgement. Outline
 CS 5321: Advanced Algorithms Analysis Using Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating
CS 5321: Advanced Algorithms Analysis Using Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating
Data selection. Lower complexity bound for sorting
 Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
1 Terminology and setup
 15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
In-Class Soln 1. CS 361, Lecture 4. Today s Outline. In-Class Soln 2
 In-Class Soln 1 Let f(n) be an always positive function and let g(n) = f(n) log n. Show that f(n) = o(g(n)) CS 361, Lecture 4 Jared Saia University of New Mexico For any positive constant c, we want to
In-Class Soln 1 Let f(n) be an always positive function and let g(n) = f(n) log n. Show that f(n) = o(g(n)) CS 361, Lecture 4 Jared Saia University of New Mexico For any positive constant c, we want to
b + O(n d ) where a 1, b > 1, then O(n d log n) if a = b d d ) if a < b d O(n log b a ) if a > b d
 CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
CSE101: Design and Analysis of Algorithms. Ragesh Jaiswal, CSE, UCSD
 Greedy s Greedy s Shortest path Claim 2: Let S be a subset of vertices containing s such that we know the shortest path length l(s, u) from s to any vertex in u S. Let e = (u, v) be an edge such that 1
Greedy s Greedy s Shortest path Claim 2: Let S be a subset of vertices containing s such that we know the shortest path length l(s, u) from s to any vertex in u S. Let e = (u, v) be an edge such that 1
CS173 Running Time and Big-O. Tandy Warnow
 CS173 Running Time and Big-O Tandy Warnow CS 173 Running Times and Big-O analysis Tandy Warnow Today s material We will cover: Running time analysis Review of running time analysis of Bubblesort Review
CS173 Running Time and Big-O Tandy Warnow CS 173 Running Times and Big-O analysis Tandy Warnow Today s material We will cover: Running time analysis Review of running time analysis of Bubblesort Review
Divide and Conquer. Arash Rafiey. 27 October, 2016
 27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
V. Adamchik 1. Recurrences. Victor Adamchik Fall of 2005
 V. Adamchi Recurrences Victor Adamchi Fall of 00 Plan Multiple roots. More on multiple roots. Inhomogeneous equations 3. Divide-and-conquer recurrences In the previous lecture we have showed that if the
V. Adamchi Recurrences Victor Adamchi Fall of 00 Plan Multiple roots. More on multiple roots. Inhomogeneous equations 3. Divide-and-conquer recurrences In the previous lecture we have showed that if the
Design and Analysis of Algorithms
 CSE 101, Winter 2018 Design and Analysis of Algorithms Lecture 5: Divide and Conquer (Part 2) Class URL: http://vlsicad.ucsd.edu/courses/cse101-w18/ A Lower Bound on Convex Hull Lecture 4 Task: sort the
CSE 101, Winter 2018 Design and Analysis of Algorithms Lecture 5: Divide and Conquer (Part 2) Class URL: http://vlsicad.ucsd.edu/courses/cse101-w18/ A Lower Bound on Convex Hull Lecture 4 Task: sort the
Big , and Definition Definition
 Big O, Ω, and Θ Big-O gives us only a one-way comparison; if f is O(g) then g eventually is bigger than f from that point on, but in fact f could be very small in comparison. Example; 3n is O(2 2n ). We
Big O, Ω, and Θ Big-O gives us only a one-way comparison; if f is O(g) then g eventually is bigger than f from that point on, but in fact f could be very small in comparison. Example; 3n is O(2 2n ). We
IS 709/809: Computational Methods in IS Research Fall Exam Review
 IS 709/809: Computational Methods in IS Research Fall 2017 Exam Review Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Exam When: Tuesday (11/28) 7:10pm
IS 709/809: Computational Methods in IS Research Fall 2017 Exam Review Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Exam When: Tuesday (11/28) 7:10pm
Divide & Conquer. CS 320, Fall Dr. Geri Georg, Instructor CS320 Div&Conq 1
 Divide & Conquer CS 320, Fall 2017 Dr. Geri Georg, Instructor georg@colostate.edu CS320 Div&Conq 1 Strategy 1. Divide the problem up into equal sized sub problems 2. Solve the sub problems recursively
Divide & Conquer CS 320, Fall 2017 Dr. Geri Georg, Instructor georg@colostate.edu CS320 Div&Conq 1 Strategy 1. Divide the problem up into equal sized sub problems 2. Solve the sub problems recursively
1 Substitution method
 Recurrence Relations we have discussed asymptotic analysis of algorithms and various properties associated with asymptotic notation. As many algorithms are recursive in nature, it is natural to analyze
Recurrence Relations we have discussed asymptotic analysis of algorithms and various properties associated with asymptotic notation. As many algorithms are recursive in nature, it is natural to analyze
CS 350 Algorithms and Complexity
 1 CS 350 Algorithms and Complexity Fall 2015 Lecture 15: Limitations of Algorithmic Power Introduction to complexity theory Andrew P. Black Department of Computer Science Portland State University Lower
1 CS 350 Algorithms and Complexity Fall 2015 Lecture 15: Limitations of Algorithmic Power Introduction to complexity theory Andrew P. Black Department of Computer Science Portland State University Lower
Module 1: Analyzing the Efficiency of Algorithms
 Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Based
Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Based
When we use asymptotic notation within an expression, the asymptotic notation is shorthand for an unspecified function satisfying the relation:
 CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
Algorithms and Data Structures 2016 Week 5 solutions (Tues 9th - Fri 12th February)
 Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
Data Structures and Algorithms CSE 465
 Data Structures and Algorithms CSE 465 LECTURE 3 Asymptotic Notation O-, Ω-, Θ-, o-, ω-notation Divide and Conquer Merge Sort Binary Search Sofya Raskhodnikova and Adam Smith /5/0 Review Questions If input
Data Structures and Algorithms CSE 465 LECTURE 3 Asymptotic Notation O-, Ω-, Θ-, o-, ω-notation Divide and Conquer Merge Sort Binary Search Sofya Raskhodnikova and Adam Smith /5/0 Review Questions If input
Data Structures and Algorithms CMPSC 465
 Data Structures and Algorithms CMPSC 465 LECTURE 9 Solving recurrences Substitution method Adam Smith S. Raskhodnikova and A. Smith; based on slides by E. Demaine and C. Leiserson Review question Draw
Data Structures and Algorithms CMPSC 465 LECTURE 9 Solving recurrences Substitution method Adam Smith S. Raskhodnikova and A. Smith; based on slides by E. Demaine and C. Leiserson Review question Draw
1 Quick Sort LECTURE 7. OHSU/OGI (Winter 2009) ANALYSIS AND DESIGN OF ALGORITHMS
 OHSU/OGI (Winter 2009) CS532 ANALYSIS AND DESIGN OF ALGORITHMS LECTURE 7 1 Quick Sort QuickSort 1 is a classic example of divide and conquer. The hard work is to rearrange the elements of the array A[1..n]
OHSU/OGI (Winter 2009) CS532 ANALYSIS AND DESIGN OF ALGORITHMS LECTURE 7 1 Quick Sort QuickSort 1 is a classic example of divide and conquer. The hard work is to rearrange the elements of the array A[1..n]
Concrete models and tight upper/lower bounds
 Lecture 3 Concrete models and tight upper/lower bounds 3.1 Overview In this lecture, we will examine some simple, concrete models of computation, each with a precise definition of what counts as a step,
Lecture 3 Concrete models and tight upper/lower bounds 3.1 Overview In this lecture, we will examine some simple, concrete models of computation, each with a precise definition of what counts as a step,
Divide and Conquer Algorithms. CSE 101: Design and Analysis of Algorithms Lecture 14
 Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
CS325: Analysis of Algorithms, Fall Midterm
 CS325: Analysis of Algorithms, Fall 2017 Midterm I don t know policy: you may write I don t know and nothing else to answer a question and receive 25 percent of the total points for that problem whereas
CS325: Analysis of Algorithms, Fall 2017 Midterm I don t know policy: you may write I don t know and nothing else to answer a question and receive 25 percent of the total points for that problem whereas
More Asymptotic Analysis Spring 2018 Discussion 8: March 6, 2018
 CS 61B More Asymptotic Analysis Spring 2018 Discussion 8: March 6, 2018 Here is a review of some formulas that you will find useful when doing asymptotic analysis. ˆ N i=1 i = 1 + 2 + 3 + 4 + + N = N(N+1)
CS 61B More Asymptotic Analysis Spring 2018 Discussion 8: March 6, 2018 Here is a review of some formulas that you will find useful when doing asymptotic analysis. ˆ N i=1 i = 1 + 2 + 3 + 4 + + N = N(N+1)
Grade 11/12 Math Circles Fall Nov. 5 Recurrences, Part 2
 1 Faculty of Mathematics Waterloo, Ontario Centre for Education in Mathematics and Computing Grade 11/12 Math Circles Fall 2014 - Nov. 5 Recurrences, Part 2 Running time of algorithms In computer science,
1 Faculty of Mathematics Waterloo, Ontario Centre for Education in Mathematics and Computing Grade 11/12 Math Circles Fall 2014 - Nov. 5 Recurrences, Part 2 Running time of algorithms In computer science,
Computational Complexity - Pseudocode and Recursions
 Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
Design Patterns for Data Structures. Chapter 3. Recursive Algorithms
 Chapter 3 Recursive Algorithms Writing recurrences + Writing recurrences To determine the statement execution count is a two-step problem. Write down the recurrence from the recursive code for the algorithm.
Chapter 3 Recursive Algorithms Writing recurrences + Writing recurrences To determine the statement execution count is a two-step problem. Write down the recurrence from the recursive code for the algorithm.
CS 344 Design and Analysis of Algorithms. Tarek El-Gaaly Course website:
 CS 344 Design and Analysis of Algorithms Tarek El-Gaaly tgaaly@cs.rutgers.edu Course website: www.cs.rutgers.edu/~tgaaly/cs344.html Course Outline Textbook: Algorithms by S. Dasgupta, C.H. Papadimitriou,
CS 344 Design and Analysis of Algorithms Tarek El-Gaaly tgaaly@cs.rutgers.edu Course website: www.cs.rutgers.edu/~tgaaly/cs344.html Course Outline Textbook: Algorithms by S. Dasgupta, C.H. Papadimitriou,
Algorithm Analysis, Asymptotic notations CISC4080 CIS, Fordham Univ. Instructor: X. Zhang
 Algorithm Analysis, Asymptotic notations CISC4080 CIS, Fordham Univ. Instructor: X. Zhang Last class Introduction to algorithm analysis: fibonacci seq calculation counting number of computer steps recursive
Algorithm Analysis, Asymptotic notations CISC4080 CIS, Fordham Univ. Instructor: X. Zhang Last class Introduction to algorithm analysis: fibonacci seq calculation counting number of computer steps recursive
Algorithms Test 1. Question 1. (10 points) for (i = 1; i <= n; i++) { j = 1; while (j < n) {
 Question 1. (10 points) for (i = 1; i
Question 1. (10 points) for (i = 1; i
CPSC 320 (Intermediate Algorithm Design and Analysis). Summer Instructor: Dr. Lior Malka Final Examination, July 24th, 2009
 CPSC 320 (Intermediate Algorithm Design and Analysis). Summer 2009. Instructor: Dr. Lior Malka Final Examination, July 24th, 2009 Student ID: INSTRUCTIONS: There are 6 questions printed on pages 1 7. Exam
CPSC 320 (Intermediate Algorithm Design and Analysis). Summer 2009. Instructor: Dr. Lior Malka Final Examination, July 24th, 2009 Student ID: INSTRUCTIONS: There are 6 questions printed on pages 1 7. Exam
CS483 Design and Analysis of Algorithms
 CS483 Design and Analysis of Algorithms Chapter 2 Divide and Conquer Algorithms Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: Room 5326, Engineering Building, Thursday 4:30pm -
CS483 Design and Analysis of Algorithms Chapter 2 Divide and Conquer Algorithms Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: Room 5326, Engineering Building, Thursday 4:30pm -
A point p is said to be dominated by point q if p.x=q.x&p.y=q.y 2 true. In RAM computation model, RAM stands for Random Access Model.
 In analysis the upper bound means the function grows asymptotically no faster than its largest term. 1 true A point p is said to be dominated by point q if p.x=q.x&p.y=q.y 2 true In RAM computation model,
In analysis the upper bound means the function grows asymptotically no faster than its largest term. 1 true A point p is said to be dominated by point q if p.x=q.x&p.y=q.y 2 true In RAM computation model,
Design and Analysis of Algorithms
 CSE 101, Winter 2018 Design and Analysis of Algorithms Lecture 4: Divide and Conquer (I) Class URL: http://vlsicad.ucsd.edu/courses/cse101-w18/ Divide and Conquer ( DQ ) First paradigm or framework DQ(S)
CSE 101, Winter 2018 Design and Analysis of Algorithms Lecture 4: Divide and Conquer (I) Class URL: http://vlsicad.ucsd.edu/courses/cse101-w18/ Divide and Conquer ( DQ ) First paradigm or framework DQ(S)
Exercise Sheet #1 Solutions, Computer Science, A M. Hallett, K. Smith a k n b k = n b + k. a k n b k c 1 n b k. a k n b.
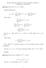 Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
15.1 Introduction to Lower Bounds Proofs
 15 Lower Bounds How do I know if I have a good algorithm to solve a problem? If my algorithm runs in Θ(n log n) time, is that good? It would be if I were sorting the records stored in an array. But it
15 Lower Bounds How do I know if I have a good algorithm to solve a problem? If my algorithm runs in Θ(n log n) time, is that good? It would be if I were sorting the records stored in an array. But it
Data Structures and Algorithm Analysis (CSC317) Randomized Algorithms (part 3)
 Data Structures and Algorithm Analysis (CSC317) Randomized Algorithms (part 3) Quicksort p r Quicksort(A, p, r) 1. If p
Data Structures and Algorithm Analysis (CSC317) Randomized Algorithms (part 3) Quicksort p r Quicksort(A, p, r) 1. If p
Outline. 1 Introduction. Merging and MergeSort. 3 Analysis. 4 Reference
 Outline Computer Science 331 Sort Mike Jacobson Department of Computer Science University of Calgary Lecture #25 1 Introduction 2 Merging and 3 4 Reference Mike Jacobson (University of Calgary) Computer
Outline Computer Science 331 Sort Mike Jacobson Department of Computer Science University of Calgary Lecture #25 1 Introduction 2 Merging and 3 4 Reference Mike Jacobson (University of Calgary) Computer
Objective. - mathematical induction, recursive definitions - arithmetic manipulations, series, products
 Recurrences Objective running time as recursive function solve recurrence for order of growth method: substitution method: iteration/recursion tree method: MASTER method prerequisite: - mathematical induction,
Recurrences Objective running time as recursive function solve recurrence for order of growth method: substitution method: iteration/recursion tree method: MASTER method prerequisite: - mathematical induction,
Fundamental Algorithms
 Chapter 2: Sorting, Winter 2018/19 1 Fundamental Algorithms Chapter 2: Sorting Jan Křetínský Winter 2018/19 Chapter 2: Sorting, Winter 2018/19 2 Part I Simple Sorts Chapter 2: Sorting, Winter 2018/19 3
Chapter 2: Sorting, Winter 2018/19 1 Fundamental Algorithms Chapter 2: Sorting Jan Křetínský Winter 2018/19 Chapter 2: Sorting, Winter 2018/19 2 Part I Simple Sorts Chapter 2: Sorting, Winter 2018/19 3
Fundamental Algorithms
 Fundamental Algorithms Chapter 2: Sorting Harald Räcke Winter 2015/16 Chapter 2: Sorting, Winter 2015/16 1 Part I Simple Sorts Chapter 2: Sorting, Winter 2015/16 2 The Sorting Problem Definition Sorting
Fundamental Algorithms Chapter 2: Sorting Harald Räcke Winter 2015/16 Chapter 2: Sorting, Winter 2015/16 1 Part I Simple Sorts Chapter 2: Sorting, Winter 2015/16 2 The Sorting Problem Definition Sorting
Asymptotic Analysis and Recurrences
 Appendix A Asymptotic Analysis and Recurrences A.1 Overview We discuss the notion of asymptotic analysis and introduce O, Ω, Θ, and o notation. We then turn to the topic of recurrences, discussing several
Appendix A Asymptotic Analysis and Recurrences A.1 Overview We discuss the notion of asymptotic analysis and introduce O, Ω, Θ, and o notation. We then turn to the topic of recurrences, discussing several
A SUMMARY OF RECURSION SOLVING TECHNIQUES
 A SUMMARY OF RECURSION SOLVING TECHNIQUES KIMMO ERIKSSON, KTH These notes are meant to be a complement to the material on recursion solving techniques in the textbook Discrete Mathematics by Biggs. In
A SUMMARY OF RECURSION SOLVING TECHNIQUES KIMMO ERIKSSON, KTH These notes are meant to be a complement to the material on recursion solving techniques in the textbook Discrete Mathematics by Biggs. In
When we use asymptotic notation within an expression, the asymptotic notation is shorthand for an unspecified function satisfying the relation:
 CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
The Divide-and-Conquer Design Paradigm
 CS473- Algorithms I Lecture 4 The Divide-and-Conquer Design Paradigm CS473 Lecture 4 1 The Divide-and-Conquer Design Paradigm 1. Divide the problem (instance) into subproblems. 2. Conquer the subproblems
CS473- Algorithms I Lecture 4 The Divide-and-Conquer Design Paradigm CS473 Lecture 4 1 The Divide-and-Conquer Design Paradigm 1. Divide the problem (instance) into subproblems. 2. Conquer the subproblems
CSCI Honor seminar in algorithms Homework 2 Solution
 CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
Introduction to Algorithms: Asymptotic Notation
 Introduction to Algorithms: Asymptotic Notation Why Should We Care? (Order of growth) CS 421 - Analysis of Algorithms 2 Asymptotic Notation O-notation (upper bounds): that 0 f(n) cg(n) for all n n. 0 CS
Introduction to Algorithms: Asymptotic Notation Why Should We Care? (Order of growth) CS 421 - Analysis of Algorithms 2 Asymptotic Notation O-notation (upper bounds): that 0 f(n) cg(n) for all n n. 0 CS
Chapter 2. Recurrence Relations. Divide and Conquer. Divide and Conquer Strategy. Another Example: Merge Sort. Merge Sort Example. Merge Sort Example
 Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
What we have learned What is algorithm Why study algorithm The time and space efficiency of algorithm The analysis framework of time efficiency Asympt
 Lecture 3 The Analysis of Recursive Algorithm Efficiency What we have learned What is algorithm Why study algorithm The time and space efficiency of algorithm The analysis framework of time efficiency
Lecture 3 The Analysis of Recursive Algorithm Efficiency What we have learned What is algorithm Why study algorithm The time and space efficiency of algorithm The analysis framework of time efficiency
2.2 Asymptotic Order of Growth. definitions and notation (2.2) examples (2.4) properties (2.2)
 2.2 Asymptotic Order of Growth definitions and notation (2.2) examples (2.4) properties (2.2) Asymptotic Order of Growth Upper bounds. T(n) is O(f(n)) if there exist constants c > 0 and n 0 0 such that
2.2 Asymptotic Order of Growth definitions and notation (2.2) examples (2.4) properties (2.2) Asymptotic Order of Growth Upper bounds. T(n) is O(f(n)) if there exist constants c > 0 and n 0 0 such that
Space Complexity of Algorithms
 Space Complexity of Algorithms So far we have considered only the time necessary for a computation Sometimes the size of the memory necessary for the computation is more critical. The amount of memory
Space Complexity of Algorithms So far we have considered only the time necessary for a computation Sometimes the size of the memory necessary for the computation is more critical. The amount of memory
Lecture 3. Big-O notation, more recurrences!!
 Lecture 3 Big-O notation, more recurrences!! Announcements! HW1 is posted! (Due Friday) See Piazza for a list of HW clarifications First recitation section was this morning, there s another tomorrow (same
Lecture 3 Big-O notation, more recurrences!! Announcements! HW1 is posted! (Due Friday) See Piazza for a list of HW clarifications First recitation section was this morning, there s another tomorrow (same
Insertion Sort. We take the first element: 34 is sorted
 Insertion Sort Idea: by Ex Given the following sequence to be sorted 34 8 64 51 32 21 When the elements 1, p are sorted, then the next element, p+1 is inserted within these to the right place after some
Insertion Sort Idea: by Ex Given the following sequence to be sorted 34 8 64 51 32 21 When the elements 1, p are sorted, then the next element, p+1 is inserted within these to the right place after some
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
Divide-and-Conquer and Recurrence Relations: Notes on Chapter 2, Dasgupta et.al. Howard A. Blair
 Divide-and-Conquer and Recurrence Relations: Notes on Chapter 2, Dasgupta et.al. Howard A. Blair 1 Multiplication Example 1.1: Carl Friedrich Gauss (1777-1855): The multiplication of two complex numbers
Divide-and-Conquer and Recurrence Relations: Notes on Chapter 2, Dasgupta et.al. Howard A. Blair 1 Multiplication Example 1.1: Carl Friedrich Gauss (1777-1855): The multiplication of two complex numbers
Divide and Conquer CPE 349. Theresa Migler-VonDollen
 Divide and Conquer CPE 349 Theresa Migler-VonDollen Divide and Conquer Divide and Conquer is a strategy that solves a problem by: 1 Breaking the problem into subproblems that are themselves smaller instances
Divide and Conquer CPE 349 Theresa Migler-VonDollen Divide and Conquer Divide and Conquer is a strategy that solves a problem by: 1 Breaking the problem into subproblems that are themselves smaller instances
Methods for solving recurrences
 Methods for solving recurrences Analyzing the complexity of mergesort The merge function Consider the following implementation: 1 int merge ( int v1, int n1, int v, int n ) { 3 int r = malloc ( ( n1+n
Methods for solving recurrences Analyzing the complexity of mergesort The merge function Consider the following implementation: 1 int merge ( int v1, int n1, int v, int n ) { 3 int r = malloc ( ( n1+n
CS 61B Asymptotic Analysis Fall 2017
 CS 61B Asymptotic Analysis Fall 2017 1 More Running Time Give the worst case and best case running time in Θ( ) notation in terms of M and N. (a) Assume that slam() Θ(1) and returns a boolean. 1 public
CS 61B Asymptotic Analysis Fall 2017 1 More Running Time Give the worst case and best case running time in Θ( ) notation in terms of M and N. (a) Assume that slam() Θ(1) and returns a boolean. 1 public
CMPS 2200 Fall Divide-and-Conquer. Carola Wenk. Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk
 CMPS 2200 Fall 2017 Divide-and-Conquer Carola Wenk Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk 1 The divide-and-conquer design paradigm 1. Divide the problem (instance)
CMPS 2200 Fall 2017 Divide-and-Conquer Carola Wenk Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk 1 The divide-and-conquer design paradigm 1. Divide the problem (instance)
Divide and Conquer. Andreas Klappenecker. [based on slides by Prof. Welch]
![Divide and Conquer. Andreas Klappenecker. [based on slides by Prof. Welch] Divide and Conquer. Andreas Klappenecker. [based on slides by Prof. Welch]](/thumbs/84/89083836.jpg) Divide and Conquer Andreas Klappenecker [based on slides by Prof. Welch] Divide and Conquer Paradigm An important general technique for designing algorithms: divide problem into subproblems recursively
Divide and Conquer Andreas Klappenecker [based on slides by Prof. Welch] Divide and Conquer Paradigm An important general technique for designing algorithms: divide problem into subproblems recursively
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
University of Toronto Department of Electrical and Computer Engineering. Final Examination. ECE 345 Algorithms and Data Structures Fall 2016
 University of Toronto Department of Electrical and Computer Engineering Final Examination ECE 345 Algorithms and Data Structures Fall 2016 Print your first name, last name, UTORid, and student number neatly
University of Toronto Department of Electrical and Computer Engineering Final Examination ECE 345 Algorithms and Data Structures Fall 2016 Print your first name, last name, UTORid, and student number neatly
ITEC2620 Introduction to Data Structures
 ITEC2620 Introduction to Data Structures Lecture 6a Complexity Analysis Recursive Algorithms Complexity Analysis Determine how the processing time of an algorithm grows with input size What if the algorithm
ITEC2620 Introduction to Data Structures Lecture 6a Complexity Analysis Recursive Algorithms Complexity Analysis Determine how the processing time of an algorithm grows with input size What if the algorithm
Divide and Conquer Strategy
 Divide and Conquer Strategy Algorithm design is more an art, less so a science. There are a few useful strategies, but no guarantee to succeed. We will discuss: Divide and Conquer, Greedy, Dynamic Programming.
Divide and Conquer Strategy Algorithm design is more an art, less so a science. There are a few useful strategies, but no guarantee to succeed. We will discuss: Divide and Conquer, Greedy, Dynamic Programming.
Agenda. We ve discussed
 Agenda We ve discussed Now Next C++ basics Some built-in data structures and their applications: stack, map, vector, array The Fibonacci example showing the importance of good algorithms and asymptotic
Agenda We ve discussed Now Next C++ basics Some built-in data structures and their applications: stack, map, vector, array The Fibonacci example showing the importance of good algorithms and asymptotic
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort
 Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
CS483 Design and Analysis of Algorithms
 CS483 Design and Analysis of Algorithms Lecture 6-8 Divide and Conquer Algorithms Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: STII, Room 443, Friday 4:00pm - 6:00pm or by appointments
CS483 Design and Analysis of Algorithms Lecture 6-8 Divide and Conquer Algorithms Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: STII, Room 443, Friday 4:00pm - 6:00pm or by appointments
Divide and Conquer Algorithms
 Divide and Conquer Algorithms T. M. Murali February 19, 2013 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
Divide and Conquer Algorithms T. M. Murali February 19, 2013 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
Bucket-Sort. Have seen lower bound of Ω(nlog n) for comparisonbased. Some cheating algorithms achieve O(n), given certain assumptions re input
 Bucket-Sort Have seen lower bound of Ω(nlog n) for comparisonbased sorting algs Some cheating algorithms achieve O(n), given certain assumptions re input One example: bucket sort Assumption: input numbers
Bucket-Sort Have seen lower bound of Ω(nlog n) for comparisonbased sorting algs Some cheating algorithms achieve O(n), given certain assumptions re input One example: bucket sort Assumption: input numbers
Data Structures and Algorithms Chapter 3
 1 Data Structures and Algorithms Chapter 3 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
1 Data Structures and Algorithms Chapter 3 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
Lower and Upper Bound Theory
 Lower and Upper Bound Theory Adnan YAZICI Dept. of Computer Engineering Middle East Technical Univ. Ankara - TURKEY 1 Lower and Upper Bound Theory How fast can we sort? Most of the sorting algorithms are
Lower and Upper Bound Theory Adnan YAZICI Dept. of Computer Engineering Middle East Technical Univ. Ankara - TURKEY 1 Lower and Upper Bound Theory How fast can we sort? Most of the sorting algorithms are
