Problem 5. Use mathematical induction to show that when n is an exact power of two, the solution of the recurrence
|
|
|
- Madeleine Washington
- 6 years ago
- Views:
Transcription
1 A. V. Gerbessiotis CS Spring 2014 PS 1 Jan 27, 2014 No points For the remainder of the course Give an algorithm means: describe an algorithm, show that it works as claimed, analyze its worst-case running time and give the expression for its worst-case running time. For mosts of the problems solutions are provided. Problem 1. (a How many bits do we need to minimally represent 2 m 1? How many for 2 m 1? How many for all integers between 2 m 1 and 2 m 1? Express the answer as a function of m. (b Use the result from (a to show that every positive integer L can be represented by lg (L + 1 bits. Problem 2. You are given the following function definition in pseudo C++/C. How much is f(91? How much is f(92? How much is f(99? How much is f(100? Explain. int f(int x // x is integer return( (x>100? (x-10 : f(f(x+11 ; Problem. Consider a modification of merge-sort in which out of n keys n/k subsequences of length k are formed and each one is sorted by insertion sort and then all subsequences are merged. The optimal k will be determined after analyzing the worst case performance of the algorithm. In other words, this new algorithm works as follows. (i Form n/k subsequences each of length k. Sort each one with insertion sort. What is the total (worst-case running time for sorting all k subsequences using insertion sort in asymptotic notation? Explain. (ii The k-long sorted subsequences can then be merged in Θ(n lg (n/k time. Show how. (iii Show that the (worst-case running time of the whole algorithm (steps (i and (ii is O(nk + n lg (n/k. (iv What is the (asymptotically largest value of k for which this algorithm is as good as merge-sort? Explain. Problem 4. Can you sort 4 keys such as a, b, c, d with at most 5 comparisons in the worst case? If yes, show your algorithm. Assume all keys are distinct, if it helps. Problem 5. Use mathematical induction to show that when n is an exact power of two, the solution of the recurrence { 8 if n = 2 T (n = 2T (n/2 + n if n = 2 k, for k > 1 is T (n = n lg n + n. Problem 6. a. Show that (n 2 = Θ(n 2 by providing the n 0, c 1, c 2 in the definition of the Θ notation. b. Rank the following function by order of growth; that is, find an arrangement g 1, g 2, g,... g 8 of the functions satisfying g 1 = Ω(g 2, g 2 = Ω(g, g = Ω(g 4,..., g 7 = Ω(g 8. Partition your list in equivalence classes such that g(n and h(n are in the same class if and only if f(n = Θ(g(n. (8 points n, (n 1!, (lg n lg n, n lg n, lg (n!, 2 lg n, n lg lg n, n!. Problem 7. Solve the following recurrences. You may assume T (1 = Θ(1, where necessary. Make your bounds as tight as possible. Use asymptotic notation to express your answers. Justify your answers. a. T (n = 4T (n/2 + n 2 b. T (n = 2T (n/4 + n 2 c. T (n = 4T (n/2 + n Problem 8. Solve exactly using the iteration method the following recurrence. You may assume that n is a power of 4, i.e. n = 4 k. T (n = 4T (n/4 + n 2, where T (1 = 4. 1
2 Problem 9. Solve the following recurrences; make your bounds as tight as possible. Use strong induction if necessary. T (n = T (n/2 + lg n, where T (2 = 1. T (n = T (n/2 + T (n/ + 2n, where T (1 = 100. Problem 10. (a What is the minimum and maximum number of elements in a heap of height h? (b Show that an n element heap has height lg n. (c Show that in any subtree of a MAX-HEAP, the root of the subtree contains the largest value occurring anywhere in that subtree. Problem 11. Min-Max. Give a divide-and-conquer algorithm that finds both the MINIMUM and the MAXIMUM of n keys x 1, x 2,..., x n by performing at most n/2 1 comparisons. You may assume that n is a power of two. Problem 12. d-heaps. Analysis of d-ary heaps. (Assume MAXheaps in the remainder. A d-ary heap is like a binary heap but non-leaf nodes have d children rather than 2. a. How would you represent a d-ary heap in an array? b. What is the height of a d-ary heap of n elements in terms of n and d? c. Give an efficient algorithm that extracts the maximum element from a d-ary max-heap. Analyze its running time in terms of n and d. d. Implement Insert for d-ary heaps and analyze its running time. e. Given an efficient implementation of an operation Increase(A,i,value which first sets A[i] = max{a[i], value} and then properly updates the d-ary max-heap. Analyze the worst-case running time of Increase. Problem 1. The following two methods are proposed to find M k, the k-th smallest of n keys stored in array A[0..n 1]. a Sort A and then output the k-th element of the sorted A. This is M k. b Build a MIN-heap out of the n elements of A, and then perform k EXTRACT-MIN operations. The last (i.e. k-th EXTRACT-MIN operation returns M k. Which of the two algorithms is asymptotically faster? Explain, i.e. provide details of efficient implementation of the various steps, and analyze their worst-case running time using asymptotic notation. Use case analysis, if necessary. Problem 14. You are given n arbitrary keys. We would like to identify which key appears most often (i.e. the highest-frequency key. Give an efficient algorithm that finds the highest-frequency key of an input of n keys. If two or more keys have the highest-frequency, then you are allowed to output any single one of these keys attaining the highest-frequency. (Example. If 10, 2, 4, 7, 4, 2, 10, 2 is an input key sequence, then the answer will be key 2. If T om, Jerry, Jerry, T om is the input, your answer can be Tom; an equally correct answer is Jerry. Problem 15. You are given n keys each one of which is an A,B,C, or D (say A means freshperson, B sophomore and so on. Sort the keys in worst-case linear time Θ(n so that in the output sequence the As are before (on the left of the Bs, which are before the Cs, which are before the Ds. Problem 16. Can you sort 5 keys with 7 comparisons in the worst case? Explain. Is it optimal? Explain. 2
3 PS 1 Solution Outline Problem 1. (a (b 2 m 1 is an 1 followed by m 1 zeroes, i.e. we need m bits. 2 m 1 is a sequence of m 1 s. So both integers need m bits to be represented. If the extremes A = 2 m 1 and B = 2 m 1 need m bits so do all integers L between A and B such that A L < B. (b Every positive integer L can be sanditched between two A, B as defined in part (b, for some integer value m. Thus 2 m 1 L 2 m 1 2 m L m 2 m 1 < L m lg (2 m 1 < lg (L + 1 lg (2 m m 1 < lg (L + 1 m The term lg (L + 1 is strictly greater than m 1 and at most m. Its ceiling lg (L + 1 = m, which is an integer can not thus be m 1, because lg (L + 1 is greater than m 1, and therefore lg (L + 1 = m must be the next greater integer, i.e. m. However, m = lg (L + 1 is the number of bits in L. This completes the proof of the problem, i.e. number of bits in L is m = lg (L + 1. Problem 2. We start establishing f(91 by using the two conditions A: (x 10 if x > 100 and B: f(x = f(f(x + 11 otherwise. f(91 = ConditionB f(f( We have just proved that f(91 = f(92. We next find f(92. = f(f(102 = ConditionA f( = f(92 f(92 = ConditionB f(f( = f(f(10 = ConditionA f(10 10 = f(9 We have just proved that f(91 = f(92 = f(9. We next find that f(91 = f(92 = f(9 = f(94, and proceeding similarly that f(91 = f(92 =... = f(100. We thus find now f(100. Therefore f(91 = f(92 =... = f(99 = f(100 = 91. f(100 = ConditionB f(f( = f(f(111 = ConditionA f( = f(101 = ConditionA = 91 Problem. i. Each sequence of length k can be sorted by insertion sort in O(k 2 worst case time. We have n/k sequences, each one requires O(k 2 time, therefore total time for all sequences is (n/k O(k 2 = O(nk.
4 Figure 1. Level SizePerSeq. #ofseq. (n 0 n/2**0 * 2**0 = n (n/2 (n/2 1 n/2**1 * 2**1 = n (n/4 (n/4 (n/4 (n/4 2 n/2**2 * 2**2 = n (n/8 (n/8 (n/8 (n/8 (n/8 (n/8 (n/8 (n/8 n/2** * 2** = n... intermediate levels (4k... 4k * n/(4k = n (2k (2k lgn-lgk+1 2k * n/(2k = n (k (k (k (k lgn-lgk k * n/k = n ii. With reference to Figure 1., at level i of the recursion we have 2 i sequences each one consisting of n/2 i keys. The base case is for i = lg (n/k = lg n lg k, where n/k subsequences have k keys each. Note that the number of subsequences and the number of elements in an individual subsequence have n as their product. The 2 i subsequences of level i are paired and merged. Each pair is merged in O(2 (n/2 i comparisons (forget about the 1 and since the number of pairs (half the number of sets is (1/22 i the total cost of merging at level i is O(n. There are lg (n/k levels thus the total cost of merging is O(n lg (n/k. iii. The running time of parts (i and (ii give a total running time of O(nk + n lg (n/k. iv. We choose k so that nk = n lg (n/k i.e. k = lg (n/k, which gives that k = Θ(lg n. Then the performance of the algorithm is O(n lg n. Problem 4. The problem is tricky. We can not use the running times of InsertionSort or MergeSort because they do not provide exact running time bounds, only asymptotic. So O(4 2 or O(4 lg 4 can be 5 or 6 or whatever other constant you like them to be. Let s say our keys are a, b, c, d and are all distinct. We can remove this assumption (distinctness but let s avoid headaches for the time being. Comparison 1. We first compare a, b using our first comparison. The output (left-to-right smallest-to-largest is either a, b or b, a depending on this outcome. Let us call this output generically x 1, x 2. Comparisons 2,. Now that we have settled a versus b, we deal with c. For c we binary search/insert c in the sorted sequence of a, b denoted x 1, x 2. That is, we first compare c to x 2 and then if necessary c to x 1. This requires one or two comparisons, i.e. two in the worst-case. Why? If c is greater than x 1 we are done: the output is x 1, x 2, c. Otherwise we need to determine whether c goes to left or right of x 1 by utilizing comparison. Let us again call the three sorted keys y 1, y 2, y, a permutation of a, b, c. Comparison 4,5. In the final step we binary search/insert d into the sorted sequence y 1, y 2, y. We can use again 2 comparisons, as many as previously, even if the keys are three and not two. How? We first compare d to y 2 (comparison 4. If d is greater than y 2, we compare d to y (comparison 5 and thus d is inserted either on the left of y or on the right depending on whether d is smaller or larger than y. If however the result of comparison 4 says d is less than y 2, then in comparison 5 we compare d to y 1 and decide whether to insert on the left or right of y 1. In 5 comparisons we managed to sort 4 keys in the worst-case. This is the best we can. We will prove later in class that no matter what we do and what algorithm we invent, sorting 4 keys in the worst-case requires at least 5 comparisons if the only operation allowed is comparison/swapping of keys. How do 4 (number of keys and 5 (number of comparisons compare? Well 5 is the smallest integer greater than lg (4!. Problem 5. We show the claim by induction. Our proposition P (n is : T (n = n + n lg n. Since we only need to show P (n not for all n but only for n being a power of two, we can transform P (n into Q(k = P (2 k using n = 2 k. Q(k is thus given by the following expression. Q(k : T (2 k = 2 k + k2 k = (k + 2 k. The recurrence T (n = 2T (n/2 + n can also be written in terms of k as We show Q(k by induction on k. T (2 k = 2T (2 k k. 4
5 Base case. For k = 1, we have n = 2 1 = 2. We substitute 1 for k in T (2 k. Thus T (2 k = T (2 = 8, which is 8 by the base case of the recurrence that was given to us. Starting from the right side of T (2 k which is (k + 2 k for k = 1 we get ( = 8 as well. Thus for k = 1 T (2 k is indeed equal to (k + 2 k. Therefore we have just shown that Q(0 is true because its left side T (2 k gives 8 by the base case and its right side (k + 2 k also gives 8 for k = 1 and thus T (2 k = (k + 2 k for the base case k = 1. Inductive Hypothesis. We show that if Q(k 1 is true, then Q(k will also be true. Inductive Step. If Q(k 1 is true, then T (2 k 1 = (k + 22 k 1. We expect to establish that Q(k is true, i.e. T (2 k = (k + 2 k, given that Q(k 1 is true. We use the recurrence T (2 k = 2T (2 k k to show that Q(k is true then. We start from the recurrence above and we substitute there for T (2 k 1 the expression obtained by the inductive hypothesis for Q(k 1. T (n = T (2 k = 2T (2 k k = 2((k + 22 k k = k2 k k + 2 k = k2 k + 2 k = (k + 2 k We have thus proved that T (2 k = (k + 2 k. We express the answer as a function of n now. Since n = 2 k we also have that k = lg n, and thus T (2 k = (k + 2 k T (n = (lg n + n T (n = n lg n + n We have thus proven that T (n = n lg n + n for all n = 2 k, where k 1. Problem 6. Part a. We show first that (n 2 = O(n 2 and then that (n 2 = Ω(n 2. Case 1. Show that (n 2 = O(n 2 For all n 1 we have that (n 2 = n 2 6n + 9 n n n n n 2 10n 2 Therefore there exist constant n 2 = 1 and c 2 = 10 such that (n 2 c 2 n 2 for all n n 2. This proves the claim. Technique 1. What we use in this proof is the fact that n 2 ± An ± B is bounded above, for positive A, B, by n 2 ± An ± B (1 + A + Bn 2. Case 2. Show that (n 2 = Ω(n 2 Technique 1 can not be used in this case. However, since 4 0 we can eliminate 4 easily. (n 2 = n 2 6n + 9 n 2 6n The next step is non-trivial. We bound n 2 6n from below by n 2 /2. This is so as long as n 2 6n n 2 /2 n 2 /2 6n n/2 6 n 12 We can do this as long as n is not zero; this is true since for all cases we assume that at least n 1. Therefore there exist constant n 1 = 12 and c 1 = 1/2 such that (n 2 n 2 /2 for all n n 1 = 12. This proves the claim. 5
6 In order to show that (n 2 = Θ(n 2 we need to establish c 1, c 2 and n 0. c 1 and c 2 are 1/2 and 10 respectively. n 0 = max(n 1, n 2 = 12. For these values the problem is thus shown. Part b. Some preliminaries R1. 2 lg n = n. R2. lg (n! = Θ(n lg n. R. n lg n = ω(n. R4. Since 2 lg n = n and 2 lg lg n = lg n, we have n lg lg n = (2 lg n lg lg n = 2 lg n lg lg n = (2 lg lg n lg n = (lg n lg n. R5. (n 1! = ω(n lg lg n. R6. n! = n (n 1!, therefore n! = ω((n 1!. A ranking of the functions would be (leftmost is asymptotically smallest, rightmost is asyptotically largest, separating equivalence classes with commas, and eliminating set notation for single-element sets/equivalence-classes. { n, 2 lg n } {, {n lg n, lg (n!}, n lg lg n, (lg n lg n}, (n 1!, n!. Problem 7. One can use the master method for all three of them. a. T (n = 4T (n/2 + n 2. It has a = 4 1, b = 2 > 1, f(n = n 2. n log b a = n lg 4 = n 2. Obviously n 2 = f(n = Θ(n log b a. Case 2 of the Master method applies and thus T (n = Θ(n 2 lg n. b. T (n = 2T (n/4 + n 2. Note that 2 2 = 1024 = 2 10, 4 5 = 1024 i.e. 4 5/2 = /2 = 2. It has a = 2 1, b = 4 > 1, f(n = n 2. n log b a = n lg 4 2 = n 5/2. Obviously n 2 = f(n = O(n log b a ɛ = O(n 2, by choosing ɛ = 1/2 > 0. Case 1 of the Master method applies and thus T (n = Θ(n 5/2. c. T (n = 4T (n/2 + n. It has a = 4 1, b = 2 > 1, f(n = n. n log b a = n lg 4 = n 2. Obviously n = f(n = Ω(n log b a+ɛ = O(n, by choosing ɛ = 1 > 0. Case of the Master method applies since also af(n/b = 4(n/2 = n /2 cn = (1/2n, by choosing c = 1/2 < 1, and thus T (n = Θ(n. Problem 8. T (n = 4T (n/4 + n 2. We use the iteration method. This first example will be done in fine detail showing all calculations. T (n = 4T (n/4 + n 2 ( 2 = 4 4T n 2 4 = 4 2 T n n2 4 0 = 4 (4T n n2 4 0 = 4 T 4 + n n n2 4 0 =... = 4 i T 4 i + n2 n i n2 4 0 ( 1 = 4 i T 4 i + n 2 4 i ( 1 = 4 i T 4 i + n i ( 1 1 = 4 i T 4 i + n 2 4 i = 4 i T 4 i + (1 4n2 14 i 6
7 The base case is T (1 = 4. We set n/4 i = 1, i.e. n = 4 i. If we solve this for i, we get i = log 4 n = lg n/2. Then T (n/4 i = T (1 = 4. In addition 4 i = n. Therfore the formula for T (n becomes. T (n = 4 i T 4 i + (1 4n2 14 i = nt (1 + 4n2 (1 1/n = 4n + 4n2 (1 1/n = 4n2 + 8n Note. It is easy to verify for example that T (1 = 4 12 solution that you have established satisfies at least the base case = 4. This can serve as a checking mechanism that the Problem 9. a. T (n = T (n/2 + lg n. We use the iteration method, noting that T (2 = 1. T (n = T + lg n ( ( 2 n = T = T =... = T ( lg n 2 + lg n lg n lg n i + lg n 2 i lg n lg n 2 0 The base case is T (2 = 1. We set n/2 i = 2, i.e. n = 2 i+1. If we solve this for i, we get i = lg n 1. Then T (n/2 i = T (2 = 1. In addition 2 i = n/2. Therfore the formula for T (n becomes. T (n = T 2 i + lg n 2 i lg n lg n ( 2 0 n n = T 2 lg n 1 + lg 2 lg n lg n lg n 2 0 = T (2 + ( lg n (lg 2 lg n ( lg n (lg 2 lg n ( lg n lg ( lg n lg 2 0 = 1 + (lg n (lg n 2 + (lg n (lg n (lg n 1 + (lg n 0 = (lg n 1 + (lg n = = lg n j j=1 lg n (lg n Therefore, T (n = lg n(lg n + 1/2. It is easy to verify that T (2 is indeed 1. b. Since T (n = T (n/2 + T (n/ + 2n we have for n = 1 from the base case that T (1 = 100. We show that T (n = Ω(n. By the recurrence we have that T (n 2n for all n > 1 since T (n/2, T (n/ are non-negative and the other term is 2n. In addition, T (1 = = 2. Therefore T (n 2n for n = 1 as well. Therefore T (n = Ω(n. We now prove that T (n = O(n or equivalently that there exist positive constants n 2, c 2 such that T (n c 2 n for all n n 2. Proof is by induction on n. Base Case. T (1 = 100 c 2 1 is true provided that c This completes the base case. Inductive Step. Let T (i c 2 i be true for all 1 i < n. We want to show that T (n c 2 n. Since T (i c 2 i for all i < n, it is also true for i = n/2 and i = n/ as well, and thus by the inductive hypothesis we obtain T (n/2 c 2 n/2 and T (n/ c 2 n/. Then we use these two inequalities in the recurrence to obtain. T (n = T (n/2 + T (n/ + 2n c 2 n/2 + c 2 n/ + 2n = 5c 2 n/6 + 2n 7
8 In order to complete the inductive step we need to prove that T (n c 2 n or equivalently 5c 2 n/6 + 2n c 2 n. The latter is equivalent to 2n c 2 n/6 or c Therefore the inductive step is completed and T (n c 2 n for any c In conclusion, combining the inductive step and the base case we obtain that T (n c 2 n for all n 1 as long as c We can fix c 2 = 192 and thus show that T (n = O(n. Therefore since T (n = O(n and T (n = Ω(n we obtain that T (n = Θ(n. The constants in the definition are 1, 192 and for n 0 we can still use 1. Problem 10. (a A heap of height h has its first h 1 levels completely filled and in the last level there exists at least one element and at most 2 h. Therefore the number of elements is h 1 + m = 2 h 1 + m, where 1 m 2 h. Therefore the minimum number of elements is 2 h and the maximum number of elements is 2 h+1 1. (b An n element heap has height h such that, by way of part (a, 2 h n 2 h+1 1 < 2 h+1. Therefore by taking logarithms base 2 of both sides h lg n < h + 1. Height h is always an integer. By the definition of the floor function we derive that h = lg n. (c Let S(u be the subtree of a heap rooted at some node u. Suppose by way of contradiction that the maximum value M stored in S(u is not at u. Let the left and right subtrees of u be LS(u and RS(u. Then the maximum of S(u must be in either LS(u or RS(u. Let the index of the heap node of S(u with the maximum M be m (note that if there are more than one nodes storing M we take the node with the minimum index value m. As the node indexed m cannot be node u it must be an internal node of S(u and therefore it must have a parent p. The index of the parent will be floor(m/2 i.e. smaller than m. The value stored in p must also be less than M as m is the lowest indexed node storing the maximum value M and therefore the value of the parent whose index is less than m must be smaller. Therefore the MAX heap-property fails for p and m, a contradiction to the assumption that S(u is a subtree of a heap. Problem 11. // MinMax(A,l,r returns (min,max, min=min(a[l..r], max=max(a[l..r], // for the subequence of A between A[l] and A[r] (inclusive of size r-l+1 // A a sequence of size n, n is a power of two ie n=2**k. MinMax(A,l,r 1. if lengthof(a[l..r] is 2 2. if (A[l] <= A[r] return (A[l],A[r] else return (A[r],A[l]; } // Split A into two halves as in mergesort. (min1,max1 = MinMax(A,l,(l+r/2; // Call this half A[l...(l+r/2] A1 4. (min2,max2 = MinMax(A,(l+r/2+1,r; // and this one A2 // and recursively find min,max of two halves. // Compare minima of two halves to find minimum 5. if min1 <= min2 then min= min1; else min= min2; // Compare maxima of two halves to find maximum 6. if max1 <= max2 then max= max2; else max= max1; 7. return((min,max; The top-level recursive call is MinMax(A,1,n The number of key comparisons T (n of MinMax(A,1,n is derived as follows. Step 2 requires one comparison; A is split as in lines 2-4 of Merge-Sort (page 1. Step requires T (n/2 comparisons and so does Step 4. We call the half of A in step, A1 and that of step 4 A2. In steps 5 and 6 we perform a total of two (2 comparisons. Note that the minimum of A is the minimum of the minima of A1 and A2. and the minimum of A is the maximum of the maxima of A1 and A2. We don t need to compare the minima to the maxima. Therefore, the recurrence for the number of comparisons becomes: T (n = 2T (n/2+2 = 2(2T (n/4+2+2 = 2 2 T (n/ = 2 lg n 1 T (2+2 lg n = n/2+( 1+n 1 = n/2 2. with T (2 = 1 by way of lines 1-2. By the iteration/recursion tree method we obtain that T (n = n/2 2, as required. [Note that the solution of the recurrence was compressed into one line.] 8
9 Problem 12. (a A d-ary heap is to be represented by an one dimensional array A. A[1] stores the root and A[2],... A[d + 1] store the d children of the root. The j-th child of node indexed i is d(i 1 + j + 1 where 1 j d. Therefore the children of i can have potential indexes d(i to di + 1. If the indexing starts from 0 i.e. the root is at A[0], then the children of i have indices starting with di + 1 through di + d. The parent of node i is floor((i 2/d + 1, in other words floor((i + d 2/d if the indexing starts from 1. If the indexing starts from zero, it is floor((i 1/d. A binary heap is a special case for d = 2. (b A heap of height h has n = 1 + d + d d h 1 + m = (d h 1/(d 1 + m elements, where 1 m d h. Therefore its height is O(lg n/ lg d. (c Extract-Max works the same way as Heap-Extract-Max for binary heaps except that Heapify(A,i on d-ary heaps works a little bit differently. It assumes that the d subtrees of node indexed i have the heap property and the maximum is taken over the value stored at i and the values stored in all d children of i. The maximum operation takes time O(d now, and Extract-Max may call Heapify O(h times. By way of part (b.b O(h = O(lg n/ lg d and therefore the time for Heapify will be O(d lg n/ lg d. (d Insert for binary heaps works fine for d-ary heaps as well (remember to use the new definition of a parent though. An upward movement is independent of the number of children of a parent. Therefore its running time is O(h = O(lg n/ lg d. (e This is similar to insertion. If the value k is at most the value of A[i] nothing changes, otherwise the value of A[i] is changed and propagated upwards just as we did in Heap-Insert. The observation is that since the value k is propagated upwards, we only need to change the value of the final destination only, just as we did in Heap-Insert. The following program demonstrates this. Note that parent(i follows the definition of part (b.a not that of a binary heap. Heap-Increase-Key (A,i,k 1. If A[i] >= k then return ; 2. while i>1 and A[parent(i] < k. do A[i] = A[parent(i]; 4. i=parent(i; 5. A[i]=k; Problem 1. The two algorithms are a. Find_M(k_a (A[1..n],n b. Find_M(k_b (A[1..n],n 1. HeapSort(A; 1. BuildMINheap(A,n; 2. return(a[k]; 2. for(i=1;i<k;i++{. z=extractmin(a; 4. } 5. return(z; The two pseudocodes are given above. Algorithm Find M(k a requires O(n lg n worst-case running time for step 1(HeapSort can be replaced by MergeSort and step 2 requires constant time. The total is O(n lg n. Algorithm Find M(k b requires O(n worst-case running time for the build-heap operation of step 1, and O(1 time for step 5. The loop involves k EXTRACT-MIN operations. Each one takes O(lg n time for a total of O(k lg n. Note that the z returned in step 5, is the result of the k-th EXTRACT-MIN operation, the k-th smallest of the n keys of the input. Total running time is O(n + k lg n. Let us asymptotically compare the performance of the two algorithms for various values of k. To make thing less confusing consider algorithm (a has performance n lg n and (b n + k lg n. Test Case 1. Let us start with small values of k. Let k = Θ(1, i.e. k be constant. The running time of (a is n lg n and (b is n + 1 lg n = O(n. The latter algorithm is asymptotically faster. How much can we increase k beyond a constant and still get the same performance? For what values of k is the term k lg n comparable to n? This is for k lg n = O(n, i.e. k = O(n/ lg n. For such values (b is Θ(n and (a is n lg n and (b is asymptotically faster. Test Case 2. Suppose that k = ω(n/ lg n. Algorithm (b has performance n + k lg n = n + ω(n/ lg n lg n which is ω(n + (n/ lg n lg n i.e. it is ω(n. Test Case. However as long as k = o(n, the term n + k lg n is still n + o(n lg n = o(n lg n, i.e. algorithm (b is still asymptotically faster that algorithm (a. Case. A. 9
10 Cases 1, 2, and can become one case: if k = o(n then (b is asymptotically faster than (a. Case B. If k is not k = o(n, then k = Θ(n, and algorithm (b has performance n + k lg n = O(n lg n and both algorithms have the same asymptotic performance. 10
11 Problem 14. Sort the keys with merge-sort. This takes O(n lg n worst-case running time. Duplicate keys appear next to each other in the sorted sequence. The most frequent of them is the desired key, i.e. we need to count the occurrences of a duplicate key. To do so we do a linear scan left to right of the output of merge-sort (i.e. O(n additional running time for the scan on the sorted array to determine the longest repetition of a given key. We use counters; every time we move from key x to a new key y, x y we reset the counters and check whether x is more frequent than the current most frequent key stored in a maxkey variable and update maxkey as needed; then we proceed to examining the frequency of y. If we go from x to y = x we update the counters (increment a frequency counter by 1. Total time is O(n lg n + O(n i.e. O(n lg n. If pseudocode is desired, the following is a good approximation. We keep track of the frequency of the current key in count, the maximum frequency in maxfreq and the index of the key attaining it (in the sorted sequence in maxkeyindex (i.e. the max frequency key has value A[maxkeyindex]. The key at A[0] is used initially as the current best (line 2 and its index (0 stored in maxkeyindex along with its current frequency (1 in maxfreq and count. In line we go through the remaining n 1 keys (C++/C notation for arrays. If the key value for A[i] is the same as before (start we increment the counter count by one. Otherwise we have a new key with possibly higher frequency. If this is so (test of line 6 we update our relevant info to reflect this (lines 7-9 otherwise we restart with this new key (count, start are updated as in line 1. The code of lines 1-16 works fine unless the highest-frequency key is the last one, i.e A[n 1]. For this we need lines 17-19, to detect and correctly record that key. HighFrequency(A[0..n-1],n //A C++ version 1. A= Sort(A,n 2. count=1; maxkeyindex = 0;maxfreq=1; start=a[0];. for(i=1;i< n;i++} { 4. if (A[i] == start count++; 5. else { 6. if (count > maxfreq { 7. maxfreq=count; 8. maxkeyindex=i-1; 9. count=1; 10. start=a[i]; 11. } 12. else { 1. count=1; start=a[i]; 14. } 15 } 16. } 17. if (count >maxfreq { 18. maxkeyindex=n-1; maxfreq=count; 19. } 20. print(a[maxkeyindex] has frequency maxfreq; // print is generic not C++/C or Java! The pseudocode is also easy to analyze. Line 1 is O(n lg n. The loop of line runs for n 1 times each time executing a constant number of operations (lines 4-15, i.e. total cost for these lines is O(n. Lines cost O(1. Total cost is O(n lg n + O(n + O(1 = O(n lg n. 11
12 Problem 15. We count the As, Bs, Cs and Ds. We go through the keys once (O(n time and count the 1 s etc in lines 2-7. Then we print enough As etc in linear time O(n (lines The solution is very simple, very inelegant but it works! More on this problem called count-sort later in class. Count124 (A,n 1. c1=c2=c=c4=0; 2. for(i=1;i<=n;i++ { //Very naive but it works!. if (A[i] == A c1++;// We don t care here about syntactice correctness cf A vs A 4. if (A[i] == B c2++;// How can you optimize these rather sloppy lines -6? 5. if (A[i] == C c++; 6. if (A[i] == D c4++; 7. } 8. c=1; // What can you do to optimize lines 9-17? 9. for(i=1;i<=c1;i++ // print as many As as c1 10. A[c++]=A; 11.for(i=1;i<=c2;i++ // print the Bs 12. A[c++]=B; 1.for(i=1;i<=c;i++ // and the Cs 14. A[c++]=C; 15.for(i=1;i<=c4;i++ // and the Ds 16. A[c++]=D; 17. return(a Problem 16. No solution is provided. It s similar to some other problem! 12
CS 577 Introduction to Algorithms: Strassen s Algorithm and the Master Theorem
 CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort
 Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Analysis of Algorithms - Using Asymptotic Bounds -
 Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
Review Of Topics. Review: Induction
 Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Data selection. Lower complexity bound for sorting
 Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
University of New Mexico Department of Computer Science. Midterm Examination. CS 361 Data Structures and Algorithms Spring, 2003
 University of New Mexico Department of Computer Science Midterm Examination CS 361 Data Structures and Algorithms Spring, 2003 Name: Email: Print your name and email, neatly in the space provided above;
University of New Mexico Department of Computer Science Midterm Examination CS 361 Data Structures and Algorithms Spring, 2003 Name: Email: Print your name and email, neatly in the space provided above;
COMP 382: Reasoning about algorithms
 Fall 2014 Unit 4: Basics of complexity analysis Correctness and efficiency So far, we have talked about correctness and termination of algorithms What about efficiency? Running time of an algorithm For
Fall 2014 Unit 4: Basics of complexity analysis Correctness and efficiency So far, we have talked about correctness and termination of algorithms What about efficiency? Running time of an algorithm For
Week 5: Quicksort, Lower bound, Greedy
 Week 5: Quicksort, Lower bound, Greedy Agenda: Quicksort: Average case Lower bound for sorting Greedy method 1 Week 5: Quicksort Recall Quicksort: The ideas: Pick one key Compare to others: partition into
Week 5: Quicksort, Lower bound, Greedy Agenda: Quicksort: Average case Lower bound for sorting Greedy method 1 Week 5: Quicksort Recall Quicksort: The ideas: Pick one key Compare to others: partition into
Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018
 CS17 Integrated Introduction to Computer Science Klein Contents Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018 1 Tree definitions 1 2 Analysis of mergesort using a binary tree 1 3 Analysis of
CS17 Integrated Introduction to Computer Science Klein Contents Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018 1 Tree definitions 1 2 Analysis of mergesort using a binary tree 1 3 Analysis of
Methods for solving recurrences
 Methods for solving recurrences Analyzing the complexity of mergesort The merge function Consider the following implementation: 1 int merge ( int v1, int n1, int v, int n ) { 3 int r = malloc ( ( n1+n
Methods for solving recurrences Analyzing the complexity of mergesort The merge function Consider the following implementation: 1 int merge ( int v1, int n1, int v, int n ) { 3 int r = malloc ( ( n1+n
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms
 CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
Divide-and-Conquer Algorithms Part Two
 Divide-and-Conquer Algorithms Part Two Recap from Last Time Divide-and-Conquer Algorithms A divide-and-conquer algorithm is one that works as follows: (Divide) Split the input apart into multiple smaller
Divide-and-Conquer Algorithms Part Two Recap from Last Time Divide-and-Conquer Algorithms A divide-and-conquer algorithm is one that works as follows: (Divide) Split the input apart into multiple smaller
Midterm Exam. CS 3110: Design and Analysis of Algorithms. June 20, Group 1 Group 2 Group 3
 Banner ID: Name: Midterm Exam CS 3110: Design and Analysis of Algorithms June 20, 2006 Group 1 Group 2 Group 3 Question 1.1 Question 2.1 Question 3.1 Question 1.2 Question 2.2 Question 3.2 Question 3.3
Banner ID: Name: Midterm Exam CS 3110: Design and Analysis of Algorithms June 20, 2006 Group 1 Group 2 Group 3 Question 1.1 Question 2.1 Question 3.1 Question 1.2 Question 2.2 Question 3.2 Question 3.3
Chapter 2. Recurrence Relations. Divide and Conquer. Divide and Conquer Strategy. Another Example: Merge Sort. Merge Sort Example. Merge Sort Example
 Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
1 Terminology and setup
 15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3
 MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
Math 391: Midterm 1.0 Spring 2016
 Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)
![Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts) Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)](/thumbs/87/95581149.jpg) Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Grade 11/12 Math Circles Fall Nov. 5 Recurrences, Part 2
 1 Faculty of Mathematics Waterloo, Ontario Centre for Education in Mathematics and Computing Grade 11/12 Math Circles Fall 2014 - Nov. 5 Recurrences, Part 2 Running time of algorithms In computer science,
1 Faculty of Mathematics Waterloo, Ontario Centre for Education in Mathematics and Computing Grade 11/12 Math Circles Fall 2014 - Nov. 5 Recurrences, Part 2 Running time of algorithms In computer science,
Algorithm runtime analysis and computational tractability
 Algorithm runtime analysis and computational tractability As soon as an Analytic Engine exists, it will necessarily guide the future course of the science. Whenever any result is sought by its aid, the
Algorithm runtime analysis and computational tractability As soon as an Analytic Engine exists, it will necessarily guide the future course of the science. Whenever any result is sought by its aid, the
3.1 Asymptotic notation
 3.1 Asymptotic notation The notations we use to describe the asymptotic running time of an algorithm are defined in terms of functions whose domains are the set of natural numbers N = {0, 1, 2,... Such
3.1 Asymptotic notation The notations we use to describe the asymptotic running time of an algorithm are defined in terms of functions whose domains are the set of natural numbers N = {0, 1, 2,... Such
b + O(n d ) where a 1, b > 1, then O(n d log n) if a = b d d ) if a < b d O(n log b a ) if a > b d
 CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
CIS 121. Analysis of Algorithms & Computational Complexity. Slides based on materials provided by Mary Wootters (Stanford University)
 CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
CSCI 3110 Assignment 6 Solutions
 CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
Problem. Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26
 Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Concrete models and tight upper/lower bounds
 Lecture 3 Concrete models and tight upper/lower bounds 3.1 Overview In this lecture, we will examine some simple, concrete models of computation, each with a precise definition of what counts as a step,
Lecture 3 Concrete models and tight upper/lower bounds 3.1 Overview In this lecture, we will examine some simple, concrete models of computation, each with a precise definition of what counts as a step,
Mergesort and Recurrences (CLRS 2.3, 4.4)
 Mergesort and Recurrences (CLRS 2.3, 4.4) We saw a couple of O(n 2 ) algorithms for sorting. Today we ll see a different approach that runs in O(n lg n) and uses one of the most powerful techniques for
Mergesort and Recurrences (CLRS 2.3, 4.4) We saw a couple of O(n 2 ) algorithms for sorting. Today we ll see a different approach that runs in O(n lg n) and uses one of the most powerful techniques for
Data Structures and Algorithms Running time and growth functions January 18, 2018
 Data Structures and Algorithms Running time and growth functions January 18, 2018 Measuring Running Time of Algorithms One way to measure the running time of an algorithm is to implement it and then study
Data Structures and Algorithms Running time and growth functions January 18, 2018 Measuring Running Time of Algorithms One way to measure the running time of an algorithm is to implement it and then study
Problem Set 2 Solutions
 Introduction to Algorithms October 1, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 9 Problem Set 2 Solutions Reading: Chapters 5-9,
Introduction to Algorithms October 1, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 9 Problem Set 2 Solutions Reading: Chapters 5-9,
Divide-and-conquer: Order Statistics. Curs: Fall 2017
 Divide-and-conquer: Order Statistics Curs: Fall 2017 The divide-and-conquer strategy. 1. Break the problem into smaller subproblems, 2. recursively solve each problem, 3. appropriately combine their answers.
Divide-and-conquer: Order Statistics Curs: Fall 2017 The divide-and-conquer strategy. 1. Break the problem into smaller subproblems, 2. recursively solve each problem, 3. appropriately combine their answers.
Taking Stock. IE170: Algorithms in Systems Engineering: Lecture 3. Θ Notation. Comparing Algorithms
 Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Data Structures and Algorithms Chapter 3
 Data Structures and Algorithms Chapter 3 1. Divide and conquer 2. Merge sort, repeated substitutions 3. Tiling 4. Recurrences Recurrences Running times of algorithms with recursive calls can be described
Data Structures and Algorithms Chapter 3 1. Divide and conquer 2. Merge sort, repeated substitutions 3. Tiling 4. Recurrences Recurrences Running times of algorithms with recursive calls can be described
The maximum-subarray problem. Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm:
 The maximum-subarray problem Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm: Brute force algorithm: At best, θ(n 2 ) time complexity 129 Can we do divide
The maximum-subarray problem Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm: Brute force algorithm: At best, θ(n 2 ) time complexity 129 Can we do divide
CS Data Structures and Algorithm Analysis
 CS 483 - Data Structures and Algorithm Analysis Lecture VII: Chapter 6, part 2 R. Paul Wiegand George Mason University, Department of Computer Science March 22, 2006 Outline 1 Balanced Trees 2 Heaps &
CS 483 - Data Structures and Algorithm Analysis Lecture VII: Chapter 6, part 2 R. Paul Wiegand George Mason University, Department of Computer Science March 22, 2006 Outline 1 Balanced Trees 2 Heaps &
CS 4407 Algorithms Lecture 3: Iterative and Divide and Conquer Algorithms
 CS 4407 Algorithms Lecture 3: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
CS 4407 Algorithms Lecture 3: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
2.2 Asymptotic Order of Growth. definitions and notation (2.2) examples (2.4) properties (2.2)
 2.2 Asymptotic Order of Growth definitions and notation (2.2) examples (2.4) properties (2.2) Asymptotic Order of Growth Upper bounds. T(n) is O(f(n)) if there exist constants c > 0 and n 0 0 such that
2.2 Asymptotic Order of Growth definitions and notation (2.2) examples (2.4) properties (2.2) Asymptotic Order of Growth Upper bounds. T(n) is O(f(n)) if there exist constants c > 0 and n 0 0 such that
Fundamental Algorithms
 Chapter 2: Sorting, Winter 2018/19 1 Fundamental Algorithms Chapter 2: Sorting Jan Křetínský Winter 2018/19 Chapter 2: Sorting, Winter 2018/19 2 Part I Simple Sorts Chapter 2: Sorting, Winter 2018/19 3
Chapter 2: Sorting, Winter 2018/19 1 Fundamental Algorithms Chapter 2: Sorting Jan Křetínský Winter 2018/19 Chapter 2: Sorting, Winter 2018/19 2 Part I Simple Sorts Chapter 2: Sorting, Winter 2018/19 3
Lecture 1: Asymptotics, Recurrences, Elementary Sorting
 Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 9 Divide and Conquer Merge sort Counting Inversions Binary Search Exponentiation Solving Recurrences Recursion Tree Method Master Theorem Sofya Raskhodnikova S. Raskhodnikova;
Algorithm Design and Analysis LECTURE 9 Divide and Conquer Merge sort Counting Inversions Binary Search Exponentiation Solving Recurrences Recursion Tree Method Master Theorem Sofya Raskhodnikova S. Raskhodnikova;
1 Substitution method
 Recurrence Relations we have discussed asymptotic analysis of algorithms and various properties associated with asymptotic notation. As many algorithms are recursive in nature, it is natural to analyze
Recurrence Relations we have discussed asymptotic analysis of algorithms and various properties associated with asymptotic notation. As many algorithms are recursive in nature, it is natural to analyze
i=1 i B[i] B[i] + A[i, j]; c n for j n downto i + 1 do c n i=1 (n i) C[i] C[i] + A[i, j]; c n
![i=1 i B[i] B[i] + A[i, j]; c n for j n downto i + 1 do c n i=1 (n i) C[i] C[i] + A[i, j]; c n i=1 i B[i] B[i] + A[i, j]; c n for j n downto i + 1 do c n i=1 (n i) C[i] C[i] + A[i, j]; c n](/thumbs/76/73723628.jpg) Fundamental Algorithms Homework #1 Set on June 25, 2009 Due on July 2, 2009 Problem 1. [15 pts] Analyze the worst-case time complexity of the following algorithms,and give tight bounds using the Theta
Fundamental Algorithms Homework #1 Set on June 25, 2009 Due on July 2, 2009 Problem 1. [15 pts] Analyze the worst-case time complexity of the following algorithms,and give tight bounds using the Theta
data structures and algorithms lecture 2
 data structures and algorithms 2018 09 06 lecture 2 recall: insertion sort Algorithm insertionsort(a, n): for j := 2 to n do key := A[j] i := j 1 while i 1 and A[i] > key do A[i + 1] := A[i] i := i 1 A[i
data structures and algorithms 2018 09 06 lecture 2 recall: insertion sort Algorithm insertionsort(a, n): for j := 2 to n do key := A[j] i := j 1 while i 1 and A[i] > key do A[i + 1] := A[i] i := i 1 A[i
Big O 2/14/13. Administrative. Does it terminate? David Kauchak cs302 Spring 2013
 /4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
/4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
Quiz 1 Solutions. (a) f 1 (n) = 8 n, f 2 (n) = , f 3 (n) = ( 3) lg n. f 2 (n), f 1 (n), f 3 (n) Solution: (b)
 Introduction to Algorithms October 14, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Srini Devadas and Constantinos (Costis) Daskalakis Quiz 1 Solutions Quiz 1 Solutions Problem
Introduction to Algorithms October 14, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Srini Devadas and Constantinos (Costis) Daskalakis Quiz 1 Solutions Quiz 1 Solutions Problem
Introduction to Divide and Conquer
 Introduction to Divide and Conquer Sorting with O(n log n) comparisons and integer multiplication faster than O(n 2 ) Periklis A. Papakonstantinou York University Consider a problem that admits a straightforward
Introduction to Divide and Conquer Sorting with O(n log n) comparisons and integer multiplication faster than O(n 2 ) Periklis A. Papakonstantinou York University Consider a problem that admits a straightforward
When we use asymptotic notation within an expression, the asymptotic notation is shorthand for an unspecified function satisfying the relation:
 CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
Fundamental Algorithms
 Fundamental Algorithms Chapter 2: Sorting Harald Räcke Winter 2015/16 Chapter 2: Sorting, Winter 2015/16 1 Part I Simple Sorts Chapter 2: Sorting, Winter 2015/16 2 The Sorting Problem Definition Sorting
Fundamental Algorithms Chapter 2: Sorting Harald Räcke Winter 2015/16 Chapter 2: Sorting, Winter 2015/16 1 Part I Simple Sorts Chapter 2: Sorting, Winter 2015/16 2 The Sorting Problem Definition Sorting
ECE608 Midterm 1 Spring 2009 THEN PUT YOUR ADDRESS ON EVERY PAGE OF THE EXAM! NAME: Neatness counts. We will not grade what we cannot read.
 ECE608 Midterm Spring 2009 Please fill in the following information. THEN PUT YOUR EMAI ADDRESS ON EVERY PAGE OF THE EXAM! NAME: Email (please put complete address): Neatness counts. We will not grade
ECE608 Midterm Spring 2009 Please fill in the following information. THEN PUT YOUR EMAI ADDRESS ON EVERY PAGE OF THE EXAM! NAME: Email (please put complete address): Neatness counts. We will not grade
Algorithm efficiency analysis
 Algorithm efficiency analysis Mădălina Răschip, Cristian Gaţu Faculty of Computer Science Alexandru Ioan Cuza University of Iaşi, Romania DS 2017/2018 Content Algorithm efficiency analysis Recursive function
Algorithm efficiency analysis Mădălina Răschip, Cristian Gaţu Faculty of Computer Science Alexandru Ioan Cuza University of Iaşi, Romania DS 2017/2018 Content Algorithm efficiency analysis Recursive function
CSCE 750, Spring 2001 Notes 2 Page 1 4 Chapter 4 Sorting ffl Reasons for studying sorting is a big deal pedagogically useful Λ the application itself
 CSCE 750, Spring 2001 Notes 2 Page 1 4 Chapter 4 Sorting ffl Reasons for studying sorting is a big deal pedagogically useful Λ the application itself is easy to understand Λ a complete analysis can often
CSCE 750, Spring 2001 Notes 2 Page 1 4 Chapter 4 Sorting ffl Reasons for studying sorting is a big deal pedagogically useful Λ the application itself is easy to understand Λ a complete analysis can often
Computational Complexity - Pseudocode and Recursions
 Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
CSCI Honor seminar in algorithms Homework 2 Solution
 CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
Asymptotic Algorithm Analysis & Sorting
 Asymptotic Algorithm Analysis & Sorting (Version of 5th March 2010) (Based on original slides by John Hamer and Yves Deville) We can analyse an algorithm without needing to run it, and in so doing we can
Asymptotic Algorithm Analysis & Sorting (Version of 5th March 2010) (Based on original slides by John Hamer and Yves Deville) We can analyse an algorithm without needing to run it, and in so doing we can
When we use asymptotic notation within an expression, the asymptotic notation is shorthand for an unspecified function satisfying the relation:
 CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
Lecture 4. Quicksort
 Lecture 4. Quicksort T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo choo@skku.edu Copyright 2000-2018 Networking
Lecture 4. Quicksort T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo choo@skku.edu Copyright 2000-2018 Networking
Divide and Conquer. Arash Rafiey. 27 October, 2016
 27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
Divide and Conquer Algorithms
 Divide and Conquer Algorithms T. M. Murali February 19, 2013 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
Divide and Conquer Algorithms T. M. Murali February 19, 2013 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
Divide and Conquer. Andreas Klappenecker
 Divide and Conquer Andreas Klappenecker The Divide and Conquer Paradigm The divide and conquer paradigm is important general technique for designing algorithms. In general, it follows the steps: - divide
Divide and Conquer Andreas Klappenecker The Divide and Conquer Paradigm The divide and conquer paradigm is important general technique for designing algorithms. In general, it follows the steps: - divide
Algorithms and Their Complexity
 CSCE 222 Discrete Structures for Computing David Kebo Houngninou Algorithms and Their Complexity Chapter 3 Algorithm An algorithm is a finite sequence of steps that solves a problem. Computational complexity
CSCE 222 Discrete Structures for Computing David Kebo Houngninou Algorithms and Their Complexity Chapter 3 Algorithm An algorithm is a finite sequence of steps that solves a problem. Computational complexity
CPS 616 DIVIDE-AND-CONQUER 6-1
 CPS 616 DIVIDE-AND-CONQUER 6-1 DIVIDE-AND-CONQUER Approach 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original (larger)
CPS 616 DIVIDE-AND-CONQUER 6-1 DIVIDE-AND-CONQUER Approach 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original (larger)
CPSC 320 Sample Final Examination December 2013
 CPSC 320 Sample Final Examination December 2013 [10] 1. Answer each of the following questions with true or false. Give a short justification for each of your answers. [5] a. 6 n O(5 n ) lim n + This is
CPSC 320 Sample Final Examination December 2013 [10] 1. Answer each of the following questions with true or false. Give a short justification for each of your answers. [5] a. 6 n O(5 n ) lim n + This is
CS383, Algorithms Spring 2009 HW1 Solutions
 Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ 21 Campanella Way, room 569 alvarez@cs.bc.edu Computer Science Department voice: (617) 552-4333 Boston College fax: (617) 552-6790 Chestnut Hill,
Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ 21 Campanella Way, room 569 alvarez@cs.bc.edu Computer Science Department voice: (617) 552-4333 Boston College fax: (617) 552-6790 Chestnut Hill,
CS Data Structures and Algorithm Analysis
 CS 483 - Data Structures and Algorithm Analysis Lecture II: Chapter 2 R. Paul Wiegand George Mason University, Department of Computer Science February 1, 2006 Outline 1 Analysis Framework 2 Asymptotic
CS 483 - Data Structures and Algorithm Analysis Lecture II: Chapter 2 R. Paul Wiegand George Mason University, Department of Computer Science February 1, 2006 Outline 1 Analysis Framework 2 Asymptotic
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Inf 2B: Sorting, MergeSort and Divide-and-Conquer
 Inf 2B: Sorting, MergeSort and Divide-and-Conquer Lecture 7 of ADS thread Kyriakos Kalorkoti School of Informatics University of Edinburgh The Sorting Problem Input: Task: Array A of items with comparable
Inf 2B: Sorting, MergeSort and Divide-and-Conquer Lecture 7 of ADS thread Kyriakos Kalorkoti School of Informatics University of Edinburgh The Sorting Problem Input: Task: Array A of items with comparable
Linear Selection and Linear Sorting
 Analysis of Algorithms Linear Selection and Linear Sorting If more than one question appears correct, choose the more specific answer, unless otherwise instructed. Concept: linear selection 1. Suppose
Analysis of Algorithms Linear Selection and Linear Sorting If more than one question appears correct, choose the more specific answer, unless otherwise instructed. Concept: linear selection 1. Suppose
1. Problem I calculated these out by hand. It was tedious, but kind of fun, in a a computer should really be doing this sort of way.
 . Problem 5.2-. I calculated these out by hand. It was tedious, but kind of fun, in a a computer should really be doing this sort of way. 2 655 95 45 243 77 33 33 93 86 5 36 8 3 5 2 4 2 2 2 4 2 2 4 4 2
. Problem 5.2-. I calculated these out by hand. It was tedious, but kind of fun, in a a computer should really be doing this sort of way. 2 655 95 45 243 77 33 33 93 86 5 36 8 3 5 2 4 2 2 2 4 2 2 4 4 2
Growth of Functions (CLRS 2.3,3)
 Growth of Functions (CLRS 2.3,3) 1 Review Last time we discussed running time of algorithms and introduced the RAM model of computation. Best-case running time: the shortest running time for any input
Growth of Functions (CLRS 2.3,3) 1 Review Last time we discussed running time of algorithms and introduced the RAM model of computation. Best-case running time: the shortest running time for any input
Randomized Sorting Algorithms Quick sort can be converted to a randomized algorithm by picking the pivot element randomly. In this case we can show th
 CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
Outline. 1 Introduction. 3 Quicksort. 4 Analysis. 5 References. Idea. 1 Choose an element x and reorder the array as follows:
 Outline Computer Science 331 Quicksort Mike Jacobson Department of Computer Science University of Calgary Lecture #28 1 Introduction 2 Randomized 3 Quicksort Deterministic Quicksort Randomized Quicksort
Outline Computer Science 331 Quicksort Mike Jacobson Department of Computer Science University of Calgary Lecture #28 1 Introduction 2 Randomized 3 Quicksort Deterministic Quicksort Randomized Quicksort
Asymptotic Analysis 1
 Asymptotic Analysis 1 Last week, we discussed how to present algorithms using pseudocode. For example, we looked at an algorithm for singing the annoying song 99 Bottles of Beer on the Wall for arbitrary
Asymptotic Analysis 1 Last week, we discussed how to present algorithms using pseudocode. For example, we looked at an algorithm for singing the annoying song 99 Bottles of Beer on the Wall for arbitrary
Algorithms Design & Analysis. Analysis of Algorithm
 Algorithms Design & Analysis Analysis of Algorithm Review Internship Stable Matching Algorithm 2 Outline Time complexity Computation model Asymptotic notions Recurrence Master theorem 3 The problem of
Algorithms Design & Analysis Analysis of Algorithm Review Internship Stable Matching Algorithm 2 Outline Time complexity Computation model Asymptotic notions Recurrence Master theorem 3 The problem of
Analysis of Algorithm Efficiency. Dr. Yingwu Zhu
 Analysis of Algorithm Efficiency Dr. Yingwu Zhu Measure Algorithm Efficiency Time efficiency How fast the algorithm runs; amount of time required to accomplish the task Our focus! Space efficiency Amount
Analysis of Algorithm Efficiency Dr. Yingwu Zhu Measure Algorithm Efficiency Time efficiency How fast the algorithm runs; amount of time required to accomplish the task Our focus! Space efficiency Amount
Solving recurrences. Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms.
 Solving recurrences Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms Example: Merge-Sort(A, p, r) 1: if p < r then 2: q (p + r)/2 3: Merge-Sort(A,
Solving recurrences Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms Example: Merge-Sort(A, p, r) 1: if p < r then 2: q (p + r)/2 3: Merge-Sort(A,
Asymptotic Analysis. Slides by Carl Kingsford. Jan. 27, AD Chapter 2
 Asymptotic Analysis Slides by Carl Kingsford Jan. 27, 2014 AD Chapter 2 Independent Set Definition (Independent Set). Given a graph G = (V, E) an independent set is a set S V if no two nodes in S are joined
Asymptotic Analysis Slides by Carl Kingsford Jan. 27, 2014 AD Chapter 2 Independent Set Definition (Independent Set). Given a graph G = (V, E) an independent set is a set S V if no two nodes in S are joined
Problem Set 1. MIT students: This problem set is due in lecture on Wednesday, September 19.
 Introduction to Algorithms September 7, 2001 Massachusetts Institute of Technology 6.046J/18.410J Singapore-MIT Alliance SMA5503 Professors Erik Demaine, Lee Wee Sun, and Charles E. Leiserson Handout 7
Introduction to Algorithms September 7, 2001 Massachusetts Institute of Technology 6.046J/18.410J Singapore-MIT Alliance SMA5503 Professors Erik Demaine, Lee Wee Sun, and Charles E. Leiserson Handout 7
Algorithms, Design and Analysis. Order of growth. Table 2.1. Big-oh. Asymptotic growth rate. Types of formulas for basic operation count
 Types of formulas for basic operation count Exact formula e.g., C(n) = n(n-1)/2 Algorithms, Design and Analysis Big-Oh analysis, Brute Force, Divide and conquer intro Formula indicating order of growth
Types of formulas for basic operation count Exact formula e.g., C(n) = n(n-1)/2 Algorithms, Design and Analysis Big-Oh analysis, Brute Force, Divide and conquer intro Formula indicating order of growth
COMP 9024, Class notes, 11s2, Class 1
 COMP 90, Class notes, 11s, Class 1 John Plaice Sun Jul 31 1::5 EST 011 In this course, you will need to know a bit of mathematics. We cover in today s lecture the basics. Some of this material is covered
COMP 90, Class notes, 11s, Class 1 John Plaice Sun Jul 31 1::5 EST 011 In this course, you will need to know a bit of mathematics. We cover in today s lecture the basics. Some of this material is covered
Fast Sorting and Selection. A Lower Bound for Worst Case
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
Divide and Conquer Algorithms
 Divide and Conquer Algorithms T. M. Murali March 17, 2014 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine solutions
Divide and Conquer Algorithms T. M. Murali March 17, 2014 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine solutions
CPSC 320 (Intermediate Algorithm Design and Analysis). Summer Instructor: Dr. Lior Malka Final Examination, July 24th, 2009
 CPSC 320 (Intermediate Algorithm Design and Analysis). Summer 2009. Instructor: Dr. Lior Malka Final Examination, July 24th, 2009 Student ID: INSTRUCTIONS: There are 6 questions printed on pages 1 7. Exam
CPSC 320 (Intermediate Algorithm Design and Analysis). Summer 2009. Instructor: Dr. Lior Malka Final Examination, July 24th, 2009 Student ID: INSTRUCTIONS: There are 6 questions printed on pages 1 7. Exam
Problem Set 1. CSE 373 Spring Out: February 9, 2016
 Problem Set 1 CSE 373 Spring 2016 Out: February 9, 2016 1 Big-O Notation Prove each of the following using the definition of big-o notation (find constants c and n 0 such that f(n) c g(n) for n > n o.
Problem Set 1 CSE 373 Spring 2016 Out: February 9, 2016 1 Big-O Notation Prove each of the following using the definition of big-o notation (find constants c and n 0 such that f(n) c g(n) for n > n o.
Asymptotic Analysis and Recurrences
 Appendix A Asymptotic Analysis and Recurrences A.1 Overview We discuss the notion of asymptotic analysis and introduce O, Ω, Θ, and o notation. We then turn to the topic of recurrences, discussing several
Appendix A Asymptotic Analysis and Recurrences A.1 Overview We discuss the notion of asymptotic analysis and introduce O, Ω, Θ, and o notation. We then turn to the topic of recurrences, discussing several
MIDTERM I CMPS Winter 2013 Warmuth
 test I 1 MIDTERM I CMPS 101 - Winter 2013 Warmuth With Solutions NAME: Student ID: This exam is closed book, notes, computer and cell phone. Show partial solutions to get partial credit. Make sure you
test I 1 MIDTERM I CMPS 101 - Winter 2013 Warmuth With Solutions NAME: Student ID: This exam is closed book, notes, computer and cell phone. Show partial solutions to get partial credit. Make sure you
CS 161 Summer 2009 Homework #2 Sample Solutions
 CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS173 Running Time and Big-O. Tandy Warnow
 CS173 Running Time and Big-O Tandy Warnow CS 173 Running Times and Big-O analysis Tandy Warnow Today s material We will cover: Running time analysis Review of running time analysis of Bubblesort Review
CS173 Running Time and Big-O Tandy Warnow CS 173 Running Times and Big-O analysis Tandy Warnow Today s material We will cover: Running time analysis Review of running time analysis of Bubblesort Review
Recurrence Relations
 Recurrence Relations Winter 2017 Recurrence Relations Recurrence Relations A recurrence relation for the sequence {a n } is an equation that expresses a n in terms of one or more of the previous terms
Recurrence Relations Winter 2017 Recurrence Relations Recurrence Relations A recurrence relation for the sequence {a n } is an equation that expresses a n in terms of one or more of the previous terms
Algorithms and Data Structures 2016 Week 5 solutions (Tues 9th - Fri 12th February)
 Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
CMPT 307 : Divide-and-Conqer (Study Guide) Should be read in conjunction with the text June 2, 2015
 CMPT 307 : Divide-and-Conqer (Study Guide) Should be read in conjunction with the text June 2, 2015 1 Introduction The divide-and-conquer strategy is a general paradigm for algorithm design. This strategy
CMPT 307 : Divide-and-Conqer (Study Guide) Should be read in conjunction with the text June 2, 2015 1 Introduction The divide-and-conquer strategy is a general paradigm for algorithm design. This strategy
Fundamental Algorithms
 Fundamental Algorithms Chapter 5: Searching Michael Bader Winter 2014/15 Chapter 5: Searching, Winter 2014/15 1 Searching Definition (Search Problem) Input: a sequence or set A of n elements (objects)
Fundamental Algorithms Chapter 5: Searching Michael Bader Winter 2014/15 Chapter 5: Searching, Winter 2014/15 1 Searching Definition (Search Problem) Input: a sequence or set A of n elements (objects)
CIS 121 Data Structures and Algorithms with Java Spring Big-Oh Notation Monday, January 22/Tuesday, January 23
 CIS 11 Data Structures and Algorithms with Java Spring 018 Big-Oh Notation Monday, January /Tuesday, January 3 Learning Goals Review Big-Oh and learn big/small omega/theta notations Discuss running time
CIS 11 Data Structures and Algorithms with Java Spring 018 Big-Oh Notation Monday, January /Tuesday, January 3 Learning Goals Review Big-Oh and learn big/small omega/theta notations Discuss running time
Advanced Analysis of Algorithms - Midterm (Solutions)
 Advanced Analysis of Algorithms - Midterm (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Solve the following recurrence using substitution:
Advanced Analysis of Algorithms - Midterm (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Solve the following recurrence using substitution:
CS361 Homework #3 Solutions
 CS6 Homework # Solutions. Suppose I have a hash table with 5 locations. I would like to know how many items I can store in it before it becomes fairly likely that I have a collision, i.e., that two items
CS6 Homework # Solutions. Suppose I have a hash table with 5 locations. I would like to know how many items I can store in it before it becomes fairly likely that I have a collision, i.e., that two items
Exercise Sheet #1 Solutions, Computer Science, A M. Hallett, K. Smith a k n b k = n b + k. a k n b k c 1 n b k. a k n b.
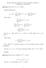 Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Problem Set 1 Solutions
 Introduction to Algorithms September 24, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 7 Problem Set 1 Solutions Exercise 1-1. Do Exercise
Introduction to Algorithms September 24, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 7 Problem Set 1 Solutions Exercise 1-1. Do Exercise
Asymptotic Notation. such that t(n) cf(n) for all n n 0. for some positive real constant c and integer threshold n 0
 Asymptotic Notation Asymptotic notation deals with the behaviour of a function in the limit, that is, for sufficiently large values of its parameter. Often, when analysing the run time of an algorithm,
Asymptotic Notation Asymptotic notation deals with the behaviour of a function in the limit, that is, for sufficiently large values of its parameter. Often, when analysing the run time of an algorithm,
Outline. 1 Introduction. Merging and MergeSort. 3 Analysis. 4 Reference
 Outline Computer Science 331 Sort Mike Jacobson Department of Computer Science University of Calgary Lecture #25 1 Introduction 2 Merging and 3 4 Reference Mike Jacobson (University of Calgary) Computer
Outline Computer Science 331 Sort Mike Jacobson Department of Computer Science University of Calgary Lecture #25 1 Introduction 2 Merging and 3 4 Reference Mike Jacobson (University of Calgary) Computer
Sorting. Chapter 11. CSE 2011 Prof. J. Elder Last Updated: :11 AM
 Sorting Chapter 11-1 - Sorting Ø We have seen the advantage of sorted data representations for a number of applications q Sparse vectors q Maps q Dictionaries Ø Here we consider the problem of how to efficiently
Sorting Chapter 11-1 - Sorting Ø We have seen the advantage of sorted data representations for a number of applications q Sparse vectors q Maps q Dictionaries Ø Here we consider the problem of how to efficiently
