Problem Set 1 Solutions
|
|
|
- Roy Houston
- 6 years ago
- Views:
Transcription
1 Introduction to Algorithms September 24, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 7 Problem Set 1 Solutions Exercise 1-1. Do Exercise on page 37 in CLRS. The following algorithm solves the problem: 1.Sort the elements in S using mergesort. 2.Remove the last element from S. Let y be the value of the removed element. 3.If S is nonempty, look for z = x y in S using binary search. 4.If S contains such an element z, then STOP, since we have found y and z such that x = y + z. Otherwise, repeat Step 2. 5.If S is empty, then no two elements in S sum to x. Notice that when we consider an element y i of S during ith iteration, we don t need to look at the elements that have already been considered in previous iterations. Suppose there exists y j S, such that x = y i + y j. If j < i, i.e. if y j has been reached prior to y i, then we would have found y i when we were searching for x y j during jth iteration and the algorithm would have terminated then. Step 1 takes Θ(n lg n) time. Step 2 takes O(1) time. Step 3 requires at most lg n time. Steps 2 4 are repeated at most n times. Thus, the total running time of this algorithm is Θ(n lg n). We can do a more precise analysis if we notice that Step 3 actually requires Θ(lg(n i)) time at ith iteration. However, if we evaluate n 1 i=1 lg(n i), we get lg(n 1)!, which is Θ(n lg n). So the total running time is still Θ(n lg n). Exercise 1-2. Do Exercise on page 50 in CLRS. Exercise 1-3. Do Exercise on page 57 in CLRS. Exercise 1-4. Do Problem 3-2 on page 58 of CLRS. Problem 1-1. Properties of Asymptotic Notation Prove or disprove each of the following properties related to asymptotic notation. In each of the following assume that f, g, and h are asymptotically nonnegative functions.
2 2 Handout 7: Problem Set 1 Solutions (a) f(n) = O(g(n)) and g(n) = O(f(n)) implies that f(n) = Θ(g(n)). This Statement is True. Since f(n) = O(g(n)), then there exists an n 0 and a c such that for all n n 0, f(n) cg(n). Similarly, since g(n) = O(f(n)), there exists an n 0 and a c such that for all 0, g ( n ) f(n). Therefore, for all n max(n 0, n 1 n n c 0), c g(n) f(n) cg(n). Hence, f(n) = Θ(g(n)). (b) f(n) + g(n) = Θ(max(f(n), g(n))). This Statement is True. For all n 1, f(n) max(f(n), g(n)) and g(n) max(f(n), g(n)). Therefore: f(n) + g(n) max(f(n), g(n)) + max(f(n), g(n)) 2 max(f(n), g(n)) and so f(n) + g(n) = O(max(f(n), g(n))). Additionally, for each n, either f(n) max(f(n), g(n)) or else g(n) max(f(n), g(n)). Therefore, for all n 1, f(n) + g(n) max(f(n), g(n)) and so f(n) + g(n) = Ω(max(f(n), g(n))). Thus, f(n) + g(n) = Θ(max(f(n), g(n))). (c) Transitivity: f(n) = O(g(n)) and g(n) = O(h(n)) implies that f(n) = O(h(n)). This Statement is True. Since f(n) = O(g(n)), then there exists an n 0 and a c such that for all n n 0, f(n) cg(n). Similarly, since g(n) = O(h(n)), there exists an n 0 and a c such that for all n n0, g( n) c h(n). Therefore, for all n max(n 0, n0), f( n) cc h(n). Hence, f(n) = O(h(n)). (d) f(n) = O(g(n)) implies that h(f(n)) = O(h(g(n)). This Statement is False. We disprove this statement by giving a counter-example. Let f(n) = n and g(n) = 3n and h(n) = 2 n. Then h(f(n)) = 2 n and h(g(n)) = 8 n. Since 2 n is not O(8 n ), this choice of f, g and h is a counter-example which disproves the theorem.
3 Handout 7: Problem Set 1 Solutions 3 (e) f (n) + o(f (n)) = Θ(f (n)). This Statement is True. Let h(n) = o(f (n)). We prove that f (n) + o(f (n)) = Θ(f (n)). Since for all n 1, f (n) + h(n) f (n), then f (n) + h(n) = Ω(f (n)). Since h(n) = o(f (n)), then there exists an n 0 such that for all n > n 0, h(n) f (n). Therefore, for all n > n 0, f (n) + h(n) 2f (n) and so f (n) + h(n) = O(f (n)). Thus, f (n) + h(n) = Θ(f (n)). (f) f (n) = o(g(n)) and g(n) = o(f (n)) implies f (n) = Θ(g(n)). This Statement is False. We disprove this statement by giving a counter-example. Consider f (n) = 1+cos(π n) and g(n) = 1 cos(π n). For all even values of n, f (n) = 2 and g(n) = 0, and there does not exist a c 1 for which f (n) c 1 g(n). Thus, f (n) is not o(g(n)), because if there does not exist a c 1 for which f (n) c 1 g(n), then it cannot be the case that for any c 1 > 0 and sufficiently large n, f (n) < c 1 g(n). For all odd values of n, f (n) = 0 and g(n) = 2, and there does not exist a c for which g(n) cf (n). By the above reasoning, it follows that g(n) is not o(f (n)). Also, there cannot exist c 2 > 0 for which c 2 g(n) f (n), because we could set c = 1/c 2 if such a c 2 existed. We have shown that there do not exist constants c 1 > 0 and c 2 > 0 such that c 2 g(n) f (n) c 1 g(n). Thus, f (n) is not Θ(g(n)). Problem 1-2. Computing Fibonacci Numbers The Fibonacci numbers are defined on page 56 of CLRS as F 0 = 0, F 1 = 1, F n = F n 1 + F n 2 for n 2. In Exercise 1-3, of this problem set, you showed that the nth Fibonacci number is F n = φn φ n, 5 where φ is the golden ratio and φ is its conjugate.
4 4 Handout 7: Problem Set 1 Solutions A fellow student comes to you with the following simple recursive algorithm for computing the nth Fibonacci number. FIB(n) 1 if n = 0 2 then return 0 3 elseif n = 1 4 then return 1 5 return FIB(n 1) + FIB(n 2) This algorithm is correct, since it directly implements the definition of the Fibonacci numbers. Let s analyze its running time. Let T (n) be the worst-case running time of FIB(n). 1 (a) Give a recurrence for T (n), and use the substitution method to show that T (n) = O(F n ). The recurrence is: T (n) = T (n 1) + T (n 2) + 1. We use the substitution method, inducting on n. Our Induction Hypothesis is: T (n) cf n b. To prove the inductive step: T (n) cf n 1 + cf n 2 b b + 1 cf n 2b + 1 Therefore, T (n) cf n b + 1 provided that b 1. We choose b = 2 and c = 10. For the base case consider n { 0, 1} and note the running time is no more than 10 2 = 8. (b) Similarly, show that T (n) = Ω(F n ), and hence, that T (n) = Θ(F n ). Again the recurrence is: T (n) = T (n 1) + T (n 2) + 1. We use the substitution method, inducting on n. Our Induction Hypothesis is: T (n) F n. To prove the inductive step: T (n) F n 1 + F n F n + 1 Therefore, T (n) F n. For the base case consider n {0, 1} and note the running time is no less than 1. 1 In this problem, please assume that all operations take unit time. In reality, the time it takes to add two numbers depends on the number of bits in the numbers being added (more precisely, on the number of memory words). However, for the purpose of this problem, the approximation of unit time addition will suffice.
5 Handout 7: Problem Set 1 Solutions 5 Professor Grigori Potemkin has recently published an improved algorithm for computing the nth Fibonacci number which uses a cleverly constructed loop to get rid of one of the recursive calls. Professor Potemkin has staked his reputation on this new algorithm, and his tenure committee has asked you to review his algorithm. FIB (n) 1 if n = 0 2 then return 0 3 elseif n = 1 4 then return sum 1 for k 1 to n 2 do sum sum + FIB (k) return sum Since it is not at all clear that this algorithm actually computes the nth Fibonacci number, let s prove that the algorithm is correct. We ll prove this by induction over n, using a loop invariant in the inductive step of the proof. (c) State the induction hypothesis and the base case of your correctness proof. To prove the algorithm is correct, we are inducting on n. Our induction hypothesis is that for all n < m, Fib (n) returns F n, the nth Fibonacci number. Our base case is m = 2. We observe that the first four lines of Potemkin guarantee that Fib (n) returns the correct value when n < 2. (d) State a loop invariant for the loop in lines 6-7. Prove, using induction over k, that your invariant is indeed invariant. Our loop invariant is that after the k = i iteration of the loop, sum = F i+2. We prove this induction using induction over k. We assume that after the k = (i 1) iteration of the loop, sum = F i+1. Our base case is i = 1. We observe that after the first pass through the loop, sum = 2 which is the 3rd Fibonacci number. To complete the induction step we observe that if sum = F i+1 after the k = (i 1) and if the call to F ib (i) on Line 7 correctly returns F i (by the induction hypothesis of our correctness proof in the previous part of the problem) then after the k = i iteration of the loop sum = F i+2. This follows immediately form the fact that F i + F i+1 = F i+2.
6 6 Handout 7: Problem Set 1 Solutions (e) Use your loop invariant to complete the inductive step of your correctness proof. To complete the inductive step of our correctness proof, we must show that if F ib (n) returns F n for all n < m then F ib (m) returns m. From the previous part we know that if F ib (n) returns F n for all n < m, then at the end of the k = i iteration of the loop sum = F i+2. We can thus conclude that after the k = m 2 iteration of the loop, sum = F m which completes our correctness proof. (f) What is the asymptotic running time, T (n), of FIB (n)? Would you recommend tenure for Professor Potemkin? We will argue that T (n) = Ω(F n ) and thus that Potemkin s algorithm, F ib does not improve upon the assymptotic performance of the simple recurrsive algorithm, F ib. Therefore we would not recommend tenure for Professor Potemkin. One way to see that T (n) = Ω(F n ) is to observe that the only constant in the program is the 1 (in lines 5 and 4). That is, in order for the program to return F n lines 5 and 4 must be executed a total of F n times. Another way to see that T (n) = Ω(F n ) is to use the substitution method with the hypothesis T (n) F n and the recurrence T (n) = cn + n 2 T (k). k=1 Problem 1-3. Polynomial multiplication One can represent a polynomial, in a symbolic variable x, with degree-bound n as an array P [0.. n] of coefficients. Consider two linear polynomials, A(x) = a 1 x + a 0 and B(x) = b 1 x + b 0, where a 1, a 0, b 1, and b 0 are numerical coefficients, which can be represented by the arrays [a 0, a 1 ] and [b 0, b 1 ], respectively. We can multiply A and B using the four coefficient multiplications m 1 = a 1 b 1, m 2 = a 1 b 0, m 3 = a 0 b 1, m 4 = a 0 b 0, as well as one numerical addition, to form the polynomial which can be represented by the array C(x) = m 1 x 2 + (m 2 + m 3 )x + m 4, [c 0, c 1, c 2 ] = [m 4, m 3 + m 2, m 1 ]. (a) Give a divide-and-conquer algorithm for multiplying two polynomials of degree-bound n, represented as coefficient arrays, based on this formula.
7 Handout 7: Problem Set 1 Solutions 7 We can use this idea to recursively multiply polynomials of degree n 1, where n is a power of 2, as follows: Let p(x) and q(x) be polynomials of degree n 1, and divide each into the upper n/2 and lower n/2 terms: p(x) = a(x)x n/2 + b(x), q(x) = c(x)x n/2 + d(x), where a(x), b(x), c(x), and d(x) are polynomials of degree n/2 1. The polynomial product is then p(x)q(x) = (a(x)x n/2 + b(x))(c(x)x n/2 + d(x)) = a(x)c(x)x n + (a(x)d(x) + b(x)c(x))x n/2 + b(x)d(x). The four polynomial products a(x)c(x), a(x)d(x), b(x)c(x), and b(x)d(x) are computed recursively. (b) Give and solve a recurrence for the worst-case running time of your algorithm. Since we can perform the dividing and combining of polynomials in time Θ(n), recursive polynomial multiplication gives us a running time of T (n) = 4T (n/2) + Θ(n) = Θ(n 2 ). (c) Show how to multiply two linear polynomials A(x) = a 1 x + a 0 and B(x) = b 1 x + b 0 using only three coefficient multiplications. We can use the following 3 multiplications: m 1 = (a + b)(c + d) = ac + ad + bc + bd, m 2 = ac, m 3 = bd, so the polynomial product is (ax + b)(cx + d) = m 2 x 2 + (m 1 m 2 m 3 )x + m 3.
8 8 Handout 7: Problem Set 1 Solutions (d) Give a divide-and-conquer algorithm for multiplying two polynomials of degree-bound n based on your formula from part (c). The algorithm is the same as in part (a), except for the fact that we need only compute three products of polynomials of degree n/2 to get the polynomial product. (e) Give and solve a recurrence for the worst-case running time of your algorithm. Similar to part (b): T (n) = 3T (n/2) + Θ(n) = Θ(n lg 3 ) Θ(n ) Alternative solution Instead of breaking a polynomial p(x) into two smaller polynomials a(x) and b(x) such that p(x) = a(x) + x n/2 b(x), as we did above, we could do the following: Collect all the even powers of p(x) and substitute y = x 2 to create the polynomial a(y). Then collect all the odd powers of p(x), factor out x and substitute y = x 2 to create the second polynomial b(y). Then we can see that p(x) = a(y) + x b(y) Both a(y) and b(y) are polynomials of (roughly) half the original size and degree, and we can proceed with our multiplications in a way analogous to what was done above. Notice that, at each level k, we need to compute y k = yk 1 2 (where y 0 = x), which takes time Θ(1) per level and does not affect the asymptotic running time.
INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR Design and Analysis of Algorithms Department of Mathematics MA21007/Assignment-2/Due: 18 Aug.
 INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR Design and Analysis of Algorithms Department of Mathematics MA21007/Assignment-2/Due: 18 Aug. 2015 Problem 1. Computing Fibonacci Numbers The Fibonacci numbers
INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR Design and Analysis of Algorithms Department of Mathematics MA21007/Assignment-2/Due: 18 Aug. 2015 Problem 1. Computing Fibonacci Numbers The Fibonacci numbers
Big O 2/14/13. Administrative. Does it terminate? David Kauchak cs302 Spring 2013
 /4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
/4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
Problem Set 1. MIT students: This problem set is due in lecture on Wednesday, September 19.
 Introduction to Algorithms September 7, 2001 Massachusetts Institute of Technology 6.046J/18.410J Singapore-MIT Alliance SMA5503 Professors Erik Demaine, Lee Wee Sun, and Charles E. Leiserson Handout 7
Introduction to Algorithms September 7, 2001 Massachusetts Institute of Technology 6.046J/18.410J Singapore-MIT Alliance SMA5503 Professors Erik Demaine, Lee Wee Sun, and Charles E. Leiserson Handout 7
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms
 CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
Lecture 2. Fundamentals of the Analysis of Algorithm Efficiency
 Lecture 2 Fundamentals of the Analysis of Algorithm Efficiency 1 Lecture Contents 1. Analysis Framework 2. Asymptotic Notations and Basic Efficiency Classes 3. Mathematical Analysis of Nonrecursive Algorithms
Lecture 2 Fundamentals of the Analysis of Algorithm Efficiency 1 Lecture Contents 1. Analysis Framework 2. Asymptotic Notations and Basic Efficiency Classes 3. Mathematical Analysis of Nonrecursive Algorithms
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort
 Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
Problem Set 2 Solutions
 Introduction to Algorithms October 1, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 9 Problem Set 2 Solutions Reading: Chapters 5-9,
Introduction to Algorithms October 1, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 9 Problem Set 2 Solutions Reading: Chapters 5-9,
CS Non-recursive and Recursive Algorithm Analysis
 CS483-04 Non-recursive and Recursive Algorithm Analysis Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 4:30pm - 5:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/
CS483-04 Non-recursive and Recursive Algorithm Analysis Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 4:30pm - 5:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/
CS 4407 Algorithms Lecture 3: Iterative and Divide and Conquer Algorithms
 CS 4407 Algorithms Lecture 3: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
CS 4407 Algorithms Lecture 3: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
Introduction to Algorithms 6.046J/18.401J/SMA5503
 Introduction to Algorithms 6.046J/8.40J/SMA5503 Lecture 3 Prof. Piotr Indyk The divide-and-conquer design paradigm. Divide the problem (instance) into subproblems. 2. Conquer the subproblems by solving
Introduction to Algorithms 6.046J/8.40J/SMA5503 Lecture 3 Prof. Piotr Indyk The divide-and-conquer design paradigm. Divide the problem (instance) into subproblems. 2. Conquer the subproblems by solving
Data Structures and Algorithms CSE 465
 Data Structures and Algorithms CSE 465 LECTURE 3 Asymptotic Notation O-, Ω-, Θ-, o-, ω-notation Divide and Conquer Merge Sort Binary Search Sofya Raskhodnikova and Adam Smith /5/0 Review Questions If input
Data Structures and Algorithms CSE 465 LECTURE 3 Asymptotic Notation O-, Ω-, Θ-, o-, ω-notation Divide and Conquer Merge Sort Binary Search Sofya Raskhodnikova and Adam Smith /5/0 Review Questions If input
Growth of Functions (CLRS 2.3,3)
 Growth of Functions (CLRS 2.3,3) 1 Review Last time we discussed running time of algorithms and introduced the RAM model of computation. Best-case running time: the shortest running time for any input
Growth of Functions (CLRS 2.3,3) 1 Review Last time we discussed running time of algorithms and introduced the RAM model of computation. Best-case running time: the shortest running time for any input
Homework 1 Solutions
 CS3510 Design & Analysis of Algorithms Section A Homework 1 Solutions Released 4pm Friday Sep 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope before
CS3510 Design & Analysis of Algorithms Section A Homework 1 Solutions Released 4pm Friday Sep 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope before
Introduction to Divide and Conquer
 Introduction to Divide and Conquer Sorting with O(n log n) comparisons and integer multiplication faster than O(n 2 ) Periklis A. Papakonstantinou York University Consider a problem that admits a straightforward
Introduction to Divide and Conquer Sorting with O(n log n) comparisons and integer multiplication faster than O(n 2 ) Periklis A. Papakonstantinou York University Consider a problem that admits a straightforward
COMP 382: Reasoning about algorithms
 Fall 2014 Unit 4: Basics of complexity analysis Correctness and efficiency So far, we have talked about correctness and termination of algorithms What about efficiency? Running time of an algorithm For
Fall 2014 Unit 4: Basics of complexity analysis Correctness and efficiency So far, we have talked about correctness and termination of algorithms What about efficiency? Running time of an algorithm For
Asymptotic Analysis. Slides by Carl Kingsford. Jan. 27, AD Chapter 2
 Asymptotic Analysis Slides by Carl Kingsford Jan. 27, 2014 AD Chapter 2 Independent Set Definition (Independent Set). Given a graph G = (V, E) an independent set is a set S V if no two nodes in S are joined
Asymptotic Analysis Slides by Carl Kingsford Jan. 27, 2014 AD Chapter 2 Independent Set Definition (Independent Set). Given a graph G = (V, E) an independent set is a set S V if no two nodes in S are joined
Introduction to Algorithms 6.046J/18.401J
 Introduction to Algorithms 6.046J/8.40J Lecture Prof. Piotr Indyk Welcome to Introduction to Algorithms, Spring 08 Handouts. Course Information. Calendar 3. Signup sheet (PLEASE return at the end of this
Introduction to Algorithms 6.046J/8.40J Lecture Prof. Piotr Indyk Welcome to Introduction to Algorithms, Spring 08 Handouts. Course Information. Calendar 3. Signup sheet (PLEASE return at the end of this
CS473 - Algorithms I
 CS473 - Algorithms I Lecture 2 Asymptotic Notation 1 O-notation: Asymptotic upper bound f(n) = O(g(n)) if positive constants c, n 0 such that 0 f(n) cg(n), n n 0 f(n) = O(g(n)) cg(n) f(n) Asymptotic running
CS473 - Algorithms I Lecture 2 Asymptotic Notation 1 O-notation: Asymptotic upper bound f(n) = O(g(n)) if positive constants c, n 0 such that 0 f(n) cg(n), n n 0 f(n) = O(g(n)) cg(n) f(n) Asymptotic running
When we use asymptotic notation within an expression, the asymptotic notation is shorthand for an unspecified function satisfying the relation:
 CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
Written Homework #1: Analysis of Algorithms
 Written Homework #1: Analysis of Algorithms CIS 121 Fall 2016 cis121-16fa-staff@googlegroups.com Due: Thursday, September 15th, 2015 before 10:30am (You must submit your homework online via Canvas. A paper
Written Homework #1: Analysis of Algorithms CIS 121 Fall 2016 cis121-16fa-staff@googlegroups.com Due: Thursday, September 15th, 2015 before 10:30am (You must submit your homework online via Canvas. A paper
Computational Complexity
 Computational Complexity S. V. N. Vishwanathan, Pinar Yanardag January 8, 016 1 Computational Complexity: What, Why, and How? Intuitively an algorithm is a well defined computational procedure that takes
Computational Complexity S. V. N. Vishwanathan, Pinar Yanardag January 8, 016 1 Computational Complexity: What, Why, and How? Intuitively an algorithm is a well defined computational procedure that takes
Homework 1 Submission
 Homework Submission Sample Solution; Due Date: Thursday, May 4, :59 pm Directions: Your solutions should be typed and submitted as a single pdf on Gradescope by the due date. L A TEX is preferred but not
Homework Submission Sample Solution; Due Date: Thursday, May 4, :59 pm Directions: Your solutions should be typed and submitted as a single pdf on Gradescope by the due date. L A TEX is preferred but not
data structures and algorithms lecture 2
 data structures and algorithms 2018 09 06 lecture 2 recall: insertion sort Algorithm insertionsort(a, n): for j := 2 to n do key := A[j] i := j 1 while i 1 and A[i] > key do A[i + 1] := A[i] i := i 1 A[i
data structures and algorithms 2018 09 06 lecture 2 recall: insertion sort Algorithm insertionsort(a, n): for j := 2 to n do key := A[j] i := j 1 while i 1 and A[i] > key do A[i + 1] := A[i] i := i 1 A[i
Analysis of Algorithms - Using Asymptotic Bounds -
 Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3
 MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
3.1 Asymptotic notation
 3.1 Asymptotic notation The notations we use to describe the asymptotic running time of an algorithm are defined in terms of functions whose domains are the set of natural numbers N = {0, 1, 2,... Such
3.1 Asymptotic notation The notations we use to describe the asymptotic running time of an algorithm are defined in terms of functions whose domains are the set of natural numbers N = {0, 1, 2,... Such
Algorithms Design & Analysis. Analysis of Algorithm
 Algorithms Design & Analysis Analysis of Algorithm Review Internship Stable Matching Algorithm 2 Outline Time complexity Computation model Asymptotic notions Recurrence Master theorem 3 The problem of
Algorithms Design & Analysis Analysis of Algorithm Review Internship Stable Matching Algorithm 2 Outline Time complexity Computation model Asymptotic notions Recurrence Master theorem 3 The problem of
CS173 Running Time and Big-O. Tandy Warnow
 CS173 Running Time and Big-O Tandy Warnow CS 173 Running Times and Big-O analysis Tandy Warnow Today s material We will cover: Running time analysis Review of running time analysis of Bubblesort Review
CS173 Running Time and Big-O Tandy Warnow CS 173 Running Times and Big-O analysis Tandy Warnow Today s material We will cover: Running time analysis Review of running time analysis of Bubblesort Review
Grade 11/12 Math Circles Fall Nov. 5 Recurrences, Part 2
 1 Faculty of Mathematics Waterloo, Ontario Centre for Education in Mathematics and Computing Grade 11/12 Math Circles Fall 2014 - Nov. 5 Recurrences, Part 2 Running time of algorithms In computer science,
1 Faculty of Mathematics Waterloo, Ontario Centre for Education in Mathematics and Computing Grade 11/12 Math Circles Fall 2014 - Nov. 5 Recurrences, Part 2 Running time of algorithms In computer science,
CS 350 Midterm Algorithms and Complexity
 It is recommended that you read through the exam before you begin. Answer all questions in the space provided. Name: Answer whether the following statements are true or false and briefly explain your answer
It is recommended that you read through the exam before you begin. Answer all questions in the space provided. Name: Answer whether the following statements are true or false and briefly explain your answer
Advanced Analysis of Algorithms - Homework I (Solutions)
 Advanced Analysis of Algorithms - Homework I (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Given an array A of n integer elements, how would
Advanced Analysis of Algorithms - Homework I (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Given an array A of n integer elements, how would
Data Structures and Algorithms Chapter 2
 1 Data Structures and Algorithms Chapter 2 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
1 Data Structures and Algorithms Chapter 2 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
Midterm Exam. CS 3110: Design and Analysis of Algorithms. June 20, Group 1 Group 2 Group 3
 Banner ID: Name: Midterm Exam CS 3110: Design and Analysis of Algorithms June 20, 2006 Group 1 Group 2 Group 3 Question 1.1 Question 2.1 Question 3.1 Question 1.2 Question 2.2 Question 3.2 Question 3.3
Banner ID: Name: Midterm Exam CS 3110: Design and Analysis of Algorithms June 20, 2006 Group 1 Group 2 Group 3 Question 1.1 Question 2.1 Question 3.1 Question 1.2 Question 2.2 Question 3.2 Question 3.3
Data structures Exercise 1 solution. Question 1. Let s start by writing all the functions in big O notation:
 Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
CIS 121. Analysis of Algorithms & Computational Complexity. Slides based on materials provided by Mary Wootters (Stanford University)
 CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
Asymptotic Notation. such that t(n) cf(n) for all n n 0. for some positive real constant c and integer threshold n 0
 Asymptotic Notation Asymptotic notation deals with the behaviour of a function in the limit, that is, for sufficiently large values of its parameter. Often, when analysing the run time of an algorithm,
Asymptotic Notation Asymptotic notation deals with the behaviour of a function in the limit, that is, for sufficiently large values of its parameter. Often, when analysing the run time of an algorithm,
CSE 101. Algorithm Design and Analysis Miles Jones Office 4208 CSE Building Lecture 1: Introduction
 CSE 101 Algorithm Design and Analysis Miles Jones mej016@eng.ucsd.edu Office 4208 CSE Building Lecture 1: Introduction LOGISTICS Book: Algorithms by Dasgupta, Papadimitriou and Vazirani Homework: Due Wednesdays
CSE 101 Algorithm Design and Analysis Miles Jones mej016@eng.ucsd.edu Office 4208 CSE Building Lecture 1: Introduction LOGISTICS Book: Algorithms by Dasgupta, Papadimitriou and Vazirani Homework: Due Wednesdays
CIS 121 Data Structures and Algorithms with Java Spring Big-Oh Notation Monday, January 22/Tuesday, January 23
 CIS 11 Data Structures and Algorithms with Java Spring 018 Big-Oh Notation Monday, January /Tuesday, January 3 Learning Goals Review Big-Oh and learn big/small omega/theta notations Discuss running time
CIS 11 Data Structures and Algorithms with Java Spring 018 Big-Oh Notation Monday, January /Tuesday, January 3 Learning Goals Review Big-Oh and learn big/small omega/theta notations Discuss running time
Algorithm efficiency analysis
 Algorithm efficiency analysis Mădălina Răschip, Cristian Gaţu Faculty of Computer Science Alexandru Ioan Cuza University of Iaşi, Romania DS 2017/2018 Content Algorithm efficiency analysis Recursive function
Algorithm efficiency analysis Mădălina Răschip, Cristian Gaţu Faculty of Computer Science Alexandru Ioan Cuza University of Iaşi, Romania DS 2017/2018 Content Algorithm efficiency analysis Recursive function
Cpt S 223. School of EECS, WSU
 Algorithm Analysis 1 Purpose Why bother analyzing code; isn t getting it to work enough? Estimate time and memory in the average case and worst case Identify bottlenecks, i.e., where to reduce time Compare
Algorithm Analysis 1 Purpose Why bother analyzing code; isn t getting it to work enough? Estimate time and memory in the average case and worst case Identify bottlenecks, i.e., where to reduce time Compare
Asymptotic Analysis. Thomas A. Anastasio. January 7, 2004
 Asymptotic Analysis Thomas A. Anastasio January 7, 004 1 Introduction As a programmer, you often have a choice of data structures and algorithms. Choosing the best one for a particular job involves, among
Asymptotic Analysis Thomas A. Anastasio January 7, 004 1 Introduction As a programmer, you often have a choice of data structures and algorithms. Choosing the best one for a particular job involves, among
CS 577 Introduction to Algorithms: Strassen s Algorithm and the Master Theorem
 CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
CS 4407 Algorithms Lecture 2: Growth Functions
 CS 4407 Algorithms Lecture 2: Growth Functions Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline Growth Functions Mathematical specification of growth functions
CS 4407 Algorithms Lecture 2: Growth Functions Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline Growth Functions Mathematical specification of growth functions
Data Structures and Algorithms Running time and growth functions January 18, 2018
 Data Structures and Algorithms Running time and growth functions January 18, 2018 Measuring Running Time of Algorithms One way to measure the running time of an algorithm is to implement it and then study
Data Structures and Algorithms Running time and growth functions January 18, 2018 Measuring Running Time of Algorithms One way to measure the running time of an algorithm is to implement it and then study
Divide and Conquer. Arash Rafiey. 27 October, 2016
 27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
Big O (Asymptotic Upper Bound)
 Big O (Asymptotic Upper Bound) Linear search takes O(n) time. Binary search takes O(lg(n)) time. (lg means log 2 ) Bubble sort takes O(n 2 ) time. n 2 + 2n + 1 O(n 2 ), n 2 + 2n + 1 O(n) Definition: f
Big O (Asymptotic Upper Bound) Linear search takes O(n) time. Binary search takes O(lg(n)) time. (lg means log 2 ) Bubble sort takes O(n 2 ) time. n 2 + 2n + 1 O(n 2 ), n 2 + 2n + 1 O(n) Definition: f
Agenda. We ve discussed
 Agenda We ve discussed Now Next C++ basics Some built-in data structures and their applications: stack, map, vector, array The Fibonacci example showing the importance of good algorithms and asymptotic
Agenda We ve discussed Now Next C++ basics Some built-in data structures and their applications: stack, map, vector, array The Fibonacci example showing the importance of good algorithms and asymptotic
Input Decidable Language -- Program Halts on all Input Encoding of Input -- Natural Numbers Encoded in Binary or Decimal, Not Unary
 Complexity Analysis Complexity Theory Input Decidable Language -- Program Halts on all Input Encoding of Input -- Natural Numbers Encoded in Binary or Decimal, Not Unary Output TRUE or FALSE Time and Space
Complexity Analysis Complexity Theory Input Decidable Language -- Program Halts on all Input Encoding of Input -- Natural Numbers Encoded in Binary or Decimal, Not Unary Output TRUE or FALSE Time and Space
Lecture 1: Asymptotics, Recurrences, Elementary Sorting
 Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
Mathematical Background. Unsigned binary numbers. Powers of 2. Logs and exponents. Mathematical Background. Today, we will review:
 Mathematical Background Mathematical Background CSE 373 Data Structures Today, we will review: Logs and eponents Series Recursion Motivation for Algorithm Analysis 5 January 007 CSE 373 - Math Background
Mathematical Background Mathematical Background CSE 373 Data Structures Today, we will review: Logs and eponents Series Recursion Motivation for Algorithm Analysis 5 January 007 CSE 373 - Math Background
Lecture 3. Big-O notation, more recurrences!!
 Lecture 3 Big-O notation, more recurrences!! Announcements! HW1 is posted! (Due Friday) See Piazza for a list of HW clarifications First recitation section was this morning, there s another tomorrow (same
Lecture 3 Big-O notation, more recurrences!! Announcements! HW1 is posted! (Due Friday) See Piazza for a list of HW clarifications First recitation section was this morning, there s another tomorrow (same
When we use asymptotic notation within an expression, the asymptotic notation is shorthand for an unspecified function satisfying the relation:
 CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
CS 4104 Data and Algorithm Analysis. Recurrence Relations. Modeling Recursive Function Cost. Solving Recurrences. Clifford A. Shaffer.
 Department of Computer Science Virginia Tech Blacksburg, Virginia Copyright c 2010,2017 by Clifford A. Shaffer Data and Algorithm Analysis Title page Data and Algorithm Analysis Clifford A. Shaffer Spring
Department of Computer Science Virginia Tech Blacksburg, Virginia Copyright c 2010,2017 by Clifford A. Shaffer Data and Algorithm Analysis Title page Data and Algorithm Analysis Clifford A. Shaffer Spring
Divide and Conquer algorithms
 Divide and Conquer algorithms Another general method for constructing algorithms is given by the Divide and Conquer strategy. We assume that we have a problem with input that can be split into parts in
Divide and Conquer algorithms Another general method for constructing algorithms is given by the Divide and Conquer strategy. We assume that we have a problem with input that can be split into parts in
Asymptotic Analysis 1
 Asymptotic Analysis 1 Last week, we discussed how to present algorithms using pseudocode. For example, we looked at an algorithm for singing the annoying song 99 Bottles of Beer on the Wall for arbitrary
Asymptotic Analysis 1 Last week, we discussed how to present algorithms using pseudocode. For example, we looked at an algorithm for singing the annoying song 99 Bottles of Beer on the Wall for arbitrary
Mergesort and Recurrences (CLRS 2.3, 4.4)
 Mergesort and Recurrences (CLRS 2.3, 4.4) We saw a couple of O(n 2 ) algorithms for sorting. Today we ll see a different approach that runs in O(n lg n) and uses one of the most powerful techniques for
Mergesort and Recurrences (CLRS 2.3, 4.4) We saw a couple of O(n 2 ) algorithms for sorting. Today we ll see a different approach that runs in O(n lg n) and uses one of the most powerful techniques for
Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)
![Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts) Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)](/thumbs/87/95581149.jpg) Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Md Momin Al Aziz. Analysis of Algorithms. Asymptotic Notations 3 COMP Computer Science University of Manitoba
 Md Momin Al Aziz azizmma@cs.umanitoba.ca Computer Science University of Manitoba Analysis of Algorithms Asymptotic Notations 3 COMP 2080 Outline 1. Visualization 2. Little notations 3. Properties of Asymptotic
Md Momin Al Aziz azizmma@cs.umanitoba.ca Computer Science University of Manitoba Analysis of Algorithms Asymptotic Notations 3 COMP 2080 Outline 1. Visualization 2. Little notations 3. Properties of Asymptotic
Big-O Notation and Complexity Analysis
 Big-O Notation and Complexity Analysis Jonathan Backer backer@cs.ubc.ca Department of Computer Science University of British Columbia May 28, 2007 Problems Reading: CLRS: Growth of Functions 3 GT: Algorithm
Big-O Notation and Complexity Analysis Jonathan Backer backer@cs.ubc.ca Department of Computer Science University of British Columbia May 28, 2007 Problems Reading: CLRS: Growth of Functions 3 GT: Algorithm
Topic 17. Analysis of Algorithms
 Topic 17 Analysis of Algorithms Analysis of Algorithms- Review Efficiency of an algorithm can be measured in terms of : Time complexity: a measure of the amount of time required to execute an algorithm
Topic 17 Analysis of Algorithms Analysis of Algorithms- Review Efficiency of an algorithm can be measured in terms of : Time complexity: a measure of the amount of time required to execute an algorithm
Analysis of Multithreaded Algorithms
 Analysis of Multithreaded Algorithms Marc Moreno Maza University of Western Ontario, London, Ontario (Canada) CS 4435 - CS 9624 (Moreno Maza) Analysis of Multithreaded Algorithms CS 4435 - CS 9624 1 /
Analysis of Multithreaded Algorithms Marc Moreno Maza University of Western Ontario, London, Ontario (Canada) CS 4435 - CS 9624 (Moreno Maza) Analysis of Multithreaded Algorithms CS 4435 - CS 9624 1 /
Review Of Topics. Review: Induction
 Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Lecture 2: Asymptotic Notation CSCI Algorithms I
 Lecture 2: Asymptotic Notation CSCI 700 - Algorithms I Andrew Rosenberg September 2, 2010 Last Time Review Insertion Sort Analysis of Runtime Proof of Correctness Today Asymptotic Notation Its use in analyzing
Lecture 2: Asymptotic Notation CSCI 700 - Algorithms I Andrew Rosenberg September 2, 2010 Last Time Review Insertion Sort Analysis of Runtime Proof of Correctness Today Asymptotic Notation Its use in analyzing
In-Class Soln 1. CS 361, Lecture 4. Today s Outline. In-Class Soln 2
 In-Class Soln 1 Let f(n) be an always positive function and let g(n) = f(n) log n. Show that f(n) = o(g(n)) CS 361, Lecture 4 Jared Saia University of New Mexico For any positive constant c, we want to
In-Class Soln 1 Let f(n) be an always positive function and let g(n) = f(n) log n. Show that f(n) = o(g(n)) CS 361, Lecture 4 Jared Saia University of New Mexico For any positive constant c, we want to
Recommended readings: Description of Quicksort in my notes, Ch7 of your CLRS text.
 Chapter 1 Quicksort 1.1 Prerequisites You need to be familiar with the divide-and-conquer paradigm, standard notations for expressing the time-complexity of an algorithm, like the big-oh, big-omega notations.
Chapter 1 Quicksort 1.1 Prerequisites You need to be familiar with the divide-and-conquer paradigm, standard notations for expressing the time-complexity of an algorithm, like the big-oh, big-omega notations.
Chapter 2. Recurrence Relations. Divide and Conquer. Divide and Conquer Strategy. Another Example: Merge Sort. Merge Sort Example. Merge Sort Example
 Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
Solving Recurrences. Lecture 23 CS2110 Fall 2011
 Solving Recurrences Lecture 23 CS2110 Fall 2011 1 Announcements Makeup Prelim 2 Monday 11/21 7:30-9pm Upson 5130 Please do not discuss the prelim with your classmates! Quiz 4 next Tuesday in class Topics:
Solving Recurrences Lecture 23 CS2110 Fall 2011 1 Announcements Makeup Prelim 2 Monday 11/21 7:30-9pm Upson 5130 Please do not discuss the prelim with your classmates! Quiz 4 next Tuesday in class Topics:
Chapter 4 Divide-and-Conquer
 Chapter 4 Divide-and-Conquer 1 About this lecture (1) Recall the divide-and-conquer paradigm, which we used for merge sort: Divide the problem into a number of subproblems that are smaller instances of
Chapter 4 Divide-and-Conquer 1 About this lecture (1) Recall the divide-and-conquer paradigm, which we used for merge sort: Divide the problem into a number of subproblems that are smaller instances of
Design and Analysis of Algorithms Recurrence. Prof. Chuhua Xian School of Computer Science and Engineering
 Design and Analysis of Algorithms Recurrence Prof. Chuhua Xian Email: chhxian@scut.edu.cn School of Computer Science and Engineering Course Information Instructor: Chuhua Xian ( 冼楚华 ) Email: chhxian@scut.edu.cn
Design and Analysis of Algorithms Recurrence Prof. Chuhua Xian Email: chhxian@scut.edu.cn School of Computer Science and Engineering Course Information Instructor: Chuhua Xian ( 冼楚华 ) Email: chhxian@scut.edu.cn
Divide and Conquer. CSE21 Winter 2017, Day 9 (B00), Day 6 (A00) January 30,
 Divide and Conquer CSE21 Winter 2017, Day 9 (B00), Day 6 (A00) January 30, 2017 http://vlsicad.ucsd.edu/courses/cse21-w17 Merging sorted lists: WHAT Given two sorted lists a 1 a 2 a 3 a k b 1 b 2 b 3 b
Divide and Conquer CSE21 Winter 2017, Day 9 (B00), Day 6 (A00) January 30, 2017 http://vlsicad.ucsd.edu/courses/cse21-w17 Merging sorted lists: WHAT Given two sorted lists a 1 a 2 a 3 a k b 1 b 2 b 3 b
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 9 Divide and Conquer Merge sort Counting Inversions Binary Search Exponentiation Solving Recurrences Recursion Tree Method Master Theorem Sofya Raskhodnikova S. Raskhodnikova;
Algorithm Design and Analysis LECTURE 9 Divide and Conquer Merge sort Counting Inversions Binary Search Exponentiation Solving Recurrences Recursion Tree Method Master Theorem Sofya Raskhodnikova S. Raskhodnikova;
Module 1: Analyzing the Efficiency of Algorithms
 Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Based
Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Based
EECS 477: Introduction to algorithms. Lecture 5
 EECS 477: Introduction to algorithms. Lecture 5 Prof. Igor Guskov guskov@eecs.umich.edu September 19, 2002 1 Lecture outline Asymptotic notation: applies to worst, best, average case performance, amortized
EECS 477: Introduction to algorithms. Lecture 5 Prof. Igor Guskov guskov@eecs.umich.edu September 19, 2002 1 Lecture outline Asymptotic notation: applies to worst, best, average case performance, amortized
5 + 9(10) + 3(100) + 0(1000) + 2(10000) =
 Chapter 5 Analyzing Algorithms So far we have been proving statements about databases, mathematics and arithmetic, or sequences of numbers. Though these types of statements are common in computer science,
Chapter 5 Analyzing Algorithms So far we have been proving statements about databases, mathematics and arithmetic, or sequences of numbers. Though these types of statements are common in computer science,
Divide and Conquer CPE 349. Theresa Migler-VonDollen
 Divide and Conquer CPE 349 Theresa Migler-VonDollen Divide and Conquer Divide and Conquer is a strategy that solves a problem by: 1 Breaking the problem into subproblems that are themselves smaller instances
Divide and Conquer CPE 349 Theresa Migler-VonDollen Divide and Conquer Divide and Conquer is a strategy that solves a problem by: 1 Breaking the problem into subproblems that are themselves smaller instances
COMP 9024, Class notes, 11s2, Class 1
 COMP 90, Class notes, 11s, Class 1 John Plaice Sun Jul 31 1::5 EST 011 In this course, you will need to know a bit of mathematics. We cover in today s lecture the basics. Some of this material is covered
COMP 90, Class notes, 11s, Class 1 John Plaice Sun Jul 31 1::5 EST 011 In this course, you will need to know a bit of mathematics. We cover in today s lecture the basics. Some of this material is covered
Asymptotic Running Time of Algorithms
 Asymptotic Complexity: leading term analysis Asymptotic Running Time of Algorithms Comparing searching and sorting algorithms so far: Count worst-case of comparisons as function of array size. Drop lower-order
Asymptotic Complexity: leading term analysis Asymptotic Running Time of Algorithms Comparing searching and sorting algorithms so far: Count worst-case of comparisons as function of array size. Drop lower-order
Fast Convolution; Strassen s Method
 Fast Convolution; Strassen s Method 1 Fast Convolution reduction to subquadratic time polynomial evaluation at complex roots of unity interpolation via evaluation at complex roots of unity 2 The Master
Fast Convolution; Strassen s Method 1 Fast Convolution reduction to subquadratic time polynomial evaluation at complex roots of unity interpolation via evaluation at complex roots of unity 2 The Master
Analysis of Algorithms
 September 29, 2017 Analysis of Algorithms CS 141, Fall 2017 1 Analysis of Algorithms: Issues Correctness/Optimality Running time ( time complexity ) Memory requirements ( space complexity ) Power I/O utilization
September 29, 2017 Analysis of Algorithms CS 141, Fall 2017 1 Analysis of Algorithms: Issues Correctness/Optimality Running time ( time complexity ) Memory requirements ( space complexity ) Power I/O utilization
Introduction to Algorithms
 Introduction to Algorithms (2 nd edition) by Cormen, Leiserson, Rivest & Stein Chapter 3: Growth of Functions (slides enhanced by N. Adlai A. DePano) Overview Order of growth of functions provides a simple
Introduction to Algorithms (2 nd edition) by Cormen, Leiserson, Rivest & Stein Chapter 3: Growth of Functions (slides enhanced by N. Adlai A. DePano) Overview Order of growth of functions provides a simple
Mid-term Exam Answers and Final Exam Study Guide CIS 675 Summer 2010
 Mid-term Exam Answers and Final Exam Study Guide CIS 675 Summer 2010 Midterm Problem 1: Recall that for two functions g : N N + and h : N N +, h = Θ(g) iff for some positive integer N and positive real
Mid-term Exam Answers and Final Exam Study Guide CIS 675 Summer 2010 Midterm Problem 1: Recall that for two functions g : N N + and h : N N +, h = Θ(g) iff for some positive integer N and positive real
CSCI Honor seminar in algorithms Homework 2 Solution
 CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
Divide and Conquer. Maximum/minimum. Median finding. CS125 Lecture 4 Fall 2016
 CS125 Lecture 4 Fall 2016 Divide and Conquer We have seen one general paradigm for finding algorithms: the greedy approach. We now consider another general paradigm, known as divide and conquer. We have
CS125 Lecture 4 Fall 2016 Divide and Conquer We have seen one general paradigm for finding algorithms: the greedy approach. We now consider another general paradigm, known as divide and conquer. We have
CS 361, Lecture 14. Outline
 Bucket Sort CS 361, Lecture 14 Jared Saia University of New Mexico Bucket sort assumes that the input is drawn from a uniform distribution over the range [0, 1) Basic idea is to divide the interval [0,
Bucket Sort CS 361, Lecture 14 Jared Saia University of New Mexico Bucket sort assumes that the input is drawn from a uniform distribution over the range [0, 1) Basic idea is to divide the interval [0,
Divide and Conquer. Andreas Klappenecker
 Divide and Conquer Andreas Klappenecker The Divide and Conquer Paradigm The divide and conquer paradigm is important general technique for designing algorithms. In general, it follows the steps: - divide
Divide and Conquer Andreas Klappenecker The Divide and Conquer Paradigm The divide and conquer paradigm is important general technique for designing algorithms. In general, it follows the steps: - divide
Taking Stock. IE170: Algorithms in Systems Engineering: Lecture 3. Θ Notation. Comparing Algorithms
 Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Math 324 Summer 2012 Elementary Number Theory Notes on Mathematical Induction
 Math 4 Summer 01 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
Math 4 Summer 01 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
CSC Design and Analysis of Algorithms. Lecture 1
 CSC 8301- Design and Analysis of Algorithms Lecture 1 Introduction Analysis framework and asymptotic notations What is an algorithm? An algorithm is a finite sequence of unambiguous instructions for solving
CSC 8301- Design and Analysis of Algorithms Lecture 1 Introduction Analysis framework and asymptotic notations What is an algorithm? An algorithm is a finite sequence of unambiguous instructions for solving
LECTURE NOTES ON DESIGN AND ANALYSIS OF ALGORITHMS
 G.PULLAIAH COLLEGE OF ENGINEERING AND TECHNOLOGY LECTURE NOTES ON DESIGN AND ANALYSIS OF ALGORITHMS Department of Computer Science and Engineering 1 UNIT 1 Basic Concepts Algorithm An Algorithm is a finite
G.PULLAIAH COLLEGE OF ENGINEERING AND TECHNOLOGY LECTURE NOTES ON DESIGN AND ANALYSIS OF ALGORITHMS Department of Computer Science and Engineering 1 UNIT 1 Basic Concepts Algorithm An Algorithm is a finite
Section 5.2 Solving Recurrence Relations
 Section 5.2 Solving Recurrence Relations If a g(n) = f (a g(0),a g(1),..., a g(n 1) ) find a closed form or an expression for a g(n). Recall: nth degree polynomials have n roots: a n x n + a n 1 x n 1
Section 5.2 Solving Recurrence Relations If a g(n) = f (a g(0),a g(1),..., a g(n 1) ) find a closed form or an expression for a g(n). Recall: nth degree polynomials have n roots: a n x n + a n 1 x n 1
Lecture 4. Quicksort
 Lecture 4. Quicksort T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo choo@skku.edu Copyright 2000-2018 Networking
Lecture 4. Quicksort T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo choo@skku.edu Copyright 2000-2018 Networking
Analysis of Algorithm Efficiency. Dr. Yingwu Zhu
 Analysis of Algorithm Efficiency Dr. Yingwu Zhu Measure Algorithm Efficiency Time efficiency How fast the algorithm runs; amount of time required to accomplish the task Our focus! Space efficiency Amount
Analysis of Algorithm Efficiency Dr. Yingwu Zhu Measure Algorithm Efficiency Time efficiency How fast the algorithm runs; amount of time required to accomplish the task Our focus! Space efficiency Amount
Problem 5. Use mathematical induction to show that when n is an exact power of two, the solution of the recurrence
 A. V. Gerbessiotis CS 610-102 Spring 2014 PS 1 Jan 27, 2014 No points For the remainder of the course Give an algorithm means: describe an algorithm, show that it works as claimed, analyze its worst-case
A. V. Gerbessiotis CS 610-102 Spring 2014 PS 1 Jan 27, 2014 No points For the remainder of the course Give an algorithm means: describe an algorithm, show that it works as claimed, analyze its worst-case
COMP 555 Bioalgorithms. Fall Lecture 3: Algorithms and Complexity
 COMP 555 Bioalgorithms Fall 2014 Lecture 3: Algorithms and Complexity Study Chapter 2.1-2.8 Topics Algorithms Correctness Complexity Some algorithm design strategies Exhaustive Greedy Recursion Asymptotic
COMP 555 Bioalgorithms Fall 2014 Lecture 3: Algorithms and Complexity Study Chapter 2.1-2.8 Topics Algorithms Correctness Complexity Some algorithm design strategies Exhaustive Greedy Recursion Asymptotic
CS F-01 Algorithm Analysis 1
 CS673-016F-01 Algorithm Analysis 1 01-0: Syllabus Office Hours Course Text Prerequisites Test Dates & Testing Policies Try to combine tests Grading Policies 01-1: How to Succeed Come to class. Pay attention.
CS673-016F-01 Algorithm Analysis 1 01-0: Syllabus Office Hours Course Text Prerequisites Test Dates & Testing Policies Try to combine tests Grading Policies 01-1: How to Succeed Come to class. Pay attention.
A design paradigm. Divide and conquer: (When) does decomposing a problem into smaller parts help? 09/09/ EECS 3101
 A design paradigm Divide and conquer: (When) does decomposing a problem into smaller parts help? 09/09/17 112 Multiplying complex numbers (from Jeff Edmonds slides) INPUT: Two pairs of integers, (a,b),
A design paradigm Divide and conquer: (When) does decomposing a problem into smaller parts help? 09/09/17 112 Multiplying complex numbers (from Jeff Edmonds slides) INPUT: Two pairs of integers, (a,b),
Exercise Sheet #1 Solutions, Computer Science, A M. Hallett, K. Smith a k n b k = n b + k. a k n b k c 1 n b k. a k n b.
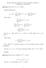 Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
The Growth of Functions and Big-O Notation
 The Growth of Functions and Big-O Notation Big-O Notation Big-O notation allows us to describe the aymptotic growth of a function without concern for i) constant multiplicative factors, and ii) lower-order
The Growth of Functions and Big-O Notation Big-O Notation Big-O notation allows us to describe the aymptotic growth of a function without concern for i) constant multiplicative factors, and ii) lower-order
