Electric fields in matter
|
|
|
- Jordan Robinson
- 6 years ago
- Views:
Transcription
1 Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to move in the E direction and the positive nuclei tend to move in the direction of the field. In the simplest circumstances, this creates a dipole moment within the material, and within the material this dipole field, E dipole generally opposes the applied field. The total electric field is therefore reduced to E E dipole within the material. Similarly, an electron approaching a spherical atom will alter the atom. In the simplest model of what happens, we have a sphere of negative charge around an equal but positively charged center. As the additional electron approaches, it repels the electron sphere and attracts the nucleus, so the cloud of electrons moves slightly away and the nucleus moves nearer, creating a slight dipole. This electric field points in the direction from the nucleus toward the approaching electron, and therefore attracts the approaching negative charge. These are highly simplified pictures. What happens in realistic situations may be different in different directions, and may depend nonlinearly on the applied electric field. Here we consider only the linear approximation. We divide materials into two types: conductors and insulators. Conductors have free charges that rearrange to offset any applied fields, but in insulators the charges stay in their respective atoms or molecules. We call these latter materials dielectrics. Effects of an electric field on molecules. Non-polar molecules The effect of an electric field on a molecule can be quite simple or highly complex. The simplest situation is for a non-polar atom or molecule, where the charge distribution is nearly spherical. In this case, the positively charged nucleus will experiencen a force in the direction of the field while the electron cloud shifts in the opposite direction. For atoms, this is the linear Stark effect, often computed as a perturbation of the quantum states. The net effect is a dipole in the direction opposite to the field, p αe The constant α is called the atomic polarizability. If the molecule is not spherically symmetric, the polarizability is likely to be different along different axes. In this case there is a more general linear relationship, p i 3 α ij E j i The polarizability tensor, α ij is symmetric. For example, the x component of the polarization due to an electric field in the y direction turns out to be the same as the y component of polarization from an electric field in the x direction. As a result, we may always diagonalize α ij along three principal axes. For strong electric fields, the dipole moment is no longer linear in the electric field. We will consider dipole moments produced by a simple linear response, p αe.
2 .2 Polar molecules Polar molecules already have a dipole moment, p, and an applied electric field acts directly on the separated plus and minus charges to produce a torque. Write the dipole moment as the charge q at the positive end times an average displacement from the center, 2 d, p 2 qd This charge experiences a force F + qe. The negative end, at 2 d experiences a force F qe, so there is a net torque, τ r a F a a+, 2 d p E qe + 2 d qe The direction of this torque tends to align p with E. If the molecule is free to rotate, it will turn until the torque vanishes, when the dipole moment is in the direction of the electric field..3 Net force If a polar molecule is in a nonuniform electric field, then the ends of the dipole do not experience the same field, so there is a net force on the dipole: d F total qe + q E d 2 2 If d 2 is small, we may expand the electric field in a Taylor series, d E 2 E d 2 d E + 2 E E + d2 E so that substituting into the total force gives d F total q E + 2 E + q E + d2 E qd qd qe + 2 E qe + 2 E p E 2 The potential produced by a polarized material We will assume that the polarization of materials is linear in both magnitude and direction, so that each atom in the material acquires a dipole moment p proportional to the applied field p E. Suppose the applied electric field varies slowly enough that we can average this dipole moment over an effectively infinitesimal volume but containing many molecules, d 3 x, so that the dipole moment of the small volume is given by p Pd 3 x. It may be that E and P depend on position within the material. Then P is the dipole moment per unit volume. 2
3 We need to compute the electric potential produced by this polarization, which will then combine with the applied potential to give a total electric potential in the material. Since a single dipole at the origin produces a potential at x given by V x p x x 3 we may shift the origin to see that a single dipole at postion x produces a potential at x of V x p x x x x 3 Now we can add up the combined contributions of small volumes, Pd 3 x, over a finite volume, V x ˆ P x x x x x 3 d 3 x V where V is the volume of dielectric. Now, recall from our discussion of potential that the gradient of x x with respect to the observation point x is x x x x x x x 3 The differentiation with respect to x gives the same, but with the opposite sign, x x x x x x x 3 This lets us rewrite the potential: V x ˆ V ˆ V P x x x x x 3 d 3 x P x x x d 3 x Now the identity fv f v + f v lets us replace P P x x x x x x x x x P Then the potential becomes V x ˆ V S P x x x P ˆn x x ˆ V x x x P d 3 x x P x x d3 x The first term on the right has the form of the potential due to a surface charge σ b P ˆn, while the second has the form of the potential due to a charge density ρ b P. We define the bound surface charge density and the bound charge density, σ b P ˆn ρ b P x 2 3
4 In terms of these the final potential is V x S σ b x x + ˆ V ρ b x x d3 x Once we know the dipole moment per unit volume, P x we can compute σ b and ρ b and find the electric potential directly. 3 Electric displacement in linear materials We could like to characterize the electric field inside a dielectric, or in regions which include dielectrics. We write the charge density as the effective bound charge density due to the polarization, together with any other charges free charges in the system, inside or outside the dielectric, ρ ρ b + ρ f The free charges from the familiar charge density. The bound charges arise only from the polarization of the material according to eqs. and 2. Then Gauss s law is ɛ E ρ ρ f P Bringing both divergence terms to the left side of the equation so that ɛ E + P ρ f, we defining the electric displacement, D ɛ E + P so that D ρ f The electric field is now replaced by the electric displacement and the charge density is given by the free charge density. Notice that in general there is no potential for D since we may have D P. Next, we assume a linear material so that the dipole moment per unit volume is proportional to the electric field in that volume. It is convenient to write the proportionality as P ɛ χ e E The constant χ e is called the electric susceptibility. Clearly this lets us write the electric displacement as D ɛ + χ e E ɛe where ɛ ɛ + χ e. These things all have names: ɛ ɛ χ e ɛ ɛ permitivity of free space permitivity, dielectric constant susceptibiliby dielectric constant 4
5 We can also simplify our relations for the bound charge densities in linear materials. P ɛ χ e E, and using Gauss s law, Starting from Solving for ρ b, ρ b P ɛ χ e E ɛ χ e ɛ ρ χ e ρ χ e ρ f + ρ b χ e ρ b x ρ f x + χ e This holds point by point for all x, so if there is no free charge suspended in the dielectric then there is no bound charge either, ρ f ρ b We may re-express the bound surface charge in terms of the potential. P ɛ χ e V gives σ b ˆn P ɛ χ e V n Setting E V so that where ˆn V V n is the directional derivative of V in the outward normal direction. The bound surface charge is therefore proportional to the normal derivative of the potential at the boundary. 4 Boundary conditions Recall the discussion of boundary conditions when we introduced Maxwell s equations for electrostatics. We now modify those results to include the presence of a linear material. Integrating the divergence of the displacement over a volume, and using the divergence theorem, we have ˆ ˆ D d 3 x ρ f d 3 x V S V D ˆn d 2 x f and we can find the boundary condition at an interface by integrating over a small cylinder that pierces the surface. Making the sides of the cylinder vanishingly small so that the charge density reduces to the surface density and the surface integral is essentially the contribution of the top and bottom of the cylinder, we have D top ˆn D bottom ˆn A σ f A and therefore the change in the normal component of the electric displacement is D out D in σ f For the tangential component of the displacement, we take the curl of D ɛ E + P, D ɛ E + P P 5
6 since the curl of E vanishes. Choose an elongated rectangle with one long side of length L and direction ˆm parallel to the surface on the outside and one long side parallel to the surface on the inside. Let the short sides have length d L. Now take the dot product of the normal to this surface with the curl, and integrate over the surface, n D d 2 x n P d 2 x Using Stokes theorem this becomes the line integral around the boundary, D dl P dl Neglecting any contribution from the short sides you may take the limit as d, L D out ˆm D in ˆm L P out ˆm P in ˆm Cancel L; now, since this relation holds for any ˆm parallel to the surface, we must have D out D in Pout P in Recall that the same computation with E gave us E out E in. In linear materials, we may simply use the equality of parallel components of the electric field, and compute D from E. 5 Summary In the presence of linear materials we have D ρ f Since there is always a potential for the electric field, we may write D ɛe ɛ V so that we have the Poisson equation in terms of the free charge density as before, but with ɛ replaced by ɛ: The boundary conditions change to 2 V ρ f ɛ D out D in σ f E out E in With free charges absent, ρ f ρ b and σ f, so for the interior or exterior regions we are solving only the Laplace equation 2 V in 2 V out and the boundary conditions are simple continuity of the normal component of D and the parallel component of E: D out D in E in E out 6
7 If we have azimuthal symmetry, the solutions may be written as V in r, θ V out r, θ and we need only impose the boundary conditions. A l r l + B l r l+ P l cos θ A l r l + B l r l+ P l cos θ 6 Solution to the Laplace equation in cylindrical coordinates First, we need the solution to the Laplace equation in cylindrical coordinates, ρ V + 2 V ρ ρ ρ ρ 2 ϕ V z 2 Using separation of variables, we write V R ρ Φ ϕ Z z, substitute, then divide by V, ΦZ d ρ dr + RZ d 2 Φ ρ dρ dρ ρ 2 dϕ 2 + Z RΦd2 dz 2 d R ρ dρ ρ dr dρ + d 2 Φ Φ ρ 2 dϕ 2 + Z The only z-dependence is in the final term, so we must have d 2 Z Z dz 2 α 2 d 2 Z dz 2 α2 Z d 2 Z dz 2 so that for α 2 >, Z Ae αz + Be αz. Then, multiplying by ρ 2 we have ρ d ρ dr + d 2 Φ R dρ dρ Φ dϕ 2 + α2 ρ 2 leaving the ϕ dependence isolated in the middle term. Therefore, since we need periodicity in ϕ, we set d 2 Φ Φ dϕ 2 β 2 d 2 Φ dϕ 2 + β2 Φ to get Φ C cos βϕ + D sin βϕ. Since we require the full azimuthal angle, ϕ : 2π, we must have β m for some integer m. Finally, we are left with ρ d ρ dr + α 2 ρ 2 β 2 R dρ dρ This is the Bessel equation. We will only solve a simpler version of this here. We do not need the full solution to the Bessel equation, since the current problem has no z dependence. Setting α 2 and β m gives a simpler equation, ρ d dρ ρ dr dρ m 2 R 7
8 When m, powers of ρ work. Let R ρ λ. Then ρ d ρλρ a m 2 ρ a dρ λ 2 ρ a m 2 ρ a so that λ ±m. Finally, when m, we have d dρ ρ dr dρ ρ dr dρ b and integrating, dr b ρ dρ R a + b ln ρ The full solution when V V ρ, ϕ only is therefore 7 Examples V ρ, ϕ a + b ln ρ + 7. Infinite half-space m a m ρ m + b m ρ m c m cos mϕ + d m sin mϕ Let the x > half of space be filled with a uniform linear dielectric with permitivity ɛ, while the region x < remains empty. Suppose there is a constant electric field, E out Ex outî + Eout y ĵ in the free space region outside the dielectric x <. Find the electric field in the dielectric. The boundary conditions are: D out D in E in E out Let the field outside the dielectric, E E x î + E y ĵ, be E out, and let be the field inside the dielectric. Then E in E in x î + Ein y ĵ + Ein k ˆk and E out Ey out E out Ex out E in E in y ĵ + Ein k ˆk E in Ex in Imposing the boundary conditions, with D out ɛ E out and D in ɛe in ɛ E out x ɛe in x Ey out ĵ Ein y ĵ Einˆk k 8
9 and therefore and the field inside the dielectric is ɛex in ɛ Ex out Ey in Ey out Ez in E in ɛ ɛ Eout x î + Eoutĵ Suppose we write this in terms of angles. The normal to the surface is î. Let the incoming electric field make an angle θ with this normal. Then E out E î out sin θ + ĵ cos θ so that Ex out E cos θ Ey out E sin θ Similarly, if the electric field in the dielectric makes an angle θ with î then y Equating components, E in E in ɛ ɛ Eout x î cos θ + ĵ sin θ î + Eoutĵ y E in cos θ ɛ ɛ Eout x ɛ ɛ E cos θ E in sin θ E sin θ we have E in sin θ E in cos θ E sin θ ɛ ɛ E cos θ sin θ cos θ ɛ sin θ ɛ cos θ ɛ tan θ ɛ tan θ This is not the same as Snell s law, which holds for electromagnetic waves at a similar interface and depends on the index of refraction, n, and not just the dielectric constant. 7.2 Infinite half-space with a charge 7.2. The induced bound charge density Let the z < half of space be filled with a uniform linear dielectric with permitivity ɛ, while the region x > remains empty except for a single charge on the z axis at a distance d >. Find the electric field on the positive z axis and compute the force on the charge. 9
10 The solution for the potential in the upper region is a linear combination of the potential of the given charge and the response of the dielectric. Since ρ b χe +χ e ρ f and there is no free charge inside the dielectric, ρ b. However, there will be a surface charge density given by σ b ɛ χ e V n ɛ χ e V z at the boundary, where the potential at the boundary is: V x x 2 + y 2 + z d 2 + V b x To take the derivative to find σ b, we need to find the potential V b due to σ b. This isn t as circular as it seems, since sufficiently near the surface the field is the same as for an infinite plane with charge per unit area σ b, E b above surface σ b 2ɛ ˆn Integrating gives the electric field, V b z σ b z 2ɛ for small z. The surface charge therefore satisfies σ b ɛ χ e + σ bz z x 2 + y 2 + z d 2 2ɛ Solving for σ b, χ e 4π χ e 4π + χ e 2 z d x 2 + y 2 + z d 2 3/2 2 χ eσ b d x 2 + y 2 + z d 2 3/2 2 χ eσ b σ b χ e 4π d z z x 2 + y 2 + d 2 3/2 σ b χ e d 2π 2 + χ e x 2 + y 2 + d 2 3/2 Once we know this, it is possible to find the potential using the method of images. The result follows by placing a charge q at dˆk and matching the boundary conditions Doing it the hard way optional! It is also possible to find the full potential without the method of images, while still avoiding elliptic integrals. First, notice that given σ b, we may compute V b everywhere by direct integration, but the form of the integral is daunting. V b x S σ b x x z
11 ˆ ˆ χ e d 2π 2 + χ e σ b dxdy x x ˆ ˆ z dxdy /2 x x 2 + y y 2 + z 2 x 2 + y 2 + d 2 3/2 Instead of tackling this straight on, we first restrict to the positive z-axis. From there we can use a Legendre series to write the potential for all z >. Finally, we recognize the expansion as the sum of two Coulomb potentials. To begin, we rewrite χ e d V b z 2π 2 + χ e ˆ ˆ in cylindrical coordinates. With the observation point at the potential becomes χ e d V b z 2π 2 + χ e Now let ξ ρ 2 so that dξ 2ρdρ. Then dxdy x 2 + y 2 + z 2/2 x 2 + y 2 + d 2 3/2 x z ˆk ˆ 2π ˆ dϕρdρ ρ 2 + z 2/2 ρ 2 + d 2 3/2 χ ˆ e d ρdρ 2 + χ e ρ 2 + z 2 /2 ρ 2 + d 2 3/2 V b z χ ˆ e d dξ 2 + χ e 8πɛ ξ + z 2/2 ξ + d 2 3/2 [ ξ + z 2 /2 ] ξ + d 2 /2 2 ξ + z 2/2 ξ + d 2 ξ + z 2 /2 /2 2 ξ + d 2 3/2 [ ] ξ + d 2 2 ξ + z 2/2 ξ + d 2 ξ + z2 3/2 ξ + z 2/2 ξ + d 2 3/2 d 2 z 2 2 ξ + z 2/2 ξ + d 2 3/2 With a little help from Wolfram integrator, we have [ V b z χ e d 2 ξ + z 2 /2 ] 2 + χ e 8πɛ d 2 z 2 ξ + d 2 /2 χ e d 2 2z 2 + χ e 8πɛ d 2 z 2 d d 2 z 2 χ e 2 + χ e d 2 z 2 d z χ e 2 + χ e d + z
12 Therefore, the potential on the zaxis is dropping the subscript on z V z χ e z d χ e d + z Notice that this already has the form of two Coulomb potentials restricted to the z axis. We can show rigorously that the full solution is exactly two Coulomb potentials. For z > d, we may expand in Taylor series, V z z d χ e 2 + χ e d + z z d χ e 2 + χ z e + d z n d χ n e n d z z 2 + χ n e z χ n e n d z 2 + χ n e z χ e n d n 2 + χ e z n+ n If we compare this to the expansion in Legendre polynomials when r z and θ, V z A l z l + B l z l+ P l n χ e n d n 2 + χ e z n+ A l z l + B l z l+ we see that n and this determines the whole series: V r, θ But we know that we can expand so we recognize V r, θ as A l B l χ e n 2 + χ e n x x n d n χ e n d l 2 + χ e z l+ P l cos θ r l n r l+ P l cos θ V r, θ χ e x dˆk 2 + χ e x + dˆk and this is just the potential of the original charge together with that of an image charge χe 2+χ e at dˆk. The same reasoning lets us show the result for z < d, or we can show that this V satisfies the correct boundary conditions. 2
13 7.3 Dielectric sphere in a uniform field A sphere of radius R, made of linear dielectric material is placed in an otherwise uniform electric field E. Find the resulting field inside and outside the sphere. The susceptibility is χ e. First, choose the z-axis in the direction of the uniform electric field. Then the boundary condition at infinity is V E r cos θ Solving the Laplace equation for the potential outside the sphere, we have V out r, θ A l r l + B l r l+ P l cos θ As r, the B l terms become negligibly small. The r l terms grow large, but we must nevertheless have a term linear in r, V r, θ E r cos θ A l r l P l cos θ so A E, with all other A l. Therefore, putting in the single nonzero A l term explicitly, we have B l V out r, θ E r cos θ + r l+ P l cos θ for the exterior solution. To find the constants B l, we must match this to the interior solution. In the interior of the sphere, we have the free and bound charge densities related by ρ b χ e ρ f χ e but there is no free charge so both vanish, and we again solve the Laplace equation, V in r, θ C l r l + D l r l+ P l cos θ This time, regularity at the origin tells us that D l for all l, so V in r, θ C l r l P l cos θ The boundary conditions at r R are: Now, compute the electric field: D out D in σ f E out E in E out V out r, θ ˆr r + ˆθ E r cos θ + r θ ˆr E cos θ + l + B l r l+2 P l ˆθ E in V in r, θ ˆr r + ˆθ C l r l P l r θ ˆr lc l r l P l ˆθ C l r l P l θ l l 3 B l r l+ P l E sin θ + l B l P l r l+2 θ
14 where we use P θ in the second sum. The parallel components are those in the ˆθ direction. For the parallel components at r R E out E in B l P l ˆθ E sin θ + R l+2 ˆθ θ l l B l P l P R l+2 C θ θ + P E θ + B P R 3 + θ l2 C l R l P l θ l2 C l R l P l θ where we separate out the l terms. The derivative terms are all independent see optional section below, so each coefficient must vanish. For each l 2, this implies while for the l term, C l B l R 2l+ C E + B R 3 This fixes all of the C l in terms of the B l. Now we look at the normal components of D. Again, there is no free surface charge, so we have continuity of the normal components at R ɛ E P + ɛ where we have written P for cos θ. For l, For l, D out D in l + B l R l+2 P l ɛ lc l R l P l B ɛ R 2 B ɛ E P + ɛ 2B R 3 P ɛc P l 2B ɛ E + ɛ R 3 ɛc 2B ɛ E + ɛ R 3 ɛ E + B R 3 2ɛ + ɛ R 3 B ɛ ɛ E ɛ ɛ B E R 3 2ɛ + ɛ Finally, for the remaining l, ɛ l + B l R l+2 ɛlc l R l 4
15 Substituting the values for C l, l + B l ɛ R l+2 ɛl l + B l ɛ R l+2 + ɛl Rl R2l+ R l+2 B l ɛ l + + ɛl B l and therefore B l and C l for all l 2, while for the l term, B l Rl R2l+ The potential is C E + B R 3 E + R 3 ɛ ɛ 2ɛ + ɛ 3ɛ 2ɛ + ɛ E E R 3 At the boundary, we check continuity: The final electric fields are ɛ ɛ R 3 V out r, θ E r cos θ + 2ɛ + ɛ r 2 E cos θ V in r, θ 3ɛ 2ɛ + ɛ E r cos θ V out R, θ E R cos θ + E out E in 3ɛ E 2ɛ + ɛ E in 3ɛ 2ɛ + ɛ E R cos θ V in R, θ + 2R3 ɛ ɛ r 3 2ɛ + ɛ + 2R3 ɛ ɛ r 3 2ɛ + ɛ 3ɛ 2ɛ + ɛ E ˆk cos θˆr sin θˆθ ɛ ɛ E R cos θ 2ɛ + ɛ E cos θˆr sin θˆθ E ˆk Notice that the polarization density is in the same direction as the electric field. 7.4 Proof of the orthogonality of derivatives of Legendre polynomials optional In solving this, we had the equality E sin θ B R 3 sin θ+b 2 R 4 θ P 2 cos θ+ l3 B l R l+2 θ P l cos θ A sin θ+a 2R θ P 2 cos θ+ 5 A lr l θ P l cos θ
16 It s not hard to guess that E sin θ A sin θ but let s look in detail at more general derivative terms. For P 2 2 Notice two things: θ P 2 cos θ 3 cos 2 θ θ 2 3 cos θ sin θ. The derivative is of the same order as P 2 in trig functions 2. The expression involves sin θ, which is indepenent of cos θ 3x 2 we have These derivatives must be expressed in terms the associated Legendre polynomials, which give the θ-dependence of the spherical harmonics which also depend on ϕ. All of these are orthogonal to the rest. To show the independence of two of the derivative terms, we may integrate, To change to x cos θ, we need and the integral becomes ˆπ ˆπ θ P l cos θ, θ P l cos θ θ P l cos θ θ P l cos θ sin θdθ θ θ P l cos θ θ P l cos θ sin θdθ x θ x sin θ x ˆ ˆ sin 2 θ x P l x x P l x dx Without loss of generality, suppose l < l. Then we may integrate by parts ˆ P l P l x 2 dx x x ˆ x P l x x P l x x 2 dx P l P l x 2 ˆ Pl dx P l x 2 dx x x x x Pl x x 2 is a polynomial of order x l +2 x l But P l x is a polynomial of order xl so that x and therefore expressible in terms of Legendre polynomials of order l or less. Since this linear combination, Pl x 2 x x l k α k P k x is multiplied by P l with l > k, each term in the sum is orthogonal and the integral vanishes. This proves that θ P l cos θ and θ P l cos θ are orthogonal if l l. You may assume this when working these problems. 6
17 8 Exercises 8. Parallel plate capacitor Consider two parallel rectangular conducting plates of area A and with separation d, with d A.. Neglecting edge effects, compute the capacitance when there is no material between the plates. 2. Recompute the capacitance if a uniform, linear dielectric material of permitivity ɛ fills the region between the plates. 8.2 Plane and dielectric The region below the xy-plane is filled with a dielectric material of permitivity ɛ. An infinite conducting plane with surface charge density σ is held at z d parallel to the surface of the dielectric. Find the bound surface charge density of the dielectric. 8.3 Spherical shell A hollow dielectric sphere extends from r a to r b. The region with r < a and the region with r > b are empty except for a charge placed at the origin.. Find the electric potential and electric field everywhere. 2. Find the bound surface charge on both spherical surfaces at a and at b. 3. Integrate your answers to part 2 over each surface to find the total bound charge on each surface. 8.4 Charge outside a dielectric half-space Repeat the example above of a single charge a distance d from an infinite half-space filled with a material of permitivity ɛ using the method of images. 8.5 Dielectric cylinder A solid dielectric cylinder of radius ρ R and infinitely long lies centered along the z-axis. There is a uniform electric field in the x-direction, E E î, perpendicular to the axis of the cylinder. Find the electric potential everywhere. 7
Chapter 4. Electrostatic Fields in Matter
 Chapter 4. Electrostatic Fields in Matter 4.1. Polarization 4.2. The Field of a Polarized Object 4.3. The Electric Displacement 4.4. Linear Dielectrics 4.5. Energy in dielectric systems 4.6. Forces on
Chapter 4. Electrostatic Fields in Matter 4.1. Polarization 4.2. The Field of a Polarized Object 4.3. The Electric Displacement 4.4. Linear Dielectrics 4.5. Energy in dielectric systems 4.6. Forces on
Electromagnetism: Worked Examples. University of Oxford Second Year, Part A2
 Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
1. (3) Write Gauss Law in differential form. Explain the physical meaning.
 Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
Maxwell s equations for electrostatics
 Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3
 Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 2017
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
l=0 The expansion coefficients can be determined, for example, by finding the potential on the z-axis and expanding that result in z.
 Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
Problem Set #4: 4.1,4.7,4.9 (Due Monday, March 25th)
 Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
E&M. 1 Capacitors. January 2009
 E&M January 2009 1 Capacitors Consider a spherical capacitor which has the space between its plates filled with a dielectric of permittivity ɛ. The inner sphere has radius r 1 and the outer sphere has
E&M January 2009 1 Capacitors Consider a spherical capacitor which has the space between its plates filled with a dielectric of permittivity ɛ. The inner sphere has radius r 1 and the outer sphere has
lim = F F = F x x + F y y + F z
 Physics 361 Summary of Results from Lecture Physics 361 Derivatives of Scalar and Vector Fields The gradient of a scalar field f( r) is given by g = f. coordinates f g = ê x x + ê f y y + ê f z z Expressed
Physics 361 Summary of Results from Lecture Physics 361 Derivatives of Scalar and Vector Fields The gradient of a scalar field f( r) is given by g = f. coordinates f g = ê x x + ê f y y + ê f z z Expressed
Chapter 4. Electric Fields in Matter
 Chapter 4. Electric Fields in Matter 4.1.2 Induced Dipoles What happens to a neutral atom when it is placed in an electric field E? The atom now has a tiny dipole moment p, in the same direction as E.
Chapter 4. Electric Fields in Matter 4.1.2 Induced Dipoles What happens to a neutral atom when it is placed in an electric field E? The atom now has a tiny dipole moment p, in the same direction as E.
Dielectrics. Lecture 20: Electromagnetic Theory. Professor D. K. Ghosh, Physics Department, I.I.T., Bombay
 What are dielectrics? Dielectrics Lecture 20: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay So far we have been discussing electrostatics in either vacuum or in a conductor.
What are dielectrics? Dielectrics Lecture 20: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay So far we have been discussing electrostatics in either vacuum or in a conductor.
A cylinder in a magnetic field (Jackson)
 Problem 1. A cylinder in a magnetic field (Jackson) A very long hollow cylinder of inner radius a and outer radius b of permeability µ is placed in an initially uniform magnetic field B o at right angles
Problem 1. A cylinder in a magnetic field (Jackson) A very long hollow cylinder of inner radius a and outer radius b of permeability µ is placed in an initially uniform magnetic field B o at right angles
Physics 505 Fall 2005 Homework Assignment #7 Solutions
 Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Dielectrics - III. Lecture 22: Electromagnetic Theory. Professor D. K. Ghosh, Physics Department, I.I.T., Bombay
 Dielectrics - III Lecture 22: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We continue with our discussion of dielectric medium. Example : Dielectric Sphere in a uniform
Dielectrics - III Lecture 22: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We continue with our discussion of dielectric medium. Example : Dielectric Sphere in a uniform
1 Fundamentals. 1.1 Overview. 1.2 Units: Physics 704 Spring 2018
 Physics 704 Spring 2018 1 Fundamentals 1.1 Overview The objective of this course is: to determine and fields in various physical systems and the forces and/or torques resulting from them. The domain of
Physics 704 Spring 2018 1 Fundamentals 1.1 Overview The objective of this course is: to determine and fields in various physical systems and the forces and/or torques resulting from them. The domain of
Physics 3323, Fall 2016 Problem Set 2 due Sep 9, 2016
 Physics 3323, Fall 26 Problem Set 2 due Sep 9, 26. What s my charge? A spherical region of radius R is filled with a charge distribution that gives rise to an electric field inside of the form E E /R 2
Physics 3323, Fall 26 Problem Set 2 due Sep 9, 26. What s my charge? A spherical region of radius R is filled with a charge distribution that gives rise to an electric field inside of the form E E /R 2
Physics GRE: Electromagnetism. G. J. Loges 1. University of Rochester Dept. of Physics & Astronomy. xkcd.com/567/
 Physics GRE: Electromagnetism G. J. Loges University of Rochester Dept. of Physics & stronomy xkcd.com/567/ c Gregory Loges, 206 Contents Electrostatics 2 Magnetostatics 2 3 Method of Images 3 4 Lorentz
Physics GRE: Electromagnetism G. J. Loges University of Rochester Dept. of Physics & stronomy xkcd.com/567/ c Gregory Loges, 206 Contents Electrostatics 2 Magnetostatics 2 3 Method of Images 3 4 Lorentz
Problem Set #3: 2.11, 2.15, 2.21, 2.26, 2.40, 2.42, 2.43, 2.46 (Due Thursday Feb. 27th)
 Chapter Electrostatics Problem Set #3:.,.5,.,.6,.40,.4,.43,.46 (Due Thursday Feb. 7th). Coulomb s Law Coulomb showed experimentally that for two point charges the force is - proportional to each of the
Chapter Electrostatics Problem Set #3:.,.5,.,.6,.40,.4,.43,.46 (Due Thursday Feb. 7th). Coulomb s Law Coulomb showed experimentally that for two point charges the force is - proportional to each of the
Additional Mathematical Tools: Detail
 Additional Mathematical Tools: Detail September 9, 25 The material here is not required, but gives more detail on the additional mathmatical tools: coordinate systems, rotations, the Dirac delta function
Additional Mathematical Tools: Detail September 9, 25 The material here is not required, but gives more detail on the additional mathmatical tools: coordinate systems, rotations, the Dirac delta function
Junior-level Electrostatics Content Review
 Junior-level Electrostatics Content Review Please fill out the following exam to the best of your ability. This will not count towards your final grade in the course. Do your best to get to all the questions
Junior-level Electrostatics Content Review Please fill out the following exam to the best of your ability. This will not count towards your final grade in the course. Do your best to get to all the questions
Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay. Poisson s and Laplace s Equations
 Poisson s and Laplace s Equations Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We will spend some time in looking at the mathematical foundations of electrostatics.
Poisson s and Laplace s Equations Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We will spend some time in looking at the mathematical foundations of electrostatics.
Electrostatics. Chapter Maxwell s Equations
 Chapter 1 Electrostatics 1.1 Maxwell s Equations Electromagnetic behavior can be described using a set of four fundamental relations known as Maxwell s Equations. Note that these equations are observed,
Chapter 1 Electrostatics 1.1 Maxwell s Equations Electromagnetic behavior can be described using a set of four fundamental relations known as Maxwell s Equations. Note that these equations are observed,
Electrodynamics I Midterm - Part A - Closed Book KSU 2005/10/17 Electro Dynamic
 Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
CHAPTER 3 POTENTIALS 10/13/2016. Outlines. 1. Laplace s equation. 2. The Method of Images. 3. Separation of Variables. 4. Multipole Expansion
 CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
1. (3) Write Gauss Law in differential form. Explain the physical meaning.
 Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about the physics involved,
Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about the physics involved,
Scattering. March 20, 2016
 Scattering March 0, 06 The scattering of waves of any kind, by a compact object, has applications on all scales, from the scattering of light from the early universe by intervening galaxies, to the scattering
Scattering March 0, 06 The scattering of waves of any kind, by a compact object, has applications on all scales, from the scattering of light from the early universe by intervening galaxies, to the scattering
A half submerged metal sphere (UIC comprehensive
 Problem 1. exam) A half submerged metal sphere (UIC comprehensive A very light neutral hollow metal spherical shell of mass m and radius a is slightly submerged by a distance b a below the surface of a
Problem 1. exam) A half submerged metal sphere (UIC comprehensive A very light neutral hollow metal spherical shell of mass m and radius a is slightly submerged by a distance b a below the surface of a
Multipole moments. November 9, 2015
 Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
1. ELECTRIC CHARGES AND FIELDS
 1. ELECTRIC CHARGES AND FIELDS 1. What are point charges? One mark questions with answers A: Charges whose sizes are very small compared to the distance between them are called point charges 2. The net
1. ELECTRIC CHARGES AND FIELDS 1. What are point charges? One mark questions with answers A: Charges whose sizes are very small compared to the distance between them are called point charges 2. The net
3/22/2016. Chapter 27 Gauss s Law. Chapter 27 Preview. Chapter 27 Preview. Chapter Goal: To understand and apply Gauss s law. Slide 27-2.
 Chapter 27 Gauss s Law Chapter Goal: To understand and apply Gauss s law. Slide 27-2 Chapter 27 Preview Slide 27-3 Chapter 27 Preview Slide 27-4 1 Chapter 27 Preview Slide 27-5 Chapter 27 Preview Slide
Chapter 27 Gauss s Law Chapter Goal: To understand and apply Gauss s law. Slide 27-2 Chapter 27 Preview Slide 27-3 Chapter 27 Preview Slide 27-4 1 Chapter 27 Preview Slide 27-5 Chapter 27 Preview Slide
3 Chapter. Gauss s Law
 3 Chapter Gauss s Law 3.1 Electric Flux... 3-2 3.2 Gauss s Law (see also Gauss s Law Simulation in Section 3.10)... 3-4 Example 3.1: Infinitely Long Rod of Uniform Charge Density... 3-9 Example 3.2: Infinite
3 Chapter Gauss s Law 3.1 Electric Flux... 3-2 3.2 Gauss s Law (see also Gauss s Law Simulation in Section 3.10)... 3-4 Example 3.1: Infinitely Long Rod of Uniform Charge Density... 3-9 Example 3.2: Infinite
3.3 Capacitance, relative permittivity & dielectrics 4
 3.3 Capacitance, relative permittivity & dielectrics 4 +Q d E Gaussian surface Voltage, V Q Fig. 3.2. Parallel plate capacitor with the plates separated by a distance d which have been charged by a power
3.3 Capacitance, relative permittivity & dielectrics 4 +Q d E Gaussian surface Voltage, V Q Fig. 3.2. Parallel plate capacitor with the plates separated by a distance d which have been charged by a power
Electric Field. Electric field direction Same direction as the force on a positive charge Opposite direction to the force on an electron
 Electric Field Electric field Space surrounding an electric charge (an energetic aura) Describes electric force Around a charged particle obeys inverse-square law Force per unit charge Electric Field Electric
Electric Field Electric field Space surrounding an electric charge (an energetic aura) Describes electric force Around a charged particle obeys inverse-square law Force per unit charge Electric Field Electric
Where k = 1. The electric field produced by a point charge is given by
 Ch 21 review: 1. Electric charge: Electric charge is a property of a matter. There are two kinds of charges, positive and negative. Charges of the same sign repel each other. Charges of opposite sign attract.
Ch 21 review: 1. Electric charge: Electric charge is a property of a matter. There are two kinds of charges, positive and negative. Charges of the same sign repel each other. Charges of opposite sign attract.
Flux. Flux = = va. This is the same as asking What is the flux of water through the rectangle? The answer depends on:
 Ch. 22: Gauss s Law Gauss s law is an alternative description of Coulomb s law that allows for an easier method of determining the electric field for situations where the charge distribution contains symmetry.
Ch. 22: Gauss s Law Gauss s law is an alternative description of Coulomb s law that allows for an easier method of determining the electric field for situations where the charge distribution contains symmetry.
y=1 1 J (a x ) dy dz dx dz 10 4 sin(2)e 2y dy dz sin(2)e 2y
 Chapter 5 Odd-Numbered 5.. Given the current density J = 4 [sin(x)e y a x + cos(x)e y a y ]ka/m : a) Find the total current crossing the plane y = in the a y direction in the region
Chapter 5 Odd-Numbered 5.. Given the current density J = 4 [sin(x)e y a x + cos(x)e y a y ]ka/m : a) Find the total current crossing the plane y = in the a y direction in the region
ELECTRO MAGNETIC FIELDS
 SET - 1 1. a) State and explain Gauss law in differential form and also list the limitations of Guess law. b) A square sheet defined by -2 x 2m, -2 y 2m lies in the = -2m plane. The charge density on the
SET - 1 1. a) State and explain Gauss law in differential form and also list the limitations of Guess law. b) A square sheet defined by -2 x 2m, -2 y 2m lies in the = -2m plane. The charge density on the
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 2, 3, and 4, and Di Bartolo, Chap. 2. 2π nx i a. ( ) = G n.
 Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
MP204 Electricity and Magnetism
 MATHEMATICAL PHYSICS SEMESTER 2, REPEAT 2016 2017 MP204 Electricity and Magnetism Prof. S. J. Hands, Dr. M. Haque and Dr. J.-I. Skullerud Time allowed: 1 1 2 hours Answer ALL questions MP204, 2016 2017,
MATHEMATICAL PHYSICS SEMESTER 2, REPEAT 2016 2017 MP204 Electricity and Magnetism Prof. S. J. Hands, Dr. M. Haque and Dr. J.-I. Skullerud Time allowed: 1 1 2 hours Answer ALL questions MP204, 2016 2017,
PHYSICS. Chapter 24 Lecture FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E RANDALL D. KNIGHT
 PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 24 Lecture RANDALL D. KNIGHT Chapter 24 Gauss s Law IN THIS CHAPTER, you will learn about and apply Gauss s law. Slide 24-2 Chapter
PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 24 Lecture RANDALL D. KNIGHT Chapter 24 Gauss s Law IN THIS CHAPTER, you will learn about and apply Gauss s law. Slide 24-2 Chapter
Solutions to Laplace s Equations- II
 Solutions to Laplace s Equations- II Lecture 15: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Laplace s Equation in Spherical Coordinates : In spherical coordinates
Solutions to Laplace s Equations- II Lecture 15: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Laplace s Equation in Spherical Coordinates : In spherical coordinates
Physics 6303 Lecture 11 September 24, LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation
 Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
Summary: Curvilinear Coordinates
 Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
Magnetostatics and the vector potential
 Magnetostatics and the vector potential December 8, 2015 1 The divergence of the magnetic field Starting with the general form of the Biot-Savart law, B (x 0 ) we take the divergence of both sides with
Magnetostatics and the vector potential December 8, 2015 1 The divergence of the magnetic field Starting with the general form of the Biot-Savart law, B (x 0 ) we take the divergence of both sides with
Electrodynamics Exam Solutions
 Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Physics (
 Question 2.12: A charge of 8 mc is located at the origin. Calculate the work done in taking a small charge of 2 10 9 C from a point P (0, 0, 3 cm) to a point Q (0, 4 cm, 0), via a point R (0, 6 cm, 9 cm).
Question 2.12: A charge of 8 mc is located at the origin. Calculate the work done in taking a small charge of 2 10 9 C from a point P (0, 0, 3 cm) to a point Q (0, 4 cm, 0), via a point R (0, 6 cm, 9 cm).
Conductors and Insulators
 Conductors and Insulators Lecture 11: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Self Energy of a Charge Distribution : In Lecture 1 we briefly discussed what we called
Conductors and Insulators Lecture 11: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Self Energy of a Charge Distribution : In Lecture 1 we briefly discussed what we called
Chapter 21 Electric Charge and the Electric Field
 Chapter 21 Electric Charge and the Electric Field 1 Electric Charge Electrostatics is the study of charges when they are stationery. Figure 1: This is Fig. 21.1 and it shows how negatively charged objects
Chapter 21 Electric Charge and the Electric Field 1 Electric Charge Electrostatics is the study of charges when they are stationery. Figure 1: This is Fig. 21.1 and it shows how negatively charged objects
A) 1, 2, 3, 4 B) 4, 3, 2, 1 C) 2, 3, 1, 4 D) 2, 4, 1, 3 E) 3, 2, 4, 1. Page 2
 1. Two parallel-plate capacitors with different plate separation but the same capacitance are connected in series to a battery. Both capacitors are filled with air. The quantity that is NOT the same for
1. Two parallel-plate capacitors with different plate separation but the same capacitance are connected in series to a battery. Both capacitors are filled with air. The quantity that is NOT the same for
DIVERGENCE AND CURL THEOREMS
 This document is stored in Documents/4C/Gausstokes.tex. with LaTex. Compile it November 29, 2014 Hans P. Paar DIVERGENCE AND CURL THEOREM 1 Introduction We discuss the theorems of Gauss and tokes also
This document is stored in Documents/4C/Gausstokes.tex. with LaTex. Compile it November 29, 2014 Hans P. Paar DIVERGENCE AND CURL THEOREM 1 Introduction We discuss the theorems of Gauss and tokes also
SUMMARY PHYSICS 707 Electrostatics. E(x) = 4πρ(x) and E(x) = 0 (1)
 SUMMARY PHYSICS 707 Electrostatics The basic differential equations of electrostatics are E(x) = 4πρ(x) and E(x) = 0 (1) where E(x) is the electric field and ρ(x) is the electric charge density. The field
SUMMARY PHYSICS 707 Electrostatics The basic differential equations of electrostatics are E(x) = 4πρ(x) and E(x) = 0 (1) where E(x) is the electric field and ρ(x) is the electric charge density. The field
Class XII Chapter 1 Electric Charges And Fields Physics
 Class XII Chapter 1 Electric Charges And Fields Physics Question 1.1: What is the force between two small charged spheres having charges of 2 10 7 C and 3 10 7 C placed 30 cm apart in air? Answer: Repulsive
Class XII Chapter 1 Electric Charges And Fields Physics Question 1.1: What is the force between two small charged spheres having charges of 2 10 7 C and 3 10 7 C placed 30 cm apart in air? Answer: Repulsive
Appendix: Orthogonal Curvilinear Coordinates. We define the infinitesimal spatial displacement vector dx in a given orthogonal coordinate system with
 Appendix: Orthogonal Curvilinear Coordinates Notes: Most of the material presented in this chapter is taken from Anupam G (Classical Electromagnetism in a Nutshell 2012 (Princeton: New Jersey)) Chap 2
Appendix: Orthogonal Curvilinear Coordinates Notes: Most of the material presented in this chapter is taken from Anupam G (Classical Electromagnetism in a Nutshell 2012 (Princeton: New Jersey)) Chap 2
Homework Assignment 4 Solution Set
 Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
Electrodynamics Qualifier Examination
 Electrodynamics Qualifier Examination August 15, 2007 General Instructions: In all cases, be sure to state your system of units. Show all your work, write only on one side of the designated paper, and
Electrodynamics Qualifier Examination August 15, 2007 General Instructions: In all cases, be sure to state your system of units. Show all your work, write only on one side of the designated paper, and
r r 1 r r 1 2 = q 1 p = qd and it points from the negative charge to the positive charge.
 MP204, Important Equations page 1 Below is a list of important equations that we meet in our study of Electromagnetism in the MP204 module. For your exam, you are expected to understand all of these, and
MP204, Important Equations page 1 Below is a list of important equations that we meet in our study of Electromagnetism in the MP204 module. For your exam, you are expected to understand all of these, and
INDIAN SCHOOL MUSCAT FIRST TERM EXAMINATION PHYSICS
 Roll Number SET NO. General Instructions: INDIAN SCHOOL MUSCAT FIRST TERM EXAMINATION PHYSICS CLASS: XII Sub. Code: 04 Time Allotted: Hrs 0.04.08 Max. Marks: 70. All questions are compulsory. There are
Roll Number SET NO. General Instructions: INDIAN SCHOOL MUSCAT FIRST TERM EXAMINATION PHYSICS CLASS: XII Sub. Code: 04 Time Allotted: Hrs 0.04.08 Max. Marks: 70. All questions are compulsory. There are
Chapter 6. Magnetostatic Fields in Matter
 Chapter 6. Magnetostatic Fields in Matter 6.1. Magnetization Any macroscopic object consists of many atoms or molecules, each having electric charges in motion. With each electron in an atom or molecule
Chapter 6. Magnetostatic Fields in Matter 6.1. Magnetization Any macroscopic object consists of many atoms or molecules, each having electric charges in motion. With each electron in an atom or molecule
Reading: Electrostatics 3. Key concepts: Capacitance, energy storage, dielectrics, energy in the E-field.
 Reading: Electrostatics 3. Key concepts: Capacitance, energy storage, dielectrics, energy in the E-field. 1.! Questions about charging and discharging capacitors. When an uncharged capacitor is connected
Reading: Electrostatics 3. Key concepts: Capacitance, energy storage, dielectrics, energy in the E-field. 1.! Questions about charging and discharging capacitors. When an uncharged capacitor is connected
Class 6 : Insulating Materials
 Class 6 : Insulating Materials What is an insulator? Electric dipoles Polarization of an insulator, and how it modifies electric field Electric displacement Boundary conditions for E Recap (1) Maxwell
Class 6 : Insulating Materials What is an insulator? Electric dipoles Polarization of an insulator, and how it modifies electric field Electric displacement Boundary conditions for E Recap (1) Maxwell
Electric Flux. If we know the electric field on a Gaussian surface, we can find the net charge enclosed by the surface.
 Chapter 23 Gauss' Law Instead of considering the electric fields of charge elements in a given charge distribution, Gauss' law considers a hypothetical closed surface enclosing the charge distribution.
Chapter 23 Gauss' Law Instead of considering the electric fields of charge elements in a given charge distribution, Gauss' law considers a hypothetical closed surface enclosing the charge distribution.
Chapter 2 Basics of Electricity and Magnetism
 Chapter 2 Basics of Electricity and Magnetism My direct path to the special theory of relativity was mainly determined by the conviction that the electromotive force induced in a conductor moving in a
Chapter 2 Basics of Electricity and Magnetism My direct path to the special theory of relativity was mainly determined by the conviction that the electromotive force induced in a conductor moving in a
Problem Solving 1: The Mathematics of 8.02 Part I. Coordinate Systems
 Problem Solving 1: The Mathematics of 8.02 Part I. Coordinate Systems In 8.02 we regularly use three different coordinate systems: rectangular (Cartesian), cylindrical and spherical. In order to become
Problem Solving 1: The Mathematics of 8.02 Part I. Coordinate Systems In 8.02 we regularly use three different coordinate systems: rectangular (Cartesian), cylindrical and spherical. In order to become
free space (vacuum) permittivity [ F/m]
![free space (vacuum) permittivity [ F/m] free space (vacuum) permittivity [ F/m]](/thumbs/79/79624275.jpg) Electrostatic Fields Electrostatic fields are static (time-invariant) electric fields produced by static (stationary) charge distributions. The mathematical definition of the electrostatic field is derived
Electrostatic Fields Electrostatic fields are static (time-invariant) electric fields produced by static (stationary) charge distributions. The mathematical definition of the electrostatic field is derived
Consider a point P on the line joining the two charges, as shown in the given figure.
 Question 2.1: Two charges 5 10 8 C and 3 10 8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Question 2.1: Two charges 5 10 8 C and 3 10 8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Boundary value problems
 1 Introduction Boundary value problems Lecture 5 We have found that the electric potential is a solution of the partial differential equation; 2 V = ρ/ǫ 0 The above is Poisson s equation where ρ is the
1 Introduction Boundary value problems Lecture 5 We have found that the electric potential is a solution of the partial differential equation; 2 V = ρ/ǫ 0 The above is Poisson s equation where ρ is the
This is known as charge quantization. Neutral particles, like neutron and photon have zero charge.
 Electrostatics Quantization of Charge Objectives In this lecture you will learn the following Quantization Of Charge and its measurement Coulomb's Law of force between electric charge Superposition principle
Electrostatics Quantization of Charge Objectives In this lecture you will learn the following Quantization Of Charge and its measurement Coulomb's Law of force between electric charge Superposition principle
Downloaded from
 Question 1.1: What is the force between two small charged spheres having charges of 2 10 7 C and 3 10 7 C placed 30 cm apart in air? Repulsive force of magnitude 6 10 3 N Charge on the first sphere, q
Question 1.1: What is the force between two small charged spheres having charges of 2 10 7 C and 3 10 7 C placed 30 cm apart in air? Repulsive force of magnitude 6 10 3 N Charge on the first sphere, q
(b) For the system in question, the electric field E, the displacement D, and the polarization P = D ɛ 0 E are as follows. r2 0 inside the sphere,
 PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
MATH 280 Multivariate Calculus Fall Integrating a vector field over a surface
 MATH 280 Multivariate Calculus Fall 2011 Definition Integrating a vector field over a surface We are given a vector field F in space and an oriented surface in the domain of F as shown in the figure below
MATH 280 Multivariate Calculus Fall 2011 Definition Integrating a vector field over a surface We are given a vector field F in space and an oriented surface in the domain of F as shown in the figure below
Physics 2212 GH Quiz #2 Solutions Spring 2015
 Physics 2212 GH uiz #2 Solutions Spring 2015 Fundamental Charge e = 1.602 10 19 C Mass of an Electron m e = 9.109 10 31 kg Coulomb constant K = 8.988 10 9 N m 2 /C 2 Vacuum Permittivity ϵ 0 = 8.854 10
Physics 2212 GH uiz #2 Solutions Spring 2015 Fundamental Charge e = 1.602 10 19 C Mass of an Electron m e = 9.109 10 31 kg Coulomb constant K = 8.988 10 9 N m 2 /C 2 Vacuum Permittivity ϵ 0 = 8.854 10
Integral Theorems. September 14, We begin by recalling the Fundamental Theorem of Calculus, that the integral is the inverse of the derivative,
 Integral Theorems eptember 14, 215 1 Integral of the gradient We begin by recalling the Fundamental Theorem of Calculus, that the integral is the inverse of the derivative, F (b F (a f (x provided f (x
Integral Theorems eptember 14, 215 1 Integral of the gradient We begin by recalling the Fundamental Theorem of Calculus, that the integral is the inverse of the derivative, F (b F (a f (x provided f (x
Physics 9 Spring 2012 Midterm 1 Solutions
 Physics 9 Spring 22 NAME: TA: Physics 9 Spring 22 Midterm s For the midterm, you may use one sheet of notes with whatever you want to put on it, front and back. Please sit every other seat, and please
Physics 9 Spring 22 NAME: TA: Physics 9 Spring 22 Midterm s For the midterm, you may use one sheet of notes with whatever you want to put on it, front and back. Please sit every other seat, and please
Expansion of 1/r potential in Legendre polynomials
 Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
Review of Electrostatics. Define the gradient operation on a field F = F(x, y, z) by;
 Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
Lecture 4-1 Physics 219 Question 1 Aug Where (if any) is the net electric field due to the following two charges equal to zero?
 Lecture 4-1 Physics 219 Question 1 Aug.31.2016. Where (if any) is the net electric field due to the following two charges equal to zero? y Q Q a x a) at (-a,0) b) at (2a,0) c) at (a/2,0) d) at (0,a) and
Lecture 4-1 Physics 219 Question 1 Aug.31.2016. Where (if any) is the net electric field due to the following two charges equal to zero? y Q Q a x a) at (-a,0) b) at (2a,0) c) at (a/2,0) d) at (0,a) and
2014 F 2014 AI. 1. Why must electrostatic field at the surface of a charged conductor be normal to the surface at every point? Give reason.
 2014 F 1. Why must electrostatic field at the surface of a charged conductor be normal to the surface at every point? Give reason. 2. Figure shows the field lines on a positive charge. Is the work done
2014 F 1. Why must electrostatic field at the surface of a charged conductor be normal to the surface at every point? Give reason. 2. Figure shows the field lines on a positive charge. Is the work done
PHYS 1441 Section 002 Lecture #6
 PHYS 1441 Section 002 Lecture #6 Monday, Sept. 18, 2017 Chapter 21 Motion of a Charged Particle in an Electric Field Electric Dipoles Chapter 22 Electric Flux Gauss Law with many charges What is Gauss
PHYS 1441 Section 002 Lecture #6 Monday, Sept. 18, 2017 Chapter 21 Motion of a Charged Particle in an Electric Field Electric Dipoles Chapter 22 Electric Flux Gauss Law with many charges What is Gauss
Chapter 1 The Electric Force
 Chapter 1 The Electric Force 1. Properties of the Electric Charges 1- There are two kinds of the electric charges in the nature, which are positive and negative charges. - The charges of opposite sign
Chapter 1 The Electric Force 1. Properties of the Electric Charges 1- There are two kinds of the electric charges in the nature, which are positive and negative charges. - The charges of opposite sign
Solution Set Eight. 1 Problem #1: Toroidal Electromagnet with Gap Problem #4: Self-Inductance of a Long Solenoid. 9
 : Solution Set Eight Northwestern University, Electrodynamics I Wednesday, March 9, 6 Contents Problem #: Toroidal Electromagnet with Gap. Problem #: Electromagnetic Momentum. 3 3 Problem #3: Type I Superconductor.
: Solution Set Eight Northwestern University, Electrodynamics I Wednesday, March 9, 6 Contents Problem #: Toroidal Electromagnet with Gap. Problem #: Electromagnetic Momentum. 3 3 Problem #3: Type I Superconductor.
Summary: Applications of Gauss Law
 Physics 2460 Electricity and Magnetism I, Fall 2006, Lecture 15 1 Summary: Applications of Gauss Law 1. Field outside of a uniformly charged sphere of radius a: 2. An infinite, uniformly charged plane
Physics 2460 Electricity and Magnetism I, Fall 2006, Lecture 15 1 Summary: Applications of Gauss Law 1. Field outside of a uniformly charged sphere of radius a: 2. An infinite, uniformly charged plane
Exam 1 Solutions. Note that there are several variations of some problems, indicated by choices in parentheses. Problem 1
 Exam 1 Solutions Note that there are several variations of some problems, indicated by choices in parentheses. Problem 1 A rod of charge per unit length λ is surrounded by a conducting, concentric cylinder
Exam 1 Solutions Note that there are several variations of some problems, indicated by choices in parentheses. Problem 1 A rod of charge per unit length λ is surrounded by a conducting, concentric cylinder
Review of Electrostatics
 Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
APPLICATIONS OF GAUSS S LAW
 APPLICATIONS OF GAUSS S LAW Although Gauss s Law is always correct it is generally only useful in cases with strong symmetries. The basic problem is that it gives the integral of E rather than E itself.
APPLICATIONS OF GAUSS S LAW Although Gauss s Law is always correct it is generally only useful in cases with strong symmetries. The basic problem is that it gives the integral of E rather than E itself.
Magnetic Materials. 1. Magnetization 2. Potential and field of a magnetized object
 Magnetic Materials 1. Magnetization 2. Potential and field of a magnetized object 3. H-field 4. Susceptibility and permeability 5. Boundary conditions 6. Magnetic field energy and magnetic pressure 1 Magnetic
Magnetic Materials 1. Magnetization 2. Potential and field of a magnetized object 3. H-field 4. Susceptibility and permeability 5. Boundary conditions 6. Magnetic field energy and magnetic pressure 1 Magnetic
Solution to Homework 1. Vector Analysis (P201)
 Solution to Homework 1. Vector Analysis (P1) Q1. A = 3î + ĵ ˆk, B = î + 3ĵ + 4ˆk, C = 4î ĵ 6ˆk. The sides AB, BC and AC are, AB = 4î ĵ 6ˆk AB = 7.48 BC = 5î + 5ĵ + 1ˆk BC = 15 1.5 CA = î 3ĵ 4ˆk CA = 6
Solution to Homework 1. Vector Analysis (P1) Q1. A = 3î + ĵ ˆk, B = î + 3ĵ + 4ˆk, C = 4î ĵ 6ˆk. The sides AB, BC and AC are, AB = 4î ĵ 6ˆk AB = 7.48 BC = 5î + 5ĵ + 1ˆk BC = 15 1.5 CA = î 3ĵ 4ˆk CA = 6
Welcome. to Electrostatics
 Welcome to Electrostatics Outline 1. Coulomb s Law 2. The Electric Field - Examples 3. Gauss Law - Examples 4. Conductors in Electric Field Coulomb s Law Coulomb s law quantifies the magnitude of the electrostatic
Welcome to Electrostatics Outline 1. Coulomb s Law 2. The Electric Field - Examples 3. Gauss Law - Examples 4. Conductors in Electric Field Coulomb s Law Coulomb s law quantifies the magnitude of the electrostatic
Electrostatic Potential and Capacitance Examples from NCERT Text Book
 Electrostatic Potential and Capacitance Examples from NCERT Text Book 1. (a) Calculate the potential at a point P due to a charge of 4 10 located 9 cm away. (b) Hence obtain the done in bringing a charge
Electrostatic Potential and Capacitance Examples from NCERT Text Book 1. (a) Calculate the potential at a point P due to a charge of 4 10 located 9 cm away. (b) Hence obtain the done in bringing a charge
Course Notes Math 275 Boise State University. Shari Ultman
 Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
Electromagnetism Answers to Problem Set 8 Spring Jackson Prob. 4.1: Multipole expansion for various charge distributions
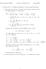 Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th)
 Chapter 5 Magnetostatics Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th) 5.1 Biot-Savart Law So far we were concerned with static configuration of charges known as electrostatics. We now switch to
Chapter 5 Magnetostatics Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th) 5.1 Biot-Savart Law So far we were concerned with static configuration of charges known as electrostatics. We now switch to
How to define the direction of A??
 Chapter Gauss Law.1 Electric Flu. Gauss Law. A charged Isolated Conductor.4 Applying Gauss Law: Cylindrical Symmetry.5 Applying Gauss Law: Planar Symmetry.6 Applying Gauss Law: Spherical Symmetry You will
Chapter Gauss Law.1 Electric Flu. Gauss Law. A charged Isolated Conductor.4 Applying Gauss Law: Cylindrical Symmetry.5 Applying Gauss Law: Planar Symmetry.6 Applying Gauss Law: Spherical Symmetry You will
A Brief Revision of Vector Calculus and Maxwell s Equations
 A Brief Revision of Vector Calculus and Maxwell s Equations Debapratim Ghosh Electronic Systems Group Department of Electrical Engineering Indian Institute of Technology Bombay e-mail: dghosh@ee.iitb.ac.in
A Brief Revision of Vector Calculus and Maxwell s Equations Debapratim Ghosh Electronic Systems Group Department of Electrical Engineering Indian Institute of Technology Bombay e-mail: dghosh@ee.iitb.ac.in
Physics 2049 Exam 1 Spring 2002
 Physics 49 Exam 1 Spring q r1 q1 r13 q3 1. In the figure q 1 = 3µC, q = 4µC, q 3 = 5µC, r 1 = 9m, r 13 = 1m. Compute the magnitude of the total force on q 3. F 3NET = F 31 + F 3 = kq 3q 1 î + kq ( 3q )
Physics 49 Exam 1 Spring q r1 q1 r13 q3 1. In the figure q 1 = 3µC, q = 4µC, q 3 = 5µC, r 1 = 9m, r 13 = 1m. Compute the magnitude of the total force on q 3. F 3NET = F 31 + F 3 = kq 3q 1 î + kq ( 3q )
NYU Physics Preliminary Examination in Electricity & Magnetism Fall 2011
 This is a closed-book exam. No reference materials of any sort are permitted. Full credit will be given for complete solutions to the following five questions. 1. An impenetrable sphere of radius a carries
This is a closed-book exam. No reference materials of any sort are permitted. Full credit will be given for complete solutions to the following five questions. 1. An impenetrable sphere of radius a carries
Chapter 23. Gauss Law. Copyright 2014 John Wiley & Sons, Inc. All rights reserved.
 Chapter 23 Gauss Law Copyright 23-1 Electric Flux Electric field vectors and field lines pierce an imaginary, spherical Gaussian surface that encloses a particle with charge +Q. Now the enclosed particle
Chapter 23 Gauss Law Copyright 23-1 Electric Flux Electric field vectors and field lines pierce an imaginary, spherical Gaussian surface that encloses a particle with charge +Q. Now the enclosed particle
Chap. 1 Fundamental Concepts
 NE 2 Chap. 1 Fundamental Concepts Important Laws in Electromagnetics Coulomb s Law (1785) Gauss s Law (1839) Ampere s Law (1827) Ohm s Law (1827) Kirchhoff s Law (1845) Biot-Savart Law (1820) Faradays
NE 2 Chap. 1 Fundamental Concepts Important Laws in Electromagnetics Coulomb s Law (1785) Gauss s Law (1839) Ampere s Law (1827) Ohm s Law (1827) Kirchhoff s Law (1845) Biot-Savart Law (1820) Faradays
Magnetostatics. Lecture 23: Electromagnetic Theory. Professor D. K. Ghosh, Physics Department, I.I.T., Bombay
 Magnetostatics Lecture 23: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Magnetostatics Up until now, we have been discussing electrostatics, which deals with physics
Magnetostatics Lecture 23: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Magnetostatics Up until now, we have been discussing electrostatics, which deals with physics
