Electromagnetism: Worked Examples. University of Oxford Second Year, Part A2
|
|
|
- Marcus Hardy
- 6 years ago
- Views:
Transcription
1 Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics Michaelmas Term 2017
2 2
3 Contents 1 Potentials Potential of an infinite line charge Vector potential of an infinite wire Potential of a sphere with a charge density σ = k cos θ Multipole expansion Electric dipole moment Electric fields in matter Field of a uniformly polarized sphere D and E of an insulated straight wire D and E of a cylinder with polarization along the axis Linear dielectric sphere with a charge at the center Magnetic fields in matter Field of a uniformly magnetized sphere Field of a cylinder with circular magnetization H and B of a cylinder with magnetization along the axis H and B of a linear insulated straight wire
4 Most of the problems are taken from: David J. Griffiths, Introduction to Electrodynamics, 4th edition (Cambridge University Press) 4
5 Chapter 1 Potentials 1.1 Potential of an infinite line charge (a) A straight wire, assumed infinitely long, has a constant linear charge density λ. Calculate the electric field due to the wire. Use this result to calculate the electric potential. Given the symmetry of the system, the electric field at the point P is: ˆ λdz E = cos θ. 4πɛ 0 d2 wire Using d = r/ cos θ and z = r tan θ, which yields dz = rdθ/ cos 2 θ, we get: E = λ ˆ π/2 cos θdθ = 4πɛ 0 r π/2 λ 2πɛ 0 r. Using cylindrical coordinates, E = V yields: V = λ ln r + C, 2πɛ 0 where C is a constant. We see that the reference point for V cannot be taken at infinity (that is, we cannot have V = 0 when r + ). (b) Show that equation (1.12) from the lecture notes cannot be used to calculate the potential. Using equation (1.12) would yield: V = λ 4πɛ 0 ˆ + dz r 2 + z 2 = λ 4πɛ 0 [arcsinh(x)] +, which gives an infinite result. Equation (1.12) is not valid here because it assumes that the reference point for the potential is at infinity, which cannot be satisfied when the wire extends to infinity. 5
6 1.2 Vector potential of an infinite wire (a) A straight wire, assumed infinitely long, carries a current I. Calculate the magnetic field due to the wire. Use this result to calculate the vector potential. Assuming the current is along the z direction, Ampère s gives the magnetic field: B = µ 0I 2πr ˆθ, where ˆθ is the unit vector in the azimuthal direction. We look for A such that A = B = Bˆθ. In cylindrial coordinates, the θ component of the curl is A r / z A z / r. Given the symmetry of the system, A cannot depend on z, so that we are left with: A z r = µ 0I 2πr = A = µ 0I ln r ẑ. 2π Note that any vector with zero curl could be added to this solution. (b) Show that equation (1.13) (or equation [1.16]) from the lecture notes cannot be used to calculate the vector potential. Using the z component of equation (1.16) would yield: which gives an infinite result. A z = µ ˆ + 0 Idz 4π r 2 + z = µ 0 2 4π [arcsinh(x)]+, As in the case of the infinite line charge above, equation (1.16) is not valid here because it assumes that the reference point for the vector potential is at infinity, which cannot be satisfied when the wire extends to infinity. 6
7 1.3 Potential of a sphere with a charge density σ = k cos θ We consider a sphere of radius R and a spherical coordinate system (r, θ, ϕ) with origin at the centre of the sphere. A charge density σ = k cos θ is glued over the surface of the sphere. Calculate the potential inside and outside the sphere using separation of variables. There is no charge inside and outside the sphere so that the potential V satisfies Laplace s equation 2 V = 0 at any r R. As the charge density does not depend on ϕ, V is also independent of ϕ. The general solution of Laplace s equation in the asisymmetric case is given by equation (1.32) from the lecture notes. We can then write the potential inside and outside the sphere as: Boundary conditions: V in (r, θ) = V out (r, θ) = l=0 ( l=0 ( αl in r l + βin l α out l r l+1 r l + βout l r l+1 ) P l (cos θ), ) P l (cos θ). (1.1) (i) V out (r, θ) 0 as r +, (ii) (iii) (iv) V in (r, θ) finite inside the sphere, V in (R, θ) = V out (R, θ) (V continuous), E out E in = σ V out + V in ɛ 0 r r = k cos θ ɛ 0. General method (always works): we use the boundary conditions to calculate all the coefficients. Condition (i) implies αl out equations (1.1) become: = 0 l, condition (ii) implies β in l = 0 l, so that Then condition (iii) implies: V in (r, θ) = V out (r, θ) = l=0 l=0 α in l r l P l (cos θ), β out l r l+1 P l(cos θ). (1.2) l=0 α in l R l P l (cos θ) = 7 l =0 βl out R l +1 P l (cos θ),
8 where we have renamed the index of summation l in the right hand side to make things more clear. We now multiply each side of this equality by P m (cos θ) sin θ and integrate from 0 to π: l=0 α in l R l ˆ π 0 P l (cos θ)p m (cos θ) sin θdθ = l =0 Using the orthogonality of the Legendre polynomials: ˆ π we obtain α in mr m = β out m /R m+1 0 P l (cos θ)p m (cos θ) sin θdθ = 2 2l + 1 δ l,m, βl out ˆ π P R l +1 l (cos θ)p m (cos θ) sin θdθ. 0 m. Therefore, equations (1.2) become: Then condition (iv) implies: V in (r, θ) = V out (r, θ) = l=0 l=0 α in l r l P l (cos θ), αl in R 2l+1 r l+1 P l(cos θ). (1.3) l=0 (2l + 1)α in l R l 1 P l (cos θ) = k cos θ ɛ 0 where we have used the fact that cos θ = P 1 (cos θ). = k ɛ 0 P 1 (cos θ), Here again, we multiply each side of this equality by P m (cos θ) sin θ and integrate from 0 to π: l=0 (2l+1)α in l R l 1 ˆ π 0 P l (cos θ)p m (cos θ) sin θdθ = k ˆ π P 1 (cos θ)p m (cos θ) sin θdθ ɛ 0 The orthogonality of the Legendre polynomials then yields: 2α in mr m 1 = 2k 3ɛ 0 δ 1,m, that is, α in m = 0 for m 1 and α in 1 = k/(3ɛ 0). Finally, equations (1.3) then become: 0 V in (r, θ) = V out (r, θ) = k r cos θ, 3ɛ 0 k R 3 cos θ. 3ɛ 0 r2 (1.4) 8
9 Shorter method (works in this particular case): we guess some of the coefficients and use the boundary conditions to calculate the others. As the surface charge density is proportional to cos θ, we expect that the potential itself is propotional to cos θ. Therefore, we can assume that all the terms in equations (1.1) are 0 except for l = 1. We will check a posteriori that this assumption is correct. We then write directly: ) V in (r, θ) = (α in r + βin r 2 cos θ, ) V out (r, θ) = (α out r + βout cos θ. r 2 (1.5) As above, the boundary conditions (i) and (ii) yield β in = 0 and α out = 0. Conditions (iii) and (iv) can then be used to calculate α in and β out. Finally, we have found a solution that satisfies Laplace s equation and the boundary conditions. As the solution is unique, this is the correct one, and that justifies a posteriori the assumption we have made to start with. 9
10 1.4 Multipole expansion A sphere of radius R, centered at the origin, carries charge density: ρ(r, θ) = k R (R 2r) sin θ, r2 where k is a constant, and r, θ are the usual spherical coordinates. Find the approximate potential for points on the z axis, far from the sphere. We use equation (1.35) from the lecture notes with O the center of the sphere and M on the z axis, so that γ = θ and r = z. Monopole term: V 0 (z) = 1 ρ(r)dτ = 4πɛ 0 z V Q 4πɛ 0 z, with dτ = r 2 sin θ dr dθ dϕ and Q is the total charge of the sphere. Here: ˆ R ˆ 2π ˆ π Q = kr (R 2r) dr dϕ sin 2 θdθ. r=0 ϕ=0 θ=0 The integral over r is 0 so that V 0 (z) = 0. Dipole term: Here: V 1 (z) = 1 4πɛ 0 z 2 r cos θρ(r)dτ. V V 1 (z) = kr ˆ R ˆ 2π ˆ π 4πɛ 0 z 2 (R 2r) rdr dϕ sin 2 θ cos θdθ. r=0 ϕ=0 θ=0 The integral over θ is 0 so that V 1 (z) = 0. Quadrupole term: Here: V 2 (z) = V 2 (z) = 1 4πɛ 0 z 3 r 2 1 ( 3 cos 2 θ 1 ) ρ(r)dτ. V 2 kr ˆ R ˆ 2π ˆ π 8πɛ 0 z 3 (R 2r) r 2 ( dr dϕ 3 cos 2 θ 1 ) sin 2 θdθ. r=0 ϕ=0 θ=0 The integral over r is R 4 /6 and the integral over θ is π/8, so that: V (z) V 3 (z) = 1 4πɛ 0 kπ 2 R 5 48z 3. 10
11 1.5 Electric dipole moment Four charges are placed as shown. Calculate the electric dipole moment of the distribution and find an approximate formula for the potential, valid far from the origin (use spherical coordinates). Since the total charge is 0, the monopole term is also 0. The dipole term in the expansion of the potential is given by: V 1 (r) = 1 4πɛ 0 p ˆr r 2, (equation 1.37 from the lecture notes) where r is the position vector, ˆr is the unit vector along the radial direction in spherical coordinates and p is the electric dipole moment. We have: p = i q i r i, where r i denotes the position of the charge q i. Since the total charge is 0, p does not depend on the choice of the origin from which we measure the positions. We use O as the origin. Then we have: p = (3qa qa)ẑ + ( 2qa + 2qa)ŷ = 2qaẑ, where ẑ and ŷ are unit vectors. Therefore: where we have used ẑ ˆr = cos θ. V (r) V 1 (r) = 1 4πɛ 0 2qa cos θ r 2, 11
12 12
13 Chapter 2 Electric fields in matter 2.1 Field of a uniformly polarized sphere (a) Find the electric field produced by a uniformly polarized sphere of radius R. (Hint: use the results of example 1.3) Inside the sphere, the volume charge density is ρ p = P which is 0 as the polarization is uniform. At the surface of the sphere, there is a surface charge density σ p = P ˆr, where ˆr is the unit vector in the radial direction. We choose the z axis in the direction of P, so that σ p = P cos θ in spherical coordinates. In example 1.3 we have calculated the potential of a sphere with a surface charge density proportional to cos θ: V (r, θ) = P 3ɛ 0 r cos θ, for r R, V (r, θ) = P R 3 cos θ, for r R. 3ɛ 0 r2 (2.1) The electric field is: E = V = V r ˆr 1 V r θ ˆθ, where ˆθ is the unit vector in the azimuthal direction. Therefore: 13
14 E = P ẑ, for r < R, 3ɛ 0 2p cos θ p sin θ E = ˆr + 4πɛ 0 r3 4πɛ 0 r ˆθ, 3 for r > R, (2.2) where we have used r cos θ = z and we have defined the total dipole moment of the sphere p = (4/3)πR 3 P. We see that the field inside the sphere is uniform, whereas the field outside the sphere is that of a perfect dipole p at the origin. (b) Calculate the potential directly using equation 2.7 from the lecture notes. Equation 2.7 gives: V (r) = 1 P(r )dτ (r r ) 4πɛ 0 V r r 3, (2.3) where V is the volume of the sphere. We have seen in the lectures that this expression is valid for calculating the potential both inside and outside the sphere. Since P is uniform, it can be taken out of the integral, so that we obtain: [ 1 V (r) = P 4πɛ 0 V (r r )dτ ] r r 3. (2.4) The term in brackets is the electric field E 1 of a sphere with a uniform charge density equal to unity. This electric field can be calculated using Gauss s law and is given by: E 1 = E 1 = r 3ɛ 0 ˆr, for r < R, V = P E 1 can then be used to recover the potential. (2.5) R3 3ɛ 0 r 2 ˆr, for r > R. Note that the parallel component of E at the surface, E θ (R), is continuous, whereas the perpendicular component, E r (R), is discontinuous: E out E in = σ ˆr. ɛ 0 14
15 2.2 D and E of an insulated straight wire A long straight wire, carrying uniform line charge λ, is surrounded by rubber insulation out to a radius a. Find the electric displacement and the electric field. Gauss s law (2.16) from the lecture notes can be used to calculate D. Given the symmetry of the problem, and using cylindrical coordinates, D depends only on the distance r to the wire and is in the radial direction. We choose the Gaussian surface to be a cylinder of radius r and length L around the wire. Then Gauss s law yields D 2πrL = λl, that is: D = 2πrˆr, λ where ˆr is the unit vector in the radial direction. This is true for all r > 0. Outside the insulation, P = 0 so that: E = D ɛ 0 = λ 2πɛ 0 rˆr. Inside the insulation, E = (D P)/ɛ 0, which we cannot calculate as we do not know P. 2.3 D and E of a cylinder with polarization along the axis A cylinder of finite size carries a frozen in uniform polarization P, parallel to its axis. (Such a cylinder is know as a bar electret). Find the polarization charges, sketch the electric field and the electric displacement (use the boundary conditions). Polarization charges: there is no volume charge as P is uniform, and the surface charge is P ˆn = +σ on one end and σ on the other end. Electric field: The bar is therefore like a physical dipole. Note that electric field lines terminate on charges, whether they are bound or free, with E pointing towards the negative charge. (Figure from Purcell.) 15
16 The perpendicular component of E is discontinuous at the surfaces: E out E in = ±σ ɛ 0 ˆn, whereas the parallel component of E is continuous across the lateral surface. Electric displacement: D = ɛ 0 E + P, therefore D = E outside the cylinder. Since there is no free charge at the surfaces, the perpendicular component of D is continuous there, so that D inside the cylinder goes from left to right. Note that D lines terminate on free charges. As there are no free charges here, D lines are continuous: We see that even though there is no polarization outside the cylinder, D is non zero there. This is because the polarization is discontinuous at the surface of the cylinder, and along the lateral surface we have (see equation [2.22] from the lecture notes): D in D out = P. The discontinuity of P generates a non zero D outside. 2.4 Linear dielectric sphere with a charge at the center A point charge q is embedded at the center of a sphere of linear dielectric material (with susceptibility χ e and radius R). Find the electric field, the polarization, and the polarization charge densities, ρ p and σ p. What is the total polarization charge on the surface? Where is the compensating negative polarization charge located? Electric displacement: Given the symmetry of the problem, in spherical coordinates, Gauss s law yields: D = q 4πr 2 ˆr, for all r > 0, where ˆr is the unit vector in the radial direction. Electric field: Inside the sphere, E = D/ɛ with ɛ = ɛ 0 (1 + χ e ). Therefore: E = and E = D/ɛ 0 outside the sphere. q ˆr, for r < R, 4πɛ 0 (1 + χ e )r2 16
17 Polarization: P = ɛ 0 χ e E inside the sphere, that is: P = Volume polarization charge: χ e q ˆr, for r < R. 4π(1 + χ e )r2 χ e q ρ p = P = 4π(1 + χ e ) Using the definition of the δ function in 3 dimensions: ( ) ˆr r 2 = 4πδ 3 (r), ( ) ˆr r 2. we get: χ e ρ p = q δ 3 (r). 1 + χ e Surface polarization charge: σ p = P(R) ˆr = Therefore, the total surface charge is: Q surf = σ p 4πR 2 = χ e q 4π(1 + χ e )R 2. χ e 1 + χ e q. The compensating negative charge is at the center, which is implied by the fact that the δ 3 function is non zero only at r = 0. As P is radial, the dipoles in the sphere are all aligned in the radial direction, leaving a net charge at the center and at the surface only. 17
18 18
19 Chapter 3 Magnetic fields in matter 3.1 Field of a uniformly magnetized sphere (a) Find the magnetic field produced by a uniformly magnetized sphere of radius R. (Hint: use the results of Problem 7 in Problem Set 1) Inside the sphere, the volume current density is J m = M which is 0 as the magnetization is uniform. At the surface of the sphere, there is a surface current density K m = M ˆr. We choose the z axis in the direction of M, so that K m = M sin θ ˆϕ in spherical coordinates. In Problem 7, Problem Set 1, we have calculated the magnetic field due to a spinning sphere, which has a surface current density K proportional to sin θ in the ˆϕ direction. By making the appropriate replacement, we therefore get: B = 2 3 µ 0M, for r < R, B = µ 0MR 3 ( ) 3r 3 2 cos θˆr + sin θˆθ, for r > R. (3.1) We see that the field inside the sphere is uniform. 19
20 We define the total dipole moment of the sphere m = (4/3)πR 3 M. Then the field outside the sphere can be written as: B = µ ( ) 0m 4πr 3 2 cos θˆr + sin θˆθ, which is the field of a perfect dipole m at the origin. (b) Calculate the vector potential A directly using equation 3.13 from the lecture notes. Derive the magnetic field from A. Equation 3.13 gives: A(r) = µ 0 M(r )dτ (r r ) 4π V r r 3, (3.2) where V is the volume of the sphere. We have seen in the lectures that this expression is valid for calculating the potential both inside and outside the sphere. Since M is uniform, it can be taken out of the integral, so that we obtain: [ µ0 A(r) = M 4π V (r r )dτ ] r r 3. (3.3) The term in brackets is the electric field E of a sphere with a uniform charge density equal to µ 0 ɛ 0. This electric field can be calculated using Gauss s law and is given by: A = M E if then equal to: E = µ 0r ˆr, for r < R, 3 E = µ 0R 3 (3.4) 3r 2 ˆr, for r > R. A = µ 0Mr 3 sin θ ˆϕ, for r < R, A = µ 0MR 3 3r 2 sin θ ˆϕ, for r > R. (3.5) The magnetic field is given by: B = A = 1 r sin θ which leads to the same expressions as in (a). θ (sin θ A) ˆr 1 r (ra) ˆθ, r 20
21 Field lines of a uniformly magnetized sphere. Note that the perpendicular component of B at the surface, B r (R), is continuous, whereas the parallel component, B θ (R), is discontinuous: B out B in = µ 0K mˆθ. 3.2 Field of a cylinder with circular magnetization A long circular cylinder of radius R carries a magnetization M = kr 2 ˆϕ, where k is a constant, r the radius in cylindrical coordinates and ˆϕ the unit vector in the azimuthal direction. Find the magnetic field due to M inside and outside the cylinder. Calculate H using B and M and, independently, using the current distribution. The volume current density is: The surface current density is: J m = M = 1 r d (rm) ẑ = 3krẑ. dr K m = M(R) ˆr = kr 2 ẑ. Note that the current is flowing up in the volume of the cylinder and returns down along the surface. For a length L of the cylinder, the total current is: I tot = K m 2πRL + L as expected. ˆ R 0 J m 2πrdr = 2πkR 3 Lẑ + 6πkLẑ ˆ R Given the symmetry of the system, and using Ampère s law, we obtain: 0 r 2 dr = 0, and ˆ r 2πrB = µ 0 ˆϕ J m 2πrdr = B = µ 0 kr 2 ˆϕ = µ 0 M for r < R, 0 2πrB = µ 0 ˆϕI tot = B = 0 for r > R. To get H we use H = B/µ 0 M. Then H = 0 everywhere. This is consistent with Ampère s law, as H = J f = 0 and the symmetry of the problem leads to 2πrH = 0ˆϕ. Note however that, in general, there may be a non zero H even when there is no free current (see below). 21
22 3.3 H and B of a cylinder with magnetization along the axis A cylinder of finite size carries a frozen in uniform magnetization M, parallel to its axis. (Such a cylinder is know as a bar magnet). Find the magnetization currents, sketch the magnetic field B and the auxiliary field H (use the boundary conditions). Magnetization currents: Since the magnetization is uniform, the volume current density is J m = M = 0. The surface current density is K m = M ˆn, that is K m = M ˆϕ on the lateral surface. Magnetic field: The bar is like a finite size solenoid. (Figure from Purcell.) The perpendicular component of B is continuous across the surfaces, whereas: B in B out = µ 0K m ẑ. Auxiliary field: H = B/µ 0 M, therefore H = B/µ 0 outside the cylinder. Since there is no free current at the surfaces, the parallel component of H is continuous there, so that H inside the cylinder goes from right to left. We see that even though there is no magnetization outside the cylinder, H is non zero there. This is because the magnetization is discontinuous at the surface of the cylinder: H out H in = B out µ 0 B in µ 0 + M = M. The discontinuity of M generates a non zero H outside. 22
23 3.4 H and B of a linear insulated straight wire A current I flows along a straight wire or radius a. If the wire is made of linear material with susceptibility χ m, and the current is distributed uniformly, what is the magnetic field a distance r from the axis? Find all the magnetization currents. What is the net magnetization current flowing along the wire? We define the volume density of free current: J f = I/(πa 2 ), and we assume that the current I flows up along the z axis. Given the symmetry of the system, and using cylindrical coordinates, Ampère s law gives: H 2πr = πr 2 J f ˆθ = H = Ir 2πa 2 ˆθ for r < a, and: H 2πr = I ˆθ = H = I 2πr ˆθ for r > a. Therefore, B = µh, with µ = µ 0 (1 + χ m ) inside the insulated material and µ = µ 0 outside, yields: B = µ 0(1 + χ m )Ir 2πa 2 ˆθ for r < a, B = µ 0I 2πr ˆθ for r > a. Volume density of magnetization current: J m = M = (χ m H) = χ m H, that is: J m = χ m J f ẑ. Surface density of magnetization current: K m = M ˆr = χ m H(a) ˆr, that is: K m = χ m Iẑ/(2πa). Net magnetization current along the wire: as expected. ˆ a 0 J m 2πrdr + K m 2πa = 0, 23
Department of Physics IIT Kanpur, Semester II,
 Department of Physics IIT Kanpur, Semester II, 7-8 PHYA: Physics II Solution # 4 Instructors: AKJ & SC Solution 4.: Force with image charges (Griffiths rd ed. Prob.6 As far as force is concerned, this
Department of Physics IIT Kanpur, Semester II, 7-8 PHYA: Physics II Solution # 4 Instructors: AKJ & SC Solution 4.: Force with image charges (Griffiths rd ed. Prob.6 As far as force is concerned, this
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3
 Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
Summary: Applications of Gauss Law
 Physics 2460 Electricity and Magnetism I, Fall 2006, Lecture 15 1 Summary: Applications of Gauss Law 1. Field outside of a uniformly charged sphere of radius a: 2. An infinite, uniformly charged plane
Physics 2460 Electricity and Magnetism I, Fall 2006, Lecture 15 1 Summary: Applications of Gauss Law 1. Field outside of a uniformly charged sphere of radius a: 2. An infinite, uniformly charged plane
Homework Assignment 4 Solution Set
 Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
1. (3) Write Gauss Law in differential form. Explain the physical meaning.
 Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
Solution Set Eight. 1 Problem #1: Toroidal Electromagnet with Gap Problem #4: Self-Inductance of a Long Solenoid. 9
 : Solution Set Eight Northwestern University, Electrodynamics I Wednesday, March 9, 6 Contents Problem #: Toroidal Electromagnet with Gap. Problem #: Electromagnetic Momentum. 3 3 Problem #3: Type I Superconductor.
: Solution Set Eight Northwestern University, Electrodynamics I Wednesday, March 9, 6 Contents Problem #: Toroidal Electromagnet with Gap. Problem #: Electromagnetic Momentum. 3 3 Problem #3: Type I Superconductor.
Electric fields in matter
 Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Electrodynamics I Midterm - Part A - Closed Book KSU 2005/10/17 Electro Dynamic
 Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
l=0 The expansion coefficients can be determined, for example, by finding the potential on the z-axis and expanding that result in z.
 Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
Physics 3323, Fall 2016 Problem Set 2 due Sep 9, 2016
 Physics 3323, Fall 26 Problem Set 2 due Sep 9, 26. What s my charge? A spherical region of radius R is filled with a charge distribution that gives rise to an electric field inside of the form E E /R 2
Physics 3323, Fall 26 Problem Set 2 due Sep 9, 26. What s my charge? A spherical region of radius R is filled with a charge distribution that gives rise to an electric field inside of the form E E /R 2
Problem Set #4: 4.1,4.7,4.9 (Due Monday, March 25th)
 Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 110A. Homework #7. Benjamin Stahl. March 3, 2015
 UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #7 Benjamin Stahl March 3, 5 GRIFFITHS, 5.34 It will be shown that the magnetic field of a dipole can written in the following
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #7 Benjamin Stahl March 3, 5 GRIFFITHS, 5.34 It will be shown that the magnetic field of a dipole can written in the following
Physics 505 Fall 2005 Homework Assignment #7 Solutions
 Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
University of Illinois at Chicago Department of Physics
 University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 110A. Homework #6. Benjamin Stahl. February 17, 2015
 UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #6 Benjamin Stahl February 7, 5 GRIFFITHS, 5.9 The magnetic field at a point, P, will be found for each of the steady current
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #6 Benjamin Stahl February 7, 5 GRIFFITHS, 5.9 The magnetic field at a point, P, will be found for each of the steady current
Second Year Electromagnetism Summer 2018 Caroline Terquem. Vacation work: Problem set 0. Revisions
 Second Year Electromagnetism Summer 2018 Caroline Terquem Vacation work: Problem set 0 Revisions At the start of the second year, you will receive the second part of the Electromagnetism course. This vacation
Second Year Electromagnetism Summer 2018 Caroline Terquem Vacation work: Problem set 0 Revisions At the start of the second year, you will receive the second part of the Electromagnetism course. This vacation
FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 2017
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
Physics 7B Midterm 2 Solutions - Fall 2017 Professor R. Birgeneau
 Problem 1 Physics 7B Midterm 2 Solutions - Fall 217 Professor R. Birgeneau (a) Since the wire is a conductor, the electric field on the inside is simply zero. To find the electric field in the exterior
Problem 1 Physics 7B Midterm 2 Solutions - Fall 217 Professor R. Birgeneau (a) Since the wire is a conductor, the electric field on the inside is simply zero. To find the electric field in the exterior
(b) For the system in question, the electric field E, the displacement D, and the polarization P = D ɛ 0 E are as follows. r2 0 inside the sphere,
 PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
Electrostatics. Chapter Maxwell s Equations
 Chapter 1 Electrostatics 1.1 Maxwell s Equations Electromagnetic behavior can be described using a set of four fundamental relations known as Maxwell s Equations. Note that these equations are observed,
Chapter 1 Electrostatics 1.1 Maxwell s Equations Electromagnetic behavior can be described using a set of four fundamental relations known as Maxwell s Equations. Note that these equations are observed,
Magnetostatics III Magnetic Vector Potential (Griffiths Chapter 5: Section 4)
 Dr. Alain Brizard Electromagnetic Theory I PY ) Magnetostatics III Magnetic Vector Potential Griffiths Chapter 5: Section ) Vector Potential The magnetic field B was written previously as Br) = Ar), 1)
Dr. Alain Brizard Electromagnetic Theory I PY ) Magnetostatics III Magnetic Vector Potential Griffiths Chapter 5: Section ) Vector Potential The magnetic field B was written previously as Br) = Ar), 1)
ECE 3209 Electromagnetic Fields Final Exam Example. University of Virginia Solutions
 ECE 3209 Electromagnetic Fields Final Exam Example University of Virginia Solutions (print name above) This exam is closed book and closed notes. Please perform all work on the exam sheets in a neat and
ECE 3209 Electromagnetic Fields Final Exam Example University of Virginia Solutions (print name above) This exam is closed book and closed notes. Please perform all work on the exam sheets in a neat and
Junior-level Electrostatics Content Review
 Junior-level Electrostatics Content Review Please fill out the following exam to the best of your ability. This will not count towards your final grade in the course. Do your best to get to all the questions
Junior-level Electrostatics Content Review Please fill out the following exam to the best of your ability. This will not count towards your final grade in the course. Do your best to get to all the questions
Tutorial 3 - Solutions Electromagnetic Waves
 Tutorial 3 - Solutions Electromagnetic Waves You can find formulas you require for vector calculus at the end of this tutorial. 1. Find the Divergence and Curl of the following functions - (a) k r ˆr f
Tutorial 3 - Solutions Electromagnetic Waves You can find formulas you require for vector calculus at the end of this tutorial. 1. Find the Divergence and Curl of the following functions - (a) k r ˆr f
lim = F F = F x x + F y y + F z
 Physics 361 Summary of Results from Lecture Physics 361 Derivatives of Scalar and Vector Fields The gradient of a scalar field f( r) is given by g = f. coordinates f g = ê x x + ê f y y + ê f z z Expressed
Physics 361 Summary of Results from Lecture Physics 361 Derivatives of Scalar and Vector Fields The gradient of a scalar field f( r) is given by g = f. coordinates f g = ê x x + ê f y y + ê f z z Expressed
ELECTRO MAGNETIC FIELDS
 SET - 1 1. a) State and explain Gauss law in differential form and also list the limitations of Guess law. b) A square sheet defined by -2 x 2m, -2 y 2m lies in the = -2m plane. The charge density on the
SET - 1 1. a) State and explain Gauss law in differential form and also list the limitations of Guess law. b) A square sheet defined by -2 x 2m, -2 y 2m lies in the = -2m plane. The charge density on the
Applications of Ampere s Law
 Applications of Ampere s Law In electrostatics, the electric field due to any known charge distribution ρ(x, y, z) may alwaysbeobtainedfromthecoulomblaw it sauniversal tool buttheactualcalculation is often
Applications of Ampere s Law In electrostatics, the electric field due to any known charge distribution ρ(x, y, z) may alwaysbeobtainedfromthecoulomblaw it sauniversal tool buttheactualcalculation is often
Topic 7. Electric flux Gauss s Law Divergence of E Application of Gauss Law Curl of E
 Topic 7 Electric flux Gauss s Law Divergence of E Application of Gauss Law Curl of E urface enclosing an electric dipole. urface enclosing charges 2q and q. Electric flux Flux density : The number of field
Topic 7 Electric flux Gauss s Law Divergence of E Application of Gauss Law Curl of E urface enclosing an electric dipole. urface enclosing charges 2q and q. Electric flux Flux density : The number of field
Classical Field Theory: Electrostatics-Magnetostatics
 Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Summary: Curvilinear Coordinates
 Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
0.4. math. r r = r 2 + r 2 2r r cos(θ ) 0.5. Coordiates.
 .. Electrostatics... Multipole. F = E(r) = E(r) = S n qq i r r i 3 (r r i) i= n i= q i r r i 3 (r r i) d 3 r ρ(r ) 3 (r r ) ds E(r) = 4πQ enclosed E(r) = 4πρ(r ) E(r) = Φ(r) d 3 r ρ(r ) r dl E W = q(φ(r
.. Electrostatics... Multipole. F = E(r) = E(r) = S n qq i r r i 3 (r r i) i= n i= q i r r i 3 (r r i) d 3 r ρ(r ) 3 (r r ) ds E(r) = 4πQ enclosed E(r) = 4πρ(r ) E(r) = Φ(r) d 3 r ρ(r ) r dl E W = q(φ(r
2nd Year Electromagnetism 2012:.Exam Practice
 2nd Year Electromagnetism 2012:.Exam Practice These are sample questions of the type of question that will be set in the exam. They haven t been checked the way exam questions are checked so there may
2nd Year Electromagnetism 2012:.Exam Practice These are sample questions of the type of question that will be set in the exam. They haven t been checked the way exam questions are checked so there may
Electric Flux. To investigate this, we have to understand electric flux.
 Problem 21.72 A charge q 1 = +5. nc is placed at the origin of an xy-coordinate system, and a charge q 2 = -2. nc is placed on the positive x-axis at x = 4. cm. (a) If a third charge q 3 = +6. nc is now
Problem 21.72 A charge q 1 = +5. nc is placed at the origin of an xy-coordinate system, and a charge q 2 = -2. nc is placed on the positive x-axis at x = 4. cm. (a) If a third charge q 3 = +6. nc is now
QUALIFYING EXAMINATION, Part 1. Solutions. Problem 1: Mathematical Methods. r r r 2 r r2 = 0 r 2. d 3 r. t 0 e t dt = e t
 QUALIFYING EXAMINATION, Part 1 Solutions Problem 1: Mathematical Methods (a) For r > we find 2 ( 1 r ) = 1 ( ) 1 r 2 r r2 = 1 ( 1 ) r r r 2 r r2 = r 2 However for r = we get 1 because of the factor in
QUALIFYING EXAMINATION, Part 1 Solutions Problem 1: Mathematical Methods (a) For r > we find 2 ( 1 r ) = 1 ( ) 1 r 2 r r2 = 1 ( 1 ) r r r 2 r r2 = r 2 However for r = we get 1 because of the factor in
Expansion of 1/r potential in Legendre polynomials
 Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
1. (3) Write Gauss Law in differential form. Explain the physical meaning.
 Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about the physics involved,
Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about the physics involved,
Ch 30 - Sources of Magnetic Field
 Ch 30 - Sources of Magnetic Field Currents produce Magnetism? 1820, Hans Christian Oersted: moving charges produce a magnetic field. The direction of the field is determined using a RHR. Oersted (1820)
Ch 30 - Sources of Magnetic Field Currents produce Magnetism? 1820, Hans Christian Oersted: moving charges produce a magnetic field. The direction of the field is determined using a RHR. Oersted (1820)
7 Curvilinear coordinates
 7 Curvilinear coordinates Read: Boas sec. 5.4, 0.8, 0.9. 7. Review of spherical and cylindrical coords. First I ll review spherical and cylindrical coordinate systems so you can have them in mind when
7 Curvilinear coordinates Read: Boas sec. 5.4, 0.8, 0.9. 7. Review of spherical and cylindrical coords. First I ll review spherical and cylindrical coordinate systems so you can have them in mind when
Dielectrics - III. Lecture 22: Electromagnetic Theory. Professor D. K. Ghosh, Physics Department, I.I.T., Bombay
 Dielectrics - III Lecture 22: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We continue with our discussion of dielectric medium. Example : Dielectric Sphere in a uniform
Dielectrics - III Lecture 22: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We continue with our discussion of dielectric medium. Example : Dielectric Sphere in a uniform
xy 2 e 2z dx dy dz = 8 3 (1 e 4 ) = 2.62 mc. 12 x2 y 3 e 2z 2 m 2 m 2 m Figure P4.1: Cube of Problem 4.1.
 Problem 4.1 A cube m on a side is located in the first octant in a Cartesian coordinate system, with one of its corners at the origin. Find the total charge contained in the cube if the charge density
Problem 4.1 A cube m on a side is located in the first octant in a Cartesian coordinate system, with one of its corners at the origin. Find the total charge contained in the cube if the charge density
Magnetic Fields Part 2: Sources of Magnetic Fields
 Magnetic Fields Part 2: Sources of Magnetic Fields Last modified: 08/01/2018 Contents Links What Causes a Magnetic Field? Moving Charges Right Hand Grip Rule Permanent Magnets Biot-Savart Law Magnetic
Magnetic Fields Part 2: Sources of Magnetic Fields Last modified: 08/01/2018 Contents Links What Causes a Magnetic Field? Moving Charges Right Hand Grip Rule Permanent Magnets Biot-Savart Law Magnetic
Gauss s Law. Chapter 22. Electric Flux Gauss s Law: Definition. Applications of Gauss s Law
 Electric Flux Gauss s Law: Definition Chapter 22 Gauss s Law Applications of Gauss s Law Uniform Charged Sphere Infinite Line of Charge Infinite Sheet of Charge Two infinite sheets of charge Phys 2435:
Electric Flux Gauss s Law: Definition Chapter 22 Gauss s Law Applications of Gauss s Law Uniform Charged Sphere Infinite Line of Charge Infinite Sheet of Charge Two infinite sheets of charge Phys 2435:
PHYS 110B - HW #4 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 11B - HW #4 Spring 4, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased [1.] Problem 8. from Griffiths Reference problem 7.31 figure 7.43. a Let
PHYS 11B - HW #4 Spring 4, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased [1.] Problem 8. from Griffiths Reference problem 7.31 figure 7.43. a Let
PHY481 - Outline of solutions to Homework 3
 1 PHY481 - Outline of solutions to Homework 3 Problem 3.8: We consider a charge outside a conducting sphere that is neutral. In order that the sphere be neutral, we have to introduce a new image charge
1 PHY481 - Outline of solutions to Homework 3 Problem 3.8: We consider a charge outside a conducting sphere that is neutral. In order that the sphere be neutral, we have to introduce a new image charge
1. ELECTRIC CHARGES AND FIELDS
 1. ELECTRIC CHARGES AND FIELDS 1. What are point charges? One mark questions with answers A: Charges whose sizes are very small compared to the distance between them are called point charges 2. The net
1. ELECTRIC CHARGES AND FIELDS 1. What are point charges? One mark questions with answers A: Charges whose sizes are very small compared to the distance between them are called point charges 2. The net
Chapter 5. Magnetostatics
 Chapter 5. Magnetostatics 5.4 Magnetic Vector Potential 5.1.1 The Vector Potential In electrostatics, E Scalar potential (V) In magnetostatics, B E B V A Vector potential (A) (Note) The name is potential,
Chapter 5. Magnetostatics 5.4 Magnetic Vector Potential 5.1.1 The Vector Potential In electrostatics, E Scalar potential (V) In magnetostatics, B E B V A Vector potential (A) (Note) The name is potential,
Steady and unsteady diffusion
 Chapter 5 Steady and unsteady diffusion In this chapter, we solve the diffusion and forced convection equations, in which it is necessary to evaluate the temperature or concentration fields when the velocity
Chapter 5 Steady and unsteady diffusion In this chapter, we solve the diffusion and forced convection equations, in which it is necessary to evaluate the temperature or concentration fields when the velocity
CHAPTER 3 POTENTIALS 10/13/2016. Outlines. 1. Laplace s equation. 2. The Method of Images. 3. Separation of Variables. 4. Multipole Expansion
 CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
Lecture notes for ELECTRODYNAMICS.
 Lecture notes for 640-343 ELECTRODYNAMICS. 1 Summary of Electrostatics 1.1 Coulomb s Law Force between two point charges F 12 = 1 4πɛ 0 Q 1 Q 2ˆr 12 r 1 r 2 2 (1.1.1) 1.2 Electric Field For a charge distribution:
Lecture notes for 640-343 ELECTRODYNAMICS. 1 Summary of Electrostatics 1.1 Coulomb s Law Force between two point charges F 12 = 1 4πɛ 0 Q 1 Q 2ˆr 12 r 1 r 2 2 (1.1.1) 1.2 Electric Field For a charge distribution:
The dielectrophoretic force on dielectric spherical objects
 10064 - Physics Project The dielectrophoretic force on dielectric spherical objects Andreas Ammitzbøll s042191 Janosch Michael Cristoph Rauba s042606 Marco Haller Schultz s042357 Supervisors: Niels Asger
10064 - Physics Project The dielectrophoretic force on dielectric spherical objects Andreas Ammitzbøll s042191 Janosch Michael Cristoph Rauba s042606 Marco Haller Schultz s042357 Supervisors: Niels Asger
Physics 202, Lecture 14
 Physics 202, Lecture 14 Today s Topics Sources of the Magnetic Field (Ch. 27) Review of Biot-Savart Law Ampere s Law Magnetism in Matter Magnetic Fields (Biot-Savart): Summary Current loop, distance on
Physics 202, Lecture 14 Today s Topics Sources of the Magnetic Field (Ch. 27) Review of Biot-Savart Law Ampere s Law Magnetism in Matter Magnetic Fields (Biot-Savart): Summary Current loop, distance on
Electromagnetism Answers to Problem Set 9 Spring 2006
 Electromagnetism 70006 Answers to Problem et 9 pring 006. Jackson Prob. 5.: Reformulate the Biot-avart law in terms of the solid angle subtended at the point of observation by the current-carrying circuit.
Electromagnetism 70006 Answers to Problem et 9 pring 006. Jackson Prob. 5.: Reformulate the Biot-avart law in terms of the solid angle subtended at the point of observation by the current-carrying circuit.
Problems in Magnetostatics
 Problems in Magnetostatics 8th February 27 Some of the later problems are quite challenging. This is characteristic of problems in magnetism. There are trivial problems and there are tough problems. Very
Problems in Magnetostatics 8th February 27 Some of the later problems are quite challenging. This is characteristic of problems in magnetism. There are trivial problems and there are tough problems. Very
Electrodynamics Exam Solutions
 Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
E & M TEST BANK. August 2016
 August 2016 E & M TEST BANK 1. Charge in an Atom [500 level] A certain charge distribution ρ(r) generates an electric potential Φ(r) = e 0a e 2r/a ( a r + 1), with constants e 0 and a. (a) Find the electric
August 2016 E & M TEST BANK 1. Charge in an Atom [500 level] A certain charge distribution ρ(r) generates an electric potential Φ(r) = e 0a e 2r/a ( a r + 1), with constants e 0 and a. (a) Find the electric
(a) Consider a sphere of charge with radius a and charge density ρ(r) that varies with radius as. ρ(r) = Ar n for r a
 Physics 7B Midterm 2 - Fall 207 Professor R. Birgeneau Total Points: 00 ( Problems) This exam is out of 00 points. Show all your work and take particular care to explain your steps. Partial credit will
Physics 7B Midterm 2 - Fall 207 Professor R. Birgeneau Total Points: 00 ( Problems) This exam is out of 00 points. Show all your work and take particular care to explain your steps. Partial credit will
Electromagnetism - Lecture 10. Magnetic Materials
 Electromagnetism - Lecture 10 Magnetic Materials Magnetization Vector M Magnetic Field Vectors B and H Magnetic Susceptibility & Relative Permeability Diamagnetism Paramagnetism Effects of Magnetic Materials
Electromagnetism - Lecture 10 Magnetic Materials Magnetization Vector M Magnetic Field Vectors B and H Magnetic Susceptibility & Relative Permeability Diamagnetism Paramagnetism Effects of Magnetic Materials
Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 2, 3, and 4, and Di Bartolo, Chap. 2. 2π nx i a. ( ) = G n.
 Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
d 1 µ 2 Θ = 0. (4.1) consider first the case of m = 0 where there is no azimuthal dependence on the angle φ.
 4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
E. not enough information given to decide
 Q22.1 A spherical Gaussian surface (#1) encloses and is centered on a point charge +q. A second spherical Gaussian surface (#2) of the same size also encloses the charge but is not centered on it. Compared
Q22.1 A spherical Gaussian surface (#1) encloses and is centered on a point charge +q. A second spherical Gaussian surface (#2) of the same size also encloses the charge but is not centered on it. Compared
PHYS152 Lecture 8. Eunil Won Korea University. Ch 30 Magnetic Fields Due to Currents. Fundamentals of Physics by Eunil Won, Korea University
 PHYS152 Lecture 8 Ch 3 Magnetic Fields Due to Currents Eunil Won Korea University Calculating the Magnetic Field Due to a Current Recall that we had the formula for the electrostatic force: d E = 1 ɛ dq
PHYS152 Lecture 8 Ch 3 Magnetic Fields Due to Currents Eunil Won Korea University Calculating the Magnetic Field Due to a Current Recall that we had the formula for the electrostatic force: d E = 1 ɛ dq
MP204 Electricity and Magnetism
 MATHEMATICAL PHYSICS SEMESTER 2, REPEAT 2016 2017 MP204 Electricity and Magnetism Prof. S. J. Hands, Dr. M. Haque and Dr. J.-I. Skullerud Time allowed: 1 1 2 hours Answer ALL questions MP204, 2016 2017,
MATHEMATICAL PHYSICS SEMESTER 2, REPEAT 2016 2017 MP204 Electricity and Magnetism Prof. S. J. Hands, Dr. M. Haque and Dr. J.-I. Skullerud Time allowed: 1 1 2 hours Answer ALL questions MP204, 2016 2017,
Examples of Dielectric Problems and the Electric Susceptability. 2 A Dielectric Sphere in a Uniform Electric Field
 Examples of Dielectric Problems and the Electric Susceptability Lecture 10 1 A Dielectric Filled Parallel Plate Capacitor Suppose an infinite, parallel plate capacitor filled with a dielectric of dielectric
Examples of Dielectric Problems and the Electric Susceptability Lecture 10 1 A Dielectric Filled Parallel Plate Capacitor Suppose an infinite, parallel plate capacitor filled with a dielectric of dielectric
Electromagnetism Answers to Problem Set 8 Spring Jackson Prob. 4.1: Multipole expansion for various charge distributions
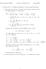 Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
A cylinder in a magnetic field (Jackson)
 Problem 1. A cylinder in a magnetic field (Jackson) A very long hollow cylinder of inner radius a and outer radius b of permeability µ is placed in an initially uniform magnetic field B o at right angles
Problem 1. A cylinder in a magnetic field (Jackson) A very long hollow cylinder of inner radius a and outer radius b of permeability µ is placed in an initially uniform magnetic field B o at right angles
Scattering. March 20, 2016
 Scattering March 0, 06 The scattering of waves of any kind, by a compact object, has applications on all scales, from the scattering of light from the early universe by intervening galaxies, to the scattering
Scattering March 0, 06 The scattering of waves of any kind, by a compact object, has applications on all scales, from the scattering of light from the early universe by intervening galaxies, to the scattering
Currents (1) Line charge λ (C/m) with velocity v : in time t, This constitutes a current I = λv (vector). Magnetic force on a segment of length dl is
 Magnetostatics 1. Currents 2. Relativistic origin of magnetic field 3. Biot-Savart law 4. Magnetic force between currents 5. Applications of Biot-Savart law 6. Ampere s law in differential form 7. Magnetic
Magnetostatics 1. Currents 2. Relativistic origin of magnetic field 3. Biot-Savart law 4. Magnetic force between currents 5. Applications of Biot-Savart law 6. Ampere s law in differential form 7. Magnetic
arxiv: v2 [physics.acc-ph] 27 Oct 2014
![arxiv: v2 [physics.acc-ph] 27 Oct 2014 arxiv: v2 [physics.acc-ph] 27 Oct 2014](/thumbs/90/101197166.jpg) Maxwell s equations for magnets A. Wolski University of Liverpool, Liverpool, UK and the Cockcroft Institute, Daresbury, UK arxiv:1103.0713v2 [physics.acc-ph] 27 Oct 2014 Abstract Magnetostatic fields
Maxwell s equations for magnets A. Wolski University of Liverpool, Liverpool, UK and the Cockcroft Institute, Daresbury, UK arxiv:1103.0713v2 [physics.acc-ph] 27 Oct 2014 Abstract Magnetostatic fields
Columbia University Department of Physics QUALIFYING EXAMINATION
 Columbia University Department of Physics QUALIFYING EXAMINATION Monday, January 9, 217 3:PM to 5:PM Classical Physics Section 2. Electricity, Magnetism & Electrodynamics Two hours are permitted for the
Columbia University Department of Physics QUALIFYING EXAMINATION Monday, January 9, 217 3:PM to 5:PM Classical Physics Section 2. Electricity, Magnetism & Electrodynamics Two hours are permitted for the
PHYS 110B - HW #4 Fall 2005, Solutions by David Pace Equations referenced as EQ. # are from Griffiths Problem statements are paraphrased
 PHYS B - HW #4 Fall 5, Solutions by David Pace Equations referenced as EQ. # are from Griffiths Problem statements are paraphrased [.] Problem 8. from Griffiths Reference problem 7.3 figure 7.43. a Let
PHYS B - HW #4 Fall 5, Solutions by David Pace Equations referenced as EQ. # are from Griffiths Problem statements are paraphrased [.] Problem 8. from Griffiths Reference problem 7.3 figure 7.43. a Let
Linear and Nonlinear Magnetic Media (Griffiths Chapter 6: Sections 3-4) Auxiliary Field H We write the total current density flowing through matter as
 Dr. Alain Brizard Electromagnetic Theory I (PY 02) Linear and Nonlinear Magnetic Media (Griffiths Chapter 6: Sections -4) Auxiliary Field H We write the total current density flowing through matter as
Dr. Alain Brizard Electromagnetic Theory I (PY 02) Linear and Nonlinear Magnetic Media (Griffiths Chapter 6: Sections -4) Auxiliary Field H We write the total current density flowing through matter as
8.1 Conservation of Charge and Energy. ρ + J =0, (8.1) t can be derived by considering the flow of charges from a given volume, Q t =
 Chapter 8 Conservation Laws 8. Conservation of Charge and Energy As was already shown, the continuity equation ρ + J =, (8.) can be derived by considering the flow of charges from a given volume, Q = ρ(r)d
Chapter 8 Conservation Laws 8. Conservation of Charge and Energy As was already shown, the continuity equation ρ + J =, (8.) can be derived by considering the flow of charges from a given volume, Q = ρ(r)d
Chapter 28 Sources of Magnetic Field
 Chapter 28 Sources of Magnetic Field In this chapter we investigate the sources of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents), Ampere s Law is introduced
Chapter 28 Sources of Magnetic Field In this chapter we investigate the sources of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents), Ampere s Law is introduced
INGENIERÍA EN NANOTECNOLOGÍA
 ETAPA DISCIPLINARIA TAREAS 385 TEORÍA ELECTROMAGNÉTICA Prof. E. Efren García G. Ensenada, B.C. México 206 Tarea. Two uniform line charges of ρ l = 4 nc/m each are parallel to the z axis at x = 0, y = ±4
ETAPA DISCIPLINARIA TAREAS 385 TEORÍA ELECTROMAGNÉTICA Prof. E. Efren García G. Ensenada, B.C. México 206 Tarea. Two uniform line charges of ρ l = 4 nc/m each are parallel to the z axis at x = 0, y = ±4
Introduction to Electrodynamics David J. Griffiths Fourth Edition
 Introduction to Electrodynamics David J. Griffiths Fourth Edition Pearson Education Limited Edinburgh Gate Harlow Essex CM20 2JE England and Associated Companies throughout the world Visit us on the World
Introduction to Electrodynamics David J. Griffiths Fourth Edition Pearson Education Limited Edinburgh Gate Harlow Essex CM20 2JE England and Associated Companies throughout the world Visit us on the World
E&M. 1 Capacitors. January 2009
 E&M January 2009 1 Capacitors Consider a spherical capacitor which has the space between its plates filled with a dielectric of permittivity ɛ. The inner sphere has radius r 1 and the outer sphere has
E&M January 2009 1 Capacitors Consider a spherical capacitor which has the space between its plates filled with a dielectric of permittivity ɛ. The inner sphere has radius r 1 and the outer sphere has
Chapter 27 Sources of Magnetic Field
 Chapter 27 Sources of Magnetic Field In this chapter we investigate the sources of magnetic of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents). Ampere s Law
Chapter 27 Sources of Magnetic Field In this chapter we investigate the sources of magnetic of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents). Ampere s Law
Chapter 28 Sources of Magnetic Field
 Chapter 28 Sources of Magnetic Field In this chapter we investigate the sources of magnetic of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents). Ampere s Law
Chapter 28 Sources of Magnetic Field In this chapter we investigate the sources of magnetic of magnetic field, in particular, the magnetic field produced by moving charges (i.e., currents). Ampere s Law
Errata Instructor s Solutions Manual Introduction to Electrodynamics, 3rd ed Author: David Griffiths Date: September 1, 2004
 Errata Instructor s Solutions Manual Introduction to Electrodynamics, 3rd ed Author: David Griffiths Date: September, 004 Page 4, Prob..5 (b): last expression should read y +z +3x. Page 4, Prob..6: at
Errata Instructor s Solutions Manual Introduction to Electrodynamics, 3rd ed Author: David Griffiths Date: September, 004 Page 4, Prob..5 (b): last expression should read y +z +3x. Page 4, Prob..6: at
Chapter 4. Electrostatic Fields in Matter
 Chapter 4. Electrostatic Fields in Matter 4.1. Polarization 4.2. The Field of a Polarized Object 4.3. The Electric Displacement 4.4. Linear Dielectrics 4.5. Energy in dielectric systems 4.6. Forces on
Chapter 4. Electrostatic Fields in Matter 4.1. Polarization 4.2. The Field of a Polarized Object 4.3. The Electric Displacement 4.4. Linear Dielectrics 4.5. Energy in dielectric systems 4.6. Forces on
Contents. Notes based on Fundamentals of Applied Electromagnetics (Ulaby et al) for ECE331, PSU.
 1 Contents 5 Magnetostatics 3 5.1 Magnetic forces and torques............... 4 5.1.1 Magnetic force on a current-carrying conductor 8 5.1.2 Magnetic torque on a current-carrying loop.. 16 5.2 Biot-Savart
1 Contents 5 Magnetostatics 3 5.1 Magnetic forces and torques............... 4 5.1.1 Magnetic force on a current-carrying conductor 8 5.1.2 Magnetic torque on a current-carrying loop.. 16 5.2 Biot-Savart
week 3 chapter 28 - Gauss s Law
 week 3 chapter 28 - Gauss s Law Here is the central idea: recall field lines... + + q 2q q (a) (b) (c) q + + q q + +q q/2 + q (d) (e) (f) The number of electric field lines emerging from minus the number
week 3 chapter 28 - Gauss s Law Here is the central idea: recall field lines... + + q 2q q (a) (b) (c) q + + q q + +q q/2 + q (d) (e) (f) The number of electric field lines emerging from minus the number
Make sure you show all your work and justify your answers in order to get full credit.
 PHYSICS 7B, Lecture 3 Spring 5 Final exam, C. Bordel Tuesday, May, 5 8- am Make sure you show all your work and justify your answers in order to get full credit. Problem : Thermodynamic process ( points)
PHYSICS 7B, Lecture 3 Spring 5 Final exam, C. Bordel Tuesday, May, 5 8- am Make sure you show all your work and justify your answers in order to get full credit. Problem : Thermodynamic process ( points)
Dielectrics. Lecture 20: Electromagnetic Theory. Professor D. K. Ghosh, Physics Department, I.I.T., Bombay
 What are dielectrics? Dielectrics Lecture 20: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay So far we have been discussing electrostatics in either vacuum or in a conductor.
What are dielectrics? Dielectrics Lecture 20: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay So far we have been discussing electrostatics in either vacuum or in a conductor.
3 Chapter. Gauss s Law
 3 Chapter Gauss s Law 3.1 Electric Flux... 3-2 3.2 Gauss s Law (see also Gauss s Law Simulation in Section 3.10)... 3-4 Example 3.1: Infinitely Long Rod of Uniform Charge Density... 3-9 Example 3.2: Infinite
3 Chapter Gauss s Law 3.1 Electric Flux... 3-2 3.2 Gauss s Law (see also Gauss s Law Simulation in Section 3.10)... 3-4 Example 3.1: Infinitely Long Rod of Uniform Charge Density... 3-9 Example 3.2: Infinite
PHY752, Fall 2016, Assigned Problems
 PHY752, Fall 26, Assigned Problems For clarification or to point out a typo (or worse! please send email to curtright@miami.edu [] Find the URL for the course webpage and email it to curtright@miami.edu
PHY752, Fall 26, Assigned Problems For clarification or to point out a typo (or worse! please send email to curtright@miami.edu [] Find the URL for the course webpage and email it to curtright@miami.edu
Physics 217 Practice Final Exam
 Physics 217 Practice Final Exam Fall 2002 If this were a real exam, you would be reminded here of the exam rules: You may consult only one page of formulas and constants and a calculator while taking this
Physics 217 Practice Final Exam Fall 2002 If this were a real exam, you would be reminded here of the exam rules: You may consult only one page of formulas and constants and a calculator while taking this
G( x x, t) = 1 (2π) 3. d 3 k e k2 t/µσ e i k ( x x ) A( k, t)e k x d 3 k. A( x, t) = 1
 Physics 505 Fall 2005 Homework Assignment #10 Solutions Textbook problems: Ch. 6: 6.3, 6.4, 6.14, 6.18 6.3 The homogeneous diffusion equation (5.160) for the vector potential for quasi-static fields in
Physics 505 Fall 2005 Homework Assignment #10 Solutions Textbook problems: Ch. 6: 6.3, 6.4, 6.14, 6.18 6.3 The homogeneous diffusion equation (5.160) for the vector potential for quasi-static fields in
Multiple Integrals and Vector Calculus (Oxford Physics) Synopsis and Problem Sets; Hilary 2015
 Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
3: Gauss s Law July 7, 2008
 3: Gauss s Law July 7, 2008 3.1 Electric Flux In order to understand electric flux, it is helpful to take field lines very seriously. Think of them almost as real things that stream out from positive charges
3: Gauss s Law July 7, 2008 3.1 Electric Flux In order to understand electric flux, it is helpful to take field lines very seriously. Think of them almost as real things that stream out from positive charges
Vector Potential for the Magnetic Field
 Vector Potential for the Magnetic Field Let me start with two two theorems of Vector Calculus: Theorem 1: If a vector field has zero curl everywhere in space, then that field is a gradient of some scalar
Vector Potential for the Magnetic Field Let me start with two two theorems of Vector Calculus: Theorem 1: If a vector field has zero curl everywhere in space, then that field is a gradient of some scalar
PHYS 3327 PRELIM 1. Prof. Itai Cohen, Fall 2010 Friday, 10/15/10. Name: Read all of the following information before starting the exam:
 PHYS 3327 PRELIM 1 Prof. Itai Cohen, Fall 2010 Friday, 10/15/10 Name: Read all of the following information before starting the exam: Put your name on the exam now. Show all work, clearly and in order,
PHYS 3327 PRELIM 1 Prof. Itai Cohen, Fall 2010 Friday, 10/15/10 Name: Read all of the following information before starting the exam: Put your name on the exam now. Show all work, clearly and in order,
B r Solved Problems Magnetic Field of a Straight Wire
 (4) Equate Iencwith d s to obtain I π r = NI NI = = ni = l π r 9. Solved Problems 9.. Magnetic Field of a Straight Wire Consider a straight wire of length L carrying a current I along the +x-direction,
(4) Equate Iencwith d s to obtain I π r = NI NI = = ni = l π r 9. Solved Problems 9.. Magnetic Field of a Straight Wire Consider a straight wire of length L carrying a current I along the +x-direction,
Solutions to PS 2 Physics 201
 Solutions to PS Physics 1 1. ke dq E = i (1) r = i = i k eλ = i k eλ = i k eλ k e λ xdx () (x x) (x x )dx (x x ) + x dx () (x x ) x ln + x x + x x (4) x + x ln + x (5) x + x To find the field for x, we
Solutions to PS Physics 1 1. ke dq E = i (1) r = i = i k eλ = i k eλ = i k eλ k e λ xdx () (x x) (x x )dx (x x ) + x dx () (x x ) x ln + x x + x x (4) x + x ln + x (5) x + x To find the field for x, we
Chapter 6. Magnetostatic Fields in Matter
 Chapter 6. Magnetostatic Fields in Matter 6.1. Magnetization Any macroscopic object consists of many atoms or molecules, each having electric charges in motion. With each electron in an atom or molecule
Chapter 6. Magnetostatic Fields in Matter 6.1. Magnetization Any macroscopic object consists of many atoms or molecules, each having electric charges in motion. With each electron in an atom or molecule
CYK\2009\PH102\Tutorial 10
 CYK\2009\PH02\Tutorial 0 Physics II. [G 6.3] Find the force of attraction between two magnetic dipoles, m and m 2, oriented as shown in the Fig., a distance r apart, (a) using F = 2πIRB cos θ, and (b)
CYK\2009\PH02\Tutorial 0 Physics II. [G 6.3] Find the force of attraction between two magnetic dipoles, m and m 2, oriented as shown in the Fig., a distance r apart, (a) using F = 2πIRB cos θ, and (b)
Physics 6C Review 1. Eric Reichwein Department of Physics University of California, Santa Cruz. July 16, Figure 1: Coulombs Law
 Physics 6C Review 1 Eric Reichwein Department of Physics University of California, Santa Cruz July 16, 2012 1 Review 1.1 Coulombs Law Figure 1: Coulombs Law The steps for solving any problem of this type
Physics 6C Review 1 Eric Reichwein Department of Physics University of California, Santa Cruz July 16, 2012 1 Review 1.1 Coulombs Law Figure 1: Coulombs Law The steps for solving any problem of this type
AMPERE'S LAW. B dl = 0
 AMPERE'S LAW The figure below shows a basic result of an experiment done by Hans Christian Oersted in 1820. It shows the magnetic field produced by a current in a long, straight length of current-carrying
AMPERE'S LAW The figure below shows a basic result of an experiment done by Hans Christian Oersted in 1820. It shows the magnetic field produced by a current in a long, straight length of current-carrying
Lecture 3. Electric Field Flux, Gauss Law. Last Lecture: Electric Field Lines
 Lecture 3. Electric Field Flux, Gauss Law Last Lecture: Electric Field Lines 1 iclicker Charged particles are fixed on grids having the same spacing. Each charge has the same magnitude Q with signs given
Lecture 3. Electric Field Flux, Gauss Law Last Lecture: Electric Field Lines 1 iclicker Charged particles are fixed on grids having the same spacing. Each charge has the same magnitude Q with signs given
A half submerged metal sphere (UIC comprehensive
 Problem 1. exam) A half submerged metal sphere (UIC comprehensive A very light neutral hollow metal spherical shell of mass m and radius a is slightly submerged by a distance b a below the surface of a
Problem 1. exam) A half submerged metal sphere (UIC comprehensive A very light neutral hollow metal spherical shell of mass m and radius a is slightly submerged by a distance b a below the surface of a
