) k ( 1 λ ) n k. ) n n e. k!(n k)! n
|
|
|
- Ezra Goodwin
- 5 years ago
- Views:
Transcription
1
2 k ) λ ) k λ ) λk k! e λ ) π/!. e α + α) /α e k ) λ ) k λ )! λ k! k)! ) λ k λ k! λk e λ k! λk e λ. k! ) k λ ) k k + k k k ) k ) k e k λ e k ) k EX EX V arx) X Nα, σ ) Bp) Eα) Πλ) U, θ) X Nα, σ ) E ) X α σ E X α ) σ EX α V arx) σ EX EX) + V arx) α + σ X Bp) EX P X ) p EX P X ) p V arx) EX EX) p p X Eα) EX xαe αx dx yαx α ye y dy α Γ) α, EX x αe αx dx α y e y dy α Γ3) α V arx) EX EX) α X Πλ) EX λ k k k )! e λ λ k λk k! e λ λ EX k kλ k k )! e λ k k )λ k k )! e λ + V arx) EX EX) λ + λ λ λ X U, θ) EX θ x θ dx θ EX θ k x θ λ k k )! e λ λ k λ k k! e λ + EX λ + λ, θ θ dx 3 V arx) 3 θ 4 θ θ U[, θ] fx θ) θ x θ, < θ <
3 m θ) E θ X θ m θ) E θ X θ 3 θ m X) X, θ m X ) 3 X. θ θ V ar θ X) m θ )) ) θ. θ E θ X 4 X θ E θ e tx e tx tθ dx etθ ) k θ tθ k + )!. E θ e tx k tk k! E θ X k E θ X k θk k+ E θ X 4 θ4 5 V ar θ X 4 θ ) m θ )) θ > 5 θ θ 45 7 k 9 θ 3 4. λ Πλ) φλ) i d d φλ) λ + λ dλ dλ px i λ) λ i X i i X i! e λ. ) i X i X i! + X i. λ i λ < i X i φx) λ > i X i φx) φλ) λ i X i λ Πλ) λ i X i α Eα) φα) px i α) [, ) X i ) α e α i Xi [, ) Y ), i Y X,, X } φα) φα) i i d d φα) dα dα α α X i ) α d dα φα) α <. φα) α α / X i Xi i X i X α Eα)
4 e θ x x θ fx θ) x < θ, < θ < θ φθ) e θ i Xi [θ, )Y ) e θ i X i θ Y θ > Y, Y X,, X } e θ i X i θ φθ) θ Y θ θ X,, X } fx θ) e x θ < x <, < θ < θ φθ) e i Xi θ. m X d E X m ) E X d ). d X x x i x i m i x i d, m x,, x } d d x,, x } φθ) θ X X θ X X Iλ) Πλ) fx λ) λx x! e λ lx λ) λ+x λ x! l x λ) x λ Iλ) E λ l X λ) E λx λ λ Iα) Nα, σ ) σ α x α) lx α) e σ πσ Iα) σ x α) σ πσ) l x α) σ Bp) p
5 fx p) p x p) x e x p p p) ap)bx)e cp)dx), ap) p bx) cp) p p dx) x S i dx i) i X i X E p S p X p Nα, σ ) σ σ α α fx α) πσ e x σ e α σ e αx σ fx α) aα) e α x σ bx) e σ πσ cα) α σ dx) x S i dx i) i X i X E α S α X α p p p X X p ξp) Bα, β) E[p] α α+β.5 E[p X,, X ].9 α β p ξx X x,, X x ) P p x X x,, X x ) P X x,, X x p x)p p x) P X x,, X x p y)p p y)dy Cx i x i x) i x i) x α x) β Cx i xi+α x) β+ i xi) C ξp x X x,, X x ) x Γ + α + β) C Γ i x i + α)γ i x i) + β), α 7 E[p X,, X ] β 9 7 xp p x X X )dx Γ + α + β) x Γα)Γ + β) xα x) +β dx α + α + β +. α α+β.5 α+ α+β+.9,
6 p p ξ.).7 ξ.).3. p ξ. X x,, X x ) P p. X x,, X x ) P X x,, X x p.)p p.) P X x,, X x p.)p p.) + P X x,, X x p.)p p.) ξ. X x,, X x ) θ θ θ Γα, β) E[θ] α β V arθ) α β α β α β 5, α β Eα) α α α ξx) α Γa, b) E[α] a b. V arα) a b a 5 b 5 ξx X x,, X x ) P X x,, X x α x)p α x) P X x,, X x α y)p α y)dy x e x i x i b a Γa) xa e bx Costat b + i x i) +a x +a e b+ i xi)x Γ + a) +a b + X) x +a e b+ X)x. Γ + a) X 3.8 a 5 b 5 α p p α 5 β p
7 p Γα + β + ) ξx X,, X ) Γα + i X i)γβ + i X i) xα+ i Xi) x) β+ i X i). p p E[p X,, X ] x Γ35)x5 x) 8 dx 6 Γ6)Γ9) 35. Πλ) λ λ α 3 β λ λ ξx X,, X ) λ E[λ X,, X ] β + )α+ i Xi x α+ Γα + i X i) i Xi e β+)x x 3+3 x 3+3 e x dx 8. Γ3 + 3). Γα, β) β α Γα, β) β [ ] β α fx,, x α) x x ) α e β i x i x,,x Γα) } ux,, x )vt x,, x ), α), ux,, x ) e β [ ] i x i x,,x } vt, α) β α Γα) T α T x,, x ) i x i T X,, X ) i X i fx θ) aθ)bx)e cθ)dx) X X fx,, x θ) aθ) i bx i )e cθ) i dxi) ux,, x )vt x,, x ), θ), T x,, x ) i dx i) vt, θ) aθ) e tcθ) ux,, x ) i bx i) T X,, X ) i dx i)
8 Γα, β) β α fx,, x α, β) [ ] β α x x ) α e β i xi x,,x Γα) } ux,, x )vt x,, x ), T x,, x ), α, β), [ ] ux,, x ) x,,x } vt, t, α, β) β α Γα) t α e βt T x,, x ) i x i T x,, x ) i x i i X i, i X i) X X Eα) α α Eα) fx,, x α) α e α i xi x,,x }. x,, x } < fx,, x α) x,, x } α α fx,, x α) α α α i x x. i T x,, x ) x ux,, x ) x,,x } vt, α) α e α t fx,, x α) ux,, x )vt x,, x ), α) α α X α X X U[, θ] Y X,, X }. θ cy E θ cy θ). θ cy Y t t θ} E θ cy θ) θ ct θ) t dt + c ) + c + θ +. 86, 8, 76, 49, 84, 9, 58, 39, 75, 48, 5,, 4, 53, 9, 57, 3, 49, 35, 3 µ σ
9 X X X X) c c c P χ 9 c ) P χ 9 c ) α.5 P t 9 c) P t 9 c) α.5 c c 3.4 c.79 σ [ X X) ), X X) ] ) [33.8, 43.] c c µ [ ] X c X X) ), X + c X X) ) [48., 65.6]. f x) f x) x f x) f x) x x X fx) f x) f x) H : fx) f x), H : fx) f x). αδ) + βδ) αδ) + βδ) αδ) βδ) αδ) P δ H ) βδ) P δ H ) ξ) 3 ξ) 3 ξ)p δ H ) + ξ)p δ H ) f X) f ξ) X) X ξ) H : X < 4 δ H : X > 4 H H : X 4. δ H : X δ 4 H : X > 4. αδ ) + βδ ) P δ H ) + P δ H ) P X > 4 ) + P X 4 ) 4 4 dx + xdx 7 8.
10 αδ). βδ) βδ) c ) f X) P f X) < c.. c 5 9 ) ) f X) P f X) < c P X < c P X > c ) c } c ).. δ H : X 5 9 H : X < 5 9 αδ). βδ) βδ) P δ H ) P X 9.8. H H H P p. H P p.4 X X α.5 fx,, x p) p i x i p) i x i) f X, X ). X+X.8 X+X) f X, X ).4 X+X.6 X+X) f X, X ) f X, X ).5X +X ) X +X 4 ). 3 c P f X,X ) f X,X ) < c ) α.5 ) f X, X ) P f X, X ) < c 6 9 <c} <c} <c}.3. c p ) ) f X, X ) P f X, X ) < c f X, X ) + p)p f X, X ) c.5. ) P f X,X ) f X,X ) < c ) P f X,X ) f X,X ) c c 3.5 c 4, 3 ].4 + p)p X, X X, X ).5,
11 p 3 3 α.5 H :.5 X+X 4 X+X ) 3) > 3 δ H :.5 X+X 4 X+X ) 3) < 3 H H :.5 X+X 4 X+X ) 3) H p 3 3 H p 3 ) ) f X, X ) P δ H ) P f X, X ) < c f X, X ) + p)p f X, X ) c P X X ) + 3 P X, X X, X ) , X X µ σ H : µ H : µ δ α δ).5 } f X,, X ) f X,, X ) i [X i µ ) X i µ ) ] σ ) f X,, X P f X,, X ) < c P i X i < c) i e X i. ) i P X i ) c < σ σ ) c Φ. ) Φ c.5 c.88 δ i H : e X i.88 δ i H : e X i <.88. ) i P δ H ) P e X i < c ) c + Φ.94.
12 α.5 Aa /4 AA / Aa /4 aa Aa AA Aa aa χ p P AA) p P Aa) p 3 P aa) H : p p, p p, p 3 p 3 H :, p, p p 3 4 v i X i AA} v i X i Aa} v 3 i X i aa} T 3 k v k p k ) p k χ δ H : T c H : T > c, c.5 α χ 3 c, ) c 5.99 T
13 χ x.84 x.53 x 3.53 x 4.84 Φx k ).k k,, 3, 4) B,.84] B.84,.53] B 3.53,.53] B 4.53,.84] B 5.84, ) p k P X B k ) k,, 3, 4, 5) H : p p p 3 p 4 p 5. H :. v k i X i B k } k,, 3, 4, 5) v 5 v v 3 7 v 4 v v k 5.) T 5. k 5.4. χ δ H : T c H : T > c, c.5 α χ 5 c, ) c H N N 6 θ θ H N, N 36, N 3 4, N 4 36, N 5, N 6 4. Q H fθ, θ ) θ N θ N θ θ ) N 3 θ θ ) N 4 [θ θ θ )] N 5 [θ θ θ )] N 6. A <
14 fθ, θ ) N θ + N θ + N 3 θ θ ) + N 4 + θ + θ ) +N 5 [ + θ + θ θ )] + N 6 [ + θ + θ θ )]. fθ, θ ) θ θ N3+N5+N6 θ θ θ fθ, θ ) N+N4+N5 θ θ fθ, θ ) N +N 4 +N 6 θ N 3+N 5 +N 6 θ θ. θ θ N i θ θ θ. θ.5 T N 5. ) 5. + N 5.5 ) N ) N 4 5.) + N 5 5.) + N 6 5.3) T χ 6 χ 3 c 7.85 χ 3c, ).5 T c T 4.37 < c θ < θ < ) p θ) 4, p 4θ θ) 3, p 6θ θ), p 3 4θ 3 θ), p 4 θ 4. H : p θ) 4, p 4θ θ) 3, p 6θ θ), p 3 4θ 3 θ), p 4 θ 4, θ, ) H :. fθ) 4 i i pn i i N i fθ) 4N θ) + N [ 4 + θ + 3 θ)] + N [ 6 + θ + θ)] +N 3 [ θ + θ)] + 4N 4 θ.
15 θ θ θ.4 p θ).96 p θ).3456 p θ).3456 p 3 θ).536 p 4 θ).56 T χ 33.96) ) ) 9.56) ).3456 T χ 5 χ 3 α c χ 3c, ) α H : T c δ H : T > c α c 7.85 χ 3c, ).5 T > c N 7 N 6 N 3 5 N 3 N 3 N 3 9 N + 7 N + 5 N + 47 N + 9 N +3 4 χ T [7 7 47/478) /7 47) /478) /7 9) /478) /7 4) /478) /5 47) /478) /5 9) /478) /5 4)] α : T c δ : T > c, c χ )3 )c, ) α δ α c 5.99 χ c, ).5 T > 5.99 T
16 O A B AB Rh O A B AB Rh Rh N 8 N 89 N 3 54 N 4 9 N 3 N 7 N 3 7 N 4 9 N + 44 N + 56 N + 95 N + 6 N +3 6 N +4 8 χ T 8.6. [ /3) /44 95) /3) /44 6) /3) /44 6) /3) /44 8) /3) /56 95) /3) /56 6) /3) /56 6) /3) /56 8)] 3 α : T c δ : T > c, c χ )4 )c, ) α δ α c 7.85 χ 3c, ).5 T >
17 N 57 N 4 N 3 5 N 87 N N 3 4 N 3 3 N 3 6 N N + 49 N + 5 N N + 47 N + 9 N +3 4 T α : T c δ : T > c, c χ 3 )3 )c, ) α δ α c χ 4c, ).5 T > [, ] H : H : F x) F x) x. H : D.35 δ H : D >.35 D x F x) x 5 D A
18 x.4 F x) F x) D H fx) 3 < x fx) < x <. fx) x 3 F x) x < x x+ < x < x. H : H : F x) F x). H : D.35 δ H : D >.35 D
19 x.66 F x) F x) D H / [, ] / θ θ [, ] θ θ P θ ) P θ ).5 P θ X x,, X 5 x 5 ) P X x,, X 5 x 5 θ )P θ ) P X x,, X 5 x 5 θ )P θ ) + P X x,, X 5 x 5 θ )P θ ) P X x,, X 5 x 5 θ ) P X x,, X 5 x 5 θ ) + P X x,, X 5 x 5 θ ) i <x i.5} i.5<x i<} β β σ y x.5 β i x i y i i x i y i β β σ β XY XȲ X X) , β Ȳ β X.47, σ Y i β β X i ).45. i α. α α χ, c ) α.5 χ c, ) α.5 c.736 c σ [ σ c, σ c ] [.9,.65] β c t c, c) α.9 c.8595 β [ ] β c [.88,.5876]. σ ) X X) ), β + c σ ) X X) )
20 β [ σ β c + X) ) X X), β + c σ + X) )] [.64,.38]. X X) x.5 ŷ y β + β.5.8 y x.5 [ σ Ŷ c + + X ) X) X X), Ŷ + c σ + + X )] X) [.386,.94]. X X) H : β H : β <, β N ) X X) β β ) σ σ σ β X X) ) T ) β β σ σ σ ) X X) ) ) σ β, X X) ) χ β β t β T T H : T > c δ H : T c, c t 8, c). c.3968 T 5.3 > c H σ )
Recursive Route to Mixed Poisson Distributions using Integration by Parts
 ISSN 2224-584 (Paper) ISSN 2225-522 (Online) Vol.4, No.4, 24 Recursive Route to Mixed Poisson Distributions using Integration by Parts Abstract Rachel Sarguta * Joseph A. M. Ottieno School of Mathematics,
ISSN 2224-584 (Paper) ISSN 2225-522 (Online) Vol.4, No.4, 24 Recursive Route to Mixed Poisson Distributions using Integration by Parts Abstract Rachel Sarguta * Joseph A. M. Ottieno School of Mathematics,
B.Sc. MATHEMATICS I YEAR
 B.Sc. MATHEMATICS I YEAR DJMB : ALGEBRA AND SEQUENCES AND SERIES SYLLABUS Unit I: Theory of equation: Every equation f(x) = 0 of n th degree has n roots, Symmetric functions of the roots in terms of the
B.Sc. MATHEMATICS I YEAR DJMB : ALGEBRA AND SEQUENCES AND SERIES SYLLABUS Unit I: Theory of equation: Every equation f(x) = 0 of n th degree has n roots, Symmetric functions of the roots in terms of the
Solutions 2017 AB Exam
 1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
Exercises for Chap. 2
 1 Exercises for Chap..1 For the Riemann-Liouville fractional integral of the first kind of order α, 1,(a,x) f, evaluate the fractional integral if (i): f(t)= tν, (ii): f(t)= (t c) ν for some constant c,
1 Exercises for Chap..1 For the Riemann-Liouville fractional integral of the first kind of order α, 1,(a,x) f, evaluate the fractional integral if (i): f(t)= tν, (ii): f(t)= (t c) ν for some constant c,
Lecture 17: The Exponential and Some Related Distributions
 Lecture 7: The Exponential and Some Related Distributions. Definition Definition: A continuous random variable X is said to have the exponential distribution with parameter if the density of X is e x if
Lecture 7: The Exponential and Some Related Distributions. Definition Definition: A continuous random variable X is said to have the exponential distribution with parameter if the density of X is e x if
Direction: This test is worth 250 points and each problem worth points. DO ANY SIX
 Term Test 3 December 5, 2003 Name Math 52 Student Number Direction: This test is worth 250 points and each problem worth 4 points DO ANY SIX PROBLEMS You are required to complete this test within 50 minutes
Term Test 3 December 5, 2003 Name Math 52 Student Number Direction: This test is worth 250 points and each problem worth 4 points DO ANY SIX PROBLEMS You are required to complete this test within 50 minutes
Stat410 Probability and Statistics II (F16)
 Stat4 Probability and Statistics II (F6 Exponential, Poisson and Gamma Suppose on average every /λ hours, a Stochastic train arrives at the Random station. Further we assume the waiting time between two
Stat4 Probability and Statistics II (F6 Exponential, Poisson and Gamma Suppose on average every /λ hours, a Stochastic train arrives at the Random station. Further we assume the waiting time between two
Practice Examination # 3
 Practice Examination # 3 Sta 23: Probability December 13, 212 This is a closed-book exam so do not refer to your notes, the text, or any other books (please put them on the floor). You may use a single
Practice Examination # 3 Sta 23: Probability December 13, 212 This is a closed-book exam so do not refer to your notes, the text, or any other books (please put them on the floor). You may use a single
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: = 0 : homogeneous equation.
 Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Chapter 3 Second Order Linear Equations
 Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
APPLIED MATHEMATICS. Part 1: Ordinary Differential Equations. Wu-ting Tsai
 APPLIED MATHEMATICS Part 1: Ordinary Differential Equations Contents 1 First Order Differential Equations 3 1.1 Basic Concepts and Ideas................... 4 1.2 Separable Differential Equations................
APPLIED MATHEMATICS Part 1: Ordinary Differential Equations Contents 1 First Order Differential Equations 3 1.1 Basic Concepts and Ideas................... 4 1.2 Separable Differential Equations................
Continuous Random Variables
 Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
arxiv: v1 [math.ho] 4 Jul 2007
![arxiv: v1 [math.ho] 4 Jul 2007 arxiv: v1 [math.ho] 4 Jul 2007](/thumbs/81/84180043.jpg) arxiv:0707.0699v [math.ho] 4 Jul 2007 A double demonstration of a theorem of Newton, which gives a relation between the coefficient of an algebraic equation and the sums of the powers of its roots Leonhard
arxiv:0707.0699v [math.ho] 4 Jul 2007 A double demonstration of a theorem of Newton, which gives a relation between the coefficient of an algebraic equation and the sums of the powers of its roots Leonhard
P (x). all other X j =x j. If X is a continuous random vector (see p.172), then the marginal distributions of X i are: f(x)dx 1 dx n
 JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
LIST OF FORMULAS FOR STK1100 AND STK1110
 LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
More on Bayes and conjugate forms
 More on Bayes and conjugate forms Saad Mneimneh A cool function, Γ(x) (Gamma) The Gamma function is defined as follows: Γ(x) = t x e t dt For x >, if we integrate by parts ( udv = uv vdu), we have: Γ(x)
More on Bayes and conjugate forms Saad Mneimneh A cool function, Γ(x) (Gamma) The Gamma function is defined as follows: Γ(x) = t x e t dt For x >, if we integrate by parts ( udv = uv vdu), we have: Γ(x)
Our task The optimization principle Available choices Preferences and utility functions Describing the representative consumer preferences
 X Y U U(x, y), x X y Y (x, y ) U(x, y ) (x, y ) (x, y ) (x, y ) (x, y ) (x, y ) U(x, y ) > U(x, y ) (x, y ) (x, y ) U(x, y ) < U(x, y ) U(x, y ) = U(x, y ) X Y U x y U x > x 0 U(x, y) U(x 0, y), y y >
X Y U U(x, y), x X y Y (x, y ) U(x, y ) (x, y ) (x, y ) (x, y ) (x, y ) (x, y ) U(x, y ) > U(x, y ) (x, y ) (x, y ) U(x, y ) < U(x, y ) U(x, y ) = U(x, y ) X Y U x y U x > x 0 U(x, y) U(x 0, y), y y >
Random Variables. Random variables. A numerically valued map X of an outcome ω from a sample space Ω to the real line R
 In probabilistic models, a random variable is a variable whose possible values are numerical outcomes of a random phenomenon. As a function or a map, it maps from an element (or an outcome) of a sample
In probabilistic models, a random variable is a variable whose possible values are numerical outcomes of a random phenomenon. As a function or a map, it maps from an element (or an outcome) of a sample
Solutions for MAS277 Problems
 Solutions for MAS77 Problems Solutions for Chapter problems: Inner product spaces 1. No. The only part that fails, however, is the condition that f, f should mean that f. If f is a non-zero function that
Solutions for MAS77 Problems Solutions for Chapter problems: Inner product spaces 1. No. The only part that fails, however, is the condition that f, f should mean that f. If f is a non-zero function that
Solutions to Dynamical Systems 2010 exam. Each question is worth 25 marks.
 Solutions to Dynamical Systems exam Each question is worth marks [Unseen] Consider the following st order differential equation: dy dt Xy yy 4 a Find and classify all the fixed points of Hence draw the
Solutions to Dynamical Systems exam Each question is worth marks [Unseen] Consider the following st order differential equation: dy dt Xy yy 4 a Find and classify all the fixed points of Hence draw the
Formulas for probability theory and linear models SF2941
 Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
Conditional distributions. Conditional expectation and conditional variance with respect to a variable.
 Conditional distributions Conditional expectation and conditional variance with respect to a variable Probability Theory and Stochastic Processes, summer semester 07/08 80408 Conditional distributions
Conditional distributions Conditional expectation and conditional variance with respect to a variable Probability Theory and Stochastic Processes, summer semester 07/08 80408 Conditional distributions
Mathematical Statistics
 Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Actuarial Science Exam 1/P
 Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
2017 Financial Mathematics Orientation - Statistics
 2017 Financial Mathematics Orientation - Statistics Written by Long Wang Edited by Joshua Agterberg August 21, 2018 Contents 1 Preliminaries 5 1.1 Samples and Population............................. 5
2017 Financial Mathematics Orientation - Statistics Written by Long Wang Edited by Joshua Agterberg August 21, 2018 Contents 1 Preliminaries 5 1.1 Samples and Population............................. 5
Probability Theory and Statistics. Peter Jochumzen
 Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
Homework 10 (due December 2, 2009)
 Homework (due December, 9) Problem. Let X and Y be independent binomial random variables with parameters (n, p) and (n, p) respectively. Prove that X + Y is a binomial random variable with parameters (n
Homework (due December, 9) Problem. Let X and Y be independent binomial random variables with parameters (n, p) and (n, p) respectively. Prove that X + Y is a binomial random variable with parameters (n
Exercises and Answers to Chapter 1
 Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
x k 34 k 34. x 3
 A A A A A B A =, C =. f k k x k l f f 3 = k 3 k 3 x k 34 k 34 x 3 k 3 l 3 k 34 l 34. f 4 x 4 K K = [ ] 4 K = K (K) = (K) I m m R I m m = [e, e,, e m ] R = [a, a,, a m ] R = (r ij ) r r r m R = r r m. r
A A A A A B A =, C =. f k k x k l f f 3 = k 3 k 3 x k 34 k 34 x 3 k 3 l 3 k 34 l 34. f 4 x 4 K K = [ ] 4 K = K (K) = (K) I m m R I m m = [e, e,, e m ] R = [a, a,, a m ] R = (r ij ) r r r m R = r r m. r
Let X be a continuous random variable, < X < f(x) is the so called probability density function (pdf) if
 University of California, Los Angeles Department of Statistics Statistics 1A Instructor: Nicolas Christou Continuous probability distributions Let X be a continuous random variable, < X < f(x) is the so
University of California, Los Angeles Department of Statistics Statistics 1A Instructor: Nicolas Christou Continuous probability distributions Let X be a continuous random variable, < X < f(x) is the so
Brief Review of Probability
 Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
Theory of Higher-Order Linear Differential Equations
 Chapter 6 Theory of Higher-Order Linear Differential Equations 6.1 Basic Theory A linear differential equation of order n has the form a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x) = b(x), (6.1.1)
Chapter 6 Theory of Higher-Order Linear Differential Equations 6.1 Basic Theory A linear differential equation of order n has the form a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x) = b(x), (6.1.1)
Multiple Random Variables
 Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
An Introduction to Bessel Functions
 An Introduction to R. C. Trinity University Partial Differential Equations March 25, 2014 Bessel s equation Given p 0, the ordinary differential equation x 2 y +xy +(x 2 p 2 )y = 0, x > 0 (1) is known
An Introduction to R. C. Trinity University Partial Differential Equations March 25, 2014 Bessel s equation Given p 0, the ordinary differential equation x 2 y +xy +(x 2 p 2 )y = 0, x > 0 (1) is known
arxiv: v1 [math.na] 15 Nov 2013
![arxiv: v1 [math.na] 15 Nov 2013 arxiv: v1 [math.na] 15 Nov 2013](/thumbs/72/66588802.jpg) NUMERICAL APPROXIMATIONS FOR FRACTIONAL DIFFERENTIAL EQUATIONS arxiv:1311.3935v1 [math.na] 15 Nov 013 Yuri Dimitrov Department of Applied Mathematics and Statistics University of Rousse 8 Studentsa str.
NUMERICAL APPROXIMATIONS FOR FRACTIONAL DIFFERENTIAL EQUATIONS arxiv:1311.3935v1 [math.na] 15 Nov 013 Yuri Dimitrov Department of Applied Mathematics and Statistics University of Rousse 8 Studentsa str.
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
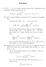 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
ECE353: Probability and Random Processes. Lecture 7 -Continuous Random Variable
 ECE353: Probability and Random Processes Lecture 7 -Continuous Random Variable Xiao Fu School of Electrical Engineering and Computer Science Oregon State University E-mail: xiao.fu@oregonstate.edu Continuous
ECE353: Probability and Random Processes Lecture 7 -Continuous Random Variable Xiao Fu School of Electrical Engineering and Computer Science Oregon State University E-mail: xiao.fu@oregonstate.edu Continuous
MAS223 Statistical Modelling and Inference Examples
 Chapter MAS3 Statistical Modelling and Inference Examples Example : Sample spaces and random variables. Let S be the sample space for the experiment of tossing two coins; i.e. Define the random variables
Chapter MAS3 Statistical Modelling and Inference Examples Example : Sample spaces and random variables. Let S be the sample space for the experiment of tossing two coins; i.e. Define the random variables
u =0with u(0,x)=f(x), (x) =
 PDE LECTURE NOTES, MATH 37A-B 69. Heat Equation The heat equation for a function u : R + R n C is the partial differential equation (.) µ t u =0with u(0,x)=f(x), where f is a given function on R n. By
PDE LECTURE NOTES, MATH 37A-B 69. Heat Equation The heat equation for a function u : R + R n C is the partial differential equation (.) µ t u =0with u(0,x)=f(x), where f is a given function on R n. By
Chp 4. Expectation and Variance
 Chp 4. Expectation and Variance 1 Expectation In this chapter, we will introduce two objectives to directly reflect the properties of a random variable or vector, which are the Expectation and Variance.
Chp 4. Expectation and Variance 1 Expectation In this chapter, we will introduce two objectives to directly reflect the properties of a random variable or vector, which are the Expectation and Variance.
MA 519 Probability: Review
 MA 519 : Review Yingwei Wang Department of Mathematics, Purdue University, West Lafayette, IN, USA Contents 1 How to compute the expectation? 1.1 Tail........................................... 1. Index..........................................
MA 519 : Review Yingwei Wang Department of Mathematics, Purdue University, West Lafayette, IN, USA Contents 1 How to compute the expectation? 1.1 Tail........................................... 1. Index..........................................
Exercises for Chapter 7
 Exercises for Chapter 7 Exercise 7.1 The following simple macroeconomic model has four equations relating government policy variables to aggregate income and investment. Aggregate income equals consumption
Exercises for Chapter 7 Exercise 7.1 The following simple macroeconomic model has four equations relating government policy variables to aggregate income and investment. Aggregate income equals consumption
Measure-theoretic probability
 Measure-theoretic probability Koltay L. VEGTMAM144B November 28, 2012 (VEGTMAM144B) Measure-theoretic probability November 28, 2012 1 / 27 The probability space De nition The (Ω, A, P) measure space is
Measure-theoretic probability Koltay L. VEGTMAM144B November 28, 2012 (VEGTMAM144B) Measure-theoretic probability November 28, 2012 1 / 27 The probability space De nition The (Ω, A, P) measure space is
Second Order ODEs. Second Order ODEs. In general second order ODEs contain terms involving y, dy But here only consider equations of the form
 Second Order ODEs Second Order ODEs In general second order ODEs contain terms involving y, dy But here only consider equations of the form A d2 y dx 2 + B dy dx + Cy = 0 dx, d2 y dx 2 and F(x). where
Second Order ODEs Second Order ODEs In general second order ODEs contain terms involving y, dy But here only consider equations of the form A d2 y dx 2 + B dy dx + Cy = 0 dx, d2 y dx 2 and F(x). where
Summer 2017 MATH Solution to Exercise 5
 Summer 07 MATH00 Solution to Exercise 5. Find the partial derivatives of the following functions: (a (xy 5z/( + x, (b x/ x + y, (c arctan y/x, (d log((t + 3 + ts, (e sin(xy z 3, (f x α, x = (x,, x n. (a
Summer 07 MATH00 Solution to Exercise 5. Find the partial derivatives of the following functions: (a (xy 5z/( + x, (b x/ x + y, (c arctan y/x, (d log((t + 3 + ts, (e sin(xy z 3, (f x α, x = (x,, x n. (a
Riemann integral and volume are generalized to unbounded functions and sets. is an admissible set, and its volume is a Riemann integral, 1l E,
 Tel Aviv University, 26 Analysis-III 9 9 Improper integral 9a Introduction....................... 9 9b Positive integrands................... 9c Special functions gamma and beta......... 4 9d Change of
Tel Aviv University, 26 Analysis-III 9 9 Improper integral 9a Introduction....................... 9 9b Positive integrands................... 9c Special functions gamma and beta......... 4 9d Change of
Starting from Heat Equation
 Department of Applied Mathematics National Chiao Tung University Hsin-Chu 30010, TAIWAN 20th August 2009 Analytical Theory of Heat The differential equations of the propagation of heat express the most
Department of Applied Mathematics National Chiao Tung University Hsin-Chu 30010, TAIWAN 20th August 2009 Analytical Theory of Heat The differential equations of the propagation of heat express the most
Probability Density Functions
 Probability Density Functions Probability Density Functions Definition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that
Probability Density Functions Probability Density Functions Definition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that
INTRODUCTION TO BAYESIAN METHODS II
 INTRODUCTION TO BAYESIAN METHODS II Abstract. We will revisit point estimation and hypothesis testing from the Bayesian perspective.. Bayes estimators Let X = (X,..., X n ) be a random sample from the
INTRODUCTION TO BAYESIAN METHODS II Abstract. We will revisit point estimation and hypothesis testing from the Bayesian perspective.. Bayes estimators Let X = (X,..., X n ) be a random sample from the
SOLUTION FOR HOMEWORK 12, STAT 4351
 SOLUTION FOR HOMEWORK 2, STAT 435 Welcome to your 2th homework. It looks like this is the last one! As usual, try to find mistakes and get extra points! Now let us look at your problems.. Problem 7.22.
SOLUTION FOR HOMEWORK 2, STAT 435 Welcome to your 2th homework. It looks like this is the last one! As usual, try to find mistakes and get extra points! Now let us look at your problems.. Problem 7.22.
Continuous Distributions
 A normal distribution and other density functions involving exponential forms play the most important role in probability and statistics. They are related in a certain way, as summarized in a diagram later
A normal distribution and other density functions involving exponential forms play the most important role in probability and statistics. They are related in a certain way, as summarized in a diagram later
Interval Estimation. Chapter 9
 Chapter 9 Interval Estimation 9.1 Introduction Definition 9.1.1 An interval estimate of a real-values parameter θ is any pair of functions, L(x 1,..., x n ) and U(x 1,..., x n ), of a sample that satisfy
Chapter 9 Interval Estimation 9.1 Introduction Definition 9.1.1 An interval estimate of a real-values parameter θ is any pair of functions, L(x 1,..., x n ) and U(x 1,..., x n ), of a sample that satisfy
HOMEWORK 3 - GEOMETRY OF CURVES AND SURFACES. where ν is the unit normal consistent with the orientation of α (right hand rule).
 HOMEWORK 3 - GEOMETRY OF CURVES AND SURFACES ANDRÉ NEVES ) If α : I R 2 is a curve on the plane parametrized by arc length and θ is the angle that α makes with the x-axis, show that α t) = dθ dt ν, where
HOMEWORK 3 - GEOMETRY OF CURVES AND SURFACES ANDRÉ NEVES ) If α : I R 2 is a curve on the plane parametrized by arc length and θ is the angle that α makes with the x-axis, show that α t) = dθ dt ν, where
Math 222 Spring 2013 Exam 3 Review Problem Answers
 . (a) By the Chain ule, Math Spring 3 Exam 3 eview Problem Answers w s w x x s + w y y s (y xy)() + (xy x )( ) (( s + 4t) (s 3t)( s + 4t)) ((s 3t)( s + 4t) (s 3t) ) 8s 94st + 3t (b) By the Chain ule, w
. (a) By the Chain ule, Math Spring 3 Exam 3 eview Problem Answers w s w x x s + w y y s (y xy)() + (xy x )( ) (( s + 4t) (s 3t)( s + 4t)) ((s 3t)( s + 4t) (s 3t) ) 8s 94st + 3t (b) By the Chain ule, w
Problem Y is an exponential random variable with parameter λ = 0.2. Given the event A = {Y < 2},
 ECE32 Spring 25 HW Solutions April 6, 25 Solutions to HW Note: Most of these solutions were generated by R. D. Yates and D. J. Goodman, the authors of our textbook. I have added comments in italics where
ECE32 Spring 25 HW Solutions April 6, 25 Solutions to HW Note: Most of these solutions were generated by R. D. Yates and D. J. Goodman, the authors of our textbook. I have added comments in italics where
Chapter 3. Second Order Linear PDEs
 Chapter 3. Second Order Linear PDEs 3.1 Introduction The general class of second order linear PDEs are of the form: ax, y)u xx + bx, y)u xy + cx, y)u yy + dx, y)u x + ex, y)u y + f x, y)u = gx, y). 3.1)
Chapter 3. Second Order Linear PDEs 3.1 Introduction The general class of second order linear PDEs are of the form: ax, y)u xx + bx, y)u xy + cx, y)u yy + dx, y)u x + ex, y)u y + f x, y)u = gx, y). 3.1)
Chapter 2 Continuous Distributions
 Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
arxiv: v1 [math.co] 6 Jan 2019
![arxiv: v1 [math.co] 6 Jan 2019 arxiv: v1 [math.co] 6 Jan 2019](/thumbs/93/113597801.jpg) BENT FUNCTIONS FROM TRIPLES OF PERMUTATION POLYNOMIALS arxiv:1901.02359v1 [math.co] 6 Jan 2019 DANIELE BARTOLI, MARIA MONTANUCCI, AND GIOVANNI ZINI Abstract. We provide constructions of bent functions
BENT FUNCTIONS FROM TRIPLES OF PERMUTATION POLYNOMIALS arxiv:1901.02359v1 [math.co] 6 Jan 2019 DANIELE BARTOLI, MARIA MONTANUCCI, AND GIOVANNI ZINI Abstract. We provide constructions of bent functions
Chapter 2 Vector-matrix Differential Equation and Numerical Inversion of Laplace Transform
 Chapter 2 Vector-matrix Differential Equation and Numerical Inversion of Laplace Transform 2.1 Vector-matrix Differential Equation A differential equation and a set of differential (simultaneous linear
Chapter 2 Vector-matrix Differential Equation and Numerical Inversion of Laplace Transform 2.1 Vector-matrix Differential Equation A differential equation and a set of differential (simultaneous linear
Lecture 5: Moment generating functions
 Lecture 5: Moment generating functions Definition 2.3.6. The moment generating function (mgf) of a random variable X is { x e tx f M X (t) = E(e tx X (x) if X has a pmf ) = etx f X (x)dx if X has a pdf
Lecture 5: Moment generating functions Definition 2.3.6. The moment generating function (mgf) of a random variable X is { x e tx f M X (t) = E(e tx X (x) if X has a pmf ) = etx f X (x)dx if X has a pdf
SEVERAL RESULTS OF FRACTIONAL DERIVATIVES IN D (R + ) Chenkuan Li. Author's Copy
 RESEARCH PAPER SEVERAL RESULTS OF FRACTIONAL DERIVATIVES IN D (R ) Chenkuan Li Abstract In this paper, we define fractional derivative of arbitrary complex order of the distributions concentrated on R,
RESEARCH PAPER SEVERAL RESULTS OF FRACTIONAL DERIVATIVES IN D (R ) Chenkuan Li Abstract In this paper, we define fractional derivative of arbitrary complex order of the distributions concentrated on R,
Continuous Random Variables and Continuous Distributions
 Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
Final Exam # 3. Sta 230: Probability. December 16, 2012
 Final Exam # 3 Sta 230: Probability December 16, 2012 This is a closed-book exam so do not refer to your notes, the text, or any other books (please put them on the floor). You may use the extra sheets
Final Exam # 3 Sta 230: Probability December 16, 2012 This is a closed-book exam so do not refer to your notes, the text, or any other books (please put them on the floor). You may use the extra sheets
a P (A) f k(x) = A k g k " g k (x) = ( 1) k x ą k. $ & g k (x) = x k (0, 1) f k, f, g : [0, 8) Ñ R f k (x) ď g(x) k P N x P [0, 8) g(x)dx g(x)dx ă 8
 M M, d A Ď M f k : A Ñ R A a P A f kx = A k xña k P N ta k u 8 k=1 f kx = f k x. xña kñ8 kñ8 xña M, d N, ρ A Ď M f k : A Ñ N tf k u 8 k=1 f : A Ñ N A f A 8ř " x ď k, g k x = 1 k x ą k. & g k x = % g k
M M, d A Ď M f k : A Ñ R A a P A f kx = A k xña k P N ta k u 8 k=1 f kx = f k x. xña kñ8 kñ8 xña M, d N, ρ A Ď M f k : A Ñ N tf k u 8 k=1 f : A Ñ N A f A 8ř " x ď k, g k x = 1 k x ą k. & g k x = % g k
Xt i Xs i N(0, σ 2 (t s)) and they are independent. This implies that the density function of X t X s is a product of normal density functions:
 174 BROWNIAN MOTION 8.4. Brownian motion in R d and the heat equation. The heat equation is a partial differential equation. We are going to convert it into a probabilistic equation by reversing time.
174 BROWNIAN MOTION 8.4. Brownian motion in R d and the heat equation. The heat equation is a partial differential equation. We are going to convert it into a probabilistic equation by reversing time.
1 Random Variable: Topics
 Note: Handouts DO NOT replace the book. In most cases, they only provide a guideline on topics and an intuitive feel. 1 Random Variable: Topics Chap 2, 2.1-2.4 and Chap 3, 3.1-3.3 What is a random variable?
Note: Handouts DO NOT replace the book. In most cases, they only provide a guideline on topics and an intuitive feel. 1 Random Variable: Topics Chap 2, 2.1-2.4 and Chap 3, 3.1-3.3 What is a random variable?
Introduction and preliminaries
 Chapter Introduction and preliminaries Partial differential equations What is a partial differential equation? ODEs Ordinary Differential Equations) have one variable x). PDEs Partial Differential Equations)
Chapter Introduction and preliminaries Partial differential equations What is a partial differential equation? ODEs Ordinary Differential Equations) have one variable x). PDEs Partial Differential Equations)
Name: Math Homework Set # 5. March 12, 2010
 Name: Math 4567. Homework Set # 5 March 12, 2010 Chapter 3 (page 79, problems 1,2), (page 82, problems 1,2), (page 86, problems 2,3), Chapter 4 (page 93, problems 2,3), (page 98, problems 1,2), (page 102,
Name: Math 4567. Homework Set # 5 March 12, 2010 Chapter 3 (page 79, problems 1,2), (page 82, problems 1,2), (page 86, problems 2,3), Chapter 4 (page 93, problems 2,3), (page 98, problems 1,2), (page 102,
A Very Brief Summary of Bayesian Inference, and Examples
 A Very Brief Summary of Bayesian Inference, and Examples Trinity Term 009 Prof Gesine Reinert Our starting point are data x = x 1, x,, x n, which we view as realisations of random variables X 1, X,, X
A Very Brief Summary of Bayesian Inference, and Examples Trinity Term 009 Prof Gesine Reinert Our starting point are data x = x 1, x,, x n, which we view as realisations of random variables X 1, X,, X
ESTIMATION THEORY. Chapter Estimation of Random Variables
 Chapter ESTIMATION THEORY. Estimation of Random Variables Suppose X,Y,Y 2,...,Y n are random variables defined on the same probability space (Ω, S,P). We consider Y,...,Y n to be the observed random variables
Chapter ESTIMATION THEORY. Estimation of Random Variables Suppose X,Y,Y 2,...,Y n are random variables defined on the same probability space (Ω, S,P). We consider Y,...,Y n to be the observed random variables
Math 201 Solutions to Assignment 1. 2ydy = x 2 dx. y = C 1 3 x3
 Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
BMIR Lecture Series on Probability and Statistics Fall 2015 Discrete RVs
 Lecture #7 BMIR Lecture Series on Probability and Statistics Fall 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University 7.1 Function of Single Variable Theorem
Lecture #7 BMIR Lecture Series on Probability and Statistics Fall 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University 7.1 Function of Single Variable Theorem
Exam 1 Review: Questions and Answers. Part I. Finding solutions of a given differential equation.
 Exam 1 Review: Questions and Answers Part I. Finding solutions of a given differential equation. 1. Find the real numbers r such that y = e x is a solution of y y 30y = 0. Answer: r = 6, 5 2. Find the
Exam 1 Review: Questions and Answers Part I. Finding solutions of a given differential equation. 1. Find the real numbers r such that y = e x is a solution of y y 30y = 0. Answer: r = 6, 5 2. Find the
Optimization: Problem Set Solutions
 Optimization: Problem Set Solutions Annalisa Molino University of Rome Tor Vergata annalisa.molino@uniroma2.it Fall 20 Compute the maxima minima or saddle points of the following functions a. f(x y) =
Optimization: Problem Set Solutions Annalisa Molino University of Rome Tor Vergata annalisa.molino@uniroma2.it Fall 20 Compute the maxima minima or saddle points of the following functions a. f(x y) =
Miscellaneous Errors in the Chapter 6 Solutions
 Miscellaneous Errors in the Chapter 6 Solutions 3.30(b In this problem, early printings of the second edition use the beta(a, b distribution, but later versions use the Poisson(λ distribution. If your
Miscellaneous Errors in the Chapter 6 Solutions 3.30(b In this problem, early printings of the second edition use the beta(a, b distribution, but later versions use the Poisson(λ distribution. If your
Continuous random variables
 Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Ordinary Differential Equations (ODEs)
 Chapter 13 Ordinary Differential Equations (ODEs) We briefly review how to solve some of the most standard ODEs. 13.1 First Order Equations 13.1.1 Separable Equations A first-order ordinary differential
Chapter 13 Ordinary Differential Equations (ODEs) We briefly review how to solve some of the most standard ODEs. 13.1 First Order Equations 13.1.1 Separable Equations A first-order ordinary differential
Random Variables. Cumulative Distribution Function (CDF) Amappingthattransformstheeventstotherealline.
 Random Variables Amappingthattransformstheeventstotherealline. Example 1. Toss a fair coin. Define a random variable X where X is 1 if head appears and X is if tail appears. P (X =)=1/2 P (X =1)=1/2 Example
Random Variables Amappingthattransformstheeventstotherealline. Example 1. Toss a fair coin. Define a random variable X where X is 1 if head appears and X is if tail appears. P (X =)=1/2 P (X =1)=1/2 Example
Solution to Assignment 3
 The Chinese University of Hong Kong ENGG3D: Probability and Statistics for Engineers 5-6 Term Solution to Assignment 3 Hongyang Li, Francis Due: 3:pm, March Release Date: March 8, 6 Dear students, The
The Chinese University of Hong Kong ENGG3D: Probability and Statistics for Engineers 5-6 Term Solution to Assignment 3 Hongyang Li, Francis Due: 3:pm, March Release Date: March 8, 6 Dear students, The
March Algebra 2 Question 1. March Algebra 2 Question 1
 March Algebra 2 Question 1 If the statement is always true for the domain, assign that part a 3. If it is sometimes true, assign it a 2. If it is never true, assign it a 1. Your answer for this question
March Algebra 2 Question 1 If the statement is always true for the domain, assign that part a 3. If it is sometimes true, assign it a 2. If it is never true, assign it a 1. Your answer for this question
THE UNIVERSITY OF HONG KONG DEPARTMENT OF STATISTICS AND ACTUARIAL SCIENCE
 THE UNIVERSITY OF HONG KONG DEPARTMENT OF STATISTICS AND ACTUARIAL SCIENCE STAT131 PROBABILITY AND STATISTICS I EXAMPLE CLASS 8 Review Conditional Distributions and Conditional Expectation For any two
THE UNIVERSITY OF HONG KONG DEPARTMENT OF STATISTICS AND ACTUARIAL SCIENCE STAT131 PROBABILITY AND STATISTICS I EXAMPLE CLASS 8 Review Conditional Distributions and Conditional Expectation For any two
Homework 9 (due November 24, 2009)
 Homework 9 (due November 4, 9) Problem. The join probability density function of X and Y is given by: ( f(x, y) = c x + xy ) < x
Homework 9 (due November 4, 9) Problem. The join probability density function of X and Y is given by: ( f(x, y) = c x + xy ) < x
Chapter 7. Basic Probability Theory
 Chapter 7. Basic Probability Theory I-Liang Chern October 20, 2016 1 / 49 What s kind of matrices satisfying RIP Random matrices with iid Gaussian entries iid Bernoulli entries (+/ 1) iid subgaussian entries
Chapter 7. Basic Probability Theory I-Liang Chern October 20, 2016 1 / 49 What s kind of matrices satisfying RIP Random matrices with iid Gaussian entries iid Bernoulli entries (+/ 1) iid subgaussian entries
RECHERCHES. sur plusieurs points d analyse relatifs à différens endroits des M. DE LA LAGRANGE
 RECHERCHES sur plusieurs points d analyse relatifs à différens endroits des Mémoires précédens. M. DE LA LAGRANGE Mémoires de l Académie Royale des Sciences et Belles-Lettres 179 3 Berlin (1798), pp. 47
RECHERCHES sur plusieurs points d analyse relatifs à différens endroits des Mémoires précédens. M. DE LA LAGRANGE Mémoires de l Académie Royale des Sciences et Belles-Lettres 179 3 Berlin (1798), pp. 47
S6880 #7. Generate Non-uniform Random Number #1
 S6880 #7 Generate Non-uniform Random Number #1 Outline 1 Inversion Method Inversion Method Examples Application to Discrete Distributions Using Inversion Method 2 Composition Method Composition Method
S6880 #7 Generate Non-uniform Random Number #1 Outline 1 Inversion Method Inversion Method Examples Application to Discrete Distributions Using Inversion Method 2 Composition Method Composition Method
Galois Theory Overview/Example Part 1: Extension Fields. Overview:
 Galois Theory Overview/Example Part 1: Extension Fields I ll start by outlining very generally the way Galois theory works. Then, I will work through an example that will illustrate the Fundamental Theorem
Galois Theory Overview/Example Part 1: Extension Fields I ll start by outlining very generally the way Galois theory works. Then, I will work through an example that will illustrate the Fundamental Theorem
HADAMARD OPERATORS ON D (R d )
 HADAMARD OPERATORS ON D (R d DIETMAR VOGT BERGISCHE UNIVERSITÄT WUPPERTAL FB MATH.-NAT., GAUSS-STR. 20, D-42119 WUPPERTAL, GERMANY E-MAIL: DVOGT@MATH.UNI-WUPPERTAL.DE Dedicated to the memory of Paweª Doma«ski
HADAMARD OPERATORS ON D (R d DIETMAR VOGT BERGISCHE UNIVERSITÄT WUPPERTAL FB MATH.-NAT., GAUSS-STR. 20, D-42119 WUPPERTAL, GERMANY E-MAIL: DVOGT@MATH.UNI-WUPPERTAL.DE Dedicated to the memory of Paweª Doma«ski
Virtuality Distributions and γγ π 0 Transition at Handbag Level
 and γγ π Transition at Handbag Level A.V. Radyushkin form hard Physics Department, Old Dominion University & Theory Center, Jefferson Lab May 16, 214, QCD Evolution 214, Santa Fe Transverse Momentum form
and γγ π Transition at Handbag Level A.V. Radyushkin form hard Physics Department, Old Dominion University & Theory Center, Jefferson Lab May 16, 214, QCD Evolution 214, Santa Fe Transverse Momentum form
Section Let A =. Then A has characteristic equation λ. 2 4λ + 3 = 0 or (λ 3)(λ 1) = 0. Hence the eigenvalues of A are λ 1 = 3 and λ 2 = 1.
 Sectio 63 4 3 Let A The A has characteristic equatio λ 2 4λ + 3 or (λ 3)(λ ) Hece the eigevalues of A are λ 3 ad λ 2 λ 3 The correspodig eigevectors satisfy (A λ I 2 )X, or 3 3 or equivaletly x 3y Hece
Sectio 63 4 3 Let A The A has characteristic equatio λ 2 4λ + 3 or (λ 3)(λ ) Hece the eigevalues of A are λ 3 ad λ 2 λ 3 The correspodig eigevectors satisfy (A λ I 2 )X, or 3 3 or equivaletly x 3y Hece
Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama
 Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama Instructions This exam has 7 pages in total, numbered 1 to 7. Make sure your exam has all the pages. This exam will be 2 hours
Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama Instructions This exam has 7 pages in total, numbered 1 to 7. Make sure your exam has all the pages. This exam will be 2 hours
On Kummer s distributions of type two and generalized Beta distributions
 On Kummer s distributions of type two and generalized Beta distributions Marwa Hamza and Pierre Vallois 2 March 20, 205 Université de Lorraine, Institut de Mathématiques Elie Cartan, INRIA-BIGS, CNRS UMR
On Kummer s distributions of type two and generalized Beta distributions Marwa Hamza and Pierre Vallois 2 March 20, 205 Université de Lorraine, Institut de Mathématiques Elie Cartan, INRIA-BIGS, CNRS UMR
Statistics (1): Estimation
 Statistics (1): Estimation Marco Banterlé, Christian Robert and Judith Rousseau Practicals 2014-2015 L3, MIDO, Université Paris Dauphine 1 Table des matières 1 Random variables, probability, expectation
Statistics (1): Estimation Marco Banterlé, Christian Robert and Judith Rousseau Practicals 2014-2015 L3, MIDO, Université Paris Dauphine 1 Table des matières 1 Random variables, probability, expectation
Applied Stochastic Models (SS 09)
 University of Karlsruhe Institute of Stochastics Prof Dr P R Parthasarathy Dipl-Math D Gentner Applied Stochastic Models (SS 9) Problem Set Problem Let X, X 2 U(θ /2, θ + /2) be independent Show that the
University of Karlsruhe Institute of Stochastics Prof Dr P R Parthasarathy Dipl-Math D Gentner Applied Stochastic Models (SS 9) Problem Set Problem Let X, X 2 U(θ /2, θ + /2) be independent Show that the
First and Second Order ODEs
 Civil Engineering 2 Mathematics Autumn 211 M. Ottobre First and Second Order ODEs Warning: all the handouts that I will provide during the course are in no way exhaustive, they are just short recaps. Notation
Civil Engineering 2 Mathematics Autumn 211 M. Ottobre First and Second Order ODEs Warning: all the handouts that I will provide during the course are in no way exhaustive, they are just short recaps. Notation
ECE 302 Division 1 MWF 10:30-11:20 (Prof. Pollak) Final Exam Solutions, 5/3/2004. Please read the instructions carefully before proceeding.
 NAME: ECE 302 Division MWF 0:30-:20 (Prof. Pollak) Final Exam Solutions, 5/3/2004. Please read the instructions carefully before proceeding. If you are not in Prof. Pollak s section, you may not take this
NAME: ECE 302 Division MWF 0:30-:20 (Prof. Pollak) Final Exam Solutions, 5/3/2004. Please read the instructions carefully before proceeding. If you are not in Prof. Pollak s section, you may not take this
IRREDUCIBILITY OF ELLIPTIC CURVES AND INTERSECTION WITH LINES.
 IRREDUCIBILITY OF ELLIPTIC CURVES AND INTERSECTION WITH LINES. IAN KIMING 1. Non-singular points and tangents. Suppose that k is a field and that F (x 1,..., x n ) is a homogeneous polynomial in n variables
IRREDUCIBILITY OF ELLIPTIC CURVES AND INTERSECTION WITH LINES. IAN KIMING 1. Non-singular points and tangents. Suppose that k is a field and that F (x 1,..., x n ) is a homogeneous polynomial in n variables
2015 School Year. Graduate School Entrance Examination Problem Booklet. Mathematics
 2015 School Year Graduate School Entrance Examination Problem Booklet Mathematics Examination Time: 10:00 to 12:30 Instructions 1. Do not open this problem booklet until the start of the examination is
2015 School Year Graduate School Entrance Examination Problem Booklet Mathematics Examination Time: 10:00 to 12:30 Instructions 1. Do not open this problem booklet until the start of the examination is
Solutions to old Exam 3 problems
 Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
Calculus I (Math 241) (In Progress)
 Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
Random Variables and Their Distributions
 Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
