Probability Density Functions
|
|
|
- Ruby Dorsey
- 5 years ago
- Views:
Transcription
1 Probability Density Functions
2 Probability Density Functions Definition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that for any two numbers a and b with a b, P(a X b) = b a f (x)dx That is, the probability that X takes on a value in the interval [a, b] is the area above this interval and under the graph of the density function. The graph of f (x) is often referred to as the density curve.
3 Probability Density Functions
4 Probability Density Functions Figure: P(60 X 70)
5 Probability Density Functions
6 Probability Density Functions Definition A continuous rv X is said to have a uniform distribution on the interval [A, B], if the pdf of X is f (x; A, B) = { 1 B A A x B 0 otherwise
7 Probability Density Functions Definition A continuous rv X is said to have a uniform distribution on the interval [A, B], if the pdf of X is f (x; A, B) = { 1 B A A x B 0 otherwise The graph of any uniform pdf looks like the graph in the previous example:
8 Cumulative Distribution Functions
9 Cumulative Distribution Functions Definition The cumulative distribution function F (x) for a continuous rv X is defined for every number x by F (x) = P(X x) = x f (y)dy For each x, F (x) is the area under the density curve to the left of x.
10 Cumulative Distribution Functions
11 Cumulative Distribution Functions Proposition Let X be a continuous rv with pdf f (x) and cdf F (x). Then for any number a, P(X > a) = 1 F (a) and for any two numbers a and b with a < b, P(a X b) = F (b) F (a).
12 Cumulative Distribution Functions Proposition Let X be a continuous rv with pdf f (x) and cdf F (x). Then for any number a, P(X > a) = 1 F (a) and for any two numbers a and b with a < b, P(a X b) = F (b) F (a).
13 Cumulative Distribution Functions
14 Cumulative Distribution Functions Proposition If X is a continuous rv with pdf f (x) and cdf F (x), then at every x at which the derivative F (x) exists, F (x) = f (x).
15 Cumulative Distribution Functions
16 Cumulative Distribution Functions Definition The expected value or mean valued of a continuous rv X with pdf f (x) is µ X = E(X ) = x f (x)dx
17 Cumulative Distribution Functions Definition The expected value or mean valued of a continuous rv X with pdf f (x) is µ X = E(X ) = x f (x)dx Definition The variance of a continuous random variable X with pdf f (x) and mean value µ is σx 2 = V (X ) = (x µ) 2 f (x)dx = E[(X µ) 2 ] The standard deviation (SD) of X is σ X = V (X ).
18 Cumulative Distribution Functions
19 Cumulative Distribution Functions Definition Let p be a number between 0 and 1. The (100p)th percentile of the distribution of a continuous rv X, denoted by η(p), is defined by p = F (η(p)) = η(p) f (y)dy
20 Normal Distribution
21 Normal Distribution Definition A continuous rv X is said to have a normal distribution with parameter µ and σ (µ and σ 2 ), where < µ < and σ > 0, if the pdf of X is f (x; µ, σ) = 1 2πσ e (x µ)2 /(2σ 2 ) We use the notation X N(µ, σ 2 ) to denote that X is rormally distributed with parameters µ and σ 2.
22 Normal Distribution Definition A continuous rv X is said to have a normal distribution with parameter µ and σ (µ and σ 2 ), where < µ < and σ > 0, if the pdf of X is f (x; µ, σ) = 1 2πσ e (x µ)2 /(2σ 2 ) We use the notation X N(µ, σ 2 ) to denote that X is rormally distributed with parameters µ and σ 2. Remark: 1. Obviously, f (x) 0 for all x; 2. It is guaranteed that 1 2πσ e (y µ)2 /(2σ 2) dy = 1.
23 Normal Distribution
24 Normal Distribution Proposition For X N(µ, σ 2 ), we have E(X ) = µ and V (X ) = σ 2
25 Normal Distribution Proposition For X N(µ, σ 2 ), we have E(X ) = µ and V (X ) = σ 2 σ = 1 σ = 2 σ = 0.5
26
27 Normal Distribution
28 Normal Distribution The cdf of a normal random variable X is F (x) = P(X x) = = x x f (y; µ, σ)dy 1 2πσ e (y µ)2 /(2σ 2) dy = 1 x µ e (z)2 /(2σ 2) dz change of variable:z = y µ 2πσ = 1 x µ σ 2πσ = x µ σ e (w)2 /2 σdw 1 2π e (w)2 /2 dw change of variable:w = z σ
29 Normal Distribution
30 Normal Distribution Definition The normal distribution with parameter values µ = 0 and σ = 1 is called the standard normal distribution. A random variable having a standard normal distribution is called a standard normal random variable and will be denoted by Z. The pdf of Z is f (z; 0, 1) = 1 2π e z2 /2 < z < The graph of f (z; 0, 1) is called the standard normal (or z) curve. The cdf of Z is P(Z z) = z f (y; 0, 1)dy, which we will denote by Φ(z).
31 Normal Distribution
32 Normal Distribution Shaded area = Φ(0.5)
33 Normal Distribution
34 Normal Distribution Table A.3 Standard Normal Curve Areas z
35 Normal Distribution
36 Normal Distribution Z N(0, 1), calculate (a)p(z 1.61); (b)p(z > 1.12); and (c)p( 1.12 < Z 1.61).
37 Normal Distribution Z N(0, 1), calculate (a)p(z 1.61); (b)p(z > 1.12); and (c)p( 1.12 < Z 1.61). z
38 Normal Distribution Z N(0, 1), calculate (a)p(z 1.61); (b)p(z > 1.12); and (c)p( 1.12 < Z 1.61). z P(Z 1.61) = ;
39 Normal Distribution Z N(0, 1), calculate (a)p(z 1.61); (b)p(z > 1.12); and (c)p( 1.12 < Z 1.61). z P(Z 1.61) = ; P(Z > 1.12) = 1 P(Z 1.12) = = ;
40 Normal Distribution Z N(0, 1), calculate (a)p(z 1.61); (b)p(z > 1.12); and (c)p( 1.12 < Z 1.61). z P(Z 1.61) = ; P(Z > 1.12) = 1 P(Z 1.12) = = ; P( 1.12 < Z 1.61) = P(Z 1.61) P(Z 1.12) = =
41 Normal Distribution
42 Normal Distribution Many tables for the normal distribution contain only the nonnegative part.
43 Normal Distribution Many tables for the normal distribution contain only the nonnegative part. z What is P(Z < 1.63)?
44 Normal Distribution Many tables for the normal distribution contain only the nonnegative part. z What is P(Z < 1.63)? By symmetry of the pdf of Z, we know that P(Z < 1.63) = P(Z > 1.63) = 1 P(Z 1.63) = =
45 Normal Distribution Many tables for the normal distribution contain only the nonnegative part. z What is P(Z < 1.63)? By symmetry of the pdf of Z, we know that P(Z < 1.63) = P(Z > 1.63) = 1 P(Z 1.63) = =
46 Normal Distribution
47 Normal Distribution Recall: The (100p)th percentile of the distribution of a continuous rv X, η(p), is defined by p = F (η(p)) = η(p) f (y)dy
48 Normal Distribution Recall: The (100p)th percentile of the distribution of a continuous rv X, η(p), is defined by p = F (η(p)) = η(p) f (y)dy Similarly, the (100p)th percentile of the standard normal rv Z is defined by η(p) 1 p = F (η(p)) = e y 2 /2 dy 2π
49 Normal Distribution Recall: The (100p)th percentile of the distribution of a continuous rv X, η(p), is defined by p = F (η(p)) = η(p) f (y)dy Similarly, the (100p)th percentile of the standard normal rv Z is defined by η(p) 1 p = F (η(p)) = e y 2 /2 dy 2π We need to use the table for normal distribution to find (100p)th percentile.
50 Normal Distribution
51 Normal Distribution e.g. Find the 95th percentile for the standard normal rv Z
52 Normal Distribution e.g. Find the 95th percentile for the standard normal rv Z z
53 Normal Distribution e.g. Find the 95th percentile for the standard normal rv Z z η(95) = 1.645, a linear interpolation of 1.64 and 1.65.
54 Normal Distribution e.g. Find the 95th percentile for the standard normal rv Z z η(95) = 1.645, a linear interpolation of 1.64 and Remark: If p does not appear in the table, we can either use the number closest to it, or use the linear interpolation of the closest two.
55 Normal Distribution
56 Normal Distribution In statistical inference, the percentiles corresponding to right small tails are heavily used. Notation z α will denote the value on the z axis for which α of the area under the z curve lies to the right of z α.
57 Normal Distribution In statistical inference, the percentiles corresponding to right small tails are heavily used. Notation z α will denote the value on the z axis for which α of the area under the z curve lies to the right of z α. z α
58 Normal Distribution
59 Normal Distribution Remark: 1. z α is the 100(1 α)th percentile of the standard normal distribution.
60 Normal Distribution Remark: 1. z α is the 100(1 α)th percentile of the standard normal distribution. 2. By symmetry the area under the standard normal curve to the left of z α is also α.
61 Normal Distribution Remark: 1. z α is the 100(1 α)th percentile of the standard normal distribution. 2. By symmetry the area under the standard normal curve to the left of z α is also α. 3. The z α s are usually referred to as z critical values. Percentile α (tail area) z α
62 Normal Distribution
63 Normal Distribution Proposition If X has a normal distribution with mean µ and stadard deviation σ, then Z = X µ σ has a standard normal distribution. Thus P(a X b) = P( a µ Z b µ σ σ ) = Φ( b µ σ ) Φ(a µ σ ) P(X a) = Φ( a µ µ ) P(X b) = 1 Φ(b σ σ )
64 Normal Distribution
65 Normal Distribution Example (Problem 38): There are two machines available for cutting corks intended for use in wine bottles. The first produces corks with diameters that are normally distributed with mean 3cm and standard deviation 0.1cm. The second produces corks with diameters that have a normal distribution with mean 3.04cm and standard deviation 0.02cm. Acceptable corks have diameters between 2.9cm and 3.1cm. Which machine is more likely to produce an acceptable cork?
66 Normal Distribution Example (Problem 38): There are two machines available for cutting corks intended for use in wine bottles. The first produces corks with diameters that are normally distributed with mean 3cm and standard deviation 0.1cm. The second produces corks with diameters that have a normal distribution with mean 3.04cm and standard deviation 0.02cm. Acceptable corks have diameters between 2.9cm and 3.1cm. Which machine is more likely to produce an acceptable cork? P(2.9 X 1 3.1) = P( Z ) = P( 1 Z 1) = = P(2.9 X 2 3.1) = P( Z ) = P( 7 Z 3) = =
67 Normal Distribution
68 Normal Distribution Example (Problem 44): If bolt thread length is normally distributed, what is the probability that the thread length of a randomly selected bolt is (a)within 1.5 SDs of its mean value? (b)between 1 and 2 SDs from its mean value?
69 Normal Distribution Example (Problem 44): If bolt thread length is normally distributed, what is the probability that the thread length of a randomly selected bolt is (a)within 1.5 SDs of its mean value? (b)between 1 and 2 SDs from its mean value? P(µ 1.5σ X 1 µ + 1.5σ) = P( µ 1.5σ µ Z µ + 1.5σ µ ) σ σ = P( 1.5 Z 1.5) = =
70 Normal Distribution Example (Problem 44): If bolt thread length is normally distributed, what is the probability that the thread length of a randomly selected bolt is (a)within 1.5 SDs of its mean value? (b)between 1 and 2 SDs from its mean value? P(µ 1.5σ X 1 µ + 1.5σ) = P( µ 1.5σ µ Z µ + 1.5σ µ ) σ σ = P( 1.5 Z 1.5) = = P(µ + σ X 1 µ + 2σ) = 2P( µ + σ µ Z µ + 2σ µ ) σ σ = 2P(1 Z 2) = 2( ) =
71 Normal Distribution
72 Normal Distribution Proposition {(100p)th percentile for N(µ, σ 2 )} = µ + {(100p)th percentile for N(0, 1)} σ
73 Normal Distribution Proposition {(100p)th percentile for N(µ, σ 2 )} = µ + {(100p)th percentile for N(0, 1)} σ Example (Problem 39) The width of a line etched on an integrated circuit chip is normally distributed with mean µm and standard deviation What width value separates the widest 10% of all such lines from the other 90%?
74 Normal Distribution Proposition {(100p)th percentile for N(µ, σ 2 )} = µ + {(100p)th percentile for N(0, 1)} σ Example (Problem 39) The width of a line etched on an integrated circuit chip is normally distributed with mean µm and standard deviation What width value separates the widest 10% of all such lines from the other 90%? η N(3, )(90) = η N(0,1) (90) = =
75 Normal Distribution
76 Normal Distribution Proposition Let X be a binomial rv based on n trials with success probability p. Then if the binomial probability histogram is not too skewed, X has approximately a normal distribution with µ = np and σ = npq, where q = 1 p. In particular, for x = a posible value of X, ( ) area under the normal curve P(X x) = B(x; n, p) to the left of x+0.5 x+0.5 np = Φ( ) npq In practice, the approximation is adequate provided that both np 10 and nq 10, since there is then enough symmetry in the underlying binomial distribution.
77 Normal Distribution
78 Normal Distribution A graphical explanation for ( ) area under the normal curve P(X x) = B(x; n, p) to the left of x+0.5 x+0.5 np = Φ( ) npq
79 Normal Distribution A graphical explanation for ( ) area under the normal curve P(X x) = B(x; n, p) to the left of x+0.5 x+0.5 np = Φ( ) npq
80 Normal Distribution
81 Normal Distribution Example (Problem 54) Suppose that 10% of all steel shafts produced by a certain process are nonconforming but can be reworked (rather than having to be scrapped). Consider a random sample of 200 shafts, and let X denote the number among these that are nonconforming and can be reworked. What is the (approximate) probability that X is between 15 and 25 (inclusive)?
82 Normal Distribution Example (Problem 54) Suppose that 10% of all steel shafts produced by a certain process are nonconforming but can be reworked (rather than having to be scrapped). Consider a random sample of 200 shafts, and let X denote the number among these that are nonconforming and can be reworked. What is the (approximate) probability that X is between 15 and 25 (inclusive)? In this problem n = 200, p = 0.1 and q = 1 p = 0.9. Thus np = 20 > 10 and nq = 180 > 10
83 Normal Distribution Example (Problem 54) Suppose that 10% of all steel shafts produced by a certain process are nonconforming but can be reworked (rather than having to be scrapped). Consider a random sample of 200 shafts, and let X denote the number among these that are nonconforming and can be reworked. What is the (approximate) probability that X is between 15 and 25 (inclusive)? In this problem n = 200, p = 0.1 and q = 1 p = 0.9. Thus np = 20 > 10 and nq = 180 > 10 P(15 X 25) = Bin(25; 200, 0.1) Bin(14; 200, 0.1) Φ( ) Φ( ) = Φ(0.3056) Φ( ) = =
84 Exponential Distribution
85 Exponential Distribution Definition X is said to have an exponential distribution with parameter λ(λ > 0) if the pdf of X is { λe λx x 0 f (x; λ) = 0 otherwise
86 Exponential Distribution Definition X is said to have an exponential distribution with parameter λ(λ > 0) if the pdf of X is { λe λx x 0 f (x; λ) = 0 otherwise Remark: 1. Usually we use X EXP(λ) to denote that the random variable X has an exponential distribution with parameter λ.
87 Exponential Distribution Definition X is said to have an exponential distribution with parameter λ(λ > 0) if the pdf of X is { λe λx x 0 f (x; λ) = 0 otherwise Remark: 1. Usually we use X EXP(λ) to denote that the random variable X has an exponential distribution with parameter λ. 2. In some sources, the pdf of exponential distribution is given by { 1 f (x; θ) = θ e x θ x 0 0 otherwise The difference is that λ 1 θ.
88 Exponential Distribution
89 Exponential Distribution
90 Exponential Distribution
91 Exponential Distribution Proposition If X EXP(λ), then And the cdf for X is E(X ) = 1 λ and V (X ) = 1 λ 2 F (x; λ) = { 1 e λx x 0 0 x < 0
92 Exponential Distribution
93 Exponential Distribution Proof: E(X ) = = 1 λ = 1 λ xλe λx dx (λx)e λx d(λx) ye y dy = 1 λ [ ye y 0 + = 1 λ [0 + ( e y 0 )] 0 e y dy] y = λx integration by parts: u = y, v = e y = 1 λ
94 Exponential Distribution
95 Exponential Distribution Proof (continued): E(X 2 ) = 0 x 2 λe λx dx = 1 λ 2 (λx) 2 e λx d(λx) 0 = 1 λ 2 y 2 e y dy 0 = 1 λ 2 [ y 2 e y 0 + = 1 λ 2 [0 + 2( ye y 0 + = 1 λ 2 2[0 + ( ye y 0 )] 0 2ye y dy] 0 e y dy)] y = λx integration by parts integration by parts = 2 λ 2
96 Exponential Distribution
97 Exponential Distribution Proof (continued): V (X ) = E(X 2 ) [E(X )] 2 = 2 λ 2 ( 1 λ )2 = 1 λ 2 F (x) = = = x 0 x 0 λx 0 λe λy dy e λy d(λy) e z dz = e z λx 0 = 1 e λx z = λy
98 Exponential Distribution
99 Exponential Distribution Example (Problem 108) The article Determination of the MTF of Positive Photoresists Using the Monte Carlo method (Photographic Sci. and Engr., 1983: ) proposes the exponential distribution with parameter λ = 0.93 as a model for the distribution of a photon s free path length (µm) under certain circumstances. Suppose this is the correct model.
100 Exponential Distribution Example (Problem 108) The article Determination of the MTF of Positive Photoresists Using the Monte Carlo method (Photographic Sci. and Engr., 1983: ) proposes the exponential distribution with parameter λ = 0.93 as a model for the distribution of a photon s free path length (µm) under certain circumstances. Suppose this is the correct model. a. What is the expected path length, and what is the standard deviation of path length?
101 Exponential Distribution Example (Problem 108) The article Determination of the MTF of Positive Photoresists Using the Monte Carlo method (Photographic Sci. and Engr., 1983: ) proposes the exponential distribution with parameter λ = 0.93 as a model for the distribution of a photon s free path length (µm) under certain circumstances. Suppose this is the correct model. a. What is the expected path length, and what is the standard deviation of path length? b. What is the probability that path length exceeds 3.0?
102 Exponential Distribution Example (Problem 108) The article Determination of the MTF of Positive Photoresists Using the Monte Carlo method (Photographic Sci. and Engr., 1983: ) proposes the exponential distribution with parameter λ = 0.93 as a model for the distribution of a photon s free path length (µm) under certain circumstances. Suppose this is the correct model. a. What is the expected path length, and what is the standard deviation of path length? b. What is the probability that path length exceeds 3.0? c. What value is exceeded by only 10% of all path lengths?
103 Exponential Distribution
104 Exponential Distribution Proposition Suppose that the number of events occurring in any time interval of length t has a Poisson distribution with parameter αt (where α, the rate of the event process, is the expected number of events occurring in 1 unit of time) and that numbers of occurrences in nonoverlappong intervals are independent of one another. Then the distribution of elapsed time between the occurrence of two successive events is exponential with parameter λ = α.
105 Exponential Distribution Proposition Suppose that the number of events occurring in any time interval of length t has a Poisson distribution with parameter αt (where α, the rate of the event process, is the expected number of events occurring in 1 unit of time) and that numbers of occurrences in nonoverlappong intervals are independent of one another. Then the distribution of elapsed time between the occurrence of two successive events is exponential with parameter λ = α. e.g. the number of customers visiting Costco in each hour = Poisson distribution;
106 Exponential Distribution Proposition Suppose that the number of events occurring in any time interval of length t has a Poisson distribution with parameter αt (where α, the rate of the event process, is the expected number of events occurring in 1 unit of time) and that numbers of occurrences in nonoverlappong intervals are independent of one another. Then the distribution of elapsed time between the occurrence of two successive events is exponential with parameter λ = α. e.g. the number of customers visiting Costco in each hour = Poisson distribution; the time between every two successive customers visiting Costco = Exponential distribution.
107 Exponential Distribution
108 Exponential Distribution Example (Example 4.22) Suppose that calls are received at a 24-hour hotline according to a Poisson process with rate α = 0.5 call per day.
109 Exponential Distribution Example (Example 4.22) Suppose that calls are received at a 24-hour hotline according to a Poisson process with rate α = 0.5 call per day. Then the number of days X between successive calls has an exponential distribution with parameter value 0.5.
110 Exponential Distribution Example (Example 4.22) Suppose that calls are received at a 24-hour hotline according to a Poisson process with rate α = 0.5 call per day. Then the number of days X between successive calls has an exponential distribution with parameter value 0.5. The probability that more than 3 days elapse between calls is P(X > 3) = 1 P(X 3) = 1 F (3; 0.5) = e =
111 Exponential Distribution Example (Example 4.22) Suppose that calls are received at a 24-hour hotline according to a Poisson process with rate α = 0.5 call per day. Then the number of days X between successive calls has an exponential distribution with parameter value 0.5. The probability that more than 3 days elapse between calls is P(X > 3) = 1 P(X 3) = 1 F (3; 0.5) = e = The expected time between successive calls is 1/0.5 = 2 days.
112 Exponential Distribution
113 Exponential Distribution Memoryless Property Let X = the time certain component lasts (in hours) and we assume the component lifetime is exponentially distributed with parameter λ. Then what is the probability that the component can last at least an additional t hours after working for t 0 hours, i.e. what is P(X t + t 0 X t 0 )?
114 Exponential Distribution Memoryless Property Let X = the time certain component lasts (in hours) and we assume the component lifetime is exponentially distributed with parameter λ. Then what is the probability that the component can last at least an additional t hours after working for t 0 hours, i.e. what is P(X t + t 0 X t 0 )? P(X t + t 0 X t 0 ) = P({X t + t 0} {X t 0 }) P(X t 0 ) = P(X t + t 0) P(X t 0 ) = 1 F (t + t 0; λ) F (t 0 ; λ) = e λt
115 Exponential Distribution
116 Exponential Distribution Memoryless Property However, we have P(X t) = 1 F (t; λ) = e λt
117 Exponential Distribution Memoryless Property However, we have Therefore, we have for any positive t and t 0. P(X t) = 1 F (t; λ) = e λt P(X t) = P(X t + t 0 X t 0 )
118 Exponential Distribution Memoryless Property However, we have Therefore, we have P(X t) = 1 F (t; λ) = e λt P(X t) = P(X t + t 0 X t 0 ) for any positive t and t 0. In words, the distribution of additional lifetime is exactly the same as the original distribution of lifetime, so at each point in time the component shows no effect of wear. In other words, the distribution of remaining lifetime is independent of current age.
119 Gamma Distribution
120 Gamma Distribution Definition For α > 0, the gamma function Γ(α) is defined by Γ(α) = 0 x α 1 e x dx
121 Gamma Distribution Definition For α > 0, the gamma function Γ(α) is defined by Γ(α) = 0 x α 1 e x dx Properties for gamma function: 1. For any α > 1, Γ(α) = (α 1) Γ(α 1) [via integration by parts];
122 Gamma Distribution Definition For α > 0, the gamma function Γ(α) is defined by Γ(α) = 0 x α 1 e x dx Properties for gamma function: 1. For any α > 1, Γ(α) = (α 1) Γ(α 1) [via integration by parts]; 2. For any positive integer, n, Γ(n) = (n 1)!;
123 Gamma Distribution Definition For α > 0, the gamma function Γ(α) is defined by Γ(α) = 0 x α 1 e x dx Properties for gamma function: 1. For any α > 1, Γ(α) = (α 1) Γ(α 1) [via integration by parts]; 2. For any positive integer, n, Γ(n) = (n 1)!; 3. Γ( 1 2 ) = π.
124 Gamma Distribution Definition For α > 0, the gamma function Γ(α) is defined by Γ(α) = 0 x α 1 e x dx Properties for gamma function: 1. For any α > 1, Γ(α) = (α 1) Γ(α 1) [via integration by parts]; 2. For any positive integer, n, Γ(n) = (n 1)!; 3. Γ( 1 2 ) = π. e.g. Γ(4) = (4 1)! = 6 and Γ( 5 2 ) = 3 2 Γ( 3 2 ) = 3 2 [ 1 2 Γ( 1 2 )] = 3 4 π
125 Gamma Distribution
126 Gamma Distribution Definition A continuous random variable X is said to have a gamma distribution if the pdf of X is { 1 β f (x; α, β) = α Γ(α) x α 1 e x/β x 0 0 otherwise where the parameters α and β satisfy α > 0, β > 0. The standard gamma distribution has β = 1, so the pdf of a standard gamma rv is { 1 Γ(α) f (x; α) = x α 1 e x x 0 0 otherwise
127 Gamma Distribution
128 Gamma Distribution Remark: 1. We use X GAM(α, β) to denote that the rv X has a gamma distribution with parameter α and β.
129 Gamma Distribution Remark: 1. We use X GAM(α, β) to denote that the rv X has a gamma distribution with parameter α and β. 2. If we let α = 1 and β = 1/λ, then we get the exponential distribution: f (x; 1, 1 λ ) = { 1 1 λ Γ(1)x 1 1 e x/ 1 λ = λe λx x 0 0 otherwise
130 Gamma Distribution Remark: 1. We use X GAM(α, β) to denote that the rv X has a gamma distribution with parameter α and β. 2. If we let α = 1 and β = 1/λ, then we get the exponential distribution: { f (x; 1, 1 1 λ ) = 1 Γ(1)x 1 1 e x/ 1 λ = λe λx x 0 λ 0 otherwise 3. When X is a standard gamma rv (β = 1), the cdf of X, F (x; α) = x 0 y α 1 e y Γ(α) dy is called the incomplete gamma function.
131 Gamma Distribution Remark: 1. We use X GAM(α, β) to denote that the rv X has a gamma distribution with parameter α and β. 2. If we let α = 1 and β = 1/λ, then we get the exponential distribution: { f (x; 1, 1 1 λ ) = 1 Γ(1)x 1 1 e x/ 1 λ = λe λx x 0 λ 0 otherwise 3. When X is a standard gamma rv (β = 1), the cdf of X, F (x; α) = x 0 y α 1 e y Γ(α) dy is called the incomplete gamma function. There are extensive tables of F (x; α) available (Appendix Table A.4).
132 Gamma Distribution
133 Gamma Distribution
134 Gamma Distribution
135 Gamma Distribution Proposition If X GAM(α, β), then E(X ) = αβ and V (X ) = αβ 2 Furthermore, for any x > 0, the cdf of X is given by ( ) x P(X x) = F (x; α, β) = F β ; α where F ( ; α) is the incomplete gamma function.
136 Gamma Distribution
137 Gamma Distribution Example: The survival time (in days) of a white rat that was subjected to a certain level of X-ray radiation is a random variable X GAM(5, 4). Then what is a. the probability that the survival time is at most 16 days;
138 Gamma Distribution Example: The survival time (in days) of a white rat that was subjected to a certain level of X-ray radiation is a random variable X GAM(5, 4). Then what is a. the probability that the survival time is at most 16 days; b. the probability that the survival time is between 16 days and 20 days (not inclusive);
139 Gamma Distribution Example: The survival time (in days) of a white rat that was subjected to a certain level of X-ray radiation is a random variable X GAM(5, 4). Then what is a. the probability that the survival time is at most 16 days; b. the probability that the survival time is between 16 days and 20 days (not inclusive); c. the expected survival time.
140 Gamma Distribution Example: The survival time (in days) of a white rat that was subjected to a certain level of X-ray radiation is a random variable X GAM(5, 4). Then what is a. the probability that the survival time is at most 16 days; b. the probability that the survival time is between 16 days and 20 days (not inclusive); c. the expected survival time.
141 Chi-Squared Distribution
142 Chi-Squared Distribution Definition Let ν be a positive integer. Then a random variable X is said to have a chi-squared distribution with parameter ν if the pdf of X is the gamma density with α = ν/2 and β = 2. The pdf of a chi-squared rv is thus f (x; ν) = { 1 2 ν/2 Γ(ν/2) x (ν/2) 1 e x/2 x 0 0 x < 0 The parameter ν is called the number of degrees of freedom (df) of X. The symbol χ 2 is often used in place of chi-squared.
143 Chi-Squared Distribution
144 Chi-Squared Distribution Remark: 1. Usually, we use X χ 2 (ν) to denote that X is a chi-squared rv with parameter ν;
145 Chi-Squared Distribution Remark: 1. Usually, we use X χ 2 (ν) to denote that X is a chi-squared rv with parameter ν; 2. If X 1, X 2,..., X n is n independent standard normal rv s, then X X X 2 n has the same distribution as χ 2 (n).
146 Chi-Squared Distribution
147 Chi-Squared Distribution
Standard Normal Curve Areas z
 Table A.3 Standard Normal Curve Areas z.00.01.02.03.04.09-1.2 0.1151 0.1131 0.1112 0.1094 0.1075 0.0985-1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1170 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9545 1.7 0.9554
Table A.3 Standard Normal Curve Areas z.00.01.02.03.04.09-1.2 0.1151 0.1131 0.1112 0.1094 0.1075 0.0985-1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1170 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9545 1.7 0.9554
Continuous Random Variables and Continuous Distributions
 Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
Continuous Random Variables and Probability Distributions
 Continuous Random Variables and Probability Distributions Instructor: Lingsong Zhang 1 4.1 Probability Density Functions Probability Density Functions Recall from Chapter 3 that a random variable X is
Continuous Random Variables and Probability Distributions Instructor: Lingsong Zhang 1 4.1 Probability Density Functions Probability Density Functions Recall from Chapter 3 that a random variable X is
Common ontinuous random variables
 Common ontinuous random variables CE 311S Earlier, we saw a number of distribution families Binomial Negative binomial Hypergeometric Poisson These were useful because they represented common situations:
Common ontinuous random variables CE 311S Earlier, we saw a number of distribution families Binomial Negative binomial Hypergeometric Poisson These were useful because they represented common situations:
Continuous Random Variables. and Probability Distributions. Continuous Random Variables and Probability Distributions ( ) ( ) Chapter 4 4.
 UCLA STAT 11 A Applied Probability & Statistics for Engineers Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Christopher Barr University of California, Los Angeles,
UCLA STAT 11 A Applied Probability & Statistics for Engineers Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Christopher Barr University of California, Los Angeles,
STAT Chapter 5 Continuous Distributions
 STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
Probability Distributions for Continuous Variables. Probability Distributions for Continuous Variables
 Probability Distributions for Continuous Variables Probability Distributions for Continuous Variables Let X = lake depth at a randomly chosen point on lake surface If we draw the histogram so that the
Probability Distributions for Continuous Variables Probability Distributions for Continuous Variables Let X = lake depth at a randomly chosen point on lake surface If we draw the histogram so that the
Continuous random variables
 Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Chapter 4: Continuous Probability Distributions
 Chapter 4: Continuous Probability Distributions Seungchul Baek Department of Statistics, University of South Carolina STAT 509: Statistics for Engineers 1 / 57 Continuous Random Variable A continuous random
Chapter 4: Continuous Probability Distributions Seungchul Baek Department of Statistics, University of South Carolina STAT 509: Statistics for Engineers 1 / 57 Continuous Random Variable A continuous random
BMIR Lecture Series on Probability and Statistics Fall, 2015 Uniform Distribution
 Lecture #5 BMIR Lecture Series on Probability and Statistics Fall, 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University s 5.1 Definition ( ) A continuous random
Lecture #5 BMIR Lecture Series on Probability and Statistics Fall, 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University s 5.1 Definition ( ) A continuous random
Continuous Random Variables
 Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
Chapter 4: Continuous Random Variables and Probability Distributions
 Chapter 4: and Probability Distributions Walid Sharabati Purdue University February 14, 2014 Professor Sharabati (Purdue University) Spring 2014 (Slide 1 of 37) Chapter Overview Continuous random variables
Chapter 4: and Probability Distributions Walid Sharabati Purdue University February 14, 2014 Professor Sharabati (Purdue University) Spring 2014 (Slide 1 of 37) Chapter Overview Continuous random variables
Exponential, Gamma and Normal Distribuions
 Exponential, Gamma and Normal Distribuions Sections 5.4, 5.5 & 6.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy Poliak,
Exponential, Gamma and Normal Distribuions Sections 5.4, 5.5 & 6.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy Poliak,
STAT509: Continuous Random Variable
 University of South Carolina September 23, 2014 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite or infinite) of real numbers for its range.
University of South Carolina September 23, 2014 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite or infinite) of real numbers for its range.
CHAPTER 6 SOME CONTINUOUS PROBABILITY DISTRIBUTIONS. 6.2 Normal Distribution. 6.1 Continuous Uniform Distribution
 CHAPTER 6 SOME CONTINUOUS PROBABILITY DISTRIBUTIONS Recall that a continuous random variable X is a random variable that takes all values in an interval or a set of intervals. The distribution of a continuous
CHAPTER 6 SOME CONTINUOUS PROBABILITY DISTRIBUTIONS Recall that a continuous random variable X is a random variable that takes all values in an interval or a set of intervals. The distribution of a continuous
Chapter 4: Continuous Random Variable
 Chapter 4: Continuous Random Variable Shiwen Shen University of South Carolina 2017 Summer 1 / 57 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite
Chapter 4: Continuous Random Variable Shiwen Shen University of South Carolina 2017 Summer 1 / 57 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite
X = lifetime of transistor
 Kelley Problem 4-57 /3 Suppose that when a transistor of a certain type is subjected to an accelerated life test, the lifetime, X (in weeks) has a gamma distribution with mean 24 weeks and standard deviation
Kelley Problem 4-57 /3 Suppose that when a transistor of a certain type is subjected to an accelerated life test, the lifetime, X (in weeks) has a gamma distribution with mean 24 weeks and standard deviation
Continuous Random Variables. and Probability Distributions. Continuous Random Variables and Probability Distributions ( ) ( )
 UCLA STAT 35 Applied Computational and Interactive Probability Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Chris Barr Continuous Random Variables and Probability
UCLA STAT 35 Applied Computational and Interactive Probability Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Chris Barr Continuous Random Variables and Probability
Ching-Han Hsu, BMES, National Tsing Hua University c 2015 by Ching-Han Hsu, Ph.D., BMIR Lab. = a + b 2. b a. x a b a = 12
 Lecture 5 Continuous Random Variables BMIR Lecture Series in Probability and Statistics Ching-Han Hsu, BMES, National Tsing Hua University c 215 by Ching-Han Hsu, Ph.D., BMIR Lab 5.1 1 Uniform Distribution
Lecture 5 Continuous Random Variables BMIR Lecture Series in Probability and Statistics Ching-Han Hsu, BMES, National Tsing Hua University c 215 by Ching-Han Hsu, Ph.D., BMIR Lab 5.1 1 Uniform Distribution
Gamma and Normal Distribuions
 Gamma and Normal Distribuions Sections 5.4 & 5.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 15-3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
Gamma and Normal Distribuions Sections 5.4 & 5.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 15-3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
STA 256: Statistics and Probability I
 Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. Exercise 4.1 Let X be a random variable with p(x)
Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. Exercise 4.1 Let X be a random variable with p(x)
Random Variables and Their Distributions
 Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Probability and Distributions
 Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
15 Discrete Distributions
 Lecture Note 6 Special Distributions (Discrete and Continuous) MIT 4.30 Spring 006 Herman Bennett 5 Discrete Distributions We have already seen the binomial distribution and the uniform distribution. 5.
Lecture Note 6 Special Distributions (Discrete and Continuous) MIT 4.30 Spring 006 Herman Bennett 5 Discrete Distributions We have already seen the binomial distribution and the uniform distribution. 5.
Chapter 2 Continuous Distributions
 Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
3 Modeling Process Quality
 3 Modeling Process Quality 3.1 Introduction Section 3.1 contains basic numerical and graphical methods. familiar with these methods. It is assumed the student is Goal: Review several discrete and continuous
3 Modeling Process Quality 3.1 Introduction Section 3.1 contains basic numerical and graphical methods. familiar with these methods. It is assumed the student is Goal: Review several discrete and continuous
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models
 System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 20, 2012 Introduction Introduction The world of the model-builder
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 20, 2012 Introduction Introduction The world of the model-builder
S n = x + X 1 + X X n.
 0 Lecture 0 0. Gambler Ruin Problem Let X be a payoff if a coin toss game such that P(X = ) = P(X = ) = /2. Suppose you start with x dollars and play the game n times. Let X,X 2,...,X n be payoffs in each
0 Lecture 0 0. Gambler Ruin Problem Let X be a payoff if a coin toss game such that P(X = ) = P(X = ) = /2. Suppose you start with x dollars and play the game n times. Let X,X 2,...,X n be payoffs in each
Continuous Distributions
 Chapter 3 Continuous Distributions 3.1 Continuous-Type Data In Chapter 2, we discuss random variables whose space S contains a countable number of outcomes (i.e. of discrete type). In Chapter 3, we study
Chapter 3 Continuous Distributions 3.1 Continuous-Type Data In Chapter 2, we discuss random variables whose space S contains a countable number of outcomes (i.e. of discrete type). In Chapter 3, we study
Topic 4: Continuous random variables
 Topic 4: Continuous random variables Course 003, 2018 Page 0 Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative
Topic 4: Continuous random variables Course 003, 2018 Page 0 Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative
Stat410 Probability and Statistics II (F16)
 Stat4 Probability and Statistics II (F6 Exponential, Poisson and Gamma Suppose on average every /λ hours, a Stochastic train arrives at the Random station. Further we assume the waiting time between two
Stat4 Probability and Statistics II (F6 Exponential, Poisson and Gamma Suppose on average every /λ hours, a Stochastic train arrives at the Random station. Further we assume the waiting time between two
Topic 4: Continuous random variables
 Topic 4: Continuous random variables Course 3, 216 Page Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative function
Topic 4: Continuous random variables Course 3, 216 Page Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative function
MATH : EXAM 2 INFO/LOGISTICS/ADVICE
 MATH 3342-004: EXAM 2 INFO/LOGISTICS/ADVICE INFO: WHEN: Friday (03/11) at 10:00am DURATION: 50 mins PROBLEM COUNT: Appropriate for a 50-min exam BONUS COUNT: At least one TOPICS CANDIDATE FOR THE EXAM:
MATH 3342-004: EXAM 2 INFO/LOGISTICS/ADVICE INFO: WHEN: Friday (03/11) at 10:00am DURATION: 50 mins PROBLEM COUNT: Appropriate for a 50-min exam BONUS COUNT: At least one TOPICS CANDIDATE FOR THE EXAM:
Expected Values, Exponential and Gamma Distributions
 Expected Values, Exponential and Gamma Distributions Sections 5.2-5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 14-3339 Cathy Poliak,
Expected Values, Exponential and Gamma Distributions Sections 5.2-5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 14-3339 Cathy Poliak,
Math438 Actuarial Probability
 Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
1 Probability and Random Variables
 1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
Sampling Distributions
 Sampling Distributions In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of
Sampling Distributions In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of
Exponential & Gamma Distributions
 Exponential & Gamma Distributions Engineering Statistics Section 4.4 Josh Engwer TTU 7 March 26 Josh Engwer (TTU) Exponential & Gamma Distributions 7 March 26 / 2 PART I PART I: EXPONENTIAL DISTRIBUTION
Exponential & Gamma Distributions Engineering Statistics Section 4.4 Josh Engwer TTU 7 March 26 Josh Engwer (TTU) Exponential & Gamma Distributions 7 March 26 / 2 PART I PART I: EXPONENTIAL DISTRIBUTION
Applied Statistics and Probability for Engineers. Sixth Edition. Chapter 4 Continuous Random Variables and Probability Distributions.
 Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE Random
Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE Random
Chapter 4 Continuous Random Variables and Probability Distributions
 Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE 4-1
Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE 4-1
Continuous Distributions
 A normal distribution and other density functions involving exponential forms play the most important role in probability and statistics. They are related in a certain way, as summarized in a diagram later
A normal distribution and other density functions involving exponential forms play the most important role in probability and statistics. They are related in a certain way, as summarized in a diagram later
Expectation, Variance and Standard Deviation for Continuous Random Variables Class 6, Jeremy Orloff and Jonathan Bloom
 Expectation, Variance and Standard Deviation for Continuous Random Variables Class 6, 8.5 Jeremy Orloff and Jonathan Bloom Learning Goals. Be able to compute and interpret expectation, variance, and standard
Expectation, Variance and Standard Deviation for Continuous Random Variables Class 6, 8.5 Jeremy Orloff and Jonathan Bloom Learning Goals. Be able to compute and interpret expectation, variance, and standard
Continuous random variables and probability distributions
 and probability distributions Sta. 113 Chapter 4 of Devore March 12, 2010 Table of contents 1 2 Mathematical definition Definition A random variable X is continuous if its set of possible values is an
and probability distributions Sta. 113 Chapter 4 of Devore March 12, 2010 Table of contents 1 2 Mathematical definition Definition A random variable X is continuous if its set of possible values is an
Basics of Stochastic Modeling: Part II
 Basics of Stochastic Modeling: Part II Continuous Random Variables 1 Sandip Chakraborty Department of Computer Science and Engineering, INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR August 10, 2016 1 Reference
Basics of Stochastic Modeling: Part II Continuous Random Variables 1 Sandip Chakraborty Department of Computer Science and Engineering, INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR August 10, 2016 1 Reference
Probability Distributions Columns (a) through (d)
 Discrete Probability Distributions Columns (a) through (d) Probability Mass Distribution Description Notes Notation or Density Function --------------------(PMF or PDF)-------------------- (a) (b) (c)
Discrete Probability Distributions Columns (a) through (d) Probability Mass Distribution Description Notes Notation or Density Function --------------------(PMF or PDF)-------------------- (a) (b) (c)
Stat 5101 Notes: Brand Name Distributions
 Stat 5101 Notes: Brand Name Distributions Charles J. Geyer September 5, 2012 Contents 1 Discrete Uniform Distribution 2 2 General Discrete Uniform Distribution 2 3 Uniform Distribution 3 4 General Uniform
Stat 5101 Notes: Brand Name Distributions Charles J. Geyer September 5, 2012 Contents 1 Discrete Uniform Distribution 2 2 General Discrete Uniform Distribution 2 3 Uniform Distribution 3 4 General Uniform
Chapter 6 Continuous Probability Distributions
 Math 3 Chapter 6 Continuous Probability Distributions The observations generated by different statistical experiments have the same general type of behavior. The followings are the probability distributions
Math 3 Chapter 6 Continuous Probability Distributions The observations generated by different statistical experiments have the same general type of behavior. The followings are the probability distributions
Moments. Raw moment: February 25, 2014 Normalized / Standardized moment:
 Moments Lecture 10: Central Limit Theorem and CDFs Sta230 / Mth 230 Colin Rundel Raw moment: Central moment: µ n = EX n ) µ n = E[X µ) 2 ] February 25, 2014 Normalized / Standardized moment: µ n σ n Sta230
Moments Lecture 10: Central Limit Theorem and CDFs Sta230 / Mth 230 Colin Rundel Raw moment: Central moment: µ n = EX n ) µ n = E[X µ) 2 ] February 25, 2014 Normalized / Standardized moment: µ n σ n Sta230
Lecture 17: The Exponential and Some Related Distributions
 Lecture 7: The Exponential and Some Related Distributions. Definition Definition: A continuous random variable X is said to have the exponential distribution with parameter if the density of X is e x if
Lecture 7: The Exponential and Some Related Distributions. Definition Definition: A continuous random variable X is said to have the exponential distribution with parameter if the density of X is e x if
3 Continuous Random Variables
 Jinguo Lian Math437 Notes January 15, 016 3 Continuous Random Variables Remember that discrete random variables can take only a countable number of possible values. On the other hand, a continuous random
Jinguo Lian Math437 Notes January 15, 016 3 Continuous Random Variables Remember that discrete random variables can take only a countable number of possible values. On the other hand, a continuous random
Let X be a continuous random variable, < X < f(x) is the so called probability density function (pdf) if
 University of California, Los Angeles Department of Statistics Statistics 1A Instructor: Nicolas Christou Continuous probability distributions Let X be a continuous random variable, < X < f(x) is the so
University of California, Los Angeles Department of Statistics Statistics 1A Instructor: Nicolas Christou Continuous probability distributions Let X be a continuous random variable, < X < f(x) is the so
Chapter 4 - Lecture 3 The Normal Distribution
 Chapter 4 - Lecture 3 The October 28th, 2009 Chapter 4 - Lecture 3 The Standard Chapter 4 - Lecture 3 The Standard Normal distribution is a statistical unicorn It is the most important distribution in
Chapter 4 - Lecture 3 The October 28th, 2009 Chapter 4 - Lecture 3 The Standard Chapter 4 - Lecture 3 The Standard Normal distribution is a statistical unicorn It is the most important distribution in
Smoking Habits. Moderate Smokers Heavy Smokers Total. Hypertension No Hypertension Total
 Math 3070. Treibergs Final Exam Name: December 7, 00. In an experiment to see how hypertension is related to smoking habits, the following data was taken on individuals. Test the hypothesis that the proportions
Math 3070. Treibergs Final Exam Name: December 7, 00. In an experiment to see how hypertension is related to smoking habits, the following data was taken on individuals. Test the hypothesis that the proportions
Chapter Learning Objectives. Probability Distributions and Probability Density Functions. Continuous Random Variables
 Chapter 4: Continuous Random Variables and Probability s 4-1 Continuous Random Variables 4-2 Probability s and Probability Density Functions 4-3 Cumulative Functions 4-4 Mean and Variance of a Continuous
Chapter 4: Continuous Random Variables and Probability s 4-1 Continuous Random Variables 4-2 Probability s and Probability Density Functions 4-3 Cumulative Functions 4-4 Mean and Variance of a Continuous
Expected Values, Exponential and Gamma Distributions
 Expected Values, Exponential and Gamma Distributions Sections 5.2 & 5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13-3339 Cathy
Expected Values, Exponential and Gamma Distributions Sections 5.2 & 5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13-3339 Cathy
Slides 8: Statistical Models in Simulation
 Slides 8: Statistical Models in Simulation Purpose and Overview The world the model-builder sees is probabilistic rather than deterministic: Some statistical model might well describe the variations. An
Slides 8: Statistical Models in Simulation Purpose and Overview The world the model-builder sees is probabilistic rather than deterministic: Some statistical model might well describe the variations. An
Brief Review of Probability
 Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
18.440: Lecture 28 Lectures Review
 18.440: Lecture 28 Lectures 18-27 Review Scott Sheffield MIT Outline Outline It s the coins, stupid Much of what we have done in this course can be motivated by the i.i.d. sequence X i where each X i is
18.440: Lecture 28 Lectures 18-27 Review Scott Sheffield MIT Outline Outline It s the coins, stupid Much of what we have done in this course can be motivated by the i.i.d. sequence X i where each X i is
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R
 Random Variables Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R As such, a random variable summarizes the outcome of an experiment
Random Variables Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R As such, a random variable summarizes the outcome of an experiment
1.1 Review of Probability Theory
 1.1 Review of Probability Theory Angela Peace Biomathemtics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
1.1 Review of Probability Theory Angela Peace Biomathemtics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
Probability distributions. Probability Distribution Functions. Probability distributions (contd.) Binomial distribution
 Probability distributions Probability Distribution Functions G. Jogesh Babu Department of Statistics Penn State University September 27, 2011 http://en.wikipedia.org/wiki/probability_distribution We discuss
Probability distributions Probability Distribution Functions G. Jogesh Babu Department of Statistics Penn State University September 27, 2011 http://en.wikipedia.org/wiki/probability_distribution We discuss
Exponential Distribution and Poisson Process
 Exponential Distribution and Poisson Process Stochastic Processes - Lecture Notes Fatih Cavdur to accompany Introduction to Probability Models by Sheldon M. Ross Fall 215 Outline Introduction Exponential
Exponential Distribution and Poisson Process Stochastic Processes - Lecture Notes Fatih Cavdur to accompany Introduction to Probability Models by Sheldon M. Ross Fall 215 Outline Introduction Exponential
Special distributions
 Special distributions August 22, 2017 STAT 101 Class 4 Slide 1 Outline of Topics 1 Motivation 2 Bernoulli and binomial 3 Poisson 4 Uniform 5 Exponential 6 Normal STAT 101 Class 4 Slide 2 What distributions
Special distributions August 22, 2017 STAT 101 Class 4 Slide 1 Outline of Topics 1 Motivation 2 Bernoulli and binomial 3 Poisson 4 Uniform 5 Exponential 6 Normal STAT 101 Class 4 Slide 2 What distributions
LIST OF FORMULAS FOR STK1100 AND STK1110
 LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
Closed book and notes. 60 minutes. Cover page and four pages of exam. No calculators.
 IE 230 Seat # Closed book and notes. 60 minutes. Cover page and four pages of exam. No calculators. Score Exam #3a, Spring 2002 Schmeiser Closed book and notes. 60 minutes. 1. True or false. (for each,
IE 230 Seat # Closed book and notes. 60 minutes. Cover page and four pages of exam. No calculators. Score Exam #3a, Spring 2002 Schmeiser Closed book and notes. 60 minutes. 1. True or false. (for each,
Outline PMF, CDF and PDF Mean, Variance and Percentiles Some Common Distributions. Week 5 Random Variables and Their Distributions
 Week 5 Random Variables and Their Distributions Week 5 Objectives This week we give more general definitions of mean value, variance and percentiles, and introduce the first probability models for discrete
Week 5 Random Variables and Their Distributions Week 5 Objectives This week we give more general definitions of mean value, variance and percentiles, and introduce the first probability models for discrete
Random variables. DS GA 1002 Probability and Statistics for Data Science.
 Random variables DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Motivation Random variables model numerical quantities
Random variables DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Motivation Random variables model numerical quantities
1 Review of Probability and Distributions
 Random variables. A numerically valued function X of an outcome ω from a sample space Ω X : Ω R : ω X(ω) is called a random variable (r.v.), and usually determined by an experiment. We conventionally denote
Random variables. A numerically valued function X of an outcome ω from a sample space Ω X : Ω R : ω X(ω) is called a random variable (r.v.), and usually determined by an experiment. We conventionally denote
This does not cover everything on the final. Look at the posted practice problems for other topics.
 Class 7: Review Problems for Final Exam 8.5 Spring 7 This does not cover everything on the final. Look at the posted practice problems for other topics. To save time in class: set up, but do not carry
Class 7: Review Problems for Final Exam 8.5 Spring 7 This does not cover everything on the final. Look at the posted practice problems for other topics. To save time in class: set up, but do not carry
Sampling Distributions
 In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of random sample. For example,
In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of random sample. For example,
Chapter 3, 4 Random Variables ENCS Probability and Stochastic Processes. Concordia University
 Chapter 3, 4 Random Variables ENCS6161 - Probability and Stochastic Processes Concordia University ENCS6161 p.1/47 The Notion of a Random Variable A random variable X is a function that assigns a real
Chapter 3, 4 Random Variables ENCS6161 - Probability and Stochastic Processes Concordia University ENCS6161 p.1/47 The Notion of a Random Variable A random variable X is a function that assigns a real
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models
 System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 29, 2014 Introduction Introduction The world of the model-builder
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 29, 2014 Introduction Introduction The world of the model-builder
Math Spring Practice for the Second Exam.
 Math 4 - Spring 27 - Practice for the Second Exam.. Let X be a random variable and let F X be the distribution function of X: t < t 2 t < 4 F X (t) : + t t < 2 2 2 2 t < 4 t. Find P(X ), P(X ), P(X 2),
Math 4 - Spring 27 - Practice for the Second Exam.. Let X be a random variable and let F X be the distribution function of X: t < t 2 t < 4 F X (t) : + t t < 2 2 2 2 t < 4 t. Find P(X ), P(X ), P(X 2),
STAT 430/510 Probability Lecture 12: Central Limit Theorem and Exponential Distribution
 STAT 430/510 Probability Lecture 12: Central Limit Theorem and Exponential Distribution Pengyuan (Penelope) Wang June 15, 2011 Review Discussed Uniform Distribution and Normal Distribution Normal Approximation
STAT 430/510 Probability Lecture 12: Central Limit Theorem and Exponential Distribution Pengyuan (Penelope) Wang June 15, 2011 Review Discussed Uniform Distribution and Normal Distribution Normal Approximation
Continuous random variables
 Continuous random variables Can take on an uncountably infinite number of values Any value within an interval over which the variable is definied has some probability of occuring This is different from
Continuous random variables Can take on an uncountably infinite number of values Any value within an interval over which the variable is definied has some probability of occuring This is different from
28. Let ^ be a standard normal random variable and calculate the following probabilities, drawing pictures wherever appropriate.
 Exercises Section 4.3 [page 154] 28. Let ^ be a standard normal random variable and calculate the following probabilities, drawing pictures wherever appropriate. a. T Ð! Ÿ ^ Ÿ #Þ"(Ñ b. TÐ! Ÿ ^ Ÿ "Ñ c.
Exercises Section 4.3 [page 154] 28. Let ^ be a standard normal random variable and calculate the following probabilities, drawing pictures wherever appropriate. a. T Ð! Ÿ ^ Ÿ #Þ"(Ñ b. TÐ! Ÿ ^ Ÿ "Ñ c.
Will Landau. Feb 28, 2013
 Iowa State University The F Feb 28, 2013 Iowa State University Feb 28, 2013 1 / 46 Outline The F The F Iowa State University Feb 28, 2013 2 / 46 The normal (Gaussian) distribution A random variable X is
Iowa State University The F Feb 28, 2013 Iowa State University Feb 28, 2013 1 / 46 Outline The F The F Iowa State University Feb 28, 2013 2 / 46 The normal (Gaussian) distribution A random variable X is
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Review for the previous lecture
 Lecture 1 and 13 on BST 631: Statistical Theory I Kui Zhang, 09/8/006 Review for the previous lecture Definition: Several discrete distributions, including discrete uniform, hypergeometric, Bernoulli,
Lecture 1 and 13 on BST 631: Statistical Theory I Kui Zhang, 09/8/006 Review for the previous lecture Definition: Several discrete distributions, including discrete uniform, hypergeometric, Bernoulli,
Chapter 5. Statistical Models in Simulations 5.1. Prof. Dr. Mesut Güneş Ch. 5 Statistical Models in Simulations
 Chapter 5 Statistical Models in Simulations 5.1 Contents Basic Probability Theory Concepts Discrete Distributions Continuous Distributions Poisson Process Empirical Distributions Useful Statistical Models
Chapter 5 Statistical Models in Simulations 5.1 Contents Basic Probability Theory Concepts Discrete Distributions Continuous Distributions Poisson Process Empirical Distributions Useful Statistical Models
Chapter 3 Common Families of Distributions
 Lecture 9 on BST 631: Statistical Theory I Kui Zhang, 9/3/8 and 9/5/8 Review for the previous lecture Definition: Several commonly used discrete distributions, including discrete uniform, hypergeometric,
Lecture 9 on BST 631: Statistical Theory I Kui Zhang, 9/3/8 and 9/5/8 Review for the previous lecture Definition: Several commonly used discrete distributions, including discrete uniform, hypergeometric,
Topic 2: Probability & Distributions. Road Map Probability & Distributions. ECO220Y5Y: Quantitative Methods in Economics. Dr.
 Topic 2: Probability & Distributions ECO220Y5Y: Quantitative Methods in Economics Dr. Nick Zammit University of Toronto Department of Economics Room KN3272 n.zammit utoronto.ca November 21, 2017 Dr. Nick
Topic 2: Probability & Distributions ECO220Y5Y: Quantitative Methods in Economics Dr. Nick Zammit University of Toronto Department of Economics Room KN3272 n.zammit utoronto.ca November 21, 2017 Dr. Nick
Chapter 7: Theoretical Probability Distributions Variable - Measured/Categorized characteristic
 BSTT523: Pagano & Gavreau, Chapter 7 1 Chapter 7: Theoretical Probability Distributions Variable - Measured/Categorized characteristic Random Variable (R.V.) X Assumes values (x) by chance Discrete R.V.
BSTT523: Pagano & Gavreau, Chapter 7 1 Chapter 7: Theoretical Probability Distributions Variable - Measured/Categorized characteristic Random Variable (R.V.) X Assumes values (x) by chance Discrete R.V.
MATH 56A: STOCHASTIC PROCESSES CHAPTER 6
 MATH 56A: STOCHASTIC PROCESSES CHAPTER 6 6. Renewal Mathematically, renewal refers to a continuous time stochastic process with states,, 2,. N t {,, 2, 3, } so that you only have jumps from x to x + and
MATH 56A: STOCHASTIC PROCESSES CHAPTER 6 6. Renewal Mathematically, renewal refers to a continuous time stochastic process with states,, 2,. N t {,, 2, 3, } so that you only have jumps from x to x + and
The exponential distribution and the Poisson process
 The exponential distribution and the Poisson process 1-1 Exponential Distribution: Basic Facts PDF f(t) = { λe λt, t 0 0, t < 0 CDF Pr{T t) = 0 t λe λu du = 1 e λt (t 0) Mean E[T] = 1 λ Variance Var[T]
The exponential distribution and the Poisson process 1-1 Exponential Distribution: Basic Facts PDF f(t) = { λe λt, t 0 0, t < 0 CDF Pr{T t) = 0 t λe λu du = 1 e λt (t 0) Mean E[T] = 1 λ Variance Var[T]
THE QUEEN S UNIVERSITY OF BELFAST
 THE QUEEN S UNIVERSITY OF BELFAST 0SOR20 Level 2 Examination Statistics and Operational Research 20 Probability and Distribution Theory Wednesday 4 August 2002 2.30 pm 5.30 pm Examiners { Professor R M
THE QUEEN S UNIVERSITY OF BELFAST 0SOR20 Level 2 Examination Statistics and Operational Research 20 Probability and Distribution Theory Wednesday 4 August 2002 2.30 pm 5.30 pm Examiners { Professor R M
Chapter 4 Multiple Random Variables
 Review for the previous lecture Theorems and Examples: How to obtain the pmf (pdf) of U = g ( X Y 1 ) and V = g ( X Y) Chapter 4 Multiple Random Variables Chapter 43 Bivariate Transformations Continuous
Review for the previous lecture Theorems and Examples: How to obtain the pmf (pdf) of U = g ( X Y 1 ) and V = g ( X Y) Chapter 4 Multiple Random Variables Chapter 43 Bivariate Transformations Continuous
Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is
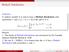 Weibull Distribution Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is { α β x α 1 e f (x; α, β) = α (x/β)α x 0 0 x < 0 Remark:
Weibull Distribution Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is { α β x α 1 e f (x; α, β) = α (x/β)α x 0 0 x < 0 Remark:
18.440: Lecture 28 Lectures Review
 18.440: Lecture 28 Lectures 17-27 Review Scott Sheffield MIT 1 Outline Continuous random variables Problems motivated by coin tossing Random variable properties 2 Outline Continuous random variables Problems
18.440: Lecture 28 Lectures 17-27 Review Scott Sheffield MIT 1 Outline Continuous random variables Problems motivated by coin tossing Random variable properties 2 Outline Continuous random variables Problems
Northwestern University Department of Electrical Engineering and Computer Science
 Northwestern University Department of Electrical Engineering and Computer Science EECS 454: Modeling and Analysis of Communication Networks Spring 2008 Probability Review As discussed in Lecture 1, probability
Northwestern University Department of Electrical Engineering and Computer Science EECS 454: Modeling and Analysis of Communication Networks Spring 2008 Probability Review As discussed in Lecture 1, probability
Continuous Probability Distributions. Uniform Distribution
 Continuous Probability Distributions Uniform Distribution Important Terms & Concepts Learned Probability Mass Function (PMF) Cumulative Distribution Function (CDF) Complementary Cumulative Distribution
Continuous Probability Distributions Uniform Distribution Important Terms & Concepts Learned Probability Mass Function (PMF) Cumulative Distribution Function (CDF) Complementary Cumulative Distribution
18.440: Lecture 19 Normal random variables
 18.440 Lecture 19 18.440: Lecture 19 Normal random variables Scott Sheffield MIT Outline Tossing coins Normal random variables Special case of central limit theorem Outline Tossing coins Normal random
18.440 Lecture 19 18.440: Lecture 19 Normal random variables Scott Sheffield MIT Outline Tossing coins Normal random variables Special case of central limit theorem Outline Tossing coins Normal random
Computer Science, Informatik 4 Communication and Distributed Systems. Simulation. Discrete-Event System Simulation. Dr.
 Simulation Discrete-Event System Simulation Chapter 4 Statistical Models in Simulation Purpose & Overview The world the model-builder sees is probabilistic rather than deterministic. Some statistical model
Simulation Discrete-Event System Simulation Chapter 4 Statistical Models in Simulation Purpose & Overview The world the model-builder sees is probabilistic rather than deterministic. Some statistical model
Small-Sample CI s for Normal Pop. Variance
 Small-Sample CI s for Normal Pop. Variance Engineering Statistics Section 7.4 Josh Engwer TTU 06 April 2016 Josh Engwer (TTU) Small-Sample CI s for Normal Pop. Variance 06 April 2016 1 / 16 PART I PART
Small-Sample CI s for Normal Pop. Variance Engineering Statistics Section 7.4 Josh Engwer TTU 06 April 2016 Josh Engwer (TTU) Small-Sample CI s for Normal Pop. Variance 06 April 2016 1 / 16 PART I PART
Continuous-Valued Probability Review
 CS 6323 Continuous-Valued Probability Review Prof. Gregory Provan Department of Computer Science University College Cork 2 Overview Review of discrete distributions Continuous distributions 3 Discrete
CS 6323 Continuous-Valued Probability Review Prof. Gregory Provan Department of Computer Science University College Cork 2 Overview Review of discrete distributions Continuous distributions 3 Discrete
3.4. The Binomial Probability Distribution
 3.4. The Binomial Probability Distribution Objectives. Binomial experiment. Binomial random variable. Using binomial tables. Mean and variance of binomial distribution. 3.4.1. Four Conditions that determined
3.4. The Binomial Probability Distribution Objectives. Binomial experiment. Binomial random variable. Using binomial tables. Mean and variance of binomial distribution. 3.4.1. Four Conditions that determined
Continuous RVs. 1. Suppose a random variable X has the following probability density function: π, zero otherwise. f ( x ) = sin x, 0 < x < 2
 STAT 4 Exam I Continuous RVs Fall 7 Practice. Suppose a random variable X has the following probability density function: f ( x ) = sin x, < x < π, zero otherwise. a) Find P ( X < 4 π ). b) Find µ = E
STAT 4 Exam I Continuous RVs Fall 7 Practice. Suppose a random variable X has the following probability density function: f ( x ) = sin x, < x < π, zero otherwise. a) Find P ( X < 4 π ). b) Find µ = E
2 Functions of random variables
 2 Functions of random variables A basic statistical model for sample data is a collection of random variables X 1,..., X n. The data are summarised in terms of certain sample statistics, calculated as
2 Functions of random variables A basic statistical model for sample data is a collection of random variables X 1,..., X n. The data are summarised in terms of certain sample statistics, calculated as
