Continuous Random Variables. and Probability Distributions. Continuous Random Variables and Probability Distributions ( ) ( ) Chapter 4 4.
|
|
|
- Rudolph McKenzie
- 5 years ago
- Views:
Transcription
1 UCLA STAT 11 A Applied Probability & Statistics for Engineers Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Christopher Barr University of California, Los Angeles, Fall 4 Chapter 4 Continuous Random Variables and Probability Distributions Slide 1 Slide 4.1 Continuous Random Variables and Probability Distributions Continuous Random Variables A random variable X is continuous if its set of possible values is an entire interval of numbers (If A < B, then any number x between A and B is possible). Slide 3 Slide 4 Probability Distribution Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that for any two numbers a and b, b ( ) ( ) P a X b = f x dx a The graph of f is the density curve. Probability Density Function For f (x) to be a pdf 1. f (x) > for all values of x..the area of the region between the graph of f and the x axis is equal to 1. Area = 1 y = f( x) Slide 5 Slide 6 1
2 Probability Density Function Pa ( X b) is given by the area of the shaded region. y = f( x) Continuous RV s A RV is continuous if it can take on any real value in a non-trivial interval (a ; b). PDF, probability density function, for a cont. RV, Y, is a non-negative function p Y (y), for any real value y, such that for each interval (a; b), the probability that Y takes on a value in (a; b), P(a<Y<b) equals the area under p Y (y) over the interval (a: b). p Y (y) P(a<Y<b) a b a b Slide 7 Slide 8 Convergence of density histograms to the PDF For a continuous RV the density histograms converge to the PDF as the size of the bins goes to zero. AdditionalInstructorAids\BirthdayDistribution_1978_systat.SYD Convergence of density histograms to the PDF For a continuous RV the density histograms converge to the PDF as the size of the bins goes to zero. Slide 9 Slide 1 Uniform Distribution A continuous rv X is said to have a uniform distribution on the interval [A, B] if the pdf of X is 1 A x B f ( x; A, B) = B A otherwise Probability for a Continuous rv If X is a continuous rv, then for any number c, P(x = c) =. For any two numbers a and b with a < b, P( a X b) = P( a< X b) = P( a X < b) = P( a< X < b) Slide 11 Slide 1
3 4. Cumulative Distribution Functions and Expected Values The Cumulative Distribution Function The cumulative distribution function, F(x) for a continuous rv X is defined for every number x by = ( ) = x F( x) P X x f( y) dy For each x, F(x) is the area under the density curve to the left of x. Slide 13 Slide 14 Using F(x) to Compute Probabilities Let X be a continuous rv with pdf f(x) and cdf F(x). Then for any number a, P ( X > a) = 1 F( a) and for any numbers a and b with a < b, Obtaining f(x) from F(x) If X is a continuous rv with pdf f(x) and cdf F(x), then at every number x for which the derivative F x F ( x) = f( x). ( ) exists, P ( a X b) = F( b) F( a) Slide 15 Slide 16 Percentiles Median Let p be a number between and 1. The (1p)th percentile of the distribution of a continuous rv X denoted by η( p), is defined by η = ( η ) = ( p) p F ( p) f( y) dy The median of a continuous distribution, denoted by µ%, is the 5 th percentile. So µ% satisfies.5 = F ( % µ ). That is, half the area under the density curve is to the left of µ%. Slide 17 Slide 18 3
4 Expected Value The expected or mean value of a continuous rv X with pdf f (x) is ( ) ( ) µ X = E X = x f x dx Expected Value of h(x) If X is a continuous rv with pdf f(x) and h(x) is any function of X, then [ ] µ hx ( ) E hx ( ) = = hx ( ) f( xdx ) Slide 19 Slide Variance and Standard Deviation The variance of continuous rv X with pdf f(x) and mean µ is σ X = V( x) = ( x µ ) f( x) dx = E[ X µ ] ( ) The standard deviation isσ = X V( x). Short-cut Formula for Variance ( ) [ ] V( X) = E X E( X) Slide 1 Slide Normal Distributions 4.3 The Normal Distribution A continuous rv X is said to have a normal distribution with parameters µ and σ, where < µ < and < σ, if the pdf of X is 1 ( x µ ) /( σ ) f( x) = e < x< σ π Slide 3 Slide 4 4
5 Standard Normal Distributions The normal distribution with parameter values µ = and σ = 1 is called a standard normal distribution. The random variable is denoted by Z. The pdf is 1 z f(;,1) z = e / σ π The cdf is z Φ ( z) = PZ ( z) = f( y;,1) dy Slide 5 < z < Standard Normal Cumulative Areas Standard normal curve z Slide 6 Shaded area = Φ( z) Standard Normal Distribution Let Z be the standard normal variable. Find (from table) a. PZ (.85) Area to the left of.85 =.83 b. P(Z > 1.3) 1 PZ ( 1.3) =.934 c. P(.1 Z 1.78) Find the area to the left of 1.78 then subtract the area to the left of.1. = PZ ( 1.78) PZ (.1) = =.9446 Slide 7 Slide 8 z α Notation z α will denote the value on the measurement axis for which the area under the z curve lies to the right of z α. Slide 9 Shaded area = PZ ( z α ) = α z α Ex. Let Z be the standard normal variable. Find z if a. P(Z < z) =.978. Look at the table and find an entry =.978 then read back to find z = b. P( z < Z < z) =.813 P(z < Z < z ) = P( < Z < z) = [P(z < Z ) ½] = P(z < Z ) 1 =.813 P(z < Z ) =.966 z = 1.3 Slide 3 5
6 Nonstandard Normal Distributions If X has a normal distribution with mean µ and standard deviation σ, then X µ Z = σ has a standard normal distribution. Normal Curve Approximate percentage of area within given standard deviations (empirical rule). 99.7% 95% 68% Slide 31 Slide 3 Ex. Let X be a normal random variable with µ = 8 and σ =. Find PX ( 65) P( X 65) = P Z (.75) = P Z =.66 Ex. A particular rash shown up at an elementary school. It has been determined that the length of time that the rash will last is normally distributed with µ = 6 days and σ = 1.5 days. Find the probability that for a student selected at random, the rash will last for between 3.75 and 9 days. Slide 33 Slide P( 3.75 X 9) = P Z ( 1.5 Z ) = P = Percentiles of an Arbitrary Normal Distribution (1p)th percentile for normal µ, σ ( ) (1 p)th for = µ + σ standard normal =.914 Slide 35 Slide 36 6
7 Normal Approximation to the Binomial Distribution Let X be a binomial rv based on n trials, each with probability of success p. If the binomial probability histogram is not too skewed, X may be approximated by a normal distribution with µ = np and σ = npq. x+.5 np PX ( x) Φ npq Ex. At a particular small college the pass rate of Intermediate Algebra is 7%. If 5 students enroll in a semester determine the probability that at least 375 students pass. µ = np = 5(.7) = 36 σ = npq = 5(.7)(.8) PX ( 375) Φ =Φ(1.55) 1 =.9394 Slide 37 Slide 38 Normal approximation to Binomial Suppose Y~Binomial(n, p) Then Y=Y 1 + Y + Y Y n, where Y k ~Bernoulli(p), E(Y k )=p & Var(Y k )=p(1-p) E(Y)=np & Var(Y)=np(1-p), SD(Y)= (np(1- p)) 1/ Standardize Y: Z=(Y-np) / (np(1-p)) 1/ By CLT Z ~ N(, 1). So, Y ~ N [np, (np(1- p)) 1/ ] Normal Approx to Binomial is reasonable when np >=1 & n(1- p)>1 (p & (1-p) are NOT too small relative to Slide 39 n) Normal approximation to Binomial Example Roulette wheel investigation: Compute P(Y>=58), where Y~Binomial(1,.47) The proportion of the Binomial(1,.47) population having more than 58 reds (successes) out of 1 roulette spins (trials). Roulette has 38 slots Since np=47>=1 & n(1-p)=53>1 18red 18black neutral Normal approx is justified. Z=(Y-np)/Sqrt(np(1-p)) = 58 1*.47)/Sqrt(1*.47*.53)=. P(Y>=58) P(Z>=.) =.139 True P(Y>=58) =.177, using SOCR (demo!) Slide 4 Binomial approx useful when no access to SOCR Normal approximation to Poisson Let X 1 ~Poisson(λ) & X ~Poisson(µ) X 1 + X ~Poisson(λ+µ) Let X 1, X, X 3,, X k ~ Poisson(λ), and independent, Y k = X 1 + X + + X k ~ Poisson(kλ), E(Y k )=Var(Y k )=kλ. The random variables in the sum on the right are independent and each has the Poisson distribution with parameter λ. By CLT the distribution of the standardized variable (Y k kλ) / (kλ) 1/ N(, 1), as k increases to infinity. Slide 41 S f k > 1 Z {(Y k )/(k ) 1/ } Normal approximation to Poisson example Let X 1 ~Poisson(λ) & X ~Poisson(µ) X 1 + X ~Poisson(λ+µ) Let X 1, X, X 3,, X ~ Poisson(), and independent, Y k = X 1 + X + + X k ~ Poisson(4), E(Y k )=Var(Y k )=4. By CLT the distribution of the standardized variable (Y k 4) / (4) 1/ N(, 1), as k increases to infinity. Z k = (Y k 4) / ~ N(,1) Y k ~ N(4, 4). P( < Y k < 4) = (std z & 4) = Slide 4 P( ( 4)/ < Z k < (4 4)/ ) = P( -< 7
8 Poisson or Normal approximation to Binomial? Poisson Approximation (Binomial(n, p n ) Poisson(λ) ): y y WHY? λ n p y n ( 1 p ) n y n n p n λ n>=1 & p<=.1 & λ =n p <= Normal Approximation (Binomial(n, p) N ( np, (np(1-p)) 1/ ) ) np >=1 & n(1-p)>1 Slide 43 n e λ y! 4.4 The Gamma Distribution and Its Relatives Slide 44 The Gamma Function For α >, the gamma function Γ( α ) is defined by α 1 x Γ ( α ) = x e dx Gamma Distribution A continuous rv X has a gamma distribution if the pdf is 1 α 1 x / β x e x α f( x; αβ, ) = β Γ( α) otherwise where the parameters satisfyα >, β >. The standard gamma distribution has β = 1. Slide 45 Slide 46 Mean and Variance The mean and variance of a random variable X having the gamma distribution f( x; α, β ) are Slide 47 EX ( ) = µ = αβ VX ( ) = σ = αβ Probabilities from the Gamma Distribution Let X have a gamma distribution with parameters α and β. Then for any x >, the cdf of X is given by x PX ( x) = Fx ( ; α, β ) = F ; α β where x α 1 y y e F( x; α) = dy Γ( α) Slide 48 8
9 Exponential Distribution A continuous rv X has an exponential distribution with parameter λ if the pdf is λx λe x f( x; λ) = otherwise Mean and Variance The mean and variance of a random variable X having the exponential distribution 1 1 µ = αβ = σ = αβ = λ λ Slide 49 Slide 5 Probabilities from the Gamma Distribution Let X have a exponential distribution Then the cdf of X is given by x < F( x; λ) = λx 1 e x Slide 51 Applications of the Exponential Distribution Suppose that the number of events occurring in any time interval of length t has a Poisson distribution with parameter αt and that the numbers of occurrences in nonoverlapping intervals are independent of one another. Then the distribution of elapsed time between the occurrences of two successive events is exponential with parameter λ = α. Slide 5 The Chi-Squared Distribution Let v be a positive integer. Then a random variable X is said to have a chisquared distribution with parameter v if the pdf of X is the gamma density with α = v / and β =. The pdf is 1 ( v/) 1 x/ x e x v / f( x; v) = Γ( v /) x < The Chi-Squared Distribution The parameter v is called the number of degrees of freedom (df) of X. The symbol χ is often used in place of chisquared. Slide 53 Slide 54 9
10 Identifying Common Distributions QQ plots Quantile-Quantile plots indicate how well the model distribution agrees with the data. q -th quantile, for <q<1, is the (data-space) value, V q, at or below which lies a proportion q of the data. 1 Graph of the CDF, F Y (y)=p(y<=v q )=q q Slide 55 V q Constructing QQ plots Start off with data {y 1, y, y 3,, y n } Order statistics y (1) <= y () <= y (3) <= <= y (n) Compute quantile rank, q (k), for each observation, y (k), P(Y<= q (k) ) = (k-.375) / (n+.5), where Y is a RV from the (target) model distribution. Finally, plot the points (y (k), q (k) ) in D plane, 1<=k<=n. Note: Different statistical packages use slightly different formulas for the computation of q (k). However, the results are quite similar. This is the formulas employed in SAS. Basic idea: Probability that: Slide 56 P((model)Y<=(data)y )~ 1/n; Example - Constructing QQ plots Start off with data {y 1, y, y 3,, y n }. Plot the points (y (k), q (k) ) in D plane, 1<=k<=n. Expected Value for Normal Distribution Slide 57 C:\Ivo.dir\UCLA_Classes\Winter\AdditionalInstructorA ids BirthdayDistribution_1978_systat.SYD SYSTAT, Graph Probability Plot, Var4, Normal Distribution 4.5 Other Continuous Distributions Slide 58 The Weibull Distribution A continuous rv X has a Weibull distribution if the pdf is α α α 1 ( x / β) x e x α f( x; αβ, ) = β x < where the parameters satisfy α >, β >. Mean and Variance The mean and variance of a random variable X having the Weibull distribution are 1 1 µ = βγ 1+ σ = β Γ 1+ Γ 1+ α α α Slide 59 Slide 6 1
11 Weibull Distribution The cdf of a Weibull rv having parameters α and β is α ( x / β ) 1 e x F( x; αβ, ) = x < Lognormal Distribution A nonnegative rv X has a lognormal distribution if the rv Y = ln(x) has a normal distribution the resulting pdf has parameters µ and σ and is 1 [ln( x) µ ] /( σ ) e x f( x; µσ, ) = παx x < Slide 61 Slide 6 Mean and Variance The mean and variance of a variable X having the lognormal distribution are µ + σ / µ + σ σ ( ) E( X) = e V( X) = e e 1 Lognormal Distribution The cdf of the lognormal distribution is given by F( x; µ, α ) = P( X x) = P[ln( X) ln( x)] ln( x) µ ln( x) µ = P Z =Φ σ σ Slide 63 Slide 64 Beta Distribution A rv X is said to have a beta distribution with parameters A, B, α >, and β > if the pdf of X is f( x; αβ,, A, B) = 1 Γ ( α + β) x A B x B A Γ( α) Γ( β) B A B A otherwise α 1 β 1 x Mean and Variance The mean and variance of a variable X having the beta distribution are α µ = A+ ( B A) α + β ( B A) αβ σ = ( α + β) ( α + β + 1) Slide 65 Slide 66 11
12 4.6 Probability Plots Sample Percentile Order the n-sample observations from smallest to largest. The ith smallest observation in the list is taken to be the [1(i.5)/n]th sample percentile. Slide 67 Slide 68 Probability Plot [1( i.5) / n]th percentile ith smallest sample of the distribution observation If the sample percentiles are close to the corresponding population distribution percentiles, the first number will roughly equal the second., Normal Probability Plot A plot of the pairs ([1( i.5) / n]th z percentile, ith smallest observation) On a two-dimensional coordinate system is called a normal probability plot. If the drawn from a normal distribution the points should fall close to a line with slope σ and intercept µ. Slide 69 Slide 7 Beyond Normality Consider a family of probability distributions involving two parameters θ Let denote the 1 and θ. F( x; θ1, θ) corresponding cdf s. The parameters θ1 and θ are said to location and scale parameters if x θ1 F( x; θ1, θ) is a function of. θ Lognormal (Y) µ,σ Relation among Distributions Normal (X) µ,σ X = lny X Y = e Uniform(X) α, β α U = X β α Beta α, β α = β = 1 χ Uniform(U),1 µ Z = X σ = n i= 1 Z i X = ( β α) U + α Normal (Z),1 Chi-square ( χ ) n α = n /, β = Gamma α, β n= α =1 X = β lnu df Weibull γ, β df γ = 1 Exponential(X) β T df=n (,1) 1 Cauchy (,1) Slide 71 Slide 7 1
Continuous Random Variables. and Probability Distributions. Continuous Random Variables and Probability Distributions ( ) ( )
 UCLA STAT 35 Applied Computational and Interactive Probability Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Chris Barr Continuous Random Variables and Probability
UCLA STAT 35 Applied Computational and Interactive Probability Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Chris Barr Continuous Random Variables and Probability
Probability Density Functions
 Probability Density Functions Probability Density Functions Definition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that
Probability Density Functions Probability Density Functions Definition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that
Probability Distributions for Continuous Variables. Probability Distributions for Continuous Variables
 Probability Distributions for Continuous Variables Probability Distributions for Continuous Variables Let X = lake depth at a randomly chosen point on lake surface If we draw the histogram so that the
Probability Distributions for Continuous Variables Probability Distributions for Continuous Variables Let X = lake depth at a randomly chosen point on lake surface If we draw the histogram so that the
Chapter 4: Continuous Random Variables and Probability Distributions
 Chapter 4: and Probability Distributions Walid Sharabati Purdue University February 14, 2014 Professor Sharabati (Purdue University) Spring 2014 (Slide 1 of 37) Chapter Overview Continuous random variables
Chapter 4: and Probability Distributions Walid Sharabati Purdue University February 14, 2014 Professor Sharabati (Purdue University) Spring 2014 (Slide 1 of 37) Chapter Overview Continuous random variables
Continuous Random Variables and Probability Distributions
 Continuous Random Variables and Probability Distributions Instructor: Lingsong Zhang 1 4.1 Probability Density Functions Probability Density Functions Recall from Chapter 3 that a random variable X is
Continuous Random Variables and Probability Distributions Instructor: Lingsong Zhang 1 4.1 Probability Density Functions Probability Density Functions Recall from Chapter 3 that a random variable X is
Continuous Random Variables and Continuous Distributions
 Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
MATH : EXAM 2 INFO/LOGISTICS/ADVICE
 MATH 3342-004: EXAM 2 INFO/LOGISTICS/ADVICE INFO: WHEN: Friday (03/11) at 10:00am DURATION: 50 mins PROBLEM COUNT: Appropriate for a 50-min exam BONUS COUNT: At least one TOPICS CANDIDATE FOR THE EXAM:
MATH 3342-004: EXAM 2 INFO/LOGISTICS/ADVICE INFO: WHEN: Friday (03/11) at 10:00am DURATION: 50 mins PROBLEM COUNT: Appropriate for a 50-min exam BONUS COUNT: At least one TOPICS CANDIDATE FOR THE EXAM:
Sampling Distributions of Statistics Corresponds to Chapter 5 of Tamhane and Dunlop
 Sampling Distributions of Statistics Corresponds to Chapter 5 of Tamhane and Dunlop Slides prepared by Elizabeth Newton (MIT), with some slides by Jacqueline Telford (Johns Hopkins University) 1 Sampling
Sampling Distributions of Statistics Corresponds to Chapter 5 of Tamhane and Dunlop Slides prepared by Elizabeth Newton (MIT), with some slides by Jacqueline Telford (Johns Hopkins University) 1 Sampling
STAT Chapter 5 Continuous Distributions
 STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models
 System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 20, 2012 Introduction Introduction The world of the model-builder
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 20, 2012 Introduction Introduction The world of the model-builder
Brief Review of Probability
 Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
15 Discrete Distributions
 Lecture Note 6 Special Distributions (Discrete and Continuous) MIT 4.30 Spring 006 Herman Bennett 5 Discrete Distributions We have already seen the binomial distribution and the uniform distribution. 5.
Lecture Note 6 Special Distributions (Discrete and Continuous) MIT 4.30 Spring 006 Herman Bennett 5 Discrete Distributions We have already seen the binomial distribution and the uniform distribution. 5.
1 Review of Probability and Distributions
 Random variables. A numerically valued function X of an outcome ω from a sample space Ω X : Ω R : ω X(ω) is called a random variable (r.v.), and usually determined by an experiment. We conventionally denote
Random variables. A numerically valued function X of an outcome ω from a sample space Ω X : Ω R : ω X(ω) is called a random variable (r.v.), and usually determined by an experiment. We conventionally denote
Continuous random variables
 Continuous random variables Can take on an uncountably infinite number of values Any value within an interval over which the variable is definied has some probability of occuring This is different from
Continuous random variables Can take on an uncountably infinite number of values Any value within an interval over which the variable is definied has some probability of occuring This is different from
Chapter Learning Objectives. Probability Distributions and Probability Density Functions. Continuous Random Variables
 Chapter 4: Continuous Random Variables and Probability s 4-1 Continuous Random Variables 4-2 Probability s and Probability Density Functions 4-3 Cumulative Functions 4-4 Mean and Variance of a Continuous
Chapter 4: Continuous Random Variables and Probability s 4-1 Continuous Random Variables 4-2 Probability s and Probability Density Functions 4-3 Cumulative Functions 4-4 Mean and Variance of a Continuous
Review for the previous lecture
 Lecture 1 and 13 on BST 631: Statistical Theory I Kui Zhang, 09/8/006 Review for the previous lecture Definition: Several discrete distributions, including discrete uniform, hypergeometric, Bernoulli,
Lecture 1 and 13 on BST 631: Statistical Theory I Kui Zhang, 09/8/006 Review for the previous lecture Definition: Several discrete distributions, including discrete uniform, hypergeometric, Bernoulli,
Applied Statistics and Probability for Engineers. Sixth Edition. Chapter 4 Continuous Random Variables and Probability Distributions.
 Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE Random
Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE Random
Chapter 4 Continuous Random Variables and Probability Distributions
 Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE 4-1
Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE 4-1
Probability Distributions Columns (a) through (d)
 Discrete Probability Distributions Columns (a) through (d) Probability Mass Distribution Description Notes Notation or Density Function --------------------(PMF or PDF)-------------------- (a) (b) (c)
Discrete Probability Distributions Columns (a) through (d) Probability Mass Distribution Description Notes Notation or Density Function --------------------(PMF or PDF)-------------------- (a) (b) (c)
Review 1: STAT Mark Carpenter, Ph.D. Professor of Statistics Department of Mathematics and Statistics. August 25, 2015
 Review : STAT 36 Mark Carpenter, Ph.D. Professor of Statistics Department of Mathematics and Statistics August 25, 25 Support of a Random Variable The support of a random variable, which is usually denoted
Review : STAT 36 Mark Carpenter, Ph.D. Professor of Statistics Department of Mathematics and Statistics August 25, 25 Support of a Random Variable The support of a random variable, which is usually denoted
Test Problems for Probability Theory ,
 1 Test Problems for Probability Theory 01-06-16, 010-1-14 1. Write down the following probability density functions and compute their moment generating functions. (a) Binomial distribution with mean 30
1 Test Problems for Probability Theory 01-06-16, 010-1-14 1. Write down the following probability density functions and compute their moment generating functions. (a) Binomial distribution with mean 30
Let X be a continuous random variable, < X < f(x) is the so called probability density function (pdf) if
 University of California, Los Angeles Department of Statistics Statistics 1A Instructor: Nicolas Christou Continuous probability distributions Let X be a continuous random variable, < X < f(x) is the so
University of California, Los Angeles Department of Statistics Statistics 1A Instructor: Nicolas Christou Continuous probability distributions Let X be a continuous random variable, < X < f(x) is the so
STA 256: Statistics and Probability I
 Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. Exercise 4.1 Let X be a random variable with p(x)
Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. Exercise 4.1 Let X be a random variable with p(x)
Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R
 Random Variables Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R As such, a random variable summarizes the outcome of an experiment
Random Variables Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R As such, a random variable summarizes the outcome of an experiment
Exponential, Gamma and Normal Distribuions
 Exponential, Gamma and Normal Distribuions Sections 5.4, 5.5 & 6.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy Poliak,
Exponential, Gamma and Normal Distribuions Sections 5.4, 5.5 & 6.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy Poliak,
2 Functions of random variables
 2 Functions of random variables A basic statistical model for sample data is a collection of random variables X 1,..., X n. The data are summarised in terms of certain sample statistics, calculated as
2 Functions of random variables A basic statistical model for sample data is a collection of random variables X 1,..., X n. The data are summarised in terms of certain sample statistics, calculated as
MIT Spring 2015
 Assessing Goodness Of Fit MIT 8.443 Dr. Kempthorne Spring 205 Outline 2 Poisson Distribution Counts of events that occur at constant rate Counts in disjoint intervals/regions are independent If intervals/regions
Assessing Goodness Of Fit MIT 8.443 Dr. Kempthorne Spring 205 Outline 2 Poisson Distribution Counts of events that occur at constant rate Counts in disjoint intervals/regions are independent If intervals/regions
Continuous Distributions
 Chapter 3 Continuous Distributions 3.1 Continuous-Type Data In Chapter 2, we discuss random variables whose space S contains a countable number of outcomes (i.e. of discrete type). In Chapter 3, we study
Chapter 3 Continuous Distributions 3.1 Continuous-Type Data In Chapter 2, we discuss random variables whose space S contains a countable number of outcomes (i.e. of discrete type). In Chapter 3, we study
BMIR Lecture Series on Probability and Statistics Fall, 2015 Uniform Distribution
 Lecture #5 BMIR Lecture Series on Probability and Statistics Fall, 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University s 5.1 Definition ( ) A continuous random
Lecture #5 BMIR Lecture Series on Probability and Statistics Fall, 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University s 5.1 Definition ( ) A continuous random
Statistical Methods in Particle Physics
 Statistical Methods in Particle Physics Lecture 3 October 29, 2012 Silvia Masciocchi, GSI Darmstadt s.masciocchi@gsi.de Winter Semester 2012 / 13 Outline Reminder: Probability density function Cumulative
Statistical Methods in Particle Physics Lecture 3 October 29, 2012 Silvia Masciocchi, GSI Darmstadt s.masciocchi@gsi.de Winter Semester 2012 / 13 Outline Reminder: Probability density function Cumulative
Ching-Han Hsu, BMES, National Tsing Hua University c 2015 by Ching-Han Hsu, Ph.D., BMIR Lab. = a + b 2. b a. x a b a = 12
 Lecture 5 Continuous Random Variables BMIR Lecture Series in Probability and Statistics Ching-Han Hsu, BMES, National Tsing Hua University c 215 by Ching-Han Hsu, Ph.D., BMIR Lab 5.1 1 Uniform Distribution
Lecture 5 Continuous Random Variables BMIR Lecture Series in Probability and Statistics Ching-Han Hsu, BMES, National Tsing Hua University c 215 by Ching-Han Hsu, Ph.D., BMIR Lab 5.1 1 Uniform Distribution
Continuous random variables
 Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
1 Probability and Random Variables
 1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
Random Variables and Their Distributions
 Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Continuous Random Variables
 Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
Slides 8: Statistical Models in Simulation
 Slides 8: Statistical Models in Simulation Purpose and Overview The world the model-builder sees is probabilistic rather than deterministic: Some statistical model might well describe the variations. An
Slides 8: Statistical Models in Simulation Purpose and Overview The world the model-builder sees is probabilistic rather than deterministic: Some statistical model might well describe the variations. An
Common ontinuous random variables
 Common ontinuous random variables CE 311S Earlier, we saw a number of distribution families Binomial Negative binomial Hypergeometric Poisson These were useful because they represented common situations:
Common ontinuous random variables CE 311S Earlier, we saw a number of distribution families Binomial Negative binomial Hypergeometric Poisson These were useful because they represented common situations:
Special distributions
 Special distributions August 22, 2017 STAT 101 Class 4 Slide 1 Outline of Topics 1 Motivation 2 Bernoulli and binomial 3 Poisson 4 Uniform 5 Exponential 6 Normal STAT 101 Class 4 Slide 2 What distributions
Special distributions August 22, 2017 STAT 101 Class 4 Slide 1 Outline of Topics 1 Motivation 2 Bernoulli and binomial 3 Poisson 4 Uniform 5 Exponential 6 Normal STAT 101 Class 4 Slide 2 What distributions
MATH Notebook 5 Fall 2018/2019
 MATH442601 2 Notebook 5 Fall 2018/2019 prepared by Professor Jenny Baglivo c Copyright 2004-2019 by Jenny A. Baglivo. All Rights Reserved. 5 MATH442601 2 Notebook 5 3 5.1 Sequences of IID Random Variables.............................
MATH442601 2 Notebook 5 Fall 2018/2019 prepared by Professor Jenny Baglivo c Copyright 2004-2019 by Jenny A. Baglivo. All Rights Reserved. 5 MATH442601 2 Notebook 5 3 5.1 Sequences of IID Random Variables.............................
Chapter 5. Statistical Models in Simulations 5.1. Prof. Dr. Mesut Güneş Ch. 5 Statistical Models in Simulations
 Chapter 5 Statistical Models in Simulations 5.1 Contents Basic Probability Theory Concepts Discrete Distributions Continuous Distributions Poisson Process Empirical Distributions Useful Statistical Models
Chapter 5 Statistical Models in Simulations 5.1 Contents Basic Probability Theory Concepts Discrete Distributions Continuous Distributions Poisson Process Empirical Distributions Useful Statistical Models
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
Math438 Actuarial Probability
 Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
Sampling Distributions
 Sampling Distributions In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of
Sampling Distributions In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of
MATH4427 Notebook 4 Fall Semester 2017/2018
 MATH4427 Notebook 4 Fall Semester 2017/2018 prepared by Professor Jenny Baglivo c Copyright 2009-2018 by Jenny A. Baglivo. All Rights Reserved. 4 MATH4427 Notebook 4 3 4.1 K th Order Statistics and Their
MATH4427 Notebook 4 Fall Semester 2017/2018 prepared by Professor Jenny Baglivo c Copyright 2009-2018 by Jenny A. Baglivo. All Rights Reserved. 4 MATH4427 Notebook 4 3 4.1 K th Order Statistics and Their
Random Variate Generation
 Random Variate Generation 28-1 Overview 1. Inverse transformation 2. Rejection 3. Composition 4. Convolution 5. Characterization 28-2 Random-Variate Generation General Techniques Only a few techniques
Random Variate Generation 28-1 Overview 1. Inverse transformation 2. Rejection 3. Composition 4. Convolution 5. Characterization 28-2 Random-Variate Generation General Techniques Only a few techniques
A Few Special Distributions and Their Properties
 A Few Special Distributions and Their Properties Econ 690 Purdue University Justin L. Tobias (Purdue) Distributional Catalog 1 / 20 Special Distributions and Their Associated Properties 1 Uniform Distribution
A Few Special Distributions and Their Properties Econ 690 Purdue University Justin L. Tobias (Purdue) Distributional Catalog 1 / 20 Special Distributions and Their Associated Properties 1 Uniform Distribution
This does not cover everything on the final. Look at the posted practice problems for other topics.
 Class 7: Review Problems for Final Exam 8.5 Spring 7 This does not cover everything on the final. Look at the posted practice problems for other topics. To save time in class: set up, but do not carry
Class 7: Review Problems for Final Exam 8.5 Spring 7 This does not cover everything on the final. Look at the posted practice problems for other topics. To save time in class: set up, but do not carry
ECE 302 Division 2 Exam 2 Solutions, 11/4/2009.
 NAME: ECE 32 Division 2 Exam 2 Solutions, /4/29. You will be required to show your student ID during the exam. This is a closed-book exam. A formula sheet is provided. No calculators are allowed. Total
NAME: ECE 32 Division 2 Exam 2 Solutions, /4/29. You will be required to show your student ID during the exam. This is a closed-book exam. A formula sheet is provided. No calculators are allowed. Total
Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is
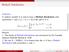 Weibull Distribution Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is { α β x α 1 e f (x; α, β) = α (x/β)α x 0 0 x < 0 Remark:
Weibull Distribution Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is { α β x α 1 e f (x; α, β) = α (x/β)α x 0 0 x < 0 Remark:
Some worked exercises from Ch 4: Ex 10 p 151
 Some worked exercises from Ch 4: Ex 0 p 5 a) It looks like this density depends on two parameters how are we going to plot it for general k and θ? But note that we can re-write the density as a constant
Some worked exercises from Ch 4: Ex 0 p 5 a) It looks like this density depends on two parameters how are we going to plot it for general k and θ? But note that we can re-write the density as a constant
Independent Events. Two events are independent if knowing that one occurs does not change the probability of the other occurring
 Independent Events Two events are independent if knowing that one occurs does not change the probability of the other occurring Conditional probability is denoted P(A B), which is defined to be: P(A and
Independent Events Two events are independent if knowing that one occurs does not change the probability of the other occurring Conditional probability is denoted P(A B), which is defined to be: P(A and
3 Continuous Random Variables
 Jinguo Lian Math437 Notes January 15, 016 3 Continuous Random Variables Remember that discrete random variables can take only a countable number of possible values. On the other hand, a continuous random
Jinguo Lian Math437 Notes January 15, 016 3 Continuous Random Variables Remember that discrete random variables can take only a countable number of possible values. On the other hand, a continuous random
Probability and Distributions
 Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Expected Values, Exponential and Gamma Distributions
 Expected Values, Exponential and Gamma Distributions Sections 5.2-5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 14-3339 Cathy Poliak,
Expected Values, Exponential and Gamma Distributions Sections 5.2-5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 14-3339 Cathy Poliak,
Chapter 4: Continuous Probability Distributions
 Chapter 4: Continuous Probability Distributions Seungchul Baek Department of Statistics, University of South Carolina STAT 509: Statistics for Engineers 1 / 57 Continuous Random Variable A continuous random
Chapter 4: Continuous Probability Distributions Seungchul Baek Department of Statistics, University of South Carolina STAT 509: Statistics for Engineers 1 / 57 Continuous Random Variable A continuous random
Chapter 3 Common Families of Distributions
 Lecture 9 on BST 631: Statistical Theory I Kui Zhang, 9/3/8 and 9/5/8 Review for the previous lecture Definition: Several commonly used discrete distributions, including discrete uniform, hypergeometric,
Lecture 9 on BST 631: Statistical Theory I Kui Zhang, 9/3/8 and 9/5/8 Review for the previous lecture Definition: Several commonly used discrete distributions, including discrete uniform, hypergeometric,
Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama
 Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama Instructions This exam has 7 pages in total, numbered 1 to 7. Make sure your exam has all the pages. This exam will be 2 hours
Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama Instructions This exam has 7 pages in total, numbered 1 to 7. Make sure your exam has all the pages. This exam will be 2 hours
The Binomial distribution. Probability theory 2. Example. The Binomial distribution
 Probability theory Tron Anders Moger September th 7 The Binomial distribution Bernoulli distribution: One experiment X i with two possible outcomes, probability of success P. If the experiment is repeated
Probability theory Tron Anders Moger September th 7 The Binomial distribution Bernoulli distribution: One experiment X i with two possible outcomes, probability of success P. If the experiment is repeated
1 Presessional Probability
 1 Presessional Probability Probability theory is essential for the development of mathematical models in finance, because of the randomness nature of price fluctuations in the markets. This presessional
1 Presessional Probability Probability theory is essential for the development of mathematical models in finance, because of the randomness nature of price fluctuations in the markets. This presessional
MA/ST 810 Mathematical-Statistical Modeling and Analysis of Complex Systems
 MA/ST 810 Mathematical-Statistical Modeling and Analysis of Complex Systems Review of Basic Probability The fundamentals, random variables, probability distributions Probability mass/density functions
MA/ST 810 Mathematical-Statistical Modeling and Analysis of Complex Systems Review of Basic Probability The fundamentals, random variables, probability distributions Probability mass/density functions
IC 102: Data Analysis and Interpretation
 IC 102: Data Analysis and Interpretation Instructor: Guruprasad PJ Dept. Aerospace Engineering Indian Institute of Technology Bombay Powai, Mumbai 400076 Email: pjguru@aero.iitb.ac.in Phone no.: 2576 7142
IC 102: Data Analysis and Interpretation Instructor: Guruprasad PJ Dept. Aerospace Engineering Indian Institute of Technology Bombay Powai, Mumbai 400076 Email: pjguru@aero.iitb.ac.in Phone no.: 2576 7142
ECON 4130 Supplementary Exercises 1-4
 HG Set. 0 ECON 430 Sulementary Exercises - 4 Exercise Quantiles (ercentiles). Let X be a continuous random variable (rv.) with df f( x ) and cdf F( x ). For 0< < we define -th quantile (or 00-th ercentile),
HG Set. 0 ECON 430 Sulementary Exercises - 4 Exercise Quantiles (ercentiles). Let X be a continuous random variable (rv.) with df f( x ) and cdf F( x ). For 0< < we define -th quantile (or 00-th ercentile),
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
1: PROBABILITY REVIEW
 1: PROBABILITY REVIEW Marek Rutkowski School of Mathematics and Statistics University of Sydney Semester 2, 2016 M. Rutkowski (USydney) Slides 1: Probability Review 1 / 56 Outline We will review the following
1: PROBABILITY REVIEW Marek Rutkowski School of Mathematics and Statistics University of Sydney Semester 2, 2016 M. Rutkowski (USydney) Slides 1: Probability Review 1 / 56 Outline We will review the following
Special Discrete RV s. Then X = the number of successes is a binomial RV. X ~ Bin(n,p).
 Sect 3.4: Binomial RV Special Discrete RV s 1. Assumptions and definition i. Experiment consists of n repeated trials ii. iii. iv. There are only two possible outcomes on each trial: success (S) or failure
Sect 3.4: Binomial RV Special Discrete RV s 1. Assumptions and definition i. Experiment consists of n repeated trials ii. iii. iv. There are only two possible outcomes on each trial: success (S) or failure
Chapter 3.3 Continuous distributions
 Chapter 3.3 Continuous distributions In this section we study several continuous distributions and their properties. Here are a few, classified by their support S X. There are of course many, many more.
Chapter 3.3 Continuous distributions In this section we study several continuous distributions and their properties. Here are a few, classified by their support S X. There are of course many, many more.
IV. The Normal Distribution
 IV. The Normal Distribution The normal distribution (a.k.a., the Gaussian distribution or bell curve ) is the by far the best known random distribution. It s discovery has had such a far-reaching impact
IV. The Normal Distribution The normal distribution (a.k.a., the Gaussian distribution or bell curve ) is the by far the best known random distribution. It s discovery has had such a far-reaching impact
Continuous random variables and probability distributions
 and probability distributions Sta. 113 Chapter 4 of Devore March 12, 2010 Table of contents 1 2 Mathematical definition Definition A random variable X is continuous if its set of possible values is an
and probability distributions Sta. 113 Chapter 4 of Devore March 12, 2010 Table of contents 1 2 Mathematical definition Definition A random variable X is continuous if its set of possible values is an
Continuous RVs. 1. Suppose a random variable X has the following probability density function: π, zero otherwise. f ( x ) = sin x, 0 < x < 2
 STAT 4 Exam I Continuous RVs Fall 7 Practice. Suppose a random variable X has the following probability density function: f ( x ) = sin x, < x < π, zero otherwise. a) Find P ( X < 4 π ). b) Find µ = E
STAT 4 Exam I Continuous RVs Fall 7 Practice. Suppose a random variable X has the following probability density function: f ( x ) = sin x, < x < π, zero otherwise. a) Find P ( X < 4 π ). b) Find µ = E
Chapter 4 Multiple Random Variables
 Review for the previous lecture Theorems and Examples: How to obtain the pmf (pdf) of U = g ( X Y 1 ) and V = g ( X Y) Chapter 4 Multiple Random Variables Chapter 43 Bivariate Transformations Continuous
Review for the previous lecture Theorems and Examples: How to obtain the pmf (pdf) of U = g ( X Y 1 ) and V = g ( X Y) Chapter 4 Multiple Random Variables Chapter 43 Bivariate Transformations Continuous
Lecture 13. Poisson Distribution. Text: A Course in Probability by Weiss 5.5. STAT 225 Introduction to Probability Models February 16, 2014
 Lecture 13 Text: A Course in Probability by Weiss 5.5 STAT 225 Introduction to Probability Models February 16, 2014 Whitney Huang Purdue University 13.1 Agenda 1 2 3 13.2 Review So far, we have seen discrete
Lecture 13 Text: A Course in Probability by Weiss 5.5 STAT 225 Introduction to Probability Models February 16, 2014 Whitney Huang Purdue University 13.1 Agenda 1 2 3 13.2 Review So far, we have seen discrete
Mathematical Statistics 1 Math A 6330
 Mathematical Statistics 1 Math A 6330 Chapter 2 Transformations and Expectations Mohamed I. Riffi Department of Mathematics Islamic University of Gaza September 14, 2015 Outline 1 Distributions of Functions
Mathematical Statistics 1 Math A 6330 Chapter 2 Transformations and Expectations Mohamed I. Riffi Department of Mathematics Islamic University of Gaza September 14, 2015 Outline 1 Distributions of Functions
Computer Science, Informatik 4 Communication and Distributed Systems. Simulation. Discrete-Event System Simulation. Dr.
 Simulation Discrete-Event System Simulation Chapter 4 Statistical Models in Simulation Purpose & Overview The world the model-builder sees is probabilistic rather than deterministic. Some statistical model
Simulation Discrete-Event System Simulation Chapter 4 Statistical Models in Simulation Purpose & Overview The world the model-builder sees is probabilistic rather than deterministic. Some statistical model
Chapter 4 - Lecture 3 The Normal Distribution
 Chapter 4 - Lecture 3 The October 28th, 2009 Chapter 4 - Lecture 3 The Standard Chapter 4 - Lecture 3 The Standard Normal distribution is a statistical unicorn It is the most important distribution in
Chapter 4 - Lecture 3 The October 28th, 2009 Chapter 4 - Lecture 3 The Standard Chapter 4 - Lecture 3 The Standard Normal distribution is a statistical unicorn It is the most important distribution in
II. The Normal Distribution
 II. The Normal Distribution The normal distribution (a.k.a., a the Gaussian distribution or bell curve ) is the by far the best known random distribution. It s discovery has had such a far-reaching impact
II. The Normal Distribution The normal distribution (a.k.a., a the Gaussian distribution or bell curve ) is the by far the best known random distribution. It s discovery has had such a far-reaching impact
Expected Values, Exponential and Gamma Distributions
 Expected Values, Exponential and Gamma Distributions Sections 5.2 & 5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13-3339 Cathy
Expected Values, Exponential and Gamma Distributions Sections 5.2 & 5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13-3339 Cathy
Gamma and Normal Distribuions
 Gamma and Normal Distribuions Sections 5.4 & 5.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 15-3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
Gamma and Normal Distribuions Sections 5.4 & 5.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 15-3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
STAT509: Continuous Random Variable
 University of South Carolina September 23, 2014 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite or infinite) of real numbers for its range.
University of South Carolina September 23, 2014 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite or infinite) of real numbers for its range.
S6880 #7. Generate Non-uniform Random Number #1
 S6880 #7 Generate Non-uniform Random Number #1 Outline 1 Inversion Method Inversion Method Examples Application to Discrete Distributions Using Inversion Method 2 Composition Method Composition Method
S6880 #7 Generate Non-uniform Random Number #1 Outline 1 Inversion Method Inversion Method Examples Application to Discrete Distributions Using Inversion Method 2 Composition Method Composition Method
Probability Density Functions
 Statistical Methods in Particle Physics / WS 13 Lecture II Probability Density Functions Niklaus Berger Physics Institute, University of Heidelberg Recap of Lecture I: Kolmogorov Axioms Ingredients: Set
Statistical Methods in Particle Physics / WS 13 Lecture II Probability Density Functions Niklaus Berger Physics Institute, University of Heidelberg Recap of Lecture I: Kolmogorov Axioms Ingredients: Set
3 Modeling Process Quality
 3 Modeling Process Quality 3.1 Introduction Section 3.1 contains basic numerical and graphical methods. familiar with these methods. It is assumed the student is Goal: Review several discrete and continuous
3 Modeling Process Quality 3.1 Introduction Section 3.1 contains basic numerical and graphical methods. familiar with these methods. It is assumed the student is Goal: Review several discrete and continuous
Week 1 Quantitative Analysis of Financial Markets Distributions A
 Week 1 Quantitative Analysis of Financial Markets Distributions A Christopher Ting http://www.mysmu.edu/faculty/christophert/ Christopher Ting : christopherting@smu.edu.sg : 6828 0364 : LKCSB 5036 October
Week 1 Quantitative Analysis of Financial Markets Distributions A Christopher Ting http://www.mysmu.edu/faculty/christophert/ Christopher Ting : christopherting@smu.edu.sg : 6828 0364 : LKCSB 5036 October
Continuous Random Variables. What continuous random variables are and how to use them. I can give a definition of a continuous random variable.
 Continuous Random Variables Today we are learning... What continuous random variables are and how to use them. I will know if I have been successful if... I can give a definition of a continuous random
Continuous Random Variables Today we are learning... What continuous random variables are and how to use them. I will know if I have been successful if... I can give a definition of a continuous random
Outline PMF, CDF and PDF Mean, Variance and Percentiles Some Common Distributions. Week 5 Random Variables and Their Distributions
 Week 5 Random Variables and Their Distributions Week 5 Objectives This week we give more general definitions of mean value, variance and percentiles, and introduce the first probability models for discrete
Week 5 Random Variables and Their Distributions Week 5 Objectives This week we give more general definitions of mean value, variance and percentiles, and introduce the first probability models for discrete
Mathematical Statistics 1 Math A 6330
 Mathematical Statistics 1 Math A 6330 Chapter 3 Common Families of Distributions Mohamed I. Riffi Department of Mathematics Islamic University of Gaza September 28, 2015 Outline 1 Subjects of Lecture 04
Mathematical Statistics 1 Math A 6330 Chapter 3 Common Families of Distributions Mohamed I. Riffi Department of Mathematics Islamic University of Gaza September 28, 2015 Outline 1 Subjects of Lecture 04
Chapter 5. Chapter 5 sections
 1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
1.6 Families of Distributions
 Your text 1.6. FAMILIES OF DISTRIBUTIONS 15 F(x) 0.20 1.0 0.15 0.8 0.6 Density 0.10 cdf 0.4 0.05 0.2 0.00 a b c 0.0 x Figure 1.1: N(4.5, 2) Distribution Function and Cumulative Distribution Function for
Your text 1.6. FAMILIES OF DISTRIBUTIONS 15 F(x) 0.20 1.0 0.15 0.8 0.6 Density 0.10 cdf 0.4 0.05 0.2 0.00 a b c 0.0 x Figure 1.1: N(4.5, 2) Distribution Function and Cumulative Distribution Function for
Continuous Probability Distributions. Uniform Distribution
 Continuous Probability Distributions Uniform Distribution Important Terms & Concepts Learned Probability Mass Function (PMF) Cumulative Distribution Function (CDF) Complementary Cumulative Distribution
Continuous Probability Distributions Uniform Distribution Important Terms & Concepts Learned Probability Mass Function (PMF) Cumulative Distribution Function (CDF) Complementary Cumulative Distribution
(Ch 3.4.1, 3.4.2, 4.1, 4.2, 4.3)
 3 Probability Distributions (Ch 3.4.1, 3.4.2, 4.1, 4.2, 4.3) Probability Distribution Functions Probability distribution function (pdf): Function for mapping random variables to real numbers. Discrete
3 Probability Distributions (Ch 3.4.1, 3.4.2, 4.1, 4.2, 4.3) Probability Distribution Functions Probability distribution function (pdf): Function for mapping random variables to real numbers. Discrete
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models
 System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 29, 2014 Introduction Introduction The world of the model-builder
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 29, 2014 Introduction Introduction The world of the model-builder
Stat 5101 Notes: Brand Name Distributions
 Stat 5101 Notes: Brand Name Distributions Charles J. Geyer February 14, 2003 1 Discrete Uniform Distribution DiscreteUniform(n). Discrete. Rationale Equally likely outcomes. The interval 1, 2,..., n of
Stat 5101 Notes: Brand Name Distributions Charles J. Geyer February 14, 2003 1 Discrete Uniform Distribution DiscreteUniform(n). Discrete. Rationale Equally likely outcomes. The interval 1, 2,..., n of
PROBABILITY DISTRIBUTION
 PROBABILITY DISTRIBUTION DEFINITION: If S is a sample space with a probability measure and x is a real valued function defined over the elements of S, then x is called a random variable. Types of Random
PROBABILITY DISTRIBUTION DEFINITION: If S is a sample space with a probability measure and x is a real valued function defined over the elements of S, then x is called a random variable. Types of Random
APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 651 APPENDIX B. BIBLIOGRAPHY 677 APPENDIX C. ANSWERS TO SELECTED EXERCISES 679
 APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 1 Table I Summary of Common Probability Distributions 2 Table II Cumulative Standard Normal Distribution Table III Percentage Points, 2 of the Chi-Squared
APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 1 Table I Summary of Common Probability Distributions 2 Table II Cumulative Standard Normal Distribution Table III Percentage Points, 2 of the Chi-Squared
Statistics for Data Analysis. Niklaus Berger. PSI Practical Course Physics Institute, University of Heidelberg
 Statistics for Data Analysis PSI Practical Course 2014 Niklaus Berger Physics Institute, University of Heidelberg Overview You are going to perform a data analysis: Compare measured distributions to theoretical
Statistics for Data Analysis PSI Practical Course 2014 Niklaus Berger Physics Institute, University of Heidelberg Overview You are going to perform a data analysis: Compare measured distributions to theoretical
Statistics, Data Analysis, and Simulation SS 2015
 Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Mainz, 27. April 2015 Dr. Michael O. Distler
Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Mainz, 27. April 2015 Dr. Michael O. Distler
Chapter 2. Continuous random variables
 Chapter 2 Continuous random variables Outline Review of probability: events and probability Random variable Probability and Cumulative distribution function Review of discrete random variable Introduction
Chapter 2 Continuous random variables Outline Review of probability: events and probability Random variable Probability and Cumulative distribution function Review of discrete random variable Introduction
EXAM. Exam #1. Math 3342 Summer II, July 21, 2000 ANSWERS
 EXAM Exam # Math 3342 Summer II, 2 July 2, 2 ANSWERS i pts. Problem. Consider the following data: 7, 8, 9, 2,, 7, 2, 3. Find the first quartile, the median, and the third quartile. Make a box and whisker
EXAM Exam # Math 3342 Summer II, 2 July 2, 2 ANSWERS i pts. Problem. Consider the following data: 7, 8, 9, 2,, 7, 2, 3. Find the first quartile, the median, and the third quartile. Make a box and whisker
functions Poisson distribution Normal distribution Arbitrary functions
 Physics 433: Computational Physics Lecture 6 Random number distributions Generation of random numbers of various distribuition functions Normal distribution Poisson distribution Arbitrary functions Random
Physics 433: Computational Physics Lecture 6 Random number distributions Generation of random numbers of various distribuition functions Normal distribution Poisson distribution Arbitrary functions Random
(Ch 3.4.1, 3.4.2, 4.1, 4.2, 4.3)
 3 Probability Distributions (Ch 3.4.1, 3.4.2, 4.1, 4.2, 4.3) Probability Distribution Functions Probability distribution function (pdf): Function for mapping random variables to real numbers. Discrete
3 Probability Distributions (Ch 3.4.1, 3.4.2, 4.1, 4.2, 4.3) Probability Distribution Functions Probability distribution function (pdf): Function for mapping random variables to real numbers. Discrete
