2 a Substituting (1,4,7) and the coefficients. c The normal vector of the plane
|
|
|
- Jared Gregory
- 5 years ago
- Views:
Transcription
1 Exam-style practice: Paper 1 1 a First we find y and d x. y t t ( = + y = t t y t t t t = x= t+ t = 1+ t. We now find the limits in terms of t. x= t = x=.75= t+ t t t +.75= 1± t = We neglect the negative solution, so the upper limit is t = ( ( V = π t t t + t t 5 ( = π t t t + t + t t t = π t + t + t + t unit. = Since we have that a unit is 1 cm, this means: ( V = cm 11cm b A criticism of the model is that it does not take into account the thickness of the clay. 1.5 a Substituting (1,,7 and the coefficients of x+ yz 1= into dist = gives dist = ax + by + cz + d = 1 = 1 1 Thus a=. 1 a + b + c ( ( ( ( + + b Since v = 5i+ jk is perpendicular to ( ( a r= λ i j+ k + µ i+ j k, we know that r.v =. rv. ( λ ( i j k µ ( ai j k.( 5i j k (( λ µ a i ( λ µ j ( λ µ k.( 5i j k = = = 5λ + 5µ a λ + µ λ + µ = 5µ a+ 5µ = a= c The normal vector of the plane 1 is v1 = i+ jk, the plane has a perpendicular vectorv = 5i+ jk. θ v. v 1 = arccos v 1 v = arccos 1 = arccos = arccos 7 =.9 ( 5 + ( 1 + ( ( ( Pearson Education Ltd 18. Copying permitted for purchasing institution only. This material is not copyright free. 1
2 a The base case n= 1, = 1 1 is true. 1 1 Assume the result is true for n= k. b i 1 1 k k For n= k, 1 = 1 k 1 1 For n = k + 1, k k k k 1 = 1 1 k = 1 k k+ k + k+ 1 ( k+ 1 ( k+ 1 = 1 ( k+ 1 1 Thus the result is true for n= k+ 1. The result is true for n= 1 and if it is true for n= k, then it is true for n= k+ 1. By mathematical induction the result is true for all positive integers n. 1 M only exists if the discriminant is non-zero. So for the discriminant to be zero, we find discrim = 1 1 (( ( (( ( 1 ( ( + k ( + = k + 16 = k+ 1= k = 7. b ii Using A a b c = d e f g h i e f c b b c h i i h e f 1 f d a c c a = A i g g i f d d e b a a b g h h g d e we may compute k k k = 1 k k 1 1 k ( k = 1 8 1k k + 1 ( k + 1 a Using z= cosθ + isinθ (since the modulus is 1 we don t need a coefficient we may write n n z = ( cosθ + isinθ = cos( nθ + isin( nθ and n n z = ( cosθ + isinθ = cos( nθ isin( nθ by De Moivre s theorem. We find the difference of these terms and get n n z z = cos( nθ + isin( nθ cos( nθ isin( nθ = isin ( nθ. ( Pearson Education Ltd 18. Copying permitted for purchasing institution only. This material is not copyright free.
3 b We use ( z z = ( isinθ = 16sin θ (from part a with n= 1 in order to obtain 1 8sin θ = ( zz 1 = ( z z + 6 z + z 1 = ( z + z ( z + z + = cos θ cos θ +. ( ( Note that we have used the fact that n n z + z = cos nθ. ( 5 a The litres of liquid in the vat after t minutes is given by V = 5 15t + t = t Let x grams be the amount of sugar in the vat after t minutes. Concentration of sugar after t minutes is x Conc = grams per litre t The rate of the sugar into the vat is Rate = 5= 75 grams per SugIn minute. The rate of the sugar out of the vat is x x RateSugOut = 15 = t 1 + t grams per minute. Hence we have the rate of change of sugar in grams with respect to time in minutes as d x 75 x =. 1+ t 5 b We write down the equation above, in the form d x Px Q. + = x + = t Now use an integrating factor to solve the differential equation. P IF = e = e = e 1+ t ( + t ln 1 = 1+. t Multiplying our original equation through by the integrating factor gives ( 1+ t + x= 75( 1+ t d ( 1 x+ tx = t. Integrating both sides with respect to t gives 1x+ tx = 75 t+ 115 t + c. Using the initial conditions t =, x= we find that + = + + c c=. Thus the equation is 1x+ tx = 75 t+ 115t. So after 1 minutes 1x+ x = x= 665g 1 c The model could be refined to reflect pressure caused by the volume of oil which would effect rate of leaking. Could take into account that sugar does not disperse uniformly throughout the vat on entry. Pearson Education Ltd 18. Copying permitted for purchasing institution only. This material is not copyright free.
4 6 a We convert z+ 1+ 5i = 1 into Cartesian form and then to polar. Since we know that this locus of points is a circle with radius 1, centred at (, 5, we know that the appropriate Cartesian equation is ( x ( y = 169. We convert this equation to polar form via x= rcosθ and y = rsin θ, giving ( r θ ( r θ r r r cos sin + 5 = cosθ + 1 sinθ = ( θ θ r = 1 cos + 5sin when r. b The set of points A= { z: z+ 1+ 5i1 } z: πargz π defines the segment of a disc (filled circle with radius 1, centred at (, 5 between the half lines π θ = π and θ =. 6 c To find the area of the region defined by A, we use the polar form r = 1cosθ + 5sinθ to calculate π π ( 1 A= ( (1cos θ+ 5sin d θ θ π (1cos 1cos sin = θ+ θ θ+ 5sin θ dθ π π 5 = (7(1 + cos θ + 6 sin θ+ (1cos θd θ π 5 (7( 1sin 1 = θ+ θ cos θ+ ( θ sin θ 57π 119 = + ( 69π = π+ 5 units π π Pearson Education Ltd 18. Copying permitted for purchasing institution only. This material is not copyright free.
5 7 a Differentiating the equation =.x+.y+ 1 with respect to t gives the expression d x dy =. +.. We remove y from the system of equations by dy.. =..x+.y+ 1..x+.y ( ( ( =. +. x+. and so we can write d y in terms of x as dy. =. ((. +. x+.. Combining the first expression we found d x for with the expression for d y, we get d x dy =. +. =. +. (. +. x+. =.6 (.1x+.. ( Multiplying through by 1 and rearranging to have all terms on the left-hand side gives us d x x+ = 7 b The auxiliary equation is 1m 6m+ 1=, with solutions 6± 65 m= i = ±. 1 5 Thus we have the complementary function.t x = e Acos.t + Bsin. t. c ( For the particular integral, we try x= C with differentials d x = and d x =. Substituting these expressions into our differential equation gives + 1C + = C =. 1 So the general solution for x is ( cos. sin. xg = e A t+ B t 1.t c By differentiating ( cos. sin. xg = e A t+ B t 1 with respect to t, we obtain G.t (.t =.e B cos.ta sin.t (.t +.e A cos.t+ B sin.t.t =.e ( B cos.t A sin.t +.xg + 1 and since we have d x.x.y 1, = + + we can rewrite G.t =.e ( B cos.t Asin.t +.xg + 1 =.x +.y + 1 G G After cancelling.x G from both sides, we solve for.t.e ( Bcos.t Asin.t = yg +.t.yg =.e ( Bcos.t Asin.t +. 1.t yg = e ( Bcos.t Asin.t t yg = e ( Bcos.t Asin.t 1 Pearson Education Ltd 18. Copying permitted for purchasing institution only. This material is not copyright free. 5
6 7 d Using the initial conditions t =, x= 1, y = 5 in the general solutions for x and y gives ( B 1= e Acos+ sin 1 16 A= 1 and. 5= e ( BcosAsin 1 85 B=. 1 Thus, we have particular solutions.t x= e cos.t+ sin.t t y = e cos.t sin.t e y( = e cos.6 sin The concentration on the right side of the model is predicted to be negative after hours. This is clearly nonsense, so the model is not suitable. Pearson Education Ltd 18. Copying permitted for purchasing institution only. This material is not copyright free. 6
Proof by induction ME 8
 Proof by induction ME 8 n Let f ( n) 9, where n. f () 9 8, which is divisible by 8. f ( n) is divisible by 8 when n =. Assume that for n =, f ( ) 9 is divisible by 8 for. f ( ) 9 9.9 9(9 ) f ( ) f ( )
Proof by induction ME 8 n Let f ( n) 9, where n. f () 9 8, which is divisible by 8. f ( n) is divisible by 8 when n =. Assume that for n =, f ( ) 9 is divisible by 8 for. f ( ) 9 9.9 9(9 ) f ( ) f ( )
Review exercise 2. 1 The equation of the line is: = 5 a The gradient of l1 is 3. y y x x. So the gradient of l2 is. The equation of line l2 is: y =
 Review exercise The equation of the line is: y y x x y y x x y 8 x+ 6 8 + y 8 x+ 6 y x x + y 0 y ( ) ( x 9) y+ ( x 9) y+ x 9 x y 0 a, b, c Using points A and B: y y x x y y x x y x 0 k 0 y x k ky k x a
Review exercise The equation of the line is: y y x x y y x x y 8 x+ 6 8 + y 8 x+ 6 y x x + y 0 y ( ) ( x 9) y+ ( x 9) y+ x 9 x y 0 a, b, c Using points A and B: y y x x y y x x y x 0 k 0 y x k ky k x a
Mixed exercise 3. x y. cosh t sinh t 1 Substituting the values for cosh t and sinht in the equation for the hyperbola H. = θ =
 Mixed exercise x x a Parametric equations: cosθ and sinθ 9 cos θ + sin θ Substituting the values for cos θ and sinθ in the equation for ellipse E gives the Cartesian equation: + 9 b Comparing with the
Mixed exercise x x a Parametric equations: cosθ and sinθ 9 cos θ + sin θ Substituting the values for cos θ and sinθ in the equation for ellipse E gives the Cartesian equation: + 9 b Comparing with the
AH Complex Numbers.notebook October 12, 2016
 Complex Numbers Complex Numbers Complex Numbers were first introduced in the 16th century by an Italian mathematician called Cardano. He referred to them as ficticious numbers. Given an equation that does
Complex Numbers Complex Numbers Complex Numbers were first introduced in the 16th century by an Italian mathematician called Cardano. He referred to them as ficticious numbers. Given an equation that does
9 Mixed Exercise. vector equation is. 4 a
 9 Mixed Exercise a AB r i j k j k c OA AB 7 i j 7 k A7,, and B,,8 8 AB 6 A vector equation is 7 r x 7 y z (i j k) j k a x y z a a 7, Pearson Education Ltd 7. Copying permitted for purchasing institution
9 Mixed Exercise a AB r i j k j k c OA AB 7 i j 7 k A7,, and B,,8 8 AB 6 A vector equation is 7 r x 7 y z (i j k) j k a x y z a a 7, Pearson Education Ltd 7. Copying permitted for purchasing institution
Candidates sitting FP2 may also require those formulae listed under Further Pure Mathematics FP1 and Core Mathematics C1 C4. e π.
 F Further IAL Pure PAPERS: Mathematics FP 04-6 AND SPECIMEN Candidates sitting FP may also require those formulae listed under Further Pure Mathematics FP and Core Mathematics C C4. Area of a sector A
F Further IAL Pure PAPERS: Mathematics FP 04-6 AND SPECIMEN Candidates sitting FP may also require those formulae listed under Further Pure Mathematics FP and Core Mathematics C C4. Area of a sector A
Draft Version 1 Mark scheme Further Maths Core Pure (AS/Year 1) Unit Test 1: Complex numbers 1
 1 w z k k States or implies that 4 i TBC Uses the definition of argument to write 4 k π tan 1 k 4 Makes an attempt to solve for k, for example 4 + k = k is seen. M1.a Finds k = 6 (4 marks) Pearson Education
1 w z k k States or implies that 4 i TBC Uses the definition of argument to write 4 k π tan 1 k 4 Makes an attempt to solve for k, for example 4 + k = k is seen. M1.a Finds k = 6 (4 marks) Pearson Education
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 Chapter 5 COMPLEX NUMBERS AND QUADRATIC EQUATIONS 5. Overview We know that the square of a real number is always non-negative e.g. (4) 6 and ( 4) 6. Therefore, square root of 6 is ± 4. What about the square
Chapter 5 COMPLEX NUMBERS AND QUADRATIC EQUATIONS 5. Overview We know that the square of a real number is always non-negative e.g. (4) 6 and ( 4) 6. Therefore, square root of 6 is ± 4. What about the square
Further Mathematics AS/F1/D17 AS PAPER 1
 Surname Other Names Candidate Signature Centre Number Candidate Number Examiner Comments Total Marks Further Mathematics AS PAPER 1 CM December Mock Exam (AQA Version) Time allowed: 1 hour and 30 minutes
Surname Other Names Candidate Signature Centre Number Candidate Number Examiner Comments Total Marks Further Mathematics AS PAPER 1 CM December Mock Exam (AQA Version) Time allowed: 1 hour and 30 minutes
Mark scheme Pure Mathematics Year 1 (AS) Unit Test 2: Coordinate geometry in the (x, y) plane
 Mark scheme Pure Mathematics Year 1 (AS) Unit Test : Coordinate in the (x, y) plane Q Scheme Marks AOs Pearson 1a Use of the gradient formula to begin attempt to find k. k 1 ( ) or 1 (k 4) ( k 1) (i.e.
Mark scheme Pure Mathematics Year 1 (AS) Unit Test : Coordinate in the (x, y) plane Q Scheme Marks AOs Pearson 1a Use of the gradient formula to begin attempt to find k. k 1 ( ) or 1 (k 4) ( k 1) (i.e.
Circles, Mixed Exercise 6
 Circles, Mixed Exercise 6 a QR is the diameter of the circle so the centre, C, is the midpoint of QR ( 5) 0 Midpoint = +, + = (, 6) C(, 6) b Radius = of diameter = of QR = of ( x x ) + ( y y ) = of ( 5
Circles, Mixed Exercise 6 a QR is the diameter of the circle so the centre, C, is the midpoint of QR ( 5) 0 Midpoint = +, + = (, 6) C(, 6) b Radius = of diameter = of QR = of ( x x ) + ( y y ) = of ( 5
b UVW is a right-angled triangle, therefore VW is the diameter of the circle. Centre of circle = Midpoint of VW = (8 2) + ( 2 6) = 100
 Circles 6F a U(, 8), V(7, 7) and W(, ) UV = ( x x ) ( y y ) = (7 ) (7 8) = 8 VW = ( 7) ( 7) = 64 UW = ( ) ( 8) = 8 Use Pythagoras' theorem to show UV UW = VW 8 8 = 64 = VW Therefore, UVW is a right-angled
Circles 6F a U(, 8), V(7, 7) and W(, ) UV = ( x x ) ( y y ) = (7 ) (7 8) = 8 VW = ( 7) ( 7) = 64 UW = ( ) ( 8) = 8 Use Pythagoras' theorem to show UV UW = VW 8 8 = 64 = VW Therefore, UVW is a right-angled
FP2 Mark Schemes from old P4, P5, P6 and FP1, FP2, FP3 papers (back to June 2002)
 FP Mark Schemes from old P, P5, P6 and FP, FP, FP papers (back to June 00) Please note that the following pages contain mark schemes for questions from past papers. The standard of the mark schemes is
FP Mark Schemes from old P, P5, P6 and FP, FP, FP papers (back to June 00) Please note that the following pages contain mark schemes for questions from past papers. The standard of the mark schemes is
The branch of mechanics which deals with the motion of object is called dynamics. It is divided into two branches:
 M th KINEMATICS 4 CHAPTER INTRODUCTION The branch of mechanics which deals with the motion of object is called dynamics. It is divided into two branches: Kinematics: (i) Kinematics (ii) Kinetics The branch
M th KINEMATICS 4 CHAPTER INTRODUCTION The branch of mechanics which deals with the motion of object is called dynamics. It is divided into two branches: Kinematics: (i) Kinematics (ii) Kinetics The branch
The gradient of the radius from the centre of the circle ( 1, 6) to (2, 3) is: ( 6)
 Circles 6E a (x + ) + (y + 6) = r, (, ) Substitute x = and y = into the equation (x + ) + (y + 6) = r + + + 6 = r ( ) ( ) 9 + 8 = r r = 90 = 0 b The line has equation x + y = 0 y = x + y = x + The gradient
Circles 6E a (x + ) + (y + 6) = r, (, ) Substitute x = and y = into the equation (x + ) + (y + 6) = r + + + 6 = r ( ) ( ) 9 + 8 = r r = 90 = 0 b The line has equation x + y = 0 y = x + y = x + The gradient
2011 Mathematics Extension 1 HSC Examination Sample Answers
 0 Mathematics Extension HSC Examination Sample Answers When examination committees develop questions for the examination, they may write sample answers or, in the case of some questions, answers could
0 Mathematics Extension HSC Examination Sample Answers When examination committees develop questions for the examination, they may write sample answers or, in the case of some questions, answers could
MATHEMATICS: SPECIALIST UNITS 3C AND 3D FORMULA SHEET 2015
 MATHEMATICS: SPECIALIST UNITS 3C AND 3D FORMULA SHEET 05 Copyright School Curriculum and Standards Authority, 05 This document apart from any third party copyright material contained in it may be freely
MATHEMATICS: SPECIALIST UNITS 3C AND 3D FORMULA SHEET 05 Copyright School Curriculum and Standards Authority, 05 This document apart from any third party copyright material contained in it may be freely
Precalculus Notes: Unit 6 Vectors, Parametrics, Polars, & Complex Numbers. A: Initial Point (start); B: Terminal Point (end) : ( ) ( )
 Syllabus Objectives: 5.1 The student will explore methods of vector addition and subtraction. 5. The student will develop strategies for computing a vector s direction angle and magnitude given its coordinates.
Syllabus Objectives: 5.1 The student will explore methods of vector addition and subtraction. 5. The student will develop strategies for computing a vector s direction angle and magnitude given its coordinates.
Taylor Series 6B. lim s x. 1 a We can evaluate the limit directly since there are no singularities: b Again, there are no singularities, so:
 Taylor Series 6B a We can evaluate the it directly since there are no singularities: 7+ 7+ 7 5 5 5 b Again, there are no singularities, so: + + c Here we should divide through by in the numerator and denominator
Taylor Series 6B a We can evaluate the it directly since there are no singularities: 7+ 7+ 7 5 5 5 b Again, there are no singularities, so: + + c Here we should divide through by in the numerator and denominator
Parametric Equations and Polar Coordinates
 Parametric Equations and Polar Coordinates Parametrizations of Plane Curves In previous chapters, we have studied curves as the graphs of functions or equations involving the two variables x and y. Another
Parametric Equations and Polar Coordinates Parametrizations of Plane Curves In previous chapters, we have studied curves as the graphs of functions or equations involving the two variables x and y. Another
MATHEMATICS AS/M/P1 AS PAPER 1
 Surname Other Names Candidate Signature Centre Number Candidate Number Examiner Comments Total Marks MATHEMATICS AS PAPER 1 Bronze Set B (Edexcel Version) CM Time allowed: 2 hours Instructions to candidates:
Surname Other Names Candidate Signature Centre Number Candidate Number Examiner Comments Total Marks MATHEMATICS AS PAPER 1 Bronze Set B (Edexcel Version) CM Time allowed: 2 hours Instructions to candidates:
cos + i sin = cos + i sin = cos 2π iθ
 Complx numbrs 1C cosθ + sinθ = cosθ + i sin θ 1 a cosθ + sin θ = cos12θ + i sin12θ b 4 c d f 2 a b c d π π π π cos + isin = cos + isin 8 i = + π π 8π 8π 2π 2π cos + isin = cos + isin = cos + isin 1 i =
Complx numbrs 1C cosθ + sinθ = cosθ + i sin θ 1 a cosθ + sin θ = cos12θ + i sin12θ b 4 c d f 2 a b c d π π π π cos + isin = cos + isin 8 i = + π π 8π 8π 2π 2π cos + isin = cos + isin = cos + isin 1 i =
a Write down the coordinates of the point on the curve where t = 2. b Find the value of t at the point on the curve with coordinates ( 5 4, 8).
 Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Chapter 8. Complex Numbers, Polar Equations, and Parametric Equations. Section 8.1: Complex Numbers. 26. { ± 6i}
 Chapter 8 Complex Numbers, Polar Equations, and Parametric Equations 6. { ± 6i} Section 8.1: Complex Numbers 1. true. true. true 4. true 5. false (Every real number is a complex number. 6. true 7. 4 is
Chapter 8 Complex Numbers, Polar Equations, and Parametric Equations 6. { ± 6i} Section 8.1: Complex Numbers 1. true. true. true 4. true 5. false (Every real number is a complex number. 6. true 7. 4 is
Q Scheme Marks AOs Pearson ( ) 2. Notes. Deduces that 21a 168 = 0 and solves to find a = 8 A1* 2.2a
 Further Maths Core Pure (AS/Year 1) Unit Test : Matrices Q Scheme Marks AOs Pearson Finds det M = 3 p p+ 4 = p + 4 p+ 6 1 ( )( ) ( )( ) ( ) Completes the square to show p + 4p+ 6= p+ + M1.a Concludes that
Further Maths Core Pure (AS/Year 1) Unit Test : Matrices Q Scheme Marks AOs Pearson Finds det M = 3 p p+ 4 = p + 4 p+ 6 1 ( )( ) ( )( ) ( ) Completes the square to show p + 4p+ 6= p+ + M1.a Concludes that
Chapter 5 Trigonometric Functions of Angles
 Chapter 5 Trigonometric Functions of Angles Section 3 Points on Circles Using Sine and Cosine Signs Signs I Signs (+, +) I Signs II (+, +) I Signs II (, +) (+, +) I Signs II (, +) (+, +) I III Signs II
Chapter 5 Trigonometric Functions of Angles Section 3 Points on Circles Using Sine and Cosine Signs Signs I Signs (+, +) I Signs II (+, +) I Signs II (, +) (+, +) I Signs II (, +) (+, +) I III Signs II
HIGHER SCHOOL CERTIFICATE EXAMINATION MATHEMATICS 4 UNIT (ADDITIONAL) Time allowed Three hours (Plus 5 minutes reading time)
 N E W S O U T H W A L E S HIGHER SCHOOL CERTIFICATE EXAMINATION 996 MATHEMATICS 4 UNIT (ADDITIONAL) Time allowed Three hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions.
N E W S O U T H W A L E S HIGHER SCHOOL CERTIFICATE EXAMINATION 996 MATHEMATICS 4 UNIT (ADDITIONAL) Time allowed Three hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions.
COMPLEX NUMBERS
 COMPLEX NUMBERS 1. Any number of the form x+iy where x, y R and i -1 is called a Complex Number.. In the complex number x+iy, x is called the real part and y is called the imaginary part of the complex
COMPLEX NUMBERS 1. Any number of the form x+iy where x, y R and i -1 is called a Complex Number.. In the complex number x+iy, x is called the real part and y is called the imaginary part of the complex
Mathematics Extension 2
 00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
CHAPTER 4 Stress Transformation
 CHAPTER 4 Stress Transformation ANALYSIS OF STRESS For this topic, the stresses to be considered are not on the perpendicular and parallel planes only but also on other inclined planes. A P a a b b P z
CHAPTER 4 Stress Transformation ANALYSIS OF STRESS For this topic, the stresses to be considered are not on the perpendicular and parallel planes only but also on other inclined planes. A P a a b b P z
abc Mathematics Further Pure General Certificate of Education SPECIMEN UNITS AND MARK SCHEMES
 abc General Certificate of Education Mathematics Further Pure SPECIMEN UNITS AND MARK SCHEMES ADVANCED SUBSIDIARY MATHEMATICS (56) ADVANCED SUBSIDIARY PURE MATHEMATICS (566) ADVANCED SUBSIDIARY FURTHER
abc General Certificate of Education Mathematics Further Pure SPECIMEN UNITS AND MARK SCHEMES ADVANCED SUBSIDIARY MATHEMATICS (56) ADVANCED SUBSIDIARY PURE MATHEMATICS (566) ADVANCED SUBSIDIARY FURTHER
Pure Mathematics Year 1 (AS) Unit Test 1: Algebra and Functions
 Pure Mathematics Year (AS) Unit Test : Algebra and Functions Simplify 6 4, giving your answer in the form p 8 q, where p and q are positive rational numbers. f( x) x ( k 8) x (8k ) a Find the discriminant
Pure Mathematics Year (AS) Unit Test : Algebra and Functions Simplify 6 4, giving your answer in the form p 8 q, where p and q are positive rational numbers. f( x) x ( k 8) x (8k ) a Find the discriminant
ALGEBRAIC LONG DIVISION
 QUESTIONS: 2014; 2c 2013; 1c ALGEBRAIC LONG DIVISION x + n ax 3 + bx 2 + cx +d Used to find factors and remainders of functions for instance 2x 3 + 9x 2 + 8x + p This process is useful for finding factors
QUESTIONS: 2014; 2c 2013; 1c ALGEBRAIC LONG DIVISION x + n ax 3 + bx 2 + cx +d Used to find factors and remainders of functions for instance 2x 3 + 9x 2 + 8x + p This process is useful for finding factors
Some commonly encountered sets and their notations
 NATIONAL UNIVERSITY OF SINGAPORE DEPARTMENT OF MATHEMATICS (This notes are based on the book Introductory Mathematics by Ng Wee Seng ) LECTURE SETS & FUNCTIONS Some commonly encountered sets and their
NATIONAL UNIVERSITY OF SINGAPORE DEPARTMENT OF MATHEMATICS (This notes are based on the book Introductory Mathematics by Ng Wee Seng ) LECTURE SETS & FUNCTIONS Some commonly encountered sets and their
MATHEMATICS EXTENSION 2
 PETRUS KY COLLEGE NEW SOUTH WALES in partnership with VIETNAMESE COMMUNITY IN AUSTRALIA NSW CHAPTER JULY 006 MATHEMATICS EXTENSION PRE-TRIAL TEST HIGHER SCHOOL CERTIFICATE (HSC) Student Number: Student
PETRUS KY COLLEGE NEW SOUTH WALES in partnership with VIETNAMESE COMMUNITY IN AUSTRALIA NSW CHAPTER JULY 006 MATHEMATICS EXTENSION PRE-TRIAL TEST HIGHER SCHOOL CERTIFICATE (HSC) Student Number: Student
= + then for all n N. n= is true, now assume the statement is. ) clearly the base case 1 ( ) ( ) ( )( ) θ θ θ θ ( θ θ θ θ)
 Complex numbers mixed exercise i a We have e cos + isin hence i i ( e + e ) ( cos + isin + cos + isin ) ( cos + isin + cos sin) cos Where we have used the fact that cos cos sin sin b We have ia ia ib ib
Complex numbers mixed exercise i a We have e cos + isin hence i i ( e + e ) ( cos + isin + cos + isin ) ( cos + isin + cos sin) cos Where we have used the fact that cos cos sin sin b We have ia ia ib ib
Study guide for Exam 1. by William H. Meeks III October 26, 2012
 Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
MAT 211 Final Exam. Spring Jennings. Show your work!
 MAT 211 Final Exam. pring 215. Jennings. how your work! Hessian D = f xx f yy (f xy ) 2 (for optimization). Polar coordinates x = r cos(θ), y = r sin(θ), da = r dr dθ. ylindrical coordinates x = r cos(θ),
MAT 211 Final Exam. pring 215. Jennings. how your work! Hessian D = f xx f yy (f xy ) 2 (for optimization). Polar coordinates x = r cos(θ), y = r sin(θ), da = r dr dθ. ylindrical coordinates x = r cos(θ),
Q Scheme Marks AOs Pearson. Notes. Deduces that 21a 168 = 0 and solves to find a = 8 A1* 2.2a
 Further Maths Core Pure (AS/Year 1) Unit Test : Matrices Q Scheme Marks AOs Pearson Finds det M 3 p p 4 p 4 p 6 1 Completes the square to show p 4 p 6 p M1.a Concludes that (p + ) + > 0 for all values
Further Maths Core Pure (AS/Year 1) Unit Test : Matrices Q Scheme Marks AOs Pearson Finds det M 3 p p 4 p 4 p 6 1 Completes the square to show p 4 p 6 p M1.a Concludes that (p + ) + > 0 for all values
University of Alberta. Math 214 Sample Exam Math 214 Solutions
 University of Alberta Math 14 Sample Exam Math 14 Solutions 1. Test the following series for convergence or divergence (a) ( n +n+1 3n +n+1 )n, (b) 3 n (n +1) (c) SOL: n!, arccos( n n +1 ), (a) ( n +n+1
University of Alberta Math 14 Sample Exam Math 14 Solutions 1. Test the following series for convergence or divergence (a) ( n +n+1 3n +n+1 )n, (b) 3 n (n +1) (c) SOL: n!, arccos( n n +1 ), (a) ( n +n+1
( ) Applications of forces 7D. 1 Suppose that the rod has length 2a. Taking moments about A: acos30 3
 Applications of forces 7D Suppose that the rod has length a. Taking moments about A: at 80 acos0 T 80 T 0. 6 N R( ), F T sin0 0 7. N R, T cos0 + R 80 R 80 0 50N In order for the rod to remain in equilibrium,
Applications of forces 7D Suppose that the rod has length a. Taking moments about A: at 80 acos0 T 80 T 0. 6 N R( ), F T sin0 0 7. N R, T cos0 + R 80 R 80 0 50N In order for the rod to remain in equilibrium,
SECTION A. f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes.
 SECTION A 1. State the maximal domain and range of the function f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes. 2. By evaluating f(0),
SECTION A 1. State the maximal domain and range of the function f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes. 2. By evaluating f(0),
Advanced Higher Grade
 Prelim Eamination / 5 (Assessing Units & ) MATHEMATICS Advanced Higher Grade Time allowed - hours Read Carefully. Full credit will be given only where the solution contains appropriate woring.. Calculators
Prelim Eamination / 5 (Assessing Units & ) MATHEMATICS Advanced Higher Grade Time allowed - hours Read Carefully. Full credit will be given only where the solution contains appropriate woring.. Calculators
Created by T. Madas LINE INTEGRALS. Created by T. Madas
 LINE INTEGRALS LINE INTEGRALS IN 2 DIMENSIONAL CARTESIAN COORDINATES Question 1 Evaluate the integral ( x + 2y) dx, C where C is the path along the curve with equation y 2 = x + 1, from ( ) 0,1 to ( )
LINE INTEGRALS LINE INTEGRALS IN 2 DIMENSIONAL CARTESIAN COORDINATES Question 1 Evaluate the integral ( x + 2y) dx, C where C is the path along the curve with equation y 2 = x + 1, from ( ) 0,1 to ( )
Core Mathematics C4. You must have: Mathematical Formulae and Statistical Tables (Pink)
 Write your name here Surname Other names Pearson Edexcel GCE Centre Number Core Mathematics C4 Advanced Candidate Number Friday 23 June 2017 Morning Time: 1 hour 30 minutes Paper Reference 6666/01 You
Write your name here Surname Other names Pearson Edexcel GCE Centre Number Core Mathematics C4 Advanced Candidate Number Friday 23 June 2017 Morning Time: 1 hour 30 minutes Paper Reference 6666/01 You
MATH 135: COMPLEX NUMBERS
 MATH 135: COMPLEX NUMBERS (WINTER, 010) The complex numbers C are important in just about every branch of mathematics. These notes 1 present some basic facts about them. 1. The Complex Plane A complex
MATH 135: COMPLEX NUMBERS (WINTER, 010) The complex numbers C are important in just about every branch of mathematics. These notes 1 present some basic facts about them. 1. The Complex Plane A complex
Core Mathematics C34
 Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Candidate Number Core Mathematics C34 Advanced Monday 16 June 2014 Morning Time: 2 hours 30 minutes You
Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Candidate Number Core Mathematics C34 Advanced Monday 16 June 2014 Morning Time: 2 hours 30 minutes You
THE NCUK INTERNATIONAL FOUNDATION YEAR (IFY) Further Mathematics
 IFYFM00 Further Maths THE NCUK INTERNATIONAL FOUNDATION YEAR (IFY) Further Mathematics Examination Session Summer 009 Time Allowed hours 0 minutes (Including 0 minutes reading time) INSTRUCTIONS TO STUDENTS
IFYFM00 Further Maths THE NCUK INTERNATIONAL FOUNDATION YEAR (IFY) Further Mathematics Examination Session Summer 009 Time Allowed hours 0 minutes (Including 0 minutes reading time) INSTRUCTIONS TO STUDENTS
Paper Reference. Core Mathematics C4 Advanced. Tuesday 18 June 2013 Morning Time: 1 hour 30 minutes
 Centre No. Candidate No. Paper Reference(s) 6666/01 Edexcel GCE Core Mathematics C4 Advanced Tuesday 18 June 2013 Morning Time: 1 hour 30 minutes Materials required for examination Mathematical Formulae
Centre No. Candidate No. Paper Reference(s) 6666/01 Edexcel GCE Core Mathematics C4 Advanced Tuesday 18 June 2013 Morning Time: 1 hour 30 minutes Materials required for examination Mathematical Formulae
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 3 2, 5 2 C) - 5 2
 Test Review (chap 0) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Find the point on the curve x = sin t, y = cos t, -
Test Review (chap 0) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Find the point on the curve x = sin t, y = cos t, -
International Advanced Level Further Pure Mathematics F2 Advanced/Advanced Subsidiary
 Write your name here Surname Other names Centre Number Pearson Edexcel International Advanced Level Further Pure Mathematics F2 Advanced/Advanced Subsidiary Sample Assessment Material Time: 1 hour 30 minutes
Write your name here Surname Other names Centre Number Pearson Edexcel International Advanced Level Further Pure Mathematics F2 Advanced/Advanced Subsidiary Sample Assessment Material Time: 1 hour 30 minutes
G H. Extended Unit Tests B L L. Higher Still Advanced Higher Mathematics. (more demanding tests covering all levels) Contents. 3 Extended Unit Tests
 M A T H E M A T I C S H I G H E R Higher Still Advanced Higher Mathematics S T I L L Etended Unit Tests B (more demanding tests covering all levels) Contents 3 Etended Unit Tests Detailed marking schemes
M A T H E M A T I C S H I G H E R Higher Still Advanced Higher Mathematics S T I L L Etended Unit Tests B (more demanding tests covering all levels) Contents 3 Etended Unit Tests Detailed marking schemes
a k 0, then k + 1 = 2 lim 1 + 1
 Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
i j k i j k i j k
 Vectors D a The equation of the line is (r a) b0 r ba b. This gives: r (i+j k)(i+j+k) (i+j k) r (i+j k) i+0j k b The equation of the line is (r a) b0 r ba b. This gives: r ( i+ j+ k) (i k) ( i+ j+ k) 0
Vectors D a The equation of the line is (r a) b0 r ba b. This gives: r (i+j k)(i+j+k) (i+j k) r (i+j k) i+0j k b The equation of the line is (r a) b0 r ba b. This gives: r ( i+ j+ k) (i k) ( i+ j+ k) 0
Elastic strings and springs Mixed exercise 3
 Elastic strings and springs Mixed exercise ( )T cosθ mg By Hooke s law 5mgx T 6a a sinθ a + x () () () a 4 5mg Ifcos θ, T from () 5 8 5mg 5mgx so, from () 8 6a a x 4 If cos θ, then sinθ 5 5 a sinθ from
Elastic strings and springs Mixed exercise ( )T cosθ mg By Hooke s law 5mgx T 6a a sinθ a + x () () () a 4 5mg Ifcos θ, T from () 5 8 5mg 5mgx so, from () 8 6a a x 4 If cos θ, then sinθ 5 5 a sinθ from
Math 113 Final Exam Practice
 Math Final Exam Practice The Final Exam is comprehensive. You should refer to prior reviews when studying material in chapters 6, 7, 8, and.-9. This review will cover.0- and chapter 0. This sheet has three
Math Final Exam Practice The Final Exam is comprehensive. You should refer to prior reviews when studying material in chapters 6, 7, 8, and.-9. This review will cover.0- and chapter 0. This sheet has three
Exam 1 Review SOLUTIONS
 1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document
 Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
Further Pure Mathematics F2
 Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Further Pure Mathematics F2 Advanced/Advanced Subsidiary Wednesday 8 June 2016 Morning Time: 1 hour 30
Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Further Pure Mathematics F2 Advanced/Advanced Subsidiary Wednesday 8 June 2016 Morning Time: 1 hour 30
Paper Reference. Further Pure Mathematics FP3 Advanced/Advanced Subsidiary. Tuesday 26 June 2007 Afternoon Time: 1 hour 30 minutes
 Centre No. Candidate No. Paper Reference 6 6 7 6 0 1 Surname Signature Paper Reference(s) 6676/01 Edexcel GCE Further Pure Mathematics FP3 Advanced/Advanced Subsidiary Tuesday 26 June 2007 Afternoon Time:
Centre No. Candidate No. Paper Reference 6 6 7 6 0 1 Surname Signature Paper Reference(s) 6676/01 Edexcel GCE Further Pure Mathematics FP3 Advanced/Advanced Subsidiary Tuesday 26 June 2007 Afternoon Time:
Review Exercise 2. 1 a Chemical A 5x+ Chemical B 2x+ 2y12 [ x+ Chemical C [ 4 12]
![Review Exercise 2. 1 a Chemical A 5x+ Chemical B 2x+ 2y12 [ x+ Chemical C [ 4 12] Review Exercise 2. 1 a Chemical A 5x+ Chemical B 2x+ 2y12 [ x+ Chemical C [ 4 12]](/thumbs/82/84751684.jpg) Review Exercise a Chemical A 5x+ y 0 Chemical B x+ y [ x+ y 6] b Chemical C 6 [ ] x+ y x+ y x, y 0 c T = x+ y d ( x, y) = (, ) T = Pearson Education Ltd 08. Copying permitted for purchasing institution
Review Exercise a Chemical A 5x+ y 0 Chemical B x+ y [ x+ y 6] b Chemical C 6 [ ] x+ y x+ y x, y 0 c T = x+ y d ( x, y) = (, ) T = Pearson Education Ltd 08. Copying permitted for purchasing institution
Introduction. The first chapter of FP1 introduces you to imaginary and complex numbers
 Introduction The first chapter of FP1 introduces you to imaginary and complex numbers You will have seen at GCSE level that some quadratic equations cannot be solved Imaginary and complex numbers will
Introduction The first chapter of FP1 introduces you to imaginary and complex numbers You will have seen at GCSE level that some quadratic equations cannot be solved Imaginary and complex numbers will
( ) ( ) 2 1 ( ) Conic Sections 1 2E. 1 a. 1 dy. At (16, 8), d y 2 1 Tangent is: dx. Tangent at,8. is 1
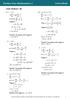 Conic Sections E a y y so At (6, ), d y y ( 6) y 6 y+ 6 y 6+ y+ 6 d y y At, 6 When, y, angent at, is y 6 y 6+ 6+ y 6+ y 6 y y so,, d y At y ( ) y ( ) y y+ y + y+ e 6+ y 6 y 7 7 y 7 so d d y 7 At ( 7, 7),
Conic Sections E a y y so At (6, ), d y y ( 6) y 6 y+ 6 y 6+ y+ 6 d y y At, 6 When, y, angent at, is y 6 y 6+ 6+ y 6+ y 6 y y so,, d y At y ( ) y ( ) y y+ y + y+ e 6+ y 6 y 7 7 y 7 so d d y 7 At ( 7, 7),
Since x + we get x² + 2x = 4, or simplifying it, x² = 4. Therefore, x² + = 4 2 = 2. Ans. (C)
 SAT II - Math Level 2 Test #01 Solution 1. x + = 2, then x² + = Since x + = 2, by squaring both side of the equation, (A) - (B) 0 (C) 2 (D) 4 (E) -2 we get x² + 2x 1 + 1 = 4, or simplifying it, x² + 2
SAT II - Math Level 2 Test #01 Solution 1. x + = 2, then x² + = Since x + = 2, by squaring both side of the equation, (A) - (B) 0 (C) 2 (D) 4 (E) -2 we get x² + 2x 1 + 1 = 4, or simplifying it, x² + 2
MTH4101 CALCULUS II REVISION NOTES. 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) ax 2 + bx + c = 0. x = b ± b 2 4ac 2a. i = 1.
 MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
Condensed. Mathematics. General Certificate of Education Advanced Level Examination June Unit Further Pure 2. Time allowed * 1 hour 30 minutes
 General Certificate of Education Advanced Level Examination June 011 Mathematics MFP Unit Further Pure Monday 13 June 011 9.00 am to 10.30 am For this paper you must have: the blue AQA booklet of formulae
General Certificate of Education Advanced Level Examination June 011 Mathematics MFP Unit Further Pure Monday 13 June 011 9.00 am to 10.30 am For this paper you must have: the blue AQA booklet of formulae
G H. Extended Unit Tests A L L. Higher Still Advanced Higher Mathematics. (more demanding tests covering all levels) Contents. 3 Extended Unit Tests
 M A T H E M A T I C S H I G H E R Higher Still Advanced Higher Mathematics S T I L L Extended Unit Tests A (more demanding tests covering all levels) Contents Extended Unit Tests Detailed marking schemes
M A T H E M A T I C S H I G H E R Higher Still Advanced Higher Mathematics S T I L L Extended Unit Tests A (more demanding tests covering all levels) Contents Extended Unit Tests Detailed marking schemes
Mathematics Extension 2
 0 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Etension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Black pen is preferred Board-approved calculators
0 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Etension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Black pen is preferred Board-approved calculators
Mathematics Extension 1
 009 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
009 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
National Quali cations
 National Quali cations AH08 X747/77/ Mathematics THURSDAY, MAY 9:00 AM :00 NOON Total marks 00 Attempt ALL questions. You may use a calculator. Full credit will be given only to solutions which contain
National Quali cations AH08 X747/77/ Mathematics THURSDAY, MAY 9:00 AM :00 NOON Total marks 00 Attempt ALL questions. You may use a calculator. Full credit will be given only to solutions which contain
( ) ( ) or ( ) ( ) Review Exercise 1. 3 a 80 Use. 1 a. bc = b c 8 = 2 = 4. b 8. Use = 16 = First find 8 = 1+ = 21 8 = =
 Review Eercise a Use m m a a, so a a a Use c c 6 5 ( a ) 5 a First find Use a 5 m n m n m a m ( a ) or ( a) 5 5 65 m n m a n m a m a a n m or m n (Use a a a ) cancelling y 6 ecause n n ( 5) ( 5)( 5) (
Review Eercise a Use m m a a, so a a a Use c c 6 5 ( a ) 5 a First find Use a 5 m n m n m a m ( a ) or ( a) 5 5 65 m n m a n m a m a a n m or m n (Use a a a ) cancelling y 6 ecause n n ( 5) ( 5)( 5) (
Mark Scheme Summer 2009
 Mark Summer 009 GCE GCE Mathematics (6668/0) Edecel is one of the leading eamining and awarding bodies in the UK and throughout the world. We provide a wide range of qualifications including academic,
Mark Summer 009 GCE GCE Mathematics (6668/0) Edecel is one of the leading eamining and awarding bodies in the UK and throughout the world. We provide a wide range of qualifications including academic,
physicsandmathstutor.com 4727 Mark Scheme June 2010
 477 Mark Scheme June 00 Direction of l = k[7, 0, 0] Direction of l = k[,, ] EITHER n = [7, 0, 0] [,, ] For both directions [ x, y, z]. [7,0, 0] = 0 7x 0z = 0 OR [ x, y, z]. [,, ] = 0 x y z = 0 n = k[0,,
477 Mark Scheme June 00 Direction of l = k[7, 0, 0] Direction of l = k[,, ] EITHER n = [7, 0, 0] [,, ] For both directions [ x, y, z]. [7,0, 0] = 0 7x 0z = 0 OR [ x, y, z]. [,, ] = 0 x y z = 0 n = k[0,,
Edexcel Core Mathematics 4 Parametric equations.
 Edexcel Core Mathematics 4 Parametric equations. Edited by: K V Kumaran kumarmaths.weebly.com 1 Co-ordinate Geometry A parametric equation of a curve is one which does not give the relationship between
Edexcel Core Mathematics 4 Parametric equations. Edited by: K V Kumaran kumarmaths.weebly.com 1 Co-ordinate Geometry A parametric equation of a curve is one which does not give the relationship between
HIGHER SCHOOL CERTIFICATE EXAMINATION MATHEMATICS 3 UNIT (ADDITIONAL) AND 3/4 UNIT (COMMON) Time allowed Two hours (Plus 5 minutes reading time)
 HIGHER SCHOOL CERTIFICATE EXAMINATION 000 MATHEMATICS UNIT (ADDITIONAL) AND /4 UNIT (COMMON) Time allowed Two hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions. ALL questions
HIGHER SCHOOL CERTIFICATE EXAMINATION 000 MATHEMATICS UNIT (ADDITIONAL) AND /4 UNIT (COMMON) Time allowed Two hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions. ALL questions
) z r θ ( ) ( ) ( ) = then. Complete Solutions to Examination Questions Complete Solutions to Examination Questions 10.
 Complete Solutions to Examination Questions 0 Complete Solutions to Examination Questions 0. (i We need to determine + given + j, j: + + j + j (ii The product ( ( + j6 + 6 j 8 + j is given by ( + j( j
Complete Solutions to Examination Questions 0 Complete Solutions to Examination Questions 0. (i We need to determine + given + j, j: + + j + j (ii The product ( ( + j6 + 6 j 8 + j is given by ( + j( j
Mark Scheme (Results) June GCE Further Pure FP2 (6668) Paper 1
 Mark (Results) June 0 GCE Further Pure FP (6668) Paper Edexcel is one of the leading examining and awarding bodies in the UK and throughout the world. We provide a wide range of qualifications including
Mark (Results) June 0 GCE Further Pure FP (6668) Paper Edexcel is one of the leading examining and awarding bodies in the UK and throughout the world. We provide a wide range of qualifications including
Edexcel past paper questions. Core Mathematics 4. Parametric Equations
 Edexcel past paper questions Core Mathematics 4 Parametric Equations Edited by: K V Kumaran Email: kvkumaran@gmail.com C4 Maths Parametric equations Page 1 Co-ordinate Geometry A parametric equation of
Edexcel past paper questions Core Mathematics 4 Parametric Equations Edited by: K V Kumaran Email: kvkumaran@gmail.com C4 Maths Parametric equations Page 1 Co-ordinate Geometry A parametric equation of
PRACTICE PAPER 6 SOLUTIONS
 PRACTICE PAPER 6 SOLUTIONS SECTION A I.. Find the value of k if the points (, ) and (k, 3) are conjugate points with respect to the circle + y 5 + 8y + 6. Sol. Equation of the circle is + y 5 + 8y + 6
PRACTICE PAPER 6 SOLUTIONS SECTION A I.. Find the value of k if the points (, ) and (k, 3) are conjugate points with respect to the circle + y 5 + 8y + 6. Sol. Equation of the circle is + y 5 + 8y + 6
SPECIALIST MATHEMATICS
 Victorian Certificate of Education 06 SUPERVISOR TO ATTACH PROCESSING LABEL HERE Letter STUDENT NUMBER SPECIALIST MATHEMATICS Section Written examination Monday 7 November 06 Reading time:.5 am to.00 noon
Victorian Certificate of Education 06 SUPERVISOR TO ATTACH PROCESSING LABEL HERE Letter STUDENT NUMBER SPECIALIST MATHEMATICS Section Written examination Monday 7 November 06 Reading time:.5 am to.00 noon
or i 2 = -1 i 4 = 1 Example : ( i ),, 7 i and 0 are complex numbers. and Imaginary part of z = b or img z = b
 1 A- LEVEL MATHEMATICS P 3 Complex Numbers (NOTES) 1. Given a quadratic equation : x 2 + 1 = 0 or ( x 2 = -1 ) has no solution in the set of real numbers, as there does not exist any real number whose
1 A- LEVEL MATHEMATICS P 3 Complex Numbers (NOTES) 1. Given a quadratic equation : x 2 + 1 = 0 or ( x 2 = -1 ) has no solution in the set of real numbers, as there does not exist any real number whose
2013 HSC Mathematics Extension 2 Marking Guidelines
 3 HSC Mathematics Extension Marking Guidelines Section I Multiple-choice Answer Key Question Answer B A 3 D 4 A 5 B 6 D 7 C 8 C 9 B A 3 HSC Mathematics Extension Marking Guidelines Section II Question
3 HSC Mathematics Extension Marking Guidelines Section I Multiple-choice Answer Key Question Answer B A 3 D 4 A 5 B 6 D 7 C 8 C 9 B A 3 HSC Mathematics Extension Marking Guidelines Section II Question
12 th Class Mathematics Paper
 th Class Mathematics Paper Maimum Time: hours Maimum Marks: 00 General Instructions: (i) All questions are compulsory. (ii) The question paper consists of 9 questions divided into four sections A, B, C
th Class Mathematics Paper Maimum Time: hours Maimum Marks: 00 General Instructions: (i) All questions are compulsory. (ii) The question paper consists of 9 questions divided into four sections A, B, C
Methods in differential equations mixed exercise 7
 Methos in ifferential equations mie eercise 7 tan lnsec The integrating factor is e = e = sec Multiplying the equation by this factor gives: sec + ysectan= sec ( sec sec y = y sec= sec = tan+ c y= sin+
Methos in ifferential equations mie eercise 7 tan lnsec The integrating factor is e = e = sec Multiplying the equation by this factor gives: sec + ysectan= sec ( sec sec y = y sec= sec = tan+ c y= sin+
Calculus III. Exam 2
 Calculus III Math 143 Spring 011 Professor Ben Richert Exam Solutions Problem 1. (0pts) Computational mishmash. For this problem (and only this problem), you are not required to supply any English explanation.
Calculus III Math 143 Spring 011 Professor Ben Richert Exam Solutions Problem 1. (0pts) Computational mishmash. For this problem (and only this problem), you are not required to supply any English explanation.
A-LEVEL Mathematics. Further Pure 2 MFP2 Mark scheme June Version/Stage: Final
 A-LEVEL Mathematics Further Pure MFP Mark scheme 660 June 04 Version/Stage: Final Mark schemes are prepared by the Lead Assessment Writer and considered, together with the relevant questions, by a panel
A-LEVEL Mathematics Further Pure MFP Mark scheme 660 June 04 Version/Stage: Final Mark schemes are prepared by the Lead Assessment Writer and considered, together with the relevant questions, by a panel
z = a + ib (4.1) i 2 = 1. (4.2) <(z) = a, (4.3) =(z) = b. (4.4)
 Chapter 4 Complex Numbers 4.1 Definition of Complex Numbers A complex number is a number of the form where a and b are real numbers and i has the property that z a + ib (4.1) i 2 1. (4.2) a is called the
Chapter 4 Complex Numbers 4.1 Definition of Complex Numbers A complex number is a number of the form where a and b are real numbers and i has the property that z a + ib (4.1) i 2 1. (4.2) a is called the
Math 263 Final. (b) The cross product is. i j k c. =< c 1, 1, 1 >
 Math 63 Final Problem 1: [ points, 5 points to each part] Given the points P : (1, 1, 1), Q : (1,, ), R : (,, c 1), where c is a parameter, find (a) the vector equation of the line through P and Q. (b)
Math 63 Final Problem 1: [ points, 5 points to each part] Given the points P : (1, 1, 1), Q : (1,, ), R : (,, c 1), where c is a parameter, find (a) the vector equation of the line through P and Q. (b)
FURTHER MATHEMATICS A2/FM/CP1 A LEVEL CORE PURE 1
 Surname Other Names Candidate Signature Centre Number Candidate Number Examiner Comments Total Marks FURTHER MATHEMATICS A LEVEL CORE PURE 1 CM Bronze Set A (Edexcel Version) Time allowed: 1 hour and 30
Surname Other Names Candidate Signature Centre Number Candidate Number Examiner Comments Total Marks FURTHER MATHEMATICS A LEVEL CORE PURE 1 CM Bronze Set A (Edexcel Version) Time allowed: 1 hour and 30
A Level Maths. Bronze Set B, Paper 1 (Edexcel version) 2018 crashmaths Limited
 A Level Maths Bronze Set B, Paper (Edexcel version) 08 crashmaths Limited A Level Maths CM Practice Paper (for Edexcel) / Bronze Set B Question Solution Partial Marks Guidance dy dx = x x e x oe Method
A Level Maths Bronze Set B, Paper (Edexcel version) 08 crashmaths Limited A Level Maths CM Practice Paper (for Edexcel) / Bronze Set B Question Solution Partial Marks Guidance dy dx = x x e x oe Method
2017 HSC Mathematics Extension 2 Marking Guidelines
 07 HSC Mathematics Etension Marking Guidelines Section I Multiple-choice Answer Key Question Answer C B 3 D 4 C 5 B 6 A 7 A 8 B 9 C 0 B NESA 07 HSC Mathematics Etension Sample Answers Section II Question
07 HSC Mathematics Etension Marking Guidelines Section I Multiple-choice Answer Key Question Answer C B 3 D 4 C 5 B 6 A 7 A 8 B 9 C 0 B NESA 07 HSC Mathematics Etension Sample Answers Section II Question
National Quali cations AHEXEMPLAR PAPER ONLY
 National Quali cations AHEXEMPLAR PAPER ONLY EP/AH/0 Mathematics Date Not applicable Duration hours Total marks 00 Attempt ALL questions. You may use a calculator. Full credit will be given only to solutions
National Quali cations AHEXEMPLAR PAPER ONLY EP/AH/0 Mathematics Date Not applicable Duration hours Total marks 00 Attempt ALL questions. You may use a calculator. Full credit will be given only to solutions
Rotation of Axes. By: OpenStaxCollege
 Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
Mathematics Extension 2
 00 HIGHER SCHOOL CERTIFICATE TRIAL EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Approved scientific calculators and templates
00 HIGHER SCHOOL CERTIFICATE TRIAL EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Approved scientific calculators and templates
Power Series. x n. Using the ratio test. n n + 1. x n+1 n 3. = lim x. lim n + 1. = 1 < x < 1. Then r = 1 and I = ( 1, 1) ( 1) n 1 x n.
 .8 Power Series. n x n x n n Using the ratio test. lim x n+ n n + lim x n n + so r and I (, ). By the ratio test. n Then r and I (, ). n x < ( ) n x n < x < n lim x n+ n (n + ) x n lim xn n (n + ) x
.8 Power Series. n x n x n n Using the ratio test. lim x n+ n n + lim x n n + so r and I (, ). By the ratio test. n Then r and I (, ). n x < ( ) n x n < x < n lim x n+ n (n + ) x n lim xn n (n + ) x
MTH 234 Exam 1 February 20th, Without fully opening the exam, check that you have pages 1 through 11.
 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 11. Show all your work on the standard
Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 11. Show all your work on the standard
Extra FP3 past paper - A
 Mark schemes for these "Extra FP3" papers at https://mathsmartinthomas.files.wordpress.com/04//extra_fp3_markscheme.pdf Extra FP3 past paper - A More FP3 practice papers, with mark schemes, compiled from
Mark schemes for these "Extra FP3" papers at https://mathsmartinthomas.files.wordpress.com/04//extra_fp3_markscheme.pdf Extra FP3 past paper - A More FP3 practice papers, with mark schemes, compiled from
Review Exercise 2. , æ. ç ø. ç ø. ç ø. ç ø. = -0.27, 0 x 2p. 1 Crosses y-axis when x = 0 at sin 3p 4 = 1 2. ö ø. æ Crosses x-axis when sin x + 3p è
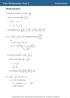 Review Exercise 1 Crosses y-axis when x 0 at sin p 4 1 Crosses x-axis when sin x + p 4 ö 0 x + p 4 -p, 0, p, p x - 7p 4, - p 4, p 4, 5p 4 So coordinates are 0, 1 ö, - 7p 4,0 ö, - p 4,0 ö, p 4,0 ö, 5p 4,0
Review Exercise 1 Crosses y-axis when x 0 at sin p 4 1 Crosses x-axis when sin x + p 4 ö 0 x + p 4 -p, 0, p, p x - 7p 4, - p 4, p 4, 5p 4 So coordinates are 0, 1 ö, - 7p 4,0 ö, - p 4,0 ö, p 4,0 ö, 5p 4,0
Trigonometry and modelling 7E
 Trigonometry and modelling 7E sinq +cosq º sinq cosa + cosq sina Comparing sin : cos Comparing cos : sin Divide the equations: sin tan cos Square and add the equations: cos sin (cos sin ) since cos sin
Trigonometry and modelling 7E sinq +cosq º sinq cosa + cosq sina Comparing sin : cos Comparing cos : sin Divide the equations: sin tan cos Square and add the equations: cos sin (cos sin ) since cos sin
MTH 362: Advanced Engineering Mathematics
 MTH 362: Advanced Engineering Mathematics Lecture 1 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 7, 2017 Course Name and number: MTH 362: Advanced Engineering
MTH 362: Advanced Engineering Mathematics Lecture 1 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 7, 2017 Course Name and number: MTH 362: Advanced Engineering
