Review Exercise 2. 1 a Chemical A 5x+ Chemical B 2x+ 2y12 [ x+ Chemical C [ 4 12]
|
|
|
- Louisa Hensley
- 5 years ago
- Views:
Transcription
1 Review Exercise a Chemical A 5x+ y 0 Chemical B x+ y [ x+ y 6] b Chemical C 6 [ ] x+ y x+ y x, y 0 c T = x+ y d ( x, y) = (, ) T = Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
2 a Maximise P= 00x+ 500y b Finishing.5x+ y56 x+ 8y (o.e.) Packing x+ y0 x+ y 0 (o.e.) c d For example, point testing Test all corner points in feasible region. Find profit at each and select point yielding maximum. profit line Draw profit lines. Select point on profit line furthest from the origin. e Using a correct, complete method. Making 6 Oxford and York gives a profit = 500 integer (6, ) 500 (.,.) (, ) 00 (6, 0) 800 (0, 0) 5000 f The line.5x+ y = 9 passes through (6, ) so reduce finishing by hours. Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
3 a Objective: maximise P= 0x+ 0 y (or P= 0.x+ 0. y ) subject to: x+ y00 x+ y500 0 x ( x+ y ) xy 00 x 0 ( x+ y ) x y 00 x, y 0 b c Visible use of objective line method objective line drawn or vertex testing all vertices tested Vertex testing (0, 60) 600 (80, 0) 00 (00, 00) (00, 00) 8000 Intersection of y= x and x+ y = 500 (00, 00) profit 90 (or 9000 p) Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
4 a b Visible use of objective line method objective line drawn or vertex testing. 5, 5 8, (, 8) 8(, 6) Optimal point, 6 with value 5 6 c Visible use of objective line method objective line drawn, or vertex testing all vertices tested. 5, 6 8, not an integer try (, ) 0 (, 8) 8 not an integer try (8, ) (, 6) Optimal point (8, ) with value, so Becky should use kg of bird feeder and.5 kg of bird table food. Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
5 5 a Objective: maximise P= 0.x+ 0. y ( P= 0x+ 0 y ) subject to: x6.5 y8 x+ y yx x, y0 b Visible use of objective line method objective line drawn (e.g. from (, 0) to (0, )) or all 5 points tested. vertex testing (0, 0) 0;(, 8).;(, 8).;(6.5, 5.5).;(6.5, 0).6 [ ] Optimal point is (6.5, 5.5) type X and 5500 type Y c P = 0.(6500) + 0.(5500) = 00 Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 5
6 6 a Maximise P = 50x + 80y + 60z Subject to x+ y+ z 0 x+ y+ z0 x+ y+ z50 where x, y, z 0 b Initialising tableau b.v. x y z r s t value r s t P Choose correct pivot, divide R by State correct row operation R R, R R, R + 80R, R c The solution found after one iteration has a slack of 0 units of black per day d i b.v. x y z r s t value r y t P (given) b.v. x y z r s t value z R y R R t R no change P R + 0R ii Not optimal, as there is a negative value in profit row iii x= 0 y= 6 z = 6 P=. r= 0, s= 0, t = 0 Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 6
7 a Objective: Maximise P= x+ 5y+ z Subject to x+ y+ z 5 x+ y+ z0 b x+ y+ z b.v. x y z r s r s 0 0 y 0 0 P t value R R R R 6 R 5 0 R + 5R b.v. x y z r s 5 x 0 0 s y P P= x=, y=, z = 0 t value R R + R R R R + R c There is some slack on s, so do not increase blending: therefore increase Processing and Packing which are both at their limit at present. Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
8 8 a x+ y+ z b i x+ y+ z+ s = ii s ( 0) is the slack time on the machine in hours c euro d b.v. x y z r s value r 0 R 6R z 0 6 R P R + R b.v. x y z t s value y 0 R 5 5 z 0 R R 8 8 P 0 0 R + R Profit = euros y = z =.5 x = r = s = 0 e Cannot make a lamp f e.g. (0, 0, 0) or (0, 6, ) or (,, ) checks in both inequalities Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 8
9 9 a Small (x) Board (m) Time (R) 0 Medium (y) 0 0 Large (z) 5 50 Available Board Time x+ y+ z x+ y+ 6z0 0x+ 0y+ 50z000 x+ y+ 5z00 b P= 0x+ 0y+ 8z c b.v. x y z r s values r s P θ = 0, θ = 50; pivot d Row b.v. x y z r s value operation y 0 0 R s 0 0 R R P R + 0R θ = 0, θ = 80;pivot Row b.v. x y z r s value operation y 0 0 R R x 0 80 R P R + 5R e This tableau is optimal as there are no negative numbers in the profit line. f Small 80, medium 0; large 0 Profit 000 Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 9
10 0 a The constraints include a mixture of and variables. b x + y + z + s = 0 x + y + z + s = 5 x + y + z s + a = c The purpose is to maximise I = a which =x+ y+ zs So Ixy z+ s = This gives the final row of the tableau. d The smallest value in the bottom row is and the smallest θ value is a (6) so this is the pivot and we obtain: b.v. x y z s s s a value s s x P I e There are no negative values in the bottom row, so the optimal value of I is 0 when a = 0 f There is a negative value in the bottom row. g b.v. x y z s s s Value z 0 0 y 0 0 x 0 0 P The maximum value of P is 0 = 6 which occurs when x = 5, y=, z=, s = s = s = Row operation R R R R R R+ R Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 0
11 a x + y + z + s = 8 x + y + z s + a = 6 x + 5y + z s + a = 0 b New objective is maximise I = (a + a ) a = x + y + z s 6 a = x + 5y + z s 0 In terms of non-basic variables, the new objective is maximise I = 5x + 6y + z s s 6 c b.v. x y z s s s a a value s a a P I d st iteration Pivot is y-column a row Row b.v. x y z s s s a a Value operation s R R 5 a R R 5 y R 6 P R R I R5 + R nd iteration Pivot is x column a row Row b.v. x y z s s s a a Value operation s R R x R y R R P R + R I R5+ R Basic feasible solution is x= 0, y=, z= 0, s 8 =, s = s = a = a = 0 Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
12 a x + y + z + s = 5x + y + z + s = 60 x s + a = b P = x + y + z Ma = x + y + z M( x + s ) P = x( + M) + y + z M Ms P ( + M)x y z + Ms = M c b.v. x y z s s s a value s s a P ( + M) 0 0 M 0 M d The most negative value in the P row is in the x-column so, in the first iteration, x enters the basic variables. e st iteration x column a row is the pivot b.v. x y z s s s a Value Row operation s R R s R 5R x P ( + M) R+ ( + M) R nd iteration z column s row is the pivot b.v. x y z s s s a Value Row operation z s 0 0 R R x P M R+ R All entries in the P row are non-negative so the tableau represents the optimal solution. x =, y = 0, z = 8, s = 0, s =, s = 0, a = 0 Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
13 a x + y + z + s = 6 x + z + s = 5 x + y s + a = 0 b Maximise P = x + y z Ma = x + y z M(0 x y + s ) = x(m ) + y(m + ) z 0M Ms Rearranging gives P (M )x (M + )y + z + Ms = 0M c b.v. x y z s s s a value s s a P (M ) (M + ) 0 0 M 0 0M d st iteration y column a row is the pivot b.v. x y z s s s a Value Row operation s R R s y P M + 0 R + ( M + ) R nd iteration s column s row is the pivot Row b.v. x y z s s s a Value operation s 0 0 R s y R + R P M 6 R+ R Maximum value of P = 6 Minimum value of C = 6 This occurs when x = 0, y =, z = 0, s = 0, s = 5, s = Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
14 5 a 6 a b Here we have that I and J depend only on E, whereas H depends on C, D, E and F. Hence we need separate nodes with a dummy. b D will only be critical if it lies on the longest path Path A to G Length A B E G A C F G 5 A C D E G + x So we need + x to be the longest, or equal longest +x5 x Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
15 a b Total float on A = = 5 Total float on H = 9 = Total float on B = = 0 Total float on I = 9 = 0 Total float on C = 0 = Total float on J = 5 8 = Total float on D = = Total float on K = 5 = 0 Total float on E = 0 0 = Total float on L = 5 8 = 0 Total float on F = = 0 Total float on M = 5 = 9 Total float on G = 8 = c Critical activities: B, F, I, K and L length of critical path is 5 days d New critical path is B F H L length of new critical path is 6 days 8 a x = 0 y = [latest out of ( + ) and (5 + )] z = 9 [Earliest out of ( ) and (9 ) and (6 )] b Length is Critical activities: B, D, E and L c i Total float on N = = 5 ii Total float on H = 6 5 = 8 Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 5
16 9 a For example, it shows dependence but it is not an activity. G depends on A and C only but H and I depend on A, C and D. b c So B, C, E, F, I, J and L d Total float on A = 0 9 = Total float on H = 5 = Total float on D = = Total float on K = 5 6 = Total float on G =8 5 = e Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 6
17 0 a Critical activities are B, F, J, K and N length of critical path is 5 hours I is not critical. b Total float on A = 5 0 = Total float on H = 6 = Total float on C = = Total float on I = = Total float on D = = 5 Total float on L = = Total float on E = 9 = Total float on M = 6 = Total float on G = 9 = Total float on P = 5 8 = c a d Look at 6.5 in the chart in c. F, E and G b 6 days, workers c Delay the start of H until time d Activity H would have to take place on its own so the project will be delayed by at least days. Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
18 a b 8 days c ADFIKN d e workers f e.g. delay the start times of: E to time G to time H to time J to time 0 L to time M to time 6 Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 8
19 a b A, C, G, H, J, K and L All critical activities have a zero total float. c Total float = 5 = d Either 6 8 =.6 ( d.p.) so at least workers needed (here 6 is the total number of hours required for all the activities) or 69 hours into the project activities J, K, I and M must be happening so at least workers will be needed. e New shortest time is 89 hours. Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 9
20 a b Critical activities: A, C, F and H; length of critical path = c Total float on B = 0 5 = Total float on E = = Total float on D = 9 = Total float on G = 9 8 = d e For example; Minimum time for workers is days. Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free. 0
21 Challenge a Optimal values x = y = 5 b x =, y = P = x = 5, y = P = 5 c x =, y = P = d If the gradient of the objective line is similar to the gradient of a constraint that runs through the optimal vertex, then the optimal integer solution may not lie close to the optimal vertex. Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
22 Challenge We need to maximise D= x+ y z subject to the constraints x+ y+ z6 x+ z5 x+ y0 We rewrite these using slack, surplus and artificial variables to obtain: x+ y+ z+ s = 6 x+ z+ s = 5 x+ y s+ a = 0 The new objective function is: I = a = x+ ys 0 So Ix y+ s =0 So the initial tableau is: b.v. x y z s s s a Value s s a D I Both the x and y columns have the same value in the I row. But sin the x-column has the smallest θ value (9) so we use that as the pivot. We then obtain: b.v. x y z s s Row s a Value operation x R s 0 R R a 0 5 R R D 0 9 R R I R5 + R Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
23 Challenge continued The y-column still has a negative value in the I row and only the x-row has a positive θ value so we need to use that as the pivot giving. Row b.v. x y z s s s a Value operation y R s R+ R a R+ 5R D R+ 6R I R5 + R There are now no negative entries in the bottom two rows so we have reached the optimal solution: y =, x = z = 0 and C = 6 Pearson Education Ltd 08. Copying permitted for purchasing institution only. This material is not copyright free.
Slide 1 Math 1520, Lecture 10
 Slide 1 Math 1520, Lecture 10 In this lecture, we study the simplex method which is a powerful method for solving maximization/minimization problems developed in the late 1940 s. It has been implemented
Slide 1 Math 1520, Lecture 10 In this lecture, we study the simplex method which is a powerful method for solving maximization/minimization problems developed in the late 1940 s. It has been implemented
Standard Form An LP is in standard form when: All variables are non-negativenegative All constraints are equalities Putting an LP formulation into sta
 Chapter 4 Linear Programming: The Simplex Method An Overview of the Simplex Method Standard Form Tableau Form Setting Up the Initial Simplex Tableau Improving the Solution Calculating the Next Tableau
Chapter 4 Linear Programming: The Simplex Method An Overview of the Simplex Method Standard Form Tableau Form Setting Up the Initial Simplex Tableau Improving the Solution Calculating the Next Tableau
4.3 Minimizing & Mixed Constraints
 Mathematics : Mattingly, Fall 6 8 4. Minimizing & Mixed Constraints So far, you have seen how to solve one type of problem: Standard Maximum. The objective function is to be maximized.. Constraints use..
Mathematics : Mattingly, Fall 6 8 4. Minimizing & Mixed Constraints So far, you have seen how to solve one type of problem: Standard Maximum. The objective function is to be maximized.. Constraints use..
Moments Mixed exercise 4
 Moments Mixed exercise 4 1 a The plank is in equilibrium. Let the reaction forces at the supports be R and R D. Considering moments about point D: R (6 1.5 1) = (100+ 145) (3 1.5) 3.5R = 245 1.5 3.5R =
Moments Mixed exercise 4 1 a The plank is in equilibrium. Let the reaction forces at the supports be R and R D. Considering moments about point D: R (6 1.5 1) = (100+ 145) (3 1.5) 3.5R = 245 1.5 3.5R =
Decision Mathematics D1 (6689) Practice paper A mark scheme
 Decision Mathematics D1 (6689) Practice paper A mark scheme 1. e.g. C 2 = A 5 = E 4 cs C = 2 A = 5 E = 4 M1 F 1 = B 3 = D 6 cs F = 1 B = 3 D = 6 M1 A =1, B = 3, C = 2, D = 6, E = 4, F = 1 (5) (5 marks)
Decision Mathematics D1 (6689) Practice paper A mark scheme 1. e.g. C 2 = A 5 = E 4 cs C = 2 A = 5 E = 4 M1 F 1 = B 3 = D 6 cs F = 1 B = 3 D = 6 M1 A =1, B = 3, C = 2, D = 6, E = 4, F = 1 (5) (5 marks)
Proof by induction ME 8
 Proof by induction ME 8 n Let f ( n) 9, where n. f () 9 8, which is divisible by 8. f ( n) is divisible by 8 when n =. Assume that for n =, f ( ) 9 is divisible by 8 for. f ( ) 9 9.9 9(9 ) f ( ) f ( )
Proof by induction ME 8 n Let f ( n) 9, where n. f () 9 8, which is divisible by 8. f ( n) is divisible by 8 when n =. Assume that for n =, f ( ) 9 is divisible by 8 for. f ( ) 9 9.9 9(9 ) f ( ) f ( )
Decision Mathematics D1
 Pearson Edexcel International Advanced Level Decision Mathematics D1 Advanced/Advanced Subsidiary Friday 17 June 016 Afternoon Time: 1 hour 30 minutes Paper Reference WDM01/01 You must have: D1 Answer
Pearson Edexcel International Advanced Level Decision Mathematics D1 Advanced/Advanced Subsidiary Friday 17 June 016 Afternoon Time: 1 hour 30 minutes Paper Reference WDM01/01 You must have: D1 Answer
Mark scheme Pure Mathematics Year 1 (AS) Unit Test 2: Coordinate geometry in the (x, y) plane
 Mark scheme Pure Mathematics Year 1 (AS) Unit Test : Coordinate in the (x, y) plane Q Scheme Marks AOs Pearson 1a Use of the gradient formula to begin attempt to find k. k 1 ( ) or 1 (k 4) ( k 1) (i.e.
Mark scheme Pure Mathematics Year 1 (AS) Unit Test : Coordinate in the (x, y) plane Q Scheme Marks AOs Pearson 1a Use of the gradient formula to begin attempt to find k. k 1 ( ) or 1 (k 4) ( k 1) (i.e.
1. Introduce slack variables for each inequaility to make them equations and rewrite the objective function in the form ax by cz... + P = 0.
 3.4 Simplex Method If a linear programming problem has more than 2 variables, solving graphically is not the way to go. Instead, we ll use a more methodical, numeric process called the Simplex Method.
3.4 Simplex Method If a linear programming problem has more than 2 variables, solving graphically is not the way to go. Instead, we ll use a more methodical, numeric process called the Simplex Method.
Mathematics (JAN12MD0201) General Certificate of Education Advanced Level Examination January Unit Decision TOTAL.
 Centre Number Candidate Number For Examiner s Use Surname Other Names Candidate Signature Examiner s Initials Mathematics Unit Decision 2 Wednesday 25 January 2012 General Certificate of Education Advanced
Centre Number Candidate Number For Examiner s Use Surname Other Names Candidate Signature Examiner s Initials Mathematics Unit Decision 2 Wednesday 25 January 2012 General Certificate of Education Advanced
Decision Mathematics D1
 Pearson Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Friday 16 June 2017 Afternoon Time: 1 hour 30 minutes Paper Reference 6689/01 You must have: D1 Answer Book Candidates may use any
Pearson Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Friday 16 June 2017 Afternoon Time: 1 hour 30 minutes Paper Reference 6689/01 You must have: D1 Answer Book Candidates may use any
Review exercise 2. 1 The equation of the line is: = 5 a The gradient of l1 is 3. y y x x. So the gradient of l2 is. The equation of line l2 is: y =
 Review exercise The equation of the line is: y y x x y y x x y 8 x+ 6 8 + y 8 x+ 6 y x x + y 0 y ( ) ( x 9) y+ ( x 9) y+ x 9 x y 0 a, b, c Using points A and B: y y x x y y x x y x 0 k 0 y x k ky k x a
Review exercise The equation of the line is: y y x x y y x x y 8 x+ 6 8 + y 8 x+ 6 y x x + y 0 y ( ) ( x 9) y+ ( x 9) y+ x 9 x y 0 a, b, c Using points A and B: y y x x y y x x y x 0 k 0 y x k ky k x a
Slack Variable. Max Z= 3x 1 + 4x 2 + 5X 3. Subject to: X 1 + X 2 + X x 1 + 4x 2 + X X 1 + X 2 + 4X 3 10 X 1 0, X 2 0, X 3 0
 Simplex Method Slack Variable Max Z= 3x 1 + 4x 2 + 5X 3 Subject to: X 1 + X 2 + X 3 20 3x 1 + 4x 2 + X 3 15 2X 1 + X 2 + 4X 3 10 X 1 0, X 2 0, X 3 0 Standard Form Max Z= 3x 1 +4x 2 +5X 3 + 0S 1 + 0S 2
Simplex Method Slack Variable Max Z= 3x 1 + 4x 2 + 5X 3 Subject to: X 1 + X 2 + X 3 20 3x 1 + 4x 2 + X 3 15 2X 1 + X 2 + 4X 3 10 X 1 0, X 2 0, X 3 0 Standard Form Max Z= 3x 1 +4x 2 +5X 3 + 0S 1 + 0S 2
Core Mathematics C1 (AS) Unit C1
 Core Mathematics C1 (AS) Unit C1 Algebraic manipulation of polynomials, including expanding brackets and collecting like terms, factorisation. Graphs of functions; sketching curves defined by simple equations.
Core Mathematics C1 (AS) Unit C1 Algebraic manipulation of polynomials, including expanding brackets and collecting like terms, factorisation. Graphs of functions; sketching curves defined by simple equations.
UNIT-4 Chapter6 Linear Programming
 UNIT-4 Chapter6 Linear Programming Linear Programming 6.1 Introduction Operations Research is a scientific approach to problem solving for executive management. It came into existence in England during
UNIT-4 Chapter6 Linear Programming Linear Programming 6.1 Introduction Operations Research is a scientific approach to problem solving for executive management. It came into existence in England during
Math 354 Summer 2004 Solutions to review problems for Midterm #1
 Solutions to review problems for Midterm #1 First: Midterm #1 covers Chapter 1 and 2. In particular, this means that it does not explicitly cover linear algebra. Also, I promise there will not be any proofs.
Solutions to review problems for Midterm #1 First: Midterm #1 covers Chapter 1 and 2. In particular, this means that it does not explicitly cover linear algebra. Also, I promise there will not be any proofs.
Pearson Edexcel GCE Decision Mathematics D2. Advanced/Advanced Subsidiary
 Pearson Edexcel GCE Decision Mathematics D2 Advanced/Advanced Subsidiary Friday 23 June 2017 Morning Time: 1 hour 30 minutes Paper Reference 6690/01 You must have: D2 Answer Book Candidates may use any
Pearson Edexcel GCE Decision Mathematics D2 Advanced/Advanced Subsidiary Friday 23 June 2017 Morning Time: 1 hour 30 minutes Paper Reference 6690/01 You must have: D2 Answer Book Candidates may use any
Decision Mathematics D1
 Pearson Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Friday 17 June 2016 Afternoon Time: 1 hour 30 minutes Paper Reference 6689/01 You must have: D1 Answer Book Candidates may use any
Pearson Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Friday 17 June 2016 Afternoon Time: 1 hour 30 minutes Paper Reference 6689/01 You must have: D1 Answer Book Candidates may use any
Summary of the simplex method
 MVE165/MMG631,Linear and integer optimization with applications The simplex method: degeneracy; unbounded solutions; starting solutions; infeasibility; alternative optimal solutions Ann-Brith Strömberg
MVE165/MMG631,Linear and integer optimization with applications The simplex method: degeneracy; unbounded solutions; starting solutions; infeasibility; alternative optimal solutions Ann-Brith Strömberg
Professor Alan H. Stein October 31, 2007
 Mathematics 05 Professor Alan H. Stein October 3, 2007 SOLUTIONS. For most maximum problems, the contraints are in the form l(x) k, where l(x) is a linear polynomial and k is a positive constant. Explain
Mathematics 05 Professor Alan H. Stein October 3, 2007 SOLUTIONS. For most maximum problems, the contraints are in the form l(x) k, where l(x) is a linear polynomial and k is a positive constant. Explain
The Simplex Method of Linear Programming
 The Simplex Method of Linear Programming Online Tutorial 3 Tutorial Outline CONVERTING THE CONSTRAINTS TO EQUATIONS SETTING UP THE FIRST SIMPLEX TABLEAU SIMPLEX SOLUTION PROCEDURES SUMMARY OF SIMPLEX STEPS
The Simplex Method of Linear Programming Online Tutorial 3 Tutorial Outline CONVERTING THE CONSTRAINTS TO EQUATIONS SETTING UP THE FIRST SIMPLEX TABLEAU SIMPLEX SOLUTION PROCEDURES SUMMARY OF SIMPLEX STEPS
Example. 1 Rows 1,..., m of the simplex tableau remain lexicographically positive
 3.4 Anticycling Lexicographic order In this section we discuss two pivoting rules that are guaranteed to avoid cycling. These are the lexicographic rule and Bland s rule. Definition A vector u R n is lexicographically
3.4 Anticycling Lexicographic order In this section we discuss two pivoting rules that are guaranteed to avoid cycling. These are the lexicographic rule and Bland s rule. Definition A vector u R n is lexicographically
Systems Analysis in Construction
 Systems Analysis in Construction CB312 Construction & Building Engineering Department- AASTMT by A h m e d E l h a k e e m & M o h a m e d S a i e d 3. Linear Programming Optimization Simplex Method 135
Systems Analysis in Construction CB312 Construction & Building Engineering Department- AASTMT by A h m e d E l h a k e e m & M o h a m e d S a i e d 3. Linear Programming Optimization Simplex Method 135
Prelude to the Simplex Algorithm. The Algebraic Approach The search for extreme point solutions.
 Prelude to the Simplex Algorithm The Algebraic Approach The search for extreme point solutions. 1 Linear Programming-1 x 2 12 8 (4,8) Max z = 6x 1 + 4x 2 Subj. to: x 1 + x 2
Prelude to the Simplex Algorithm The Algebraic Approach The search for extreme point solutions. 1 Linear Programming-1 x 2 12 8 (4,8) Max z = 6x 1 + 4x 2 Subj. to: x 1 + x 2
MATH2070 Optimisation
 MATH2070 Optimisation Linear Programming Semester 2, 2012 Lecturer: I.W. Guo Lecture slides courtesy of J.R. Wishart Review The standard Linear Programming (LP) Problem Graphical method of solving LP problem
MATH2070 Optimisation Linear Programming Semester 2, 2012 Lecturer: I.W. Guo Lecture slides courtesy of J.R. Wishart Review The standard Linear Programming (LP) Problem Graphical method of solving LP problem
Dr. S. Bourazza Math-473 Jazan University Department of Mathematics
 Dr. Said Bourazza Department of Mathematics Jazan University 1 P a g e Contents: Chapter 0: Modelization 3 Chapter1: Graphical Methods 7 Chapter2: Simplex method 13 Chapter3: Duality 36 Chapter4: Transportation
Dr. Said Bourazza Department of Mathematics Jazan University 1 P a g e Contents: Chapter 0: Modelization 3 Chapter1: Graphical Methods 7 Chapter2: Simplex method 13 Chapter3: Duality 36 Chapter4: Transportation
b UVW is a right-angled triangle, therefore VW is the diameter of the circle. Centre of circle = Midpoint of VW = (8 2) + ( 2 6) = 100
 Circles 6F a U(, 8), V(7, 7) and W(, ) UV = ( x x ) ( y y ) = (7 ) (7 8) = 8 VW = ( 7) ( 7) = 64 UW = ( ) ( 8) = 8 Use Pythagoras' theorem to show UV UW = VW 8 8 = 64 = VW Therefore, UVW is a right-angled
Circles 6F a U(, 8), V(7, 7) and W(, ) UV = ( x x ) ( y y ) = (7 ) (7 8) = 8 VW = ( 7) ( 7) = 64 UW = ( ) ( 8) = 8 Use Pythagoras' theorem to show UV UW = VW 8 8 = 64 = VW Therefore, UVW is a right-angled
Chapter 4 The Simplex Algorithm Part I
 Chapter 4 The Simplex Algorithm Part I Based on Introduction to Mathematical Programming: Operations Research, Volume 1 4th edition, by Wayne L. Winston and Munirpallam Venkataramanan Lewis Ntaimo 1 Modeling
Chapter 4 The Simplex Algorithm Part I Based on Introduction to Mathematical Programming: Operations Research, Volume 1 4th edition, by Wayne L. Winston and Munirpallam Venkataramanan Lewis Ntaimo 1 Modeling
Non-Standard Constraints. Setting up Phase 1 Phase 2
 Non-Standard Constraints Setting up Phase 1 Phase 2 Maximizing with Mixed Constraints Some maximization problems contain mixed constraints, like this: maximize 3x 1 + 2x 2 subject to 2x 1 + x 2 50 (standard)
Non-Standard Constraints Setting up Phase 1 Phase 2 Maximizing with Mixed Constraints Some maximization problems contain mixed constraints, like this: maximize 3x 1 + 2x 2 subject to 2x 1 + x 2 50 (standard)
Lesson 27 Linear Programming; The Simplex Method
 Lesson Linear Programming; The Simplex Method Math 0 April 9, 006 Setup A standard linear programming problem is to maximize the quantity c x + c x +... c n x n = c T x subject to constraints a x + a x
Lesson Linear Programming; The Simplex Method Math 0 April 9, 006 Setup A standard linear programming problem is to maximize the quantity c x + c x +... c n x n = c T x subject to constraints a x + a x
Decision Mathematics D1 Advanced/Advanced Subsidiary. Tuesday 9 June 2015 Morning Time: 1 hour 30 minutes
 Paper Reference(s) 6689/01 Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Tuesday 9 June 2015 Morning Time: 1 hour 30 minutes Materials required for examination Nil Items included with
Paper Reference(s) 6689/01 Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Tuesday 9 June 2015 Morning Time: 1 hour 30 minutes Materials required for examination Nil Items included with
9 Mixed Exercise. vector equation is. 4 a
 9 Mixed Exercise a AB r i j k j k c OA AB 7 i j 7 k A7,, and B,,8 8 AB 6 A vector equation is 7 r x 7 y z (i j k) j k a x y z a a 7, Pearson Education Ltd 7. Copying permitted for purchasing institution
9 Mixed Exercise a AB r i j k j k c OA AB 7 i j 7 k A7,, and B,,8 8 AB 6 A vector equation is 7 r x 7 y z (i j k) j k a x y z a a 7, Pearson Education Ltd 7. Copying permitted for purchasing institution
DEPARTMENT OF STATISTICS AND OPERATIONS RESEARCH OPERATIONS RESEARCH DETERMINISTIC QUALIFYING EXAMINATION. Part I: Short Questions
 DEPARTMENT OF STATISTICS AND OPERATIONS RESEARCH OPERATIONS RESEARCH DETERMINISTIC QUALIFYING EXAMINATION Part I: Short Questions August 12, 2008 9:00 am - 12 pm General Instructions This examination is
DEPARTMENT OF STATISTICS AND OPERATIONS RESEARCH OPERATIONS RESEARCH DETERMINISTIC QUALIFYING EXAMINATION Part I: Short Questions August 12, 2008 9:00 am - 12 pm General Instructions This examination is
9.5 THE SIMPLEX METHOD: MIXED CONSTRAINTS
 SECTION 9.5 THE SIMPLEX METHOD: MIXED CONSTRAINTS 557 9.5 THE SIMPLEX METHOD: MIXED CONSTRAINTS In Sections 9. and 9., you looked at linear programming problems that occurred in standard form. The constraints
SECTION 9.5 THE SIMPLEX METHOD: MIXED CONSTRAINTS 557 9.5 THE SIMPLEX METHOD: MIXED CONSTRAINTS In Sections 9. and 9., you looked at linear programming problems that occurred in standard form. The constraints
Review Questions, Final Exam
 Review Questions, Final Exam A few general questions 1. What does the Representation Theorem say (in linear programming)? 2. What is the Fundamental Theorem of Linear Programming? 3. What is the main idea
Review Questions, Final Exam A few general questions 1. What does the Representation Theorem say (in linear programming)? 2. What is the Fundamental Theorem of Linear Programming? 3. What is the main idea
Pure Mathematics Year 1 (AS) Unit Test 1: Algebra and Functions
 Pure Mathematics Year (AS) Unit Test : Algebra and Functions Simplify 6 4, giving your answer in the form p 8 q, where p and q are positive rational numbers. f( x) x ( k 8) x (8k ) a Find the discriminant
Pure Mathematics Year (AS) Unit Test : Algebra and Functions Simplify 6 4, giving your answer in the form p 8 q, where p and q are positive rational numbers. f( x) x ( k 8) x (8k ) a Find the discriminant
min 4x 1 5x 2 + 3x 3 s.t. x 1 + 2x 2 + x 3 = 10 x 1 x 2 6 x 1 + 3x 2 + x 3 14
 The exam is three hours long and consists of 4 exercises. The exam is graded on a scale 0-25 points, and the points assigned to each question are indicated in parenthesis within the text. If necessary,
The exam is three hours long and consists of 4 exercises. The exam is graded on a scale 0-25 points, and the points assigned to each question are indicated in parenthesis within the text. If necessary,
April 2003 Mathematics 340 Name Page 2 of 12 pages
 April 2003 Mathematics 340 Name Page 2 of 12 pages Marks [8] 1. Consider the following tableau for a standard primal linear programming problem. z x 1 x 2 x 3 s 1 s 2 rhs 1 0 p 0 5 3 14 = z 0 1 q 0 1 0
April 2003 Mathematics 340 Name Page 2 of 12 pages Marks [8] 1. Consider the following tableau for a standard primal linear programming problem. z x 1 x 2 x 3 s 1 s 2 rhs 1 0 p 0 5 3 14 = z 0 1 q 0 1 0
Solutionbank Edexcel AS and A Level Modular Mathematics
 Page of Exercise A, Question The curve C, with equation y = x ln x, x > 0, has a stationary point P. Find, in terms of e, the coordinates of P. (7) y = x ln x, x > 0 Differentiate as a product: = x + x
Page of Exercise A, Question The curve C, with equation y = x ln x, x > 0, has a stationary point P. Find, in terms of e, the coordinates of P. (7) y = x ln x, x > 0 Differentiate as a product: = x + x
A-LEVEL Further Mathematics
 A-LEVEL Further Mathematics Discrete Mark scheme Specimen Version 1.1 Mark schemes are prepared by the Lead Assessment Writer and considered, together with the relevant questions, by a panel of subject
A-LEVEL Further Mathematics Discrete Mark scheme Specimen Version 1.1 Mark schemes are prepared by the Lead Assessment Writer and considered, together with the relevant questions, by a panel of subject
AM 121: Intro to Optimization
 AM 121: Intro to Optimization Models and Methods Lecture 6: Phase I, degeneracy, smallest subscript rule. Yiling Chen SEAS Lesson Plan Phase 1 (initialization) Degeneracy and cycling Smallest subscript
AM 121: Intro to Optimization Models and Methods Lecture 6: Phase I, degeneracy, smallest subscript rule. Yiling Chen SEAS Lesson Plan Phase 1 (initialization) Degeneracy and cycling Smallest subscript
Special cases of linear programming
 Special cases of linear programming Infeasible solution Multiple solution (infinitely many solution) Unbounded solution Degenerated solution Notes on the Simplex tableau 1. The intersection of any basic
Special cases of linear programming Infeasible solution Multiple solution (infinitely many solution) Unbounded solution Degenerated solution Notes on the Simplex tableau 1. The intersection of any basic
REVISION SHEET DECISION MATHS 2 DECISION ANALYSIS
 REVISION SHEET DECISION MATHS 2 DECISION ANALYSIS The main ideas are covered in AQA Edexcel MEI OCR D2 Before the exam you should know The meaning of the different kinds of node. Be able to construct a
REVISION SHEET DECISION MATHS 2 DECISION ANALYSIS The main ideas are covered in AQA Edexcel MEI OCR D2 Before the exam you should know The meaning of the different kinds of node. Be able to construct a
Decision Mathematics D1 Advanced/Advanced Subsidiary. Wednesday 23 January 2013 Morning Time: 1 hour 30 minutes
 Paper Reference(s) 6689/01 Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Wednesday 23 January 2013 Morning Time: 1 hour 30 minutes Materials required for examination Nil Items included
Paper Reference(s) 6689/01 Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Wednesday 23 January 2013 Morning Time: 1 hour 30 minutes Materials required for examination Nil Items included
LINEAR PROGRAMMING 2. In many business and policy making situations the following type of problem is encountered:
 LINEAR PROGRAMMING 2 In many business and policy making situations the following type of problem is encountered: Maximise an objective subject to (in)equality constraints. Mathematical programming provides
LINEAR PROGRAMMING 2 In many business and policy making situations the following type of problem is encountered: Maximise an objective subject to (in)equality constraints. Mathematical programming provides
Linear Programming II NOT EXAMINED
 Chapter 9 Linear Programming II NOT EXAMINED 9.1 Graphical solutions for two variable problems In last week s lecture we discussed how to formulate a linear programming problem; this week, we consider
Chapter 9 Linear Programming II NOT EXAMINED 9.1 Graphical solutions for two variable problems In last week s lecture we discussed how to formulate a linear programming problem; this week, we consider
Linear Programming and the Simplex method
 Linear Programming and the Simplex method Harald Enzinger, Michael Rath Signal Processing and Speech Communication Laboratory Jan 9, 2012 Harald Enzinger, Michael Rath Jan 9, 2012 page 1/37 Outline Introduction
Linear Programming and the Simplex method Harald Enzinger, Michael Rath Signal Processing and Speech Communication Laboratory Jan 9, 2012 Harald Enzinger, Michael Rath Jan 9, 2012 page 1/37 Outline Introduction
c) Place the Coefficients from all Equations into a Simplex Tableau, labeled above with variables indicating their respective columns
 BUILDING A SIMPLEX TABLEAU AND PROPER PIVOT SELECTION Maximize : 15x + 25y + 18 z s. t. 2x+ 3y+ 4z 60 4x+ 4y+ 2z 100 8x+ 5y 80 x 0, y 0, z 0 a) Build Equations out of each of the constraints above by introducing
BUILDING A SIMPLEX TABLEAU AND PROPER PIVOT SELECTION Maximize : 15x + 25y + 18 z s. t. 2x+ 3y+ 4z 60 4x+ 4y+ 2z 100 8x+ 5y 80 x 0, y 0, z 0 a) Build Equations out of each of the constraints above by introducing
Decision Mathematics D1
 Pearson Edexcel International Advanced Level Decision Mathematics D1 Advanced/Advanced Subsidiary Monday 1 February 2016 Afternoon Time: 1 hour 30 minutes Paper Reference WDM01/01 You must have: D1 Answer
Pearson Edexcel International Advanced Level Decision Mathematics D1 Advanced/Advanced Subsidiary Monday 1 February 2016 Afternoon Time: 1 hour 30 minutes Paper Reference WDM01/01 You must have: D1 Answer
1. Algebraic and geometric treatments Consider an LP problem in the standard form. x 0. Solutions to the system of linear equations
 The Simplex Method Most textbooks in mathematical optimization, especially linear programming, deal with the simplex method. In this note we study the simplex method. It requires basically elementary linear
The Simplex Method Most textbooks in mathematical optimization, especially linear programming, deal with the simplex method. In this note we study the simplex method. It requires basically elementary linear
Circles, Mixed Exercise 6
 Circles, Mixed Exercise 6 a QR is the diameter of the circle so the centre, C, is the midpoint of QR ( 5) 0 Midpoint = +, + = (, 6) C(, 6) b Radius = of diameter = of QR = of ( x x ) + ( y y ) = of ( 5
Circles, Mixed Exercise 6 a QR is the diameter of the circle so the centre, C, is the midpoint of QR ( 5) 0 Midpoint = +, + = (, 6) C(, 6) b Radius = of diameter = of QR = of ( x x ) + ( y y ) = of ( 5
Draft Version 1 Mark scheme Further Maths Core Pure (AS/Year 1) Unit Test 1: Complex numbers 1
 1 w z k k States or implies that 4 i TBC Uses the definition of argument to write 4 k π tan 1 k 4 Makes an attempt to solve for k, for example 4 + k = k is seen. M1.a Finds k = 6 (4 marks) Pearson Education
1 w z k k States or implies that 4 i TBC Uses the definition of argument to write 4 k π tan 1 k 4 Makes an attempt to solve for k, for example 4 + k = k is seen. M1.a Finds k = 6 (4 marks) Pearson Education
Section 4.1 Solving Systems of Linear Inequalities
 Section 4.1 Solving Systems of Linear Inequalities Question 1 How do you graph a linear inequality? Question 2 How do you graph a system of linear inequalities? Question 1 How do you graph a linear inequality?
Section 4.1 Solving Systems of Linear Inequalities Question 1 How do you graph a linear inequality? Question 2 How do you graph a system of linear inequalities? Question 1 How do you graph a linear inequality?
Chapter 1: Linear Programming
 Chapter 1: Linear Programming Math 368 c Copyright 2013 R Clark Robinson May 22, 2013 Chapter 1: Linear Programming 1 Max and Min For f : D R n R, f (D) = {f (x) : x D } is set of attainable values of
Chapter 1: Linear Programming Math 368 c Copyright 2013 R Clark Robinson May 22, 2013 Chapter 1: Linear Programming 1 Max and Min For f : D R n R, f (D) = {f (x) : x D } is set of attainable values of
Linear Programming, Lecture 4
 Linear Programming, Lecture 4 Corbett Redden October 3, 2016 Simplex Form Conventions Examples Simplex Method To run the simplex method, we start from a Linear Program (LP) in the following standard simplex
Linear Programming, Lecture 4 Corbett Redden October 3, 2016 Simplex Form Conventions Examples Simplex Method To run the simplex method, we start from a Linear Program (LP) in the following standard simplex
Ω R n is called the constraint set or feasible set. x 1
 1 Chapter 5 Linear Programming (LP) General constrained optimization problem: minimize subject to f(x) x Ω Ω R n is called the constraint set or feasible set. any point x Ω is called a feasible point We
1 Chapter 5 Linear Programming (LP) General constrained optimization problem: minimize subject to f(x) x Ω Ω R n is called the constraint set or feasible set. any point x Ω is called a feasible point We
CSC Design and Analysis of Algorithms. LP Shader Electronics Example
 CSC 80- Design and Analysis of Algorithms Lecture (LP) LP Shader Electronics Example The Shader Electronics Company produces two products:.eclipse, a portable touchscreen digital player; it takes hours
CSC 80- Design and Analysis of Algorithms Lecture (LP) LP Shader Electronics Example The Shader Electronics Company produces two products:.eclipse, a portable touchscreen digital player; it takes hours
Decision Mathematics D2 Advanced/Advanced Subsidiary. Thursday 6 June 2013 Morning Time: 1 hour 30 minutes
 Paper Reference(s) 6690/01R Edexcel GE Decision Mathematics D2 Advanced/Advanced Subsidiary Thursday 6 June 2013 Morning Time: 1 hour 30 minutes Materials required for examination Nil Items included with
Paper Reference(s) 6690/01R Edexcel GE Decision Mathematics D2 Advanced/Advanced Subsidiary Thursday 6 June 2013 Morning Time: 1 hour 30 minutes Materials required for examination Nil Items included with
Decision Mathematics D1 Advanced/Advanced Subsidiary. Friday 17 May 2013 Morning Time: 1 hour 30 minutes
 Paper Reference(s) 6689/01 Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Friday 17 May 2013 Morning Time: 1 hour 30 minutes Materials required for examination Nil Items included with
Paper Reference(s) 6689/01 Edexcel GCE Decision Mathematics D1 Advanced/Advanced Subsidiary Friday 17 May 2013 Morning Time: 1 hour 30 minutes Materials required for examination Nil Items included with
2. Linear Programming Problem
 . Linear Programming Problem. Introduction to Linear Programming Problem (LPP). When to apply LPP or Requirement for a LPP.3 General form of LPP. Assumptions in LPP. Applications of Linear Programming.6
. Linear Programming Problem. Introduction to Linear Programming Problem (LPP). When to apply LPP or Requirement for a LPP.3 General form of LPP. Assumptions in LPP. Applications of Linear Programming.6
PLC Papers. Created For:
 PLC Papers Created For: Algebra and proof 2 Grade 8 Objective: Use algebra to construct proofs Question 1 a) If n is a positive integer explain why the expression 2n + 1 is always an odd number. b) Use
PLC Papers Created For: Algebra and proof 2 Grade 8 Objective: Use algebra to construct proofs Question 1 a) If n is a positive integer explain why the expression 2n + 1 is always an odd number. b) Use
In Chapters 3 and 4 we introduced linear programming
 SUPPLEMENT The Simplex Method CD3 In Chapters 3 and 4 we introduced linear programming and showed how models with two variables can be solved graphically. We relied on computer programs (WINQSB, Excel,
SUPPLEMENT The Simplex Method CD3 In Chapters 3 and 4 we introduced linear programming and showed how models with two variables can be solved graphically. We relied on computer programs (WINQSB, Excel,
Part III: A Simplex pivot
 MA 3280 Lecture 31 - More on The Simplex Method Friday, April 25, 2014. Objectives: Analyze Simplex examples. We were working on the Simplex tableau The matrix form of this system of equations is called
MA 3280 Lecture 31 - More on The Simplex Method Friday, April 25, 2014. Objectives: Analyze Simplex examples. We were working on the Simplex tableau The matrix form of this system of equations is called
Review Solutions, Exam 2, Operations Research
 Review Solutions, Exam 2, Operations Research 1. Prove the weak duality theorem: For any x feasible for the primal and y feasible for the dual, then... HINT: Consider the quantity y T Ax. SOLUTION: To
Review Solutions, Exam 2, Operations Research 1. Prove the weak duality theorem: For any x feasible for the primal and y feasible for the dual, then... HINT: Consider the quantity y T Ax. SOLUTION: To
Taylor Series 6B. lim s x. 1 a We can evaluate the limit directly since there are no singularities: b Again, there are no singularities, so:
 Taylor Series 6B a We can evaluate the it directly since there are no singularities: 7+ 7+ 7 5 5 5 b Again, there are no singularities, so: + + c Here we should divide through by in the numerator and denominator
Taylor Series 6B a We can evaluate the it directly since there are no singularities: 7+ 7+ 7 5 5 5 b Again, there are no singularities, so: + + c Here we should divide through by in the numerator and denominator
Lecture 11 Linear programming : The Revised Simplex Method
 Lecture 11 Linear programming : The Revised Simplex Method 11.1 The Revised Simplex Method While solving linear programming problem on a digital computer by regular simplex method, it requires storing
Lecture 11 Linear programming : The Revised Simplex Method 11.1 The Revised Simplex Method While solving linear programming problem on a digital computer by regular simplex method, it requires storing
MATH 4211/6211 Optimization Linear Programming
 MATH 4211/6211 Optimization Linear Programming Xiaojing Ye Department of Mathematics & Statistics Georgia State University Xiaojing Ye, Math & Stat, Georgia State University 0 The standard form of a Linear
MATH 4211/6211 Optimization Linear Programming Xiaojing Ye Department of Mathematics & Statistics Georgia State University Xiaojing Ye, Math & Stat, Georgia State University 0 The standard form of a Linear
PhysicsAndMathsTutor.com. Mark Scheme (Results) Summer Pearson Edexcel GCE Decision Mathematics /01
 Mark (Results) Summer 2016 Pearson Edexcel GCE Decision Mathematics 2 6690/01 Edexcel and BTEC Qualifications Edexcel and BTEC qualifications are awarded by Pearson, the UK s largest awarding body. We
Mark (Results) Summer 2016 Pearson Edexcel GCE Decision Mathematics 2 6690/01 Edexcel and BTEC Qualifications Edexcel and BTEC qualifications are awarded by Pearson, the UK s largest awarding body. We
Math Models of OR: Some Definitions
 Math Models of OR: Some Definitions John E. Mitchell Department of Mathematical Sciences RPI, Troy, NY 12180 USA September 2018 Mitchell Some Definitions 1 / 20 Active constraints Outline 1 Active constraints
Math Models of OR: Some Definitions John E. Mitchell Department of Mathematical Sciences RPI, Troy, NY 12180 USA September 2018 Mitchell Some Definitions 1 / 20 Active constraints Outline 1 Active constraints
Gauss-Jordan Elimination for Solving Linear Equations Example: 1. Solve the following equations: (3)
 The Simple Method Gauss-Jordan Elimination for Solving Linear Equations Eample: Gauss-Jordan Elimination Solve the following equations: + + + + = 4 = = () () () - In the first step of the procedure, we
The Simple Method Gauss-Jordan Elimination for Solving Linear Equations Eample: Gauss-Jordan Elimination Solve the following equations: + + + + = 4 = = () () () - In the first step of the procedure, we
Constant acceleration, Mixed Exercise 9
 Constant acceleration, Mixed Exercise 9 a 45 000 45 km h = m s 3600 =.5 m s 3 min = 80 s b s= ( a+ bh ) = (60 + 80).5 = 5 a The distance from A to B is 5 m. b s= ( a+ bh ) 5 570 = (3 + 3 + T ) 5 ( T +
Constant acceleration, Mixed Exercise 9 a 45 000 45 km h = m s 3600 =.5 m s 3 min = 80 s b s= ( a+ bh ) = (60 + 80).5 = 5 a The distance from A to B is 5 m. b s= ( a+ bh ) 5 570 = (3 + 3 + T ) 5 ( T +
The augmented form of this LP is the following linear system of equations:
 1 Consider the following LP given in standard form: max z = 5 x_1 + 2 x_2 Subject to 3 x_1 + 2 x_2 2400 x_2 800 2 x_1 1200 x_1, x_2 >= 0 The augmented form of this LP is the following linear system of
1 Consider the following LP given in standard form: max z = 5 x_1 + 2 x_2 Subject to 3 x_1 + 2 x_2 2400 x_2 800 2 x_1 1200 x_1, x_2 >= 0 The augmented form of this LP is the following linear system of
 Duality in LPP Every LPP called the primal is associated with another LPP called dual. Either of the problems is primal with the other one as dual. The optimal solution of either problem reveals the information
Duality in LPP Every LPP called the primal is associated with another LPP called dual. Either of the problems is primal with the other one as dual. The optimal solution of either problem reveals the information
...(iii), x 2 Example 7: Geetha Perfume Company produces both perfumes and body spray from two flower extracts F 1. The following data is provided:
 The LP formulation is Linear Programming: Graphical Method Maximize, Z = 2x + 7x 2 Subject to constraints, 2x + x 2 200...(i) x 75...(ii) x 2 00...(iii) where x, x 2 ³ 0 Example 7: Geetha Perfume Company
The LP formulation is Linear Programming: Graphical Method Maximize, Z = 2x + 7x 2 Subject to constraints, 2x + x 2 200...(i) x 75...(ii) x 2 00...(iii) where x, x 2 ³ 0 Example 7: Geetha Perfume Company
Mathematics (JUN13MD0201) General Certificate of Education Advanced Level Examination June Unit Decision TOTAL.
 Centre Number Candidate Number For Examiner s Use Surname Other Names Candidate Signature Examiner s Initials Mathematics Unit Decision 2 Thursday 13 June 2013 General Certificate of Education Advanced
Centre Number Candidate Number For Examiner s Use Surname Other Names Candidate Signature Examiner s Initials Mathematics Unit Decision 2 Thursday 13 June 2013 General Certificate of Education Advanced
Chapter 5 Linear Programming (LP)
 Chapter 5 Linear Programming (LP) General constrained optimization problem: minimize f(x) subject to x R n is called the constraint set or feasible set. any point x is called a feasible point We consider
Chapter 5 Linear Programming (LP) General constrained optimization problem: minimize f(x) subject to x R n is called the constraint set or feasible set. any point x is called a feasible point We consider
Introduction to Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras
 Introduction to Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Module - 03 Simplex Algorithm Lecture 15 Infeasibility In this class, we
Introduction to Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Module - 03 Simplex Algorithm Lecture 15 Infeasibility In this class, we
i j k i j k i j k
 Vectors D a The equation of the line is (r a) b0 r ba b. This gives: r (i+j k)(i+j+k) (i+j k) r (i+j k) i+0j k b The equation of the line is (r a) b0 r ba b. This gives: r ( i+ j+ k) (i k) ( i+ j+ k) 0
Vectors D a The equation of the line is (r a) b0 r ba b. This gives: r (i+j k)(i+j+k) (i+j k) r (i+j k) i+0j k b The equation of the line is (r a) b0 r ba b. This gives: r ( i+ j+ k) (i k) ( i+ j+ k) 0
Q Scheme Marks AOs Pearson. Notes. Deduces that 21a 168 = 0 and solves to find a = 8 A1* 2.2a
 Further Maths Core Pure (AS/Year 1) Unit Test : Matrices Q Scheme Marks AOs Pearson Finds det M 3 p p 4 p 4 p 6 1 Completes the square to show p 4 p 6 p M1.a Concludes that (p + ) + > 0 for all values
Further Maths Core Pure (AS/Year 1) Unit Test : Matrices Q Scheme Marks AOs Pearson Finds det M 3 p p 4 p 4 p 6 1 Completes the square to show p 4 p 6 p M1.a Concludes that (p + ) + > 0 for all values
9.1 Linear Programs in canonical form
 9.1 Linear Programs in canonical form LP in standard form: max (LP) s.t. where b i R, i = 1,..., m z = j c jx j j a ijx j b i i = 1,..., m x j 0 j = 1,..., n But the Simplex method works only on systems
9.1 Linear Programs in canonical form LP in standard form: max (LP) s.t. where b i R, i = 1,..., m z = j c jx j j a ijx j b i i = 1,..., m x j 0 j = 1,..., n But the Simplex method works only on systems
4. Duality Duality 4.1 Duality of LPs and the duality theorem. min c T x x R n, c R n. s.t. ai Tx = b i i M a i R n
 2 4. Duality of LPs and the duality theorem... 22 4.2 Complementary slackness... 23 4.3 The shortest path problem and its dual... 24 4.4 Farkas' Lemma... 25 4.5 Dual information in the tableau... 26 4.6
2 4. Duality of LPs and the duality theorem... 22 4.2 Complementary slackness... 23 4.3 The shortest path problem and its dual... 24 4.4 Farkas' Lemma... 25 4.5 Dual information in the tableau... 26 4.6
( ) ( ) 2 1 ( ) Conic Sections 1 2E. 1 a. 1 dy. At (16, 8), d y 2 1 Tangent is: dx. Tangent at,8. is 1
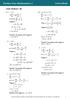 Conic Sections E a y y so At (6, ), d y y ( 6) y 6 y+ 6 y 6+ y+ 6 d y y At, 6 When, y, angent at, is y 6 y 6+ 6+ y 6+ y 6 y y so,, d y At y ( ) y ( ) y y+ y + y+ e 6+ y 6 y 7 7 y 7 so d d y 7 At ( 7, 7),
Conic Sections E a y y so At (6, ), d y y ( 6) y 6 y+ 6 y 6+ y+ 6 d y y At, 6 When, y, angent at, is y 6 y 6+ 6+ y 6+ y 6 y y so,, d y At y ( ) y ( ) y y+ y + y+ e 6+ y 6 y 7 7 y 7 so d d y 7 At ( 7, 7),
UNIVERSITY OF KWA-ZULU NATAL
 UNIVERSITY OF KWA-ZULU NATAL EXAMINATIONS: June 006 Solutions Subject, course and code: Mathematics 34 MATH34P Multiple Choice Answers. B. B 3. E 4. E 5. C 6. A 7. A 8. C 9. A 0. D. C. A 3. D 4. E 5. B
UNIVERSITY OF KWA-ZULU NATAL EXAMINATIONS: June 006 Solutions Subject, course and code: Mathematics 34 MATH34P Multiple Choice Answers. B. B 3. E 4. E 5. C 6. A 7. A 8. C 9. A 0. D. C. A 3. D 4. E 5. B
MA 162: Finite Mathematics - Section 3.3/4.1
 MA 162: Finite Mathematics - Section 3.3/4.1 Fall 2014 Ray Kremer University of Kentucky October 6, 2014 Announcements: Homework 3.3 due Tuesday at 6pm. Homework 4.1 due Friday at 6pm. Exam scores were
MA 162: Finite Mathematics - Section 3.3/4.1 Fall 2014 Ray Kremer University of Kentucky October 6, 2014 Announcements: Homework 3.3 due Tuesday at 6pm. Homework 4.1 due Friday at 6pm. Exam scores were
The Graphical Method & Algebraic Technique for Solving LP s. Métodos Cuantitativos M. En C. Eduardo Bustos Farías 1
 The Graphical Method & Algebraic Technique for Solving LP s Métodos Cuantitativos M. En C. Eduardo Bustos Farías The Graphical Method for Solving LP s If LP models have only two variables, they can be
The Graphical Method & Algebraic Technique for Solving LP s Métodos Cuantitativos M. En C. Eduardo Bustos Farías The Graphical Method for Solving LP s If LP models have only two variables, they can be
Master of Intelligent Systems - French-Czech Double Diploma. Hough transform
 Hough transform I- Introduction The Hough transform is used to isolate features of a particular shape within an image. Because it requires that the desired features be specified in some parametric form,
Hough transform I- Introduction The Hough transform is used to isolate features of a particular shape within an image. Because it requires that the desired features be specified in some parametric form,
The Simplex Method. Lecture 5 Standard and Canonical Forms and Setting up the Tableau. Lecture 5 Slide 1. FOMGT 353 Introduction to Management Science
 The Simplex Method Lecture 5 Standard and Canonical Forms and Setting up the Tableau Lecture 5 Slide 1 The Simplex Method Formulate Constrained Maximization or Minimization Problem Convert to Standard
The Simplex Method Lecture 5 Standard and Canonical Forms and Setting up the Tableau Lecture 5 Slide 1 The Simplex Method Formulate Constrained Maximization or Minimization Problem Convert to Standard
Mark Scheme (Results) June GCE Decision D2 (6690) Paper 1
 Mark (Results) June 20 GCE Decision D2 (6690) Paper Edexcel is one of the leading examining and awarding bodies in the UK and throughout the world. We provide a wide range of qualifications including academic,
Mark (Results) June 20 GCE Decision D2 (6690) Paper Edexcel is one of the leading examining and awarding bodies in the UK and throughout the world. We provide a wide range of qualifications including academic,
Introduction to the Simplex Algorithm Active Learning Module 3
 Introduction to the Simplex Algorithm Active Learning Module 3 J. René Villalobos and Gary L. Hogg Arizona State University Paul M. Griffin Georgia Institute of Technology Background Material Almost any
Introduction to the Simplex Algorithm Active Learning Module 3 J. René Villalobos and Gary L. Hogg Arizona State University Paul M. Griffin Georgia Institute of Technology Background Material Almost any
The Simplex Algorithm and Goal Programming
 The Simplex Algorithm and Goal Programming In Chapter 3, we saw how to solve two-variable linear programming problems graphically. Unfortunately, most real-life LPs have many variables, so a method is
The Simplex Algorithm and Goal Programming In Chapter 3, we saw how to solve two-variable linear programming problems graphically. Unfortunately, most real-life LPs have many variables, so a method is
56:171 Operations Research Fall 1998
 56:171 Operations Research Fall 1998 Quiz Solutions D.L.Bricker Dept of Mechanical & Industrial Engineering University of Iowa 56:171 Operations Research Quiz
56:171 Operations Research Fall 1998 Quiz Solutions D.L.Bricker Dept of Mechanical & Industrial Engineering University of Iowa 56:171 Operations Research Quiz
IE 400 Principles of Engineering Management. The Simplex Algorithm-I: Set 3
 IE 4 Principles of Engineering Management The Simple Algorithm-I: Set 3 So far, we have studied how to solve two-variable LP problems graphically. However, most real life problems have more than two variables!
IE 4 Principles of Engineering Management The Simple Algorithm-I: Set 3 So far, we have studied how to solve two-variable LP problems graphically. However, most real life problems have more than two variables!
( y) ( ) ( ) ( ) ( ) ( ) Trigonometric ratios, Mixed Exercise 9. 2 b. Using the sine rule. a Using area of ABC = sin x sin80. So 10 = 24sinθ.
 Trigonometric ratios, Mixed Exercise 9 b a Using area of ABC acsin B 0cm 6 8 sinθ cm So 0 4sinθ So sinθ 0 4 θ 4.6 or 3 s.f. (.) As θ is obtuse, ABC 3 s.f b Using the cosine rule b a + c ac cos B AC 8 +
Trigonometric ratios, Mixed Exercise 9 b a Using area of ABC acsin B 0cm 6 8 sinθ cm So 0 4sinθ So sinθ 0 4 θ 4.6 or 3 s.f. (.) As θ is obtuse, ABC 3 s.f b Using the cosine rule b a + c ac cos B AC 8 +
OPTIMISATION 3: NOTES ON THE SIMPLEX ALGORITHM
 OPTIMISATION 3: NOTES ON THE SIMPLEX ALGORITHM Abstract These notes give a summary of the essential ideas and results It is not a complete account; see Winston Chapters 4, 5 and 6 The conventions and notation
OPTIMISATION 3: NOTES ON THE SIMPLEX ALGORITHM Abstract These notes give a summary of the essential ideas and results It is not a complete account; see Winston Chapters 4, 5 and 6 The conventions and notation
Understanding the Simplex algorithm. Standard Optimization Problems.
 Understanding the Simplex algorithm. Ma 162 Spring 2011 Ma 162 Spring 2011 February 28, 2011 Standard Optimization Problems. A standard maximization problem can be conveniently described in matrix form
Understanding the Simplex algorithm. Ma 162 Spring 2011 Ma 162 Spring 2011 February 28, 2011 Standard Optimization Problems. A standard maximization problem can be conveniently described in matrix form
Solutionbank Edexcel AS and A Level Modular Mathematics
 Page of Exercise A, Question Use the binomial theorem to expand, x
Page of Exercise A, Question Use the binomial theorem to expand, x
Simplex Method in different guises
 Simplex Method in different guises The Furniture problem Max 0x + 0x 2 + 20x, subject to x 0, 8x + x 2 + 2x 48, 4x + 2x 2 +.x 20, 2x +.x 2 +.x 8. Canonical form: slack variables s = (s, s 2, s ) 0. Constraints
Simplex Method in different guises The Furniture problem Max 0x + 0x 2 + 20x, subject to x 0, 8x + x 2 + 2x 48, 4x + 2x 2 +.x 20, 2x +.x 2 +.x 8. Canonical form: slack variables s = (s, s 2, s ) 0. Constraints
( ) ( ) or ( ) ( ) Review Exercise 1. 3 a 80 Use. 1 a. bc = b c 8 = 2 = 4. b 8. Use = 16 = First find 8 = 1+ = 21 8 = =
 Review Eercise a Use m m a a, so a a a Use c c 6 5 ( a ) 5 a First find Use a 5 m n m n m a m ( a ) or ( a) 5 5 65 m n m a n m a m a a n m or m n (Use a a a ) cancelling y 6 ecause n n ( 5) ( 5)( 5) (
Review Eercise a Use m m a a, so a a a Use c c 6 5 ( a ) 5 a First find Use a 5 m n m n m a m ( a ) or ( a) 5 5 65 m n m a n m a m a a n m or m n (Use a a a ) cancelling y 6 ecause n n ( 5) ( 5)( 5) (
Lecture 2: The Simplex method
 Lecture 2 1 Linear and Combinatorial Optimization Lecture 2: The Simplex method Basic solution. The Simplex method (standardform, b>0). 1. Repetition of basic solution. 2. One step in the Simplex algorithm.
Lecture 2 1 Linear and Combinatorial Optimization Lecture 2: The Simplex method Basic solution. The Simplex method (standardform, b>0). 1. Repetition of basic solution. 2. One step in the Simplex algorithm.
The Big M Method. Modify the LP
 The Big M Method Modify the LP 1. If any functional constraints have negative constants on the right side, multiply both sides by 1 to obtain a constraint with a positive constant. Big M Simplex: 1 The
The Big M Method Modify the LP 1. If any functional constraints have negative constants on the right side, multiply both sides by 1 to obtain a constraint with a positive constant. Big M Simplex: 1 The
