Power Series. x n. Using the ratio test. n n + 1. x n+1 n 3. = lim x. lim n + 1. = 1 < x < 1. Then r = 1 and I = ( 1, 1) ( 1) n 1 x n.
|
|
|
- Beverly Wilkerson
- 5 years ago
- Views:
Transcription
1 .8 Power Series. n x n x n n Using the ratio test. lim x n+ n n + lim x n n + so r and I (, ). By the ratio test. n Then r and I (, ). n x < ( ) n x n < x < n lim x n+ n (n + ) x n lim xn n (n + ) x < < x < By the ratio test lim x ( n + ) n! n (n + )! x n lim x n n + < so r and I (, ) x n n!
2 4. ( ) n x n 4 n By the ratio test lim n+ x n+ 4 n n 4 n + n x n lim x 4 n n 4 < n + x < x < < x < So r and I ( /, /) 5. By the Ratio Test n (x + )n ( ) n n lim n So r and I ( 4, ) (x + ) n+ n n (n + ) n+ (x + ) n lim n(x + ) n n + < x + < x + < 4 < x < 6. (x ) n 5 n n
3 By the Ratio test lim (x ) n+ 5 n n n 5 n+ n + (x ) n lim (x ) n n 5 n + < x 5 < x < 5 x < 5 x < 5 5 < x < 5 < x < So r 5 and I (, ).9 Representing Functions as Power Series. f(x) + x Using the formula for the sum of a geometric series r n r We find that + x ( x) x n ( ) n x n By the properties of geometric series we know that so I (, ) x < x <
4 . Using Geometric series f(x) x x (x ) n x n as r x x < So I (, ). x 5 Using the same methodology as before x x 5 ( x ) n 5 x n 5 n+ The radius of convergence is 5 and the interval of convergence is (-5,5) x n 5 n 4. x 9 + x 4
5 Using the same methodology with slightly more manipulation x 9 + x x 9 ( x ) x 9 ( x ) 9 x ( x 9 9 ) n ( ) n xn+ 9 n+ I use the ratio test to find the radius of convergence: Now we can calculate that lim x (n+)+ 9 n+ n 9 n+ x n+ lim n lim n x 9 x n++ 9x n+ x 9 x 9 < x < 9 x < So the radius of convergence is and the interval of convergence is (-,) 5. x We will apply the exact same procedure. yes there is a pattern here... x x x n n x n n+ 5
6 By the properties of the geometric series, this power series converges when x < Which is the case when x < So the Radius of convergence is and the interval of convergence is (-,) 6. Note that (x ) ( x) also note that ( ) x ( x) From here it is possible to use integration to find the power series of this function: x (x ) x ( x) x ( x x ( x n n ) x n n+ nx n n+ We need to start the power series at to avoid negative exponents, so we get: x nx n n+ 7. If you think that computing t t dt 8 ) nx n+ n+ is going to be a pain in the butt, then you and I are in agreement dear reader. We can use the following property to solve the integral using a power series. c n (x a) n dx c n (x a) n dx 6
7 So first we turn the integrand into a power series: and we integrate: t t t 8 t 8 t t 8n t 8n+ t 8n+ dt t8n+ 8n + + C and find that the integral is equal to C + t 8n+ 8n +. Taylor and Maclaurin Series. Find the Maclaurin series for f(x). Find the radius of convergence. a. f(x) xcos(x) Recall that the formula for a Maclaurin series is n f n () (x a) n n! The best way to start this problem is to write out a few terms to identify the pattern. I start with Derivatives: f(x) x cos(x) f() f (x) cos(x) x sin(x) f () f () (x) sin(x) x cos(x) f () () f () (x) cos(x) + x sin(x) f () f 4 (x) 4 sin(x) + x cos(x) f 4 () f 5 (x) 5 cos(x) x sin(x) f 5 () 5 7
8 And so the first few terms of the series looks like this: x! x + 5 5! x5... and the so in summation notation: ( ) n (n)! xn+ b. n f(x) ln( + x) Note that the nth derivative (n ) of this function is given by and so evaluated at f n (x) ( )n+ (n )! ( + x) n f n () ( ) n+ (n )! Note that f(). So using this in the formula for a taylor series we get that : f(x) ( ) n (n )! + x n ( ) n+ x n n! n c. f(x) e 5x Note that the nth derivative of f(x) is given by and so d. f(x) f n (x) 5 n e 5x 5 n e 5() x n n! n xe x n 5 n n! xn Note that the nth derivative of e x n e x we can use this to get the Maclaurin series like this: f(x) xe n x x n! xn 8 n n n n! xn+
9 . find the Taylor series for f(x) centered at a a. a so f(x) + x + x f(x) + x + x f (x) x + f (x) f() 8f () 5f () and consequently the taylor series is finite, given by the polynomial: (x ) +! (x ) 7 + 5(x ) + (x ) b. f(x) e x a Note that the nth derivative of e x is e x so: f n () e So we can use this to get our Taylor series : n e (x )n n! c. a π f(x) cos(x) lets do some derivatives and figure the series out from there: f(x) cos x f(π) f (x) sin x f (π) f (x) cos x f (π) f (x) sin x f (π) clearly the derivatives follow this pattern, so we can construct the series: f(x) n ( ) n+ (x π) n (n)! 9
10 d. a 9 f(x) x Let s take some derivatives and search out a pattern f(x) x f(9) f (x) x f (9) 9 f (x) 4 x 5 f (9) 9 f (x) 5 8 x 7 f (9) 5 9 So in general because of the power rule, the nth derivative of f at 9 will be f (n) (9) ( )n ( 5 n ) n 9 n and so the taylor series centred at 9 will be n ( ) n ( 5 n ) (x 9) n n! n 9 n. Applications of Taylor Series. Find T (x) for each function a. for a So T is We need derivatives: f(x) e x sin(x) f(x) e x sin(x) f() f (x) e x (cos x sin x) f () f (x) e x cos x f () f (x) e x (cos x sin x) f () T x x + x
11 b. f(x) x cos x a Use the derivatives we found in part a from. to get T T + x + x! x x x c. f(x) tan (x) a Taking some derivatives: f(x) tan (x) f() π 4 f (x) + x f () f (x) x f () ( + x ) f (x) 6x ( + x ) f (x) and so T π 4 + x + 4 x + x d. a Using the same process, f(x) ln( + x) f(x) ln( + x) f() ln() f (x) f () + x f 4 (x) f () 4 ( + x) 9 f 6 (x) f () 6 ( + x) 7 and so T ln() + x + 9 x x
12 . Parametric Equations Eliminate the parameter and find the Cartesian coordinates a. x sin(θ) y cos(θ) Note that sin (θ) + cos (θ) so we know also that x + y and since θ runs from to π we can conclude that the plot is a half circle in the lower portion of the plane, so y b. First we solve for a parameter: x 4 cos(θ)y 5 sin(θ) x 4 cos(θ) θ cos x 4 then use that to eliminate the parameter in the other equation. y 5 sin(cos ( x )) () 4 y 5 4 ± 6 x () You can use a triangle to get from line to line like this B 4 6 x C x A we can work it out from there. for x y 5 6 (6 x ) y 5 x 6 y 5 + x 6 the angle with vertex C is θ and so
13 c. Solve for cos(θ) x + cos(θ) y cos(θ) so and so we get that: for x d. x + cos(θ) x + cos(θ) y cos(θ) y + c cos(θ) y + cos(θ) x + y + x t y x solving for t in the x equation we get y t x t x t so we can sub that into the y equation to get for x e. y x x t 5 y t + Solving solving for t in the x equation we find that t x + 5 and so substituting to eliminate the parameter we find that: y x y x + + y x +
14 4. Calculus of parametric curves. At what point does the curve x cos (t), y tan(t)( cos (t) Cross itself? Find the equations for both tangents at that point. The curve corsses itself at (,), so we can solve for θ by x cos (t) cos (t) t cos (± ) we can conclude that t is equal to π 4 and 7π 4 So Computing the slope of tangent I can use the following formula, and so dy dy dx dt dx dt dx 4 cos(t) sin(t) dt dy dt sec (t) 4 sin (t) dy dx sec (t) 4 sin (t) 4 cos(t) sin(t) () and evaluating at π we get and evaluating at 7π we get - so the equations for those lines are easy to get since we have a slope and a point (,) 4 4 we get y x and y x. evaluate derivatives and determine concavity for x t t and y t I ll first get my derivatives using the formula above and using the identity that d d dy y dx dt dx dx dt 4
15 so and consequently dx dt t (4) dy t (5) dy dx dt t t (6) (t ) (t)(6t) fracd ydx (t ) t 6(t + 4) (t ) 6(t + 4) 7(t 4) (t + 4) 9(t 4) The second derivative is never zero, but it doesn t exist for t ± so those will be the inflection points. for t < the second derivative is negative, for < t < the second derivative is positive, and for t > the second derivative is negative. its concave up between - and.. find the are of the region enclosed by the Asteroid given by x a cos (θ) and y a sin (θ) Recall that the Area under a parametric curve is given by A β α g(t)f (t)dt for x f(t) and y g(t) note that the asteroid is symetric about both axes and so we can evaluate our integral from to π and multiply by four in order to find the area. f (t) a cos (t) sin(t) 5
16 so we will evaluate the integral: 4 a sin (t)( a cos (t) sin(t)dt a a a ( pi ) a π 8 sin 4 (t)cos (t)dt sin 4 (t) sin 6 (t)dt I used an integration table for this one, Wolfram Alpha has a great step by step for it. 5 Set up but don t evaluate the following arc length integrals a. x t t, y 4 t Recall that arclength is given by the formula β (dx ) ( ) dy L + dt dt dt α So we can set it up by first taking some derivatives dx dt tdy dt 5 t and so we just plug it in on the bounds we re given, which is simplified to L L ( t) + (t 5 ) dt 4t + 4t 5 dt t + t dt 5 6
17 b. x t + cos(t) using the same strategy as above: so the arc length is given by dx dt sin(t) y t sin(t) dy dt cos(t) ( sin t) + ( cos t) dt sin(t) + sin t + cos(t) + cos tdt using the Pythagorean Identity I can reduce + (sin (t) + cos (t)) sin(t) cos(t)dt (sin(t) + cos(t))dt 5. find the length of the curve given by x +t and y 4 + t setting up the integral as before: dx dt 6tdy dt 6t 6t + 6t 4 dt 6 t + t dt u + t ( u udu ( ) 6. polar coordinates du t. find the slopes of tangent lines at specified points r sin(θ) at π 6 following formula: recall that polar derivatives can be attained using the dr dy dy sin(θ) + r cos(θ) dθ cos(θ) r sin(θ) dr dθ 7
18 so evaluating the derivative and so the derivative is evaluating at π 6 I get dr dθ cos(θ) sin(θ) cos(θ) + sin(θ)cos(θ) cos(θ)cos(θ) sin(θ)sin(θ) tan(θ) b. r at θ π Let s do it like the last one. θ so sin(θ) dy dx + cos(θ) θ θ cos(θ) dr dθ θ evaluating at π I get an answer of π θ sin(θ) θ. Area and length in polar coordinates. find the area enclosed by the curve a. r ( + cos(θ)) The period is to π and is symmetric about the x-axis so we will integrate from to π and multiply by. recall that the area of a polar curve is given by b r dθ a 8
19 So the area will be: b. (( + cos(θ)) dθ cos(θ) + cos (θ)dθ + cos(θ) + ( cos(θ) + )dθ 9(θ + sin(θ) + ( 9(θ + sin(θ) + θ + 4 sin(θ) 9(π + + π + ) 9( π ) 7π r cos(θ) + cos(θ)dθ) The three petals of the flower are equal, so I will calculate the first one an multiply by. Note also that the first half of the first petal is traced from θ to θ π so we can take the integral from to π and solve multiply the whole thing by 6. 6 ( cos(θ)dθ) 6 cos (θ)dθ ( + cos(6θ)dθ cos(6θ)dθ + 6θ sin(6θ) + 6θ π π c. r + sin(6θ) 9
20 note that the graph is symetric about the origin, so we can take the integral from to π and then multiply by to get the area. ( + sin(6θ)dθ + 4sin(6θ) + 4 sin (6θ)dθ θ 4 6 cos(6θ) + 4 sin (6θ)dθ θ 4 6 cos(6θ) + 4( t sin(θ) ) π 4 π π π Find the area inside the first curve and outside the second curve. a. r 4sin(θ) and r If we find the points of intersection, we can integrate the first curve between them. so we set them equal and solve for θ 4 sin(θ) sin(θ) θ π 6, 5π 6 those will be our bounds of integration. We will integrate each and take there difference, which can be solved as a single integral like this: 5π 6 π 6 ((4 sin(θ)) () )dθ 8 5π 6 π 6 5π 6 π 6 5π 6 π 6 6sin (θ) 4dθ 4sin (θ) dθ sin (θ)dθ θ 4θ sin(θ) θ 5π 6 π 6 θ sin(θ) 5π + π + 4π +
21 b. r cos(θ) and r +cos(θ) using the same procedure as above, I find that a point of intersection is π and since the curves are both symmetric about the x axis, we can integrate this from to π and multiply by. So I get ( cos(θ)) ( + cos(θ)) dθ 4 8 cos ( θ) cos(θ) dθ cos (θ)dθ + sin(θ) + θ θ sin(θ) + sin(θ) + θ π θ π sin(θ) + sin(θ) π + π So multiplying the answer by we find that the area in question is equal to π c. r + sin(θ) and r sin(θ) The only point of intersection here is at π. note that the second curve is contained completely within the first curve. so we can take the area contained by the first curve and subtract the area of the second. we are going to do two integrals for this, the first gets us from to π and the second will be the absolute value of the integral from π to. we add these and multiply by to get what the area of the outside curve. we can then subtract the area within the second curve which we find using an integral sin(θ) + sin (θ)dθ sin(θ) + sin (θ)dθ π 4θ 4 cos(θ) + θ sin(θ) cos(θ) π + 4θ 4 cos(θ) + θ sin(θ) cos(θ) π So we find the area of the second curve, which is a circle of radius 9π 9π We know 9π its area will be 9π 4
22 Subtracting one from the second from the first, we find that the area of the first curve without the second one is 9π 9π 4 9π 4 Find the exact Length of the polar curve a. r sin(θ) Recall that arc length in polar coordinates is given by the following Formula: b L ( dr dθ ) + r dθ so lets first take the derivative: and subbing into the formula: a r cos(θ) 9cos (θ) + 9 sin (θ)dθ dθ θ π π b. r θ r θ L 4θ + θ 4 dθ θ 4 + θ dθ udu (4 + θ ) π (4 + π) r e θ r e θ
23 L (e θ ) + (e θ ) dθ 4e 4θ + e 4θ dθ e θ 5dθ 5 eθ π 5 (e4π + )
Practice Problems: Exam 2 MATH 230, Spring 2011 Instructor: Dr. Zachary Kilpatrick Show all your work. Simplify as much as possible.
 Practice Problems: Exam MATH, Spring Instructor: Dr. Zachary Kilpatrick Show all your work. Simplify as much as possible.. Write down a table of x and y values associated with a few t values. Then, graph
Practice Problems: Exam MATH, Spring Instructor: Dr. Zachary Kilpatrick Show all your work. Simplify as much as possible.. Write down a table of x and y values associated with a few t values. Then, graph
Math 113 Final Exam Practice
 Math Final Exam Practice The Final Exam is comprehensive. You should refer to prior reviews when studying material in chapters 6, 7, 8, and.-9. This review will cover.0- and chapter 0. This sheet has three
Math Final Exam Practice The Final Exam is comprehensive. You should refer to prior reviews when studying material in chapters 6, 7, 8, and.-9. This review will cover.0- and chapter 0. This sheet has three
Math 181, Exam 2, Study Guide 2 Problem 1 Solution. 1 + dx. 1 + (cos x)2 dx. 1 + cos2 xdx. = π ( 1 + cos π 2
 Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
Mathematics Engineering Calculus III Fall 13 Test #1
 Mathematics 2153-02 Engineering Calculus III Fall 13 Test #1 Instructor: Dr. Alexandra Shlapentokh (1) Which of the following statements is always true? (a) If x = f(t), y = g(t) and f (1) = 0, then dy/dx(1)
Mathematics 2153-02 Engineering Calculus III Fall 13 Test #1 Instructor: Dr. Alexandra Shlapentokh (1) Which of the following statements is always true? (a) If x = f(t), y = g(t) and f (1) = 0, then dy/dx(1)
a k 0, then k + 1 = 2 lim 1 + 1
 Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
Math156 Review for Exam 4
 Math56 Review for Eam 4. What will be covered in this eam: Representing functions as power series, Taylor and Maclaurin series, calculus with parametric curves, calculus with polar coordinates.. Eam Rules:
Math56 Review for Eam 4. What will be covered in this eam: Representing functions as power series, Taylor and Maclaurin series, calculus with parametric curves, calculus with polar coordinates.. Eam Rules:
You can learn more about the services offered by the teaching center by visiting
 MAC 232 Exam 3 Review Spring 209 This review, produced by the Broward Teaching Center, contains a collection of questions which are representative of the type you may encounter on the exam. Other resources
MAC 232 Exam 3 Review Spring 209 This review, produced by the Broward Teaching Center, contains a collection of questions which are representative of the type you may encounter on the exam. Other resources
Math 226 Calculus Spring 2016 Exam 2V1
 Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Spring 2015, MA 252, Calculus II, Final Exam Preview Solutions
 Spring 5, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card,
Spring 5, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card,
Math 1310 Final Exam
 Math 1310 Final Exam December 11, 2014 NAME: INSTRUCTOR: Write neatly and show all your work in the space provided below each question. You may use the back of the exam pages if you need additional space
Math 1310 Final Exam December 11, 2014 NAME: INSTRUCTOR: Write neatly and show all your work in the space provided below each question. You may use the back of the exam pages if you need additional space
Parametric Curves. Calculus 2 Lia Vas
 Calculus Lia Vas Parametric Curves In the past, we mostly worked with curves in the form y = f(x). However, this format does not encompass all the curves one encounters in applications. For example, consider
Calculus Lia Vas Parametric Curves In the past, we mostly worked with curves in the form y = f(x). However, this format does not encompass all the curves one encounters in applications. For example, consider
Taylor and Maclaurin Series. Approximating functions using Polynomials.
 Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Friday 09/15/2017 Midterm I 50 minutes
 Fa 17: MATH 2924 040 Differential and Integral Calculus II Noel Brady Friday 09/15/2017 Midterm I 50 minutes Name: Student ID: Instructions. 1. Attempt all questions. 2. Do not write on back of exam sheets.
Fa 17: MATH 2924 040 Differential and Integral Calculus II Noel Brady Friday 09/15/2017 Midterm I 50 minutes Name: Student ID: Instructions. 1. Attempt all questions. 2. Do not write on back of exam sheets.
10.1 Review of Parametric Equations
 10.1 Review of Parametric Equations Recall that often, instead of representing a curve using just x and y (called a Cartesian equation), it is more convenient to define x and y using parametric equations
10.1 Review of Parametric Equations Recall that often, instead of representing a curve using just x and y (called a Cartesian equation), it is more convenient to define x and y using parametric equations
y = x 3 and y = 2x 2 x. 2x 2 x = x 3 x 3 2x 2 + x = 0 x(x 2 2x + 1) = 0 x(x 1) 2 = 0 x = 0 and x = (x 3 (2x 2 x)) dx
 Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
APPM 1360 Final Exam Spring 2016
 APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
Calculus III. George Voutsadakis 1. LSSU Math 251. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus III George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 251 George Voutsadakis (LSSU) Calculus III January 2016 1 / 76 Outline 1 Parametric Equations,
Calculus III George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 251 George Voutsadakis (LSSU) Calculus III January 2016 1 / 76 Outline 1 Parametric Equations,
SOLUTIONS FOR PRACTICE FINAL EXAM
 SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
Fall 2016, MA 252, Calculus II, Final Exam Preview Solutions
 Fall 6, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card, and
Fall 6, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card, and
Review Problems for the Final
 Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
More Final Practice Problems
 8.0 Calculus Jason Starr Final Exam at 9:00am sharp Fall 005 Tuesday, December 0, 005 More 8.0 Final Practice Problems Here are some further practice problems with solutions for the 8.0 Final Exam. Many
8.0 Calculus Jason Starr Final Exam at 9:00am sharp Fall 005 Tuesday, December 0, 005 More 8.0 Final Practice Problems Here are some further practice problems with solutions for the 8.0 Final Exam. Many
1 4 (1 cos(4θ))dθ = θ 4 sin(4θ)
 M48M Final Exam Solutions, December 9, 5 ) A polar curve Let C be the portion of the cloverleaf curve r = sin(θ) that lies in the first quadrant a) Draw a rough sketch of C This looks like one quarter
M48M Final Exam Solutions, December 9, 5 ) A polar curve Let C be the portion of the cloverleaf curve r = sin(θ) that lies in the first quadrant a) Draw a rough sketch of C This looks like one quarter
Math Final Exam Review
 Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Math 230 Mock Final Exam Detailed Solution
 Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
SECTION A. f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes.
 SECTION A 1. State the maximal domain and range of the function f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes. 2. By evaluating f(0),
SECTION A 1. State the maximal domain and range of the function f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes. 2. By evaluating f(0),
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 3 2, 5 2 C) - 5 2
 Test Review (chap 0) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Find the point on the curve x = sin t, y = cos t, -
Test Review (chap 0) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Find the point on the curve x = sin t, y = cos t, -
(x 3)(x + 5) = (x 3)(x 1) = x + 5. sin 2 x e ax bx 1 = 1 2. lim
 SMT Calculus Test Solutions February, x + x 5 Compute x x x + Answer: Solution: Note that x + x 5 x x + x )x + 5) = x )x ) = x + 5 x x + 5 Then x x = + 5 = Compute all real values of b such that, for fx)
SMT Calculus Test Solutions February, x + x 5 Compute x x x + Answer: Solution: Note that x + x 5 x x + x )x + 5) = x )x ) = x + 5 x x + 5 Then x x = + 5 = Compute all real values of b such that, for fx)
Final Exam 2011 Winter Term 2 Solutions
 . (a Find the radius of convergence of the series: ( k k+ x k. Solution: Using the Ratio Test, we get: L = lim a k+ a k = lim ( k+ k+ x k+ ( k k+ x k = lim x = x. Note that the series converges for L
. (a Find the radius of convergence of the series: ( k k+ x k. Solution: Using the Ratio Test, we get: L = lim a k+ a k = lim ( k+ k+ x k+ ( k k+ x k = lim x = x. Note that the series converges for L
There are some trigonometric identities given on the last page.
 MA 114 Calculus II Fall 2015 Exam 4 December 15, 2015 Name: Section: Last 4 digits of student ID #: No books or notes may be used. Turn off all your electronic devices and do not wear ear-plugs during
MA 114 Calculus II Fall 2015 Exam 4 December 15, 2015 Name: Section: Last 4 digits of student ID #: No books or notes may be used. Turn off all your electronic devices and do not wear ear-plugs during
Spring 2011 solutions. We solve this via integration by parts with u = x 2 du = 2xdx. This is another integration by parts with u = x du = dx and
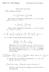 Math - 8 Rahman Final Eam Practice Problems () We use disks to solve this, Spring solutions V π (e ) d π e d. We solve this via integration by parts with u du d and dv e d v e /, V π e π e d. This is another
Math - 8 Rahman Final Eam Practice Problems () We use disks to solve this, Spring solutions V π (e ) d π e d. We solve this via integration by parts with u du d and dv e d v e /, V π e π e d. This is another
Chapter 9 Overview: Parametric and Polar Coordinates
 Chapter 9 Overview: Parametric and Polar Coordinates As we saw briefly last year, there are axis systems other than the Cartesian System for graphing (vector coordinates, polar coordinates, rectangular
Chapter 9 Overview: Parametric and Polar Coordinates As we saw briefly last year, there are axis systems other than the Cartesian System for graphing (vector coordinates, polar coordinates, rectangular
SET 1. (1) Solve for x: (a) e 2x = 5 3x
 () Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
() Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
3. On the grid below, sketch and label graphs of the following functions: y = sin x, y = cos x, and y = sin(x π/2). π/2 π 3π/2 2π 5π/2
 AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
University of Alberta. Math 214 Sample Exam Math 214 Solutions
 University of Alberta Math 14 Sample Exam Math 14 Solutions 1. Test the following series for convergence or divergence (a) ( n +n+1 3n +n+1 )n, (b) 3 n (n +1) (c) SOL: n!, arccos( n n +1 ), (a) ( n +n+1
University of Alberta Math 14 Sample Exam Math 14 Solutions 1. Test the following series for convergence or divergence (a) ( n +n+1 3n +n+1 )n, (b) 3 n (n +1) (c) SOL: n!, arccos( n n +1 ), (a) ( n +n+1
Parametric Equations and Polar Coordinates
 Parametric Equations and Polar Coordinates Parametrizations of Plane Curves In previous chapters, we have studied curves as the graphs of functions or equations involving the two variables x and y. Another
Parametric Equations and Polar Coordinates Parametrizations of Plane Curves In previous chapters, we have studied curves as the graphs of functions or equations involving the two variables x and y. Another
Assignment 6 Solution. Please do not copy and paste my answer. You will get similar questions but with different numbers!
 Assignment 6 Solution Please do not copy and paste my answer. You will get similar questions but with different numbers! This question tests you the following points: Integration by Parts: Let u = x, dv
Assignment 6 Solution Please do not copy and paste my answer. You will get similar questions but with different numbers! This question tests you the following points: Integration by Parts: Let u = x, dv
Completion Date: Monday February 11, 2008
 MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
Section 5.8. Taylor Series
 Difference Equations to Differential Equations Section 5.8 Taylor Series In this section we will put together much of the work of Sections 5.-5.7 in the context of a discussion of Taylor series. We begin
Difference Equations to Differential Equations Section 5.8 Taylor Series In this section we will put together much of the work of Sections 5.-5.7 in the context of a discussion of Taylor series. We begin
Mathematics 104 Fall Term 2006 Solutions to Final Exam. sin(ln t) dt = e x sin(x) dx.
 Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Practice problems from old exams for math 132 William H. Meeks III
 Practice problems from old exams for math 32 William H. Meeks III Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These practice tests are
Practice problems from old exams for math 32 William H. Meeks III Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These practice tests are
Ma 530 Power Series II
 Ma 530 Power Series II Please note that there is material on power series at Visual Calculus. Some of this material was used as part of the presentation of the topics that follow. Operations on Power Series
Ma 530 Power Series II Please note that there is material on power series at Visual Calculus. Some of this material was used as part of the presentation of the topics that follow. Operations on Power Series
n=0 ( 1)n /(n + 1) converges, but not
 Math 07H Topics for the third exam (and beyond) (Technically, everything covered on the first two exams plus...) Absolute convergence and alternating series A series a n converges absolutely if a n converges.
Math 07H Topics for the third exam (and beyond) (Technically, everything covered on the first two exams plus...) Absolute convergence and alternating series A series a n converges absolutely if a n converges.
Taylor and Maclaurin Series
 Taylor and Maclaurin Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background We have seen that some power series converge. When they do, we can think of them as
Taylor and Maclaurin Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background We have seen that some power series converge. When they do, we can think of them as
Homework Problem Answers
 Homework Problem Answers Integration by Parts. (x + ln(x + x. 5x tan 9x 5 ln sec 9x 9 8 (. 55 π π + 6 ln 4. 9 ln 9 (ln 6 8 8 5. (6 + 56 0/ 6. 6 x sin x +6cos x. ( + x e x 8. 4/e 9. 5 x [sin(ln x cos(ln
Homework Problem Answers Integration by Parts. (x + ln(x + x. 5x tan 9x 5 ln sec 9x 9 8 (. 55 π π + 6 ln 4. 9 ln 9 (ln 6 8 8 5. (6 + 56 0/ 6. 6 x sin x +6cos x. ( + x e x 8. 4/e 9. 5 x [sin(ln x cos(ln
1969 AP Calculus BC: Section I
 969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
BC Exam 1 - Part I 28 questions No Calculator Allowed - Solutions C = 2. Which of the following must be true?
 BC Exam 1 - Part I 8 questions No Calculator Allowed - Solutions 6x 5 8x 3 1. Find lim x 0 9x 3 6x 5 A. 3 B. 8 9 C. 4 3 D. 8 3 E. nonexistent ( ) f ( 4) f x. Let f be a function such that lim x 4 x 4 I.
BC Exam 1 - Part I 8 questions No Calculator Allowed - Solutions 6x 5 8x 3 1. Find lim x 0 9x 3 6x 5 A. 3 B. 8 9 C. 4 3 D. 8 3 E. nonexistent ( ) f ( 4) f x. Let f be a function such that lim x 4 x 4 I.
MATH 31B: MIDTERM 2 REVIEW. sin 2 x = 1 cos(2x) dx = x 2 sin(2x) 4. + C = x 2. dx = x sin(2x) + C = x sin x cos x
 MATH 3B: MIDTERM REVIEW JOE HUGHES. Evaluate sin x and cos x. Solution: Recall the identities cos x = + cos(x) Using these formulas gives cos(x) sin x =. Trigonometric Integrals = x sin(x) sin x = cos(x)
MATH 3B: MIDTERM REVIEW JOE HUGHES. Evaluate sin x and cos x. Solution: Recall the identities cos x = + cos(x) Using these formulas gives cos(x) sin x =. Trigonometric Integrals = x sin(x) sin x = cos(x)
8.7 Taylor s Inequality Math 2300 Section 005 Calculus II. f(x) = ln(1 + x) f(0) = 0
 8.7 Taylor s Inequality Math 00 Section 005 Calculus II Name: ANSWER KEY Taylor s Inequality: If f (n+) is continuous and f (n+) < M between the center a and some point x, then f(x) T n (x) M x a n+ (n
8.7 Taylor s Inequality Math 00 Section 005 Calculus II Name: ANSWER KEY Taylor s Inequality: If f (n+) is continuous and f (n+) < M between the center a and some point x, then f(x) T n (x) M x a n+ (n
Study Guide for Final Exam
 Study Guide for Final Exam. You are supposed to be able to calculate the cross product a b of two vectors a and b in R 3, and understand its geometric meaning. As an application, you should be able to
Study Guide for Final Exam. You are supposed to be able to calculate the cross product a b of two vectors a and b in R 3, and understand its geometric meaning. As an application, you should be able to
Math 113 (Calculus 2) Exam 4
 Math 3 (Calculus ) Exam 4 November 0 November, 009 Sections 0, 3 7 Name Student ID Section Instructor In some cases a series may be seen to converge or diverge for more than one reason. For such problems
Math 3 (Calculus ) Exam 4 November 0 November, 009 Sections 0, 3 7 Name Student ID Section Instructor In some cases a series may be seen to converge or diverge for more than one reason. For such problems
Practice Final Exam Solutions
 Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Problem Set 6 Math 213, Fall 2016
 Problem Set 6 Math 213, Fall 216 Directions: Name: Show all your work. You are welcome and encouraged to use Mathematica, or similar software, to check your answers and aid in your understanding of the
Problem Set 6 Math 213, Fall 216 Directions: Name: Show all your work. You are welcome and encouraged to use Mathematica, or similar software, to check your answers and aid in your understanding of the
Taylor and Maclaurin Series. Approximating functions using Polynomials.
 Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
MATH 1080 Test 2 -Version A-SOLUTIONS Fall a. (8 pts) Find the exact length of the curve on the given interval.
 MATH 8 Test -Version A-SOLUTIONS Fall 4. Consider the curve defined by y = ln( sec x), x. a. (8 pts) Find the exact length of the curve on the given interval. sec x tan x = = tan x sec x L = + tan x =
MATH 8 Test -Version A-SOLUTIONS Fall 4. Consider the curve defined by y = ln( sec x), x. a. (8 pts) Find the exact length of the curve on the given interval. sec x tan x = = tan x sec x L = + tan x =
M152: Calculus II Midterm Exam Review
 M52: Calculus II Midterm Exam Review Chapter 4. 4.2 : Mean Value Theorem. - Know the statement and idea of Mean Value Theorem. - Know how to find values of c making the theorem true. - Realize the importance
M52: Calculus II Midterm Exam Review Chapter 4. 4.2 : Mean Value Theorem. - Know the statement and idea of Mean Value Theorem. - Know how to find values of c making the theorem true. - Realize the importance
Exam 1 Review SOLUTIONS
 1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
8.3 Trigonometric Substitution
 8.3 8.3 Trigonometric Substitution Three Basic Substitutions Recall the derivative formulas for the inverse trigonometric functions of sine, secant, tangent. () () (3) d d d ( sin x ) = ( tan x ) = +x
8.3 8.3 Trigonometric Substitution Three Basic Substitutions Recall the derivative formulas for the inverse trigonometric functions of sine, secant, tangent. () () (3) d d d ( sin x ) = ( tan x ) = +x
Things to Know and Be Able to Do Understand the meaning of equations given in parametric and polar forms, and develop a sketch of the appropriate
 AP Calculus BC Review Chapter (Parametric Equations and Polar Coordinates) Things to Know and Be Able to Do Understand the meaning of equations given in parametric and polar forms, and develop a sketch
AP Calculus BC Review Chapter (Parametric Equations and Polar Coordinates) Things to Know and Be Able to Do Understand the meaning of equations given in parametric and polar forms, and develop a sketch
Calculus II Practice Test 1 Problems: , 6.5, Page 1 of 10
 Calculus II Practice Test Problems: 6.-6.3, 6.5, 7.-7.3 Page of This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for the test: review homework,
Calculus II Practice Test Problems: 6.-6.3, 6.5, 7.-7.3 Page of This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for the test: review homework,
5.9 Representations of Functions as a Power Series
 5.9 Representations of Functions as a Power Series Example 5.58. The following geometric series x n + x + x 2 + x 3 + x 4 +... will converge when < x
5.9 Representations of Functions as a Power Series Example 5.58. The following geometric series x n + x + x 2 + x 3 + x 4 +... will converge when < x
2018 FREE RESPONSE QUESTION TENTATIVE SOLUTIONS
 8 FREE RESPONSE QUESTION TENTATIVE SOLUTIONS L. MARIZZA A BAILEY Problem. People enter a line for an escalator at a rate modeled by the function, r given by { 44( t r(t) = ) ( t )7 ) t t > where r(t) is
8 FREE RESPONSE QUESTION TENTATIVE SOLUTIONS L. MARIZZA A BAILEY Problem. People enter a line for an escalator at a rate modeled by the function, r given by { 44( t r(t) = ) ( t )7 ) t t > where r(t) is
False. 1 is a number, the other expressions are invalid.
 Ma1023 Calculus III A Term, 2013 Pseudo-Final Exam Print Name: Pancho Bosphorus 1. Mark the following T and F for false, and if it cannot be determined from the given information. 1 = 0 0 = 1. False. 1
Ma1023 Calculus III A Term, 2013 Pseudo-Final Exam Print Name: Pancho Bosphorus 1. Mark the following T and F for false, and if it cannot be determined from the given information. 1 = 0 0 = 1. False. 1
10550 PRACTICE FINAL EXAM SOLUTIONS. x 2 4. x 2 x 2 5x +6 = lim x +2. x 2 x 3 = 4 1 = 4.
 55 PRACTICE FINAL EXAM SOLUTIONS. First notice that x 2 4 x 2x + 2 x 2 5x +6 x 2x. This function is undefined at x 2. Since, in the it as x 2, we only care about what happens near x 2 an for x less than
55 PRACTICE FINAL EXAM SOLUTIONS. First notice that x 2 4 x 2x + 2 x 2 5x +6 x 2x. This function is undefined at x 2. Since, in the it as x 2, we only care about what happens near x 2 an for x less than
Material for review. By Lei. May, 2011
 Material for review. By Lei. May, 20 You shouldn t only use this to do the review. Read your book and do the example problems. Do the problems in Midterms and homework once again to have a review. Some
Material for review. By Lei. May, 20 You shouldn t only use this to do the review. Read your book and do the example problems. Do the problems in Midterms and homework once again to have a review. Some
Jim Lambers MAT 169 Fall Semester Practice Final Exam
 Jim Lambers MAT 169 Fall Semester 2010-11 Practice Final Exam 1. A ship is moving northwest at a speed of 50 mi/h. A passenger is walking due southeast on the deck at 4 mi/h. Find the speed of the passenger
Jim Lambers MAT 169 Fall Semester 2010-11 Practice Final Exam 1. A ship is moving northwest at a speed of 50 mi/h. A passenger is walking due southeast on the deck at 4 mi/h. Find the speed of the passenger
1. (13%) Find the orthogonal trajectories of the family of curves y = tan 1 (kx), where k is an arbitrary constant. Solution: For the original curves:
 5 微甲 6- 班期末考解答和評分標準. (%) Find the orthogonal trajectories of the family of curves y = tan (kx), where k is an arbitrary constant. For the original curves: dy dx = tan y k = +k x x sin y cos y = +tan y
5 微甲 6- 班期末考解答和評分標準. (%) Find the orthogonal trajectories of the family of curves y = tan (kx), where k is an arbitrary constant. For the original curves: dy dx = tan y k = +k x x sin y cos y = +tan y
Math 142, Final Exam. 12/7/10.
 Math 4, Final Exam. /7/0. No notes, calculator, or text. There are 00 points total. Partial credit may be given. Write your full name in the upper right corner of page. Number the pages in the upper right
Math 4, Final Exam. /7/0. No notes, calculator, or text. There are 00 points total. Partial credit may be given. Write your full name in the upper right corner of page. Number the pages in the upper right
Math 323 Exam 1 Practice Problem Solutions
 Math Exam Practice Problem Solutions. For each of the following curves, first find an equation in x and y whose graph contains the points on the curve. Then sketch the graph of C, indicating its orientation.
Math Exam Practice Problem Solutions. For each of the following curves, first find an equation in x and y whose graph contains the points on the curve. Then sketch the graph of C, indicating its orientation.
PARAMETRIC EQUATIONS AND POLAR COORDINATES
 10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES We have seen how to represent curves by parametric equations. Now, we apply the methods of calculus to these parametric
10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES We have seen how to represent curves by parametric equations. Now, we apply the methods of calculus to these parametric
MTH Calculus with Analytic Geom I TEST 1
 MTH 229-105 Calculus with Analytic Geom I TEST 1 Name Please write your solutions in a clear and precise manner. SHOW your work entirely. (1) Find the equation of a straight line perpendicular to the line
MTH 229-105 Calculus with Analytic Geom I TEST 1 Name Please write your solutions in a clear and precise manner. SHOW your work entirely. (1) Find the equation of a straight line perpendicular to the line
GEORGE ANDROULAKIS THE 7 INDETERMINATE FORMS OF LIMITS : usually we use L Hospital s rule. Two important such limits are lim
 MATH 4 (CALCULUS II) IN ORDER TO OBTAIN A PERFECT SCORE IN ANDROULAKIS MATH 4 CLASS YOU NEED TO MEMORIZE THIS HANDOUT AND SOLVE THE ASSIGNED HOMEWORK ON YOUR OWN GEORGE ANDROULAKIS TRIGONOMETRY θ sin(θ)
MATH 4 (CALCULUS II) IN ORDER TO OBTAIN A PERFECT SCORE IN ANDROULAKIS MATH 4 CLASS YOU NEED TO MEMORIZE THIS HANDOUT AND SOLVE THE ASSIGNED HOMEWORK ON YOUR OWN GEORGE ANDROULAKIS TRIGONOMETRY θ sin(θ)
6.2 Trigonometric Integrals and Substitutions
 Arkansas Tech University MATH 9: Calculus II Dr. Marcel B. Finan 6. Trigonometric Integrals and Substitutions In this section, we discuss integrals with trigonometric integrands and integrals that can
Arkansas Tech University MATH 9: Calculus II Dr. Marcel B. Finan 6. Trigonometric Integrals and Substitutions In this section, we discuss integrals with trigonometric integrands and integrals that can
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
Limits. Final Exam Study Guide. Calculus I. 1. Basic Limits I: Evaluate each limit exactly. (a) lim. (c) lim. 2t 15 3 (g) lim. (e) lim. (f) lim.
 Limits 1. Basic Limits I: Evaluate each limit eactly. 3 ( +5 8) (c) lim(sin(α) 5cos(α)) α π 6 (e) lim t t 15 3 (g) lim t 0 t (4t 3 8t +1) t 1 (tan(θ) cot(θ)+1) θ π 4 (f) lim 16 ( 5 (h) lim t 0 3 t ). Basic
Limits 1. Basic Limits I: Evaluate each limit eactly. 3 ( +5 8) (c) lim(sin(α) 5cos(α)) α π 6 (e) lim t t 15 3 (g) lim t 0 t (4t 3 8t +1) t 1 (tan(θ) cot(θ)+1) θ π 4 (f) lim 16 ( 5 (h) lim t 0 3 t ). Basic
MA 162 FINAL EXAM PRACTICE PROBLEMS Spring Find the angle between the vectors v = 2i + 2j + k and w = 2i + 2j k. C.
 MA 6 FINAL EXAM PRACTICE PROBLEMS Spring. Find the angle between the vectors v = i + j + k and w = i + j k. cos 8 cos 5 cos D. cos 7 E. cos. Find a such that u = i j + ak and v = i + j + k are perpendicular.
MA 6 FINAL EXAM PRACTICE PROBLEMS Spring. Find the angle between the vectors v = i + j + k and w = i + j k. cos 8 cos 5 cos D. cos 7 E. cos. Find a such that u = i j + ak and v = i + j + k are perpendicular.
Chapter 4 Notes, Calculus I with Precalculus 3e Larson/Edwards
 4.1 The Derivative Recall: For the slope of a line we need two points (x 1,y 1 ) and (x 2,y 2 ). Then the slope is given by the formula: m = y x = y 2 y 1 x 2 x 1 On a curve we can find the slope of a
4.1 The Derivative Recall: For the slope of a line we need two points (x 1,y 1 ) and (x 2,y 2 ). Then the slope is given by the formula: m = y x = y 2 y 1 x 2 x 1 On a curve we can find the slope of a
Math 113/113H Winter 2006 Departmental Final Exam
 Name KEY Instructor Section No. Student Number Math 3/3H Winter 26 Departmental Final Exam Instructions: The time limit is 3 hours. Problems -6 short-answer questions, each worth 2 points. Problems 7 through
Name KEY Instructor Section No. Student Number Math 3/3H Winter 26 Departmental Final Exam Instructions: The time limit is 3 hours. Problems -6 short-answer questions, each worth 2 points. Problems 7 through
AP Calculus Testbank (Chapter 9) (Mr. Surowski)
 AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK. Summer Examination 2009.
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
Note: Unless otherwise specified, the domain of a function f is assumed to be the set of all real numbers x for which f (x) is a real number.
 997 AP Calculus BC: Section I, Part A 5 Minutes No Calculator Note: Unless otherwise specified, the domain of a function f is assumed to be the set of all real numbers for which f () is a real number..
997 AP Calculus BC: Section I, Part A 5 Minutes No Calculator Note: Unless otherwise specified, the domain of a function f is assumed to be the set of all real numbers for which f () is a real number..
Brief answers to assigned even numbered problems that were not to be turned in
 Brief answers to assigned even numbered problems that were not to be turned in Section 2.2 2. At point (x 0, x 2 0) on the curve the slope is 2x 0. The point-slope equation of the tangent line to the curve
Brief answers to assigned even numbered problems that were not to be turned in Section 2.2 2. At point (x 0, x 2 0) on the curve the slope is 2x 0. The point-slope equation of the tangent line to the curve
Mathematics 111 (Calculus II) Laboratory Manual
 Mathematics (Calculus II) Laboratory Manual Department of Mathematics & Statistics University of Regina nd edition prepared by Patrick Maidorn, Fotini Labropulu, and Robert Petry University of Regina Department
Mathematics (Calculus II) Laboratory Manual Department of Mathematics & Statistics University of Regina nd edition prepared by Patrick Maidorn, Fotini Labropulu, and Robert Petry University of Regina Department
Final Exam Review Quesitons
 Final Exam Review Quesitons. Compute the following integrals. (a) x x 4 (x ) (x + 4) dx. The appropriate partial fraction form is which simplifies to x x 4 (x ) (x + 4) = A x + B (x ) + C x + 4 + Dx x
Final Exam Review Quesitons. Compute the following integrals. (a) x x 4 (x ) (x + 4) dx. The appropriate partial fraction form is which simplifies to x x 4 (x ) (x + 4) = A x + B (x ) + C x + 4 + Dx x
1. (4 % each, total 20 %) Answer each of the following. (No need to show your work for this problem). 3 n. n!? n=1
 NAME: EXAM 4 - Math 56 SOlutions Instruction: Circle your answers and show all your work CLEARLY Partial credit will be given only when you present what belongs to part of a correct solution (4 % each,
NAME: EXAM 4 - Math 56 SOlutions Instruction: Circle your answers and show all your work CLEARLY Partial credit will be given only when you present what belongs to part of a correct solution (4 % each,
CHALLENGE! (0) = 5. Construct a polynomial with the following behavior at x = 0:
 TAYLOR SERIES Construct a polynomial with the following behavior at x = 0: CHALLENGE! P( x) = a + ax+ ax + ax + ax 2 3 4 0 1 2 3 4 P(0) = 1 P (0) = 2 P (0) = 3 P (0) = 4 P (4) (0) = 5 Sounds hard right?
TAYLOR SERIES Construct a polynomial with the following behavior at x = 0: CHALLENGE! P( x) = a + ax+ ax + ax + ax 2 3 4 0 1 2 3 4 P(0) = 1 P (0) = 2 P (0) = 3 P (0) = 4 P (4) (0) = 5 Sounds hard right?
Final Exam SOLUTIONS MAT 131 Fall 2011
 1. Compute the following its. (a) Final Exam SOLUTIONS MAT 131 Fall 11 x + 1 x 1 x 1 The numerator is always positive, whereas the denominator is negative for numbers slightly smaller than 1. Also, as
1. Compute the following its. (a) Final Exam SOLUTIONS MAT 131 Fall 11 x + 1 x 1 x 1 The numerator is always positive, whereas the denominator is negative for numbers slightly smaller than 1. Also, as
18.01 Final Answers. 1. (1a) By the product rule, (x 3 e x ) = 3x 2 e x + x 3 e x = e x (3x 2 + x 3 ). (1b) If f(x) = sin(2x), then
 8. Final Answers. (a) By the product rule, ( e ) = e + e = e ( + ). (b) If f() = sin(), then f (7) () = 8 cos() since: f () () = cos() f () () = 4 sin() f () () = 8 cos() f (4) () = 6 sin() f (5) () =
8. Final Answers. (a) By the product rule, ( e ) = e + e = e ( + ). (b) If f() = sin(), then f (7) () = 8 cos() since: f () () = cos() f () () = 4 sin() f () () = 8 cos() f (4) () = 6 sin() f (5) () =
4.1 Analysis of functions I: Increase, decrease and concavity
 4.1 Analysis of functions I: Increase, decrease and concavity Definition Let f be defined on an interval and let x 1 and x 2 denote points in that interval. a) f is said to be increasing on the interval
4.1 Analysis of functions I: Increase, decrease and concavity Definition Let f be defined on an interval and let x 1 and x 2 denote points in that interval. a) f is said to be increasing on the interval
for 2 1/3 < t 3 1/3 parametrizes
 Solution to Set 4, due Friday April 1) Section 5.1, Problem ) Explain why the path parametrized by ft) = t, t 1 ) is not smooth. Note this is true more specifically if the interval of t contains t = 1
Solution to Set 4, due Friday April 1) Section 5.1, Problem ) Explain why the path parametrized by ft) = t, t 1 ) is not smooth. Note this is true more specifically if the interval of t contains t = 1
AP Calculus BC Spring Final Part IA. Calculator NOT Allowed. Name:
 AP Calculus BC 6-7 Spring Final Part IA Calculator NOT Allowed Name: . Find the derivative if the function if f ( x) = x 5 8 2x a) f b) f c) f d) f ( ) ( x) = x4 40 x 8 2x ( ) ( x) = x4 40 +x 8 2x ( )
AP Calculus BC 6-7 Spring Final Part IA Calculator NOT Allowed Name: . Find the derivative if the function if f ( x) = x 5 8 2x a) f b) f c) f d) f ( ) ( x) = x4 40 x 8 2x ( ) ( x) = x4 40 +x 8 2x ( )
Math 115 HW #5 Solutions
 Math 5 HW #5 Solutions From 29 4 Find the power series representation for the function and determine the interval of convergence Answer: Using the geometric series formula, f(x) = 3 x 4 3 x 4 = 3(x 4 )
Math 5 HW #5 Solutions From 29 4 Find the power series representation for the function and determine the interval of convergence Answer: Using the geometric series formula, f(x) = 3 x 4 3 x 4 = 3(x 4 )
Math 101 Fall 2006 Exam 1 Solutions Instructor: S. Cautis/M. Simpson/R. Stong Thursday, October 5, 2006
 Math 101 Fall 2006 Exam 1 Solutions Instructor: S. Cautis/M. Simpson/R. Stong Thursday, October 5, 2006 Instructions: This is a closed book, closed notes exam. Use of calculators is not permitted. You
Math 101 Fall 2006 Exam 1 Solutions Instructor: S. Cautis/M. Simpson/R. Stong Thursday, October 5, 2006 Instructions: This is a closed book, closed notes exam. Use of calculators is not permitted. You
Math 2414 Activity 1 (Due by end of class July 23) Precalculus Problems: 3,0 and are tangent to the parabola axis. Find the other line.
 Math 44 Activity (Due by end of class July 3) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
Math 44 Activity (Due by end of class July 3) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
a Write down the coordinates of the point on the curve where t = 2. b Find the value of t at the point on the curve with coordinates ( 5 4, 8).
 Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Examples. 1. (Solution) (a) Suppose f is an increasing function, and let A(x) = x
 Math 31A Final Exam Practice Problems Austin Christian December 1, 15 Here are some practice problems for the final. You ll notice that these problems all come from material since the last exam. You are,
Math 31A Final Exam Practice Problems Austin Christian December 1, 15 Here are some practice problems for the final. You ll notice that these problems all come from material since the last exam. You are,
Mth Review Problems for Test 2 Stewart 8e Chapter 3. For Test #2 study these problems, the examples in your notes, and the homework.
 For Test # study these problems, the examples in your notes, and the homework. Derivative Rules D [u n ] = nu n 1 du D [ln u] = du u D [log b u] = du u ln b D [e u ] = e u du D [a u ] = a u ln a du D [sin
For Test # study these problems, the examples in your notes, and the homework. Derivative Rules D [u n ] = nu n 1 du D [ln u] = du u D [log b u] = du u ln b D [e u ] = e u du D [a u ] = a u ln a du D [sin
Math 190 (Calculus II) Final Review
 Math 90 (Calculus II) Final Review. Sketch the region enclosed by the given curves and find the area of the region. a. y = 7 x, y = x + 4 b. y = cos ( πx ), y = x. Use the specified method to find the
Math 90 (Calculus II) Final Review. Sketch the region enclosed by the given curves and find the area of the region. a. y = 7 x, y = x + 4 b. y = cos ( πx ), y = x. Use the specified method to find the
Let s Get Series(ous)
 Department of Mathematics, Computer Science, and Statistics Bloomsburg University Bloomsburg, Pennsylvania 785 Let s Get Series(ous) Summary Presenting infinite series can be (used to be) a tedious and
Department of Mathematics, Computer Science, and Statistics Bloomsburg University Bloomsburg, Pennsylvania 785 Let s Get Series(ous) Summary Presenting infinite series can be (used to be) a tedious and
Math 113 Winter 2005 Key
 Name Student Number Section Number Instructor Math Winter 005 Key Departmental Final Exam Instructions: The time limit is hours. Problem consists of short answer questions. Problems through are multiple
Name Student Number Section Number Instructor Math Winter 005 Key Departmental Final Exam Instructions: The time limit is hours. Problem consists of short answer questions. Problems through are multiple
Virginia Tech Math 1226 : Past CTE problems
 Virginia Tech Math 16 : Past CTE problems 1. It requires 1 in-pounds of work to stretch a spring from its natural length of 1 in to a length of 1 in. How much additional work (in inch-pounds) is done in
Virginia Tech Math 16 : Past CTE problems 1. It requires 1 in-pounds of work to stretch a spring from its natural length of 1 in to a length of 1 in. How much additional work (in inch-pounds) is done in
