THE QUADRATIC APPROXIMATION LEMMA AND DECOMPOSITIONS OF SUPERLATIVE INDEXES. W. Erwin Diewert. October Discussion Paper No.
|
|
|
- Andra Norman
- 5 years ago
- Views:
Transcription
1 1 THE QUADRATIC APPROXIMATION LEMMA AND DECOMPOSITIONS OF SUPERLATIVE INDEXES by W. Erwin Diewert October 2 Discussion Paper No.: -15 DEPARTMENT OF ECONOMICS THE UNIVERSITY OF BRITISH COLUMBIA VANCOUVER, CANADA V6T 1Z1
2 2 THE QUADRATIC APPROXIMATION LEMMA AND DECOMPOSITIONS OF SUPERLATIVE INDEXES Abstract W. Erwin Diewert, 1 October 3,2 version. Department of Economics, University of British Columbia, Vancouver, B. C., Canada, V6T 1Z1. diewert@econ.ubc.ca It was shown in 1976 that a difference in a quadratic function of N variables evaluated at two points is exactly equal to the sum of the arithmetic average of the first order partial derivatives of the function evaluated at the two points times the differences in the independent variables. In the present paper, this result is generalized and the resulting generalized quadratic approximation lemma is used to establish all of the superlative index number formulae that were derived in Diewert (1976). In addition, some new exact decompositions of the percentage change in the Fisher and Walsh superlative indexes into N components are derived. Each component in this decomposition represents the contribution of a change in a single independent variable to the overall percentage change in the index. Finally, these components are given economic interpretations. Keywords Superlative index, quadratic approximations, percentage change decompositions, price indexes, quantity indexes, Fisher ideal index. Journal of Economic Literature Classification Numbers C43, E31,O47 1 University of British Columbia and NBER. The author thanks the Social Sciences and Humanities Research Council of Canada for financial support and Bert Balk and Rolf Färe for helpful comments.
3 1 THE QUADRATIC APPROXIMATION LEMMA AND DECOMPOSITIONS OF SUPERLATIVE INDEXES 1. Introduction W. Erwin Diewert, 1 October 3, 2 version. Department of Economics, University of British Columbia, Vancouver, B. C., Canada, V6T 1Z1. diewert@econ.ubc.ca Let F(z 1,,z N ) be a quadratic function of N variables, (z 1,,z N ) z; i.e., define F as follows: (1) F(z) a + n=1 N a n z n + i=1 N j=1 N a ij z i z j where a ij = a ji for all i and j. It is well known that a second order Taylor series approximation to a quadratic function will exactly reproduce the quadratic function. It is not so well known that the arithmetic average of two linear approximations will also reproduce a quadratic function exactly. To see this, write the linear approximation to F(z) around the point z (z 1,,z N ) as (2) F(z) F(z ) + F(z ) [z z ] F(z ) + n=1 N F n (z )[z n z n ] where F(z ) [ F(z )/ z 1,, F(z )/ z N ] [F 1 (z ),,F N (z )] is the vector of first order partial derivatives of F evaluated at the point z and x y n=1 N x n y n denotes the inner product of the vectors x and y. The linear approximation to F around another point z 1 is (3) F(z) F(z 1 ) + F(z 1 ) [z z 1 ] F(z 1 ) + n=1 N F n (z 1 )[z n z n 1 ]. Now let z = z 1 in (2) and z = z in (3) and treat the two approximations as equalities. Taking the arithmetic average of the resulting two equations and rearranging terms yields the following equation: (4) F(z 1 ) F(z ) = (1/2)[ F(z ) + F(z 1 )] [z 1 z ] = n=1 N (1/2)[F n (z ) + F n (z 1 )][z n 1 z n ]. It can be verified by substituting the F defined by (1) into (4) that if F is quadratic, then (4) holds exactly for any two points, z and z 1. 2 Note that this result shows that taking an 1 University of British Columbia and NBER. The author thanks the Social Sciences and Humanities Research Council of Canada for financial support and Bert Balk and Rolf Färe for helpful comments. 2 Diewert (1976; 118) and Lau (1979) showed that the converse result also holds; i.e., if (4) holds, then F must be quadratic. Diewert called this result the quadratic approximation lemma.
4 4 average of two first order approximations yields the equivalent of a second order approximation. Diewert (1976; ) used the fact that (4) holds as an identity for quadratic functions to prove that the Törnqvist (1936) (1937) quantity index is exact for a translog aggregator function and that the Törnqvist price index is exact for a translog unit cost function. 4 Diewert established these results by taking a simple transformation of (4). It turns out that other transformations of the quadratic identity (4) can be used to establish the exactness of all of the major families of superlative index numbers. 5 We show this in section 4 below. In section 2, we provide the economic framework for our index number results. In section 3, we provide a rather general transformation of the quadratic identity (4). We then show how a special case of this general result yields the translog results. In section 4, we specialize our general transformation of (4) to yield the exactness of the quadratic mean of order r indexes. Thus our transformation of (4) provides a unified framework for deriving the commonly used superlative index number formulae. In section 5, we specialize the results of section 4 to the case where r equals 2. This specialization allows us to obtain additive percentage change decompositions for the Fisher (1922) ideal price and quantity indexes. In section 6, we specialize the results of section 4 to the case where r equals 1. This specialization allows us to obtain additive percentage change decompositions for some indexes that were originally defined by Walsh (191) (1921). In section 5, we find that our additive percentage change decompositions for the Fisher ideal price and quantity indexes are not unique. Thus it is important to provide some sort of an axiomatic or economic justification for any particular additive percentage change decomposition. In section 7, we provide economic interpretations for our preferred decompositions. Section 8 concludes. We conclude that the decompositions that we obtain for the Törnqvist 6, Fisher and Walsh indexes are particularly attractive. 2. The Economic Framework For simplicity, we consider a consumer 7 who minimizes the cost of achieving a given utility level in two periods where the utility or aggregator function f(q) is (positively) 4 The translog functional form was introduced into the economics literature by Christensen, Jorgenson and Lau (1971) (1973). 5 A superlative index number formula is exact for a flexible functional form; see Diewert (1976). 6 The Törnqvist decomposition was obtained earlier by Diewert and Morrison (1986) and Kohli (199).
5 5 linearly homogeneous, positive for positive q, nondecreasing and concave function in the N variables, q (q 1,,q N ). We assume that we can observe the price vectors that the consumer faces during these two periods, say p t (p 1 t,,p N t ) for t =,1, and the quantity vectors chosen for the two periods, say q t (q 1 t,,q N t ) for t =,1. The unit cost function c that corresponds to the aggregator function f is defined as the minimum cost of achieving the utility level 1; i.e., for each vector of positive commodity prices p, define c by: 8 (5) c(p) min q {p q : f(q) = 1}. Under our assumptions on consumer behavior, the observed period t expenditure on the N commodities, p t q t = n=1 N p n t q n t, will equal the product of the period t utility level, f(q t ), times the period t unit cost, c(p t ): 9 (6) p t q t = c(p t )f(q t ) ; t =,1. Thus taking ratios of the period 1 expenditures on the N commodities to the period observed expenditures, we obtain: (7) p 1 q 1 / p q = [c(p 1 )f(q 1 )]/[c(p )f(q )] = [c(p 1 )/c(p )][f(q 1 )/f(q )]. The term [c(p 1 )/c(p )] on the right hand side of (7) can be interpreted as the consumer s true price index 1 and the term [f(q 1 )/f(q )] can be interpreted as the consumer s true quantity index. If the unit cost function c(p) is differentiable with respect to the components of the price vector p, then Shephard s (1953; 11) Lemma implies the following useful equations: 11 (8) c(p t )/c(p t ) = q t /p t q t ; t =,1. If the aggregator function f(q) is differentiable with respect to the components of q, the Wold s (1944; 69-71) (1953; 145) Identity implies the following equally useful equations: 12 (9) f(q t )/f(q t ) = p t /p t q t ; t =,1. 7 Alternatively, the same theory applies to a producer who minimizes the cost of achieving a given level of output in two periods, where f(q 1,,q N ) is the maximum output that can be produced by the vector of inputs q (q 1,,q N ). This is the framework used by Shephard (1953), Samuelson and Swamy (1974) and Diewert (1976). 8 For additional material on unit cost functions and the other theoretical results used in this section, see Diewert (1974) (1993). 9 See Shephard (1953) or Diewert (1976; 12). 1 This concept for a price index is due to Konüs (1924). 11 See Diewert (1976; 12) for more details. 12 In deriving (9), we also used f(q t ) = f(q t ) q t which follows from Euler s Theorem on homogeneous functions.
6 6 With the above economic preliminaries out of the way, we can derive a generalization of the Quadratic Identity, (4). 3. A Transformed Quadratic Identity We now suppose that our aggregator function f(q) has the following transformed quadratic functional form: (1) g[f(q)] a + n=1 N a n h(q n ) + i=1 N j=1 N a ij h(q i )h(q j ) ; a ij = a ji where the a n and the a ij are constants and the functions g and h are continuous monotonic functions of one variable with nonzero derivatives. Later, we will specialize the general functional form f defined by (1) by choosing specific functions for g and h and we will place some restrictions on the coefficients a n and a ij so that the resulting f will be linearly homogeneous. It is fairly obvious that (1) can be rewritten as a quadratic function of the type defined by (1) if we make some transformations of variables. Thus define: (11) z n h(q n ) ; n = 1,2,,N. Due to the assumed continuity and monotonicity of the function h, we can invert equations (11): (12) q n = h 1 (z n ) ; n = 1,2,,N. We rewrite the N equations in (12) in vector notation as follows: (13) q = H 1 (z) where q (q 1,,q N ) and z (z 1,,z N ). Now define the function of N variables F(z) by: (14) F(z) g[f{h 1 (z)}]. Substituting (11)-(14) into (1) shows that the F defined by (14) is the quadratic function of z defined by (1). We now need to express the first order partial derivatives of F, F n (z) F(z)/ z n, in terms of f, g and h. First note that since h (q n ) by assumption, we have (15) dh 1 (z n )/dz n = 1/h (q n ) ; n = 1,2,,N. Now differentiate (14) with respect to z n : (16) F n (z) = g [f{h 1 (z)}] f n {H 1 (z)} dh 1 (z n )/dz n
7 7 = g [f(q)] f n (q) dh 1 (z n )/dz n using (13) = g [f(q)] f n (q) / h (q n ) using (15). Now substitute (16) into (4) and we obtain the following identity: (17) g[f(q 1 )] g[f(q )] = n=1 N (1/2)[F n (z ) + F n (z 1 )][h(q n 1 ) h(q n )] = n=1 N (1/2)[{f n (q )g [f(q )]/h (q n )} + {f n (q 1 )g [f(q 1 )]/h (q n 1 )}][ h(q n 1 ) h(q n )]. Equation (17) is our generalized quadratic identity and it holds as an identity for all functions f defined by (1). To illustrate the usefulness of (17), let g and h be the natural logarithm functions; i.e., define: (18) g(y) ln y and h(y) ln y. Using g (y) = 1/y and h (y) = 1/y, (17) becomes (19) ln f(q 1 ) ln f(q ) = n=1 N (1/2)[{f n (q )q n /f(q )} + {f n (q 1 )q n 1 /f(q 1 )}][ln q n 1 ln q n ] and (1) becomes (2) ln f(q) a + n=1 N a n ln q n + i=1 N j=1 N a ij ln q i ln q j ; a ij = a ji. Note that the f(q) defined by (2) becomes the well known translog aggregator function. 13 In order to make the f(q) defined by (2) linearly homogeneous, we require the following restrictions: (21) n=1 N a n = 1 ; j=1 N a ij = ; i = 1,2,,N. With the restrictions (21) imposed, f(q) defined by (2) is linearly homogeneous and we can apply Wold s identity (9), f n (q t ) = f(q t )p n t /p t q t, for t =,1 and n = 1,2,,N. Substituting these relations into (19) yields: (22) ln [f(q 1 )/f(q )] = (1/2) n=1 N [s n + s n 1 ] ln [q n 1 /q n ] where s n t p n t q n t /p t q t is the share of period t expenditure on commodity n for t =,1 and n = 1,2,,N. The right hand side of (22) is the logarithm of the Törnqvist quantity index, Q T (p,p 1,q,q 1 ), and the left hand side of (22) is the logarithm of the true quantity index, f(q 1 )/f(q ). Thus we have 13 This functional form was introduced into the economics literature by Christensen, Jorgenson and Lau (1971) (1973).
8 8 (23) f(q 1 )/f(q ) = Q T (p,p 1,q,q 1 ). Note that the right hand sides of (22) and (23) can be calculated using observable data. The above algebra can be repeated for the translog unit cost function, which can be defined by (2), except that c(p) replaces f(q) and ln p n replaces ln q n. The counterpart to (19) becomes (24) ln c(p 1 ) ln c(p ) = n=1 N (1/2)[{c n (p )p n /c(p )} + {c n (p 1 )p n 1 /c(p 1 )}][ln p n 1 ln p n ]. Again, we assume that the restrictions (21) hold so that the translog unit cost function c(p) is linearly homogeneous in the components of p. Now use Shephard s lemma (8), c n (p t ) = c(p t )q n t /p t q t, for t =,1 and n = 1,2,,N. Substituting these relations into (24) yields: (25) ln [c(p 1 )/c(p )] = (1/2) n=1 N [s n + s n 1 ] ln [p n 1 /p n ]. The right hand side of (25) is the logarithm of the Törnqvist price index, P T (p,p 1,q,q 1 ), and the left hand side of (25) is the logarithm of the true price index, c(p 1 )/c(p ). Thus we have (26) c(p 1 )/c(p ) = P T (p,p 1,q,q 1 ). The exact index number results (23) and (26) illustrate the usefulness of the generalized quadratic identity (17) even though these results are not new. 14 In the following section, we provide some new applications of (17). 4. The Generalized Quadratic Identity and Mean of Order r Indexes Recall the generalized quadratic functional form defined by (1) above. We now place the following restrictions on the coefficients a n : (27) a n = ; n =,1,.,N. We also assume that the functions g and h which appear in the definition of f are defined as follows: (28) g(y) y r ; h(y) y 1/2r ; r. Using the restrictions (27) and (28), the function f defined by (1) becomes the following quadratic mean of order r aggregator function: (29) f(q) [ i=1 N j=1 N a ij q i 1/2r q j 1/2r ] 1/r ; a ij = a ji. 14 See Diewert (1976; ).
9 9 It can be shown that f(q) defined by (29) is linearly homogeneous flexible functional form; that is, it can provide a second order approximation to an arbitrary twice continuously differentiable linearly homogeneous function. 15 Substituting the restrictions and definitions (27) and (28) into the generalized quadratic identity (17) yields the following identity: (3) [f(q 1 )] r [f(q )] r = (1/2) n=1 N [{f n (q )r[f(q )] r 1 /[(r/2)(q n ) (r/2) 1 ]} + {f n (q 1 )r[f(q 1 )] r 1 /[(r/2)(q n 1 ) (r/2) 1 ]}[(q n 1 ) r/2 (q n ) r/2 ] or (31) [f 1 ] r [f ] r = n=1 N [f n {f } r 1 (q n ) 1 r/2 + f n 1 {f 1 } r 1 (q n 1 ) 1 r/2 ][(q n 1 ) r/2 (q n ) r/2 ] where we have simplified the notation by defining (32) f f(q ) ; f 1 f(q 1 ) ; f n t f n (q t ) f(q t )/ q n ; t =,1 ; n = 1,2,,N. Since the f(q) defined by (29) is linearly homogeneous, we may use Wold s identity (9) to replace the partial derivatives f n t by p n t f t /p t q t. The notation will be simplified if we define the period t normalized price for commodity n, w n t, as follows: (33) w t n p t n /p t q t t =,1 ; n = 1,2,,N =[1/f(q t )] f(q t )/ q n using Wold s identity, (9) = ln f(q t )/ q n = f t n / f t using the notation in (32). Thus w n t is the period t price for commodity n, p n t, divided by period t expenditure on all commodities in the aggregate, p t q t n=1 N p n t q n t. Using Wold s identity, the normalized price w n t is equal to the logarithmic derivative of the aggregator function with respect to commodity n evaluated at the period t data, ln f(q t )/ q n. Making use of (33), (31) can be rewritten as follows: (34) [f 1 ] r [f ] r = n=1 N [w n {f } r (q n ) 1 r/2 + w n 1 {f 1 } r (q n 1 ) 1 r/2 ][(q n 1 ) r/2 (q n ) r/2 ]. Now divide both sides of (34) through by [f ] r to obtain: (35) [f 1 /f ] r 1 = n=1 N [w n (q n ) 1 r/2 + w n 1 {f 1 /f } r (q n 1 ) 1 r/2 ][(q n 1 ) r/2 (q n ) r/2 ]. Now f 1 /f is the true quantity index, Q r f(q 1 )/f(q ). Replace f 1 /f in (35) by Q r and solve the resulting equation for Q r. We obtain the following solution: 15 See Diewert (1976; 13). Färe and Sung (1986) showed that the translog case considered earlier and the present normalized quadratic function are the only special cases of the family of generalized quadratic functions that are also linearly homogeneous.
10 1 (36) Q r = [ n=1 N (q n 1 /q n ) r/2 s n ] 1/r [ n=1 N (q n 1 /q n ) r/2 s n 1 ] 1/r where s n t is the period t expenditure share for commodity n; i.e., (37) s t n p t n q t n /p t q t ; t =,1 ; n = 1,2,,N = w t t n q n using definitions (33). The index number formula on the right hand side of (36) depends only on the observed prices and quantities pertaining to the two periods under consideration and it is equal to the quadratic mean of order r quantity index defined by Diewert (1976; 13). The above results show that it is exactly equal to f(q 1 )/f(q ) where f is the quadratic mean of order r aggregator function defined by (29). Thus we have used the generalized quadratic identity (17) in order to establish this exactness result. The above algebra for quantity indexes has its counterpart for price indexes as we now show. Define the quadratic mean of order r unit cost function c(p) by: (38) c(p) [ i=1 N j=1 N a ij p i 1/2r p j 1/2r ] 1/r ; a ij = a ji. Define the period t normalized quantity for commodity n, v n t, as follows: (39) v t n q t n /p t q t t =,1 ; n = 1,2,,N = [ c(p t )/ p n ]/c(p t ) using Shephard s lemma, (8) = ln c(p t )/ p n. Let the level of unit cost in period be c c(p ) and the level of unit cost in period 1 be c 1 c(p 1 ). The counterpart to (35) is now (4) [c 1 /c ] r 1 = n=1 N [v n (p n ) 1 r/2 + v n 1 {c 1 /c } r (p n 1 ) 1 r/2 ][(p n 1 ) r/2 (p n ) r/2 ]. Note that c 1 /c c(p 1 )/c(p ) P r is the true price index that corresponds to the unit cost function defined by (38). Now replace c 1 /c in equation (4) by P r and solve the resulting equation for P r. We obtain the following solution: (41) P r = [ n=1 N (p n 1 /p n ) r/2 s n ] 1/r [ n=1 N (p n 1 /p n ) r/2 s n 1 ] 1/r where s n t is the period t expenditure share for commodity n defined earlier by (37). The index number formula on the right hand side of (41) depends only on the observed prices and quantities pertaining to the two periods under consideration and it is equal to the quadratic mean of order r price index defined by Diewert (1976; 131). The above results show that it is exactly equal to c(p 1 )/c(p ) where c is the quadratic mean of order r unit cost function defined by (38). Thus again we have used the generalized quadratic identity (17) in order to establish this exactness result. In the following two sections, we examine equations (35) and (4) more closely for the special cases when r = 1 or 2.
11 11 5. Additive Percentage Change Decompositions for the Fisher Ideal Indexes It can be verified that when r = 2, Q 2 defined by (36) turns out to equal the Fisher (1922) ideal quantity index Q F ; i.e., we have (42) Q 2 = Q F (p,p 1,q,q 1 ) [{p q 1 /p q }{p 1 q 1 /p 1 q }] 1/2. Using (34) when r = 2, we have the following decomposition: 16 (43) [f 1 ] 2 [f ] 2 = n=1 N [w n {f } 2 + w n 1 {f 1 } 2 ][q n 1 q n ] where the normalized prices w n t are defined by (33). From elementary algebra, we have: (44) [f 1 ] 2 [f ] 2 = [f 1 f ] [f 1 + f ]. Now divide both sides of (43) by f 1 + f. Using (44), the resulting equation becomes: (45) f 1 f = f n=1 N {(f /[f + f 1 ])w n + (f 1 /f ){(f 1 /[f + f 1 ])w n 1 }{q n 1 q n }. Divide both sides of (45) by f and using Q F = f 1 /f, we have the following additive percentage change decomposition for the Fisher ideal quantity index: 17 (46) Q F 1 = n=1 N {(1/[1 + Q F ])w n + (Q F /[1 +Q F ]) Q F w n 1 }{q n 1 q n }. In the above decomposition, the term in front of the change in quantity n going from period to 1, Q Fn, the nth percentage change quantity weight, is defined as follows: (47) Q Fn (1/[1 + Q F ])w n + (Q F /[1 +Q F ]) Q F w n 1. Note that the nth percentage change quantity weight is almost a weighted average (with weights (1/[1 + Q F ]) and (Q F /[1 +Q F ]) which sum to unity) of the two normalized prices t t for commodity n in the two periods under consideration, w n p n /p t q t for t =,1. However, the period 1 normalized price w 1 n gets an extra weighting factor equal to Q F, the value of the Fisher quantity index going from period to 1. If Q F = 1, then Q Fn is equal to the arithmetic average of the normalized prices for commodity n, (1/2)w n + (1/2)w 1 n. In a manner analogous to the derivation of (46), we can obtain the following additive percentage change decomposition for the Fisher ideal price index: (48) P F 1 = n=1 N {(1/[1 + P F ])v n + (P F /[1 +P F ]) P F v n 1 }{p n 1 p n } 16 This decomposition was used already by Reinsdorf, Diewert and Ehemann (2). 17 If we solve equation (46) for Q F, we obtain the Fisher ideal index defined by (42) as the solution. This shows that (46) is an identity, which is valid for all p,p 1,q,q 1.
12 12 where the Fisher ideal price index P F is defined as follows: (49) P F (p,p 1,q,q 1 ) [{p 1 q /p q }{p 1 q 1 /p q 1 }] 1/2 = p 1 q 1 /p q Q F (p,p 1,q,q 1 ) where Q F is the Fisher ideal quantity index defined earlier by (42). In the decomposition (48), the term in front of the change in price n going from period to 1, P Fn, the nth percentage change price weight, is defined as follows: (5) P Fn (1/[1 + P F ])v n + (P F /[1 +P F ]) P F v n 1 where the normalized quantities, v n t are equal to q n t /p t q t for t =,1. It should be noted that the concept of a price or quantity index number formula having an additive percentage change decomposition is not quite the same as an index number formula having the property of additivity. We now explain the difference. A price index, P(p,p 1,q,q 1 ), is said to be additive if it can be written as follows: (51) P(p,p 1,q,q 1 ) = n=1 N q n *p n 1 / n=1 N q n *p n where the quantity weights q n * are usually taken to be some sort of average of the base and current period quantities for commodity n, q n and q n 1. However, in principle, more complicated quantity weighting could be used: the important factor in the definition of additivity given by (51) is that the quantity weights be the same in the numerator and the denominator of the right hand side of (51). In a similar manner, a quantity index, Q(p,p 1,q,q 1 ), is said to be additive if it can be written as follows: (52) Q(p,p 1,q,q 1 ) = n=1 N p n *q n 1 / n=1 N p n *q n where the price weights p n * are usually taken to be some sort of average of the base and current period prices for commodity n, p n and p n 1. However, in principle, more complicated price weighting could be used: as before, the important factor in the definition of additivity given by (52) is that the price weights be the same in the numerator and the denominator of the right hand side of (52). It is straightforward to show that additive price and quantity indexes have additive percentage change decompositions. For example, suppose we have an additive quantity index of the type defined by (52) above. Then we have: (53) Q(p,p 1,q,q 1 ) 1 = [ n=1 N p n *q n 1 / n=1 N p n *q n ] 1 using (52) = [ n=1 N p n *q n 1 / n=1 N p n *q n ] [ n=1 N p n *q n / n=1 N p n *q n ] = [ n=1 N p n *{q n 1 q n }] / n=1 N p n *q n
13 13 = n=1 N Q n {q n 1 q n } where the nth percentage change quantity weight Q n is defined as (54) Q n p n */ n=1 N p n *q n ; n = 1,,N. Thus we can always find an additive percentage change decomposition for an additive price or quantity index. However, it is not always possible to go from an additive percentage change decomposition to a corresponding additive index number formula. 18 Unfortunately, the additive percentage change decompositions (46) and (48) that we obtained for the Fisher quantity and price indexes are not unique. For example, Van Ijzeren (1987;6) chose the following values for the quantity weights q n * which appear in (51) above: (55) q n * (1/2)q n + (1/2)q n 1 /Q F (p,p 1,q,q 1 ) ; n = 1,2,,N where Q F is the Fisher quantity index defined by (42). Thus the reference quantity for commodity n in formula (51), q n *, is chosen to be the arithmetic mean of the period and period 1 observed use of commodity n, except that the period 1 use, q n 1, is deflated by the Fisher quantity index, Q F, for the entire group of commodities in the aggregate. To show that the resulting price index defined by (51) is the Fisher ideal price index, replace Q F in (55) by p 1 q 1 /p q P if necessary. Now solve (51) using the weights defined by (55) for P; i.e., solve the resulting equation for P: (56) P = n=1 N (1/2)[q n + q n 1 /Q}]p n 1 / n=1 N (1/2)[q n + q n 1 /Q]p n = [p 1 q + p 1 q 1 /Q] / [p q + p q 1 /Q] or PQp q + p q 1 P = Qp 1 q + p 1 q 1 or [p 1 q 1 /p q ] p q + p q 1 P = Qp 1 q + p 1 q 1 using PQ = [p 1 q 1 /p q ] or p q 1 P = Qp 1 q canceling terms or p q 1 P = [p 1 q 1 /p q P]p 1 q using Q = p 1 q 1 /p q P or P 2 = [p 1 q 1 /p q 1 ][ p 1 q /p q ] or (57) P = {[p 1 q 1 /p q 1 ][ p 1 q /p q ]} 1/2 P F. Thus (51) and (55) provide an exact additive representation for the Fisher ideal price index. In a similar fashion, Van Ijzeren (1987;6) showed that if we choose the following values for the price weights p n * which appear in (52) above: 18 It does not seem to be possible to go from the additive percentage change decomposition for the Fisher quantity index given by (46) to a corresponding additive representation of the form defined by (52).
14 14 (58) p n * (1/2)p n + (1/2)p n 1 /P F (p,p 1,q,q 1 ) ; n = 1,2,,N where P F is the Fisher price index defined by (49), then (52) and (58) provide an exact additive representation for the Fisher ideal quantity index. Since an additive representation for index number formula implies an additive percentage change decomposition for the formula, we see that our additive percentage change decompositions for the Fisher ideal price and quantity indexes given by (48) and (46) above are not unique. 19 In retrospect, it is not surprising that additive percentage change decompositions of any index number formula are not unique (unless the decomposition has to satisfy further properties). To see this, look at the right hand side of equation (52), which is homogeneous of degree in p 1 *,,p N *. Thus given an index value Q, we can never determine the scale of the p n *. Hence, let us impose a normalization on the p n *, such as: (59) n=1 N p n *q n = 1. Using (59), equation (52), which defines an additive representation for the quantity index Q, can be rewritten as follows: (6) n=1 N p n *q n 1 = Q. Equations (59) and (6) can be regarded as two simultaneous linear equations in the N unknowns, p 1 *,,p N *. Obviously, as soon as N exceeds 2, there will be an infinite number of solutions to (59) and (6) in general. Thus the quest for unique additive representations or unique additive percentage change decompositions of an index number formula is doomed to failure. Hence any particular additive percentage change decomposition needs to be justified on axiomatic grounds or on its economic interpretation. We will return to this topic after the following section. In the following section, we examine equations (35) and (4) for the special case when r equals Additive Percentage Change Decompositions for the Implicit Walsh Indexes Our goal in this section is to provide some additive percentage change decompositions for some indexes defined by Walsh. 19 In fact, two additional additive percentage change decompositions for the Fisher indexes may be found in Reinsdorf, Diewert and Ehemann (2). The first of these two decompositions turns out to be equivalent to the decomposition of Van Ijzeren (1987; 6), which was also independently derived by Dikhanov (1997). The Van Ijzeren decomposition is currently being used by Bureau of Economic Analysis; see Moulton and Seskin (1999; 16) and Ehemann, Katz and Moulton (2).
15 15 Walsh(191; 398) (1921; 97) defined the following very useful price index: 2 (61) P W (p,p 1,q,q 1 ) n=1 N [q n q n 1 ] 1/2 p n 1 / n=1 N [q n q n 1 ] 1/2 p n. Thus the Walsh price index is an additive price index of the type defined by (51) where the quantity weights q n * are equal to the geometric means of the period and 1 consumption of commodity n, [q n q n 1 ] 1/2. As indicated in the previous section, the Walsh price index necessarily has an additive percentage change decomposition. Using the fact that the price index times the quantity index should equal the value ratio for the two periods under consideration; i.e., using 21 (62) P W (p,p 1,q,q 1 ) Q W *(p,p 1,q,q 1 ) = p 1 q 1 /p q, we can define the implicit Walsh quantity index Q W * that corresponds to P W defined by (61) as follows: (63) Q W *(p,p 1,q,q 1 ) [p 1 q 1 /p q ]/P W (p,p 1,q,q 1 ) = { n=1 N [q n q n 1 ] 1/2 p n /p q }/{ n=1 N [q n q n 1 ] 1/2 p n 1 / p 1 q 1 } using (61) = { n=1 N [q n 1 /q n ] 1/2 p n q n /p q }/{ n=1 N [q n /q n 1 ] 1/2 p n 1 q n 1 / p 1 q 1 } = { n=1 N [q n 1 /q n ] 1/2 s n }/{ n=1 N [q n /q n 1 ] 1/2 s n 1 } using (37) = Q 1 (p,p 1,q,q 1 ) where Q 1 is a quadratic mean of order r quantity index defined by (36) when r = 1. Thus the Walsh implicit quantity index, Q W *, is equal to a special case of the quadratic mean of order quantity indexes defined earlier. It is not at all obvious what an additive percentage change decomposition for the implicit Walsh quantity index would look like. However, using the decomposition (35) for r = 1 yields the following equation: (64) Q 1 1 = n=1 N [w n (q n ) 1/2 + w n 1 {Q 1 }(q n 1 ) 1/2 ][(q n 1 ) 1/2 (q n ) 1/2 ] where Q 1 is defined by (63). Now multiply the numerator and the denominator of the nth term on the right hand side of (64) by (q n 1 ) 1/2 + (q n 1 ) 1/2 for n = 1,,N. The resulting equation is: (65) Q 1 1 = n=1 N [w n {(q n ) 1/2 /[(q n 1 ) 1/2 + (q n 1 ) 1/2 ]} + w n 1 Q 1 {(q n 1 ) 1/2 /[(q n 1 ) 1/2 + (q n 1 ) 1/2 ]}[q n 1 q n ] = n=1 N Q 1n [q n 1 q n ] 2 Diewert (2) made a case for this index being the best pure price or fixed basket type index. The Australian statistician Knibbs (1924; 43-44) was perhaps the first to define the class of fixed basket type indexes, which he called unequivocal indexes. 21 See (7) above. Fisher (1911) was the first to suggest that that the product of the price and quantity indexes should equal the value ratio between the two periods under consideration.
16 16 where the nth Walsh percentage change quantity weight Q 1n is defined as (66) Q 1n w n {(q n ) 1/2 /[(q n 1 ) 1/2 + (q n 1 ) 1/2 ]} + w n 1 Q 1 {(q n 1 ) 1/2 /[(q n 1 ) 1/2 + (q n 1 ) 1/2 ]}. Note that the nth percentage change quantity weight is almost a weighted average (with weights (q n ) 1/2 /[(q n 1 ) 1/2 + (q n 1 ) 1/2 ] and (q n 1 ) 1/2 /[(q n 1 ) 1/2 + (q n 1 ) 1/2 ] which sum to unity) of the two normalized prices for commodity n in the two periods under consideration, w n t p n t /p t q t for t =,1. However, as was the case with the Fisher decomposition defined earlier by (46) and (47), the period 1 normalized price w n 1 gets an extra weighting factor equal to Q 1, the value of the Walsh implicit quantity index going from period to 1. The counterpart to the Walsh price index defined by (61) above is the Walsh (1921; 13) quantity index Q W defined as follows: 22 (67) Q W (p,p 1,q,q 1 ) n=1 N [p n p n 1 ] 1/2 q n 1 / n=1 N [p n p n 1 ] 1/2 q n. It is easy to see that the Walsh quantity index has the additive form defined by (52) where the nth price weight p n * is the geometric mean of the period and 1 prices for commodity n, [p n p n 1 ] 1/2. Thus the Walsh quantity index also has an additive percentage change decomposition; recall (53) and (54) above. The Walsh (1921; 13) implicit price index that corresponds to the Walsh quantity index Q W defined by (67) is defined as follows: (68) P W *(p,p 1,q,q 1 ) [p 1 q 1 /p q ]/Q W (p,p 1,q,q 1 ) = { n=1 N [p n p n 1 ] 1/2 q n /p q }/{ n=1 N [p n p n 1 ] 1/2 q n 1 / p 1 q 1 } using (67) = { n=1 N [p n 1 /p n ] 1/2 p n q n /p q }/{ n=1 N [p n /p n 1 ] 1/2 p n 1 q n 1 / p 1 q 1 } = { n=1 N [p n 1 /p n ] 1/2 s n }/{ n=1 N [p n /p n 1 ] 1/2 s n 1 } using (37) = P 1 (p,p 1,q,q 1 ) where P 1 is a quadratic mean of order r price index defined by (42) when r = 1. Thus the Walsh implicit price index, P W *, is equal to a special case of the quadratic mean of order quantity indexes defined earlier. We can repeat the algebra associated with (64) and (65) above using the decomposition (4) in place of (35) to show that the Walsh implicit price index has the following additive percentage change decomposition: (69) P 1 1 = n=1 N P 1n [p n 1 p n ] where the nth Walsh percentage change price weight P 1n is defined as (7) P 1n v n {(p n ) 1/2 /[(p n 1 ) 1/2 + (p n 1 ) 1/2 ]} + v n 1 P 1 {(p n 1 ) 1/2 /[(p n 1 ) 1/2 + (p n 1 ) 1/2 ]}. 22 The Walsh quantity index is a special case of Knibb s (1924; 43-44) class of unequivocal quantity indexes. See Diewert (2) for further discussion.
17 17 Note that the nth percentage change price weight is almost a weighted average (with weights (p n ) 1/2 /[(p n 1 ) 1/2 + (p n 1 ) 1/2 ] and (p n 1 ) 1/2 /[(p n 1 ) 1/2 + (p n 1 ) 1/2 ] which sum to unity) of the two normalized quantities for commodity n in the two periods under consideration, v n t q n t /p t q t for t =,1. However, as was the case with the Fisher decomposition defined earlier by (48), the period 1 normalized quantity v n 1 gets an extra weighting factor equal to P 1, the value of the Walsh implicit price index going from period to 1. The results in this section show that all four of the Walsh price and quantity indexes have additive percentage change decompositions. In the following section, we will attempt to provide economic interpretations for the terms in two of these additive decompositions. 7. Economic Interpretations for Some Additive Percentage Change Decompositions Given that in general an infinite number of additive percentage change decompositions are possible for any given price or quantity index, it will be useful to find decompositions such that each term in the decomposition has an economic interpretation. In this section, we shall show how this can be done for some of the most commonly used superlative index number formulae. 23 We first need to provide an exact interpretation for each of the N terms on the right hand side of the quadratic identity (4) above. Let F(z) be the quadratic function defined by (1) and consider a change in the vector z from the base period situation z (z 1,z 2,,z N ) to (z 1 1,z 2,,z N ); i.e., only the first component of z changes from the base period value z 1 to the period 1 value z 1 1. Then since F(z 1,z 2,,z N ) is quadratic in z 1, we can apply the quadratic identity (4) to this change and get the following equation: (71) F(z 1 1,z 2,,z N ) F(z 1,z 2,,z N ) = (1/2)[F 1 (z 1,z 2,,z N ) + F 1 (z 1 1,z 2,,z N )][z 1 1 z 1 ] = (1/2)[a 1 +2a 11 z 1 + i=2 N 2a 1i z i + a 1 +2a 11 z i=2 N 2a 1i z i ][ z 1 1 z 1 ] partially differentiating the F defined by (1) = (1/2)[ F 1 (z 1,z 2,,z N )+2a 11 (z 1 1 z 1 )+F 1 (z 1,z 2,,z N )][ z 1 1 z 1 ] = [F 1 (z 1,z 2,,z N )+a 11 (z 1 1 z 1 )][ z 1 1 z 1 ]. Now consider a change in z from (z 1,z 2 1,,z N 1 ) to z 1 (z 1 1,z 2 1,,z N 1 ). In a manner analogous to our derivation of (71), we can show that (72) F(z 1 1,z 2 1,,z N 1 ) F(z 1,z 2 1,,z N 1 ) = (1/2)[F 1 (z 1,z 2 1,,z N 1 ) + F 1 (z 1 1,z 2 1,,z N 1 )][z 1 1 z 1 ] = (1/2)[a 1 +2a 11 z 1 + i=2 N 2a 1i z i 1 + a 1 +2a 11 z i=2 N 2a 1i z i 1 ][ z 1 1 z 1 ] partially differentiating the F defined by (1) = (1/2)[ F 1 (z 1 1,z 2 1,,z N 1 )+2a 11 (z 1 z 1 1 )+F 1 (z 1 1,z 2 1,,z N 1 )][ z 1 1 z 1 ] = [F 1 (z 1 1,z 2 1,,z N 1 ) a 11 (z 1 1 z 1 )][ z 1 1 z 1 ]. 23 For the Törnqvist price and quantity indexes, we will obtain multiplicative decompositions rather than additive ones.
18 18 Finally, take the arithmetic average of equations (71) and (72) and we obtain the following exact identity: (73) (1/2)[F(z 1 1,z 2,,z N ) F(z 1,z 2,,z N )]+(1/2)[F(z 1 1,z 2 1,,z N 1 ) F(z 1,z 2 1,,z N 1 )] = (1/2)[F 1 (z 1,z 2,,z N ) + F 1 (z 1 1,z 2 1,,z N 1 )][ z 1 1 z 1 ]. Note that the right hand side of (73) is the first term on the right hand side of the quadratic identity (4). Thus this first term is equal to the arithmetic average of two differences in the level of F(z) where only the first component of the z vector changes in each of these two differences. We define the left hand side of (73) as the first difference effect, δ 1. In general, define the nth difference effect, δ n, as follows: (74) δ n (1/2)[F(z 1,,z n 1,z n 1,z n+1,z N ) F(z 1,z 2,,z N )] + (1/2)[F(z 1 1,z 2 1,,z N 1 ) F(z 1 1, z n 1 1,z n,z n+1 1,z N 1 )] ; n = 1,2,,N. Thus δ n is the arithmetic average of two hypothetical changes in F(z) where in the first (second) change, only the nth component changes from its period level of z n to its period 1 level z n 1 and all other components of z are held constant at their period (1) levels. In a manner analogous to our derivation of (73), we can show that δ n is equal to the nth term on the right hand side of the quadratic identity (4); i.e., we have: (75) δ n = (1/2)[F n (z 1,z 2,,z N ) + F n (z 1 1,z 2 1,,z N 1 )][ z n 1 z n ] n = 1,2,,N. We now have to translate equations (74) and (75) into our generalized quadratic identity framework. If f(q) is defined by (1), it is straightforward to show that the counterpart to (75) is (76) δ n = (1/2)[{f n (q )g [f(q )]/h (q n )} + {f n (q 1 )g [f(q 1 )]/h (q n 1 )}][ h(q n 1 ) h(q n )] ; n = 1,2,,N where δ n is now defined as follows: (77) δ n (1/2){g[f(q 1,,q n 1,q n 1,q n+1,q N )] g[f(q 1,q 2,,q N )]} + (1/2){g[f(q 1 1,q 2 1,,q N 1 )] g[f(q 1 1, q n 1 1,q n,q n+1 1,q N 1 )]} ; n = 1,2,,N. Note that the right hand side of (76) is the nth term in our generalized quadratic identity and (77) gives an economic interpretation for this term in terms of differences in g[f(q)] where only the nth component of q changes. Thus each of the N terms on the right hand side of the generalized quadratic identity (17) has an economic interpretation as an average of two finite differences in the level of our transformed aggregator function g[f(q)] where only one component of q changes in each of the finite differences. We now specialize (76) and (77) by considering specific functions for g and h.
19 19 The first special case that we consider is the case where g and h are the natural logarithm functions (recall (18) above), which gave rise to the translog aggregator function defined by (2) and (21). In this case, the generalized quadratic identity (17) became (22). Thus we have: (78) ln [f(q 1 )/f(q )] = n=1 N (1/2)[s n + s n 1 ] ln [q n 1 /q n ] = n=1 N δ n where δ n is defined by (77) where g is the logarithm function in this special case. It is useful to introduce some additional notation at this point. Define the base period nth quantity effect σ n as the relative change in the aggregate going from the base period quantities q to new quantities where we only change q n to the period 1 level, q n 1 ; i.e., define σ n as follows: (79) σ n f(q 1,,q n 1,q n 1,q n+1,q N )/f(q 1,q 2,,q N ) ; n = 1,2,,N. Define the current period nth quantity effect σ n 1 as the relative change in the aggregate going to the current period quantities q 1 from quantities where all quantities are at their period 1 levels except q n is equal to the period level, q n ; i.e., define σ n 1 as follows: (8) σ n 1 f(q 1 1,q 2 1,,q N 1 )/f(q 1 1, q n 1 1,q n,q n+1 1,q N 1 ) ; n = 1,2,,N. Finally, define the nth quantity effect c n as the geometric mean of the base and current period quantity effects defined by (79) and (8); i.e., define (81) c n [σ n σ n 1 ] 1/2 ; n = 1,2,,N. Using this new notation and exponentiating both sides of (78), we obtain the following decomposition for the Törnqvist quantity index, Q T (p,p 1,q,q 1 ) (recall (23) above): 24 (82) f(q 1 )/f(q ) = Q T (p,p 1,q,q 1 ) = n=1 N exp[δ n ] where exp[y] e y = n=1 N [σ n σ n 1 ] 1/2 = n=1 N c n. Thus we have an exact multiplicative decomposition of the Törnqvist quantity index Q T into a product of N quantity effects, n=1 N c n, where each quantity effect is a quantity index which shows the effect of changing just the nth quantity from q n to q n 1 ; see (79) to (81) above. 24 For similar decompositions in the profit or revenue function context, see Diewert and Morrison (1986; ) and Kohli (199).
20 2 The same algebra works for a multiplicative decomposition for the Törnqvist price index P T defined earlier by (25) and (26). Again, we introduce some additional notation in order to define the terms in the decomposition. Define the base period nth price effect ρ n as the relative change in the aggregate going from the base period prices p to new prices where we only change p n to the period 1 level, p n 1 ; i.e., define ρ n as follows: (83) ρ n c(p 1,,p n 1,p n 1,p n+1,p N )/c(p 1,p 2,,p N ) ; n = 1,2,,N where c(p) is the translog unit cost function defined in section 3 above. Define the current period nth price effect ρ n 1 as the relative change in the aggregate going to the current period prices p 1 from prices where all prices are at their period 1 levels except p n is equal to the period level, p n ; i.e., define ρ n 1 as follows: (84) ρ n 1 c(p 1 1,p 2 1,,p N 1 )/c(p 1 1, p n 1 1,p n,p n+1 1,p N 1 ) ; n = 1,2,,N. Finally, define the nth price effect b n as the geometric mean of the base and current period quantity effects defined by (83) and (84); i.e., define (85) b n [ρ n ρ n 1 ] 1/2 ; n = 1,2,,N. Using this new notation, we obtain the following decomposition for the Törnqvist price index, P T (p,p 1,q,q 1 ) (recall (26) above): 25 (86) c(p 1 )/c(p ) = P T (p,p 1,q,q 1 ) = n=1 N exp{(1/2) [s n + s n 1 ] ln [p n 1 /p n ]} = n=1 N [ρ n ρ n 1 ] 1/2 = n=1 N b n. Thus we have an exact multiplicative decomposition of the Törnqvist price index P T into a product of N price effects, n=1 N b n, where each price effect is a price index which shows the effect of changing just the nth price from p n to p n 1. We turn now to our second special case of (76) and (77) where g and h are defined by (28) for r and the restrictions (27) are satisfied. Thus f(q) is the quadratic mean of order r aggregator function defined by (29) for r. Using (76) and (77) above, the generalized quadratic identity (34) in this case becomes: (87) [f 1 ] r [f ] r = n=1 N [w n {f } r (q n ) 1 r/2 + w n 1 {f 1 } r (q n 1 ) 1 r/2 ][(q n 1 ) r/2 (q n ) r/2 ] = n=1 N δ n where δ n defined in general by (77) becomes the following expression when the restrictions (27) and (28) are satisfied: 25 See Diewert and Morrison (1986; ) and Kohli (199) for similar decompositions.
21 21 (88) δ n = (1/2){[f(q 1,,q n 1,q n 1,q n+1,q N )] r [f(q 1,q 2,,q N )] r } + (1/2){[f(q 1 1,q 2 1,,q N 1 )] r [f(q 1 1, q n 1 1,q n,q n+1 1,q N 1 )] r } ; n = 1,2,,N = (1/2)[f ] r {[σ n ] r 1} + (1/2)[f 1 ] r {1 [1/σ n 1 ] r } where the quantity effects σ n and σ n 1 are defined by (79) and (8). Now specialize (87) to the case where r = 1. Upon dividing both sides of (87) by f, we obtain the following additive percentage change decomposition for the implicit Walsh quantity index Q 1 defined earlier by (63): (89) Q 1 1 = n=1 N δ n / f where δ n / f is defined as (9) δ n / f (1/2){σ n 1} + (1/2)Q 1 {1 [1/σ n 1 ]} ; n = 1,2,,N = Q 1n [q n 1 q n ] and where the nth Walsh percentage change quantity weight Q 1n was defined by (66). Thus the nth term in the additive percentage change decomposition for Q 1 given by (65), Q 1n [q n 1 q n ], can be interpreted as a weighted sum of the percentage changes in the two single variable changes, σ n 1 and 1 [1/σ n 1 ], where σ n and σ n 1 are defined by (79) and (8). The weighted sum is an arithmetic average of the changes σ n 1 and 1 [1/σ n 1 ] if the index Q 1 is equal to one. 26 The above algebra can be adapted to provide an economic interpretation for the terms in the additive percentage change decomposition (69) that we obtained earlier for the Walsh implicit price index P 1. Thus we have (91) P 1n [p n 1 p n ] = (1/2){ρ n 1} + (1/2)P 1 {1 [1/ρ n 1 ]} ; n = 1,2,,N where the nth Walsh percentage change price weight P 1n was defined earlier by (7) and the base period nth price effects ρ n and the current period nth price effects ρ n 1 were defined by (83) and (84). Thus the nth term in the additive percentage change decomposition for P 1 given by (69), P 1n [p n 1 p n ], can be interpreted as a weighted sum of the percentage changes in the two single variable changes, ρ n 1 and 1 [1/ρ n 1 ], where ρ n and ρ n 1 are defined by (83) and (84). The weighted sum is an arithmetic average of the changes ρ n 1 and 1 [1/ρ n 1 ] if the overall price index P 1 is equal to one. Now specialize (87) to the case where r = 2. Upon dividing both sides of (87) by f [f + f 1 ], we obtain the following additive percentage change decomposition for the Fisher ideal quantity index Q 2 = Q F defined earlier by (42): 26 If σ n 1 is close to one, then 1 [1/σ n 1 ] will be close to σ n 1 1. These two expressions have the same first order Taylor series approximations around the point of approximation σ n 1 = 1.
22 22 (92) Q F 1 = n=1 N δ n / f [f + f 1 ] where δ n / f [f + f 1 ] is defined for n = 1,2,,N as (93) δ n / f [f + f 1 ] [(1/2)[f ] 2 {[σ n ] 2 1} + (1/2)[f 1 ] 2 {1 [1/σ n 1 ] 2 }/f [f + f 1 ] = (1/2){f /[f + f 1 ]}{[σ n ] 2 1} + (1/2)Q F {f 1 /[f + f 1 ]}{1 [1/σ n 1 ] 2 } = (1/2){1/[1 + Q F ]}{[σ n ] 2 1} + (1/2)[Q F ] 2 {1/[1 + Q F ]}{1 [1/σ n 1 ] 2 } = Q Fn [q n 1 q n ] and where the nth Fisher percentage change quantity weight Q Fn was defined by (47). Thus the nth term in the additive percentage change decomposition for Q F given by (46), Q Fn [q n 1 q n ], can be interpreted as a weighted sum of the changes in the two single variable changes, [σ n ] 2 1 and 1 [1/σ n 1 ] 2, where σ n and σ n 1 are defined by (79) and (8). If the Fisher quantity index Q F equals 1, then (93) becomes: (94) Q Fn [q n 1 q n ] = (1/4){[σ n ] 2 1} + (1/4){1 [1/σ n 1 ] 2 } = (1/4){[σ n 1][σ n + 1]} + (1/4){[1 (1/σ n 1 )][1 + (1/σ n 1 )]} (1/2)[σ n 1] + (1/2)[1 (1/σ n 1 )] where the last approximation follows if the two quantity effects σ n and σ n 1 are close to one. Thus under normal conditions when all of the quantity indexes are close to one, the nth term in the additive percentage change decomposition for Q F given by (46), Q Fn [q n 1 q n ], will be approximately equal to the arithmetic average of the two single variable index changes, σ n 1 and 1 (1/σ n 1 ). 27 Of course, the above algebra can be adapted to provide an economic interpretation for the terms in the additive percentage change decomposition (48) that we obtained earlier for the Fisher price index P 2 = P F. Thus we have for n = 1,2,,N: (95) P Fn [p n 1 p n ] = (1/2){1/[1+P F ]}{[ρ n ] 2 1} + (1/2)[P F ] 2 {1/[1+P F ]}{1 [1/ρ n 1 ] 2 } where the nth Fisher percentage change price weight P Fn was defined earlier by (5) and the base period nth price effects ρ n and the current period nth price effects ρ n 1 were defined by (83) and (84). Thus if P F, ρ n and ρ n 1 are all close to one, then the nth term in the additive percentage change decomposition for P F given by (48), P Fn [p n 1 p n ], is approximately equal to the arithmetic average of the percentage changes in the two single variable changes, ρ n 1 and 1 [1/ρ n 1 ], where ρ n and ρ n 1 are defined by (83) and (84). 8. Conclusion The results in the previous sections demonstrate that the quadratic identity (4) and its generalizations provide a unifying framework for deriving all of the most commonly used 27 Thus under these conditions, the terms in (9) will closely approximate the terms in (93).
23 23 superlative index number formula. In addition, the single variable quadratic identity (73) and its generalizations have proven to be very useful in providing economic interpretations for some additive percentage change decompositions for these commonly used superlative indexes. 28 References Christensen, L.R., D.W. Jorgenson and L.J. Lau (1971), Conjugate Duality and the Transcendental Logarithmic Production Function, Econometrica 39, Christensen, L.R., D.W. Jorgenson and L.J. Lau (1973), Transcendental Logarithmic Production Frontiers, Review of Economics and Statistics 55, Diewert, W.E., Applications of Duality Theory, pp in M.D. Intriligator and D.A. Kendrick (ed.), Frontiers of Quantitative Economics, Vol. II, Amsterdam: North-Holland. Diewert, W.E. (1976), Exact and Superlative Index Numbers, Journal of Econometrics 4, Diewert, W.E. (1993), Duality Approaches To Microeconomic Theory, in Essays in Index Number Theory, pp in Volume I, Contributions to Economic Analysis 217, W.E. Diewert and A.O. Nakamura (eds.), Amsterdam: North Holland. Diewert, W.E. (2), The Consumer Price Index and Index Number Purpose, Discussion Paper -2, Department of Economics, University of British Columbia, Vancouver, Canada, V6T 1Z1, 69 pp. Diewert, W.E. and C.J. Morrison (1986), Adjusting Output and Productivity Indexes for Changes in the Terms of Trade, The Economic Journal 96, Dikhanov, Y. (1997), The Sensitivity of PPP-Based Income Estimates to Choice of Aggregation Procedures, mimeo, International Economics Department, The World Bank, Washington D.C., January. Ehemann, C., A.J. Katz and B.R. Moulton (2), The Chain-Additivity Issue and the U.S. National Accounts, mimeo, Bureau of Economic Analysis, U.S. Department of Commerce, Washington D.C. 223, September. Färe, R. and K.J. Sung (1986), On Second Order Taylor s Series Approximation and Linear Homogeneity, Aequationes Mathematicae 3, Fisher, I. (1911), The Purchasing Power of Money, London: Macmillan. 28 For the Törnqvist price and quantity indexes, we obtained multiplicative decompositions rather than additive ones.
ADDITIVE DECOMPOSITIONS FOR FISHER, TÖRNQVIST AND GEOMETRIC MEAN INDEXES
 ADDITIVE DECOMPOSITIONS FOR FISHER, TÖRNQVIST AND GEOMETRIC MEAN INDEXES by Marshall B. Reinsdorf, W. Erwin Diewert & Christian Ehemann DECEMBER 2000 Discussion Paper No.: 01-01 DEPARTMENT OF ECONOMICS
ADDITIVE DECOMPOSITIONS FOR FISHER, TÖRNQVIST AND GEOMETRIC MEAN INDEXES by Marshall B. Reinsdorf, W. Erwin Diewert & Christian Ehemann DECEMBER 2000 Discussion Paper No.: 01-01 DEPARTMENT OF ECONOMICS
SCHOOL OF ECONOMICS. Productivity Measurement using. Differences rather than. Ratios: A Note. W. Erwin Diewert 2000/1 DISCUSSION PAPER
 Productivity Measurement using Differences rather than Ratios: A Note W. Erwin Diewert 2000/1 ISSN 1323-8949 ISBN 0 7334 0702 1 SCHOOL OF ECONOMICS DISCUSSION PAPER 2 Productivity Measurement Using Differences
Productivity Measurement using Differences rather than Ratios: A Note W. Erwin Diewert 2000/1 ISSN 1323-8949 ISBN 0 7334 0702 1 SCHOOL OF ECONOMICS DISCUSSION PAPER 2 Productivity Measurement Using Differences
By W.E. Diewert, January, CHAPTER 5: The Theory of the Cost of Living Index: The Many Consumer Case
 1 INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS By W.E. Diewert, January, 2015. CHAPTER 5: The Theory of the Cost of Living Index: The Many Consumer Case 1. Introduction In previous chapters, we have considered
1 INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS By W.E. Diewert, January, 2015. CHAPTER 5: The Theory of the Cost of Living Index: The Many Consumer Case 1. Introduction In previous chapters, we have considered
Quality Adjustment and Hedonics: An Attempt at a Unified Approach
 Quality Adjustment and Hedonics: An Attempt at a Unified Approach by Erwin Diewert University of British Columbia and University of New South Wales EMG 2018 Workshop University of New South Wales Centre
Quality Adjustment and Hedonics: An Attempt at a Unified Approach by Erwin Diewert University of British Columbia and University of New South Wales EMG 2018 Workshop University of New South Wales Centre
The Difference Approach to Productivity Measurement and Exact Indicators November 25, 2017
 1 The Difference Approach to Productivity Measurement and Exact Indicators November 25, 2017 Erwin Diewert and Kevin J. Fox, 1 Discussion Paper 17-08, Vancouver School of Economics, University of British
1 The Difference Approach to Productivity Measurement and Exact Indicators November 25, 2017 Erwin Diewert and Kevin J. Fox, 1 Discussion Paper 17-08, Vancouver School of Economics, University of British
Lowe and Cobb-Douglas CPIs and their Substitution Bias
 Lowe and Cobb-Douglas CPIs and their Substitution Bias Bert M. Balk Rotterdam School of Management Erasmus University Rotterdam E-mail bbalk@rsm.nl and Statistics Netherlands The Hague Draft, April 16,
Lowe and Cobb-Douglas CPIs and their Substitution Bias Bert M. Balk Rotterdam School of Management Erasmus University Rotterdam E-mail bbalk@rsm.nl and Statistics Netherlands The Hague Draft, April 16,
INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS. By W.E. Diewert. March 15, 2015.
 1 INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS By W.E. Diewert. March 15, 2015. University of British Columbia and the University of New South Wales Email: erwin.diewert@ubc.ca Website: http://www.economics.ubc.ca/faculty-and-staff/w-erwin-diewert/
1 INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS By W.E. Diewert. March 15, 2015. University of British Columbia and the University of New South Wales Email: erwin.diewert@ubc.ca Website: http://www.economics.ubc.ca/faculty-and-staff/w-erwin-diewert/
Chapter 3: An Introduction to Multilateral Index Number Theory
 1 Notes on Price Measurement 1 July 22, 2014. Chapter 3: An Introduction to Multilateral Index Number Theory W. Erwin Diewert University of British Columbia and the University of New South Wales Email:
1 Notes on Price Measurement 1 July 22, 2014. Chapter 3: An Introduction to Multilateral Index Number Theory W. Erwin Diewert University of British Columbia and the University of New South Wales Email:
SCHOOL OF ECONOMICS DISCUSSION PAPER
 An Economic Justification for the EKS Multilateral Index Kevin J Fox 2000/3 SCHOOL OF ECONOMICS DISCUSSION PAPER ISSN 1323-8949 ISBN 0 7334 0788 9 An Economic Justification for the EKS Multilateral Index
An Economic Justification for the EKS Multilateral Index Kevin J Fox 2000/3 SCHOOL OF ECONOMICS DISCUSSION PAPER ISSN 1323-8949 ISBN 0 7334 0788 9 An Economic Justification for the EKS Multilateral Index
Methods of Aggregation above the Basic Heading Level within Regions
 Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized International Comparison Program [06.01] Methods of Aggregation above the Basic Heading
Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized International Comparison Program [06.01] Methods of Aggregation above the Basic Heading
INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS. By W.E. Diewert. May, CHAPTER 13: The Economic Approach to the Producer Price Index
 1 INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS By W.E. Diewert. May, 2013. CHAPTER 13: The Economic Approach to the Producer Price Index 1. Introduction Producer Price Indexes provide price indexes to
1 INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS By W.E. Diewert. May, 2013. CHAPTER 13: The Economic Approach to the Producer Price Index 1. Introduction Producer Price Indexes provide price indexes to
Measuring Real GDP and Changes in the Terms of Trade across space and time. WANG Yan, DUFE Presented at BNU
 Measuring Real GDP and Changes in the Terms of Trade across space and time WANG Yan, DUFE Presented at BNU 2018.10.29 Main Contents 1. Introduction 2. Literature Review 3. Measurement Framework 4. Conclusion
Measuring Real GDP and Changes in the Terms of Trade across space and time WANG Yan, DUFE Presented at BNU 2018.10.29 Main Contents 1. Introduction 2. Literature Review 3. Measurement Framework 4. Conclusion
Chapter 13 Fisher Ideal Output, Input and Productivity Indexes Revisited* W.E. Diewert. 1. Introduction
 Chapter 13 Fisher Ideal Output, Input and Productivity Indexes Revisited* W.E. Diewert 1. Introduction Essays in Index Number Theory, Volume I W.E. Diewert and A.O. Nakamura (Editors) c 1993 Elsevier Science
Chapter 13 Fisher Ideal Output, Input and Productivity Indexes Revisited* W.E. Diewert 1. Introduction Essays in Index Number Theory, Volume I W.E. Diewert and A.O. Nakamura (Editors) c 1993 Elsevier Science
By W.E. Diewert. December 13, 2008
 1 APPLIED ECONOMICS By W.E. Diewert. December 13, 2008 Chapter 9: Flexible Functional Forms 1. Introduction In this chapter, we will take an in depth look at the problems involved in choosing functional
1 APPLIED ECONOMICS By W.E. Diewert. December 13, 2008 Chapter 9: Flexible Functional Forms 1. Introduction In this chapter, we will take an in depth look at the problems involved in choosing functional
Economic Theory of Spatial Costs. of Living Indices with. Application to Thailand
 Economic Theory of Spatial Costs of Living Indices with Application to Thailand spatial 5/10/97 ECONOMIC THEORY OF SPATIAL COSTS OF LIVING INDICES WITH APPLICATION TO THAILAND by N.Kakwani* School of Economics
Economic Theory of Spatial Costs of Living Indices with Application to Thailand spatial 5/10/97 ECONOMIC THEORY OF SPATIAL COSTS OF LIVING INDICES WITH APPLICATION TO THAILAND by N.Kakwani* School of Economics
C02, C32, C43, D24, D42, D92, E01, E22, F11, H44, L51, M40, O47
 1 Duality in Production W. Erwin Diewert. 1 February 5, 2018. Discussion Paper 18-02, Vancouver School of Economics, University of British Columbia, Vancouver, B.C., Canada, V6T 1L4. Email: erwin.diewert@ubc.ca
1 Duality in Production W. Erwin Diewert. 1 February 5, 2018. Discussion Paper 18-02, Vancouver School of Economics, University of British Columbia, Vancouver, B.C., Canada, V6T 1L4. Email: erwin.diewert@ubc.ca
Decomposing Malmquist Productivity Indexes into Explanatory Factors
 1 Decomposing Malmquist Productivity Indexes into Explanatory Factors September 16, 2013 Erwin Diewert, 1 Kevin Fox, Discussion Paper 13-09, School of Economics, School of Economics, University of New
1 Decomposing Malmquist Productivity Indexes into Explanatory Factors September 16, 2013 Erwin Diewert, 1 Kevin Fox, Discussion Paper 13-09, School of Economics, School of Economics, University of New
W. Erwin Diewert From The New Palgrave Dictionary of Economics, Second Edition, 2008 Edited by Steven N. Durlauf and Lawrence E.
 index numbers W. Erwin Diewert From The New Palgrave Dictionary of Economics, Second Edition, 2008 Edited by Steven N. Durlauf and Lawrence E. Blume Abstract Index numbers are used to aggregate detailed
index numbers W. Erwin Diewert From The New Palgrave Dictionary of Economics, Second Edition, 2008 Edited by Steven N. Durlauf and Lawrence E. Blume Abstract Index numbers are used to aggregate detailed
Lecture 1 Introduction and Historical Notes
 Lecture and Historical Notes s 5415 Index Number Theory Winter 2019 Outline Test 2 3 4 5 6 Test 7 Required Readings Test Diewert, W.E. (1993) Early History of Price Index Research, in Diewert and Nakamura
Lecture and Historical Notes s 5415 Index Number Theory Winter 2019 Outline Test 2 3 4 5 6 Test 7 Required Readings Test Diewert, W.E. (1993) Early History of Price Index Research, in Diewert and Nakamura
Derivative Properties of Directional Technology Distance Functions
 Derivative Properties of Directional Technology Distance Functions Lane Blume Hudgins 1 and Daniel Primont 2 1 Department of Economics Southern Illinois University Carbondale Carbondale, Illinois 62901,
Derivative Properties of Directional Technology Distance Functions Lane Blume Hudgins 1 and Daniel Primont 2 1 Department of Economics Southern Illinois University Carbondale Carbondale, Illinois 62901,
NEW APPROACH TO GROSS DOMESTIC PRODUCT DECOMPOSITION
 NEW APPROACH TO GROSS DOMESTIC PRODUCT DECOMPOSITION Ante Rozga, University of Split, Faculty of Economics/Split - Cvite Fiskovića 5, 21 000 Split; CROATIA e-mail: ante.rozga@efst.hr Elza Jurun, University
NEW APPROACH TO GROSS DOMESTIC PRODUCT DECOMPOSITION Ante Rozga, University of Split, Faculty of Economics/Split - Cvite Fiskovića 5, 21 000 Split; CROATIA e-mail: ante.rozga@efst.hr Elza Jurun, University
Lecture 2 Test Approach
 Economics 5415 Number Theory Winter 2017 Outline Required Readings Balk, Bert M. (1995) Price Theory: A Survey, International Statistical Review, 63(1), 69 93. Diewert, W.E. (1992) Fisher Ideal Output,
Economics 5415 Number Theory Winter 2017 Outline Required Readings Balk, Bert M. (1995) Price Theory: A Survey, International Statistical Review, 63(1), 69 93. Diewert, W.E. (1992) Fisher Ideal Output,
2. The Accounting Framework
 Diewert Discussion of Aggregate Productivity and the Productivity of the Aggregate: Connecting the Bottom- Up and Top-Down Approaches by Bert M. Balk Rotterdam School of Management Erasmus University,
Diewert Discussion of Aggregate Productivity and the Productivity of the Aggregate: Connecting the Bottom- Up and Top-Down Approaches by Bert M. Balk Rotterdam School of Management Erasmus University,
Exact and superlative measurement of the Luenberger-Hicks- Moorsteen productivity indicator DISCUSSION PAPER SERIES DPS17.02
 DISCUSSION PAPER SERIES DPS17.02 JANUARY 2017 Exact and superlative measurement of the Luenberger-Hicks- Moorsteen productivity indicator Frederic ANG and Pieter Jan KERSTENS Department of Economics Faculty
DISCUSSION PAPER SERIES DPS17.02 JANUARY 2017 Exact and superlative measurement of the Luenberger-Hicks- Moorsteen productivity indicator Frederic ANG and Pieter Jan KERSTENS Department of Economics Faculty
Chapter 11: Benchmarking and the Nonparametric Approach to Production Theory
 1 APPLIED ECONOMICS By W.E. Diewert. 1 July, 2013. Chapter 11: Benchmarking and the Nonparametric Approach to Production Theory 1. Introduction Data Envelopment Analysis or (DEA) is the term used by Charnes
1 APPLIED ECONOMICS By W.E. Diewert. 1 July, 2013. Chapter 11: Benchmarking and the Nonparametric Approach to Production Theory 1. Introduction Data Envelopment Analysis or (DEA) is the term used by Charnes
PROFIT FUNCTIONS. 1. REPRESENTATION OF TECHNOLOGY 1.1. Technology Sets. The technology set for a given production process is defined as
 PROFIT FUNCTIONS 1. REPRESENTATION OF TECHNOLOGY 1.1. Technology Sets. The technology set for a given production process is defined as T {x, y : x ɛ R n, y ɛ R m : x can produce y} where x is a vector
PROFIT FUNCTIONS 1. REPRESENTATION OF TECHNOLOGY 1.1. Technology Sets. The technology set for a given production process is defined as T {x, y : x ɛ R n, y ɛ R m : x can produce y} where x is a vector
Malmquist and Törnqvist Productivity Indexes: Returns to scale and technical progress with imperfect competition. W. Erwin Diewert. Kevin J.
 Malmquist and Törnqvist Productivity Indexes: Returns to scale and technical progress with imperfect competition by W. Erwin Diewert University of British Columbia and Kevin J. Fox University of New South
Malmquist and Törnqvist Productivity Indexes: Returns to scale and technical progress with imperfect competition by W. Erwin Diewert University of British Columbia and Kevin J. Fox University of New South
EC487 Advanced Microeconomics, Part I: Lecture 2
 EC487 Advanced Microeconomics, Part I: Lecture 2 Leonardo Felli 32L.LG.04 6 October, 2017 Properties of the Profit Function Recall the following property of the profit function π(p, w) = max x p f (x)
EC487 Advanced Microeconomics, Part I: Lecture 2 Leonardo Felli 32L.LG.04 6 October, 2017 Properties of the Profit Function Recall the following property of the profit function π(p, w) = max x p f (x)
Week 9: Topics in Consumer Theory (Jehle and Reny, Chapter 2)
 Week 9: Topics in Consumer Theory (Jehle and Reny, Chapter 2) Tsun-Feng Chiang *School of Economics, Henan University, Kaifeng, China November 15, 2015 Microeconomic Theory Week 9: Topics in Consumer Theory
Week 9: Topics in Consumer Theory (Jehle and Reny, Chapter 2) Tsun-Feng Chiang *School of Economics, Henan University, Kaifeng, China November 15, 2015 Microeconomic Theory Week 9: Topics in Consumer Theory
Econometrics Lecture 10: Applied Demand Analysis
 Econometrics Lecture 10: Applied Demand Analysis R. G. Pierse 1 Introduction In this lecture we look at the estimation of systems of demand equations. Demand equations were some of the earliest economic
Econometrics Lecture 10: Applied Demand Analysis R. G. Pierse 1 Introduction In this lecture we look at the estimation of systems of demand equations. Demand equations were some of the earliest economic
Hedonic Imputation versus Time Dummy Hedonic Indexes
 WP/07/234 Hedonic Imputation versus Time Dummy Hedonic Indexes Erwin Diewert, Saeed Heravi, and Mick Silver 2007 International Monetary Fund WP/07/234 IMF Working Paper Statistics Department Hedonic Imputation
WP/07/234 Hedonic Imputation versus Time Dummy Hedonic Indexes Erwin Diewert, Saeed Heravi, and Mick Silver 2007 International Monetary Fund WP/07/234 IMF Working Paper Statistics Department Hedonic Imputation
St. Gallen, Switzerland, August 22-28, 2010
 Session Number: Parallel Session 7C Time: Friday, August 27, AM Paper Prepared for the 31st General Conference of The International Association for Research in Income and Wealth St. Gallen, Switzerland,
Session Number: Parallel Session 7C Time: Friday, August 27, AM Paper Prepared for the 31st General Conference of The International Association for Research in Income and Wealth St. Gallen, Switzerland,
Price Index Basics* (pg. 146 of Foundations of Economic Analysis)
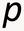 Price Index Basics* The fundamental problem upon which all the analysis rests is that of determining merely from price and quantity data which of two situations is higher up on an individual s preference
Price Index Basics* The fundamental problem upon which all the analysis rests is that of determining merely from price and quantity data which of two situations is higher up on an individual s preference
Economics 401 Sample questions 2
 Economics 401 Sample questions 1. What does it mean to say that preferences fit the Gorman polar form? Do quasilinear preferences fit the Gorman form? Do aggregate demands based on the Gorman form have
Economics 401 Sample questions 1. What does it mean to say that preferences fit the Gorman polar form? Do quasilinear preferences fit the Gorman form? Do aggregate demands based on the Gorman form have
By W.E. Diewert, April 7, 2006.
 1 INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS By W.E. Diewert, April 7, 2006. CHAPTER 8: Fixed Base Versus Chained Indexes 1. Introduction In this chapter 1, the merits of using the chain system for
1 INDEX NUMBER THEORY AND MEASUREMENT ECONOMICS By W.E. Diewert, April 7, 2006. CHAPTER 8: Fixed Base Versus Chained Indexes 1. Introduction In this chapter 1, the merits of using the chain system for
The Multi-Output Firm
 Prerequisites Almost essential Firm: Optimisation Useful, but optional Firm: Demand and Supply The Multi-Output Firm MICROECONOMICS Principles and Analysis Frank Cowell October 2006 Introduction This presentation
Prerequisites Almost essential Firm: Optimisation Useful, but optional Firm: Demand and Supply The Multi-Output Firm MICROECONOMICS Principles and Analysis Frank Cowell October 2006 Introduction This presentation
4) Univariate and multivariate functions
 30C00300 Mathematical Methods for Economists (6 cr) 4) Univariate and multivariate functions Simon & Blume chapters: 13, 15 Slides originally by: Timo Kuosmanen Slides amended by: Anna Lukkarinen Lecture
30C00300 Mathematical Methods for Economists (6 cr) 4) Univariate and multivariate functions Simon & Blume chapters: 13, 15 Slides originally by: Timo Kuosmanen Slides amended by: Anna Lukkarinen Lecture
Preface by W. Erwin Diewert to Functional Structure and Approximation in Econometrics, William A. Barnett and Jane Binner, editors. October 1, 2003.
 1 Preface by W. Erwin Diewert to Functional Structure and Approximation in Econometrics, William A. Barnett and Jane Binner, editors. October 1, 2003. This book deals with five of the most fundamental
1 Preface by W. Erwin Diewert to Functional Structure and Approximation in Econometrics, William A. Barnett and Jane Binner, editors. October 1, 2003. This book deals with five of the most fundamental
Linear Algebra. The analysis of many models in the social sciences reduces to the study of systems of equations.
 POLI 7 - Mathematical and Statistical Foundations Prof S Saiegh Fall Lecture Notes - Class 4 October 4, Linear Algebra The analysis of many models in the social sciences reduces to the study of systems
POLI 7 - Mathematical and Statistical Foundations Prof S Saiegh Fall Lecture Notes - Class 4 October 4, Linear Algebra The analysis of many models in the social sciences reduces to the study of systems
CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS. W. Erwin Diewert January 31, 2008.
 1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
1. First and Second Order Conditions for A Local Min or Max.
 1 MATH CHAPTER 3: UNCONSTRAINED OPTIMIZATION W. Erwin Diewert 1. First and Second Order Conditions for A Local Min or Max. Consider the problem of maximizing or minimizing a function of N variables, f(x
1 MATH CHAPTER 3: UNCONSTRAINED OPTIMIZATION W. Erwin Diewert 1. First and Second Order Conditions for A Local Min or Max. Consider the problem of maximizing or minimizing a function of N variables, f(x
September Math Course: First Order Derivative
 September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
Beyond CES: Three Alternative Classes of Flexible Homothetic Demand Systems
 Beyond CES: Three Alternative Classes of Flexible Homothetic Demand Systems Kiminori Matsuyama 1 Philip Ushchev 2 October 2017 1 Department of Economics, Northwestern University, Evanston, USA. Email:
Beyond CES: Three Alternative Classes of Flexible Homothetic Demand Systems Kiminori Matsuyama 1 Philip Ushchev 2 October 2017 1 Department of Economics, Northwestern University, Evanston, USA. Email:
Problems of operationalizing the concept of a cost-of-living index
 MPRA Munich Personal RePEc Archive Problems of operationalizing the concept of a cost-of-living index Breuer, Claus C. and von der Lippe, Peter M. Universität Duisburg-Essen 19. June 2011 Online at http://mpra.ub.uni-muenchen.de/32902/
MPRA Munich Personal RePEc Archive Problems of operationalizing the concept of a cost-of-living index Breuer, Claus C. and von der Lippe, Peter M. Universität Duisburg-Essen 19. June 2011 Online at http://mpra.ub.uni-muenchen.de/32902/
Week 10: Theory of the Firm (Jehle and Reny, Chapter 3)
 Week 10: Theory of the Firm (Jehle and Reny, Chapter 3) Tsun-Feng Chiang* *School of Economics, Henan University, Kaifeng, China November 22, 2015 First Last (shortinst) Short title November 22, 2015 1
Week 10: Theory of the Firm (Jehle and Reny, Chapter 3) Tsun-Feng Chiang* *School of Economics, Henan University, Kaifeng, China November 22, 2015 First Last (shortinst) Short title November 22, 2015 1
Erasmus Research Institute of Management. KEI Workshop, Leuven, 5-6 September 2006
 Price and Quantity Indices as Role Models for Composite Indicators Bert M. Balk Erasmus Research Institute of Management and Statistics Netherlands bbalk@rsm.nl KEI Workshop, Leuven, 5-6 September 2006
Price and Quantity Indices as Role Models for Composite Indicators Bert M. Balk Erasmus Research Institute of Management and Statistics Netherlands bbalk@rsm.nl KEI Workshop, Leuven, 5-6 September 2006
( )! ±" and g( x)! ±" ], or ( )! 0 ] as x! c, x! c, x! c, or x! ±". If f!(x) g!(x) "!,
![( )! ± and g( x)! ± ], or ( )! 0 ] as x! c, x! c, x! c, or x! ±. If f!(x) g!(x) !, ( )! ± and g( x)! ± ], or ( )! 0 ] as x! c, x! c, x! c, or x! ±. If f!(x) g!(x) !,](/thumbs/81/83782563.jpg) IV. MORE CALCULUS There are some miscellaneous calculus topics to cover today. Though limits have come up a couple of times, I assumed prior knowledge, or at least that the idea makes sense. Limits are
IV. MORE CALCULUS There are some miscellaneous calculus topics to cover today. Though limits have come up a couple of times, I assumed prior knowledge, or at least that the idea makes sense. Limits are
Dual Preference in Leontief Production Problem and Its Extension
 Vietnam Journal of Mathematics 32:2 (2004) 209 218 9LHWQDP -RXUQDO RI 0$7+(0$7,&6 9$67 Dual Preference in Leontief Production Problem and Its Extension P. T. Thach Institute of Mathematics, 18 Hoang Quoc
Vietnam Journal of Mathematics 32:2 (2004) 209 218 9LHWQDP -RXUQDO RI 0$7+(0$7,&6 9$67 Dual Preference in Leontief Production Problem and Its Extension P. T. Thach Institute of Mathematics, 18 Hoang Quoc
Introduction to General Equilibrium: Framework.
 Introduction to General Equilibrium: Framework. Economy: I consumers, i = 1,...I. J firms, j = 1,...J. L goods, l = 1,...L Initial Endowment of good l in the economy: ω l 0, l = 1,...L. Consumer i : preferences
Introduction to General Equilibrium: Framework. Economy: I consumers, i = 1,...I. J firms, j = 1,...J. L goods, l = 1,...L Initial Endowment of good l in the economy: ω l 0, l = 1,...L. Consumer i : preferences
Duality. for The New Palgrave Dictionary of Economics, 2nd ed. Lawrence E. Blume
 Duality for The New Palgrave Dictionary of Economics, 2nd ed. Lawrence E. Blume Headwords: CONVEXITY, DUALITY, LAGRANGE MULTIPLIERS, PARETO EFFICIENCY, QUASI-CONCAVITY 1 Introduction The word duality is
Duality for The New Palgrave Dictionary of Economics, 2nd ed. Lawrence E. Blume Headwords: CONVEXITY, DUALITY, LAGRANGE MULTIPLIERS, PARETO EFFICIENCY, QUASI-CONCAVITY 1 Introduction The word duality is
CES functions and Dixit-Stiglitz Formulation
 CES functions and Dixit-Stiglitz Formulation Weijie Chen Department of Political and Economic Studies University of Helsinki September, 9 4 8 3 7 Labour 6 5 4 5 Labour 5 Capital 3 4 6 8 Capital Any suggestion
CES functions and Dixit-Stiglitz Formulation Weijie Chen Department of Political and Economic Studies University of Helsinki September, 9 4 8 3 7 Labour 6 5 4 5 Labour 5 Capital 3 4 6 8 Capital Any suggestion
Microeconomic Theory -1- Introduction
 Microeconomic Theory -- Introduction. Introduction. Profit maximizing firm with monopoly power 6 3. General results on maximizing with two variables 8 4. Model of a private ownership economy 5. Consumer
Microeconomic Theory -- Introduction. Introduction. Profit maximizing firm with monopoly power 6 3. General results on maximizing with two variables 8 4. Model of a private ownership economy 5. Consumer
Unit 2: Index Numbers
 Unit 2: Index Numbers Index Number Index numbers are statistical devices designed to measrure the relative changes in the level of phenomenon with respect to time, geographical location or other characteristics
Unit 2: Index Numbers Index Number Index numbers are statistical devices designed to measrure the relative changes in the level of phenomenon with respect to time, geographical location or other characteristics
Beyond CES: Three Alternative Classes of Flexible Homothetic Demand Systems
 Beyond CES: Three Alternative Classes of Flexible Homothetic Demand Systems Kiminori Matsuyama 1 Philip Ushchev 2 December 19, 2017, Keio University December 20. 2017, University of Tokyo 1 Department
Beyond CES: Three Alternative Classes of Flexible Homothetic Demand Systems Kiminori Matsuyama 1 Philip Ushchev 2 December 19, 2017, Keio University December 20. 2017, University of Tokyo 1 Department
Chapter 3a Topics in differentiation. Problems in differentiation. Problems in differentiation. LC Abueg: mathematical economics
 Chapter 3a Topics in differentiation Lectures in Mathematical Economics L Cagandahan Abueg De La Salle University School of Economics Problems in differentiation Problems in differentiation Problem 1.
Chapter 3a Topics in differentiation Lectures in Mathematical Economics L Cagandahan Abueg De La Salle University School of Economics Problems in differentiation Problems in differentiation Problem 1.
The Di erential Approach to Demand Analysis and the Rotterdam Model
 The Di erential Approach to Demand Analysis and the Rotterdam Model William A. Barnett y Department of Economics University of Kansas Lawrence, Kansas, 66045 and Apostolos Serletis Department of Economics
The Di erential Approach to Demand Analysis and the Rotterdam Model William A. Barnett y Department of Economics University of Kansas Lawrence, Kansas, 66045 and Apostolos Serletis Department of Economics
Econ Slides from Lecture 10
 Econ 205 Sobel Econ 205 - Slides from Lecture 10 Joel Sobel September 2, 2010 Example Find the tangent plane to {x x 1 x 2 x 2 3 = 6} R3 at x = (2, 5, 2). If you let f (x) = x 1 x 2 x3 2, then this is
Econ 205 Sobel Econ 205 - Slides from Lecture 10 Joel Sobel September 2, 2010 Example Find the tangent plane to {x x 1 x 2 x 2 3 = 6} R3 at x = (2, 5, 2). If you let f (x) = x 1 x 2 x3 2, then this is
Birmingham MSc International Macro Autumn Lecture 7: Deviations from purchasing power parity explored and explained
 Birmingham MSc International Macro Autumn 2015 Lecture 7: Deviations from purchasing power parity explored and explained 1. Some definitions: PPP, LOOP, absolute and relative [hese notes are very heavily
Birmingham MSc International Macro Autumn 2015 Lecture 7: Deviations from purchasing power parity explored and explained 1. Some definitions: PPP, LOOP, absolute and relative [hese notes are very heavily
The General Neoclassical Trade Model
 The General Neoclassical Trade Model J. Peter Neary University of Oxford October 15, 2013 J.P. Neary (University of Oxford) Neoclassical Trade Model October 15, 2013 1 / 28 Plan of Lectures 1 Review of
The General Neoclassical Trade Model J. Peter Neary University of Oxford October 15, 2013 J.P. Neary (University of Oxford) Neoclassical Trade Model October 15, 2013 1 / 28 Plan of Lectures 1 Review of
On Hotelling s Stability in Competition
 On Hotelling s Stability in Competition Claude d Aspremont, Jean Jaskold Gabszewicz and Jacques-François Thisse Manuscript received March, 1978; revision received June, 1978 Abstract The purpose of this
On Hotelling s Stability in Competition Claude d Aspremont, Jean Jaskold Gabszewicz and Jacques-François Thisse Manuscript received March, 1978; revision received June, 1978 Abstract The purpose of this
Birmingham MSc International Macro Autumn Deviations from purchasing power parity explored and explained
 Birmingham MSc International Macro Autumn 2015 Deviations from purchasing power parity explored and explained 1. Some definitions: PPP, LOOP, absolute and relative [hese notes are very heavily derivative
Birmingham MSc International Macro Autumn 2015 Deviations from purchasing power parity explored and explained 1. Some definitions: PPP, LOOP, absolute and relative [hese notes are very heavily derivative
AN ELEMENTARY PROOF OF THE SPECTRAL RADIUS FORMULA FOR MATRICES
 AN ELEMENTARY PROOF OF THE SPECTRAL RADIUS FORMULA FOR MATRICES JOEL A. TROPP Abstract. We present an elementary proof that the spectral radius of a matrix A may be obtained using the formula ρ(a) lim
AN ELEMENTARY PROOF OF THE SPECTRAL RADIUS FORMULA FOR MATRICES JOEL A. TROPP Abstract. We present an elementary proof that the spectral radius of a matrix A may be obtained using the formula ρ(a) lim
Test code: ME I/ME II, 2004 Syllabus for ME I. Matrix Algebra: Matrices and Vectors, Matrix Operations, Determinants,
 Test code: ME I/ME II, 004 Syllabus for ME I Matri Algebra: Matrices and Vectors, Matri Operations, Determinants, Nonsingularity, Inversion, Cramer s rule. Calculus: Limits, Continuity, Differentiation
Test code: ME I/ME II, 004 Syllabus for ME I Matri Algebra: Matrices and Vectors, Matri Operations, Determinants, Nonsingularity, Inversion, Cramer s rule. Calculus: Limits, Continuity, Differentiation
Chapter Five Schneider s Solution to Hilbert s Seventh Problem (and Beyond) (Revised January 2, 2011)
 Chapter Five Schneider s Solution to Hilbert s Seventh Problem (and Beyond) (Revised January 2, 2011) In this lecture we will briefly examine Schneider s solution to Hilbert s Seventh Problem and then
Chapter Five Schneider s Solution to Hilbert s Seventh Problem (and Beyond) (Revised January 2, 2011) In this lecture we will briefly examine Schneider s solution to Hilbert s Seventh Problem and then
Mathematical Foundations -1- Constrained Optimization. Constrained Optimization. An intuitive approach 2. First Order Conditions (FOC) 7
 Mathematical Foundations -- Constrained Optimization Constrained Optimization An intuitive approach First Order Conditions (FOC) 7 Constraint qualifications 9 Formal statement of the FOC for a maximum
Mathematical Foundations -- Constrained Optimization Constrained Optimization An intuitive approach First Order Conditions (FOC) 7 Constraint qualifications 9 Formal statement of the FOC for a maximum
ECON2285: Mathematical Economics
 ECON2285: Mathematical Economics Yulei Luo FBE, HKU September 2, 2018 Luo, Y. (FBE, HKU) ME September 2, 2018 1 / 35 Course Outline Economics: The study of the choices people (consumers, firm managers,
ECON2285: Mathematical Economics Yulei Luo FBE, HKU September 2, 2018 Luo, Y. (FBE, HKU) ME September 2, 2018 1 / 35 Course Outline Economics: The study of the choices people (consumers, firm managers,
Tutorial 2: Comparative Statics
 Tutorial 2: Comparative Statics ECO42F 20 Derivatives and Rules of Differentiation For each of the functions below: (a) Find the difference quotient. (b) Find the derivative dx. (c) Find f (4) and f (3)..
Tutorial 2: Comparative Statics ECO42F 20 Derivatives and Rules of Differentiation For each of the functions below: (a) Find the difference quotient. (b) Find the derivative dx. (c) Find f (4) and f (3)..
The New Palgrave: Separability
 The New Palgrave: Separability Charles Blackorby Daniel Primont R. Robert Russell 1. Introduction July 29, 2006 Separability, as discussed here, refers to certain restrictions on functional representations
The New Palgrave: Separability Charles Blackorby Daniel Primont R. Robert Russell 1. Introduction July 29, 2006 Separability, as discussed here, refers to certain restrictions on functional representations
Consumer theory Topics in consumer theory. Microeconomics. Joana Pais. Fall Joana Pais
 Microeconomics Fall 2016 Indirect utility and expenditure Properties of consumer demand The indirect utility function The relationship among prices, incomes, and the maximised value of utility can be summarised
Microeconomics Fall 2016 Indirect utility and expenditure Properties of consumer demand The indirect utility function The relationship among prices, incomes, and the maximised value of utility can be summarised
Sometimes the domains X and Z will be the same, so this might be written:
 II. MULTIVARIATE CALCULUS The first lecture covered functions where a single input goes in, and a single output comes out. Most economic applications aren t so simple. In most cases, a number of variables
II. MULTIVARIATE CALCULUS The first lecture covered functions where a single input goes in, and a single output comes out. Most economic applications aren t so simple. In most cases, a number of variables
Lecture Notes 6: Dynamic Equations Part C: Linear Difference Equation Systems
 University of Warwick, EC9A0 Maths for Economists Peter J. Hammond 1 of 45 Lecture Notes 6: Dynamic Equations Part C: Linear Difference Equation Systems Peter J. Hammond latest revision 2017 September
University of Warwick, EC9A0 Maths for Economists Peter J. Hammond 1 of 45 Lecture Notes 6: Dynamic Equations Part C: Linear Difference Equation Systems Peter J. Hammond latest revision 2017 September
The Measurement of Macroeconomic Price Level Changes. Ludwig von Auer. Research Papers in Economics No. 1/09
 The Measurement of Macroeconomic Price Level Changes Ludwig von Auer Research Papers in Economics No. /9 The Measurement of Macroeconomic Price Level Changes by Ludwig von Auer Universität Trier, Germany
The Measurement of Macroeconomic Price Level Changes Ludwig von Auer Research Papers in Economics No. /9 The Measurement of Macroeconomic Price Level Changes by Ludwig von Auer Universität Trier, Germany
ECON0702: Mathematical Methods in Economics
 ECON0702: Mathematical Methods in Economics Yulei Luo SEF of HKU January 14, 2009 Luo, Y. (SEF of HKU) MME January 14, 2009 1 / 44 Comparative Statics and The Concept of Derivative Comparative Statics
ECON0702: Mathematical Methods in Economics Yulei Luo SEF of HKU January 14, 2009 Luo, Y. (SEF of HKU) MME January 14, 2009 1 / 44 Comparative Statics and The Concept of Derivative Comparative Statics
Queen s University. Department of Economics. Instructor: Kevin Andrew
 Figure 1: 1b) GDP Queen s University Department of Economics Instructor: Kevin Andrew Econ 320: Math Assignment Solutions 1. (10 Marks) On the course website is provided an Excel file containing quarterly
Figure 1: 1b) GDP Queen s University Department of Economics Instructor: Kevin Andrew Econ 320: Math Assignment Solutions 1. (10 Marks) On the course website is provided an Excel file containing quarterly
Advanced Microeconomic Analysis, Lecture 6
 Advanced Microeconomic Analysis, Lecture 6 Prof. Ronaldo CARPIO April 10, 017 Administrative Stuff Homework # is due at the end of class. I will post the solutions on the website later today. The midterm
Advanced Microeconomic Analysis, Lecture 6 Prof. Ronaldo CARPIO April 10, 017 Administrative Stuff Homework # is due at the end of class. I will post the solutions on the website later today. The midterm
The Non-Existence of Representative Agents
 The Non-Existence of Representative Agents Matthew O. Jackson and Leeat Yariv November 2015 Abstract We characterize environments in which there exists a representative agent: an agent who inherits the
The Non-Existence of Representative Agents Matthew O. Jackson and Leeat Yariv November 2015 Abstract We characterize environments in which there exists a representative agent: an agent who inherits the
A note on national income in a dynamic economy
 Available online at www.sciencedirect.com Economics Letters 98 (28) 2 8 www.elsevier.com/locate/econbase A note on national income in a dynamic economy Geoffrey Heal a,, Bengt Kriström b a Columbia Business
Available online at www.sciencedirect.com Economics Letters 98 (28) 2 8 www.elsevier.com/locate/econbase A note on national income in a dynamic economy Geoffrey Heal a,, Bengt Kriström b a Columbia Business
The Firm: Demand and Supply
 Almost essential Firm: Optimisation The Firm: Demand and Supply MICROECONOMICS Principles and Analysis Frank Cowell October 2005 Moving on from the optimum... We derive the firm's reactions to changes
Almost essential Firm: Optimisation The Firm: Demand and Supply MICROECONOMICS Principles and Analysis Frank Cowell October 2005 Moving on from the optimum... We derive the firm's reactions to changes
Standard forms for writing numbers
 Standard forms for writing numbers In order to relate the abstract mathematical descriptions of familiar number systems to the everyday descriptions of numbers by decimal expansions and similar means,
Standard forms for writing numbers In order to relate the abstract mathematical descriptions of familiar number systems to the everyday descriptions of numbers by decimal expansions and similar means,
Lecture 9. = 1+z + 2! + z3. 1 = 0, it follows that the radius of convergence of (1) is.
 The Exponential Function Lecture 9 The exponential function 1 plays a central role in analysis, more so in the case of complex analysis and is going to be our first example using the power series method.
The Exponential Function Lecture 9 The exponential function 1 plays a central role in analysis, more so in the case of complex analysis and is going to be our first example using the power series method.
PRESENTATION OF MATHEMATICAL ECONOMICS SYLLABUS FOR ECONOMICS HONOURS UNDER CBCS, UNIVERSITY OF CALCUTTA
 PRESENTATION OF MATHEMATICAL ECONOMICS SYLLABUS FOR ECONOMICS HONOURS UNDER CBCS, UNIVERSITY OF CALCUTTA Kausik Gupta Professor of Economics, University of Calcutta Introductory Remarks The paper/course
PRESENTATION OF MATHEMATICAL ECONOMICS SYLLABUS FOR ECONOMICS HONOURS UNDER CBCS, UNIVERSITY OF CALCUTTA Kausik Gupta Professor of Economics, University of Calcutta Introductory Remarks The paper/course
The Demand for Liquid Assets: Evidence from the Minflex Laurent Demand System with Conditionally Heteroscedastic Errors
 The Demand for Liquid Assets: Evidence from the Minflex Laurent Demand System with Conditionally Heteroscedastic Errors Dongfeng Chang School of Economics Shandong University Jinan, Shandong 250100 and
The Demand for Liquid Assets: Evidence from the Minflex Laurent Demand System with Conditionally Heteroscedastic Errors Dongfeng Chang School of Economics Shandong University Jinan, Shandong 250100 and
2. Matrix Algebra and Random Vectors
 2. Matrix Algebra and Random Vectors 2.1 Introduction Multivariate data can be conveniently display as array of numbers. In general, a rectangular array of numbers with, for instance, n rows and p columns
2. Matrix Algebra and Random Vectors 2.1 Introduction Multivariate data can be conveniently display as array of numbers. In general, a rectangular array of numbers with, for instance, n rows and p columns
Elementary Aggregation Using the Country Product Dummy (CPD) Method
 Chapter 23 Elementary Aggregation Using the Country Product Dummy (CPD) Method he country product dummy (CPD) regression has been used by the International Comparison Program (ICP) since the program was
Chapter 23 Elementary Aggregation Using the Country Product Dummy (CPD) Method he country product dummy (CPD) regression has been used by the International Comparison Program (ICP) since the program was
STATE COUNCIL OF EDUCATIONAL RESEARCH AND TRAINING TNCF DRAFT SYLLABUS
 STATE COUNCIL OF EDUCATIONAL RESEARCH AND TRAINING TNCF 2017 - DRAFT SYLLABUS Subject :Business Maths Class : XI Unit 1 : TOPIC Matrices and Determinants CONTENT Determinants - Minors; Cofactors; Evaluation
STATE COUNCIL OF EDUCATIONAL RESEARCH AND TRAINING TNCF 2017 - DRAFT SYLLABUS Subject :Business Maths Class : XI Unit 1 : TOPIC Matrices and Determinants CONTENT Determinants - Minors; Cofactors; Evaluation
GARP and Afriat s Theorem Production
 GARP and Afriat s Theorem Production Econ 2100 Fall 2017 Lecture 8, September 21 Outline 1 Generalized Axiom of Revealed Preferences 2 Afriat s Theorem 3 Production Sets and Production Functions 4 Profits
GARP and Afriat s Theorem Production Econ 2100 Fall 2017 Lecture 8, September 21 Outline 1 Generalized Axiom of Revealed Preferences 2 Afriat s Theorem 3 Production Sets and Production Functions 4 Profits
Chapter 1 Consumer Theory Part II
 Chapter 1 Consumer Theory Part II Economics 5113 Microeconomic Theory Kam Yu Winter 2018 Outline 1 Introduction to Duality Theory Indirect Utility and Expenditure Functions Ordinary and Compensated Demand
Chapter 1 Consumer Theory Part II Economics 5113 Microeconomic Theory Kam Yu Winter 2018 Outline 1 Introduction to Duality Theory Indirect Utility and Expenditure Functions Ordinary and Compensated Demand
Chapter 2 THE MATHEMATICS OF OPTIMIZATION. Copyright 2005 by South-Western, a division of Thomson Learning. All rights reserved.
 Chapter THE MATHEMATICS OF OPTIMIZATION Copyright 005 by South-Western, a division of Thomson Learning. All rights reserved. 1 The Mathematics of Optimization Many economic theories begin with the assumption
Chapter THE MATHEMATICS OF OPTIMIZATION Copyright 005 by South-Western, a division of Thomson Learning. All rights reserved. 1 The Mathematics of Optimization Many economic theories begin with the assumption
Linear Algebra. Min Yan
 Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
3.1 Derivative Formulas for Powers and Polynomials
 3.1 Derivative Formulas for Powers and Polynomials First, recall that a derivative is a function. We worked very hard in 2.2 to interpret the derivative of a function visually. We made the link, in Ex.
3.1 Derivative Formulas for Powers and Polynomials First, recall that a derivative is a function. We worked very hard in 2.2 to interpret the derivative of a function visually. We made the link, in Ex.
Considering our result for the sum and product of analytic functions, this means that for (a 0, a 1,..., a N ) C N+1, the polynomial.
 Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
Consumers' SulVus as an Exact and Superlative Cardinal We /fare Indicator
 378.752 D34 W-96-3 Consumers' SulVus as an Exact and Superlative Cardinal We /fare Indicator by Robert G. Chambers WP 96-03 Revised May 1997 Waite Library Dept. of Applied Economics University of Minnesota
378.752 D34 W-96-3 Consumers' SulVus as an Exact and Superlative Cardinal We /fare Indicator by Robert G. Chambers WP 96-03 Revised May 1997 Waite Library Dept. of Applied Economics University of Minnesota
Heterogeneity. Krishna Pendakur. May 24, Krishna Pendakur () Heterogeneity May 24, / 21
 Heterogeneity Krishna Pendakur May 24, 2015 Krishna Pendakur () Heterogeneity May 24, 2015 1 / 21 Introduction People are heterogeneous. Some heterogeneity is observed, some is not observed. Some heterogeneity
Heterogeneity Krishna Pendakur May 24, 2015 Krishna Pendakur () Heterogeneity May 24, 2015 1 / 21 Introduction People are heterogeneous. Some heterogeneity is observed, some is not observed. Some heterogeneity
LECTURE NOTES ON MICROECONOMICS
 LECTURE NOTES ON MICROECONOMICS ANALYZING MARKETS WITH BASIC CALCULUS William M. Boal Part : Mathematical tools Chapter : Introduction to multivariate calculus But those skilled in mathematical analysis
LECTURE NOTES ON MICROECONOMICS ANALYZING MARKETS WITH BASIC CALCULUS William M. Boal Part : Mathematical tools Chapter : Introduction to multivariate calculus But those skilled in mathematical analysis
Generators for Continuous Coordinate Transformations
 Page 636 Lecture 37: Coordinate Transformations: Continuous Passive Coordinate Transformations Active Coordinate Transformations Date Revised: 2009/01/28 Date Given: 2009/01/26 Generators for Continuous
Page 636 Lecture 37: Coordinate Transformations: Continuous Passive Coordinate Transformations Active Coordinate Transformations Date Revised: 2009/01/28 Date Given: 2009/01/26 Generators for Continuous
Chapter One Hilbert s 7th Problem: It s statement and origins
 Chapter One Hilbert s 7th Problem: It s statement and origins At the second International Congress of athematicians in Paris, 900, the mathematician David Hilbert was invited to deliver a keynote address,
Chapter One Hilbert s 7th Problem: It s statement and origins At the second International Congress of athematicians in Paris, 900, the mathematician David Hilbert was invited to deliver a keynote address,
Contents CONTENTS 1. 1 Straight Lines and Linear Equations 1. 2 Systems of Equations 6. 3 Applications to Business Analysis 11.
 CONTENTS 1 Contents 1 Straight Lines and Linear Equations 1 2 Systems of Equations 6 3 Applications to Business Analysis 11 4 Functions 16 5 Quadratic Functions and Parabolas 21 6 More Simple Functions
CONTENTS 1 Contents 1 Straight Lines and Linear Equations 1 2 Systems of Equations 6 3 Applications to Business Analysis 11 4 Functions 16 5 Quadratic Functions and Parabolas 21 6 More Simple Functions
Cowles Foundation for Research in Economics at Yale University
 Cowles Foundation for Research in Economics at Yale University Cowles Foundation Discussion Paper No. 1904 Afriat from MaxMin John D. Geanakoplos August 2013 An author index to the working papers in the
Cowles Foundation for Research in Economics at Yale University Cowles Foundation Discussion Paper No. 1904 Afriat from MaxMin John D. Geanakoplos August 2013 An author index to the working papers in the
Hicksian Demand and Expenditure Function Duality, Slutsky Equation
 Hicksian Demand and Expenditure Function Duality, Slutsky Equation Econ 2100 Fall 2017 Lecture 6, September 14 Outline 1 Applications of Envelope Theorem 2 Hicksian Demand 3 Duality 4 Connections between
Hicksian Demand and Expenditure Function Duality, Slutsky Equation Econ 2100 Fall 2017 Lecture 6, September 14 Outline 1 Applications of Envelope Theorem 2 Hicksian Demand 3 Duality 4 Connections between
THE FIRM: DEMAND AND SUPPLY
 Prerequisites Almost essential Firm: Optimisation THE FIRM: DEMAND AND SUPPLY MICROECONOMICS Principles and Analysis Frank Cowell July 2017 1 Moving on from the optimum We derive the firm's reactions to
Prerequisites Almost essential Firm: Optimisation THE FIRM: DEMAND AND SUPPLY MICROECONOMICS Principles and Analysis Frank Cowell July 2017 1 Moving on from the optimum We derive the firm's reactions to
