Pre-Calculus Notes from Week 6
|
|
|
- Kerry Farmer
- 5 years ago
- Views:
Transcription
1 1-105 Pre-Calculus Notes from Week 6 Logarithmic Functions: Let a > 0, a 1 be a given base (as in, base of an exponential function), and let x be any positive number. By our properties of exponential functions, we know that the function f(t) = a t has range (0, ), all positive numbers, so x is in the range of a t. That means there is a y with a y = x. And, because f(t) = a t is either always increasing or always decreasing, we know that if there s a z with a z = x, then a y = a z, and hence y = z. What this means is that there s only one number y with a y = x. Definition: Let a > 0, a 1, and x > 0 be given. Let y be the unique real number such that a y = x. (We just showed y exists in the previous paragraph.) We call y the logarithm of x with base a, and we write y = log a (x). Example: Find log (8). Solution: We can write 8 = 3, so 3 is the number we raise to in order to get 8, so log (8) = log ( 3 ) = 3. Example: Find log 3 (1/9). so Solution: 1 9 = 1 3 = 3, ( ) 1 log 3 = log 9 3 (3 ) =. Example: Find log 7 (7 15 ). Solution: 7 15 is already written as a power of 7, so log 7 (7 15 ) = 15. From how we defined f(x) = log a (x) (where a is any base), we can see that the domain is (0, ) (we only can put positive numbers in) and the range is (, ) (we can get any number out), which is the opposite of what g(x) = a x has. This isn t a coincidence! Exponential Functions and Logarithmic Functions are Inverse to Each Other! For a > 0, a 1, let f(x) = log a (x) and let g(x) = a x. Then, for any number x, (f g)(x) = f(g(x)) = f(a x ) = log a (a x ) = x,
2 and for any x > 0, (g f)(x) = g(f(x)) = g(log a (x)) = a log a (x) = x. (Remember, we defined log a (x) to be the number you raise a to in order to get x out.) So f and g are inverse functions by our very definition: what this means for us is that exponential functions and logarithms can be used to cancel out each other, which is how we ll use them when solving problems. Notation: Just as we wrote sin x instead of sin(x) and cos x instead of cos(x), we ll often write log a x instead of log a (x), when the meaning won t be lost. Important Properties of Logarithmic Functions: Assume a > 0, a log a (1) = 0. This is because a 0 = 1 for all a.. log a (a) = 1, since a = a For A, B, both positive (and here A a: lower-case letter and capital letters are different variables in most math textbooks!), we have log a (A B) = log a A + log a B and ( ) A log a = log B a A log a B. To see why this is true, let s let r = log a A and s = log a B, so A = a r and B = a s. Then A B = a r a s = a r+s and A B = ar a s = ar s, and by the definition of the logarithm, that means that log a (A B) = r+s and log a ( A B ) = r s. Substituting log a A in for r and log b B in for s gives us the formulas. 4. For A > 0, k any number, log a (A k ) = k log a (A). To see why this is true, again let r = log a A, so A = a r. Then A k = (a r ) k = a r k, so log a (A k ) = r k, and the result follows from substituting log a A in for r. 5. If a > 1, the graph looks like
3 If 0 < a < 1, the graph looks like Graph of y = log a (x), a > 1. Graph of y = log a (x), 0 < a < 1. (You may notice a similarity to the graphs of a x for a > 1 and 0 < a < 1 here. This is because the functions log a (x) and a x are inverse functions. Though I didn t discuss it in class, inverse functions have the property that each looks like the graph of the other, but flipped over the line y = x. You can see more of this in your textbook in Section of Appendix B, but I won t be testing on it.) 6. From the graphs, we get that if a > 1, then log a (x) is strictly increasing, and log a (x) gets very, very negative as x gets close to 0, and gets positive (slowly) as x gets larger. If 0 < a < 1, log a (x) is decreasing, and becomes very, very positive as x gets close to 0, and becomes negative (slowly) as x gets larger. Since log a (1) = 0, the x-intercept of log a (x) is always 1.
4 Before we go further, we need two definitions: Definition: We define the common logarithm to be the function f(x) = log 10 (x), the logarithm with base 10, and we write log(x) instead of log 10 (x). Definition: We define the natural logarithm to be the function f(x) = log e (x), the logarithm with base e, where e is the natural exponential base. We write ln(x) instead of log e (x). The ln comes from logarithme naturel, which is, of course, French for natural logarithm. Just as we have Euler (pronounced oiler, not yooler ) to blame for the choice of the letter e for the natural exponential base, so too do we have him to blame for this notation. Euler was Swiss, so it s very likely he spoke French. Note: For various reasons, older textbooks (many textbooks written pre-1970), and some newer textbooks, use log(x) to denote the natural logarithm and not the common logarithm. While this isn t a common occurrence, when you see log(x) written in books, make sure you know which one the author is referring to! To recap: for x > 0, and for any x, e ln(x) = x and 10 log x = x, ln(e x ) = x and log(10 x ) = x. Example: Solve 9 x +x = 1 using logarithms. Solution: Since we want to use logarithms, we look to see if there s a good base to pick: since we have 9 x +x, we guess that 9 might be a good choice. Since we re solving for x, we want to bring it out of the exponent, so we take the logarithm (with base 9) of both sides: 9 x +x = 1, so log 9 (9 x +x ) = log 9 (1), and by properties of logarithms, the left-hand side becomes x + x and the right-hand side becomes 0, leaving us with x + x = 0. Factoring an x out gives us x(x + 1) = 0, so x = 0 or x = 1. Checking our answers, we see that = 9 0 = 1 and 9 ( 1) +( 1) = = 9 0 = 1,
5 so our solutions are x = 0 and x = 1. Notice that this is the same answer we get as if we had used our previous method of substituting 9 0 in for 1, so 9 x +x = 9 0 means x + x = 0 by the equality of exponents. Logarithms, it will turn out, let us not only solve the exponential functions we ve already seen, but many that are more complicated. Example: Solve ln x + ln(x + 1) = 0. Solution: By our logarithm rules, since ln(x) and ln(x + 1) have the same base, ln x + ln(x + 1) = ln(x(x + 1)) = ln(x + x), so ln(x + x) = 0. Since we want to get rid of the ln and just deal with x, and since e is the base of the logarithms we re dealing with, we raise e to both sides: e ln(x +x) = e 0. Since e x and ln(x) are inverse functions, e ln(x +x) = x + x, and we know e 0 = 1, so we re left with x + x = 1, or x + x 1 = 0. Since this is a quadratic, we can use the quadratic formula to solve: x = (1) ± (1) 4(1)( 1) (1) = 1 ± 5, so we get x = 1 5 and x = But our original equation is ln(x) + ln(x + 1) = 0, so we must have x > 0 and x + 1 > 0 (the domain of ln is positive numbers), so x > 0 and x > 1 must both be true, and we see that x > 0 is the most restrictive of the two. But 1 5 < 0 (it s the opposite of the golden ratio), so it can t be a solution to this equation. But since 5 > 4 = > 1, therefore > = 0, 1+ 5 > 0 and therefore it is a solution. So x = Remember, we can only put positive numbers into logs! This makes solving logarithmic equations slightly trickier than solving regular equations, since now we have to make sure that everything inside the log stays positive! Example: Solve log 9 x = 3. Solution: Since we want to get rid of the log 9, we raise 9 to both sides: 9 log 9 x = x and 9 3/ = ( 9) 3 = 3 3 = 7, so x = 7,
6 and we re done. Change of Base Suppose we can calculate log a (x) very easily, but what we actually want to find is log b (x), where a and b are different bases (so both are positive and neither is equal to 1). We can do this, but it requires a little finesse: First, we note that x = b log b (x) since b x and log b x are inverse functions. Then, we note that b = a log a (b) for essentially the same reason. So But this means that x = b log b (x) = (a log a (b) ) log b (x) = a log a (b) log b (x). log a (x) = log a (b) log b (x). Since log a (b) 0 (as b 1), this means we can solve for log b (x), which gives us the change of base formula: log b (x) = log a(x) log a (b). Why would we want to know how to do this? Well, one reason is that computers can calculate binary logarithms (log (x)) very quickly as a result of how they re built, and this formula lets us calculate log a (x) for any a by simply computing log (x)/ log (a). But a more important result is that log a (x) = ln(x) ln(a), which means that every single logarithmic function is a multiple of ln(x)! So we only need to understand the properties of ln(x) and we ll get the properties of log a (x) as a result. Similarly, since a = e ln(a) for every a, we have a x = ( e ln(a)) x = e ln(a) x, so every single exponential function can be formed from e x, and it s enough to understand the properties of e x to figure out the properties of a x. Example: Find log 4 ( 178 ). Solution: Looking at 178, we see it s written as to some power, which means that taking the logarithm with base of it is easy. What that suggests is we should use our change of base formula: log 4 ( 178 ) = log ( 178 ) log (4).
7 So log ( 178 ) = 178 by the fact that x and log (x) are inverse functions, and since 4 =, we have log (4) =, so log 4 ( 178 ) = 178 = 89. Now, let s look at some more general equations, and see how to solve them: Example: Solve 5 x+1 = 6 x. Solution: Since neither 5 nor 6 can be written as a simple power of each other, it doesn t look like there s a good choice of base for logarithms. But we do want to apply logarithms, since we know they undo exponential functions, so we ll use the common log: log(5 x+1 ) = log(6 x ). We might be tempted to move everything to one side of the equation and simplify using our rules for differences of logs, but what we ll find is that, if we do that, it doesn t make the problem any easier. What we ll do instead is use Property 4 of logarithms: log a (A k ) = k log a (A). Applying this idea to both sides, we get (x + 1) log(5) = (x ) log(6). Distributing the log(5) and log(6) terms, we get ( log(5))x + log(5) = (log(6))x ( log(6)), and since log(5) and log(6) are just fixed numbers (albeit complicated ones), we see that this new equation is a linear equation in x, so we can solve it by moving the x terms to the left, the constant terms to the right, and dividing by x s coefficient: ( log(5))x + log(5) = (log(6))x ( log(6)), ( log(5))x (log(6))x = log(5) ( log(6)), ( log(5) log(6) ) x = log(5) log(6), x = log(5) log(6) log(5) log(6). Now, the right-hand side of our value of x looks complicated and unpleasant, but what s important is that there are no x s over there: the right-hand side is a specific number, though it s not pleasant to compute by hand. However, just to make it look a little nicer, let s simplify the numerator and denominator some: log(5) log(6) = (log 5 + log 6) = (log 5 + log 6 ) = (log(5 6 )) = log(180), and ( ) 5 log(5) log(6) = log(5 ) log(6) = log = log 6 ( ) 5, 6
8 so our final answer is x = log(180) log( 5). 6 Example: Solve 5 x 5 x = 3. Solution: This is by far the trickiest problem we ve looked at, because the left-hand side can t clearly be simplified into a single constant to some power. In fact, taking logs here won t help: we need to simplify some other way. The first thing we ll do is multiply both sides by, to get 5 x 5 x = 6. While that doesn t seem to have helped, we can now rewrite the left-hand side: 5 x 5 x = 5 x 1 5 x, and we ll multiply through by 5 x (which is always positive) to get rid of the fraction, and simplify some: (5 x 5 x )5 x = 6 5 x (5 x )(5 x ) (5 x )(5 x ) = 6 5 x (5 x ) 5 x+x 6 5 x = 0 (5 x ) x = 0 (5 x ) 6 5 x 1 = 0. While we could have written (5 x ) as 5 x, writing it like this gives us the missing clue: let u = 5 x. Then our equation is u 6u 1 = 0, a quadratic! We can use the quadratic formula (just like when we solved higher-degree polynomial equations) to get u = ( 6) ± ( 6) 4(1)( 1) (1) = 6 ± 40 = 6 ± 4 10 = 3 ± 10. But u = 5 x > 0, and 3 10 < 0, so the only solution is u = (Remember, we have to pay more attention to the signs of numbers when solving exponential and logarithmic equations!) Therefore 5 x = ,
9 and we can solve this by taking the natural log of both sides: ln(5 x ) = ln(3 + 10), x ln(5) = ln(3 + 10), x = ln(3 + 10). ln(5) Right now, you might be asking yourself, But why didn t we just take log 5 of both sides, since we had 5 x on the left?. Well, the answer is: no reason at all: log 5 (5 x ) = log 5 (3 + 10), so x = log 5 (3 + 10). While this answer isn t identical to ours in how it s written, the two are equal because of the change of base formula: log 5 (3 + 10) = ln(3 + 10). ln(5) Example: Solve log( 3 x) = log x for x. Solution: The first thing we notice is that 3 x = x 1/3. This means that log( 3 x) = log(x 1/3 ) = (1/3) log(x), giving us 1 3 log(x) = log(x). Squaring both sides to get rid of the radical gives us 1 9 (log(x)) = log(x), or 1 9 (log(x)) log(x) = 0. Factoring out log(x) from the left-hand side gives us ( ) 1 log(x) 9 log(x) 1 = 0, so log(x) = 0 or (1/9) log(x) 1 = 0. If log(x) = 0, then taking 10 to both sides gives us x = 10 log(x) = 10 0 = 1, so x = 1. Now, we check to make sure it works in our original equation: log( 3 1) = log(1) = 0, and log(1) = 0 = 0, so both sides are defined and equal: x = 1 is a solution.
10 If (1/9) log(x) 1 = 0, then log(x) = 9 and therefore x = 10 9 : log( ) = log(10 9/3 ) = log(10 3 ) = 3 and log(109 ) = 9 = 3, so x = 10 9 is also a solution.
Math 5a Reading Assignments for Sections
 Math 5a Reading Assignments for Sections 4.1 4.5 Due Dates for Reading Assignments Note: There will be a very short online reading quiz (WebWork) on each reading assignment due one hour before class on
Math 5a Reading Assignments for Sections 4.1 4.5 Due Dates for Reading Assignments Note: There will be a very short online reading quiz (WebWork) on each reading assignment due one hour before class on
ln(9 4x 5 = ln(75) (4x 5) ln(9) = ln(75) 4x 5 = ln(75) ln(9) ln(75) ln(9) = 1. You don t have to simplify the exact e x + 4e x
 Math 11. Exponential and Logarithmic Equations Fall 016 Instructions. Work in groups of 3 to solve the following problems. Turn them in at the end of class for credit. Names. 1. Find the (a) exact solution
Math 11. Exponential and Logarithmic Equations Fall 016 Instructions. Work in groups of 3 to solve the following problems. Turn them in at the end of class for credit. Names. 1. Find the (a) exact solution
5.6 Logarithmic and Exponential Equations
 SECTION 5.6 Logarithmic and Exponential Equations 305 5.6 Logarithmic and Exponential Equations PREPARING FOR THIS SECTION Before getting started, review the following: Solving Equations Using a Graphing
SECTION 5.6 Logarithmic and Exponential Equations 305 5.6 Logarithmic and Exponential Equations PREPARING FOR THIS SECTION Before getting started, review the following: Solving Equations Using a Graphing
a factors The exponential 0 is a special case. If b is any nonzero real number, then
 0.1 Exponents The expression x a is an exponential expression with base x and exponent a. If the exponent a is a positive integer, then the expression is simply notation that counts how many times the
0.1 Exponents The expression x a is an exponential expression with base x and exponent a. If the exponent a is a positive integer, then the expression is simply notation that counts how many times the
+ i sin. + i sin. = 2 cos
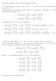 Math 11 Lesieutre); Exam review I; December 4, 017 1. a) Find all complex numbers z for which z = 8. Write your answers in rectangular non-polar) form. We are going to use de Moivre s theorem. For 1, r
Math 11 Lesieutre); Exam review I; December 4, 017 1. a) Find all complex numbers z for which z = 8. Write your answers in rectangular non-polar) form. We are going to use de Moivre s theorem. For 1, r
Algebra & Trig Review
 Algebra & Trig Review 1 Algebra & Trig Review This review was originally written for my Calculus I class, but it should be accessible to anyone needing a review in some basic algebra and trig topics. The
Algebra & Trig Review 1 Algebra & Trig Review This review was originally written for my Calculus I class, but it should be accessible to anyone needing a review in some basic algebra and trig topics. The
Algebra Exam. Solutions and Grading Guide
 Algebra Exam Solutions and Grading Guide You should use this grading guide to carefully grade your own exam, trying to be as objective as possible about what score the TAs would give your responses. Full
Algebra Exam Solutions and Grading Guide You should use this grading guide to carefully grade your own exam, trying to be as objective as possible about what score the TAs would give your responses. Full
Self-Directed Course: Transitional Math Module 4: Algebra
 Lesson #1: Solving for the Unknown with no Coefficients During this unit, we will be dealing with several terms: Variable a letter that is used to represent an unknown number Coefficient a number placed
Lesson #1: Solving for the Unknown with no Coefficients During this unit, we will be dealing with several terms: Variable a letter that is used to represent an unknown number Coefficient a number placed
8.7 Taylor s Inequality Math 2300 Section 005 Calculus II. f(x) = ln(1 + x) f(0) = 0
 8.7 Taylor s Inequality Math 00 Section 005 Calculus II Name: ANSWER KEY Taylor s Inequality: If f (n+) is continuous and f (n+) < M between the center a and some point x, then f(x) T n (x) M x a n+ (n
8.7 Taylor s Inequality Math 00 Section 005 Calculus II Name: ANSWER KEY Taylor s Inequality: If f (n+) is continuous and f (n+) < M between the center a and some point x, then f(x) T n (x) M x a n+ (n
LECTURE 11 - PARTIAL DIFFERENTIATION
 LECTURE 11 - PARTIAL DIFFERENTIATION CHRIS JOHNSON Abstract Partial differentiation is a natural generalization of the differentiation of a function of a single variable that you are familiar with 1 Introduction
LECTURE 11 - PARTIAL DIFFERENTIATION CHRIS JOHNSON Abstract Partial differentiation is a natural generalization of the differentiation of a function of a single variable that you are familiar with 1 Introduction
1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
 Math120 - Precalculus. Final Review. Fall, 2011 Prepared by Dr. P. Babaali 1 Algebra 1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
Math120 - Precalculus. Final Review. Fall, 2011 Prepared by Dr. P. Babaali 1 Algebra 1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
Math 111: Final Review
 Math 111: Final Review Suggested Directions: Start by reviewing the new material with the first portion of the review sheet. Then take every quiz again as if it were a test. No book. No notes. Limit yourself
Math 111: Final Review Suggested Directions: Start by reviewing the new material with the first portion of the review sheet. Then take every quiz again as if it were a test. No book. No notes. Limit yourself
MATH 408N PRACTICE MIDTERM 1
 02/0/202 Bormashenko MATH 408N PRACTICE MIDTERM Show your work for all the problems. Good luck! () (a) [5 pts] Solve for x if 2 x+ = 4 x Name: TA session: Writing everything as a power of 2, 2 x+ = (2
02/0/202 Bormashenko MATH 408N PRACTICE MIDTERM Show your work for all the problems. Good luck! () (a) [5 pts] Solve for x if 2 x+ = 4 x Name: TA session: Writing everything as a power of 2, 2 x+ = (2
Mathematic 108, Fall 2015: Solutions to assignment #7
 Mathematic 08, Fall 05: Solutions to assignment #7 Problem # Suppose f is a function with f continuous on the open interval I and so that f has a local maximum at both x = a and x = b for a, b I with a
Mathematic 08, Fall 05: Solutions to assignment #7 Problem # Suppose f is a function with f continuous on the open interval I and so that f has a local maximum at both x = a and x = b for a, b I with a
Math Lecture 23 Notes
 Math 1010 - Lecture 23 Notes Dylan Zwick Fall 2009 In today s lecture we ll expand upon the concept of radicals and radical expressions, and discuss how we can deal with equations involving these radical
Math 1010 - Lecture 23 Notes Dylan Zwick Fall 2009 In today s lecture we ll expand upon the concept of radicals and radical expressions, and discuss how we can deal with equations involving these radical
How to use these notes
 Chapter How to use these notes These notes were prepared for the University of Utah s Math 00 refresher course. They asssume that the user has had the Math 00 course Intermediate Algebra or its equivalent
Chapter How to use these notes These notes were prepared for the University of Utah s Math 00 refresher course. They asssume that the user has had the Math 00 course Intermediate Algebra or its equivalent
SUMMER REVIEW PACKET. Name:
 Wylie East HIGH SCHOOL SUMMER REVIEW PACKET For students entering Regular PRECALCULUS Name: Welcome to Pre-Calculus. The following packet needs to be finished and ready to be turned the first week of the
Wylie East HIGH SCHOOL SUMMER REVIEW PACKET For students entering Regular PRECALCULUS Name: Welcome to Pre-Calculus. The following packet needs to be finished and ready to be turned the first week of the
Page 1. These are all fairly simple functions in that wherever the variable appears it is by itself. What about functions like the following, ( ) ( )
 Chain Rule Page We ve taken a lot of derivatives over the course of the last few sections. However, if you look back they have all been functions similar to the following kinds of functions. 0 w ( ( tan
Chain Rule Page We ve taken a lot of derivatives over the course of the last few sections. However, if you look back they have all been functions similar to the following kinds of functions. 0 w ( ( tan
Examples 2: Composite Functions, Piecewise Functions, Partial Fractions
 Examples 2: Composite Functions, Piecewise Functions, Partial Fractions September 26, 206 The following are a set of examples to designed to complement a first-year calculus course. objectives are listed
Examples 2: Composite Functions, Piecewise Functions, Partial Fractions September 26, 206 The following are a set of examples to designed to complement a first-year calculus course. objectives are listed
If a function has an inverse then we can determine the input if we know the output. For example if the function
 1 Inverse Functions We know what it means for a relation to be a function. Every input maps to only one output, it passes the vertical line test. But not every function has an inverse. A function has no
1 Inverse Functions We know what it means for a relation to be a function. Every input maps to only one output, it passes the vertical line test. But not every function has an inverse. A function has no
5.2 Infinite Series Brian E. Veitch
 5. Infinite Series Since many quantities show up that cannot be computed exactly, we need some way of representing it (or approximating it). One way is to sum an infinite series. Recall that a n is the
5. Infinite Series Since many quantities show up that cannot be computed exactly, we need some way of representing it (or approximating it). One way is to sum an infinite series. Recall that a n is the
Bishop Kelley High School Summer Math Program Course: Honors Pre-Calculus
 017 018 Summer Math Program Course: Honors Pre-Calculus NAME: DIRECTIONS: Show all work in the packet. Make sure you are aware of the calculator policy for this course. No matter when you have math, this
017 018 Summer Math Program Course: Honors Pre-Calculus NAME: DIRECTIONS: Show all work in the packet. Make sure you are aware of the calculator policy for this course. No matter when you have math, this
Chapter Five Notes N P U2C5
 Chapter Five Notes N P UC5 Name Period Section 5.: Linear and Quadratic Functions with Modeling In every math class you have had since algebra you have worked with equations. Most of those equations have
Chapter Five Notes N P UC5 Name Period Section 5.: Linear and Quadratic Functions with Modeling In every math class you have had since algebra you have worked with equations. Most of those equations have
Albertson AP Calculus AB AP CALCULUS AB SUMMER PACKET DUE DATE: The beginning of class on the last class day of the first week of school.
 Albertson AP Calculus AB Name AP CALCULUS AB SUMMER PACKET 2015 DUE DATE: The beginning of class on the last class day of the first week of school. This assignment is to be done at you leisure during the
Albertson AP Calculus AB Name AP CALCULUS AB SUMMER PACKET 2015 DUE DATE: The beginning of class on the last class day of the first week of school. This assignment is to be done at you leisure during the
1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
 Math120 - Precalculus. Final Review Prepared by Dr. P. Babaali 1 Algebra 1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents. (a) 5
Math120 - Precalculus. Final Review Prepared by Dr. P. Babaali 1 Algebra 1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents. (a) 5
2.5 The Chain Rule Brian E. Veitch
 2.5 The Chain Rule This is our last ifferentiation rule for this course. It s also one of the most use. The best way to memorize this (along with the other rules) is just by practicing until you can o
2.5 The Chain Rule This is our last ifferentiation rule for this course. It s also one of the most use. The best way to memorize this (along with the other rules) is just by practicing until you can o
APPENDIX : PARTIAL FRACTIONS
 APPENDIX : PARTIAL FRACTIONS Appendix : Partial Fractions Given the expression x 2 and asked to find its integral, x + you can use work from Section. to give x 2 =ln( x 2) ln( x + )+c x + = ln k x 2 x+
APPENDIX : PARTIAL FRACTIONS Appendix : Partial Fractions Given the expression x 2 and asked to find its integral, x + you can use work from Section. to give x 2 =ln( x 2) ln( x + )+c x + = ln k x 2 x+
AP Calculus AB Summer Math Packet
 Name Date Section AP Calculus AB Summer Math Packet This assignment is to be done at you leisure during the summer. It is meant to help you practice mathematical skills necessary to be successful in Calculus
Name Date Section AP Calculus AB Summer Math Packet This assignment is to be done at you leisure during the summer. It is meant to help you practice mathematical skills necessary to be successful in Calculus
Partial Fractions. June 27, In this section, we will learn to integrate another class of functions: the rational functions.
 Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
Hello Future Calculus Level One Student,
 Hello Future Calculus Level One Student, This assignment must be completed and handed in on the first day of class. This assignment will serve as the main review for a test on this material. The test will
Hello Future Calculus Level One Student, This assignment must be completed and handed in on the first day of class. This assignment will serve as the main review for a test on this material. The test will
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
Regents Review Session #3 Functions
 Regents Review Session #3 Functions A relation is a set of ordered pairs. A function is a relation in which each element of the domain corresponds t exactly one element in the range. (Each x value is paired
Regents Review Session #3 Functions A relation is a set of ordered pairs. A function is a relation in which each element of the domain corresponds t exactly one element in the range. (Each x value is paired
Solution: f( 1) = 3 1)
 Gateway Questions How to Evaluate Functions at a Value Using the Rules Identify the independent variable in the rule of function. Replace the independent variable with big parenthesis. Plug in the input
Gateway Questions How to Evaluate Functions at a Value Using the Rules Identify the independent variable in the rule of function. Replace the independent variable with big parenthesis. Plug in the input
Core Mathematics 3 Differentiation
 http://kumarmaths.weebly.com/ Core Mathematics Differentiation C differentiation Page Differentiation C Specifications. By the end of this unit you should be able to : Use chain rule to find the derivative
http://kumarmaths.weebly.com/ Core Mathematics Differentiation C differentiation Page Differentiation C Specifications. By the end of this unit you should be able to : Use chain rule to find the derivative
POD. A) Graph: y = 2e x +2 B) Evaluate: (e 2x e x ) 2 2e -x. e 7x 2
 POD A) Graph: y = 2e x +2 B) Evaluate: (e 2x e x ) 2 2e -x e 7x 2 4.4 Evaluate Logarithms & Graph Logarithmic Functions What is a logarithm? How do you read it? What relationship exists between logs and
POD A) Graph: y = 2e x +2 B) Evaluate: (e 2x e x ) 2 2e -x e 7x 2 4.4 Evaluate Logarithms & Graph Logarithmic Functions What is a logarithm? How do you read it? What relationship exists between logs and
University Calculus I. Worksheet # 8 Mar b. sin tan e. sin 2 sin 1 5. b. tan. c. sec sin 1 ( x )) cos 1 ( x )) f. csc. c.
 MATH 6 WINTER 06 University Calculus I Worksheet # 8 Mar. 06-0 The topic covered by this worksheet is: Derivative of Inverse Functions and the Inverse Trigonometric functions. SamplesolutionstoallproblemswillbeavailableonDL,
MATH 6 WINTER 06 University Calculus I Worksheet # 8 Mar. 06-0 The topic covered by this worksheet is: Derivative of Inverse Functions and the Inverse Trigonometric functions. SamplesolutionstoallproblemswillbeavailableonDL,
M155 Exam 2 Concept Review
 M155 Exam 2 Concept Review Mark Blumstein DERIVATIVES Product Rule Used to take the derivative of a product of two functions u and v. u v + uv Quotient Rule Used to take a derivative of the quotient of
M155 Exam 2 Concept Review Mark Blumstein DERIVATIVES Product Rule Used to take the derivative of a product of two functions u and v. u v + uv Quotient Rule Used to take a derivative of the quotient of
Summer Packet A Math Refresher For Students Entering IB Mathematics SL
 Summer Packet A Math Refresher For Students Entering IB Mathematics SL Name: PRECALCULUS SUMMER PACKET Directions: This packet is required if you are registered for Precalculus for the upcoming school
Summer Packet A Math Refresher For Students Entering IB Mathematics SL Name: PRECALCULUS SUMMER PACKET Directions: This packet is required if you are registered for Precalculus for the upcoming school
Find the domain and range of each function. Use interval notation (parenthesis or square brackets).
 Page of 10 I. Functions & Composition of Functions A function is a set of points (x, y) such that for every x, there is one and only one y. In short, in a function, the x-values cannot repeat while the
Page of 10 I. Functions & Composition of Functions A function is a set of points (x, y) such that for every x, there is one and only one y. In short, in a function, the x-values cannot repeat while the
MSM120 1M1 First year mathematics for civil engineers Revision notes 3
 MSM0 M First year mathematics for civil engineers Revision notes Professor Robert. Wilson utumn 00 Functions Definition of a function: it is a rule which, given a value of the independent variable (often
MSM0 M First year mathematics for civil engineers Revision notes Professor Robert. Wilson utumn 00 Functions Definition of a function: it is a rule which, given a value of the independent variable (often
Practice Calculus Test without Trig
 Practice Calculus Test without Trig The problems here are similar to those on the practice test Slight changes have been made 1 What is the domain of the function f (x) = 3x 1? Express the answer in interval
Practice Calculus Test without Trig The problems here are similar to those on the practice test Slight changes have been made 1 What is the domain of the function f (x) = 3x 1? Express the answer in interval
MATH 250 TOPIC 13 INTEGRATION. 13B. Constant, Sum, and Difference Rules
 Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
UNIT 3: DERIVATIVES STUDY GUIDE
 Calculus I UNIT 3: Derivatives REVIEW Name: Date: UNIT 3: DERIVATIVES STUDY GUIDE Section 1: Section 2: Limit Definition (Derivative as the Slope of the Tangent Line) Calculating Rates of Change (Average
Calculus I UNIT 3: Derivatives REVIEW Name: Date: UNIT 3: DERIVATIVES STUDY GUIDE Section 1: Section 2: Limit Definition (Derivative as the Slope of the Tangent Line) Calculating Rates of Change (Average
Logarithms Dr. Laura J. Pyzdrowski
 1 Names: (8 communication points) About this Laboratory An exponential function of the form f(x) = a x, where a is a positive real number not equal to 1, is an example of a one-to-one function. This means
1 Names: (8 communication points) About this Laboratory An exponential function of the form f(x) = a x, where a is a positive real number not equal to 1, is an example of a one-to-one function. This means
f(x) = 2x + 5 3x 1. f 1 (x) = x + 5 3x 2. f(x) = 102x x
 1. Let f(x) = x 3 + 7x 2 x 2. Use the fact that f( 1) = 0 to factor f completely. (2x-1)(3x+2)(x+1). 2. Find x if log 2 x = 5. x = 1/32 3. Find the vertex of the parabola given by f(x) = 2x 2 + 3x 4. (Give
1. Let f(x) = x 3 + 7x 2 x 2. Use the fact that f( 1) = 0 to factor f completely. (2x-1)(3x+2)(x+1). 2. Find x if log 2 x = 5. x = 1/32 3. Find the vertex of the parabola given by f(x) = 2x 2 + 3x 4. (Give
Section 4.6 Negative Exponents
 Section 4.6 Negative Exponents INTRODUCTION In order to understand negative exponents the main topic of this section we need to make sure we understand the meaning of the reciprocal of a number. Reciprocals
Section 4.6 Negative Exponents INTRODUCTION In order to understand negative exponents the main topic of this section we need to make sure we understand the meaning of the reciprocal of a number. Reciprocals
Math Exam Jam Solutions. Contents. 1 Linear Inequalities and Absolute Value Equations 2
 Math 11100 Exam Jam Solutions Contents 1 Linear Inequalities and Absolute Value Equations 2 2 Linear Equations, Graphing and Solving Systems of Equations 4 3 Polynomials and Rational Expressions 13 4 Radical
Math 11100 Exam Jam Solutions Contents 1 Linear Inequalities and Absolute Value Equations 2 2 Linear Equations, Graphing and Solving Systems of Equations 4 3 Polynomials and Rational Expressions 13 4 Radical
Ch 21: Logarithmic Fcts
 Ch 21: Logarithmic Fcts WARM UP You do: 1) Draw the graph of f(x)=2 x. List its domain and range. Is it invertible? Domain: R f(x)=2 x Range: (0, ), or y>0 Yes. It s one-to-one, so it s invertible. Draw
Ch 21: Logarithmic Fcts WARM UP You do: 1) Draw the graph of f(x)=2 x. List its domain and range. Is it invertible? Domain: R f(x)=2 x Range: (0, ), or y>0 Yes. It s one-to-one, so it s invertible. Draw
Module 6 Lecture Notes
 Module 6 Lecture Notes Contents 6. An Introduction to Logarithms....................... 6. Evaluating Logarithmic Expressions.................... 4 6.3 Graphs of Logarithmic Functions......................
Module 6 Lecture Notes Contents 6. An Introduction to Logarithms....................... 6. Evaluating Logarithmic Expressions.................... 4 6.3 Graphs of Logarithmic Functions......................
CALCULUS ASSESSMENT REVIEW
 CALCULUS ASSESSMENT REVIEW DEPARTMENT OF MATHEMATICS CHRISTOPHER NEWPORT UNIVERSITY 1. Introduction and Topics The purpose of these notes is to give an idea of what to expect on the Calculus Readiness
CALCULUS ASSESSMENT REVIEW DEPARTMENT OF MATHEMATICS CHRISTOPHER NEWPORT UNIVERSITY 1. Introduction and Topics The purpose of these notes is to give an idea of what to expect on the Calculus Readiness
Math 230 Mock Final Exam Detailed Solution
 Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
Math 12 Final Exam Review 1
 Math 12 Final Exam Review 1 Part One Calculators are NOT PERMITTED for this part of the exam. 1. a) The sine of angle θ is 1 What are the 2 possible values of θ in the domain 0 θ 2π? 2 b) Draw these angles
Math 12 Final Exam Review 1 Part One Calculators are NOT PERMITTED for this part of the exam. 1. a) The sine of angle θ is 1 What are the 2 possible values of θ in the domain 0 θ 2π? 2 b) Draw these angles
Instructor Quick Check: Question Block 12
 Instructor Quick Check: Question Block 2 How to Administer the Quick Check: The Quick Check consists of two parts: an Instructor portion which includes solutions and a Student portion with problems for
Instructor Quick Check: Question Block 2 How to Administer the Quick Check: The Quick Check consists of two parts: an Instructor portion which includes solutions and a Student portion with problems for
Solutions to Final Review Sheet. The Math 5a final exam will be Tuesday, May 1 from 9:15 am 12:15 p.m.
 Math 5a Solutions to Final Review Sheet The Math 5a final exam will be Tuesday, May 1 from 9:15 am 1:15 p.m. Location: Gerstenzang 1 The final exam is cumulative (i.e., it will cover all the material we
Math 5a Solutions to Final Review Sheet The Math 5a final exam will be Tuesday, May 1 from 9:15 am 1:15 p.m. Location: Gerstenzang 1 The final exam is cumulative (i.e., it will cover all the material we
SET 1. (1) Solve for x: (a) e 2x = 5 3x
 () Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
() Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
5.3. Polynomials and Polynomial Functions
 5.3 Polynomials and Polynomial Functions Polynomial Vocabulary Term a number or a product of a number and variables raised to powers Coefficient numerical factor of a term Constant term which is only a
5.3 Polynomials and Polynomial Functions Polynomial Vocabulary Term a number or a product of a number and variables raised to powers Coefficient numerical factor of a term Constant term which is only a
Math 221 Notes on Rolle s Theorem, The Mean Value Theorem, l Hôpital s rule, and the Taylor-Maclaurin formula. 1. Two theorems
 Math 221 Notes on Rolle s Theorem, The Mean Value Theorem, l Hôpital s rule, and the Taylor-Maclaurin formula 1. Two theorems Rolle s Theorem. If a function y = f(x) is differentiable for a x b and if
Math 221 Notes on Rolle s Theorem, The Mean Value Theorem, l Hôpital s rule, and the Taylor-Maclaurin formula 1. Two theorems Rolle s Theorem. If a function y = f(x) is differentiable for a x b and if
The above statement is the false product rule! The correct product rule gives g (x) = 3x 4 cos x+ 12x 3 sin x. for all angles θ.
 Math 7A Practice Midterm III Solutions Ch. 6-8 (Ebersole,.7-.4 (Stewart DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You
Math 7A Practice Midterm III Solutions Ch. 6-8 (Ebersole,.7-.4 (Stewart DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You
Chapter 1- Polynomial Functions
 Chapter 1- Polynomial Functions Lesson Package MHF4U Chapter 1 Outline Unit Goal: By the end of this unit, you will be able to identify and describe some key features of polynomial functions, and make
Chapter 1- Polynomial Functions Lesson Package MHF4U Chapter 1 Outline Unit Goal: By the end of this unit, you will be able to identify and describe some key features of polynomial functions, and make
Math 180, Exam 2, Practice Fall 2009 Problem 1 Solution. f(x) = arcsin(2x + 1) = sin 1 (3x + 1), lnx
 Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Chapter 3. Exponential and Logarithmic Functions. 3.2 Logarithmic Functions
 Chapter 3 Exponential and Logarithmic Functions 3.2 Logarithmic Functions 1/23 Chapter 3 Exponential and Logarithmic Functions 3.2 4, 8, 14, 16, 18, 20, 22, 30, 31, 32, 33, 34, 39, 42, 54, 56, 62, 68,
Chapter 3 Exponential and Logarithmic Functions 3.2 Logarithmic Functions 1/23 Chapter 3 Exponential and Logarithmic Functions 3.2 4, 8, 14, 16, 18, 20, 22, 30, 31, 32, 33, 34, 39, 42, 54, 56, 62, 68,
Introduction. So, why did I even bother to write this?
 Introduction This review was originally written for my Calculus I class, but it should be accessible to anyone needing a review in some basic algebra and trig topics. The review contains the occasional
Introduction This review was originally written for my Calculus I class, but it should be accessible to anyone needing a review in some basic algebra and trig topics. The review contains the occasional
POLYNOMIAL EXPRESSIONS PART 1
 POLYNOMIAL EXPRESSIONS PART 1 A polynomial is an expression that is a sum of one or more terms. Each term consists of one or more variables multiplied by a coefficient. Coefficients can be negative, so
POLYNOMIAL EXPRESSIONS PART 1 A polynomial is an expression that is a sum of one or more terms. Each term consists of one or more variables multiplied by a coefficient. Coefficients can be negative, so
function independent dependent domain range graph of the function The Vertical Line Test
 Functions A quantity y is a function of another quantity x if there is some rule (an algebraic equation, a graph, a table, or as an English description) by which a unique value is assigned to y by a corresponding
Functions A quantity y is a function of another quantity x if there is some rule (an algebraic equation, a graph, a table, or as an English description) by which a unique value is assigned to y by a corresponding
Internet Mat117 Formulas and Concepts. d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. ( x 1 + x 2 2., y 1 + y 2. (x h) 2 + (y k) 2 = r 2. m = y 2 y 1 x 2 x 1
 Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
4 Exponential and Logarithmic Functions
 4 Exponential and Logarithmic Functions 4.1 Exponential Functions Definition 4.1 If a > 0 and a 1, then the exponential function with base a is given by fx) = a x. Examples: fx) = x, gx) = 10 x, hx) =
4 Exponential and Logarithmic Functions 4.1 Exponential Functions Definition 4.1 If a > 0 and a 1, then the exponential function with base a is given by fx) = a x. Examples: fx) = x, gx) = 10 x, hx) =
Manipulating Equations
 Manipulating Equations Now that you know how to set up an equation, the next thing you need to do is solve for the value that the question asks for. Above all, the most important thing to remember when
Manipulating Equations Now that you know how to set up an equation, the next thing you need to do is solve for the value that the question asks for. Above all, the most important thing to remember when
Rational Functions. Elementary Functions. Algebra with mixed fractions. Algebra with mixed fractions
 Rational Functions A rational function f (x) is a function which is the ratio of two polynomials, that is, Part 2, Polynomials Lecture 26a, Rational Functions f (x) = where and are polynomials Dr Ken W
Rational Functions A rational function f (x) is a function which is the ratio of two polynomials, that is, Part 2, Polynomials Lecture 26a, Rational Functions f (x) = where and are polynomials Dr Ken W
SOLUTIONS FOR PROBLEMS 1-30
 . Answer: 5 Evaluate x x + 9 for x SOLUTIONS FOR PROBLEMS - 0 When substituting x in x be sure to do the exponent before the multiplication by to get (). + 9 5 + When multiplying ( ) so that ( 7) ( ).
. Answer: 5 Evaluate x x + 9 for x SOLUTIONS FOR PROBLEMS - 0 When substituting x in x be sure to do the exponent before the multiplication by to get (). + 9 5 + When multiplying ( ) so that ( 7) ( ).
1.10 Continuity Brian E. Veitch
 1.10 Continuity Definition 1.5. A function is continuous at x = a if 1. f(a) exists 2. lim x a f(x) exists 3. lim x a f(x) = f(a) If any of these conditions fail, f is discontinuous. Note: From algebra
1.10 Continuity Definition 1.5. A function is continuous at x = a if 1. f(a) exists 2. lim x a f(x) exists 3. lim x a f(x) = f(a) If any of these conditions fail, f is discontinuous. Note: From algebra
Calculus I Review Solutions
 Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Solving Equations with Addition and Subtraction. Solving Equations with Addition and Subtraction. Solving Equations with Addition and Subtraction
 OBJECTIVE: You need to be able to solve equations by using addition and subtraction. In math, when you say two things are equal to each other, you mean they represent the same value. We use the sign to
OBJECTIVE: You need to be able to solve equations by using addition and subtraction. In math, when you say two things are equal to each other, you mean they represent the same value. We use the sign to
MATH 124. Midterm 2 Topics
 MATH 124 Midterm 2 Topics Anything you ve learned in class (from lecture and homework) so far is fair game, but here s a list of some main topics since the first midterm that you should be familiar with:
MATH 124 Midterm 2 Topics Anything you ve learned in class (from lecture and homework) so far is fair game, but here s a list of some main topics since the first midterm that you should be familiar with:
Internet Mat117 Formulas and Concepts. d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2., y 1 + y 2. ( x 1 + x 2 2
 Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
Section 6.3: Exponential Equations and Inequalities, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D.
 Section 6.3: Exponential Equations and Inequalities, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-
Section 6.3: Exponential Equations and Inequalities, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-
1.5 Inverse Trigonometric Functions
 1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
Skill 6 Exponential and Logarithmic Functions
 Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Section 1.6 Inverse Functions
 0 Chapter 1 Section 1.6 Inverse Functions A fashion designer is travelling to Milan for a fashion show. He asks his assistant, Betty, what 7 degrees Fahrenheit is in Celsius, and after a quick search on
0 Chapter 1 Section 1.6 Inverse Functions A fashion designer is travelling to Milan for a fashion show. He asks his assistant, Betty, what 7 degrees Fahrenheit is in Celsius, and after a quick search on
A2TH MIDTERM REVIEW (at home) CHAPTER 1/2 NUMBERS/FUNCTIONS. 2) Solve the inequality, write the solution set, and graph in the specified domain:
 A2TH MIDTERM REVIEW (at home) )Simplify 3 2[ 2x 3(x + 4) 3(4 x) ] CHAPTER /2 NUMBERS/FUNCTIONS 2) Solve the inequality, write the solution set, and graph in the specified domain: a) 5x 3< 22 {integers}
A2TH MIDTERM REVIEW (at home) )Simplify 3 2[ 2x 3(x + 4) 3(4 x) ] CHAPTER /2 NUMBERS/FUNCTIONS 2) Solve the inequality, write the solution set, and graph in the specified domain: a) 5x 3< 22 {integers}
NAME: DATE: CLASS: AP CALCULUS AB SUMMER MATH 2018
 NAME: DATE: CLASS: AP CALCULUS AB SUMMER MATH 2018 A] Refer to your pre-calculus notebook, the internet, or the sheets/links provided for assistance. B] Do not wait until the last minute to complete this
NAME: DATE: CLASS: AP CALCULUS AB SUMMER MATH 2018 A] Refer to your pre-calculus notebook, the internet, or the sheets/links provided for assistance. B] Do not wait until the last minute to complete this
Skill 6 Exponential and Logarithmic Functions
 Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Topics from Algebra and Pre-Calculus. (Key contains solved problems)
 Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
MAC Module 8. Exponential and Logarithmic Functions I. Learning Objectives. - Exponential Functions - Logarithmic Functions
 MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
Algebra. Here are a couple of warnings to my students who may be here to get a copy of what happened on a day that you missed.
 This document was written and copyrighted by Paul Dawkins. Use of this document and its online version is governed by the Terms and Conditions of Use located at. The online version of this document is
This document was written and copyrighted by Paul Dawkins. Use of this document and its online version is governed by the Terms and Conditions of Use located at. The online version of this document is
MAC Module 8 Exponential and Logarithmic Functions I. Rev.S08
 MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
Review Sheet for Math 5a Final Exam. The Math 5a final exam will be Tuesday, May 1 from 9:15 am 12:15 p.m.
 Review Sheet for Math 5a Final Exam The Math 5a final exam will be Tuesday, May from 9:5 am :5 p.m. Location: Gerstenzang The final exam is cumulative (i.e., it will cover all the material we covered in
Review Sheet for Math 5a Final Exam The Math 5a final exam will be Tuesday, May from 9:5 am :5 p.m. Location: Gerstenzang The final exam is cumulative (i.e., it will cover all the material we covered in
MATH 408N PRACTICE FINAL
 2/03/20 Bormashenko MATH 408N PRACTICE FINAL Show your work for all the problems. Good luck! () Let f(x) = ex e x. (a) [5 pts] State the domain and range of f(x). Name: TA session: Since e x is defined
2/03/20 Bormashenko MATH 408N PRACTICE FINAL Show your work for all the problems. Good luck! () Let f(x) = ex e x. (a) [5 pts] State the domain and range of f(x). Name: TA session: Since e x is defined
Sections 7.1, 7.2: Sums, differences, products of polynomials CHAPTER 7: POLYNOMIALS
 Sections 7.1, 7.2: Sums, differences, products of polynomials CHAPTER 7: POLYNOMIALS Quiz results Average 73%: high h score 100% Problems: Keeping track of negative signs x = + = + Function notation f(x)
Sections 7.1, 7.2: Sums, differences, products of polynomials CHAPTER 7: POLYNOMIALS Quiz results Average 73%: high h score 100% Problems: Keeping track of negative signs x = + = + Function notation f(x)
Math101, Sections 2 and 3, Spring 2008 Review Sheet for Exam #2:
 Math101, Sections 2 and 3, Spring 2008 Review Sheet for Exam #2: 03 17 08 3 All about lines 3.1 The Rectangular Coordinate System Know how to plot points in the rectangular coordinate system. Know the
Math101, Sections 2 and 3, Spring 2008 Review Sheet for Exam #2: 03 17 08 3 All about lines 3.1 The Rectangular Coordinate System Know how to plot points in the rectangular coordinate system. Know the
Aim: How do we prepare for AP Problems on limits, continuity and differentiability? f (x)
 Name AP Calculus Date Supplemental Review 1 Aim: How do we prepare for AP Problems on limits, continuity and differentiability? Do Now: Use the graph of f(x) to evaluate each of the following: 1. lim x
Name AP Calculus Date Supplemental Review 1 Aim: How do we prepare for AP Problems on limits, continuity and differentiability? Do Now: Use the graph of f(x) to evaluate each of the following: 1. lim x
Math Boot Camp Functions and Algebra
 Fall 017 Math Boot Camp Functions and Algebra FUNCTIONS Much of mathematics relies on functions, the pairing (relation) of one object (typically a real number) with another object (typically a real number).
Fall 017 Math Boot Camp Functions and Algebra FUNCTIONS Much of mathematics relies on functions, the pairing (relation) of one object (typically a real number) with another object (typically a real number).
3 Inequalities Absolute Values Inequalities and Intervals... 18
 Contents 1 Real Numbers, Exponents, and Radicals 1.1 Rationalizing the Denominator................................... 1. Factoring Polynomials........................................ 1. Algebraic and Fractional
Contents 1 Real Numbers, Exponents, and Radicals 1.1 Rationalizing the Denominator................................... 1. Factoring Polynomials........................................ 1. Algebraic and Fractional
Reference Material /Formulas for Pre-Calculus CP/ H Summer Packet
 Reference Material /Formulas for Pre-Calculus CP/ H Summer Packet Week # 1 Order of Operations Step 1 Evaluate expressions inside grouping symbols. Order of Step 2 Evaluate all powers. Operations Step
Reference Material /Formulas for Pre-Calculus CP/ H Summer Packet Week # 1 Order of Operations Step 1 Evaluate expressions inside grouping symbols. Order of Step 2 Evaluate all powers. Operations Step
Algebra 2 Segment 1 Lesson Summary Notes
 Algebra 2 Segment 1 Lesson Summary Notes For each lesson: Read through the LESSON SUMMARY which is located. Read and work through every page in the LESSON. Try each PRACTICE problem and write down the
Algebra 2 Segment 1 Lesson Summary Notes For each lesson: Read through the LESSON SUMMARY which is located. Read and work through every page in the LESSON. Try each PRACTICE problem and write down the
Higher Mathematics Course Notes
 Higher Mathematics Course Notes Equation of a Line (i) Collinearity: (ii) Gradient: If points are collinear then they lie on the same straight line. i.e. to show that A, B and C are collinear, show that
Higher Mathematics Course Notes Equation of a Line (i) Collinearity: (ii) Gradient: If points are collinear then they lie on the same straight line. i.e. to show that A, B and C are collinear, show that
Section 4.2 Logarithmic Functions & Applications
 34 Section 4.2 Logarithmic Functions & Applications Recall that exponential functions are one-to-one since every horizontal line passes through at most one point on the graph of y = b x. So, an exponential
34 Section 4.2 Logarithmic Functions & Applications Recall that exponential functions are one-to-one since every horizontal line passes through at most one point on the graph of y = b x. So, an exponential
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... 7 Introduction... 7 Integer Exponents... 8 Rational Exponents...5 Radicals... Polynomials...30 Factoring Polynomials...36
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... 7 Introduction... 7 Integer Exponents... 8 Rational Exponents...5 Radicals... Polynomials...30 Factoring Polynomials...36
y+2 x 1 is in the range. We solve x as x =
 Dear Students, Here are sample solutions. The most fascinating thing about mathematics is that you can solve the same problem in many different ways. The correct answer will always be the same. Be creative
Dear Students, Here are sample solutions. The most fascinating thing about mathematics is that you can solve the same problem in many different ways. The correct answer will always be the same. Be creative
Solving Linear Equations
 Solving Linear Equations Golden Rule of Algebra: Do unto one side of the equal sign as you will do to the other Whatever you do on one side of the equal sign, you MUST do the same exact thing on the other
Solving Linear Equations Golden Rule of Algebra: Do unto one side of the equal sign as you will do to the other Whatever you do on one side of the equal sign, you MUST do the same exact thing on the other
Composition of Functions
 Math 120 Intermediate Algebra Sec 9.1: Composite and Inverse Functions Composition of Functions The composite function f g, the composition of f and g, is defined as (f g)(x) = f(g(x)). Recall that a function
Math 120 Intermediate Algebra Sec 9.1: Composite and Inverse Functions Composition of Functions The composite function f g, the composition of f and g, is defined as (f g)(x) = f(g(x)). Recall that a function
