Other quantum algorithms
|
|
|
- Melina Charles
- 5 years ago
- Views:
Transcription
1 Chapte 3 Othe uatum agoithms 3. Quick emide of Gove s agoithm We peset hee a uick emide of Gove s agoithm. Iput: a fuctio f : {0,}! {0,}. Goa: fid x such that f (x) =. Seach pobem We have a uatum access to f i.e. we have access to the uatum uitay O f satisfyig: 8x {0,}, O f ( xi 0i) = xi f (x)i. Gove s agoithm: if thee ae T soutios, fids oe with O( eo( T Time(f )) whee we use the otatio eo(b()) = O Gove s agoithm T ) cas to O f ad i time fo ay b(). b() poyog(b()). Ceate the state i=o P f / x{0,} xi 0i = p P x{0,} xi f (x)i.. Decompose ito the good x ad bad x (eca thee ae T soutios). i= = T X x:f (x)= p xi f (x)i+ T X T x:f (x)=0 xi f (x)i T {z } Good i Bad i {z } T Goodi+ T Badi 3. Ateate the foowig opeatios to tasfom i ito a state cose to Good i Phase fip ove f (x) egiste: O Z ( xi f (x)i=( ) f (x) xi f (x)i. Refexio ove i: Ref i( i) = i ; Ref i(? i) = i? fo ay i? othogoa to i. 4. Geometica itepetatio i the subspace { Good i, Bad i}. 0
2 O Z is a efexio ove Bad i. Ref i is a efexio ove i. O Z ± Ref i is a µ coute cockwise otatio whee cos(µ):=h Bad i h Bad i= T T so µ º whe T ø. 5. Pefom this otatio µ times to be cose to Goodi. Pictuig the agoithm Phase estimatio Ou fist potoco is a diect appicatio of the uatum Fouie tasfom. Phase estimatio Iput: a uatum uitay U actig o ubits. A eigevecto i of U with eigevaue give as a uatum state. Goa: output. Reca that a eigevecto i of U with eigevaue meas that U( i) = i. Because U is a uitay, = so we ca wite = e iº fo some ea umbe [0,) ([0,[ i Fech otatio). We assume fist that ca be fuy descibed with bits of pecisio, i.e. thee exists a atua umbe C such that = C. We coside a uatum uitay Q satisfyig Q( ki i) = kiu k ( i). fo ay k {0,..., } ad ay state i. We pefom the foowig agoithm:
3 . Stat fom 0i i ad appy F o the fist egiste. The esutig state is. Appy Q o both egistes. X p ki i. X p U k ki i= p X k ki i = p X e iºkc ki i. 3. Appy the ivese Fouie tasfom F o the fist egiste. The esutig state is Ci i. It is the easy to ecove fom C. Geea case If caot be witte with bits of pecisio, we coside the cosest appoximatio of of the fom C. A eo aaysis (ot detaied hee) shows that the above pocedue wi fid this C with pobabiity at east 4 º. By pefomig sevea iteatios of this pocedue, we ca fid the coect C, i.e. a good appoximatio of with a pobabiity that expoetiay coveges to i the umbe of iteatios. Efficiecy of the agoithm If U ca be computed efficiety ad if, fo ay k {0,..., }, U k ca be computed efficiety the Q ca be computed efficiety ad the whoe agoithm is efficiet. This meas that if we wat ou agoithm to u i time poy() (assumig U ca be computed i time poy()), we have to take = O(og()). 3.. Appicatio : Coutig agoithm Iput: a fuctio f : {0,}! {0,}. Goa: output T = {x : f (x) = }. Seach pobem Desciptio of the agoithm: coside the state i ad the opeatios Ref i ad O Z fom the Gove s agoithm sectio (Sectio 3.) ad et U = O Z ±Ref i. Fom the aaysis of Gove s agoithm, U is a µ coute cockwise otatio i the basis { Bad i, Good i} with µ = accos(h Bad i) = accos( T ). µ cos(µ) si(µ) We ca theefoe wite U = i this basis. si(µ) cos(µ) U has eigevaues e 0 i= p Bad i+i Good i ad e i= p Bad i i Good i with espective eigevaues e iº(µ) ad e iº(µ). Take the state T i= Goodi+ T Badi = Æ e i+ø e i fo some Æ,Ø C which is efficiety computabe. What happes whe we appy the phase estimatio agoithm o i ad U? We, i is ot a eigestate of U but a supepositio of its eigestates. The agoithm wi
4 output µ (actuay º µ) with pobabiity Æ ad µ with pobabiity Ø. We ca easiy distiguish betwee the cases ad aways output the good vaue fo µ. Fom thee, usig the eatio betwee µ ad T, we ca ecove T. If we wat a agoithm uig i poy() the we ca do this up to a additive eo of poy() i the age µ we fid. 3.. Appicatio : Fouie tasfom F fo ay I Chapte, we showed how to pefom the Fouie tasfom F whe = fo some. Hee, we show how to pefom the Fouie tasfom fo ay. F wi act o a uatum egiste that ca take vaues fom 0 to ad 8k {0,..., }, F ( ki) = p X! k i. whee! := e iº. Let U ad U two uitaies that do the foowig, 8k {0,..., }. U ( ki 0i) = kif ( ki) ; U (F ki 0i) = F ( ki) ki. Fom those two uitaies, we ca pefom F as foows SW AP ki 0i U! kif ( ki)! F ( ki) ki U! F ( ki) 0i. what is eft to show is how to pefom U ad U. U ca be pefomed uite easiy. Let S a uatum uitay such that S ( 0i) = p P i. Sice is ot a powe of, S caot be expessed as Hadamads but we ca sti easiy costuct such a uitay. Let aso O mut satisfyig O mut ( ki i 0i) = ki i k mod i. Let s ow costuct U.. Stat fom ki 0i 0i ad appy S o the secod egiste. The esutig state is. Appy O mut o the thee egistes. kip X i 0i. kip X i k mod i. 3. Appy the uitay xi!! x xi o the thid egiste. 4. Appy O o the thee egistes. We obtai mut kip X! k i k mod i. kip X! k i 0i= kif ( ki) 0i. 3
5 Swappig egistes is the easy. What is eft to do is to pefom uitay U. We coside the uitay O add such that O add ( ki) = k + mod i. The idea is that F ( ki) is a eigevecto of O add with eigevaue k ad that it wi be easy to ecove k fom k. Doig this i a coheet way wi give U. Fist see that O add F ( ki) = p X! k + mod i=! k X p! k i which meas that F ( ki) is a eigevecto of O add with eigevaue! k =! k. If we appy the phase estimatio fom the pevious sectio, with =dog()e, we obtai F ( ki) 0i Phase Estimatio with O add! F ( ki) ki. Which by appyig xi! xi gives the coect esut. Actuay, the phase estimatio wi oy give k with some (high) pobabiity so this whoe pocess wi costuct a appoximatio of U. Puttig eveythig togethe, we maaged to costuct F ( ki). This uitay has may appicatios, fo exampe fo the Discete Log uatum agoithm. 3.3 Coisio agoithm Coisio pobem Iput: a adom fuctio f : {0,}! {0,}. Goa: fid (x, y) such that f (x) = f (y). Because f is adom, may such coupes. Cassica agoithm. Pick a paamete. Pick a adom subset I µ {0,} of size. Costuct the ist L = {f (i)} ii ad sot it.. Compute f (x) fo adom vaues x I uti we fid f (x) L. Sice f is adom, this takes aveage time fo each x tested this way. This agoithm uses the we kow bithday paadox. The fist step takes time O( og( ) ad the secod oe O( og( ) ). By takig = /, we have a agoithm uig i time O(poy() / ). We exted this to the uatum settig The BHT Agoithm. Pick a paamete. Pick a adom subset I µ {0,} of size. Costuct the ist {f (i)} ii.. Let g : {0,}! {0,} satisfyig g (x) =, x I ad 9i I, f (x) = f (i). º soutios whe ø. 3. Appy Gove o g.fidy such that g (y) =. 4. Fid i I st. f (i) = f (y). Output (i, y). 4
6 3.3. Time aaysis of BHT Fo simpicity, Time(f ) = ad we igoe eo. List ceatio: time. Gove o g. We defie i= P / x{0,} xi g (x)i QTime = + 0 B i) + {z} A. Ref Bad i Reca that if we have a uitay U( 0i) = i the we ca costuct Ref i usig U twice ad a phase fip. If QTime(Ref i) = the take = /3 ad the tota uig time of the agoithm is /3 (as good as adom waks). If we ae iteested i uey compexity, i.e. the cas to O f the we ca sove the pobem the coisio pobem with eo( /3 ) ueies to O f. Ambaiis showed that it is aso possibe to do this i ea uatum time eo( /3 ) (with a adeuate uatum data stuctue). 5
Merging to ordered sequences. Efficient (Parallel) Sorting. Merging (cont.)
 Efficient (Paae) Soting One of the most fequent opeations pefomed by computes is oganising (soting) data The access to soted data is moe convenient/faste Thee is a constant need fo good soting agoithms
Efficient (Paae) Soting One of the most fequent opeations pefomed by computes is oganising (soting) data The access to soted data is moe convenient/faste Thee is a constant need fo good soting agoithms
By the end of this section you will be able to prove the Chinese Remainder Theorem apply this theorem to solve simultaneous linear congruences
 Chapte : Theoy of Modula Aithmetic 8 Sectio D Chiese Remaide Theoem By the ed of this sectio you will be able to pove the Chiese Remaide Theoem apply this theoem to solve simultaeous liea cogueces The
Chapte : Theoy of Modula Aithmetic 8 Sectio D Chiese Remaide Theoem By the ed of this sectio you will be able to pove the Chiese Remaide Theoem apply this theoem to solve simultaeous liea cogueces The
MATH Midterm Solutions
 MATH 2113 - Midtem Solutios Febuay 18 1. A bag of mables cotais 4 which ae ed, 4 which ae blue ad 4 which ae gee. a How may mables must be chose fom the bag to guaatee that thee ae the same colou? We ca
MATH 2113 - Midtem Solutios Febuay 18 1. A bag of mables cotais 4 which ae ed, 4 which ae blue ad 4 which ae gee. a How may mables must be chose fom the bag to guaatee that thee ae the same colou? We ca
Using Counting Techniques to Determine Probabilities
 Kowledge ticle: obability ad Statistics Usig outig Techiques to Detemie obabilities Tee Diagams ad the Fudametal outig iciple impotat aspect of pobability theoy is the ability to detemie the total umbe
Kowledge ticle: obability ad Statistics Usig outig Techiques to Detemie obabilities Tee Diagams ad the Fudametal outig iciple impotat aspect of pobability theoy is the ability to detemie the total umbe
Lecture 24: Observability and Constructibility
 ectue 24: Obsevability ad Costuctibility 7 Obsevability ad Costuctibility Motivatio: State feedback laws deped o a kowledge of the cuet state. I some systems, xt () ca be measued diectly, e.g., positio
ectue 24: Obsevability ad Costuctibility 7 Obsevability ad Costuctibility Motivatio: State feedback laws deped o a kowledge of the cuet state. I some systems, xt () ca be measued diectly, e.g., positio
Seidel s Trapezoidal Partitioning Algorithm
 CS68: Geometic Agoithms Handout #6 Design and Anaysis Oigina Handout #6 Stanfod Univesity Tuesday, 5 Febuay 99 Oigina Lectue #7: 30 Januay 99 Topics: Seide s Tapezoida Patitioning Agoithm Scibe: Michae
CS68: Geometic Agoithms Handout #6 Design and Anaysis Oigina Handout #6 Stanfod Univesity Tuesday, 5 Febuay 99 Oigina Lectue #7: 30 Januay 99 Topics: Seide s Tapezoida Patitioning Agoithm Scibe: Michae
CHAPTER 5 : SERIES. 5.2 The Sum of a Series Sum of Power of n Positive Integers Sum of Series of Partial Fraction Difference Method
 CHAPTER 5 : SERIES 5.1 Seies 5. The Sum of a Seies 5..1 Sum of Powe of Positive Iteges 5.. Sum of Seies of Patial Factio 5..3 Diffeece Method 5.3 Test of covegece 5.3.1 Divegece Test 5.3. Itegal Test 5.3.3
CHAPTER 5 : SERIES 5.1 Seies 5. The Sum of a Seies 5..1 Sum of Powe of Positive Iteges 5.. Sum of Seies of Patial Factio 5..3 Diffeece Method 5.3 Test of covegece 5.3.1 Divegece Test 5.3. Itegal Test 5.3.3
Quantum Mechanics Lecture Notes 10 April 2007 Meg Noah
 The -Patice syste: ˆ H V This is difficut to sove. y V 1 ˆ H V 1 1 1 1 ˆ = ad with 1 1 Hˆ Cete of Mass ˆ fo Patice i fee space He Reative Haitoia eative coodiate of the tota oetu Pˆ the tota oetu tota
The -Patice syste: ˆ H V This is difficut to sove. y V 1 ˆ H V 1 1 1 1 ˆ = ad with 1 1 Hˆ Cete of Mass ˆ fo Patice i fee space He Reative Haitoia eative coodiate of the tota oetu Pˆ the tota oetu tota
THE ANALYTIC LARGE SIEVE
 THE ANALYTIC LAGE SIEVE 1. The aalytic lage sieve I the last lectue we saw how to apply the aalytic lage sieve to deive a aithmetic fomulatio of the lage sieve, which we applied to the poblem of boudig
THE ANALYTIC LAGE SIEVE 1. The aalytic lage sieve I the last lectue we saw how to apply the aalytic lage sieve to deive a aithmetic fomulatio of the lage sieve, which we applied to the poblem of boudig
= 5! 3! 2! = 5! 3! (5 3)!. In general, the number of different groups of r items out of n items (when the order is ignored) is given by n!
 0 Combiatoial Aalysis Copyight by Deiz Kalı 4 Combiatios Questio 4 What is the diffeece betwee the followig questio i How may 3-lette wods ca you wite usig the lettes A, B, C, D, E ii How may 3-elemet
0 Combiatoial Aalysis Copyight by Deiz Kalı 4 Combiatios Questio 4 What is the diffeece betwee the followig questio i How may 3-lette wods ca you wite usig the lettes A, B, C, D, E ii How may 3-elemet
Counting Functions and Subsets
 CHAPTER 1 Coutig Fuctios ad Subsets This chapte of the otes is based o Chapte 12 of PJE See PJE p144 Hee ad below, the efeeces to the PJEccles book ae give as PJE The goal of this shot chapte is to itoduce
CHAPTER 1 Coutig Fuctios ad Subsets This chapte of the otes is based o Chapte 12 of PJE See PJE p144 Hee ad below, the efeeces to the PJEccles book ae give as PJE The goal of this shot chapte is to itoduce
Homework 1 Solutions CSE 101 Summer 2017
 Homewok 1 Soutions CSE 101 Summe 2017 1 Waming Up 1.1 Pobem and Pobem Instance Find the smaest numbe in an aay of n integes a 1, a 2,..., a n. What is the input? What is the output? Is this a pobem o a
Homewok 1 Soutions CSE 101 Summe 2017 1 Waming Up 1.1 Pobem and Pobem Instance Find the smaest numbe in an aay of n integes a 1, a 2,..., a n. What is the input? What is the output? Is this a pobem o a
Minimization of the quadratic test function
 Miimizatio of the quadatic test fuctio A quadatic fom is a scala quadatic fuctio of a vecto with the fom f ( ) A b c with b R A R whee A is assumed to be SPD ad c is a scala costat Note: A symmetic mati
Miimizatio of the quadatic test fuctio A quadatic fom is a scala quadatic fuctio of a vecto with the fom f ( ) A b c with b R A R whee A is assumed to be SPD ad c is a scala costat Note: A symmetic mati
Consider unordered sample of size r. This sample can be used to make r! Ordered samples (r! permutations). unordered sample
 Uodeed Samples without Replacemet oside populatio of elemets a a... a. y uodeed aagemet of elemets is called a uodeed sample of size. Two uodeed samples ae diffeet oly if oe cotais a elemet ot cotaied
Uodeed Samples without Replacemet oside populatio of elemets a a... a. y uodeed aagemet of elemets is called a uodeed sample of size. Two uodeed samples ae diffeet oly if oe cotais a elemet ot cotaied
SOME ARITHMETIC PROPERTIES OF OVERPARTITION K -TUPLES
 #A17 INTEGERS 9 2009), 181-190 SOME ARITHMETIC PROPERTIES OF OVERPARTITION K -TUPLES Deick M. Keiste Depatmet of Mathematics, Pe State Uivesity, Uivesity Pak, PA 16802 dmk5075@psu.edu James A. Selles Depatmet
#A17 INTEGERS 9 2009), 181-190 SOME ARITHMETIC PROPERTIES OF OVERPARTITION K -TUPLES Deick M. Keiste Depatmet of Mathematics, Pe State Uivesity, Uivesity Pak, PA 16802 dmk5075@psu.edu James A. Selles Depatmet
Quantum Fourier Transform
 Chapte 5 Quantum Fouie Tansfom Many poblems in physics and mathematics ae solved by tansfoming a poblem into some othe poblem with a known solution. Some notable examples ae Laplace tansfom, Legende tansfom,
Chapte 5 Quantum Fouie Tansfom Many poblems in physics and mathematics ae solved by tansfoming a poblem into some othe poblem with a known solution. Some notable examples ae Laplace tansfom, Legende tansfom,
MATH /19: problems for supervision in week 08 SOLUTIONS
 MATH10101 2018/19: poblems fo supevisio i week 08 Q1. Let A be a set. SOLUTIONS (i Pove that the fuctio c: P(A P(A, defied by c(x A \ X, is bijective. (ii Let ow A be fiite, A. Use (i to show that fo each
MATH10101 2018/19: poblems fo supevisio i week 08 Q1. Let A be a set. SOLUTIONS (i Pove that the fuctio c: P(A P(A, defied by c(x A \ X, is bijective. (ii Let ow A be fiite, A. Use (i to show that fo each
Progression. CATsyllabus.com. CATsyllabus.com. Sequence & Series. Arithmetic Progression (A.P.) n th term of an A.P.
 Pogessio Sequece & Seies A set of umbes whose domai is a eal umbe is called a SEQUENCE ad sum of the sequece is called a SERIES. If a, a, a, a 4,., a, is a sequece, the the expessio a + a + a + a 4 + a
Pogessio Sequece & Seies A set of umbes whose domai is a eal umbe is called a SEQUENCE ad sum of the sequece is called a SERIES. If a, a, a, a 4,., a, is a sequece, the the expessio a + a + a + a 4 + a
Construction of mixed estimation for solving the first edge problem for the equation of non-isotropic diffusion
 ISSN: 350-038 Iteatioa Joua of AdvacedReseach i Sciece, Egieeig ad echoogy Vo. 5, Issue, Decembe 08 Costuctio of mixed estimatio fo sovig the fist edge pobem fo the equatio of o-isotopic diffusio okhi
ISSN: 350-038 Iteatioa Joua of AdvacedReseach i Sciece, Egieeig ad echoogy Vo. 5, Issue, Decembe 08 Costuctio of mixed estimatio fo sovig the fist edge pobem fo the equatio of o-isotopic diffusio okhi
Multivector Functions
 I: J. Math. Aal. ad Appl., ol. 24, No. 3, c Academic Pess (968) 467 473. Multivecto Fuctios David Hestees I a pevious pape [], the fudametals of diffeetial ad itegal calculus o Euclidea -space wee expessed
I: J. Math. Aal. ad Appl., ol. 24, No. 3, c Academic Pess (968) 467 473. Multivecto Fuctios David Hestees I a pevious pape [], the fudametals of diffeetial ad itegal calculus o Euclidea -space wee expessed
BINOMIAL THEOREM An expression consisting of two terms, connected by + or sign is called a
 BINOMIAL THEOREM hapte 8 8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4 5y, etc., ae all biomial epessios. 8.. Biomial theoem If
BINOMIAL THEOREM hapte 8 8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4 5y, etc., ae all biomial epessios. 8.. Biomial theoem If
Chapter 2 Sampling distribution
 [ 05 STAT] Chapte Samplig distibutio. The Paamete ad the Statistic Whe we have collected the data, we have a whole set of umbes o desciptios witte dow o a pape o stoed o a compute file. We ty to summaize
[ 05 STAT] Chapte Samplig distibutio. The Paamete ad the Statistic Whe we have collected the data, we have a whole set of umbes o desciptios witte dow o a pape o stoed o a compute file. We ty to summaize
Discrete Fourier Transform
 Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
BINOMIAL THEOREM NCERT An expression consisting of two terms, connected by + or sign is called a
 8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4, etc., ae all biomial 5y epessios. 8.. Biomial theoem BINOMIAL THEOREM If a ad b ae
8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4, etc., ae all biomial 5y epessios. 8.. Biomial theoem BINOMIAL THEOREM If a ad b ae
EDEXCEL NATIONAL CERTIFICATE UNIT 28 FURTHER MATHEMATICS FOR TECHNICIANS OUTCOME 2- ALGEBRAIC TECHNIQUES TUTORIAL 1 - PROGRESSIONS
 EDEXCEL NATIONAL CERTIFICATE UNIT 8 FURTHER MATHEMATICS FOR TECHNICIANS OUTCOME - ALGEBRAIC TECHNIQUES TUTORIAL - PROGRESSIONS CONTENTS Be able to apply algebaic techiques Aithmetic pogessio (AP): fist
EDEXCEL NATIONAL CERTIFICATE UNIT 8 FURTHER MATHEMATICS FOR TECHNICIANS OUTCOME - ALGEBRAIC TECHNIQUES TUTORIAL - PROGRESSIONS CONTENTS Be able to apply algebaic techiques Aithmetic pogessio (AP): fist
Technical Report: Bessel Filter Analysis
 Sasa Mahmoodi 1 Techical Repot: Bessel Filte Aalysis 1 School of Electoics ad Compute Sciece, Buildig 1, Southampto Uivesity, Southampto, S17 1BJ, UK, Email: sm3@ecs.soto.ac.uk I this techical epot, we
Sasa Mahmoodi 1 Techical Repot: Bessel Filte Aalysis 1 School of Electoics ad Compute Sciece, Buildig 1, Southampto Uivesity, Southampto, S17 1BJ, UK, Email: sm3@ecs.soto.ac.uk I this techical epot, we
LESSON 15: COMPOUND INTEREST
 High School: Expoeial Fuctios LESSON 15: COMPOUND INTEREST 1. You have see this fomula fo compoud ieest. Paamete P is the picipal amou (the moey you stat with). Paamete is the ieest ate pe yea expessed
High School: Expoeial Fuctios LESSON 15: COMPOUND INTEREST 1. You have see this fomula fo compoud ieest. Paamete P is the picipal amou (the moey you stat with). Paamete is the ieest ate pe yea expessed
2012 GCE A Level H2 Maths Solution Paper Let x,
 GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
Math 7409 Homework 2 Fall from which we can calculate the cycle index of the action of S 5 on pairs of vertices as
 Math 7409 Hoewok 2 Fall 2010 1. Eueate the equivalece classes of siple gaphs o 5 vetices by usig the patte ivetoy as a guide. The cycle idex of S 5 actig o 5 vetices is 1 x 5 120 1 10 x 3 1 x 2 15 x 1
Math 7409 Hoewok 2 Fall 2010 1. Eueate the equivalece classes of siple gaphs o 5 vetices by usig the patte ivetoy as a guide. The cycle idex of S 5 actig o 5 vetices is 1 x 5 120 1 10 x 3 1 x 2 15 x 1
Auchmuty High School Mathematics Department Sequences & Series Notes Teacher Version
 equeces ad eies Auchmuty High chool Mathematics Depatmet equeces & eies Notes Teache Vesio A sequece takes the fom,,7,0,, while 7 0 is a seies. Thee ae two types of sequece/seies aithmetic ad geometic.
equeces ad eies Auchmuty High chool Mathematics Depatmet equeces & eies Notes Teache Vesio A sequece takes the fom,,7,0,, while 7 0 is a seies. Thee ae two types of sequece/seies aithmetic ad geometic.
The Pigeonhole Principle 3.4 Binomial Coefficients
 Discete M athematic Chapte 3: Coutig 3. The Pigeohole Piciple 3.4 Biomial Coefficiets D Patic Cha School of Compute Sciece ad Egieeig South Chia Uivesity of Techology Ageda Ch 3. The Pigeohole Piciple
Discete M athematic Chapte 3: Coutig 3. The Pigeohole Piciple 3.4 Biomial Coefficiets D Patic Cha School of Compute Sciece ad Egieeig South Chia Uivesity of Techology Ageda Ch 3. The Pigeohole Piciple
a) The average (mean) of the two fractions is halfway between them: b) The answer is yes. Assume without loss of generality that p < r.
 Solutios to MAML Olympiad Level 00. Factioated a) The aveage (mea) of the two factios is halfway betwee them: p ps+ q ps+ q + q s qs qs b) The aswe is yes. Assume without loss of geeality that p
Solutios to MAML Olympiad Level 00. Factioated a) The aveage (mea) of the two factios is halfway betwee them: p ps+ q ps+ q + q s qs qs b) The aswe is yes. Assume without loss of geeality that p
Math 166 Week-in-Review - S. Nite 11/10/2012 Page 1 of 5 WIR #9 = 1+ r eff. , where r. is the effective interest rate, r is the annual
 Math 66 Week-i-Review - S. Nite // Page of Week i Review #9 (F-F.4, 4.-4.4,.-.) Simple Iteest I = Pt, whee I is the iteest, P is the picipal, is the iteest ate, ad t is the time i yeas. P( + t), whee A
Math 66 Week-i-Review - S. Nite // Page of Week i Review #9 (F-F.4, 4.-4.4,.-.) Simple Iteest I = Pt, whee I is the iteest, P is the picipal, is the iteest ate, ad t is the time i yeas. P( + t), whee A
SVD ( ) Linear Algebra for. A bit of repetition. Lecture: 8. Let s try the factorization. Is there a generalization? = Q2Λ2Q (spectral theorem!
 Liea Algeba fo Wieless Commuicatios Lectue: 8 Sigula Value Decompositio SVD Ove Edfos Depatmet of Electical ad Ifomatio echology Lud Uivesity it 00-04-06 Ove Edfos A bit of epetitio A vey useful matix
Liea Algeba fo Wieless Commuicatios Lectue: 8 Sigula Value Decompositio SVD Ove Edfos Depatmet of Electical ad Ifomatio echology Lud Uivesity it 00-04-06 Ove Edfos A bit of epetitio A vey useful matix
Nuclear Physics (9 th lecture)
 Nucea Physics (9 th ectue) Cotet The ucea she mode (cotd.) The successes ad faiues of the ucea she mode o Nucea spi ad paity o Nucea magetic momets o Nucea quadupoe momets Nucea modes #4: The ucea coective
Nucea Physics (9 th ectue) Cotet The ucea she mode (cotd.) The successes ad faiues of the ucea she mode o Nucea spi ad paity o Nucea magetic momets o Nucea quadupoe momets Nucea modes #4: The ucea coective
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
EXAMPLES. Leader in CBSE Coaching. Solutions of BINOMIAL THEOREM A.V.T.E. by AVTE (avte.in) Class XI
 avtei EXAMPLES Solutios of AVTE by AVTE (avtei) lass XI Leade i BSE oachig 1 avtei SHORT ANSWER TYPE 1 Fid the th tem i the epasio of 1 We have T 1 1 1 1 1 1 1 1 1 1 Epad the followig (1 + ) 4 Put 1 y
avtei EXAMPLES Solutios of AVTE by AVTE (avtei) lass XI Leade i BSE oachig 1 avtei SHORT ANSWER TYPE 1 Fid the th tem i the epasio of 1 We have T 1 1 1 1 1 1 1 1 1 1 Epad the followig (1 + ) 4 Put 1 y
Discrete Fourier Transform
 Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Lecture 6: October 16, 2017
 Ifomatio ad Codig Theoy Autum 207 Lectue: Madhu Tulsiai Lectue 6: Octobe 6, 207 The Method of Types Fo this lectue, we will take U to be a fiite uivese U, ad use x (x, x 2,..., x to deote a sequece of
Ifomatio ad Codig Theoy Autum 207 Lectue: Madhu Tulsiai Lectue 6: Octobe 6, 207 The Method of Types Fo this lectue, we will take U to be a fiite uivese U, ad use x (x, x 2,..., x to deote a sequece of
Discretizing the 3-D Schrödinger equation for a Central Potential
 Discetizing the 3-D Schödinge equation fo a Centa Potentia By now, you ae faiia with the Discete Schodinge Equation fo one Catesian diension. We wi now conside odifying it to hande poa diensions fo a centa
Discetizing the 3-D Schödinge equation fo a Centa Potentia By now, you ae faiia with the Discete Schodinge Equation fo one Catesian diension. We wi now conside odifying it to hande poa diensions fo a centa
Finite q-identities related to well-known theorems of Euler and Gauss. Johann Cigler
 Fiite -idetities elated to well-ow theoems of Eule ad Gauss Joha Cigle Faultät fü Mathemati Uivesität Wie A-9 Wie, Nodbegstaße 5 email: oha.cigle@uivie.ac.at Abstact We give geealizatios of a fiite vesio
Fiite -idetities elated to well-ow theoems of Eule ad Gauss Joha Cigle Faultät fü Mathemati Uivesität Wie A-9 Wie, Nodbegstaße 5 email: oha.cigle@uivie.ac.at Abstact We give geealizatios of a fiite vesio
A NOTE ON DOMINATION PARAMETERS IN RANDOM GRAPHS
 Discussioes Mathematicae Gaph Theoy 28 (2008 335 343 A NOTE ON DOMINATION PARAMETERS IN RANDOM GRAPHS Athoy Boato Depatmet of Mathematics Wilfid Lauie Uivesity Wateloo, ON, Caada, N2L 3C5 e-mail: aboato@oges.com
Discussioes Mathematicae Gaph Theoy 28 (2008 335 343 A NOTE ON DOMINATION PARAMETERS IN RANDOM GRAPHS Athoy Boato Depatmet of Mathematics Wilfid Lauie Uivesity Wateloo, ON, Caada, N2L 3C5 e-mail: aboato@oges.com
Using Difference Equations to Generalize Results for Periodic Nested Radicals
 Usig Diffeece Equatios to Geealize Results fo Peiodic Nested Radicals Chis Lyd Uivesity of Rhode Islad, Depatmet of Mathematics South Kigsto, Rhode Islad 2 2 2 2 2 2 2 π = + + +... Vieta (593) 2 2 2 =
Usig Diffeece Equatios to Geealize Results fo Peiodic Nested Radicals Chis Lyd Uivesity of Rhode Islad, Depatmet of Mathematics South Kigsto, Rhode Islad 2 2 2 2 2 2 2 π = + + +... Vieta (593) 2 2 2 =
DANIEL YAQUBI, MADJID MIRZAVAZIRI AND YASIN SAEEDNEZHAD
 MIXED -STIRLING NUMERS OF THE SEOND KIND DANIEL YAQUI, MADJID MIRZAVAZIRI AND YASIN SAEEDNEZHAD Abstact The Stilig umbe of the secod id { } couts the umbe of ways to patitio a set of labeled balls ito
MIXED -STIRLING NUMERS OF THE SEOND KIND DANIEL YAQUI, MADJID MIRZAVAZIRI AND YASIN SAEEDNEZHAD Abstact The Stilig umbe of the secod id { } couts the umbe of ways to patitio a set of labeled balls ito
The Discrete Fourier Transform
 (7) The Discete Fouie Tasfom The Discete Fouie Tasfom hat is Discete Fouie Tasfom (DFT)? (ote: It s ot DTFT discete-time Fouie tasfom) A liea tasfomatio (mati) Samples of the Fouie tasfom (DTFT) of a apeiodic
(7) The Discete Fouie Tasfom The Discete Fouie Tasfom hat is Discete Fouie Tasfom (DFT)? (ote: It s ot DTFT discete-time Fouie tasfom) A liea tasfomatio (mati) Samples of the Fouie tasfom (DTFT) of a apeiodic
Bertrand s Postulate
 Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Ch 3.4 Binomial Coefficients. Pascal's Identit y and Triangle. Chapter 3.2 & 3.4. South China University of Technology
 Disc ete Mathem atic Chapte 3: Coutig 3. The Pigeohole Piciple 3.4 Biomial Coefficiets D Patic Cha School of Compute Sciece ad Egieeig South Chia Uivesity of Techology Pigeohole Piciple Suppose that a
Disc ete Mathem atic Chapte 3: Coutig 3. The Pigeohole Piciple 3.4 Biomial Coefficiets D Patic Cha School of Compute Sciece ad Egieeig South Chia Uivesity of Techology Pigeohole Piciple Suppose that a
EVALUATION OF SUMS INVOLVING GAUSSIAN q-binomial COEFFICIENTS WITH RATIONAL WEIGHT FUNCTIONS
 EVALUATION OF SUMS INVOLVING GAUSSIAN -BINOMIAL COEFFICIENTS WITH RATIONAL WEIGHT FUNCTIONS EMRAH KILIÇ AND HELMUT PRODINGER Abstact We coside sums of the Gaussia -biomial coefficiets with a paametic atioal
EVALUATION OF SUMS INVOLVING GAUSSIAN -BINOMIAL COEFFICIENTS WITH RATIONAL WEIGHT FUNCTIONS EMRAH KILIÇ AND HELMUT PRODINGER Abstact We coside sums of the Gaussia -biomial coefficiets with a paametic atioal
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
On ARMA(1,q) models with bounded and periodically correlated solutions
 Reseach Repot HSC/03/3 O ARMA(,q) models with bouded ad peiodically coelated solutios Aleksade Weo,2 ad Agieszka Wy oma ska,2 Hugo Steihaus Cete, Woc aw Uivesity of Techology 2 Istitute of Mathematics,
Reseach Repot HSC/03/3 O ARMA(,q) models with bouded ad peiodically coelated solutios Aleksade Weo,2 ad Agieszka Wy oma ska,2 Hugo Steihaus Cete, Woc aw Uivesity of Techology 2 Istitute of Mathematics,
Lower Bounds for Cover-Free Families
 Loe Bouds fo Cove-Fee Families Ali Z. Abdi Covet of Nazaeth High School Gade, Abas 7, Haifa Nade H. Bshouty Dept. of Compute Sciece Techio, Haifa, 3000 Apil, 05 Abstact Let F be a set of blocks of a t-set
Loe Bouds fo Cove-Fee Families Ali Z. Abdi Covet of Nazaeth High School Gade, Abas 7, Haifa Nade H. Bshouty Dept. of Compute Sciece Techio, Haifa, 3000 Apil, 05 Abstact Let F be a set of blocks of a t-set
MATHS FOR ENGINEERS ALGEBRA TUTORIAL 8 MATHEMATICAL PROGRESSIONS AND SERIES
 MATHS FOR ENGINEERS ALGEBRA TUTORIAL 8 MATHEMATICAL PROGRESSIONS AND SERIES O completio of this ttoial yo shold be able to do the followig. Eplai aithmetical ad geometic pogessios. Eplai factoial otatio
MATHS FOR ENGINEERS ALGEBRA TUTORIAL 8 MATHEMATICAL PROGRESSIONS AND SERIES O completio of this ttoial yo shold be able to do the followig. Eplai aithmetical ad geometic pogessios. Eplai factoial otatio
Complementary Dual Subfield Linear Codes Over Finite Fields
 1 Complemetay Dual Subfield Liea Codes Ove Fiite Fields Kiagai Booiyoma ad Somphog Jitma,1 Depatmet of Mathematics, Faculty of Sciece, Silpao Uivesity, Naho Pathom 73000, hailad e-mail : ai_b_555@hotmail.com
1 Complemetay Dual Subfield Liea Codes Ove Fiite Fields Kiagai Booiyoma ad Somphog Jitma,1 Depatmet of Mathematics, Faculty of Sciece, Silpao Uivesity, Naho Pathom 73000, hailad e-mail : ai_b_555@hotmail.com
PH 425 Quantum Measurement and Spin Winter SPINS Lab 1
 PH 425 Quatum Measuremet ad Spi Witer 23 SPIS Lab Measure the spi projectio S z alog the z-axis This is the experimet that is ready to go whe you start the program, as show below Each atom is measured
PH 425 Quatum Measuremet ad Spi Witer 23 SPIS Lab Measure the spi projectio S z alog the z-axis This is the experimet that is ready to go whe you start the program, as show below Each atom is measured
Conditional Convergence of Infinite Products
 Coditioal Covegece of Ifiite Poducts William F. Tech Ameica Mathematical Mothly 106 1999), 646-651 I this aticle we evisit the classical subject of ifiite poducts. Fo stadad defiitios ad theoems o this
Coditioal Covegece of Ifiite Poducts William F. Tech Ameica Mathematical Mothly 106 1999), 646-651 I this aticle we evisit the classical subject of ifiite poducts. Fo stadad defiitios ad theoems o this
RELIABILITY ASSESSMENT OF SYSTEMS WITH PERIODIC MAINTENANCE UNDER RARE FAILURES OF ITS ELEMENTS
 Y Geis ELIABILITY ASSESSMENT OF SYSTEMS WITH PEIODIC MAINTENANCE UNDE AE FAILUES OF ITS ELEMENTS T&A # (6) (Vol) 2, Mach ELIABILITY ASSESSMENT OF SYSTEMS WITH PEIODIC MAINTENANCE UNDE AE FAILUES OF ITS
Y Geis ELIABILITY ASSESSMENT OF SYSTEMS WITH PEIODIC MAINTENANCE UNDE AE FAILUES OF ITS ELEMENTS T&A # (6) (Vol) 2, Mach ELIABILITY ASSESSMENT OF SYSTEMS WITH PEIODIC MAINTENANCE UNDE AE FAILUES OF ITS
A note on random minimum length spanning trees
 A ote o adom miimum legth spaig tees Ala Fieze Miklós Ruszikó Lubos Thoma Depatmet of Mathematical Scieces Caegie Mello Uivesity Pittsbugh PA15213, USA ala@adom.math.cmu.edu, usziko@luta.sztaki.hu, thoma@qwes.math.cmu.edu
A ote o adom miimum legth spaig tees Ala Fieze Miklós Ruszikó Lubos Thoma Depatmet of Mathematical Scieces Caegie Mello Uivesity Pittsbugh PA15213, USA ala@adom.math.cmu.edu, usziko@luta.sztaki.hu, thoma@qwes.math.cmu.edu
Lesson 5. Chapter 7. Wiener Filters. Bengt Mandersson. r x k We assume uncorrelated noise v(n). LTH. September 2010
 Optimal Sigal Poceig Leo 5 Chapte 7 Wiee Filte I thi chapte we will ue the model how below. The igal ito the eceive i ( ( iga. Nomally, thi igal i ditubed by additive white oie v(. The ifomatio i i (.
Optimal Sigal Poceig Leo 5 Chapte 7 Wiee Filte I thi chapte we will ue the model how below. The igal ito the eceive i ( ( iga. Nomally, thi igal i ditubed by additive white oie v(. The ifomatio i i (.
Physics 235 Final Examination December 4, 2006 Solutions
 Physics 35 Fi Emitio Decembe, 6 Soutios.. Fist coside the two u quks. They e idetic spi ½ ptices, so the tot spi c be eithe o. The Pui Picipe equies tht the ove wvefuctio be echge tisymmetic. Sice the
Physics 35 Fi Emitio Decembe, 6 Soutios.. Fist coside the two u quks. They e idetic spi ½ ptices, so the tot spi c be eithe o. The Pui Picipe equies tht the ove wvefuctio be echge tisymmetic. Sice the
Range Symmetric Matrices in Minkowski Space
 BULLETIN of the Bull. alaysia ath. Sc. Soc. (Secod Seies) 3 (000) 45-5 LYSIN THETICL SCIENCES SOCIETY Rae Symmetic atices i ikowski Space.R. EENKSHI Depatmet of athematics, amalai Uivesity, amalaiaa 608
BULLETIN of the Bull. alaysia ath. Sc. Soc. (Secod Seies) 3 (000) 45-5 LYSIN THETICL SCIENCES SOCIETY Rae Symmetic atices i ikowski Space.R. EENKSHI Depatmet of athematics, amalai Uivesity, amalaiaa 608
5.6 Absolute Convergence and The Ratio and Root Tests
 5.6 Absolute Covergece ad The Ratio ad Root Tests Bria E. Veitch 5.6 Absolute Covergece ad The Ratio ad Root Tests Recall from our previous sectio that diverged but ( ) coverged. Both of these sequeces
5.6 Absolute Covergece ad The Ratio ad Root Tests Bria E. Veitch 5.6 Absolute Covergece ad The Ratio ad Root Tests Recall from our previous sectio that diverged but ( ) coverged. Both of these sequeces
Advanced Physical Geodesy
 Supplemetal Notes Review of g Tems i Moitz s Aalytic Cotiuatio Method. Advaced hysical Geodesy GS887 Chistophe Jekeli Geodetic Sciece The Ohio State Uivesity 5 South Oval Mall Columbus, OH 4 7 The followig
Supplemetal Notes Review of g Tems i Moitz s Aalytic Cotiuatio Method. Advaced hysical Geodesy GS887 Chistophe Jekeli Geodetic Sciece The Ohio State Uivesity 5 South Oval Mall Columbus, OH 4 7 The followig
Disjoint Sets { 9} { 1} { 11} Disjoint Sets (cont) Operations. Disjoint Sets (cont) Disjoint Sets (cont) n elements
 Disjoit Sets elemets { x, x, } X =, K Opeatios x Patitioed ito k sets (disjoit sets S, S,, K Fid-Set(x - etu set cotaiig x Uio(x,y - make a ew set by combiig the sets cotaiig x ad y (destoyig them S k
Disjoit Sets elemets { x, x, } X =, K Opeatios x Patitioed ito k sets (disjoit sets S, S,, K Fid-Set(x - etu set cotaiig x Uio(x,y - make a ew set by combiig the sets cotaiig x ad y (destoyig them S k
( ) 1 Comparison Functions. α is strictly increasing since ( r) ( r ) α = for any positive real number c. = 0. It is said to belong to
 Compaiso Fuctios I this lesso, we study stability popeties of the oautoomous system = f t, x The difficulty is that ay solutio of this system statig at x( t ) depeds o both t ad t = x Thee ae thee special
Compaiso Fuctios I this lesso, we study stability popeties of the oautoomous system = f t, x The difficulty is that ay solutio of this system statig at x( t ) depeds o both t ad t = x Thee ae thee special
The picture in figure 1.1 helps us to see that the area represents the distance traveled. Figure 1: Area represents distance travelled
 1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
Areas and Distances. We can easily find areas of certain geometric figures using well-known formulas:
 Areas ad Distaces We ca easily fid areas of certai geometric figures usig well-kow formulas: However, it is t easy to fid the area of a regio with curved sides: METHOD: To evaluate the area of the regio
Areas ad Distaces We ca easily fid areas of certai geometric figures usig well-kow formulas: However, it is t easy to fid the area of a regio with curved sides: METHOD: To evaluate the area of the regio
Linear Convolution Using DFT
 Liea Covoutio Usig DFT Reca that iea covoutio is x3 x x whe the egths of x ad x ae L ad P espectivey the egth of x3 is LP-. Thus a usefu popety is that the cicua covoutio of two fiite-egth sequeces with
Liea Covoutio Usig DFT Reca that iea covoutio is x3 x x whe the egths of x ad x ae L ad P espectivey the egth of x3 is LP-. Thus a usefu popety is that the cicua covoutio of two fiite-egth sequeces with
Alternative Orthogonal Polynomials. Vladimir Chelyshkov
 Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Greatest term (numerically) in the expansion of (1 + x) Method 1 Let T
 BINOMIAL THEOREM_SYNOPSIS Geatest tem (umeically) i the epasio of ( + ) Method Let T ( The th tem) be the geatest tem. Fid T, T, T fom the give epasio. Put T T T ad. Th will give a iequality fom whee value
BINOMIAL THEOREM_SYNOPSIS Geatest tem (umeically) i the epasio of ( + ) Method Let T ( The th tem) be the geatest tem. Fid T, T, T fom the give epasio. Put T T T ad. Th will give a iequality fom whee value
KEY. Math 334 Midterm II Fall 2007 section 004 Instructor: Scott Glasgow
 KEY Math 334 Midtem II Fall 7 sectio 4 Istucto: Scott Glasgow Please do NOT wite o this exam. No cedit will be give fo such wok. Rathe wite i a blue book, o o you ow pape, pefeably egieeig pape. Wite you
KEY Math 334 Midtem II Fall 7 sectio 4 Istucto: Scott Glasgow Please do NOT wite o this exam. No cedit will be give fo such wok. Rathe wite i a blue book, o o you ow pape, pefeably egieeig pape. Wite you
= ρ. Since this equation is applied to an arbitrary point in space, we can use it to determine the charge density once we know the field.
 Gauss s Law In diffeentia fom D = ρ. ince this equation is appied to an abita point in space, we can use it to detemine the chage densit once we know the fied. (We can use this equation to ve fo the fied
Gauss s Law In diffeentia fom D = ρ. ince this equation is appied to an abita point in space, we can use it to detemine the chage densit once we know the fied. (We can use this equation to ve fo the fied
On composite conformal mapping of an annulus to a plane with two holes
 O composite cofomal mappig of a aulus to a plae with two holes Mila Batista (July 07) Abstact I the aticle we coside the composite cofomal map which maps aulus to ifiite egio with symmetic hole ad ealy
O composite cofomal mappig of a aulus to a plae with two holes Mila Batista (July 07) Abstact I the aticle we coside the composite cofomal map which maps aulus to ifiite egio with symmetic hole ad ealy
Einstein Classes, Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road New Delhi , Ph. : ,
 MB BINOMIAL THEOREM Biomial Epessio : A algebaic epessio which cotais two dissimila tems is called biomial epessio Fo eample :,,, etc / ( ) Statemet of Biomial theoem : If, R ad N, the : ( + ) = a b +
MB BINOMIAL THEOREM Biomial Epessio : A algebaic epessio which cotais two dissimila tems is called biomial epessio Fo eample :,,, etc / ( ) Statemet of Biomial theoem : If, R ad N, the : ( + ) = a b +
THE ANALYSIS OF SOME MODELS FOR CLAIM PROCESSING IN INSURANCE COMPANIES
 Please cite this atle as: Mhal Matalyck Tacaa Romaiuk The aalysis of some models fo claim pocessig i isuace compaies Scietif Reseach of the Istitute of Mathemats ad Compute Sciece 004 Volume 3 Issue pages
Please cite this atle as: Mhal Matalyck Tacaa Romaiuk The aalysis of some models fo claim pocessig i isuace compaies Scietif Reseach of the Istitute of Mathemats ad Compute Sciece 004 Volume 3 Issue pages
BBU Codes Overview. Outline Introduction Beam transport Equation How to solve (BBU-R, TDBBUU, bi, MATBBU etc.) Comparison of BBU codes
 BBU Codes Oveview asau Sawamua ad Ryoichi Hajima JAERI Outie Itoductio Beam tasot Equatio How to sove BBU-R, DBBUU, bi, ABBU etc. Comaiso of BBU codes Itoductio ERL cuet imited by Beam Beaku asvese defect
BBU Codes Oveview asau Sawamua ad Ryoichi Hajima JAERI Outie Itoductio Beam tasot Equatio How to sove BBU-R, DBBUU, bi, ABBU etc. Comaiso of BBU codes Itoductio ERL cuet imited by Beam Beaku asvese defect
The Solutions of the Classical Relativistic Two-Body Equation
 T. J. of Physics (998), 07 4. c TÜBİTAK The Soutions of the Cassica Reativistic Two-Body Equation Coşkun ÖNEM Eciyes Univesity, Physics Depatment, 38039, Kaysei - TURKEY Received 3.08.996 Abstact With
T. J. of Physics (998), 07 4. c TÜBİTAK The Soutions of the Cassica Reativistic Two-Body Equation Coşkun ÖNEM Eciyes Univesity, Physics Depatment, 38039, Kaysei - TURKEY Received 3.08.996 Abstact With
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
The number of r element subsets of a set with n r elements
 Popositio: is The umbe of elemet subsets of a set with elemets Poof: Each such subset aises whe we pick a fist elemet followed by a secod elemet up to a th elemet The umbe of such choices is P But this
Popositio: is The umbe of elemet subsets of a set with elemets Poof: Each such subset aises whe we pick a fist elemet followed by a secod elemet up to a th elemet The umbe of such choices is P But this
Sums of Involving the Harmonic Numbers and the Binomial Coefficients
 Ameica Joual of Computatioal Mathematics 5 5 96-5 Published Olie Jue 5 i SciRes. http://www.scip.og/oual/acm http://dx.doi.og/.46/acm.5.58 Sums of Ivolvig the amoic Numbes ad the Biomial Coefficiets Wuyugaowa
Ameica Joual of Computatioal Mathematics 5 5 96-5 Published Olie Jue 5 i SciRes. http://www.scip.og/oual/acm http://dx.doi.og/.46/acm.5.58 Sums of Ivolvig the amoic Numbes ad the Biomial Coefficiets Wuyugaowa
Riemann Sums y = f (x)
 Riema Sums Recall that we have previously discussed the area problem I its simplest form we ca state it this way: The Area Problem Let f be a cotiuous, o-egative fuctio o the closed iterval [a, b] Fid
Riema Sums Recall that we have previously discussed the area problem I its simplest form we ca state it this way: The Area Problem Let f be a cotiuous, o-egative fuctio o the closed iterval [a, b] Fid
On randomly generated non-trivially intersecting hypergraphs
 O adomly geeated o-tivially itesectig hypegaphs Balázs Patkós Submitted: May 5, 009; Accepted: Feb, 010; Published: Feb 8, 010 Mathematics Subject Classificatio: 05C65, 05D05, 05D40 Abstact We popose two
O adomly geeated o-tivially itesectig hypegaphs Balázs Patkós Submitted: May 5, 009; Accepted: Feb, 010; Published: Feb 8, 010 Mathematics Subject Classificatio: 05C65, 05D05, 05D40 Abstact We popose two
Capacity of Data Collection in Arbitrary Wireless Sensor Networks
 This fu text pape was pee eviewed at the diection of IEEE Communications Society subject matte expets fo pubication in the IEEE INFOCOM 2010 poceedings This pape was pesented as pat of the Mini-Confeence
This fu text pape was pee eviewed at the diection of IEEE Communications Society subject matte expets fo pubication in the IEEE INFOCOM 2010 poceedings This pape was pesented as pat of the Mini-Confeence
19 Fourier Series and Practical Harmonic Analysis
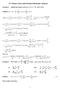 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Here are some solutions to the sample problems concerning series solution of differential equations with non-constant coefficients (Chapter 12).
 Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Stanford University CS259Q: Quantum Computing Handout 8 Luca Trevisan October 18, 2012
 Stanfod Univesity CS59Q: Quantum Computing Handout 8 Luca Tevisan Octobe 8, 0 Lectue 8 In which we use the quantum Fouie tansfom to solve the peiod-finding poblem. The Peiod Finding Poblem Let f : {0,...,
Stanfod Univesity CS59Q: Quantum Computing Handout 8 Luca Tevisan Octobe 8, 0 Lectue 8 In which we use the quantum Fouie tansfom to solve the peiod-finding poblem. The Peiod Finding Poblem Let f : {0,...,
Chapter 3: Theory of Modular Arithmetic 38
 Chapte 3: Theoy of Modula Aithmetic 38 Section D Chinese Remainde Theoem By the end of this section you will be able to pove the Chinese Remainde Theoem apply this theoem to solve simultaneous linea conguences
Chapte 3: Theoy of Modula Aithmetic 38 Section D Chinese Remainde Theoem By the end of this section you will be able to pove the Chinese Remainde Theoem apply this theoem to solve simultaneous linea conguences
ELEMENTARY AND COMPOUND EVENTS PROBABILITY
 Euopea Joual of Basic ad Applied Scieces Vol. 5 No., 08 ELEMENTARY AND COMPOUND EVENTS PROBABILITY William W.S. Che Depatmet of Statistics The Geoge Washigto Uivesity Washigto D.C. 003 E-mail: williamwsche@gmail.com
Euopea Joual of Basic ad Applied Scieces Vol. 5 No., 08 ELEMENTARY AND COMPOUND EVENTS PROBABILITY William W.S. Che Depatmet of Statistics The Geoge Washigto Uivesity Washigto D.C. 003 E-mail: williamwsche@gmail.com
Electron states in a periodic potential. Assume the electrons do not interact with each other. Solve the single electron Schrodinger equation: KJ =
 Electo states i a peiodic potetial Assume the electos do ot iteact with each othe Solve the sigle electo Schodige equatio: 2 F h 2 + I U ( ) Ψ( ) EΨ( ). 2m HG KJ = whee U(+R)=U(), R is ay Bavais lattice
Electo states i a peiodic potetial Assume the electos do ot iteact with each othe Solve the sigle electo Schodige equatio: 2 F h 2 + I U ( ) Ψ( ) EΨ( ). 2m HG KJ = whee U(+R)=U(), R is ay Bavais lattice
Fuzzy Erlangian Queuing System with State Dependent Service Rate, Balking, Reneging and Retention of Reneged customers
 Iteatioa Joa of Basic & Aied Scieces IJBAS-IJENS Vo:4 No: 6 Fzzy Eagia Qeig System with State Deedet Sevice Rate Bakig Reegig ad Retetio of Reeged cstomes MS E Paomy Deatmet of Statistics Facty of Commece
Iteatioa Joa of Basic & Aied Scieces IJBAS-IJENS Vo:4 No: 6 Fzzy Eagia Qeig System with State Deedet Sevice Rate Bakig Reegig ad Retetio of Reeged cstomes MS E Paomy Deatmet of Statistics Facty of Commece
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
4. PERMUTATIONS AND COMBINATIONS Quick Review
 4 ERMUTATIONS AND COMBINATIONS Quick Review A aagemet that ca be fomed by takig some o all of a fiite set of thigs (o objects) is called a emutatio A emutatio is said to be a liea emutatio if the objects
4 ERMUTATIONS AND COMBINATIONS Quick Review A aagemet that ca be fomed by takig some o all of a fiite set of thigs (o objects) is called a emutatio A emutatio is said to be a liea emutatio if the objects
Machine Learning for Data Science (CS 4786)
 Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
How to Maximize a Function without Really Trying
 How to Maximize a Fuctio without Really Tryig MARK FLANAGAN School of Electrical, Electroic ad Commuicatios Egieerig Uiversity College Dubli We will prove a famous elemetary iequality called The Rearragemet
How to Maximize a Fuctio without Really Tryig MARK FLANAGAN School of Electrical, Electroic ad Commuicatios Egieerig Uiversity College Dubli We will prove a famous elemetary iequality called The Rearragemet
6.895 Essential Coding Theory October 20, Lecture 11. This lecture is focused in comparisons of the following properties/parameters of a code:
 6.895 Essetial Codig Theory October 0, 004 Lecture 11 Lecturer: Madhu Suda Scribe: Aastasios Sidiropoulos 1 Overview This lecture is focused i comparisos of the followig properties/parameters of a code:
6.895 Essetial Codig Theory October 0, 004 Lecture 11 Lecturer: Madhu Suda Scribe: Aastasios Sidiropoulos 1 Overview This lecture is focused i comparisos of the followig properties/parameters of a code:
Lecture 4: Unique-SAT, Parity-SAT, and Approximate Counting
 Advaced Complexity Theory Sprig 206 Lecture 4: Uique-SAT, Parity-SAT, ad Approximate Coutig Prof. Daa Moshkovitz Scribe: Aoymous Studet Scribe Date: Fall 202 Overview I this lecture we begi talkig about
Advaced Complexity Theory Sprig 206 Lecture 4: Uique-SAT, Parity-SAT, ad Approximate Coutig Prof. Daa Moshkovitz Scribe: Aoymous Studet Scribe Date: Fall 202 Overview I this lecture we begi talkig about
Self-Consistent Simulations of Beam and Plasma Systems Final Exam ( take-home )
 Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
PHYS 705: Classical Mechanics. Central Force Problems I
 1 PHYS 705: Cassica Mechanics Centa Foce Pobems I Two-Body Centa Foce Pobem Histoica Backgound: Kepe s Laws on ceestia bodies (~1605) - Based his 3 aws on obsevationa data fom Tycho Bahe - Fomuate his
1 PHYS 705: Cassica Mechanics Centa Foce Pobems I Two-Body Centa Foce Pobem Histoica Backgound: Kepe s Laws on ceestia bodies (~1605) - Based his 3 aws on obsevationa data fom Tycho Bahe - Fomuate his
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
