EXACT SOLUTIONS OF A GENERALIZED BRATU EQUATION
|
|
|
- Juniper Bates
- 5 years ago
- Views:
Transcription
1 EXACT SOLUTIONS OF A GENERALIZED BRATU EQUATION LAZHAR BOUGOFFA Department of Mathematics, Faculty of Science, Al Imam Mohammad Ibn Saud Islamic University (IMSIU), P.O. Box 90950, Riyadh 1163, Saudi Arabia bougoffa@hotmail.com, lbbougoffa@imamu.edu.sa Received October 4, 016 Abstract. In this short article, we derive the closed-form solutions of a generalized Bratu equation, which arises in many fields of science and engineering such as radiative heat transfer, combustion theory, and nanotechnology. Key words: Bratu equation; generalized Bratu equation; exact solution. 1. INTRODUCTION Bratu solved in 1914 the following boundary value problem in one-dimensional planar coordinates u + λe u = 0, 0 < x < 1 (1) and u(0) = u(1) = 0, () which is a basic one-dimensional (1-D) model in combustion theory [1] that was revisited by Gelfand in 1963 []. Equations (1)-() arises in many fields of science and engineering such as radiative heat transfer, combustion theory, and nanotechnology. For λ > 0, the exact solution of Eqs. (1)-() is given by [3] ) u(x) = ln cosh( (x 1 ) θ cosh( θ 4 ), (3) where θ satisfies θ = ( ) θ λcosh. (4) 4 The Bratu problem has zero, one or two solutions when λ > λ c, λ = λ c, and λ < λ c, respectively, where the critical value λ c satisfies the equation 1 = 4 1 ( ) θ λc sinh, (5) 4 and the numerical value of λ c is computed and given by λ c = In this short article, we are interested in the general nonlinear differential equations, which contains the classical Bratu equation as a special case, Romanian Journal of Physics 6, 110 (017) u + e au = f(x), (6) v..0* #6597f710
2 Article no. 110 Lazhar Bougoffa where > 0, f(x) are two functions and a is a constant. The purpose of this work is to present new exact solutions of this generalized Bratu equation under suitable conditions on the functions and f(x). Thus We make the change of variables. THE EXACT SOLUTIONS.1. THE FIRST SOLUTION au(x) = ln ( ) v(x). (7) au (x) = v (x) v(x) λ (x). (8) Eq. (6) becomes (x) ( λ ) (x) + av(x) = f(x). (9) v(x) ( ) If we assume that f(x) + λ (x) = 0, that is, f(x) + (ln) = 0, then by the change of variables w(x) = v (x) v(x), (10) and in view of v(x) = v (x), Eq.(9) reduces to w(x) w (x) + av (x) w(x) = 0, (11) which is a separable ordinary differential equation (ODE). It follows that w(x)w (x) + av (x) = 0. (1) Integrating Eq. (1) with respect to x, we obtain where c 1 is a constant of integration. So that Hence w(x) = ± av(x) + c 1, (13) v (x) v(x) = ± av(x) + c 1. (14) dv v av + c 1 = ±dx. (15)
3 3 Exact solutions of a generalized Bratu equation Article no. 110 Consequently, we have where c is another constant of integration. Thus we have Consequently, ( ) tanh 1 c1 av c1 = ±x + c, (16) c1 v(x) = c 1 a c 1 a tanh v(x) = c 1 a Now using the given boundary conditions () we get c 1a 1 ) = λ 0, ( c1 c1 c x ). (17) ( 1 cosh ). (18) c1 c1 c x cosh ( c1 c c 1a 1 cosh ( c1 c1 c ) = λ 1, where λ 0 = λ(0) and λ 1 = λ(1). c1 We choose θ 1 = and θ = ±c, then cosh(θ 1 θ ) = aλ 0 θ 1, cosh(θ 1 + θ 1 θ ) = aλ 1 θ 1. Thus we have cosh(θ 1 + θ 1 θ ) cosh(θ 1 θ ) = (19) (0) λ0 λ 1, θ 1 0. (1) We have thus proved Theorem 1 Let λ be a positive function. If we assume that f(x) + (ln) = 0, then the exact solution to the general boundary value problem (6) with () is given as u(x) = 1 a lnv(x) 1 ln, () a where v(x) = θ 1 1 a cosh (3) (θ 1 (x + θ )) and the constants θ 1 and θ satisfy Eq. (1). Now we consider the simplest case of Theorem 1, namely the case when = λ > 0 and a = 1. Thus f(x) = 0, and the condition of this theorem is satisfied. Hence ( ) θ u(x) = ln 1 ln(cosh(θ 1 (x + θ ))). (4) λ
4 Article no. 110 Lazhar Bougoffa 4 A simple calculation leads to u(x) = ln cosh(θ 1(x + θ )) λ θ 1. (5) From (1) we get θ = 1 that could make Eq. (1) true and solvable. Thus u(x) = ln cosh( θ 1 (x 1 )) λ θ 1, (6) where θ 1 satisfies (0), that is cosh( θ 1 ) = θ 1 λ. Replacing the constant θ instead of θ 1 into this solution, we obtain the same Bratu s solution... THE SECOND SOLUTION WHEN f(x) > 0 We make the change of variables ( ) f(x)v(x) au(x) = ln, (7) where f(x) is a positive differentiable function. Equation (6) reduces to (x) ( + ln( f(x) ) v(x) ) + af(x)v(x) = af(x). (8) ( ) If we assume that ln( f(x) ) = 0, then Eq. (8) becomes (x) + af(x)v(x) = af(x). (9) v(x) Clearly, v(x) = 1 is a solution of Eq. (9). We then get from Eq. (7) u(x) = 1 ( ) f(x) a ln, f(x) > 0 (30) and u(x) = 0 as long as f(x) = at x = 0 and x = 1. (31) Thus we have proved ( ) Theorem Let f and λ be two positive functions. If we assume that ln( f(x) ) = 0, then the exact solution to the general boundary value problem (6) with () is given by (30)-(31).
5 5 Exact solutions of a generalized Bratu equation Article no CONCLUSION In this paper, we have considered a generalization of the Bratu equation. When the functions and f(x) in Eq. (6) are replaced by the constant λ and by 0, respectively, then Eq. (6) becomes the standard Bratu equation. We have demonstrated that the closed-form solutions of this problem can be obtained in a straightforward manner by a direct method under suitable conditions on the functions and f(x). REFERENCES 1. G. Bratu, Bull. M. Soc. France 4, (1914).. I. M. Gelfand, AMS Trans. Ser. (9) (1963). 3. A. M. Wazwaz, Rom. J. Phys. 61, (016).
FURTHER SOLUTIONS OF THE FALKNER-SKAN EQUATION
 FURTHER SOLUTIONS OF THE FALKNER-SKAN EQUATION LAZHAR BOUGOFFA a, RUBAYYI T. ALQAHTANI b Department of Mathematics and Statistics, College of Science, Al-Imam Mohammad Ibn Saud Islamic University (IMSIU),
FURTHER SOLUTIONS OF THE FALKNER-SKAN EQUATION LAZHAR BOUGOFFA a, RUBAYYI T. ALQAHTANI b Department of Mathematics and Statistics, College of Science, Al-Imam Mohammad Ibn Saud Islamic University (IMSIU),
Differential Equations DIRECT INTEGRATION. Graham S McDonald
 Differential Equations DIRECT INTEGRATION Graham S McDonald A Tutorial Module introducing ordinary differential equations and the method of direct integration Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
Differential Equations DIRECT INTEGRATION Graham S McDonald A Tutorial Module introducing ordinary differential equations and the method of direct integration Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
Exact solutions of Bratu and Liouville equations
 Exact solutions of Bratu and Liouville equations Nir Cohen and Julia V. Toledo Benavides Departamento de Matemática, CCET, UFRN, 59078-970, Natal, RN. E-mail: nir@ccet.ufrn.br, julia@ccet.ufrn.br Abstract:
Exact solutions of Bratu and Liouville equations Nir Cohen and Julia V. Toledo Benavides Departamento de Matemática, CCET, UFRN, 59078-970, Natal, RN. E-mail: nir@ccet.ufrn.br, julia@ccet.ufrn.br Abstract:
Benha University Faculty of Science Department of Mathematics. (Curriculum Vitae)
 Benha University Faculty of Science Department of Mathematics (Curriculum Vitae) (1) General *Name : Mohamed Meabed Bayuomi Khader *Date of Birth : 24 May 1973 *Marital Status: Married *Nationality : Egyptian
Benha University Faculty of Science Department of Mathematics (Curriculum Vitae) (1) General *Name : Mohamed Meabed Bayuomi Khader *Date of Birth : 24 May 1973 *Marital Status: Married *Nationality : Egyptian
Sixth Order Newton-Type Method For Solving System Of Nonlinear Equations And Its Applications
 Applied Mathematics E-Notes, 17(017), 1-30 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Sixth Order Newton-Type Method For Solving System Of Nonlinear Equations
Applied Mathematics E-Notes, 17(017), 1-30 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Sixth Order Newton-Type Method For Solving System Of Nonlinear Equations
Analytical solution for determination the control parameter in the inverse parabolic equation using HAM
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 12, Issue 2 (December 2017, pp. 1072 1087 Applications and Applied Mathematics: An International Journal (AAM Analytical solution
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 12, Issue 2 (December 2017, pp. 1072 1087 Applications and Applied Mathematics: An International Journal (AAM Analytical solution
Maejo International Journal of Science and Technology
 Full Paper Maejo International Journal of Science and Technology ISSN 905-7873 Available online at www.mijst.mju.ac.th New eact travelling wave solutions of generalised sinh- ordon and ( + )-dimensional
Full Paper Maejo International Journal of Science and Technology ISSN 905-7873 Available online at www.mijst.mju.ac.th New eact travelling wave solutions of generalised sinh- ordon and ( + )-dimensional
New approach for tanh and extended-tanh methods with applications on Hirota-Satsuma equations
 Volume 28, N. 1, pp. 1 14, 2009 Copyright 2009 SBMAC ISSN 0101-8205 www.scielo.br/cam New approach for tanh and extended-tanh methods with applications on Hirota-Satsuma equations HASSAN A. ZEDAN Mathematics
Volume 28, N. 1, pp. 1 14, 2009 Copyright 2009 SBMAC ISSN 0101-8205 www.scielo.br/cam New approach for tanh and extended-tanh methods with applications on Hirota-Satsuma equations HASSAN A. ZEDAN Mathematics
Exact Solutions for the Nonlinear (2+1)-Dimensional Davey-Stewartson Equation Using the Generalized ( G. )-Expansion Method
 Journal of Mathematics Research; Vol. 6, No. ; 04 ISSN 96-9795 E-ISSN 96-9809 Published by Canadian Center of Science and Education Exact Solutions for the Nonlinear +-Dimensional Davey-Stewartson Equation
Journal of Mathematics Research; Vol. 6, No. ; 04 ISSN 96-9795 E-ISSN 96-9809 Published by Canadian Center of Science and Education Exact Solutions for the Nonlinear +-Dimensional Davey-Stewartson Equation
On exact and numerical solutions of the one-dimensional planar Bratu problem
 On exact and numerical solutions of the one-dimensional planar Bratu problem by Ron Buckmire Mathematics Department Occidental College 16 Campus Road Los Angeles, CA 91-3338, U.S.A. June 1, 3 The nonlinear
On exact and numerical solutions of the one-dimensional planar Bratu problem by Ron Buckmire Mathematics Department Occidental College 16 Campus Road Los Angeles, CA 91-3338, U.S.A. June 1, 3 The nonlinear
PDE: The Method of Characteristics Page 1
 PDE: The Method of Characteristics Page y u x (x, y) + x u y (x, y) =, () u(, y) = cos y 2. Solution The partial differential equation given can be rewritten as follows: u(x, y) y, x =, (2) where = / x,
PDE: The Method of Characteristics Page y u x (x, y) + x u y (x, y) =, () u(, y) = cos y 2. Solution The partial differential equation given can be rewritten as follows: u(x, y) y, x =, (2) where = / x,
PH.D. PRELIMINARY EXAMINATION MATHEMATICS
 UNIVERSITY OF CALIFORNIA, BERKELEY SPRING SEMESTER 207 Dept. of Civil and Environmental Engineering Structural Engineering, Mechanics and Materials NAME PH.D. PRELIMINARY EXAMINATION MATHEMATICS Problem
UNIVERSITY OF CALIFORNIA, BERKELEY SPRING SEMESTER 207 Dept. of Civil and Environmental Engineering Structural Engineering, Mechanics and Materials NAME PH.D. PRELIMINARY EXAMINATION MATHEMATICS Problem
Second Midterm Exam Name: Practice Problems March 10, 2015
 Math 160 1. Treibergs Second Midterm Exam Name: Practice Problems March 10, 015 1. Determine the singular points of the function and state why the function is analytic everywhere else: z 1 fz) = z + 1)z
Math 160 1. Treibergs Second Midterm Exam Name: Practice Problems March 10, 015 1. Determine the singular points of the function and state why the function is analytic everywhere else: z 1 fz) = z + 1)z
ANALYTICAL APPROXIMATE SOLUTIONS OF THE ZAKHAROV-KUZNETSOV EQUATIONS
 (c) Romanian RRP 66(No. Reports in 2) Physics, 296 306 Vol. 2014 66, No. 2, P. 296 306, 2014 ANALYTICAL APPROXIMATE SOLUTIONS OF THE ZAKHAROV-KUZNETSOV EQUATIONS A. JAFARIAN 1, P. GHADERI 2, ALIREZA K.
(c) Romanian RRP 66(No. Reports in 2) Physics, 296 306 Vol. 2014 66, No. 2, P. 296 306, 2014 ANALYTICAL APPROXIMATE SOLUTIONS OF THE ZAKHAROV-KUZNETSOV EQUATIONS A. JAFARIAN 1, P. GHADERI 2, ALIREZA K.
Soliton and Periodic Solutions to the Generalized Hirota-Satsuma Coupled System Using Trigonometric and Hyperbolic Function Methods.
 ISSN 1749-889 (print), 1749-897 (online) International Journal of Nonlinear Science Vol.14(01) No.,pp.150-159 Soliton and Periodic Solutions to the Generalized Hirota-Satsuma Coupled System Using Trigonometric
ISSN 1749-889 (print), 1749-897 (online) International Journal of Nonlinear Science Vol.14(01) No.,pp.150-159 Soliton and Periodic Solutions to the Generalized Hirota-Satsuma Coupled System Using Trigonometric
MATH 220: PROBLEM SET 1, SOLUTIONS DUE FRIDAY, OCTOBER 2, 2015
 MATH 220: PROBLEM SET 1, SOLUTIONS DUE FRIDAY, OCTOBER 2, 2015 Problem 1 Classify the following PDEs by degree of non-linearity (linear, semilinear, quasilinear, fully nonlinear: (1 (cos x u x + u y =
MATH 220: PROBLEM SET 1, SOLUTIONS DUE FRIDAY, OCTOBER 2, 2015 Problem 1 Classify the following PDEs by degree of non-linearity (linear, semilinear, quasilinear, fully nonlinear: (1 (cos x u x + u y =
A curvature-unified equation for a non-newtonian power-law fluid flow
 Int. J. Adv. Appl. Math. and Mech. 2(3) (215) 72-77 (ISSN: 2347-2529) Journal homepage: www.ijaamm.com International Journal of Advances in Applied Mathematics and Mechanics A curvature-unified equation
Int. J. Adv. Appl. Math. and Mech. 2(3) (215) 72-77 (ISSN: 2347-2529) Journal homepage: www.ijaamm.com International Journal of Advances in Applied Mathematics and Mechanics A curvature-unified equation
Mathematical Techniques: Revision Notes
 Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
DIFFERENT DIFFERENCES
 DIFFERENT DIFFERENCES Ron Buckmire ron@oxy.edu Professor of Mathematics Occidental College Los Angeles, CA Pomona College Claremont, CA March 21, 2016 ABSTRACT From calculus we know that a derivative of
DIFFERENT DIFFERENCES Ron Buckmire ron@oxy.edu Professor of Mathematics Occidental College Los Angeles, CA Pomona College Claremont, CA March 21, 2016 ABSTRACT From calculus we know that a derivative of
Extended Adomian s polynomials for solving. non-linear fractional differential equations
 Theoretical Mathematics & Applications, vol.5, no.2, 25, 89-4 ISSN: 792-9687 (print), 792-979 (online) Scienpress Ltd, 25 Extended Adomian s polynomials for solving non-linear fractional differential equations
Theoretical Mathematics & Applications, vol.5, no.2, 25, 89-4 ISSN: 792-9687 (print), 792-979 (online) Scienpress Ltd, 25 Extended Adomian s polynomials for solving non-linear fractional differential equations
Solving Analytically Singular Sixth-Order Boundary Value Problems
 Int. Journal of Math. Analysis, Vol. 3, 009, no. 39, 1945-195 Solving Analytically Singular Sixth-Order Boundary Value Problems Fazhan Geng 1 Department of Mathematics, Changshu Institute of Technology
Int. Journal of Math. Analysis, Vol. 3, 009, no. 39, 1945-195 Solving Analytically Singular Sixth-Order Boundary Value Problems Fazhan Geng 1 Department of Mathematics, Changshu Institute of Technology
Existence and uniqueness: Picard s theorem
 Existence and uniqueness: Picard s theorem First-order equations Consider the equation y = f(x, y) (not necessarily linear). The equation dictates a value of y at each point (x, y), so one would expect
Existence and uniqueness: Picard s theorem First-order equations Consider the equation y = f(x, y) (not necessarily linear). The equation dictates a value of y at each point (x, y), so one would expect
First order Partial Differential equations
 First order Partial Differential equations 0.1 Introduction Definition 0.1.1 A Partial Deferential equation is called linear if the dependent variable and all its derivatives have degree one and not multiple
First order Partial Differential equations 0.1 Introduction Definition 0.1.1 A Partial Deferential equation is called linear if the dependent variable and all its derivatives have degree one and not multiple
The comparison of optimal homotopy asymptotic method and homotopy perturbation method to solve Fisher equation
 Computational Methods for Differential Equations http://cmdetabrizuacir Vol 4, No, 206, pp 43-53 The comparison of optimal homotopy asymptotic method and homotopy perturbation method to solve Fisher equation
Computational Methods for Differential Equations http://cmdetabrizuacir Vol 4, No, 206, pp 43-53 The comparison of optimal homotopy asymptotic method and homotopy perturbation method to solve Fisher equation
EXACT SOLUTIONS OF WAVE-TYPE EQUATIONS BY THE ABOODH DECOMPOSITION METHOD
 Stochastic Modeling and Applications Vol.21 No. 1(June 2017) 23-30 EXACT SOLUTIONS OF WAVE-TYPE EQUATIONS BY THE ABOODH DECOMPOSITION METHOD RAHMATULLAH IBRAHIM NURUDDEEN AND AMINU M. NASS* Abstract. This
Stochastic Modeling and Applications Vol.21 No. 1(June 2017) 23-30 EXACT SOLUTIONS OF WAVE-TYPE EQUATIONS BY THE ABOODH DECOMPOSITION METHOD RAHMATULLAH IBRAHIM NURUDDEEN AND AMINU M. NASS* Abstract. This
JUST THE MATHS UNIT NUMBER DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 104 DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) by AJHobson 1041 Products 1042 Quotients 1043 Logarithmic differentiation 1044 Exercises 1045 Answers
JUST THE MATHS UNIT NUMBER 104 DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) by AJHobson 1041 Products 1042 Quotients 1043 Logarithmic differentiation 1044 Exercises 1045 Answers
Application of Taylor-Padé technique for obtaining approximate solution for system of linear Fredholm integro-differential equations
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 12, Issue 1 (June 2017), pp. 392 404 Applications and Applied Mathematics: An International Journal (AAM) Application of Taylor-Padé
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 12, Issue 1 (June 2017), pp. 392 404 Applications and Applied Mathematics: An International Journal (AAM) Application of Taylor-Padé
Parametric Spline Method for Solving Bratu s Problem
 ISSN 749-3889 print, 749-3897 online International Journal of Nonlinear Science Vol4202 No,pp3-0 Parametric Spline Metod for Solving Bratu s Problem M Zarebnia, Z Sarvari 2,2 Department of Matematics,
ISSN 749-3889 print, 749-3897 online International Journal of Nonlinear Science Vol4202 No,pp3-0 Parametric Spline Metod for Solving Bratu s Problem M Zarebnia, Z Sarvari 2,2 Department of Matematics,
Application of Reduced Differential Transform Method for Solving Nonlinear Reaction-Diffusion-Convection Problems
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 10, Issue 1 (June 2015), pp. 162 170 Applications and Applied Mathematics: An International Journal (AAM) Application of Reduced
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 10, Issue 1 (June 2015), pp. 162 170 Applications and Applied Mathematics: An International Journal (AAM) Application of Reduced
Exact Solutions for a Class of Singular Two-Point Boundary Value Problems Using Adomian Decomposition Method
 Applied Mathematical Sciences, Vol 6, 212, no 122, 697-618 Exact Solutions for a Class of Singular Two-Point Boundary Value Problems Using Adomian Decomposition Method Abdelhalim Ebaid 1 and Mona D Aljoufi
Applied Mathematical Sciences, Vol 6, 212, no 122, 697-618 Exact Solutions for a Class of Singular Two-Point Boundary Value Problems Using Adomian Decomposition Method Abdelhalim Ebaid 1 and Mona D Aljoufi
The (2+1) and (3+1)-Dimensional CBS Equations: Multiple Soliton Solutions and Multiple Singular Soliton Solutions
 The (+1) and (3+1)-Dimensional CBS Equations: Multiple Soliton Solutions and Multiple Singular Soliton Solutions Abdul-Majid Wazwaz Department of Mathematics, Saint Xavier University, Chicago, IL 60655,
The (+1) and (3+1)-Dimensional CBS Equations: Multiple Soliton Solutions and Multiple Singular Soliton Solutions Abdul-Majid Wazwaz Department of Mathematics, Saint Xavier University, Chicago, IL 60655,
Mathematics II. Tutorial 2 First order differential equations. Groups: B03 & B08
 Tutorial 2 First order differential equations Groups: B03 & B08 February 1, 2012 Department of Mathematics National University of Singapore 1/15 : First order linear differential equations In this question,
Tutorial 2 First order differential equations Groups: B03 & B08 February 1, 2012 Department of Mathematics National University of Singapore 1/15 : First order linear differential equations In this question,
EXP-FUNCTION AND -EXPANSION METHODS
 SOLVIN NONLINEAR FRACTIONAL DIFFERENTIAL EQUATIONS USIN EXP-FUNCTION AND -EXPANSION METHODS AHMET BEKIR 1, ÖZKAN ÜNER 2, ALI H. BHRAWY 3,4, ANJAN BISWAS 3,5 1 Eskisehir Osmangazi University, Art-Science
SOLVIN NONLINEAR FRACTIONAL DIFFERENTIAL EQUATIONS USIN EXP-FUNCTION AND -EXPANSION METHODS AHMET BEKIR 1, ÖZKAN ÜNER 2, ALI H. BHRAWY 3,4, ANJAN BISWAS 3,5 1 Eskisehir Osmangazi University, Art-Science
The Lorentz Transformation
 The Lorentz Transformation This is a derivation of the Lorentz transformation of Special Relativity. The basic idea is to derive a relationship between the spacetime coordinates, y, z, t as seen by observer
The Lorentz Transformation This is a derivation of the Lorentz transformation of Special Relativity. The basic idea is to derive a relationship between the spacetime coordinates, y, z, t as seen by observer
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS Chapter 1 Introduction and Basic Terminology Most of the phenomena studied in the sciences and engineering involve processes that change with time. For example, it is well known
DIFFERENTIAL EQUATIONS Chapter 1 Introduction and Basic Terminology Most of the phenomena studied in the sciences and engineering involve processes that change with time. For example, it is well known
The Modified Adomian Decomposition Method for. Solving Nonlinear Coupled Burger s Equations
 Nonlinear Analysis and Differential Equations, Vol. 3, 015, no. 3, 111-1 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/nade.015.416 The Modified Adomian Decomposition Method for Solving Nonlinear
Nonlinear Analysis and Differential Equations, Vol. 3, 015, no. 3, 111-1 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/nade.015.416 The Modified Adomian Decomposition Method for Solving Nonlinear
Completion Date: Monday February 11, 2008
 MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
FINAL EXAM, MATH 353 SUMMER I 2015
 FINAL EXAM, MATH 353 SUMMER I 25 9:am-2:pm, Thursday, June 25 I have neither given nor received any unauthorized help on this exam and I have conducted myself within the guidelines of the Duke Community
FINAL EXAM, MATH 353 SUMMER I 25 9:am-2:pm, Thursday, June 25 I have neither given nor received any unauthorized help on this exam and I have conducted myself within the guidelines of the Duke Community
Introduction to Differential Equations
 Chapter 1 Introduction to Differential Equations 1.1 Basic Terminology Most of the phenomena studied in the sciences and engineering involve processes that change with time. For example, it is well known
Chapter 1 Introduction to Differential Equations 1.1 Basic Terminology Most of the phenomena studied in the sciences and engineering involve processes that change with time. For example, it is well known
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
Computers and Mathematics with Applications
 Computers and Mathematics with Applications 60 (00) 3088 3097 Contents lists available at ScienceDirect Computers and Mathematics with Applications journal homepage: www.elsevier.com/locate/camwa Symmetry
Computers and Mathematics with Applications 60 (00) 3088 3097 Contents lists available at ScienceDirect Computers and Mathematics with Applications journal homepage: www.elsevier.com/locate/camwa Symmetry
First-Order Ordinary Differntial Equations: Classification and Linear Equations. David Levermore Department of Mathematics University of Maryland
 First-Order Ordinary Differntial Equations: Classification and Linear Equations David Levermore Department of Mathematics University of Maryland 1 February 2009 These notes cover some of the material that
First-Order Ordinary Differntial Equations: Classification and Linear Equations David Levermore Department of Mathematics University of Maryland 1 February 2009 These notes cover some of the material that
Extended Jacobi Elliptic Function Expansion Method for Nonlinear Benjamin-Bona-Mahony Equations
 International Mathematical Forum, Vol. 7, 2, no. 53, 239-249 Extended Jacobi Elliptic Function Expansion Method for Nonlinear Benjamin-Bona-Mahony Equations A. S. Alofi Department of Mathematics, Faculty
International Mathematical Forum, Vol. 7, 2, no. 53, 239-249 Extended Jacobi Elliptic Function Expansion Method for Nonlinear Benjamin-Bona-Mahony Equations A. S. Alofi Department of Mathematics, Faculty
Numerical solution of nonlinear sine-gordon equation with local RBF-based finite difference collocation method
 Numerical solution of nonlinear sine-gordon equation with local RBF-based finite difference collocation method Y. Azari Keywords: Local RBF-based finite difference (LRBF-FD), Global RBF collocation, sine-gordon
Numerical solution of nonlinear sine-gordon equation with local RBF-based finite difference collocation method Y. Azari Keywords: Local RBF-based finite difference (LRBF-FD), Global RBF collocation, sine-gordon
Homotopy Perturbation Method for the Fisher s Equation and Its Generalized
 ISSN 749-889 (print), 749-897 (online) International Journal of Nonlinear Science Vol.8(2009) No.4,pp.448-455 Homotopy Perturbation Method for the Fisher s Equation and Its Generalized M. Matinfar,M. Ghanbari
ISSN 749-889 (print), 749-897 (online) International Journal of Nonlinear Science Vol.8(2009) No.4,pp.448-455 Homotopy Perturbation Method for the Fisher s Equation and Its Generalized M. Matinfar,M. Ghanbari
Existence, Uniqueness Solution of a Modified. Predator-Prey Model
 Nonlinear Analysis and Differential Equations, Vol. 4, 6, no. 4, 669-677 HIKARI Ltd, www.m-hikari.com https://doi.org/.988/nade.6.6974 Existence, Uniqueness Solution of a Modified Predator-Prey Model M.
Nonlinear Analysis and Differential Equations, Vol. 4, 6, no. 4, 669-677 HIKARI Ltd, www.m-hikari.com https://doi.org/.988/nade.6.6974 Existence, Uniqueness Solution of a Modified Predator-Prey Model M.
Numerical Simulation of the Generalized Hirota-Satsuma Coupled KdV Equations by Variational Iteration Method
 ISSN 1749-3889 (print), 1749-3897 (online) International Journal of Nonlinear Science Vol.7(29) No.1,pp.67-74 Numerical Simulation of the Generalized Hirota-Satsuma Coupled KdV Equations by Variational
ISSN 1749-3889 (print), 1749-3897 (online) International Journal of Nonlinear Science Vol.7(29) No.1,pp.67-74 Numerical Simulation of the Generalized Hirota-Satsuma Coupled KdV Equations by Variational
Periodic and Solitary Wave Solutions of the Davey-Stewartson Equation
 Applied Mathematics & Information Sciences 4(2) (2010), 253 260 An International Journal c 2010 Dixie W Publishing Corporation, U. S. A. Periodic and Solitary Wave Solutions of the Davey-Stewartson Equation
Applied Mathematics & Information Sciences 4(2) (2010), 253 260 An International Journal c 2010 Dixie W Publishing Corporation, U. S. A. Periodic and Solitary Wave Solutions of the Davey-Stewartson Equation
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
HOMOTOPY ANALYSIS METHOD FOR SOLVING COUPLED RAMANI EQUATIONS
 HOMOTOPY ANALYSIS METHOD FOR SOLVING COUPLED RAMANI EQUATIONS A. JAFARIAN 1, P. GHADERI 2, ALIREZA K. GOLMANKHANEH 3, D. BALEANU 4,5,6 1 Department of Mathematics, Uremia Branch, Islamic Azan University,
HOMOTOPY ANALYSIS METHOD FOR SOLVING COUPLED RAMANI EQUATIONS A. JAFARIAN 1, P. GHADERI 2, ALIREZA K. GOLMANKHANEH 3, D. BALEANU 4,5,6 1 Department of Mathematics, Uremia Branch, Islamic Azan University,
New Exact Travelling Wave Solutions for Regularized Long-wave, Phi-Four and Drinfeld-Sokolov Equations
 ISSN 1749-3889 print), 1749-3897 online) International Journal of Nonlinear Science Vol.008) No.1,pp.4-5 New Exact Travelling Wave Solutions for Regularized Long-wave, Phi-Four and Drinfeld-Sokolov Euations
ISSN 1749-3889 print), 1749-3897 online) International Journal of Nonlinear Science Vol.008) No.1,pp.4-5 New Exact Travelling Wave Solutions for Regularized Long-wave, Phi-Four and Drinfeld-Sokolov Euations
NONLINEAR SINGULAR HYPERBOLIC INITIAL BOUNDARY VALUE PROBLEMS
 Electronic Journal of Differential Equations, Vol. 217 (217, No. 277, pp. 1 11. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu NONLINEAR SINGULAR HYPERBOLIC INITIAL BOUNDARY
Electronic Journal of Differential Equations, Vol. 217 (217, No. 277, pp. 1 11. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu NONLINEAR SINGULAR HYPERBOLIC INITIAL BOUNDARY
Group analysis, nonlinear self-adjointness, conservation laws, and soliton solutions for the mkdv systems
 ISSN 139-5113 Nonlinear Analysis: Modelling Control, 017, Vol., No. 3, 334 346 https://doi.org/10.15388/na.017.3.4 Group analysis, nonlinear self-adjointness, conservation laws, soliton solutions for the
ISSN 139-5113 Nonlinear Analysis: Modelling Control, 017, Vol., No. 3, 334 346 https://doi.org/10.15388/na.017.3.4 Group analysis, nonlinear self-adjointness, conservation laws, soliton solutions for the
Campus Academic Resource Program Chain Rule
 This handout will: Provide a strategy to identify composite functions Provide a strategy to find chain rule by using a substitution method. Identifying Composite Functions This section will provide a strategy
This handout will: Provide a strategy to identify composite functions Provide a strategy to find chain rule by using a substitution method. Identifying Composite Functions This section will provide a strategy
MAS153/MAS159. MAS153/MAS159 1 Turn Over SCHOOL OF MATHEMATICS AND STATISTICS hours. Mathematics (Materials) Mathematics For Chemists
 Data provided: Formula sheet MAS53/MAS59 SCHOOL OF MATHEMATICS AND STATISTICS Mathematics (Materials Mathematics For Chemists Spring Semester 203 204 3 hours All questions are compulsory. The marks awarded
Data provided: Formula sheet MAS53/MAS59 SCHOOL OF MATHEMATICS AND STATISTICS Mathematics (Materials Mathematics For Chemists Spring Semester 203 204 3 hours All questions are compulsory. The marks awarded
JUST THE MATHS UNIT NUMBER DIFFERENTIATION 3 (Elementary techniques of differentiation) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 10.3 DIFFERENTIATION 3 (Elementary techniques of differentiation) by A.J.Hobson 10.3.1 Standard derivatives 10.3.2 Rules of differentiation 10.3.3 Exercises 10.3.4 Answers to
JUST THE MATHS UNIT NUMBER 10.3 DIFFERENTIATION 3 (Elementary techniques of differentiation) by A.J.Hobson 10.3.1 Standard derivatives 10.3.2 Rules of differentiation 10.3.3 Exercises 10.3.4 Answers to
THE ADOMIAN DECOMPOSITION METHOD FOR SOLVING DELAY DIFFERENTIAL EQUATION
 International Journal of Computer Mathematics Vol. 00, No. 0, Month 004, pp. 1 6 THE ADOMIAN DECOMPOSITION METHOD FOR SOLVING DELAY DIFFERENTIAL EQUATION D. J. EVANS a and K. R. RASLAN b, a Faculty of
International Journal of Computer Mathematics Vol. 00, No. 0, Month 004, pp. 1 6 THE ADOMIAN DECOMPOSITION METHOD FOR SOLVING DELAY DIFFERENTIAL EQUATION D. J. EVANS a and K. R. RASLAN b, a Faculty of
13 PDEs on spatially bounded domains: initial boundary value problems (IBVPs)
 13 PDEs on spatially bounded domains: initial boundary value problems (IBVPs) A prototypical problem we will discuss in detail is the 1D diffusion equation u t = Du xx < x < l, t > finite-length rod u(x,
13 PDEs on spatially bounded domains: initial boundary value problems (IBVPs) A prototypical problem we will discuss in detail is the 1D diffusion equation u t = Du xx < x < l, t > finite-length rod u(x,
The (G'/G) - Expansion Method for Finding Traveling Wave Solutions of Some Nonlinear Pdes in Mathematical Physics
 Vol.3, Issue., Jan-Feb. 3 pp-369-376 ISSN: 49-6645 The ('/) - Expansion Method for Finding Traveling Wave Solutions of Some Nonlinear Pdes in Mathematical Physics J.F.Alzaidy Mathematics Department, Faculty
Vol.3, Issue., Jan-Feb. 3 pp-369-376 ISSN: 49-6645 The ('/) - Expansion Method for Finding Traveling Wave Solutions of Some Nonlinear Pdes in Mathematical Physics J.F.Alzaidy Mathematics Department, Faculty
Application of the Differential Transform Method for the Nonlinear Differential Equations
 American Journal of Applied Mathematics 27; 5(): 4- http://www.sciencepublishinggroup.com//aam doi:.64/.aam.275.2 ISSN: 233-43 (Print); ISSN: 233-6X (Online) Application of the Differential Transform Method
American Journal of Applied Mathematics 27; 5(): 4- http://www.sciencepublishinggroup.com//aam doi:.64/.aam.275.2 ISSN: 233-43 (Print); ISSN: 233-6X (Online) Application of the Differential Transform Method
Available online at J. Math. Comput. Sci. 2 (2012), No. 1, ISSN:
 Available online at http://scik.org J. Math. Comput. Sci. 2 (2012), No. 1, 15-22 ISSN: 1927-5307 BRIGHT AND DARK SOLITON SOLUTIONS TO THE OSTROVSKY-BENJAMIN-BONA-MAHONY (OS-BBM) EQUATION MARWAN ALQURAN
Available online at http://scik.org J. Math. Comput. Sci. 2 (2012), No. 1, 15-22 ISSN: 1927-5307 BRIGHT AND DARK SOLITON SOLUTIONS TO THE OSTROVSKY-BENJAMIN-BONA-MAHONY (OS-BBM) EQUATION MARWAN ALQURAN
Integration by parts Integration by parts is a direct reversal of the product rule. By integrating both sides, we get:
 Integration by parts Integration by parts is a direct reversal of the proct rule. By integrating both sides, we get: u dv dx x n sin mx dx (make u = x n ) dx = uv v dx dx When to use integration by parts
Integration by parts Integration by parts is a direct reversal of the proct rule. By integrating both sides, we get: u dv dx x n sin mx dx (make u = x n ) dx = uv v dx dx When to use integration by parts
MA 242 Review Exponential and Log Functions Notes for today s class can be found at
 MA 242 Review Exponential and Log Functions Notes for today s class can be found at www.xecu.net/jacobs/index242.htm Example: If y = x n If y = x 2 then then dy dx = nxn 1 dy dx = 2x1 = 2x Power Function
MA 242 Review Exponential and Log Functions Notes for today s class can be found at www.xecu.net/jacobs/index242.htm Example: If y = x n If y = x 2 then then dy dx = nxn 1 dy dx = 2x1 = 2x Power Function
Chapter 2 Vector-matrix Differential Equation and Numerical Inversion of Laplace Transform
 Chapter 2 Vector-matrix Differential Equation and Numerical Inversion of Laplace Transform 2.1 Vector-matrix Differential Equation A differential equation and a set of differential (simultaneous linear
Chapter 2 Vector-matrix Differential Equation and Numerical Inversion of Laplace Transform 2.1 Vector-matrix Differential Equation A differential equation and a set of differential (simultaneous linear
Brief Notes on Differential Equations
 Brief Notes on Differential Equations (A) Searable First-Order Differential Equations Solve the following differential equations b searation of variables: (a) (b) Solution ( 1 ) (a) The ODE becomes d and
Brief Notes on Differential Equations (A) Searable First-Order Differential Equations Solve the following differential equations b searation of variables: (a) (b) Solution ( 1 ) (a) The ODE becomes d and
Problem set 3: Solutions Math 207B, Winter Suppose that u(x) is a non-zero solution of the eigenvalue problem. (u ) 2 dx, u 2 dx.
 Problem set 3: Solutions Math 27B, Winter 216 1. Suppose that u(x) is a non-zero solution of the eigenvalue problem u = λu < x < 1, u() =, u(1) =. Show that λ = (u ) 2 dx u2 dx. Deduce that every eigenvalue
Problem set 3: Solutions Math 27B, Winter 216 1. Suppose that u(x) is a non-zero solution of the eigenvalue problem u = λu < x < 1, u() =, u(1) =. Show that λ = (u ) 2 dx u2 dx. Deduce that every eigenvalue
Travelling waves. Chapter 8. 1 Introduction
 Chapter 8 Travelling waves 1 Introduction One of the cornerstones in the study of both linear and nonlinear PDEs is the wave propagation. A wave is a recognizable signal which is transferred from one part
Chapter 8 Travelling waves 1 Introduction One of the cornerstones in the study of both linear and nonlinear PDEs is the wave propagation. A wave is a recognizable signal which is transferred from one part
Strauss PDEs 2e: Section Exercise 4 Page 1 of 6
 Strauss PDEs 2e: Section 5.3 - Exercise 4 Page of 6 Exercise 4 Consider the problem u t = ku xx for < x < l, with the boundary conditions u(, t) = U, u x (l, t) =, and the initial condition u(x, ) =, where
Strauss PDEs 2e: Section 5.3 - Exercise 4 Page of 6 Exercise 4 Consider the problem u t = ku xx for < x < l, with the boundary conditions u(, t) = U, u x (l, t) =, and the initial condition u(x, ) =, where
Math 106 Fall 2014 Exam 2.1 October 31, ln(x) x 3 dx = 1. 2 x 2 ln(x) + = 1 2 x 2 ln(x) + 1. = 1 2 x 2 ln(x) 1 4 x 2 + C
 Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
Exact Solutions of the Generalized- Zakharov (GZ) Equation by the Infinite Series Method
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 05, Issue (December 010), pp. 61 68 (Previously, Vol. 05, Issue 10, pp. 1718 175) Applications and Applied Mathematics: An International
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 05, Issue (December 010), pp. 61 68 (Previously, Vol. 05, Issue 10, pp. 1718 175) Applications and Applied Mathematics: An International
( 2) ( ) Hyperbolic Functions 6E. cosh d (cosh sech ) d sinh tanh. cosh. x x x x x x C. x 1 x. 2 a. x x x = + = + cosh dx sinh C 3sinh C.
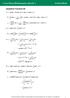 Hyperolic Functions 6E a (sinh+ cosh ) cosh+ sinh+ + cosh cosh (cosh sech ) sinh tanh sinh sinh sechtanh sech+ cosh cosh cosh c a a sinh cosh+ cosh sinh sinh + + ( ) + + ( ) ( ) ( ) ( ) arcosh + ( ) +
Hyperolic Functions 6E a (sinh+ cosh ) cosh+ sinh+ + cosh cosh (cosh sech ) sinh tanh sinh sinh sechtanh sech+ cosh cosh cosh c a a sinh cosh+ cosh sinh sinh + + ( ) + + ( ) ( ) ( ) ( ) arcosh + ( ) +
MATH 251 Final Examination May 4, 2015 FORM A. Name: Student Number: Section:
 MATH 251 Final Examination May 4, 2015 FORM A Name: Student Number: Section: This exam has 16 questions for a total of 150 points. In order to obtain full credit for partial credit problems, all work must
MATH 251 Final Examination May 4, 2015 FORM A Name: Student Number: Section: This exam has 16 questions for a total of 150 points. In order to obtain full credit for partial credit problems, all work must
More Techniques. for Solving First Order ODE'S. and. a Classification Scheme for Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 1 A COLLECTION OF HANDOUTS ON FIRST ORDER ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 1 A COLLECTION OF HANDOUTS ON FIRST ORDER ORDINARY DIFFERENTIAL
Some notes on a second-order random boundary value problem
 ISSN 1392-5113 Nonlinear Analysis: Modelling and Control, 217, Vol. 22, No. 6, 88 82 https://doi.org/1.15388/na.217.6.6 Some notes on a second-order random boundary value problem Fairouz Tchier a, Calogero
ISSN 1392-5113 Nonlinear Analysis: Modelling and Control, 217, Vol. 22, No. 6, 88 82 https://doi.org/1.15388/na.217.6.6 Some notes on a second-order random boundary value problem Fairouz Tchier a, Calogero
M412 Assignment 5 Solutions
 M41 Assignment 5 Solutions 1. [1 pts] Haberman.5.1 (a). Solution. Setting u(x, y) =X(x)Y(y), we find that X and Y satisfy X + λx = Y λy =, X () = X () = Y() =. In this case, we find from the X equation
M41 Assignment 5 Solutions 1. [1 pts] Haberman.5.1 (a). Solution. Setting u(x, y) =X(x)Y(y), we find that X and Y satisfy X + λx = Y λy =, X () = X () = Y() =. In this case, we find from the X equation
Some tight polynomial-exponential lower bounds for an exponential function
 Some tight polynomial-exponential lower bounds for an exponential function Christophe Chesneau To cite this version: Christophe Chesneau. Some tight polynomial-exponential lower bounds for an exponential
Some tight polynomial-exponential lower bounds for an exponential function Christophe Chesneau To cite this version: Christophe Chesneau. Some tight polynomial-exponential lower bounds for an exponential
Calculus for Engineers II - Sample Problems on Integrals Manuela Kulaxizi
 Calculus for Engineers II - Sample Problems on Integrals Manuela Kulaxizi Question : Solve the following integrals:. π sin x. x 4 3. 4. sinh 8 x cosh x sin x cos 7 x 5. x 5 ln x 6. 8x + 6 3x + x 7. 8..
Calculus for Engineers II - Sample Problems on Integrals Manuela Kulaxizi Question : Solve the following integrals:. π sin x. x 4 3. 4. sinh 8 x cosh x sin x cos 7 x 5. x 5 ln x 6. 8x + 6 3x + x 7. 8..
Atangana-Baleanu derivative with fractional order applied to the model of groundwater within an unconfined aquifer
 1 Atangana-Baleanu derivative with fractional order applied to the model of groundwater within an unconfined aquifer Rubayyi T. Alqahtani Department of Mathematics and Statistics, College of Science, Al-Imam
1 Atangana-Baleanu derivative with fractional order applied to the model of groundwater within an unconfined aquifer Rubayyi T. Alqahtani Department of Mathematics and Statistics, College of Science, Al-Imam
Exact solutions through symmetry reductions for a new integrable equation
 Exact solutions through symmetry reductions for a new integrable equation MARIA LUZ GANDARIAS University of Cádiz Department of Mathematics PO.BOX, 1151 Puerto Real, Cádiz SPAIN marialuz.gandarias@uca.es
Exact solutions through symmetry reductions for a new integrable equation MARIA LUZ GANDARIAS University of Cádiz Department of Mathematics PO.BOX, 1151 Puerto Real, Cádiz SPAIN marialuz.gandarias@uca.es
Math 2930 Worksheet Final Exam Review
 Math 293 Worksheet Final Exam Review Week 14 November 3th, 217 Question 1. (* Solve the initial value problem y y = 2xe x, y( = 1 Question 2. (* Consider the differential equation: y = y y 3. (a Find the
Math 293 Worksheet Final Exam Review Week 14 November 3th, 217 Question 1. (* Solve the initial value problem y y = 2xe x, y( = 1 Question 2. (* Consider the differential equation: y = y y 3. (a Find the
Diffusion equation in one spatial variable Cauchy problem. u(x, 0) = φ(x)
 Diffusion equation in one spatial variable Cauchy problem. u t (x, t) k u xx (x, t) = f(x, t), x R, t > u(x, ) = φ(x) 1 Some more mathematics { if x < Θ(x) = 1 if x > is the Heaviside step function. It
Diffusion equation in one spatial variable Cauchy problem. u t (x, t) k u xx (x, t) = f(x, t), x R, t > u(x, ) = φ(x) 1 Some more mathematics { if x < Θ(x) = 1 if x > is the Heaviside step function. It
A Simple Algorithm for Calculating Adomian Polynomials
 Int. J. Contemp. Math. Sciences, Vol. 2, 2007, no. 20, 975-982 A Simple Algorithm for Calculating Aomian Polynomials J. Biazar an S. M. Shafiof Department of Mathematics, Faculty of Science University
Int. J. Contemp. Math. Sciences, Vol. 2, 2007, no. 20, 975-982 A Simple Algorithm for Calculating Aomian Polynomials J. Biazar an S. M. Shafiof Department of Mathematics, Faculty of Science University
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georgia Tech PHYS 612 Mathematical Methods of Physics I Instructor: Predrag Cvitanović Fall semester 2012 Homework Set #5 due October 2, 2012 == show all your work for maximum credit, == put labels, title,
Georgia Tech PHYS 612 Mathematical Methods of Physics I Instructor: Predrag Cvitanović Fall semester 2012 Homework Set #5 due October 2, 2012 == show all your work for maximum credit, == put labels, title,
A note on Abundant new exact solutions for the (3+1)-dimensional Jimbo-Miwa equation
 A note on Abundant new exact solutions for the (3+1)-dimensional Jimbo-Miwa equation Nikolay A. Kudryashov, Dmitry I. Sinelshchikov Deartment of Alied Mathematics, National Research Nuclear University
A note on Abundant new exact solutions for the (3+1)-dimensional Jimbo-Miwa equation Nikolay A. Kudryashov, Dmitry I. Sinelshchikov Deartment of Alied Mathematics, National Research Nuclear University
The Solitary Wave Solutions of Zoomeron Equation
 Applied Mathematical Sciences, Vol. 5, 011, no. 59, 943-949 The Solitary Wave Solutions of Zoomeron Equation Reza Abazari Deparment of Mathematics, Ardabil Branch Islamic Azad University, Ardabil, Iran
Applied Mathematical Sciences, Vol. 5, 011, no. 59, 943-949 The Solitary Wave Solutions of Zoomeron Equation Reza Abazari Deparment of Mathematics, Ardabil Branch Islamic Azad University, Ardabil, Iran
Ordinary Differential Equations II
 Ordinary Differential Equations II February 23 2017 Separation of variables Wave eq. (PDE) 2 u t (t, x) = 2 u 2 c2 (t, x), x2 c > 0 constant. Describes small vibrations in a homogeneous string. u(t, x)
Ordinary Differential Equations II February 23 2017 Separation of variables Wave eq. (PDE) 2 u t (t, x) = 2 u 2 c2 (t, x), x2 c > 0 constant. Describes small vibrations in a homogeneous string. u(t, x)
CHAPTER 1: FURTHER TRANSCENDENTAL FUNCTIONS
 SSCE1693 ENGINEERING MATHEMATICS CHAPTER 1: FURTHER TRANSCENDENTAL FUNCTIONS WAN RUKAIDA BT WAN ABDULLAH YUDARIAH BT MOHAMMAD YUSOF SHAZIRAWATI BT MOHD PUZI NUR ARINA BAZILAH BT AZIZ ZUHAILA BT ISMAIL
SSCE1693 ENGINEERING MATHEMATICS CHAPTER 1: FURTHER TRANSCENDENTAL FUNCTIONS WAN RUKAIDA BT WAN ABDULLAH YUDARIAH BT MOHAMMAD YUSOF SHAZIRAWATI BT MOHD PUZI NUR ARINA BAZILAH BT AZIZ ZUHAILA BT ISMAIL
MATH 251 Final Examination December 16, 2015 FORM A. Name: Student Number: Section:
 MATH 5 Final Examination December 6, 5 FORM A Name: Student Number: Section: This exam has 7 questions for a total of 5 points. In order to obtain full credit for partial credit problems, all work must
MATH 5 Final Examination December 6, 5 FORM A Name: Student Number: Section: This exam has 7 questions for a total of 5 points. In order to obtain full credit for partial credit problems, all work must
Received May 20, 2009; accepted October 21, 2009
 MATHEMATICAL COMMUNICATIONS 43 Math. Commun., Vol. 4, No., pp. 43-44 9) Geodesics and geodesic spheres in SL, R) geometry Blaženka Divjak,, Zlatko Erjavec, Barnabás Szabolcs and Brigitta Szilágyi Faculty
MATHEMATICAL COMMUNICATIONS 43 Math. Commun., Vol. 4, No., pp. 43-44 9) Geodesics and geodesic spheres in SL, R) geometry Blaženka Divjak,, Zlatko Erjavec, Barnabás Szabolcs and Brigitta Szilágyi Faculty
Negative Even Grade mkdv Hierarchy and its Soliton Solutions
 Journal of Physics: Conference Series Negative Even Grade mkdv Hierarchy and its Soliton Solutions To cite this article: J F Gomes et al 2011 J. Phys.: Conf. Ser. 284 012030 View the article online for
Journal of Physics: Conference Series Negative Even Grade mkdv Hierarchy and its Soliton Solutions To cite this article: J F Gomes et al 2011 J. Phys.: Conf. Ser. 284 012030 View the article online for
Multiple-Soliton Solutions for Extended Shallow Water Wave Equations
 Studies in Mathematical Sciences Vol. 1, No. 1, 2010, pp. 21-29 www.cscanada.org ISSN 1923-8444 [Print] ISSN 1923-8452 [Online] www.cscanada.net Multiple-Soliton Solutions for Extended Shallow Water Wave
Studies in Mathematical Sciences Vol. 1, No. 1, 2010, pp. 21-29 www.cscanada.org ISSN 1923-8444 [Print] ISSN 1923-8452 [Online] www.cscanada.net Multiple-Soliton Solutions for Extended Shallow Water Wave
An Introduction to Numerical Continuation Methods. with Application to some Problems from Physics. Eusebius Doedel. Cuzco, Peru, May 2013
 An Introduction to Numerical Continuation Methods with Application to some Problems from Physics Eusebius Doedel Cuzco, Peru, May 2013 Persistence of Solutions Newton s method for solving a nonlinear equation
An Introduction to Numerical Continuation Methods with Application to some Problems from Physics Eusebius Doedel Cuzco, Peru, May 2013 Persistence of Solutions Newton s method for solving a nonlinear equation
On Symmetry Group Properties of the Benney Equations
 Proceedings of Institute of Mathematics of NAS of Ukraine 2004, Vol. 50, Part 1, 214 218 On Symmetry Group Properties of the Benney Equations Teoman ÖZER Istanbul Technical University, Faculty of Civil
Proceedings of Institute of Mathematics of NAS of Ukraine 2004, Vol. 50, Part 1, 214 218 On Symmetry Group Properties of the Benney Equations Teoman ÖZER Istanbul Technical University, Faculty of Civil
The first integral method and traveling wave solutions to Davey Stewartson equation
 18 Nonlinear Analysis: Modelling Control 01 Vol. 17 No. 18 193 The first integral method traveling wave solutions to Davey Stewartson equation Hossein Jafari a1 Atefe Sooraki a Yahya Talebi a Anjan Biswas
18 Nonlinear Analysis: Modelling Control 01 Vol. 17 No. 18 193 The first integral method traveling wave solutions to Davey Stewartson equation Hossein Jafari a1 Atefe Sooraki a Yahya Talebi a Anjan Biswas
CDS 101/110a: Lecture 2.1 Dynamic Behavior
 CDS 11/11a: Lecture 2.1 Dynamic Behavior Richard M. Murray 6 October 28 Goals: Learn to use phase portraits to visualize behavior of dynamical systems Understand different types of stability for an equilibrium
CDS 11/11a: Lecture 2.1 Dynamic Behavior Richard M. Murray 6 October 28 Goals: Learn to use phase portraits to visualize behavior of dynamical systems Understand different types of stability for an equilibrium
Computational study of some nonlinear shallow water equations
 Shiraz University of Technology From the SelectedWorks of Habibolla Latifizadeh 013 Computational study of some nonlinear shallow water equations Habibolla Latifizadeh, Shiraz University of Technology
Shiraz University of Technology From the SelectedWorks of Habibolla Latifizadeh 013 Computational study of some nonlinear shallow water equations Habibolla Latifizadeh, Shiraz University of Technology
CLASSIFICATION AND PRINCIPLE OF SUPERPOSITION FOR SECOND ORDER LINEAR PDE
 CLASSIFICATION AND PRINCIPLE OF SUPERPOSITION FOR SECOND ORDER LINEAR PDE 1. Linear Partial Differential Equations A partial differential equation (PDE) is an equation, for an unknown function u, that
CLASSIFICATION AND PRINCIPLE OF SUPERPOSITION FOR SECOND ORDER LINEAR PDE 1. Linear Partial Differential Equations A partial differential equation (PDE) is an equation, for an unknown function u, that
Exact Solutions of Time-dependent Navier-Stokes Equations by Hodograph-Legendre Transformation Method
 Tamsui Oxford Journal of Mathematical Sciences 24(3) (2008) 257-268 Aletheia University Exact Solutions of Time-dependent Navier-Stokes Equations by Hodograph-Legendre Transformation Method Muhammad R.
Tamsui Oxford Journal of Mathematical Sciences 24(3) (2008) 257-268 Aletheia University Exact Solutions of Time-dependent Navier-Stokes Equations by Hodograph-Legendre Transformation Method Muhammad R.
MATH 412 Fourier Series and PDE- Spring 2010 SOLUTIONS to HOMEWORK 6
 MATH 412 Fourier Series and PDE- Spring 21 SOLUTIONS to HOMEWORK 6 Problem 1. Solve the following problem u t u xx =1+xcos t
MATH 412 Fourier Series and PDE- Spring 21 SOLUTIONS to HOMEWORK 6 Problem 1. Solve the following problem u t u xx =1+xcos t
