LSMR: An iterative algorithm for least-squares problems
|
|
|
- Brendan Blair
- 5 years ago
- Views:
Transcription
1 LSMR: An iterative algorithm for least-squares problems David Fong Michael Saunders Institute for Computational and Mathematical Engineering (icme) Stanford University Copper Mountain Conference on Iterative Methods Copper Mountain, Colorado Apr 5 9, 2010 David Fong, Michael Saunders LSMR Algorithm 1/31
2 LSMR in one slide solve Ax = b min Ax b 2 David Fong, Michael Saunders LSMR Algorithm 2/31
3 LSMR in one slide solve Ax = b min Ax b 2 ) ( ) min A b ( x λi 0 2 David Fong, Michael Saunders LSMR Algorithm 2/31
4 LSMR in one slide solve Ax = b min Ax b 2 ) ( ) min A b ( x λi 0 2 LSQR CG on the normal equation LSMR MINRES on the normal equation David Fong, Michael Saunders LSMR Algorithm 2/31
5 LSMR in one slide solve Ax = b min Ax b 2 ) ( ) min A b ( x λi 0 2 LSQR CG on the normal equation LSMR MINRES on the normal equation Almost same complexity as LSQR Better convergence properties for inexact solves David Fong, Michael Saunders LSMR Algorithm 2/31
6 LSQR Iterative algorithm for ( ) ( min A b x λi 0) 2 David Fong, Michael Saunders LSMR Algorithm 3/31
7 LSQR Iterative algorithm for Properties ( ) ( min A b x λi 0) 2 A is rectangular (m n) and often sparse A can be an operator CG on the normal equation (A T A + λ 2 I)x = A T b Av, A T u plus O(m + n) operations per iteration David Fong, Michael Saunders LSMR Algorithm 3/31
8 Monotone convergence of residual Measure of Convergence r = b Ax r ˆr, A T r 0 David Fong, Michael Saunders LSMR Algorithm 4/31
9 Monotone convergence of residual Measure of Convergence r = b Ax r ˆr, A T r 0 LSQR r LSQR log A T r Name:lp fit1p, Dim:1677x627, nnz:9868, id=80 2 Name:lp fit1p, Dim:1677x627, nnz:9868, id= r log A T r iteration count iteration count David Fong, Michael Saunders LSMR Algorithm 4/31
10 Monotone convergence of residual Measure of Convergence r = b Ax r ˆr, A T r 0 LSQR LSMR r log A T r Name:lp fit1p, Dim:1677x627, nnz:9868, id=80 lsqr lsmr 2 1 Name:lp fit1p, Dim:1677x627, nnz:9868, id=80 lsqr lsmr r log A T r iteration count iteration count David Fong, Michael Saunders LSMR Algorithm 4/31
11 LSMR Algorithm David Fong, Michael Saunders LSMR Algorithm 5/31
12 Golub-Kahan bidiagonalization Given A (m n) and b (m 1) Direct bidiagonalization U T AV = B David Fong, Michael Saunders LSMR Algorithm 6/31
13 Golub-Kahan bidiagonalization Given A (m n) and b (m 1) Direct bidiagonalization U T AV = B Iterative bidiagonalization 1 β 1 u 1 = b, α 1 v 1 = A T u 1 2 for = 1, 2,..., set β +1 u +1 = Av α u α +1 v +1 = A T u +1 β +1 v David Fong, Michael Saunders LSMR Algorithm 6/31
14 Golub-Kahan bidiagonalization (2) The process can be summarized by AV = U +1 B A T U +1 = V +1 L T +1 where α 1 β 2 α 2 L = β α α 1, B β 2 α 2 = β α β +1 = ( L β +1 e T ) David Fong, Michael Saunders LSMR Algorithm 7/31
15 Golub-Kahan bidiagonalization (3) V spans the Krylov subspace: span{v 1,..., v } = span{a T b, (A T A)A T b,..., (A T A) 1 A T b} Define x = V y Subproblem to solve min r = min β 1 e 1 B y (LSQR) y y ( ) min A T r = min y y β B T 1 e 1 B β +1 e T y (LSMR) where r = b Ax, β = α β David Fong, Michael Saunders LSMR Algorithm 8/31
16 Golub-Kahan bidiagonalization (3) V spans the Krylov subspace: span{v 1,..., v } = span{a T b, (A T A)A T b,..., (A T A) 1 A T b} Define x = V y Subproblem to solve min r = min β 1 e 1 B y (LSQR) y y ( ) min A T r = min y y β B T 1 e 1 B β +1 e T y (LSMR) where r = b Ax, β = α β David Fong, Michael Saunders LSMR Algorithm 8/31
17 Least squares subproblem min y ( ) B β T B 1e 1 y β +1 e T David Fong, Michael Saunders LSMR Algorithm 9/31
18 Least squares subproblem min y = min y ( ) B β T B 1e 1 y β +1 e T ( ) R β T R 1e 1 y q T Q +1 B = R ( ) R, R T q 0 = β +1 e David Fong, Michael Saunders LSMR Algorithm 9/31
19 Least squares subproblem min y = min y = min t ( ) B β T B 1e 1 y β +1 e T ( ) R β T R ( ) R 1e 1 y q T Q +1 B =, R T q R 0 = β +1 e ( ) R β T 1e 1 t ϕ e T t = R y, q = ( β +1 /(R ), )e = ϕ e David Fong, Michael Saunders LSMR Algorithm 9/31
20 Least squares subproblem min y = min y = min t = min t ( ) B β T B 1e 1 y β +1 e T ( ) R β T R ( ) R 1e 1 y q T Q +1 B =, R T q R 0 = β +1 e ( ) R β T 1e 1 t ϕ e T t = R y, q = ( β +1 /(R ), )e = ϕ e ( ) ( ) ( ) ( ) z R R T β1e 1 R z t ζ +1 0 Q+1 = ϕ e T 0 0 ζ+1 David Fong, Michael Saunders LSMR Algorithm 9/31
21 Least squares subproblem min y = min y = min t = min t ( ) B β T B 1e 1 y β +1 e T ( ) R β T R ( ) R 1e 1 y q T Q +1 B =, R T q R 0 = β +1 e ( ) R β T 1e 1 t ϕ e T t = R y, q = ( β +1 /(R ), )e = ϕ e ( ) ( ) ( ) ( ) z R R T β1e 1 R z t ζ +1 0 Q+1 = ϕ e T 0 0 ζ+1 Things to note x = V y, t = R y, z = R t, two cheap QRs David Fong, Michael Saunders LSMR Algorithm 9/31
22 Least squares subproblem (2) Remember x = V y, t = R y, z = R t David Fong, Michael Saunders LSMR Algorithm 10/31
23 Least squares subproblem (2) Remember x = V y, t = R y, z = R t Key steps to compute x x = V y David Fong, Michael Saunders LSMR Algorithm 10/31
24 Least squares subproblem (2) Remember x = V y, t = R y, z = R t Key steps to compute x x = V y = W t R T W T = V T David Fong, Michael Saunders LSMR Algorithm 10/31
25 Least squares subproblem (2) Remember x = V y, t = R y, z = R t Key steps to compute x x = V y = W t R T W T = V T = W z RT W T = W T David Fong, Michael Saunders LSMR Algorithm 10/31
26 Least squares subproblem (2) Remember x = V y, t = R y, z = R t Key steps to compute x x = V y = W t R T W T = V T = W z RT W T = W T = x 1 + ζ w where z = ( ζ 1 ζ 2 ζ ) T David Fong, Michael Saunders LSMR Algorithm 10/31
27 Flow chart of LSMR A,b Golub-Kahan bidiagonalization QR decompositions Update x Estimate bacward error large small Solution x David Fong, Michael Saunders LSMR Algorithm 11/31
28 Flow chart of LSMR Computational cost A,b Av, A T v, 3m + 3n Golub-Kahan bidiagonalization O(1) QR decompositions 3n Update x O(1) Estimate bacward error small Solution x large David Fong, Michael Saunders LSMR Algorithm 11/31
29 Computational and storage requirement Storage Wor m n m n MINRES on A T Ax = A T b Av 1 x, v 1, v 2, w 1, w 2 8 LSQR Av, u x, v, w 3 5 LSMR Av, u x, v, h, h 3 6 where h, h are scalar multiples of w, w David Fong, Michael Saunders LSMR Algorithm 12/31
30 Numerical experiments Test Data University of Florida Sparse Matrix Collection LPnetlib: Linear Programming Problems A = (Problem.A) b = Problem.c (127 problems) David Fong, Michael Saunders LSMR Algorithm 13/31
31 Numerical experiments Test Data University of Florida Sparse Matrix Collection LPnetlib: Linear Programming Problems A = (Problem.A) b = Problem.c (127 problems) Solve min Ax b 2 with LSQR and LSMR Bacward error tests: nnz(a) Reorthogonalization: nnz(a) David Fong, Michael Saunders LSMR Algorithm 13/31
32 Bacward errors - optimal Optimal bacward error µ(x) min E E s.t. (A + E)T (A + E)x = (A + E) T b David Fong, Michael Saunders LSMR Algorithm 14/31
33 Bacward errors - optimal Optimal bacward error µ(x) min E E s.t. (A + E)T (A + E)x = (A + E) T b Higham 1995: µ(x) = σ min (C), C [ A ( )] r x I rrt. r 2 Cheaper estimate (Grcar, Saunders, & Su 2007): ( ) ( ) A r K = r v = y = argmin Ky v x 0 y µ(x) = Ky x David Fong, Michael Saunders LSMR Algorithm 14/31
34 Bacward error estimates - E 1, E 2 Again, (A + E i ) T (A + E i )x = (A + E i ) T b Two estimates given by Stewart (1975 and 1977): E 1 = ext x 2, E 1 = e x, e = ˆr r E 2 = rrt A r 2, E 2 = AT r r where ˆr is the residual for the exact solution David Fong, Michael Saunders LSMR Algorithm 15/31
35 r for LSQR and LSMR Name:lp greenbeb, Dim:5598x2392, nnz:31070, id=100 lsqr lsmr r iteration count David Fong, Michael Saunders LSMR Algorithm 16/31
36 log 10 ( E 2 ) for LSQR and LSMR 0 Name:lp pilot ja, Dim:2267x940, nnz:14977, id=88 E2 LSQR E2 LSMR log(e2) iteration count David Fong, Michael Saunders LSMR Algorithm 17/31
37 Bacward errors for LSQR 1 0 Name:lp cre a, Dim:7248x3516, nnz:18168, id=93 E1 LSQR E2 LSQR Optimal LSQR 1 2 log(bacward Error) iteration count David Fong, Michael Saunders LSMR Algorithm 18/31
38 Bacward errors for LSMR 1 0 Name:lp cre a, Dim:7248x3516, nnz:18168, id=93 E1 LSMR E2 LSMR Optimal LSMR 1 2 log(bacward Error) iteration count David Fong, Michael Saunders LSMR Algorithm 19/31
39 Optimal bacward errors for LSQR and LSMR 0 Name:lp pilot, Dim:4860x1441, nnz:44375, id=107 Optimal LSQR Optimal LSMR 1 2 log( A T r / r ) iteration count David Fong, Michael Saunders LSMR Algorithm 20/31
40 Space-time trade-offs LSMR is well-suited for limited memory computations. What if we have more memory Av expensive Can we speed things up? David Fong, Michael Saunders LSMR Algorithm 21/31
41 Space-time trade-offs LSMR is well-suited for limited memory computations. What if we have more memory Av expensive Can we speed things up? Some ideas: Reorthogonalization Restarting Local reorthogonalization David Fong, Michael Saunders LSMR Algorithm 21/31
42 Reorthogonalization Golub-Kahan process Infinite precision Finite precision U, V orthonormal Lose orthogonality At most min(m, n) iterations Could tae 10n or more David Fong, Michael Saunders LSMR Algorithm 22/31
43 Reorthogonalization Golub-Kahan process Infinite precision Finite precision U, V orthonormal Lose orthogonality At most min(m, n) iterations Could tae 10n or more Apply modified Gram-Schmidt to u +1 and/or v +1 : u u (u T j u)u j j =, 1, 2,... (similarly for v) David Fong, Michael Saunders LSMR Algorithm 22/31
44 Effects of reorthogonalization on various problems 1 0 Name:lp ship12l, Dim:5533x1151, nnz:16276, id=91 NoOrtho OrthoU OrthoV OrthoUV 1 0 Name:lp scfxm2, Dim:1200x660, nnz:5469, id=62 NoOrtho OrthoU OrthoV OrthoUV log(e2) 3 4 log(e2) iteration count iteration count 1 0 Name:lp agg2, Dim:758x516, nnz:4740, id=58 NoOrtho OrthoU OrthoV OrthoUV 0 1 Name:lpi gran, Dim:2525x2658, nnz:20111, id=94 NoOrtho OrthoU OrthoV OrthoUV log(e2) log(e2) iteration count iteration count David Fong, Michael Saunders LSMR Algorithm 23/31
45 Orthogonality of U Original MGS on U MGS on V MGS on U,V David Fong, Michael Saunders LSMR Algorithm 24/31
46 Orthogonality of V Original MGS on U MGS on V MGS on U,V David Fong, Michael Saunders LSMR Algorithm 25/31
47 What we learnt so far Reorthogonalizing V (only) is sufficient Reorthogonalizing U (only) is nearly as good x converges the same for all options What can be improved May still use too much memory Need more flexibility for space-time trade-off David Fong, Michael Saunders LSMR Algorithm 26/31
48 Reorthogonalization with Restarting Restarting LSMR r = b Ax min A x r David Fong, Michael Saunders LSMR Algorithm 27/31
49 Reorthogonalization with Restarting Restarting LSMR r = b Ax min A x r Restarting leads to stagnation 0 1 Name:lp maros, Dim:1966x846, nnz:10137, id=81 NoOrtho Restart5 Restart10 Restart50 NoRestart 1 0 Name:lp cre c, Dim:6411x3068, nnz:15977, id=90 NoOrtho Restart5 Restart10 Restart50 NoRestart Bacward Error 3 4 Bacward Error iteration count iteration count David Fong, Michael Saunders LSMR Algorithm 27/31
50 Local reorthogonalization Reorthogonalize wrto only the last l vectors Partial speed-up Less memory Depends on efficiency of Av and A T u David Fong, Michael Saunders LSMR Algorithm 28/31
51 Local reorthogonalization Reorthogonalize wrto only the last l vectors Partial speed-up Less memory Depends on efficiency of Av and A T u Speed up with local reorthogonalization Name:lp fit1p, Dim:1677x627, nnz:9868, id=80 NoOrtho Local5 Local10 Local50 FullOrtho 2 1 Name:lp bnl2, Dim:4486x2324, nnz:14996, id=89 NoOrtho Local5 Local10 Local50 FullOrtho Bacward Error Bacward Error iteration count iteration count David Fong, Michael Saunders LSMR Algorithm 28/31
52 Conclusions Advantages of LSMR All the good properties of LSQR Monotone convergence of A T r r still monotonic Cheap near-optimal bacward error estimate reliable stopping rule Bacward error almost surely monotonic David Fong, Michael Saunders LSMR Algorithm 29/31
53 Acnowledgement Michael Saunders Chris Paige Stanford Graduate Fellowship David Fong, Michael Saunders LSMR Algorithm 30/31
54 Questions LSMR in MATLAB and slides for this tal are downloadable at David Fong, Michael Saunders LSMR Algorithm 31/31
CG and MINRES: An empirical comparison
 School of Engineering CG and MINRES: An empirical comparison Prequel to LSQR and LSMR: Two least-squares solvers David Fong and Michael Saunders Institute for Computational and Mathematical Engineering
School of Engineering CG and MINRES: An empirical comparison Prequel to LSQR and LSMR: Two least-squares solvers David Fong and Michael Saunders Institute for Computational and Mathematical Engineering
CG versus MINRES on Positive Definite Systems
 School of Engineering CG versus MINRES on Positive Definite Systems Michael Saunders SOL and ICME, Stanford University Joint work with David Fong Recent Advances on Optimization In honor of Philippe Toint
School of Engineering CG versus MINRES on Positive Definite Systems Michael Saunders SOL and ICME, Stanford University Joint work with David Fong Recent Advances on Optimization In honor of Philippe Toint
AMS subject classifications. 15A06, 65F10, 65F20, 65F22, 65F25, 65F35, 65F50, 93E24
 : AN IERAIVE ALGORIHM FOR SPARSE LEAS-SQUARES PROBLEMS DAVID CHIN-LUNG FONG AND MICHAEL SAUNDERS Abstract. An iterative method is presented for solving linear systems Ax = b and leastsquares problems min
: AN IERAIVE ALGORIHM FOR SPARSE LEAS-SQUARES PROBLEMS DAVID CHIN-LUNG FONG AND MICHAEL SAUNDERS Abstract. An iterative method is presented for solving linear systems Ax = b and leastsquares problems min
Experiments with iterative computation of search directions within interior methods for constrained optimization
 Experiments with iterative computation of search directions within interior methods for constrained optimization Santiago Akle and Michael Saunders Institute for Computational Mathematics and Engineering
Experiments with iterative computation of search directions within interior methods for constrained optimization Santiago Akle and Michael Saunders Institute for Computational Mathematics and Engineering
Generalized MINRES or Generalized LSQR?
 Generalized MINRES or Generalized LSQR? Michael Saunders Systems Optimization Laboratory (SOL) Institute for Computational Mathematics and Engineering (ICME) Stanford University New Frontiers in Numerical
Generalized MINRES or Generalized LSQR? Michael Saunders Systems Optimization Laboratory (SOL) Institute for Computational Mathematics and Engineering (ICME) Stanford University New Frontiers in Numerical
Block Bidiagonal Decomposition and Least Squares Problems
 Block Bidiagonal Decomposition and Least Squares Problems Åke Björck Department of Mathematics Linköping University Perspectives in Numerical Analysis, Helsinki, May 27 29, 2008 Outline Bidiagonal Decomposition
Block Bidiagonal Decomposition and Least Squares Problems Åke Björck Department of Mathematics Linköping University Perspectives in Numerical Analysis, Helsinki, May 27 29, 2008 Outline Bidiagonal Decomposition
Math 310 Final Project Recycled subspaces in the LSMR Krylov method
 Math 310 Final Project Recycled subspaces in the LSMR Krylov method Victor Minden November 25, 2013 1 Introduction In many applications, it is the case that we are interested not only in solving a single
Math 310 Final Project Recycled subspaces in the LSMR Krylov method Victor Minden November 25, 2013 1 Introduction In many applications, it is the case that we are interested not only in solving a single
The Lanczos and conjugate gradient algorithms
 The Lanczos and conjugate gradient algorithms Gérard MEURANT October, 2008 1 The Lanczos algorithm 2 The Lanczos algorithm in finite precision 3 The nonsymmetric Lanczos algorithm 4 The Golub Kahan bidiagonalization
The Lanczos and conjugate gradient algorithms Gérard MEURANT October, 2008 1 The Lanczos algorithm 2 The Lanczos algorithm in finite precision 3 The nonsymmetric Lanczos algorithm 4 The Golub Kahan bidiagonalization
CG VERSUS MINRES: AN EMPIRICAL COMPARISON
 VERSUS : AN EMPIRICAL COMPARISON DAVID CHIN-LUNG FONG AND MICHAEL SAUNDERS Abstract. For iterative solution of symmetric systems Ax = b, the conjugate gradient method () is commonly used when A is positive
VERSUS : AN EMPIRICAL COMPARISON DAVID CHIN-LUNG FONG AND MICHAEL SAUNDERS Abstract. For iterative solution of symmetric systems Ax = b, the conjugate gradient method () is commonly used when A is positive
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 23: GMRES and Other Krylov Subspace Methods; Preconditioning
 AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 23: GMRES and Other Krylov Subspace Methods; Preconditioning Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 18 Outline
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 23: GMRES and Other Krylov Subspace Methods; Preconditioning Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 18 Outline
CG VERSUS MINRES: AN EMPIRICAL COMPARISON
 VERSUS : AN EMPIRICAL COMPARISON DAVID CHIN-LUNG FONG AND MICHAEL SAUNDERS Abstract. For iterative solution of symmetric systems Ax = b, the conjugate gradient method () is commonly used when A is positive
VERSUS : AN EMPIRICAL COMPARISON DAVID CHIN-LUNG FONG AND MICHAEL SAUNDERS Abstract. For iterative solution of symmetric systems Ax = b, the conjugate gradient method () is commonly used when A is positive
LARGE SPARSE EIGENVALUE PROBLEMS. General Tools for Solving Large Eigen-Problems
 LARGE SPARSE EIGENVALUE PROBLEMS Projection methods The subspace iteration Krylov subspace methods: Arnoldi and Lanczos Golub-Kahan-Lanczos bidiagonalization General Tools for Solving Large Eigen-Problems
LARGE SPARSE EIGENVALUE PROBLEMS Projection methods The subspace iteration Krylov subspace methods: Arnoldi and Lanczos Golub-Kahan-Lanczos bidiagonalization General Tools for Solving Large Eigen-Problems
LARGE SPARSE EIGENVALUE PROBLEMS
 LARGE SPARSE EIGENVALUE PROBLEMS Projection methods The subspace iteration Krylov subspace methods: Arnoldi and Lanczos Golub-Kahan-Lanczos bidiagonalization 14-1 General Tools for Solving Large Eigen-Problems
LARGE SPARSE EIGENVALUE PROBLEMS Projection methods The subspace iteration Krylov subspace methods: Arnoldi and Lanczos Golub-Kahan-Lanczos bidiagonalization 14-1 General Tools for Solving Large Eigen-Problems
4.8 Arnoldi Iteration, Krylov Subspaces and GMRES
 48 Arnoldi Iteration, Krylov Subspaces and GMRES We start with the problem of using a similarity transformation to convert an n n matrix A to upper Hessenberg form H, ie, A = QHQ, (30) with an appropriate
48 Arnoldi Iteration, Krylov Subspaces and GMRES We start with the problem of using a similarity transformation to convert an n n matrix A to upper Hessenberg form H, ie, A = QHQ, (30) with an appropriate
On the loss of orthogonality in the Gram-Schmidt orthogonalization process
 CERFACS Technical Report No. TR/PA/03/25 Luc Giraud Julien Langou Miroslav Rozložník On the loss of orthogonality in the Gram-Schmidt orthogonalization process Abstract. In this paper we study numerical
CERFACS Technical Report No. TR/PA/03/25 Luc Giraud Julien Langou Miroslav Rozložník On the loss of orthogonality in the Gram-Schmidt orthogonalization process Abstract. In this paper we study numerical
FEM and sparse linear system solving
 FEM & sparse linear system solving, Lecture 9, Nov 19, 2017 1/36 Lecture 9, Nov 17, 2017: Krylov space methods http://people.inf.ethz.ch/arbenz/fem17 Peter Arbenz Computer Science Department, ETH Zürich
FEM & sparse linear system solving, Lecture 9, Nov 19, 2017 1/36 Lecture 9, Nov 17, 2017: Krylov space methods http://people.inf.ethz.ch/arbenz/fem17 Peter Arbenz Computer Science Department, ETH Zürich
Key words. conjugate gradients, normwise backward error, incremental norm estimation.
 Proceedings of ALGORITMY 2016 pp. 323 332 ON ERROR ESTIMATION IN THE CONJUGATE GRADIENT METHOD: NORMWISE BACKWARD ERROR PETR TICHÝ Abstract. Using an idea of Duff and Vömel [BIT, 42 (2002), pp. 300 322
Proceedings of ALGORITMY 2016 pp. 323 332 ON ERROR ESTIMATION IN THE CONJUGATE GRADIENT METHOD: NORMWISE BACKWARD ERROR PETR TICHÝ Abstract. Using an idea of Duff and Vömel [BIT, 42 (2002), pp. 300 322
A DISSERTATION. Extensions of the Conjugate Residual Method. by Tomohiro Sogabe. Presented to
 A DISSERTATION Extensions of the Conjugate Residual Method ( ) by Tomohiro Sogabe Presented to Department of Applied Physics, The University of Tokyo Contents 1 Introduction 1 2 Krylov subspace methods
A DISSERTATION Extensions of the Conjugate Residual Method ( ) by Tomohiro Sogabe Presented to Department of Applied Physics, The University of Tokyo Contents 1 Introduction 1 2 Krylov subspace methods
Applied Mathematics 205. Unit II: Numerical Linear Algebra. Lecturer: Dr. David Knezevic
 Applied Mathematics 205 Unit II: Numerical Linear Algebra Lecturer: Dr. David Knezevic Unit II: Numerical Linear Algebra Chapter II.3: QR Factorization, SVD 2 / 66 QR Factorization 3 / 66 QR Factorization
Applied Mathematics 205 Unit II: Numerical Linear Algebra Lecturer: Dr. David Knezevic Unit II: Numerical Linear Algebra Chapter II.3: QR Factorization, SVD 2 / 66 QR Factorization 3 / 66 QR Factorization
Ax=b. Zack 10/4/2013
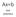 Ax=b Zack 10/4/2013 Iteration method Ax=b v 1, v 2 x k = V k y k Given (A, b) standard orthonormal base v 1, v 2 x k = V k y k For symmetric A, the method to generate V k is called Lanczos Method Lanczos
Ax=b Zack 10/4/2013 Iteration method Ax=b v 1, v 2 x k = V k y k Given (A, b) standard orthonormal base v 1, v 2 x k = V k y k For symmetric A, the method to generate V k is called Lanczos Method Lanczos
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME MS&E 38 (CME 338 Large-Scale Numerical Optimization Course description Instructor: Michael Saunders Spring 28 Notes : Review The course teaches
Stanford University, Management Science & Engineering (and ICME MS&E 38 (CME 338 Large-Scale Numerical Optimization Course description Instructor: Michael Saunders Spring 28 Notes : Review The course teaches
Course Notes: Week 1
 Course Notes: Week 1 Math 270C: Applied Numerical Linear Algebra 1 Lecture 1: Introduction (3/28/11) We will focus on iterative methods for solving linear systems of equations (and some discussion of eigenvalues
Course Notes: Week 1 Math 270C: Applied Numerical Linear Algebra 1 Lecture 1: Introduction (3/28/11) We will focus on iterative methods for solving linear systems of equations (and some discussion of eigenvalues
Lanczos Bidiagonalization with Subspace Augmentation for Discrete Inverse Problems
 Lanczos Bidiagonalization with Subspace Augmentation for Discrete Inverse Problems Per Christian Hansen Technical University of Denmark Ongoing work with Kuniyoshi Abe, Gifu Dedicated to Dianne P. O Leary
Lanczos Bidiagonalization with Subspace Augmentation for Discrete Inverse Problems Per Christian Hansen Technical University of Denmark Ongoing work with Kuniyoshi Abe, Gifu Dedicated to Dianne P. O Leary
Inexactness and flexibility in linear Krylov solvers
 Inexactness and flexibility in linear Krylov solvers Luc Giraud ENSEEIHT (N7) - IRIT, Toulouse Matrix Analysis and Applications CIRM Luminy - October 15-19, 2007 in honor of Gérard Meurant for his 60 th
Inexactness and flexibility in linear Krylov solvers Luc Giraud ENSEEIHT (N7) - IRIT, Toulouse Matrix Analysis and Applications CIRM Luminy - October 15-19, 2007 in honor of Gérard Meurant for his 60 th
Math 3191 Applied Linear Algebra
 Math 9 Applied Linear Algebra Lecture : Orthogonal Projections, Gram-Schmidt Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./ Orthonormal Sets A set of vectors {u, u,...,
Math 9 Applied Linear Algebra Lecture : Orthogonal Projections, Gram-Schmidt Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./ Orthonormal Sets A set of vectors {u, u,...,
F as a function of the approximate solution x
 ESTIMATES OF OPTIMAL BACKWARD PERTURBATIONS FOR LINEAR LEAST SQUARES PROBLEMS JOSEPH F. GRCAR, MICHAEL A. SAUNDERS, AND ZHENG SU Abstract. Numerical tests are used to validate a practical estimate for
ESTIMATES OF OPTIMAL BACKWARD PERTURBATIONS FOR LINEAR LEAST SQUARES PROBLEMS JOSEPH F. GRCAR, MICHAEL A. SAUNDERS, AND ZHENG SU Abstract. Numerical tests are used to validate a practical estimate for
Computation of eigenvalues and singular values Recall that your solutions to these questions will not be collected or evaluated.
 Math 504, Homework 5 Computation of eigenvalues and singular values Recall that your solutions to these questions will not be collected or evaluated 1 Find the eigenvalues and the associated eigenspaces
Math 504, Homework 5 Computation of eigenvalues and singular values Recall that your solutions to these questions will not be collected or evaluated 1 Find the eigenvalues and the associated eigenspaces
MATH 304 Linear Algebra Lecture 20: The Gram-Schmidt process (continued). Eigenvalues and eigenvectors.
 MATH 304 Linear Algebra Lecture 20: The Gram-Schmidt process (continued). Eigenvalues and eigenvectors. Orthogonal sets Let V be a vector space with an inner product. Definition. Nonzero vectors v 1,v
MATH 304 Linear Algebra Lecture 20: The Gram-Schmidt process (continued). Eigenvalues and eigenvectors. Orthogonal sets Let V be a vector space with an inner product. Definition. Nonzero vectors v 1,v
Numerical Methods in Matrix Computations
 Ake Bjorck Numerical Methods in Matrix Computations Springer Contents 1 Direct Methods for Linear Systems 1 1.1 Elements of Matrix Theory 1 1.1.1 Matrix Algebra 2 1.1.2 Vector Spaces 6 1.1.3 Submatrices
Ake Bjorck Numerical Methods in Matrix Computations Springer Contents 1 Direct Methods for Linear Systems 1 1.1 Elements of Matrix Theory 1 1.1.1 Matrix Algebra 2 1.1.2 Vector Spaces 6 1.1.3 Submatrices
Worksheet for Lecture 25 Section 6.4 Gram-Schmidt Process
 Worksheet for Lecture Name: Section.4 Gram-Schmidt Process Goal For a subspace W = Span{v,..., v n }, we want to find an orthonormal basis of W. Example Let W = Span{x, x } with x = and x =. Give an orthogonal
Worksheet for Lecture Name: Section.4 Gram-Schmidt Process Goal For a subspace W = Span{v,..., v n }, we want to find an orthonormal basis of W. Example Let W = Span{x, x } with x = and x =. Give an orthogonal
AM 205: lecture 8. Last time: Cholesky factorization, QR factorization Today: how to compute the QR factorization, the Singular Value Decomposition
 AM 205: lecture 8 Last time: Cholesky factorization, QR factorization Today: how to compute the QR factorization, the Singular Value Decomposition QR Factorization A matrix A R m n, m n, can be factorized
AM 205: lecture 8 Last time: Cholesky factorization, QR factorization Today: how to compute the QR factorization, the Singular Value Decomposition QR Factorization A matrix A R m n, m n, can be factorized
Last Time. Social Network Graphs Betweenness. Graph Laplacian. Girvan-Newman Algorithm. Spectral Bisection
 Eigenvalue Problems Last Time Social Network Graphs Betweenness Girvan-Newman Algorithm Graph Laplacian Spectral Bisection λ 2, w 2 Today Small deviation into eigenvalue problems Formulation Standard eigenvalue
Eigenvalue Problems Last Time Social Network Graphs Betweenness Girvan-Newman Algorithm Graph Laplacian Spectral Bisection λ 2, w 2 Today Small deviation into eigenvalue problems Formulation Standard eigenvalue
Lab 1: Iterative Methods for Solving Linear Systems
 Lab 1: Iterative Methods for Solving Linear Systems January 22, 2017 Introduction Many real world applications require the solution to very large and sparse linear systems where direct methods such as
Lab 1: Iterative Methods for Solving Linear Systems January 22, 2017 Introduction Many real world applications require the solution to very large and sparse linear systems where direct methods such as
Charles University Faculty of Mathematics and Physics DOCTORAL THESIS. Krylov subspace approximations in linear algebraic problems
 Charles University Faculty of Mathematics and Physics DOCTORAL THESIS Iveta Hnětynková Krylov subspace approximations in linear algebraic problems Department of Numerical Mathematics Supervisor: Doc. RNDr.
Charles University Faculty of Mathematics and Physics DOCTORAL THESIS Iveta Hnětynková Krylov subspace approximations in linear algebraic problems Department of Numerical Mathematics Supervisor: Doc. RNDr.
Residual statics analysis by LSQR
 Residual statics analysis by LSQR Residual statics analysis by LSQR Yan Yan, Zhengsheng Yao, Gary F. Margrave and R. James Brown ABSRAC Residual statics corrections can be formulated as a linear inverse
Residual statics analysis by LSQR Residual statics analysis by LSQR Yan Yan, Zhengsheng Yao, Gary F. Margrave and R. James Brown ABSRAC Residual statics corrections can be formulated as a linear inverse
Homework 5. (due Wednesday 8 th Nov midnight)
 Homework (due Wednesday 8 th Nov midnight) Use this definition for Column Space of a Matrix Column Space of a matrix A is the set ColA of all linear combinations of the columns of A. In other words, if
Homework (due Wednesday 8 th Nov midnight) Use this definition for Column Space of a Matrix Column Space of a matrix A is the set ColA of all linear combinations of the columns of A. In other words, if
EECS 275 Matrix Computation
 EECS 275 Matrix Computation Ming-Hsuan Yang Electrical Engineering and Computer Science University of California at Merced Merced, CA 95344 http://faculty.ucmerced.edu/mhyang Lecture 20 1 / 20 Overview
EECS 275 Matrix Computation Ming-Hsuan Yang Electrical Engineering and Computer Science University of California at Merced Merced, CA 95344 http://faculty.ucmerced.edu/mhyang Lecture 20 1 / 20 Overview
Golub-Kahan iterative bidiagonalization and determining the noise level in the data
 Golub-Kahan iterative bidiagonalization and determining the noise level in the data Iveta Hnětynková,, Martin Plešinger,, Zdeněk Strakoš, * Charles University, Prague ** Academy of Sciences of the Czech
Golub-Kahan iterative bidiagonalization and determining the noise level in the data Iveta Hnětynková,, Martin Plešinger,, Zdeněk Strakoš, * Charles University, Prague ** Academy of Sciences of the Czech
Lanczos tridigonalization and Golub - Kahan bidiagonalization: Ideas, connections and impact
 Lanczos tridigonalization and Golub - Kahan bidiagonalization: Ideas, connections and impact Zdeněk Strakoš Academy of Sciences and Charles University, Prague http://www.cs.cas.cz/ strakos Hong Kong, February
Lanczos tridigonalization and Golub - Kahan bidiagonalization: Ideas, connections and impact Zdeněk Strakoš Academy of Sciences and Charles University, Prague http://www.cs.cas.cz/ strakos Hong Kong, February
STAT 309: MATHEMATICAL COMPUTATIONS I FALL 2018 LECTURE 9
 STAT 309: MATHEMATICAL COMPUTATIONS I FALL 2018 LECTURE 9 1. qr and complete orthogonal factorization poor man s svd can solve many problems on the svd list using either of these factorizations but they
STAT 309: MATHEMATICAL COMPUTATIONS I FALL 2018 LECTURE 9 1. qr and complete orthogonal factorization poor man s svd can solve many problems on the svd list using either of these factorizations but they
Chapter 7 Iterative Techniques in Matrix Algebra
 Chapter 7 Iterative Techniques in Matrix Algebra Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 128B Numerical Analysis Vector Norms Definition
Chapter 7 Iterative Techniques in Matrix Algebra Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 128B Numerical Analysis Vector Norms Definition
A short course on: Preconditioned Krylov subspace methods. Yousef Saad University of Minnesota Dept. of Computer Science and Engineering
 A short course on: Preconditioned Krylov subspace methods Yousef Saad University of Minnesota Dept. of Computer Science and Engineering Universite du Littoral, Jan 19-3, 25 Outline Part 1 Introd., discretization
A short course on: Preconditioned Krylov subspace methods Yousef Saad University of Minnesota Dept. of Computer Science and Engineering Universite du Littoral, Jan 19-3, 25 Outline Part 1 Introd., discretization
Solving large sparse Ax = b.
 Bob-05 p.1/69 Solving large sparse Ax = b. Stopping criteria, & backward stability of MGS-GMRES. Chris Paige (McGill University); Miroslav Rozložník & Zdeněk Strakoš (Academy of Sciences of the Czech Republic)..pdf
Bob-05 p.1/69 Solving large sparse Ax = b. Stopping criteria, & backward stability of MGS-GMRES. Chris Paige (McGill University); Miroslav Rozložník & Zdeněk Strakoš (Academy of Sciences of the Czech Republic)..pdf
Summary of Iterative Methods for Non-symmetric Linear Equations That Are Related to the Conjugate Gradient (CG) Method
 Summary of Iterative Methods for Non-symmetric Linear Equations That Are Related to the Conjugate Gradient (CG) Method Leslie Foster 11-5-2012 We will discuss the FOM (full orthogonalization method), CG,
Summary of Iterative Methods for Non-symmetric Linear Equations That Are Related to the Conjugate Gradient (CG) Method Leslie Foster 11-5-2012 We will discuss the FOM (full orthogonalization method), CG,
Krylov Space Methods. Nonstationary sounds good. Radu Trîmbiţaş ( Babeş-Bolyai University) Krylov Space Methods 1 / 17
 Krylov Space Methods Nonstationary sounds good Radu Trîmbiţaş Babeş-Bolyai University Radu Trîmbiţaş ( Babeş-Bolyai University) Krylov Space Methods 1 / 17 Introduction These methods are used both to solve
Krylov Space Methods Nonstationary sounds good Radu Trîmbiţaş Babeş-Bolyai University Radu Trîmbiţaş ( Babeş-Bolyai University) Krylov Space Methods 1 / 17 Introduction These methods are used both to solve
Lecture 9: Krylov Subspace Methods. 2 Derivation of the Conjugate Gradient Algorithm
 CS 622 Data-Sparse Matrix Computations September 19, 217 Lecture 9: Krylov Subspace Methods Lecturer: Anil Damle Scribes: David Eriksson, Marc Aurele Gilles, Ariah Klages-Mundt, Sophia Novitzky 1 Introduction
CS 622 Data-Sparse Matrix Computations September 19, 217 Lecture 9: Krylov Subspace Methods Lecturer: Anil Damle Scribes: David Eriksson, Marc Aurele Gilles, Ariah Klages-Mundt, Sophia Novitzky 1 Introduction
The conjugate gradient method
 The conjugate gradient method Michael S. Floater November 1, 2011 These notes try to provide motivation and an explanation of the CG method. 1 The method of conjugate directions We want to solve the linear
The conjugate gradient method Michael S. Floater November 1, 2011 These notes try to provide motivation and an explanation of the CG method. 1 The method of conjugate directions We want to solve the linear
COMPUTING PROJECTIONS WITH LSQR*
 BIT 37:1(1997), 96-104. COMPUTING PROJECTIONS WITH LSQR* MICHAEL A. SAUNDERS t Abstract. Systems Optimization Laboratory, Department of EES ~4 OR Stanford University, Stanford, CA 94305-4023, USA. email:
BIT 37:1(1997), 96-104. COMPUTING PROJECTIONS WITH LSQR* MICHAEL A. SAUNDERS t Abstract. Systems Optimization Laboratory, Department of EES ~4 OR Stanford University, Stanford, CA 94305-4023, USA. email:
The QR Factorization
 The QR Factorization How to Make Matrices Nicer Radu Trîmbiţaş Babeş-Bolyai University March 11, 2009 Radu Trîmbiţaş ( Babeş-Bolyai University) The QR Factorization March 11, 2009 1 / 25 Projectors A projector
The QR Factorization How to Make Matrices Nicer Radu Trîmbiţaş Babeş-Bolyai University March 11, 2009 Radu Trîmbiţaş ( Babeş-Bolyai University) The QR Factorization March 11, 2009 1 / 25 Projectors A projector
Gram-Schmidt Orthogonalization: 100 Years and More
 Gram-Schmidt Orthogonalization: 100 Years and More September 12, 2008 Outline of Talk Early History (1795 1907) Middle History 1. The work of Åke Björck Least squares, Stability, Loss of orthogonality
Gram-Schmidt Orthogonalization: 100 Years and More September 12, 2008 Outline of Talk Early History (1795 1907) Middle History 1. The work of Åke Björck Least squares, Stability, Loss of orthogonality
Conjugate Gradient algorithm. Storage: fixed, independent of number of steps.
 Conjugate Gradient algorithm Need: A symmetric positive definite; Cost: 1 matrix-vector product per step; Storage: fixed, independent of number of steps. The CG method minimizes the A norm of the error,
Conjugate Gradient algorithm Need: A symmetric positive definite; Cost: 1 matrix-vector product per step; Storage: fixed, independent of number of steps. The CG method minimizes the A norm of the error,
ECS231 Handout Subspace projection methods for Solving Large-Scale Eigenvalue Problems. Part I: Review of basic theory of eigenvalue problems
 ECS231 Handout Subspace projection methods for Solving Large-Scale Eigenvalue Problems Part I: Review of basic theory of eigenvalue problems 1. Let A C n n. (a) A scalar λ is an eigenvalue of an n n A
ECS231 Handout Subspace projection methods for Solving Large-Scale Eigenvalue Problems Part I: Review of basic theory of eigenvalue problems 1. Let A C n n. (a) A scalar λ is an eigenvalue of an n n A
Iterative Linear Solvers
 Chapter 10 Iterative Linear Solvers In the previous two chapters, we developed strategies for solving a new class of problems involving minimizing a function f ( x) with or without constraints on x. In
Chapter 10 Iterative Linear Solvers In the previous two chapters, we developed strategies for solving a new class of problems involving minimizing a function f ( x) with or without constraints on x. In
SOLVING SPARSE LINEAR SYSTEMS OF EQUATIONS. Chao Yang Computational Research Division Lawrence Berkeley National Laboratory Berkeley, CA, USA
 1 SOLVING SPARSE LINEAR SYSTEMS OF EQUATIONS Chao Yang Computational Research Division Lawrence Berkeley National Laboratory Berkeley, CA, USA 2 OUTLINE Sparse matrix storage format Basic factorization
1 SOLVING SPARSE LINEAR SYSTEMS OF EQUATIONS Chao Yang Computational Research Division Lawrence Berkeley National Laboratory Berkeley, CA, USA 2 OUTLINE Sparse matrix storage format Basic factorization
Iterative Methods for Linear Systems of Equations
 Iterative Methods for Linear Systems of Equations Projection methods (3) ITMAN PhD-course DTU 20-10-08 till 24-10-08 Martin van Gijzen 1 Delft University of Technology Overview day 4 Bi-Lanczos method
Iterative Methods for Linear Systems of Equations Projection methods (3) ITMAN PhD-course DTU 20-10-08 till 24-10-08 Martin van Gijzen 1 Delft University of Technology Overview day 4 Bi-Lanczos method
Least Squares. Tom Lyche. October 26, Centre of Mathematics for Applications, Department of Informatics, University of Oslo
 Least Squares Tom Lyche Centre of Mathematics for Applications, Department of Informatics, University of Oslo October 26, 2010 Linear system Linear system Ax = b, A C m,n, b C m, x C n. under-determined
Least Squares Tom Lyche Centre of Mathematics for Applications, Department of Informatics, University of Oslo October 26, 2010 Linear system Linear system Ax = b, A C m,n, b C m, x C n. under-determined
Computing tomographic resolution matrices using Arnoldi s iterative inversion algorithm
 Stanford Exploration Project, Report 82, May 11, 2001, pages 1 176 Computing tomographic resolution matrices using Arnoldi s iterative inversion algorithm James G. Berryman 1 ABSTRACT Resolution matrices
Stanford Exploration Project, Report 82, May 11, 2001, pages 1 176 Computing tomographic resolution matrices using Arnoldi s iterative inversion algorithm James G. Berryman 1 ABSTRACT Resolution matrices
Math 407: Linear Optimization
 Math 407: Linear Optimization Lecture 16: The Linear Least Squares Problem II Math Dept, University of Washington February 28, 2018 Lecture 16: The Linear Least Squares Problem II (Math Dept, University
Math 407: Linear Optimization Lecture 16: The Linear Least Squares Problem II Math Dept, University of Washington February 28, 2018 Lecture 16: The Linear Least Squares Problem II (Math Dept, University
Sparse BLAS-3 Reduction
 Sparse BLAS-3 Reduction to Banded Upper Triangular (Spar3Bnd) Gary Howell, HPC/OIT NC State University gary howell@ncsu.edu Sparse BLAS-3 Reduction p.1/27 Acknowledgements James Demmel, Gene Golub, Franc
Sparse BLAS-3 Reduction to Banded Upper Triangular (Spar3Bnd) Gary Howell, HPC/OIT NC State University gary howell@ncsu.edu Sparse BLAS-3 Reduction p.1/27 Acknowledgements James Demmel, Gene Golub, Franc
Introduction to Arnoldi method
 Introduction to Arnoldi method SF2524 - Matrix Computations for Large-scale Systems KTH Royal Institute of Technology (Elias Jarlebring) 2014-11-07 KTH Royal Institute of Technology (Elias Jarlebring)Introduction
Introduction to Arnoldi method SF2524 - Matrix Computations for Large-scale Systems KTH Royal Institute of Technology (Elias Jarlebring) 2014-11-07 KTH Royal Institute of Technology (Elias Jarlebring)Introduction
2017 Society for Industrial and Applied Mathematics
 SIAM J. SCI. COMPUT. Vol. 39, No. 5, pp. S24 S46 2017 Society for Industrial and Applied Mathematics GENERALIZED HYBRID ITERATIVE METHODS FOR LARGE-SCALE BAYESIAN INVERSE PROBLEMS JULIANNE CHUNG AND ARVIND
SIAM J. SCI. COMPUT. Vol. 39, No. 5, pp. S24 S46 2017 Society for Industrial and Applied Mathematics GENERALIZED HYBRID ITERATIVE METHODS FOR LARGE-SCALE BAYESIAN INVERSE PROBLEMS JULIANNE CHUNG AND ARVIND
Research Article Some Generalizations and Modifications of Iterative Methods for Solving Large Sparse Symmetric Indefinite Linear Systems
 Abstract and Applied Analysis Article ID 237808 pages http://dxdoiorg/055/204/237808 Research Article Some Generalizations and Modifications of Iterative Methods for Solving Large Sparse Symmetric Indefinite
Abstract and Applied Analysis Article ID 237808 pages http://dxdoiorg/055/204/237808 Research Article Some Generalizations and Modifications of Iterative Methods for Solving Large Sparse Symmetric Indefinite
Dot product and linear least squares problems
 Dot product and linear least squares problems Dot Product For vectors u,v R n we define the dot product Note that we can also write this as u v = u,,u n u v = u v + + u n v n v v n = u v + + u n v n The
Dot product and linear least squares problems Dot Product For vectors u,v R n we define the dot product Note that we can also write this as u v = u,,u n u v = u v + + u n v n v v n = u v + + u n v n The
Some minimization problems
 Week 13: Wednesday, Nov 14 Some minimization problems Last time, we sketched the following two-step strategy for approximating the solution to linear systems via Krylov subspaces: 1. Build a sequence of
Week 13: Wednesday, Nov 14 Some minimization problems Last time, we sketched the following two-step strategy for approximating the solution to linear systems via Krylov subspaces: 1. Build a sequence of
REORTHOGONALIZATION FOR THE GOLUB KAHAN LANCZOS BIDIAGONAL REDUCTION: PART I SINGULAR VALUES
 REORTHOGONALIZATION FOR THE GOLUB KAHAN LANCZOS BIDIAGONAL REDUCTION: PART I SINGULAR VALUES JESSE L. BARLOW Department of Computer Science and Engineering, The Pennsylvania State University, University
REORTHOGONALIZATION FOR THE GOLUB KAHAN LANCZOS BIDIAGONAL REDUCTION: PART I SINGULAR VALUES JESSE L. BARLOW Department of Computer Science and Engineering, The Pennsylvania State University, University
Iterative Methods for Sparse Linear Systems
 Iterative Methods for Sparse Linear Systems Luca Bergamaschi e-mail: berga@dmsa.unipd.it - http://www.dmsa.unipd.it/ berga Department of Mathematical Methods and Models for Scientific Applications University
Iterative Methods for Sparse Linear Systems Luca Bergamaschi e-mail: berga@dmsa.unipd.it - http://www.dmsa.unipd.it/ berga Department of Mathematical Methods and Models for Scientific Applications University
Applied Mathematics 205. Unit V: Eigenvalue Problems. Lecturer: Dr. David Knezevic
 Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.4: Krylov Subspace Methods 2 / 51 Krylov Subspace Methods In this chapter we give
Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.4: Krylov Subspace Methods 2 / 51 Krylov Subspace Methods In this chapter we give
Conjugate gradient method. Descent method. Conjugate search direction. Conjugate Gradient Algorithm (294)
 Conjugate gradient method Descent method Hestenes, Stiefel 1952 For A N N SPD In exact arithmetic, solves in N steps In real arithmetic No guaranteed stopping Often converges in many fewer than N steps
Conjugate gradient method Descent method Hestenes, Stiefel 1952 For A N N SPD In exact arithmetic, solves in N steps In real arithmetic No guaranteed stopping Often converges in many fewer than N steps
5 Selected Topics in Numerical Linear Algebra
 5 Selected Topics in Numerical Linear Algebra In this chapter we will be concerned mostly with orthogonal factorizations of rectangular m n matrices A The section numbers in the notes do not align with
5 Selected Topics in Numerical Linear Algebra In this chapter we will be concerned mostly with orthogonal factorizations of rectangular m n matrices A The section numbers in the notes do not align with
Notes on Some Methods for Solving Linear Systems
 Notes on Some Methods for Solving Linear Systems Dianne P. O Leary, 1983 and 1999 and 2007 September 25, 2007 When the matrix A is symmetric and positive definite, we have a whole new class of algorithms
Notes on Some Methods for Solving Linear Systems Dianne P. O Leary, 1983 and 1999 and 2007 September 25, 2007 When the matrix A is symmetric and positive definite, we have a whole new class of algorithms
Lecture 9 Least Square Problems
 March 26, 2018 Lecture 9 Least Square Problems Consider the least square problem Ax b (β 1,,β n ) T, where A is an n m matrix The situation where b R(A) is of particular interest: often there is a vectors
March 26, 2018 Lecture 9 Least Square Problems Consider the least square problem Ax b (β 1,,β n ) T, where A is an n m matrix The situation where b R(A) is of particular interest: often there is a vectors
6.4 Krylov Subspaces and Conjugate Gradients
 6.4 Krylov Subspaces and Conjugate Gradients Our original equation is Ax = b. The preconditioned equation is P Ax = P b. When we write P, we never intend that an inverse will be explicitly computed. P
6.4 Krylov Subspaces and Conjugate Gradients Our original equation is Ax = b. The preconditioned equation is P Ax = P b. When we write P, we never intend that an inverse will be explicitly computed. P
Section 6.4. The Gram Schmidt Process
 Section 6.4 The Gram Schmidt Process Motivation The procedures in 6 start with an orthogonal basis {u, u,..., u m}. Find the B-coordinates of a vector x using dot products: x = m i= x u i u i u i u i Find
Section 6.4 The Gram Schmidt Process Motivation The procedures in 6 start with an orthogonal basis {u, u,..., u m}. Find the B-coordinates of a vector x using dot products: x = m i= x u i u i u i u i Find
PROJECTED GMRES AND ITS VARIANTS
 PROJECTED GMRES AND ITS VARIANTS Reinaldo Astudillo Brígida Molina rastudillo@kuaimare.ciens.ucv.ve bmolina@kuaimare.ciens.ucv.ve Centro de Cálculo Científico y Tecnológico (CCCT), Facultad de Ciencias,
PROJECTED GMRES AND ITS VARIANTS Reinaldo Astudillo Brígida Molina rastudillo@kuaimare.ciens.ucv.ve bmolina@kuaimare.ciens.ucv.ve Centro de Cálculo Científico y Tecnológico (CCCT), Facultad de Ciencias,
Bindel, Fall 2016 Matrix Computations (CS 6210) Notes for
 1 Arnoldi Notes for 2016-11-16 Krylov subspaces are good spaces for approximation schemes. But the power basis (i.e. the basis A j b for j = 0,..., k 1) is not good for numerical work. The vectors in the
1 Arnoldi Notes for 2016-11-16 Krylov subspaces are good spaces for approximation schemes. But the power basis (i.e. the basis A j b for j = 0,..., k 1) is not good for numerical work. The vectors in the
Orthogonalization and least squares methods
 Chapter 3 Orthogonalization and least squares methods 31 QR-factorization (QR-decomposition) 311 Householder transformation Definition 311 A complex m n-matrix R = [r ij is called an upper (lower) triangular
Chapter 3 Orthogonalization and least squares methods 31 QR-factorization (QR-decomposition) 311 Householder transformation Definition 311 A complex m n-matrix R = [r ij is called an upper (lower) triangular
Alternative correction equations in the Jacobi-Davidson method
 Chapter 2 Alternative correction equations in the Jacobi-Davidson method Menno Genseberger and Gerard Sleijpen Abstract The correction equation in the Jacobi-Davidson method is effective in a subspace
Chapter 2 Alternative correction equations in the Jacobi-Davidson method Menno Genseberger and Gerard Sleijpen Abstract The correction equation in the Jacobi-Davidson method is effective in a subspace
The parallel rational Arnoldi algorithm
 The parallel rational Arnoldi algorithm Mario Berljafa Stefan Güttel May 016 Contents 1 Introduction 1 Parallelization strategies 1 3 Basic usage 1 Near-optimal continuation strategy 3 5 Links to numerical
The parallel rational Arnoldi algorithm Mario Berljafa Stefan Güttel May 016 Contents 1 Introduction 1 Parallelization strategies 1 3 Basic usage 1 Near-optimal continuation strategy 3 5 Links to numerical
Non-stationary extremal eigenvalue approximations in iterative solutions of linear systems and estimators for relative error
 on-stationary extremal eigenvalue approximations in iterative solutions of linear systems and estimators for relative error Divya Anand Subba and Murugesan Venatapathi* Supercomputer Education and Research
on-stationary extremal eigenvalue approximations in iterative solutions of linear systems and estimators for relative error Divya Anand Subba and Murugesan Venatapathi* Supercomputer Education and Research
Topics. The CG Algorithm Algorithmic Options CG s Two Main Convergence Theorems
 Topics The CG Algorithm Algorithmic Options CG s Two Main Convergence Theorems What about non-spd systems? Methods requiring small history Methods requiring large history Summary of solvers 1 / 52 Conjugate
Topics The CG Algorithm Algorithmic Options CG s Two Main Convergence Theorems What about non-spd systems? Methods requiring small history Methods requiring large history Summary of solvers 1 / 52 Conjugate
Lecture 8 Fast Iterative Methods for linear systems of equations
 CGLS Select x 0 C n x = x 0, r = b Ax 0 u = 0, ρ = 1 while r 2 > tol do s = A r ρ = ρ, ρ = s s, β = ρ/ρ u s βu, c = Au σ = c c, α = ρ/σ r r αc x x+αu end while Graig s method Select x 0 C n x = x 0, r
CGLS Select x 0 C n x = x 0, r = b Ax 0 u = 0, ρ = 1 while r 2 > tol do s = A r ρ = ρ, ρ = s s, β = ρ/ρ u s βu, c = Au σ = c c, α = ρ/σ r r αc x x+αu end while Graig s method Select x 0 C n x = x 0, r
This manuscript is for review purposes only.
 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 8 9 30 31 3 33 34 35 36 37 38 39 40 41 4 A GOLUB-KAHAN DAVIDSON METHOD FOR ACCURATELY COMPUTING A FEW SINGULAR TRIPLETS OF LARGE SPARSE MATRICES
1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 8 9 30 31 3 33 34 35 36 37 38 39 40 41 4 A GOLUB-KAHAN DAVIDSON METHOD FOR ACCURATELY COMPUTING A FEW SINGULAR TRIPLETS OF LARGE SPARSE MATRICES
REORTHOGONALIZATION FOR GOLUB KAHAN LANCZOS BIDIAGONAL REDUCTION: PART II SINGULAR VECTORS
 REORTHOGONALIZATION FOR GOLUB KAHAN LANCZOS BIDIAGONAL REDUCTION: PART II SINGULAR VECTORS JESSE L. BARLOW Department of Computer Science and Engineering, The Pennsylvania State University, University
REORTHOGONALIZATION FOR GOLUB KAHAN LANCZOS BIDIAGONAL REDUCTION: PART II SINGULAR VECTORS JESSE L. BARLOW Department of Computer Science and Engineering, The Pennsylvania State University, University
Review of some mathematical tools
 MATHEMATICAL FOUNDATIONS OF SIGNAL PROCESSING Fall 2016 Benjamín Béjar Haro, Mihailo Kolundžija, Reza Parhizkar, Adam Scholefield Teaching assistants: Golnoosh Elhami, Hanjie Pan Review of some mathematical
MATHEMATICAL FOUNDATIONS OF SIGNAL PROCESSING Fall 2016 Benjamín Béjar Haro, Mihailo Kolundžija, Reza Parhizkar, Adam Scholefield Teaching assistants: Golnoosh Elhami, Hanjie Pan Review of some mathematical
Assignment #9: Orthogonal Projections, Gram-Schmidt, and Least Squares. Name:
 Assignment 9: Orthogonal Projections, Gram-Schmidt, and Least Squares Due date: Friday, April 0, 08 (:pm) Name: Section Number Assignment 9: Orthogonal Projections, Gram-Schmidt, and Least Squares Due
Assignment 9: Orthogonal Projections, Gram-Schmidt, and Least Squares Due date: Friday, April 0, 08 (:pm) Name: Section Number Assignment 9: Orthogonal Projections, Gram-Schmidt, and Least Squares Due
AMS526: Numerical Analysis I (Numerical Linear Algebra)
 AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 23: GMRES and Other Krylov Subspace Methods Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 9 Minimizing Residual CG
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 23: GMRES and Other Krylov Subspace Methods Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 9 Minimizing Residual CG
Linear Algebra- Final Exam Review
 Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Householder reflectors are matrices of the form. P = I 2ww T, where w is a unit vector (a vector of 2-norm unity)
 Householder QR Householder reflectors are matrices of the form P = I 2ww T, where w is a unit vector (a vector of 2-norm unity) w Px x Geometrically, P x represents a mirror image of x with respect to
Householder QR Householder reflectors are matrices of the form P = I 2ww T, where w is a unit vector (a vector of 2-norm unity) w Px x Geometrically, P x represents a mirror image of x with respect to
DS-GA 1002 Lecture notes 0 Fall Linear Algebra. These notes provide a review of basic concepts in linear algebra.
 DS-GA 1002 Lecture notes 0 Fall 2016 Linear Algebra These notes provide a review of basic concepts in linear algebra. 1 Vector spaces You are no doubt familiar with vectors in R 2 or R 3, i.e. [ ] 1.1
DS-GA 1002 Lecture notes 0 Fall 2016 Linear Algebra These notes provide a review of basic concepts in linear algebra. 1 Vector spaces You are no doubt familiar with vectors in R 2 or R 3, i.e. [ ] 1.1
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences)
 AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 1: Course Overview; Matrix Multiplication Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 1: Course Overview; Matrix Multiplication Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
Krylov subspace projection methods
 I.1.(a) Krylov subspace projection methods Orthogonal projection technique : framework Let A be an n n complex matrix and K be an m-dimensional subspace of C n. An orthogonal projection technique seeks
I.1.(a) Krylov subspace projection methods Orthogonal projection technique : framework Let A be an n n complex matrix and K be an m-dimensional subspace of C n. An orthogonal projection technique seeks
A Hybrid LSQR Regularization Parameter Estimation Algorithm for Large Scale Problems
 A Hybrid LSQR Regularization Parameter Estimation Algorithm for Large Scale Problems Rosemary Renaut Joint work with Jodi Mead and Iveta Hnetynkova SIAM Annual Meeting July 10, 2009 National Science Foundation:
A Hybrid LSQR Regularization Parameter Estimation Algorithm for Large Scale Problems Rosemary Renaut Joint work with Jodi Mead and Iveta Hnetynkova SIAM Annual Meeting July 10, 2009 National Science Foundation:
Solution of eigenvalue problems. Subspace iteration, The symmetric Lanczos algorithm. Harmonic Ritz values, Jacobi-Davidson s method
 Solution of eigenvalue problems Introduction motivation Projection methods for eigenvalue problems Subspace iteration, The symmetric Lanczos algorithm Nonsymmetric Lanczos procedure; Implicit restarts
Solution of eigenvalue problems Introduction motivation Projection methods for eigenvalue problems Subspace iteration, The symmetric Lanczos algorithm Nonsymmetric Lanczos procedure; Implicit restarts
5.) For each of the given sets of vectors, determine whether or not the set spans R 3. Give reasons for your answers.
 Linear Algebra - Test File - Spring Test # For problems - consider the following system of equations. x + y - z = x + y + 4z = x + y + 6z =.) Solve the system without using your calculator..) Find the
Linear Algebra - Test File - Spring Test # For problems - consider the following system of equations. x + y - z = x + y + 4z = x + y + 6z =.) Solve the system without using your calculator..) Find the
IDR(s) as a projection method
 Delft University of Technology Faculty of Electrical Engineering, Mathematics and Computer Science Delft Institute of Applied Mathematics IDR(s) as a projection method A thesis submitted to the Delft Institute
Delft University of Technology Faculty of Electrical Engineering, Mathematics and Computer Science Delft Institute of Applied Mathematics IDR(s) as a projection method A thesis submitted to the Delft Institute
The quadratic eigenvalue problem (QEP) is to find scalars λ and nonzero vectors u satisfying
 I.2 Quadratic Eigenvalue Problems 1 Introduction The quadratic eigenvalue problem QEP is to find scalars λ and nonzero vectors u satisfying where Qλx = 0, 1.1 Qλ = λ 2 M + λd + K, M, D and K are given
I.2 Quadratic Eigenvalue Problems 1 Introduction The quadratic eigenvalue problem QEP is to find scalars λ and nonzero vectors u satisfying where Qλx = 0, 1.1 Qλ = λ 2 M + λd + K, M, D and K are given
Linear least squares problem: Example
 Linear least squares problem: Example We want to determine n unknown parameters c,,c n using m measurements where m n Here always denotes the -norm v = (v + + v n) / Example problem Fit the experimental
Linear least squares problem: Example We want to determine n unknown parameters c,,c n using m measurements where m n Here always denotes the -norm v = (v + + v n) / Example problem Fit the experimental
The Conjugate Gradient Method
 The Conjugate Gradient Method Classical Iterations We have a problem, We assume that the matrix comes from a discretization of a PDE. The best and most popular model problem is, The matrix will be as large
The Conjugate Gradient Method Classical Iterations We have a problem, We assume that the matrix comes from a discretization of a PDE. The best and most popular model problem is, The matrix will be as large
Total least squares. Gérard MEURANT. October, 2008
 Total least squares Gérard MEURANT October, 2008 1 Introduction to total least squares 2 Approximation of the TLS secular equation 3 Numerical experiments Introduction to total least squares In least squares
Total least squares Gérard MEURANT October, 2008 1 Introduction to total least squares 2 Approximation of the TLS secular equation 3 Numerical experiments Introduction to total least squares In least squares
Large-scale eigenvalue problems
 ELE 538B: Mathematics of High-Dimensional Data Large-scale eigenvalue problems Yuxin Chen Princeton University, Fall 208 Outline Power method Lanczos algorithm Eigenvalue problems 4-2 Eigendecomposition
ELE 538B: Mathematics of High-Dimensional Data Large-scale eigenvalue problems Yuxin Chen Princeton University, Fall 208 Outline Power method Lanczos algorithm Eigenvalue problems 4-2 Eigendecomposition
