Multiple Imputation. Paul E. Johnson 1 2. Why Impute? Amelia mice mi aregimpute Making Sense out of All of This. 1 Department of Political Science
|
|
|
- Benjamin Boone
- 5 years ago
- Views:
Transcription
1 Multiple Imputation Paul E. Johnson Department of Political Science 2 Center for Research Methods and Data Analysis, University of Kansas 2013 Descriptive 1 / 96 K.U.
2 Overview Why Impute? Amelia mice mi aregimpute Descriptive 2 / 96 K.U.
3 Listwise Deletion In almost all software, listwise deletion has been the default. If any variable is missing, a case is completely dropped from the analysis. Most people seem to agree that is bad biased parameter estimates Until recently, practitioners ignored the problem. Research on this has been steadily accumulating since 1970s Statistical researchers are trying to find a more-or-less convenient, idiot proof procedure Descriptive 3 / 96 K.U.
4 Rubin proposed Multiple Imputation Jargon: MAR ( Missing at Random ) means that the chance of a missing score is predictable using information in other variables (and not predictable by other unmeasured forces) Rubin s proposal 1 Use many variables, including the dependent variable and variables not planned for inclusion in the final model, to predict missings 2 Create several Imputed data sets. 3 Run Each analysis on Each Imputed Dataset 4 Combine the estimates, weight them to take uncertainty into account. Descriptive 4 / 96 K.U.
5 Do You Do It Yourself? Rubin suggested the imputations could be done at a data center when they supply the dataset. MI would be done once and for all, and the imputed missings would be distributed as one collection. That approach was impractical for a number of reasons. Many routines to impute missing values have been proposed. This research area is still under active development Caution: I m not an MI authority (just a guy demonstrating some R packages) Descriptive 5 / 96 K.U.
6 What are we looking for? What format does a routine expect from our data? Are the imputations returned in a manageable format? Is it difficult to conduct the analysis on each separate dataset? How to best pool the estimates together and summarize them? Descriptive 6 / 96 K.U.
7 Points of Concern Calculation of imputation averaged results Good theory/method exists for MLE of slope coefficients. Rubin s Rules for slope & variance estimates For slope estimates, average the imputed, ˆβ = m i=1 ˆβ j Variance estimate for ˆβ combines 1 average of Var( ˆβ m j ), i=1 = Var( ˆβ j ), plus 2 1 a penalty for uncertainty between ˆβ j, 1+m ( ˆβ j ˆβ) 2. Less good theory/tools on other statistics (R 2, deviance, etc.) Difficult choices about openness and interoperability with other R functions Caution about terminology: imputation sometimes means The candidates to fill in for NAs A completed data frame with the NAs are replaced by the candidates Descriptive 7 / 96 K.U.
8 Amelia King, Gary, James Honaker, Anne Joseph, and Kenneth Scheve Analyzing Incomplete Political Science Data: An Alternative Algorithm for Multiple Imputation. The American Political Science Review 95(1): James Honaker, Gary King, Matthew Blackwell (2011). Amelia II: A Program for Missing Data. Journal of Statistical Software, 45(7), URL Descriptive 8 / 96 K.U.
9 Rough Sketch of Amelia Assume all variables are drawn from one Multivariate Normal Distribution, MVN(µ, Σ) Conduct series of complicated algorithms to estimate µ and Σ After estimating µ and Σ, then draw random samples from the MVN to fill in missing values Basic idea similar to Norm (J. Schafer), but algorithm may be faster (EM with importance sampling ) Descriptive 9 / 96 K.U.
10 Interface a m e l i a ( x, m = 5, p2s = 1, f r o n t e n d = FALSE, i d v a r s = NULL, t s = NULL, cs = NULL, p o l y t i m e = NULL, s p l i n e t i m e = NULL, i n t e r c s = FALSE, l a g s = NULL, l e a d s = NULL, s t a r t v a l s = 0, t o l e r a n c e = , l o g s = NULL, s q r t s = NULL, l g s t c = NULL, noms = NULL, o r d s = NULL, i n c h e c k = TRUE, c o l l e c t = FALSE, a r g l i s t = NULL, empri = NULL, p r i o r s = NULL, a u t o p r i = 0.05, emburn = c ( 0, 0 ), bounds = NULL, max.resample = 100,... ) Note: amelia uses all of the supplied variables in imputations except vars declared as idvars. To save memory, one should remove all extraneous variables first, rather than use the idvars feature to ask amelia to ignore them. Descriptive 10 / 96 K.U.
11 Surprising, Possibly True Most people say but my variables are not Normal. (gender, survey scales, etc) King (and others) argue the approximation is not harmful (various reasons) Amelia allows user to specify variables as nominal and ordinal Nominal variables: The normal imputations are rounded off to values in the observed scale {0,1,2} Ordinal variables: Optionally rounded off to integers, but instructions discourage that They suggest a 7 point scale might meaningfully have imputed values in-between the integers Descriptive 11 / 96 K.U.
12 Grab Some Data, Impose Some Missings Thanks to Chuck Cleland who suggested this example in r-help o p t i o n s ( d i g i t s =2) i f (! f i l e. e x i s t s ( examples ) ) d i r. c r e a t e ( examples ) i f (! f i l e. e x i s t s ( examples / t i t a n i c. t x t ) ) d o w n l o a d. f i l e ( h t t p : // l i b. s t a t. c m u. e d u /S/ H a r r e l l / data / a s c i i / t i t a n i c. t x t, examples / t i t a n i c. t x t ) t i t a n i c < r e a d. t a b l e ( examples / t i t a n i c. t x t, sep = ', ', header = TRUE) t i t a n i c 0 < t i t a n i c s a v e ( t i t a n i c 0, f i l e = examples / t i t a n i c 0. r d a ) s e t. s e e d (4321) t i t a n i c $ s e x [ sample ( nrow ( t i t a n i c ), 10) ] < NA t i t a n i c $ p c l a s s [ sample ( nrow ( t i t a n i c ), 10) ] < NA t i t a n i c $ s u r v i v e d [ sample ( nrow ( t i t a n i c ), 10) ] < NA Descriptive 12 / 96 K.U.
13 The Most Complete Version of the Data Says... f u l l g l m < glm ( s u r v i v e d p c l a s s + s e x + age, f a m i l y = b i n o m i a l, data = t i t a n i c 0 ) l i b r a r y ( x t a b l e ) t o u t < x t a b l e ( f u l l g l m ) p r i n t ( tout, type = l a t e x ) Estimate Std. Error z value Pr(> z ) (Intercept) pclass2nd pclass3rd sexmale age Descriptive 13 / 96 K.U.
14 After Imposing some more Missings, The ListWise Deletion Results ldglm < glm ( s u r v i v e d p c l a s s + s e x + age, = b i n o m i a l, data = t i t a n i c ) l i b r a r y ( x t a b l e ) t o u t < x t a b l e ( ldglm ) p r i n t ( tout, type = l a t e x ) f a m i l y Estimate Std. Error z value Pr(> z ) (Intercept) pclass2nd pclass3rd sexmale age Descriptive 14 / 96 K.U.
15 Use Amelia to create Imputed Data Sets l i b r a r y ( Amelia ) # generate multiple imputations t i t a n i c. a m e l i a < a m e l i a ( s u b s e t ( t i t a n i c, s e l e c t = c ( ' s u r v i v e d ', ' p c l a s s ', ' s e x ', ' age ', ' embarked ' ) ), m = 10, noms = c ( ' s u r v i v e d ', ' p c l a s s ', ' s e x ', ' embarked ' ), emburn = c (500, 500), p2s = F) p2s=f turns off screen output that overflows the presentation software Descriptive 15 / 96 K.U.
16 Note: Now use tools not from Amelia to Analyze the Data and Summarize it Lets try to use general purpose tools to estimate and summarize these models. The imputations are in an R list, so the general lapply function can be used to fit any kind of model that can accept a data frame as an argument. The R package mitools (Thomas Lumley) has tools to combine estimates of slopes and calcuate the Rubin-adjusted standard errors. Descriptive 16 / 96 K.U.
17 lapply Conducts the glm for Each Imputed Set a l l i m p l o g r e g < l a p p l y ( t i t a n i c. a m e l i a $ i m p u t a t i o n s, f u n c t i o n ( x ) { glm ( s u r v i v e d p c l a s s + s e x + age, f a m i l y = b i n o m i a l, data = x ) }) Descriptive 17 / 96 K.U.
18 Post Processing with mitools o p t i o n s ( d i g i t s =2) l i b r a r y ( m i t o o l s ) # MIextract b e t a s < M I e x t r a c t ( a l l i m p l o g r e g, fun = c o e f ) v a r s < M I e x t r a c t ( a l l i m p l o g r e g, fun = vcov ) summary ( MIcombine ( betas, v a r s ) ) M u l t i p l e i m p u t a t i o n r e s u l t s : M I c o m b i n e. d e f a u l t ( betas, v a r s ) r e s u l t s s e ( l o w e r upper ) m i s s I n f o ( I n t e r c e p t ) % p c l a s s 2 n d % p c l a s s 3 r d % s e x m a l e % age % Descriptive 18 / 96 K.U.
19 mi.inference from mix offers effective df and fm l i b r a r y ( mix ) s e. g l m < M I e x t r a c t ( a l l i m p l o g r e g, fun = f u n c t i o n ( x ) { s q r t ( d i a g ( vcov ( x ) ) ) }) a s. d a t a. f r a m e ( m i. i n f e r e n c e ( betas, s e. g l m ) ) e s t s t d. e r r d f s i g n i f l o w e r upper r f m i n f ( I n t e r c e p t ) e p c l a s s 2 n d e p c l a s s 3 r d e s e x m a l e e age e df: degrees of freedom associated with the t reference distribution used for interval estimates. r: estimated relative increases in variance due to nonresponse. fminf: estimated fractions of missing information. Descriptive 19 / 96 K.U.
20 Compare Side-by-Side: MI and LD results d f 1 < a s. d a t a. f r a m e ( m i. i n f e r e n c e ( betas, s e. g l m ) ) d f 2 < c b i n d ( d f 1 [, 1 : 2 ], l d b e t a = c o e f ( l d g l m ), l d s e = s q r t ( d i a g ( vcov ( l d g l m ) ) ) ) d f 2 e s t s t d. e r r l d b e t a l d s e ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d sexmale age Descriptive 20 / 96 K.U.
21 Make the Missings Worse! s e t. s e e d (234234) t i t a n i c < t i t a n i c 0 t i t a n i c $ s e x [ sample ( nrow ( t i t a n i c ), 400) ] < NA t i t a n i c $ p c l a s s [ sample ( nrow ( t i t a n i c ), 400) ] < NA t i t a n i c $ s u r v i v e d [ sample ( nrow ( t i t a n i c ), 400) ] < NA Then estimate new ldglm (listwise deletion estimate) 10 fresh imputed datasets and regressions for each Descriptive 21 / 96 K.U.
22 New Listwise Deletion Model ldglm ldglm < glm ( s u r v i v e d p c l a s s + s e x + age, =b i n o m i a l, data = t i t a n i c ) l i b r a r y ( x t a b l e ) t o u t < x t a b l e ( ldglm ) p r i n t ( tout, type = l a t e x ) f a m i l y Estimate Std. Error z value Pr(> z ) (Intercept) pclass2nd pclass3rd sexmale age Descriptive 22 / 96 K.U.
23 MI summary estimates summary ( MIcombine ( betas, v a r s ) ) M u l t i p l e i m p u t a t i o n r e s u l t s : M I c o m b i n e. d e f a u l t ( betas, v a r s ) r e s u l t s s e ( l o w e r upper ) m i s s I n f o ( I n t e r c e p t ) % p c l a s s 2 n d % p c l a s s 3 r d % sexmale % age % Descriptive 23 / 96 K.U.
24 Compare Side-by-Side: MI and LD results d f 2. 1 < a s. d a t a. f r a m e ( m i. i n f e r e n c e ( betas, s e. g l m ) ) d f 2. 2 < c b i n d ( MI, d f 2. 1 [, 1 : 2 ], LD, l d b e t a = c o e f ( l d g l m ), l d s e = s q r t ( d i a g ( vcov ( l d g l m ) ) ), f u l l, e s t = c o e f ( f u l l g l m ) ) d f 2. 2 MI e s t s t d. e r r LD l d b e t a l d s e f u l l e s t ( I n t e r c e p t ) MI LD f u l l p c l a s s 2 n d MI LD f u l l p c l a s s 3 r d MI LD f u l l sexmale MI LD f u l l age MI LD f u l l Descriptive 24 / 96 K.U.
25 Maybe confidence intervals help e s t l o w e r upper f u l l b e t a 2. 5 % % ( I n t e r c e p t ) f u l l p c l a s s 2 n d f u l l p c l a s s 3 r d f u l l sexmale f u l l age f u l l LDbeta 2. 5 % % ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d s e x m a l e age Descriptive 25 / 96 K.U.
26 Multiple Imputation via Chained Equations Stef van Buuren, Karin Groothuis-Oudshoorn (2011). MICE: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software, 45(3): Stef van Buuren (2012). Flexible Imputation of Missing Data. Boca Raton, FL: Chapman & Hall/CRC Press. Descriptive 26 / 96 K.U.
27 Rough Sketch Strategy quite different from Amelia and other MVN based theories MICE: separately process each column, predicting it from all the others. The algorithm imputes an incomplete column (the target column) by generating plausible synthetic values given other columns in the data. Cycle through columns over and over, until model converges (in MCMC sense), then draw samples to impute. Descriptive 27 / 96 K.U.
28 Recommends predictive mean matching to select imputed values When filling in missings, find cases with similar predicted values to the case in question From among those cases, collect their list of actual observed scores Draw imputations from that subset of actual scores Automatically solves the problem that imputations might have impossible values Imputations for categorical variables always match the original scale (sex is always 0 or 1, never 0.64) When a variable is badly skewed, the PMM always selects a realistic value. Descriptive 28 / 96 K.U.
29 The mice Interface mice ( data, m = 5, method = v e c t o r ( c h a r a c t e r, l e n g t h=n c o l ( data ) ), p r e d i c t o r M a t r i x = (1 d i a g ( 1, n c o l ( data ) ) ), v i s i t S e q u e n c e = ( 1 : n c o l ( data ) ) [ a p p l y ( i s. n a ( data ), 2, any ) ], p o s t = v e c t o r ( c h a r a c t e r, l e n g t h = n c o l ( data ) ), defaultmethod = c ( pmm, l o g r e g, p o l y r e g, p o l r ), maxit = 5, d i a g n o s t i c s = TRUE, p r i n t F l a g = TRUE, seed = NA,... ) Descriptive 29 / 96 K.U.
30 Special mice features fine grained management of imputation algorithms for different types of data Defaults: data type default also available numeric pmm (predictive mean matching) norm, 2level binary logreg (logistic regression) lda factor polyreg (Bayesian polytomous regression) factor: ordinal polr (prop. odds logistic (MASS)) Possible to add user-defined predictive tools control the sequence of column processing Descriptive 30 / 96 K.U.
31 Other Handy mice Features complete: function can return any of the individual imputed data frames return all data frames combined in the long format (rows stacked together) return all frames combined in the wide format (columns side-by-side) pool: outputs many of Rubin s suggested diagnostic formulae (param, var, R 2 ) summary(pool( )): distills parameter estimates Descriptive 31 / 96 K.U.
32 nhanes: small test data frame supplied with mice l i b r a r y ( mice ) nhanes age bmi hyp c h l 1 1 NA NA NA NA NA NA NA NA NA NA NA NA 11 1 NA NA NA 12 2 NA NA NA NA 16 1 NA NA NA NA 21 1 NA NA NA Descriptive 32 / 96 K.U.
33 nhanes: small test data frame supplied with mice NA Descriptive 33 / 96 K.U.
34 Test That Out imp < mice ( nhanes, p r i n t F l a g = FALSE) f i t < with ( data = imp, exp = lm ( bmi hyp + c h l ) ) f i t p o o l < p o o l ( f i t ) f i t p o o l C a l l : p o o l ( o b j e c t = f i t ) Pooled c o e f f i c i e n t s : ( I n t e r c e p t ) hyp c h l F r a c t i o n o f i n f o r m a t i o n about the c o e f f i c i e n t s m i s s i n g due to n o n r e s p o n s e : ( I n t e r c e p t ) hyp c h l Descriptive 34 / 96 K.U.
35 What s all that? Inside the outpute object from pool, there is a wealth of information that previous editions of mi did report automatically. That structure includes f i t < l i s t ( c a l l = c a l l, c a l l 1 = o b j e c t $ c a l l, c a l l 2 = o b j e c t $ c a l l 1, nmis = o b j e c t $ nmis, m = m, qhat = qhat, u = u, qbar = qbar, ubar = ubar, b = b, t = t, r = r, dfcom = dfcom, d f = df, fmi = fmi, lambda = lambda ) qhat: matrix of m complete data fits b: within imputation variance r: rel. incr var due to nonresponse t: total variance of pooled estimates qbar: pooled estimate u: Variance matrices from m fits (var var m) ubar: mean of variances across m fits dfcom: df in complete analysis gamma: prop. variance explained by imputations df: df for pooled estimates fmi: fraction missing information Descriptive 35 / 96 K.U.
36 summary of pooled fit round ( summary ( p o o l ( f i t ) ) [, c ( 1 : 4, 6 : 9 ) ], 2 ) e s t s e t d f l o 95 h i 95 nmis fmi ( I n t e r c e p t ) NA hyp c h l Descriptive 36 / 96 K.U.
37 It Gracefully Handles Factor Variables n h a n e s f < nhanes n h a n e s f $ age < f a c t o r ( n h a n e s f $ age, l a b e l s = c ( 20 39, 40 59, ) ) n h a n e s f $ hyp < f a c t o r ( n h a n e s f $hyp, l a b e l s = c ( no, y e s ) ) imp2 < mice ( nhanes, p r i n t F l a g = FALSE) f i t 2 < w i t h ( data = imp2, exp = lm ( bmi hyp+c h l ) ) p o o l ( f i t 2 ) C a l l : p o o l ( o b j e c t = f i t 2 ) Pooled c o e f f i c i e n t s : ( I n t e r c e p t ) hyp c h l F r a c t i o n o f i n f o r m a t i o n about t h e c o e f f i c i e n t s m i s s i n g due to nonresponse : ( I n t e r c e p t ) hyp c h l Descriptive 37 / 96 K.U.
38 Compare real and 2 imputed sets c b i n d ( F, nhanes, imp1, complete ( imp2, 3 ), imp2, complete ( imp, 3 ) ) F age bmi hyp c h l imp1 age bmi hyp c h l imp2 age bmi hyp c h l 1 F 1 NA NA NA imp imp F imp imp F 1 NA imp imp F 3 NA NA NA imp imp F imp imp F 3 NA NA 184 imp imp F imp imp F imp imp F imp imp F 2 NA NA NA imp imp F 1 NA NA NA imp imp F 2 NA NA NA imp imp F imp imp F imp imp F NA imp imp F 1 NA NA NA imp imp F imp imp F imp imp F imp imp F NA imp imp F 1 NA NA NA imp imp F imp imp Descriptive 38 / 96 K.U.
39 Compare real and 2 imputed sets F imp imp F NA imp imp F imp imp Descriptive 39 / 96 K.U.
40 How About the Titanic Data? l o a d ( /home/ p a u l j o h n /SVN/SVN guides/ Rcourse / DataSets / t i t a n i c 0. r d a ) s e t. s e e d (234234) t i t a n i c < t i t a n i c 0 t i t a n i c $ s e x [ sample ( nrow ( t i t a n i c ), 400) ] < NA t i t a n i c $ p c l a s s [ sample ( nrow ( t i t a n i c ), 400) ] < NA t i t a n i c $ s u r v i v e d [ sample ( nrow ( t i t a n i c ), 400) ] < NA m i c e T i t a n i c < mice ( s u b s e t ( t i t a n i c, s e l e c t = c ( ' s u r v i v e d ', ' p c l a s s ', ' s e x ', ' age ', ' embarked ' ) ), m = 10, maxit = 10, p r i n t F l a g=false) m i c e F i t T i t a n i c < w i t h ( data = m i c e T i t a n i c, exp = glm ( s u r v i v e d p c l a s s + s e x + age, f a m i l y = b i n o m i a l ) ) p o o l ( m i c e F i t T i t a n i c ) C a l l : p o o l ( o b j e c t = m i c e F i t T i t a n i c ) Pooled c o e f f i c i e n t s : ( I n t e r c e p t ) p c l a s s 2 p c l a s s 3 s e x 2 age F r a c t i o n o f i n f o r m a t i o n about t h e c o e f f i c i e n t s m i s s i n g due to nonresponse : ( I n t e r c e p t ) p c l a s s 2 p c l a s s 3 s e x 2 age Here s the error you see if you forget to subset the variables with select Descriptive 40 / 96 K.U.
41 How About the Titanic Data?... E r r o r : chunk 7 ( l a b e l=mice70 ) E r r o r i n n n e t. d e f a u l t (X, Y, w, mask = mask, s i z e = 0, s k i p = TRUE, softmax = TRUE, : too many ( 3210) w e i g h t s E x e c u t i o n h a l t e d Descriptive 41 / 96 K.U.
42 summary of pooled fit round ( summary ( p o o l ( m i c e F i t T i t a n i c ) ), 2) e s t s e t d f Pr ( > t ) l o 95 h i 95 nmis fmi lambda ( I n t e r c e p t ) NA p c l a s s NA p c l a s s NA s e x NA age Descriptive 42 / 96 K.U.
43 The mi Package (Gelman s Columbia U Team) Yu-Sung Su, Andrew Gelman, Jennifer Hill, Masanao Yajima Multiple Imputation with Diagnostics (mi) in R: Opening Windows into the Black Box. Journal of Statistical Software. 45(2) Kobi Abayomi, Andrew Gelman and Marc Levy. (2008). Diagnostics for multivariate imputations. Applied Statistics 57, Part 3: Generate a multiply imputed matrix applying the elementary functions iteratively to the variables with missingness in the data randomly imputing each variable and looping through until approximate convergence. Descriptive 43 / 96 K.U.
44 Rough Sketch Strategy similar to mice and aregimpute: proceed one-variable-at-a-time Predict each variable from each of the others Start with median/mode for NAs Conduct n.iter iterations, or until convergence Provides a large set of mi.xxx functions to impute variables of different types Draw bootstrap sample to create imputed values Allows limited preprocessing of numeric variables (similar idea to aregimpute s use of avas) As Opening Windows into the Black Box implies, this is intended to be less mysterious, more informative, and easier to diagnose MI processes. Descriptive 44 / 96 K.U.
45 Type-Dependent Imputation Methods type mi name model binary mi.binary logistic unordered mi.categorical multinomial ordinal mi.polr continuation logistic continuous mi.continous regression count mi.count Bayesian Poisson (w overdispersion) Descriptive 45 / 96 K.U.
46 Interface mi ( o b j e c t, i n f o, n.imp = 3, n. i t e r = 30, R.hat = 1.1, max.minutes = 20, rand.imp.method= b o o t s t r a p, r u n. p a s t. c o n v e r g e n c e = FALSE, seed = NA, c h e c k. c o e f. c o n v e r g e n c e = FALSE, a d d. n o i s e = n o i s e. c o n t r o l ( ) ) Descriptive 46 / 96 K.U.
47 Steps to Use mi 1 Create an information table 2 Use mi to create imputations Runs 1 separate chain for each desired imputation 3 pooling methods implemented for common R estimators like lm.mi, glm.mi, lmer.mi These cycle through all imputed data frames create estimates for each 4 display or other extractor methods can present results Descriptive 47 / 96 K.U.
48 Information Table for nhanes data with factor variables in it i n f < m i. i n f o ( nhanes2 ) i n f names i n c l u d e o r d e r number.mis a l l. m i s type c o l l i n e a r 1 age Yes NA 0 No u n o r d e r e d c a t e g o r i c a l No 2 bmi Yes 1 9 No p o s i t i v e c o n t i n u o u s No 3 hyp Yes 2 8 No b i n a r y No 4 c h l Yes 3 10 No p o s i t i v e c o n t i n u o u s No Can customize variable types at this stage Descriptive 48 / 96 K.U.
49 Run mi Caution: runtime errors were observed with n.imp = 10, only 8 will succeed. miimputenhanes2 < mi ( nhanes2, i n f o = i n f, n.imp = 8, n. i t e r = 500, a d d. n o i s e = FALSE) Descriptive 49 / 96 K.U.
50 Regression: mi Summary for 10 Imputations M1 < lm.mi ( bmi hyp + chl, miimputenhanes2 ) d i s p l a y (M1) ======================================= Separate E s tim ate s f o r each Imputation ======================================= ** Chain 1 ** lm ( f o r m u l a = formula, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) hypyes c h l n = 25, k = 3 r e s i d u a l sd = 4.72, R Squared = ** Chain 2 ** lm ( f o r m u l a = formula, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) hypyes c h l n = 25, k = 3 Descriptive 50 / 96 K.U.
51 Regression: mi Summary for 10 Imputations... r e s i d u a l sd = 5.18, R Squared = ** Chain 3 ** lm ( f o r m u l a = formula, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) hypyes c h l n = 25, k = 3 r e s i d u a l sd = 4.79, R Squared = ** Chain 4 ** lm ( f o r m u l a = formula, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) hypyes c h l n = 25, k = 3 r e s i d u a l sd = 4.26, R Squared = ** Chain 5 ** lm ( f o r m u l a = formula, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) Descriptive 51 / 96 K.U.
52 Regression: mi Summary for 10 Imputations... hypyes c h l n = 25, k = 3 r e s i d u a l sd = 4.40, R Squared = ** Chain 6 ** lm ( f o r m u l a = formula, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) hypyes c h l n = 25, k = 3 r e s i d u a l sd = 4.96, R Squared = ** Chain 7 ** lm ( f o r m u l a = formula, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) hypyes c h l n = 25, k = 3 r e s i d u a l sd = 4.09, R Squared = Descriptive 52 / 96 K.U.
53 Regression: mi Summary for 10 Imputations... ** Chain 8 ** lm ( f o r m u l a = formula, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) hypyes c h l n = 25, k = 3 r e s i d u a l sd = 6.24, R Squared = ======================================= Pooled E s t i m a t e s ======================================= lm.mi ( f o r m u l a = bmi hyp + c h l, m i. o b j e c t = miimputenhanes2 ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) hypyes c h l c b i n d ( b=c o e f (M1), s e=s e. c o e f (M1), t=c o e f (M1) / s e. c o e f (M1) ) Descriptive 53 / 96 K.U.
54 Regression: mi Summary for 10 Imputations... b s e t ( I n t e r c e p t ) hypyes c h l Descriptive 54 / 96 K.U.
55 Titanic, Featuring Kate Winslet and Leonardo DiCaprio l o a d ( /home/ p a u l j o h n /SVN/SVN guides/ Rcourse / DataSets / t i t a n i c 0. r d a ) s e t. s e e d (234234) t i t a n i c < t i t a n i c 0 t i t a n i c $ s e x [ sample ( nrow ( t i t a n i c ), 400) ] < NA t i t a n i c $ p c l a s s [ sample ( nrow ( t i t a n i c ), 400) ] < NA t i t a n i c $ s u r v i v e d [ sample ( nrow ( t i t a n i c ), 400) ] < NA Descriptive 55 / 96 K.U.
56 Grab Subset, then compute min.info (prepare for imputation) Subset required to avoid use of extraneous variables by imputer. Can customize inf to change variable types, if desired. Note, mi did not converge with embarked included as predictor, so it was omitted here s s < s u b s e t ( t i t a n i c, s e l e c t = c ( ' s u r v i v e d ', ' p c l a s s ', ' s e x ', ' age ' ) ) i n f < m i. i n f o ( s s ) i n f names i n c l u d e o r d e r number.mis a l l. m i s t y p e c o l l i n e a r 1 s u r v i v e d Yes No b i n a r y No 2 p c l a s s Yes No u n o r d e r e d c a t e g o r i c a l No 3 s e x Yes No b i n a r y No 4 age Yes No p o s i t i v e c o n t i n u o u s No Descriptive 56 / 96 K.U.
57 Create 10 Titanics m i I m p T i t a n i c < mi ( ss, i n f o = i n f, n.imp = 10, n. i t e r = 400, a d d. n o i s e = FALSE) n.iter set higher, convergence can take more than 100 iterations Descriptive 57 / 96 K.U.
58 Use glm.mi from mi on the List of Imputed Datasets M2 < glm.mi ( s u r v i v e d p c l a s s + s e x + age, miimptitanic, f a m i l y = b i n o m i a l ( l i n k = l o g i t ) ) d i s p l a y (M2) ======================================= Separate E s tim ate s f o r each Imputation ======================================= ** Chain 1 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = , n u l l d e v i a n c e = ( d i f f e r e n c e = ) ** Chain 2 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) Descriptive 58 / 96 K.U.
59 Use glm.mi from mi on the List of Imputed Datasets... p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = 929.3, n u l l d e v i a n c e = ( d i f f e r e n c e = ) ** Chain 3 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = , n u l l d e v i a n c e = ( d i f f e r e n c e = ) ** Chain 4 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) Descriptive 59 / 96 K.U.
60 Use glm.mi from mi on the List of Imputed Datasets... p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = 967.6, n u l l d e v i a n c e = ( d i f f e r e n c e = ) ** Chain 5 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = , n u l l d e v i a n c e = ( d i f f e r e n c e = ) ** Chain 6 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) Descriptive 60 / 96 K.U.
61 Use glm.mi from mi on the List of Imputed Datasets... p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = 937.2, n u l l d e v i a n c e = ( d i f f e r e n c e = ) ** Chain 7 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = , n u l l d e v i a n c e = ( d i f f e r e n c e = ) ** Chain 8 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) Descriptive 61 / 96 K.U.
62 Use glm.mi from mi on the List of Imputed Datasets... p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = , n u l l d e v i a n c e = ( d i f f e r e n c e = ) ** Chain 9 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = 918.0, n u l l d e v i a n c e = ( d i f f e r e n c e = ) ** Chain 10 ** glm ( f o r m u l a = formula, f a m i l y = f a m i l y, data = m i. d a t a [ [ i ] ] ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) Descriptive 62 / 96 K.U.
63 Use glm.mi from mi on the List of Imputed Datasets... p c l a s s 2 n d p c l a s s 3 r d sexmale age n = 1313, k = 5 r e s i d u a l d e v i a n c e = , n u l l d e v i a n c e = ( d i f f e r e n c e = ) ======================================= Pooled E s t i m a t e s ======================================= glm.mi ( f o r m u l a = s u r v i v e d p c l a s s + s e x + age, m i. o b j e c t = miimptitanic, f a m i l y = b i n o m i a l ( l i n k = l o g i t ) ) c o e f. e s t c o e f. s e ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d sexmale age Descriptive 63 / 96 K.U.
64 ( m i T i t a n i c R e s u l t < c b i n d ( b = c o e f (M2), s e = s e. c o e f (M2), t = c o e f ( M2) / s e. c o e f (M2) ) ) b s e t ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d sexmale age Descriptive 64 / 96 K.U.
65 The Hmisc & rms Packages Harrell, Frank E Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. Springer. Frank E Harrell Jr (2013). rms: Regression Modeling Strategies. R package version aregimpute takes all aspects of uncertainty in the imputations into account by using the bootstrap to approximate the process of drawing predicted values from a full Bayesian predictive distribution. Different bootstrap resamples are used for each of the multiple imputations, i.e., for the i th imputation of a sometimes missing variable, i=1,2,... n.impute, a flexible additive model is fitted on a sample with replacement from the original data and this model is used to predict all of the original missing and non-missing values for the target variable. Descriptive 65 / 96 K.U.
66 Rough Sketch Predict each variable from each of the others Start with random selections for NAs Do this burnin + n.impute times Draw bootstrap sample, fit a flexible model to it, predict outcomes for all cases from that model. Default uses predictive mean matching to select an imputed value for each NA. (regression extrapolation is alternative) Note: Special emphasis on nonlinearity in imputation fitting (similar to avas) Descriptive 66 / 96 K.U.
67 What s Avas? From:Squeeze and Stretch Variables To: Estimate, Convert Back Gross Domestic Product Infant Mortality (per 1000 live births) avas transformed x avas transformed y Descriptive 67 / 96 K.U.
68 Interface aregimpute ( formula, data, subset, n. i m pute = 5, group = NULL, nk = 3, t l i n e a r = TRUE, type = c ( 'pmm ', ' r e g r e s s i o n ' ), match = c ( ' weighted ', ' c l o s e s t ' ), f w e i g h t e d = 0.2, c u r t a i l = TRUE, boot.method = c ( ' s i m p l e ', ' approximate b a y e s i a n ' ), b u r n i n = 3, x = FALSE, pr = TRUE, p l o t T r a n s = FALSE, t o l e r a n c e = NULL, B = 75) Descriptive 68 / 96 K.U.
69 Important Detail about rms Prof. Harrell is a long-standing, highly distinguished programmer and statistician (SAS PROC Logistic in mid 1980s) He has developed his own set of fitting functions in S over 2 decades and they are not perfectly interchangeable with R functions rms ols is not exactly same as R s lm rms lrm is not exactly same as R s glm(y x, family=binomial(link= logit )) aregimpute and other rms functions are tailored for rms fitting routines, but tolerate some R routines (with warnings). Summary and Plotting functions for rms objects are usually expecting different options than functions in base R Descriptive 69 / 96 K.U.
70 Syntax Example [ 1 ] f < aregimpute ( age + bmi + hyp + chl, data= nhanesf, nk=0) Can t actually run that, though, because of this error (which I have not solved) E r r o r i n aregimpute ( age + bmi + hyp + chl, data = nhanesf, nk = 0) : a b o o t s t r a p r e s a m p l e had too few unique v a l u e s o f the f o l l o w i n g v a r i a b l e s : age E x e c u t i o n h a l t e d Warning i n aregimpute ( age + bmi + hyp + chl, data = nhanesf, nk = 1) : hyp has the f o l l o w i n g l e v e l s with < 5 o b s e r v a t i o n s : y e s C o n s i d e r u s i n g the group parameter to b a l a n c e b o o t s t r a p samples Descriptive 70 / 96 K.U.
71 If that did work, we would run fit.mult.impute fmi < f i t. m u l t. i m p u t e ( bmi hyp + chl, lm, f, data = n h a n e s f ) s q r t ( d i a g ( vcov ( fmi ) ) ) Even if aregimpute did create imputations, it would be accompanied by this warning Warning i n f i t. m u l t. i m p u t e ( bmi hyp + chl, lm, f, data = n h a n e s f ) : Not u s i n g a Design f i t t i n g f u n c t i o n ; summary ( f i t ) w i l l use s t a n d a r d e r r o r s, t, P from l a s t i m p u t a t i o n o n l y. Use vcov ( f i t ) to get the c o r r e c t c o v a r i a n c e matrix, s q r t ( d i a g ( vcov ( f i t ) ) ) to get s. e. Caused by my use of R s lm, rather than rms s own function ols Descriptive 71 / 96 K.U.
72 The Titanic Rises Again l o a d ( /home/ p a u l j o h n /SVN/SVN guides/ Rcourse / DataSets / t i t a n i c 0. r d a ) s e t. s e e d (234234) t i t a n i c < t i t a n i c 0 t i t a n i c $ s e x [ sample ( nrow ( t i t a n i c ), 400) ] < NA t i t a n i c $ p c l a s s [ sample ( nrow ( t i t a n i c ), 400) ] < NA t i t a n i c $ s u r v i v e d [ sample ( nrow ( t i t a n i c ), 400) ] < NA r m s I m p u t e T i t a n i c < a r e g I m p u t e ( s u r v i v e d + p c l a s s + s e x + age + embarked, n. i m p u t e =10, data=t i t a n i c, nk=3) I t e r a t i o n 1 I t e r a t i o n 2 I t e r a t i o n 3 I t e r a t i o n 4 I t e r a t i o n 5 I t e r a t i o n 6 I t e r a t i o n 7 I t e r a t i o n 8 I t e r a t i o n 9 I t e r a t i o n 10 I t e r a t i o n 11 I t e r a t i o n 12 I t e r a t i o n 13 Descriptive 72 / 96 K.U.
73 Use glm in fit.mult.impute r m s F m i T i t a n i c < f i t. m u l t. i m p u t e ( s u r v i v e d p c l a s s + s e x + age, glm, f a m i l y=b i n o m i a l ( l i n k=l o g i t ), r m s I m p u t e T i t a n i c, data= t i t a n i c, f i t. r e p s =TRUE) V a r i a n c e I n f l a t i o n F a c t o r s Due to I m p u t a t i o n : ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d s e x m a l e age Rate o f M i s s i n g I n f o r m a t i o n : ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d s e x m a l e age d. f. f o r t d i s t r i b u t i o n f o r T e s t s o f S i n g l e C o e f f i c i e n t s : ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d s e x m a l e age The f o l l o w i n g f i t components were a v e r a g e d o v e r t h e 10 model f i t s : f i t t e d. v a l u e s l i n e a r. p r e d i c t o r s summary ( r m s F m i T i t a n i c ) Descriptive 73 / 96 K.U.
74 Use glm in fit.mult.impute... C a l l : f i t t e r ( f o r m u l a = formula, f a m i l y =.. 1, data = c o m p l e t e d. d a t a ) Deviance R e s i d u a l s : Min 1Q Median 3Q Max C o e f f i c i e n t s : E s t i m a t e S t d. E r r o r z v a l u e Pr ( > z ) ( I n t e r c e p t ) < 2e 16 *** p c l a s s 2 n d e 11 *** p c l a s s 3 r d < 2e 16 *** sexmale < 2e 16 *** age < 2e 16 *** S i g n i f. c o des : 0 ' *** ' ' ** ' ' * ' '. ' 0. 1 ' ' 1 ( D i s p e r s i o n p a r a m e t e r f o r b i n o m i a l f a m i l y taken to be 1) N u l l d e v i a n c e : on 1312 d e g r e e s o f freedom R e s i d u a l d e v i a n c e : on 1308 d e g r e e s o f freedom AIC : 1159 Number o f F i s h e r S c o r i n g i t e r a t i o n s : 5 Descriptive 74 / 96 K.U.
75 Recall the Cautionary Warning about Fitting Functions? fit.mult.impute warns the user that when a fitting routine is not from rms, then the standard errors and significance tests are based only on the last fitted model One should instead extract the standard errors from the covariance matrix Which I do on the next slide Descriptive 75 / 96 K.U.
76 Create a Homemade Summary for the Fit.Mult.Impute Output s q r t ( d i a g ( vcov ( r m s F m i T i t a n i c ) ) ) ( I n t e r c e p t ) p c l a s s 2 n d p c l a s s 3 r d s e x m a l e age ( r m s T i t a n i c R e s u l t < c b i n d ( b=r m s F m i T i t a n i c $ c o e f f i c i e n t s, s e=d i a g ( vcov ( r m s F m i T i t a n i c ) ) ) ) b s e ( I n t e r c e p t ) e 02 p c l a s s 2 n d e 02 p c l a s s 3 r d e 02 s e x m a l e e 02 age e 05 Descriptive 76 / 96 K.U.
77 Here s a Problem: I don t believe the se result. Compare mitools r e q u i r e ( m i t o o l s ) r m s b e t a s < M I e x t r a c t ( r m s F m i T i t a n i c $ f i t s, fun=c o e f ) r m s v a r s < M I e x t r a c t ( r m s F m i T i t a n i c $ f i t s, fun=vcov ) r m s T i t a n i c M I t o o l s < summary ( MIcombine ( rmsbetas, r m s v a r s ) ) M u l t i p l e i m p u t a t i o n r e s u l t s : M I c o m b i n e. d e f a u l t ( rmsbetas, r m s v a r s ) r e s u l t s s e ( l o w e r upper ) m i s s I n f o ( I n t e r c e p t ) % p c l a s s 2 n d % p c l a s s 3 r d % sexmale % age % Descriptive 77 / 96 K.U.
78 Notice the fit.reps=t option? It allows inspection of each fitted model f o r ( i i n 1 : l e n g t h ( r m s F m i T i t a n i c $ f i t s ) ) p r i n t ( summary ( r m s F m i T i t a n i c $ f i t s [ [ i ] ] ) ) C a l l : f i t t e r ( f o r m u l a = formula, f a m i l y =.. 1, data = c o m p l e t e d. d a t a ) Deviance R e s i d u a l s : Min 1Q Median 3Q Max C o e f f i c i e n t s : E s t i m a t e S t d. E r r o r z v a l u e Pr ( > z ) ( I n t e r c e p t ) < 2e 16 *** p c l a s s 2 n d e 09 *** p c l a s s 3 r d < 2e 16 *** sexmale < 2e 16 *** age < 2e 16 *** S i g n i f. c o des : 0 ' *** ' ' ** ' ' * ' '. ' 0. 1 ' ' 1 ( D i s p e r s i o n p a r a m e t e r f o r b i n o m i a l f a m i l y taken to be 1) N u l l d e v i a n c e : on 1312 d e g r e e s o f freedom Descriptive 78 / 96 K.U.
79 Notice the fit.reps=t option? It allows inspection of each fitted model... R e s i d u a l d e v i a n c e : on 1308 d e g r e e s o f freedom AIC : 1159 Number o f F i s h e r S c o r i n g i t e r a t i o n s : 5 C a l l : f i t t e r ( f o r m u l a = formula, f a m i l y =.. 1, data = c o m p l e t e d. d a t a ) Deviance R e s i d u a l s : Min 1Q Median 3Q Max C o e f f i c i e n t s : E s t i m a t e S t d. E r r o r z v a l u e Pr ( > z ) ( I n t e r c e p t ) < 2e 16 *** p c l a s s 2 n d e 15 *** p c l a s s 3 r d < 2e 16 *** sexmale < 2e 16 *** age < 2e 16 *** S i g n i f. c o des : 0 ' *** ' ' ** ' ' * ' '. ' 0. 1 ' ' 1 ( D i s p e r s i o n p a r a m e t e r f o r b i n o m i a l f a m i l y taken to be 1) Descriptive 79 / 96 K.U.
80 Notice the fit.reps=t option? It allows inspection of each fitted model... N u l l d e v i a n c e : on 1312 d e g r e e s o f freedom R e s i d u a l d e v i a n c e : on 1308 d e g r e e s o f freedom AIC : 1113 Number o f F i s h e r S c o r i n g i t e r a t i o n s : 5 C a l l : f i t t e r ( f o r m u l a = formula, f a m i l y =.. 1, data = c o m p l e t e d. d a t a ) Deviance R e s i d u a l s : Min 1Q Median 3Q Max C o e f f i c i e n t s : E s t i m a t e S t d. E r r o r z v a l u e Pr ( > z ) ( I n t e r c e p t ) < 2e 16 *** p c l a s s 2 n d e 13 *** p c l a s s 3 r d < 2e 16 *** sexmale < 2e 16 *** age < 2e 16 *** S i g n i f. c o des : 0 ' *** ' ' ** ' ' * ' '. ' 0. 1 ' ' 1 Descriptive 80 / 96 K.U.
81 Notice the fit.reps=t option? It allows inspection of each fitted model... ( D i s p e r s i o n p a r a m e t e r f o r b i n o m i a l f a m i l y taken to be 1) N u l l d e v i a n c e : on 1312 d e g r e e s o f freedom R e s i d u a l d e v i a n c e : on 1308 d e g r e e s o f freedom AIC : 1060 Number o f F i s h e r S c o r i n g i t e r a t i o n s : 5 C a l l : f i t t e r ( f o r m u l a = formula, f a m i l y =.. 1, data = c o m p l e t e d. d a t a ) Deviance R e s i d u a l s : Min 1Q Median 3Q Max C o e f f i c i e n t s : E s t i m a t e S t d. E r r o r z v a l u e Pr ( > z ) ( I n t e r c e p t ) < 2e 16 *** p c l a s s 2 n d e 11 *** p c l a s s 3 r d < 2e 16 *** sexmale < 2e 16 *** age < 2e 16 *** Descriptive 81 / 96 K.U.
82 Notice the fit.reps=t option? It allows inspection of each fitted model... S i g n i f. c o des : 0 ' *** ' ' ** ' ' * ' '. ' 0. 1 ' ' 1 ( D i s p e r s i o n p a r a m e t e r f o r b i n o m i a l f a m i l y taken to be 1) N u l l d e v i a n c e : on 1312 d e g r e e s o f freedom R e s i d u a l d e v i a n c e : on 1308 d e g r e e s o f freedom AIC : 1119 Number o f F i s h e r S c o r i n g i t e r a t i o n s : 5 C a l l : f i t t e r ( f o r m u l a = formula, f a m i l y =.. 1, data = c o m p l e t e d. d a t a ) Deviance R e s i d u a l s : Min 1Q Median 3Q Max C o e f f i c i e n t s : E s t i m a t e S t d. E r r o r z v a l u e Pr ( > z ) ( I n t e r c e p t ) <2e 16 *** p c l a s s 2 n d e 12 *** p c l a s s 3 r d <2e 16 *** Descriptive 82 / 96 K.U.
83 Notice the fit.reps=t option? It allows inspection of each fitted model... sexmale <2e 16 *** age <2e 16 *** S i g n i f. c o des : 0 ' *** ' ' ** ' ' * ' '. ' 0. 1 ' ' 1 ( D i s p e r s i o n p a r a m e t e r f o r b i n o m i a l f a m i l y taken to be 1) N u l l d e v i a n c e : on 1312 d e g r e e s o f freedom R e s i d u a l d e v i a n c e : on 1308 d e g r e e s o f freedom AIC : 1130 Number o f F i s h e r S c o r i n g i t e r a t i o n s : 5 C a l l : f i t t e r ( f o r m u l a = formula, f a m i l y =.. 1, data = c o m p l e t e d. d a t a ) Deviance R e s i d u a l s : Min 1Q Median 3Q Max C o e f f i c i e n t s : E s t i m a t e S t d. E r r o r z v a l u e Pr ( > z ) ( I n t e r c e p t ) < 2e 16 *** Descriptive 83 / 96 K.U.
84 Notice the fit.reps=t option? It allows inspection of each fitted model... p c l a s s 2 n d e 10 *** p c l a s s 3 r d < 2e 16 *** sexmale < 2e 16 *** age < 2e 16 *** S i g n i f. c o des : 0 ' *** ' ' ** ' ' * ' '. ' 0. 1 ' ' 1 ( D i s p e r s i o n p a r a m e t e r f o r b i n o m i a l f a m i l y taken to be 1) N u l l d e v i a n c e : on 1312 d e g r e e s o f freedom R e s i d u a l d e v i a n c e : on 1308 d e g r e e s o f freedom AIC : 1182 Number o f F i s h e r S c o r i n g i t e r a t i o n s : 5 C a l l : f i t t e r ( f o r m u l a = formula, f a m i l y =.. 1, data = c o m p l e t e d. d a t a ) Deviance R e s i d u a l s : Min 1Q Median 3Q Max C o e f f i c i e n t s : Descriptive 84 / 96 K.U.
85 Notice the fit.reps=t option? It allows inspection of each fitted model... E s t i m a t e S t d. E r r o r z v a l u e Pr ( > z ) ( I n t e r c e p t ) < 2e 16 *** p c l a s s 2 n d e 09 *** p c l a s s 3 r d < 2e 16 *** sexmale < 2e 16 *** age < 2e 16 *** S i g n i f. c o des : 0 ' *** ' ' ** ' ' * ' '. ' 0. 1 ' ' 1 ( D i s p e r s i o n p a r a m e t e r f o r b i n o m i a l f a m i l y taken to be 1) N u l l d e v i a n c e : on 1312 d e g r e e s o f freedom R e s i d u a l d e v i a n c e : on 1308 d e g r e e s o f freedom AIC : 1110 Number o f F i s h e r S c o r i n g i t e r a t i o n s : 5 C a l l : f i t t e r ( f o r m u l a = formula, f a m i l y =.. 1, data = c o m p l e t e d. d a t a ) Deviance R e s i d u a l s : Min 1Q Median 3Q Max Descriptive 85 / 96 K.U.
The mice package. Stef van Buuren 1,2. amst-r-dam, Oct. 29, TNO, Leiden. 2 Methodology and Statistics, FSBS, Utrecht University
 The mice package 1,2 1 TNO, Leiden 2 Methodology and Statistics, FSBS, Utrecht University amst-r-dam, Oct. 29, 2012 > The problem of missing data Consequences of missing data Less information than planned
The mice package 1,2 1 TNO, Leiden 2 Methodology and Statistics, FSBS, Utrecht University amst-r-dam, Oct. 29, 2012 > The problem of missing data Consequences of missing data Less information than planned
Statistical Methods. Missing Data snijders/sm.htm. Tom A.B. Snijders. November, University of Oxford 1 / 23
 1 / 23 Statistical Methods Missing Data http://www.stats.ox.ac.uk/ snijders/sm.htm Tom A.B. Snijders University of Oxford November, 2011 2 / 23 Literature: Joseph L. Schafer and John W. Graham, Missing
1 / 23 Statistical Methods Missing Data http://www.stats.ox.ac.uk/ snijders/sm.htm Tom A.B. Snijders University of Oxford November, 2011 2 / 23 Literature: Joseph L. Schafer and John W. Graham, Missing
Missing Data and Multiple Imputation
 Maximum Likelihood Methods for the Social Sciences POLS 510 CSSS 510 Missing Data and Multiple Imputation Christopher Adolph Political Science and CSSS University of Washington, Seattle Vincent van Gogh
Maximum Likelihood Methods for the Social Sciences POLS 510 CSSS 510 Missing Data and Multiple Imputation Christopher Adolph Political Science and CSSS University of Washington, Seattle Vincent van Gogh
Don t be Fancy. Impute Your Dependent Variables!
 Don t be Fancy. Impute Your Dependent Variables! Kyle M. Lang, Todd D. Little Institute for Measurement, Methodology, Analysis & Policy Texas Tech University Lubbock, TX May 24, 2016 Presented at the 6th
Don t be Fancy. Impute Your Dependent Variables! Kyle M. Lang, Todd D. Little Institute for Measurement, Methodology, Analysis & Policy Texas Tech University Lubbock, TX May 24, 2016 Presented at the 6th
Pooling multiple imputations when the sample happens to be the population.
 Pooling multiple imputations when the sample happens to be the population. Gerko Vink 1,2, and Stef van Buuren 1,3 arxiv:1409.8542v1 [math.st] 30 Sep 2014 1 Department of Methodology and Statistics, Utrecht
Pooling multiple imputations when the sample happens to be the population. Gerko Vink 1,2, and Stef van Buuren 1,3 arxiv:1409.8542v1 [math.st] 30 Sep 2014 1 Department of Methodology and Statistics, Utrecht
Handling Missing Data in R with MICE
 Handling Missing Data in R with MICE Handling Missing Data in R with MICE Stef van Buuren 1,2 1 Methodology and Statistics, FSBS, Utrecht University 2 Netherlands Organization for Applied Scientific Research
Handling Missing Data in R with MICE Handling Missing Data in R with MICE Stef van Buuren 1,2 1 Methodology and Statistics, FSBS, Utrecht University 2 Netherlands Organization for Applied Scientific Research
MULTILEVEL IMPUTATION 1
 MULTILEVEL IMPUTATION 1 Supplement B: MCMC Sampling Steps and Distributions for Two-Level Imputation This document gives technical details of the full conditional distributions used to draw regression
MULTILEVEL IMPUTATION 1 Supplement B: MCMC Sampling Steps and Distributions for Two-Level Imputation This document gives technical details of the full conditional distributions used to draw regression
Logistic Regression. James H. Steiger. Department of Psychology and Human Development Vanderbilt University
 Logistic Regression James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) Logistic Regression 1 / 38 Logistic Regression 1 Introduction
Logistic Regression James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) Logistic Regression 1 / 38 Logistic Regression 1 Introduction
EPSY 905: Fundamentals of Multivariate Modeling Online Lecture #7
 Introduction to Generalized Univariate Models: Models for Binary Outcomes EPSY 905: Fundamentals of Multivariate Modeling Online Lecture #7 EPSY 905: Intro to Generalized In This Lecture A short review
Introduction to Generalized Univariate Models: Models for Binary Outcomes EPSY 905: Fundamentals of Multivariate Modeling Online Lecture #7 EPSY 905: Intro to Generalized In This Lecture A short review
Regression Methods for Survey Data
 Regression Methods for Survey Data Professor Ron Fricker! Naval Postgraduate School! Monterey, California! 3/26/13 Reading:! Lohr chapter 11! 1 Goals for this Lecture! Linear regression! Review of linear
Regression Methods for Survey Data Professor Ron Fricker! Naval Postgraduate School! Monterey, California! 3/26/13 Reading:! Lohr chapter 11! 1 Goals for this Lecture! Linear regression! Review of linear
Generalized Linear Models for Non-Normal Data
 Generalized Linear Models for Non-Normal Data Today s Class: 3 parts of a generalized model Models for binary outcomes Complications for generalized multivariate or multilevel models SPLH 861: Lecture
Generalized Linear Models for Non-Normal Data Today s Class: 3 parts of a generalized model Models for binary outcomes Complications for generalized multivariate or multilevel models SPLH 861: Lecture
Package hot.deck. January 4, 2016
 Type Package Title Multiple Hot-Deck Imputation Version 1.1 Date 2015-11-19 Package hot.deck January 4, 2016 Author Skyler Cranmer, Jeff Gill, Natalie Jackson, Andreas Murr, Dave Armstrong Maintainer Dave
Type Package Title Multiple Hot-Deck Imputation Version 1.1 Date 2015-11-19 Package hot.deck January 4, 2016 Author Skyler Cranmer, Jeff Gill, Natalie Jackson, Andreas Murr, Dave Armstrong Maintainer Dave
Simple logistic regression
 Simple logistic regression Biometry 755 Spring 2009 Simple logistic regression p. 1/47 Model assumptions 1. The observed data are independent realizations of a binary response variable Y that follows a
Simple logistic regression Biometry 755 Spring 2009 Simple logistic regression p. 1/47 Model assumptions 1. The observed data are independent realizations of a binary response variable Y that follows a
LOGISTIC REGRESSION Joseph M. Hilbe
 LOGISTIC REGRESSION Joseph M. Hilbe Arizona State University Logistic regression is the most common method used to model binary response data. When the response is binary, it typically takes the form of
LOGISTIC REGRESSION Joseph M. Hilbe Arizona State University Logistic regression is the most common method used to model binary response data. When the response is binary, it typically takes the form of
BMI 541/699 Lecture 22
 BMI 541/699 Lecture 22 Where we are: 1. Introduction and Experimental Design 2. Exploratory Data Analysis 3. Probability 4. T-based methods for continous variables 5. Power and sample size for t-based
BMI 541/699 Lecture 22 Where we are: 1. Introduction and Experimental Design 2. Exploratory Data Analysis 3. Probability 4. T-based methods for continous variables 5. Power and sample size for t-based
Multilevel Models in Matrix Form. Lecture 7 July 27, 2011 Advanced Multivariate Statistical Methods ICPSR Summer Session #2
 Multilevel Models in Matrix Form Lecture 7 July 27, 2011 Advanced Multivariate Statistical Methods ICPSR Summer Session #2 Today s Lecture Linear models from a matrix perspective An example of how to do
Multilevel Models in Matrix Form Lecture 7 July 27, 2011 Advanced Multivariate Statistical Methods ICPSR Summer Session #2 Today s Lecture Linear models from a matrix perspective An example of how to do
Multinomial Logistic Regression Models
 Stat 544, Lecture 19 1 Multinomial Logistic Regression Models Polytomous responses. Logistic regression can be extended to handle responses that are polytomous, i.e. taking r>2 categories. (Note: The word
Stat 544, Lecture 19 1 Multinomial Logistic Regression Models Polytomous responses. Logistic regression can be extended to handle responses that are polytomous, i.e. taking r>2 categories. (Note: The word
A comparison of fully Bayesian and two-stage imputation strategies for missing covariate data
 A comparison of fully Bayesian and two-stage imputation strategies for missing covariate data Alexina Mason, Sylvia Richardson and Nicky Best Department of Epidemiology and Biostatistics, Imperial College
A comparison of fully Bayesian and two-stage imputation strategies for missing covariate data Alexina Mason, Sylvia Richardson and Nicky Best Department of Epidemiology and Biostatistics, Imperial College
Linear Regression Models P8111
 Linear Regression Models P8111 Lecture 25 Jeff Goldsmith April 26, 2016 1 of 37 Today s Lecture Logistic regression / GLMs Model framework Interpretation Estimation 2 of 37 Linear regression Course started
Linear Regression Models P8111 Lecture 25 Jeff Goldsmith April 26, 2016 1 of 37 Today s Lecture Logistic regression / GLMs Model framework Interpretation Estimation 2 of 37 Linear regression Course started
Time-Invariant Predictors in Longitudinal Models
 Time-Invariant Predictors in Longitudinal Models Topics: What happens to missing predictors Effects of time-invariant predictors Fixed vs. systematically varying vs. random effects Model building strategies
Time-Invariant Predictors in Longitudinal Models Topics: What happens to missing predictors Effects of time-invariant predictors Fixed vs. systematically varying vs. random effects Model building strategies
Hierarchical Generalized Linear Models. ERSH 8990 REMS Seminar on HLM Last Lecture!
 Hierarchical Generalized Linear Models ERSH 8990 REMS Seminar on HLM Last Lecture! Hierarchical Generalized Linear Models Introduction to generalized models Models for binary outcomes Interpreting parameter
Hierarchical Generalized Linear Models ERSH 8990 REMS Seminar on HLM Last Lecture! Hierarchical Generalized Linear Models Introduction to generalized models Models for binary outcomes Interpreting parameter
Linear Regression. Data Model. β, σ 2. Process Model. ,V β. ,s 2. s 1. Parameter Model
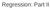 Regression: Part II Linear Regression y~n X, 2 X Y Data Model β, σ 2 Process Model Β 0,V β s 1,s 2 Parameter Model Assumptions of Linear Model Homoskedasticity No error in X variables Error in Y variables
Regression: Part II Linear Regression y~n X, 2 X Y Data Model β, σ 2 Process Model Β 0,V β s 1,s 2 Parameter Model Assumptions of Linear Model Homoskedasticity No error in X variables Error in Y variables
Predictive mean matching imputation of semicontinuous variables
 61 Statistica Neerlandica (2014) Vol. 68, nr. 1, pp. 61 90 doi:10.1111/stan.12023 Predictive mean matching imputation of semicontinuous variables Gerko Vink* Department of Methodology and Statistics, Utrecht
61 Statistica Neerlandica (2014) Vol. 68, nr. 1, pp. 61 90 doi:10.1111/stan.12023 Predictive mean matching imputation of semicontinuous variables Gerko Vink* Department of Methodology and Statistics, Utrecht
WinLTA USER S GUIDE for Data Augmentation
 USER S GUIDE for Version 1.0 (for WinLTA Version 3.0) Linda M. Collins Stephanie T. Lanza Joseph L. Schafer The Methodology Center The Pennsylvania State University May 2002 Dev elopment of this program
USER S GUIDE for Version 1.0 (for WinLTA Version 3.0) Linda M. Collins Stephanie T. Lanza Joseph L. Schafer The Methodology Center The Pennsylvania State University May 2002 Dev elopment of this program
An Introduction to Path Analysis
 An Introduction to Path Analysis PRE 905: Multivariate Analysis Lecture 10: April 15, 2014 PRE 905: Lecture 10 Path Analysis Today s Lecture Path analysis starting with multivariate regression then arriving
An Introduction to Path Analysis PRE 905: Multivariate Analysis Lecture 10: April 15, 2014 PRE 905: Lecture 10 Path Analysis Today s Lecture Path analysis starting with multivariate regression then arriving
LCA_Distal_LTB Stata function users guide (Version 1.1)
 LCA_Distal_LTB Stata function users guide (Version 1.1) Liying Huang John J. Dziak Bethany C. Bray Aaron T. Wagner Stephanie T. Lanza Penn State Copyright 2017, Penn State. All rights reserved. NOTE: the
LCA_Distal_LTB Stata function users guide (Version 1.1) Liying Huang John J. Dziak Bethany C. Bray Aaron T. Wagner Stephanie T. Lanza Penn State Copyright 2017, Penn State. All rights reserved. NOTE: the
Investigating Models with Two or Three Categories
 Ronald H. Heck and Lynn N. Tabata 1 Investigating Models with Two or Three Categories For the past few weeks we have been working with discriminant analysis. Let s now see what the same sort of model might
Ronald H. Heck and Lynn N. Tabata 1 Investigating Models with Two or Three Categories For the past few weeks we have been working with discriminant analysis. Let s now see what the same sort of model might
STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis. 1. Indicate whether each of the following is true (T) or false (F).
 STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis 1. Indicate whether each of the following is true (T) or false (F). (a) T In 2 2 tables, statistical independence is equivalent to a population
STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis 1. Indicate whether each of the following is true (T) or false (F). (a) T In 2 2 tables, statistical independence is equivalent to a population
Generalized Models: Part 1
 Generalized Models: Part 1 Topics: Introduction to generalized models Introduction to maximum likelihood estimation Models for binary outcomes Models for proportion outcomes Models for categorical outcomes
Generalized Models: Part 1 Topics: Introduction to generalized models Introduction to maximum likelihood estimation Models for binary outcomes Models for proportion outcomes Models for categorical outcomes
Using R in 200D Luke Sonnet
 Using R in 200D Luke Sonnet Contents Working with data frames 1 Working with variables........................................... 1 Analyzing data............................................... 3 Random
Using R in 200D Luke Sonnet Contents Working with data frames 1 Working with variables........................................... 1 Analyzing data............................................... 3 Random
Exam Applied Statistical Regression. Good Luck!
 Dr. M. Dettling Summer 2011 Exam Applied Statistical Regression Approved: Tables: Note: Any written material, calculator (without communication facility). Attached. All tests have to be done at the 5%-level.
Dr. M. Dettling Summer 2011 Exam Applied Statistical Regression Approved: Tables: Note: Any written material, calculator (without communication facility). Attached. All tests have to be done at the 5%-level.
Lecture 14: Introduction to Poisson Regression
 Lecture 14: Introduction to Poisson Regression Ani Manichaikul amanicha@jhsph.edu 8 May 2007 1 / 52 Overview Modelling counts Contingency tables Poisson regression models 2 / 52 Modelling counts I Why
Lecture 14: Introduction to Poisson Regression Ani Manichaikul amanicha@jhsph.edu 8 May 2007 1 / 52 Overview Modelling counts Contingency tables Poisson regression models 2 / 52 Modelling counts I Why
Modelling counts. Lecture 14: Introduction to Poisson Regression. Overview
 Modelling counts I Lecture 14: Introduction to Poisson Regression Ani Manichaikul amanicha@jhsph.edu Why count data? Number of traffic accidents per day Mortality counts in a given neighborhood, per week
Modelling counts I Lecture 14: Introduction to Poisson Regression Ani Manichaikul amanicha@jhsph.edu Why count data? Number of traffic accidents per day Mortality counts in a given neighborhood, per week
STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis. 1. Indicate whether each of the following is true (T) or false (F).
 STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis 1. Indicate whether each of the following is true (T) or false (F). (a) (b) (c) (d) (e) In 2 2 tables, statistical independence is equivalent
STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis 1. Indicate whether each of the following is true (T) or false (F). (a) (b) (c) (d) (e) In 2 2 tables, statistical independence is equivalent
Modeling Overdispersion
 James H. Steiger Department of Psychology and Human Development Vanderbilt University Regression Modeling, 2009 1 Introduction 2 Introduction In this lecture we discuss the problem of overdispersion in
James H. Steiger Department of Psychology and Human Development Vanderbilt University Regression Modeling, 2009 1 Introduction 2 Introduction In this lecture we discuss the problem of overdispersion in
EDF 7405 Advanced Quantitative Methods in Educational Research. Data are available on IQ of the child and seven potential predictors.
 EDF 7405 Advanced Quantitative Methods in Educational Research Data are available on IQ of the child and seven potential predictors. Four are medical variables available at the birth of the child: Birthweight
EDF 7405 Advanced Quantitative Methods in Educational Research Data are available on IQ of the child and seven potential predictors. Four are medical variables available at the birth of the child: Birthweight
Class Notes: Week 8. Probit versus Logit Link Functions and Count Data
 Ronald Heck Class Notes: Week 8 1 Class Notes: Week 8 Probit versus Logit Link Functions and Count Data This week we ll take up a couple of issues. The first is working with a probit link function. While
Ronald Heck Class Notes: Week 8 1 Class Notes: Week 8 Probit versus Logit Link Functions and Count Data This week we ll take up a couple of issues. The first is working with a probit link function. While
LCA Distal Stata function users guide (Version 1.0)
 LCA Distal Stata function users guide (Version 1.0) Liying Huang John J. Dziak Bethany C. Bray Aaron T. Wagner Stephanie T. Lanza Penn State Copyright 2016, Penn State. All rights reserved. Please send
LCA Distal Stata function users guide (Version 1.0) Liying Huang John J. Dziak Bethany C. Bray Aaron T. Wagner Stephanie T. Lanza Penn State Copyright 2016, Penn State. All rights reserved. Please send
Statistical Distribution Assumptions of General Linear Models
 Statistical Distribution Assumptions of General Linear Models Applied Multilevel Models for Cross Sectional Data Lecture 4 ICPSR Summer Workshop University of Colorado Boulder Lecture 4: Statistical Distributions
Statistical Distribution Assumptions of General Linear Models Applied Multilevel Models for Cross Sectional Data Lecture 4 ICPSR Summer Workshop University of Colorado Boulder Lecture 4: Statistical Distributions
Propensity Score Matching
 Methods James H. Steiger Department of Psychology and Human Development Vanderbilt University Regression Modeling, 2009 Methods 1 Introduction 2 3 4 Introduction Why Match? 5 Definition Methods and In
Methods James H. Steiger Department of Psychology and Human Development Vanderbilt University Regression Modeling, 2009 Methods 1 Introduction 2 3 4 Introduction Why Match? 5 Definition Methods and In
A Re-Introduction to General Linear Models (GLM)
 A Re-Introduction to General Linear Models (GLM) Today s Class: You do know the GLM Estimation (where the numbers in the output come from): From least squares to restricted maximum likelihood (REML) Reviewing
A Re-Introduction to General Linear Models (GLM) Today s Class: You do know the GLM Estimation (where the numbers in the output come from): From least squares to restricted maximum likelihood (REML) Reviewing
Generalized Linear Models
 Generalized Linear Models Assumptions of Linear Model Homoskedasticity Model variance No error in X variables Errors in variables No missing data Missing data model Normally distributed error Error in
Generalized Linear Models Assumptions of Linear Model Homoskedasticity Model variance No error in X variables Errors in variables No missing data Missing data model Normally distributed error Error in
Basics of Modern Missing Data Analysis
 Basics of Modern Missing Data Analysis Kyle M. Lang Center for Research Methods and Data Analysis University of Kansas March 8, 2013 Topics to be Covered An introduction to the missing data problem Missing
Basics of Modern Missing Data Analysis Kyle M. Lang Center for Research Methods and Data Analysis University of Kansas March 8, 2013 Topics to be Covered An introduction to the missing data problem Missing
Logistic Regression - problem 6.14
 Logistic Regression - problem 6.14 Let x 1, x 2,, x m be given values of an input variable x and let Y 1,, Y m be independent binomial random variables whose distributions depend on the corresponding values
Logistic Regression - problem 6.14 Let x 1, x 2,, x m be given values of an input variable x and let Y 1,, Y m be independent binomial random variables whose distributions depend on the corresponding values
R-squared for Bayesian regression models
 R-squared for Bayesian regression models Andrew Gelman Ben Goodrich Jonah Gabry Imad Ali 8 Nov 2017 Abstract The usual definition of R 2 (variance of the predicted values divided by the variance of the
R-squared for Bayesian regression models Andrew Gelman Ben Goodrich Jonah Gabry Imad Ali 8 Nov 2017 Abstract The usual definition of R 2 (variance of the predicted values divided by the variance of the
Topic 1. Definitions
 S Topic. Definitions. Scalar A scalar is a number. 2. Vector A vector is a column of numbers. 3. Linear combination A scalar times a vector plus a scalar times a vector, plus a scalar times a vector...
S Topic. Definitions. Scalar A scalar is a number. 2. Vector A vector is a column of numbers. 3. Linear combination A scalar times a vector plus a scalar times a vector, plus a scalar times a vector...
LISA Short Course Series Generalized Linear Models (GLMs) & Categorical Data Analysis (CDA) in R. Liang (Sally) Shan Nov. 4, 2014
 LISA Short Course Series Generalized Linear Models (GLMs) & Categorical Data Analysis (CDA) in R Liang (Sally) Shan Nov. 4, 2014 L Laboratory for Interdisciplinary Statistical Analysis LISA helps VT researchers
LISA Short Course Series Generalized Linear Models (GLMs) & Categorical Data Analysis (CDA) in R Liang (Sally) Shan Nov. 4, 2014 L Laboratory for Interdisciplinary Statistical Analysis LISA helps VT researchers
Introduction to Generalized Models
 Introduction to Generalized Models Today s topics: The big picture of generalized models Review of maximum likelihood estimation Models for binary outcomes Models for proportion outcomes Models for categorical
Introduction to Generalized Models Today s topics: The big picture of generalized models Review of maximum likelihood estimation Models for binary outcomes Models for proportion outcomes Models for categorical
Generalized Linear Models
 Generalized Linear Models Methods@Manchester Summer School Manchester University July 2 6, 2018 Generalized Linear Models: a generic approach to statistical modelling www.research-training.net/manchester2018
Generalized Linear Models Methods@Manchester Summer School Manchester University July 2 6, 2018 Generalized Linear Models: a generic approach to statistical modelling www.research-training.net/manchester2018
Bayesian Networks in Educational Assessment
 Bayesian Networks in Educational Assessment Estimating Parameters with MCMC Bayesian Inference: Expanding Our Context Roy Levy Arizona State University Roy.Levy@asu.edu 2017 Roy Levy MCMC 1 MCMC 2 Posterior
Bayesian Networks in Educational Assessment Estimating Parameters with MCMC Bayesian Inference: Expanding Our Context Roy Levy Arizona State University Roy.Levy@asu.edu 2017 Roy Levy MCMC 1 MCMC 2 Posterior
MS&E 226: Small Data
 MS&E 226: Small Data Lecture 15: Examples of hypothesis tests (v5) Ramesh Johari ramesh.johari@stanford.edu 1 / 32 The recipe 2 / 32 The hypothesis testing recipe In this lecture we repeatedly apply the
MS&E 226: Small Data Lecture 15: Examples of hypothesis tests (v5) Ramesh Johari ramesh.johari@stanford.edu 1 / 32 The recipe 2 / 32 The hypothesis testing recipe In this lecture we repeatedly apply the
Part 8: GLMs and Hierarchical LMs and GLMs
 Part 8: GLMs and Hierarchical LMs and GLMs 1 Example: Song sparrow reproductive success Arcese et al., (1992) provide data on a sample from a population of 52 female song sparrows studied over the course
Part 8: GLMs and Hierarchical LMs and GLMs 1 Example: Song sparrow reproductive success Arcese et al., (1992) provide data on a sample from a population of 52 female song sparrows studied over the course
Various Issues in Fitting Contingency Tables
 Various Issues in Fitting Contingency Tables Statistics 149 Spring 2006 Copyright 2006 by Mark E. Irwin Complete Tables with Zero Entries In contingency tables, it is possible to have zero entries in a
Various Issues in Fitting Contingency Tables Statistics 149 Spring 2006 Copyright 2006 by Mark E. Irwin Complete Tables with Zero Entries In contingency tables, it is possible to have zero entries in a
Logistic Regression 21/05
 Logistic Regression 21/05 Recall that we are trying to solve a classification problem in which features x i can be continuous or discrete (coded as 0/1) and the response y is discrete (0/1). Logistic regression
Logistic Regression 21/05 Recall that we are trying to solve a classification problem in which features x i can be continuous or discrete (coded as 0/1) and the response y is discrete (0/1). Logistic regression
Known unknowns : using multiple imputation to fill in the blanks for missing data
 Known unknowns : using multiple imputation to fill in the blanks for missing data James Stanley Department of Public Health University of Otago, Wellington james.stanley@otago.ac.nz Acknowledgments Cancer
Known unknowns : using multiple imputation to fill in the blanks for missing data James Stanley Department of Public Health University of Otago, Wellington james.stanley@otago.ac.nz Acknowledgments Cancer
Statistical Methods III Statistics 212. Problem Set 2 - Answer Key
 Statistical Methods III Statistics 212 Problem Set 2 - Answer Key 1. (Analysis to be turned in and discussed on Tuesday, April 24th) The data for this problem are taken from long-term followup of 1423
Statistical Methods III Statistics 212 Problem Set 2 - Answer Key 1. (Analysis to be turned in and discussed on Tuesday, April 24th) The data for this problem are taken from long-term followup of 1423
MIXED MODELS FOR REPEATED (LONGITUDINAL) DATA PART 2 DAVID C. HOWELL 4/1/2010
 MIXED MODELS FOR REPEATED (LONGITUDINAL) DATA PART 2 DAVID C. HOWELL 4/1/2010 Part 1 of this document can be found at http://www.uvm.edu/~dhowell/methods/supplements/mixed Models for Repeated Measures1.pdf
MIXED MODELS FOR REPEATED (LONGITUDINAL) DATA PART 2 DAVID C. HOWELL 4/1/2010 Part 1 of this document can be found at http://www.uvm.edu/~dhowell/methods/supplements/mixed Models for Repeated Measures1.pdf
An Introduction to Mplus and Path Analysis
 An Introduction to Mplus and Path Analysis PSYC 943: Fundamentals of Multivariate Modeling Lecture 10: October 30, 2013 PSYC 943: Lecture 10 Today s Lecture Path analysis starting with multivariate regression
An Introduction to Mplus and Path Analysis PSYC 943: Fundamentals of Multivariate Modeling Lecture 10: October 30, 2013 PSYC 943: Lecture 10 Today s Lecture Path analysis starting with multivariate regression
STA 303 H1S / 1002 HS Winter 2011 Test March 7, ab 1cde 2abcde 2fghij 3
 STA 303 H1S / 1002 HS Winter 2011 Test March 7, 2011 LAST NAME: FIRST NAME: STUDENT NUMBER: ENROLLED IN: (circle one) STA 303 STA 1002 INSTRUCTIONS: Time: 90 minutes Aids allowed: calculator. Some formulae
STA 303 H1S / 1002 HS Winter 2011 Test March 7, 2011 LAST NAME: FIRST NAME: STUDENT NUMBER: ENROLLED IN: (circle one) STA 303 STA 1002 INSTRUCTIONS: Time: 90 minutes Aids allowed: calculator. Some formulae
Univariate Normal Distribution; GLM with the Univariate Normal; Least Squares Estimation
 Univariate Normal Distribution; GLM with the Univariate Normal; Least Squares Estimation PRE 905: Multivariate Analysis Spring 2014 Lecture 4 Today s Class The building blocks: The basics of mathematical
Univariate Normal Distribution; GLM with the Univariate Normal; Least Squares Estimation PRE 905: Multivariate Analysis Spring 2014 Lecture 4 Today s Class The building blocks: The basics of mathematical
Models for Count and Binary Data. Poisson and Logistic GWR Models. 24/07/2008 GWR Workshop 1
 Models for Count and Binary Data Poisson and Logistic GWR Models 24/07/2008 GWR Workshop 1 Outline I: Modelling counts Poisson regression II: Modelling binary events Logistic Regression III: Poisson Regression
Models for Count and Binary Data Poisson and Logistic GWR Models 24/07/2008 GWR Workshop 1 Outline I: Modelling counts Poisson regression II: Modelling binary events Logistic Regression III: Poisson Regression
Review: what is a linear model. Y = β 0 + β 1 X 1 + β 2 X 2 + A model of the following form:
 Outline for today What is a generalized linear model Linear predictors and link functions Example: fit a constant (the proportion) Analysis of deviance table Example: fit dose-response data using logistic
Outline for today What is a generalized linear model Linear predictors and link functions Example: fit a constant (the proportion) Analysis of deviance table Example: fit dose-response data using logistic
Let s see if we can predict whether a student returns or does not return to St. Ambrose for their second year.
 Assignment #13: GLM Scenario: Over the past few years, our first-to-second year retention rate has ranged from 77-80%. In other words, 77-80% of our first-year students come back to St. Ambrose for their
Assignment #13: GLM Scenario: Over the past few years, our first-to-second year retention rate has ranged from 77-80%. In other words, 77-80% of our first-year students come back to St. Ambrose for their
Review of Multiple Regression
 Ronald H. Heck 1 Let s begin with a little review of multiple regression this week. Linear models [e.g., correlation, t-tests, analysis of variance (ANOVA), multiple regression, path analysis, multivariate
Ronald H. Heck 1 Let s begin with a little review of multiple regression this week. Linear models [e.g., correlation, t-tests, analysis of variance (ANOVA), multiple regression, path analysis, multivariate
A Generalized Linear Model for Binomial Response Data. Copyright c 2017 Dan Nettleton (Iowa State University) Statistics / 46
 A Generalized Linear Model for Binomial Response Data Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 1 / 46 Now suppose that instead of a Bernoulli response, we have a binomial response
A Generalized Linear Model for Binomial Response Data Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 1 / 46 Now suppose that instead of a Bernoulli response, we have a binomial response
Time-Invariant Predictors in Longitudinal Models
 Time-Invariant Predictors in Longitudinal Models Today s Class (or 3): Summary of steps in building unconditional models for time What happens to missing predictors Effects of time-invariant predictors
Time-Invariant Predictors in Longitudinal Models Today s Class (or 3): Summary of steps in building unconditional models for time What happens to missing predictors Effects of time-invariant predictors
STAT 7030: Categorical Data Analysis
 STAT 7030: Categorical Data Analysis 5. Logistic Regression Peng Zeng Department of Mathematics and Statistics Auburn University Fall 2012 Peng Zeng (Auburn University) STAT 7030 Lecture Notes Fall 2012
STAT 7030: Categorical Data Analysis 5. Logistic Regression Peng Zeng Department of Mathematics and Statistics Auburn University Fall 2012 Peng Zeng (Auburn University) STAT 7030 Lecture Notes Fall 2012
Introduction to lnmle: An R Package for Marginally Specified Logistic-Normal Models for Longitudinal Binary Data
 Introduction to lnmle: An R Package for Marginally Specified Logistic-Normal Models for Longitudinal Binary Data Bryan A. Comstock and Patrick J. Heagerty Department of Biostatistics University of Washington
Introduction to lnmle: An R Package for Marginally Specified Logistic-Normal Models for Longitudinal Binary Data Bryan A. Comstock and Patrick J. Heagerty Department of Biostatistics University of Washington
9 Generalized Linear Models
 9 Generalized Linear Models The Generalized Linear Model (GLM) is a model which has been built to include a wide range of different models you already know, e.g. ANOVA and multiple linear regression models
9 Generalized Linear Models The Generalized Linear Model (GLM) is a model which has been built to include a wide range of different models you already know, e.g. ANOVA and multiple linear regression models
Chapter 1 Statistical Inference
 Chapter 1 Statistical Inference causal inference To infer causality, you need a randomized experiment (or a huge observational study and lots of outside information). inference to populations Generalizations
Chapter 1 Statistical Inference causal inference To infer causality, you need a randomized experiment (or a huge observational study and lots of outside information). inference to populations Generalizations
MODULE 6 LOGISTIC REGRESSION. Module Objectives:
 MODULE 6 LOGISTIC REGRESSION Module Objectives: 1. 147 6.1. LOGIT TRANSFORMATION MODULE 6. LOGISTIC REGRESSION Logistic regression models are used when a researcher is investigating the relationship between
MODULE 6 LOGISTIC REGRESSION Module Objectives: 1. 147 6.1. LOGIT TRANSFORMATION MODULE 6. LOGISTIC REGRESSION Logistic regression models are used when a researcher is investigating the relationship between
A Practitioner s Guide to Generalized Linear Models
 A Practitioners Guide to Generalized Linear Models Background The classical linear models and most of the minimum bias procedures are special cases of generalized linear models (GLMs). GLMs are more technically
A Practitioners Guide to Generalized Linear Models Background The classical linear models and most of the minimum bias procedures are special cases of generalized linear models (GLMs). GLMs are more technically
Bootstrapping, Randomization, 2B-PLS
 Bootstrapping, Randomization, 2B-PLS Statistics, Tests, and Bootstrapping Statistic a measure that summarizes some feature of a set of data (e.g., mean, standard deviation, skew, coefficient of variation,
Bootstrapping, Randomization, 2B-PLS Statistics, Tests, and Bootstrapping Statistic a measure that summarizes some feature of a set of data (e.g., mean, standard deviation, skew, coefficient of variation,
This manual is Copyright 1997 Gary W. Oehlert and Christopher Bingham, all rights reserved.
 This file consists of Chapter 4 of MacAnova User s Guide by Gary W. Oehlert and Christopher Bingham, issued as Technical Report Number 617, School of Statistics, University of Minnesota, March 1997, describing
This file consists of Chapter 4 of MacAnova User s Guide by Gary W. Oehlert and Christopher Bingham, issued as Technical Report Number 617, School of Statistics, University of Minnesota, March 1997, describing
ST3241 Categorical Data Analysis I Multicategory Logit Models. Logit Models For Nominal Responses
 ST3241 Categorical Data Analysis I Multicategory Logit Models Logit Models For Nominal Responses 1 Models For Nominal Responses Y is nominal with J categories. Let {π 1,, π J } denote the response probabilities
ST3241 Categorical Data Analysis I Multicategory Logit Models Logit Models For Nominal Responses 1 Models For Nominal Responses Y is nominal with J categories. Let {π 1,, π J } denote the response probabilities
Generalised linear models. Response variable can take a number of different formats
 Generalised linear models Response variable can take a number of different formats Structure Limitations of linear models and GLM theory GLM for count data GLM for presence \ absence data GLM for proportion
Generalised linear models Response variable can take a number of different formats Structure Limitations of linear models and GLM theory GLM for count data GLM for presence \ absence data GLM for proportion
Diagnostics and Transformations Part 2
 Diagnostics and Transformations Part 2 Bivariate Linear Regression James H. Steiger Department of Psychology and Human Development Vanderbilt University Multilevel Regression Modeling, 2009 Diagnostics
Diagnostics and Transformations Part 2 Bivariate Linear Regression James H. Steiger Department of Psychology and Human Development Vanderbilt University Multilevel Regression Modeling, 2009 Diagnostics
Implications of Missing Data Imputation for Agricultural Household Surveys: An Application to Technology Adoption
 Implications of Missing Data Imputation for Agricultural Household Surveys: An Application to Technology Adoption Haluk Gedikoglu Assistant Professor of Agricultural Economics Cooperative Research Programs
Implications of Missing Data Imputation for Agricultural Household Surveys: An Application to Technology Adoption Haluk Gedikoglu Assistant Professor of Agricultural Economics Cooperative Research Programs
STAT 510 Final Exam Spring 2015
 STAT 510 Final Exam Spring 2015 Instructions: The is a closed-notes, closed-book exam No calculator or electronic device of any kind may be used Use nothing but a pen or pencil Please write your name and
STAT 510 Final Exam Spring 2015 Instructions: The is a closed-notes, closed-book exam No calculator or electronic device of any kind may be used Use nothing but a pen or pencil Please write your name and
Review of Statistics 101
 Review of Statistics 101 We review some important themes from the course 1. Introduction Statistics- Set of methods for collecting/analyzing data (the art and science of learning from data). Provides methods
Review of Statistics 101 We review some important themes from the course 1. Introduction Statistics- Set of methods for collecting/analyzing data (the art and science of learning from data). Provides methods
Introduction to Bayesian Statistics and Markov Chain Monte Carlo Estimation. EPSY 905: Multivariate Analysis Spring 2016 Lecture #10: April 6, 2016
 Introduction to Bayesian Statistics and Markov Chain Monte Carlo Estimation EPSY 905: Multivariate Analysis Spring 2016 Lecture #10: April 6, 2016 EPSY 905: Intro to Bayesian and MCMC Today s Class An
Introduction to Bayesian Statistics and Markov Chain Monte Carlo Estimation EPSY 905: Multivariate Analysis Spring 2016 Lecture #10: April 6, 2016 EPSY 905: Intro to Bayesian and MCMC Today s Class An
UNIVERSITY OF TORONTO. Faculty of Arts and Science APRIL 2010 EXAMINATIONS STA 303 H1S / STA 1002 HS. Duration - 3 hours. Aids Allowed: Calculator
 UNIVERSITY OF TORONTO Faculty of Arts and Science APRIL 2010 EXAMINATIONS STA 303 H1S / STA 1002 HS Duration - 3 hours Aids Allowed: Calculator LAST NAME: FIRST NAME: STUDENT NUMBER: There are 27 pages
UNIVERSITY OF TORONTO Faculty of Arts and Science APRIL 2010 EXAMINATIONS STA 303 H1S / STA 1002 HS Duration - 3 hours Aids Allowed: Calculator LAST NAME: FIRST NAME: STUDENT NUMBER: There are 27 pages
Flexible multiple imputation by chained equations of the AVO-95 Survey
 PG/VGZ/99.045 Flexible multiple imputation by chained equations of the AVO-95 Survey TNO Prevention and Health Public Health Wassenaarseweg 56 P.O.Box 2215 2301 CE Leiden The Netherlands Tel + 31 71 518
PG/VGZ/99.045 Flexible multiple imputation by chained equations of the AVO-95 Survey TNO Prevention and Health Public Health Wassenaarseweg 56 P.O.Box 2215 2301 CE Leiden The Netherlands Tel + 31 71 518
Linear Regression. In this lecture we will study a particular type of regression model: the linear regression model
 1 Linear Regression 2 Linear Regression In this lecture we will study a particular type of regression model: the linear regression model We will first consider the case of the model with one predictor
1 Linear Regression 2 Linear Regression In this lecture we will study a particular type of regression model: the linear regression model We will first consider the case of the model with one predictor
Stat 8053, Fall 2013: Multinomial Logistic Models
 Stat 8053, Fall 2013: Multinomial Logistic Models Here is the example on page 269 of Agresti on food preference of alligators: s is size class, g is sex of the alligator, l is name of the lake, and f is
Stat 8053, Fall 2013: Multinomial Logistic Models Here is the example on page 269 of Agresti on food preference of alligators: s is size class, g is sex of the alligator, l is name of the lake, and f is
Linear, Generalized Linear, and Mixed-Effects Models in R. Linear and Generalized Linear Models in R Topics
 Linear, Generalized Linear, and Mixed-Effects Models in R John Fox McMaster University ICPSR 2018 John Fox (McMaster University) Statistical Models in R ICPSR 2018 1 / 19 Linear and Generalized Linear
Linear, Generalized Linear, and Mixed-Effects Models in R John Fox McMaster University ICPSR 2018 John Fox (McMaster University) Statistical Models in R ICPSR 2018 1 / 19 Linear and Generalized Linear
arxiv: v5 [stat.me] 13 Feb 2018
![arxiv: v5 [stat.me] 13 Feb 2018 arxiv: v5 [stat.me] 13 Feb 2018](/thumbs/77/75239018.jpg) arxiv: arxiv:1602.07933 BOOTSTRAP INFERENCE WHEN USING MULTIPLE IMPUTATION By Michael Schomaker and Christian Heumann University of Cape Town and Ludwig-Maximilians Universität München arxiv:1602.07933v5
arxiv: arxiv:1602.07933 BOOTSTRAP INFERENCE WHEN USING MULTIPLE IMPUTATION By Michael Schomaker and Christian Heumann University of Cape Town and Ludwig-Maximilians Universität München arxiv:1602.07933v5
Generalized linear models
 Generalized linear models Douglas Bates November 01, 2010 Contents 1 Definition 1 2 Links 2 3 Estimating parameters 5 4 Example 6 5 Model building 8 6 Conclusions 8 7 Summary 9 1 Generalized Linear Models
Generalized linear models Douglas Bates November 01, 2010 Contents 1 Definition 1 2 Links 2 3 Estimating parameters 5 4 Example 6 5 Model building 8 6 Conclusions 8 7 Summary 9 1 Generalized Linear Models
The pan Package. April 2, Title Multiple imputation for multivariate panel or clustered data
 The pan Package April 2, 2005 Version 0.2-3 Date 2005-3-23 Title Multiple imputation for multivariate panel or clustered data Author Original by Joseph L. Schafer . Maintainer Jing hua
The pan Package April 2, 2005 Version 0.2-3 Date 2005-3-23 Title Multiple imputation for multivariate panel or clustered data Author Original by Joseph L. Schafer . Maintainer Jing hua
Lecture Notes: Some Core Ideas of Imputation for Nonresponse in Surveys. Tom Rosenström University of Helsinki May 14, 2014
 Lecture Notes: Some Core Ideas of Imputation for Nonresponse in Surveys Tom Rosenström University of Helsinki May 14, 2014 1 Contents 1 Preface 3 2 Definitions 3 3 Different ways to handle MAR data 4 4
Lecture Notes: Some Core Ideas of Imputation for Nonresponse in Surveys Tom Rosenström University of Helsinki May 14, 2014 1 Contents 1 Preface 3 2 Definitions 3 3 Different ways to handle MAR data 4 4
Simulating MLM. Paul E. Johnson 1 2. Descriptive 1 / Department of Political Science
 Descriptive 1 / 76 Simulating MLM Paul E. Johnson 1 2 1 Department of Political Science 2 Center for Research Methods and Data Analysis, University of Kansas 2015 Descriptive 2 / 76 Outline 1 Orientation:
Descriptive 1 / 76 Simulating MLM Paul E. Johnson 1 2 1 Department of Political Science 2 Center for Research Methods and Data Analysis, University of Kansas 2015 Descriptive 2 / 76 Outline 1 Orientation:
Bayesian methods for missing data: part 1. Key Concepts. Nicky Best and Alexina Mason. Imperial College London
 Bayesian methods for missing data: part 1 Key Concepts Nicky Best and Alexina Mason Imperial College London BAYES 2013, May 21-23, Erasmus University Rotterdam Missing Data: Part 1 BAYES2013 1 / 68 Outline
Bayesian methods for missing data: part 1 Key Concepts Nicky Best and Alexina Mason Imperial College London BAYES 2013, May 21-23, Erasmus University Rotterdam Missing Data: Part 1 BAYES2013 1 / 68 Outline
ECLT 5810 Linear Regression and Logistic Regression for Classification. Prof. Wai Lam
 ECLT 5810 Linear Regression and Logistic Regression for Classification Prof. Wai Lam Linear Regression Models Least Squares Input vectors is an attribute / feature / predictor (independent variable) The
ECLT 5810 Linear Regression and Logistic Regression for Classification Prof. Wai Lam Linear Regression Models Least Squares Input vectors is an attribute / feature / predictor (independent variable) The
Generalized linear models for binary data. A better graphical exploratory data analysis. The simple linear logistic regression model
 Stat 3302 (Spring 2017) Peter F. Craigmile Simple linear logistic regression (part 1) [Dobson and Barnett, 2008, Sections 7.1 7.3] Generalized linear models for binary data Beetles dose-response example
Stat 3302 (Spring 2017) Peter F. Craigmile Simple linear logistic regression (part 1) [Dobson and Barnett, 2008, Sections 7.1 7.3] Generalized linear models for binary data Beetles dose-response example
ZERO INFLATED POISSON REGRESSION
 STAT 6500 ZERO INFLATED POISSON REGRESSION FINAL PROJECT DEC 6 th, 2013 SUN JEON DEPARTMENT OF SOCIOLOGY UTAH STATE UNIVERSITY POISSON REGRESSION REVIEW INTRODUCING - ZERO-INFLATED POISSON REGRESSION SAS
STAT 6500 ZERO INFLATED POISSON REGRESSION FINAL PROJECT DEC 6 th, 2013 SUN JEON DEPARTMENT OF SOCIOLOGY UTAH STATE UNIVERSITY POISSON REGRESSION REVIEW INTRODUCING - ZERO-INFLATED POISSON REGRESSION SAS
Ronald Christensen. University of New Mexico. Albuquerque, New Mexico. Wesley Johnson. University of California, Irvine. Irvine, California
 Texts in Statistical Science Bayesian Ideas and Data Analysis An Introduction for Scientists and Statisticians Ronald Christensen University of New Mexico Albuquerque, New Mexico Wesley Johnson University
Texts in Statistical Science Bayesian Ideas and Data Analysis An Introduction for Scientists and Statisticians Ronald Christensen University of New Mexico Albuquerque, New Mexico Wesley Johnson University
Business Analytics and Data Mining Modeling Using R Prof. Gaurav Dixit Department of Management Studies Indian Institute of Technology, Roorkee
 Business Analytics and Data Mining Modeling Using R Prof. Gaurav Dixit Department of Management Studies Indian Institute of Technology, Roorkee Lecture - 04 Basic Statistics Part-1 (Refer Slide Time: 00:33)
Business Analytics and Data Mining Modeling Using R Prof. Gaurav Dixit Department of Management Studies Indian Institute of Technology, Roorkee Lecture - 04 Basic Statistics Part-1 (Refer Slide Time: 00:33)
CHAPTER 11 ASDA ANALYSIS EXAMPLES REPLICATION
 CHAPTER 11 ASDA ANALYSIS EXAMPLES REPLICATION GENERAL NOTES ABOUT ANALYSIS EXAMPLES REPLICATION These examples are intended to provide guidance on how to use the commands/procedures for analysis of complex
CHAPTER 11 ASDA ANALYSIS EXAMPLES REPLICATION GENERAL NOTES ABOUT ANALYSIS EXAMPLES REPLICATION These examples are intended to provide guidance on how to use the commands/procedures for analysis of complex
Statistics Boot Camp. Dr. Stephanie Lane Institute for Defense Analyses DATAWorks 2018
 Statistics Boot Camp Dr. Stephanie Lane Institute for Defense Analyses DATAWorks 2018 March 21, 2018 Outline of boot camp Summarizing and simplifying data Point and interval estimation Foundations of statistical
Statistics Boot Camp Dr. Stephanie Lane Institute for Defense Analyses DATAWorks 2018 March 21, 2018 Outline of boot camp Summarizing and simplifying data Point and interval estimation Foundations of statistical
A Note on Bayesian Inference After Multiple Imputation
 A Note on Bayesian Inference After Multiple Imputation Xiang Zhou and Jerome P. Reiter Abstract This article is aimed at practitioners who plan to use Bayesian inference on multiplyimputed datasets in
A Note on Bayesian Inference After Multiple Imputation Xiang Zhou and Jerome P. Reiter Abstract This article is aimed at practitioners who plan to use Bayesian inference on multiplyimputed datasets in
