STAT 450: Final Examination Version 1. Richard Lockhart 16 December 2002
|
|
|
- Jordan Barrie Cunningham
- 5 years ago
- Views:
Transcription
1 Name: Last Name 1, First Name 1 Stdnt # StudentNumber1 STAT 450: Final Examination Version 1 Richard Lockhart 16 December 2002 Instructions: This is an open book exam. You may use notes, books and a calculator. You may not use calculators capable of remote communication nor may you use cellular phones. The exam is out of 50. There are 14 pages including this one and two pages of extra working space. Question Maximum Mark Question Maximum Mark 1a 5 1b 5 2a 4 2b 1 3a 2 3b 2 3c 2 3d 3 4a 1 4b 1 4c 5 4d 5 4e 3 4f 1 5a 3 5b 1 5c 1 5d 5 Total Out of 50 1
2 1. Suppose that X 1,...,X n are independent random variables. Suppose that the density X k is { } 1 f k (x;σ) = 2k2 πσ exp x2 2k 2 σ 2 where the unknown parameter σ belongs to (0, ). (a) Find the UMVUE of σ 2. (5 marks) 2
3 (b) Find the Cramér-Rao Lower Bound for the variance of unbiased estimators of σ 4. (5 marks) 3
4 2. Suppose X 1,...,X n are a sample from the density 2φ(x 2) 2φ 1 2 x 3 f(x;φ) = 0 otherwise (a) Find the moment generating function of 6log(X 1 2). (4 marks) (b) What is the distribution of 6 n i=1 log(x i 2)? (1 mark) 4
5 3. Suppose X 1,...,X n are iid random variables with (1 θ) (1+x)/2 θ (1 x)/2 x = 1, 1 P(X = x;θ) = 0 otherwise for an unknown θ [0,1]. (a) Find constants a, b, c, and d such that T = (ax 1 +b)(cx 2 +d) is an unbiased estimator of φ (2θ 1) 2. (2 marks) (b) Find the variance of the estimator T above. (2 marks) 5
6 (c) Find constants a, b and c so that T = a X2 +b X +c is an unbiased estimate of φ. (2 marks) (d) Which estimate, T or T has smaller variance. Explain clearly how you know. (3 marks) 6
7 4. Suppose that X 1,X 2,X 3 are 3 random variables. Assume i) Given X 1 = x 1 and X 2 = x 2 the random variable X 3 has a normal distribution with mean 2ρx 2 and variance σ 2, ii) Given X 1 = x 1 the random variable X 2 has a normal distribution with mean 2ρx 1 and variance σ 2. iii) The random variable X 1 has a N(0,σ 2 ) distribution. (a) What is the joint density of X 1 and X 2? (1 mark) (b) What is the joint density of X 1, X 2 and X 3? (1 mark) 7
8 (c) Show that X 1, X 2 2ρX 1 and X 3 2ρX 2 are independent N(0,σ 2 ) random variables. NOTE: you may use this fact in the rest of the problem even if you could not do this part. (3 marks) (d) What is the distribution of X 2 1 +(X 2 2ρX 1 ) 2 σ 2 (1 mark) 8
9 (e) Find the MLE of (ρ,σ) if we observe X 1,X 2,X 3. (5 marks) 9
10 (f) Find the Fisher information matrix for this problem. (5 marks) 10
11 5. Suppose X, Y have joint density φ e x xy > 1,x > 0,y > 0 x f(x,y;φ) = φ y φ+1 0 otherwise for some unknown φ > 0. (a) Suppose we use the rejection region R = {(x,y) : x > log(4)} What is the power function of this rejection region. (3 marks) (b) If the null hypothesis is φ 1 what is the level (or size) of the test? (1 mark) (c) What is the probability of a type II error if φ = 2? (1 mark) 11
12 (d) Find the Uniformly Most Powerful test at level α of φ = 1 against φ > 1. Express the rejection region in the form S(X 1,...,X n ) < k for some statistic S and give an explicit formula for k. (5 marks) 12
13 Extra Page 13
14 Extra Page 14
15 Name: Last Name2, First Name 2 Stdnt # StudentNumber1 STAT 450: Final Examination Version 2 Richard Lockhart 16 December 2002 Instructions: This is an open book exam. You may use notes, books and a calculator. You may not use calculators capable of remote communication nor may you use cellular phones. The exam is out of 50. There are 14 pages including this one and two pages of extra working space. Question Maximum Mark Question Maximum Mark 1a 5 1b 5 2a 4 2b 1 3a 2 3b 2 3c 2 3d 3 4a 1 4b 1 4c 5 4d 5 4e 3 4f 1 5a 3 5b 1 5c 1 5d 5 Total Out of 50 1
16 1. Suppose that X 1,...,X n are independent random variables. Suppose that the density X k is { } 1 f k (x;σ) = 2k3 πσ exp x2 2k 3 σ 2 where the unknown parameter σ belongs to (0, ). (a) Find the UMVUE of σ 2. (5 marks) 2
17 (b) Find the Cramér-Rao Lower Bound for the variance of unbiased estimators of σ 3. (5 marks) 3
18 2. Suppose X 1,...,X n are a sample from the density 3θ(x 4) 3θ 1 4 x 5 f(x;θ) = 0 otherwise (a) Find the moment generating function of 5log(X 1 4). (4 marks) (b) What is the distribution of 5 n i=1 log(x i 4)? (1 mark) 4
19 3. Suppose X 1,...,X n are iid random variables with ψ (1+x)/2 (1 ψ) (1 x)/2 x = 1, 1 P(X = x;ψ) = 0 otherwise for an unknown ψ [0,1]. (a) Find constants r, s, t, and u such that S = (rx 1 +s)(tx 2 +u) is an unbiased estimator of γ (1 2ψ) 2. (2 marks) (b) Find the variance of the estimator S above. (2 marks) 5
20 (c) Find constants r, s and t so that S = r X2 +s X +t is an unbiased estimate of γ. (2 marks) (d) Which estimate, S or S has smaller variance. Explain clearly how you know. (3 marks) 6
21 4. Suppose that X 1,X 2,X 3 are 3 random variables. Assume i) Given X 1 = x 1 and X 2 = x 2 the random variable X 3 has a normal distribution with mean 3ρx 2 and variance σ 2, ii) Given X 1 = x 1 the random variable X 2 has a normal distribution with mean 3ρx 1 and variance σ 2. iii) The random variable X 1 has a N(0,σ 2 ) distribution. (a) What is the joint density of X 1 and X 2? (1 mark) (b) What is the joint density of X 1, X 2 and X 3? (1 mark) 7
22 (c) Show that X 1, X 2 3ρX 1 and X 3 3ρX 2 are independent N(0,σ 2 ) random variables. NOTE: you may use this fact in the rest of the problem even if you could not do this part. (3 marks) (d) What is the distribution of X 2 1 +(X 2 3ρX 1 ) 2 σ 2 (1 mark) 8
23 (e) Find the MLE of (ρ,σ) if we observe X 1,X 2,X 3. (5 marks) 9
24 (f) Find the Fisher information matrix for this problem. (5 marks) 10
25 5. Suppose X, Y have joint density φ e x xy > 1,x > 0,y > 0 x f(x,y;φ) = φ y φ+1 0 otherwise for some unknown φ > 0. (a) Suppose we use the rejection region R = {(x,y) : x > log(5)} What is the power function of this rejection region. (3 marks) (b) If the null hypothesis is φ 1 what is the level (or size) of the test? (1 mark) (c) What is the probability of a type II error if φ = 2? (1 mark) 11
26 (d) Find the Uniformly Most Powerful test at level α of φ = 1 against φ > 1. Express the rejection region in the form S(X 1,...,X n ) < k for some statistic S and give an explicit formula for k. (5 marks) 12
27 Extra Page 13
28 Extra Page 14
29 Name: Last Name 3, First Name 3 Stdnt # StudentNumber1 STAT 450: Final Examination Version 3 Richard Lockhart 16 December 2002 Instructions: This is an open book exam. You may use notes, books and a calculator. You may not use calculators capable of remote communication nor may you use cellular phones. The exam is out of 50. There are 14 pages including this one and two pages of extra working space. Question Maximum Mark Question Maximum Mark 1a 5 1b 5 2a 4 2b 1 3a 2 3b 2 3c 2 3d 3 4a 1 4b 1 4c 5 4d 5 4e 3 4f 1 5a 3 5b 1 5c 1 5d 5 Total Out of 50 1
30 1. Suppose that X 1,...,X n are independent random variables. Suppose that the density X k is { } 1 f k (x;τ) = 2k4 πτ exp x2 2k 4 τ 2 where the unknown parameter τ belongs to (0, ). (a) Find the UMVUE of τ 2. (5 marks) 2
31 (b) Find the Cramér-Rao Lower Bound for the variance of unbiased estimators of τ 5. (5 marks) 3
32 2. Suppose X 1,...,X n are a sample from the density 3θ(x 6) 3θ 1 6 x 7 f(x;θ) = 0 otherwise (a) Find the moment generating function of 3log(X 1 6). (4 marks) (b) What is the distribution of 3 n i=1 log(x i 6)? (1 mark) 4
33 3. Suppose X 1,...,X n are iid random variables with (1 γ) (1+x)/2 γ (1 x)/2 x = 1, 1 P(X = x;γ) = 0 otherwise for an unknown γ [0,1]. (a) Find constants a, b, c, and d such that U = (ax 3 +c)(bx 4 +d) is an unbiased estimator of φ (2γ 1) 2. (2 marks) (b) Find the variance of the estimator U above. (2 marks) 5
34 (c) Find constants a, b and c so that U = a +b X2 +c X is an unbiased estimate of φ. (2 marks) (d) Which estimate, U or U has smaller variance. Explain clearly how you know. (3 marks) 6
35 4. Suppose that X 1,X 2,X 3 are 3 random variables. Assume i) Given X 1 = x 1 and X 2 = x 2 the random variable X 3 has a normal distribution with mean 4ρx 2 and variance τ 2, ii) Given X 1 = x 1 the random variable X 2 has a normal distribution with mean 4ρx 1 and variance τ 2. iii) The random variable X 1 has a N(0,τ 2 ) distribution. (a) What is the joint density of X 1 and X 2? (1 mark) (b) What is the joint density of X 1, X 2 and X 3? (1 mark) 7
36 (c) Show that X 1, X 2 4ρX 1 and X 3 4ρX 2 are independent N(0,τ 2 ) random variables. NOTE: you may use this fact in the rest of the problem even if you could not do this part. (3 marks) (d) What is the distribution of X 2 1 +(X 2 4ρX 1 ) 2 τ 2 (1 mark) 8
37 (e) Find the MLE of (ρ,τ) if we observe X 1,X 2,X 3. (5 marks) 9
38 (f) Find the Fisher information matrix for this problem. (5 marks) 10
39 5. Suppose X, Y have joint density φ e x xy > 1,x > 0,y > 0 x f(x,y;φ) = φ y φ+1 0 otherwise for some unknown φ > 0. (a) Suppose we use the rejection region R = {(x,y) : x > log(6)} What is the power function of this rejection region. (3 marks) (b) If the null hypothesis is φ 1 what is the level (or size) of the test? (1 mark) (c) What is the probability of a type II error if φ = 2? (1 mark) 11
40 (d) Find the Uniformly Most Powerful test at level α of φ = 1 against φ > 1. Express the rejection region in the form S(X 1,...,X n ) < k for some statistic S and give an explicit formula for k. (5 marks) 12
41 Extra Page 13
42 Extra Page 14
43 Name: Last Name 4, First Name4 Stdnt # StudentNumber1 STAT 450: Final Examination Version 4 Richard Lockhart 16 December 2002 Instructions: This is an open book exam. You may use notes, books and a calculator. You may not use calculators capable of remote communication nor may you use cellular phones. The exam is out of 50. There are 14 pages including this one and two pages of extra working space. Question Maximum Mark Question Maximum Mark 1a 5 1b 5 2a 4 2b 1 3a 2 3b 2 3c 2 3d 3 4a 1 4b 1 4c 5 4d 5 4e 3 4f 1 5a 3 5b 1 5c 1 5d 5 Total Out of 50 1
44 1. Suppose that X 1,...,X n are independent random variables. Suppose that the density X k is { } 1 f k (x;τ) = 2k5 πτ exp x2 2k 5 τ 2 where the unknown parameter τ belongs to (0, ). (a) Find the UMVUE of τ 2. (5 marks) 2
45 (b) Find the Cramér-Rao Lower Bound for the variance of unbiased estimators of τ 6. (5 marks) 3
46 2. Suppose X 1,...,X n are a sample from the density 3θ(x 8) 3θ 1 8 x 9 f(x;θ) = 0 otherwise (a) Find the moment generating function of 4log(X 1 8). (4 marks) (b) What is the distribution of 4 n i=1 log(x i 8)? (1 mark) 4
47 3. Suppose X 1,...,X n are iid random variables with (1 δ) (1+x)/2 δ (1 x)/2 x = 1, 1 P(X = x;δ) = 0 otherwise for an unknown δ [0,1]. (a) Find constants a, b, c, and d such that V = (ax 3 +c)(dx 4 +b) is an unbiased estimator of ψ (2δ 1) 2. (2 marks) (b) Find the variance of the estimator V above. (2 marks) 5
48 (c) Find constants a, b and c so that V = a +b X +c X2 is an unbiased estimate of ψ. (2 marks) (d) Which estimate, V or V has smaller variance. Explain clearly how you know. (3 marks) 6
49 4. Suppose that X 1,X 2,X 3 are 3 random variables. Assume i) Given X 1 = x 1 and X 2 = x 2 the random variable X 3 has a normal distribution with mean 5ρx 2 and variance τ 2, ii) Given X 1 = x 1 the random variable X 2 has a normal distribution with mean 5ρx 1 and variance τ 2. iii) The random variable X 1 has a N(0,τ 2 ) distribution. (a) What is the joint density of X 1 and X 2? (1 mark) (b) What is the joint density of X 1, X 2 and X 3? (1 mark) 7
50 (c) Show that X 1, X 2 5ρX 1 and X 3 5ρX 2 are independent N(0,τ 2 ) random variables. NOTE: you may use this fact in the rest of the problem even if you could not do this part. (3 marks) (d) What is the distribution of X 2 1 +(X 2 5ρX 1 ) 2 τ 2 (1 mark) 8
51 (e) Find the MLE of (ρ,τ) if we observe X 1,X 2,X 3. (5 marks) 9
52 (f) Find the Fisher information matrix for this problem. (5 marks) 10
53 5. Suppose X, Y have joint density φ e x xy > 1,x > 0,y > 0 x f(x,y;φ) = φ y φ+1 0 otherwise for some unknown φ > 0. (a) Suppose we use the rejection region R = {(x,y) : x > log(7)} What is the power function of this rejection region. (3 marks) (b) If the null hypothesis is φ 1 what is the level (or size) of the test? (1 mark) (c) What is the probability of a type II error if φ = 2? (1 mark) 11
54 (d) Find the Uniformly Most Powerful test at level α of φ = 1 against φ > 1. Express the rejection region in the form S(X 1,...,X n ) < k for some statistic S and give an explicit formula for k. (5 marks) 12
55 Extra Page 13
56 Extra Page 14
Economics 520. Lecture Note 19: Hypothesis Testing via the Neyman-Pearson Lemma CB 8.1,
 Economics 520 Lecture Note 9: Hypothesis Testing via the Neyman-Pearson Lemma CB 8., 8.3.-8.3.3 Uniformly Most Powerful Tests and the Neyman-Pearson Lemma Let s return to the hypothesis testing problem
Economics 520 Lecture Note 9: Hypothesis Testing via the Neyman-Pearson Lemma CB 8., 8.3.-8.3.3 Uniformly Most Powerful Tests and the Neyman-Pearson Lemma Let s return to the hypothesis testing problem
Mathematics Ph.D. Qualifying Examination Stat Probability, January 2018
 Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Problem Selected Scores
 Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
McGill University. Faculty of Science. Department of Mathematics and Statistics. Part A Examination. Statistics: Theory Paper
 McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
Mathematics Qualifying Examination January 2015 STAT Mathematical Statistics
 Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Final Exam. 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given.
 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
Review. December 4 th, Review
 December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
Spring 2012 Math 541A Exam 1. X i, S 2 = 1 n. n 1. X i I(X i < c), T n =
 Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Mathematical statistics
 October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
All other items including (and especially) CELL PHONES must be left at the front of the room.
 TEST #2 / STA 5327 (Inference) / Spring 2017 (April 24, 2017) Name: Directions This exam is closed book and closed notes. You will be supplied with scratch paper, and a copy of the Table of Common Distributions
TEST #2 / STA 5327 (Inference) / Spring 2017 (April 24, 2017) Name: Directions This exam is closed book and closed notes. You will be supplied with scratch paper, and a copy of the Table of Common Distributions
7 Likelihood and Maximum Likelihood Estimation
 7 Likelihood and Maximum Likelihood Estimation Exercice 7.1. Let X be a random variable admitting the following probability density : x +1 I x 1 where > 0. It is in fact a particular Pareto law. Consider
7 Likelihood and Maximum Likelihood Estimation Exercice 7.1. Let X be a random variable admitting the following probability density : x +1 I x 1 where > 0. It is in fact a particular Pareto law. Consider
Statistics & Data Sciences: First Year Prelim Exam May 2018
 Statistics & Data Sciences: First Year Prelim Exam May 2018 Instructions: 1. Do not turn this page until instructed to do so. 2. Start each new question on a new sheet of paper. 3. This is a closed book
Statistics & Data Sciences: First Year Prelim Exam May 2018 Instructions: 1. Do not turn this page until instructed to do so. 2. Start each new question on a new sheet of paper. 3. This is a closed book
Probability and Statistics qualifying exam, May 2015
 Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
STAT 730 Chapter 4: Estimation
 STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Review Quiz. 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the
 Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
Chapter 4 HOMEWORK ASSIGNMENTS. 4.1 Homework #1
 Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee
 Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
1. (Regular) Exponential Family
 1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
Masters Comprehensive Examination Department of Statistics, University of Florida
 Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002
 Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Stat 5102 Final Exam May 14, 2015
 Stat 5102 Final Exam May 14, 2015 Name Student ID The exam is closed book and closed notes. You may use three 8 1 11 2 sheets of paper with formulas, etc. You may also use the handouts on brand name distributions
Stat 5102 Final Exam May 14, 2015 Name Student ID The exam is closed book and closed notes. You may use three 8 1 11 2 sheets of paper with formulas, etc. You may also use the handouts on brand name distributions
Math 494: Mathematical Statistics
 Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed
 18.466 Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed 1. MLEs in exponential families Let f(x,θ) for x X and θ Θ be a likelihood function, that is, for present purposes,
18.466 Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed 1. MLEs in exponential families Let f(x,θ) for x X and θ Θ be a likelihood function, that is, for present purposes,
Theory of Statistics.
 Theory of Statistics. Homework V February 5, 00. MT 8.7.c When σ is known, ˆµ = X is an unbiased estimator for µ. If you can show that its variance attains the Cramer-Rao lower bound, then no other unbiased
Theory of Statistics. Homework V February 5, 00. MT 8.7.c When σ is known, ˆµ = X is an unbiased estimator for µ. If you can show that its variance attains the Cramer-Rao lower bound, then no other unbiased
t x 1 e t dt, and simplify the answer when possible (for example, when r is a positive even number). In particular, confirm that EX 4 = 3.
 Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
f (1 0.5)/n Z =
 Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Statistics Ph.D. Qualifying Exam: Part II November 3, 2001
 Statistics Ph.D. Qualifying Exam: Part II November 3, 2001 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Statistics Ph.D. Qualifying Exam: Part II November 3, 2001 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Statement: With my signature I confirm that the solutions are the product of my own work. Name: Signature:.
 MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
STAT215: Solutions for Homework 2
 STAT25: Solutions for Homework 2 Due: Wednesday, Feb 4. (0 pt) Suppose we take one observation, X, from the discrete distribution, x 2 0 2 Pr(X x θ) ( θ)/4 θ/2 /2 (3 θ)/2 θ/4, 0 θ Find an unbiased estimator
STAT25: Solutions for Homework 2 Due: Wednesday, Feb 4. (0 pt) Suppose we take one observation, X, from the discrete distribution, x 2 0 2 Pr(X x θ) ( θ)/4 θ/2 /2 (3 θ)/2 θ/4, 0 θ Find an unbiased estimator
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Mathematical Statistics
 Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Estimation theory. Parametric estimation. Properties of estimators. Minimum variance estimator. Cramer-Rao bound. Maximum likelihood estimators
 Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
STA 6857 Estimation ( 3.6)
 STA 6857 Estimation ( 3.6) Outline 1 Yule-Walker 2 Least Squares 3 Maximum Likelihood Arthur Berg STA 6857 Estimation ( 3.6) 2/ 19 Outline 1 Yule-Walker 2 Least Squares 3 Maximum Likelihood Arthur Berg
STA 6857 Estimation ( 3.6) Outline 1 Yule-Walker 2 Least Squares 3 Maximum Likelihood Arthur Berg STA 6857 Estimation ( 3.6) 2/ 19 Outline 1 Yule-Walker 2 Least Squares 3 Maximum Likelihood Arthur Berg
STATS 200: Introduction to Statistical Inference. Lecture 29: Course review
 STATS 200: Introduction to Statistical Inference Lecture 29: Course review Course review We started in Lecture 1 with a fundamental assumption: Data is a realization of a random process. The goal throughout
STATS 200: Introduction to Statistical Inference Lecture 29: Course review Course review We started in Lecture 1 with a fundamental assumption: Data is a realization of a random process. The goal throughout
Central Limit Theorem ( 5.3)
 Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic
 Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Brief Review on Estimation Theory
 Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Asymptotic Statistics-III. Changliang Zou
 Asymptotic Statistics-III Changliang Zou The multivariate central limit theorem Theorem (Multivariate CLT for iid case) Let X i be iid random p-vectors with mean µ and and covariance matrix Σ. Then n (
Asymptotic Statistics-III Changliang Zou The multivariate central limit theorem Theorem (Multivariate CLT for iid case) Let X i be iid random p-vectors with mean µ and and covariance matrix Σ. Then n (
Introduction to Normal Distribution
 Introduction to Normal Distribution Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 17-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Introduction
Introduction to Normal Distribution Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 17-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Introduction
Exercises and Answers to Chapter 1
 Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
AMCS243/CS243/EE243 Probability and Statistics. Fall Final Exam: Sunday Dec. 8, 3:00pm- 5:50pm VERSION A
 AMCS243/CS243/EE243 Probability and Statistics Fall 2013 Final Exam: Sunday Dec. 8, 3:00pm- 5:50pm VERSION A *********************************************************** ID: ***********************************************************
AMCS243/CS243/EE243 Probability and Statistics Fall 2013 Final Exam: Sunday Dec. 8, 3:00pm- 5:50pm VERSION A *********************************************************** ID: ***********************************************************
STAT 285: Fall Semester Final Examination Solutions
 Name: Student Number: STAT 285: Fall Semester 2014 Final Examination Solutions 5 December 2014 Instructor: Richard Lockhart Instructions: This is an open book test. As such you may use formulas such as
Name: Student Number: STAT 285: Fall Semester 2014 Final Examination Solutions 5 December 2014 Instructor: Richard Lockhart Instructions: This is an open book test. As such you may use formulas such as
Lecture 8: Information Theory and Statistics
 Lecture 8: Information Theory and Statistics Part II: Hypothesis Testing and I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 23, 2015 1 / 50 I-Hsiang
Lecture 8: Information Theory and Statistics Part II: Hypothesis Testing and I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 23, 2015 1 / 50 I-Hsiang
This exam is closed book and closed notes. (You will have access to a copy of the Table of Common Distributions given in the back of the text.
 TEST #3 STA 536 December, 00 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. You will have access to a copy
TEST #3 STA 536 December, 00 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. You will have access to a copy
M(t) = 1 t. (1 t), 6 M (0) = 20 P (95. X i 110) i=1
 Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
Lecture 7 Introduction to Statistical Decision Theory
 Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
Lecture 12 November 3
 STATS 300A: Theory of Statistics Fall 2015 Lecture 12 November 3 Lecturer: Lester Mackey Scribe: Jae Hyuck Park, Christian Fong Warning: These notes may contain factual and/or typographic errors. 12.1
STATS 300A: Theory of Statistics Fall 2015 Lecture 12 November 3 Lecturer: Lester Mackey Scribe: Jae Hyuck Park, Christian Fong Warning: These notes may contain factual and/or typographic errors. 12.1
Bayesian statistics, simulation and software
 Module 10: Bayesian prediction and model checking Department of Mathematical Sciences Aalborg University 1/15 Prior predictions Suppose we want to predict future data x without observing any data x. Assume:
Module 10: Bayesian prediction and model checking Department of Mathematical Sciences Aalborg University 1/15 Prior predictions Suppose we want to predict future data x without observing any data x. Assume:
BEST TESTS. Abstract. We will discuss the Neymann-Pearson theorem and certain best test where the power function is optimized.
 BEST TESTS Abstract. We will discuss the Neymann-Pearson theorem and certain best test where the power function is optimized. 1. Most powerful test Let {f θ } θ Θ be a family of pdfs. We will consider
BEST TESTS Abstract. We will discuss the Neymann-Pearson theorem and certain best test where the power function is optimized. 1. Most powerful test Let {f θ } θ Θ be a family of pdfs. We will consider
Direction: This test is worth 250 points and each problem worth points. DO ANY SIX
 Term Test 3 December 5, 2003 Name Math 52 Student Number Direction: This test is worth 250 points and each problem worth 4 points DO ANY SIX PROBLEMS You are required to complete this test within 50 minutes
Term Test 3 December 5, 2003 Name Math 52 Student Number Direction: This test is worth 250 points and each problem worth 4 points DO ANY SIX PROBLEMS You are required to complete this test within 50 minutes
Answer Key for STAT 200B HW No. 7
 Answer Key for STAT 200B HW No. 7 May 5, 2007 Problem 2.2 p. 649 Assuming binomial 2-sample model ˆπ =.75, ˆπ 2 =.6. a ˆτ = ˆπ 2 ˆπ =.5. From Ex. 2.5a on page 644: ˆπ ˆπ + ˆπ 2 ˆπ 2.75.25.6.4 = + =.087;
Answer Key for STAT 200B HW No. 7 May 5, 2007 Problem 2.2 p. 649 Assuming binomial 2-sample model ˆπ =.75, ˆπ 2 =.6. a ˆτ = ˆπ 2 ˆπ =.5. From Ex. 2.5a on page 644: ˆπ ˆπ + ˆπ 2 ˆπ 2.75.25.6.4 = + =.087;
Statistics Masters Comprehensive Exam March 21, 2003
 Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Qualifying Exam in Probability and Statistics.
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
Principles of Statistics
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 81 Paper 4, Section II 28K Let g : R R be an unknown function, twice continuously differentiable with g (x) M for
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 81 Paper 4, Section II 28K Let g : R R be an unknown function, twice continuously differentiable with g (x) M for
Variations. ECE 6540, Lecture 10 Maximum Likelihood Estimation
 Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama
 Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama Instructions This exam has 7 pages in total, numbered 1 to 7. Make sure your exam has all the pages. This exam will be 2 hours
Qualifying Exam CS 661: System Simulation Summer 2013 Prof. Marvin K. Nakayama Instructions This exam has 7 pages in total, numbered 1 to 7. Make sure your exam has all the pages. This exam will be 2 hours
ECE 275B Homework # 1 Solutions Version Winter 2015
 ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
Estimation Theory. as Θ = (Θ 1,Θ 2,...,Θ m ) T. An estimator
 Estimation Theory Estimation theory deals with finding numerical values of interesting parameters from given set of data. We start with formulating a family of models that could describe how the data were
Estimation Theory Estimation theory deals with finding numerical values of interesting parameters from given set of data. We start with formulating a family of models that could describe how the data were
Final Examination. STA 215: Statistical Inference. Saturday, 2001 May 5, 9:00am 12:00 noon
 Final Examination Saturday, 2001 May 5, 9:00am 12:00 noon This is an open-book examination, but you may not share materials. A normal distribution table, a PMF/PDF handout, and a blank worksheet are attached
Final Examination Saturday, 2001 May 5, 9:00am 12:00 noon This is an open-book examination, but you may not share materials. A normal distribution table, a PMF/PDF handout, and a blank worksheet are attached
Statement: With my signature I confirm that the solutions are the product of my own work. Name: Signature:.
 MATHEMATICAL STATISTICS Take-home final examination February 1 st -February 8 th, 019 Instructions You do not need to edit the solutions Just make sure the handwriting is legible The final solutions should
MATHEMATICAL STATISTICS Take-home final examination February 1 st -February 8 th, 019 Instructions You do not need to edit the solutions Just make sure the handwriting is legible The final solutions should
Two hours. To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER. 21 June :45 11:45
 Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
COS513 LECTURE 8 STATISTICAL CONCEPTS
 COS513 LECTURE 8 STATISTICAL CONCEPTS NIKOLAI SLAVOV AND ANKUR PARIKH 1. MAKING MEANINGFUL STATEMENTS FROM JOINT PROBABILITY DISTRIBUTIONS. A graphical model (GM) represents a family of probability distributions
COS513 LECTURE 8 STATISTICAL CONCEPTS NIKOLAI SLAVOV AND ANKUR PARIKH 1. MAKING MEANINGFUL STATEMENTS FROM JOINT PROBABILITY DISTRIBUTIONS. A graphical model (GM) represents a family of probability distributions
Lecture 34: Properties of the LSE
 Lecture 34: Properties of the LSE The following results explain why the LSE is popular. Gauss-Markov Theorem Assume a general linear model previously described: Y = Xβ + E with assumption A2, i.e., Var(E
Lecture 34: Properties of the LSE The following results explain why the LSE is popular. Gauss-Markov Theorem Assume a general linear model previously described: Y = Xβ + E with assumption A2, i.e., Var(E
Spring 2012 Math 541B Exam 1
 Spring 2012 Math 541B Exam 1 1. A sample of size n is drawn without replacement from an urn containing N balls, m of which are red and N m are black; the balls are otherwise indistinguishable. Let X denote
Spring 2012 Math 541B Exam 1 1. A sample of size n is drawn without replacement from an urn containing N balls, m of which are red and N m are black; the balls are otherwise indistinguishable. Let X denote
λ(x + 1)f g (x) > θ 0
 Stat 8111 Final Exam December 16 Eleven students took the exam, the scores were 92, 78, 4 in the 5 s, 1 in the 4 s, 1 in the 3 s and 3 in the 2 s. 1. i) Let X 1, X 2,..., X n be iid each Bernoulli(θ) where
Stat 8111 Final Exam December 16 Eleven students took the exam, the scores were 92, 78, 4 in the 5 s, 1 in the 4 s, 1 in the 3 s and 3 in the 2 s. 1. i) Let X 1, X 2,..., X n be iid each Bernoulli(θ) where
STAT 830 Bayesian Estimation
 STAT 830 Bayesian Estimation Richard Lockhart Simon Fraser University STAT 830 Fall 2011 Richard Lockhart (Simon Fraser University) STAT 830 Bayesian Estimation STAT 830 Fall 2011 1 / 23 Purposes of These
STAT 830 Bayesian Estimation Richard Lockhart Simon Fraser University STAT 830 Fall 2011 Richard Lockhart (Simon Fraser University) STAT 830 Bayesian Estimation STAT 830 Fall 2011 1 / 23 Purposes of These
IIT JAM : MATHEMATICAL STATISTICS (MS) 2013
 IIT JAM : MATHEMATICAL STATISTICS (MS 2013 Question Paper with Answer Keys Ctanujit Classes Of Mathematics, Statistics & Economics Visit our website for more: www.ctanujit.in IMPORTANT NOTE FOR CANDIDATES
IIT JAM : MATHEMATICAL STATISTICS (MS 2013 Question Paper with Answer Keys Ctanujit Classes Of Mathematics, Statistics & Economics Visit our website for more: www.ctanujit.in IMPORTANT NOTE FOR CANDIDATES
Probability on a Riemannian Manifold
 Probability on a Riemannian Manifold Jennifer Pajda-De La O December 2, 2015 1 Introduction We discuss how we can construct probability theory on a Riemannian manifold. We make comparisons to this and
Probability on a Riemannian Manifold Jennifer Pajda-De La O December 2, 2015 1 Introduction We discuss how we can construct probability theory on a Riemannian manifold. We make comparisons to this and
Statistics GIDP Ph.D. Qualifying Exam Theory Jan 11, 2016, 9:00am-1:00pm
 Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
ECE 275B Homework # 1 Solutions Winter 2018
 ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
Definition 1.1 (Parametric family of distributions) A parametric distribution is a set of distribution functions, each of which is determined by speci
 Definition 1.1 (Parametric family of distributions) A parametric distribution is a set of distribution functions, each of which is determined by specifying one or more values called parameters. The number
Definition 1.1 (Parametric family of distributions) A parametric distribution is a set of distribution functions, each of which is determined by specifying one or more values called parameters. The number
Chapter 3. Point Estimation. 3.1 Introduction
 Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
ECE 275A Homework 7 Solutions
 ECE 275A Homework 7 Solutions Solutions 1. For the same specification as in Homework Problem 6.11 we want to determine an estimator for θ using the Method of Moments (MOM). In general, the MOM estimator
ECE 275A Homework 7 Solutions Solutions 1. For the same specification as in Homework Problem 6.11 we want to determine an estimator for θ using the Method of Moments (MOM). In general, the MOM estimator
Statistics Ph.D. Qualifying Exam
 Department of Statistics Carnegie Mellon University May 7 2008 Statistics Ph.D. Qualifying Exam You are not expected to solve all five problems. Complete solutions to few problems will be preferred to
Department of Statistics Carnegie Mellon University May 7 2008 Statistics Ph.D. Qualifying Exam You are not expected to solve all five problems. Complete solutions to few problems will be preferred to
Point Estimation. Maximum likelihood estimation for a binomial distribution. CSE 446: Machine Learning
 Point Estimation Emily Fox University of Washington January 6, 2017 Maximum likelihood estimation for a binomial distribution 1 Your first consulting job A bored Seattle billionaire asks you a question:
Point Estimation Emily Fox University of Washington January 6, 2017 Maximum likelihood estimation for a binomial distribution 1 Your first consulting job A bored Seattle billionaire asks you a question:
Mathematical statistics
 October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
ECE534, Spring 2018: Solutions for Problem Set #3
 ECE534, Spring 08: Solutions for Problem Set #3 Jointly Gaussian Random Variables and MMSE Estimation Suppose that X, Y are jointly Gaussian random variables with µ X = µ Y = 0 and σ X = σ Y = Let their
ECE534, Spring 08: Solutions for Problem Set #3 Jointly Gaussian Random Variables and MMSE Estimation Suppose that X, Y are jointly Gaussian random variables with µ X = µ Y = 0 and σ X = σ Y = Let their
STAT763: Applied Regression Analysis. Multiple linear regression. 4.4 Hypothesis testing
 STAT763: Applied Regression Analysis Multiple linear regression 4.4 Hypothesis testing Chunsheng Ma E-mail: cma@math.wichita.edu 4.4.1 Significance of regression Null hypothesis (Test whether all β j =
STAT763: Applied Regression Analysis Multiple linear regression 4.4 Hypothesis testing Chunsheng Ma E-mail: cma@math.wichita.edu 4.4.1 Significance of regression Null hypothesis (Test whether all β j =
Comprehensive Examination Quantitative Methods Spring, 2018
 Comprehensive Examination Quantitative Methods Spring, 2018 Instruction: This exam consists of three parts. You are required to answer all the questions in all the parts. 1 Grading policy: 1. Each part
Comprehensive Examination Quantitative Methods Spring, 2018 Instruction: This exam consists of three parts. You are required to answer all the questions in all the parts. 1 Grading policy: 1. Each part
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Statistics. Statistics
 The main aims of statistics 1 1 Choosing a model 2 Estimating its parameter(s) 1 point estimates 2 interval estimates 3 Testing hypotheses Distributions used in statistics: χ 2 n-distribution 2 Let X 1,
The main aims of statistics 1 1 Choosing a model 2 Estimating its parameter(s) 1 point estimates 2 interval estimates 3 Testing hypotheses Distributions used in statistics: χ 2 n-distribution 2 Let X 1,
Economics 573 Problem Set 5 Fall 2002 Due: 4 October b. The sample mean converges in probability to the population mean.
 Economics 573 Problem Set 5 Fall 00 Due: 4 October 00 1. In random sampling from any population with E(X) = and Var(X) =, show (using Chebyshev's inequality) that sample mean converges in probability to..
Economics 573 Problem Set 5 Fall 00 Due: 4 October 00 1. In random sampling from any population with E(X) = and Var(X) =, show (using Chebyshev's inequality) that sample mean converges in probability to..
STAT420 Midterm Exam. University of Illinois Urbana-Champaign October 19 (Friday), :00 4:15p. SOLUTIONS (Yellow)
 STAT40 Midterm Exam University of Illinois Urbana-Champaign October 19 (Friday), 018 3:00 4:15p SOLUTIONS (Yellow) Question 1 (15 points) (10 points) 3 (50 points) extra ( points) Total (77 points) Points
STAT40 Midterm Exam University of Illinois Urbana-Champaign October 19 (Friday), 018 3:00 4:15p SOLUTIONS (Yellow) Question 1 (15 points) (10 points) 3 (50 points) extra ( points) Total (77 points) Points
Parameter Estimation
 Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
[y i α βx i ] 2 (2) Q = i=1
![[y i α βx i ] 2 (2) Q = i=1 [y i α βx i ] 2 (2) Q = i=1](/thumbs/75/72005858.jpg) Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
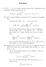 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
FINAL EXAM: Monday 8-10am
 ECE 30: Probabilistic Methods in Electrical and Computer Engineering Fall 016 Instructor: Prof. A. R. Reibman FINAL EXAM: Monday 8-10am Fall 016, TTh 3-4:15pm (December 1, 016) This is a closed book exam.
ECE 30: Probabilistic Methods in Electrical and Computer Engineering Fall 016 Instructor: Prof. A. R. Reibman FINAL EXAM: Monday 8-10am Fall 016, TTh 3-4:15pm (December 1, 016) This is a closed book exam.
Completeness. On the other hand, the distribution of an ancillary statistic doesn t depend on θ at all.
 Completeness A minimal sufficient statistic achieves the maximum amount of data reduction while retaining all the information the sample has concerning θ. On the other hand, the distribution of an ancillary
Completeness A minimal sufficient statistic achieves the maximum amount of data reduction while retaining all the information the sample has concerning θ. On the other hand, the distribution of an ancillary
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
GEOMETRIC -discrete A discrete random variable R counts number of times needed before an event occurs
 STATISTICS 4 Summary Notes. Geometric and Exponential Distributions GEOMETRIC -discrete A discrete random variable R counts number of times needed before an event occurs P(X = x) = ( p) x p x =,, 3,...
STATISTICS 4 Summary Notes. Geometric and Exponential Distributions GEOMETRIC -discrete A discrete random variable R counts number of times needed before an event occurs P(X = x) = ( p) x p x =,, 3,...
Problem 1 (20) Log-normal. f(x) Cauchy
 ORF 245. Rigollet Date: 11/21/2008 Problem 1 (20) f(x) f(x) 0.0 0.1 0.2 0.3 0.4 0.0 0.2 0.4 0.6 0.8 4 2 0 2 4 Normal (with mean -1) 4 2 0 2 4 Negative-exponential x x f(x) f(x) 0.0 0.1 0.2 0.3 0.4 0.5
ORF 245. Rigollet Date: 11/21/2008 Problem 1 (20) f(x) f(x) 0.0 0.1 0.2 0.3 0.4 0.0 0.2 0.4 0.6 0.8 4 2 0 2 4 Normal (with mean -1) 4 2 0 2 4 Negative-exponential x x f(x) f(x) 0.0 0.1 0.2 0.3 0.4 0.5
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments
 STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
