REPRESENTATIVE HYDRAULIC CONDUCTIVITIES IN SATURATED GROUNDWATER FLOW
|
|
|
- Jessica Christina Malone
- 5 years ago
- Views:
Transcription
1 REPRESENTATIE HYDRAULIC CONDUCTIITIES IN SATURATED GROUNDWATER FLOW Xavier Sanchez-ila, 1 Alberto Guadagnini, 2 and Jesus Carrera 1 Received 24 March 2005; revised 5 January 2006; accepted 5 May 2006; published 23 September [1] Heterogeneity is the single most salient feature of hydrogeology. An enormous amount of work has been devoted during the last 30 years to addressing this issue. Our objective is to synthesize and to offer a critical appraisal of results related to the problem of finding representative hydraulic conductivities. By representative hydraulic conductivity we mean a parameter controlling the average behavior of groundwater flow within an aquifer at a given scale. Three related concepts are defined: effective hydraulic conductivity, which relates the ensemble averages of flux and head gradient; equivalent conductivity, which relates the spatial averages of flux and head gradient within a given volume of an aquifer; and interpreted conductivity, which is the one derived from interpretation of field data. Most theoretical results are related to effective conductivity, and their application to real world scenarios relies on ergodic assumptions. Fortunately, a number of results are available suggesting that conventional hydraulic test interpretations yield (interpreted) hydraulic conductivity values that can be closely linked to equivalent and/or effective hydraulic conductivities. Complex spatial distributions of geologic hydrofacies and flow conditions have a strong impact upon the existence and the actual values of representative parameters. Therefore it is not surprising that a large body of literature provides particular solutions for simplified boundary conditions and geological settings, which are, nevertheless, useful for many practical applications. Still, frequent observations of scale effects imply that efforts should be directed at characterizing well-connected stochastic random fields and at evaluating the corresponding representative hydraulic conductivities. Citation: Sanchez-ila, X., A. Guadagnini, and J. Carrera (2006), Representative hydraulic conductivities in saturated groundwater flow, Rev. Geophys., 44,, doi: /2005rg INTRODUCTION 1.1. Significance of Hydraulic Conductivity to Earth Sciences [2] The concept of hydraulic conductivity dates back to the middle nineteenth century, when Darcy [1856] performed experiments to show that fluid displacement in porous materials is governed by a linear relationship between velocity and hydraulic gradient. Dupuit [1863] noticed the parallelism with heat conduction and, being heavily influenced by the work of Fourier [1822], expanded the work of Darcy, providing the mathematical framework that led to the generalized form of Darcy s law as it is used nowadays: qx ðþ¼ Kx ðþrhðþ; x where x is a vector of space coordinates, q is a seepage velocity vector, h is hydraulic head, and K is the hydraulic 1 Department of Geotechnical Engineering and Geosciences, Technical University of Catalonia, Barcelona, Spain. 2 Dipartimento di Ingegneria Idraulica, Ambientale, Infrastrutture iarie, Rilevamento, Politecnico di Milano, Milan, Italy. ð1þ conductivity tensor. This tensor can be written as K = krg/m, where k is the intrinsic permeability tensor, r is fluid density, g is the acceleration of gravity, and m is viscosity. That is, K depends on the properties of the medium through k (the larger and better connected the pores, the larger k is) and the fluid through r and m. Hydraulic conductivity is a key parameter in several branches of Earth sciences and engineering, notably hydrogeology, soil sciences, geotechnics, and petroleum engineering. Because of the broad spectrum of disciplines some nomenclature ambiguities have arisen. In civil engineering, hydraulic conductivity is often termed permeability, which is the way geologists and petroleum engineers term intrinsic permeability. Here we will use the term hydraulic conductivity. [3] Darcy s law is an empirical law resulting from experimental evidence. However, it can be viewed from at least two other perspectives. Historically, early developments in groundwater flow arose from potential theory because hydraulic head is the energy per unit weight of water. Under slow laminar flow conditions, water flux is linearly proportional to head loss, which is another way of stating Darcy s law. This linearity between potential loss and flux is observed in many other phenomena, starting from Fourier s Copyright 2006 by the American Geophysical Union /06/2005RG Reviews of Geophysics, 44, / of46 Paper number 2005RG000169
2 law, where thermal conductivity relates heat flux and temperature gradient. In fact, the publication of Fourier s [1822] book led to many laws equivalent to (1) [Narasimhan, 1999]: Ohm s law, which relates electricity current to the gradient of electrical potential through electrical conductivity; Fick s law, which relates diffusive fluxes of matter to the gradient of concentration through the molecular diffusion coefficient; Hooke s law that relates mechanical stress to the gradient of displacements through the elasticity modulus, etc. All these phenomena are historically and mathematically equivalent to water flux in porous media. As we will see, the singularity of hydraulic conductivity results from its large but structured variability. [4] Darcy s law can also be viewed as an expression of Newton s second law: momentum conservation. For a given pore geometry and velocity field the force that the solid exerts over a Newtonian fluid is proportional to the flux. In the absence of gravity this force must be balanced by a pressure drop to maintain equilibrium. Therefore flux is proportional to pressure drop, which is yet another way of stating Darcy s law. As a consequence, Darcy s law can also be viewed as the porous medium version of Navier-Stokes equations. [5] By controlling the direction and magnitude of flow, hydraulic conductivity plays a key role in many applications, including the protection of natural groundwater bodies, the restoration of polluted bodies, the preservation of wetlands, and long-term storage of toxic or radioactive materials. Since groundwater accounts for a large percentage of the total water consumption throughout the world, it is clear that proper understanding of hydraulic conductivity is crucial in planning and providing solutions to many environmental, economic, and societal challenges Motivation and Background [6] To some extent the difficulties in properly understanding and identifying hydraulic conductivity can be traced to its almost intrinsic spatial variability. Over 30 years have passed since Freeze [1975] published a paper pointing to the effect of heterogeneity on groundwater flow across a column. While the paper had some limitations [Dagan, 1976; Gelhar et al., 1977], it brought to the attention of most hydrogeologists the importance of accounting for heterogeneity in hydrologic analysis. Actually, hydraulic conductivity (K) is arguably one of the most variable parameters in the Earth sciences. Laboratory measurements of K span more than 12 orders of magnitude. Even in seemingly homogeneous aquifers, measured values of K may range over some orders of magnitude. This realization spurred a large amount of work on the problem of finding the effect of heterogeneity on flow and transport. Since hydrologic analyses of flow are largely based on the concept of hydraulic conductivity, an immediate question is whether the heterogeneous distribution can be substituted by a representative value, and, if so, what would such a value be. In short, one could ask two key questions: (1) Which are the actual values that can be considered representative? (2) How can one obtain them? These questions, in turn, generate some additional considerations, including whether representative values can actually be defined and how accurately can they be obtained on the basis of available data and information. [7] The aim of this paper is precisely to address all of these questions. We will only review works dealing with representative hydraulic conductivities. Still, we must stress the large volume of literature produced in a number of disciplines with the aim of finding representative parameters in the theory of conductive media. Such disciplines would include electrical conductivity (see, e.g., Fokin [1996] for a review and Kaganova [2003]), thermal conductivity [e.g., Caldimi and Mahajan, 1999; Boomsma and Poulikakos, 2001], galvanomagnetic conductivity [e.g., Kaganova and Kaganov, 2004; Bergman and Stroud, 2000], and electronic conductivity [e.g., Du et al., 2004]. [8] Either a deterministic or a random model may be chosen to face real problems in hydrogeology. As discussed by Dagan [1997], the choice is always affected by how uncertainty is viewed. Deterministic approaches are based on viewing parameters as unique, but uncertain, local quantities at some given scale. Stochastic approaches are based on viewing reality as one among the ensemble of possible spatial distributions (realizations) of the parameter. This is motivated by recognizing that spatial variability is important yet impossible to describe in a precise manner. This view implies that parameters and state variables are inherently uncertain and require a nondeterministic framework of analysis. The formalism adopted for studying spatial variability and its associated uncertainty considers the independent or dependent groundwater variables as regionalized, i.e., as realizations of random functions. A spatial random function (SRF), (x, w), is a function of space coordinate, x, whose outcome is nondeterministic; that is, it has a component defined in a probability space (this variation is represented by another coordinate, w, which is usually suppressed to simplify notation). For a given point, x 1,(x 1, w) is a random variable. For two given points, x 1 and x 2,(x 1, w) and (x 2, w) are two (generally) nonindependent random variables. Their dependence is usually characterized by the correlation between these two variables, which is a function of location and separation distance. On the other hand, fixing w = w 0 (i.e., providing an individual realization of the SRF) renders a single space function. The collection of all the space functions for the different w values is called the ensemble. When spatial and ensemble averages coincide, the SRF is said to be ergodic. The topic of spatial random functions is a large one by itself and is needed for understanding much of what is written here. Fortunately, many comprehensive reviews are available, including those of Matheron [1965], Journel and Huijbregts [1978], Dagan [1989], Samper and Carrera [1990], Gelhar [1993], and Rubin [2003]. [9] In this paper we address saturated groundwater flow in both a deterministic and a stochastic framework. Under steady state the governing equation is obtained from mass balance and reads r½kx ð ÞrhðÞ x Š ¼ QðÞ; x ð2þ 2of46
3 where Q is an external sink/source term. This equation is valid at a certain spatial scale, which is generally referred to as support volume. [10] When the approach is stochastic, the variables that appear in (2) become random, so that we can formally write it as r½kx; ð wþrhðx; wþš ¼ QðxÞ: Notice that considering the independent variable K as a SRF turns the dependent variable, h, into another SRF, while Q can be either random (the notation would then be Q(x, w)) or deterministic. Equation (3) is then a stochastic partial differential equation The Problem of Scales [11] The above definitions carry implicitly the validity of the flow equation at some local (support) scale. We will be seeking representative values of K at different scales. So some formalization is required regarding scales. Several attempts have been made at defining them. Dagan [1986, 1989] considered spatial variability at three different scales: pore, formation, and regional. This concept has been further elaborated by Gelhar [1993]. At the pore scale, physical variables are defined in terms of averages over a volume containing many molecules (classical continuum mechanics). In modeling natural formations, heterogeneity at the pore scale is not explicity accounted for. The local (or formation) scale is of the order of the formation thickness, and flow and transport are generally of a three-dimensional nature at this scale. Many problems of interest in hydrogeology, such as pumping tests in the vicinity of the well and solute transport near the source, occur at this scale. The regional or aquifer scale is much larger than the aquifer thickness. Hydraulic parameters are averaged over depth, and flow is mainly two-dimensional. Local-scale variations can be smoothed out. This scale is of interest in applications such as management and longrange pollution. [12] ariability of hydraulic conductivity at the local scale in sedimentary aquifers occurs over lengths (closely related to the concept of correlation distance) of the order of meters in the horizontal direction and about 1 order of magnitude smaller in the vertical direction [Gelhar, 1986]. On the other hand, characteristic lengths at the regional scale are of the order of hundreds to thousands of meters [Delhomme, 1979; Clifton and Neuman, 1982; Hoeksema and Kitanidis, 1985]. In fact, field evidence suggests that the correlation length of K(x) consistently increases with the domain size. This is in line with recent geological models based on process-imitating concepts and sequential stratigraphy [Teles et al., 2004, and references therein], and it suggests that stationarity of K(x) is not a real property of the medium but an artifact of the scale of observation. This prompted Neuman [1990, 1994] to model K as a process that is distributed over a continuous hierarchy of scales, forming a self-similar random variable with homogeneous increments. ð3þ 3of46 [13] Normally, we are not interested in hydraulic heads or fluxes at individual volumes that coincide exactly with the support volume at which equation (3) was obtained. Thus we need to specify the equations that are valid at different (in our case larger) scales. At this stage we should ask ourselves some fundamental questions: (1) Is the formal structure of the equation maintained after a change in the scale of the problem? (2) If not, what is the proper representation of flow processes at a predefined scale? (3) If so, what are the different parameters values to be used at each scale? (4) Is there a way to bridge parameter values across different scales? Much of what follows in this paper is devoted to answering these questions. The traditional approach in hydrogeology, which might be questionable in some cases (as we will explore later), consists of applying to aquifers similar laws to those derived at the local scale. The issue is then to find the representative parameters to be used at that particular scale. The main question is, How representative are representative parameters? The answer is that ideally a representative parameter should yield an average behavior of the aquifer at a given scale. Depending on the averaging procedure, starting from Darcy s law we can obtain effective, equivalent, or interpreted parameters, defined as follows Effective Parameters [14] Effective parameters are based on averaging over the ensemble of realizations. Thus the definition of effective hydraulic conductivity is obtained from the generalization of Darcy s law that results from relating the expected values of specific discharge and head gradient hqi ¼ K eff rhhi; where angle brackets indicate ensemble averaging in the probability space of hydraulic conductivity, that is, averaging all the possible head and specific discharge fields that could be obtained with the ensemble of hydraulic conductivity fields. If the value that relates both expectations, K eff, exists, it is a second-order tensor and is called the effective hydraulic conductivity. The tensorial nature of K eff may be a consequence of statistical anisotropy, boundary conditions, or domain geometry, as will be analyzed in sections 2.2 and Pseudoeffective or Apparent Parameters [15] The name effective is used only when the value appearing in (4) is constant throughout the domain. In this case the effective parameter can be considered as a characteristic property of the medium. The presence of boundaries or sink/sources would cause K eff in (4) to be variable in space (actually, the most important variations would arise near the boundaries or the sources). Then even though (4) is still a proper definition, the resulting parameter is a function of space and cannot (in principle) be termed effective. In such cases some authors introduced the term pseudoeffective parameters [e.g., Sanchez-ila, 1997]. Dagan [2001] coined the term apparent conductivity for this K eff being a function of location, which has then been used in a ð4þ
4 number of publications [e.g., Riva et al., 2001; Tartakovsky et al., 2002; Guadagnini et al., 2003]. Still, we prefer to use the term pseudoeffective to emphasize that average quantities appearing in the definition of this parameter are computed in the probability space. The only difference with the concept of effective parameters is that a pseudoeffective value is not a characteristic of the medium but changes with location and is influenced by the presence of a boundary or by the nonstationarity of the medium (we will address this topic in sections 2.3, 2.6, and 2.8). We will use this terminology throughout the paper Equivalent Parameters (or Block-Averaged Parameters) [16] A different approach to the problem relies on averaging in physical space. The resulting representative parameter is termed equivalent. Alternative terminologies that are often employed are block-averaged or volume-averaged parameters. Several authors refer to these as upscaled parameters, since these are usually representative of some average behavior observed over blocks larger than the support scale. Along these lines an equivalent hydraulic conductivity, K b, can be defined by means of an averaged version of (1). q ¼ K b rh: Here the over bar refers to averaging in the spatial (volumetric) sense, that is, q ¼ 1 qd rh ¼ 1 rh d: Even if K is isotropic at the local scale, upscaling may lead to a tensorial K b. Notice that an expression equivalent to (5) would be Krh ¼ K b rh: A discussion about conditions of existence and properties of such parameters will be presented in sections 3 and 4. [17] When the averaging volume is very large, with a representative size that is several times larger than the integral scale of the underlying (random) heterogeneous parameter, the averaging process comprises all scales of heterogeneity. In such a case, ergodicity would imply that equivalent and effective (or pseudoeffective) parameters be identical. A comprehensive discussion about conditions under which subsurface can be characterized by a unique integral scale within a predefined observation window is presented by Neuman and Di Federico [2003] Interpreted Parameters (or Estimated Parameters) [18] Interpreted parameters are again defined in physical space, as the ones obtained from the interpretation of field data, although this is often restricted to the interpretation of hydraulic tests. Thus they can also be termed estimated parameters. This causes the definition to be quite loose, as it ð5þ ð6þ ð7þ involves interpretation issues. In general, tests are analyzed with some underlying simplifying hypotheses that are not completely met in reality. A clear example is the assumption of medium homogeneity, while reality is heterogeneous. When applying standard interpretation methods to a hydraulic test, one obtains a set of parameter values that are somehow representative of the global behavior of the aquifer at the scale of the test. The key point here is that the values obtained depend on the interpretation method and therefore do not have direct physical meaning. An example would be the estimation of transmissivity from a hydraulic test. Field hydrogeologists would interpret the test using a classical method (Theis or Cooper-Jacob) to obtain a value that they would later use in their models or calculations. Since interpreted parameters are the ones used in practice, the salient question here is whether interpreted parameters bear any relationship to effective, pseudoeffective, or equivalent parameters Structure of the Paper [19] The objective of this paper is to review literature results regarding representative (i.e., effective, pseudoeffective, equivalent, and interpreted) hydraulic conductivities. Unfortunately, these concepts (including the existence and the actual values of such parameters) depend on the flow regime, boundary conditions, and assumptions regarding the underlying structure of the spatial random function hydraulic conductivity. This has led to a large variety of methods and results. We classify existing results on representative parameters according to flow configurations. Section 2 is devoted to effective and pseudoeffective hydraulic conductivity for mean parallel flow, where most results are available, including the pioneering results on the topic. Most methods will be reviewed in section 2. Equivalent values derived under the same flow conditions are presented in section 3. Section 4 is devoted to convergent flow, where, apart from effective, pseudoeffective, and equivalent parameters, interpreted values become relevant. A discussion on issues arising from scale effects is presented in section 4. Section 5 is devoted to other flow configurations. The paper ends with some discussion about relationships between classical and modern approaches and major results. A set of key conclusions and an appraisal of remaining challenges are then proposed. 2. MEAN PARALLEL FLOW: EFFECTIE AND PSEUDOEFFECTIE PARAMETERS [20] This section is devoted to compiling the most important methodologies and relevant results available in the literature regarding effective and pseudoeffective hydraulic conductivity for mean parallel flow. Section 2 is structured over increasing levels of difficulty: It starts with isotropic, unbounded, and stationary media under steady state conditions and progresses to consider anisotropic media, bounded domains, and transient flow. The remainder of section 2 is devoted to different types of nonstationary media. arious reviews covering part of the topics 4of46
5 addressed here are already available in the literature. The most recent ones are those of Dagan [2001], Rubin [2003], and Neuman and Di Federico [2003] Isotropic Stationary Media, Steady State Flow, and Unbounded Domains [21] As will become clear in the following, steady state parallel flow in stationary media is one of the particular situations where effective hydraulic conductivity exists Bounds of the Principal alues of Effective Hydraulic Conductivity [22] The evaluation of K eff has been the subject of several studies since the 1960s. Matheron [1967] obtained the upper and lower bounds for K eff in any given direction by using energy dissipation considerations. He found that K eff was bounded by the arithmetic (K A ) and the harmonic mean (K H ) of the point values of conductivity. Mathematically, the principal values of the K eff tensor are bounded by K H ¼hK 1 i 1 K eff;ii hki ¼K A ; i ¼ 1;...; n; n being space dimensionality. [23] The solution for K eff in an unbounded domain under the assumption that the SRF K(x, w) is isotropic is K eff =K eff I (I being the identity tensor). Matheron [1967] demonstrated that in a two-dimensional infinite domain, and under not very restrictive conditions, K eff is equal to the geometric mean, K G, of the point values of K. The conditions for this equation to hold are that the ensemble of all multivariate moments for K/hKi and hki/k are equal and invariant to rotation. These conditions are met, for example, when K(x, w) is a multilognormal stationary random function with isotropic correlation structure. Later, Adler and Mityushev [2003] proved that the actual necessary conditions for K eff =K G are a little less restrictive than those imposed by Matheron Perturbative Methods Perturbations: General Ideas and Main Results [24] Most of the results regarding effective parameters in heterogeneous media have been obtained using perturbation methods. This general methodology is widely applied in many other fields in science. It allows deriving analytical results or simplifying the numerical burden associated with Monte Carlo methods. The essence of small perturbations techniques is to expand the dependent variable in an asymptotic sequence and to derive different partial differential equations (PDEs) for each of the terms in the expansion. By solving them, we obtain the solution for the dependent variable (heads in the case of saturated groundwater flow) as a sequence. Closure and convergence analysis then become critical. [25] The starting point consists of expanding the independent variable about its expected value, which is, in general, a function of x. In hydrogeological problems, while some authors use as an independent variable K(x), most prefer to use Y(x) = ln K(x). In the latter case we can use Reynolds decomposition to write YðxÞ ¼ hyðxþiþy 0 ðþ; x ð8þ ð9þ where Y 0 (x) is a zero-mean perturbation of the variable around its expected value, hy(x)i. Exponentiating each side of equation (9) and noticing that K G (x) = exp[hy(x)i], an alternative expression for K reads: K(x) =K G (x) exp[y 0 (x)]. In the special case of stationary media, K G is not a function of location. [26] The next step consists in formally expanding h(x) [Dagan, 1989]: hðxþ ¼ h ðþ 0 ðxþþ h ðþ 1 ðþþ x h ðþ 2 ðþþ x...: ð10þ Strictly speaking, an expansion of this kind, widely used in the stochastic literature, does not constitute an asymptotic sequence. This is so since random quantities defined on infinite probabilistic support, such as h (i) (x), can take arbitrarily large values. The crucial points here are that the method relies on computing only statistical moments of the random variables involved, and moments are amenable to asymptotic expansions. Incorporating (9) and (10) into Darcy s law, and expanding exp(y 0 (x)) into a Mac Laurin series, yields q ¼ K G X! Y 0 j ½ ðxþš r j! j0 X! h ðþ i ðþ x : ð11þ The effective hydraulic conductivity can then be obtained by ensemble averaging (11): * X! Y 0 j ½ ðxþš hqi ¼ K G r X! + h ðþ i ðþ x : ð12þ j! j0 [27] To provide an expression that formally looks like (4), we need to obtain expressions for the different terms in the expansion of (12), which formally include h (i) (x). These terms can be obtained by performing a similar expansion in the groundwater flow equation (3), considering no external sources (even though they could be incorporated). Under conditions of stationarity in Y (i.e., rhy(x)i = 0) we can write the steady state flow equation as the following set of sequential equations: r 2 h ðþ 0 ðþ¼0 x r 2 h ðþ i ðþþry x 0 ðþrh x ði 1 Þ x i0 i0 ð13þ ðþ¼0 i 1: ð14þ [28] From (13), and noticing that the domain is infinite, h (0) (x) is a deterministic function. Moreover, for mean uniform flow conditions, h (0) (x) hh(x)i, arising from the fact that hh (j) (x)i = 0 for j > 0 [e.g., Dagan, 1989]. On the contrary, from (14) and as Y 0 is an SRF, all the h (i) (x), i = 1, 2,...terms are the solution of the different stochastic PDEs and therefore are random as well. In (12), there is a double infinite series of ensemble averages of products of Y 0j and rh (i) (x). Each term is assigned an order equal to (i + j). The terminology small perturbations in itself means that the terms of increasing order are of lesser significance. Using the small perturbations argument, we can truncate the 5of46
6 expansion of (12). By retaining only terms up to second order in the expansion we arrive at D E hqi ¼ K G 1 þ s2 Y rhhðþ x iþ Y 0 rh ðþ 1 ðxþ : ð15þ 2 Here s 2 Y is the variance of the natural logarithm, Y, of hydraulic conductivity. An expression similar to (15) but formally incorporating all higher-order terms (before truncation) was already presented by Gelhar and Axness [1983]. When s 2 Y is small, the small perturbation methodology applied to (12) converges to the exact solution, and truncation after a few terms, such as in (15), provides acceptable to very good results. [29] The last step in the methodology is to write the last term on the right-hand side of (15) in terms of rhh(x)i. As we will show later in this section, this is generally not possible. Whenever it is possible, we actually arrive at an expression formally equal to (4), so that a low-order approximation for K eff is readily obtained. [30] The first applications of the methodology for the derivation of effective parameters were performed by Shvidler [1962] and subsequently by Matheron [1967]. These authors already concluded that K eff ¼hKiþO s 2 Y ; ð16þ where the O(s Y 2 ) term is always negative. This last term in (16) was called the deterioration of permeability by Matheron and was already found to depend on the problem dimensionality. Notice that for lognormal hydraulic conductivity fields hki =K G exp(s Y 2 /2) K G (1 + s Y 2 /2). Thus there is a direct relation between (15) and (16), pointing out that when an effective conductivity value exists, the hy 0 rh (1) (x)i term must be negative. [31] The first compact expression for (15) for mean uniform flow conditions and stationary isotropic conductivity fields was presented by Gutjahr et al. [1978] as D E Y 0 rh ð1þ ðxþ ¼ s2 Y n r h hðxþ i; rhhðþi¼ x constant; ð17þ n being the number of space dimensions. Direct comparison of (15) and (4) allowed Gutjahr et al. to obtain the following expression for K eff K eff ¼ K G 1 þ s 2 Y : ð18þ n [32] From (18), Gelhar and Axness [1983] conjectured an extrapolation valid for large s 2 Y by suggesting that it is possible to consider (18) as the sum of the first two terms in the expansion of an exponential (this is known in hydrogeology as Matheron s conjecture [Matheron, 1967]), so that the equation becomes 1 K eff ¼ K G exp 2 1 n s 2 Y : ð19þ [33] This avoids the problem of having negative K eff values in one dimension for large s Y 2 values, as would be the case in (18). [34] Assuming that the univariate distribution of K(x 0 )is lognormal, alternative equations to (19) are given as K eff ¼ K A n 1 n KH 1 n K eff ¼hK n 2 n i n n 2 : ð20aþ ð20bþ Equation (20a) was already conjectured by Matheron [1967], even though it was not rigorously proved. Actually, Matheron arrives at a different analytical expression: K eff ¼ n 1 K A þ 1 n n K H; ð21þ which is not correct. He found that (21) constituted a very low order approximation and conjectured (20a) as a potential exact solution to the problem. Equations (19) and (20a) are rigorously valid for n = 1, 2. Dagan [1993] 4 derived, using small perturbations, the terms up to order s Y for the expression of K eff and found these to be in agreement with the expansion of (19). Later, De Wit [1995] derived the term of order s 6 Y, providing the following expression " K eff ¼ K G 1 þ s 2 Y n þ s 4 Y n 2 þ # 3 s 6 Y n 6 þ e e ¼ s6 Y 3n 3 þ b n : ð22aþ ð22bþ The quantity e in (22b) vanishes for n = 1, 2. This is not the case for three-dimensional flows, where it is found numerically that e is approximately equal to s Y 6 for a Gaussian log conductivity field. De Wit s solution is also valid for nonsymmetric log conductivity configurations, and then the value of b is obtained as a ninedimensional integral. Figure 1 illustrates these results depicting the normalized effective conductivity for threedimensional mean uniform flows as obtained by means of the exponential conjecture (19) (solid curve) together with the sixth-order (in s Y ) approximation (22a) with b = s Y 6 /(3 n 2 ) (dash-dotted curve) and e = s Y 6 or e = s Y 6 for log conductivity field characterized by an exponential (dashed curve) or Gaussian (dotted curve) covariance function, respectively. Similar methodology and results for the Gaussian case were presented at about the same time by Abramovich and Indelman [1995] Small Perturbations Combined With Green s Functions [35] Several methods can be used to derive (17). Because of their applicability to more complex problems we present the main steps of some of these methodologies when 6of46
7 Figure 1. Normalized effective conductivity for threedimensional mean uniform flows as obtained by means of the exponential conjecture (19) (solid curve). For comparison, the dash-dotted curve is the sixth-order (in s Y ) approximation (22a) with b = s 6 Y /(3 n 2 ), and the dashed and dotted curves are (22a) with e = s 6 Y or e = s 6 Y, representing a log conductivity field characterized by an exponential or Gaussian covariance function, respectively. Reprinted with permission from De Wit [1995]. Copyright 1995, American Institute of Physics Small Perturbations Combined With Covariance Spectra [37] An alternative to the use of Green s functions is based on the spectral representation theorem. Under the condition that K(x, w) is a stationary random function, both Y 0 (x, w) and h (1) (x, w) can be represented through a Fourier-Stieltjes integral [Gelhar, 1986]. Then, the first stochastic PDE in (14) becomes a linear equation with constant coefficients in the spectral space. It is then possible to write the spectral density of hydraulic heads from the spectral density of log conductivities. This approach has been successfully used in works by Bakr et al. [1978], Mizell et al. [1982], and Gelhar and Axness [1983] among many others. The methodology was explained in detail by Gelhar [1993]. [38] The spectral representation theorem states that any stationary SRF (in general, a stationary random process) can be written in terms of a stochastic process,, with orthogonal increments, as follows: Y 0 ðxþ ¼ þ1 1 expðik xþd Y ðkþ: ð26þ Here k =(k 1,k 2,k 3 ) is the wave vector in spectral space. By using the same type of representation for h (1) (x) and from (14) we can relate the stochastic processes Y and h, respectively, for log conductivity and heads applied to unbounded domains. The Green s function methodology is based on obtaining a formal mathematical expression for hy 0 rh (1) (x)i. We start by writing the formal random solution to (14) as h ðþ i ðxþ ¼ r x 0Y 0 ðx 0 Þr x 0h ði 1Þ ðx 0 ÞGðx; x 0 Þd ð23þ i ¼ 1; 2;...; where is the domain and G(x, x 0 ) is the deterministic Green s function for the Laplace equation in, i.e., the solution to r 2 Gðx; x 0 Þ ¼ dðjx x 0 jþ ð24þ in, subject to homogeneous boundary conditions. Some boundary integrals also appear in the general solution in a bounded domain. From (24), and taking advantage of the fact that rh (0) (x) =rhh(x)i = constant, we can write D E Y 0 rh ðþ 1 ðþ x ¼ hy 0 ðxþr x 0Y 0 ðx 0 ÞirGðx; x 0 Þd rhi: h ð25þ Now the integral appearing in (25) is a deterministic quantity and can be evaluated analytically or numerically. Evaluating (25) in unbounded domains would lead to (17). [36] A very similar approach, also based on Green s function, was taken initially by Shvidler [1962] and Matheron [1967] in the study of effective parameters under different flow configurations and was applied to other problems by Dagan [1982, 1987]. The methodology was explained in detail by Dagan [1989]. 7of46 d h ðkþ ¼ ik J jkj 2 d YðkÞ: ð27þ After some manipulations in Fourier space it is possible to express the last term in (15) in terms of the spectral density function of Y(x). The results for isotropic media coincide with those obtained using a Green s function approach. Applications of the methodology to bounded domains lead to a truncated, and thus approximated, spectral representation of the random processes involved Residual Flux Theory Approach [39] Neuman and coworkers [Neuman and Orr, 1993; Neuman et al., 1996; Tartakovsky and Neuman, 1998a, 1998b; Guadagnini and Neuman, 1999a, 1999b; Riva et al., 2001; Tartakovsky et al., 2002; Guadagnini et al., 2003] analyzed effective and pseudoeffective hydraulic conductivity by means of moment equations of transient and steady state groundwater flow. Under steady state the predictor of the flux, hqi, is written as hqi ¼ hkirhhiþr; r ¼ hk 0 rh 0 i; ð28þ where it can be easily recognized that hqi is expressed in terms of a Darcian component, which is governed by the hydraulic conductivity predictor, hki, and a (generally) non- Darcian one, which is termed residual flux, r. It has been shown by Neuman and Orr [1993] and Neuman et al. [1996] that for a bounded domain, W, with impermeable Neumann boundaries, the residual flux is given exactly by the compact explicit expression rx ð Þ ¼ ay; ð xþr y h c ðyþdy: ð29þ W
8 Here h c is the solution of the following deterministic flow problem r½hkðxþirh c ðxþšþhfðþi¼0; x ð30þ where hf(x)i is the mean source term and the boundary conditions are provided in terms of (ensemble) mean quantities. The kernel D E ay; ð xþ ¼ K 0 ðþk x 0 ðyþr x r T y G rðy; xþ ð31þ is a second-rank positive semidefinite symmetric tensor, G r (y, x) being the random Green s function associated with the groundwater flow problem, i.e., the solution of the (random) groundwater flow equation for the case where the source function is replaced by the Dirac delta function d(x y), subject to homogeneous boundary conditions [Greenberg, 1971]. In the general case of prescribed nonzero (random) flux along Neumann boundaries, (29) has to be supplemented with a series of boundary integrals. As an alternative the residual flux can be expressed by means of an implicit expression: rx ð Þ ¼ ay; ð xþr y hhðþ y idy þ W W dy; ð xþry ðþdy; ð32þ where a is given by (31) and d forms a second-order, positive semidefinite tensor given by D E dy; ð xþ ¼ K 0 ðxþr x r T y Gðy; xþ : ð33þ It is precisely the integrodifferential nature of the residual flux that renders the flux predictor nonlocal and thus non- Darcian, so that a (pseudo)effective conductivity does not exist with the exception of a few particular cases. This is a very important point to emphasize, since the methodologies directly based on perturbations of random quantities do not allow recognizing general conditions of existence of effective conductivities. A discussion about generally nonuniform flow configurations will be presented in sections 4 and 5. In the special case of flow in an infinite domain with (statistically) homogeneous hydraulic conductivity under a uniform mean hydraulic gradient rh c = rhhi = const, the second integral in (32) must vanish, and therefore the residual flux can be localized exactly, i.e., r(x) = K C (x) rhh(x)i. [40] Owing to symmetry considerations, applicable only to infinite domains, K C (x) is constant throughout the domain, and an effective conductivity value can be defined as K eff ¼hKiI K C ; K C ¼ K C ðxþ ¼ ay; ð xþdy: ð34þ W The salient feature of this expression is that the evaluation of the integral term in (34) requires a closure model. Closure can be obtained by a large eddy diffusivity approximation [e.g., Kraichnan, 1987], leading to ay; ð xþ hk 0 ðþk x 0 ðyþir x r T y G ð y; x Þ; ð35þ where G is a deterministic Green s function defined as the solution of the deterministic groundwater flow equation, with K = hki. Alternatively, one can use perturbation expansion techniques. By doing so, the equations recovered for infinite domain provide the same solutions as the methodologies presented so far. We emphasize that a key theoretical advantage of the residual flux based approach is that the variables expanded are deterministic moments rather than random quantities. Expansion of moments is performed in series of a parameter representing a measure of the standard deviation of log-hydraulic conductivity, the smallness of which can be assessed. Key advantages of this methodology, as opposed to the others, are that (1) it does not require restrictions about the probability density function (pdf) of K and (2) it can incorporate conditioning on different types of information. An important application is the possibility of addressing bounded domains, as we will see in section Other Perturbative Techniques [41] Another method also based on perturbations is stochastic diagrammatic analysis. The basic idea is to perform a perturbation expansion similar to the one defined by (9) and (10). The difference lies in the way the resulting equations are treated. The resulting terms involving the integral of n-point correlations are presented in a concise form using Feynman s diagrams. These diagrams are applicable in bounded domains and are not restricted to small perturbations. Christakos et al. [1995] used this method to discuss the existence of an effective conductivity in heterogeneous media, arriving essentially at the same conclusions that can be drawn by means of the residual flux approach. An additional advantage of the diagrammatic method is that it allows obtaining results for partial summations at any given order in the expansion of (12) thus providing some insight to the solution in a number of cases. These partial summations cannot provide the full solution to any given order, and therefore the method is limited when applied to obtaining higher-order results in closed form. [42] Stepanyants and Teodorovich [2003] used a different perturbative approach based on the decomposition of seepage velocity into a potential plus a solenoidal function. Then they expanded the product K 1 (x)q(x) in terms of perturbations. Using a diagrammatic method, they can compute the low-order terms of the effective conductivity, providing the following result: K eff ¼ K G exp s 2 Y =2 " n 1 1 s 2 Y n þ 1 # n s 4 Y 2 n : ð36þ This result cannot be directly applied to large s 2 Y values, since these would provide a decreasing K eff value for increasing degree of heterogeneity in three dimensions. In addition to this it does not provide the exact solution K eff = K G in two dimensions. On the other hand, when Matheron s conjecture is applied to (36), the final results are in agreement with (19). [43] Another perturbative technique was initially used by Noetinger [1994]. His approach consisted of expanding in a 8of46
9 geometrical series the inverse of a linear integral operator that involves a Green s series. Noetinger then writes the effective conductivity as the sum of an infinite number of terms: K eff ¼ X1 N¼0 K N ; ð37þ where each K N term includes high-order correlation functions such as hexp(y 0 (r)y 0 (r 1 )...Y 0 (r N )i. For lognormal conductivity media, Noetinger [1994] summed up all the terms that do not include correlations between different points. This is equivalent to finding the exact expression for K eff for vanishing correlation length. The final expression corresponds exactly to (19), thus revealing that (19) is an exact result for negligible correlation length. Unfortunately, this methodology provides no additional insight with respect to other methodologies when applied to correlated conductivity fields Nonperturbative Methods Self-Consistent Approach [44] The self-consistent approach, also termed embedding matrix approach [Dagan, 1981], is based on the following idea: We start with a homogenized medium with a hydraulic conductivity value equal to K eff, which is unknown. An inclusion is incorporated into this medium. The shape and dimension of the inclusion depend on the problem analyzed, typically an n-dimensional sphere in isotropic media. The K value assigned to the inclusion, K inclusion, is drawn at random from a predefined pdf of K, p(k). For each particular value of K inclusion, there is a different head distribution solution. The K eff value is defined as that of a homogeneous medium whose head distribution equals the average of the inclusion head distributions. It is clear from the definition that the solution must always be obtained through an iterative process. In an isotropic medium, Dagan [1981] obtained the following solution for K eff : 2 K eff ¼ 1 4 n pk ð Þ dk5 K þ ðn 1ÞK eff 1 : ð38þ This methodology is not limited to small variances of the log conductivity field. Moreover, if p(k) is assumed to be lognormal, it provides the exact solution both for the one- (K eff = K H ) and the two-dimensional (K eff = K G ) cases [Dagan, 1993]. However, equation (38) leads to an underestimation of K eff in three dimensions. The selfconsistent approach has been widely used to derive effective parameters in anisotropic media and bimodal conductivity fields, as will be presented in sections 2.2 and Method of Moments [45] The method of moments [Kitanidis, 1990] takes advantage of the formalism of periodic media. Kitanidis assumed that the conductivity field is periodic in the threedimensional space and that the period in all three directions is known. Ergodicity can then be invoked by setting the periodic distance to infinity. The equivalence of ensemble parameters to those obtained by large periodization volume averaging has been demonstrated rigorously by Owhadi [2003]. The method consists of averaging out in real space (not in the ensemble) the effects of gradually varying flow (steady state being the limit for infinite time). Under these conditions, Kitanidis [1990] obtains that the effective conductivity is given by a volume integral over one single period. The volume integral involves functions that satisfy a Poisson-type PDE with periodic boundary conditions. By considering a volume which tends to infinity, he recovers an expression for K eff which coincides with (18). This method involves a rigorous mathematical formalism, and though it has not been widely used in the hydrogeological literature, it is commonly applied in other branches of physics ariational Method [46] The variational method consists of writing the actual expression for effective conductivity in Fourier space in order to eliminate the nonlocalities that arise from the solution to the flow equation using Green s functions. Auxiliary correlation functions are obtained through variational principles in an optimization process. Using this method, Hristopulos and Christakos [1997] provided an expression for effective hydraulic conductivity in an n- dimensional isotropic unbounded domain, 2 K eff ¼ hki 41 þ 1 4s2 K 2 nk h i 2! 1=2 3 5; ð39þ s K 2 being the variance of hydraulic conductivity. In the case of a small heterogeneity, equation (39) reduces to K eff ¼ hki s2 K nk h i : ð40þ According to Bulgadaev [2003], equation (40) was already obtained by Landau and Lifshitz [1960] in the field of electrodynamics. The solutions provided in (40) are subject to serious restrictions. For instance, in the case of lognormal hydraulic conductivity these reduce to ( K eff ¼ K r ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi) G 2 exp s2 Y =2 1 þ 1 4 ½ n exp ð s2 YÞ 1Š ð41aþ K eff ¼ K G exp s 2 Y =2 1 1 n exp s2 Y 1 : ð41bþ Then, for two-dimensional flow, values of s 2 Y larger than 0.4 would lead to imaginary values for K eff in (41a), while 2 s Y > 1.1 leads to negative values in (41b). Similar restrictions apply in three dimensions. All these results contradict the claim of Hristopulos and Christakos [1997] that the solution is not restricted to moderate heterogeneity Renormalization Methods [47] Noetinger [1994, 2000] used a renormalization group method to develop the K eff value for a lognormal 9of46
10 hydraulic conductivity field. The approach consists of defining a cutoff value in Fourier space, L, and then finding an analytical relationship between K eff (L +dl) and K eff (L). By considering the limit of L which tends to zero, Noetinger found out that (19) is an exact result, thus criticizing the results of De Wit [1995] obtained by a perturbations approach. Since De Wit s correction is very small for the usual range of s Y 2 values found in practical applications, this discrepancy between the two methods is very difficult to assess and not completely significant Other Methods [48] Madden [1976] modeled two-dimensional heterogeneous media as a random network and concluded that the geometric mean can be used to predict conductivity of heterogeneous mixtures of materials. His result is in line with later findings that the geometric mean of locally random hydraulic conductivities can be used, under certain flow conditions, as representative of the overall conductivity of the medium. [49] An approach in principle similar to that of Noetinger [1994] was presented by Teodorovich [1997, 2000]. Again, the idea is to expand the inverse of an operator. While the approach of Noetinger [1994] was in terms of perturbations, Teodorovich [1997, 2000] wrote it in terms of a Feynman path integral. This allows the author to work without perturbations. In any case the results obtained by this method are quite different from those reflected in the literature. The final expression for Teodorovich [1997, 2000] in a three-dimensional isotropic medium is given by "! # 1 s 2 K K eff ¼ hki hki 2 ½1 erfðs Y =2ÞŠ ; ð42þ where erf( ) stands for error function. This solution is not in agreement with solutions presented in section 2.1 (and validated numerically), thus questioning the applicability of the method to the problem of finding effective conductivities Anisotropic Media [50] The limiting case for an anisotropic medium is that of a perfectly stratified aquifer. When a head gradient is imposed parallel to stratification, the total flow equals that of a homogeneous medium with hydraulic conductivity K A (arithmetic mean of point K values). Contrariwise, if flow is perpendicular to stratification, the homogenous counterpart for hydraulic conductivity would be K H. These results can be traced back at least to Terzaghi and Peck [1948]. Invoking ergodic arguments, we can state that the effective hydraulic conductivities for flow parallel or perpendicular to stratification are hki and hk 1 i 1, respectively. [51] We return now to fields where heterogeneity is not deterministic. Let us consider a heterogeneous domain where K(x, w) is taken as locally isotropic but statistically anisotropic, meaning that a covariance structure exists and is directionally dependent. Let l 1, l 2, and l 3 be the correlation scales in the principal directions of correlation. If the global coordinate system (x 1, x 2, x 3 ) is taken to coincide with these principal directions, the effective conductivity expressed in these coordinates will exist and will be a diagonal tensor. [52] To our knowledge, Gelhar and Axness [1983] were the first to address the problem of effective conductivity in a two-dimensional anisotropic infinite domain under mean uniform flow conditions (actually they did it as the limiting case l 3!1in a three-dimensional problem). They found that K eff is a diagonal tensor whose principal components are given by K eff;i ¼ K G 1 þ s 2 1 Y 2 l j ; i; j ¼ 1; 2 and i 6¼ j: l 1 þ l 2 ð43þ It is more convenient to write the solution to the effective conductivity for the two-dimensional case in terms of the anisotropy ratio of the correlation structure. If we define the anisotropy ratio e = l 2 /l 1 (1) and we further consider (43) as the first terms of an exponential expansion, we can write 1 K eff;1 ¼ K G exp 2 e 1 þ e 1 K eff;2 ¼ K G exp þ e s 2 Y s 2 Y ð44aþ : ð44bþ [53] In Figure 2, K eff,1 and K eff,2 are presented as a function of e and s Y 2 based on (44). The asymptotic limits are well known. For e = 1 we get K eff,1 =K eff,2 =K G, thus recovering (18) and (19). The other limiting case is that of e! 0, which is equivalent to a layered system and allows recovering K eff,1 = hki and K eff,2 = hk 1 i 1. Other interesting results that can be extracted from (44a) are that for any given value of the anisotropic ratio, e, we obtain pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi K eff;1 K eff;2 ¼ K G ð45aþ K eff;1 ¼ exp 1 e K eff;2 e þ 1 s2 Y : ð45bþ [54] The last expression shows that the nonlinear relationship between the anisotropy ratios of the effective hydraulic conductivity and that of the log conductivity correlation scales [Sanchez-ila and Carrera, 1997]. From (45), and if one has information about e (coming from geostatistical analysis of data or geological analogues) and s Y 2 and K G (coming from laboratory- or field-based data), it would be possible (in principle) to evaluate the individual directional effective parameters and assess the principle directions of the effective conductivity tensor. [55] Since Gelhar and Axness [1983] several authors have considered the case of anisotropic correlation structures in three dimensions. The closed-form results were 10 of 46
Simple closed form formulas for predicting groundwater flow model uncertainty in complex, heterogeneous trending media
 WATER RESOURCES RESEARCH, VOL. 4,, doi:0.029/2005wr00443, 2005 Simple closed form formulas for predicting groundwater flow model uncertainty in complex, heterogeneous trending media Chuen-Fa Ni and Shu-Guang
WATER RESOURCES RESEARCH, VOL. 4,, doi:0.029/2005wr00443, 2005 Simple closed form formulas for predicting groundwater flow model uncertainty in complex, heterogeneous trending media Chuen-Fa Ni and Shu-Guang
Ensemble Kalman filter assimilation of transient groundwater flow data via stochastic moment equations
 Ensemble Kalman filter assimilation of transient groundwater flow data via stochastic moment equations Alberto Guadagnini (1,), Marco Panzeri (1), Monica Riva (1,), Shlomo P. Neuman () (1) Department of
Ensemble Kalman filter assimilation of transient groundwater flow data via stochastic moment equations Alberto Guadagnini (1,), Marco Panzeri (1), Monica Riva (1,), Shlomo P. Neuman () (1) Department of
Assessment of Hydraulic Conductivity Upscaling Techniques and. Associated Uncertainty
 CMWRXVI Assessment of Hydraulic Conductivity Upscaling Techniques and Associated Uncertainty FARAG BOTROS,, 4, AHMED HASSAN 3, 4, AND GREG POHLL Division of Hydrologic Sciences, University of Nevada, Reno
CMWRXVI Assessment of Hydraulic Conductivity Upscaling Techniques and Associated Uncertainty FARAG BOTROS,, 4, AHMED HASSAN 3, 4, AND GREG POHLL Division of Hydrologic Sciences, University of Nevada, Reno
Deterministic solution of stochastic groundwater flow equations by nonlocalfiniteelements A. Guadagnini^ & S.P. Neuman^
 Deterministic solution of stochastic groundwater flow equations by nonlocalfiniteelements A. Guadagnini^ & S.P. Neuman^ Milano, Italy; ^Department of. Hydrology & Water Resources, The University ofarizona,
Deterministic solution of stochastic groundwater flow equations by nonlocalfiniteelements A. Guadagnini^ & S.P. Neuman^ Milano, Italy; ^Department of. Hydrology & Water Resources, The University ofarizona,
MOMENT DIFFERENTIAL EQUATIONS FOR FLOW IN HIGHLY HETEROGENEOUS POROUS MEDIA
 MOMENT DIFFERENTIAL EQUATIONS FOR FLOW IN HIGHLY HETEROGENEOUS POROUS MEDIA C.L. WINTER Mathematical Modeling & Analysis Group and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos,
MOMENT DIFFERENTIAL EQUATIONS FOR FLOW IN HIGHLY HETEROGENEOUS POROUS MEDIA C.L. WINTER Mathematical Modeling & Analysis Group and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos,
Type-curve estimation of statistical heterogeneity
 WATER RESOURCES RESEARCH, VOL. 40,, doi:10.1029/2003wr002405, 2004 Type-curve estimation of statistical heterogeneity Shlomo P. Neuman Department of Hydrology and Water Resources, University of Arizona,
WATER RESOURCES RESEARCH, VOL. 40,, doi:10.1029/2003wr002405, 2004 Type-curve estimation of statistical heterogeneity Shlomo P. Neuman Department of Hydrology and Water Resources, University of Arizona,
6. GRID DESIGN AND ACCURACY IN NUMERICAL SIMULATIONS OF VARIABLY SATURATED FLOW IN RANDOM MEDIA: REVIEW AND NUMERICAL ANALYSIS
 Harter Dissertation - 1994-132 6. GRID DESIGN AND ACCURACY IN NUMERICAL SIMULATIONS OF VARIABLY SATURATED FLOW IN RANDOM MEDIA: REVIEW AND NUMERICAL ANALYSIS 6.1 Introduction Most numerical stochastic
Harter Dissertation - 1994-132 6. GRID DESIGN AND ACCURACY IN NUMERICAL SIMULATIONS OF VARIABLY SATURATED FLOW IN RANDOM MEDIA: REVIEW AND NUMERICAL ANALYSIS 6.1 Introduction Most numerical stochastic
Hydraulic tomography: Development of a new aquifer test method
 WATER RESOURCES RESEARCH, VOL. 36, NO. 8, PAGES 2095 2105, AUGUST 2000 Hydraulic tomography: Development of a new aquifer test method T.-C. Jim Yeh and Shuyun Liu Department of Hydrology and Water Resources,
WATER RESOURCES RESEARCH, VOL. 36, NO. 8, PAGES 2095 2105, AUGUST 2000 Hydraulic tomography: Development of a new aquifer test method T.-C. Jim Yeh and Shuyun Liu Department of Hydrology and Water Resources,
Type curve interpretation of late-time pumping test data in randomly heterogeneous aquifers
 WATER RESOURCES RESEARCH, VOL. 43,, doi:10.1029/2007wr005871, 2007 Type curve interpretation of late-time pumping test data in randomly heterogeneous aquifers Shlomo P. Neuman, 1 Ayelet Blattstein, 1,2
WATER RESOURCES RESEARCH, VOL. 43,, doi:10.1029/2007wr005871, 2007 Type curve interpretation of late-time pumping test data in randomly heterogeneous aquifers Shlomo P. Neuman, 1 Ayelet Blattstein, 1,2
In all of the following equations, is the coefficient of permeability in the x direction, and is the hydraulic head.
 Groundwater Seepage 1 Groundwater Seepage Simplified Steady State Fluid Flow The finite element method can be used to model both steady state and transient groundwater flow, and it has been used to incorporate
Groundwater Seepage 1 Groundwater Seepage Simplified Steady State Fluid Flow The finite element method can be used to model both steady state and transient groundwater flow, and it has been used to incorporate
Use of the Fourier Laplace transform and of diagrammatical methods to interpret pumping tests in heterogeneous reservoirs
 PII: S39-78(97)4-6 Advances in Water Resources, Vol. 2, pp. 58 59, 998 998 Elsevier Science Limited All rights reserved. Printed in Great Britain 39-78/98/$9. +. Use of the Fourier Laplace transform and
PII: S39-78(97)4-6 Advances in Water Resources, Vol. 2, pp. 58 59, 998 998 Elsevier Science Limited All rights reserved. Printed in Great Britain 39-78/98/$9. +. Use of the Fourier Laplace transform and
Reactive Transport in Porous Media
 Reactive Transport in Porous Media Daniel M. Tartakovsky Department of Mechanical & Aerospace Engineering University of California, San Diego Alberto Guadagnini, Politecnico di Milano, Italy Peter C. Lichtner,
Reactive Transport in Porous Media Daniel M. Tartakovsky Department of Mechanical & Aerospace Engineering University of California, San Diego Alberto Guadagnini, Politecnico di Milano, Italy Peter C. Lichtner,
BME STUDIES OF STOCHASTIC DIFFERENTIAL EQUATIONS REPRESENTING PHYSICAL LAW
 7 VIII. BME STUDIES OF STOCHASTIC DIFFERENTIAL EQUATIONS REPRESENTING PHYSICAL LAW A wide variety of natural processes are described using physical laws. A physical law may be expressed by means of an
7 VIII. BME STUDIES OF STOCHASTIC DIFFERENTIAL EQUATIONS REPRESENTING PHYSICAL LAW A wide variety of natural processes are described using physical laws. A physical law may be expressed by means of an
B005 A NEW FAST FOURIER TRANSFORM ALGORITHM FOR FLUID FLOW SIMULATION
 1 B5 A NEW FAST FOURIER TRANSFORM ALGORITHM FOR FLUID FLOW SIMULATION LUDOVIC RICARD, MICAËLE LE RAVALEC-DUPIN, BENOÎT NOETINGER AND YVES GUÉGUEN Institut Français du Pétrole, 1& 4 avenue Bois Préau, 92852
1 B5 A NEW FAST FOURIER TRANSFORM ALGORITHM FOR FLUID FLOW SIMULATION LUDOVIC RICARD, MICAËLE LE RAVALEC-DUPIN, BENOÎT NOETINGER AND YVES GUÉGUEN Institut Français du Pétrole, 1& 4 avenue Bois Préau, 92852
Darcy's Law. Laboratory 2 HWR 531/431
 Darcy's Law Laboratory HWR 531/431-1 Introduction In 1856, Henry Darcy, a French hydraulic engineer, published a report in which he described a series of experiments he had performed in an attempt to quantify
Darcy's Law Laboratory HWR 531/431-1 Introduction In 1856, Henry Darcy, a French hydraulic engineer, published a report in which he described a series of experiments he had performed in an attempt to quantify
= _(2,r)af OG(x, a) 0p(a, y da (2) Aj(r) = (2*r)a (Oh(x)y,(y)) A (r) = -(2,r) a Ox Oxj G(x, a)p(a, y) da
 WATER RESOURCES RESEARCH, VOL. 35, NO. 7, PAGES 2273-2277, JULY 999 A general method for obtaining analytical expressions for the first-order velocity covariance in heterogeneous porous media Kuo-Chin
WATER RESOURCES RESEARCH, VOL. 35, NO. 7, PAGES 2273-2277, JULY 999 A general method for obtaining analytical expressions for the first-order velocity covariance in heterogeneous porous media Kuo-Chin
RATE OF FLUID FLOW THROUGH POROUS MEDIA
 RATE OF FLUID FLOW THROUGH POROUS MEDIA Submitted by Xu Ming Xin Kiong Min Yi Kimberly Yip Juen Chen Nicole A project presented to the Singapore Mathematical Society Essay Competition 2013 1 Abstract Fluid
RATE OF FLUID FLOW THROUGH POROUS MEDIA Submitted by Xu Ming Xin Kiong Min Yi Kimberly Yip Juen Chen Nicole A project presented to the Singapore Mathematical Society Essay Competition 2013 1 Abstract Fluid
Inverse Modelling for Flow and Transport in Porous Media
 Inverse Modelling for Flow and Transport in Porous Media Mauro Giudici 1 Dipartimento di Scienze della Terra, Sezione di Geofisica, Università degli Studi di Milano, Milano, Italy Lecture given at the
Inverse Modelling for Flow and Transport in Porous Media Mauro Giudici 1 Dipartimento di Scienze della Terra, Sezione di Geofisica, Università degli Studi di Milano, Milano, Italy Lecture given at the
Prediction of transient flow in random porous media by conditional moments
 Prediction of transient flow in random porous media by conditional moments Item Type Dissertation-Reproduction (electronic); text Authors Tartakovsky, Daniel. Publisher The University of Arizona. Rights
Prediction of transient flow in random porous media by conditional moments Item Type Dissertation-Reproduction (electronic); text Authors Tartakovsky, Daniel. Publisher The University of Arizona. Rights
New Renormalization Schemes for Conductivity Upscaling in Heterogeneous Media
 Transp Porous Med () 85:677 69 DOI.7/s4--9585-9 New Renormalization Schemes for Conductivity Upscaling in Heterogeneous Media M. R. Karim K. Krabbenhoft Received: 8 February / Accepted: April / Published
Transp Porous Med () 85:677 69 DOI.7/s4--9585-9 New Renormalization Schemes for Conductivity Upscaling in Heterogeneous Media M. R. Karim K. Krabbenhoft Received: 8 February / Accepted: April / Published
Lecture 6: Introduction to Partial Differential Equations
 Introductory lecture notes on Partial Differential Equations - c Anthony Peirce. Not to be copied, used, or revised without explicit written permission from the copyright owner. 1 Lecture 6: Introduction
Introductory lecture notes on Partial Differential Equations - c Anthony Peirce. Not to be copied, used, or revised without explicit written permission from the copyright owner. 1 Lecture 6: Introduction
A hybrid Marquardt-Simulated Annealing method for solving the groundwater inverse problem
 Calibration and Reliability in Groundwater Modelling (Proceedings of the ModelCARE 99 Conference held at Zurich, Switzerland, September 1999). IAHS Publ. no. 265, 2000. 157 A hybrid Marquardt-Simulated
Calibration and Reliability in Groundwater Modelling (Proceedings of the ModelCARE 99 Conference held at Zurich, Switzerland, September 1999). IAHS Publ. no. 265, 2000. 157 A hybrid Marquardt-Simulated
CHAPTER V. Brownian motion. V.1 Langevin dynamics
 CHAPTER V Brownian motion In this chapter, we study the very general paradigm provided by Brownian motion. Originally, this motion is that a heavy particle, called Brownian particle, immersed in a fluid
CHAPTER V Brownian motion In this chapter, we study the very general paradigm provided by Brownian motion. Originally, this motion is that a heavy particle, called Brownian particle, immersed in a fluid
(Refer Slide Time: 02:10)
 Soil Mechanics Prof. B.V.S. Viswanathan Department of Civil Engineering Indian Institute of Technology, Bombay Lecture 24 Flow of water through soils-v Welcome to lecture five of flow of water through
Soil Mechanics Prof. B.V.S. Viswanathan Department of Civil Engineering Indian Institute of Technology, Bombay Lecture 24 Flow of water through soils-v Welcome to lecture five of flow of water through
Introduction to Environment System Modeling
 Introduction to Environment System Modeling (3 rd week:modeling with differential equation) Department of Environment Systems, Graduate School of Frontier Sciences, the University of Tokyo Masaatsu AICHI
Introduction to Environment System Modeling (3 rd week:modeling with differential equation) Department of Environment Systems, Graduate School of Frontier Sciences, the University of Tokyo Masaatsu AICHI
Conditional moment analysis of steady state unsaturated flow in bounded, randomly heterogeneous soils
 WATR RSOURCS RSARCH, VOL. 38, NO. 4, 10.109/001WR00078, 00 Conditional moment analysis of steady state unsaturated flow in bounded, randomly heterogeneous soils himing Lu and Shlomo P. Neuman Department
WATR RSOURCS RSARCH, VOL. 38, NO. 4, 10.109/001WR00078, 00 Conditional moment analysis of steady state unsaturated flow in bounded, randomly heterogeneous soils himing Lu and Shlomo P. Neuman Department
On stochastic modeling of flow in multimodal heterogeneous formations
 WATER RESOURCES RESEARCH, VOL. 38, NO. 10, 1190, doi:10.109/001wr00106, 00 On stochastic modeling of flow in multimodal heterogeneous formations Zhiming Lu and Dongxiao Zhang Hydrology, Geochemistry, and
WATER RESOURCES RESEARCH, VOL. 38, NO. 10, 1190, doi:10.109/001wr00106, 00 On stochastic modeling of flow in multimodal heterogeneous formations Zhiming Lu and Dongxiao Zhang Hydrology, Geochemistry, and
Effective unsaturated hydraulic conductivity for one-dimensional structured heterogeneity
 WATER RESOURCES RESEARCH, VOL. 41, W09406, doi:10.1029/2005wr003988, 2005 Effective unsaturated hydraulic conductivity for one-dimensional structured heterogeneity A. W. Warrick Department of Soil, Water
WATER RESOURCES RESEARCH, VOL. 41, W09406, doi:10.1029/2005wr003988, 2005 Effective unsaturated hydraulic conductivity for one-dimensional structured heterogeneity A. W. Warrick Department of Soil, Water
*** ***! " " ) * % )!( & ' % # $. 0 1 %./ +, - 7 : %8% 9 ) 7 / ( * 7 : %8% 9 < ;14. " > /' ;-,=. / ١
 ١ ******!" #$ % & '!( ) % * ") +,-./ % 01. 3 ( 4 56 7/4 ) 8%9 % : 7 ;14 < 8%9 % : *7./ = ;-, >/'." Soil Permeability & Seepage ٢ Soil Permeability- Definition ٣ What is Permeability? Permeability is the
١ ******!" #$ % & '!( ) % * ") +,-./ % 01. 3 ( 4 56 7/4 ) 8%9 % : 7 ;14 < 8%9 % : *7./ = ;-, >/'." Soil Permeability & Seepage ٢ Soil Permeability- Definition ٣ What is Permeability? Permeability is the
Hydraulic properties of porous media
 PART 5 Hydraulic properties of porous media Porosity Definition: Void space: n V void /V total total porosity e V void /V solid Primary porosity - between grains Secondary porosity - fracture or solution
PART 5 Hydraulic properties of porous media Porosity Definition: Void space: n V void /V total total porosity e V void /V solid Primary porosity - between grains Secondary porosity - fracture or solution
Tailing of the breakthrough curve in aquifer contaminant transport: equivalent longitudinal macrodispersivity and occurrence of anomalous transport
 5 GQ7: Securing Groundwater Quality in Urban and Industrial Environments (Proc. 6th International Groundwater Quality Conference held in Fremantle, Western Australia, 2 7 December 27). IAHS Publ. no. XXX,
5 GQ7: Securing Groundwater Quality in Urban and Industrial Environments (Proc. 6th International Groundwater Quality Conference held in Fremantle, Western Australia, 2 7 December 27). IAHS Publ. no. XXX,
Flow in unsaturated random porous media, nonlinear numerical analysis and comparison to analytical stochastic models
 Advances in Water Resources Vol. 22, No. 3, pp. 257 272, 1998 1998 Elsevier Science Ltd Printed in Great Britain. All rights reserved PII:S0309-1708(98)00010-4 0309-1708/98/$ - see front matter Flow in
Advances in Water Resources Vol. 22, No. 3, pp. 257 272, 1998 1998 Elsevier Science Ltd Printed in Great Britain. All rights reserved PII:S0309-1708(98)00010-4 0309-1708/98/$ - see front matter Flow in
Darcy s law in 3-D. K * xx K * yy K * zz
 PART 7 Equations of flow Darcy s law in 3-D Specific discarge (vector) is calculated by multiplying te ydraulic conductivity (second-order tensor) by te ydraulic gradient (vector). We obtain a general
PART 7 Equations of flow Darcy s law in 3-D Specific discarge (vector) is calculated by multiplying te ydraulic conductivity (second-order tensor) by te ydraulic gradient (vector). We obtain a general
A continuous time random walk approach to transient flow in heterogeneous porous media
 WATER RESOURCES RESEARCH, VOL. 42,, doi:10.1029/2006wr005227, 2006 A continuous time random walk approach to transient flow in heterogeneous porous media Andrea Cortis 1 and Christen Knudby 2 Received
WATER RESOURCES RESEARCH, VOL. 42,, doi:10.1029/2006wr005227, 2006 A continuous time random walk approach to transient flow in heterogeneous porous media Andrea Cortis 1 and Christen Knudby 2 Received
A GENERALIZED CONVECTION-DIFFUSION MODEL FOR SUBGRID TRANSPORT IN POROUS MEDIA
 MULTISCALE MODEL. SIMUL. Vol. 1, No. 3, pp. 504 526 c 2003 Society for Industrial and Applied Mathematics A GENERALIZED CONVECTION-DIFFUSION MODEL FOR SUBGRID TRANSPORT IN POROUS MEDIA Y. EFENDIEV AND
MULTISCALE MODEL. SIMUL. Vol. 1, No. 3, pp. 504 526 c 2003 Society for Industrial and Applied Mathematics A GENERALIZED CONVECTION-DIFFUSION MODEL FOR SUBGRID TRANSPORT IN POROUS MEDIA Y. EFENDIEV AND
Capturing aquifer heterogeneity: Comparison of approaches through controlled sandbox experiments
 WATER RESOURCES RESEARCH, VOL. 47, W09514, doi:10.1029/2011wr010429, 2011 Capturing aquifer heterogeneity: Comparison of approaches through controlled sandbox experiments Steven J. Berg 1 and Walter A.
WATER RESOURCES RESEARCH, VOL. 47, W09514, doi:10.1029/2011wr010429, 2011 Capturing aquifer heterogeneity: Comparison of approaches through controlled sandbox experiments Steven J. Berg 1 and Walter A.
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION
 CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
7 The Navier-Stokes Equations
 18.354/12.27 Spring 214 7 The Navier-Stokes Equations In the previous section, we have seen how one can deduce the general structure of hydrodynamic equations from purely macroscopic considerations and
18.354/12.27 Spring 214 7 The Navier-Stokes Equations In the previous section, we have seen how one can deduce the general structure of hydrodynamic equations from purely macroscopic considerations and
Kernel-based Approximation. Methods using MATLAB. Gregory Fasshauer. Interdisciplinary Mathematical Sciences. Michael McCourt.
 SINGAPORE SHANGHAI Vol TAIPEI - Interdisciplinary Mathematical Sciences 19 Kernel-based Approximation Methods using MATLAB Gregory Fasshauer Illinois Institute of Technology, USA Michael McCourt University
SINGAPORE SHANGHAI Vol TAIPEI - Interdisciplinary Mathematical Sciences 19 Kernel-based Approximation Methods using MATLAB Gregory Fasshauer Illinois Institute of Technology, USA Michael McCourt University
Energy minimization for the flow in ducts and networks
 Energy minimization for the flow in ducts and networks Taha Sochi University College London, Department of Physics & Astronomy, Gower Street, London, WC1E 6BT Email: t.sochi@ucl.ac.uk. Abstract The present
Energy minimization for the flow in ducts and networks Taha Sochi University College London, Department of Physics & Astronomy, Gower Street, London, WC1E 6BT Email: t.sochi@ucl.ac.uk. Abstract The present
3. DIFFERENT MODEL TYPES
 3-1 3. DIFFERENT MODEL TYPES It is important for us to fully understand a physical problem before we can select a solution strategy for it. Models are convenient tools that enhance our understanding and
3-1 3. DIFFERENT MODEL TYPES It is important for us to fully understand a physical problem before we can select a solution strategy for it. Models are convenient tools that enhance our understanding and
4. The Green Kubo Relations
 4. The Green Kubo Relations 4.1 The Langevin Equation In 1828 the botanist Robert Brown observed the motion of pollen grains suspended in a fluid. Although the system was allowed to come to equilibrium,
4. The Green Kubo Relations 4.1 The Langevin Equation In 1828 the botanist Robert Brown observed the motion of pollen grains suspended in a fluid. Although the system was allowed to come to equilibrium,
18 Single vertical fractures
 18 Single vertical fractures 18.1 Introduction If a well intersects a single vertical fracture, the aquifer s unsteady drawdown response to pumping differs significantly from that predicted by the Theis
18 Single vertical fractures 18.1 Introduction If a well intersects a single vertical fracture, the aquifer s unsteady drawdown response to pumping differs significantly from that predicted by the Theis
1.72, Groundwater Hydrology Prof. Charles Harvey Lecture Packet #4: Continuity and Flow Nets
 1.7, Groundwater Hydrology Prof. Charles Harvey Lecture Packet #4: Continuity and Flow Nets Equation of Continuity Our equations of hydrogeology are a combination of o Conservation of mass o Some empirical
1.7, Groundwater Hydrology Prof. Charles Harvey Lecture Packet #4: Continuity and Flow Nets Equation of Continuity Our equations of hydrogeology are a combination of o Conservation of mass o Some empirical
Numerical methods for the Navier- Stokes equations
 Numerical methods for the Navier- Stokes equations Hans Petter Langtangen 1,2 1 Center for Biomedical Computing, Simula Research Laboratory 2 Department of Informatics, University of Oslo Dec 6, 2012 Note:
Numerical methods for the Navier- Stokes equations Hans Petter Langtangen 1,2 1 Center for Biomedical Computing, Simula Research Laboratory 2 Department of Informatics, University of Oslo Dec 6, 2012 Note:
Conditional Distribution Fitting of High Dimensional Stationary Data
 Conditional Distribution Fitting of High Dimensional Stationary Data Miguel Cuba and Oy Leuangthong The second order stationary assumption implies the spatial variability defined by the variogram is constant
Conditional Distribution Fitting of High Dimensional Stationary Data Miguel Cuba and Oy Leuangthong The second order stationary assumption implies the spatial variability defined by the variogram is constant
dynamics of f luids in porous media
 dynamics of f luids in porous media Jacob Bear Department of Civil Engineering Technion Israel Institute of Technology, Haifa DOVER PUBLICATIONS, INC. New York Contents Preface xvii CHAPTER 1 Introduction
dynamics of f luids in porous media Jacob Bear Department of Civil Engineering Technion Israel Institute of Technology, Haifa DOVER PUBLICATIONS, INC. New York Contents Preface xvii CHAPTER 1 Introduction
2 GOVERNING EQUATIONS
 2 GOVERNING EQUATIONS 9 2 GOVERNING EQUATIONS For completeness we will take a brief moment to review the governing equations for a turbulent uid. We will present them both in physical space coordinates
2 GOVERNING EQUATIONS 9 2 GOVERNING EQUATIONS For completeness we will take a brief moment to review the governing equations for a turbulent uid. We will present them both in physical space coordinates
Game Physics. Game and Media Technology Master Program - Utrecht University. Dr. Nicolas Pronost
 Game and Media Technology Master Program - Utrecht University Dr. Nicolas Pronost Soft body physics Soft bodies In reality, objects are not purely rigid for some it is a good approximation but if you hit
Game and Media Technology Master Program - Utrecht University Dr. Nicolas Pronost Soft body physics Soft bodies In reality, objects are not purely rigid for some it is a good approximation but if you hit
Macrodispersivity for transport in arbitrary nonuniform flow fields: Asymptotic and preasymptotic results
 WATER RESOURCES RESEARCH, VOL. 38, NO. 1, 1187, doi:1.129/21wr123, 22 Macrodispersivity for transport in arbitrary nonuniform flow fields: Asymptotic and preasymptotic results Ivan Lunati, Sabine Attinger,
WATER RESOURCES RESEARCH, VOL. 38, NO. 1, 1187, doi:1.129/21wr123, 22 Macrodispersivity for transport in arbitrary nonuniform flow fields: Asymptotic and preasymptotic results Ivan Lunati, Sabine Attinger,
On the formation of breakthrough curves tailing during convergent flow tracer tests in three-dimensional heterogeneous aquifers
 WATER RESOURCES RESEARCH, VOL. 49, 1 17, doi:10.1002/wrcr.20330, 2013 On the formation of breakthrough curves tailing during convergent flow tracer tests in three-dimensional heterogeneous aquifers D.
WATER RESOURCES RESEARCH, VOL. 49, 1 17, doi:10.1002/wrcr.20330, 2013 On the formation of breakthrough curves tailing during convergent flow tracer tests in three-dimensional heterogeneous aquifers D.
Introduction to Well Hydraulics Fritz R. Fiedler
 Introduction to Well Hydraulics Fritz R. Fiedler A well is a pipe placed in a drilled hole that has slots (screen) cut into it that allow water to enter the well, but keep the aquifer material out. A well
Introduction to Well Hydraulics Fritz R. Fiedler A well is a pipe placed in a drilled hole that has slots (screen) cut into it that allow water to enter the well, but keep the aquifer material out. A well
Basics of Point-Referenced Data Models
 Basics of Point-Referenced Data Models Basic tool is a spatial process, {Y (s), s D}, where D R r Chapter 2: Basics of Point-Referenced Data Models p. 1/45 Basics of Point-Referenced Data Models Basic
Basics of Point-Referenced Data Models Basic tool is a spatial process, {Y (s), s D}, where D R r Chapter 2: Basics of Point-Referenced Data Models p. 1/45 Basics of Point-Referenced Data Models Basic
Elements of Continuum Elasticity. David M. Parks Mechanics and Materials II February 25, 2004
 Elements of Continuum Elasticity David M. Parks Mechanics and Materials II 2.002 February 25, 2004 Solid Mechanics in 3 Dimensions: stress/equilibrium, strain/displacement, and intro to linear elastic
Elements of Continuum Elasticity David M. Parks Mechanics and Materials II 2.002 February 25, 2004 Solid Mechanics in 3 Dimensions: stress/equilibrium, strain/displacement, and intro to linear elastic
Chapter 1 Direct Modeling for Computational Fluid Dynamics
 Chapter 1 Direct Modeling for Computational Fluid Dynamics Computational fluid dynamics (CFD) is a scientific discipline, which aims to capture fluid motion in a discretized space. The description of the
Chapter 1 Direct Modeling for Computational Fluid Dynamics Computational fluid dynamics (CFD) is a scientific discipline, which aims to capture fluid motion in a discretized space. The description of the
Natalia Tronko S.V.Nazarenko S. Galtier
 IPP Garching, ESF Exploratory Workshop Natalia Tronko University of York, York Plasma Institute In collaboration with S.V.Nazarenko University of Warwick S. Galtier University of Paris XI Outline Motivations:
IPP Garching, ESF Exploratory Workshop Natalia Tronko University of York, York Plasma Institute In collaboration with S.V.Nazarenko University of Warwick S. Galtier University of Paris XI Outline Motivations:
7 Geostatistics. Figure 7.1 Focus of geostatistics
 7 Geostatistics 7.1 Introduction Geostatistics is the part of statistics that is concerned with geo-referenced data, i.e. data that are linked to spatial coordinates. To describe the spatial variation
7 Geostatistics 7.1 Introduction Geostatistics is the part of statistics that is concerned with geo-referenced data, i.e. data that are linked to spatial coordinates. To describe the spatial variation
Numerical Solution of the Two-Dimensional Time-Dependent Transport Equation. Khaled Ismail Hamza 1 EXTENDED ABSTRACT
 Second International Conference on Saltwater Intrusion and Coastal Aquifers Monitoring, Modeling, and Management. Mérida, México, March 3-April 2 Numerical Solution of the Two-Dimensional Time-Dependent
Second International Conference on Saltwater Intrusion and Coastal Aquifers Monitoring, Modeling, and Management. Mérida, México, March 3-April 2 Numerical Solution of the Two-Dimensional Time-Dependent
Exact transverse macro dispersion coefficients for transport in heterogeneous porous media
 Stochastic Environmental Resea (2004) 18: 9 15 Ó Springer-Verlag 2004 DOI 10.1007/s00477-003-0160-6 ORIGINAL PAPER S. Attinger Æ M. Dentz Æ W. Kinzelbach Exact transverse macro dispersion coefficients
Stochastic Environmental Resea (2004) 18: 9 15 Ó Springer-Verlag 2004 DOI 10.1007/s00477-003-0160-6 ORIGINAL PAPER S. Attinger Æ M. Dentz Æ W. Kinzelbach Exact transverse macro dispersion coefficients
Upscaled flow and transport properties for heterogeneous unsaturated media
 WATER RESOURCES RESEARCH, VOL. 38, NO. 5, 1053, 10.1029/2000WR000072, 2002 Upscaled flow and transport properties for heterogeneous unsaturated media Raziuddin Khaleel Fluor Federal Services, Richland,
WATER RESOURCES RESEARCH, VOL. 38, NO. 5, 1053, 10.1029/2000WR000072, 2002 Upscaled flow and transport properties for heterogeneous unsaturated media Raziuddin Khaleel Fluor Federal Services, Richland,
Uncertainty quantification for flow in highly heterogeneous porous media
 695 Uncertainty quantification for flow in highly heterogeneous porous media D. Xiu and D.M. Tartakovsky a a Theoretical Division, Los Alamos National Laboratory, Mathematical Modeling and Analysis Group
695 Uncertainty quantification for flow in highly heterogeneous porous media D. Xiu and D.M. Tartakovsky a a Theoretical Division, Los Alamos National Laboratory, Mathematical Modeling and Analysis Group
Introduction to Aspects of Multiscale Modeling as Applied to Porous Media
 Introduction to Aspects of Multiscale Modeling as Applied to Porous Media Part II Todd Arbogast Department of Mathematics and Center for Subsurface Modeling, Institute for Computational Engineering and
Introduction to Aspects of Multiscale Modeling as Applied to Porous Media Part II Todd Arbogast Department of Mathematics and Center for Subsurface Modeling, Institute for Computational Engineering and
CENG 501 Examination Problem: Estimation of Viscosity with a Falling - Cylinder Viscometer
 CENG 501 Examination Problem: Estimation of Viscosity with a Falling - Cylinder Viscometer You are assigned to design a fallingcylinder viscometer to measure the viscosity of Newtonian liquids. A schematic
CENG 501 Examination Problem: Estimation of Viscosity with a Falling - Cylinder Viscometer You are assigned to design a fallingcylinder viscometer to measure the viscosity of Newtonian liquids. A schematic
Characterization of heterogeneous hydraulic conductivity field via Karhunen-Loève expansions and a measure-theoretic computational method
 Characterization of heterogeneous hydraulic conductivity field via Karhunen-Loève expansions and a measure-theoretic computational method Jiachuan He University of Texas at Austin April 15, 2016 Jiachuan
Characterization of heterogeneous hydraulic conductivity field via Karhunen-Loève expansions and a measure-theoretic computational method Jiachuan He University of Texas at Austin April 15, 2016 Jiachuan
Stochastic uncertainty analysis for solute transport in randomly heterogeneous media using a Karhunen-Loève-based moment equation approach
 WATER RESOURCES RESEARCH, VOL. 43,, doi:10.1029/2006wr005193, 2007 Stochastic uncertainty analysis for solute transport in randomly heterogeneous media using a Karhunen-Loève-based moment equation approach
WATER RESOURCES RESEARCH, VOL. 43,, doi:10.1029/2006wr005193, 2007 Stochastic uncertainty analysis for solute transport in randomly heterogeneous media using a Karhunen-Loève-based moment equation approach
centrifugal acceleration, whose magnitude is r cos, is zero at the poles and maximum at the equator. This distribution of the centrifugal acceleration
 Lecture 10. Equations of Motion Centripetal Acceleration, Gravitation and Gravity The centripetal acceleration of a body located on the Earth's surface at a distance from the center is the force (per unit
Lecture 10. Equations of Motion Centripetal Acceleration, Gravitation and Gravity The centripetal acceleration of a body located on the Earth's surface at a distance from the center is the force (per unit
If we want to analyze experimental or simulated data we might encounter the following tasks:
 Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Stochastic Structural Dynamics Prof. Dr. C. S. Manohar Department of Civil Engineering Indian Institute of Science, Bangalore
 Stochastic Structural Dynamics Prof. Dr. C. S. Manohar Department of Civil Engineering Indian Institute of Science, Bangalore Lecture No. # 33 Probabilistic methods in earthquake engineering-2 So, we have
Stochastic Structural Dynamics Prof. Dr. C. S. Manohar Department of Civil Engineering Indian Institute of Science, Bangalore Lecture No. # 33 Probabilistic methods in earthquake engineering-2 So, we have
Benefits of Collaboration between Centrifuge Modeling and Numerical Modeling. Xiangwu Zeng Case Western Reserve University, Cleveland, Ohio
 Benefits of Collaboration between Centrifuge Modeling and Numerical Modeling Xiangwu Zeng Case Western Reserve University, Cleveland, Ohio ABSTRACT There is little doubt that collaboration between centrifuge
Benefits of Collaboration between Centrifuge Modeling and Numerical Modeling Xiangwu Zeng Case Western Reserve University, Cleveland, Ohio ABSTRACT There is little doubt that collaboration between centrifuge
Receiver. Johana Brokešová Charles University in Prague
 Propagation of seismic waves - theoretical background Receiver Johana Brokešová Charles University in Prague Seismic waves = waves in elastic continuum a model of the medium through which the waves propagate
Propagation of seismic waves - theoretical background Receiver Johana Brokešová Charles University in Prague Seismic waves = waves in elastic continuum a model of the medium through which the waves propagate
11280 Electrical Resistivity Tomography Time-lapse Monitoring of Three-dimensional Synthetic Tracer Test Experiments
 11280 Electrical Resistivity Tomography Time-lapse Monitoring of Three-dimensional Synthetic Tracer Test Experiments M. Camporese (University of Padova), G. Cassiani* (University of Padova), R. Deiana
11280 Electrical Resistivity Tomography Time-lapse Monitoring of Three-dimensional Synthetic Tracer Test Experiments M. Camporese (University of Padova), G. Cassiani* (University of Padova), R. Deiana
Journal of Hydrology
 Journal of Hydrology 387 (21) 32 327 Contents lists available at ScienceDirect Journal of Hydrology journal homepage: www.elsevier.com/locate/jhydrol Steady-state discharge into tunnels in formations with
Journal of Hydrology 387 (21) 32 327 Contents lists available at ScienceDirect Journal of Hydrology journal homepage: www.elsevier.com/locate/jhydrol Steady-state discharge into tunnels in formations with
Upscaling of Richards equation for soil moisture dynamics to be utilized in mesoscale atmospheric models
 Exchange Processes at the imnd Surface for a Range of Space and Time Scales (Proceedings of the Yokohama Symposium, July 1993). [AHS Publ. no. 212, 1993. 125 Upscaling of Richards equation for soil moisture
Exchange Processes at the imnd Surface for a Range of Space and Time Scales (Proceedings of the Yokohama Symposium, July 1993). [AHS Publ. no. 212, 1993. 125 Upscaling of Richards equation for soil moisture
On the advective-diffusive transport in porous media in the presence of time-dependent velocities
 GEOPHYSICAL RESEARCH LETTERS, VOL. 3, L355, doi:.29/24gl9646, 24 On the advective-diffusive transport in porous media in the presence of time-dependent velocities A. P. S. Selvadurai Department of Civil
GEOPHYSICAL RESEARCH LETTERS, VOL. 3, L355, doi:.29/24gl9646, 24 On the advective-diffusive transport in porous media in the presence of time-dependent velocities A. P. S. Selvadurai Department of Civil
Technical note: Analytical drawdown solution for steady-state pumping tests in two-dimensional isotropic heterogeneous aquifers
 Hydrol. Earth Syst. Sci., 0, 655 667, 06 www.hydrol-earth-syst-sci.net/0/655/06/ doi:0.594/hess-0-655-06 Authors 06. CC Attribution 3.0 License. Technical note: Analytical drawdown solution for steady-state
Hydrol. Earth Syst. Sci., 0, 655 667, 06 www.hydrol-earth-syst-sci.net/0/655/06/ doi:0.594/hess-0-655-06 Authors 06. CC Attribution 3.0 License. Technical note: Analytical drawdown solution for steady-state
Stokes Flow in a Slowly Varying Two-Dimensional Periodic Pore
 Transport in Porous Media 6: 89 98, 997. 89 c 997 Kluwer Academic Publishers. Printed in the Netherlands. Stokes Flow in a Slowly Varying Two-Dimensional Periodic Pore PETER K. KITANIDIS? and BRUCE B.
Transport in Porous Media 6: 89 98, 997. 89 c 997 Kluwer Academic Publishers. Printed in the Netherlands. Stokes Flow in a Slowly Varying Two-Dimensional Periodic Pore PETER K. KITANIDIS? and BRUCE B.
RENORMALIZATION OF DYSON S VECTOR-VALUED HIERARCHICAL MODEL AT LOW TEMPERATURES
 RENORMALIZATION OF DYSON S VECTOR-VALUED HIERARCHICAL MODEL AT LOW TEMPERATURES P. M. Bleher (1) and P. Major (2) (1) Keldysh Institute of Applied Mathematics of the Soviet Academy of Sciences Moscow (2)
RENORMALIZATION OF DYSON S VECTOR-VALUED HIERARCHICAL MODEL AT LOW TEMPERATURES P. M. Bleher (1) and P. Major (2) (1) Keldysh Institute of Applied Mathematics of the Soviet Academy of Sciences Moscow (2)
Euler equation and Navier-Stokes equation
 Euler equation and Navier-Stokes equation WeiHan Hsiao a a Department of Physics, The University of Chicago E-mail: weihanhsiao@uchicago.edu ABSTRACT: This is the note prepared for the Kadanoff center
Euler equation and Navier-Stokes equation WeiHan Hsiao a a Department of Physics, The University of Chicago E-mail: weihanhsiao@uchicago.edu ABSTRACT: This is the note prepared for the Kadanoff center
On The Determination of Transmissibility and Storage Coefficients from Pumping Test Data
 Circular No. 38 1952 STATE OF ILLINOIS On The Determination of Transmissibility and Storage Coefficients from Pumping Test Data Issued by Department of Registration and Education C. HOBART ENGLE, Director
Circular No. 38 1952 STATE OF ILLINOIS On The Determination of Transmissibility and Storage Coefficients from Pumping Test Data Issued by Department of Registration and Education C. HOBART ENGLE, Director
DATA ASSIMILATION FOR COMPLEX SUBSURFACE FLOW FIELDS
 POLITECNICO DI MILANO Department of Civil and Environmental Engineering Doctoral Programme in Environmental and Infrastructure Engineering XXVI Cycle DATA ASSIMILATION FOR COMPLEX SUBSURFACE FLOW FIELDS
POLITECNICO DI MILANO Department of Civil and Environmental Engineering Doctoral Programme in Environmental and Infrastructure Engineering XXVI Cycle DATA ASSIMILATION FOR COMPLEX SUBSURFACE FLOW FIELDS
Modeling Seepage Control in Hydraulic Structures
 Number 3 Volume 13 September2006 Journal of Engineering Dr. Rafa H. El-Suhaili Professor Environmental Engineering Department College of Engineering Fawaz M. Aziz Al-Joubori M.Sc Student Irrigation and
Number 3 Volume 13 September2006 Journal of Engineering Dr. Rafa H. El-Suhaili Professor Environmental Engineering Department College of Engineering Fawaz M. Aziz Al-Joubori M.Sc Student Irrigation and
Fundamentals of Fluid Dynamics: Elementary Viscous Flow
 Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Direct Modeling for Computational Fluid Dynamics
 Direct Modeling for Computational Fluid Dynamics Kun Xu February 20, 2013 Computational fluid dynamics (CFD) is new emerging scientific discipline, and targets to simulate fluid motion in different scales.
Direct Modeling for Computational Fluid Dynamics Kun Xu February 20, 2013 Computational fluid dynamics (CFD) is new emerging scientific discipline, and targets to simulate fluid motion in different scales.
PROBABILISTIC PREDICTIONS OF INFILTRATION INTO HETEROGENEOUS MEDIA WITH UNCERTAIN HYDRAULIC PARAMETERS
 International Journal for Uncertainty Quantification, 1(1):35 47, 211 PROBABILISTIC PREDICTIONS OF INFILTRATION INTO HETEROGENEOUS MEDIA WITH UNCERTAIN HYDRAULIC PARAMETERS Peng Wang & Daniel M. Tartakovsky
International Journal for Uncertainty Quantification, 1(1):35 47, 211 PROBABILISTIC PREDICTIONS OF INFILTRATION INTO HETEROGENEOUS MEDIA WITH UNCERTAIN HYDRAULIC PARAMETERS Peng Wang & Daniel M. Tartakovsky
Homogenization and numerical Upscaling. Unsaturated flow and two-phase flow
 Homogenization and numerical Upscaling Unsaturated flow and two-phase flow Insa Neuweiler Institute of Hydromechanics, University of Stuttgart Outline Block 1: Introduction and Repetition Homogenization
Homogenization and numerical Upscaling Unsaturated flow and two-phase flow Insa Neuweiler Institute of Hydromechanics, University of Stuttgart Outline Block 1: Introduction and Repetition Homogenization
One-Dimensional Steady State Infiltration in Heterogeneous Soils
 WATER RESOURCES RESEARCH, VOL. 25, NO. 10, PAGES 2149-2158, OCTOBER 1989 One-Dimensional Steady State Infiltration in Heterogeneous Soils T.-C. JIM YEI Department of Hydrology and Water Resources, University
WATER RESOURCES RESEARCH, VOL. 25, NO. 10, PAGES 2149-2158, OCTOBER 1989 One-Dimensional Steady State Infiltration in Heterogeneous Soils T.-C. JIM YEI Department of Hydrology and Water Resources, University
36. TURBULENCE. Patriotism is the last refuge of a scoundrel. - Samuel Johnson
 36. TURBULENCE Patriotism is the last refuge of a scoundrel. - Samuel Johnson Suppose you set up an experiment in which you can control all the mean parameters. An example might be steady flow through
36. TURBULENCE Patriotism is the last refuge of a scoundrel. - Samuel Johnson Suppose you set up an experiment in which you can control all the mean parameters. An example might be steady flow through
Turbulence: Basic Physics and Engineering Modeling
 DEPARTMENT OF ENERGETICS Turbulence: Basic Physics and Engineering Modeling Numerical Heat Transfer Pietro Asinari, PhD Spring 2007, TOP UIC Program: The Master of Science Degree of the University of Illinois
DEPARTMENT OF ENERGETICS Turbulence: Basic Physics and Engineering Modeling Numerical Heat Transfer Pietro Asinari, PhD Spring 2007, TOP UIC Program: The Master of Science Degree of the University of Illinois
Sequential Monte Carlo methods for filtering of unobservable components of multidimensional diffusion Markov processes
 Sequential Monte Carlo methods for filtering of unobservable components of multidimensional diffusion Markov processes Ellida M. Khazen * 13395 Coppermine Rd. Apartment 410 Herndon VA 20171 USA Abstract
Sequential Monte Carlo methods for filtering of unobservable components of multidimensional diffusion Markov processes Ellida M. Khazen * 13395 Coppermine Rd. Apartment 410 Herndon VA 20171 USA Abstract
Lecture Introduction
 Lecture 1 1.1 Introduction The theory of Partial Differential Equations (PDEs) is central to mathematics, both pure and applied. The main difference between the theory of PDEs and the theory of Ordinary
Lecture 1 1.1 Introduction The theory of Partial Differential Equations (PDEs) is central to mathematics, both pure and applied. The main difference between the theory of PDEs and the theory of Ordinary
APPLICATION OF THE TRUNCATED PLURIGAUSSIAN METHOD TO DELINEATE HYDROFACIES DISTRIBUTION IN HETEROGENEOUS AQUIFERS
 XIX International Conference on Water Resources CMWR 2012 University of Illinois at Urbana-Champaign June 17-22, 2012 APPLICATION OF THE TRUNCATED PLURIGAUSSIAN METHOD TO DELINEATE HYDROFACIES DISTRIBUTION
XIX International Conference on Water Resources CMWR 2012 University of Illinois at Urbana-Champaign June 17-22, 2012 APPLICATION OF THE TRUNCATED PLURIGAUSSIAN METHOD TO DELINEATE HYDROFACIES DISTRIBUTION
Computer Applications in Engineering and Construction Programming Assignment #9 Principle Stresses and Flow Nets in Geotechnical Design
 CVEN 302-501 Computer Applications in Engineering and Construction Programming Assignment #9 Principle Stresses and Flow Nets in Geotechnical Design Date distributed : 12/2/2015 Date due : 12/9/2015 at
CVEN 302-501 Computer Applications in Engineering and Construction Programming Assignment #9 Principle Stresses and Flow Nets in Geotechnical Design Date distributed : 12/2/2015 Date due : 12/9/2015 at
Brownian motion and the Central Limit Theorem
 Brownian motion and the Central Limit Theorem Amir Bar January 4, 3 Based on Shang-Keng Ma, Statistical Mechanics, sections.,.7 and the course s notes section 6. Introduction In this tutorial we shall
Brownian motion and the Central Limit Theorem Amir Bar January 4, 3 Based on Shang-Keng Ma, Statistical Mechanics, sections.,.7 and the course s notes section 6. Introduction In this tutorial we shall
A Constitutive Framework for the Numerical Analysis of Organic Soils and Directionally Dependent Materials
 Dublin, October 2010 A Constitutive Framework for the Numerical Analysis of Organic Soils and Directionally Dependent Materials FracMan Technology Group Dr Mark Cottrell Presentation Outline Some Physical
Dublin, October 2010 A Constitutive Framework for the Numerical Analysis of Organic Soils and Directionally Dependent Materials FracMan Technology Group Dr Mark Cottrell Presentation Outline Some Physical
Continuum Mechanics Fundamentals
 Continuum Mechanics Fundamentals James R. Rice, notes for ES 220, 12 November 2009; corrections 9 December 2009 Conserved Quantities Let a conseved quantity have amount F per unit volume. Examples are
Continuum Mechanics Fundamentals James R. Rice, notes for ES 220, 12 November 2009; corrections 9 December 2009 Conserved Quantities Let a conseved quantity have amount F per unit volume. Examples are
Site Characterization & Hydrogeophysics
 Site Characterization & Hydrogeophysics (Source: Matthew Becker, California State University) Site Characterization Definition: quantitative description of the hydraulic, geologic, and chemical properties
Site Characterization & Hydrogeophysics (Source: Matthew Becker, California State University) Site Characterization Definition: quantitative description of the hydraulic, geologic, and chemical properties
Two-dimensional flow in a porous medium with general anisotropy
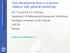 Two-dimensional flow in a porous medium with general anisotropy P.A. Tyvand & A.R.F. Storhaug Norwegian University of Life Sciences 143 Ås Norway peder.tyvand@umb.no 1 Darcy s law for flow in an isotropic
Two-dimensional flow in a porous medium with general anisotropy P.A. Tyvand & A.R.F. Storhaug Norwegian University of Life Sciences 143 Ås Norway peder.tyvand@umb.no 1 Darcy s law for flow in an isotropic
Chapter 7 Permeability and Seepage
 Permeability and Seepage - N. Sivakugan (2005) 1 7.1 INTRODUCTION Chapter 7 Permeability and Seepage Permeability, as the name implies (ability to permeate), is a measure of how easily a fluid can flow
Permeability and Seepage - N. Sivakugan (2005) 1 7.1 INTRODUCTION Chapter 7 Permeability and Seepage Permeability, as the name implies (ability to permeate), is a measure of how easily a fluid can flow
KOZENY-CARMAN EQUATION REVISITED. Jack Dvorkin Abstract
 KOZENY-CARMAN EQUATION REVISITED Jack Dvorkin -- 009 Abstract The Kozeny-Carman equation is often presented as permeability versus porosity, grain size, and tortuosity. When it is used to estimate permeability
KOZENY-CARMAN EQUATION REVISITED Jack Dvorkin -- 009 Abstract The Kozeny-Carman equation is often presented as permeability versus porosity, grain size, and tortuosity. When it is used to estimate permeability
Algorithms for Uncertainty Quantification
 Algorithms for Uncertainty Quantification Lecture 9: Sensitivity Analysis ST 2018 Tobias Neckel Scientific Computing in Computer Science TUM Repetition of Previous Lecture Sparse grids in Uncertainty Quantification
Algorithms for Uncertainty Quantification Lecture 9: Sensitivity Analysis ST 2018 Tobias Neckel Scientific Computing in Computer Science TUM Repetition of Previous Lecture Sparse grids in Uncertainty Quantification
