Scientific Computing. Roots of Equations
|
|
|
- Emil Fleming
- 5 years ago
- Views:
Transcription
1 ECE257 Numerical Methods and Scientific Computing Roots of Equations
2 Today s s class: Roots of Equations Polynomials
3 Polynomials A polynomial is of the form: ( x) = a 0 + a 1 x + a 2 x 2 +L+ a n x n f n The roots of a polynomial follow these rules: There will be n roots to an n-th order polynomial. The roots may be real or complex and need not be distinct If complex roots exist, they exist in conjugate pairs (λ+µi i and λ-µi) If n is odd, there is at least one real root
4 Polynomials Uses in electrical engineering Solving for poles and zeros in transfer functions Solving characteristic equations in linear ordinary differential equations
5 Polynomials f n ( x) = a 0 + a 1 x + a 2 x 2 +L+ a n x n F=A[0] FOR I=1 to N K = A[I] FOR J=1 to I K = K * X ENDFOR F = F + K ENDFOR n( n +1) 2 n additions multiplications
6 Polynomials f n ( ( )) ( x) = a 0 + x a 1 + x a 2 +L+ xa n F=A[N] FOR I=N-1 to 0 F = F*X + A[I] ENDFOR n additions n multiplications
7 Polynomial Deflation Given a polynomial and a single known root, deflating the polynomial can reduce the order of the polynomial and remove possible redundant roots Example: x 4 8x 3 20x x 576 Root x=4 is known
8 Polynomial Deflation x 4 x 3 4 x 2 36x +144 x 4 8x 3 20x x 576 x 4 4x 3 4x 3 20x 2 4 x 3 +16x 2 36x x 36x x 144 x x 576 0
9 Polynomial Deflation Synthetic Division x 4 8x 3 20x x
10 Polynomial Deflation Synthetic Division x 3 4x 2 36x
11 Polynomial Deflation Synthetic Division a 0 + a 1 x + a 2 x 2 +L+ a n x n = ( b 0 + b 1 x + b 2 x 2 +L+ b n 1 x n 1 )( x t) + r r=a[n] b[n]=0 for i=n-1 to 0 b[i]=r r = r*t+a[i] endfor n additions n multiplications
12 Polynomial Deflation If the known root is a calculated root, approximation error in that root may be compounded during the deflation process With forward deflation, i.e. new polynomial coefficients are calculated in descending order, it is better to divide by roots of smallest absolute value first Round-off errors can also be reduced by using root polishing.
13 Roots of polynomials Previous methods (Newton-Raphson, bracketing, etc.) have a few problems when applied to polynomials Must determine an initial guess of the root Can not find complex roots May not converge Polynomial-specific methods Müller s s method Bairstow s s method
14 Müller s s method Similar idea to secant method Instead of projecting a straight line through two points to estimate the root, project a parabola through three points to estimate the root
15 Müller s method From Numerical Methods for Engineers, Chapra and Canale, Copyright The McGraw-Hill Companies, Inc.
16 Müller s s method Find a parabola f 2 ( x) = a( x x 2 ) 2 + b( x x 2 ) + c such that it intersects the function at three points x 0, x 1, and x 2 f ( x 0 ) = f 2 ( x 0 ) = a( x 0 x 2 ) 2 + b( x 0 x 2 ) + c f ( x 1 ) = f 2 ( x 1 ) = a( x 1 x 2 ) 2 + b( x 1 x 2 ) + c f ( x 2 ) = f 2 ( x 2 ) = a( x 2 x 2 ) 2 + b( x 2 x 2 ) + c
17 Müller s s method Solve for c c = f ( x 2 ) Substitute back into set of equations f ( x 0 ) f ( x 2 ) = a( x 0 x 2 ) 2 + b( x 0 x 2 ) f ( x 1 ) f ( x 2 ) = a( x 1 x 2 ) 2 + b( x 1 x 2 ) Define new set of variables h 0 = ( x 1 x 0 ) h 1 = ( x 2 x 1 ) ( ) f ( x 0 ) ( ) f ( x 1 ) δ 0 = f x 1 x 1 x 0 δ 1 = f x 2 x 2 x 1
18 Müller s s method Substitute new variables back into equations Solve for a and b h 0 δ 0 + h 1 δ 1 = b( h 0 + h 1 ) a( h 0 + h 1 ) 2 h 1 δ = bh 1 ah 1 2 a = δ 1 δ 0 h 0 + h 1 b = ah 1 + δ 1
19 Müller s s method Now that we have found the coefficients of the parabola, find where it intersects the x-axis to get the next root estimate The intersection point with the x-axis is simply the root of the parabola which we can find using the quadratic formula f 2 ( x r ) = a x r x 2 ( ) 2 + b( x r x 2 ) + c = 0 x r x 2 = b ± b2 4ac 2a = b ± 2c b 2 4ac
20 Müller s s method x r = x 2 + b ± 2c b 2 4ac Which of the two quadratic roots do you choose? Choose the sign that makes the denominator the largest That will bring x r closer to x 2
21 Müller s s method How do you pick the three points for the next iteration? If there are only real roots, choose x r and the closer two of the orignal three roots to x r. If there are complex roots, use a sequential approach: use x r, x 2, and x 1.
22 Example Find roots of f(x)=x 3-13x-12 Use x 0 =4.5, x 1 =5.5, and x 2 =5 as the initial guesses ( ) = f ( 4.5) = ( ) = f ( 5.5) = ( ) = f ( 5) = 48 f x 0 f x 1 f x 2 ( ) = =1.0 ( ) f ( x 0 ) h 0 = x 1 x 0 δ 0 = f x 1 = x 1 x = ( ) = = 0.5 ( ) f ( x 1 ) h 1 = x 2 x 1 δ 1 = f x 2 = x 2 x = 69.75
23 Example x r = x 2 + = a = δ 1 δ 0 h 0 + h 1 = b = ah 1 + δ 1 = c = f x =15 ( ) = ( ) = 48 2c b ± b 2 4ac = ( ) ε a = x x r 2 = x r = 25.74%
24 Example i x r ε a (%)
25 Bairstow s s method Based on dividing the polynomial by (x-t) where t is the root estimate If there is no remainder, we found the root If not, we adjust the guess
26 Bairstow s s method f ( x) = a 0 + a 1 x + a 2 x 2 +L+ a n x n Factor by x-t f ( x) = ( x t) ( b 1 + b 2 x + b 3 x 2 +L+ b n x n 1 ) + b 0 Factor by x 2 -rx-s f ( x) = x 2 rx s b n = a n b i = a i + b i+1 t for i = n 1 to 0 ( )( b 2 + b 3 x + b 4 x 2 +L+ b n x n 2 ) + b 1 (x r) + b 0
27 Bairstow s s method b n = a n We have to find values of r and s such that the remainder is 0 The remainder is 0 if b 1 =b 0 =0 b 1 and b 0 are both functions of r and s, so we can give a Taylor series expansion of both b 1 ( r + Δr,s + Δs) b 1 ( r,s) + b 1( r,s) Δr + b 1( r,s) Δs r s b 0 ( r + Δr,s + Δs) b 0 ( r,s) + b 0( r,s) Δr + b 0( r,s) Δs r s b n 1 = a n 1 + rb n b i = a i + rb i+1 + sb i+2 for i = n 2 to 0
28 Bairstow s s method 0 = b 1 r,s 0 = b 0 r,s c n = b n ( ) + b 1( r,s) r ( ) + b 0( r,s) r Δr + b 1( r,s) c 2 Δr + c 3 Δs = b 1 r,s c 1 Δr + c 2 Δs = b 0 Δs s Δr + b 0( r,s) Δs s ( ) ( r,s) c n 1 = b n 1 + rc n c i = b i + rc i+1 + sc i+2 for i = n 2 to 1
29 Bairstow s s method Solve for r r and s ( ) ( r,s) c 2 Δr + c 3 Δs = b 1 r,s c 1 Δr + c 2 Δs = b 0 Use the results to adjust r and s and iterate Stop when the approximate error in r and s is sufficient ε a,r = Δr r and ε a,s = Δs s
30 Example Find roots of f(x)=x 5-3.5x x x x+1.25 Use s=-1, r=-1 as the initial guesses b 5 = a 5 =1 b 4 = a 4 + rb 5 = 4.5 b 3 = a 3 + rb 4 + sb 5 = 6.25 b 2 = a 2 + rb 3 + sb 4 = b 1 = a 1 + rb 2 + sb 3 = b 0 = a 0 + rb 1 + sb 2 = c 5 = b 5 =1 c 4 = b 4 + rc 5 = 5.5 c 3 = b 3 + rc 4 + sc 5 =10.75 c 2 = b 2 + rc 3 + sc 4 = c 1 = b 1 + rc 2 + sc 3 =
31 Example Solve linear system ( ) ( r,s) c 2 Δr + c 3 Δs = b 1 r,s c 1 Δr + c 2 Δs = b Δr Δs = Δr 4.875Δs = Δr = Δs = New s and r r = 1+ Δr = s = 1+ Δs =
32 Example Use s=0.1381, r= b 5 = a 5 =1 b 4 = a 4 + rb 5 = b 3 = a 3 + rb 4 + sb 5 = b 2 = a 2 + rb 3 + sb 4 = b 1 = a 1 + rb 2 + sb 3 = b 0 = a 0 + rb 1 + sb 2 = c 5 = b 5 =1 c 4 = b 4 + rc 5 = c 3 = b 3 + rc 4 + sc 5 = c 2 = b 2 + rc 3 + sc 4 = c 1 = b 1 + rc 2 + sc 3 =
33 Example Solve linear system ( ) ( r,s) c 2 Δr + c 3 Δs = b 1 r,s c 1 Δr + c 2 Δs = b Δr Δs = Δr Δs = Δr = Δs = New s and r r = Δr = s = Δs =
34 Example Keep going until s=0.5 and r=-0.5 Then solve the following: x 2 rx s = 0 x 2 + x = 0 x = 0.5 ± ( 0.5) ( 0.5) 2 = 0.5,1.0
35 Example The quotient coefficients are as follows b 5 = a 5 =1 b 4 = a 4 + rb 5 = 4 b 3 = a 3 + rb 4 + sb 5 = 5.25 b 2 = a 2 + rb 3 + sb 4 = -2.5 b 1 = a 1 + rb 2 + sb 3 = 0 b 0 = a 0 + rb 1 + sb 2 = 0 Now we have to solve: f ( x) = x 3 4 x x 2.5 = 0
36 Bairstow s s method If no s or r are known, start with s=0, r=0 Converges fast May diverge
37 Roots of equations Bisection 2 initial guesses, slow convergence, will not diverge False-position 2 initial guesses, slow-medium convergence, will not diverge
38 Roots of equations Newton-Raphson 1 initial guess, fast convergence, may diverge Secant 2 initial guesses, medium-fast convergence, may diverge
39 Roots of equations Muller 3 initial guesses, medium-fast convergence, may diverge, only polynomials, complex roots Bairstow 2 initial guesses, medium-fast convergence, may diverge, only polynomials, complex roots
40 Next Lecture Linear algebraic equations Read Chapter PT3, 9 HW3 due 9/30 Exam 1 on Tuesday 10/04
by Martin Mendez, UASLP Copyright 2006 The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
 Chapter 5 by Martin Mendez, 1 Roots of Equations Part Why? b m b a + b + c = 0 = aa 4ac But a 5 4 3 + b + c + d + e + f = 0 sin + = 0 =? =? by Martin Mendez, Nonlinear Equation Solvers Bracketing Graphical
Chapter 5 by Martin Mendez, 1 Roots of Equations Part Why? b m b a + b + c = 0 = aa 4ac But a 5 4 3 + b + c + d + e + f = 0 sin + = 0 =? =? by Martin Mendez, Nonlinear Equation Solvers Bracketing Graphical
ECE257 Numerical Methods and Scientific Computing. Ordinary Differential Equations
 ECE257 Numerical Methods and Scientific Computing Ordinary Differential Equations Today s s class: Stiffness Multistep Methods Stiff Equations Stiffness occurs in a problem where two or more independent
ECE257 Numerical Methods and Scientific Computing Ordinary Differential Equations Today s s class: Stiffness Multistep Methods Stiff Equations Stiffness occurs in a problem where two or more independent
Today s class. Numerical differentiation Roots of equation Bracketing methods. Numerical Methods, Fall 2011 Lecture 4. Prof. Jinbo Bi CSE, UConn
 Today s class Numerical differentiation Roots of equation Bracketing methods 1 Numerical Differentiation Finite divided difference First forward difference First backward difference Lecture 3 2 Numerical
Today s class Numerical differentiation Roots of equation Bracketing methods 1 Numerical Differentiation Finite divided difference First forward difference First backward difference Lecture 3 2 Numerical
2.29 Numerical Fluid Mechanics Spring 2015 Lecture 4
 2.29 Spring 2015 Lecture 4 Review Lecture 3 Truncation Errors, Taylor Series and Error Analysis Taylor series: 2 3 n n i1 i i i i i n f( ) f( ) f '( ) f ''( ) f '''( )... f ( ) R 2! 3! n! n1 ( n1) Rn f
2.29 Spring 2015 Lecture 4 Review Lecture 3 Truncation Errors, Taylor Series and Error Analysis Taylor series: 2 3 n n i1 i i i i i n f( ) f( ) f '( ) f ''( ) f '''( )... f ( ) R 2! 3! n! n1 ( n1) Rn f
CHAPTER 2 EXTRACTION OF THE QUADRATICS FROM REAL ALGEBRAIC POLYNOMIAL
 24 CHAPTER 2 EXTRACTION OF THE QUADRATICS FROM REAL ALGEBRAIC POLYNOMIAL 2.1 INTRODUCTION Polynomial factorization is a mathematical problem, which is often encountered in applied sciences and many of
24 CHAPTER 2 EXTRACTION OF THE QUADRATICS FROM REAL ALGEBRAIC POLYNOMIAL 2.1 INTRODUCTION Polynomial factorization is a mathematical problem, which is often encountered in applied sciences and many of
Review. Numerical Methods Lecture 22. Prof. Jinbo Bi CSE, UConn
 Review Taylor Series and Error Analysis Roots of Equations Linear Algebraic Equations Optimization Numerical Differentiation and Integration Ordinary Differential Equations Partial Differential Equations
Review Taylor Series and Error Analysis Roots of Equations Linear Algebraic Equations Optimization Numerical Differentiation and Integration Ordinary Differential Equations Partial Differential Equations
Chapter 3: Root Finding. September 26, 2005
 Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
S56 (5.1) Polynomials.notebook August 25, 2016
 Q1. Simplify Daily Practice 28.6.2016 Q2. Evaluate Today we will be learning about Polynomials. Q3. Write in completed square form x 2 + 4x + 7 Q4. State the equation of the line joining (0, 3) and (4,
Q1. Simplify Daily Practice 28.6.2016 Q2. Evaluate Today we will be learning about Polynomials. Q3. Write in completed square form x 2 + 4x + 7 Q4. State the equation of the line joining (0, 3) and (4,
PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435
 PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435 Professor Biswa Nath Datta Department of Mathematical Sciences Northern Illinois University DeKalb, IL. 60115 USA E mail: dattab@math.niu.edu
PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435 Professor Biswa Nath Datta Department of Mathematical Sciences Northern Illinois University DeKalb, IL. 60115 USA E mail: dattab@math.niu.edu
Section 4.1: Polynomial Functions and Models
 Section 4.1: Polynomial Functions and Models Learning Objectives: 1. Identify Polynomial Functions and Their Degree 2. Graph Polynomial Functions Using Transformations 3. Identify the Real Zeros of a Polynomial
Section 4.1: Polynomial Functions and Models Learning Objectives: 1. Identify Polynomial Functions and Their Degree 2. Graph Polynomial Functions Using Transformations 3. Identify the Real Zeros of a Polynomial
Scientific Computing. Roots of Equations
 ECE257 Numerical Methods and Scientific Computing Roots of Equations Today s s class: Roots of Equations Bracketing Methods Roots of Equations Given a function f(x), the roots are those values of x that
ECE257 Numerical Methods and Scientific Computing Roots of Equations Today s s class: Roots of Equations Bracketing Methods Roots of Equations Given a function f(x), the roots are those values of x that
Numerical Methods. Roots of Equations
 Roots of Equations by Norhayati Rosli & Nadirah Mohd Nasir Faculty of Industrial Sciences & Technology norhayati@ump.edu.my, nadirah@ump.edu.my Description AIMS This chapter is aimed to compute the root(s)
Roots of Equations by Norhayati Rosli & Nadirah Mohd Nasir Faculty of Industrial Sciences & Technology norhayati@ump.edu.my, nadirah@ump.edu.my Description AIMS This chapter is aimed to compute the root(s)
Solution of Algebric & Transcendental Equations
 Page15 Solution of Algebric & Transcendental Equations Contents: o Introduction o Evaluation of Polynomials by Horner s Method o Methods of solving non linear equations o Bracketing Methods o Bisection
Page15 Solution of Algebric & Transcendental Equations Contents: o Introduction o Evaluation of Polynomials by Horner s Method o Methods of solving non linear equations o Bracketing Methods o Bisection
ROOT FINDING REVIEW MICHELLE FENG
 ROOT FINDING REVIEW MICHELLE FENG 1.1. Bisection Method. 1. Root Finding Methods (1) Very naive approach based on the Intermediate Value Theorem (2) You need to be looking in an interval with only one
ROOT FINDING REVIEW MICHELLE FENG 1.1. Bisection Method. 1. Root Finding Methods (1) Very naive approach based on the Intermediate Value Theorem (2) You need to be looking in an interval with only one
Roots of Polynomials
 Roots of Polynomials (Com S 477/577 Notes) Yan-Bin Jia Sep 26, 2017 A direct corollary of the fundamental theorem of algebra is that p(x) can be factorized over the complex domain into a product a n (x
Roots of Polynomials (Com S 477/577 Notes) Yan-Bin Jia Sep 26, 2017 A direct corollary of the fundamental theorem of algebra is that p(x) can be factorized over the complex domain into a product a n (x
Computational Methods CMSC/AMSC/MAPL 460. Solving nonlinear equations and zero finding. Finding zeroes of functions
 Computational Methods CMSC/AMSC/MAPL 460 Solving nonlinear equations and zero finding Ramani Duraiswami, Dept. of Computer Science Where does it arise? Finding zeroes of functions Solving functional equations
Computational Methods CMSC/AMSC/MAPL 460 Solving nonlinear equations and zero finding Ramani Duraiswami, Dept. of Computer Science Where does it arise? Finding zeroes of functions Solving functional equations
M.SC. PHYSICS - II YEAR
 MANONMANIAM SUNDARANAR UNIVERSITY DIRECTORATE OF DISTANCE & CONTINUING EDUCATION TIRUNELVELI 627012, TAMIL NADU M.SC. PHYSICS - II YEAR DKP26 - NUMERICAL METHODS (From the academic year 2016-17) Most Student
MANONMANIAM SUNDARANAR UNIVERSITY DIRECTORATE OF DISTANCE & CONTINUING EDUCATION TIRUNELVELI 627012, TAMIL NADU M.SC. PHYSICS - II YEAR DKP26 - NUMERICAL METHODS (From the academic year 2016-17) Most Student
Roots of Equations Roots of Polynomials
 Roots of Equations Roots of Polynomials Content Roots of Polynomials Birge Vieta Method Lin Bairstow Method Roots of Polynomials The methods used to get all roots (real and complex) of a polynomial are:
Roots of Equations Roots of Polynomials Content Roots of Polynomials Birge Vieta Method Lin Bairstow Method Roots of Polynomials The methods used to get all roots (real and complex) of a polynomial are:
( 3) ( ) ( ) ( ) ( ) ( )
 81 Instruction: Determining the Possible Rational Roots using the Rational Root Theorem Consider the theorem stated below. Rational Root Theorem: If the rational number b / c, in lowest terms, is a root
81 Instruction: Determining the Possible Rational Roots using the Rational Root Theorem Consider the theorem stated below. Rational Root Theorem: If the rational number b / c, in lowest terms, is a root
Numerical Analysis Solution of Algebraic Equation (non-linear equation) 1- Trial and Error. 2- Fixed point
 Numerical Analysis Solution of Algebraic Equation (non-linear equation) 1- Trial and Error In this method we assume initial value of x, and substitute in the equation. Then modify x and continue till we
Numerical Analysis Solution of Algebraic Equation (non-linear equation) 1- Trial and Error In this method we assume initial value of x, and substitute in the equation. Then modify x and continue till we
EAD 115. Numerical Solution of Engineering and Scientific Problems. David M. Rocke Department of Applied Science
 EAD 115 Numerical Solution of Engineering and Scientific Problems David M. Rocke Department of Applied Science Taylor s Theorem Can often approximate a function by a polynomial The error in the approximation
EAD 115 Numerical Solution of Engineering and Scientific Problems David M. Rocke Department of Applied Science Taylor s Theorem Can often approximate a function by a polynomial The error in the approximation
Solving Non-Linear Equations (Root Finding)
 Solving Non-Linear Equations (Root Finding) Root finding Methods What are root finding methods? Methods for determining a solution of an equation. Essentially finding a root of a function, that is, a zero
Solving Non-Linear Equations (Root Finding) Root finding Methods What are root finding methods? Methods for determining a solution of an equation. Essentially finding a root of a function, that is, a zero
Chapter 7 Polynomial Functions. Factoring Review. We will talk about 3 Types: ALWAYS FACTOR OUT FIRST! Ex 2: Factor x x + 64
 Chapter 7 Polynomial Functions Factoring Review We will talk about 3 Types: 1. 2. 3. ALWAYS FACTOR OUT FIRST! Ex 1: Factor x 2 + 5x + 6 Ex 2: Factor x 2 + 16x + 64 Ex 3: Factor 4x 2 + 6x 18 Ex 4: Factor
Chapter 7 Polynomial Functions Factoring Review We will talk about 3 Types: 1. 2. 3. ALWAYS FACTOR OUT FIRST! Ex 1: Factor x 2 + 5x + 6 Ex 2: Factor x 2 + 16x + 64 Ex 3: Factor 4x 2 + 6x 18 Ex 4: Factor
CHAPTER 2 POLYNOMIALS KEY POINTS
 CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
Math 473: Practice Problems for Test 1, Fall 2011, SOLUTIONS
 Math 473: Practice Problems for Test 1, Fall 011, SOLUTIONS Show your work: 1. (a) Compute the Taylor polynomials P n (x) for f(x) = sin x and x 0 = 0. Solution: Compute f(x) = sin x, f (x) = cos x, f
Math 473: Practice Problems for Test 1, Fall 011, SOLUTIONS Show your work: 1. (a) Compute the Taylor polynomials P n (x) for f(x) = sin x and x 0 = 0. Solution: Compute f(x) = sin x, f (x) = cos x, f
Numerical Methods. Root Finding
 Numerical Methods Solving Non Linear 1-Dimensional Equations Root Finding Given a real valued function f of one variable (say ), the idea is to find an such that: f() 0 1 Root Finding Eamples Find real
Numerical Methods Solving Non Linear 1-Dimensional Equations Root Finding Given a real valued function f of one variable (say ), the idea is to find an such that: f() 0 1 Root Finding Eamples Find real
Secondary Math 3 Honors - Polynomial and Polynomial Functions Test Review
 Name: Class: Date: Secondary Math 3 Honors - Polynomial and Polynomial Functions Test Review 1 Write 3x 2 ( 2x 2 5x 3 ) in standard form State whether the function is even, odd, or neither Show your work
Name: Class: Date: Secondary Math 3 Honors - Polynomial and Polynomial Functions Test Review 1 Write 3x 2 ( 2x 2 5x 3 ) in standard form State whether the function is even, odd, or neither Show your work
Rational Exponents. Polynomial function of degree n: with leading coefficient,, with maximum number of turning points is given by (n-1)
 Useful Fact Sheet Final Exam Interval, Set Builder Notation (a,b) = {x a
Useful Fact Sheet Final Exam Interval, Set Builder Notation (a,b) = {x a
SAZ3C NUMERICAL AND STATISTICAL METHODS Unit : I -V
 SAZ3C NUMERICAL AND STATISTICAL METHODS Unit : I -V UNIT-I Introduction Mathematical Preliminaries Errors: Computations, Formula Errors in a Series Approximation Roots of Equations Linear Equations Bisection
SAZ3C NUMERICAL AND STATISTICAL METHODS Unit : I -V UNIT-I Introduction Mathematical Preliminaries Errors: Computations, Formula Errors in a Series Approximation Roots of Equations Linear Equations Bisection
Polynomial Functions and Models
 1 CA-Fall 2011-Jordan College Algebra, 4 th edition, Beecher/Penna/Bittinger, Pearson/Addison Wesley, 2012 Chapter 4: Polynomial Functions and Rational Functions Section 4.1 Polynomial Functions and Models
1 CA-Fall 2011-Jordan College Algebra, 4 th edition, Beecher/Penna/Bittinger, Pearson/Addison Wesley, 2012 Chapter 4: Polynomial Functions and Rational Functions Section 4.1 Polynomial Functions and Models
Numerical Analysis Fall. Roots: Open Methods
 Numerical Analysis 2015 Fall Roots: Open Methods Open Methods Open methods differ from bracketing methods, in that they require only a single starting value or two starting values that do not necessarily
Numerical Analysis 2015 Fall Roots: Open Methods Open Methods Open methods differ from bracketing methods, in that they require only a single starting value or two starting values that do not necessarily
Numerical Analysis MTH603
 Numerical Analysis Course Contents Solution of Non Linear Equations Solution of Linear System of Equations Approximation of Eigen Values Interpolation and Polynomial Approximation Numerical Differentiation
Numerical Analysis Course Contents Solution of Non Linear Equations Solution of Linear System of Equations Approximation of Eigen Values Interpolation and Polynomial Approximation Numerical Differentiation
Lesson 2.1: Quadratic Functions
 Quadratic Functions: Lesson 2.1: Quadratic Functions Standard form (vertex form) of a quadratic function: Vertex: (h, k) Algebraically: *Use completing the square to convert a quadratic equation into standard
Quadratic Functions: Lesson 2.1: Quadratic Functions Standard form (vertex form) of a quadratic function: Vertex: (h, k) Algebraically: *Use completing the square to convert a quadratic equation into standard
More Polynomial Equations Section 6.4
 MATH 11009: More Polynomial Equations Section 6.4 Dividend: The number or expression you are dividing into. Divisor: The number or expression you are dividing by. Synthetic division: Synthetic division
MATH 11009: More Polynomial Equations Section 6.4 Dividend: The number or expression you are dividing into. Divisor: The number or expression you are dividing by. Synthetic division: Synthetic division
Program : M.A./M.Sc. (Mathematics) M.A./M.Sc. (Final) Paper Code:MT-08 Numerical Analysis Section A (Very Short Answers Questions)
 Program : M../M.Sc. (Mathematics) M../M.Sc. (Final) Paper Code:MT-08 Numerical nalysis Section (Very Short nswers Questions) 1. Write two examples of transcendental equations. (i) x 3 + sin x = 0 (ii)
Program : M../M.Sc. (Mathematics) M../M.Sc. (Final) Paper Code:MT-08 Numerical nalysis Section (Very Short nswers Questions) 1. Write two examples of transcendental equations. (i) x 3 + sin x = 0 (ii)
3.3 Dividing Polynomials. Copyright Cengage Learning. All rights reserved.
 3.3 Dividing Polynomials Copyright Cengage Learning. All rights reserved. Objectives Long Division of Polynomials Synthetic Division The Remainder and Factor Theorems 2 Dividing Polynomials In this section
3.3 Dividing Polynomials Copyright Cengage Learning. All rights reserved. Objectives Long Division of Polynomials Synthetic Division The Remainder and Factor Theorems 2 Dividing Polynomials In this section
Course Name: MAT 135 Spring 2017 Master Course Code: N/A. ALEKS Course: Intermediate Algebra Instructor: Master Templates
 Course Name: MAT 135 Spring 2017 Master Course Code: N/A ALEKS Course: Intermediate Algebra Instructor: Master Templates Course Dates: Begin: 01/15/2017 End: 05/31/2017 Course Content: 279 Topics (207
Course Name: MAT 135 Spring 2017 Master Course Code: N/A ALEKS Course: Intermediate Algebra Instructor: Master Templates Course Dates: Begin: 01/15/2017 End: 05/31/2017 Course Content: 279 Topics (207
SOLUTION OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS BISECTION METHOD
 BISECTION METHOD If a function f(x) is continuous between a and b, and f(a) and f(b) are of opposite signs, then there exists at least one root between a and b. It is shown graphically as, Let f a be negative
BISECTION METHOD If a function f(x) is continuous between a and b, and f(a) and f(b) are of opposite signs, then there exists at least one root between a and b. It is shown graphically as, Let f a be negative
cha1873x_p02.qxd 3/21/05 1:01 PM Page 104 PART TWO
 cha1873x_p02.qxd 3/21/05 1:01 PM Page 104 PART TWO ROOTS OF EQUATIONS PT2.1 MOTIVATION Years ago, you learned to use the quadratic formula x = b ± b 2 4ac 2a to solve f(x) = ax 2 + bx + c = 0 (PT2.1) (PT2.2)
cha1873x_p02.qxd 3/21/05 1:01 PM Page 104 PART TWO ROOTS OF EQUATIONS PT2.1 MOTIVATION Years ago, you learned to use the quadratic formula x = b ± b 2 4ac 2a to solve f(x) = ax 2 + bx + c = 0 (PT2.1) (PT2.2)
A Partial List of Topics: Math Spring 2009
 A Partial List of Topics: Math 112 - Spring 2009 This is a partial compilation of a majority of the topics covered this semester and may not include everything which might appear on the exam. The purpose
A Partial List of Topics: Math 112 - Spring 2009 This is a partial compilation of a majority of the topics covered this semester and may not include everything which might appear on the exam. The purpose
Math 4329: Numerical Analysis Chapter 03: Newton s Method. Natasha S. Sharma, PhD
 Mathematical question we are interested in numerically answering How to find the x-intercepts of a function f (x)? These x-intercepts are called the roots of the equation f (x) = 0. Notation: denote the
Mathematical question we are interested in numerically answering How to find the x-intercepts of a function f (x)? These x-intercepts are called the roots of the equation f (x) = 0. Notation: denote the
3 Polynomial and Rational Functions
 3 Polynomial and Rational Functions 3.1 Polynomial Functions and their Graphs So far, we have learned how to graph polynomials of degree 0, 1, and. Degree 0 polynomial functions are things like f(x) =,
3 Polynomial and Rational Functions 3.1 Polynomial Functions and their Graphs So far, we have learned how to graph polynomials of degree 0, 1, and. Degree 0 polynomial functions are things like f(x) =,
Final Exam C Name i D) 2. Solve the equation by factoring. 4) x2 = x + 72 A) {1, 72} B) {-8, 9} C) {-8, -9} D) {8, 9} 9 ± i
 Final Exam C Name First, write the value(s) that make the denominator(s) zero. Then solve the equation. 7 ) x + + 3 x - = 6 (x + )(x - ) ) A) No restrictions; {} B) x -, ; C) x -; {} D) x -, ; {2} Add
Final Exam C Name First, write the value(s) that make the denominator(s) zero. Then solve the equation. 7 ) x + + 3 x - = 6 (x + )(x - ) ) A) No restrictions; {} B) x -, ; C) x -; {} D) x -, ; {2} Add
Numerical Solution of f(x) = 0
 Numerical Solution of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@pdx.edu ME 350: Finding roots of f(x) = 0 Overview Topics covered in these slides
Numerical Solution of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@pdx.edu ME 350: Finding roots of f(x) = 0 Overview Topics covered in these slides
NUMERICAL AND STATISTICAL COMPUTING (MCA-202-CR)
 NUMERICAL AND STATISTICAL COMPUTING (MCA-202-CR) Autumn Session UNIT 1 Numerical analysis is the study of algorithms that uses, creates and implements algorithms for obtaining numerical solutions to problems
NUMERICAL AND STATISTICAL COMPUTING (MCA-202-CR) Autumn Session UNIT 1 Numerical analysis is the study of algorithms that uses, creates and implements algorithms for obtaining numerical solutions to problems
Trigonometry Self-study: Reading: Red Bostock and Chandler p , p , p
 Trigonometry Self-study: Reading: Red Bostock Chler p137-151, p157-234, p244-254 Trigonometric functions be familiar with the six trigonometric functions, i.e. sine, cosine, tangent, cosecant, secant,
Trigonometry Self-study: Reading: Red Bostock Chler p137-151, p157-234, p244-254 Trigonometric functions be familiar with the six trigonometric functions, i.e. sine, cosine, tangent, cosecant, secant,
STOP, a i+ 1 is the desired root. )f(a i) > 0. Else If f(a i+ 1. Set a i+1 = a i+ 1 and b i+1 = b Else Set a i+1 = a i and b i+1 = a i+ 1
 53 17. Lecture 17 Nonlinear Equations Essentially, the only way that one can solve nonlinear equations is by iteration. The quadratic formula enables one to compute the roots of p(x) = 0 when p P. Formulas
53 17. Lecture 17 Nonlinear Equations Essentially, the only way that one can solve nonlinear equations is by iteration. The quadratic formula enables one to compute the roots of p(x) = 0 when p P. Formulas
MATH 1902: Mathematics for the Physical Sciences I
 MATH 1902: Mathematics for the Physical Sciences I Dr Dana Mackey School of Mathematical Sciences Room A305 A Email: Dana.Mackey@dit.ie Dana Mackey (DIT) MATH 1902 1 / 46 Module content/assessment Functions
MATH 1902: Mathematics for the Physical Sciences I Dr Dana Mackey School of Mathematical Sciences Room A305 A Email: Dana.Mackey@dit.ie Dana Mackey (DIT) MATH 1902 1 / 46 Module content/assessment Functions
15 Nonlinear Equations and Zero-Finders
 15 Nonlinear Equations and Zero-Finders This lecture describes several methods for the solution of nonlinear equations. In particular, we will discuss the computation of zeros of nonlinear functions f(x).
15 Nonlinear Equations and Zero-Finders This lecture describes several methods for the solution of nonlinear equations. In particular, we will discuss the computation of zeros of nonlinear functions f(x).
Numerical Analysis MTH603. Virtual University of Pakistan Knowledge beyond the boundaries
 Numerical Analysis MTH6 Virtual University of Pakistan Knowledge beyond the boundaries Table of Contents Lecture # Topics Page # Lecture Introduction Lecture Errors in Computations 6 Lecture Solution of
Numerical Analysis MTH6 Virtual University of Pakistan Knowledge beyond the boundaries Table of Contents Lecture # Topics Page # Lecture Introduction Lecture Errors in Computations 6 Lecture Solution of
x 2 x n r n J(x + t(x x ))(x x )dt. For warming-up we start with methods for solving a single equation of one variable.
 Maria Cameron 1. Fixed point methods for solving nonlinear equations We address the problem of solving an equation of the form (1) r(x) = 0, where F (x) : R n R n is a vector-function. Eq. (1) can be written
Maria Cameron 1. Fixed point methods for solving nonlinear equations We address the problem of solving an equation of the form (1) r(x) = 0, where F (x) : R n R n is a vector-function. Eq. (1) can be written
Chapter 4. Solution of Non-linear Equation. Module No. 1. Newton s Method to Solve Transcendental Equation
 Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-713209 email: anita.buie@gmail.com 1 . Chapter 4 Solution of Non-linear
Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-713209 email: anita.buie@gmail.com 1 . Chapter 4 Solution of Non-linear
Comparative Analysis of Convergence of Various Numerical Methods
 Journal of Computer and Mathematical Sciences, Vol.6(6),290-297, June 2015 (An International Research Journal), www.compmath-journal.org ISSN 0976-5727 (Print) ISSN 2319-8133 (Online) Comparative Analysis
Journal of Computer and Mathematical Sciences, Vol.6(6),290-297, June 2015 (An International Research Journal), www.compmath-journal.org ISSN 0976-5727 (Print) ISSN 2319-8133 (Online) Comparative Analysis
CHAPTER 4 ROOTS OF EQUATIONS
 CHAPTER 4 ROOTS OF EQUATIONS Chapter 3 : TOPIC COVERS (ROOTS OF EQUATIONS) Definition of Root of Equations Bracketing Method Graphical Method Bisection Method False Position Method Open Method One-Point
CHAPTER 4 ROOTS OF EQUATIONS Chapter 3 : TOPIC COVERS (ROOTS OF EQUATIONS) Definition of Root of Equations Bracketing Method Graphical Method Bisection Method False Position Method Open Method One-Point
Polynomials. Exponents. End Behavior. Writing. Solving Factoring. Graphing. End Behavior. Polynomial Notes. Synthetic Division.
 Polynomials Polynomials 1. P 1: Exponents 2. P 2: Factoring Polynomials 3. P 3: End Behavior 4. P 4: Fundamental Theorem of Algebra Writing real root x= 10 or (x+10) local maximum Exponents real root x=10
Polynomials Polynomials 1. P 1: Exponents 2. P 2: Factoring Polynomials 3. P 3: End Behavior 4. P 4: Fundamental Theorem of Algebra Writing real root x= 10 or (x+10) local maximum Exponents real root x=10
Chapter 6. Nonlinear Equations. 6.1 The Problem of Nonlinear Root-finding. 6.2 Rate of Convergence
 Chapter 6 Nonlinear Equations 6. The Problem of Nonlinear Root-finding In this module we consider the problem of using numerical techniques to find the roots of nonlinear equations, f () =. Initially we
Chapter 6 Nonlinear Equations 6. The Problem of Nonlinear Root-finding In this module we consider the problem of using numerical techniques to find the roots of nonlinear equations, f () =. Initially we
Roots of Equations. ITCS 4133/5133: Introduction to Numerical Methods 1 Roots of Equations
 Roots of Equations Direct Search, Bisection Methods Regula Falsi, Secant Methods Newton-Raphson Method Zeros of Polynomials (Horner s, Muller s methods) EigenValue Analysis ITCS 4133/5133: Introduction
Roots of Equations Direct Search, Bisection Methods Regula Falsi, Secant Methods Newton-Raphson Method Zeros of Polynomials (Horner s, Muller s methods) EigenValue Analysis ITCS 4133/5133: Introduction
Numerical Methods Lecture 3
 Numerical Methods Lecture 3 Nonlinear Equations by Pavel Ludvík Introduction Definition (Root or zero of a function) A root (or a zero) of a function f is a solution of an equation f (x) = 0. We learn
Numerical Methods Lecture 3 Nonlinear Equations by Pavel Ludvík Introduction Definition (Root or zero of a function) A root (or a zero) of a function f is a solution of an equation f (x) = 0. We learn
Newton-Raphson. Relies on the Taylor expansion f(x + δ) = f(x) + δ f (x) + ½ δ 2 f (x) +..
 2008 Lecture 7 starts here Newton-Raphson When the derivative of f(x) is known, and when f(x) is well behaved, the celebrated (and ancient) Newton- Raphson method gives the fastest convergence of all (
2008 Lecture 7 starts here Newton-Raphson When the derivative of f(x) is known, and when f(x) is well behaved, the celebrated (and ancient) Newton- Raphson method gives the fastest convergence of all (
Polynomial and Rational Functions. Chapter 3
 Polynomial and Rational Functions Chapter 3 Quadratic Functions and Models Section 3.1 Quadratic Functions Quadratic function: Function of the form f(x) = ax 2 + bx + c (a, b and c real numbers, a 0) -30
Polynomial and Rational Functions Chapter 3 Quadratic Functions and Models Section 3.1 Quadratic Functions Quadratic function: Function of the form f(x) = ax 2 + bx + c (a, b and c real numbers, a 0) -30
Lecture 8. Root finding II
 1 Introduction Lecture 8 Root finding II In the previous lecture we considered the bisection root-bracketing algorithm. It requires only that the function be continuous and that we have a root bracketed
1 Introduction Lecture 8 Root finding II In the previous lecture we considered the bisection root-bracketing algorithm. It requires only that the function be continuous and that we have a root bracketed
Finding the Roots of f(x) = 0. Gerald W. Recktenwald Department of Mechanical Engineering Portland State University
 Finding the Roots of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@me.pdx.edu These slides are a supplement to the book Numerical Methods with Matlab:
Finding the Roots of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@me.pdx.edu These slides are a supplement to the book Numerical Methods with Matlab:
Computational Methods. Solving Equations
 Computational Methods Solving Equations Manfred Huber 2010 1 Solving Equations Solving scalar equations is an elemental task that arises in a wide range of applications Corresponds to finding parameters
Computational Methods Solving Equations Manfred Huber 2010 1 Solving Equations Solving scalar equations is an elemental task that arises in a wide range of applications Corresponds to finding parameters
Finding the Roots of f(x) = 0
 Finding the Roots of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@me.pdx.edu These slides are a supplement to the book Numerical Methods with Matlab:
Finding the Roots of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@me.pdx.edu These slides are a supplement to the book Numerical Methods with Matlab:
6x 3 12x 2 7x 2 +16x 7x 2 +14x 2x 4
 2.3 Real Zeros of Polynomial Functions Name: Pre-calculus. Date: Block: 1. Long Division of Polynomials. We have factored polynomials of degree 2 and some specific types of polynomials of degree 3 using
2.3 Real Zeros of Polynomial Functions Name: Pre-calculus. Date: Block: 1. Long Division of Polynomials. We have factored polynomials of degree 2 and some specific types of polynomials of degree 3 using
Exam 2. Average: 85.6 Median: 87.0 Maximum: Minimum: 55.0 Standard Deviation: Numerical Methods Fall 2011 Lecture 20
 Exam 2 Average: 85.6 Median: 87.0 Maximum: 100.0 Minimum: 55.0 Standard Deviation: 10.42 Fall 2011 1 Today s class Multiple Variable Linear Regression Polynomial Interpolation Lagrange Interpolation Newton
Exam 2 Average: 85.6 Median: 87.0 Maximum: 100.0 Minimum: 55.0 Standard Deviation: 10.42 Fall 2011 1 Today s class Multiple Variable Linear Regression Polynomial Interpolation Lagrange Interpolation Newton
SYSTEMS OF NONLINEAR EQUATIONS
 SYSTEMS OF NONLINEAR EQUATIONS Widely used in the mathematical modeling of real world phenomena. We introduce some numerical methods for their solution. For better intuition, we examine systems of two
SYSTEMS OF NONLINEAR EQUATIONS Widely used in the mathematical modeling of real world phenomena. We introduce some numerical methods for their solution. For better intuition, we examine systems of two
p 1 p 0 (p 1, f(p 1 )) (p 0, f(p 0 )) The geometric construction of p 2 for the se- cant method.
 80 CHAP. 2 SOLUTION OF NONLINEAR EQUATIONS f (x) = 0 y y = f(x) (p, 0) p 2 p 1 p 0 x (p 1, f(p 1 )) (p 0, f(p 0 )) The geometric construction of p 2 for the se- Figure 2.16 cant method. Secant Method The
80 CHAP. 2 SOLUTION OF NONLINEAR EQUATIONS f (x) = 0 y y = f(x) (p, 0) p 2 p 1 p 0 x (p 1, f(p 1 )) (p 0, f(p 0 )) The geometric construction of p 2 for the se- Figure 2.16 cant method. Secant Method The
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane.
 Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 3 Lecture 3 3.1 General remarks March 4, 2018 This
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 3 Lecture 3 3.1 General remarks March 4, 2018 This
( ) y 2! 4. ( )( y! 2)
 1. Dividing: 4x3! 8x 2 + 6x 2x 5.7 Division of Polynomials = 4x3 2x! 8x2 2x + 6x 2x = 2x2! 4 3. Dividing: 1x4 + 15x 3! 2x 2!5x 2 = 1x4!5x 2 + 15x3!5x 2! 2x2!5x 2 =!2x2! 3x + 4 5. Dividing: 8y5 + 1y 3!
1. Dividing: 4x3! 8x 2 + 6x 2x 5.7 Division of Polynomials = 4x3 2x! 8x2 2x + 6x 2x = 2x2! 4 3. Dividing: 1x4 + 15x 3! 2x 2!5x 2 = 1x4!5x 2 + 15x3!5x 2! 2x2!5x 2 =!2x2! 3x + 4 5. Dividing: 8y5 + 1y 3!
CHAPTER-II ROOTS OF EQUATIONS
 CHAPTER-II ROOTS OF EQUATIONS 2.1 Introduction The roots or zeros of equations can be simply defined as the values of x that makes f(x) =0. There are many ways to solve for roots of equations. For some
CHAPTER-II ROOTS OF EQUATIONS 2.1 Introduction The roots or zeros of equations can be simply defined as the values of x that makes f(x) =0. There are many ways to solve for roots of equations. For some
Power and Polynomial Functions. College Algebra
 Power and Polynomial Functions College Algebra Power Function A power function is a function that can be represented in the form f x = kx % where k and p are real numbers, and k is known as the coefficient.
Power and Polynomial Functions College Algebra Power Function A power function is a function that can be represented in the form f x = kx % where k and p are real numbers, and k is known as the coefficient.
Section 3.1 Quadratic Functions
 Chapter 3 Lecture Notes Page 1 of 72 Section 3.1 Quadratic Functions Objectives: Compare two different forms of writing a quadratic function Find the equation of a quadratic function (given points) Application
Chapter 3 Lecture Notes Page 1 of 72 Section 3.1 Quadratic Functions Objectives: Compare two different forms of writing a quadratic function Find the equation of a quadratic function (given points) Application
COURSE SYLLABUS Part I Course Title: MATH College Algebra Credit Hours: 4, (4 Lecture 0 Lab G) OTM-TMM001
 COURSE SYLLABUS Part I Course Title: MATH 1340 - College Algebra Credit Hours: 4, (4 Lecture 0 Lab G) OTM-TMM001 Course Description: College Algebra in conjunction with MATH 1350, Pre-Calculus, provides
COURSE SYLLABUS Part I Course Title: MATH 1340 - College Algebra Credit Hours: 4, (4 Lecture 0 Lab G) OTM-TMM001 Course Description: College Algebra in conjunction with MATH 1350, Pre-Calculus, provides
Algebra 2 Khan Academy Video Correlations By SpringBoard Activity
 SB Activity Activity 1 Creating Equations 1-1 Learning Targets: Create an equation in one variable from a real-world context. Solve an equation in one variable. 1-2 Learning Targets: Create equations in
SB Activity Activity 1 Creating Equations 1-1 Learning Targets: Create an equation in one variable from a real-world context. Solve an equation in one variable. 1-2 Learning Targets: Create equations in
Final Exam A Name. 20 i C) Solve the equation by factoring. 4) x2 = x + 30 A) {-5, 6} B) {5, 6} C) {1, 30} D) {-5, -6} -9 ± i 3 14
 Final Exam A Name First, write the value(s) that make the denominator(s) zero. Then solve the equation. 1 1) x + 3 + 5 x - 3 = 30 (x + 3)(x - 3) 1) A) x -3, 3; B) x -3, 3; {4} C) No restrictions; {3} D)
Final Exam A Name First, write the value(s) that make the denominator(s) zero. Then solve the equation. 1 1) x + 3 + 5 x - 3 = 30 (x + 3)(x - 3) 1) A) x -3, 3; B) x -3, 3; {4} C) No restrictions; {3} D)
Algebra 2 Khan Academy Video Correlations By SpringBoard Activity
 SB Activity Activity 1 Creating Equations 1-1 Learning Targets: Create an equation in one variable from a real-world context. Solve an equation in one variable. 1-2 Learning Targets: Create equations in
SB Activity Activity 1 Creating Equations 1-1 Learning Targets: Create an equation in one variable from a real-world context. Solve an equation in one variable. 1-2 Learning Targets: Create equations in
Dividing Polynomials: Remainder and Factor Theorems
 Dividing Polynomials: Remainder and Factor Theorems When we divide one polynomial by another, we obtain a quotient and a remainder. If the remainder is zero, then the divisor is a factor of the dividend.
Dividing Polynomials: Remainder and Factor Theorems When we divide one polynomial by another, we obtain a quotient and a remainder. If the remainder is zero, then the divisor is a factor of the dividend.
Example - Newton-Raphson Method
 Eample - Newton-Raphson Method We now consider the following eample: minimize f( 3 3 + -- 4 4 Since f ( 3 2 + 3 3 and f ( 6 + 9 2 we form the following iteration: + n 3 ( n 3 3( n 2 ------------------------------------
Eample - Newton-Raphson Method We now consider the following eample: minimize f( 3 3 + -- 4 4 Since f ( 3 2 + 3 3 and f ( 6 + 9 2 we form the following iteration: + n 3 ( n 3 3( n 2 ------------------------------------
The standard form for a general polynomial of degree n is written. Examples of a polynomial in standard form
 Section 4 1A: The Rational Zeros (Roots) of a Polynomial The standard form for a general polynomial of degree n is written f (x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0 where the highest degree term
Section 4 1A: The Rational Zeros (Roots) of a Polynomial The standard form for a general polynomial of degree n is written f (x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0 where the highest degree term
Complex Numbers: Definition: A complex number is a number of the form: z = a + bi where a, b are real numbers and i is a symbol with the property: i
 Complex Numbers: Definition: A complex number is a number of the form: z = a + bi where a, b are real numbers and i is a symbol with the property: i 2 = 1 Sometimes we like to think of i = 1 We can treat
Complex Numbers: Definition: A complex number is a number of the form: z = a + bi where a, b are real numbers and i is a symbol with the property: i 2 = 1 Sometimes we like to think of i = 1 We can treat
MAT116 Final Review Session Chapter 3: Polynomial and Rational Functions
 MAT116 Final Review Session Chapter 3: Polynomial and Rational Functions Quadratic Function A quadratic function is defined by a quadratic or second-degree polynomial. Standard Form f x = ax 2 + bx + c,
MAT116 Final Review Session Chapter 3: Polynomial and Rational Functions Quadratic Function A quadratic function is defined by a quadratic or second-degree polynomial. Standard Form f x = ax 2 + bx + c,
. As x gets really large, the last terms drops off and f(x) ½x
 Pre-AP Algebra 2 Unit 8 -Lesson 3 End behavior of rational functions Objectives: Students will be able to: Determine end behavior by dividing and seeing what terms drop out as x Know that there will be
Pre-AP Algebra 2 Unit 8 -Lesson 3 End behavior of rational functions Objectives: Students will be able to: Determine end behavior by dividing and seeing what terms drop out as x Know that there will be
PreCalculus Notes. MAT 129 Chapter 5: Polynomial and Rational Functions. David J. Gisch. Department of Mathematics Des Moines Area Community College
 PreCalculus Notes MAT 129 Chapter 5: Polynomial and Rational Functions David J. Gisch Department of Mathematics Des Moines Area Community College September 2, 2011 1 Chapter 5 Section 5.1: Polynomial Functions
PreCalculus Notes MAT 129 Chapter 5: Polynomial and Rational Functions David J. Gisch Department of Mathematics Des Moines Area Community College September 2, 2011 1 Chapter 5 Section 5.1: Polynomial Functions
Math 120, Sample Final Fall 2015
 Math 10, Sample Final Fall 015 Disclaimer: This sample final is intended to help students prepare for the final exam The final exam will be similar in structure and type of problems, however the actual
Math 10, Sample Final Fall 015 Disclaimer: This sample final is intended to help students prepare for the final exam The final exam will be similar in structure and type of problems, however the actual
SOLVING EQUATIONS OF ONE VARIABLE
 1 SOLVING EQUATIONS OF ONE VARIABLE ELM1222 Numerical Analysis Some of the contents are adopted from Laurene V. Fausett, Applied Numerical Analysis using MATLAB. Prentice Hall Inc., 1999 2 Today s lecture
1 SOLVING EQUATIONS OF ONE VARIABLE ELM1222 Numerical Analysis Some of the contents are adopted from Laurene V. Fausett, Applied Numerical Analysis using MATLAB. Prentice Hall Inc., 1999 2 Today s lecture
A Review of Bracketing Methods for Finding Zeros of Nonlinear Functions
 Applied Mathematical Sciences, Vol 1, 018, no 3, 137-146 HIKARI Ltd, wwwm-hikaricom https://doiorg/101988/ams018811 A Review of Bracketing Methods for Finding Zeros of Nonlinear Functions Somkid Intep
Applied Mathematical Sciences, Vol 1, 018, no 3, 137-146 HIKARI Ltd, wwwm-hikaricom https://doiorg/101988/ams018811 A Review of Bracketing Methods for Finding Zeros of Nonlinear Functions Somkid Intep
Order of convergence
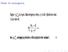 Order of convergence Linear and Quadratic Order of convergence Computing square root with Newton s Method Given a > 0, p def = a is positive root of equation Newton s Method p k+1 = p k p2 k a 2p k = 1
Order of convergence Linear and Quadratic Order of convergence Computing square root with Newton s Method Given a > 0, p def = a is positive root of equation Newton s Method p k+1 = p k p2 k a 2p k = 1
x 20 f ( x ) = x Determine the implied domain of the given function. Express your answer in interval notation.
 Test 2 Review 1. Given the following relation: 5 2 + = -6 - y Step 1. Rewrite the relation as a function of. Step 2. Using the answer from step 1, evaluate the function at = -1. Step. Using the answer
Test 2 Review 1. Given the following relation: 5 2 + = -6 - y Step 1. Rewrite the relation as a function of. Step 2. Using the answer from step 1, evaluate the function at = -1. Step. Using the answer
PART 1: USING SCIENTIFIC CALCULATORS (41 PTS.) 1) The Vertex Form for the equation of a parabola in the usual xy-plane is given by y = 3 x + 4
 MIDTERM SOLUTIONS (CHAPTERS AND 3: POLYNOMIAL, RATIONAL, EXP L, LOG FUNCTIONS) MATH 141 FALL 018 KUNIYUKI 150 POINTS TOTAL: 41 FOR PART 1, AND 109 FOR PART PART 1: USING SCIENTIFIC CALCULATORS (41 PTS.)
MIDTERM SOLUTIONS (CHAPTERS AND 3: POLYNOMIAL, RATIONAL, EXP L, LOG FUNCTIONS) MATH 141 FALL 018 KUNIYUKI 150 POINTS TOTAL: 41 FOR PART 1, AND 109 FOR PART PART 1: USING SCIENTIFIC CALCULATORS (41 PTS.)
Practice Test - Chapter 2
 Graph and analyze each function. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing. 1. f (x) = 0.25x 3 Evaluate the function for several
Graph and analyze each function. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing. 1. f (x) = 0.25x 3 Evaluate the function for several
Polynomial Functions
 Polynomial Functions Polynomials A Polynomial in one variable, x, is an expression of the form a n x 0 a 1 x n 1... a n 2 x 2 a n 1 x a n The coefficients represent complex numbers (real or imaginary),
Polynomial Functions Polynomials A Polynomial in one variable, x, is an expression of the form a n x 0 a 1 x n 1... a n 2 x 2 a n 1 x a n The coefficients represent complex numbers (real or imaginary),
Section 4.2 Polynomial Functions of Higher Degree
 Section 4.2 Polynomial Functions of Higher Degree Polynomial Function P(x) P(x) = a degree 0 P(x) = ax +b (degree 1) Graph Horizontal line through (0,a) line with y intercept (0,b) and slope a P(x) = ax
Section 4.2 Polynomial Functions of Higher Degree Polynomial Function P(x) P(x) = a degree 0 P(x) = ax +b (degree 1) Graph Horizontal line through (0,a) line with y intercept (0,b) and slope a P(x) = ax
Bisection Method. and compute f (p 1 ). repeat with p 2 = a 2+b 2
 Bisection Method Given continuous function f (x) on the interval [a, b] with f (a) f (b) < 0, there must be a root in (a, b). To find a root: set [a 1, b 1 ] = [a, b]. set p 1 = a 1+b 1 2 and compute f
Bisection Method Given continuous function f (x) on the interval [a, b] with f (a) f (b) < 0, there must be a root in (a, b). To find a root: set [a 1, b 1 ] = [a, b]. set p 1 = a 1+b 1 2 and compute f
2.1 Quadratic Functions
 Date:.1 Quadratic Functions Precalculus Notes: Unit Polynomial Functions Objective: The student will sketch the graph of a quadratic equation. The student will write the equation of a quadratic function.
Date:.1 Quadratic Functions Precalculus Notes: Unit Polynomial Functions Objective: The student will sketch the graph of a quadratic equation. The student will write the equation of a quadratic function.
Chapter 2 Formulas and Definitions:
 Chapter 2 Formulas and Definitions: (from 2.1) Definition of Polynomial Function: Let n be a nonnegative integer and let a n,a n 1,...,a 2,a 1,a 0 be real numbers with a n 0. The function given by f (x)
Chapter 2 Formulas and Definitions: (from 2.1) Definition of Polynomial Function: Let n be a nonnegative integer and let a n,a n 1,...,a 2,a 1,a 0 be real numbers with a n 0. The function given by f (x)
ALGEBRA 2 FINAL EXAM REVIEW
 Class: Date: ALGEBRA 2 FINAL EXAM REVIEW Multiple Choice Identify the choice that best completes the statement or answers the question.. Classify 6x 5 + x + x 2 + by degree. quintic c. quartic cubic d.
Class: Date: ALGEBRA 2 FINAL EXAM REVIEW Multiple Choice Identify the choice that best completes the statement or answers the question.. Classify 6x 5 + x + x 2 + by degree. quintic c. quartic cubic d.
p324 Section 5.2: The Natural Logarithmic Function: Integration
 p324 Section 5.2: The Natural Logarithmic Function: Integration Theorem 5.5: Log Rule for Integration Let u be a differentiable function of x 1. 2. Example 1: Using the Log Rule for Integration ** Note:
p324 Section 5.2: The Natural Logarithmic Function: Integration Theorem 5.5: Log Rule for Integration Let u be a differentiable function of x 1. 2. Example 1: Using the Log Rule for Integration ** Note:
Section 9.7 and 9.10: Taylor Polynomials and Approximations/Taylor and Maclaurin Series
 Section 9.7 and 9.10: Taylor Polynomials and Approximations/Taylor and Maclaurin Series Power Series for Functions We can create a Power Series (or polynomial series) that can approximate a function around
Section 9.7 and 9.10: Taylor Polynomials and Approximations/Taylor and Maclaurin Series Power Series for Functions We can create a Power Series (or polynomial series) that can approximate a function around
Section 3.6 Complex Zeros
 04 Chapter Section 6 Complex Zeros When finding the zeros of polynomials, at some point you're faced with the problem x = While there are clearly no real numbers that are solutions to this equation, leaving
04 Chapter Section 6 Complex Zeros When finding the zeros of polynomials, at some point you're faced with the problem x = While there are clearly no real numbers that are solutions to this equation, leaving
