Backward Stochastic Differential Equations with Financial Applications (Part I) Jin Ma

Transcription

1 Backward Sochasic Differenial Equaions wih Financial Applicaions (Par I) Jin Ma 2nd SMAI European Summer School in Financial Mahemaics Paris, France, Augus 24 29, 2009 Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

2 Ouline 1 Inroducion 2 BSDEs in Finance (A Firs Glance) 3 Wellposedness of BSDEs 4 Well-posedness of FBSDEs 5 Some Imporan facs of BSDEs/FBSDEs 6 Weak Soluion for FBSDEs 7 Backward Sochasic PDEs 8 BSPDEs and FBSDEs 9 References Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

3 1. Inroducion Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

4 Why BSDEs and FBSDEs? An Example: A sandard LQ sochasic conrol problem: dx u = (ax u + bu )d + dw, X0 u = x; J(u) = 1 { } 2 E { X u 2 + u 2 }d + XT u 2, 0 where W is a sandard Brownian moion and F = {F W } 0 is he naural filraion generaed by W ; u = {u } is he conrol process; and J(u) is he cos funcional. The problem: Find u U ad L 2 F (Ω [0, T ]) such ha J(u ) = inf J(u). u U ad Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

5 A necessary condiion (Ponryagin s Maximum Principle): Assume u is opimal. Then ε > 0 and v U ad, one has J(u + εv) J(u ) = 0 d { dε J(u +εv) = E ε=0 0 {X u ξ + u v }d + XT u ξ T where ξ = d dε X u +εv ε=0 is he soluion o he variaional equaion: dξ = {aξ + bv }d, ξ 0 = 0. (1) }, Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

6 A necessary condiion (Ponryagin s Maximum Principle): Assume u is opimal. Then ε > 0 and v U ad, one has J(u + εv) J(u ) = 0 d { dε J(u +εv) = E ε=0 0 {X u ξ + u v }d + XT u ξ T where ξ = d dε X u +εv ε=0 is he soluion o he variaional equaion: dξ = {aξ + bv }d, ξ 0 = 0. (1) }, A Lucky Guess (?): Assume ha η is he soluion o he following adjoin equaion of (1): dη = (aη + X u )d, η T = XT u. (2) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

7 Then, inegraion by pars yields ξ T η T = E { ξ X u {u v + bη v }d = {u + bη }v d = + bη v }d { } E {X u ξ + u v }d + XT u ξ T {X u ξ + u v }d + XT u ξ T Since v L 2 F (Ω [0, T ]) is arbirary, u = bη,, a.s. u = bη should have all he reasons o be an opimal conrol excep... Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

8 Then, inegraion by pars yields ξ T η T = E { ξ X u {u v + bη v }d = {u + bη }v d = + bη v }d { } E {X u ξ + u v }d + XT u ξ T {X u ξ + u v }d + XT u ξ T Since v L 2 F (Ω [0, T ]) is arbirary, u = bη,, a.s. u = bη should have all he reasons o be an opimal conrol excep... A Problem: u / U ad! (since i is no adaped!!) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

9 BSDE o he rescue: Example { dy = 0; Y T = ξ L 2 (F T ). Same Problem: The unique soluion Y ξ is no adaped! (3) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

10 BSDE o he rescue: Example { dy = 0; Y T = ξ L 2 (F T ). Same Problem: The unique soluion Y ξ is no adaped! The Soluion: Define Y = E{ξ F }, [0, T ]. Then Y becomes an L 2 -maringale, and by Maringale Represenaion Theorem (Iô, 1951), here exiss Z L 2 F (Ω [0, T ]) such ha Y = E{ξ} + Z dw, [0, T ]. 0 = Y = ξ Z dw, [0, T ] A BSDE! (4) (3) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

11 Back o he LQ problem: Consider he modified adjoin equaion (as a BSDE): { dη = (aη + X u )d+z dw, η T = XT u. (5) The Conclusion Suppose ha one can find a pair of process (η, Z) ha is he soluion o (5). Then define u = bη,, we obain an opimal conrol! Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

12 Back o he LQ problem: Consider he modified adjoin equaion (as a BSDE): { dη = (aη + X u )d+z dw, η T = XT u. (5) The Conclusion Suppose ha one can find a pair of process (η, Z) ha is he soluion o (5). Then define u = bη,, we obain an opimal conrol! Observaion: The close-loop sysem is hen dx u = (ax b 2 η )d + dw, dη = (aη + X u )d + Z dw, X0 u = x η T = X u T, An FBSDE! Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

13 A Brief Hisory Bismu ( 73) Linear BSDEs (Maximum Principle) Pardoux-Peng ( 90, 92) Nonlinear BSDEs Anonelli ( 93) FBSDEs (Sochasic Recursive Uiliy Duffie-Epsain ( 92)) Ma-Yong/Ma-Proer-Yong ( 93, 94) Four Sep Scheme El Karoui-Kapoudjian-Pardoux-Peng-Quenez, Cvianic-Karazas, ( 97) BSDEs wih reflecions Ma-Yong ( 96-98) BSPDEs Ma-Yong ( 99) Book (LNM 1702) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

14 A Brief Hisory Bismu ( 73) Linear BSDEs (Maximum Principle) Pardoux-Peng ( 90, 92) Nonlinear BSDEs Anonelli ( 93) FBSDEs (Sochasic Recursive Uiliy Duffie-Epsain ( 92)) Ma-Yong/Ma-Proer-Yong ( 93, 94) Four Sep Scheme El Karoui-Kapoudjian-Pardoux-Peng-Quenez, Cvianic-Karazas, ( 97) BSDEs wih reflecions Ma-Yong ( 96-98) BSPDEs Ma-Yong ( 99) Book (LNM 1702) Oher Developmens Lepelier-San Marin ( 97) BSDEs wih con. coefficiens Kobylanski ( 01) BSDEs wih quadraic growh (in Z) Delarue ( 02) FBSDE wih Lipschiz coefficiens Ma-Zhang-Zheng ( 08) Weak soluion and FBMP Soner-Touzi-Zhang (09?) 2BSDEs Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

15 2. BSDEs/FBSDEs in Finance Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

16 Opion Pricing The (Black-Scholes) marke model: ds 0 = S 0 r d, S0 0 = s 0, (Bond/Money Marke) { d } ds i = S i bd i + σ ij dw j, S0 i = s i, 1 i d, (Socks) j=1 S 0, S i prices of bond/(i-h) socks (per share) a ime r ineres rae a ime {b} i d i=1 appreciaion raes a ime [σ ij ] volailiy marix a ime More general form of he underlying asse price: ds = S {b(, S )d + σ(, S )dw }, S 0 = s. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

17 The Wealh Equaion: Denoe: Y dollar amoun of he oal wealh of an invesor a ime π i dollars invesed in i-h sock a ime, i = 1,, N C cumulaed consumpion up o ime Then, he wealh process Y saisfies an SDE: for [0, T ], Y = y + where 1 = (1,, 1). The Coningen Claims: 0 {r s Y s + π s, [b s r s 1] }ds + π s, σ s dw s C, 0 Any ξ F T. In paricular, ξ = g(s T ) Opions. E.g., ξ = (S 1 T q)+ European call ξ = (S 1 τ q) + American call (τ-sopping ime) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

18 European Opions (Fixed exercise ime T ) Define he fair price of an opion o be p = inf{v : (π, C), such ha Y y,π,c T ξ}. Then (El Karoui-Peng-Quenez, 96), he price p and he hedging sraegy (π, C) can be deermined by: C 0, p = Y 0 = y, and π = (σ T ) 1 Z ; (Y, Z) solves he BSDE: Y = ξ Fair price for American Opion: {r s Y s + Z s, σs 1 [b s r s 1] }ds Z s, dw s. p = inf{v : (π, C), such ha Y y,π,c τ g(s τ ), τ}. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

19 American Opions (El Karoui-Kapoudjian-Pardoux-Peng-Quenez, 97) For ξ = g(s τ ), where τ is exercise ime (any {F }-sopping ime). Then he price, hedging sraegy, and he opimal exercise ime are solved as: p = Y 0 = y, C = 0, (Y, Z, K) solves a BSDE wih reflecion: Y = g(s T ) Y g(s ), {r s Y s + Z s, σ 1 s Z s, dw s +K T K ; [0, T ], a.s.; The opimal exercise ime is given by τ = inf{ > 0 : Y = g(s )}. 0 [b s r s 1] }ds (Y g(s ))dk = 0. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

20 Large Invesors Problem Conrary o he Black-Scholes heory, one may assume ha some invesors are large. The price-wealh pair saisfies an FBSDE: dx = X {b(, X, Y, Z )d + σ(, X, Y, Z )dw }, dy = {r Y + Z [b(, X, Y, Z ) r 1]}d Z σ(, )dw + C T C. X 0 = x, Y T = g(x T ). Hedging wihou consrain (Cvianic-Ma, 1996) Hedging wih consrain (Buckdahn-Hu, 1998) American game opion (FBSDER, Cvianic-Ma, 2000) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

21 Sochasic Recursive Uiliy Duffie-Epsain ( 92) defined he SRU by a BSDE: U = Φ(Y T ) + f (s, c s, U s, V s )ds V s dw s, Y wealh; Φ uiliy funcion f sandard driver or aggregaor V 2 = d d U he variabiliy process c consumpion (rae) process Sandard Uiliy: f (c, u, v) = ϕ(c) βu. Uzawa Uiliy: f (c, u, v) = ϕ(c) β(c)u. Generalized Uzawa Uiliy: f (c, u, v) = ϕ(c) βu γ v, (Chen-Epsein (1999)). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

22 Porfolio/Consumpion Opimizaion Problems General wealh equaion wih porfolio-consumpion sraegy (π, c): dy = b(, c, Y, σ T π )d π, σ dw. (6) Porfolio/consumpion opimizaion problem Find (π, c) so as o maximize cerain uiliy : { } U(y, π, c) = E Φ(Y y,π,c T ) + h(, c, Y y,π,c )d. 0 A sochasic conrol problem! Wih Sochasic Recursive Uiliy: { U y,π,c 0 = E Φ(Y y,π,c T ) + 0 f (, c, Y y,π,c = A sochasic conrol problem for FBSDEs!, U y,π,c }, V y,π,c )d. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

23 Term Srucure of Ineres Raes. Brennan-Schwarz s Term srucure model: (1979) { dr = µ(r, R )d + α(r, R )dw dr = ν(r, R )d + β(r, R )dw, where r shor rae, R consol rae (consol = perpeual annuiy). This model was laer dispued by M. Hogan, by counerexample, which leads o Consol Rae Conjecure by Fisher Black: Assume ha he consol price Y = R 1, where R is he consol rae. Then, under a mos echnical condiions, µ and α, A(, ) such ha { dr = µ(r, Y )d + α(r, Y )dw (7) dy = (r Y 1)d + A(r, Y )dw, Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

24 Assume r = h(x ) for some facor process X and h( ) > 0, X saisfies an SDE depending on R (or equivalen Y ). Then he erm srucure SDEs (7) becomes an FBSDE wih infinie horizon: dx = b(x {, Y )d + σ(x, Y )dw, X 0 = x, Y = E e } s h(xu)du ds F, [0, ), (8) where Y is uniformly bounded for [0, ). Or equivalenly, dx = b(x, Y )d + σ(x, Y )dw, Y = (h(x )Y 1)d + A(X, Y )dw, X 0 = x, esssup ω sup [0, ) Y (ω) <. (9) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

25 Soluion of Black s Consol Rae Conjecure This resul (Duffie-Ma-Yong, 1993) was one of he early successful applicaions of FBSDE in finance, and he firs applicaion using he Four Sep Scheme. Theorem Under some echnical condiions, here exiss a unique funcion A(x, y) = σ(x, y) T θ x (x) such ha (X, Y ) in (8) saisfies (9), and θ is he unique classical soluion o he PDE: 1 2 σσt (x, θ)θ xx + b(x, θ)θ x h(x)θ + 1 = 0. Moreover, Y = θ(x ) for any [0, ). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

26 BSDEs and g-expecaions Consider a Backward SDE of he following general form: Y = ξ + g(, Y s, Z s )ds Z s db s, [0, T ], (10) where ξ L 2 (F T ) is he erminal condiion and g(, y, z) is he generaor. g-expecaion via BSDE (Peng, 93) If he BSDE (10) is well-posed, hen he soluion mapping E g : ξ Y 0 is called a g-expecaion. For any [0, T ], he condiional g-expecaion of ξ given F is defined by E g [ξ F ] = Y. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

27 BSDEs and g-expecaions Properies of g-expecaions: Assume ha g z=0 = 0. Consan-preserving: E g [ξ F ] = ξ, P-a.s., ξ L 2 (F ); In paricular, E g [c] = c, c R; Time-consisency: E g [ E g [ξ F ] F s ] = E g [ξ F s ], P-a.s., 0 s T ; (Sric) Monooniciy: If ξ η, hen E g [ξ F ] E g [η F ], P-a.s., [0, T ]; Moreover if = holds for some, hen ξ = η, P-a.s.; Zero-one Law: E g [1 A ξ F ] = 1 A E g [ξ F ], P-a.s., A F ; Translaion Invariance: If g is independen of y, hen E g [ξ + η F ] = E g [ξ F ] + η, P-a.s., η L 2 (F ). Convexiy: If g is convex (in z), hen so is E g [ F ]. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

28 g-expecaions and Risk Measures Axioms for Risk Measures (Arzner e al., Barrieu-El Karoui,...) A (saic) RM is a mapping ρ : X R (for some space of random variables X ), s.., Monooniciy: ξ η = ρ(ξ) ρ(η); Translaion Invariance: ρ(ξ + m) = ρ(ξ) m, m R; Coheren: if Subaddiiviy: ρ(ξ + η) ρ(ξ) + ρ(η) Posiive homogeneiy: ρ(αξ) = αρ(ξ), α 0; Convex: (Föllmer and Schied, 02) ρ ( αξ + (1 α)η ) αρ(ξ) + (1 α)ρ(η), α [0, 1]. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

29 g-expecaions and Risk Measures Axioms for Risk Measures (Arzner e al., Barrieu-El Karoui,...) A (saic) RM is a mapping ρ : X R (for some space of random variables X ), s.., Monooniciy: ξ η = ρ(ξ) ρ(η); Translaion Invariance: ρ(ξ + m) = ρ(ξ) m, m R; Coheren: if Subaddiiviy: ρ(ξ + η) ρ(ξ) + ρ(η) Posiive homogeneiy: ρ(αξ) = αρ(ξ), α 0; Convex: (Föllmer and Schied, 02) ρ ( αξ + (1 α)η ) αρ(ξ) + (1 α)ρ(η), α [0, 1]. A (dynamic) RM is a family of mappings ρ : X L 0 (F ), [0, T ], s.. ξ, η X, Monoonciy: If ξ η, hen ρ (ξ) ρ (η), P-a.s., ; Translaion Invariance: ρ (ξ + η) = ρ (ξ) η, η F. ρ 0 is a saic risk measure ρ T (ξ) = ξ for any ξ X. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

30 Example Wors-case Dynamic Risk Measure: ρ (ξ) = esssupe Q [ ξ F ], [0, T ], Q P P Enropic Dynamic Risk{ Measure: ρ γ (ξ) = γ ln E [ e 1 ξ ] γ F }, [0, T ]. Convex Dynamic Risk Measure: ρ (ξ) = esssup Q P P { EQ [ ξ F ] F (Q) }, [0, T ], where F is he penaly funcion of ρ for any. {ρ } [0,T ] is called convex (or coheren) if each ρ is. (e.g., Wors case coheren; Enropic convex.) {ρ } [0,T ] is said o be ime-consisen if Convex RM ρ 0 [ξ1 A ] = ρ 0 [ ρ (ξ)1 A ], [0, T ], ξ X, A F. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

31 g-expecaions and Risk Measures Le g be generaor wih g z=0 = 0, and is Lipschiz in (y, z). ρ(ξ) = E g [ ξ] defines a saic risk measure on X = L 2 (F T ). ρ (ξ) = E g [ ξ F ], [0, T ], defines a dynamic risk measure on X = L 2 (F T ). The risk measure (resp. dynamic risk measure) is convex if g is convex in z. The risk measure (resp. dynamic risk measure) is coheren if g is furher independen of y. Quesion: Does every risk measure have o be a g-expecaion?? Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

32 Nonlinear Expecaions Definiion Le (Ω, F, P, {F }) be a given probabiliy space. A funcional E : L 2 (F T ) R is called a nonlinear expecaion if i saisfies he following axioms: Monooniciy: ξ η, P-a.s. = E [ξ] E [η] E [ξ] = E [η] ξ = η, P-a.s. Consan-preserving: E [c] = c, c R. A nonlinear expecaion E is called {F }-consisen if i saisfies for all [0, T ] and ξ L 2 (F T ), here exiss η F such ha E [1 A ξ] = E [1 A η], A F s Will denoe η = E {ξ F }, for obvious reasons. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

33 Nonlinear Expecaions Definiion An {F }-consisan nonlinear expecaion E is said o be dominaed by E µ = E gµ (µ > 0) if Convex RM E [ξ + η] E [ξ] E µ [η], ξ, η L 2 (F T ). (11) where E µ = E gµ is he g-expecaion wih g µ z. Furher, E is said o saisfy he ranslabiliy condiion if E [ξ + α F ] = E [ξ F ] + α, ξ L 2 (F T ), α L 2 (F ). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

34 Nonlinear Expecaions Definiion An {F }-consisan nonlinear expecaion E is said o be dominaed by E µ = E gµ (µ > 0) if Convex RM E [ξ + η] E [ξ] E µ [η], ξ, η L 2 (F T ). (11) where E µ = E gµ is he g-expecaion wih g µ z. Furher, E is said o saisfy he ranslabiliy condiion if E [ξ + α F ] = E [ξ F ] + α, ξ L 2 (F T ), α L 2 (F ). Represenaion Theorem (Coque e al. 02) If E is a ranslable {F }-expecaion dominaed by E µ, for some µ > 0, hen! (deerminisic) funcion g, independen of y, such ha g(, z) µ z, and ha E [ξ] = E g [ξ], for all ξ L 2 (F T ). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

35 Represening Risk Measures as g-expecaions A direc consequence of he Represenaion Theorem for nonlinear expecaion is he following represenaion heorem for dynamic coheren risk measures. Some Facs: Le {ρ } be a dynamic, coheren, ime-consisen risk measure on X = L 2 (F T ). Define E (ξ) = ρ ( ξ), [0, T ]; and E = E 0. Then E is a nonlinear expecaion E { } = E { F } is he nonlinear condiional expecaion ( ime-consisency = {F }-consisency!) Consequenly, if E is furher E µ -dominaed for some µ > 0, hen here exiss a unique Lipschiz generaor g such ha ρ 0 (ξ) = E g ( ξ), ρ (ξ) = E g { ξ F }, ξ L 2 (F T ). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

36 3. Wellposedness of BSDEs Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

37 Wellposedness for BSDEs Consider he BSDE Y = ξ + f (s, Y s, Z s )ds Z s dw s, (12) where ξ L 2 F T (Ω; R n ), W is a d-dimensional Brownian moion. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

38 Wellposedness for BSDEs Consider he BSDE Y = ξ + f (s, Y s, Z s )ds Z s dw s, (12) where ξ L 2 F T (Ω; R n ), W is a d-dimensional Brownian moion. Some spaces: For any β 0 and Euclidean space H, define Sβ 2 (0, T ; H ) o be he space of all H -valued, coninuous, F-adaped { processes X }, such ha E sup 0 T e β X 2 < H 2 β (0, T ; E) o be he space of all H -valued, F-adaped { } processes X such ha E e β X 2 d < N β [0, T ] = S 2 β (0, T ; Rn ) H 2 β (0, T ; Rn d ) 0 Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

39 Main resul: Assumpion f is Lipschiz in (y, z) wih a uniform Lipschiz consan L > 0. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

40 Main resul: Assumpion f is Lipschiz in (y, z) wih a uniform Lipschiz consan L > 0. Theorem Under he above assumpions on f, for any ξ L 2 F T (Ω; R n ), (12) admis a unique soluion (Y, Z) N 0 [0, T ]. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

41 Main resul: Assumpion f is Lipschiz in (y, z) wih a uniform Lipschiz consan L > 0. Theorem Under he above assumpions on f, for any ξ L 2 F T (Ω; R n ), (12) admis a unique soluion (Y, Z) N 0 [0, T ]. Observaions: Since N β [0, T ] is equivalen o N 0 [0, T ], we need only find he soluion (Y, Z) N β (0, T ) for some β > 0. (y, z) N [0, T ], le h( ) = f (, y, z ) L 2 F (Ω [0, T ]; Rn ). { T Then, M = E ξ + h(s)ds } F, [0, T ] is an L 2 (F)-maringale. 0 Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

42 The Firs Sep: By he Mar. Rep. Thm, Z L 2 F (0, T ; Rn d ), such ha M = M Z s dw s, [0, T ]. (13) Define Y = M 0 h(s)ds. Then M 0 = Y 0, and ξ + Consequenly, Y = M = ξ+ = ξ h(s)ds = M T = Y 0 + h(s)ds = Y 0 + h(s)ds h(s)ds 0 0 Z s dw s 0 Z s dw s. Z s dw s 0 h(s)ds + 0 h(s)ds 0 Z s dw s Z s dw s. (14) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

43 A Priori Esimaes For any (y, z) N β [0, T ], le (Y, Z) be he soluion o (14). Applying Iô s formula o F (, Y ) = e β Y 2, hen aking expecaion and applying Faou: { E e β Y 2} + βe e βt E ξ 2 + 2E e βs Y s 2 ds + E e βs Y s, h(s) ds. Using he rick: 2ab εa 2 + b 2 /ε, ε > 0, we have E {e β Y 2} +(β 1 ε )E e βs Y s 2 ds +E e βt E ξ 2 + εe e βs h(s) 2 ds. e βs Z s 2 ds e βs Z s 2 ds Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

44 Coninuing from before, one has Y 2 ε H 2 β (εβ 1) { e βt E ξ 2 + ε h 2 H 2 β Z 2 H e βt E ξ 2 + ε h 2 2 β Hβ. 2 } ; (15) Using Burkholder-Davis-Gundy s inequaliy, one hen derive ha Y 2 S 2 β 2(1 + C 1 (β, ε))e βt E ξ 2 + 2εC 1 (β, ε) h 2 H 2 β, (16) where C 1 (β, ε) = 1 + ε εβ 1 + 2(1 + C)2, and C is he universal consan in he Burkholder-Davis-Gundy inequaliy. = (Y, Z) N β [0, T ]. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

45 Furhermore, For (y, z), (ȳ, z) N β [0, T ], le (Y, Z), (Ȳ, Z) N β [0, T ] be he corresponding soluions of (14), respecively. Define ζ = ζ ζ, ζ = y, z, Y, Z, and H(s) = f (s, y s, z s ) f (s, ȳ s, z s ). Then, H(s) L( ŷ s + ẑ s ), Ŷ T = ξ = 0; Choosing β = β(ε) and ε > 0 small enough, show ha (Ŷ, Ẑ) 2 N β [0,T ] C(ε) (ŷ, ẑ) 2 N β [0,T ], where C(ε) < 1. Thus he mapping (y, z) (Y, Z) is a conracion on N β [0, T ], proving he heorem. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

46 Comparison Theorems Suppose ha (Y i, Z i ), i = 1, 2 are soluions o he following wo BSDEs: for [0, T ], Y i = ξ i + f i (s, Ys i, Zs i )ds Zs i dw s, i = 1, 2. (17) Quesion: Assume ha ξ 1 ξ 2, P-a.s.; f 1 (, y, z) f 2 (, y, z), (, y, z). Can we conclude ha Y 1 Y 2, [0, T ]? Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

47 Comparison Theorems Suppose ha (Y i, Z i ), i = 1, 2 are soluions o he following wo BSDEs: for [0, T ], Y i = ξ i + f i (s, Ys i, Zs i )ds Zs i dw s, i = 1, 2. (17) Quesion: Assume ha ξ 1 ξ 2, P-a.s.; f 1 (, y, z) f 2 (, y, z), (, y, z). Can we conclude ha Y 1 Y 2, [0, T ]? Answer: Yes, provided f 2 is uniformly Lipschiz in (y, z)!! Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

48 Comparison Theorems Define Y = Y 1 Y 2 and Z = Z 1 Z 2. Then f 1 (, Y 1, Z 1 ) f 2 (, Y 2, Z 2 )=δf ()+α() Y + β(), Z, where δf () = f 1 (, Y 1, Z 1 ) f 2 (, Y 1, Z 1 ), and α() = f 2 (, Y 1, Z 1 ) f 2 (, Y 2, Z 1 ) 1 Y { Y 0}; β i () = f 2 (, Y 2, Z 1,i ) f 2 (, Y 2, Z 2,i ) 1 { Z i 0}, In oher words, we have Y = ξ + Z i {δf (s) + α(s) Y s + β(s), Z s }ds Z s, dw s. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

49 Comparison Theorems Noe: Since f 2 is uniformly Lipschiz, boh α and β are bounded, adaped processes!! Two Tricks: 1. (Change of Measure:) Define Θ() = exp { 0 β(s)dw s β s 2 ds } ; and dq dp = Θ(T ). Since β is bounded, by Girsanov Theorem we know ha Θ is a P-maringale, and W 1 = W + 0 β sds is a Q-Brownian moion. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

50 Comparison Theorems 2. (Exponeniaing:) Define Γ = exp { 0 α(s)ds}. Then applying Iô we have, for [0, T ], Γ T Y T Γ Y = Γ s δf (s)ds + Γ s Z s, dws 1. Now aking condiional expecaion on boh sides above, we have Γ Y = E Q{ Γ T ξ + Γ s δf (s)ds F }, [0, T ], P-a.s. Since ξ = ξ 1 ξ 2 0, P-a.s. (hence Q-a.s.!); and δf () = f 1 (, Y 1, Z 1 ) f 2 (, Y 1, Z 1 ) 0,, Q-a.s., we conclude ha Γ Y 0,, Q-a.s. This implies ha Y 0,, P-a.s., proving he comparison heorem. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

51 BSDEs wih Coninuous Coefficiens Theorem (Lepelier-San Marin, 1997) Assume f : [0, T ] Ω R R d R is a P B(R d+1 ) m able funcion, s.. for fixed, ω, he mapping (y, z) f (, ω, y, z) is coninuous, and K > 0, s.. (, ω, y, z), f (, w, y, z) K(1 + y + z ). Then for any ξ L 2 (Ω, F T, P) he BSDE Y = ξ + f (s, Y s, Z s )ds Z s dw s (18) has an adaped soluion (Y, Z) H 2 (R d+1 ), where Y is a coninuous process and Z is predicable. Also, here is a minimal soluion (Y, Z) of equaion (1), in he sense ha for any oher soluion (Y, Z) of (1) we have Y Y. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

52 BSDEs wih Coninuous Coefficiens Lemma 1 Le f : R p R be a coninuous funcion wih linear growh, ha is: K > 0 such ha x R p f (x) K(1 + x ). Then he sequence of funcions f n (x) = is well defined for n K and i saisfies: (i) Linear growh: x R p inf y Qp{f (y) + n x y } (19) f n (x) K(1 + x ); (ii) Monooniciy in n: x R p f n (x) ; (iii) Lipschiz condiion: x, y R p f n (x) f n (y) n x y ; (iv) srong convergence: if x n x as n, hen f n (x n ) f (x), as n. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

53 Proof of Lemma 1 Since f n f (= f n (x) K(1 + x )), and f n (x) inf y Q p{ K K y + K x y } = K(1 + x ), = (i) holds. (ii) is eviden from he definiion of he sequence (f n ). ε > 0, choose y ε Q p so ha f n (x) f (y ε ) + n x y ε ε f (y ε ) + n y y ε + n x y ε n y y ε ε f (y ε ) + n y y ε n x y ε f n (y) n x y ε. Exchanging he roles of x and y, and since ε is arbirary we deduce ha f n (x) f n (y) n x y, proving (iii). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

54 Proof of Lemma 1 To see (iv), assume x n x as n. For every n, le y n Q p be such ha f (x n ) f n (x n ) f (y n ) + n x n y n 1/n. Since {x n } is bounded and f has linear growh, we deduce ha {y n } is bounded, and so is {f (y n )}. Consequenly lim n n y n x n <, and in paricular y n x, as n. Moreover, from which he resul follows. f (x n ) f n (x n ) f (y n ) 1/n, Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

55 Proof of he Theorem Define, for fixed (, ω), a sequence f n (, ω, y, z), associaed o f by Lemma 1; and h(, ω, y, z) = K(1 + y + z ). Then consider he following wo BSDEs: Y n = ξ + U = ξ + f n (s, Ys n, Zs n )ds Z n s dws, h(u s, V s )ds V s dw s. By Comparison Theorem we obain ha n K n m K Y m Y n U d dp a.s. = A > 0, depending only on K, T and E(ξ 2 ), s.. U A, V A, and hence n K, Y n A. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

56 Proof of he Theorem Claim: Z n A as well. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

57 Proof of he Theorem Claim: Z n A as well. Le λ 2 > K, and applying Iô o (Y n ) 2 : ξ 2 = (Y n ) (Z n s ) 2 ds. Y n s f n (s, Y n s, Z n s )ds + 2 Taking expecaion on boh sides, we deduce E((Y n ) 2 )+E (Z n s ) 2 ds =E(ξ 2 ) + 2E Y n s Z n s dw s Y n s f n (s, Y n s, Z n s )ds. Therefore we obain from he uniform linear growh condiion on f n (see (i) of Lemma 1), for = 0 Z n 2 E(ξ 2 ) + 2K Y n 2 + 2KE 0 Y n s (1 + Z n s )ds. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

58 Proof of he Theorem Using 2a a 2 λ λ 2 and and 2ab a 2 λ 2 + b2 λ 2, we have 2K Y n s (1 + Z n s ) K{ 1 λ 2 + 2λ2 Y n s λ 2 Z n s 2 }, Z n 2 E(ξ 2 ) + KT λ 2 + 2K(λ2 + 1) Y n 2 + K λ 2 Z n 2. Since λ 2 > K we deduce for n K proving he claim. Z n 2 E(ξ2 ) + KT /λ 2 + 2K(λ 2 + 1)B 2 1 K/λ 2 = A, Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

59 Proof of he Theorem Now fix n 0 K. Since {Y n } is increasing and bounded in H 2 (R), i converges in H 2 (R) o a limi Y. Then, for n, m n 0 : = 2E E( Y0 n Y0 m 2 ) + E 0 0 Z n u Z m u 2 du (Y n u Y m u )(f n (u, Y n u, Z n u ) f m (u, Y m u, Z m u ))du. Applying Cauchy-Schwarz, and noing he uniform linear growh of {f n } and boundedness of { (Y n, Z n ) } we obain for all n, m n 0, Z n Z m 2 2C Y n Y m. = {Z n } is Cauchy in H 2 (R d ), and hus converge o Z H(R d ). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

60 Proof of he Theorem I hen can be checked ha, possibly along a subsequence: as n, P-almos surely, sup Y n Y T 0 + sup T f n (s, Y n s, Z n s ) f (s, Y s, Z s ) ds Zs n dw s Z s dw s 0, = Y is coninuous, and since {Y n } is monoone, by Dini he convergence is uniform. = One can hen pass all he necessary limis o show ha (Y, Z) is an adaped soluion of he original equaion (18). Finally, le (Ŷ, Ẑ) any H 2 soluion of (18). By Comparison Thm we ge ha n Y n Ŷ and herefore Y Ŷ proving ha Y is he minimal soluion. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

61 BSDEs wih Reflecions We now consider he following BSDE wih Reflecion (cf. e.g., El Karoui-Kapoudjian-Pardoux-Peng-Quenez, 1997): where Y = ξ + f (s, Y s, Z s )ds Z s dw s + K T K, Y S, [0, T ], (20) S, [0, T ] is he obsacle process, which is assumed o be coninuous, and E{sup 0 T S 2 } < ; and is given as a parameer of he equaion. K, [0, T ] is he reflecing process, which is assumed o be coninuous and increasing, and saisfies: K 0 = 0, 0 (Y S )dk = 0; and i is defined as a par of he soluion o he BSDE (20)(!) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

62 BSDEs wih Reflecions Recall he well-known Skorohod Problem: Le x be a coninuous funcion on [0, ) such ha x 0 0. Then here exiss a unique pair (y, k) of funcions on [0, ) such ha y = x + k; y 0, ; k is coninuous, increasing, k 0 = 0, and 0 y dk = 0. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

63 BSDEs wih Reflecions Recall he well-known Skorohod Problem: Le x be a coninuous funcion on [0, ) such ha x 0 0. Then here exiss a unique pair (y, k) of funcions on [0, ) such ha y = x + k; y 0, ; k is coninuous, increasing, k 0 = 0, and 0 y dk = 0. I is known ha he soluion o he Skorohod Problem for x has an explici form: k = sup s x s, 0. In he BSDE case we have Proposiion Le (Y, Z, K) be a soluion o he BSDE (20). Then for all [0, T ], i holds ha { }. K T K = ξ + f (s, Y s, Z s )ds Z s dw s S u sup u T u u Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

64 Oher Observaions Proposiion Le (Y, Z, K) be a soluion o (20). Then for each [0, T ], { v Y = esssup E f (s, Y s, Z s )ds + S v 1 {v<t } + ξ1 {v=t }, }, v T where T is he se of all sopping imes v, s.. v T. Suppose furher ha he obsacle process S is an Iô process: S = S U s ds + 0 V s, dw s, 0, where U, V L 2 F ([0, T ] Ω). Then Z = V, dp d-a.e. on he se {Y = S }; 0 dk 1 {Y=S }[f (, S, V ) + U ] d. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

65 A Priori Esimaes Lemma 1 Le (Y, Z, K) be a soluion o (20). Then C > 0 such ha { } E Y 2 + Z 2 d + KT 2 sup 0 T { CE ξ Proof. Firs apply Iô s formula o ge Y 2 + Z s 2 ds = ξ f 2 (, 0, 0)d + s sup 0 T Y s f (s, Y s, Z s )ds Y s Z s, dw s. s Then use 0 (Y S )dk = 0, Hölder, and Gronwall. (S + ) 2}. (21) s Y s dk s Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

66 A Priori Esimaes Lemma 2 Le (Y i, Z i, K i ), i = 1, 2 be soluions o BSDEs (20) wih parameers (ξ i, f i, S i ), i = 1, 2, respecively. Then C > 0 s.. { E ( Y ) 2 + Z 2 d + ( K T ) 2} sup 0 T { CE ( ξ) 2 + [ ( +C E sup 0 T 0 0 } [ f (, 0, 0)] 2 d ( S + ) 2)] 1/2 Ψ 1/2 T, where X { = X 1 X 2, for X = ξ, f, S, Y, Z, and K; and 2 Ψ T = E i=1 ( ξi 2 + } T 0 f i (, 0, 0) 2 d + sup 0 T S i 2 ). (22) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

67 A Priori Esimaes Lemma 2 Le (Y i, Z i, K i ), i = 1, 2 be soluions o BSDEs (20) wih parameers (ξ i, f i, S i ), i = 1, 2, respecively. Then C > 0 s.. { E ( Y ) 2 + Z 2 d + ( K T ) 2} sup 0 T { CE ( ξ) 2 + [ ( +C E sup 0 T 0 0 } [ f (, 0, 0)] 2 d ( S + ) 2)] 1/2 Ψ 1/2 T, where X { = X 1 X 2, for X = ξ, f, S, Y, Z, and K; and 2 Ψ T = E i=1 ( ξi 2 + } T 0 f i (, 0, 0) 2 d + sup 0 T S i 2 ). Noe: The uniqueness of BSDE follows direcly from Lemma 2! (22) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

68 Comparison Theorem Theorem Le (Y i, Z i, K i ), i = 1, 2 be soluions o BSDEs (20) wih parameers (ξ i, f i, S i ), i = 1, 2, respecively. Suppose ha ξ 1 ξ 2, f 1 f 2, S 1 S 2, 0 T, a.s. Then Y 1 Y 2, 0 T, a.s. Proof. Apply Iô s formula o ( Y ) + 2, and aking expecaion. Then use he fac ha Y 1 > S 2 S 1 on { Y > 0} o ge ( Y ) + (dk 1 dk 2 ) = ( Y ) + dk 2 0. Then apply Gronwall o ge ( Y ) + 0 = Y 1 Y 2. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

69 Well-Posdedness of he Refleced BSDEs The exisence and uniqueness of he adaped soluion o he refleced BSDE (20) can be proved using a sandard Picard ieraion (see EK-K-P-P-Q). However, he following penalizaion mehod has been used more ofen for is clariy on he srucure of he soluion. Penalizaion Scheme For each n N, le (Y n, Z n ) be he soluion o he unconsrained BSDE: Y n = ξ + f (s, Ys n, Zs n )ds + KT n K n Zs n, dw s, (23) where K n = n 0 (Y n s S s ) ds, [0, T ]. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

70 Well-Posdedness of he Refleced BSDEs One can show ha (as unconsrained BSDE): E{sup 0 T Y n 2 } < C > 0, such ha { E sup 0 T Y n 2 + Z n 2 d + (KT n )2} C. 0 Since f n = f + n(y S ) f n+1, by Comparison Theorem, Y n Y n+1, 0 T, a.s. = Y n Y. { } By Faou, one has E sup 0 T Y 2 C. Apply DCT o ge E 0 (Y Y n ) 2 d 0, as n. { } Since E sup (Y n S ) 2 0, as n (no rivial!!), i follows ha {(Y n, Z n )} is Cauchy in L 2 F ([0, T ] Ω; R Rd ). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

71 Well-Posdedness of he Refleced BSDEs Thus {(Y n, Z n )} L 2 F (Ω; C([0, T ]; R) L2 F ([0, T ] Ω; Rd ) is Cauchy, and {K n } is Cauchy in L 2 F (Ω; C([0, T ]; R) as well = The limi (Y, Z, K) (of {(Y n, Z n, K n )) mus saisfy (20) To check he fla-off condiion, noe ha { } { } E sup (Y S ) 2 = lim n E sup (Y n S ) 2 = 0 = Y s S, = 0 (Y S )dk 0. On he oher hand, since 0 (Y n S )dk n = n 0 [(Y n S ) ] 2 d 0, = 0 (Y S )dk = lim n 0 (Y n S )dk n 0 = 0 (Y S )dk = 0. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

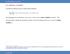
72 BSDEs wih Quadraic Growh Consider he BSDE: Y = ξ + f (s, Y s, Z s )ds Z s dw s, [0, T ]. (24) We assume ha he generaor f akes he following form: f (, y, z) = a 0 (, y, z)y + F 0 (, y, z), (25) where for consans β 0 < α 0, i holds for all (y, z) R 1+d ha (H1) { β0 a 0 (, y, z) α 0 ; F 0 (, y, z) k + c( y ) z 2 ; d dp-a.s. Noe: Under (H1) f grows linearly in y, bu quadraically in z! Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

73 BSDEs wih Quadraic Growh Theorem (Kobylanski, 2000) Suppose ha he coefficien f saisfies (H1), wih α 0, β 0, k R, and c : R + R + being coninuous and increasing. Then, for any ξ L (F T ), he BSDE (24) admis a leas one soluion (Y, Z) L F (Ω; C([0, T ]; R)) H 2 F ([0, T ]; Rd ). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

74 BSDEs wih Quadraic Growh Theorem (Kobylanski, 2000) Suppose ha he coefficien f saisfies (H1), wih α 0, β 0, k R, and c : R + R + being coninuous and increasing. Then, for any ξ L (F T ), he BSDE (24) admis a leas one soluion (Y, Z) L F (Ω; C([0, T ]; R)) H 2 F ([0, T ]; Rd ). The Power of Exponenial (Hopf-Cole) Transformaion Consider a simple quadraic BSDE: Y = ξ Z s 2 ds Z s dw s, [0, T ]. (26) Define y = exp[y ], z = yz. Then, he BSDE (26) becomes y = exp[ξ] z s dw s, [0, T ]. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

75 A Priori Esimaes Suppose ha he assumpion (H1) is replaced by { a0 (, y, z) α 0 ; (H0) F 0 (, y, z) b() + C( y ) z 2, d dp-a.s. where α 0 is consan and b L 1 ([0, T ]). Then he following a priori esimaes hold: Assume ha ξ L F T (Ω), hen [ ] +e Y sup(ξ) a sds + Ω for some consan K > 0, E Z s 2 ds K; 0 Y ξ + b α 0. s b s e aλdλ ds; (27) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

76 A Priori Esimaes Suppose ha he assumpion (H1) is replaced by (H0) { a0 (, y, z) α 0 ; F 0 (, y, z) b() + C( y ) z 2, d dp-a.s. where α 0 is consan and b L 1 ([0, T ]). Then he following a priori esimaes hold: Assume ha ξ L F T (Ω), hen Y [ ] e inf (ξ) T a sds Ω for some consan K > 0, E Z s 2 ds K; 0 Y ξ + b α 0. s b s e aλdλ ds; (28) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

77 A Priori Esimaes Idea of he Proof. Define he RHS of (27) by ϕ, hen ϕ saisfies he ODE: [ ] + T ϕ = sup(ξ) Ω (a s ϕ s + b s )ds, [0, T ]. Le Φ be a C 2 -funcion o be deermined. Applying Iô o ge Φ(Y ϕ ) = Φ(Y T ϕ T ) + Φ (Y s ϕ s )[f (s, Y s, Z s ) (a s ϕ s + β s )]ds (29) 1 T 2 Φ (Y s ϕ s ) Z s 2 ds Φ (Y s ϕ s )Z s dw s. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

78 A Priori Esimaes Denoe M = Y + ϕ, and choose { e Φ(u) = 2Cu 1 2Cu 2C 2 u 2, u [0, M] 0 u [ M, 0]. One can check ha Φ(u) 0 and Φ(u) = 0 u 0 Φ (u) 0 0 uφ (u) 2(M + 1)CΦ(u) CΦ (u) 1 2 Φ (u) 0. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

79 A Priori Esimaes Denoe M = Y + ϕ, and choose { e Φ(u) = 2Cu 1 2Cu 2C 2 u 2, u [0, M] 0 u [ M, 0]. One can check ha Φ(u) 0 and Φ(u) = 0 u 0 Φ (u) 0 0 uφ (u) 2(M + 1)CΦ(u) CΦ (u) 1 2 Φ (u) 0. Applying hese o (29) we ge, wih k = a + 2(M + 1)C, 0 Φ(Y ϕ ) k s Φ(Y s ϕ s )ds Φ (Y s ϕ s )Z s dw s, Taking expecaion and applying Gronwall one shows ha E{Φ(Y ϕ )} = 0 = Φ(Y ϕ ) = 0 = Y ϕ. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

80 A Priori Esimaes The L 2 -bound for Z can be proved by considering Φ(u) = 1 2C 2 [ exp(2c(u + M)) (1 + 2C(u + M)) ], where M = Y. Indeed, since Φ(u) 0, Φ (u) 0 0 uφ (u) M C (e4cm 1) = K Φ (u) CΦ (u) = 1, Seing ϕ 0 in (29) we can check 0 Φ(Y 0 ) Φ(Y T )+K 0 a s + ds = E Z s 2 ds Φ(M) + K 0 a + L 1 0 Z s 2 ds = K. Φ (Y s )Z s dw s, Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

81 Monoone Sabiliy Proposiion Suppose ha {(f n, ξ n )} are a sequence of parameers such ha f n f locally uniformly on R + R R d ; ξ n ξ in L. k : R + R +, k L 1 ([0, T ]), such ha for some C > 0, f n (, y, z) k +C z 2, n N, (, y, z) R + R R d. (Y n, Z n ) L F (Ω; C([0, T ]; R)) H 2 F ([0, T ]; Rd ) such ha {Y n } and Y n M. Then (Y, Z) L F (Ω; C([0, T ]; R)) H 2 F ([0, T ]; Rd ) such ha lim Y n = Y, uniformly on [0, T ]; Z n Z in H 2 n F ([0, T ]; Rd ), and (Y, Z) solves BSDE (24). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

82 Monoone Sabiliy Main Poins: {Y n } is monoone and bounded = Y, s.., Y n Y (poinwisely). {Z n } is bounded in L 2 ([0, T ] Ω) = i has a weakly convergen subsequence, denoed by iself. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

83 Monoone Sabiliy Main Poins: {Y n } is monoone and bounded = Y, s.., Y n Y (poinwisely). {Z n } is bounded in L 2 ([0, T ] Ω) = i has a weakly convergen subsequence, denoed by iself. Wan o Show: {Z n } converges Srongly in L 2 ([0, T ] Ω) (Mazur s Theorem) {Y n } converges Uniformly in (Dini s Theorem) Consequenly, one can hen show ha f n (s, Ys n, Zs n )ds Z n s dw s f (s, Y s, Z s )ds; and Z s dw s, and hus (Y, Z) solves he BSDE. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

84 Proof of he Main Resul Assumpions: There exiss α 0, β 0 R, B, C R +, such ha for all (, y, z) R + R R d, where f (, y, z) = a 0 (, y, z)y + F 0 (, y, z), β 0 a 0 (, y, z) α 0, F 0 (, y, z) B + C z 2. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

85 Proof of he Main Resul Assumpions: There exiss α 0, β 0 R, B, C R +, such ha for all (, y, z) R + R R d, where f (, y, z) = a 0 (, y, z)y + F 0 (, y, z), β 0 a 0 (, y, z) α 0, F 0 (, y, z) B + C z Exponenial Change. Define y = e 2CY and z = 2Cy Z. Then, by Iô one can check ha (y, z) solves he BSDE (24) wih parameers: y T = e 2Cξ ; F (, y, z) = 2C yf ( s, ln(y) 2C, z ) 1 z 2 2C y 2 y Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

86 Proof of he Main Resul 2. Truncaion. Define a C funcion ψ : R [0, 1] by { 1, if u [e 2CM, e 2CM ]; ψ(u) = 0, if u / [e 2C(M+1), e 2C(M+1) ]. Now, define F (, y, z) = ψ(y)f (, y, z), and le l + (y) l (y, z) Then i is easily checked ha Noe: = ψ(y)(α 0 y ln(y) + 2CBy); = ψ(y) (β 0 y ln(y) 2CBy z 2 ). y l (y, z) F (, y, z) l(y), (, y, z). (30) The funcion y l + (y) is bounded and Lipschiz! Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

87 Proof of he Main Resul 3. Approximaion. For any n N, find F n C b such ha F n+1 F n F n. Then, le φ n C be s.. φ(u) = { 1, 0 u n; 0, u n + 1. Define F n (, y, z) = F n (, y, z)φ n ( y + z )+ (l + (y)+ 1 ) 2 n [1 φ n ( y + z )]. Noe: F n s are uniformly Lipschiz (in (y, z)); For any n N and all (, y, z), i holds ha F (, y, z) F n (, y, z) F n (, y, z) l + (y) n. (31) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

88 Proof of he Main Resul 4. Synhesis. Denoe (y n, z n ) o be soluion o BSDE(F n, e 2Cξ ), via sandard heory. For n large enough F n (, e 2CM, 0) 0, and e 2CM e 2Cξ ; F n (, e 2CM, 0) 0, and e 2CM e 2Cξ, Since y e 2CM, z 0 (resp. y e 2CM, z 0) are soluions o he BSDE(e 2CM, 0) (resp. BSDE(e 2CM, 0)), by he sandard Comparison Theorem we conclude: Define Y n = ln(yn ) 2C f n (, y, z) f n (, y, z) e 2CM y n+1 y n e 2CM., Z n = zn 2Cy n, and = F n (, e 2Cy, 2Ce 2Cy z) 2Ce 2Cy + C z 2 = F n (, e 2Cy, 2Ce 2Cy z) 2Ce 2Cy + C z 2 ; Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

89 Proof of he Main Resul Then (Y n, Z n ) is he soluion o BSDE( f n, ξ), n N, and Y n s are monoone, since y n s are! Since f n f and f n f, uniformly on compacs, we can firs apply he Monoone Sabiliy Theorem, we know ha (Y, Z) L F (Ω; C([0, T ]; R)) H 2 F ([0, T ]; Rd ) such ha (Y, Z) solves BSDE( f, ξ). One can hen show ha Y M as was done in he a priori esimae, and noe ha f (, y, z) = f (, y, z), whenever y M (by he naure of he runcaion), we conclude ha (Y, Z) solves BSDE(f, ξ), proving he exisence. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

90 Uniqueness We shall assume ha he generaor f saisfies he following assumpions hroughou he uniqueness discussion. (H2) For some consans M and C > 0, and posiive funcions l( ) and k( ), i holds for all R +, y [ M, M], and z R d ha f (, y, z) l() + C z 2, a.s., f (32) z (, y, z) k() + C z 2, a.s., (H3) For some consan ε > 0 and C ε > 0, i holds for all R +, y R, and z R d ha f y (, y, z) l ε() + C z 2, a.s. (33) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

91 Uniqueness Comparison Theorem Le (Y i, Z i ), i = 1, 2 be wo soluions of BSDE(f i, ξ i ), i = 1, 2. Assume ha ξ 1 ξ 2, a.s., and f 1 f 2 ; For all ε > 0 and M > 0, here exis funcions l, l ε L 1, k L 2, and consan C R, such ha eiher f 1 or f 2 saisfies boh (H2) wih l, k, and C and (H3) wih l ε and ε. Then if (Y 1, Z 1 ) [resp. (Y 2, Z 2 ) L ( ) L 2 ( )] is a sub-soluion (resp. super-soluion) of he BSDEs wih parameers (f 1, ξ 1 ) (resp. (f 2, ξ 2 )), one has Y 1 Y 2, R +, a.s. Proof. Lenghy. (cf. Kobylanski (2000)) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

92 A Quick Summary We have sudied following ypes of BSDEs beyond he sandard ones: BSDEs wih coninuous coefficiens BSDEs wih reflecions BSDEs wih quadraic growh Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

93 A Quick Summary We have sudied following ypes of BSDEs beyond he sandard ones: BSDEs wih coninuous coefficiens BSDEs wih reflecions BSDEs wih quadraic growh Some Variaions Refleced BSDEs wih coninuous coefficiens Maoussi (1997), Hamadene-Maoussi-Lepelier (1997) BSDEs wih superlinear-quadraic coefficiens Lepelier-San Marin (1998) Refleced BSDE wih superlinear-quadraic coefficiens Kobylanski-Lepelier-Quenez-Torres (2001) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

94 Converse Comparison Theorem Consider he BSDE: Y = ξ + f (s, Y s, Z s )ds Z s dw s, 0. We know ha ξ 1 ξ 2 f 1 f 2 = Y 1 Y 2, 0 Quesion: Under wha condiion Y 1 Y 2 implies f 1 f 2? Main Assumpions (A1) The random field f : [0, T ] Ω R R d R is uniformly Lipschiz in (y, z), uniformly in (, ω). (A2) f (, 0, 0), is a square-inegrable adaped process. (A3) f (, y, 0) = 0 (A4) f (, y, z) is coninuous. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

95 Converse Comparison Theorem Theorem (Briand-Coque-Hu-Mémin-Peng, 2000) Assume (A1) (A4), and assume furher ha for any ξ L 2 (F T ), i holds ha Y 1 (ξ) Y 2 (ξ), for all [0, T ], P-a.s. Then P-almos surely, Main Tricks: f 1 0 (, y, z) f 1 0 (, y, z), (y, z) R R 6. Choose ξ ε = y + z(w +ε W ), ε > 0; and denoe = Y (ξ ε ); Y ε T Show ha 1 ε (Y ε y) g(, y, z), as ε 0; Then Y 1,ε Y 2,ε = g 1 g 2. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

96 Quadraic BSDEs wih Unbounded Terminal Value This is based on he works of Briand and Hu ( ). Consider he BSDE: Y = ξ + Main Assumpions f (s, Y s, Z s )ds Z s dw s, [0, T ] (34) β 0, γ > 0, α L 0 F ([0, T ] Ω), and ϕ : R + R + wih ϕ(0) = 0, such ha P-a.s., (i) For all [0, T ], (y, z) f (, y, z) is coninuous; (ii) (Monooniciy in y) (, z), (iii) (Quadraic growh): (, y, z), y[f (, y, z) f (, 0, z)] β y 2 ; f (, y, z) α() + ϕ( y ) + γ 2 z 2. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

97 Quadraic BSDEs wih Unbounded Terminal Value Main Purpose: Find he adaped soluion (hopefully unique!) o he BSDE (34), wih erminal value ξ saisfying: E{e γ ξ } < (ξ is said o have exponenial momen of order γ ), for some or all γ > 0. A Trick: Consider U(, Y ) = e γψ(, Y ), where ψ is a smooh funcion o be deermined. Applying Iô Tanaka: du(, Y ) γu(, Y ) = { ψ x(, Y )sgn(y )f (, Y, Z ) + ψ (, Y ) + γ 2 ψ x(, Y ) 2 Z 2 }d ψ xx(, Y ) Z 2 d +ψ x (, Y )dl + ψ x (, Y )sgn(y )Z dw, where L is he local ime of Y a zero. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

98 Quadraic BSDEs wih Unbounded Terminal Value Since sgn(y )f (, Y, Z ) = sgn(y )[f (, Y, Z ) f (, 0, Z )] +sgn(y )f (, 0, Z ) β Y + α() + γ 2 Z 2, assuming ψ x (, x) 1 for x 0, one has ψ x (, Y )sgn(y )f (, Y, Z ) ψ (, Y ) γ 2 ψ x(, Y ) 2 Z 2 ψ x (, Y )[α() + β Y ] ψ (, Y ). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

99 Quadraic BSDEs wih Unbounded Terminal Value Since sgn(y )f (, Y, Z ) = sgn(y )[f (, Y, Z ) f (, 0, Z )] +sgn(y )f (, 0, Z ) β Y + α() + γ 2 Z 2, assuming ψ x (, x) 1 for x 0, one has ψ x (, Y )sgn(y )f (, Y, Z ) ψ (, Y ) γ 2 ψ x(, Y ) 2 Z 2 ψ x (, Y )[α() + β Y ] ψ (, Y ). Idea: Look for ψ ha solves he firs order PDE for (, x) [s, T ] R: ψ (, x) (α() + βx)ψ x (, x) = 0, ψ(s, x) = x. (35) Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

100 Quadraic BSDEs wih Unbounded Terminal Value The soluion o he characerisic equaion of (35): v(u;, x) = x + u [α(r) + βv(r;, x)]dr, 0 u. (36) is v(s;, x) = xe β( s) + s α(r)eβ(r s) dr, 0 s T. Since d du ψ(u, v(u;, x)) = 0, we have for s T, ψ(, x) = ψ(, v(;, x)) = ψ(s, v(s;, x)) = v(s;, x). = ψ x (, x) 1 and ψ xx (, x) 0!! A Key Esimae e γ Ys = U(s, Y s ) U(, Y ) s γu(r, Y r )ψ x (r, Y r )sgn(y r )Z r dw r. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

101 Quadraic BSDEs wih Unbounded Terminal Value Theorem (Exisence) Assume ha he main assumpion holds. Assume also ha ξ + α 1 has an exponenial momen of order γe βt, hen he BSDE (34) has a soluion (Y, Z) such ha Y 1 { { γ log E exp γe β(t ) ξ + γ Noe: α(r)e β(r ) dr } F }. The Comparison Theorems (whence uniqueness) for quadraic BSDE were only proved for he bounded erminal value case, based essenially on he fac ha in ha case he process Z W is a BMO Maringale. Since his fac fails in he unbounded erminal case, a new idea is needed! Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

102 Quadraic BSDEs wih Convex Coefficiens in z Assumpion (A2) There exis wo consans γ > 0 and β 0, and a non-negaive, progressively measurable process α(), 0, such ha, [0, T ], y R, he mapping z f (, y, z) is convex; (, z) [0, T ] R, f (, y, z) f (, y, z ) β y y, (y, y ) R 2 ; f saisfies he growh condiion: f (, y, z) α() + β y + γ 2 z 2 ; α 1 has exponenial momen of all order. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

103 Quadraic BSDEs wih Convex Coefficiens in z Comparison Theorem Le (Y, Z) and (Y, Z ) be wo soluion o (34) w.r.. erminal condiions ξ and ξ, generaors f and f, respecively. Assume ha { for any λ > 0, E e λy + e λy } <, where Y = sup [0,T ] Y ; ξ ξ, P-a.s.; f (, y, z) f (, y, z), (, y, z) [0, T ] R R d ; f saisfies (A2). Then Y Y, for all [0, T ], P-a.s. Furhermore, if Y 0 = Y 0, hen { } P ξ = ξ, (f f )(, Y, Z )d = 0 > 0. 0 Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

104 Quadraic BSDEs wih Convex Coefficiens in z Main Trick: For any θ (0, 1), consider η θ = η θη, η = ξ, Y, Z. Le A = 0 α(s)ds, hen we have e A Y θ = e A T Y θ T + e As F s ds e As Zs θ dw s, where, denoing δf () = (f f )(, Y, Z ), F = (f (, Y, Z ) θf (, Y, Z )) α()y θ = (f (, Y, Z ) f (, Y, Z )) +(f (, Y, Z ) θf (, Y, Z )) + θδf (). Using he convexiy of f in z, one has ( f (, Y, Z ) θf (, Y, Z ) + (1 θ)f, Y Z θ ), 1 θ Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

105 Quadraic BSDEs wih Convex Coefficiens in z Using he growh condiion o ge f (, Y, Z ) θf (, Y, Z )+(1 θ)(α()+β Y )+ γ 1 θ Z θ 2. = F (1 θ)(α() + 2β Y γ ) + 2(1 θ) Z θ 2 + θδf (). Denoe P = e cea Y θ, Q = cp Z θ e A, hen P = P T + c = Y θ 1 θ { { log E exp γe 2βT( ξ + γ Leing θ 1, one obains Y Y! ( P s e As F s ceas 2 Z θ 2) ds Q s dw s. )} } G(s, Y s F )ds. Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

106 Quadraic BSDEs and Convex Risk Measures Recall he Enropic dynamic risk measure. Enropic RM I is shown by Barrieu-El Karoui ( 04) ha {ρ γ (ξ)} [0,T ] is he unique soluion of he following quadraic BSDE: ρ γ (ξ) = ξ + 1 Z s 2 ds Z s db s, [0, T ], 2γ Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

107 Quadraic BSDEs and Convex Risk Measures Recall he Enropic dynamic risk measure. Enropic RM I is shown by Barrieu-El Karoui ( 04) ha {ρ γ (ξ)} [0,T ] is he unique soluion of he following quadraic BSDE: ρ γ (ξ) = ξ + 1 Z s 2 ds Z s db s, [0, T ], 2γ Bu he generaor g = 1 2γ z 2 is quadraic, and hence NOT a consequence of he represenaion heorem! Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218

108 Quadraic BSDEs and Convex Risk Measures Recall he Enropic dynamic risk measure. Enropic RM I is shown by Barrieu-El Karoui ( 04) ha {ρ γ (ξ)} [0,T ] is he unique soluion of he following quadraic BSDE: ρ γ (ξ) = ξ + 1 Z s 2 ds Z s db s, [0, T ], 2γ Bu he generaor g = 1 2γ z 2 is quadraic, and hence NOT a consequence of he represenaion heorem! In fac, in his case he dominaion (11) fails. E.g., γ = 1: ρ 0 (ξ+η) ρ 0 (ξ) = η ( Z 2 s +Z s 2 Z 2 s 2 )ds 0 Z s db s. where Z = Z 1 Z 2. Bu 1 2 ( z2 + z 2 z 2 2 ) z z2 2 canno be dominaed by any (quadraic g). Jin Ma (Universiy of Souhern California) BSDEs in Financial Mah Paris Aug / 218