Simulation of BSDEs and. Wiener Chaos Expansions
|
|
|
- Charlene Mills
- 5 years ago
- Views:
Transcription
1 Simulaion of BSDEs and Wiener Chaos Expansions Philippe Briand Céline Labar LAMA UMR 5127, Universié de Savoie, France hp:// Workshop on BSDEs Rennes, May 22-24, 213
2 Inroducion Simulaion of BSDEs and Wiener Chaos Expansions Inroducion Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
3 Inroducion Backward Sochasic Differenial Equaions A BSDE is an equaion of he ype T T Y = ξ + f (s, Y s, Z s )ds Z s db s, T The firs resul was proved by É. Pardoux and S. Peng Theorem (Pardoux-Peng) If he generaor f is Lipschiz, and [ ] E ξ 2 + T f (s,, ) 2 ds < + hen he BSDE has a unique square inegrable soluion Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
4 Inroducion Euler s scheme for BSDEs For a SDE For a BSDE X +h = X + h b(x ) + σ(x ) (B +h B ) Y h = Y + h f (Y h, Z h ) Z h (B B h ) The correc equaion is Y h = Y + h f (Y h, Z h ) Z h (B B h ) + (N N h ) The soluion is given by Z h = h 1 E (Y (B B h ) F h ), Y h = E (Y F h ) + h f (Y h, Z h ) Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
5 Inroducion Discreizaion of BSDEs No so easy as for SDEs D. Chevance 1997, V. Bally 1997 Dynamical Programming Equaion A "sepwise consan" Brownian moion in his case (Ph. B., B. Delyon, J. Mémin 1 & 2) The speed of convergence was proved by J. Zhang 4 and B. Bouchard and N. Touzi 4 for Markovian BSDEs Error expansion by E. Gobe and C. Labar 7 L 2 regulariy E. Gobe, A. Makhlouf 1, Quadraic case A. Richou 11 Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
6 Inroducion Discreizaion of BSDEs One of he main difficulies is o compue condiional expecaions Several approaches : using Malliavin calculus, B. Bouchard and N. Touzi using regression mehods, E. Gobe, J.-P. Lemor and X. Warin using quanizaion, V. Bally and G. Pagès We propose here o use Wiener chaos expansions In he spiri, i is no so far from he regression echnics C. Bender and R. Denk 7 Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
7 Inroducion How o solve a BSDE? Two seps : The generaor does no depend on (Y, Z ) Fixed poin argumen Picard ieraions ξ, {f (s)} s T square inegrable T T Y = ξ + f (s) ds Z s db s, T. The soluion is given by Y = E ( ξ + T f (s) ds ) F Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
8 Inroducion How o solve a BSDE? T Seing F = ξ + f (s) ds, we have Y = E (F F ) f (s) ds Finally, he soluion is given by T F = E [F ] + Z s db s. Y = E (F F ) f (s) ds Z = D Y = D E (F F ) Explici formulae using Wiener chaos expansions + Picard ieraions Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
9 The Algorihm Simulaion of BSDEs and Wiener Chaos Expansions The Algorihm Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
10 The Algorihm Wiener Chaos Expansion Muliple Wiener Inegrals (Ω, F, P) complee probabiliy space B real valued Brownian moion {F } T augmened filraion of B : F = F T If F L 2 (Ω, F, P), T F =E[F ] u 1 (s 1 )db s1 + T sn T s2 u n is a deerminisic funcion defined on u 2 (s 2, s 1 )db s1 db s2 s2 u n (s n,..., s 1 )db s1... db sn +... S n (T ) := {(s 1,, s n ) [, T ] n : < s 1 <... < s n < T } Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
11 The Algorihm Wiener Chaos Expansion Muliple Wiener Inegrals If u n L 2 (S n (T )), we se J n (u n ) := T sn s2 u n (s n,, s 1 )db s1 db sn, H n := vec ( J n (u n ) : u n L 2 (S n (T )) ) We have E [ J n (u n ) 2] = sn s2 sn E [J n (u n )J m (u m )] = δ nm u 2 n(s n,..., s 1 )ds 1... ds n s2 u n (s n,..., s 1 )u m (s n,..., s 1 )ds 1... ds n Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
12 The Algorihm Wiener Chaos Expansion Muliple Wiener Inegrals To summarize, wih H = R, L 2 (Ω, F, P) = n H n Noaions : for F L 2 (Ω, F, P) P n (F) = J n (u n ) is he projecion of F on H n, C p (F) denoes he chaos decomposiion of F up o order p p p C p (F) = E[F] + P k (F) = E[F ] + J k (u k ) = E[F] + k=1 T u 1 (s 1 )db s k=1 T s2 u p (s p,..., s 1 )db s1... db sp E [ F 2] = E [F ] 2 + n 1 E [ P n (F ) 2] Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
13 The Algorihm Wiener Chaos Expansion Hermie polynomials The Hermie polynomials are defined by he expansion e x 2 /2 = H n (x) n n! = K n (x) n n n H 2 (x) = x 2 1, K 1 (x) = 1 ( x 2 1 ). 2 ( n! ) Kn is an orhonormal basis of L 2 (R, µ) n µ normal disribuion N (, 1) Le (g n ) n 1 be an orhonormal basis of L 2 (, T ) H n is he closure of he vecor field spanned by ( ) T ni! K ni g i (s)db s : (n i ) i 1 := n i = n i 1 i 1 Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
14 The Algorihm Wiener Chaos Expansion Hermie polynomials Le Λ be he se of all sequences of inegers (n i ) i 1 such ha n = i 1 n i < + The se ( ) T ni! K ni g i (s)db s : n = (n i ) i 1 Λ i 1 is an orhonormal basis of L 2 (Ω, F, P) For F L 2 (Ω, F, P), F = E[F] + k 1 n =k d n k ( ) T K ni g i (s)db s i 1 dk n = n! E F ( T K ni i 1 g i (s)db s ), n! = i 1 n i! Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
15 The Algorihm Generaor independen of (Y, Z ) We consider he BSDE Y = ξ + A simple BSDE T The soluion is given by T f (s) ds Z s db s, T T Y = E (F F ) f (s) ds, Z = D E (F F ), F = ξ + f (s) ds Compue Y and Z wih he decomposiion F = E[F] + k 1 n =k d n k ( ) T K ni g i (s)db s i 1 dk n = n! E F ( T K ni i 1 g i (s)db s ), n! = i 1 n i! Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
16 The Algorihm Generaor independen of (Y, Z ) Choice of he basis We choose an orhonormal basis of L 2 (, T ) for which compuaions are easy The firs N funcions, g 1,..., g N, are given by g i () = ( i i 1 ) 1/2 1 ]i 1, i ](), i = i T N = ih, i = 1,..., n We complee hese funcions ino an orhonormal basis of L 2 (, T ), (g i ) i 1 We can consider he Haar basis on each inerval ( i 1, i ) Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
17 The Algorihm Generaor independen of (Y, Z ) Approximaion of F We consider a finie numbers of chaos p p F C p (F) = E [F ] + dk n k=1 n =k i 1 We work only wih he funcions g 1,..., g N p F C p (F ) Cp N (F ) = E [F] + k=1 n =k p = E [F] + ( ) T K ni g i (s)db s d n k dk n k=1 n =k i=1 ( n ) T K ni g i (s)db s i=1 n K ni (G i ) dk n = n 1!... n N! E [F K n1 (G 1 )... K nn (G N )] wih he noaions n = (n 1,..., n N ), G i = ( i i 1 ) 1/2 ( ) B i B i 1 Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
18 The Algorihm Generaor independen of (Y, Z ) Approximaion of F Roughly speaking, we consider ha H k is generaed by Exemple For p = 2, C N 2 (F) = E [F ] + {K n1 (G 1 )... K nn (G N ) : n n N = k} N j=1 d e j 1 K 1(G j ) + j 1 N d e ij 2 K 1(G i )K 1 (G j ) + j=1 i=1 where (e j ) 1 j N is he canonical basis of R N, and e ij = e i + e j. For j = 1,, N and i = 1,, j 1 d e j 1 = E(FK 1(G j )), d e ij 2 = E(FK 1(G i )K 1 (G j )), d 2e j 2 = 2E(FK 2 (G j )). N j=1 d 2e j 2 K 2(G j ), Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
19 The Algorihm Generaor independen of (Y, Z ) Approximaion of (Y, Z ): coninuous ime For 1 r N and r 1 < r, wih n(r) = (n 1,..., n r ) E ( C N p (F) ) = E [F ] + Y p,n p k=1 n(r) =k d n k ( ) ( ) nr K r 1 2 B B r 1 n i<r i (G i ) Knr, h r 1 ( = E C N p F ) r 1 h f ( i 1 ) ( r 1 )f ( r 1 ), Z p,n = D E ( C N p (F ) ) = h 1/2 p k=1 n(r) =k n r > d n k i=1 ( ) nr 1 ( ) K r 1 2 B B n i<r i (G i ) K r 1 nr 1. h r 1 Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
20 The Algorihm Generaor independen of (Y, Z ) Approximaion of (Y, Z ): coninuous ime Y p,n is coninuous on [, T ] To define Z p,n we se Case p = 2, for 1 r N, Y 2,N r = E[F] + Z 2,N r = h 1/2 ( r j=1 Y p,n = E[F ] = d Z p,n = lim Z p,n = d e 1 1 = E[F B h]. h h d e j 1 K 1(G j ) + j 1 r d e ij 2 K 1(G i )K 1 (G j ) + j=1 i=1 d er 1 + d 2er 2 K 1 (G r ) + r 1 i=1 d e ir 2 K 1(G i ) ). r j=1 d 2e j 2 K 2(G j ), Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
21 The Algorihm Generaor independen of (Y, Z ) The Algorihm Saring from M rajecories of he BM B, we ge M rajecories of F We compue d = Ê [F ] = 1 M M m=1 F m d n k = n!ê [FK n 1 (G 1 )... K nn (G N )] = n! 1 M We ge M rajecories of (Y, Z ) Y p,n,m r = d + Z p,n,m r = h 1/2 p k=1 n(r) =k p k=1 n(r) =k n r > d n k d n k M F m K n1 (G1 m )... K nn (GN m ) m=1 i r K n i (G m i ) h r f m ( i 1 ), i=1 i<r K n i (G m i ) K nr 1 (G m r ). Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
22 The Algorihm The general case A BSDE wih a generaor We consider now he BSDE Y = ξ + T f (s, Y s, Z s )ds T Z s db s, T. We assume ha f : [, T ] R R d R is Lipschiz f (, y, z) f (, y, z ) L f ( y y + z z ). The algorihm consiss in wo seps The Picard scheme o remove he generaor The previous approximaion Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
23 The Algorihm The general case Picard Ieraions (Y, Z ) = (, ) and for q T Y q+1 = ξ + f ( s, Ys q, Zs q ) T ds Zs q+1 db s, T. Le ( Y q,p,n, Z q,p,n) be he approximaion of (Y q, Z q ) ( Y,p,N, Z,p,N) = (, ) F q,p,n = ξ + T f (s, Y q,p,n s, Zs q,p,n )ds Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
24 The Algorihm The general case Previous Approximaion We consruc, wih he explici formulas, for r =,..., N Y q+1,p,n r Z q+1,p,n r = E ( Cp N ( F q,p,n ) ) r ( F r h f = D r Y q+1,p,n r i=1 i 1, Y q,p,n i 1 = D r E ( Cp N ( F q,p,n ) ) F r Saring wih M rajecories of B he coefficiens of he Wiener expansions are compued by Mone-Carlo we obain M rajecories of he process ( Y q,p,n,m, Z q,p,n,m) ), Z q,p,n i 1 Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
25 Numerical Examples Simulaion of BSDEs and Wiener Chaos Expansions Numerical Examples Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
26 Numerical Examples Linear Driver - Financial Benchmark Linear Driver - Financial Benchmark Black-Scholes model in dimension d = 1 Linear generaor f (, y, z) = ry S = S e (r 1 2 σ2 )+σw, [, T ]. We consider a Discree Down and Ou Barrier Call opion The parameers are ξ = (S T K ) + 1 n [,N]Sn L r =.1, σ =.2, T = 1, K =.9, L =.85, S = 1, N = 2 By a variance reducion Mone Carlo mehod Y = , δ = Z σs =.8327 Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
27 Numerical Examples Linear Driver - Financial Benchmark Linear Driver - Financial Benchmark Evoluion of Y_ Evoluion of dela_ 134e e e e 3.64 ref y_app log(m) ref dela_app log(m) Figure : Evoluion of Y q,p,n,m and δ := Z q,p,n,m w.r.. log(m) when N = 2, p = 2, σs q = 5 -Discree Down and Ou Barrier Call opion Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
28 Numerical Examples Non linear driver - Financial Benchmark Non linear driver - Financial Benchmark Black-Scholes model in dimension d = 5 i = 1,, 5 S i = S i e (µi (σi ) 2 2 )+σ i B i. The correlaion marix of B is given by B i, B j = C i,j = ρ1 i j + 1 i=j, 1 4 < ρ < 1 The borrowing rae R is higher han he bond one r The driver is given by f (, y, z) = ry θ z + (R r)(y where θ = θ := Σ 1 (µ r1), Σ ij = σ i L ij, C = LL 5 (Σ 1 z) i ) We consider a Pu Baske Opion : ξ = (K i=1 Si T ) + i=1 Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
29 Numerical Examples Non linear driver - Financial Benchmark Non linear driver - Financial Benchmark Comparison wih resuls from É. Gobe & C. Labar 21 CPU ime = 166 when M = 5 and N = 2 Evoluion of Y_ Evoluion of dela_(1) 2.1 ref y_app 2. 45e 3 49e e e e log(m) ref dela_app 65e log(m) Figure : Evoluion of Y q,p,n,m and δ (1) w.r.. log(m) when N = 2, p = 2, q = 5, d = 5 - Baske Pu opion wih differen ineres and borrowing raes. Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
30 Numerical Examples Non linear driver - Financial Benchmark Non linear driver - Financial Benchmark We ry his example in dimension d = 1 The price and he δ are obained in 5 minues Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
31 Numerical Examples Non Linear Driver & Pah Dependen Terminal Condiion Non Linear Driver & Pah Dependen ξ The example is he following : d = 1 ξ = sup T B f (, y, z) = cos(y) Comparison beween p = 2 and p = 3 for N = 2 and M = 1 5 Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
32 Numerical Examples Non Linear Driver & Pah Dependen Terminal Condiion Non Linear Driver & Pah Dependen ξ ieraions CPU ime p = p = Table : Evoluion of Y q,p,n,m w.r.. Picard s ieraions, M = 1 5, N = 2 and CPU ime ieraions CPU ime p = p = Table : Evoluion of Z q,p,n,m w.r.. Picard s ieraions, M = 1 5, N = 2 and CPU ime Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
33 Numerical Examples Non Linear Driver & Pah Dependen Terminal Condiion + + Non Linear Driver & Pah Dependen ξ Convergence in M Evoluion of Y^q_ Evoluion of Z^q_ M=1^3 M=1^4 M=1^5.9 + M=1^3 M=1^4 M=1^ ieraions ieraions Figure : Evoluion of Y q,p,n,m and Z q,p,n,m w.r.. q and M when N = 2, p = 2, ξ = sup T B s, f (, y, z) = cos(y). Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
34 Numerical Examples Non Linear Driver & Pah Dependen Terminal Condiion Non Linear Driver & Pah Dependen ξ Convergence in N Evoluion of Y^q_ Evoluion of Z^q_ N=1 N=2 N=3 N= N=1 N=2 N=3.9 N= ieraions ieraions Figure : Evoluion of Y q,p,n,m and Z q,p,n,m w.r.. N when M = 1 5, p = 2 - ξ = sup T B s, f (, y, z) = cos(y) Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
35 Numerical Examples Non Linear Driver & Pah Dependen Terminal Condiion Conclusion The complexiy of he algorihm is he following O ( K i M p (N d) p+1) This algorihm is raher fas even when he dimension of he underlying BM is grea easy o implemen Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
36 Error Analysis Simulaion of BSDEs and Wiener Chaos Expansions Error Analysis Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
37 Error Analysis Convergence Resuls Spliing he error We wan o conrol he error [ E = E Y Y q,p,n sup T 2 + T Of course, we spli he error ino hree pars E = E q + E q,p + E q,p,n ] Z Z q,p,n 2 d Y Y q,p,n = Y Y q + Y q Y q,p + Y q,p Y q,p,n A erm is missing : Y q,p,n Y q,p,n,m which comes from "Mone Carlo expecaions" The firs par is very easy : E q C(T, L f ) 2 q, C(T, L f ) is explici Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
38 Error Analysis Convergence Resuls A lo of regulariy The generaor f smooh : f C b ξ is smooh in he Malliavin sense : ξ D Hölder coninuiy : E[D (r) s 1,,s r ξ] E[D (r) 1,, r ξ] K ξ ( s 1 1 α ξ + + s r r α ξ ) The Malliavin derivaives belongs o L p Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
39 Error Analysis Convergence Resuls Example X soluion o he SDE X = x + wih b and σ C wih bounded derivaives g : R n R C p b(x s ) ds + σ(x s ) db s, Regulariy assumpion rue ξ = g(x T ) ( ) T ξ = g X s ds Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
40 Error Analysis Convergence Resuls Error coming from a finie number of chaos We invesigae now E q,p relaed o Y q Y q,p. Proposiion Under h regulariy assumpion E q+1,p C T (T + 1)L 2 f E q,p + K p + 1 where K depends on he derivaives of f and ξ and T. Corollary We have E q,p A p + 1, A = K (C T (T + 1)L 2 f )q 1 C T (T + 1)L 2 f 1. Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
41 Error Analysis Convergence Resuls Error coming from a finie number of chaos We deduce from his resul ha lim q + lim Y q,p = Y. p + When T is small, C T (T + 1)L 2 f < 1, A does no depend on q and lim p + lim Y q,p = Y. q + The algorihm breaks he srucure of BSDEs Le us wrie (Y q+1,p, Z q+1,p ) in a backward way ( T = C p (ξ) + C p f ( s, Ys q,p Y q+1,p T + f (s, Y q,p s, Zs q,p )ds ), Zs q,p ) T ds T Zs q+1,p db s f ( s, Y q,p s, Zs q,p ) ds Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
42 Error Analysis Convergence Resuls Error coming from a finie number of chaos If lim q Y q,p exiss, hen one has Y,p = C p (ξ) + C p ( T T + f (s, Y,p s f ( s, Y,p s T, Zs,p )ds ), Zs,p ) T ds Zs,p db s f ( s, Y,p s The erminal condiion involves all he rajecory of he soluion. We were able o solve his BSDE only when T is small, Zs,p ) ds Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
43 Error Analysis Error coming from he runcaion of he basis Error coming from he runcaion of he basis Proposiion Under he regulariy assumpion, ) 2αξ 1 E q+1,p,n C 1 T (T + 1)L 2 f E q,p,n + K 1 ( T N where C 1 is a scalar and K 1 depends on he derivaives of f and ξ. Moreover, E q,p,n A 1 ( T N ) 2αξ 1, A 1 = K 1 T (T + 1)e T (C 1T (T + 1)L 2 f )q 1 C 1 T (T + 1)L 2 f 1 As before, he consan T (T + 1) appears Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
44 Error Analysis Global error Proposiion Under he regulariy assumpion, wih Convergence resul E C2 q + A ( ) 2αξ 1 T p A 1 N A = K (C T (T + 1)L 2 f )q 1 C T (T + 1)L 2 f 1 A 1 = K 1 T (T + 1)e T (C 1T (T + 1)L 2 f )q 1 C 1 T (T + 1)L 2 f 1 Corollary In paricular, lim lim q p lim Y q,p,n = Y N Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
45 Error Analysis Global error Perspecives Try o weaken he regulariy assumpion Undersand for large p and T he BSDE Y,p = C p (ξ) + C p ( T T + f (s, Y,p s f ( s, Y,p s T, Zs,p )ds ), Zs,p ) T ds Zs,p db s f ( s, Y,p s This mehod works also for he dynamic programing equaion, Zs,p ) ds Y = E (Y + h F ) + hf (, Y, Z ), Z = h 1 E (Y +h (B +h B ) F ) Numerical simulaions are no so good Error analysis Ph. Briand & C. Labar (Univ. Savoie) Simulaion of BSDEs and Wiener Chaos Expansions Rennes, May 22-24, / 46
46 Thank you for your aenion
Simulation of BSDEs and. Wiener Chaos Expansions
 Simulaion of BSDEs and Wiener Chaos Expansions Philippe Briand Céline Labar LAMA UMR 5127, Universié de Savoie, France hp://www.lama.univ-savoie.fr/ Sochasic Analysis Seminar Oxford, June 1, 213 Inroducion
Simulaion of BSDEs and Wiener Chaos Expansions Philippe Briand Céline Labar LAMA UMR 5127, Universié de Savoie, France hp://www.lama.univ-savoie.fr/ Sochasic Analysis Seminar Oxford, June 1, 213 Inroducion
Time discretization of quadratic and superquadratic Markovian BSDEs with unbounded terminal conditions
 Time discreizaion of quadraic and superquadraic Markovian BSDEs wih unbounded erminal condiions Adrien Richou Universié Bordeaux 1, INRIA équipe ALEA Oxford framework Le (Ω, F, P) be a probabiliy space,
Time discreizaion of quadraic and superquadraic Markovian BSDEs wih unbounded erminal condiions Adrien Richou Universié Bordeaux 1, INRIA équipe ALEA Oxford framework Le (Ω, F, P) be a probabiliy space,
An Introduction to Malliavin calculus and its applications
 An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
An Introduction to Backward Stochastic Differential Equations (BSDEs) PIMS Summer School 2016 in Mathematical Finance.
 1 An Inroducion o Backward Sochasic Differenial Equaions (BSDEs) PIMS Summer School 2016 in Mahemaical Finance June 25, 2016 Chrisoph Frei cfrei@ualbera.ca This inroducion is based on Touzi [14], Bouchard
1 An Inroducion o Backward Sochasic Differenial Equaions (BSDEs) PIMS Summer School 2016 in Mahemaical Finance June 25, 2016 Chrisoph Frei cfrei@ualbera.ca This inroducion is based on Touzi [14], Bouchard
Uniqueness of solutions to quadratic BSDEs. BSDEs with convex generators and unbounded terminal conditions
 Recalls and basic resuls on BSDEs Uniqueness resul Links wih PDEs On he uniqueness of soluions o quadraic BSDEs wih convex generaors and unbounded erminal condiions IRMAR, Universié Rennes 1 Châeau de
Recalls and basic resuls on BSDEs Uniqueness resul Links wih PDEs On he uniqueness of soluions o quadraic BSDEs wih convex generaors and unbounded erminal condiions IRMAR, Universié Rennes 1 Châeau de
6. Stochastic calculus with jump processes
 A) Trading sraegies (1/3) Marke wih d asses S = (S 1,, S d ) A rading sraegy can be modelled wih a vecor φ describing he quaniies invesed in each asse a each insan : φ = (φ 1,, φ d ) The value a of a porfolio
A) Trading sraegies (1/3) Marke wih d asses S = (S 1,, S d ) A rading sraegy can be modelled wih a vecor φ describing he quaniies invesed in each asse a each insan : φ = (φ 1,, φ d ) The value a of a porfolio
Backward stochastic dynamics on a filtered probability space
 Backward sochasic dynamics on a filered probabiliy space Gechun Liang Oxford-Man Insiue, Universiy of Oxford based on join work wih Terry Lyons and Zhongmin Qian Page 1 of 15 gliang@oxford-man.ox.ac.uk
Backward sochasic dynamics on a filered probabiliy space Gechun Liang Oxford-Man Insiue, Universiy of Oxford based on join work wih Terry Lyons and Zhongmin Qian Page 1 of 15 gliang@oxford-man.ox.ac.uk
and Applications Alexander Steinicke University of Graz Vienna Seminar in Mathematical Finance and Probability,
 Backward Sochasic Differenial Equaions and Applicaions Alexander Seinicke Universiy of Graz Vienna Seminar in Mahemaical Finance and Probabiliy, 6-20-2017 1 / 31 1 Wha is a BSDE? SDEs - he differenial
Backward Sochasic Differenial Equaions and Applicaions Alexander Seinicke Universiy of Graz Vienna Seminar in Mahemaical Finance and Probabiliy, 6-20-2017 1 / 31 1 Wha is a BSDE? SDEs - he differenial
Chapter 14 Wiener Processes and Itô s Lemma. Options, Futures, and Other Derivatives, 9th Edition, Copyright John C. Hull
 Chaper 14 Wiener Processes and Iô s Lemma Copyrigh John C. Hull 014 1 Sochasic Processes! Describes he way in which a variable such as a sock price, exchange rae or ineres rae changes hrough ime! Incorporaes
Chaper 14 Wiener Processes and Iô s Lemma Copyrigh John C. Hull 014 1 Sochasic Processes! Describes he way in which a variable such as a sock price, exchange rae or ineres rae changes hrough ime! Incorporaes
AMartingaleApproachforFractionalBrownian Motions and Related Path Dependent PDEs
 AMaringaleApproachforFracionalBrownian Moions and Relaed Pah Dependen PDEs Jianfeng ZHANG Universiy of Souhern California Join work wih Frederi VIENS Mahemaical Finance, Probabiliy, and PDE Conference
AMaringaleApproachforFracionalBrownian Moions and Relaed Pah Dependen PDEs Jianfeng ZHANG Universiy of Souhern California Join work wih Frederi VIENS Mahemaical Finance, Probabiliy, and PDE Conference
Chapter 3 Boundary Value Problem
 Chaper 3 Boundary Value Problem A boundary value problem (BVP) is a problem, ypically an ODE or a PDE, which has values assigned on he physical boundary of he domain in which he problem is specified. Le
Chaper 3 Boundary Value Problem A boundary value problem (BVP) is a problem, ypically an ODE or a PDE, which has values assigned on he physical boundary of he domain in which he problem is specified. Le
On a Fractional Stochastic Landau-Ginzburg Equation
 Applied Mahemaical Sciences, Vol. 4, 1, no. 7, 317-35 On a Fracional Sochasic Landau-Ginzburg Equaion Nguyen Tien Dung Deparmen of Mahemaics, FPT Universiy 15B Pham Hung Sree, Hanoi, Vienam dungn@fp.edu.vn
Applied Mahemaical Sciences, Vol. 4, 1, no. 7, 317-35 On a Fracional Sochasic Landau-Ginzburg Equaion Nguyen Tien Dung Deparmen of Mahemaics, FPT Universiy 15B Pham Hung Sree, Hanoi, Vienam dungn@fp.edu.vn
Quadratic and Superquadratic BSDEs and Related PDEs
 Quadraic and Superquadraic BSDEs and Relaed PDEs Ying Hu IRMAR, Universié Rennes 1, FRANCE hp://perso.univ-rennes1.fr/ying.hu/ ITN Marie Curie Workshop "Sochasic Conrol and Finance" Roscoff, March 21 Ying
Quadraic and Superquadraic BSDEs and Relaed PDEs Ying Hu IRMAR, Universié Rennes 1, FRANCE hp://perso.univ-rennes1.fr/ying.hu/ ITN Marie Curie Workshop "Sochasic Conrol and Finance" Roscoff, March 21 Ying
Comparison between the Discrete and Continuous Time Models
 Comparison beween e Discree and Coninuous Time Models D. Sulsky June 21, 2012 1 Discree o Coninuous Recall e discree ime model Î = AIS Ŝ = S Î. Tese equaions ell us ow e populaion canges from one day o
Comparison beween e Discree and Coninuous Time Models D. Sulsky June 21, 2012 1 Discree o Coninuous Recall e discree ime model Î = AIS Ŝ = S Î. Tese equaions ell us ow e populaion canges from one day o
Utility maximization in incomplete markets
 Uiliy maximizaion in incomplee markes Marcel Ladkau 27.1.29 Conens 1 Inroducion and general seings 2 1.1 Marke model....................................... 2 1.2 Trading sraegy.....................................
Uiliy maximizaion in incomplee markes Marcel Ladkau 27.1.29 Conens 1 Inroducion and general seings 2 1.1 Marke model....................................... 2 1.2 Trading sraegy.....................................
Hamilton- J acobi Equation: Explicit Formulas In this lecture we try to apply the method of characteristics to the Hamilton-Jacobi equation: u t
 M ah 5 2 7 Fall 2 0 0 9 L ecure 1 0 O c. 7, 2 0 0 9 Hamilon- J acobi Equaion: Explici Formulas In his lecure we ry o apply he mehod of characerisics o he Hamilon-Jacobi equaion: u + H D u, x = 0 in R n
M ah 5 2 7 Fall 2 0 0 9 L ecure 1 0 O c. 7, 2 0 0 9 Hamilon- J acobi Equaion: Explici Formulas In his lecure we ry o apply he mehod of characerisics o he Hamilon-Jacobi equaion: u + H D u, x = 0 in R n
Existence and uniqueness of solution for multidimensional BSDE with local conditions on the coefficient
 1/34 Exisence and uniqueness of soluion for mulidimensional BSDE wih local condiions on he coefficien EL HASSAN ESSAKY Cadi Ayyad Universiy Mulidisciplinary Faculy Safi, Morocco ITN Roscof, March 18-23,
1/34 Exisence and uniqueness of soluion for mulidimensional BSDE wih local condiions on he coefficien EL HASSAN ESSAKY Cadi Ayyad Universiy Mulidisciplinary Faculy Safi, Morocco ITN Roscof, March 18-23,
Simulation-Solving Dynamic Models ABE 5646 Week 2, Spring 2010
 Simulaion-Solving Dynamic Models ABE 5646 Week 2, Spring 2010 Week Descripion Reading Maerial 2 Compuer Simulaion of Dynamic Models Finie Difference, coninuous saes, discree ime Simple Mehods Euler Trapezoid
Simulaion-Solving Dynamic Models ABE 5646 Week 2, Spring 2010 Week Descripion Reading Maerial 2 Compuer Simulaion of Dynamic Models Finie Difference, coninuous saes, discree ime Simple Mehods Euler Trapezoid
MATH 5720: Gradient Methods Hung Phan, UMass Lowell October 4, 2018
 MATH 5720: Gradien Mehods Hung Phan, UMass Lowell Ocober 4, 208 Descen Direcion Mehods Consider he problem min { f(x) x R n}. The general descen direcions mehod is x k+ = x k + k d k where x k is he curren
MATH 5720: Gradien Mehods Hung Phan, UMass Lowell Ocober 4, 208 Descen Direcion Mehods Consider he problem min { f(x) x R n}. The general descen direcions mehod is x k+ = x k + k d k where x k is he curren
CH Sean Han QF, NTHU, Taiwan BFS2010. (Joint work with T.-Y. Chen and W.-H. Liu)
 CH Sean Han QF, NTHU, Taiwan BFS2010 (Join work wih T.-Y. Chen and W.-H. Liu) Risk Managemen in Pracice: Value a Risk (VaR) / Condiional Value a Risk (CVaR) Volailiy Esimaion: Correced Fourier Transform
CH Sean Han QF, NTHU, Taiwan BFS2010 (Join work wih T.-Y. Chen and W.-H. Liu) Risk Managemen in Pracice: Value a Risk (VaR) / Condiional Value a Risk (CVaR) Volailiy Esimaion: Correced Fourier Transform
f(s)dw Solution 1. Approximate f by piece-wise constant left-continuous non-random functions f n such that (f(s) f n (s)) 2 ds 0.
 Advanced Financial Models Example shee 3 - Michaelmas 217 Michael Tehranchi Problem 1. Le f : [, R be a coninuous (non-random funcion and W a Brownian moion, and le σ 2 = f(s 2 ds and assume σ 2
Advanced Financial Models Example shee 3 - Michaelmas 217 Michael Tehranchi Problem 1. Le f : [, R be a coninuous (non-random funcion and W a Brownian moion, and le σ 2 = f(s 2 ds and assume σ 2
t is a basis for the solution space to this system, then the matrix having these solutions as columns, t x 1 t, x 2 t,... x n t x 2 t...
 Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Section 3.5 Nonhomogeneous Equations; Method of Undetermined Coefficients
 Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
1. Introduction. Journal of Numerical Mathematics and Stochastics, 10(1) : 45-57, A.SGHIR 1, D.SEGHIR 2, and S. HADIRI 2
 Journal of Numerical Mahemaics and Sochasics, 1(1) : 5-57, 218 hp://www.jnmas.org/jnmas1-.pdf JNM@S Euclidean Press, LLC Online: ISSN 2151-232 Numerical Mehods for Cerain Classes of Markovian Backward
Journal of Numerical Mahemaics and Sochasics, 1(1) : 5-57, 218 hp://www.jnmas.org/jnmas1-.pdf JNM@S Euclidean Press, LLC Online: ISSN 2151-232 Numerical Mehods for Cerain Classes of Markovian Backward
Backward doubly stochastic di erential equations with quadratic growth and applications to quasilinear SPDEs
 Backward doubly sochasic di erenial equaions wih quadraic growh and applicaions o quasilinear SPDEs Badreddine MANSOURI (wih K. Bahlali & B. Mezerdi) Universiy of Biskra Algeria La Londe 14 sepember 2007
Backward doubly sochasic di erenial equaions wih quadraic growh and applicaions o quasilinear SPDEs Badreddine MANSOURI (wih K. Bahlali & B. Mezerdi) Universiy of Biskra Algeria La Londe 14 sepember 2007
EXISTENCE AND UNIQUENESS OF SOLUTIONS TO THE BACKWARD STOCHASTIC LORENZ SYSTEM
 Communicaions on Sochasic Analysis Vol. 1, No. 3 (27) 473-483 EXISTENCE AND UNIQUENESS OF SOLUTIONS TO THE BACKWARD STOCHASTIC LORENZ SYSTEM P. SUNDAR AND HONG YIN Absrac. The backward sochasic Lorenz
Communicaions on Sochasic Analysis Vol. 1, No. 3 (27) 473-483 EXISTENCE AND UNIQUENESS OF SOLUTIONS TO THE BACKWARD STOCHASTIC LORENZ SYSTEM P. SUNDAR AND HONG YIN Absrac. The backward sochasic Lorenz
arxiv: v1 [math.pr] 28 Nov 2016
![arxiv: v1 [math.pr] 28 Nov 2016 arxiv: v1 [math.pr] 28 Nov 2016](/thumbs/93/111619169.jpg) Backward Sochasic Differenial Equaions wih Nonmarkovian Singular Terminal Values Ali Devin Sezer, Thomas Kruse, Alexandre Popier Ocober 15, 2018 arxiv:1611.09022v1 mah.pr 28 Nov 2016 Absrac We solve a
Backward Sochasic Differenial Equaions wih Nonmarkovian Singular Terminal Values Ali Devin Sezer, Thomas Kruse, Alexandre Popier Ocober 15, 2018 arxiv:1611.09022v1 mah.pr 28 Nov 2016 Absrac We solve a
Empirical Process Theory
 Empirical Process heory 4.384 ime Series Analysis, Fall 27 Reciaion by Paul Schrimpf Supplemenary o lecures given by Anna Mikusheva Ocober 7, 28 Reciaion 7 Empirical Process heory Le x be a real-valued
Empirical Process heory 4.384 ime Series Analysis, Fall 27 Reciaion by Paul Schrimpf Supplemenary o lecures given by Anna Mikusheva Ocober 7, 28 Reciaion 7 Empirical Process heory Le x be a real-valued
Course Notes for EE227C (Spring 2018): Convex Optimization and Approximation
 Course Noes for EE7C Spring 018: Convex Opimizaion and Approximaion Insrucor: Moriz Hard Email: hard+ee7c@berkeley.edu Graduae Insrucor: Max Simchowiz Email: msimchow+ee7c@berkeley.edu Ocober 15, 018 3
Course Noes for EE7C Spring 018: Convex Opimizaion and Approximaion Insrucor: Moriz Hard Email: hard+ee7c@berkeley.edu Graduae Insrucor: Max Simchowiz Email: msimchow+ee7c@berkeley.edu Ocober 15, 018 3
A proof of Ito's formula using a di Title formula. Author(s) Fujita, Takahiko; Kawanishi, Yasuhi. Studia scientiarum mathematicarum H Citation
 A proof of Io's formula using a di Tile formula Auhor(s) Fujia, Takahiko; Kawanishi, Yasuhi Sudia scieniarum mahemaicarum H Ciaion 15-134 Issue 8-3 Dae Type Journal Aricle Tex Version auhor URL hp://hdl.handle.ne/186/15878
A proof of Io's formula using a di Tile formula Auhor(s) Fujia, Takahiko; Kawanishi, Yasuhi Sudia scieniarum mahemaicarum H Ciaion 15-134 Issue 8-3 Dae Type Journal Aricle Tex Version auhor URL hp://hdl.handle.ne/186/15878
Lecture 20: Riccati Equations and Least Squares Feedback Control
 34-5 LINEAR SYSTEMS Lecure : Riccai Equaions and Leas Squares Feedback Conrol 5.6.4 Sae Feedback via Riccai Equaions A recursive approach in generaing he marix-valued funcion W ( ) equaion for i for he
34-5 LINEAR SYSTEMS Lecure : Riccai Equaions and Leas Squares Feedback Conrol 5.6.4 Sae Feedback via Riccai Equaions A recursive approach in generaing he marix-valued funcion W ( ) equaion for i for he
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
T L. t=1. Proof of Lemma 1. Using the marginal cost accounting in Equation(4) and standard arguments. t )+Π RB. t )+K 1(Q RB
 Elecronic Companion EC.1. Proofs of Technical Lemmas and Theorems LEMMA 1. Le C(RB) be he oal cos incurred by he RB policy. Then we have, T L E[C(RB)] 3 E[Z RB ]. (EC.1) Proof of Lemma 1. Using he marginal
Elecronic Companion EC.1. Proofs of Technical Lemmas and Theorems LEMMA 1. Le C(RB) be he oal cos incurred by he RB policy. Then we have, T L E[C(RB)] 3 E[Z RB ]. (EC.1) Proof of Lemma 1. Using he marginal
Singular perturbation control problems: a BSDE approach
 Singular perurbaion conrol problems: a BSDE approach Join work wih Francois Delarue Universié de Nice and Giuseppina Guaeri Poliecnico di Milano Le Mans 8h of Ocober 215 Conference in honour of Vlad Bally
Singular perurbaion conrol problems: a BSDE approach Join work wih Francois Delarue Universié de Nice and Giuseppina Guaeri Poliecnico di Milano Le Mans 8h of Ocober 215 Conference in honour of Vlad Bally
arxiv:quant-ph/ v1 5 Jul 2004
 Numerical Mehods for Sochasic Differenial Equaions Joshua Wilkie Deparmen of Chemisry, Simon Fraser Universiy, Burnaby, Briish Columbia V5A 1S6, Canada Sochasic differenial equaions (sdes) play an imporan
Numerical Mehods for Sochasic Differenial Equaions Joshua Wilkie Deparmen of Chemisry, Simon Fraser Universiy, Burnaby, Briish Columbia V5A 1S6, Canada Sochasic differenial equaions (sdes) play an imporan
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Couplage du principe des grandes déviations et de l homogénisation dans le cas des EDP paraboliques: (le cas constant)
 Couplage du principe des grandes déviaions e de l homogénisaion dans le cas des EDP paraboliques: (le cas consan) Alioune COULIBALY U.F.R Sciences e Technologie Universié Assane SECK de Ziguinchor Probabilié
Couplage du principe des grandes déviaions e de l homogénisaion dans le cas des EDP paraboliques: (le cas consan) Alioune COULIBALY U.F.R Sciences e Technologie Universié Assane SECK de Ziguinchor Probabilié
Oscillation of an Euler Cauchy Dynamic Equation S. Huff, G. Olumolode, N. Pennington, and A. Peterson
 PROCEEDINGS OF THE FOURTH INTERNATIONAL CONFERENCE ON DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS May 4 7, 00, Wilmingon, NC, USA pp 0 Oscillaion of an Euler Cauchy Dynamic Equaion S Huff, G Olumolode,
PROCEEDINGS OF THE FOURTH INTERNATIONAL CONFERENCE ON DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS May 4 7, 00, Wilmingon, NC, USA pp 0 Oscillaion of an Euler Cauchy Dynamic Equaion S Huff, G Olumolode,
Generalized Snell envelope and BSDE With Two general Reflecting Barriers
 1/22 Generalized Snell envelope and BSDE Wih Two general Reflecing Barriers EL HASSAN ESSAKY Cadi ayyad Universiy Poly-disciplinary Faculy Safi Work in progress wih : M. Hassani and Y. Ouknine Iasi, July
1/22 Generalized Snell envelope and BSDE Wih Two general Reflecing Barriers EL HASSAN ESSAKY Cadi ayyad Universiy Poly-disciplinary Faculy Safi Work in progress wih : M. Hassani and Y. Ouknine Iasi, July
Approximation of backward stochastic variational inequalities
 Al. I. Cuza Universiy of Iaşi, România 10ème Colloque Franco-Roumain de Mahémaiques Appliquées Augus 27, 2010, Poiiers, France Shor hisory & moivaion Re eced Sochasic Di erenial Equaions were rs sudied
Al. I. Cuza Universiy of Iaşi, România 10ème Colloque Franco-Roumain de Mahémaiques Appliquées Augus 27, 2010, Poiiers, France Shor hisory & moivaion Re eced Sochasic Di erenial Equaions were rs sudied
MATH 128A, SUMMER 2009, FINAL EXAM SOLUTION
 MATH 28A, SUMME 2009, FINAL EXAM SOLUTION BENJAMIN JOHNSON () (8 poins) [Lagrange Inerpolaion] (a) (4 poins) Le f be a funcion defined a some real numbers x 0,..., x n. Give a defining equaion for he Lagrange
MATH 28A, SUMME 2009, FINAL EXAM SOLUTION BENJAMIN JOHNSON () (8 poins) [Lagrange Inerpolaion] (a) (4 poins) Le f be a funcion defined a some real numbers x 0,..., x n. Give a defining equaion for he Lagrange
An introduction to the theory of SDDP algorithm
 An inroducion o he heory of SDDP algorihm V. Leclère (ENPC) Augus 1, 2014 V. Leclère Inroducion o SDDP Augus 1, 2014 1 / 21 Inroducion Large scale sochasic problem are hard o solve. Two ways of aacking
An inroducion o he heory of SDDP algorihm V. Leclère (ENPC) Augus 1, 2014 V. Leclère Inroducion o SDDP Augus 1, 2014 1 / 21 Inroducion Large scale sochasic problem are hard o solve. Two ways of aacking
Georey E. Hinton. University oftoronto. Technical Report CRG-TR February 22, Abstract
 Parameer Esimaion for Linear Dynamical Sysems Zoubin Ghahramani Georey E. Hinon Deparmen of Compuer Science Universiy oftorono 6 King's College Road Torono, Canada M5S A4 Email: zoubin@cs.orono.edu Technical
Parameer Esimaion for Linear Dynamical Sysems Zoubin Ghahramani Georey E. Hinon Deparmen of Compuer Science Universiy oftorono 6 King's College Road Torono, Canada M5S A4 Email: zoubin@cs.orono.edu Technical
Most Probable Phase Portraits of Stochastic Differential Equations and Its Numerical Simulation
 Mos Probable Phase Porrais of Sochasic Differenial Equaions and Is Numerical Simulaion Bing Yang, Zhu Zeng and Ling Wang 3 School of Mahemaics and Saisics, Huazhong Universiy of Science and Technology,
Mos Probable Phase Porrais of Sochasic Differenial Equaions and Is Numerical Simulaion Bing Yang, Zhu Zeng and Ling Wang 3 School of Mahemaics and Saisics, Huazhong Universiy of Science and Technology,
Ordinary Differential Equations
 Lecure 22 Ordinary Differenial Equaions Course Coordinaor: Dr. Suresh A. Karha, Associae Professor, Deparmen of Civil Engineering, IIT Guwahai. In naure, mos of he phenomena ha can be mahemaically described
Lecure 22 Ordinary Differenial Equaions Course Coordinaor: Dr. Suresh A. Karha, Associae Professor, Deparmen of Civil Engineering, IIT Guwahai. In naure, mos of he phenomena ha can be mahemaically described
System of Linear Differential Equations
 Sysem of Linear Differenial Equaions In "Ordinary Differenial Equaions" we've learned how o solve a differenial equaion for a variable, such as: y'k5$e K2$x =0 solve DE yx = K 5 2 ek2 x C_C1 2$y''C7$y
Sysem of Linear Differenial Equaions In "Ordinary Differenial Equaions" we've learned how o solve a differenial equaion for a variable, such as: y'k5$e K2$x =0 solve DE yx = K 5 2 ek2 x C_C1 2$y''C7$y
Stochastic Modelling in Finance - Solutions to sheet 8
 Sochasic Modelling in Finance - Soluions o shee 8 8.1 The price of a defaulable asse can be modeled as ds S = µ d + σ dw dn where µ, σ are consans, (W ) is a sandard Brownian moion and (N ) is a one jump
Sochasic Modelling in Finance - Soluions o shee 8 8.1 The price of a defaulable asse can be modeled as ds S = µ d + σ dw dn where µ, σ are consans, (W ) is a sandard Brownian moion and (N ) is a one jump
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
GMM - Generalized Method of Moments
 GMM - Generalized Mehod of Momens Conens GMM esimaion, shor inroducion 2 GMM inuiion: Maching momens 2 3 General overview of GMM esimaion. 3 3. Weighing marix...........................................
GMM - Generalized Mehod of Momens Conens GMM esimaion, shor inroducion 2 GMM inuiion: Maching momens 2 3 General overview of GMM esimaion. 3 3. Weighing marix...........................................
Option pricing and implied volatilities in a 2-hypergeometric stochastic volatility model
 Opion pricing and implied volailiies in a 2-hypergeomeric sochasic volailiy model Nicolas Privaul Qihao She Division of Mahemaical Sciences School of Physical and Mahemaical Sciences Nanyang Technological
Opion pricing and implied volailiies in a 2-hypergeomeric sochasic volailiy model Nicolas Privaul Qihao She Division of Mahemaical Sciences School of Physical and Mahemaical Sciences Nanyang Technological
Essential Microeconomics : OPTIMAL CONTROL 1. Consider the following class of optimization problems
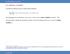 Essenial Microeconomics -- 6.5: OPIMAL CONROL Consider he following class of opimizaion problems Max{ U( k, x) + U+ ( k+ ) k+ k F( k, x)}. { x, k+ } = In he language of conrol heory, he vecor k is he vecor
Essenial Microeconomics -- 6.5: OPIMAL CONROL Consider he following class of opimizaion problems Max{ U( k, x) + U+ ( k+ ) k+ k F( k, x)}. { x, k+ } = In he language of conrol heory, he vecor k is he vecor
arxiv: v1 [math.ca] 15 Nov 2016
![arxiv: v1 [math.ca] 15 Nov 2016 arxiv: v1 [math.ca] 15 Nov 2016](/thumbs/90/102217337.jpg) arxiv:6.599v [mah.ca] 5 Nov 26 Counerexamples on Jumarie s hree basic fracional calculus formulae for non-differeniable coninuous funcions Cheng-shi Liu Deparmen of Mahemaics Norheas Peroleum Universiy
arxiv:6.599v [mah.ca] 5 Nov 26 Counerexamples on Jumarie s hree basic fracional calculus formulae for non-differeniable coninuous funcions Cheng-shi Liu Deparmen of Mahemaics Norheas Peroleum Universiy
Lecture 33: November 29
 36-705: Inermediae Saisics Fall 2017 Lecurer: Siva Balakrishnan Lecure 33: November 29 Today we will coninue discussing he boosrap, and hen ry o undersand why i works in a simple case. In he las lecure
36-705: Inermediae Saisics Fall 2017 Lecurer: Siva Balakrishnan Lecure 33: November 29 Today we will coninue discussing he boosrap, and hen ry o undersand why i works in a simple case. In he las lecure
Vehicle Arrival Models : Headway
 Chaper 12 Vehicle Arrival Models : Headway 12.1 Inroducion Modelling arrival of vehicle a secion of road is an imporan sep in raffic flow modelling. I has imporan applicaion in raffic flow simulaion where
Chaper 12 Vehicle Arrival Models : Headway 12.1 Inroducion Modelling arrival of vehicle a secion of road is an imporan sep in raffic flow modelling. I has imporan applicaion in raffic flow simulaion where
EXERCISES FOR SECTION 1.5
 1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
Singular control of SPDEs and backward stochastic partial diffe. reflection
 Singular conrol of SPDEs and backward sochasic parial differenial equaions wih reflecion Universiy of Mancheser Join work wih Bern Øksendal and Agnès Sulem Singular conrol of SPDEs and backward sochasic
Singular conrol of SPDEs and backward sochasic parial differenial equaions wih reflecion Universiy of Mancheser Join work wih Bern Øksendal and Agnès Sulem Singular conrol of SPDEs and backward sochasic
3.1.3 INTRODUCTION TO DYNAMIC OPTIMIZATION: DISCRETE TIME PROBLEMS. A. The Hamiltonian and First-Order Conditions in a Finite Time Horizon
 3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
ODEs II, Lecture 1: Homogeneous Linear Systems - I. Mike Raugh 1. March 8, 2004
 ODEs II, Lecure : Homogeneous Linear Sysems - I Mike Raugh March 8, 4 Inroducion. In he firs lecure we discussed a sysem of linear ODEs for modeling he excreion of lead from he human body, saw how o ransform
ODEs II, Lecure : Homogeneous Linear Sysems - I Mike Raugh March 8, 4 Inroducion. In he firs lecure we discussed a sysem of linear ODEs for modeling he excreion of lead from he human body, saw how o ransform
LECTURE 1: GENERALIZED RAY KNIGHT THEOREM FOR FINITE MARKOV CHAINS
 LECTURE : GENERALIZED RAY KNIGHT THEOREM FOR FINITE MARKOV CHAINS We will work wih a coninuous ime reversible Markov chain X on a finie conneced sae space, wih generaor Lf(x = y q x,yf(y. (Recall ha q
LECTURE : GENERALIZED RAY KNIGHT THEOREM FOR FINITE MARKOV CHAINS We will work wih a coninuous ime reversible Markov chain X on a finie conneced sae space, wih generaor Lf(x = y q x,yf(y. (Recall ha q
Finish reading Chapter 2 of Spivak, rereading earlier sections as necessary. handout and fill in some missing details!
 MAT 257, Handou 6: Ocober 7-2, 20. I. Assignmen. Finish reading Chaper 2 of Spiva, rereading earlier secions as necessary. handou and fill in some missing deails! II. Higher derivaives. Also, read his
MAT 257, Handou 6: Ocober 7-2, 20. I. Assignmen. Finish reading Chaper 2 of Spiva, rereading earlier secions as necessary. handou and fill in some missing deails! II. Higher derivaives. Also, read his
14 Autoregressive Moving Average Models
 14 Auoregressive Moving Average Models In his chaper an imporan parameric family of saionary ime series is inroduced, he family of he auoregressive moving average, or ARMA, processes. For a large class
14 Auoregressive Moving Average Models In his chaper an imporan parameric family of saionary ime series is inroduced, he family of he auoregressive moving average, or ARMA, processes. For a large class
THE WAVE EQUATION. part hand-in for week 9 b. Any dilation v(x, t) = u(λx, λt) of u(x, t) is also a solution (where λ is constant).
 THE WAVE EQUATION 43. (S) Le u(x, ) be a soluion of he wave equaion u u xx = 0. Show ha Q43(a) (c) is a. Any ranslaion v(x, ) = u(x + x 0, + 0 ) of u(x, ) is also a soluion (where x 0, 0 are consans).
THE WAVE EQUATION 43. (S) Le u(x, ) be a soluion of he wave equaion u u xx = 0. Show ha Q43(a) (c) is a. Any ranslaion v(x, ) = u(x + x 0, + 0 ) of u(x, ) is also a soluion (where x 0, 0 are consans).
Online Appendix to Solution Methods for Models with Rare Disasters
 Online Appendix o Soluion Mehods for Models wih Rare Disasers Jesús Fernández-Villaverde and Oren Levinal In his Online Appendix, we presen he Euler condiions of he model, we develop he pricing Calvo block,
Online Appendix o Soluion Mehods for Models wih Rare Disasers Jesús Fernández-Villaverde and Oren Levinal In his Online Appendix, we presen he Euler condiions of he model, we develop he pricing Calvo block,
PENALIZED LEAST SQUARES AND PENALIZED LIKELIHOOD
 PENALIZED LEAST SQUARES AND PENALIZED LIKELIHOOD HAN XIAO 1. Penalized Leas Squares Lasso solves he following opimizaion problem, ˆβ lasso = arg max β R p+1 1 N y i β 0 N x ij β j β j (1.1) for some 0.
PENALIZED LEAST SQUARES AND PENALIZED LIKELIHOOD HAN XIAO 1. Penalized Leas Squares Lasso solves he following opimizaion problem, ˆβ lasso = arg max β R p+1 1 N y i β 0 N x ij β j β j (1.1) for some 0.
III. Module 3. Empirical and Theoretical Techniques
 III. Module 3. Empirical and Theoreical Techniques Applied Saisical Techniques 3. Auocorrelaion Correcions Persisence affecs sandard errors. The radiional response is o rea he auocorrelaion as a echnical
III. Module 3. Empirical and Theoreical Techniques Applied Saisical Techniques 3. Auocorrelaion Correcions Persisence affecs sandard errors. The radiional response is o rea he auocorrelaion as a echnical
Optimal Investment under Dynamic Risk Constraints and Partial Information
 Opimal Invesmen under Dynamic Risk Consrains and Parial Informaion Wolfgang Puschögl Johann Radon Insiue for Compuaional and Applied Mahemaics (RICAM) Ausrian Academy of Sciences www.ricam.oeaw.ac.a 2
Opimal Invesmen under Dynamic Risk Consrains and Parial Informaion Wolfgang Puschögl Johann Radon Insiue for Compuaional and Applied Mahemaics (RICAM) Ausrian Academy of Sciences www.ricam.oeaw.ac.a 2
10. State Space Methods
 . Sae Space Mehods. Inroducion Sae space modelling was briefly inroduced in chaper. Here more coverage is provided of sae space mehods before some of heir uses in conrol sysem design are covered in he
. Sae Space Mehods. Inroducion Sae space modelling was briefly inroduced in chaper. Here more coverage is provided of sae space mehods before some of heir uses in conrol sysem design are covered in he
Local Strict Comparison Theorem and Converse Comparison Theorems for Reflected Backward Stochastic Differential Equations
 arxiv:mah/07002v [mah.pr] 3 Dec 2006 Local Sric Comparison Theorem and Converse Comparison Theorems for Refleced Backward Sochasic Differenial Equaions Juan Li and Shanjian Tang Absrac A local sric comparison
arxiv:mah/07002v [mah.pr] 3 Dec 2006 Local Sric Comparison Theorem and Converse Comparison Theorems for Refleced Backward Sochasic Differenial Equaions Juan Li and Shanjian Tang Absrac A local sric comparison
Backward Stochastic Differential Equations with Nonmarkovian Singular Terminal Values
 Backward Sochasic Differenial Equaions wih Nonmarkovian Singular Terminal Values Ali Sezer, Thomas Kruse, Alexandre Popier, Ali Sezer To cie his version: Ali Sezer, Thomas Kruse, Alexandre Popier, Ali
Backward Sochasic Differenial Equaions wih Nonmarkovian Singular Terminal Values Ali Sezer, Thomas Kruse, Alexandre Popier, Ali Sezer To cie his version: Ali Sezer, Thomas Kruse, Alexandre Popier, Ali
A FAMILY OF MARTINGALES GENERATED BY A PROCESS WITH INDEPENDENT INCREMENTS
 Theory of Sochasic Processes Vol. 14 3), no. 2, 28, pp. 139 144 UDC 519.21 JOSEP LLUÍS SOLÉ AND FREDERIC UTZET A FAMILY OF MARTINGALES GENERATED BY A PROCESS WITH INDEPENDENT INCREMENTS An explici procedure
Theory of Sochasic Processes Vol. 14 3), no. 2, 28, pp. 139 144 UDC 519.21 JOSEP LLUÍS SOLÉ AND FREDERIC UTZET A FAMILY OF MARTINGALES GENERATED BY A PROCESS WITH INDEPENDENT INCREMENTS An explici procedure
Modeling Economic Time Series with Stochastic Linear Difference Equations
 A. Thiemer, SLDG.mcd, 6..6 FH-Kiel Universiy of Applied Sciences Prof. Dr. Andreas Thiemer e-mail: andreas.hiemer@fh-kiel.de Modeling Economic Time Series wih Sochasic Linear Difference Equaions Summary:
A. Thiemer, SLDG.mcd, 6..6 FH-Kiel Universiy of Applied Sciences Prof. Dr. Andreas Thiemer e-mail: andreas.hiemer@fh-kiel.de Modeling Economic Time Series wih Sochasic Linear Difference Equaions Summary:
Chapter 6. Systems of First Order Linear Differential Equations
 Chaper 6 Sysems of Firs Order Linear Differenial Equaions We will only discuss firs order sysems However higher order sysems may be made ino firs order sysems by a rick shown below We will have a sligh
Chaper 6 Sysems of Firs Order Linear Differenial Equaions We will only discuss firs order sysems However higher order sysems may be made ino firs order sysems by a rick shown below We will have a sligh
Unit Root Time Series. Univariate random walk
 Uni Roo ime Series Univariae random walk Consider he regression y y where ~ iid N 0, he leas squares esimae of is: ˆ yy y y yy Now wha if = If y y hen le y 0 =0 so ha y j j If ~ iid N 0, hen y ~ N 0, he
Uni Roo ime Series Univariae random walk Consider he regression y y where ~ iid N 0, he leas squares esimae of is: ˆ yy y y yy Now wha if = If y y hen le y 0 =0 so ha y j j If ~ iid N 0, hen y ~ N 0, he
Dual Representation as Stochastic Differential Games of Backward Stochastic Differential Equations and Dynamic Evaluations
 arxiv:mah/0602323v1 [mah.pr] 15 Feb 2006 Dual Represenaion as Sochasic Differenial Games of Backward Sochasic Differenial Equaions and Dynamic Evaluaions Shanjian Tang Absrac In his Noe, assuming ha he
arxiv:mah/0602323v1 [mah.pr] 15 Feb 2006 Dual Represenaion as Sochasic Differenial Games of Backward Sochasic Differenial Equaions and Dynamic Evaluaions Shanjian Tang Absrac In his Noe, assuming ha he
Recursive Least-Squares Fixed-Interval Smoother Using Covariance Information based on Innovation Approach in Linear Continuous Stochastic Systems
 8 Froniers in Signal Processing, Vol. 1, No. 1, July 217 hps://dx.doi.org/1.2266/fsp.217.112 Recursive Leas-Squares Fixed-Inerval Smooher Using Covariance Informaion based on Innovaion Approach in Linear
8 Froniers in Signal Processing, Vol. 1, No. 1, July 217 hps://dx.doi.org/1.2266/fsp.217.112 Recursive Leas-Squares Fixed-Inerval Smooher Using Covariance Informaion based on Innovaion Approach in Linear
THE MYSTERY OF STOCHASTIC MECHANICS. Edward Nelson Department of Mathematics Princeton University
 THE MYSTERY OF STOCHASTIC MECHANICS Edward Nelson Deparmen of Mahemaics Princeon Universiy 1 Classical Hamilon-Jacobi heory N paricles of various masses on a Euclidean space. Incorporae he masses in he
THE MYSTERY OF STOCHASTIC MECHANICS Edward Nelson Deparmen of Mahemaics Princeon Universiy 1 Classical Hamilon-Jacobi heory N paricles of various masses on a Euclidean space. Incorporae he masses in he
On Boundedness of Q-Learning Iterates for Stochastic Shortest Path Problems
 MATHEMATICS OF OPERATIONS RESEARCH Vol. 38, No. 2, May 2013, pp. 209 227 ISSN 0364-765X (prin) ISSN 1526-5471 (online) hp://dx.doi.org/10.1287/moor.1120.0562 2013 INFORMS On Boundedness of Q-Learning Ieraes
MATHEMATICS OF OPERATIONS RESEARCH Vol. 38, No. 2, May 2013, pp. 209 227 ISSN 0364-765X (prin) ISSN 1526-5471 (online) hp://dx.doi.org/10.1287/moor.1120.0562 2013 INFORMS On Boundedness of Q-Learning Ieraes
Differential Equations
 Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
EMS SCM joint meeting. On stochastic partial differential equations of parabolic type
 EMS SCM join meeing Barcelona, May 28-30, 2015 On sochasic parial differenial equaions of parabolic ype Isván Gyöngy School of Mahemaics and Maxwell Insiue Edinburgh Universiy 1 I. Filering problem II.
EMS SCM join meeing Barcelona, May 28-30, 2015 On sochasic parial differenial equaions of parabolic ype Isván Gyöngy School of Mahemaics and Maxwell Insiue Edinburgh Universiy 1 I. Filering problem II.
Physics 127b: Statistical Mechanics. Fokker-Planck Equation. Time Evolution
 Physics 7b: Saisical Mechanics Fokker-Planck Equaion The Langevin equaion approach o he evoluion of he velociy disribuion for he Brownian paricle migh leave you uncomforable. A more formal reamen of his
Physics 7b: Saisical Mechanics Fokker-Planck Equaion The Langevin equaion approach o he evoluion of he velociy disribuion for he Brownian paricle migh leave you uncomforable. A more formal reamen of his
Theory of! Partial Differential Equations!
 hp://www.nd.edu/~gryggva/cfd-course/! Ouline! Theory o! Parial Dierenial Equaions! Gréar Tryggvason! Spring 011! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
hp://www.nd.edu/~gryggva/cfd-course/! Ouline! Theory o! Parial Dierenial Equaions! Gréar Tryggvason! Spring 011! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
Lecture 6: Wiener Process
 Lecure 6: Wiener Process Eric Vanden-Eijnden Chapers 6, 7 and 8 offer a (very) brief inroducion o sochasic analysis. These lecures are based in par on a book projec wih Weinan E. A sandard reference for
Lecure 6: Wiener Process Eric Vanden-Eijnden Chapers 6, 7 and 8 offer a (very) brief inroducion o sochasic analysis. These lecures are based in par on a book projec wih Weinan E. A sandard reference for
Ordinary differential equations. Phys 750 Lecture 7
 Ordinary differenial equaions Phys 750 Lecure 7 Ordinary Differenial Equaions Mos physical laws are expressed as differenial equaions These come in hree flavours: iniial-value problems boundary-value problems
Ordinary differenial equaions Phys 750 Lecure 7 Ordinary Differenial Equaions Mos physical laws are expressed as differenial equaions These come in hree flavours: iniial-value problems boundary-value problems
t 2 B F x,t n dsdt t u x,t dxdt
 Evoluion Equaions For 0, fixed, le U U0, where U denoes a bounded open se in R n.suppose ha U is filled wih a maerial in which a conaminan is being ranspored by various means including diffusion and convecion.
Evoluion Equaions For 0, fixed, le U U0, where U denoes a bounded open se in R n.suppose ha U is filled wih a maerial in which a conaminan is being ranspored by various means including diffusion and convecion.
Branching diffusion representation of semilinear PDEs and Monte Carlo approximation
 Branching diffusion represenaion of semilinear PDEs and Mone Carlo approximaion Pierre Henry-Labordère Nadia Oudjane Xiaolu Tan Nizar Touzi December 22, 207 Xavier Warin Absrac We provide a represenaion
Branching diffusion represenaion of semilinear PDEs and Mone Carlo approximaion Pierre Henry-Labordère Nadia Oudjane Xiaolu Tan Nizar Touzi December 22, 207 Xavier Warin Absrac We provide a represenaion
Cash Flow Valuation Mode Lin Discrete Time
 IOSR Journal of Mahemaics (IOSR-JM) e-issn: 2278-5728,p-ISSN: 2319-765X, 6, Issue 6 (May. - Jun. 2013), PP 35-41 Cash Flow Valuaion Mode Lin Discree Time Olayiwola. M. A. and Oni, N. O. Deparmen of Mahemaics
IOSR Journal of Mahemaics (IOSR-JM) e-issn: 2278-5728,p-ISSN: 2319-765X, 6, Issue 6 (May. - Jun. 2013), PP 35-41 Cash Flow Valuaion Mode Lin Discree Time Olayiwola. M. A. and Oni, N. O. Deparmen of Mahemaics
Generalized Chebyshev polynomials
 Generalized Chebyshev polynomials Clemene Cesarano Faculy of Engineering, Inernaional Telemaic Universiy UNINETTUNO Corso Viorio Emanuele II, 39 86 Roma, Ialy email: c.cesarano@unineunouniversiy.ne ABSTRACT
Generalized Chebyshev polynomials Clemene Cesarano Faculy of Engineering, Inernaional Telemaic Universiy UNINETTUNO Corso Viorio Emanuele II, 39 86 Roma, Ialy email: c.cesarano@unineunouniversiy.ne ABSTRACT
Math 10B: Mock Mid II. April 13, 2016
 Name: Soluions Mah 10B: Mock Mid II April 13, 016 1. ( poins) Sae, wih jusificaion, wheher he following saemens are rue or false. (a) If a 3 3 marix A saisfies A 3 A = 0, hen i canno be inverible. True.
Name: Soluions Mah 10B: Mock Mid II April 13, 016 1. ( poins) Sae, wih jusificaion, wheher he following saemens are rue or false. (a) If a 3 3 marix A saisfies A 3 A = 0, hen i canno be inverible. True.
Lecture 4: Processes with independent increments
 Lecure 4: Processes wih independen incremens 1. A Wienner process 1.1 Definiion of a Wienner process 1.2 Reflecion principle 1.3 Exponenial Brownian moion 1.4 Exchange of measure (Girsanov heorem) 1.5
Lecure 4: Processes wih independen incremens 1. A Wienner process 1.1 Definiion of a Wienner process 1.2 Reflecion principle 1.3 Exponenial Brownian moion 1.4 Exchange of measure (Girsanov heorem) 1.5
7 The Itô/Stratonovich dilemma
 7 The Iô/Sraonovich dilemma The dilemma: wha does he idealizaion of dela-funcion-correlaed noise mean? ẋ = f(x) + g(x)η() η()η( ) = κδ( ). (1) Previously, we argued by a limiing procedure: aking noise
7 The Iô/Sraonovich dilemma The dilemma: wha does he idealizaion of dela-funcion-correlaed noise mean? ẋ = f(x) + g(x)η() η()η( ) = κδ( ). (1) Previously, we argued by a limiing procedure: aking noise
Math 527 Lecture 6: Hamilton-Jacobi Equation: Explicit Formulas
 Mah 527 Lecure 6: Hamilon-Jacobi Equaion: Explici Formulas Sep. 23, 2 Mehod of characerisics. We r o appl he mehod of characerisics o he Hamilon-Jacobi equaion: u +Hx, Du = in R n, u = g on R n =. 2 To
Mah 527 Lecure 6: Hamilon-Jacobi Equaion: Explici Formulas Sep. 23, 2 Mehod of characerisics. We r o appl he mehod of characerisics o he Hamilon-Jacobi equaion: u +Hx, Du = in R n, u = g on R n =. 2 To
Reliability of Technical Systems
 eliabiliy of Technical Sysems Main Topics Inroducion, Key erms, framing he problem eliabiliy parameers: Failure ae, Failure Probabiliy, Availabiliy, ec. Some imporan reliabiliy disribuions Componen reliabiliy
eliabiliy of Technical Sysems Main Topics Inroducion, Key erms, framing he problem eliabiliy parameers: Failure ae, Failure Probabiliy, Availabiliy, ec. Some imporan reliabiliy disribuions Componen reliabiliy
Math 315: Linear Algebra Solutions to Assignment 6
 Mah 35: Linear Algebra s o Assignmen 6 # Which of he following ses of vecors are bases for R 2? {2,, 3, }, {4,, 7, 8}, {,,, 3}, {3, 9, 4, 2}. Explain your answer. To generae he whole R 2, wo linearly independen
Mah 35: Linear Algebra s o Assignmen 6 # Which of he following ses of vecors are bases for R 2? {2,, 3, }, {4,, 7, 8}, {,,, 3}, {3, 9, 4, 2}. Explain your answer. To generae he whole R 2, wo linearly independen
Stochastic Model for Cancer Cell Growth through Single Forward Mutation
 Journal of Modern Applied Saisical Mehods Volume 16 Issue 1 Aricle 31 5-1-2017 Sochasic Model for Cancer Cell Growh hrough Single Forward Muaion Jayabharahiraj Jayabalan Pondicherry Universiy, jayabharahi8@gmail.com
Journal of Modern Applied Saisical Mehods Volume 16 Issue 1 Aricle 31 5-1-2017 Sochasic Model for Cancer Cell Growh hrough Single Forward Muaion Jayabharahiraj Jayabalan Pondicherry Universiy, jayabharahi8@gmail.com
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Then. 1 The eigenvalues of A are inside R = n i=1 R i. 2 Union of any k circles not intersecting the other (n k)
 Ger sgorin Circle Chaper 9 Approimaing Eigenvalues Per-Olof Persson persson@berkeley.edu Deparmen of Mahemaics Universiy of California, Berkeley Mah 128B Numerical Analysis (Ger sgorin Circle) Le A be
Ger sgorin Circle Chaper 9 Approimaing Eigenvalues Per-Olof Persson persson@berkeley.edu Deparmen of Mahemaics Universiy of California, Berkeley Mah 128B Numerical Analysis (Ger sgorin Circle) Le A be
Weak error analysis via functional Itô calculus
 Weak error analysis via funcional Iô calculus Mihály Kovács and Felix Lindner arxiv:163.8756v2 [mah.pr] 14 Jun 216 Absrac We consider auonomous sochasic ordinary differenial equaions SDEs and weak approximaions
Weak error analysis via funcional Iô calculus Mihály Kovács and Felix Lindner arxiv:163.8756v2 [mah.pr] 14 Jun 216 Absrac We consider auonomous sochasic ordinary differenial equaions SDEs and weak approximaions
Matlab and Python programming: how to get started
 Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
Estimation of Poses with Particle Filters
 Esimaion of Poses wih Paricle Filers Dr.-Ing. Bernd Ludwig Chair for Arificial Inelligence Deparmen of Compuer Science Friedrich-Alexander-Universiä Erlangen-Nürnberg 12/05/2008 Dr.-Ing. Bernd Ludwig (FAU
Esimaion of Poses wih Paricle Filers Dr.-Ing. Bernd Ludwig Chair for Arificial Inelligence Deparmen of Compuer Science Friedrich-Alexander-Universiä Erlangen-Nürnberg 12/05/2008 Dr.-Ing. Bernd Ludwig (FAU
Convergence of the Neumann series in higher norms
 Convergence of he Neumann series in higher norms Charles L. Epsein Deparmen of Mahemaics, Universiy of Pennsylvania Version 1.0 Augus 1, 003 Absrac Naural condiions on an operaor A are given so ha he Neumann
Convergence of he Neumann series in higher norms Charles L. Epsein Deparmen of Mahemaics, Universiy of Pennsylvania Version 1.0 Augus 1, 003 Absrac Naural condiions on an operaor A are given so ha he Neumann
