Mitigating Balanced and Unbalanced Voltage Sag Via Shunt-Connected Voltage Source Convertor (VSC) by using Double Vector Controller
|
|
|
- Andrea Baker
- 6 years ago
- Views:
Transcription
1 sah Jounal of Appl Sns, Engnng an Thnology 6(3): , 03 ISSN: ; -ISSN: Maxwll Sntf Oganzaton, 03 Submtt: Dmb 7, 0 Apt: Mah 07, 03 Publsh: August 05, 03 Mtgatng Balan an Unbalan Voltag Sag Va Shunt-Connt Voltag Sou Convto (VSC) by usng Doubl Vto Contoll Abollah Sho, Hussan Shaf, Azah Moham an Shvn Sho Dpatmnt of Eltal, Elton an Systms Engnng, Unvst Kbangsaan, Malaysa Abstat: Ths stuy psnts a shunt-connt Voltag Sou Convto (VSC) to mtgat balan an unbalan voltag sag an gulat th g voltag at a fx lvl by nstng u atv pow at th Pont of Common Couplng (PCC). Moov, an nn Vto Cunt-Contoll (VCC) an out voltag ontoll (VVC) a appl togth to alulats th unt fns fo th VCC. Futhmo, an nuto/ apato/nuto (C) flt s pla wth th smpl -flt n btwn th VSC an th ntwo an t s onstut to u th voltag sag. ws, to ma up fo th unbalan ps, th postv an ngatv sun omponnts lat to th g voltag shoul b manag stntly. Th postv an ngatv sun omponnts lat to th g voltag shoul b manag stntly. Ths s ahv though th applaton of two npnnt ontolls fo th two suns wth an ntal asa stutu whh has bn xplat abov. Smulaton sults sgnat pop funtonng of th ontol systm whh has bn popos. Kywos: Pow ualty, atv pow ontoll, voltag an unt ontoll, voltag sag mtgaton, voltag sou onvto INTODUCTION In th nt as, pow ualty poblms spally voltag sag an hamon stoton a nown as on of th most sgnfant tops among pow systm ngns (Hngoan, 995; D Pna t al., 003; Wooly t al., 999; Jung t al., 00). Thfo, th oun of ths pow ualty vnts spally fo thos nusts whh a assoat wth nfomaton thnology systms an b vy hamful. ntly, stat-of-th-at pow lton bas ompnsatos all Custom Pow Dvs (CPD) hav bn vlop to mtgat th ngatv ffts of pow ualty poblms (Hngoan, 995). Th Ssonnt Voltag Sou Convtos (VSC), also all Stat Ss Compnsato (SSC) o Dynam Voltag sto (DV), an b atgoz as a typ of CPDs. Ths vs an b onnt n ss wth th stbuton f at th upstam s of th snstv loas to fftvly mtgat o lmnat th ffts of voltag sag, voltag mbalan an oth typs of pow ualty vnts (Hngoan, 995). Nvthlss, hgh nvstmnt an mantnan osts an omplx stutu a th man lmtatons to of Ss-onnt VSCs (Nwman an Holms, 00). Th Dstbuton Stat Synhonous Compnsato (D- STATCOM) s a typ of shunt-onnt CPDs whh s mostly bas on VSC an onnt n paalll wth snstv loas n stbuton ntwos to pott snstv loas aganst voltag sag, voltag vaaton an unt hamon stoton (Choma an Etza- Amol, 00; Esoba t al., 000). Th voltag sag ompnsaton statgy n D-STATCOM s bas on th atv pow njton at th onnton pont fo moat voltag sag, whl atv pow njton s manatoy to mtgat p voltag sags (Bolln, 999; Wang t al., 998). Thfo, a ps ontol statgy s nssay to mpov th ynam pfomans of D-STATCOMs. Suh ontolls shoul b abl to auatly ontol th voltag o unt fba loop an th swthng pattn of th nvts. Bas ontolls n D-STATCOM ontolls an b manly v nto voltag ontol an unt ontol, whh voltag ontol mo s manly ommon n Voltag ontol mo, th output AC voltag shoul ta th at fn voltag n DC uantts. Dpnng on th u ontol paamts, ths pou an b mplmnt usng (Cla an pa tansfom) fn to xtat atv atv pow an tuaat voltag omponnts as th tansfomaton valus an multplyng ths valus n th AC nstantanous voltag (Svnsson an ngn, 998). Th man lmtaton of ths thnu s th hgh snstvty of th tansfom valus to th mbalan voltag ontons, whh ma th ontol pou mo omplx. In ompason, th unt ontol mthos suh as hystss an avag unt ontolls a lss omplx an fast than voltag ontol mthos. In ths stuy, an mpov ontol mtho bas on voltag an unt gulaton s popos an usng Doubl Vto Contol (DVC) baus t has two Cosponng Autho: Abollah Sho, Dpatmnt of Eltal, Elton an Systms Engnng, Unvst Kbangsaan, Malaysa 379
2 s. J. Appl. S. Eng. Thnol., 6(3): , 03 vto-ontol loops. On of th loops s tan nto onsaton to gulat unt whl th oth loop gulats voltag at (PCC). Vto Cunt Contol (VCC) s appl fo ompnsato unt gulaton (Hngoan, 995) an Vto Voltag Contoll (VVC) wos as out ontol lop, whh tas th fn bus voltag to alz th voltag sag mtgaton. In th smulaton pogam PSCAD/EMTDC all th smulatons a a out an th lvant pfoman s manfst. wttn as Hanfos an N, 000; Wang t al., 998): u u ff pε ( u ) ff ε () (3) wh, an a th f-fowa tm an unt o at ah sampl, sptvly an:, ε ( n ) CONFIGUATION OF D-STATCOM WITH DUA VECTO CONTOE (DVC) u ω j [ ff g ] (4) DVC s manly a typ of asa ontoll sgn to ontol th u njt unt. DVC onssts of two vto ontolls namly Vto Cunt Contoll (VCC) an Vto Voltag Contoll (VVC). Vto unt ontoll: Th Vto Cunt Contoll (VCC) an b ons as a usful tool whh mas th ompnsato unt to ta th fn unt. Consng th shmat agam of th shunt-onnt VSC shown n Fg. an applyng Khhoff's voltag law to th VSC output flt by usng Cla an Pa tansfomaton un th fx two-oonat αβ fam, th voltag an unt at th Pont of Common Couplng (PCC) an b obtan as: u ( αβ ) ( t) ( αβ ) ( αβ ) αβ ) t ( g ( αβ ) ( αβ ) ( αβ ) ( αβ ) u ( t) g t () () wh, an a sstan an atan of th flt an u, g an a th VSC output voltag, PCC voltag an njt unt at th PCC, sptvly. By applyng th Synhonous fn Fam (SF),.., -oonat systm an Phas-o oop (P) n th VCC, th atv an atv unt an b spaatly ontoll. Thfo, E. () an b ε (5) Th popotonal gan, p, an th ntgal gan,, to attan th abat spons an also b fn as / T s / an K p, T s /T,, sptvly, wh, T, Th ntgato tm onstant s st to / Both atv an atv unts a ontoll npnntly wth hgh banwth, vn n ov moulaton gon usng th voltag lmtaton an Mnmum Ampltu Eo (MAE) tats (Ottstn an Svnsson, 00; Svnsson an ngn, 998). Th output voltag of VCC an b xpss n tms of SF by substtutng (4) an (5) n () as: ω u ( ) ( ) p, g u, ( )( ) ω ( ) ( ) ( ), p, g (6) (7) Vto Voltag-Contol (VVC): Th man tas of th VVC s to mantan an stablz th PCC voltag at ts Fg. : Sngl-ln agam of systm wth shunt-onnt VSC an -flt 380
3 s. J. Appl. S. Eng. Thnol., 6(3): , 03 Fg. : Blo shm of th wth ts lvant poss Fg. 3: G voltags ung 5% voltag sag. Wthout VSC at valu. In th psn of an njton tansfom wth wnng ato of : an assumng a nglgbl voltag op at th tansfom ato, th PCC voltag an b ons balan an ual to th flt apato voltag Fg. 6. Hn, th voltag at PCC an b ontoll an pt onstant. Consng Fg., th njt unt nto th g an b obtan as: ω j [ nj p, v, vε ( n ) (8) wh, ε () s th voltag o at sampl, s gvn by: ε ε AC-voltag ontoll: Th ampltu of th PCC voltag an b ontoll by njtng atv pow an also th voltag g an b hang by usng th ntwo mpan (Wooly t al., 999). Fgu shows` th omplt blo shm of th Vto Cunt-Contoll (VCC) wth ts lvant poss. Th voltag magntu o s tansmtt to th a-voltag ontoll, fom by a PI-gulato. In as of th stay-stat -voltag of wll b zo. s th g output fn atv unt, whh s f to th VCC an s th fn atv unt whh s au fom a slow -ln voltag ontoll that ompnsats fo VSC losss. Th apatv atv pow njt nto th ntwo by th VSC, has bn psnt as a blow: Thfo, ω nj nj ( ω ( ) wh, K p,v Th popotonal gan K,v Th ntgal gan ( p v ) (, v ), ) ( ) p, v (9) (0) If th ntgato tm onstant s ual to 30 ms an sttng of th unt an voltag ontoll a sptvly 70% an 5% of abat (Bongono t al., 005, Ptsson t al., 005)., v ( ) 38 Q g g () In vw of th fat that g s zo, whn th voltag of g s too low, apatv atv pow has bn njt an th unt wll b postv. Dst tm ampltu of th PI-gulato s gvn by: Tabl : Contol paamts g pamt G voltag E 400 V pu G Cunt I 40 A pu G funy f 50 HZ G nutan g. mh 0.4 pu G sstan g 0.05 Ω pu oa sstan l 0 Ω.73 pu oa nutan l 3.9 mh.3 pu DC-ln voltag u 600 V.5 pu Flt sstan 4.8 mω pu Flt nutan mh 0.09 pu g
4 Tabl : Systm paamt Cunt ontoll paamts Popotonal gan K P, 7.0(70% a bat) Intgato gan K, 0 AC- voltag ontoll paamts Popotonal gan K P,Q 0.97 Intgato tm onstant T,Q 0.0 P-ban wth α P 30 a/s Tabl 3: Injton tansfom paamts at pow S T 0 KVA.08 pu Shot-ut pow E T 30 V pu Shot-ut voltag P 4 W 0.05 pu aag nutan V 5.3 V 0.03 pu Ss sstan λ 0.3 mh 0.08 pu λ mω 0.04 [ pq g g g ] g [ TQ S s. J. Appl. S. Eng. Thnol., 6(3): , 03 ( n ) g g ( pq T )( 0.4 Q g () (3) wh, K PQ an T Q a th popotonal an ntgal gan of th gulato, sptvly. Pfoman spton: Tabls an a th ontoll an systm paamts sptvly (Wooly t al., 999). An by usng PSCAD/EMTDC, smulaton, ontol systm has bn nvstgat an tst. Fgu 3 has psnt th voltag at th PCC whn th VSC n l mo. As llustat, th voltag of PCC s un th nflun of a 5% voltag p an 9 phas-angl jump. Fgu 4 splay th VSC njt a hgh atv unt (los to 00A..) ung voltag sag to ma voltag at th PCC onstant 400V (Fg. 5). Aong to th smulaton sult t s possbl to ompnsat voltag sag wth nvstgat ontoll an by hangng -flt wth C-flt, VSC wll manag th amount of atv pow n. Systm pfoman by applyng ll-flt an atv ampng: In abov ston th VCC sb un stff g voltag, mpan of th g s appoxmatly ual to zo. If th PCC voltag stff s not nough, g wth th sam ynams of th njton unt wll hang, lang to th stablty poblm sb abov. It wll b ssntal to ovom ths poblms to shown th ynam of th g voltag at PCC. Consuntly, t shoul b mof onfguaton fo th SVC by ang a apato (C 60μμμμ) (Fg. 6). Paamts fo th njton tansfom a shown n Tabl 3. SIMUATION ANAYSIS ( n )] g g Th ontol systm, whh has bn off, has bn xamn un smla voltag p shown n n Fg. 0 an. 38 g Fg. 3. Th osllatons a vsbly snbl n Fg. 7. Instng a sst as a ampng tm n ss ( 0.5Ω) wth th flt apato wll la to th pvnton of ths phnomnon. Nonthlss, th ffowa tm n E. (4) s pt blow an Fg. 8 monstats that th PCC voltag s ajust to th pf valu whh appoxmats 0.0 pu osllatons an an b obsv n -voltag (Ptsson t al., 005,, 989): u ff [ ω j g ( ] (4) Dynam opaton ung unbalan voltag sag: Th popos ontol statgy by Smulaton sults has laf that t s only appopat fo mtgaton of balan voltag sag as you an s n Fg. 8, owng to th psn of th ngatv-sun n th masu uantts an to gan btt op wth unbalan voltag ps shoul mofy th onfguaton of th systm spaat to th ontol postv an ngatvsun of th njt unt. Mofatons of th ngatv-sun omponnts of th njt unt wll b llumnat n abov ston. Doubl vto otoll (v): To mpov th unbalan stuban ompnsaton two spaat ontols, Synhonous fn Fam (SF s ) an b us (Ptsson t al., 005, Snsama t al., 00), wh th postv an ngatv (SF) a synhonz to postv an ngatv sun omponnt of th ntwo voltag. Th sults an xplan by th blo shm of Dual Vto Contoll (DVC) (Wooly t al., 999). By Sun Spaaton Mtho (SSM) an sb sun omponnts of unt njton, voltag of apato an flt unt (Wooly t al., 999, Jung t al., 00). Euatons (3 an 3) a th sam fo th postv sun of VCC an VVC, sptvly. To ompnsat fo th unbalan stuban of th voltag, a ontol mtho s u to pou th sou fn unts of D-STATCOM n th as th ntwo voltag s unbalan. Ths fn unts nt th vto ontoll bas on whh onvto voltag a ma n phass a, b an. Th gnal tn s llustat n Fg. 9. In th Doubl Vto Contoll (DVC) (Wooly t al., 999), two ntal vto ontol blos xst whh a ffnt only n th sgn of oupl fatos btwn th an axs (Hngoan, 995). Th am s to tah th postv an ngatv omponnts of voltag an unt n th vnt of th unbalan voltag. Fou sgnals hang nto subsun omponnts. Dsptons of ths sgnals a pov )
5 s. J. Appl. S. Eng. Thnol., 6(3): , 03 Fg. 4: Injt unt of - an -omponnt as a sult of 5% voltag sag Fg. 5: Th-phas g voltags ompnsat at PCC.VSC an - flt a us Fg. 6: Shmat lat to th systm wth shunt-onnt VSC an C-output flt. Fg. 7: Th th-phas g voltags of th PCC ung th voltag sag.vsc n l mo Fg. 8: Th-phas g voltags of PCC. By applyng VSC, C-flt an atv ampng 383
6 s. J. Appl. S. Eng. Thnol., 6(3): , 03 Fg. 9: Shmat of systm (DVC) bas on oubl synhonous fn fams Fg. 0: Dsptons of ths sgnals Fg. : Dsptons of ths sgnals Fg. : Th-phas wav foms at PCC E g Ntwo voltag at PCC pont E Capato voltag of ompnsato flt I Cunt of VSC onvto I nj Injt unt to th ntwo Implmntng of ths fou sgnals s shown by E. (6, 7), (8, 9) an Fg. 0, : xx 0.5( (tt) (tt 0.005) (5) xx 0.5( (tt) (tt 0.005) (6) xx 0.5( (tt) (tt 0.005)) (7) xx 0.5( (tt) (tt 0.005)) (8) 384
7 s. J. Appl. S. Eng. Thnol., 6(3): , 03 To ompa th pfoman of th asa ontoll that w psnt n th pvous ston wth DVC un th sam unbalan voltag sag, llustat n Fg. 7, fo th-phas wavfoms an by usng Dual Vto Contoll, t wll b sussful mtgaton of th voltag sag an t s vntly vsbl n Fg.. CONCUSION Ths stuy sbs how to us VSC to mtgat voltag p. Moov, t susss an shows that VSC an ontol an mantan th ampltu of th ntwo s voltag wth ompnsatng voltag p by njtng atv pow. Nvthlss, ths n of ontol systm s ompltly snstv to th paamts vaatons of th systm. To gan at th hgh opaton an mo obust ontoll an stutu of shunt onnton, wth smpl -flt an C-flt has bn analyz. Invstgaton vals that by sltng a asa ontoll, wth VVC an VCC a mo powful ontoll an b ah. sult of th ontol systm has bn obtan n th postv an ngatv SF, n o to spaat ontol omponnts of postv an ngatv-sun of th ntwo voltag. Smulaton sults mantan that wth th popos ontol mtho, w an ahv hgh ynam pfoman by usng DVC. EFEENCES Bolln, M., 999. Unstanng Pow Qualty Poblms: Voltag Sags an Intuptons. IEEE Pss, Nw Yo. Bongono, M., J. Svnsson an A. Sannno, 005. An avan asa ontoll fo ss-onnt VSC fo voltag p mtgaton. Inusty Applatons Confn, Foutth IAS Annual Mtng Confn o of th 005, Gotbog, Swn, : Choma, K.N. an M. Etza-Amol, 00. Th applaton of a DSTATCOM to an nustal falty. IEEE Pow Engnng Soty Wnt Mtng, : D Pna, C., P. V, A. Sannno an M. Bolln, 003. Stat ss ompnsato fo voltag p mtgaton wth zo-sun njton apablty. IEEE Bologna Pow Th Confn Pongs, Italy, VO. 4. Esoba, G., A. Stanov an P. Mattavll, 000. atv Pow, mbalan an hamons ompnsaton usng -statom wth a sspatvtybas ontoll. IEEE Inusty Applatons Confn, Confn o of th 000, Boston, MA, USA, 4: Hanfos,. an H.P. N, 000. A gnal algothm fo sp an poston stmaton of AC motos. IEEE T. In. Elt., 47(): Hngoan, N.G., 995. Intoung ustom pow. IEEE Sptum, 3(6): Jung, S.Y., T.H. Km, S.I. Moon an B.M. Han, 00. Analyss an ontol of DSTATCOM fo a ln voltag gulaton. IEEE Pow Engnng Soty Wnt Mtng, South Koa, : , T.N., 989. Kompnssaton shnll vanlh blnstom ns shstomvbauhs. tzahv H. 8(B. ): Nwman, M.J. an D.G. Holms, 00. An ntgat appoah fo th potton of ss njton nvts. IEEE T. In. Appl., 38(3): Ottstn,. an J. Svnsson, 00. Vto unt ontoll voltag sou onvt-abat ontol an satuaton statgs. IEEE T. Pow Elt., 7(): Ptsson, A.,. Hanfos an T. Thng, 005. Evaluaton of unt ontol mthos fo wn tubns usng oubly-f nuton mahns. IEEE T. Pow Elt., 0(): Snsama, P., K. Paya an V. amanaayanan, 00. Analyssanpfomanvaluatonof a stbuton STATCOM fo ompnsatng voltag flutuatons. IEEE T. Pow Dlv., 6(): Svnsson, J. an M.B. ngn, 998. Vto unt ontoll g onnt voltag sou onvtnflun of nonlnats on th pfoman. 9th Annual IEEE Pow Eltons Spalsts Confn, PESC 98 o, 7- May, Gotbog, Swn, : Wang, P., N. Jnns an M. Bolln, 998. Expmntal nvstgaton of voltag sag mtgaton by an avan stat VA ompnsato. IEEE T. Pow Dlv., 3(4): Wooly, N.H.,. Mogan an A. Sunaam, 999. Expn wth an nvt-bas ynam voltag sto. IEEE T. Pow Dlv., 4(3):
Load Equations. So let s look at a single machine connected to an infinite bus, as illustrated in Fig. 1 below.
 oa Euatons Thoughout all of chapt 4, ou focus s on th machn tslf, thfo w wll only pfom a y smpl tatmnt of th ntwok n o to s a complt mol. W o that h, but alz that w wll tun to ths ssu n Chapt 9. So lt
oa Euatons Thoughout all of chapt 4, ou focus s on th machn tslf, thfo w wll only pfom a y smpl tatmnt of th ntwok n o to s a complt mol. W o that h, but alz that w wll tun to ths ssu n Chapt 9. So lt
Structure and Features
 Thust l Roll ans Thust Roll ans Stutu an atus Thust ans onsst of a psly ma a an olls. Thy hav hh ty an hh loa apats an an b us n small spas. Thust l Roll ans nopoat nl olls, whl Thust Roll ans nopoat ylnal
Thust l Roll ans Thust Roll ans Stutu an atus Thust ans onsst of a psly ma a an olls. Thy hav hh ty an hh loa apats an an b us n small spas. Thust l Roll ans nopoat nl olls, whl Thust Roll ans nopoat ylnal
Rectification and Depth Computation
 Dpatmnt of Comput Engnng Unvst of Cafona at Santa Cuz Rctfcaton an Dpth Computaton CMPE 64: mag Anass an Comput Vson Spng 0 Ha ao 4/6/0 mag cosponncs Dpatmnt of Comput Engnng Unvst of Cafona at Santa Cuz
Dpatmnt of Comput Engnng Unvst of Cafona at Santa Cuz Rctfcaton an Dpth Computaton CMPE 64: mag Anass an Comput Vson Spng 0 Ha ao 4/6/0 mag cosponncs Dpatmnt of Comput Engnng Unvst of Cafona at Santa Cuz
Analysis of a M/G/1/K Queue with Vacations Systems with Exhaustive Service, Multiple or Single Vacations
 Analyss of a M/G// uu wth aatons Systms wth Ehaustv Sv, Multpl o Sngl aatons W onsd h th fnt apaty M/G// uu wth th vaaton that th sv gos fo vaatons whn t s dl. Ths sv modl s fd to as on povdng haustv sv,
Analyss of a M/G// uu wth aatons Systms wth Ehaustv Sv, Multpl o Sngl aatons W onsd h th fnt apaty M/G// uu wth th vaaton that th sv gos fo vaatons whn t s dl. Ths sv modl s fd to as on povdng haustv sv,
Switching FOC Method for Vector Control of Single-Phase Induction Motor Drives
 Intnatonal Jounal of Elctcal an Comput Engnng (IJECE) Vol. 6, No., Apl 16, pp. 474~483 ISSN: 88-878, DOI: 1.11591/jc.6.9146 474 Swtchng FOC tho fo Vcto Contol of Sngl-Phas Inucton oto Ds ohamma Jannat*,
Intnatonal Jounal of Elctcal an Comput Engnng (IJECE) Vol. 6, No., Apl 16, pp. 474~483 ISSN: 88-878, DOI: 1.11591/jc.6.9146 474 Swtchng FOC tho fo Vcto Contol of Sngl-Phas Inucton oto Ds ohamma Jannat*,
Period vs. Length of a Pendulum
 Gaphcal Mtho n Phc Gaph Intptaton an Lnazaton Pat 1: Gaphng Tchnqu In Phc w u a vat of tool nclung wo, quaton, an gaph to mak mol of th moton of objct an th ntacton btwn objct n a tm. Gaph a on of th bt
Gaphcal Mtho n Phc Gaph Intptaton an Lnazaton Pat 1: Gaphng Tchnqu In Phc w u a vat of tool nclung wo, quaton, an gaph to mak mol of th moton of objct an th ntacton btwn objct n a tm. Gaph a on of th bt
Applications of Lagrange Equations
 Applcaton of agang Euaton Ca Stuy : Elctc Ccut ng th agang uaton of oton, vlop th athatcal ol fo th ccut hown n Fgu.Sulat th ult by SIMI. Th ccuty paat a: 0.0 H, 0.00 H, 0.00 H, C 0.0 F, C 0. F, 0 Ω, Ω
Applcaton of agang Euaton Ca Stuy : Elctc Ccut ng th agang uaton of oton, vlop th athatcal ol fo th ccut hown n Fgu.Sulat th ult by SIMI. Th ccuty paat a: 0.0 H, 0.00 H, 0.00 H, C 0.0 F, C 0. F, 0 Ω, Ω
t the propensity to consume the resource good. Maximizing U t in (9) subject to the budget constraint (8) yields
 ISB 978-9-84468-8-5 Innaonal Confn on Issus n Busnss onoms Mang an Mamas (IBMM-6) Sngapo 5-6 6 Busnss Cls Capal nvonmn an Rnabl Rsous W-Bn Zang Rsuman Asa Paf Unvs Bppu-s Japan Absa: Ts pap nfs busnss
ISB 978-9-84468-8-5 Innaonal Confn on Issus n Busnss onoms Mang an Mamas (IBMM-6) Sngapo 5-6 6 Busnss Cls Capal nvonmn an Rnabl Rsous W-Bn Zang Rsuman Asa Paf Unvs Bppu-s Japan Absa: Ts pap nfs busnss
ECE 422 Power System Operations & Planning 2 Synchronous Machine Modeling
 ECE 422 Power System Operatons & Plannng 2 Synhronous Mahne Moelng Sprng 219 Instrutor: Ka Sun 1 Outlne 2.1 Moelng of synhronous generators for Stablty Stues Synhronous Mahne Moelng Smplfe Moels for Stablty
ECE 422 Power System Operatons & Plannng 2 Synhronous Mahne Moelng Sprng 219 Instrutor: Ka Sun 1 Outlne 2.1 Moelng of synhronous generators for Stablty Stues Synhronous Mahne Moelng Smplfe Moels for Stablty
Determination of slot leakage inductance for three-phase induction motor winding using an analytical method
 ACHIVES OF EECTICA EGIEEIG VO 6 pp 569-59 DOI 78/--6 Dtnton of ot ntn fo t-p nton oto wnn n n nt to JA STASZAK Dptnt of Et Mn n Mton St K Unvt of Tnoo Tą PP 7 K Pon -: j@tp v: v: 5 Att: T t nto o pon fo
ACHIVES OF EECTICA EGIEEIG VO 6 pp 569-59 DOI 78/--6 Dtnton of ot ntn fo t-p nton oto wnn n n nt to JA STASZAK Dptnt of Et Mn n Mton St K Unvt of Tnoo Tą PP 7 K Pon -: j@tp v: v: 5 Att: T t nto o pon fo
Homework: Due
 hw-.nb: //::9:5: omwok: Du -- Ths st (#7) s du on Wdnsday, //. Th soluton fom Poblm fom th xam s found n th mdtm solutons. ü Sakua Chap : 7,,,, 5. Mbach.. BJ 6. ü Mbach. Th bass stats of angula momntum
hw-.nb: //::9:5: omwok: Du -- Ths st (#7) s du on Wdnsday, //. Th soluton fom Poblm fom th xam s found n th mdtm solutons. ü Sakua Chap : 7,,,, 5. Mbach.. BJ 6. ü Mbach. Th bass stats of angula momntum
Noise in electronic components.
 No lto opot5098, JDS No lto opot Th PN juto Th ut thouh a PN juto ha fou opot t: two ffuo ut (hol fo th paa to th aa a lto th oppot to) a thal at oty ha a (hol fo th aa to th paa a lto th oppot to, laka
No lto opot5098, JDS No lto opot Th PN juto Th ut thouh a PN juto ha fou opot t: two ffuo ut (hol fo th paa to th aa a lto th oppot to) a thal at oty ha a (hol fo th aa to th paa a lto th oppot to, laka
SYMMETRICAL COMPONENTS
 SYMMETRCA COMPONENTS Syl oponn llow ph un of volg n un o pl y h p ln yl oponn Con h ph ln oponn wh Engy Convon o 4 o o wh o, 4 o, 6 o Engy Convon SYMMETRCA COMPONENTS Dfn h opo wh o Th o of pho : pov ph
SYMMETRCA COMPONENTS Syl oponn llow ph un of volg n un o pl y h p ln yl oponn Con h ph ln oponn wh Engy Convon o 4 o o wh o, 4 o, 6 o Engy Convon SYMMETRCA COMPONENTS Dfn h opo wh o Th o of pho : pov ph
ECE 522 Power Systems Analysis II 2 Power System Modeling
 ECE 522 Power Systems Analyss II 2 Power System Moelng Sprng 218 Instrutor: Ka Sun 1 Outlne 2.1 Moelng of synhronous generators for Stablty Stues Synhronous Mahne Moelng Smplfe Moels for Stablty Stues
ECE 522 Power Systems Analyss II 2 Power System Moelng Sprng 218 Instrutor: Ka Sun 1 Outlne 2.1 Moelng of synhronous generators for Stablty Stues Synhronous Mahne Moelng Smplfe Moels for Stablty Stues
5- Scattering Stationary States
 Lctu 19 Pyscs Dpatmnt Yamou Unvsty 1163 Ibd Jodan Pys. 441: Nucla Pyscs 1 Pobablty Cunts D. Ndal Esadat ttp://ctaps.yu.du.jo/pyscs/couss/pys641/lc5-3 5- Scattng Statonay Stats Rfnc: Paagaps B and C Quantum
Lctu 19 Pyscs Dpatmnt Yamou Unvsty 1163 Ibd Jodan Pys. 441: Nucla Pyscs 1 Pobablty Cunts D. Ndal Esadat ttp://ctaps.yu.du.jo/pyscs/couss/pys641/lc5-3 5- Scattng Statonay Stats Rfnc: Paagaps B and C Quantum
Adaptive Power System Stabilizer using Artificial Neural Network
 84 NAIONAL POWER SYSEMS CONFERENCE, NPSC Adaptv Pow Systm Stablz usng Atal Nual Ntwok P.C. Panda, A.. Panda and A. Routay Abstat-- An Atal Nual Ntwok (ANN) basd adaptv PSS and ts applaton to pow systm
84 NAIONAL POWER SYSEMS CONFERENCE, NPSC Adaptv Pow Systm Stablz usng Atal Nual Ntwok P.C. Panda, A.. Panda and A. Routay Abstat-- An Atal Nual Ntwok (ANN) basd adaptv PSS and ts applaton to pow systm
Midterm Exam. CS/ECE 181B Intro to Computer Vision. February 13, :30-4:45pm
 Nam: Midtm am CS/C 8B Into to Comput Vision Fbua, 7 :-4:45pm las spa ouslvs to th dg possibl so that studnts a vnl distibutd thoughout th oom. his is a losd-boo tst. h a also a fw pags of quations, t.
Nam: Midtm am CS/C 8B Into to Comput Vision Fbua, 7 :-4:45pm las spa ouslvs to th dg possibl so that studnts a vnl distibutd thoughout th oom. his is a losd-boo tst. h a also a fw pags of quations, t.
Weighted Graphs. Weighted graphs may be either directed or undirected.
 1 In mny ppltons, o rp s n ssot numrl vlu, ll wt. Usully, t wts r nonntv ntrs. Wt rps my tr rt or unrt. T wt o n s otn rrr to s t "ost" o t. In ppltons, t wt my msur o t lnt o rout, t pty o ln, t nry rqur
1 In mny ppltons, o rp s n ssot numrl vlu, ll wt. Usully, t wts r nonntv ntrs. Wt rps my tr rt or unrt. T wt o n s otn rrr to s t "ost" o t. In ppltons, t wt my msur o t lnt o rout, t pty o ln, t nry rqur
Analysis of Data Dependency Based Intrusion Detection System *
 nalyss of Data Dnny Bas Intuson Dtton Systm * Ymk ugmanov 1, Bajna ana 1, an Y Hu 2 1 Comut Sn an Comut Engnng Datmnt Unvsty of kansas ayttvll, R 72701 {ynugmano,bana}@uak.u 2 Comut Sn Datmnt othn Kntuky
nalyss of Data Dnny Bas Intuson Dtton Systm * Ymk ugmanov 1, Bajna ana 1, an Y Hu 2 1 Comut Sn an Comut Engnng Datmnt Unvsty of kansas ayttvll, R 72701 {ynugmano,bana}@uak.u 2 Comut Sn Datmnt othn Kntuky
Integrated Optical Waveguides
 Su Opls Faha Raa Cll Uvs Chap 8 Ia Opal Wavus 7 Dl Slab Wavus 7 Iu: A va f ff a pal wavus a us f a u lh a hp Th s bas pal wavu s a slab wavus shw blw Th suu s uf h - Lh s u s h b al al fl a h -la fas Cla
Su Opls Faha Raa Cll Uvs Chap 8 Ia Opal Wavus 7 Dl Slab Wavus 7 Iu: A va f ff a pal wavus a us f a u lh a hp Th s bas pal wavu s a slab wavus shw blw Th suu s uf h - Lh s u s h b al al fl a h -la fas Cla
J. Milli Monfared K. Abbaszadeh E. Fallah Assistant Professor P.H.D Student P.H.D Student
 olng an Smulaton of Dual h Pha Inucton achn n Fault conton wo Pha cut off) an Popo A Nw Vcto Contol Appoach fo oqu Ocllaton Ructon J. ll onfa K. Abbazah E. Fallah Atant Pofo P.H.D Stunt P.H.D Stunt Amkab
olng an Smulaton of Dual h Pha Inucton achn n Fault conton wo Pha cut off) an Popo A Nw Vcto Contol Appoach fo oqu Ocllaton Ructon J. ll onfa K. Abbazah E. Fallah Atant Pofo P.H.D Stunt P.H.D Stunt Amkab
Chapter 3 Binary Image Analysis. Comunicação Visual Interactiva
 Chapt 3 Bnay Iag Analyss Counação Vsual Intatva Most oon nghbohoods Pxls and Nghbohoods Nghbohood Vznhança N 4 Nghbohood N 8 Us of ass Exapl: ogn nput output CVI - Bnay Iag Analyss Exapl 0 0 0 0 0 output
Chapt 3 Bnay Iag Analyss Counação Vsual Intatva Most oon nghbohoods Pxls and Nghbohoods Nghbohood Vznhança N 4 Nghbohood N 8 Us of ass Exapl: ogn nput output CVI - Bnay Iag Analyss Exapl 0 0 0 0 0 output
RAKE Receiver with Adaptive Interference Cancellers for a DS-CDMA System in Multipath Fading Channels
 AKE v wh Apv f Cs fo DS-CDMA Ss Muph Fg Chs JooHu Y Su M EEE JHog M EEE Shoo of E Egg Sou o Uvs Sh-og Gw-gu Sou 5-74 Ko E-: ohu@su As hs pp pv AKE v wh vs og s popos fo DS-CDMA ss uph fg hs h popos pv
AKE v wh Apv f Cs fo DS-CDMA Ss Muph Fg Chs JooHu Y Su M EEE JHog M EEE Shoo of E Egg Sou o Uvs Sh-og Gw-gu Sou 5-74 Ko E-: ohu@su As hs pp pv AKE v wh vs og s popos fo DS-CDMA ss uph fg hs h popos pv
Evaluation of Back-EMF Estimators for Sensorless Control of Permanent Magnet Synchronous Motors
 Ealuaton of Back-EMF Etmato fo Snol Contol of JPE -4- http://x.o.og/.63/jpe...4. Ealuaton of Back-EMF Etmato fo Snol Contol of Pmannt Magnt Synchonou Moto Kwang-Woon an Jung-Ik Ha Dpt. of Elctonc Eng.,
Ealuaton of Back-EMF Etmato fo Snol Contol of JPE -4- http://x.o.og/.63/jpe...4. Ealuaton of Back-EMF Etmato fo Snol Contol of Pmannt Magnt Synchonou Moto Kwang-Woon an Jung-Ik Ha Dpt. of Elctonc Eng.,
Lecture 20: Minimum Spanning Trees (CLRS 23)
 Ltur 0: Mnmum Spnnn Trs (CLRS 3) Jun, 00 Grps Lst tm w n (wt) rps (unrt/rt) n ntrou s rp voulry (vrtx,, r, pt, onnt omponnts,... ) W lso suss jny lst n jny mtrx rprsntton W wll us jny lst rprsntton unlss
Ltur 0: Mnmum Spnnn Trs (CLRS 3) Jun, 00 Grps Lst tm w n (wt) rps (unrt/rt) n ntrou s rp voulry (vrtx,, r, pt, onnt omponnts,... ) W lso suss jny lst n jny mtrx rprsntton W wll us jny lst rprsntton unlss
Optimum PSK Signal Mapping for Multi-Phase Binary-CDMA Systems
 Omum Sgnal Mappng fo Mult-Pha Bnay-CDMA Sytm Yong-Jn So and Yong-Hwan L Shool of Eltal Engnng and INMC Soul Natonal Unvty Kwanak P O Box 34 Soul 5-744 Koa -mal: yl@nuak Atat - Although th CDMA ytm an ffntly
Omum Sgnal Mappng fo Mult-Pha Bnay-CDMA Sytm Yong-Jn So and Yong-Hwan L Shool of Eltal Engnng and INMC Soul Natonal Unvty Kwanak P O Box 34 Soul 5-744 Koa -mal: yl@nuak Atat - Although th CDMA ytm an ffntly
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
PF nce. Conferen. is, FRANC. ectronics Pari. ber 6-10, 2. ustrial Ele. Novemb. EEE Indu
 Confn nc s, FRANC CE ctoncs 006 Pa ustal El b 6-0, EEE Indu Nomb 3 nd I Spd and Poston Estmaton fo PM Synchonous Moto usng Slf-Compnsatd t d Back-EMF k Obss Maco TURSINI, Robto PETRELLA, Alssa SCAFATI
Confn nc s, FRANC CE ctoncs 006 Pa ustal El b 6-0, EEE Indu Nomb 3 nd I Spd and Poston Estmaton fo PM Synchonous Moto usng Slf-Compnsatd t d Back-EMF k Obss Maco TURSINI, Robto PETRELLA, Alssa SCAFATI
Electromagnetics: The Smith Chart (9-6)
 Elctomagntcs: Th Smth Chat (9-6 Yoonchan Jong School of Elctcal Engnng, Soul Natonal Unvsty Tl: 8 (0 880 63, Fax: 8 (0 873 9953 Emal: yoonchan@snu.ac.k A Confomal Mappng ( Mappng btwn complx-valud vaabls:
Elctomagntcs: Th Smth Chat (9-6 Yoonchan Jong School of Elctcal Engnng, Soul Natonal Unvsty Tl: 8 (0 880 63, Fax: 8 (0 873 9953 Emal: yoonchan@snu.ac.k A Confomal Mappng ( Mappng btwn complx-valud vaabls:
( V ) 0 in the above equation, but retained to keep the complete vector identity for V in equation.
 Cuvlna Coodnats Outln:. Otogonal cuvlna coodnat systms. Dffntal opatos n otogonal cuvlna coodnat systms. Dvatvs of t unt vctos n otogonal cuvlna coodnat systms 4. Incompssbl N-S quatons n otogonal cuvlna
Cuvlna Coodnats Outln:. Otogonal cuvlna coodnat systms. Dffntal opatos n otogonal cuvlna coodnat systms. Dvatvs of t unt vctos n otogonal cuvlna coodnat systms 4. Incompssbl N-S quatons n otogonal cuvlna
Lecture 7 Diffusion. Our fluid equations that we developed before are: v t v mn t
 Cla ot fo EE6318/Phy 6383 Spg 001 Th doumt fo tutoal u oly ad may ot b opd o dtbutd outd of EE6318/Phy 6383 tu 7 Dffuo Ou flud quato that w dvlopd bfo a: f ( )+ v v m + v v M m v f P+ q E+ v B 13 1 4 34
Cla ot fo EE6318/Phy 6383 Spg 001 Th doumt fo tutoal u oly ad may ot b opd o dtbutd outd of EE6318/Phy 6383 tu 7 Dffuo Ou flud quato that w dvlopd bfo a: f ( )+ v v m + v v M m v f P+ q E+ v B 13 1 4 34
Diffraction. Diffraction: general Fresnel vs. Fraunhofer diffraction Several coherent oscillators Single-slit diffraction. Phys 322 Lecture 28
 Chapt 10 Phys 3 Lctu 8 Dffacton Dffacton: gnal Fsnl vs. Faunhof dffacton Sval cohnt oscllatos Sngl-slt dffacton Dffacton Gmald, 1600s: dffacto, dvaton of lght fom lna popagaton Dffacton s a consqunc of
Chapt 10 Phys 3 Lctu 8 Dffacton Dffacton: gnal Fsnl vs. Faunhof dffacton Sval cohnt oscllatos Sngl-slt dffacton Dffacton Gmald, 1600s: dffacto, dvaton of lght fom lna popagaton Dffacton s a consqunc of
An action with positive kinetic energy term for general relativity. T. Mei
 An ton wt post nt ny t fo n tty T (Dptnt of Jon Cnt Cn o Unsty Wn H PRO Pop s Rp of Cn E-: to@nn tow@pwn ) Astt: At fst w stt so sts n X: 7769 n tn sn post nt ny oont onton n y X: 7769 w psnt n ton wt
An ton wt post nt ny t fo n tty T (Dptnt of Jon Cnt Cn o Unsty Wn H PRO Pop s Rp of Cn E-: to@nn tow@pwn ) Astt: At fst w stt so sts n X: 7769 n tn sn post nt ny oont onton n y X: 7769 w psnt n ton wt
Analytical Evaluation of Multicenter Nuclear Attraction Integrals for Slater-Type Orbitals Using Guseinov Rotation-Angular Function
 I. J. Cop. Mh. S Vo. 5 o. 7 39-3 Ay Evuo of Mu u Ao Ig fo S-yp O Ug Guov Roo-Agu uo Rz Y M Ag Dp of Mh uy of uo fo g A-Khj Uvy Kgo of Su A Dp of Mh uy of S o B Auh Uvy Kgo of Su A A. Ug h Guov oo-gu fuo
I. J. Cop. Mh. S Vo. 5 o. 7 39-3 Ay Evuo of Mu u Ao Ig fo S-yp O Ug Guov Roo-Agu uo Rz Y M Ag Dp of Mh uy of uo fo g A-Khj Uvy Kgo of Su A Dp of Mh uy of S o B Auh Uvy Kgo of Su A A. Ug h Guov oo-gu fuo
Diffraction. Diffraction: general Fresnel vs. Fraunhofer diffraction Several coherent oscillators Single-slit diffraction. Phys 322 Lecture 28
 Chapt 10 Phys 3 Lctu 8 Dffacton Dffacton: gnal Fsnl vs. Faunhof dffacton Sval cohnt oscllatos Sngl-slt dffacton Dffacton Gmald, 1600s: dffacto, dvaton of lght fom lna popagaton Dffacton s a consqunc of
Chapt 10 Phys 3 Lctu 8 Dffacton Dffacton: gnal Fsnl vs. Faunhof dffacton Sval cohnt oscllatos Sngl-slt dffacton Dffacton Gmald, 1600s: dffacto, dvaton of lght fom lna popagaton Dffacton s a consqunc of
STRIPLINES. A stripline is a planar type transmission line which is well suited for microwave integrated circuitry and photolithographic fabrication.
 STIPLINES A tiplin i a plana typ tanmiion lin hih i ll uitd fo mioav intgatd iuity and photolithogaphi faiation. It i uually ontutd y thing th nt onduto of idth, on a utat of thikn and thn oving ith anoth
STIPLINES A tiplin i a plana typ tanmiion lin hih i ll uitd fo mioav intgatd iuity and photolithogaphi faiation. It i uually ontutd y thing th nt onduto of idth, on a utat of thikn and thn oving ith anoth
Analysis of Stresses and Strains in a Rotating Homogeneous Thermoelastic Circular Disk by using Finite Element Method
 Intnatonal Jounal of Comput Applcatons (0975 8887 Volum 35 No.3, Dcmb 0 Analyss of Stsss an Stans n a Rotatng Homognous Thmolastc Ccula Dsk by usng Fnt lmnt Mtho J. N. Shama Dpatmnt of Mathmatcs Natonal
Intnatonal Jounal of Comput Applcatons (0975 8887 Volum 35 No.3, Dcmb 0 Analyss of Stsss an Stans n a Rotatng Homognous Thmolastc Ccula Dsk by usng Fnt lmnt Mtho J. N. Shama Dpatmnt of Mathmatcs Natonal
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Homework 1: Solutions
 Howo : Solutos No-a Fals supposto tst but passs scal tst lthouh -f th ta as slowss [S /V] vs t th appaac of laty alty th path alo whch slowss s to b tat to obta tavl ts ps o th ol paat S o V as a cosquc
Howo : Solutos No-a Fals supposto tst but passs scal tst lthouh -f th ta as slowss [S /V] vs t th appaac of laty alty th path alo whch slowss s to b tat to obta tavl ts ps o th ol paat S o V as a cosquc
Nikon i-line Glass Series
 Nkon ln la S ln la VNTS Nkon a an vlopmn of qualy maal a alway bn la o n fo ompany opal pou. Pon ky fao. van n la noloy pn upon pon, an a Nkon xl. Nkon ln la wa vlop fo u w ln ( nm) loapy un. I lv anman
Nkon ln la S ln la VNTS Nkon a an vlopmn of qualy maal a alway bn la o n fo ompany opal pou. Pon ky fao. van n la noloy pn upon pon, an a Nkon xl. Nkon ln la wa vlop fo u w ln ( nm) loapy un. I lv anman
CHAPTER 3 KINEMATICS OF CYLINDRICAL ROLLER BEARING
 34 CHAPTER 3 KINEMATICS OF CYLINDRICAL ROLLER BEARING 3. CAGE AND ROLLER SPEED Th latv mtns f th ag spaat, th lls, an th as f ylnal llng lmnt bangs a mptant t unstan th pfman. Th latv vlts n a ball bang
34 CHAPTER 3 KINEMATICS OF CYLINDRICAL ROLLER BEARING 3. CAGE AND ROLLER SPEED Th latv mtns f th ag spaat, th lls, an th as f ylnal llng lmnt bangs a mptant t unstan th pfman. Th latv vlts n a ball bang
MODELING AND SIMULATION OF SENSORLESS CONTROL OF PMSM WITH LUENBERGER ROTOR POSITION OBSERVER AND SUI PID CONTROLLER
 Jounal of Elctcal Engnng www.j.o MODEING AND SIMUAION OF SENSORESS CONRO OF PMSM WIH UENBERGER ROOR POSIION OBSERVER AND SUI PID CONROER GHADA A. ABDE AZIZ, MOHAMED. I. ABU E- SEBAH, Elctonc Rsach Insttut,
Jounal of Elctcal Engnng www.j.o MODEING AND SIMUAION OF SENSORESS CONRO OF PMSM WIH UENBERGER ROOR POSIION OBSERVER AND SUI PID CONROER GHADA A. ABDE AZIZ, MOHAMED. I. ABU E- SEBAH, Elctonc Rsach Insttut,
CIVL 7/ D Boundary Value Problems - Axisymmetric Elements 1/8
 CIVL 7/8 -D Bounday Valu Poblms - xsymmtc Elmnts /8 xsymmtc poblms a somtms fd to as adally symmtc poblms. hy a gomtcally th-dmnsonal but mathmatcally only two-dmnsonal n th physcs of th poblm. In oth
CIVL 7/8 -D Bounday Valu Poblms - xsymmtc Elmnts /8 xsymmtc poblms a somtms fd to as adally symmtc poblms. hy a gomtcally th-dmnsonal but mathmatcally only two-dmnsonal n th physcs of th poblm. In oth
Description of Spectral Particle-in-Cell Codes from the UPIC Framework
 Dspton of Sptal Patl-n-Cll Cods fom th UPIC Famwok Vkto K. Dyk Dpatmnt of Physs and Astonomy Unvsty of Calfona, Los Angls Los Angls, Calfona 90095-1547 I. Intoduton hs doumnt psnts th mathmatal foundaton
Dspton of Sptal Patl-n-Cll Cods fom th UPIC Famwok Vkto K. Dyk Dpatmnt of Physs and Astonomy Unvsty of Calfona, Los Angls Los Angls, Calfona 90095-1547 I. Intoduton hs doumnt psnts th mathmatal foundaton
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
ILSim A compact simulation tool for interferometric lithography
 LSm A compact smulaton tool fo ntfomtc lthogaphy Yongfa an, Anatoly Bouov, Lna Zavyalova, Janmng Zhou, Anw stoff, al Laffty, Buc W. Smth Rochst nsttut of Tchnology, Mcolctonc ngnng Dpatmnt 8 Lomb Mmoal
LSm A compact smulaton tool fo ntfomtc lthogaphy Yongfa an, Anatoly Bouov, Lna Zavyalova, Janmng Zhou, Anw stoff, al Laffty, Buc W. Smth Rochst nsttut of Tchnology, Mcolctonc ngnng Dpatmnt 8 Lomb Mmoal
Massachusetts Institute of Technology Introduction to Plasma Physics
 Massachustts Insttut of Tchnology Intoducton to Plasma Physcs NAME 6.65J,8.63J,.6J R. Pak Dcmb 5 Fnal Eam :3-4:3 PM NOTES: Th a 8 pags to th am, plus on fomula sht. Mak su that you copy s complt. Each
Massachustts Insttut of Tchnology Intoducton to Plasma Physcs NAME 6.65J,8.63J,.6J R. Pak Dcmb 5 Fnal Eam :3-4:3 PM NOTES: Th a 8 pags to th am, plus on fomula sht. Mak su that you copy s complt. Each
b.) v d =? Example 2 l = 50 m, D = 1.0 mm, E = 6 V, " = 1.72 #10 $8 % & m, and r = 0.5 % a.) R =? c.) V ab =? a.) R eq =?
 xmpl : An 8-gug oppr wr hs nomnl mtr o. mm. Ths wr rrs onstnt urrnt o.67 A to W lmp. Th nsty o r ltrons s 8.5 x 8 ltrons pr u mtr. Fn th mgntu o. th urrnt nsty. th rt vloty xmpl D. mm,.67 A, n N 8.5" 8
xmpl : An 8-gug oppr wr hs nomnl mtr o. mm. Ths wr rrs onstnt urrnt o.67 A to W lmp. Th nsty o r ltrons s 8.5 x 8 ltrons pr u mtr. Fn th mgntu o. th urrnt nsty. th rt vloty xmpl D. mm,.67 A, n N 8.5" 8
n gativ b ias to phap s 5 Q mou ntd ac oss a 50 Q co-a xial l, i t whn bias no t back-bia s d, so t hat p ow fl ow wi ll not b p ositiv. Th u s, if si
 DIOD E AND ITS APPLI AT C I O N: T h diod is a p-t p, y intin s ic, n-typ diod consis ting of a naow lay of p- typ smiconducto and a naow lay of n-typ smiconducto, wi th a thick gion of intins ic o b twn
DIOD E AND ITS APPLI AT C I O N: T h diod is a p-t p, y intin s ic, n-typ diod consis ting of a naow lay of p- typ smiconducto and a naow lay of n-typ smiconducto, wi th a thick gion of intins ic o b twn
Creep damage evaluation of thick-walled spheres using a long-term creep constitutive model
 Jounal of Mhanal Sn and Thnology (009) 577~58 Jounal of Mhanal Sn and Thnology www.spnglnk.om/ontnt/78-494x DOI 0.007/s06-009-06-x Cp damag valuaton of thk-walld sphs usng a long-tm p onsttutv modl Abbas
Jounal of Mhanal Sn and Thnology (009) 577~58 Jounal of Mhanal Sn and Thnology www.spnglnk.om/ontnt/78-494x DOI 0.007/s06-009-06-x Cp damag valuaton of thk-walld sphs usng a long-tm p onsttutv modl Abbas
SHELL CANADA PIPING AND INSTRUMENT DIAGRAM QUEST CCS PROJECT LEGENDS AND SYMBOLS QUEST CCS PROJECT UNIT COMMON "!!
 .. 2 S 222... 2. SSU TON Y K PS S M P PM T S N QUST S POJT. S NON N N NSTUMNT M QUST S POJT S W NO.. 2... NT M T \\\2\WNS\UTTS\2\2..pid MO T22 PM Yahm 2. UNT 2 OMMON NS N SYMOS .. SSU T 2 2 2. TON Y K
.. 2 S 222... 2. SSU TON Y K PS S M P PM T S N QUST S POJT. S NON N N NSTUMNT M QUST S POJT S W NO.. 2... NT M T \\\2\WNS\UTTS\2\2..pid MO T22 PM Yahm 2. UNT 2 OMMON NS N SYMOS .. SSU T 2 2 2. TON Y K
Extinction Ratio and Power Penalty
 Application Not: HFAN-.. Rv.; 4/8 Extinction Ratio and ow nalty AVALABLE Backgound Extinction atio is an impotant paamt includd in th spcifications of most fib-optic tanscivs. h pupos of this application
Application Not: HFAN-.. Rv.; 4/8 Extinction Ratio and ow nalty AVALABLE Backgound Extinction atio is an impotant paamt includd in th spcifications of most fib-optic tanscivs. h pupos of this application
Exam 2 Solutions. Jonathan Turner 4/2/2012. CS 542 Advanced Data Structures and Algorithms
 CS 542 Avn Dt Stutu n Alotm Exm 2 Soluton Jontn Tun 4/2/202. (5 ont) Con n oton on t tton t tutu n w t n t 2 no. Wt t mllt num o no tt t tton t tutu oul ontn. Exln you nw. Sn n mut n you o u t n t, t n
CS 542 Avn Dt Stutu n Alotm Exm 2 Soluton Jontn Tun 4/2/202. (5 ont) Con n oton on t tton t tutu n w t n t 2 no. Wt t mllt num o no tt t tton t tutu oul ontn. Exln you nw. Sn n mut n you o u t n t, t n
K E L LY T H O M P S O N
 K E L LY T H O M P S O N S E A O LO G Y C R E ATO R, F O U N D E R, A N D PA R T N E R K e l l y T h o m p s o n i s t h e c r e a t o r, f o u n d e r, a n d p a r t n e r o f S e a o l o g y, a n e x
K E L LY T H O M P S O N S E A O LO G Y C R E ATO R, F O U N D E R, A N D PA R T N E R K e l l y T h o m p s o n i s t h e c r e a t o r, f o u n d e r, a n d p a r t n e r o f S e a o l o g y, a n e x
International Journal on Recent and Innovation Trends in Computing and Communication ISSN: Volume: 2 Issue:
 Intnational Jounal on Rnt and Innovation Tnds in Computing and Communiation ISSN: 2321-8169 Volum: 2 Issu: 6 1554 1559 Modl Rfn Adaptiv Systm (MRAS) Basd Spd Snsolss Vto Contol of Indution Moto Div P N
Intnational Jounal on Rnt and Innovation Tnds in Computing and Communiation ISSN: 2321-8169 Volum: 2 Issu: 6 1554 1559 Modl Rfn Adaptiv Systm (MRAS) Basd Spd Snsolss Vto Contol of Indution Moto Div P N
Advanced Queueing Theory. M/G/1 Queueing Systems
 Advand Quung Thory Ths slds ar rad by Dr. Yh Huang of Gorg Mason Unvrsy. Sudns rgsrd n Dr. Huang's ourss a GMU an ma a sngl mahn-radabl opy and prn a sngl opy of ah sld for hr own rfrn, so long as ah sld
Advand Quung Thory Ths slds ar rad by Dr. Yh Huang of Gorg Mason Unvrsy. Sudns rgsrd n Dr. Huang's ourss a GMU an ma a sngl mahn-radabl opy and prn a sngl opy of ah sld for hr own rfrn, so long as ah sld
The University of Sydney MATH 2009
 T Unvrsty o Syny MATH 2009 APH THEOY Tutorl 7 Solutons 2004 1. Lt t sonnt plnr rp sown. Drw ts ul, n t ul o t ul ( ). Sow tt s sonnt plnr rp, tn s onnt. Du tt ( ) s not somorp to. ( ) A onnt rp s on n
T Unvrsty o Syny MATH 2009 APH THEOY Tutorl 7 Solutons 2004 1. Lt t sonnt plnr rp sown. Drw ts ul, n t ul o t ul ( ). Sow tt s sonnt plnr rp, tn s onnt. Du tt ( ) s not somorp to. ( ) A onnt rp s on n
Optimum Maintenance of a System under two Types of Failure
 ntnatonal Jounal o Matals & tutual lablty Vol.4, o., Mah 6, 7-37 ntnatonal Jounal o Matals & tutual lablty Otmum Mantnan o a ystm un two ys o alu.. Baía * an M.D. Ba Datmnt o tatsts, C... Unvsty o Zaagoza,
ntnatonal Jounal o Matals & tutual lablty Vol.4, o., Mah 6, 7-37 ntnatonal Jounal o Matals & tutual lablty Otmum Mantnan o a ystm un two ys o alu.. Baía * an M.D. Ba Datmnt o tatsts, C... Unvsty o Zaagoza,
Matched Quick Switching Variable Sampling System with Quick Switching Attribute Sampling System
 Natur and Sn 9;7( g v, t al, Samlng Systm Mathd Quk Swthng Varabl Samlng Systm wth Quk Swthng Attrbut Samlng Systm Srramahandran G.V, Palanvl.M Dartmnt of Mathmats, Dr.Mahalngam Collg of Engnrng and Thnology,
Natur and Sn 9;7( g v, t al, Samlng Systm Mathd Quk Swthng Varabl Samlng Systm wth Quk Swthng Attrbut Samlng Systm Srramahandran G.V, Palanvl.M Dartmnt of Mathmats, Dr.Mahalngam Collg of Engnrng and Thnology,
Signal Circuit and Transistor Small-Signal Model
 Snal cut an anto Sall-Snal Mol Lctu not: Sc. 5 Sa & Sth 6 th E: Sc. 5.5 & 6.7 Sa & Sth 5 th E: Sc. 4.6 & 5.6 F. Najaba EE65 Wnt 0 anto pl lopnt Ba & Snal Ba Snal only Ba Snal - Ba? MOS... : : S... MOS...
Snal cut an anto Sall-Snal Mol Lctu not: Sc. 5 Sa & Sth 6 th E: Sc. 5.5 & 6.7 Sa & Sth 5 th E: Sc. 4.6 & 5.6 F. Najaba EE65 Wnt 0 anto pl lopnt Ba & Snal Ba Snal only Ba Snal - Ba? MOS... : : S... MOS...
Physics 111. Lecture 38 (Walker: ) Phase Change Latent Heat. May 6, The Three Basic Phases of Matter. Solid Liquid Gas
 Physics 111 Lctu 38 (Walk: 17.4-5) Phas Chang May 6, 2009 Lctu 38 1/26 Th Th Basic Phass of Matt Solid Liquid Gas Squnc of incasing molcul motion (and ngy) Lctu 38 2/26 If a liquid is put into a sald contain
Physics 111 Lctu 38 (Walk: 17.4-5) Phas Chang May 6, 2009 Lctu 38 1/26 Th Th Basic Phass of Matt Solid Liquid Gas Squnc of incasing molcul motion (and ngy) Lctu 38 2/26 If a liquid is put into a sald contain
Fourier transforms (Chapter 15) Fourier integrals are generalizations of Fourier series. The series representation
 Pof. D. I. Nass Phys57 (T-3) Sptmb 8, 03 Foui_Tansf_phys57_T3 Foui tansfoms (Chapt 5) Foui intgals a gnalizations of Foui sis. Th sis psntation a0 nπx nπx f ( x) = + [ an cos + bn sin ] n = of a function
Pof. D. I. Nass Phys57 (T-3) Sptmb 8, 03 Foui_Tansf_phys57_T3 Foui tansfoms (Chapt 5) Foui intgals a gnalizations of Foui sis. Th sis psntation a0 nπx nπx f ( x) = + [ an cos + bn sin ] n = of a function
CERTAIN RESULTS ON TIGHTENED-NORMAL-TIGHTENED REPETITIVE DEFERRED SAMPLING SCHEME (TNTRDSS) INDEXED THROUGH BASIC QUALITY LEVELS
 Intnatonal Rsach Jounal of Engnng and Tchnology (IRJET) -ISSN: 2395-0056 Volum: 03 Issu: 02 Fb-2016 www.jt.nt p-issn: 2395-0072 CERTAIN RESULTS ON TIGHTENED-NORMAL-TIGHTENED REPETITIVE DEFERRED SAMPLING
Intnatonal Rsach Jounal of Engnng and Tchnology (IRJET) -ISSN: 2395-0056 Volum: 03 Issu: 02 Fb-2016 www.jt.nt p-issn: 2395-0072 CERTAIN RESULTS ON TIGHTENED-NORMAL-TIGHTENED REPETITIVE DEFERRED SAMPLING
Handout 30. Optical Processes in Solids and the Dielectric Constant
 Haut Otal Sl a th Dlt Ctat I th ltu yu wll la: La ut Ka-Kg lat Dlt tat l Itba a Itaba tbut t th lt tat l C 47 Sg 9 Faha Raa Cll Uty Chag Dl, Dl Mt, a lazat Dty A hag l t a gat a a t hag aat by ta: Q Q
Haut Otal Sl a th Dlt Ctat I th ltu yu wll la: La ut Ka-Kg lat Dlt tat l Itba a Itaba tbut t th lt tat l C 47 Sg 9 Faha Raa Cll Uty Chag Dl, Dl Mt, a lazat Dty A hag l t a gat a a t hag aat by ta: Q Q
E F. and H v. or A r and F r are dual of each other.
 A Duality Thom: Consid th following quations as an xampl = A = F μ ε H A E A = jωa j ωμε A + β A = μ J μ A x y, z = J, y, z 4π E F ( A = jω F j ( F j β H F ωμε F + β F = ε M jβ ε F x, y, z = M, y, z 4π
A Duality Thom: Consid th following quations as an xampl = A = F μ ε H A E A = jωa j ωμε A + β A = μ J μ A x y, z = J, y, z 4π E F ( A = jω F j ( F j β H F ωμε F + β F = ε M jβ ε F x, y, z = M, y, z 4π
ECCE-ASIA), pp ; 2014
 NAOSITE: Naaak Uvty' A Ttl Autho() Ctato Stablty ompao of IPMSM o xt EMF Tuj, Mo; Mzuak, Hoh; Ha 4 Itatoal Pow Elto ECCE-ASIA), pp.393-398; 4 Iu Dat 4 URL Rht http://hl.hal.t/69/3559 4 IEEE. Poal u of
NAOSITE: Naaak Uvty' A Ttl Autho() Ctato Stablty ompao of IPMSM o xt EMF Tuj, Mo; Mzuak, Hoh; Ha 4 Itatoal Pow Elto ECCE-ASIA), pp.393-398; 4 Iu Dat 4 URL Rht http://hl.hal.t/69/3559 4 IEEE. Poal u of
6. Introduction to Transistor Amplifiers: Concepts and Small-Signal Model
 6. ntoucton to anssto mples: oncepts an Small-Sgnal Moel Lectue notes: Sec. 5 Sea & Smth 6 th E: Sec. 5.4, 5.6 & 6.3-6.4 Sea & Smth 5 th E: Sec. 4.4, 4.6 & 5.3-5.4 EE 65, Wnte203, F. Najmaba Founaton o
6. ntoucton to anssto mples: oncepts an Small-Sgnal Moel Lectue notes: Sec. 5 Sea & Smth 6 th E: Sec. 5.4, 5.6 & 6.3-6.4 Sea & Smth 5 th E: Sec. 4.4, 4.6 & 5.3-5.4 EE 65, Wnte203, F. Najmaba Founaton o
CHAPTER 13. Exercises. E13.1 The emitter current is given by the Shockley equation:
 HPT 3 xercses 3. The emtter current s gen by the Shockley equaton: S exp VT For operaton wth, we hae exp >> S >>, and we can wrte VT S exp VT Solng for, we hae 3. 0 6ln 78.4 mv 0 0.784 5 4.86 V VT ln 4
HPT 3 xercses 3. The emtter current s gen by the Shockley equaton: S exp VT For operaton wth, we hae exp >> S >>, and we can wrte VT S exp VT Solng for, we hae 3. 0 6ln 78.4 mv 0 0.784 5 4.86 V VT ln 4
9.4 Absorption and Dispersion
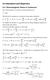 9.4 Absoon and Dsson 9.4. loagn Wavs n Conduos un dnsy n a onduo ollowng Oh s law: J Th Maxwll s uaons n a onduo lna da should b: ρ B B B J To sly h suaon w agu ha h hag dsaas uly n a aoso od. Fo h onnuy
9.4 Absoon and Dsson 9.4. loagn Wavs n Conduos un dnsy n a onduo ollowng Oh s law: J Th Maxwll s uaons n a onduo lna da should b: ρ B B B J To sly h suaon w agu ha h hag dsaas uly n a aoso od. Fo h onnuy
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
Economics 600: August, 2007 Dynamic Part: Problem Set 5. Problems on Differential Equations and Continuous Time Optimization
 THE UNIVERSITY OF MARYLAND COLLEGE PARK, MARYLAND Economcs 600: August, 007 Dynamc Part: Problm St 5 Problms on Dffrntal Equatons and Contnuous Tm Optmzaton Quston Solv th followng two dffrntal quatons.
THE UNIVERSITY OF MARYLAND COLLEGE PARK, MARYLAND Economcs 600: August, 007 Dynamc Part: Problm St 5 Problms on Dffrntal Equatons and Contnuous Tm Optmzaton Quston Solv th followng two dffrntal quatons.
GTAP Eleventh Annual Conference, 2008 "Future of Global Economy" Helsinki
 GTAP Elvth Aual Cof, 28 "Futu of Global Eooy" lsk SAM laboato as a ultobtv austt pobl Casao Maqu Laa Pñat Dpto Aálss Eoóo Aplao Uvsa Las Palas Ga Caaa (Spa aqu@aa.ulpg.s Dolos R. Satos-Pñat Dpto Métoos
GTAP Elvth Aual Cof, 28 "Futu of Global Eooy" lsk SAM laboato as a ultobtv austt pobl Casao Maqu Laa Pñat Dpto Aálss Eoóo Aplao Uvsa Las Palas Ga Caaa (Spa aqu@aa.ulpg.s Dolos R. Satos-Pñat Dpto Métoos
The Random Phase Approximation:
 Th Random Phas Appoxmaton: Elctolyts, Polym Solutons and Polylctolyts I. Why chagd systms a so mpotant: thy a wat solubl. A. bology B. nvonmntally-fndly polym pocssng II. Elctolyt solutons standad dvaton
Th Random Phas Appoxmaton: Elctolyts, Polym Solutons and Polylctolyts I. Why chagd systms a so mpotant: thy a wat solubl. A. bology B. nvonmntally-fndly polym pocssng II. Elctolyt solutons standad dvaton
Formula overview. Halit Eroglu, 04/2014 With the base formula the following fundamental constants and significant physical parameters were derived.
 Foula ovviw Halit Eolu, 0/0 With th bas foula th followin fundantal onstants and sinifiant physial paats w divd. aiabl usd: Spd of liht G Gavitational onstant h lank onstant α Fin stutu onstant h dud lank
Foula ovviw Halit Eolu, 0/0 With th bas foula th followin fundantal onstants and sinifiant physial paats w divd. aiabl usd: Spd of liht G Gavitational onstant h lank onstant α Fin stutu onstant h dud lank
Bethe-Salpeter Equation Green s Function and the Bethe-Salpeter Equation for Effective Interaction in the Ladder Approximation
 Bh-Salp Equaon n s Funcon and h Bh-Salp Equaon fo Effcv Inacon n h Ladd Appoxmaon Csa A. Z. Vasconcllos Insuo d Físca-UFRS - upo: Físca d Hadons Sngl-Pacl Popagao. Dagam xpanson of popagao. W consd as
Bh-Salp Equaon n s Funcon and h Bh-Salp Equaon fo Effcv Inacon n h Ladd Appoxmaon Csa A. Z. Vasconcllos Insuo d Físca-UFRS - upo: Físca d Hadons Sngl-Pacl Popagao. Dagam xpanson of popagao. W consd as
Week 11: Differential Amplifiers
 ELE 0A Electronc rcuts Week : Dfferental Amplfers Lecture - Large sgnal analyss Topcs to coer A analyss Half-crcut analyss eadng Assgnment: hap 5.-5.8 of Jaeger and Blalock or hap 7. - 7.3, of Sedra and
ELE 0A Electronc rcuts Week : Dfferental Amplfers Lecture - Large sgnal analyss Topcs to coer A analyss Half-crcut analyss eadng Assgnment: hap 5.-5.8 of Jaeger and Blalock or hap 7. - 7.3, of Sedra and
SHT 1 OF 3 SHT 2 AND 3 ARE -A- SIZE
 0 SH NO TYP O MOL NXT SSMLY QTY PT NUM SIPTION O MTIL ITM 00 MIN ION SOL SI K-O ION SOL SI X X 0 Y U T 0 U OM O SSY 0-0-0 V SHM 0-0-00 U U 0 O J X U 0 0 X S TIL V T 0 V U U J L U L MH U U V U0 0 U U U
0 SH NO TYP O MOL NXT SSMLY QTY PT NUM SIPTION O MTIL ITM 00 MIN ION SOL SI K-O ION SOL SI X X 0 Y U T 0 U OM O SSY 0-0-0 V SHM 0-0-00 U U 0 O J X U 0 0 X S TIL V T 0 V U U J L U L MH U U V U0 0 U U U
Unit 3: Transistor at Low Frequencies
 Unt 3: Tansst at Lw Fquncs JT Tansst Mdlng mdl s an qualnt ccut that psnts th chaactstcs f th tansst. mdl uss ccut lmnts that appxmat th ha f th tansst. Th a tw mdls cmmnly usd n small sgnal analyss f
Unt 3: Tansst at Lw Fquncs JT Tansst Mdlng mdl s an qualnt ccut that psnts th chaactstcs f th tansst. mdl uss ccut lmnts that appxmat th ha f th tansst. Th a tw mdls cmmnly usd n small sgnal analyss f
SCALARS AND VECTORS All physical quantities in engineering mechanics are measured using either scalars or vectors.
 SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
EE750 Advanced Engineering Electromagnetics Lecture 17
 EE75 Avan Engnrng Eltromagnt Ltur 7 D EM W onr a D ffrntal quaton of th form α α β f ut to p on Γ α α. n γ q on Γ whr Γ Γ Γ th ontour nlong th oman an n th unt outwar normal ot that th ounar onton ma a
EE75 Avan Engnrng Eltromagnt Ltur 7 D EM W onr a D ffrntal quaton of th form α α β f ut to p on Γ α α. n γ q on Γ whr Γ Γ Γ th ontour nlong th oman an n th unt outwar normal ot that th ounar onton ma a
FEATURES Support multi-language OSD. PM70Support IR remote control. System auto recovery after power reconnected. Support daylight saving function
 onsider it secured T 16 H PG-4 TNLN V FTU upport multi-language P70upport remote control ystem auto recovery after power reconnected upport remote control, PTZ camera operations through -485, and PTZ Hot
onsider it secured T 16 H PG-4 TNLN V FTU upport multi-language P70upport remote control ystem auto recovery after power reconnected upport remote control, PTZ camera operations through -485, and PTZ Hot
CHAPTER IV RESULTS. Grade One Test Results. The first graders took two different sets of pretests and posttests, one at the first
 33 CHAPTER IV RESULTS Gad On Tst Rsults Th fist gads tk tw diffnt sts f ptsts and psttsts, n at th fist gad lvl and n at th snd gad lvl. As displayd n Figu 4.1, n th fist gad lvl ptst th tatmnt gup had
33 CHAPTER IV RESULTS Gad On Tst Rsults Th fist gads tk tw diffnt sts f ptsts and psttsts, n at th fist gad lvl and n at th snd gad lvl. As displayd n Figu 4.1, n th fist gad lvl ptst th tatmnt gup had
A New Bargaining Game Model for Measuring Performance of Two-Stage Network Structures
 Int. J. Rsach n Inustal Engnng, pp. 7-39 Volu, Nub, 0 Intnatonal Jounal of Rsach n Inustal Engnng ounal hopag: www.nvlscnc.co/nx.php/ A Nw Baganng Ga Mol fo Masung Pfoanc of Two-tag Ntwok tuctus F. Hossnzah
Int. J. Rsach n Inustal Engnng, pp. 7-39 Volu, Nub, 0 Intnatonal Jounal of Rsach n Inustal Engnng ounal hopag: www.nvlscnc.co/nx.php/ A Nw Baganng Ga Mol fo Masung Pfoanc of Two-tag Ntwok tuctus F. Hossnzah
Divided. diamonds. Mimic the look of facets in a bracelet that s deceptively deep RIGHT-ANGLE WEAVE. designed by Peggy Brinkman Matteliano
 RIGHT-ANGLE WEAVE Dv mons Mm t look o ts n rlt tt s ptvly p sn y Py Brnkmn Mttlno Dv your mons nto trnls o two or our olors. FCT-SCON0216_BNB66 2012 Klm Pulsn Co. Ts mtrl my not rprou n ny orm wtout prmsson
RIGHT-ANGLE WEAVE Dv mons Mm t look o ts n rlt tt s ptvly p sn y Py Brnkmn Mttlno Dv your mons nto trnls o two or our olors. FCT-SCON0216_BNB66 2012 Klm Pulsn Co. Ts mtrl my not rprou n ny orm wtout prmsson
0# E % D 0 D - C AB
 5-70,- 393 %& 44 03& / / %0& / / 405 4 90//7-90/8/3 ) /7 0% 0 - @AB 5? 07 5 >0< 98 % =< < ; 98 07 &? % B % - G %0A 0@ % F0 % 08 403 08 M3 @ K0 J? F0 4< - G @ I 0 QR 4 @ 8 >5 5 % 08 OF0 80P 0O 0N 0@ 80SP
5-70,- 393 %& 44 03& / / %0& / / 405 4 90//7-90/8/3 ) /7 0% 0 - @AB 5? 07 5 >0< 98 % =< < ; 98 07 &? % B % - G %0A 0@ % F0 % 08 403 08 M3 @ K0 J? F0 4< - G @ I 0 QR 4 @ 8 >5 5 % 08 OF0 80P 0O 0N 0@ 80SP
Grid Transformations for CFD Calculations
 Coll of Ennn an Comput Scnc Mchancal Ennn Dpatmnt ME 69 Computatonal lu Dnamcs Spn Tct: 5754 Instuct: La Catto Intoucton G Tansfmatons f CD Calculatons W want to ca out ou CD analss n altnatv conat sstms.
Coll of Ennn an Comput Scnc Mchancal Ennn Dpatmnt ME 69 Computatonal lu Dnamcs Spn Tct: 5754 Instuct: La Catto Intoucton G Tansfmatons f CD Calculatons W want to ca out ou CD analss n altnatv conat sstms.
PH672 WINTER Problem Set #1. Hint: The tight-binding band function for an fcc crystal is [ ] (a) The tight-binding Hamiltonian (8.
![PH672 WINTER Problem Set #1. Hint: The tight-binding band function for an fcc crystal is [ ] (a) The tight-binding Hamiltonian (8. PH672 WINTER Problem Set #1. Hint: The tight-binding band function for an fcc crystal is [ ] (a) The tight-binding Hamiltonian (8.](/thumbs/76/73289053.jpg) PH67 WINTER 5 Poblm St # Mad, hapt, poblm # 6 Hint: Th tight-binding band function fo an fcc cstal is ( U t cos( a / cos( a / cos( a / cos( a / cos( a / cos( a / ε [ ] (a Th tight-binding Hamiltonian (85
PH67 WINTER 5 Poblm St # Mad, hapt, poblm # 6 Hint: Th tight-binding band function fo an fcc cstal is ( U t cos( a / cos( a / cos( a / cos( a / cos( a / cos( a / ε [ ] (a Th tight-binding Hamiltonian (85
ESCI 341 Atmospheric Thermodynamics Lesson 16 Pseudoadiabatic Processes Dr. DeCaria
 ESCI 34 Atmohi hmoynami on 6 Puoaiabati Po D DCaia fn: Man, A an FE obitaill, 97: A omaion of th uialnt otntial tmatu an th tati ngy, J Atmo Si, 7, 37-39 Btt, AK, 974: Futh ommnt on A omaion of th uialnt
ESCI 34 Atmohi hmoynami on 6 Puoaiabati Po D DCaia fn: Man, A an FE obitaill, 97: A omaion of th uialnt otntial tmatu an th tati ngy, J Atmo Si, 7, 37-39 Btt, AK, 974: Futh ommnt on A omaion of th uialnt
Q Q N, V, e, Quantum Statistics for Ideal Gas. The Canonical Ensemble 10/12/2009. Physics 4362, Lecture #19. Dr. Peter Kroll
 Quantum Statistics fo Idal Gas Physics 436 Lctu #9 D. Pt Koll Assistant Pofsso Dpatmnt of Chmisty & Biochmisty Univsity of Txas Alington Will psnt a lctu ntitld: Squzing Matt and Pdicting w Compounds:
Quantum Statistics fo Idal Gas Physics 436 Lctu #9 D. Pt Koll Assistant Pofsso Dpatmnt of Chmisty & Biochmisty Univsity of Txas Alington Will psnt a lctu ntitld: Squzing Matt and Pdicting w Compounds:
SHELL CANADA PIPING AND INSTRUMENT DIAGRAM UNIT REGENERATION/COMMON LEAN / RICH AMINE EXCHANGER QUEST CCS PROJECT QUEST CCS PROJECT CONSTRUCTION
 ). M 5 34 34..... / / / /......... / / / / / / / / / /. /.... 66...... / /... SSU T SPTON SHLL N NOTS: G Y K P S QUST S POJT M P PM LNT SL: NON NG N NSTUMNT GM QUST S POJT SHLL WG NO.:. 46...4.. 46. L:\\:\5\WNGS\O\46\46..pid
). M 5 34 34..... / / / /......... / / / / / / / / / /. /.... 66...... / /... SSU T SPTON SHLL N NOTS: G Y K P S QUST S POJT M P PM LNT SL: NON NG N NSTUMNT GM QUST S POJT SHLL WG NO.:. 46...4.. 46. L:\\:\5\WNGS\O\46\46..pid
(8) Gain Stage and Simple Output Stage
 EEEB23 Electoncs Analyss & Desgn (8) Gan Stage and Smple Output Stage Leanng Outcome Able to: Analyze an example of a gan stage and output stage of a multstage amplfe. efeence: Neamen, Chapte 11 8.0) ntoducton
EEEB23 Electoncs Analyss & Desgn (8) Gan Stage and Smple Output Stage Leanng Outcome Able to: Analyze an example of a gan stage and output stage of a multstage amplfe. efeence: Neamen, Chapte 11 8.0) ntoducton
ANALOG ELECTRONICS I. Transistor Amplifiers DR NORLAILI MOHD NOH
 241 ANALO LTRONI I Lectures 2&3 ngle Transstor Amplfers R NORLAILI MOH NOH 3.3 Basc ngle-transstor Amplfer tages 3 dfferent confguratons : 1. ommon-emtter ommon-source Ib B R I d I c o R o gnal appled
241 ANALO LTRONI I Lectures 2&3 ngle Transstor Amplfers R NORLAILI MOH NOH 3.3 Basc ngle-transstor Amplfer tages 3 dfferent confguratons : 1. ommon-emtter ommon-source Ib B R I d I c o R o gnal appled
An Interactive Intuitionistic Fuzzy Non-Linear Fractional Programming Problem
 o ou of pp gg R SSN - Voum Num pp - R uo p:wwwpuoom v uo uzz No- o ogmmg om zz m pm of Mm u of S w v o gp O : --- T pp vop w v mo fo ovg o fo pogmmg pom o uo fuzz o v mo f o m M pf g of - v m-m pom ov
o ou of pp gg R SSN - Voum Num pp - R uo p:wwwpuoom v uo uzz No- o ogmmg om zz m pm of Mm u of S w v o gp O : --- T pp vop w v mo fo ovg o fo pogmmg pom o uo fuzz o v mo f o m M pf g of - v m-m pom ov
Chapter 5 Transmission Lines
 ap 5 ao 5- aacc of ao ao l: a o cou ca cu o uppo a M av c M o qua-m o. Fo M o a H M H a M a µ M. cu a M av av ff caacc. A M av popaa o ff lcc a paal flco a paal ao ll occu. A ob follo ul. ll la: p a β
ap 5 ao 5- aacc of ao ao l: a o cou ca cu o uppo a M av c M o qua-m o. Fo M o a H M H a M a µ M. cu a M av av ff caacc. A M av popaa o ff lcc a paal flco a paal ao ll occu. A ob follo ul. ll la: p a β
19 The Born-Oppenheimer Approximation
 9 The Bon-Oppenheme Appoxmaton The full nonelatvstc Hamltonan fo a molecule s gven by (n a.u.) Ĥ = A M A A A, Z A + A + >j j (883) Lets ewte the Hamltonan to emphasze the goal as Ĥ = + A A A, >j j M A
9 The Bon-Oppenheme Appoxmaton The full nonelatvstc Hamltonan fo a molecule s gven by (n a.u.) Ĥ = A M A A A, Z A + A + >j j (883) Lets ewte the Hamltonan to emphasze the goal as Ĥ = + A A A, >j j M A
4/12/2018. PHY 712 Electrodynamics 9-9:50 AM MWF Olin 105. Plan for Lecture 34: Review radiating systems
 PHY 7 Eodynams 9-9:5 M MWF On 5 Pan o u : Rvw adang sysms Souon o Maxw s quaons wh sous Tm pod sous Examps //8 PHY 7 Spng 8 -- u //8 PHY 7 Spng 8 -- u Gna vw -- SI uns mosop o vauum om ( P M ): Couombs
PHY 7 Eodynams 9-9:5 M MWF On 5 Pan o u : Rvw adang sysms Souon o Maxw s quaons wh sous Tm pod sous Examps //8 PHY 7 Spng 8 -- u //8 PHY 7 Spng 8 -- u Gna vw -- SI uns mosop o vauum om ( P M ): Couombs
EFFICIENCY OPTIMIZATION OF INDUCTION MOTOR DRIVES
 Naučno-stučn spozju Engtska fkasnost ENEF 03, Banja Luka,. 3. novba 03. gon Ra po pozvu EFFICIENCY OPIMIZAION OF INUCION MOOR RIVES Banko Blanuša, Faculty of Elctcal Engnng, Rpublka Spska, Bosna an Hzgovna
Naučno-stučn spozju Engtska fkasnost ENEF 03, Banja Luka,. 3. novba 03. gon Ra po pozvu EFFICIENCY OPIMIZAION OF INUCION MOOR RIVES Banko Blanuša, Faculty of Elctcal Engnng, Rpublka Spska, Bosna an Hzgovna
Q Q N, V, e, Quantum Statistics for Ideal Gas and Black Body Radiation. The Canonical Ensemble
 Quantum Statistics fo Idal Gas and Black Body Radiation Physics 436 Lctu #0 Th Canonical Ensmbl Ei Q Q N V p i 1 Q E i i Bos-Einstin Statistics Paticls with intg valu of spin... qi... q j...... q j...
Quantum Statistics fo Idal Gas and Black Body Radiation Physics 436 Lctu #0 Th Canonical Ensmbl Ei Q Q N V p i 1 Q E i i Bos-Einstin Statistics Paticls with intg valu of spin... qi... q j...... q j...
T h e C e n t r e f o r U l t r a h i g h b a n d w i d t h D e v i c e s f o r O p t i c a l S y s t e m s ( C U D O S )
 T h f U h g h b w h D v f O p S y ( U D O S ) A N N U A R E P O R T 2006 54 Dg 2006 UDOS b g p p g f f b wh h A y. Nw hf Ivg UDOS gh w D A Mh f h M M Thgy RMIT Uvy hf Ivg. Wh RMIT w fy j h b 2008, A y
T h f U h g h b w h D v f O p S y ( U D O S ) A N N U A R E P O R T 2006 54 Dg 2006 UDOS b g p p g f f b wh h A y. Nw hf Ivg UDOS gh w D A Mh f h M M Thgy RMIT Uvy hf Ivg. Wh RMIT w fy j h b 2008, A y
Controller Design for Networked Control Systems in Multiple-packet Transmission with Random Delays
 Appled Mehans and Materals Onlne: 03-0- ISSN: 66-748, Vols. 78-80, pp 60-604 do:0.408/www.sentf.net/amm.78-80.60 03 rans eh Publatons, Swtzerland H Controller Desgn for Networed Control Systems n Multple-paet
Appled Mehans and Materals Onlne: 03-0- ISSN: 66-748, Vols. 78-80, pp 60-604 do:0.408/www.sentf.net/amm.78-80.60 03 rans eh Publatons, Swtzerland H Controller Desgn for Networed Control Systems n Multple-paet
