Applied Linear Algebra
|
|
|
- Lindsey Simon
- 5 years ago
- Views:
Transcription
1 Applied Linear Algebra OTTO BRETSCHER Chapter 4 Linear Spaces Chia-Hui Chang chia@csie.ncu.edu.tw National Central University, Taiwan October 28, 2002
2 4.1 Introduction to Linear Systems EXAMPLE 1 Consider the differential equation(de) f (x) + f(x) = 0, orf (x) = f(x) We are asked to find all functions f(x) whose second derivative is the negative of the function itself. Recalling rules from your introductory calculus class, you will (hopefully) note that sin(x) and cos(x) are solutions of this DE. Can you find any other solutions? 1
3 Definition Linear spaces A linear space V is a set endowed with (1) a rule for addition (if f and g are in V, then so is f + g) and (2) a rule for scalar multiplication (if f is in V and k in R, then kf is in V) such that these operations satisfy the following eight rules (for all f, g, h in V and all c, k in R): 1. (f + g) + h = f + (g + h) 2. f + g = g + f 3. There is a neutral element n in V such that f + n = f, for all f in V. This n is unique and denoted by 0. 2
4 4. For each f in V there is a g in V such that f + g = 0. this g is unique and denoted by ( f) 5. k(f + g) = kf + kg 6. (c + k)f = cf + kf 7. c(kf) = (ck)f 8. 1f = f
5 EXAMPLE 2 In R n, the prototype linear space, the neutral element is the zero vector, 0. EXAMPLE 3 Let F (R,R) be the set of all functions from R to R (see Example 1), with the operations and (f + g)(x) = f(x) + g(x) (kf)(x) = kf(x) Then, F(R,R) is a linear space. The neutral element is the zero function, f(x) = 0 for all x. EXAMPLE 4 If addition and scalar multiplication are given as in Definition 1.3.9, then R m n, the set of all m n matrices, is a linear space. The neutral element is the zero matrix whose entries are all zero. 3
6 EXAMPLE 5 The set of all infinite sequence of real numbers is a linear space, where addition and scalar multiplication are defined term by term: (x 0, x 1, x 2,...) + (y 0, y 1, y 2,...) = (x 0 + y 0, x 1 + y 1, x 2 + y 2,...) k(x 0, x 1, x 2,...) = (kx 0, kx 1, kx 2,...). The neutral element is the sequence (0, 0, 0,...) EXAMPLE 6 The linear equation in three unknowns, ax + by + cz = d, where a, b, c, and d are constants, from a linear space. The neutral element is the equation 0 = 0 (with a = b = c = d = 0). 4
7 Linear Combination We say that an element f of a linear space is a linear combination of the elements f 1, f 2,..., f n if f = c 1 f 1 + c 2 f c n f n for some scalars c 1, c 2,, c n. EXAMPLE Let A =. Show that A = a linear combination of A and I is Solution We have to find scalars c 1 and c 2 such that A 2 = c 1 A + c 2 I 2, or A 2 = = c c
8 Definition Subspaces A subspace W of a linear space V is called a subspace of V if 1. W contains the neutral element 0 of V 2. W is closed under addition (if f and g are in W, then so is f + g). 3. W is closed under scalar multiplication (if f is in W and k is a scalar, then kf is in W). We can summarize parts (2) and (3) by saying that W is closed under linear combinations. 6
9 EXAMPLE 10 Show that the polynomials of degree 2, of the form f(x) = a + bx + cx 2, are a subspace W of the space F(R,R) of all functions from R to R. EXAMPLE 11 Show that the differentiable functions form a subspace W of F(R,R) EXAMPLE 12 Here are three more subspaces of F(R,R): 1. C, the smooth functions, that is, functions we can differentiate as many times as we want. This subspace contains all polynomials, exponential functions, sin(x), and cos(x), for example. 2. P, the set of all polynomials. 3. P n, the set of all polynomials of degree n 7
10 EXAMPLE 13 Show that the matrices B that commute with 0 1 A = form a subspace of R Solution (a) The zero matrix 0 commutes with A. (b) If matrices B 1 and B 2 commute with A, then so does matrix B 1 + B 2. (c) If B commutes with A, then so does kb. EXAMPLE 14 Consider the set W of all noninvertible 2 2 matrices. Is W a subsequence of R 2 2? Solution =
11 Definition Span, linear independence, basis, coordinates Consider the elements f 1, f 2,..., f n of a linear space V. 1. We say that f 1, f 2,..., f n span V if every f in V can be expressed as a linear combination of f 1, f 2,..., f n. 2. We say that f 1, f 2,..., f n are (linearly) independent if the equation c 1 f 1 + c 2 f c n f n = 0 has only the trivial solution c 1 = c 2 = = c n = 0. 9
12 3. We say that elements f 1, f 2,..., f n are a basis of V if they span V and are independent. This means that every f in V can be written uniquely as a linear combination f = c 1 f 1 + c 2 f c n f n. The coefficients c 1, c 2,..., c n are called the coordinates of f with respect to the basis f 1, f 2,..., f n. Fact Dimension If a linear space V has a basis with n elements, then all other bases of V consist of n elements as well. We say that n is the dimension of V: dim(v ) = n.
13 EXAMPLE 15 Find a basis of V = R 2 2 and thus determine dim(v ). Solution We can write any 2 2 matrix a b c d = a b a b c d +c as: +d EXAMPLE 16 Find a basis of P 2, the space of all polynomials of degree 2, and thus determine the dimension of P 2. Solution We can write any polynomial f(x) of degree 2 uniquely as: f(x) = a + bx + cx 2 = a 1 + b x + c x 2 10
14 EXAMPLE 17 Find a basis of the space V of all matrices B 0 1 that commute with A =. 2 3 Solution a b We need to find all matrices B = c d a b a b that =. c d c d 2b a + 3b 2d c + 3d = c 2a + 3c d 2b + 3d such c = 2b, d = a + 3b So a typical matrix B in V is of the form a b B = = a + b 2b a + 3b = ai 2 + ba The matrices I 2 and A form a basis of V, so that dim(v)=2. 11
15 EXAMPLE 19 Let f 1, f 2,..., f n be polynomials. Explain why these polynomials do not span the space P of all polynomials. Solution Let N be the maximum of the degrees of these n polynomials. Then all linear combinations of f 1, f 2,..., f n are in P N, the space of the polynomials of degree N. Any polynomial of higher degree, such as f(x) = x N+1, will not be in the span of f 1, f 2,..., f n. This implies that the space P of all polynomials does not have a finite basis f 1, f 2,..., f n. 12
16 Definition Finite-dimensional linear spaces A linear spaces V is called finite dimensional if it has a (finite) basis f 1, f 2,..., f n, so that we can define its dimension dim(v ) = n. (See Definition ) Otherwise, the space is called inf inite dimensional. Exercises 4.1: 3, 5, 7, 8, 17, 18, 20, 33, 35 13
17 *EXAMPLE 7 Consider the plane with a point designated as the origin, O, but without a coordinate system (the coordinate-free plane). A geometric vector v in this plane is an arrow (a directed line segment) with its tail at the origin, as shown in Figure 1. The sum v + w of vectors v and w is defined by means of a parallelogram, as illustration in Figure 2. If k is a positive scalar, then vector k v points in the same direction as v, but k v is k times as long as v ; see Figure 3. 14
18 If k is negative, then k v points in the opposite direction, and it is k times as long as v ; see Figure 4. The geometric vectors in the plane with these operations forms a linear space. The neutral element is the zero vector 0, with tail and head at the origin. By introducing a coordinate system, we can identify the plane of geometric vectors with R 2 ; this was the great idea of Descartes Analytic Geometry. In Section 4.3, we will study this idea more systematically.
19 *EXAMPLE 8 Let C be the set of the complex numbers. We trust that you have at least a fleeting acquaintance with complex numbers. Without attempting a definition, we recall that a complex number can be expressed as z = a + bi, where a and b are real numbers. Addition of complex numbers is defined in a natural way, by the rule (a + bi) + (c + di) = (a + c) + i(b + d). If k is a real scalar, we define k(a + bi) = ka + i(kb). There is also a (less natural) rule for the multiplication of complex numbers, but we are not concerned with this operation here. The complex numbers C with the two operations just given form a linear space; the neutral element is the complex number 0 = 0 + 0i. 15
20 *Fact Linear differential equations The solutions of the DE f (x) + af (x) + bf(x) = 0 where a and b are constants, form a two-dimensional subspace of the space C of smooth functions. More generally, the solutions of the DE f (n) (x) + a n 1 f n 1 (x) + + a 1 f (x) + a 0 f(x) (where the a i are constants) form an n-dimensional subspace of C. A DE of this is called an nthorder linear differential equation. Fact will be proven in Section
21 *EXAMPLE 18 Find all solutions of the DE f (x) + f (x) 6f(x) = 0. (Hint: Find all exponential functions f(x) = e kx that solve the DE) An exponential function f(x) = e kx solves the DE if k = 2 or k = 3. Since k 2 e kx + ke kx 6e kx = (k 2 + k 6)e kx = (k + 3)(k 2)e kx = 0 According to Fact 4.1.5, the solution space V is two-dimensional. Thus, the two exponential functions e 2x and e 3x form a basis of V, and all solutions are of the form f(x) = c 1 e 2x + c 2 e 3x 17
Vector Spaces ปร ภ ม เวกเตอร
 Vector Spaces ปร ภ ม เวกเตอร 1 5.1 Real Vector Spaces ปร ภ ม เวกเตอร ของจ านวนจร ง Vector Space Axioms (1/2) Let V be an arbitrary nonempty set of objects on which two operations are defined, addition
Vector Spaces ปร ภ ม เวกเตอร 1 5.1 Real Vector Spaces ปร ภ ม เวกเตอร ของจ านวนจร ง Vector Space Axioms (1/2) Let V be an arbitrary nonempty set of objects on which two operations are defined, addition
Definition 1. A set V is a vector space over the scalar field F {R, C} iff. there are two operations defined on V, called vector addition
 6 Vector Spaces with Inned Product Basis and Dimension Section Objective(s): Vector Spaces and Subspaces Linear (In)dependence Basis and Dimension Inner Product 6 Vector Spaces and Subspaces Definition
6 Vector Spaces with Inned Product Basis and Dimension Section Objective(s): Vector Spaces and Subspaces Linear (In)dependence Basis and Dimension Inner Product 6 Vector Spaces and Subspaces Definition
Chapter 1 Vector Spaces
 Chapter 1 Vector Spaces Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 110 Linear Algebra Vector Spaces Definition A vector space V over a field
Chapter 1 Vector Spaces Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 110 Linear Algebra Vector Spaces Definition A vector space V over a field
EXERCISE SET 5.1. = (kx + kx + k, ky + ky + k ) = (kx + kx + 1, ky + ky + 1) = ((k + )x + 1, (k + )y + 1)
 EXERCISE SET 5. 6. The pair (, 2) is in the set but the pair ( )(, 2) = (, 2) is not because the first component is negative; hence Axiom 6 fails. Axiom 5 also fails. 8. Axioms, 2, 3, 6, 9, and are easily
EXERCISE SET 5. 6. The pair (, 2) is in the set but the pair ( )(, 2) = (, 2) is not because the first component is negative; hence Axiom 6 fails. Axiom 5 also fails. 8. Axioms, 2, 3, 6, 9, and are easily
Vector Spaces ปร ภ ม เวกเตอร
 Vector Spaces ปร ภ ม เวกเตอร 5.1 Real Vector Spaces ปร ภ ม เวกเตอร ของจ านวนจร ง Vector Space Axioms (1/2) Let V be an arbitrary nonempty set of objects on which two operations are defined, addition and
Vector Spaces ปร ภ ม เวกเตอร 5.1 Real Vector Spaces ปร ภ ม เวกเตอร ของจ านวนจร ง Vector Space Axioms (1/2) Let V be an arbitrary nonempty set of objects on which two operations are defined, addition and
CSL361 Problem set 4: Basic linear algebra
 CSL361 Problem set 4: Basic linear algebra February 21, 2017 [Note:] If the numerical matrix computations turn out to be tedious, you may use the function rref in Matlab. 1 Row-reduced echelon matrices
CSL361 Problem set 4: Basic linear algebra February 21, 2017 [Note:] If the numerical matrix computations turn out to be tedious, you may use the function rref in Matlab. 1 Row-reduced echelon matrices
Linear Algebra Practice Problems
 Linear Algebra Practice Problems Math 24 Calculus III Summer 25, Session II. Determine whether the given set is a vector space. If not, give at least one axiom that is not satisfied. Unless otherwise stated,
Linear Algebra Practice Problems Math 24 Calculus III Summer 25, Session II. Determine whether the given set is a vector space. If not, give at least one axiom that is not satisfied. Unless otherwise stated,
2 so Q[ 2] is closed under both additive and multiplicative inverses. a 2 2b 2 + b
![2 so Q[ 2] is closed under both additive and multiplicative inverses. a 2 2b 2 + b 2 so Q[ 2] is closed under both additive and multiplicative inverses. a 2 2b 2 + b](/thumbs/72/66553010.jpg) . FINITE-DIMENSIONAL VECTOR SPACES.. Fields By now you ll have acquired a fair knowledge of matrices. These are a concrete embodiment of something rather more abstract. Sometimes it is easier to use matrices,
. FINITE-DIMENSIONAL VECTOR SPACES.. Fields By now you ll have acquired a fair knowledge of matrices. These are a concrete embodiment of something rather more abstract. Sometimes it is easier to use matrices,
Math 110: Worksheet 3
 Math 110: Worksheet 3 September 13 Thursday Sept. 7: 2.1 1. Fix A M n n (F ) and define T : M n n (F ) M n n (F ) by T (B) = AB BA. (a) Show that T is a linear transformation. Let B, C M n n (F ) and a
Math 110: Worksheet 3 September 13 Thursday Sept. 7: 2.1 1. Fix A M n n (F ) and define T : M n n (F ) M n n (F ) by T (B) = AB BA. (a) Show that T is a linear transformation. Let B, C M n n (F ) and a
Math 4377/6308 Advanced Linear Algebra I Dr. Vaughn Climenhaga, PGH 651A HOMEWORK 3
 Math 4377/6308 Advanced Linear Algebra I Dr. Vaughn Climenhaga, PGH 651A Fall 2013 HOMEWORK 3 Due 4pm Wednesday, September 11. You will be graded not only on the correctness of your answers but also on
Math 4377/6308 Advanced Linear Algebra I Dr. Vaughn Climenhaga, PGH 651A Fall 2013 HOMEWORK 3 Due 4pm Wednesday, September 11. You will be graded not only on the correctness of your answers but also on
On-Line Geometric Modeling Notes VECTOR SPACES
 On-Line Geometric Modeling Notes VECTOR SPACES Kenneth I. Joy Visualization and Graphics Research Group Department of Computer Science University of California, Davis These notes give the definition of
On-Line Geometric Modeling Notes VECTOR SPACES Kenneth I. Joy Visualization and Graphics Research Group Department of Computer Science University of California, Davis These notes give the definition of
Chapter 3. Vector spaces
 Chapter 3. Vector spaces Lecture notes for MA1111 P. Karageorgis pete@maths.tcd.ie 1/22 Linear combinations Suppose that v 1,v 2,...,v n and v are vectors in R m. Definition 3.1 Linear combination We say
Chapter 3. Vector spaces Lecture notes for MA1111 P. Karageorgis pete@maths.tcd.ie 1/22 Linear combinations Suppose that v 1,v 2,...,v n and v are vectors in R m. Definition 3.1 Linear combination We say
August 23, 2017 Let us measure everything that is measurable, and make measurable everything that is not yet so. Galileo Galilei. 1.
 August 23, 2017 Let us measure everything that is measurable, and make measurable everything that is not yet so. Galileo Galilei 1. Vector spaces 1.1. Notations. x S denotes the fact that the element x
August 23, 2017 Let us measure everything that is measurable, and make measurable everything that is not yet so. Galileo Galilei 1. Vector spaces 1.1. Notations. x S denotes the fact that the element x
MTH5102 Spring 2017 HW Assignment 2: Sec. 1.3, #8, 16, 28, 31; Sec. 1.4, #5 (a), (e), (g), 10 The due date for this assignment is 1/25/17.
 MTH510 Spring 017 HW Assignment : Sec. 1. #8 16 8 1; Sec. 1.4 #5 (a (e (g 10 The due date for this assignment is 1/5/17. Sec. 1. #8. Determine whether the following sets are subspaces of the vector space
MTH510 Spring 017 HW Assignment : Sec. 1. #8 16 8 1; Sec. 1.4 #5 (a (e (g 10 The due date for this assignment is 1/5/17. Sec. 1. #8. Determine whether the following sets are subspaces of the vector space
Instructions Please answer the five problems on your own paper. These are essay questions: you should write in complete sentences.
 Instructions Please answer the five problems on your own paper. These are essay questions: you should write in complete sentences.. Recall that P 3 denotes the vector space of polynomials of degree less
Instructions Please answer the five problems on your own paper. These are essay questions: you should write in complete sentences.. Recall that P 3 denotes the vector space of polynomials of degree less
3. Vector spaces 3.1 Linear dependence and independence 3.2 Basis and dimension. 5. Extreme points and basic feasible solutions
 A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
1. Let r, s, t, v be the homogeneous relations defined on the set M = {2, 3, 4, 5, 6} by
 Seminar 1 1. Which ones of the usual symbols of addition, subtraction, multiplication and division define an operation (composition law) on the numerical sets N, Z, Q, R, C? 2. Let A = {a 1, a 2, a 3 }.
Seminar 1 1. Which ones of the usual symbols of addition, subtraction, multiplication and division define an operation (composition law) on the numerical sets N, Z, Q, R, C? 2. Let A = {a 1, a 2, a 3 }.
Linear Algebra- Final Exam Review
 Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
2.3. VECTOR SPACES 25
 2.3. VECTOR SPACES 25 2.3 Vector Spaces MATH 294 FALL 982 PRELIM # 3a 2.3. Let C[, ] denote the space of continuous functions defined on the interval [,] (i.e. f(x) is a member of C[, ] if f(x) is continuous
2.3. VECTOR SPACES 25 2.3 Vector Spaces MATH 294 FALL 982 PRELIM # 3a 2.3. Let C[, ] denote the space of continuous functions defined on the interval [,] (i.e. f(x) is a member of C[, ] if f(x) is continuous
Overview of vector calculus. Coordinate systems in space. Distance formula. (Sec. 12.1)
 Math 20C Multivariable Calculus Lecture 1 1 Coordinates in space Slide 1 Overview of vector calculus. Coordinate systems in space. Distance formula. (Sec. 12.1) Vector calculus studies derivatives and
Math 20C Multivariable Calculus Lecture 1 1 Coordinates in space Slide 1 Overview of vector calculus. Coordinate systems in space. Distance formula. (Sec. 12.1) Vector calculus studies derivatives and
Inner Product Spaces
 Inner Product Spaces Introduction Recall in the lecture on vector spaces that geometric vectors (i.e. vectors in two and three-dimensional Cartesian space have the properties of addition, subtraction,
Inner Product Spaces Introduction Recall in the lecture on vector spaces that geometric vectors (i.e. vectors in two and three-dimensional Cartesian space have the properties of addition, subtraction,
Math 601 Solutions to Homework 3
 Math 601 Solutions to Homework 3 1 Use Cramer s Rule to solve the following system of linear equations (Solve for x 1, x 2, and x 3 in terms of a, b, and c 2x 1 x 2 + 7x 3 = a 5x 1 2x 2 x 3 = b 3x 1 x
Math 601 Solutions to Homework 3 1 Use Cramer s Rule to solve the following system of linear equations (Solve for x 1, x 2, and x 3 in terms of a, b, and c 2x 1 x 2 + 7x 3 = a 5x 1 2x 2 x 3 = b 3x 1 x
Solution to Set 7, Math 2568
 Solution to Set 7, Math 568 S 5.: No. 18: Let Q be the set of all nonsingular matrices with the usual definition of addition and scalar multiplication. Show that Q is not a vector space. In particular,
Solution to Set 7, Math 568 S 5.: No. 18: Let Q be the set of all nonsingular matrices with the usual definition of addition and scalar multiplication. Show that Q is not a vector space. In particular,
Note: Every graph is a level set (why?). But not every level set is a graph. Graphs must pass the vertical line test. (Level sets may or may not.
 Curves in R : Graphs vs Level Sets Graphs (y = f(x)): The graph of f : R R is {(x, y) R y = f(x)} Example: When we say the curve y = x, we really mean: The graph of the function f(x) = x That is, we mean
Curves in R : Graphs vs Level Sets Graphs (y = f(x)): The graph of f : R R is {(x, y) R y = f(x)} Example: When we say the curve y = x, we really mean: The graph of the function f(x) = x That is, we mean
The scope of the midterm exam is up to and includes Section 2.1 in the textbook (homework sets 1-4). Below we highlight some of the important items.
 AMS 10: Review for the Midterm Exam The scope of the midterm exam is up to and includes Section 2.1 in the textbook (homework sets 1-4). Below we highlight some of the important items. Complex numbers
AMS 10: Review for the Midterm Exam The scope of the midterm exam is up to and includes Section 2.1 in the textbook (homework sets 1-4). Below we highlight some of the important items. Complex numbers
which are not all zero. The proof in the case where some vector other than combination of the other vectors in S is similar.
 It follows that S is linearly dependent since the equation is satisfied by which are not all zero. The proof in the case where some vector other than combination of the other vectors in S is similar. is
It follows that S is linearly dependent since the equation is satisfied by which are not all zero. The proof in the case where some vector other than combination of the other vectors in S is similar. is
Final A. Problem Points Score Total 100. Math115A Nadja Hempel 03/23/2017
 Final A Math115A Nadja Hempel 03/23/2017 nadja@math.ucla.edu Name: UID: Problem Points Score 1 10 2 20 3 5 4 5 5 9 6 5 7 7 8 13 9 16 10 10 Total 100 1 2 Exercise 1. (10pt) Let T : V V be a linear transformation.
Final A Math115A Nadja Hempel 03/23/2017 nadja@math.ucla.edu Name: UID: Problem Points Score 1 10 2 20 3 5 4 5 5 9 6 5 7 7 8 13 9 16 10 10 Total 100 1 2 Exercise 1. (10pt) Let T : V V be a linear transformation.
3.2 Subspace. Definition: If S is a non-empty subset of a vector space V, and S satisfies the following conditions: (i).
 . ubspace Given a vector spacev, it is possible to form another vector space by taking a subset of V and using the same operations (addition and multiplication) of V. For a set to be a vector space, it
. ubspace Given a vector spacev, it is possible to form another vector space by taking a subset of V and using the same operations (addition and multiplication) of V. For a set to be a vector space, it
Vector Spaces. (1) Every vector space V has a zero vector 0 V
 Vector Spaces 1. Vector Spaces A (real) vector space V is a set which has two operations: 1. An association of x, y V to an element x+y V. This operation is called vector addition. 2. The association of
Vector Spaces 1. Vector Spaces A (real) vector space V is a set which has two operations: 1. An association of x, y V to an element x+y V. This operation is called vector addition. 2. The association of
A matrix is a rectangular array of. objects arranged in rows and columns. The objects are called the entries. is called the size of the matrix, and
 Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
XV - Vector Spaces and Subspaces
 MATHEMATICS -NYC- Vectors and Matrices Martin Huard Fall 7 XV - Vector Spaces and Subspaces Describe the zero vector (the additive identity) for the following vector spaces 4 a) c) d) e) C, b) x, y x,
MATHEMATICS -NYC- Vectors and Matrices Martin Huard Fall 7 XV - Vector Spaces and Subspaces Describe the zero vector (the additive identity) for the following vector spaces 4 a) c) d) e) C, b) x, y x,
Contents. 2.1 Vectors in R n. Linear Algebra (part 2) : Vector Spaces (by Evan Dummit, 2017, v. 2.50) 2 Vector Spaces
 Linear Algebra (part 2) : Vector Spaces (by Evan Dummit, 2017, v 250) Contents 2 Vector Spaces 1 21 Vectors in R n 1 22 The Formal Denition of a Vector Space 4 23 Subspaces 6 24 Linear Combinations and
Linear Algebra (part 2) : Vector Spaces (by Evan Dummit, 2017, v 250) Contents 2 Vector Spaces 1 21 Vectors in R n 1 22 The Formal Denition of a Vector Space 4 23 Subspaces 6 24 Linear Combinations and
Final Exam Practice Problems Answers Math 24 Winter 2012
 Final Exam Practice Problems Answers Math 4 Winter 0 () The Jordan product of two n n matrices is defined as A B = (AB + BA), where the products inside the parentheses are standard matrix product. Is the
Final Exam Practice Problems Answers Math 4 Winter 0 () The Jordan product of two n n matrices is defined as A B = (AB + BA), where the products inside the parentheses are standard matrix product. Is the
Abstract Vector Spaces
 CHAPTER 1 Abstract Vector Spaces 1.1 Vector Spaces Let K be a field, i.e. a number system where you can add, subtract, multiply and divide. In this course we will take K to be R, C or Q. Definition 1.1.
CHAPTER 1 Abstract Vector Spaces 1.1 Vector Spaces Let K be a field, i.e. a number system where you can add, subtract, multiply and divide. In this course we will take K to be R, C or Q. Definition 1.1.
Chapter 2: Linear Independence and Bases
 MATH20300: Linear Algebra 2 (2016 Chapter 2: Linear Independence and Bases 1 Linear Combinations and Spans Example 11 Consider the vector v (1, 1 R 2 What is the smallest subspace of (the real vector space
MATH20300: Linear Algebra 2 (2016 Chapter 2: Linear Independence and Bases 1 Linear Combinations and Spans Example 11 Consider the vector v (1, 1 R 2 What is the smallest subspace of (the real vector space
A matrix is a rectangular array of. objects arranged in rows and columns. The objects are called the entries. is called the size of the matrix, and
 Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
Review 1 Math 321: Linear Algebra Spring 2010
 Department of Mathematics and Statistics University of New Mexico Review 1 Math 321: Linear Algebra Spring 2010 This is a review for Midterm 1 that will be on Thursday March 11th, 2010. The main topics
Department of Mathematics and Statistics University of New Mexico Review 1 Math 321: Linear Algebra Spring 2010 This is a review for Midterm 1 that will be on Thursday March 11th, 2010. The main topics
OHSX XM511 Linear Algebra: Multiple Choice Exercises for Chapter 2
 OHSX XM5 Linear Algebra: Multiple Choice Exercises for Chapter. In the following, a set is given together with operations of addition and scalar multiplication. Which is not a vector space under the given
OHSX XM5 Linear Algebra: Multiple Choice Exercises for Chapter. In the following, a set is given together with operations of addition and scalar multiplication. Which is not a vector space under the given
Abstract Vector Spaces and Concrete Examples
 LECTURE 18 Abstract Vector Spaces and Concrete Examples Our discussion of linear algebra so far has been devoted to discussing the relations between systems of linear equations, matrices, and vectors.
LECTURE 18 Abstract Vector Spaces and Concrete Examples Our discussion of linear algebra so far has been devoted to discussing the relations between systems of linear equations, matrices, and vectors.
Family Feud Review. Linear Algebra. October 22, 2013
 Review Linear Algebra October 22, 2013 Question 1 Let A and B be matrices. If AB is a 4 7 matrix, then determine the dimensions of A and B if A has 19 columns. Answer 1 Answer A is a 4 19 matrix, while
Review Linear Algebra October 22, 2013 Question 1 Let A and B be matrices. If AB is a 4 7 matrix, then determine the dimensions of A and B if A has 19 columns. Answer 1 Answer A is a 4 19 matrix, while
Moreover this binary operation satisfies the following properties
 Contents 1 Algebraic structures 1 1.1 Group........................................... 1 1.1.1 Definitions and examples............................. 1 1.1.2 Subgroup.....................................
Contents 1 Algebraic structures 1 1.1 Group........................................... 1 1.1.1 Definitions and examples............................. 1 1.1.2 Subgroup.....................................
Row Space, Column Space, and Nullspace
 Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
Math 54 HW 4 solutions
 Math 54 HW 4 solutions 2.2. Section 2.2 (a) False: Recall that performing a series of elementary row operations A is equivalent to multiplying A by a series of elementary matrices. Suppose that E,...,
Math 54 HW 4 solutions 2.2. Section 2.2 (a) False: Recall that performing a series of elementary row operations A is equivalent to multiplying A by a series of elementary matrices. Suppose that E,...,
MATH 167: APPLIED LINEAR ALGEBRA Chapter 2
 MATH 167: APPLIED LINEAR ALGEBRA Chapter 2 Jesús De Loera, UC Davis February 1, 2012 General Linear Systems of Equations (2.2). Given a system of m equations and n unknowns. Now m n is OK! Apply elementary
MATH 167: APPLIED LINEAR ALGEBRA Chapter 2 Jesús De Loera, UC Davis February 1, 2012 General Linear Systems of Equations (2.2). Given a system of m equations and n unknowns. Now m n is OK! Apply elementary
Vector Spaces. Addition : R n R n R n Scalar multiplication : R R n R n.
 Vector Spaces Definition: The usual addition and scalar multiplication of n-tuples x = (x 1,..., x n ) R n (also called vectors) are the addition and scalar multiplication operations defined component-wise:
Vector Spaces Definition: The usual addition and scalar multiplication of n-tuples x = (x 1,..., x n ) R n (also called vectors) are the addition and scalar multiplication operations defined component-wise:
We could express the left side as a sum of vectors and obtain the Vector Form of a Linear System: a 12 a x n. a m2
 Week 22 Equations, Matrices and Transformations Coefficient Matrix and Vector Forms of a Linear System Suppose we have a system of m linear equations in n unknowns a 11 x 1 + a 12 x 2 + + a 1n x n b 1
Week 22 Equations, Matrices and Transformations Coefficient Matrix and Vector Forms of a Linear System Suppose we have a system of m linear equations in n unknowns a 11 x 1 + a 12 x 2 + + a 1n x n b 1
Math 24 Spring 2012 Questions (mostly) from the Textbook
 Math 24 Spring 2012 Questions (mostly) from the Textbook 1. TRUE OR FALSE? (a) The zero vector space has no basis. (F) (b) Every vector space that is generated by a finite set has a basis. (c) Every vector
Math 24 Spring 2012 Questions (mostly) from the Textbook 1. TRUE OR FALSE? (a) The zero vector space has no basis. (F) (b) Every vector space that is generated by a finite set has a basis. (c) Every vector
CHAPTER 3 REVIEW QUESTIONS MATH 3034 Spring a 1 b 1
 . Let U = { A M (R) A = and b 6 }. CHAPTER 3 REVIEW QUESTIONS MATH 334 Spring 7 a b a and b are integers and a 6 (a) Let S = { A U det A = }. List the elements of S; that is S = {... }. (b) Let T = { A
. Let U = { A M (R) A = and b 6 }. CHAPTER 3 REVIEW QUESTIONS MATH 334 Spring 7 a b a and b are integers and a 6 (a) Let S = { A U det A = }. List the elements of S; that is S = {... }. (b) Let T = { A
MATH 315 Linear Algebra Homework #1 Assigned: August 20, 2018
 Homework #1 Assigned: August 20, 2018 Review the following subjects involving systems of equations and matrices from Calculus II. Linear systems of equations Converting systems to matrix form Pivot entry
Homework #1 Assigned: August 20, 2018 Review the following subjects involving systems of equations and matrices from Calculus II. Linear systems of equations Converting systems to matrix form Pivot entry
MATH2210 Notebook 3 Spring 2018
 MATH2210 Notebook 3 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2009 2018 by Jenny A. Baglivo. All Rights Reserved. 3 MATH2210 Notebook 3 3 3.1 Vector Spaces and Subspaces.................................
MATH2210 Notebook 3 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2009 2018 by Jenny A. Baglivo. All Rights Reserved. 3 MATH2210 Notebook 3 3 3.1 Vector Spaces and Subspaces.................................
Exercises Chapter II.
 Page 64 Exercises Chapter II. 5. Let A = (1, 2) and B = ( 2, 6). Sketch vectors of the form X = c 1 A + c 2 B for various values of c 1 and c 2. Which vectors in R 2 can be written in this manner? B y
Page 64 Exercises Chapter II. 5. Let A = (1, 2) and B = ( 2, 6). Sketch vectors of the form X = c 1 A + c 2 B for various values of c 1 and c 2. Which vectors in R 2 can be written in this manner? B y
Lecture Summaries for Linear Algebra M51A
 These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
Math 240, 4.3 Linear Independence; Bases A. DeCelles. 1. definitions of linear independence, linear dependence, dependence relation, basis
 Math 24 4.3 Linear Independence; Bases A. DeCelles Overview Main ideas:. definitions of linear independence linear dependence dependence relation basis 2. characterization of linearly dependent set using
Math 24 4.3 Linear Independence; Bases A. DeCelles Overview Main ideas:. definitions of linear independence linear dependence dependence relation basis 2. characterization of linearly dependent set using
The geometry of least squares
 The geometry of least squares We can think of a vector as a point in space, where the elements of the vector are the coordinates of the point. Consider for example, the following vector s: t = ( 4, 0),
The geometry of least squares We can think of a vector as a point in space, where the elements of the vector are the coordinates of the point. Consider for example, the following vector s: t = ( 4, 0),
11.10a Taylor and Maclaurin Series
 11.10a 1 11.10a Taylor and Maclaurin Series Let y = f(x) be a differentiable function at x = a. In first semester calculus we saw that (1) f(x) f(a)+f (a)(x a), for all x near a The right-hand side of
11.10a 1 11.10a Taylor and Maclaurin Series Let y = f(x) be a differentiable function at x = a. In first semester calculus we saw that (1) f(x) f(a)+f (a)(x a), for all x near a The right-hand side of
MATH 304 Linear Algebra Lecture 10: Linear independence. Wronskian.
 MATH 304 Linear Algebra Lecture 10: Linear independence. Wronskian. Spanning set Let S be a subset of a vector space V. Definition. The span of the set S is the smallest subspace W V that contains S. If
MATH 304 Linear Algebra Lecture 10: Linear independence. Wronskian. Spanning set Let S be a subset of a vector space V. Definition. The span of the set S is the smallest subspace W V that contains S. If
MATH 225 Summer 2005 Linear Algebra II Solutions to Assignment 1 Due: Wednesday July 13, 2005
 MATH 225 Summer 25 Linear Algebra II Solutions to Assignment 1 Due: Wednesday July 13, 25 Department of Mathematical and Statistical Sciences University of Alberta Question 1. [p 224. #2] The set of all
MATH 225 Summer 25 Linear Algebra II Solutions to Assignment 1 Due: Wednesday July 13, 25 Department of Mathematical and Statistical Sciences University of Alberta Question 1. [p 224. #2] The set of all
Linear Algebra. Min Yan
 Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
Linear Independence. Linear Algebra MATH Linear Algebra LI or LD Chapter 1, Section 7 1 / 1
 Linear Independence Linear Algebra MATH 76 Linear Algebra LI or LD Chapter, Section 7 / Linear Combinations and Span Suppose s, s,..., s p are scalars and v, v,..., v p are vectors (all in the same space
Linear Independence Linear Algebra MATH 76 Linear Algebra LI or LD Chapter, Section 7 / Linear Combinations and Span Suppose s, s,..., s p are scalars and v, v,..., v p are vectors (all in the same space
(1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3
 Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
EXERCISES AND SOLUTIONS IN LINEAR ALGEBRA
 EXERCISES AND SOLUTIONS IN LINEAR ALGEBRA Mahmut Kuzucuoğlu Middle East Technical University matmah@metu.edu.tr Ankara, TURKEY March 14, 015 ii TABLE OF CONTENTS CHAPTERS 0. PREFACE..................................................
EXERCISES AND SOLUTIONS IN LINEAR ALGEBRA Mahmut Kuzucuoğlu Middle East Technical University matmah@metu.edu.tr Ankara, TURKEY March 14, 015 ii TABLE OF CONTENTS CHAPTERS 0. PREFACE..................................................
SYMBOL EXPLANATION EXAMPLE
 MATH 4310 PRELIM I REVIEW Notation These are the symbols we have used in class, leading up to Prelim I, and which I will use on the exam SYMBOL EXPLANATION EXAMPLE {a, b, c, } The is the way to write the
MATH 4310 PRELIM I REVIEW Notation These are the symbols we have used in class, leading up to Prelim I, and which I will use on the exam SYMBOL EXPLANATION EXAMPLE {a, b, c, } The is the way to write the
LS.1 Review of Linear Algebra
 LS. LINEAR SYSTEMS LS.1 Review of Linear Algebra In these notes, we will investigate a way of handling a linear system of ODE s directly, instead of using elimination to reduce it to a single higher-order
LS. LINEAR SYSTEMS LS.1 Review of Linear Algebra In these notes, we will investigate a way of handling a linear system of ODE s directly, instead of using elimination to reduce it to a single higher-order
Linear algebra and differential equations (Math 54): Lecture 10
 Linear algebra and differential equations (Math 54): Lecture 10 Vivek Shende February 24, 2016 Hello and welcome to class! As you may have observed, your usual professor isn t here today. He ll be back
Linear algebra and differential equations (Math 54): Lecture 10 Vivek Shende February 24, 2016 Hello and welcome to class! As you may have observed, your usual professor isn t here today. He ll be back
Chapter 5. Linear Algebra. A linear (algebraic) equation in. unknowns, x 1, x 2,..., x n, is. an equation of the form
 Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
3 Matrix Algebra. 3.1 Operations on matrices
 3 Matrix Algebra A matrix is a rectangular array of numbers; it is of size m n if it has m rows and n columns. A 1 n matrix is a row vector; an m 1 matrix is a column vector. For example: 1 5 3 5 3 5 8
3 Matrix Algebra A matrix is a rectangular array of numbers; it is of size m n if it has m rows and n columns. A 1 n matrix is a row vector; an m 1 matrix is a column vector. For example: 1 5 3 5 3 5 8
Vector Spaces - Definition
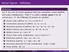 Vector Spaces - Definition Definition Let V be a set of vectors equipped with two operations: vector addition and scalar multiplication. Then V is called a vector space if for all vectors u,v V, the following
Vector Spaces - Definition Definition Let V be a set of vectors equipped with two operations: vector addition and scalar multiplication. Then V is called a vector space if for all vectors u,v V, the following
A Do It Yourself Guide to Linear Algebra
 A Do It Yourself Guide to Linear Algebra Lecture Notes based on REUs, 2001-2010 Instructor: László Babai Notes compiled by Howard Liu 6-30-2010 1 Vector Spaces 1.1 Basics Definition 1.1.1. A vector space
A Do It Yourself Guide to Linear Algebra Lecture Notes based on REUs, 2001-2010 Instructor: László Babai Notes compiled by Howard Liu 6-30-2010 1 Vector Spaces 1.1 Basics Definition 1.1.1. A vector space
MAT Linear Algebra Collection of sample exams
 MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
Chapter 8: Taylor s theorem and L Hospital s rule
 Chapter 8: Taylor s theorem and L Hospital s rule Theorem: [Inverse Mapping Theorem] Suppose that a < b and f : [a, b] R. Given that f (x) > 0 for all x (a, b) then f 1 is differentiable on (f(a), f(b))
Chapter 8: Taylor s theorem and L Hospital s rule Theorem: [Inverse Mapping Theorem] Suppose that a < b and f : [a, b] R. Given that f (x) > 0 for all x (a, b) then f 1 is differentiable on (f(a), f(b))
Vector Spaces and SubSpaces
 Vector Spaces and SubSpaces Linear Algebra MATH 2076 Linear Algebra Vector Spaces & SubSpaces Chapter 4, Section 1b 1 / 10 What is a Vector Space? A vector space is a bunch of objects that we call vectors
Vector Spaces and SubSpaces Linear Algebra MATH 2076 Linear Algebra Vector Spaces & SubSpaces Chapter 4, Section 1b 1 / 10 What is a Vector Space? A vector space is a bunch of objects that we call vectors
Functional Analysis Exercise Class
 Functional Analysis Exercise Class Week: December 4 8 Deadline to hand in the homework: your exercise class on week January 5. Exercises with solutions ) Let H, K be Hilbert spaces, and A : H K be a linear
Functional Analysis Exercise Class Week: December 4 8 Deadline to hand in the homework: your exercise class on week January 5. Exercises with solutions ) Let H, K be Hilbert spaces, and A : H K be a linear
LINEAR ALGEBRA W W L CHEN
 LINEAR ALGEBRA W W L CHEN c W W L Chen, 994, 28. This chapter is available free to all individuals, on the understanding that it is not to be used for financial gain, and may be downloaded and/or photocopied,
LINEAR ALGEBRA W W L CHEN c W W L Chen, 994, 28. This chapter is available free to all individuals, on the understanding that it is not to be used for financial gain, and may be downloaded and/or photocopied,
2. Every linear system with the same number of equations as unknowns has a unique solution.
 1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
1 Matrices and matrix algebra
 1 Matrices and matrix algebra 1.1 Examples of matrices A matrix is a rectangular array of numbers and/or variables. For instance 4 2 0 3 1 A = 5 1.2 0.7 x 3 π 3 4 6 27 is a matrix with 3 rows and 5 columns
1 Matrices and matrix algebra 1.1 Examples of matrices A matrix is a rectangular array of numbers and/or variables. For instance 4 2 0 3 1 A = 5 1.2 0.7 x 3 π 3 4 6 27 is a matrix with 3 rows and 5 columns
Review problems for MA 54, Fall 2004.
 Review problems for MA 54, Fall 2004. Below are the review problems for the final. They are mostly homework problems, or very similar. If you are comfortable doing these problems, you should be fine on
Review problems for MA 54, Fall 2004. Below are the review problems for the final. They are mostly homework problems, or very similar. If you are comfortable doing these problems, you should be fine on
Linear Algebra, 4th day, Thursday 7/1/04 REU Info:
 Linear Algebra, 4th day, Thursday 7/1/04 REU 004. Info http//people.cs.uchicago.edu/laci/reu04. Instructor Laszlo Babai Scribe Nick Gurski 1 Linear maps We shall study the notion of maps between vector
Linear Algebra, 4th day, Thursday 7/1/04 REU 004. Info http//people.cs.uchicago.edu/laci/reu04. Instructor Laszlo Babai Scribe Nick Gurski 1 Linear maps We shall study the notion of maps between vector
Polynomials over UFD s
 Polynomials over UFD s Let R be a UFD and let K be the field of fractions of R. Our goal is to compare arithmetic in the rings R[x] and K[x]. We introduce the following notion. Definition 1. A non-constant
Polynomials over UFD s Let R be a UFD and let K be the field of fractions of R. Our goal is to compare arithmetic in the rings R[x] and K[x]. We introduce the following notion. Definition 1. A non-constant
Review : Powers of a matrix
 Review : Powers of a matrix Given a square matrix A and a positive integer k, we define A k = AA A } {{ } k times Note that the multiplications AA, AAA,... make sense. Example. Suppose A=. Then A 0 2 =
Review : Powers of a matrix Given a square matrix A and a positive integer k, we define A k = AA A } {{ } k times Note that the multiplications AA, AAA,... make sense. Example. Suppose A=. Then A 0 2 =
Linear Equations in Linear Algebra
 1 Linear Equations in Linear Algebra 1.7 LINEAR INDEPENDENCE LINEAR INDEPENDENCE Definition: An indexed set of vectors {v 1,, v p } in n is said to be linearly independent if the vector equation x x x
1 Linear Equations in Linear Algebra 1.7 LINEAR INDEPENDENCE LINEAR INDEPENDENCE Definition: An indexed set of vectors {v 1,, v p } in n is said to be linearly independent if the vector equation x x x
Vector Spaces. Chapter Two
 Chapter Two Vector Spaces The first chapter began by introducing Gauss method and finished with a fair understanding, keyed on the Linear Combination Lemma, of how it finds the solution set of a linear
Chapter Two Vector Spaces The first chapter began by introducing Gauss method and finished with a fair understanding, keyed on the Linear Combination Lemma, of how it finds the solution set of a linear
GQE ALGEBRA PROBLEMS
 GQE ALGEBRA PROBLEMS JAKOB STREIPEL Contents. Eigenthings 2. Norms, Inner Products, Orthogonality, and Such 6 3. Determinants, Inverses, and Linear (In)dependence 4. (Invariant) Subspaces 3 Throughout
GQE ALGEBRA PROBLEMS JAKOB STREIPEL Contents. Eigenthings 2. Norms, Inner Products, Orthogonality, and Such 6 3. Determinants, Inverses, and Linear (In)dependence 4. (Invariant) Subspaces 3 Throughout
Ch. 7.3, 7.4: Vectors and Complex Numbers
 Ch. 7.3, 7.4: Vectors and Complex Numbers Johns Hopkins University Fall 2014 (Johns Hopkins University) Ch. 7.3, 7.4: Vectors and Complex Numbers Fall 2014 1 / 38 Vectors(1) Definition (Vector) A vector
Ch. 7.3, 7.4: Vectors and Complex Numbers Johns Hopkins University Fall 2014 (Johns Hopkins University) Ch. 7.3, 7.4: Vectors and Complex Numbers Fall 2014 1 / 38 Vectors(1) Definition (Vector) A vector
Chapter SSM: Linear Algebra Section Fails to be invertible; since det = 6 6 = Invertible; since det = = 2.
 SSM: Linear Algebra Section 61 61 Chapter 6 1 2 1 Fails to be invertible; since det = 6 6 = 0 3 6 3 5 3 Invertible; since det = 33 35 = 2 7 11 5 Invertible; since det 2 5 7 0 11 7 = 2 11 5 + 0 + 0 0 0
SSM: Linear Algebra Section 61 61 Chapter 6 1 2 1 Fails to be invertible; since det = 6 6 = 0 3 6 3 5 3 Invertible; since det = 33 35 = 2 7 11 5 Invertible; since det 2 5 7 0 11 7 = 2 11 5 + 0 + 0 0 0
Math 110, Spring 2015: Midterm Solutions
 Math 11, Spring 215: Midterm Solutions These are not intended as model answers ; in many cases far more explanation is provided than would be necessary to receive full credit. The goal here is to make
Math 11, Spring 215: Midterm Solutions These are not intended as model answers ; in many cases far more explanation is provided than would be necessary to receive full credit. The goal here is to make
Math 307: Problems for section 2.1
 Math 37: Problems for section 2. October 9 26 2. Are the vectors 2 2 3 2 2 4 9 linearly independent? You may use MAT- 7 3 LAB/Octave to perform calculations but explain your answer. Put the vectors in
Math 37: Problems for section 2. October 9 26 2. Are the vectors 2 2 3 2 2 4 9 linearly independent? You may use MAT- 7 3 LAB/Octave to perform calculations but explain your answer. Put the vectors in
CHAPTER 5. Higher Order Linear ODE'S
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 2 A COLLECTION OF HANDOUTS ON SCALAR LINEAR ORDINARY
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 2 A COLLECTION OF HANDOUTS ON SCALAR LINEAR ORDINARY
Chapter 2 Notes, Linear Algebra 5e Lay
 Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
Linear Algebra. Preliminary Lecture Notes
 Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date May 9, 29 2 Contents 1 Motivation for the course 5 2 Euclidean n dimensional Space 7 2.1 Definition of n Dimensional Euclidean Space...........
Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date May 9, 29 2 Contents 1 Motivation for the course 5 2 Euclidean n dimensional Space 7 2.1 Definition of n Dimensional Euclidean Space...........
MATH 2331 Linear Algebra. Section 2.1 Matrix Operations. Definition: A : m n, B : n p. Example: Compute AB, if possible.
 MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
Vectors. February 1, 2010
 Vectors Febrary 1, 2010 Motivation Location of projector from crrent position and orientation: direction of projector distance to projector (direction, distance=magnitde) vector Examples: Force Velocity
Vectors Febrary 1, 2010 Motivation Location of projector from crrent position and orientation: direction of projector distance to projector (direction, distance=magnitde) vector Examples: Force Velocity
Linear Algebra Homework and Study Guide
 Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
Math 350 Fall 2011 Notes about inner product spaces. In this notes we state and prove some important properties of inner product spaces.
 Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Mathematics I. Exercises with solutions. 1 Linear Algebra. Vectors and Matrices Let , C = , B = A = Determine the following matrices:
 Mathematics I Exercises with solutions Linear Algebra Vectors and Matrices.. Let A = 5, B = Determine the following matrices: 4 5, C = a) A + B; b) A B; c) AB; d) BA; e) (AB)C; f) A(BC) Solution: 4 5 a)
Mathematics I Exercises with solutions Linear Algebra Vectors and Matrices.. Let A = 5, B = Determine the following matrices: 4 5, C = a) A + B; b) A B; c) AB; d) BA; e) (AB)C; f) A(BC) Solution: 4 5 a)
1.4 Linear Transformation I
 .4. LINEAR TRANSFORMATION I.4 Linear Transformation I MATH 9 FALL 99 PRELIM # 5 9FA9PQ5.tex.4. a) Consider the vector transformation y f(x) from V to V such that if y (y ; y ); x (x ; x ); y (x + x ) p
.4. LINEAR TRANSFORMATION I.4 Linear Transformation I MATH 9 FALL 99 PRELIM # 5 9FA9PQ5.tex.4. a) Consider the vector transformation y f(x) from V to V such that if y (y ; y ); x (x ; x ); y (x + x ) p
Notes on Linear Algebra I. # 1
 Notes on Linear Algebra I. # 1 Oussama Moutaoikil Contents 1 Introduction 1 2 On Vector Spaces 5 2.1 Vectors................................... 5 2.2 Vector Spaces................................ 7 2.3
Notes on Linear Algebra I. # 1 Oussama Moutaoikil Contents 1 Introduction 1 2 On Vector Spaces 5 2.1 Vectors................................... 5 2.2 Vector Spaces................................ 7 2.3
LINEAR ALGEBRA BOOT CAMP WEEK 4: THE SPECTRAL THEOREM
 LINEAR ALGEBRA BOOT CAMP WEEK 4: THE SPECTRAL THEOREM Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F is R or C. Definition 1. A linear operator
LINEAR ALGEBRA BOOT CAMP WEEK 4: THE SPECTRAL THEOREM Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F is R or C. Definition 1. A linear operator
INTRODUCTION TO LIE ALGEBRAS. LECTURE 2.
 INTRODUCTION TO LIE ALGEBRAS. LECTURE 2. 2. More examples. Ideals. Direct products. 2.1. More examples. 2.1.1. Let k = R, L = R 3. Define [x, y] = x y the cross-product. Recall that the latter is defined
INTRODUCTION TO LIE ALGEBRAS. LECTURE 2. 2. More examples. Ideals. Direct products. 2.1. More examples. 2.1.1. Let k = R, L = R 3. Define [x, y] = x y the cross-product. Recall that the latter is defined
11.4 Dot Product Contemporary Calculus 1
 11.4 Dot Product Contemporary Calculus 1 11.4 DOT PRODUCT In the previous sections we looked at the meaning of vectors in two and three dimensions, but the only operations we used were addition and subtraction
11.4 Dot Product Contemporary Calculus 1 11.4 DOT PRODUCT In the previous sections we looked at the meaning of vectors in two and three dimensions, but the only operations we used were addition and subtraction
Linear Maps and Matrices
 Linear Maps and Matrices Maps Suppose that V and W are sets A map F : V W is a function; that is, to every v V there is assigned a unique element w F v in W Two maps F : V W and G : V W are equal if F
Linear Maps and Matrices Maps Suppose that V and W are sets A map F : V W is a function; that is, to every v V there is assigned a unique element w F v in W Two maps F : V W and G : V W are equal if F
