Lecture Notes for math111: Calculus I.
|
|
|
- Evelyn Bradford
- 5 years ago
- Views:
Transcription
1 Lecture Notes for math111: Calculus I. Dr. Vitaly A. Shneidman New Jersey Institute of Technology Fall,
2 Introduction y = f(x) Limits & Continuity Rates of change and tangents to curves 2
3 Average rate of change y x = f (x 2) f (x 1 ) x 2 x 1 (1) Equation for the secant line: Y = y x (x x 1)+f (x 1 ) Tangent - secant in the limit x 2 x 1 (Or, x 0). Slope of tangent f (x 1 ) y x, x 0 (2) (notation f is not yet in the book, but will appear later...). Equation of tangent line: Y = f (x 1 )(x x 1 )+f (x 1 ) 3
4 Example (Galileo): t instead of x or x 1, h instead of x. y(t) = 1 2 at2 where a is a constant ( acceleration ). Secant (finite h) y = y(t+h) y(t) = 1 2 a[ (t+h) 2 t 2] = 1 2 a( 2th+h 2) y t = y h = a(t+h/2) Tangent (h 0): y (t) = at (known as instantaneous velocity or instantaneous 4
5 rate of change ). Returning to math notations ( x 2 ) = 2x (3)
6 Example: y(x) = x 3 Use a 3 b 3 = (a b)(a 2 +ab+b 2 ) with a = x+h, b = x. Slope of secant (A.R.C.), finite h x: y = y(x+h) y(x) = (x+h) 3 x 3 = h [ (x+h) 2 +x(x+h)+x 2] = = h(3x 2 +3xh+h 2 ) y x = y h = 3x2 +3xh+h 2 Slope of tangent (I.R.C.) h 0: ( x 3 ) = 3x 2 (4) 5
7 Example: y(x) = x A.R.C. = y x = y h = x+h x h = x+h x h Now, no problem h 0: or x+h+ x x+h+ x = I.R.C. = 1/2 x 1 x+h+ x ( x ) = 1 2 x (5) 6
8 Continuity and Limits Continuous (left) and discontinuous (right) functions Intermediate value Theorem 11, p.99 7
9 Limit of a function Assume don t know f (x 0 ) but know f(x) for any x close to x 0. Example: sin x 1.0 x y(0) not defined. Can define y(0) = a, with any a. Why a = 1 is the best? 8
10 Limit: Example: lim x a lim f(x) = L x x 0 x 2 a 2 x a = lim x a Functions with no limit as x 0: step-function, 1/x, sin(1/x) x+a = 2a 9
11 Limit Laws - Theorem 1, p.68. If f, g have limits L & M as x c. Then, lim x c (f ±g) = L±M, lim(f g) = L M, etc. (6) x c lim x c (fn ) = L n, lim(f 1/n ) = L 1/n (7) x c Dull functions lim x c f(x) = f(c). Example 4x 2 3 = 13 lim x 2 Example: any polynomial lim x c P n (x) = P n (c) 10
12 Limits of rational functions P(x)/Q(x) as x c. If Q(c) 0 - dull, limit R(c)/Q(c). If Q(c) = 0 check P(c): if P(c) 0 - no limit; If P(c) = 0 try to simplify. Example: lim x 1 x 3 +x 2 x 2 x = lim x 1 (x 1)(x 2 +x+2) x(x 1) = 4 Other functions with limits of type 0/0. Example: x 2 +a 2 a x 2 +a 2 a x 2 +a 2 +a lim x 0 x 2 = lim x 0 x 2 = x 2 +a 2 +a = lim x 0 1/( x 2 +a 2 +a) = 1/2a 11
13 Sandwich theorem : Let f(x) g(x) and IF lim f(x) = lim x c x c g(x) = L. f(x) u(x) g(x) THEN lim x c u(x) = L 12
14 Limit (sinx)/x as x 0 B C AOC = x (in radians!) S OAC = 2 1 sinx O A S sectoroac = x 2 S OAB = 1 2 tanx Thus, sinx < x < tanx, 0 < x < π 2 (8) Divide by sinx and take the inverse, changing < to > : 1 > sinx x > cosx. Since cos0 = 1, from S.T. lim x 0 sinx x = 1 (9) 13
15 Examples (discussed in class): tanx lim = 1 (10) x 0 x sinkx lim = k (11) x 0 x 1 cosx lim = 0 (12) x 0 x 1 cosx x 2 = 1 (13) 2 lim x 0 lim x 0 tanx sinx x 3 =
16 One-sided limits (skip definition on p. 87) x x x 1 x Functions with 1-sided limits. x x lim = 1, lim x 0 + x x 0 x = 1, f(0) =? lim 1 x 2 = 0, lim x 1 + x 1 1 x 2 = 0 x 15
17 Theorem 6, p.86: Limit of f(x) for x c exists if and only if L.H. and R.H. limits at x c,c + exist and have the same value (in which case, this also will be the value of the limit of f). 16
18 x sin 1 x x sin 1 x x x Tricky functions with 2- or 1-sided limits. lim x 0 xsin1 x 0.3 = 0, lim x 0 + xsin 1 x = 0 17
19 Continuity at a point x = c (p. 93, or Continuity Test, p. 94): f(c) = lim x c f(x) for an interior point (and similarly for an endpoint with corresponding one-sided limit). Right-continuous at a point x = c : f(c) = lim x c +f(x) Left-continuous at a point x = c : f(c) = lim x c f(x) 18
20 x x 2 right-continuous integer floor function 19
21 Continuous Function (CF) CF on an interval CF Theorem 8, p. 95 f ±g, etc. Inverse of a CF is a CF: e.g. e x and lnx Composits of CF are CFs: e.g. Theorems 9, 10 on p. 97 f(x),f(x) = 1 x 2 Continuous extension to a point: e.g. F(x) = sinx/x,x 1;F(0) = 1 20
22 Limits involving x ± (skip p. 104) 2 x 2 5 x 7 x x Limits of a rational function with the same power of denom. and numerator. Horizontal asymptote(s) - lim(s) of f(x) as x ± 21
23 Non-algebraic functions x 3 x 3 +1,ex,xsin 1 x, etc. x sin 1 x x 0.2
24 Oblique and vertical asymptotes x 2 x 2 x x 10 22
25 Derivatives f f(x+h) f(x) (x) = lim = h 0 h (14) f(z) f(x) = lim z x z x (15) If the limit exists, this is derivative at a point x, a.k.a: slope of the graph at x slope of the tangent to the graph at x 23
26 rate of change of f with respect to x
27 Derivative as a function x is not frozen anymore; can consider a new function Other notations g(x) = f (x) f (x) = y = dy dx = df dx = d f(x) =... dx g(a) = df dx x=a 24
28 Examples: or d dx 1 x = lim z x 1/z 1/x z x = lim z x x z zx(z x) = 1 x 2 d dx 1 x = 1 x 2 (16) d dx 1 x 2 = lim z x 1/z 2 1/x 2 z x = lim z x x 2 z 2 z 2 x 2 (z x) = 2 1 x 3 d dx x x 1 = d dx ( 1+ 1 ) x 1 = 0 1 (x 1) 2 25
29 One-sided derivatives From right: f f(x+h) f(x) (x) = lim h 0 + h From left: f f(x+h) f(x) (x) = lim h 0 h f(z) f(x) = lim z x + z x f(z) f(x) = lim z x z x Example: x = 1 for x > 0, = 1 for x < 0 and is not defined at x = 0 where only r.-h. or l.-h. derivatives exist. (This was a corner ; other cases with no derivative may include cusp as x, vertical tangent as x 1/3 and a discontinuity of the original function as x /x. Graphics in class.) 26
30 Theorem 3.1. If f(x) has a derivative at x = c it is continuous at x = c. Consider identity f(c+h) = f(c)+ f(c+h) f(c) h h and take the limit of both sides as h 0. Note: Converse is false, e.g. x. 27
31 Differentiation rules (af(x)+bg(x)) = af +bg (17) Proof. Consider af(z)+bg(z) af(x) bg(x) z x and take the limit z x. a[f(z) f(x)]+b[g(z) g(x)] z x (f(ax)) = a df(z) dz Example: (sin(ωx)) = ωcos(ωx) (18) z=ax 28
32 [f(x) g(x)] = f g +fg (19) Proof. Consider f(z)g(z) f(x)g(x) [f(z) f(x)]g(z)+f(x)[g(z) g(x)] z x z x and take the limit z x. Example: (x x) = 1 x+x 1 = 2x 29
33 ( 1 f ) = f f 2 (20) Proof. Consider 1/f(z) 1/f(x) z x and take the limit z x. f(x) f(z) f(z)f(x)(z x) Example: (1/x) = 1/x 2 ( f g ) = f g g f g 2 (21) 30
34 Derivatives of elementary functions (x n ) = nx n 1, any n (22) (sinx) = cosx, (cosx) = sinx (23) (e x ) = e x, (a x ) = ( e xlna) = ax lna (24) (lnx) = 1/x (25) 31
35 Trigonometric functions Earlier: (sinx) = cosx, (cosx) = sinx and (tanx) = 1/cos 2 x (26) Other basic examples: 1/cosx, 1/sinx, cotx,... Simple harmonic motion: dy y(t) = Asin(ωt), = Aωcos(ωt) dt (27) d 2 y dt 2 = Aω2 sin(ωt) ω 2 y(t) (28) 32
36 Chain rule (f(g(x))) = df dg dg dx (f(g)) (g(x)) (29) Proof. Let u = g(z), v = g(x) (f(g(x))) = lim z x f(u) f(v) z x f(u) f(v) = lim u v z x u v z x = dg dg df dx Simple example: (f(ax)) = af (ax) 33
37 (u(x) n ) = nu n 1du dx (sinu(x)) = [cosu(x)] du dx (e u ) = e udu dx (lnu) = 1 du udx (30) (31) (32) (33) ( ) x = 2 x 2 +1 (2x) 34
38 Example ( e x2) = 2xe x exp x x exp x
39 Example: ( sin(x 2 ) ) = 2xcos(x 2 ) 10 5 sin x x cos x
40 Example (e e x) = e e x (e x) exp x exp x x
41 Implicit differentiation Let F(x,y) = 0 where F is a simple known function (e.g. F = x y 2 describing a parabola). Then F x dy +F y dx = 0 (34) and dy dx = F x /F y 38
42 Tangent at (x 0, y 0 ) Y = y 0 + dy (x x 0 ) (35) dx x=x0 Normal: Y = y 0 ( 1 dy (x x 0 ) (36) dx x=x0) 39
43 Parabola: Tangent and normal: y 2 = x, 2y dy dx = 1, dy dx = 1 2y Y = y y 0 (x x 0 ), Y = y 0 (2y 0 )(x x 0 ) x y
44 Ellipse: (x/a) 2 +(y/b) 2 = 1, 2x/a 2 +2y/b 2dy dx = 0, dy dx = x y Tangent and normal: 3 Y = y 0 x 0 y 0 b 2 a 2(x x 0), Y = y 0 + y 0 x 0 a 2 b 2(x x 0) b 2 a x 2 9 y
45 Hyperbola: x 2 y 2 = 1, 2x 2y dy dx = 0, dy dx = x y Tangent and normal: Y = y 0 + x 0 y 0 (x x 0 ), Y = y 0 y 0 x 0 (x x 0 ) x 2 y
46 Inverse Functions Consider y = f(x) and solve for x = F(y) (select only one branch, if several). Then, swap y and x. Then, y = F(x), with (f(f(x))) = x is the inverse function (F f 1 in textbook). Examples: f = x 2, F = x, f = e x, F = lnx, f = sinx, F = arcsinx, etc. Note: range of f becomes the domain of F, but the domain of f becomes range of F for monotonic f only. Examples: e x (monotonic) and x 2 or sinx (non-monotonic). 43
47 Note (f(f(x))) = x for all x in the domain of F, while F(f(x)) = x in the entire domain of f for monotonic f only. E.g.: e lnx = xfor0 < x <, and ln(e x ) = xfor < x < sin(arcsinx) = xfor 1 x 1, but arcsin(sinx) x, for x > π/2 44
48 Primitive example: f = x 1, F = x x 1 x
49 Primitive example: f = x/2+1, F = 2x x x 2 f(f(x)) = 1 2 (2x 2)+1 = x
50 Example: f = x 2, F = x 4 3 (f) = 2x, (F) = 1 2 x 2 x 2 x Consider (x 0 = 2, y 0 = 4), (X 0 = 4,Y 0 = 2): 1 (f) = 4, (F) =
51 Example: f = x 2 2, F = x (f) = 2x, (F) = 1 2 x+2 2 x 2 2 x 2 Consider (x 0 = 3, y 0 = 7), (X 0 = 7,Y 0 = 3): (f) = 6, (F) =
52 Example: f = e x, F = lnx exp x log x
53 Logarithm y = lnx e y = x e y y = 1 y = 1 e y = 1 x 50
54 Example: f = sinx, F = arcsinx 2 1 sin x sin 1 x
55 arcsin y = arcsinx siny = x (cosy) y = 1 y = 1 cosy = = 1 1 sin 2 y = 1 1 x 2 52
56 Example: f = tanx, F = arctanx 4 2 tan x 5 5 tan 1 x
57 arctan y = arctanx tany = x (1/cos 2 y) y = 1 y = 1 1/cos 2 y = = cos 2 y = 1 tan 2 y +1 = 1 x
58 General y = F(x) f(y) = x df dy y = 1 y df dx = 1 df dy y=f(x) 55
59 Logarithmic functions and differentiation (lnu(x)) = 1 u (u) Examples (lnbx) = b bx = 1 x (ln x ) = 1 x ( x ) = 1 x, x 0 56
60 Recall: a x = e xlna, log a x = lnx lna, a > 0,a 1 (37) (a x ) = ( e xlna) = ax lna (log a x) = 1 xlna (x n ) = ( e nlnx) = n x enlnx = nx n 1 57
61 (x x ) = ( e xlnx) ( = e xlnx lnx+ x ) x = x x (lnx+1) Remarkable limit: lim x 0 (1+x)1/x = e (38) 58
62 Logarithmic differentiation Let y = P(x)Q(x) R(x) lny = lnp +lnq lnr y /y = (P) P + (Q) Q (R) R y = P(x)Q(x) R(x) [ (P) P + (Q) Q (R) R ] 59
63 Inverse trigonometric functions (arcsinx) = (arctanx) = 1 x , x < 1 (39) 1 x2, < x < (40) Now, arccosx = π 2 arcsinx and cot 1 x = π 2 arctanx. Thus (arccosx) 1 =, x < 1 (41) 1 x2 ( cot 1 x ) = 1 x 2 +1, < x < (42) 60
64 sec 1 (x) = arccos 1 x, csc 1 (x) = arcsin 1 x ( sec 1 (x) ) ( = arccos 1 = x) (1/x) 2 x 2 = 1 x x 2 1, x > 1 ( csc 1 (x) ) = ( arcsin 1 x) = (1/x) 2 x 2 1 = x x 2 1, x > 1 61
65 Related rates Suggested notations: V - volume, A - area, L - length/distance, r, R - radii, y Y, h, H - vertical position, x, X -horizontal position, v, V velocity, t - time Sphere: V = 4 3 πr3, A = 4πR 2 (43) Cone: V = 1 3 A base h (44) 62
66 1.0 Circle: 0.5 A = πr da/dt = 2πr dr/dt:
67 1.0 Sphere: 0.5 V = 4 3 πr3 0.0 dv dt = 4πr 2 dr dt = A dr dt
68 Cone: V = 1 3 πr2 (h) h = = 1 3 π( R(H) h H) 2 h = V 0 H 3 h3 dv dt = V 0 H 3 3h2 dh dt = A(h) dh dt 65
69 Coffee maker : V 1 +V 2 = const, dv 1 dt + dv 2 dt = 0 dv 1 dt = πr 2 (h) dh dt dv 2 dt = πr 2 dy dt dy dt = 1 R 2r2 (h) dh dt 66
70 An a(t) b(t) rectangle: A = ab, P = 2(a+b), D = a 2 +b 2 dd dt = 1 2D da dt = adb dt +bda dt ( dp da dt = 2 dt + db dt d dt ( a 2 +b 2) = 1 D ) ( a da ) dt +bdb dt 67
71 Distance between two moving points: X,Y L L = (x X) 2 +(y Y) 2 x,y = 1 L dl dt = 1 d ( (x X) 2 +(y Y) 2) = 2Ldt [ (x X)( dx dt dx )+(y Y)(dy dt dt dy ] dt ) 68
72 Police car: X 0, dy/dt = V, y 0, dx/dt = v = 1 L dl dt = 1 d ( x 2 +Y 2) = 2Ldt [ x dx ] dy +Y = 1 (xv YV) dt dt L v = 1 x (L dl/dt+yv) 69
73 Angle with horizontal (X, Y = 0, L = x/cosθ): tanθ = y/x, 1 cos 2 θ dθ dt = 1 L 2 dθ dt = 1 x 2 ( x dy ) dt ydx dt ( x dy ) dt ydx dt x 2 +y 2 = Balloon: x = const, dy/dt = V. Aircraft: y = const, dx/dt = v. 70
74 y x x x 1 Tangent line and error (for a parabola): Y(x) = y(a)+y (a)(x a) y(x) Y(x) = x 2 a 2 2a(x a) = (x a) 2 71
75 x 1 x x 72
76 x sin x 0 1 x 0 sin x 0 1 x
77 Differential: dx - independent variable dy = y (x)dx 74
78 dx dy y x 75
79 f(x+dx) f(x)+df = f(x)+f (x) dx Examples (small x instead of dx; approximation only near x = 0): (1+x) 2 1+2x (45) 1/(1+x) 1 x (46) 1+x 1+x/2 (47) (1+x) k 1+kx (48) e x 1+x (49) ln(1+x) x (50) 76
80 y x sin 2 x 1 2 cos 2 x x 77
81 Absolute maximum: f(c) = M, f(x) M for every x in the domain of f. Theorem. On a closed domain [a,b] any continuous f(x) will have an absolute maximum. 78
82 Local maximum: f(c) = M, f(x) M for every x on some open interval containing c. Theorem. For any differentiable f(x) a local maximum will have a zero derivative: f(c) = M, (f(x)) x=c = 0 (51) (but, the reverse can be false: e.g. x 3 ) 79
83 Critical and end points: endpoint(s) zero derivative no derivative (e.g x or x ) 80
84 E.g.: critical point - no extrema: y x x 3 3 x
85 E.g.: critical point - no extrema: y x sgn x x sgn x Abs x 3 x x sgn x
86 y x 3 x x x 2 x x 1 83
87 y x x x x x x
88 y x x 3 3 x x 2 x x x
89 y x x log x 1 log x
90 y x 4 cos x 3 sin x 3 cos x 4 sin x
91 Rolle s Theorem: y x 88
92 Mean Value Theorem: y x 89
93 Corollary: If (f) 0, f const Corollary: If (f) (g), f g +C E.g.: a = const, v = at+v 0, x = 1 2 at2 +V 0 t+x 0 90
94 MONOTONICITY Corollary: If (f) keeps sign on (a,b), f is monotonic. y x x 3 x x 3 x 1 3x
95 1st Derivative Test (f) changes from + to - - local max. (f) changes from - to + - local min. if (f) does not change sign - no local max or min Note: Often can use 2nd derivative, but the 1st test does not require the existence of derivatives at x = c, e.g f = x. 92
96 y x sin x 2 sgn 10 x x 93
97 Concavity: y 2.0 c. up c. up c. down x x x 94
98 Concave up: (f) increasing Concave down: (f) decreasing Change of concavity: inflection point y x 3 x x x 3 x 1 3x
99 2nd Derivative Test for Concavity: Concave up: f > 0 Concave down: f < 0 Change of concavity: inflection point f = 0 or does not exist 2nd Derivative Test for Local Extrema: if f = 0 and f > 0 - local min (e.g., x 2 ) if f = 0 and f < 0 - local max (e.g., x 2 ) if f = 0 and f = 0 - test fails (e.g., x 3 or x 4 ) 96
100 y x x 4 x 2 x 4 x 2 2 x 4x x
101 y x x x 1 x x 1 1 x 2 2 x
102 y x x 2 x 1 x 2 x 1 2 x 3 6 x
103 y x 1 x 1 x 2 x x 1 x 2 x x 2 3 x 2 1 x x 3 x2 1 x
104 y x sin x Domain: f(x) : (, ) f (x) : (, ), x nπ 101
105 y x x 2 x 1 x x Domain: f(x) : [ 1, 1], f (x) : ( 1, 1) 102
106 6 y x x sin x 1 cos x sin x
107 6 y x x sin 2 x 1 2 cos 2 x 4 sin 2 x
108 y x x 2 x 3 2 3x x 2 6x 105
109 0.10 y x x 3 x 4 x 2 3 4x 6 x 1 2x
110 y x 1 x x 2 1 x 1 4 x 2 x 2 1 x x 3 x
111 l Hopital Rule If f(c) = 0 AND g(c) = 0 with g (c) 0, then: lim x c f g = f (c) g (c) (52) Demonstration (not proof): f(c+dx) 0+f (c) dx g(c+dx) 0+g (c) dx If f (c) = g (c) = 0, repeat to get f (c) / g (c), etc. 108
112 Examples 0/0 : lim x 0 lim x 0 lim x 1 lim x 0 x 2 1 x 1 = 2x = 2 1 x=1 sinx x = cosx = 1 1 x=0 tanx x 1+x 1 x = 1/cos2 x 1 x=0 = 1 = 1/(2 1+x) 1 x=0 = 1 2 Caution: f(c) = g(c) = 0 is crucial! E.g. lim x 0 sinx 1 x =, not cosx 0 1 x=0 = 1 109
113 lim x 0 x sinx x 3 = 1 cosx 3x 2 = sinx = 1 x 0 6x x 0 6 lim x 0 tanx x x 3 = 1/cos2 x 1 3x 2 = 2sinx/cos3 x = 1 x 0 6x x 0 3 lim x 0 1+x 1 x/2 x 2 = 1/(2 1+x) 1/2 2x = 1/4 ( 1+x) 3 2 x 0 = 1 8 = x 0 110
114 l Hopital Rule for / : If f(x) AND g(x) as x c with g (x) const 0, then: lim x c f g = f (x) g (53) (x) x c 111
115 lim x 0 +xn lnx = lim lnx x 0 + x n = lim nx n 1 = x 0 + 1/x = 1 n xn x 0 + = 0, n > 0 lim = 0 (54) x 0 +xlnx lim x x n e x e x = lim x x n = x lim e x =... nxn 1 = lim x e x n! 112
116 0 0/0 : lim xsin(1/x) = lim x x sin(1/x) 1/x = lim x (1/x 2 )cos(1/x) 1/x 2 = 1 0/0 : 1 sinx 1 = x sinx x x 0 xsinx = = x 0 1 cosx xcosx+sinx sinx = 0 xsinx+cosx+cosx x 0 = x 0 113
117 1 : lim x 0 +(1+zx)1/x = e z 0 0 : (both via logarithm) lim x 0 +xx = 1 114
118 Applied Optimization Best rectangle : P = 2(x+y) -fixed; S = xy = max. S = x(p/2 x), ds/dx = P/2 2x = 0 x = P/4 = y Best can : V = πr 2 h - fixed; S = 2πrh+2πr 2 = min. h = V/πr 2 S = 2π ( ) V πr +r2, 1 2π ds/dx = V πr 2 +2r = 0 r = ( V 2π ) 1/3,h = 2r 115
119 Rectangle in a semicircle: S = 2x R 2 x 2 = max. Ans.: x = R/ 2. Refraction and reflection from Fermat principle (in class). Distance from a parabola (in class). 116
120 Using linearization for approximate calculations: Let F(c) be easy to evaluate, then for small dx F(c+dx) F(c)+F (c) dx E.g. F(x) = x 1/3, F (x) = 1 3 x 2/3. Find 29 1/3. Solution: Use c = 27: (27+2) 1/ /3 2 = =
121 Alternatively (1st step of Newtons method): f(x) = x look for a root in linearized approximation; starting guess x 0 = 3 0 = f(x) f(x 0 )+(x x 0 ) f (x 0 ) x = x 0 f(x 0) f (x 0 ) same thing. = 3 ( 2)/(3 9) = 83/27 118
122 y x x 2 119
123 y x 29 x
124 General Newton s method x n+1 = x n f(x n) f (x n ) (55) E.g., f = x 2 2, starting guess x 0 = 3/2 Errors : x n+1 = x n x n, { } 3 2,17 12, , {0.25, 0.007, 10 6, } 121
125 f = x 3 29, starting guess x 0 = 3: x n+1 = 29 3x 2 n + 2x n 3 { 3, 83 27, , Errors : ( 2., 0.05, 10 5, ) } 122
126 Approximating ln3 = with Newton f(x) = e x 3 x n+1 = x n f(x n) f (x n ) = x n +3e xn 1 If start with x 0 = 1, x 1 = 1+ 3 e 1 = 3 e with error Next, x with error
127 Antiderivatives and indefinite integrals: F(x) is A.D. of f(x) if (F) = f Note: F(x)+C - also an A.D. All together - indefinite integral, f(x)dx E.g. dx = x+c (56) xdx = 1 2 x2 +C (57) dx x 2 = 1 +C (58) x 124
128 Tables (remember constant!): x n dx = 1 n+1 xn+1, n 1 (59) dx/x = ln x (60) sinxdx = cosx (61) cosxdx = sinx (62) dx/cos 2 x = tanx (63) dx/ 1 x 2 = arcsinx (64) dx/(x 2 +1) = arctanx (65) e x dx = e x (66) 125
129 Expanding the Tables: (af(x)+bg(x))dx = a f dx+b gdx+c If F(x) = f(x)dx, then f(kx)dx = 1 k F(kx)+C E.g. sin(ωt)dt = 1 ω cos(ωt)+c, e 2x dx = 1 2 e 2x +C,
130 Finding C. Let F(x) - some A.D. of f(x). We want to construct a specific A.D. which satisfies F(x 0 ) = A. The general form is F(x)+C AND F(x 0 )+C = A, i.e. C = A F(x 0 ) Thus, we solved a differential equation (F) = f with additional initial (or boundary ) condition F(x 0 ) = A. 127
131 E.g., dx/dt = 4t 3 +4t, x(0) = 7 x(t) = (4t 3 +4t)dt = t 4 +2t 2 +C, C = 7 E.g., free fall with dv/dt = g = const, v(0) = V 0, dy/dt = v, y(0) = Y 0. (2 equations) v(t) = ( g)dt = gt+c, C = V 0 y(t) = v(t)dt = 1 2 gt2 +V 0 t+c 1, C 1 = Y 0 E.g., 1-d motion with a = 4e 2t, v(0) = 7, x(0) = 3. v(t) = 2e 2t +C, C = 7 2e 0 = 5 x(t) = e 2t +5t+C 1, C 1 = 3 e = 2 128
132 Small x approximations (from l Hopital) (1+x) k 1 kx (67) e x 1 x, a x 1 xlna (68) ln(1+x) x (69) sinx tanx x (70) x sinx x 3 /6 (71) tanx x x 3 /3 (72) 1 cosx x 2 /2 (73) 129
133 More examples on limits lim x 4x 2 1 x π = 2 lim x 0 2 sinx 1 x = ln2 lim x 0 (1+2x)5/x = e 10 πx lim cos x 0 sinx = 1 ( lim e 2x +e x 1 ) 2/x = e 6 x 0 130
134 y x
135 y x 134
136 v v t t 135
137 4 y x 136
138 Σ-notations N k=1 k - dummy variable: a k = a 1 +a a N N k=1 a k = N i=1 a i = N 1 a m+1 m=0 N k=1 f(a k ) = f(a 1 )+f(a 2 )+...f(a N ) 137
139 N k=1 k = N = N(N +1) 2 (74) Indeed, consider and add (N 1)+N N +(N 1) Also, N k=1 k 2 = N 2 = N(N +1)(2N +1) 6 138
140 Area under a straight line Consider v(t) = t (acceleration = 1 and v(0) = 0) and look for displacement from t = 0 to arbitrary t (in the picture, t = 1). Use discrete t k = k t = v k, t = t N N 1 k=1 v k t = ( t) 2N(N 1) 2 = 1 2 t2 (1 1 N ) 139
141 Area under a parabola Consider y = x 2 and look for area between a = 0 and arbitrary b > 0. Use discrete x k = k x, y k = (k x) 2, x = b a N N 1 k=1 y k x = ( x) 3N(N 1)(2N 1) 6 = 1 3 b3 (1 1 N )(1 1 2N ) 140
142 Riemann Sums Partition P = { a = x 0 < x 1 < x 2 <... < x N 1 < x N = b } x k = x k x k 1, P = max[ x k ] x k 1 c k x k R.S. : N k=1 f(c k ) x k (75) f(c k ) = maxf(x), x k 1 x x k - upper sum. f(c k ) = minf(x), x k 1 x x k - lower sum. 141
143 4 y x 142
144 1.0 y x
145 Definite integral: b a f(x)dx = lim P 0 = lim N N k=1 N k=1 f(c k ) x k = (76) f(c k ) x, x = b a N (77) area = b a f(x)dx, f(x) 0, b > a (78) 144
146 Mean Value Theorem: If f(x) is continuous on [a,b] then at some a c b f(c) = f = 1 b a b a f dx Proof: From min-max inequality min f f max f. Then use I.V.T. E.g., if b a f dx = 0, there is a root of f 145
147 Fundamental Theorem of Calculus. Pt.I If f(x) is continuous on [a,b] then F(x) = x a f(t)dt is continuous and diff. on (a,b) with d dx x a f(t)dt = f(x) (79) Part II ( Evaluation Theorem ): b a f(x)dx = F(b) F(a) = F(x) b a (80) where F is any A.D. of f. 146
148 E.g. (Pt. I): d dx a (a does not matter!) d dx x a x tsintdt = xsinx tsintdt = xsinx d dx x 2 a tsintdt = (x 2 sinx 2 ) dx2 dx =
149 E.g. (Pt.II): π 0 sinxdx = cosx π 0 = 2 π/ b dx cos 2 x = tanx π/4 0 = 1 dx x 2 +1 = arctanx 1 0 = π/4 2 1 dx/x = lnx 2 1 = ln2 0 eαx dx = 1 α eαx b 0 = eαb 1 α 148
150 The net change theorem F(b) F(a) = b a F (x)dx s(t 2 ) s(t 1 ) = t2 t 1 v(t)dt 149
151 b area = f(x) dx a not convenient since don t know A.D. for f. 2π 0 sinx dx = cosx π 0 + cosx 2π π = 4 f = x(x+1)(x 2), F(x) = x 4 /4 x 3 /3 x 2 area = 0 2 f dx 1 0 f dx = F(0) F( 1) [F(2) F(0)] =
152 y x 2 3 x x F(x) = x 3 /3 3x 2 /2, A = [F( 3) F( 8)]+F(0) F( 3) [F(2) F(0)] 151
153 y x 5 x x 0 sgn x F(x) = 5 6 x6/5 x 2 /2 area = 2[F(1) F(0)] [F(2) F(1)] =
154 Substitution method f(u)u (x)dx = f(u)du (81) dx = 1 k d(kx+b) (82) xdx = d(x 2 /2) (83) dx/x 2 = d(1/x) (84) dx/x = d(ln x ) (85) sinxdx = d(cosx) (86) cosxdx = d(sinx) (87) dx/cos 2 x = d(tanx) (88) e ax dx = 1 a d(eax ) (89) 153
155 f(kx+b)dx = 1 k f(kx+b)d(kx+b) = 1 k F(kx+b)+C kx+bdx = 1 k 2 3 (kx+b)3/2 +C sec 2 (kx+b)dx = 1 k tan(kx+b)+c xe x2 dx = x 2 e x3 dx = e x2 d(x 2 /2) = 1 2 ex2 +C e x3 d(x 3 /3) = 1 3 ex3 +C 154
156 I = I = secxdx = 1 2 cosxdx cos 2 x = ( 1 1 u + 1 ) 1+u du 1 u 2, u = sinx du = 1 2 ln 1+u 1 u +C I = x 2x+1dx = u 1 u ud 2 2, u = 2x+1, x = (u 1)/2 I = 1 4 (2 5 u5/2 2 3 u3/2 )+C =... u = cosx: tanxdx = sinxdx cosx = du u = ln u +C = ln secx +C 155
157 Substitution method for definite integrals b a f(u)u (x)dx = u(b) u(a) f(u)du (90) 1 1 x2 x 3 +1dx = 1 1 x 3 +1d (x3 +1) 3 or u = x 3 +1, u( 1) = 0, u(1) = udu = u3/2 1 0 = /2 = (x3 +1) 3/2 1 1 = /2 156
158 y 1.0 f u x 2 1 x u x u 157
159 u = cotx: π/2 π/4 cotxcsc2 xdx = cot π 2 cot π 4 udu = 1 2 u2 0 1 = 1 2 u = cosx: π/4 π/4 π/4 tanxdx = π/4 sinxdx cosx = cos(π/4) cos( π/4) 2 du 1/ u = 1/... =
160 y 4 y x2 2 x x sin x 1 sin 3 x x 1.0 a a f(x)dx = 2 a 0 f dx, (f even) a a f(x)dx = 0, (f odd) 159
161 Proof I = a 0 a f(x)dx = f(x)dx+ f(x)dx = I 1 +I 2 a a 0 I 1 = 0 a a f(x)dx = f( u)du = ± f(u)du = a 0 0 = ±I 2, ( + for even, for odd) E.g. 1 1 (x4 3x 3 +4x 2 +x 2)dx = (x4 +4x 2 2)dx =
162 Area between two curves y 3 A = b a (f g)dx, f(x) g(x) x 2 x 2 x
163 f = 2 x 2, g = x Intersection: f(x) = g(x), x = 1 and x = 2 A = 2 1 (2 x2 +x)dx = (2x x 3 /3+x 2 /2) 2 1 = = 2(2+1) 1 3 (23 +1)+ 1 2 (22 1) =... > 0 162
2.1 The derivative. Rates of change. m sec = y f (a + h) f (a)
 2.1 The derivative Rates of change 1 The slope of a secant line is m sec = y f (b) f (a) = x b a and represents the average rate of change over [a, b]. Letting b = a + h, we can express the slope of the
2.1 The derivative Rates of change 1 The slope of a secant line is m sec = y f (b) f (a) = x b a and represents the average rate of change over [a, b]. Letting b = a + h, we can express the slope of the
Solutions to Math 41 Final Exam December 10, 2012
 Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
Calculus I Review Solutions
 Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Chapter 2: Differentiation
 Chapter 2: Differentiation Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 82 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Chapter 2: Differentiation Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 82 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
1.1 Definition of a Limit. 1.2 Computing Basic Limits. 1.3 Continuity. 1.4 Squeeze Theorem
 1. Limits 1.1 Definition of a Limit 1.2 Computing Basic Limits 1.3 Continuity 1.4 Squeeze Theorem 1.1 Definition of a Limit The limit is the central object of calculus. It is a tool from which other fundamental
1. Limits 1.1 Definition of a Limit 1.2 Computing Basic Limits 1.3 Continuity 1.4 Squeeze Theorem 1.1 Definition of a Limit The limit is the central object of calculus. It is a tool from which other fundamental
WORKBOOK. MATH 31. CALCULUS AND ANALYTIC GEOMETRY I.
 WORKBOOK. MATH 31. CALCULUS AND ANALYTIC GEOMETRY I. DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE Contributors: U. N. Iyer and P. Laul. (Many problems have been directly taken from Single Variable Calculus,
WORKBOOK. MATH 31. CALCULUS AND ANALYTIC GEOMETRY I. DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE Contributors: U. N. Iyer and P. Laul. (Many problems have been directly taken from Single Variable Calculus,
Final Exam Review Exercise Set A, Math 1551, Fall 2017
 Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Sec 4.1 Limits, Informally. When we calculated f (x), we first started with the difference quotient. f(x + h) f(x) h
 1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
Learning Objectives for Math 165
 Learning Objectives for Math 165 Chapter 2 Limits Section 2.1: Average Rate of Change. State the definition of average rate of change Describe what the rate of change does and does not tell us in a given
Learning Objectives for Math 165 Chapter 2 Limits Section 2.1: Average Rate of Change. State the definition of average rate of change Describe what the rate of change does and does not tell us in a given
Math 147 Exam II Practice Problems
 Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Mth Review Problems for Test 2 Stewart 8e Chapter 3. For Test #2 study these problems, the examples in your notes, and the homework.
 For Test # study these problems, the examples in your notes, and the homework. Derivative Rules D [u n ] = nu n 1 du D [ln u] = du u D [log b u] = du u ln b D [e u ] = e u du D [a u ] = a u ln a du D [sin
For Test # study these problems, the examples in your notes, and the homework. Derivative Rules D [u n ] = nu n 1 du D [ln u] = du u D [log b u] = du u ln b D [e u ] = e u du D [a u ] = a u ln a du D [sin
Chapter 2: Differentiation
 Chapter 2: Differentiation Winter 2016 Department of Mathematics Hong Kong Baptist University 1 / 75 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Chapter 2: Differentiation Winter 2016 Department of Mathematics Hong Kong Baptist University 1 / 75 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
3.4 The Chain Rule. F (x) = f (g(x))g (x) Alternate way of thinking about it: If y = f(u) and u = g(x) where both are differentiable functions, then
 3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
Chapter 1: Limits and Continuity
 Chapter 1: Limits and Continuity Winter 2015 Department of Mathematics Hong Kong Baptist University 1/69 1.1 Examples where limits arise Calculus has two basic procedures: differentiation and integration.
Chapter 1: Limits and Continuity Winter 2015 Department of Mathematics Hong Kong Baptist University 1/69 1.1 Examples where limits arise Calculus has two basic procedures: differentiation and integration.
ECM Calculus and Geometry. Revision Notes
 ECM1702 - Calculus and Geometry Revision Notes Joshua Byrne Autumn 2011 Contents 1 The Real Numbers 1 1.1 Notation.................................................. 1 1.2 Set Notation...............................................
ECM1702 - Calculus and Geometry Revision Notes Joshua Byrne Autumn 2011 Contents 1 The Real Numbers 1 1.1 Notation.................................................. 1 1.2 Set Notation...............................................
Topics and Concepts. 1. Limits
 Topics and Concepts 1. Limits (a) Evaluating its (Know: it exists if and only if the it from the left is the same as the it from the right) (b) Infinite its (give rise to vertical asymptotes) (c) Limits
Topics and Concepts 1. Limits (a) Evaluating its (Know: it exists if and only if the it from the left is the same as the it from the right) (b) Infinite its (give rise to vertical asymptotes) (c) Limits
Unit #3 : Differentiability, Computing Derivatives, Trig Review
 Unit #3 : Differentiability, Computing Derivatives, Trig Review Goals: Determine when a function is differentiable at a point Relate the derivative graph to the the graph of an original function Compute
Unit #3 : Differentiability, Computing Derivatives, Trig Review Goals: Determine when a function is differentiable at a point Relate the derivative graph to the the graph of an original function Compute
2.2 The derivative as a Function
 2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
Foundations of Calculus. November 18, 2014
 Foundations of Calculus November 18, 2014 Contents 1 Conic Sections 3 11 A review of the coordinate system 3 12 Conic Sections 4 121 Circle 4 122 Parabola 5 123 Ellipse 5 124 Hyperbola 6 2 Review of Functions
Foundations of Calculus November 18, 2014 Contents 1 Conic Sections 3 11 A review of the coordinate system 3 12 Conic Sections 4 121 Circle 4 122 Parabola 5 123 Ellipse 5 124 Hyperbola 6 2 Review of Functions
Limit. Chapter Introduction
 Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
Unit #3 : Differentiability, Computing Derivatives
 Unit #3 : Differentiability, Computing Derivatives Goals: Determine when a function is differentiable at a point Relate the derivative graph to the the graph of an original function Compute derivative
Unit #3 : Differentiability, Computing Derivatives Goals: Determine when a function is differentiable at a point Relate the derivative graph to the the graph of an original function Compute derivative
Formulas that must be memorized:
 Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
MATH 408N PRACTICE FINAL
 2/03/20 Bormashenko MATH 408N PRACTICE FINAL Show your work for all the problems. Good luck! () Let f(x) = ex e x. (a) [5 pts] State the domain and range of f(x). Name: TA session: Since e x is defined
2/03/20 Bormashenko MATH 408N PRACTICE FINAL Show your work for all the problems. Good luck! () Let f(x) = ex e x. (a) [5 pts] State the domain and range of f(x). Name: TA session: Since e x is defined
Lecture 5: Integrals and Applications
 Lecture 5: Integrals and Applications Lejla Batina Institute for Computing and Information Sciences Digital Security Version: spring 2012 Lejla Batina Version: spring 2012 Wiskunde 1 1 / 21 Outline The
Lecture 5: Integrals and Applications Lejla Batina Institute for Computing and Information Sciences Digital Security Version: spring 2012 Lejla Batina Version: spring 2012 Wiskunde 1 1 / 21 Outline The
Calculus 1 Exam 1 MAT 250, Spring 2011 D. Ivanšić. Name: Show all your work!
 Calculus 1 Exam 1 MAT 250, Spring 2011 D. Ivanšić Name: Show all your work! 1. (16pts) Use the graph of the function to answer the following. Justify your answer if a limit does not exist. lim x 2 f(x)
Calculus 1 Exam 1 MAT 250, Spring 2011 D. Ivanšić Name: Show all your work! 1. (16pts) Use the graph of the function to answer the following. Justify your answer if a limit does not exist. lim x 2 f(x)
Blue Pelican Calculus First Semester
 Blue Pelican Calculus First Semester Student Version 1.01 Copyright 2011-2013 by Charles E. Cook; Refugio, Tx Edited by Jacob Cobb (All rights reserved) Calculus AP Syllabus (First Semester) Unit 1: Function
Blue Pelican Calculus First Semester Student Version 1.01 Copyright 2011-2013 by Charles E. Cook; Refugio, Tx Edited by Jacob Cobb (All rights reserved) Calculus AP Syllabus (First Semester) Unit 1: Function
f(x 0 + h) f(x 0 ) h slope of secant line = m sec
 Derivatives Using limits, we can define the slope of a tangent line to a function. When given a function f(x), and given a point P (x 0, f(x 0 )) on f, if we want to find the slope of the tangent line
Derivatives Using limits, we can define the slope of a tangent line to a function. When given a function f(x), and given a point P (x 0, f(x 0 )) on f, if we want to find the slope of the tangent line
Chapter 3: Transcendental Functions
 Chapter 3: Transcendental Functions Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 32 Except for the power functions, the other basic elementary functions are also called the transcendental
Chapter 3: Transcendental Functions Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 32 Except for the power functions, the other basic elementary functions are also called the transcendental
AP Calculus BC Chapter 4 AP Exam Problems. Answers
 AP Calculus BC Chapter 4 AP Exam Problems Answers. A 988 AB # 48%. D 998 AB #4 5%. E 998 BC # % 5. C 99 AB # % 6. B 998 AB #80 48% 7. C 99 AB #7 65% 8. C 998 AB # 69% 9. B 99 BC # 75% 0. C 998 BC # 80%.
AP Calculus BC Chapter 4 AP Exam Problems Answers. A 988 AB # 48%. D 998 AB #4 5%. E 998 BC # % 5. C 99 AB # % 6. B 998 AB #80 48% 7. C 99 AB #7 65% 8. C 998 AB # 69% 9. B 99 BC # 75% 0. C 998 BC # 80%.
Math 180, Final Exam, Fall 2012 Problem 1 Solution
 Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
Math Exam 02 Review
 Math 10350 Exam 02 Review 1. A differentiable function g(t) is such that g(2) = 2, g (2) = 1, g (2) = 1/2. (a) If p(t) = g(t)e t2 find p (2) and p (2). (Ans: p (2) = 7e 4 ; p (2) = 28.5e 4 ) (b) If f(t)
Math 10350 Exam 02 Review 1. A differentiable function g(t) is such that g(2) = 2, g (2) = 1, g (2) = 1/2. (a) If p(t) = g(t)e t2 find p (2) and p (2). (Ans: p (2) = 7e 4 ; p (2) = 28.5e 4 ) (b) If f(t)
Inverse Trig Functions
 6.6i Inverse Trigonometric Functions Inverse Sine Function Does g(x) = sin(x) have an inverse? What restriction would we need to make so that at least a piece of this function has an inverse? Given f (x)
6.6i Inverse Trigonometric Functions Inverse Sine Function Does g(x) = sin(x) have an inverse? What restriction would we need to make so that at least a piece of this function has an inverse? Given f (x)
ORDINARY DIFFERENTIAL EQUATIONS
 ORDINARY DIFFERENTIAL EQUATIONS Basic concepts: Find y(x) where x is the independent and y the dependent varible, based on an equation involving x, y(x), y 0 (x),...e.g.: y 00 (x) = 1+y(x) y0 (x) 1+x or,
ORDINARY DIFFERENTIAL EQUATIONS Basic concepts: Find y(x) where x is the independent and y the dependent varible, based on an equation involving x, y(x), y 0 (x),...e.g.: y 00 (x) = 1+y(x) y0 (x) 1+x or,
Lecture 4: Integrals and applications
 Lecture 4: Integrals and applications Lejla Batina Institute for Computing and Information Sciences Digital Security Version: autumn 2013 Lejla Batina Version: autumn 2013 Calculus en Kansrekenen 1 / 18
Lecture 4: Integrals and applications Lejla Batina Institute for Computing and Information Sciences Digital Security Version: autumn 2013 Lejla Batina Version: autumn 2013 Calculus en Kansrekenen 1 / 18
Math 106 Calculus 1 Topics for first exam
 Math 06 Calculus Topics for first exam Precalculus = what comes before its. Lines and their slopes: slope= rise over run = (change in y-value)/(corresponding change in x value) y y 0 slope-intercept: y
Math 06 Calculus Topics for first exam Precalculus = what comes before its. Lines and their slopes: slope= rise over run = (change in y-value)/(corresponding change in x value) y y 0 slope-intercept: y
Week 1: need to know. November 14, / 20
 Week 1: need to know How to find domains and ranges, operations on functions (addition, subtraction, multiplication, division, composition), behaviors of functions (even/odd/ increasing/decreasing), library
Week 1: need to know How to find domains and ranges, operations on functions (addition, subtraction, multiplication, division, composition), behaviors of functions (even/odd/ increasing/decreasing), library
Derivative of a Function
 Derivative of a Function (x+δx,f(x+δx)) f ' (x) = (x,f(x)) provided the limit exists Can be interpreted as the slope of the tangent line to the curve at any point (x, f(x)) on the curve. This generalizes
Derivative of a Function (x+δx,f(x+δx)) f ' (x) = (x,f(x)) provided the limit exists Can be interpreted as the slope of the tangent line to the curve at any point (x, f(x)) on the curve. This generalizes
Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3)
 Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
MATH 1A - FINAL EXAM DELUXE - SOLUTIONS. x x x x x 2. = lim = 1 =0. 2) Then ln(y) = x 2 ln(x) 3) ln(x)
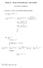 MATH A - FINAL EXAM DELUXE - SOLUTIONS PEYAM RYAN TABRIZIAN. ( points, 5 points each) Find the following limits (a) lim x x2 + x ( ) x lim x2 + x x2 + x 2 + + x x x x2 + + x x 2 + x 2 x x2 + + x x x2 +
MATH A - FINAL EXAM DELUXE - SOLUTIONS PEYAM RYAN TABRIZIAN. ( points, 5 points each) Find the following limits (a) lim x x2 + x ( ) x lim x2 + x x2 + x 2 + + x x x x2 + + x x 2 + x 2 x x2 + + x x x2 +
f(x) g(x) = [f (x)g(x) dx + f(x)g (x)dx
 Chapter 7 is concerned with all the integrals that can t be evaluated with simple antidifferentiation. Chart of Integrals on Page 463 7.1 Integration by Parts Like with the Chain Rule substitutions with
Chapter 7 is concerned with all the integrals that can t be evaluated with simple antidifferentiation. Chart of Integrals on Page 463 7.1 Integration by Parts Like with the Chain Rule substitutions with
Inverse Trigonometric Functions. September 5, 2018
 Inverse Trigonometric Functions September 5, 08 / 7 Restricted Sine Function. The trigonometric function sin x is not a one-to-one functions..0 0.5 Π 6, 5Π 6, Π Π Π Π 0.5 We still want an inverse, so what
Inverse Trigonometric Functions September 5, 08 / 7 Restricted Sine Function. The trigonometric function sin x is not a one-to-one functions..0 0.5 Π 6, 5Π 6, Π Π Π Π 0.5 We still want an inverse, so what
b n x n + b n 1 x n b 1 x + b 0
 Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
MATH 162 R E V I E W F I N A L E X A M FALL 2016
 MATH 6 R E V I E W F I N A L E X A M FALL 06 BASICS Graphs. Be able to graph basic functions, such as polynomials (eg, f(x) = x 3 x, x + ax + b, x(x ) (x + ) 3, know about the effect of multiplicity of
MATH 6 R E V I E W F I N A L E X A M FALL 06 BASICS Graphs. Be able to graph basic functions, such as polynomials (eg, f(x) = x 3 x, x + ax + b, x(x ) (x + ) 3, know about the effect of multiplicity of
Final Exam Solutions
 Final Exam Solutions Laurence Field Math, Section March, Name: Solutions Instructions: This exam has 8 questions for a total of points. The value of each part of each question is stated. The time allowed
Final Exam Solutions Laurence Field Math, Section March, Name: Solutions Instructions: This exam has 8 questions for a total of points. The value of each part of each question is stated. The time allowed
Calculus. Sungpyo Hong. Pohang University of Science and Technology
 Calculus Sungpyo Hong Pohang University of Science and Technology POSTECH 6 Preface Calculus is the most fundamental course in the study of science and engineering, whose main contents include the differentiation
Calculus Sungpyo Hong Pohang University of Science and Technology POSTECH 6 Preface Calculus is the most fundamental course in the study of science and engineering, whose main contents include the differentiation
Formulas to remember
 Complex numbers Let z = x + iy be a complex number The conjugate z = x iy Formulas to remember The real part Re(z) = x = z+z The imaginary part Im(z) = y = z z i The norm z = zz = x + y The reciprocal
Complex numbers Let z = x + iy be a complex number The conjugate z = x iy Formulas to remember The real part Re(z) = x = z+z The imaginary part Im(z) = y = z z i The norm z = zz = x + y The reciprocal
1. (16pts) Use the graph of the function to answer the following. Justify your answer if a limit does not exist. lim
 Spring 10/MAT 250/Exam 1 Name: Show all your work. 1. (16pts) Use the graph of the function to answer the following. Justify your answer if a limit does not exist. lim x 1 +f(x) = lim x 3 f(x) = lim x
Spring 10/MAT 250/Exam 1 Name: Show all your work. 1. (16pts) Use the graph of the function to answer the following. Justify your answer if a limit does not exist. lim x 1 +f(x) = lim x 3 f(x) = lim x
Math 2413 General Review for Calculus Last Updated 02/23/2016
 Math 243 General Review for Calculus Last Updated 02/23/206 Find the average velocity of the function over the given interval.. y = 6x 3-5x 2-8, [-8, ] Find the slope of the curve for the given value of
Math 243 General Review for Calculus Last Updated 02/23/206 Find the average velocity of the function over the given interval.. y = 6x 3-5x 2-8, [-8, ] Find the slope of the curve for the given value of
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
Final Exam. Math 3 December 7, 2010
 Final Exam Math 3 December 7, 200 Name: On this final examination for Math 3 in Fall 200, I will work individually, neither giving nor receiving help, guided by the Dartmouth Academic Honor Principle.
Final Exam Math 3 December 7, 200 Name: On this final examination for Math 3 in Fall 200, I will work individually, neither giving nor receiving help, guided by the Dartmouth Academic Honor Principle.
Old Math 220 Exams. David M. McClendon. Department of Mathematics Ferris State University
 Old Math 0 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Spring 05 Contents Contents General information about these exams 4 Exams from 0
Old Math 0 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Spring 05 Contents Contents General information about these exams 4 Exams from 0
f(g(x)) g (x) dx = f(u) du.
 1. Techniques of Integration Section 8-IT 1.1. Basic integration formulas. Integration is more difficult than derivation. The derivative of every rational function or trigonometric function is another
1. Techniques of Integration Section 8-IT 1.1. Basic integration formulas. Integration is more difficult than derivation. The derivative of every rational function or trigonometric function is another
Section 4.4. Using the Fundamental Theorem. Difference Equations to Differential Equations
 Difference Equations to Differential Equations Section 4.4 Using the Fundamental Theorem As we saw in Section 4.3, using the Fundamental Theorem of Integral Calculus reduces the problem of evaluating a
Difference Equations to Differential Equations Section 4.4 Using the Fundamental Theorem As we saw in Section 4.3, using the Fundamental Theorem of Integral Calculus reduces the problem of evaluating a
Friday 09/15/2017 Midterm I 50 minutes
 Fa 17: MATH 2924 040 Differential and Integral Calculus II Noel Brady Friday 09/15/2017 Midterm I 50 minutes Name: Student ID: Instructions. 1. Attempt all questions. 2. Do not write on back of exam sheets.
Fa 17: MATH 2924 040 Differential and Integral Calculus II Noel Brady Friday 09/15/2017 Midterm I 50 minutes Name: Student ID: Instructions. 1. Attempt all questions. 2. Do not write on back of exam sheets.
4 Partial Differentiation
 4 Partial Differentiation Many equations in engineering, physics and mathematics tie together more than two variables. For example Ohm s Law (V = IR) and the equation for an ideal gas, PV = nrt, which
4 Partial Differentiation Many equations in engineering, physics and mathematics tie together more than two variables. For example Ohm s Law (V = IR) and the equation for an ideal gas, PV = nrt, which
Math 226 Calculus Spring 2016 Exam 2V1
 Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Calculus II Lecture Notes
 Calculus II Lecture Notes David M. McClendon Department of Mathematics Ferris State University 206 edition Contents Contents 2 Review of Calculus I 5. Limits..................................... 7.2 Derivatives...................................3
Calculus II Lecture Notes David M. McClendon Department of Mathematics Ferris State University 206 edition Contents Contents 2 Review of Calculus I 5. Limits..................................... 7.2 Derivatives...................................3
AP Calculus ---Notecards 1 20
 AP Calculus ---Notecards 1 20 NC 1 For a it to exist, the left-handed it must equal the right sided it x c f(x) = f(x) = L + x c A function can have a it at x = c even if there is a hole in the graph at
AP Calculus ---Notecards 1 20 NC 1 For a it to exist, the left-handed it must equal the right sided it x c f(x) = f(x) = L + x c A function can have a it at x = c even if there is a hole in the graph at
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
 Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
4. Theory of the Integral
 4. Theory of the Integral 4.1 Antidifferentiation 4.2 The Definite Integral 4.3 Riemann Sums 4.4 The Fundamental Theorem of Calculus 4.5 Fundamental Integration Rules 4.6 U-Substitutions 4.1 Antidifferentiation
4. Theory of the Integral 4.1 Antidifferentiation 4.2 The Definite Integral 4.3 Riemann Sums 4.4 The Fundamental Theorem of Calculus 4.5 Fundamental Integration Rules 4.6 U-Substitutions 4.1 Antidifferentiation
2.1 The Tangent and Velocity Problems
 2.1 The Tangent and Velocity Problems Tangents What is a tangent? Tangent lines and Secant lines Estimating slopes from discrete data: Example: 1. A tank holds 1000 gallons of water, which drains from
2.1 The Tangent and Velocity Problems Tangents What is a tangent? Tangent lines and Secant lines Estimating slopes from discrete data: Example: 1. A tank holds 1000 gallons of water, which drains from
Calculus & Analytic Geometry I
 TQS 124 Autumn 2008 Quinn Calculus & Analytic Geometry I The Derivative: Analytic Viewpoint Derivative of a Constant Function. For c a constant, the derivative of f(x) = c equals f (x) = Derivative of
TQS 124 Autumn 2008 Quinn Calculus & Analytic Geometry I The Derivative: Analytic Viewpoint Derivative of a Constant Function. For c a constant, the derivative of f(x) = c equals f (x) = Derivative of
Math 1431 Final Exam Review
 Math 1431 Final Exam Review Comprehensive exam. I recommend you study all past reviews and practice exams as well. Know all rules/formulas. Make a reservation for the final exam. If you miss it, go back
Math 1431 Final Exam Review Comprehensive exam. I recommend you study all past reviews and practice exams as well. Know all rules/formulas. Make a reservation for the final exam. If you miss it, go back
M152: Calculus II Midterm Exam Review
 M52: Calculus II Midterm Exam Review Chapter 4. 4.2 : Mean Value Theorem. - Know the statement and idea of Mean Value Theorem. - Know how to find values of c making the theorem true. - Realize the importance
M52: Calculus II Midterm Exam Review Chapter 4. 4.2 : Mean Value Theorem. - Know the statement and idea of Mean Value Theorem. - Know how to find values of c making the theorem true. - Realize the importance
Test one Review Cal 2
 Name: Class: Date: ID: A Test one Review Cal 2 Short Answer. Write the following expression as a logarithm of a single quantity. lnx 2ln x 2 ˆ 6 2. Write the following expression as a logarithm of a single
Name: Class: Date: ID: A Test one Review Cal 2 Short Answer. Write the following expression as a logarithm of a single quantity. lnx 2ln x 2 ˆ 6 2. Write the following expression as a logarithm of a single
More Final Practice Problems
 8.0 Calculus Jason Starr Final Exam at 9:00am sharp Fall 005 Tuesday, December 0, 005 More 8.0 Final Practice Problems Here are some further practice problems with solutions for the 8.0 Final Exam. Many
8.0 Calculus Jason Starr Final Exam at 9:00am sharp Fall 005 Tuesday, December 0, 005 More 8.0 Final Practice Problems Here are some further practice problems with solutions for the 8.0 Final Exam. Many
Chapter 6. Techniques of Integration. 6.1 Differential notation
 Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Math 106 Calculus 1 Topics for first exam
 Chapter 2: Limits and Continuity Rates of change and its: Math 06 Calculus Topics for first exam Limit of a function f at a point a = the value the function should take at the point = the value that the
Chapter 2: Limits and Continuity Rates of change and its: Math 06 Calculus Topics for first exam Limit of a function f at a point a = the value the function should take at the point = the value that the
MATH 409 Advanced Calculus I Lecture 11: More on continuous functions.
 MATH 409 Advanced Calculus I Lecture 11: More on continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if for any ε > 0 there
MATH 409 Advanced Calculus I Lecture 11: More on continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if for any ε > 0 there
December Exam Summary
 December Exam Summary 1 Lines and Distances 1.1 List of Concepts Distance between two numbers on the real number line or on the Cartesian Plane. Increments. If A = (a 1, a 2 ) and B = (b 1, b 2 ), then
December Exam Summary 1 Lines and Distances 1.1 List of Concepts Distance between two numbers on the real number line or on the Cartesian Plane. Increments. If A = (a 1, a 2 ) and B = (b 1, b 2 ), then
AP Calculus Summer Prep
 AP Calculus Summer Prep Topics from Algebra and Pre-Calculus (Solutions are on the Answer Key on the Last Pages) The purpose of this packet is to give you a review of basic skills. You are asked to have
AP Calculus Summer Prep Topics from Algebra and Pre-Calculus (Solutions are on the Answer Key on the Last Pages) The purpose of this packet is to give you a review of basic skills. You are asked to have
Chapter 6. Techniques of Integration. 6.1 Differential notation
 Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Your signature: (1) (Pre-calculus Review Set Problems 80 and 124.)
 (1) (Pre-calculus Review Set Problems 80 an 14.) (a) Determine if each of the following statements is True or False. If it is true, explain why. If it is false, give a counterexample. (i) If a an b are
(1) (Pre-calculus Review Set Problems 80 an 14.) (a) Determine if each of the following statements is True or False. If it is true, explain why. If it is false, give a counterexample. (i) If a an b are
Math Final Exam Review
 Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
There are some trigonometric identities given on the last page.
 MA 114 Calculus II Fall 2015 Exam 4 December 15, 2015 Name: Section: Last 4 digits of student ID #: No books or notes may be used. Turn off all your electronic devices and do not wear ear-plugs during
MA 114 Calculus II Fall 2015 Exam 4 December 15, 2015 Name: Section: Last 4 digits of student ID #: No books or notes may be used. Turn off all your electronic devices and do not wear ear-plugs during
Chapter P: Preliminaries
 Chapter P: Preliminaries Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 67 Preliminaries The preliminary chapter reviews the most important things that you should know before beginning
Chapter P: Preliminaries Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 67 Preliminaries The preliminary chapter reviews the most important things that you should know before beginning
Chapter 2: Functions, Limits and Continuity
 Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
Functions and Graphs. Chapter Numbers (1.2.1, 1.2.4)
 Chapter 1 Functions and Graphs 1.1 Numbers (1.2.1, 1.2.4) The most fundamental type of number are those we use to count with: 0,1,2,... These are called the natural numbers: the set of all natural numbers
Chapter 1 Functions and Graphs 1.1 Numbers (1.2.1, 1.2.4) The most fundamental type of number are those we use to count with: 0,1,2,... These are called the natural numbers: the set of all natural numbers
Math 180, Exam 2, Practice Fall 2009 Problem 1 Solution. f(x) = arcsin(2x + 1) = sin 1 (3x + 1), lnx
 Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
SANDERSON HIGH SCHOOL AP CALCULUS AB/BC SUMMER REVIEW PACKET
 SANDERSON HIGH SCHOOL AP CALCULUS AB/BC SUMMER REVIEW PACKET 017-018 Name: 1. This packet is to be handed in on Monday August 8, 017.. All work must be shown on separate paper attached to the packet. 3.
SANDERSON HIGH SCHOOL AP CALCULUS AB/BC SUMMER REVIEW PACKET 017-018 Name: 1. This packet is to be handed in on Monday August 8, 017.. All work must be shown on separate paper attached to the packet. 3.
Day 3 Review of Basic Calculus
 Day 3 Review of Basic Calculus Sivaram sivaambi@stanford.edu Institute of Computational and Mathematical Engineering Stanford University September 21, 2011 Differential Calculus Product rule Quotient rule
Day 3 Review of Basic Calculus Sivaram sivaambi@stanford.edu Institute of Computational and Mathematical Engineering Stanford University September 21, 2011 Differential Calculus Product rule Quotient rule
Math 2250 Final Exam Practice Problem Solutions. f(x) = ln x x. 1 x. lim. lim. x x = lim. = lim 2
 Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Chapter 7: Techniques of Integration
 Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Brief answers to assigned even numbered problems that were not to be turned in
 Brief answers to assigned even numbered problems that were not to be turned in Section 2.2 2. At point (x 0, x 2 0) on the curve the slope is 2x 0. The point-slope equation of the tangent line to the curve
Brief answers to assigned even numbered problems that were not to be turned in Section 2.2 2. At point (x 0, x 2 0) on the curve the slope is 2x 0. The point-slope equation of the tangent line to the curve
This Week. Professor Christopher Hoffman Math 124
 This Week Sections 2.1-2.3,2.5,2.6 First homework due Tuesday night at 11:30 p.m. Average and instantaneous velocity worksheet Tuesday available at http://www.math.washington.edu/ m124/ (under week 2)
This Week Sections 2.1-2.3,2.5,2.6 First homework due Tuesday night at 11:30 p.m. Average and instantaneous velocity worksheet Tuesday available at http://www.math.washington.edu/ m124/ (under week 2)
Review for the Final Exam
 Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
4.1 Analysis of functions I: Increase, decrease and concavity
 4.1 Analysis of functions I: Increase, decrease and concavity Definition Let f be defined on an interval and let x 1 and x 2 denote points in that interval. a) f is said to be increasing on the interval
4.1 Analysis of functions I: Increase, decrease and concavity Definition Let f be defined on an interval and let x 1 and x 2 denote points in that interval. a) f is said to be increasing on the interval
Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued)
 Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued) Prove this Result How Can a Derivative Not Exist? Remember that the derivative at a point (or slope of a tangent line) is a LIMIT, so it doesn t exist whenever
Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued) Prove this Result How Can a Derivative Not Exist? Remember that the derivative at a point (or slope of a tangent line) is a LIMIT, so it doesn t exist whenever
PH1105 Lecture Notes on Calculus. Main Text: Calculus for the Life Sciences by. Bittenger, Brand and Quintanilla
 PH1105 Lecture Notes on Calculus Joe Ó hógáin E-mail: johog@maths.tcd.ie Main Text: Calculus for the Life Sciences by Other Text: Calculus by Bittenger, Brand and Quintanilla Anton, Bivens and Davis 1
PH1105 Lecture Notes on Calculus Joe Ó hógáin E-mail: johog@maths.tcd.ie Main Text: Calculus for the Life Sciences by Other Text: Calculus by Bittenger, Brand and Quintanilla Anton, Bivens and Davis 1
CALCULUS ASSESSMENT REVIEW
 CALCULUS ASSESSMENT REVIEW DEPARTMENT OF MATHEMATICS CHRISTOPHER NEWPORT UNIVERSITY 1. Introduction and Topics The purpose of these notes is to give an idea of what to expect on the Calculus Readiness
CALCULUS ASSESSMENT REVIEW DEPARTMENT OF MATHEMATICS CHRISTOPHER NEWPORT UNIVERSITY 1. Introduction and Topics The purpose of these notes is to give an idea of what to expect on the Calculus Readiness
Calculus I Sample Exam #01
 Calculus I Sample Exam #01 1. Sketch the graph of the function and define the domain and range. 1 a) f( x) 3 b) g( x) x 1 x c) hx ( ) x x 1 5x6 d) jx ( ) x x x 3 6 . Evaluate the following. a) 5 sin 6
Calculus I Sample Exam #01 1. Sketch the graph of the function and define the domain and range. 1 a) f( x) 3 b) g( x) x 1 x c) hx ( ) x x 1 5x6 d) jx ( ) x x x 3 6 . Evaluate the following. a) 5 sin 6
Techniques of Integration
 5 Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives
5 Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives
Math 131 Final Exam Spring 2016
 Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
1 The Derivative and Differrentiability
 1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
Calculus AB Topics Limits Continuity, Asymptotes
 Calculus AB Topics Limits Continuity, Asymptotes Consider f x 2x 1 x 3 1 x 3 x 3 Is there a vertical asymptote at x = 3? Do not give a Precalculus answer on a Calculus exam. Consider f x 2x 1 x 3 1 x 3
Calculus AB Topics Limits Continuity, Asymptotes Consider f x 2x 1 x 3 1 x 3 x 3 Is there a vertical asymptote at x = 3? Do not give a Precalculus answer on a Calculus exam. Consider f x 2x 1 x 3 1 x 3
AP Calculus Chapter 3 Testbank (Mr. Surowski)
 AP Calculus Chapter 3 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.). If f(x) = 0x 4 3 + x, then f (8) = (A) (B) 4 3 (C) 83 3 (D) 2 3 (E) 2
AP Calculus Chapter 3 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.). If f(x) = 0x 4 3 + x, then f (8) = (A) (B) 4 3 (C) 83 3 (D) 2 3 (E) 2
(e) 2 (f) 2. (c) + (d). Limits at Infinity. 2.5) 9-14,25-34,41-43,46-47,56-57, (c) (d) 2
 Math 150A. Final Review Answers, Spring 2018. Limits. 2.2) 7-10, 21-24, 28-1, 6-8, 4-44. 1. Find the values, or state they do not exist. (a) (b) 1 (c) DNE (d) 1 (e) 2 (f) 2 (g) 2 (h) 4 2. lim f(x) = 2,
Math 150A. Final Review Answers, Spring 2018. Limits. 2.2) 7-10, 21-24, 28-1, 6-8, 4-44. 1. Find the values, or state they do not exist. (a) (b) 1 (c) DNE (d) 1 (e) 2 (f) 2 (g) 2 (h) 4 2. lim f(x) = 2,
Math 229 Mock Final Exam Solution
 Name: Math 229 Mock Final Exam Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and that it
Name: Math 229 Mock Final Exam Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and that it
