Coherence with Proper Scoring Rules
|
|
|
- Rolf Austin
- 5 years ago
- Views:
Transcription
1 Coherence with Proper Scoring Rules Mark Schervish, Teddy Seidenfeld, and Joseph (Jay) Kadane Mark Schervish Joseph ( Jay ) Kadane Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
2 In this paper we explore three concepts of dominance (de Finetti) coherence : Coherence 1 for previsions of random variables with generalized betting; Coherence 2 for probability forecasts of events with Brier score penalty; Coherence 3 probability forecasts of events with various proper scoring rules. In order to show that these variations on coherence are equivalent we use Minimiax theory to relate dominance and Bayes s decisions, generally. With each proper scoring rule, assuming that (simple) mixed strategies are available, all and only non-bayes forecasts are dominated options. This extends de Finetti s result that Coherence 1 and Coherence 2 are equivalent, to include Coherence 3. However, unless the proper scoring rules are continuous, Coherence 3 is not equivalent to the other two senses without the use of incoherent mixed strategy forecasts to dominate. That is, with discontinuous proper scores, no coherent forecast may dominate particular incoherent ones. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
3 1. Structural assumptions about preference used in this presentation. 1.1 Act-state independence: no cases of moral hazards are considered so strict dominance is valid. Reminder: Consider the following binary state, two act problem, with outcomes ordinally (or cardinally) ranked so that more is better. 1 2 Act Act Act 2 strictly dominates Act 1. Nonetheless, if Prob( i Act i ) 1 (i = 1, 2), then dominance carries no force. A rational decision maker then prefers Act 1 to Act 2. We consider decision problems without moral hazards. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
4 1.2 The focus here is on normal form (aka strategic form ) games/decisions. The decision maker can commit, in advance, to contingency planning. BUT conditional previsions/forecasts are represented using the device of a called-off options. Example: A bookie s called-off prevision on event A given event B the fair betting odds yields payoff to the bookie S A [ P B (A) ] Where: is the indicator function for event A. is the indicator function for event B. S A is the total stake (positive or negative) for the wager, fixed by a rival gambler. P B (A) is the bookie s conditional prevision or called-off fair-betting odds on A, given B. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
5 So, we bypass the difficult work that is needed when the conditioning event B is null: Coherence for called-off wagers impose no substantive constraint on the conditional prevision when the conditioning event is null. We make no assumption that normal and extensive form decisions are equivalent, and generally they will not be equivalent Aside: The non-equivalence is salient in decision theories with Indeterminate/Imprecise Probabilities IP Theory. This issue is important for so-called Dynamic Book arguments Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
6 2. de Finetti s Coherence 1 of previsions. An important, and historically early application of strict dominance in decision making is de Finetti s criterion of coherence 1 of previsions. Coherence 1 de Finetti s notion of coherence 1 begins with an arbitrary partition of states, = { i : i I}, and a class of bounded real-valued variables, = {X j : j J}, defined on. For each random variable X, the rational agent has a (two-sided) prevision P(X) which is to be interpreted as a fair price (both for buying and selling) gambles. For all real > 0, small enough so that the agent is willing to pay the possible losses, the agent is willing to pay P(X) in order to buy (i.e., to receive) X in return. and, is willing to accept P(X) in order to sell (i.e., to pay) X in return. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
7 The agent will accept the gamble [X P(X)] as a change in fortune, for all sufficiently small (positive or negative). The agent is required to accept all finite sums of gambles of the preceding form. That is, for all finite n and all small, real and all, the agent will accept the combination of gambles P(X. Where i is positive, the agent buys i -units of X i for a price of i P(X i ) where it is negative, the agent sells i -units of X i for a price of i P(X i ). The previsions are incoherent 1 if there is a uniformly negative acceptable finite combination of gambles. That is, if there exists a sum of the form above and such that, for each, P(X < -. Otherwise the agent s previsions are coherent 1. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
8 Where previsions are incoherent 1, the book that indicates this constitutes a combination of gambles that is uniformly, strictly dominated by not-betting (= 0). de Finetti s Coherence 1 Theorem: A set of previsions are coherent 1 if and only if they are the expected values for the respective random variables under a (finitely additive) probability distribution over. When the variables are indicator functions for events (subsets of ), coherent previsions are exactly those in agreement with a (finitely additive) probability. And then the are the stakes in winner-takeall bets, where the previsions fix betting rates, P(X : 1-P(X Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
9 De Finetti s result applies to conditional previsions, given an event B. These use called-off gambles of the form [X P(X)] where is the indicator function for the conditioning event B. Then, with the proviso about non-null conditioning events, coherence 1 assures that coherent called off (2-sided) previsions are finitely additive conditional expectations, given the conditioning event. When the random variables, X i, include indicator functions for events, the resulting coherent 1 previsions include conditional probabilities for these events. Note well: Called-off previsions correspond only to normal form, and not to extensive form decisions. There is no dynamical coherence in de Finetti s theory. His theory covers merely static aspects of coherence 1. Thus, de Finetti s theory of coherence 1 does not require updating/learning by Bayesian conditional probabilities. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
10 3. de Finetti s Coherence 2 of forecasts with Brier-score. In a 1981 note to the BJPS de Finetti explains some of his motives for introducing (in 1974) a second, but equivalent concept of coherence. o The betting context for coherence 1 also serves as an elicitation of the bookie s previsions. But the bookie s announced previsions may reflect strategic aspects of the game-like interaction with the rival gambler. The gambler plays second, after the bookie has announced her/his fair previsions. The bookie may anticipate this and play strategically. o The bookie s previsions may change upon learning which bets the gambler has chosen. Using the ruler changes the length of the object measured. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
11 Brier score squared error loss. The loss (negative utility) that attaches to a prevision P(X) is -(X P(X)) 2. The called-off loss for a conditional prevision P(X) given event B is -B(X P(X)) 2. The combined losses from a finite set of (called-off) previsions is the sum of the individual losses just as payoffs from bets are added together with coherence 1. o Coherence 2 : A set of previsions is incoherent 2 if for some finite subset of those previsions, there exist a rival set of forecasts that dominace, by resulting in a (uniformly) smaller Brier score loss over all states. The previsions are coherent 2, otherwise. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
12 If a forecaster makes decisions by maximizing subjective expected utility, and since the mean of a distribution (uniquely) minimizes mean-squared error, then her/his announced previsions will be her/his honest previsions her/his degrees of belief when forecasting events including announcing conditional previsions for called-off forecasts. o Thus, Brier score is (strictly) proper it elicits the forecaster s conditional expected value of the variable X, given event B. De Finetti established equivalence between coherence 1 and coherence 2 with an elegant, geometric argument. The distance from an incoherent 1 forecast Q to a corner of the probability simplex is greater than the corresponding distance to that corner from the coherent 1 forecast that is the projection of Q onto the probability simplex. If P is coherent 1 forecast, hence a point in the probability simplex, there is no other point that has smaller distance to each corner of the simplex. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
13 (0, 1) P(A c ) (.60,.70) de Finetti projection (.45,.55) (0, 0) (1, 0) P(A) Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
14 4. Coherence 3 of forecasts with proper scores. Brier score is just one of an infinite class of (strictly) proper scoring rules. A scoring rule for forecasting an event A given event B, the called-off score for the forecast P(A B), is defined by two extended real-valued loss functions (g 0, g 1 ), with arguments from [0,1], as follows. if A occurs, the loss is Bg 1 ( P(A B) ) and if A c occurs, the loss is Bg 0 ( P(A B) ). As before, with a finite set of called-off forecasts, even using different scoring rules for different forecasts, the combined score is the sum of the individual scores. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
15 A scoring rule (as a loss function) for forecasting A, given B, is (strictly) proper provided that a decision maker who maximizes subjective expected utility (uniquely) minimizes expected score by using her/his conditional probability P(A B) as the called-off forecast. Thus (strictly) proper scores all elicit the same forecast as does Brier score. Savage (1971) and Schervish (1989) characterized the class of (strictly) proper scoring rules. For the results on coherence and dominance highlighted here, we do not need to review these characterizations of proper scoring rules. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
16 Surprisingly, neither de Finetti nor Savage gave us more than a brief sketch of their thinking whether (strictly) proper scoring rules all support the same concept of coherence. Do the same forecasts avoid dominance under all proper scoring rules? In what follows, we allow that the (strictly) proper scoring rule may vary with the event forecasted. {(g 0,Ai,Bi, g 1,Ai,Bi ): i = 1, } Coherence 3 : A collection of conditional forecasts for events is incoherent 3 if some finite sub-collection of those forecasts are uniformly dominated by some rival set of conditional forecasts. The forecasts are coherent 3, otherwise. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
17 Central Result: Subject to 3 mild constraints on these proper scoring rules (Assumptions 1-3, see below) and assuming that the forecaster can use simple mixed strategy forecasts then, (i) Coherence 1 and Coherence 3 are equivalent. (ii) Moreover, if the scoring rules are continuous, each incoherent forecast is dominated by some (non-mixed) coherent forecast. Assumptions: (1) For k = 0, 1 g k (x) is bounded below with g 0 (0) = g 1 (1) = 0. (2) For k = 0, 1 g k (x) is continuous at x = k. (3) For k = 0, 1 g k (x) is finite for 0 < x < 1. Aside: We give examples to support each of these assumptions. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
18 Here is an illustration (Example 3, p. 5) where in order to dominate an incoherent forecast, one must use a different incoherent forecast. This example uses a (strictly) proper scoring rule that is not continuous. Consider a binary partition {A, A c } and a common scoring rule for forecasting both events. x 2 if x < g 0 (x) = x 2 + if x > g 1 (x) = (1-x) 2 + (1-x) 2 if x < if x > The incoherent forecast pair (0.6, 0.7) with scores (1.15, 0.95) is not dominated by any coherent forecast, but the incoherent forecast pair (0.55, 0.65) dominates, with scores (1.125, 0.925). Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
19 Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
20 5. When non-bayes decisions may be dominated. Consider this decision problem on 2-states with three options. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
21 Now, consider the mixed strategy option, m which is.5f.5g. Observe that m dominates h. 1.0 Utility axis h m f g 1 P( 2 ) axis Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
22 Our approach for showing the equivalence among the different senses of coherence is to generalize this picture to apply it to forecasting under proper scoring rules. Ours is NOT a generalization of de Finetti s geometric argument, which is the focus of a paper by Predd et al. (2007). Instead we have generalized D.Pearce s (1984) game theoretic result about rationalizable strategies to cover certain semi-infinite 2-person 0-sum games. These are games where the Statistician has infinitely many pure strategy forecasts, and Nature has only finitely many pure strategies, corresponding to choosing from a finite partition of states. When the scoring rules are continuous, the game s solution set is closed (below) and pure strategies win for the Statistician. When the proper scoring rules are discontinuous, the game has a value but the solution set may be open (below), as in the Example. Then there is no Minimax solution for the Statistician. Only other non-bayes solutions may dominate a particular non-bayes forecast, as they form the epsilon-minimax strategies for the corresponding game. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
23 6. Summary and review. 1. Structural assumptions for this presentation. Moral hazards and dominance Normal versus extensive form decision making 2. de Finetti s coherence 1 of previsions. 3. de Finetti s coherence 2 of forecasts with Brier score. 4. Central result about the equivalence of all three coherence concepts An example of forecasts with a discontinuous (strictly) proper scores where no coherent forecast dominates some incoherent forecasts. 5. On dominance and rationalizability (D. Pearce s 1984 result) extended to semi-infinite 0-sum games against Nature. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
24 Example: Consider a countably infinite state space = { 1, 2,...} with its powerset serving as the -field of sets. Let the class of forecast variables be X = {W i : i = 1,...}, where W i is the indicator for event { i }. Consider a (purely) finitely additive probability with 0 probability for each atom: P( i ) = 0, i = 1,.... These form a coherent 1 set of previsions. But to secure coherence 1 only finitely many previsions may be used in betting. On the contrary, as de Finetti noted, were countably many previsions used simultaneously, then for each, choosing i = -1, yields the constant payoff: i -(W i ( ) - P[W i ]) = i -W i ( ) = -1, which is a sure loss of -1 to the bookie. However, the infinite set of forecasts {P[Wi] = 0} has a constant Brier score -1 = i -(W i ( ) - P[W i ]) 2, which is not dominated (let alone uniformly dominated) by any set of forecasts, { P [W i ] }, regardless whether or not these rival forecasts are coherent 1-or-2. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
25 This example generalizes to the following result. Proposition about coherence 2 of f.a. probability forecasts: (i) Call a set of variables {X i : i = 1,, } uniformly series-bounded, if there exists a real number b, so that for each, i X i ( ) < b When the class of forecast variables are uniformly series-bounded, it is not necessary to restrict Brier score to sums of finitely many unconditional forecasts in order that a set of finitely additive probability forecasts is undominated by a rival forecast set: coherence 2. Note: Series-boundedness is satisfied when forecasting events that form a partition. (ii) However, the previous result is modest. It does not generalize to include called-off forecasts. Then, because of non-conglomerablity of merely finitely additive conditional probabilities, their coherence 2 depends upon the clause that only finitely many Brier scores from called-off forecasts are summed up simultaneously. Coherence with Proper Scoring Rules ILC, Sun Yat-Sen University June
Three contrasts between two senses of coherence
 Three contrasts between two senses of coherence Teddy Seidenfeld Joint work with M.J.Schervish and J.B.Kadane Statistics, CMU Call an agent s choices coherent when they respect simple dominance relative
Three contrasts between two senses of coherence Teddy Seidenfeld Joint work with M.J.Schervish and J.B.Kadane Statistics, CMU Call an agent s choices coherent when they respect simple dominance relative
Dominating countably many forecasts.* T. Seidenfeld, M.J.Schervish, and J.B.Kadane. Carnegie Mellon University. May 5, 2011
 Dominating countably many forecasts.* T. Seidenfeld, M.J.Schervish, and J.B.Kadane. Carnegie Mellon University May 5, 2011 Abstract We contrast de Finetti s two criteria for coherence in settings where
Dominating countably many forecasts.* T. Seidenfeld, M.J.Schervish, and J.B.Kadane. Carnegie Mellon University May 5, 2011 Abstract We contrast de Finetti s two criteria for coherence in settings where
Three grades of coherence for non-archimedean preferences
 Teddy Seidenfeld (CMU) in collaboration with Mark Schervish (CMU) Jay Kadane (CMU) Rafael Stern (UFdSC) Robin Gong (Rutgers) 1 OUTLINE 1. We review de Finetti s theory of coherence for a (weakly-ordered)
Teddy Seidenfeld (CMU) in collaboration with Mark Schervish (CMU) Jay Kadane (CMU) Rafael Stern (UFdSC) Robin Gong (Rutgers) 1 OUTLINE 1. We review de Finetti s theory of coherence for a (weakly-ordered)
Some Finitely Additive (Statistical) Decision Theory or How Bruno de Finetti might have channeled Abraham Wald
 Some Finitely Additive (Statistical) Decision Theory or How Bruno de Finetti might have channeled Abraham Wald T.Seidenfeld ------------ Based on our T.R.: What Finite Additivity Can Add to Decision Theory
Some Finitely Additive (Statistical) Decision Theory or How Bruno de Finetti might have channeled Abraham Wald T.Seidenfeld ------------ Based on our T.R.: What Finite Additivity Can Add to Decision Theory
DOMINATING COUNTABLY MANY FORECASTS. BY M. J. SCHERVISH, TEDDY SEIDENFELD AND J. B. KADANE Carnegie Mellon University
 The Annals of Statistics 2014, Vol. 42, No. 2, 728 756 DOI: 10.1214/14-AOS1203 Institute of Mathematical Statistics, 2014 DOMINATING COUNTABLY MANY FORECASTS BY M. J. SCHERVISH, TEDDY SEIDENFELD AND J.
The Annals of Statistics 2014, Vol. 42, No. 2, 728 756 DOI: 10.1214/14-AOS1203 Institute of Mathematical Statistics, 2014 DOMINATING COUNTABLY MANY FORECASTS BY M. J. SCHERVISH, TEDDY SEIDENFELD AND J.
Coherent Choice Functions Under Uncertainty* OUTLINE
 Coherent Choice Functions Under Uncertainty* Teddy Seidenfeld joint work with Jay Kadane and Mark Schervish Carnegie Mellon University OUTLINE 1. Preliminaries a. Coherent choice functions b. The framework
Coherent Choice Functions Under Uncertainty* Teddy Seidenfeld joint work with Jay Kadane and Mark Schervish Carnegie Mellon University OUTLINE 1. Preliminaries a. Coherent choice functions b. The framework
We begin by considering a slightly more general situation than that described above, both because it strengthens the results and because the most inte
 March 13,2002 Measures of incoherence: How not to gamble if you must MARK J. SCHERVISH, TEDDY SEIDENFELD and JOSEPH B. KADANE Carnegie Mellon University, USA SUMMARY The degree of incoherence, when previsions
March 13,2002 Measures of incoherence: How not to gamble if you must MARK J. SCHERVISH, TEDDY SEIDENFELD and JOSEPH B. KADANE Carnegie Mellon University, USA SUMMARY The degree of incoherence, when previsions
Teddy Seidenfeld, Mark J. Schervish, and Joseph B. Kadane
 When coherent preferences may not preserve indifference between equivalent random variables: A price for unbounded utilities.* Teddy Seidenfeld, Mark J. Schervish, and Joseph B. Kadane Abstract We extend
When coherent preferences may not preserve indifference between equivalent random variables: A price for unbounded utilities.* Teddy Seidenfeld, Mark J. Schervish, and Joseph B. Kadane Abstract We extend
ON THE EQUIVALENCE OF CONGLOMERABILITY AND DISINTEGRABILITY FOR UNBOUNDED RANDOM VARIABLES
 Submitted to the Annals of Probability ON THE EQUIVALENCE OF CONGLOMERABILITY AND DISINTEGRABILITY FOR UNBOUNDED RANDOM VARIABLES By Mark J. Schervish, Teddy Seidenfeld, and Joseph B. Kadane, Carnegie
Submitted to the Annals of Probability ON THE EQUIVALENCE OF CONGLOMERABILITY AND DISINTEGRABILITY FOR UNBOUNDED RANDOM VARIABLES By Mark J. Schervish, Teddy Seidenfeld, and Joseph B. Kadane, Carnegie
Extensions of Expected Utility Theory and some Limitations of Pairwise Comparisons
 Extensions of Expected Utility Theory and some Limitations of Pairwise Comparisons M. J. SCHERVISH Carnegie Mellon University, USA T. SEIDENFELD Carnegie Mellon University, USA J. B. KADANE Carnegie Mellon
Extensions of Expected Utility Theory and some Limitations of Pairwise Comparisons M. J. SCHERVISH Carnegie Mellon University, USA T. SEIDENFELD Carnegie Mellon University, USA J. B. KADANE Carnegie Mellon
Non-conglomerability for countably additive measures that are not -additive* Mark Schervish, Teddy Seidenfeld, and Joseph Kadane CMU
 Non-conglomerability for countably additive measures that are not -additive* Mark Schervish, Teddy Seidenfeld, and Joseph Kadane CMU Abstract Let be an uncountable cardinal. Using the theory of conditional
Non-conglomerability for countably additive measures that are not -additive* Mark Schervish, Teddy Seidenfeld, and Joseph Kadane CMU Abstract Let be an uncountable cardinal. Using the theory of conditional
A survey of the theory of coherent lower previsions
 A survey of the theory of coherent lower previsions Enrique Miranda Abstract This paper presents a summary of Peter Walley s theory of coherent lower previsions. We introduce three representations of coherent
A survey of the theory of coherent lower previsions Enrique Miranda Abstract This paper presents a summary of Peter Walley s theory of coherent lower previsions. We introduce three representations of coherent
A gentle introduction to imprecise probability models
 A gentle introduction to imprecise probability models and their behavioural interpretation Gert de Cooman gert.decooman@ugent.be SYSTeMS research group, Ghent University A gentle introduction to imprecise
A gentle introduction to imprecise probability models and their behavioural interpretation Gert de Cooman gert.decooman@ugent.be SYSTeMS research group, Ghent University A gentle introduction to imprecise
Probability COMP 245 STATISTICS. Dr N A Heard. 1 Sample Spaces and Events Sample Spaces Events Combinations of Events...
 Probability COMP 245 STATISTICS Dr N A Heard Contents Sample Spaces and Events. Sample Spaces........................................2 Events........................................... 2.3 Combinations
Probability COMP 245 STATISTICS Dr N A Heard Contents Sample Spaces and Events. Sample Spaces........................................2 Events........................................... 2.3 Combinations
Two theories of conditional probability and non-conglomerability
 8th International Symposium on Imprecise Probability: Theories and Applications, Compiègne, France, 2013 Two theories of conditional probability and non-conglomerability Teddy Seidenfeld Mark J. Schervish
8th International Symposium on Imprecise Probability: Theories and Applications, Compiègne, France, 2013 Two theories of conditional probability and non-conglomerability Teddy Seidenfeld Mark J. Schervish
Philosophy of Science, Vol. 50, No. 3. (Sep., 1983), pp
 A Conflict between Finite Additivity and Avoiding Dutch Book Teddy Seidenfeld; Mark J. Schervish Philosophy of Science, Vol. 50, No. 3. (Sep., 1983), pp. 398-412. Stable URL: http://links.jstor.org/sici?sici=0031-8248%28198309%2950%3a3%3c398%3aacbfaa%3e2.0.co%3b2-3
A Conflict between Finite Additivity and Avoiding Dutch Book Teddy Seidenfeld; Mark J. Schervish Philosophy of Science, Vol. 50, No. 3. (Sep., 1983), pp. 398-412. Stable URL: http://links.jstor.org/sici?sici=0031-8248%28198309%2950%3a3%3c398%3aacbfaa%3e2.0.co%3b2-3
Sequential Decisions
 Sequential Decisions A Basic Theorem of (Bayesian) Expected Utility Theory: If you can postpone a terminal decision in order to observe, cost free, an experiment whose outcome might change your terminal
Sequential Decisions A Basic Theorem of (Bayesian) Expected Utility Theory: If you can postpone a terminal decision in order to observe, cost free, an experiment whose outcome might change your terminal
Bayes Correlated Equilibrium and Comparing Information Structures
 Bayes Correlated Equilibrium and Comparing Information Structures Dirk Bergemann and Stephen Morris Spring 2013: 521 B Introduction game theoretic predictions are very sensitive to "information structure"
Bayes Correlated Equilibrium and Comparing Information Structures Dirk Bergemann and Stephen Morris Spring 2013: 521 B Introduction game theoretic predictions are very sensitive to "information structure"
This corresponds to a within-subject experiment: see same subject make choices from different menus.
 Testing Revealed Preference Theory, I: Methodology The revealed preference theory developed last time applied to a single agent. This corresponds to a within-subject experiment: see same subject make choices
Testing Revealed Preference Theory, I: Methodology The revealed preference theory developed last time applied to a single agent. This corresponds to a within-subject experiment: see same subject make choices
JOSEPH B. KADANE AND JIASHUN JIN, IN HONOR OF ARNOLD ZELLNER
 UNIFORM DISTRIBUTIONS ON THE INTEGERS: A CONNECTION TO THE BERNOUILLI RANDOM WALK JOSEPH B. KADANE AND JIASHUN JIN, IN HONOR OF ARNOLD ZELLNER Abstract. Associate to each subset of the integers its almost
UNIFORM DISTRIBUTIONS ON THE INTEGERS: A CONNECTION TO THE BERNOUILLI RANDOM WALK JOSEPH B. KADANE AND JIASHUN JIN, IN HONOR OF ARNOLD ZELLNER Abstract. Associate to each subset of the integers its almost
APM 421 Probability Theory Probability Notes. Jay Taylor Fall Jay Taylor (ASU) Fall / 62
 APM 421 Probability Theory Probability Notes Jay Taylor Fall 2013 Jay Taylor (ASU) Fall 2013 1 / 62 Motivation Scientific Determinism Scientific determinism holds that we can exactly predict how a system
APM 421 Probability Theory Probability Notes Jay Taylor Fall 2013 Jay Taylor (ASU) Fall 2013 1 / 62 Motivation Scientific Determinism Scientific determinism holds that we can exactly predict how a system
Correlated Equilibrium in Games with Incomplete Information
 Correlated Equilibrium in Games with Incomplete Information Dirk Bergemann and Stephen Morris Econometric Society Summer Meeting June 2012 Robust Predictions Agenda game theoretic predictions are very
Correlated Equilibrium in Games with Incomplete Information Dirk Bergemann and Stephen Morris Econometric Society Summer Meeting June 2012 Robust Predictions Agenda game theoretic predictions are very
ENGI 3423 Introduction to Probability; Sets & Venn Diagrams Page 3-01
 ENGI 3423 Introduction to Probability; Sets & Venn Diagrams Page 3-01 Probability Decision trees θ 1 u 1 α 1 θ 2 u 2 Decision α 2 θ 1 u 3 Actions Chance nodes States of nature θ 2 u 4 Consequences; utility
ENGI 3423 Introduction to Probability; Sets & Venn Diagrams Page 3-01 Probability Decision trees θ 1 u 1 α 1 θ 2 u 2 Decision α 2 θ 1 u 3 Actions Chance nodes States of nature θ 2 u 4 Consequences; utility
Sequential Decisions
 Sequential Decisions A Basic Theorem of (Bayesian) Expected Utility Theory: If you can postpone a terminal decision in order to observe, cost free, an experiment whose outcome might change your terminal
Sequential Decisions A Basic Theorem of (Bayesian) Expected Utility Theory: If you can postpone a terminal decision in order to observe, cost free, an experiment whose outcome might change your terminal
Preference, Choice and Utility
 Preference, Choice and Utility Eric Pacuit January 2, 205 Relations Suppose that X is a non-empty set. The set X X is the cross-product of X with itself. That is, it is the set of all pairs of elements
Preference, Choice and Utility Eric Pacuit January 2, 205 Relations Suppose that X is a non-empty set. The set X X is the cross-product of X with itself. That is, it is the set of all pairs of elements
Axiomatic Foundations of Expected Utility. and Subjective Probability
 Axiomatic Foundations of Expected Utility and Subjective Probability Edi Karni Johns Hopkins University April 29, 2013 This is a chapter commissioned for the Handbook of Risk and Uncertainty (Machina and
Axiomatic Foundations of Expected Utility and Subjective Probability Edi Karni Johns Hopkins University April 29, 2013 This is a chapter commissioned for the Handbook of Risk and Uncertainty (Machina and
COHERENCE AND PROBABILITY. Rosangela H. Loschi and Sergio Wechsler. Universidade Federal de Minas Gerais e Universidade de S~ao Paulo ABSTRACT
 COHERENCE AND PROBABILITY Rosangela H. Loschi and Sergio Wechsler Universidade Federal de Minas Gerais e Universidade de S~ao Paulo ABSTRACT A process of construction of subjective probability based on
COHERENCE AND PROBABILITY Rosangela H. Loschi and Sergio Wechsler Universidade Federal de Minas Gerais e Universidade de S~ao Paulo ABSTRACT A process of construction of subjective probability based on
Imprecise Probability
 Imprecise Probability Alexander Karlsson University of Skövde School of Humanities and Informatics alexander.karlsson@his.se 6th October 2006 0 D W 0 L 0 Introduction The term imprecise probability refers
Imprecise Probability Alexander Karlsson University of Skövde School of Humanities and Informatics alexander.karlsson@his.se 6th October 2006 0 D W 0 L 0 Introduction The term imprecise probability refers
Definitions and Proofs
 Giving Advice vs. Making Decisions: Transparency, Information, and Delegation Online Appendix A Definitions and Proofs A. The Informational Environment The set of states of nature is denoted by = [, ],
Giving Advice vs. Making Decisions: Transparency, Information, and Delegation Online Appendix A Definitions and Proofs A. The Informational Environment The set of states of nature is denoted by = [, ],
Recursive Ambiguity and Machina s Examples
 Recursive Ambiguity and Machina s Examples David Dillenberger Uzi Segal May 0, 0 Abstract Machina (009, 0) lists a number of situations where standard models of ambiguity aversion are unable to capture
Recursive Ambiguity and Machina s Examples David Dillenberger Uzi Segal May 0, 0 Abstract Machina (009, 0) lists a number of situations where standard models of ambiguity aversion are unable to capture
Axiomatic Decision Theory
 Decision Theory Decision theory is about making choices It has a normative aspect what rational people should do... and a descriptive aspect what people do do Not surprisingly, it s been studied by economists,
Decision Theory Decision theory is about making choices It has a normative aspect what rational people should do... and a descriptive aspect what people do do Not surprisingly, it s been studied by economists,
SF2972 Game Theory Exam with Solutions March 15, 2013
 SF2972 Game Theory Exam with s March 5, 203 Part A Classical Game Theory Jörgen Weibull and Mark Voorneveld. (a) What are N, S and u in the definition of a finite normal-form (or, equivalently, strategic-form)
SF2972 Game Theory Exam with s March 5, 203 Part A Classical Game Theory Jörgen Weibull and Mark Voorneveld. (a) What are N, S and u in the definition of a finite normal-form (or, equivalently, strategic-form)
Should all Machine Learning be Bayesian? Should all Bayesian models be non-parametric?
 Should all Machine Learning be Bayesian? Should all Bayesian models be non-parametric? Zoubin Ghahramani Department of Engineering University of Cambridge, UK zoubin@eng.cam.ac.uk http://learning.eng.cam.ac.uk/zoubin/
Should all Machine Learning be Bayesian? Should all Bayesian models be non-parametric? Zoubin Ghahramani Department of Engineering University of Cambridge, UK zoubin@eng.cam.ac.uk http://learning.eng.cam.ac.uk/zoubin/
Models of Strategic Reasoning Lecture 2
 Models of Strategic Reasoning Lecture 2 Eric Pacuit University of Maryland, College Park ai.stanford.edu/~epacuit August 7, 2012 Eric Pacuit: Models of Strategic Reasoning 1/30 Lecture 1: Introduction,
Models of Strategic Reasoning Lecture 2 Eric Pacuit University of Maryland, College Park ai.stanford.edu/~epacuit August 7, 2012 Eric Pacuit: Models of Strategic Reasoning 1/30 Lecture 1: Introduction,
Expected Utility Framework
 Expected Utility Framework Preferences We want to examine the behavior of an individual, called a player, who must choose from among a set of outcomes. Let X be the (finite) set of outcomes with common
Expected Utility Framework Preferences We want to examine the behavior of an individual, called a player, who must choose from among a set of outcomes. Let X be the (finite) set of outcomes with common
Decision Analysis. An insightful study of the decision-making process under uncertainty and risk
 Decision Analysis An insightful study of the decision-making process under uncertainty and risk Decision Theory A philosophy, articulated by a set of logical axioms and a methodology, for analyzing the
Decision Analysis An insightful study of the decision-making process under uncertainty and risk Decision Theory A philosophy, articulated by a set of logical axioms and a methodology, for analyzing the
Inference for Stochastic Processes
 Inference for Stochastic Processes Robert L. Wolpert Revised: June 19, 005 Introduction A stochastic process is a family {X t } of real-valued random variables, all defined on the same probability space
Inference for Stochastic Processes Robert L. Wolpert Revised: June 19, 005 Introduction A stochastic process is a family {X t } of real-valued random variables, all defined on the same probability space
Selecting Efficient Correlated Equilibria Through Distributed Learning. Jason R. Marden
 1 Selecting Efficient Correlated Equilibria Through Distributed Learning Jason R. Marden Abstract A learning rule is completely uncoupled if each player s behavior is conditioned only on his own realized
1 Selecting Efficient Correlated Equilibria Through Distributed Learning Jason R. Marden Abstract A learning rule is completely uncoupled if each player s behavior is conditioned only on his own realized
Bayesian Learning in Social Networks
 Bayesian Learning in Social Networks Asu Ozdaglar Joint work with Daron Acemoglu, Munther Dahleh, Ilan Lobel Department of Electrical Engineering and Computer Science, Department of Economics, Operations
Bayesian Learning in Social Networks Asu Ozdaglar Joint work with Daron Acemoglu, Munther Dahleh, Ilan Lobel Department of Electrical Engineering and Computer Science, Department of Economics, Operations
IS IGNORANCE BLISS? By Joseph B. Kadane, Mark Schervish and Teddy Seidenfeld 1 Carnegie Mellon University
 February 16, 2007 IS IGNORANCE BLISS? By Joseph B. Kadane, Mark Schervish and Teddy Seidenfeld 1 Carnegie Mellon University...where ignorance is bliss, tis folly to be wise. Thomas Gray If ignorance were
February 16, 2007 IS IGNORANCE BLISS? By Joseph B. Kadane, Mark Schervish and Teddy Seidenfeld 1 Carnegie Mellon University...where ignorance is bliss, tis folly to be wise. Thomas Gray If ignorance were
Diachronic Coherence and Radical Probabilism
 Diachronic Coherence and Radical Probabilism Brian Skyrms The question of diachronic coherence, coherence of degrees of belief across time, is investigated within the context of Richard Jeffrey s radical
Diachronic Coherence and Radical Probabilism Brian Skyrms The question of diachronic coherence, coherence of degrees of belief across time, is investigated within the context of Richard Jeffrey s radical
The problem Countable additivity Finite additivity Conglomerability Structure Puzzle. The Measure Problem. Alexander R. Pruss
 The Measure Problem Alexander R. Pruss Department of Philosophy Baylor University July 11, 2013 The problem and the claim There are infinitely many observers (or types of observers, or observations, or
The Measure Problem Alexander R. Pruss Department of Philosophy Baylor University July 11, 2013 The problem and the claim There are infinitely many observers (or types of observers, or observations, or
Economics 3012 Strategic Behavior Andy McLennan October 20, 2006
 Economics 301 Strategic Behavior Andy McLennan October 0, 006 Lecture 11 Topics Problem Set 9 Extensive Games of Imperfect Information An Example General Description Strategies and Nash Equilibrium Beliefs
Economics 301 Strategic Behavior Andy McLennan October 0, 006 Lecture 11 Topics Problem Set 9 Extensive Games of Imperfect Information An Example General Description Strategies and Nash Equilibrium Beliefs
Making Decisions Using Sets of Probabilities: Updating, Time Consistency, and Calibration
 Journal of Artificial Intelligence Research 42 (2011) 393-426 Submitted 04/11; published 11/11 Making Decisions Using Sets of Probabilities: Updating, Time Consistency, and Calibration Peter D. Grünwald
Journal of Artificial Intelligence Research 42 (2011) 393-426 Submitted 04/11; published 11/11 Making Decisions Using Sets of Probabilities: Updating, Time Consistency, and Calibration Peter D. Grünwald
Weak Dutch Books versus Strict Consistency with Lower Previsions
 PMLR: Proceedings of Machine Learning Research, vol. 62, 85-96, 2017 ISIPTA 17 Weak Dutch Books versus Strict Consistency with Lower Previsions Chiara Corsato Renato Pelessoni Paolo Vicig University of
PMLR: Proceedings of Machine Learning Research, vol. 62, 85-96, 2017 ISIPTA 17 Weak Dutch Books versus Strict Consistency with Lower Previsions Chiara Corsato Renato Pelessoni Paolo Vicig University of
Practical implementation of possibilistic probability mass functions
 Practical implementation of possibilistic probability mass functions Leen Gilbert Gert de Cooman Etienne E. Kerre October 12, 2000 Abstract Probability assessments of events are often linguistic in nature.
Practical implementation of possibilistic probability mass functions Leen Gilbert Gert de Cooman Etienne E. Kerre October 12, 2000 Abstract Probability assessments of events are often linguistic in nature.
WHAT FINITE-ADDITIVITY CAN ADD TO DECISION THEORY
 WHAT FINITE-ADDITIVITY CAN ADD TO DECISION THEORY By Mark J. Schervish, Teddy Seidenfeld, Rafael Stern, and Joseph B. Kadane Carnegie Mellon University and Federal University of São Carlos We examine general
WHAT FINITE-ADDITIVITY CAN ADD TO DECISION THEORY By Mark J. Schervish, Teddy Seidenfeld, Rafael Stern, and Joseph B. Kadane Carnegie Mellon University and Federal University of São Carlos We examine general
P(X 1,, X n H) = P(X $ H) 1 Let H be a (simple) statistical hypothesis for the random variable X, i.e., where the conditional probability
 Standards for Modest Bayesian Credences Jessi Cisewski, Joseph B. Kadane, Mark J. Schervish, Teddy Seidenfeld, and Rafael Stern Yale U., Carnegie Mellon U. ( 3), and the Universidade Federal de São Carlos.
Standards for Modest Bayesian Credences Jessi Cisewski, Joseph B. Kadane, Mark J. Schervish, Teddy Seidenfeld, and Rafael Stern Yale U., Carnegie Mellon U. ( 3), and the Universidade Federal de São Carlos.
Practical implementation of possibilistic probability mass functions
 Soft Computing manuscript No. (will be inserted by the editor) Practical implementation of possibilistic probability mass functions Leen Gilbert, Gert de Cooman 1, Etienne E. Kerre 2 1 Universiteit Gent,
Soft Computing manuscript No. (will be inserted by the editor) Practical implementation of possibilistic probability mass functions Leen Gilbert, Gert de Cooman 1, Etienne E. Kerre 2 1 Universiteit Gent,
where u is the decision-maker s payoff function over her actions and S is the set of her feasible actions.
 Seminars on Mathematics for Economics and Finance Topic 3: Optimization - interior optima 1 Session: 11-12 Aug 2015 (Thu/Fri) 10:00am 1:00pm I. Optimization: introduction Decision-makers (e.g. consumers,
Seminars on Mathematics for Economics and Finance Topic 3: Optimization - interior optima 1 Session: 11-12 Aug 2015 (Thu/Fri) 10:00am 1:00pm I. Optimization: introduction Decision-makers (e.g. consumers,
Game Theory Lecture 10+11: Knowledge
 Game Theory Lecture 10+11: Knowledge Christoph Schottmüller University of Copenhagen November 13 and 20, 2014 1 / 36 Outline 1 (Common) Knowledge The hat game A model of knowledge Common knowledge Agree
Game Theory Lecture 10+11: Knowledge Christoph Schottmüller University of Copenhagen November 13 and 20, 2014 1 / 36 Outline 1 (Common) Knowledge The hat game A model of knowledge Common knowledge Agree
General-sum games. I.e., pretend that the opponent is only trying to hurt you. If Column was trying to hurt Row, Column would play Left, so
 General-sum games You could still play a minimax strategy in general- sum games I.e., pretend that the opponent is only trying to hurt you But this is not rational: 0, 0 3, 1 1, 0 2, 1 If Column was trying
General-sum games You could still play a minimax strategy in general- sum games I.e., pretend that the opponent is only trying to hurt you But this is not rational: 0, 0 3, 1 1, 0 2, 1 If Column was trying
Deceptive Advertising with Rational Buyers
 Deceptive Advertising with Rational Buyers September 6, 016 ONLINE APPENDIX In this Appendix we present in full additional results and extensions which are only mentioned in the paper. In the exposition
Deceptive Advertising with Rational Buyers September 6, 016 ONLINE APPENDIX In this Appendix we present in full additional results and extensions which are only mentioned in the paper. In the exposition
WEAKLY DOMINATED STRATEGIES: A MYSTERY CRACKED
 WEAKLY DOMINATED STRATEGIES: A MYSTERY CRACKED DOV SAMET Abstract. An informal argument shows that common knowledge of rationality implies the iterative elimination of strongly dominated strategies. Rationality
WEAKLY DOMINATED STRATEGIES: A MYSTERY CRACKED DOV SAMET Abstract. An informal argument shows that common knowledge of rationality implies the iterative elimination of strongly dominated strategies. Rationality
INDEPENDENT NATURAL EXTENSION
 INDEPENDENT NATURAL EXTENSION GERT DE COOMAN, ENRIQUE MIRANDA, AND MARCO ZAFFALON ABSTRACT. There is no unique extension of the standard notion of probabilistic independence to the case where probabilities
INDEPENDENT NATURAL EXTENSION GERT DE COOMAN, ENRIQUE MIRANDA, AND MARCO ZAFFALON ABSTRACT. There is no unique extension of the standard notion of probabilistic independence to the case where probabilities
Minimax and the Value of Information
 Minimax and the Value of Information Evan Sadler April 4, 2014 Abstract In his discussion of minimax decision rules, Savage (1954, p. 170) presents an example purporting to show that minimax applied to
Minimax and the Value of Information Evan Sadler April 4, 2014 Abstract In his discussion of minimax decision rules, Savage (1954, p. 170) presents an example purporting to show that minimax applied to
coherence assessed via gambling: a discussion
 coherence assessed via gambling: a discussion Christian P. Robert Université Paris-Dauphine (CEREMADE) & University of Warwick (Dept. of Statistics) http://xianblog.wordpress.com,seriesblog.net 4th Bayes,
coherence assessed via gambling: a discussion Christian P. Robert Université Paris-Dauphine (CEREMADE) & University of Warwick (Dept. of Statistics) http://xianblog.wordpress.com,seriesblog.net 4th Bayes,
Predictive inference under exchangeability
 Predictive inference under exchangeability and the Imprecise Dirichlet Multinomial Model Gert de Cooman, Jasper De Bock, Márcio Diniz Ghent University, SYSTeMS gert.decooman@ugent.be http://users.ugent.be/
Predictive inference under exchangeability and the Imprecise Dirichlet Multinomial Model Gert de Cooman, Jasper De Bock, Márcio Diniz Ghent University, SYSTeMS gert.decooman@ugent.be http://users.ugent.be/
6.207/14.15: Networks Lecture 24: Decisions in Groups
 6.207/14.15: Networks Lecture 24: Decisions in Groups Daron Acemoglu and Asu Ozdaglar MIT December 9, 2009 1 Introduction Outline Group and collective choices Arrow s Impossibility Theorem Gibbard-Satterthwaite
6.207/14.15: Networks Lecture 24: Decisions in Groups Daron Acemoglu and Asu Ozdaglar MIT December 9, 2009 1 Introduction Outline Group and collective choices Arrow s Impossibility Theorem Gibbard-Satterthwaite
Virtual Robust Implementation and Strategic Revealed Preference
 and Strategic Revealed Preference Workshop of Mathematical Economics Celebrating the 60th birthday of Aloisio Araujo IMPA Rio de Janeiro December 2006 Denitions "implementation": requires ALL equilibria
and Strategic Revealed Preference Workshop of Mathematical Economics Celebrating the 60th birthday of Aloisio Araujo IMPA Rio de Janeiro December 2006 Denitions "implementation": requires ALL equilibria
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page α 2 θ 1 u 3. wear coat. θ 2 = warm u 2 = sweaty! θ 1 = cold u 3 = brrr!
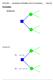 ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
Anscombe & Aumann Expected Utility Betting and Insurance
 Anscombe & Aumann Expected Utility Betting and Insurance Econ 2100 Fall 2017 Lecture 11, October 3 Outline 1 Subjective Expected Utility 2 Qualitative Probabilities 3 Allais and Ellsebrg Paradoxes 4 Utility
Anscombe & Aumann Expected Utility Betting and Insurance Econ 2100 Fall 2017 Lecture 11, October 3 Outline 1 Subjective Expected Utility 2 Qualitative Probabilities 3 Allais and Ellsebrg Paradoxes 4 Utility
II. Analysis of Linear Programming Solutions
 Optimization Methods Draft of August 26, 2005 II. Analysis of Linear Programming Solutions Robert Fourer Department of Industrial Engineering and Management Sciences Northwestern University Evanston, Illinois
Optimization Methods Draft of August 26, 2005 II. Analysis of Linear Programming Solutions Robert Fourer Department of Industrial Engineering and Management Sciences Northwestern University Evanston, Illinois
What are the laws of physics? Resisting reification
 What are the laws of physics? Resisting reification Carlton M. Caves C. M. Caves, C. A. Fuchs, and R. Schack, Subjective probability and quantum certainty, Studies in History and Philosophy of Modern Physics
What are the laws of physics? Resisting reification Carlton M. Caves C. M. Caves, C. A. Fuchs, and R. Schack, Subjective probability and quantum certainty, Studies in History and Philosophy of Modern Physics
Subjective Expected Utility in Games
 Subective Expected Utility in Games Alfredo Di Tillio Department of Economics University of Pennsylvania 3718 Locust Walk Philadelphia, PA 19104 June 23, 2004 Abstract This paper extends the scope of Savage
Subective Expected Utility in Games Alfredo Di Tillio Department of Economics University of Pennsylvania 3718 Locust Walk Philadelphia, PA 19104 June 23, 2004 Abstract This paper extends the scope of Savage
On the equivalence of conglomerability and disintegrability for unbounded random variables
 Stat Methods Appl (2014) 23:501 518 DOI 10.1007/s10260-014-0282-7 On the equivalence of conglomerability and disintegrability for unbounded random variables Mark J. Schervish Teddy Seidenfeld Joseph B.
Stat Methods Appl (2014) 23:501 518 DOI 10.1007/s10260-014-0282-7 On the equivalence of conglomerability and disintegrability for unbounded random variables Mark J. Schervish Teddy Seidenfeld Joseph B.
Computing Minmax; Dominance
 Computing Minmax; Dominance CPSC 532A Lecture 5 Computing Minmax; Dominance CPSC 532A Lecture 5, Slide 1 Lecture Overview 1 Recap 2 Linear Programming 3 Computational Problems Involving Maxmin 4 Domination
Computing Minmax; Dominance CPSC 532A Lecture 5 Computing Minmax; Dominance CPSC 532A Lecture 5, Slide 1 Lecture Overview 1 Recap 2 Linear Programming 3 Computational Problems Involving Maxmin 4 Domination
Advanced Microeconomics Note 1: Preference and choice
 Advanced Microeconomics Note 1: Preference and choice Xiang Han (SUFE) Fall 2017 Advanced microeconomics Note 1: Preference and choice Fall 2017 1 / 17 Introduction Individual decision making Suppose that
Advanced Microeconomics Note 1: Preference and choice Xiang Han (SUFE) Fall 2017 Advanced microeconomics Note 1: Preference and choice Fall 2017 1 / 17 Introduction Individual decision making Suppose that
Intro to Economic analysis
 Intro to Economic analysis Alberto Bisin - NYU 1 Rational Choice The central gure of economics theory is the individual decision-maker (DM). The typical example of a DM is the consumer. We shall assume
Intro to Economic analysis Alberto Bisin - NYU 1 Rational Choice The central gure of economics theory is the individual decision-maker (DM). The typical example of a DM is the consumer. We shall assume
Coherent conditional probabilities and proper scoring rules
 7th International Symposium on Imprecise Probability: Theories and Applications, Innsbruc, Austria, 2011 Coherent conditional probabilities and proper scoring rules Angelo Gilio Dipartimento di Scienze
7th International Symposium on Imprecise Probability: Theories and Applications, Innsbruc, Austria, 2011 Coherent conditional probabilities and proper scoring rules Angelo Gilio Dipartimento di Scienze
WHAT FINITE-ADDITIVITY CAN ADD TO DECISION THEORY
 Submitted to the Annals of Statistics WHAT FINITE-ADDITIVITY CAN ADD TO DECISION THEORY By Mark J. Schervish, Teddy Seidenfeld, Rafael Stern, and Joseph B. Kadane Carnegie Mellon University and Federal
Submitted to the Annals of Statistics WHAT FINITE-ADDITIVITY CAN ADD TO DECISION THEORY By Mark J. Schervish, Teddy Seidenfeld, Rafael Stern, and Joseph B. Kadane Carnegie Mellon University and Federal
Sequential Equilibria of Multi-Stage Games with Infinite Sets of Types and Actions
 Sequential Equilibria of Multi-Stage Games with Infinite Sets of Types and Actions by Roger B. Myerson and Philip J. Reny* Draft notes October 2011 http://home.uchicago.edu/~preny/papers/bigseqm.pdf Abstract:
Sequential Equilibria of Multi-Stage Games with Infinite Sets of Types and Actions by Roger B. Myerson and Philip J. Reny* Draft notes October 2011 http://home.uchicago.edu/~preny/papers/bigseqm.pdf Abstract:
Chapter Three. Hypothesis Testing
 3.1 Introduction The final phase of analyzing data is to make a decision concerning a set of choices or options. Should I invest in stocks or bonds? Should a new product be marketed? Are my products being
3.1 Introduction The final phase of analyzing data is to make a decision concerning a set of choices or options. Should I invest in stocks or bonds? Should a new product be marketed? Are my products being
A Theory of Bayesian Decision Making
 A Theory of Bayesian Decision Making Edi Karni November 11, 2009 Abstract This paper presents a complete, choice-based, axiomatic Bayesian decision theory. It introduces a new choice set consisting of
A Theory of Bayesian Decision Making Edi Karni November 11, 2009 Abstract This paper presents a complete, choice-based, axiomatic Bayesian decision theory. It introduces a new choice set consisting of
An AI-ish view of Probability, Conditional Probability & Bayes Theorem
 An AI-ish view of Probability, Conditional Probability & Bayes Theorem Review: Uncertainty and Truth Values: a mismatch Let action A t = leave for airport t minutes before flight. Will A 15 get me there
An AI-ish view of Probability, Conditional Probability & Bayes Theorem Review: Uncertainty and Truth Values: a mismatch Let action A t = leave for airport t minutes before flight. Will A 15 get me there
10/18/2017. An AI-ish view of Probability, Conditional Probability & Bayes Theorem. Making decisions under uncertainty.
 An AI-ish view of Probability, Conditional Probability & Bayes Theorem Review: Uncertainty and Truth Values: a mismatch Let action A t = leave for airport t minutes before flight. Will A 15 get me there
An AI-ish view of Probability, Conditional Probability & Bayes Theorem Review: Uncertainty and Truth Values: a mismatch Let action A t = leave for airport t minutes before flight. Will A 15 get me there
BELIEFS & EVOLUTIONARY GAME THEORY
 1 / 32 BELIEFS & EVOLUTIONARY GAME THEORY Heinrich H. Nax hnax@ethz.ch & Bary S. R. Pradelski bpradelski@ethz.ch May 15, 217: Lecture 1 2 / 32 Plan Normal form games Equilibrium invariance Equilibrium
1 / 32 BELIEFS & EVOLUTIONARY GAME THEORY Heinrich H. Nax hnax@ethz.ch & Bary S. R. Pradelski bpradelski@ethz.ch May 15, 217: Lecture 1 2 / 32 Plan Normal form games Equilibrium invariance Equilibrium
Definitions: A binary relation R on a set X is (a) reflexive if x X : xrx; (f) asymmetric if x, x X : [x Rx xr c x ]
![Definitions: A binary relation R on a set X is (a) reflexive if x X : xrx; (f) asymmetric if x, x X : [x Rx xr c x ] Definitions: A binary relation R on a set X is (a) reflexive if x X : xrx; (f) asymmetric if x, x X : [x Rx xr c x ]](/thumbs/72/67754492.jpg) Binary Relations Definition: A binary relation between two sets X and Y (or between the elements of X and Y ) is a subset of X Y i.e., is a set of ordered pairs (x, y) X Y. If R is a relation between X
Binary Relations Definition: A binary relation between two sets X and Y (or between the elements of X and Y ) is a subset of X Y i.e., is a set of ordered pairs (x, y) X Y. If R is a relation between X
Ex Post Cheap Talk : Value of Information and Value of Signals
 Ex Post Cheap Talk : Value of Information and Value of Signals Liping Tang Carnegie Mellon University, Pittsburgh PA 15213, USA Abstract. Crawford and Sobel s Cheap Talk model [1] describes an information
Ex Post Cheap Talk : Value of Information and Value of Signals Liping Tang Carnegie Mellon University, Pittsburgh PA 15213, USA Abstract. Crawford and Sobel s Cheap Talk model [1] describes an information
Formal Epistemology: Lecture Notes. Horacio Arló-Costa Carnegie Mellon University
 Formal Epistemology: Lecture Notes Horacio Arló-Costa Carnegie Mellon University hcosta@andrew.cmu.edu Bayesian Epistemology Radical probabilism doesn t insists that probabilities be based on certainties;
Formal Epistemology: Lecture Notes Horacio Arló-Costa Carnegie Mellon University hcosta@andrew.cmu.edu Bayesian Epistemology Radical probabilism doesn t insists that probabilities be based on certainties;
Contents. Decision Making under Uncertainty 1. Meanings of uncertainty. Classical interpretation
 Contents Decision Making under Uncertainty 1 elearning resources Prof. Ahti Salo Helsinki University of Technology http://www.dm.hut.fi Meanings of uncertainty Interpretations of probability Biases in
Contents Decision Making under Uncertainty 1 elearning resources Prof. Ahti Salo Helsinki University of Technology http://www.dm.hut.fi Meanings of uncertainty Interpretations of probability Biases in
INFINITESIMALS ARE TOO SMALL FOR COUNTABLY INFINITE FAIR LOTTERIES
 INFINITESIMALS ARE TOO SMALL FOR COUNTABLY INFINITE FAIR LOTTERIES ALEXANDER R. PRUSS Abstract. We show that infinitesimal probabilities are much too small for modeling the individual outcome of a countably
INFINITESIMALS ARE TOO SMALL FOR COUNTABLY INFINITE FAIR LOTTERIES ALEXANDER R. PRUSS Abstract. We show that infinitesimal probabilities are much too small for modeling the individual outcome of a countably
The fundamental theorems of prevision and asset pricing
 Available online at www.sciencedirect.com International Journal of Approximate Reasoning 49 (2008) 148 158 www.elsevier.com/locate/ijar The fundamental theorems of prevision and asset pricing Mark J. Schervish
Available online at www.sciencedirect.com International Journal of Approximate Reasoning 49 (2008) 148 158 www.elsevier.com/locate/ijar The fundamental theorems of prevision and asset pricing Mark J. Schervish
Microeconomic Theory (501b) Problem Set 10. Auctions and Moral Hazard Suggested Solution: Tibor Heumann
 Dirk Bergemann Department of Economics Yale University Microeconomic Theory (50b) Problem Set 0. Auctions and Moral Hazard Suggested Solution: Tibor Heumann 4/5/4 This problem set is due on Tuesday, 4//4..
Dirk Bergemann Department of Economics Yale University Microeconomic Theory (50b) Problem Set 0. Auctions and Moral Hazard Suggested Solution: Tibor Heumann 4/5/4 This problem set is due on Tuesday, 4//4..
Repeated Downsian Electoral Competition
 Repeated Downsian Electoral Competition John Duggan Department of Political Science and Department of Economics University of Rochester Mark Fey Department of Political Science University of Rochester
Repeated Downsian Electoral Competition John Duggan Department of Political Science and Department of Economics University of Rochester Mark Fey Department of Political Science University of Rochester
Tijmen Daniëls Universiteit van Amsterdam. Abstract
 Pure strategy dominance with quasiconcave utility functions Tijmen Daniëls Universiteit van Amsterdam Abstract By a result of Pearce (1984), in a finite strategic form game, the set of a player's serially
Pure strategy dominance with quasiconcave utility functions Tijmen Daniëls Universiteit van Amsterdam Abstract By a result of Pearce (1984), in a finite strategic form game, the set of a player's serially
Math-Stat-491-Fall2014-Notes-V
 Math-Stat-491-Fall2014-Notes-V Hariharan Narayanan November 18, 2014 Martingales 1 Introduction Martingales were originally introduced into probability theory as a model for fair betting games. Essentially
Math-Stat-491-Fall2014-Notes-V Hariharan Narayanan November 18, 2014 Martingales 1 Introduction Martingales were originally introduced into probability theory as a model for fair betting games. Essentially
LEXICOGRAPHIC CHOICE FUNCTIONS
 LEXICOGRAPHIC CHOICE FUNCTIONS ARTHUR VAN CAMP, GERT DE COOMAN, AND ENRIQUE MIRANDA ABSTRACT. We investigate a generalisation of the coherent choice functions considered by Seidenfeld et al. (2010), by
LEXICOGRAPHIC CHOICE FUNCTIONS ARTHUR VAN CAMP, GERT DE COOMAN, AND ENRIQUE MIRANDA ABSTRACT. We investigate a generalisation of the coherent choice functions considered by Seidenfeld et al. (2010), by
Dr. Truthlove, or How I Learned to Stop Worrying and Love Bayesian Probabilities
 Dr. Truthlove, or How I Learned to Stop Worrying and Love Bayesian Probabilities Kenny Easwaran 10/15/2014 1 Setup 1.1 The Preface Paradox Dr. Truthlove loves believing things that are true, and hates
Dr. Truthlove, or How I Learned to Stop Worrying and Love Bayesian Probabilities Kenny Easwaran 10/15/2014 1 Setup 1.1 The Preface Paradox Dr. Truthlove loves believing things that are true, and hates
Non- conglomerability for countably additive measures that are not κ- additive* T.Seidenfeld, M.J.Schervish, and J.B.Kadane
 Non- conglomerability for countably additive measures that are not κ- additive* T.Seidenfeld, M.J.Schervish, and J.B.Kadane Abstract Let κ be a successor cardinal. Using the theory of coherent conditional
Non- conglomerability for countably additive measures that are not κ- additive* T.Seidenfeld, M.J.Schervish, and J.B.Kadane Abstract Let κ be a successor cardinal. Using the theory of coherent conditional
Theory of Auctions. Carlos Hurtado. Jun 23th, Department of Economics University of Illinois at Urbana-Champaign
 Theory of Auctions Carlos Hurtado Department of Economics University of Illinois at Urbana-Champaign hrtdmrt2@illinois.edu Jun 23th, 2015 C. Hurtado (UIUC - Economics) Game Theory On the Agenda 1 Formalizing
Theory of Auctions Carlos Hurtado Department of Economics University of Illinois at Urbana-Champaign hrtdmrt2@illinois.edu Jun 23th, 2015 C. Hurtado (UIUC - Economics) Game Theory On the Agenda 1 Formalizing
2.3 Measuring Degrees of Belief
 Richard Johns From A Theory of Physical Probability, U. of T. Press, 2002 2.3 Measuring Degrees of Belief Having sketched out the nature of logical probability, let us now proceed to giving a precise account
Richard Johns From A Theory of Physical Probability, U. of T. Press, 2002 2.3 Measuring Degrees of Belief Having sketched out the nature of logical probability, let us now proceed to giving a precise account
A Rothschild-Stiglitz approach to Bayesian persuasion
 A Rothschild-Stiglitz approach to Bayesian persuasion Matthew Gentzkow and Emir Kamenica Stanford University and University of Chicago September 2015 Abstract Rothschild and Stiglitz (1970) introduce a
A Rothschild-Stiglitz approach to Bayesian persuasion Matthew Gentzkow and Emir Kamenica Stanford University and University of Chicago September 2015 Abstract Rothschild and Stiglitz (1970) introduce a
Introduction to Game Theory
 COMP323 Introduction to Computational Game Theory Introduction to Game Theory Paul G. Spirakis Department of Computer Science University of Liverpool Paul G. Spirakis (U. Liverpool) Introduction to Game
COMP323 Introduction to Computational Game Theory Introduction to Game Theory Paul G. Spirakis Department of Computer Science University of Liverpool Paul G. Spirakis (U. Liverpool) Introduction to Game
A Rothschild-Stiglitz approach to Bayesian persuasion
 A Rothschild-Stiglitz approach to Bayesian persuasion Matthew Gentzkow and Emir Kamenica Stanford University and University of Chicago December 2015 Abstract Rothschild and Stiglitz (1970) represent random
A Rothschild-Stiglitz approach to Bayesian persuasion Matthew Gentzkow and Emir Kamenica Stanford University and University of Chicago December 2015 Abstract Rothschild and Stiglitz (1970) represent random
Imprecise Bernoulli processes
 Imprecise Bernoulli processes Jasper De Bock and Gert de Cooman Ghent University, SYSTeMS Research Group Technologiepark Zwijnaarde 914, 9052 Zwijnaarde, Belgium. {jasper.debock,gert.decooman}@ugent.be
Imprecise Bernoulli processes Jasper De Bock and Gert de Cooman Ghent University, SYSTeMS Research Group Technologiepark Zwijnaarde 914, 9052 Zwijnaarde, Belgium. {jasper.debock,gert.decooman}@ugent.be
STAT:5100 (22S:193) Statistical Inference I
 STAT:5100 (22S:193) Statistical Inference I Week 3 Luke Tierney University of Iowa Fall 2015 Luke Tierney (U Iowa) STAT:5100 (22S:193) Statistical Inference I Fall 2015 1 Recap Matching problem Generalized
STAT:5100 (22S:193) Statistical Inference I Week 3 Luke Tierney University of Iowa Fall 2015 Luke Tierney (U Iowa) STAT:5100 (22S:193) Statistical Inference I Fall 2015 1 Recap Matching problem Generalized
Elicitation and Machine Learning. Part I
 Elicitation and Machine Learning a tutorial at EC 2016 Part I Rafael Frongillo and Bo Waggoner 25 July 2016 Information Elicitation Contracts to exchange information for money/goods. Scoring rules, peer
Elicitation and Machine Learning a tutorial at EC 2016 Part I Rafael Frongillo and Bo Waggoner 25 July 2016 Information Elicitation Contracts to exchange information for money/goods. Scoring rules, peer
Implementation in undominated strategies by bounded mechanisms: The Pareto Correspondence
 Implementation in undominated strategies by bounded mechanisms: The Pareto Correspondence Saptarshi Mukherjee Eve Ramaekers Arunava Sen September 5, 2016 Preliminary and Incomplete Abstract We show that
Implementation in undominated strategies by bounded mechanisms: The Pareto Correspondence Saptarshi Mukherjee Eve Ramaekers Arunava Sen September 5, 2016 Preliminary and Incomplete Abstract We show that
Quaderni di Dipartimento. A Note on the Law of Large Numbers in Economics. Patrizia Berti (Università di Modena e Reggio Emilia)
 Quaderni di Dipartimento A Note on the Law of Large Numbers in Economics Patrizia Berti (Università di Modena e Reggio Emilia) Michele Gori (Università di Firenze) Pietro Rigo (Università di Pavia) # 131
Quaderni di Dipartimento A Note on the Law of Large Numbers in Economics Patrizia Berti (Università di Modena e Reggio Emilia) Michele Gori (Università di Firenze) Pietro Rigo (Università di Pavia) # 131
