Geometry H Ch. 10 Test
|
|
|
- Lindsay Sharp
- 5 years ago
- Views:
Transcription
1 Geometry H Ch. 10 est 1. In the diagram, point is a point of tangency,, and. What is the radius of? M N J a. 76 c. 72 b. 70 d In the diagram, is tangent to at, is tangent to at,, and. Find the value of x. M N a. x = 29 c. x = 9 b. x = 99 d. x = physics experiment is set up using two pulleys, a string, and a weight as shown below. he larger pulley has a radius of 20 centimeters, and the smaller pulley has a radius of 5 centimeters. he distance between the centers of the pulleys is 51 centimeters. he string is pulled tightly across both pulleys so that is a common tangent of the pulleys. Find the length of string from to to the nearest tenth of a centimeter. J weight a cm c cm b cm d cm 4. In the diagram,. Find.
2 J H 5. In the diagram,. Find and. U a., c., b., d., 6. In the diagram, and. Find. a. = c. = b. = d. = 7. In the diagram,. Find. G E F H
3 a. = 59 c. = 29.5 b. = 118 d. = In the diagram,. Find the value of x. O 9. In the diagram,,,, and. Find the value of each variable. G F E a., c., b., d., 10. In the diagram, line m is tangent to the circle and. Find. m Find the value of x.
4 11. x G a. x = 104 c. x = 72.5 b. x = 93.5 d. x = G 40 x 115 a. x = 35 c. x = 27 b. x = 75 d. x = 77.5 C 13. satellite at point is orbiting Earth at 3600 miles. he satellite can only send a signal over the part of Earth that is visible to the satellite, represented by. What is the measure of, the portion of Earth from which the signal is visible? (Earth s radius is approximately 4000 miles.) 3600 mi C 4000 mi a. m c. m b. m 58.2 d. m In the diagram,,,, and. Find.
5 M N J L 15. In the diagram,,,, and. Find the value of x. J M N L 16. Find the value of x x In the diagram,,,, and. Find the value of x. a. x = 6 c. x = 8.1 b. x = 9.5 d. x = 10
6 18. Find. 45 x park downtown has a circular fountain with a walkway that runs tangent to the fountain. You want to find the radius of the fountain using indirect measurement. You stand on the walkway at a point 16 meters from where it meets the fountain. his point is represented by C in the diagram below and is 9 meters from the edge of the fountain. nowing is tangent to the circle, find the radius r of the fountain. C 9 m 16 m E r r a. r = 9.7 m c. r = m b. r = 7 m d. r = 19.4 m Use the diagram of circle to answer the question. V U 20. What word best describes?
7 b. chord 21. What word best describes? b. chord 22. What word best describes? b. chord 23. What word best describes? b. chord 24. What word best describes? b. chord
8 Geometry H Ch. 10 est nswer ection 1. N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: circle radius of a circle NO: Example 4 2. N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: circle tangent of a circle application NO: Example 5 3. N: : 1 IF: Level 3 EF: Geometry ec N: HG-C..2 EY: circle tangent of a circle application NO: Example 5 4. N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: inscribed angle NO: Example 1 5. N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: inscribed angle NO: Example 2 6. N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: inscribed angle NO: Example 2 7. N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: inscribed angle NO: Example 3 8. N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: inscribed polygon application NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: inscribed polygon application NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: circle measures of arcs NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: circle application measures of arcs NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: circle application measures of arcs NO: Example N: : 1 IF: Level 2 EF: Geometry ec N: HG-C..2 EY: circle application circumscribed angle NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: circle segments of a chord application NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: circle segments of a chord application NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: circle application secant segment NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 EY: circle application secant segment NO: Example N: : 1 IF: Level 2 EF: Geometry ec N: HG-C..2 EY: circle application secant segment tangent of a circle NO: Example 3-2
9 19. N: : 1 IF: Level 1 EF: Geometry ec N: HG-C..2 HG-MG..1 EY: circle application secant segment tangent of a circle NO: Example N: C : 1 IF: Level 1 EF: Geometry ec N: HG-CO..1 HG-C..2 EY: circle NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-CO..1 HG-C..2 EY: circle NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-CO..1 HG-C..2 EY: circle NO: Example N: E : 1 IF: Level 1 EF: Geometry ec N: HG-CO..1 HG-C..2 EY: circle NO: Example N: : 1 IF: Level 1 EF: Geometry ec N: HG-CO..1 HG-C..2 EY: circle NO: Example 1
Example 1: Finding angle measures: I ll do one: We ll do one together: You try one: ML and MN are tangent to circle O. Find the value of x
Ch 1: Circles 1 1 Tangent Lines 1 Chords and Arcs 1 3 Inscribed Angles 1 4 Angle Measures and Segment Lengths 1 5 Circles in the coordinate plane 1 1 Tangent Lines Focused Learning Target: I will be able
Mth 076: Applied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE
Mth 076: pplied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE INTRODUTION TO GEOMETRY Pick up Geometric Formula Sheet (This sheet may be used while testing) ssignment Eleven: Problems Involving
10.1 circles and circumference 2017 ink.notebook. March 13, Page 91. Page 92. Page 90. Ch 10 Circles Circles and Circumference.
Page 90 Page 91 Page 92 Ch 10 Circles 10.1 Circles and Circumference Lesson Objectives Page 93 Standards Lesson Notes Page 94 10.1 Circles and Circumference Press the tabs to view details. 1 Lesson Objectives
UNIT 3 CIRCLES AND VOLUME Lesson 1: Introducing Circles Instruction
Prerequisite Skills This lesson requires the use of the following skills: performing operations with fractions understanding slope, both algebraically and graphically understanding the relationship of
Tangent Lines Unit 10 Lesson 1 Example 1: Tell how many common tangents the circles have and draw them.
Tangent Lines Unit 10 Lesson 1 EQ: How can you verify that a segment is tangent to a circle? Circle: Center: Radius: Chord: Diameter: Secant: Tangent: Tangent Lines Unit 10 Lesson 1 Example 1: Tell how
Unit 10 Geometry Circles. NAME Period
Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
SM2H Unit 6 Circle Notes
Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
Chapter 12 Practice Test
hapter 12 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. ssume that lines that appear to be tangent are tangent. is the center of the circle.
Name. 9. Find the diameter and radius of A, B, and C. State the best term for the given figure in the diagram.
Name LESSON 10.1 State the best term for the given figure in the diagram. 9. Find the diameter and radius of A, B, and C. 10. Describe the point of intersection of all three circles. 11. Describe all the
Circles. II. Radius - a segment with one endpoint the center of a circle and the other endpoint on the circle.
Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
1. Draw and label a diagram to illustrate the property of a tangent to a circle.
Master 8.17 Extra Practice 1 Lesson 8.1 Properties of Tangents to a Circle 1. Draw and label a diagram to illustrate the property of a tangent to a circle. 2. Point O is the centre of the circle. Points
Replacement for a Carpenter s Square
Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
Geometry Honors Homework
Geometry Honors Homework pg. 1 12-1 Practice Form G Tangent Lines Algebra Assume that lines that appear to be tangent are tangent. O is the center of each circle. What is the value of x? 1. 2. 3. The circle
Circle Practice. D. chord 5. Which of the following is not a radius of the circle?
Name: Date: 1. In circle P, XY is a. 4. How many radii can be named in the diagram? A. radius. diameter A. 2. 3 C. 4 D. 5 C. chord D. circumference 2. In circle P, A is a. A. diameter. radius C. circumference
Name. Chapter 12: Circles
Name Chapter 12: Circles Chapter 12 Calendar Sun Mon Tue Wed Thu Fri Sat May 13 12.1 (Friday) 14 Chapter 10/11 Assessment 15 12.2 12.1 11W Due 16 12.3 12.2 HW Due 17 12.1-123 Review 12.3 HW Due 18 12.1-123
Study Guide. Exploring Circles. Example: Refer to S for Exercises 1 6.
9 1 Eploring ircles A circle is the set of all points in a plane that are a given distance from a given point in the plane called the center. Various parts of a circle are labeled in the figure at the
Honors Geometry Circle Investigation - Instructions
Honors Geometry ircle Investigation - Instructions 1. On the first circle a. onnect points and O with a line segment. b. onnect points O and also. c. Measure O. d. Estimate the degree measure of by using
Geo - CH11 Practice Test
Geo - H11 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. 1. Identify the secant that intersects ñ. a. c. b. l d. 2. satellite rotates 50 miles
C=2πr C=πd. Chapter 10 Circles Circles and Circumference. Circumference: the distance around the circle
10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
Chapter 10. Properties of Circles
Chapter 10 Properties of Circles 10.1 Use Properties of Tangents Objective: Use properties of a tangent to a circle. Essential Question: how can you verify that a segment is tangent to a circle? Terminology:
Arcs and Inscribed Angles of Circles
Arcs and Inscribed Angles of Circles Inscribed angles have: Vertex on the circle Sides are chords (Chords AB and BC) Angle ABC is inscribed in the circle AC is the intercepted arc because it is created
Apply Other Angle Relationships in Circles
0.5 pply Other ngle elationships in ircles efore You found the measures of angles formed on a circle. Now You will find the measures of angles inside or outside a circle. Why So you can determine the part
Solve problems involving tangents to a circle. Solve problems involving chords of a circle
8UNIT ircle Geometry What You ll Learn How to Solve problems involving tangents to a circle Solve problems involving chords of a circle Solve problems involving the measures of angles in a circle Why Is
15.5 Angle Relationships in Circles
ame lass ate 15.5 ngle Relationships in ircles ssential uestion: What are the relationships between angles formed by lines that intersect a circle? xplore xploring ngle Measures in ircles The sundial is
Indicate whether the statement is true or false.
PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
Ready To Go On? Skills Intervention 11-1 Lines That Intersect Circles
Name ate lass STION 11 Ready To Go On? Skills Intervention 11-1 Lines That Intersect ircles ind these vocabulary words in Lesson 11-1 and the Multilingual Glossary. Vocabulary interior of a circle exterior
( ) Chapter 10 Review Question Answers. Find the value of x mhg. m B = 1 2 ( 80 - x) H x G. E 30 = 80 - x. x = 50. Find m AXB and m Y A D X 56
hapter 10 Review Question nswers 1. ( ) Find the value of mhg 30 m = 1 2 ( 30) = 15 F 80 m = 1 2 ( 80 - ) H G E 30 = 80 - = 50 2. Find m X and m Y m X = 1 120 + 56 2 ( ) = 88 120 X 56 Y m Y = 1 120-56
10.6 Find Segment Lengths
10. Find Segment Lengths in ircles Goal p Find segment lengths in circles. Your Notes VOULRY Segments of a chord Secant segment Eternal segment THEOREM 10.14: SEGMENTS OF HORS THEOREM If two chords intersect
G.C.B.5: Arc Length 1
Regents Exam Questions G.C.B.5: Arc Length 1 www.jmap.org Name: G.C.B.5: Arc Length 1 1 A sprinkler system is set up to water the sector shown in the accompanying diagram, with angle ABC measuring 1 radian
Assuming the Earth is a sphere with radius miles, answer the following questions. Round all answers to the nearest whole number.
G-MG Satellite Alignments to Content Standards: G-MG.A.3 Task A satellite orbiting the earth uses radar to communicate with two control stations on the earth's surface. The satellite is in a geostationary
Mu Alpha Theta State 2007 Euclidean Circles
Mu Alpha Theta State 2007 Euclidean Circles 1. Joe had a bet with Mr. Federer saying that if Federer can solve the following problem in one minute, Joe would be his slave for a whole month. The problem
Review for Grade 9 Math Exam - Unit 8 - Circle Geometry
Name: Review for Grade 9 Math Exam - Unit 8 - ircle Geometry Date: Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is the centre of this circle and point
10-1 Study Guide and Intervention
opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-1 tudy Guide and Intervention ircles and ircumference arts of ircles circle consists of all points in a plane that are
G.C.B.5: Arc Length 1
Regents Exam Questions G.C.B.5: Arc Length www.jmap.org Name: G.C.B.5: Arc Length The diagram below shows circle O with radii OA and OB. The measure of angle AOB is 0, and the length of a radius is inches.
Understand and Apply Theorems about Circles
UNIT 4: CIRCLES AND VOLUME This unit investigates the properties of circles and addresses finding the volume of solids. Properties of circles are used to solve problems involving arcs, angles, sectors,
Ch 10 Review. Multiple Choice Identify the choice that best completes the statement or answers the question.
Ch 10 Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. In the diagram shown, the measure of ADC is a. 55 b. 70 c. 90 d. 180 2. What is the measure
G.C.B.5: Arc Length 1
Regents Exam Questions G.C.B.5: Arc Length 1 www.jmap.org Name: G.C.B.5: Arc Length 1 1 A sprinkler system is set up to water the sector shown in the accompanying diagram, with angle ABC measuring 1 radian
Assignment. Riding a Ferris Wheel Introduction to Circles. 1. For each term, name all of the components of circle Y that are examples of the term.
ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to Circles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. Chord b.
11.2 Start Thinking Warm Up Cumulative Review Warm Up
11.2 Start Thinking The circle in the diagram has a diameter of 14 inches. What is the area of the circle? Use the area of the circle to calculate the area of the sector created b the given measure of
Circles Test Circumference/Area Calculator Active. Clearly label the following in the circle to the right.
Circles Test Circumference/Area Calculator Active Clearly label the following in the circle to the right. 1. Point B as the center 2. Diameter AC 3. Radius BD 4. Chord EF 5. Arc FG Find the following.
New Jersey Center for Teaching and Learning. Progressive Mathematics Initiative
Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
radii: AP, PR, PB diameter: AB chords: AB, CD, AF secant: AG or AG tangent: semicircles: ACB, ARB minor arcs: AC, AR, RD, BC,
h 6 Note Sheets L Shortened Key Note Sheets hapter 6: iscovering and roving ircle roperties eview: ircles Vocabulary If you are having problems recalling the vocabulary, look back at your notes for Lesson
2 Explain 1 Proving the Intersecting Chords Angle Measure Theorem
xplain 1 Proving the Intersecting hords ngle easure Theorem In the xplore section, you discovered the effects that line segments, such as chords and secants, have on angle measures and their intercepted
Chapter-wise questions
hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
Circles in Neutral Geometry
Everything we do in this set of notes is Neutral. Definitions: 10.1 - Circles in Neutral Geometry circle is the set of points in a plane which lie at a positive, fixed distance r from some fixed point.
Riding a Ferris Wheel. Students should be able to answer these questions after Lesson 10.1:
.1 Riding a Ferris Wheel Introduction to ircles Students should be able to answer these questions after Lesson.1: What are the parts of a circle? How are the parts of a circle drawn? Read Question 1 and
So, the measure of arc TS is 144. So, the measure of arc QTS is 248. So, the measure of arc LP is Secants, Tangents, and Angle Measures
11-6 Secants, Tangents, Angle Measures Find each measure Assume that segments that appear to be tangent are tangent 4 1 5 So, the measure of arc QTS is 48 So, the measure of arc TS is 144 6 3 So, the measure
West Haven Public Schools Unit Planning Organizer
West Haven Public Schools Unit Planning Organizer Subject: Circles and Other Conic Sections Grade 10 Unit: Five Pacing: 4 weeks + 1 week Essential Question(s): 1. What is the relationship between angles
Circles. Parts of a Circle Class Work Use the diagram of the circle with center A to answer the following: Angles & Arcs Class Work
Circles Parts of a Circle Class Work Use the diagram of the circle with center A to answer the following: 1. Name the radii 2. Name the chord(s) 3. Name the diameter(s) 4. If AC= 7, what does TC=? 5. If
Using Properties of Segments that Intersect Circles
ig Idea 1 H UY I I Using roperties of egments that Intersect ircles or Your otebook You learned several relationships between tangents, secants, and chords. ome of these relationships can help you determine
Conic Section: Circles
Conic Section: Circles Circle, Center, Radius A circle is defined as the set of all points that are the same distance awa from a specific point called the center of the circle. Note that the circle consists
Unit 1. GSE Analytic Geometry EOC Review Name: Units 1 3. Date: Pd:
GSE Analytic Geometry EOC Review Name: Units 1 Date: Pd: Unit 1 1 1. Figure A B C D F is a dilation of figure ABCDF by a scale factor of. The dilation is centered at ( 4, 1). 2 Which statement is true?
Page 1
Pacing Chart Unit Week Day CCSS Standards Objective I Can Statements 121 CCSS.MATH.CONTENT.HSG.C.A.1 Prove that all circles are similar. Prove that all circles are similar. I can prove that all circles
Regents Exam Questions by Topic Page 1 ANGLES: Arc Length NAME:
Regents Exam Questions by Topic Page 1 1. 010725b As shown in the accompanying diagram, a dial in the shape of a semicircle has a radius of 4 centimeters. Find the measure of, in radians, when the pointer
Name two radii in Circle E.
A C E B D Name two radii in Circle E. Unit 4: Prerequisite Terms A C E B D ECandED Unit 4: Prerequisite Terms A C E B D Name all chords in Circle E. Unit 4: Prerequisite Terms A C E B D AD, CD, AB Unit
Geometry Final Exam Review
Name: Date: Period: Geometry Final Exam Review 1. Fill in the flow chart below with the properties that belong to each polygon. 2. Find the measure of each numbered angle: 3. Find the value of x 4. Calculate
Math 3 Quarter 4 Overview
Math 3 Quarter 4 Overview EO5 Rational Functions 13% EO6 Circles & Circular Functions 25% EO7 Inverse Functions 25% EO8 Normal Distribution 12% Q4 Final 10% EO5 Opp #1 Fri, Mar 24th Thu, Mar 23rd ML EO5
Integrated Math II. IM2.1.2 Interpret given situations as functions in graphs, formulas, and words.
Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
Pre-Test. Use the following figure to answer Questions 1 through 6. B C. 1. What is the center of the circle? The center of the circle is point G.
Pre-Test Name Date Use the following figure to answer Questions 1 through 6. A B C F G E D 1. What is the center of the circle? The center of the circle is point G. 2. Name a radius of the circle. A radius
1998 Harvard/MIT Math Tournament GEOMETRY Answer Sheet
1998 Harvard/MIT Math Tournament GEOMETRY Answer Sheet Name: School: Grade: 1 7 2 8 3 9 4 10a 5 10b 6 10c TOTAL: GEOMETRY Question One. [3 points] Quadrilateral ALEX, pictured below (but not necessarily
Page 1 Central Angles & Arc Measures
Geometry/Trig Unit 8 ll bout ircles! Name: ate: Page 1 entral ngles & rc Measures Example 1: JK is a diameter of ircle. Name two examples for each: K Minor rc:, Major rc:, M Semicircle:, Name Pair of djacent
JEFFERSON MATH PROJECT REGENTS AT RANDOM
JEFFERSON MATH PROJECT REGENTS AT RANDOM The NY Geometry Regents Exams Fall 2008-August 2009 Dear Sir I have to acknolege the reciept of your favor of May 14. in which you mention that you have finished
17. The length of a diagonal of a square is 16 inches. What is its perimeter? a. 8 2 in. b in. c in. d in. e in.
Geometry 2 nd Semester Final Review Name: 1. Pentagon FGHIJ pentagon. 2. Find the scale factor of FGHIJ to KLMNO. 3. Find x. 4. Find y. 5. Find z. 6. Find the scale factor of ABCD to EFGD. 7. Find the
Chords and Arcs. Objectives To use congruent chords, arcs, and central angles To use perpendicular bisectors to chords
- hords and rcs ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. M, M bjectives To use congruent chords, arcs, and central angles To use perpendicular
10.1 Tangents to Circles. Geometry Mrs. Spitz Spring 2005
10.1 Tangents to Circles Geometry Mrs. Spitz Spring 2005 Objectives/Assignment Identify segments and lines related to circles. Use properties of a tangent to a circle. Assignment: Chapter 10 Definitions
Circles-Tangent Properties
15 ircles-tangent roperties onstruction of tangent at a point on the circle. onstruction of tangents when the angle between radii is given. Tangents from an external point - construction and proof Touching
Circles. Riding a Ferris Wheel. Take the Wheel. Manhole Covers. Color Theory. Solar Eclipses Introduction to Circles...
Circles That s no moon. It s a picture of a solar eclipse in the making. A solar eclipse occurs when the Moon passes between the Earth and the Sun. Scientists can predict when solar eclipses will happen
ARCS An ARC is any unbroken part of the circumference of a circle. It is named using its ENDPOINTS.
ARCS An ARC is any unbroken part of the circumference of a circle. It is named using its ENDPOINTS. A B X Z Y A MINOR arc is LESS than 1/2 way around the circle. A MAJOR arc is MORE than 1/2 way around
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Semester 1Eam Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Answer the question. 1) Which one of the equations below matches the graph? 1)
Lesson 12.1 Skills Practice
Lesson 12.1 Skills Practice Introduction to ircles ircle, Radius, and iameter Vocabulary efine each term in your own words. 1. circle circle is a collection of points on the same plane equidistant from
TENTH YEAR MATHEMATICS
---------- The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION TENTH YEAR MATHEMATICS Monday, June 17, 1985 1:15 to 4:15 p.m., only The last page of the booklet is the answer sheet.
Pre-Test. Use trigonometric ratios to find the value of x. Show all your work and round your answer to the nearest tenth.
Pre-Test Name Date 1. Write the trigonometric ratios for A. Write your answers as simplified fractions. A 6 cm 10 cm sin A cos A 8 10 5 6 10 3 5 C 8 cm B tan A 8 6 3 2. Write the trigonometric ratios for
KEY STANDARDS ADDRESSED: MM2G3. Students will understand the properties of circles.
KEY STANDARDS ADDRESSED:. Students will understand the properties of circles. a. Understand and use properties of chords, tangents, and secants an application of triangle similarity. b. Understand and
Assignment. Riding a Ferris Wheel Introduction to Circles. 1. For each term, name all of the components of circle Y that are examples of the term.
ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to ircles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. hord GM, R,
Geometry Final Exam Review
1. In the figures find the missing parts. Geometry Final Eam Review 2. In the figures find the missing parts. 3. Tom is trying to put a divider diagonally to separate his animals and his play area. If
( ) Find the value of x mhg. H x G. Find m AXB and m Y A D X 56. Baroody Page 1 of 18
1. ( ) Find the value of x mhg 30 F 80 H x G E 2. Find m X and m Y 120 X 56 Y aroody age 1 of 18 3. Find mq X 70 30 Y Q 4. Find the radius of a circle in which a 48 cm. chord is 8 cm closer to the center
Math & 8.7 Circle Properties 8.6 #1 AND #2 TANGENTS AND CHORDS
Math 9 8.6 & 8.7 Circle Properties 8.6 #1 AND #2 TANGENTS AND CHORDS Property #1 Tangent Line A line that touches a circle only once is called a line. Tangent lines always meet the radius of a circle at
GEOMETRY. Part I. _,_ c. August 2010
GEOMETRY Part I nswer all 28 questions in this part. Each correct answer will receive,',"eliits. No partial credit will be allowed. For each question, write on the "pnce provided the numeral preceding
Unit 8 Circle Geometry Exploring Circle Geometry Properties. 1. Use the diagram below to answer the following questions:
Unit 8 Circle Geometry Exploring Circle Geometry Properties Name: 1. Use the diagram below to answer the following questions: a. BAC is a/an angle. (central/inscribed) b. BAC is subtended by the red arc.
b) Parallelogram Opposite Sides Converse c) Parallelogram Diagonals Converse d) Opposite sides Parallel and Congruent Theorem
Chapter 7 1. State which theorem you can use to show that the quadrilateral is a parallelogram. a) Parallelogram Opposite Angles Converse b) Parallelogram Opposite Sides Converse c) Parallelogram Diagonals
Park Forest Math Team. Meet #4. Geometry. Self-study Packet
Park Forest Math Team Meet #4 Self-study Packet Problem Categories for this Meet: 1. Mystery: Problem solving 2. : ngle measures in plane figures including supplements and complements 3. Number Theory:
2016 State Mathematics Contest Geometry Test
2016 State Mathematics Contest Geometry Test In each of the following, choose the BEST answer and record your choice on the answer sheet provided. To ensure correct scoring, be sure to make all erasures
Practice For use with pages
Name ate ON 0. ractice For use with pages 678 686 se ( to draw the described part of the circle.. raw a diameter and label it }.. raw a tangent ra and label it ###$. 3. raw a secant and label it } F. 4.
Section 3.2 Applications of Radian Measure
Section. Applications of Radian Measure 07 (continued) 88. 80 radians = = 0 5 5 80 radians = = 00 7 5 = 5 radian s 0 = 0 radian s = radian 80 89. (a) In hours, the hour hand will rotate twice around the
Math 9 Chapter 8 Practice Test
Name: Class: Date: ID: A Math 9 Chapter 8 Practice Test Short Answer 1. O is the centre of this circle and point Q is a point of tangency. Determine the value of t. If necessary, give your answer to the
Geometry Honors Final Exam Review June 2018
Geometry Honors Final Exam Review June 2018 1. Determine whether 128 feet, 136 feet, and 245 feet can be the lengths of the sides of a triangle. 2. Casey has a 13-inch television and a 52-inch television
Geometry Final Exam REVIEW
Name: Class: _ Date: _ Geometry Final Exam 09-10 - REVIEW Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the perimeter and area of the parallelogram.
Circles Print Activity. Use the Explore It mode to answer the following questions. 1. Use the diagram below to answer the following questions:
Name: Circles Print Activity Use the Explore It mode to answer the following questions. 1. Use the diagram below to answer the following questions: a. A is a/an angle. (central/inscribed) b. A is subtended
0110ge. Geometry Regents Exam Which expression best describes the transformation shown in the diagram below?
0110ge 1 In the diagram below of trapezoid RSUT, RS TU, X is the midpoint of RT, and V is the midpoint of SU. 3 Which expression best describes the transformation shown in the diagram below? If RS = 30
So, the measure of arc TS is Secants, Tangents, and Angle Measures
Find each measure. Assume that segments that appear to be tangent are tangent. 1. 3. 110 73 2. 4. So, the measure of arc TS is 144. 144 31 esolutions Manual - Powered by Cognero Page 1 5. 7. STUNTS A ramp
Chapter 10 Worksheet 1 Name: Honors Accelerated Geometry Hour:
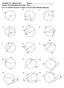hapter 10 Worksheet 1 Name: Honors ccelerated Geometry Hour: For 1-15, find the measure of angle in each of the following diagrams. 1. 2.. 258 84 140 40 4. 5. 6. 2 y 80 y 72 7. 8. 9. 50 X 40 140 4 y 10.
Due to the detail of some problems, print the contests using a normal or high quality setting.
General Contest Guidelines: Keep the contests secure. Discussion about contest questions is not permitted prior to giving the contest. Due to the detail of some problems, print the contests using a normal
Chapter 3. Radian Measure and Circular Functions. Copyright 2005 Pearson Education, Inc.
Chapter 3 Radian Measure and Circular Functions Copyright 2005 Pearson Education, Inc. 3.1 Radian Measure Copyright 2005 Pearson Education, Inc. Measuring Angles Thus far we have measured angles in degrees
0113ge. Geometry Regents Exam In the diagram below, under which transformation is A B C the image of ABC?
0113ge 1 If MNP VWX and PM is the shortest side of MNP, what is the shortest side of VWX? 1) XV ) WX 3) VW 4) NP 4 In the diagram below, under which transformation is A B C the image of ABC? In circle
Extra Test Review. 3. Use the following graph to find the area of a rectangle with vertices of ( 2, 4), ( 2, 4), (1, 4), and (1, 4).
Name: Date: 1. The sides of the outer square are about 14 inches. The sides of the inner square about 10 inches. What is a logical estimate for the circumference of the circle? 3. Use the following graph
0610ge. Geometry Regents Exam The diagram below shows a right pentagonal prism.
0610ge 1 In the diagram below of circle O, chord AB chord CD, and chord CD chord EF. 3 The diagram below shows a right pentagonal prism. Which statement must be true? 1) CE DF 2) AC DF 3) AC CE 4) EF CD
0-8 Area. Find the area of each figure. 1. SOLUTION: The area of the rectangle is 6 square centimeters. 2. SOLUTION:
Find the area of each figure. 1. The area of the rectangle is 6 square centimeters. 2. The area of the square is 36 square inches. 3. The area of the parallelogram is 120 square meters. esolutions Manual
JEFFERSON MATH PROJECT REGENTS AT RANDOM
JEFFERSON MATH PROJECT REGENTS AT RANDOM The NY Geometry Regents Exams Fall 2008-January 2010 Dear Sir I have to acknolege the reciept of your favor of May 14. in which you mention that you have finished
0609ge. Geometry Regents Exam AB DE, A D, and B E.
0609ge 1 Juliann plans on drawing ABC, where the measure of A can range from 50 to 60 and the measure of B can range from 90 to 100. Given these conditions, what is the correct range of measures possible
Trigonometric ratios:
0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses: