Mathematical Logic. Target. Chapter 01: Mathematical Logic
|
|
|
- Sherman Lynch
- 5 years ago
- Views:
Transcription
1 Trget Publictions Pvt. Ltd. Mthemticl Logic Chpter : Mthemticl Logic. + is n open sentence. It is not sttement. option (C) is correct.. Since p q is flse, when p is true nd q is flse. p (q r) is flse, p is true nd q r is flse p is true nd both q nd r re flse.. Since, contrpositive of p q is ~q ~p. contrpositive of (~p q) ~r is ~(~r) ~(~p q) r (p ~q). ~p: Rohit is short. The given sttement cn be written smbolicll s p (~p q). 5. Let p: is comple number q: is negtive number Logicl sttement is p q converse of p q is q p option (B) is correct. 6. Consider option (C) p q r ~q p ~q (p ~q) r T T T F F T T T F F F T T F T T T T T F F T T F F T T F F T F T F F F T F F T T F T F F F T F T (p ~q) r is contingenc option (C) is correct. 7. Consider option (A) p q p q p q ~(p q) (p q) (p q)) T T T T F F T F F T F F F T F T F F F F F F T F (p q) (~(p q)) is contrdiction. option (A) is correct p q ~q p q p ~q ~(p ~q) T T F T F T T F T F T F F T F F T F F F T T F T The entries in the columns nd 6 re identicl. ~(p ~q) p q sttement-l is true. Also, ll the entries in the lst column of the bove truth tble re not T. ~(p ~q) is not tutolog. sttement- is flse. option (B) is correct. 9. Consider option (C) (p q) (p r) (T T) (T F) T T T option (C) is correct.. The sttement Sumn is brillint nd dishonest iff sumn is rich cn be epressed s Q (P ~R) The negtion of this sttement is ~(Q (P ~R)). (q) (p) is contrpositive of p q. p q (~q) (~p) option (D) is true.. (~p ~q) (p q) (~p q) ~p (~q q) (p q) (~p T) (p q) ~p (p q) (~p p) (~p q) T (~p q) ~p q option (B) is correct.. Since, inverse of p q is ~p ~q. inverse of (p ~q) r is ~(p ~q) ~r i.e., ~p q ~r
2 Trget Publictions Pvt. Ltd. Mtrices Chpter : Mtrices. A A eists. () (7) + (9) 7 9 dj A 5 6 A sum of the elements of A T ( ). (dj A) A A I n A. Let A A A does not eist. tn tn sec sec tn tn tn tn T 6. tn tn tn sec tn tn tn sec tn tn cos sin sin cos B equlit of mtrices, we get cos, b sin z R R R, R R R z 5z 5 z + + z 6 7. Let A Mtri will not be invertible if A () + (9) () 9 8. Given, A nd B AB A B nd A B A B A B... A A AB nd A B re singulr.
3 Std. XII : Triumph Mths 9. (AB) B A B A. (A 8A)A A.A.A 8A.A A 8I Since, A(dj A) A.I Replcing A b dj A, we get dj A (dj(dj A)) dj A I A. A (dj(dj A)) dj A I. A (dja) A A (dj (dj A)) A.I.[ dj A A n ] A (dj (dj A)) I A (dj (dj A)) I Given, A (dj (dj A)) ki k. det A det (dj (dj A)) ( ) (det A). dj(dja) A (det A) () (n ). A. (dj A).I Since, A(dj A) A.I A From (i), A. dj A 6.(i) dj A 6 6 Also, dj (dj A) A (n ) dj(dja) dja ( ) A ()
4 Trget Publictions Pvt. Ltd. Trigonometric Functions Chpter : Trigonometric Functions. sin sin sin sin (sin sin ) cos cos cos cos (cos cos ) Given, cos cos + sin sin cos (cos + cos ) + sin ( sin sin ) cos cos cos +sin sin sin + cos sin + (cos cos + sin sin ) cos 6 + cos cos cos + cos cos cos (n + ) (n + ) But cos > ( must be in st or th Qudrnt) the possible vlues re,. 8 8 Cse II: If cos <, sin (cos ) sin 5, 7 5 7, 8 8 The vlues of stisfing the given eqution 5 7 between nd re,,, These re in A.P. with common difference.. sin cos 6 6 sin sin sin Let t 6 6 sin 6 sin. sin 8cos sin cos. 8 sin cos Cse I: If cos >, sin cos sin sin 9,,,.[ (, ), (, )] 9,,, t + 6 t t + 6 t t t + 6 (t ) (t 8) t or t 8 sin 6 sin or sin 6 8 sin or sin or sin sin or sin sin sin 6 or sin sin n ± or n ± 6 7 5,,, or,,, There re 8 solutions in [, ].
5 Std. XII : Triumph Mths. The mimum vlue of sin + b cos is b. Mimum vlue of sin + cos is nd the mimum vlue of + sin is. The given eqution will be true onl when sin + cos nd + sin If sin + cos cos + sin cos cos + sin sin cos n, n +.(i) + sin sin sin sin n + () n. n + () n..(ii) The vlue of [, ] which stisfies both (i) nd (ii) is. 5. sin + cos sin cos (sin + cos ) sin cos sin cos ( sin cos ).sin cos sin sin sin + sin (sin + ) (sin ) sin.[sin ] sin sin n + () n n + () n 5 The vlue of in [, ] re nd. There re solutions. 6. tn sec + tn ( + tn ) + tn tn + tn tn + + (tn ) 7. cos + sin 5 tn tn + tn 5 tn Let tn t t + 8t 5 + 5t 8t 8t + t t + (t ) t tn tn n + n + 8. tn + tn + tn tn tn + tn + tn tn tn ( tn ) (tn )( tn ) (tn ) ( tn ) tn 9 tn tn tn tntn tn tn tn tn n + (n + )
6 Chpter : Trigonometric Functions tn A > tn B A B A > B A B tn A B tn tn A B tn tn 5 tn A B C 85 tn C tn 5 cot C 5 tn C 5 Since, 7 > 5 tn B tn C B C B > C A > B > C > b > c. A(ABC) 9 bcsina 9 bc 9 bc 8 b c cos A bc. sin A sin. cos (b c) bc bc ( ) cm B Let B, C 5 A 5 sina sinb sinc b c sin5 sin sin 5 b c b c sin sin5 sin5 sin5 sin5 sin5 A(ABC) bc sin A sin5 sin5 sin5 5 A sin (65 ) 5 C
7 Std. XII : Triumph Mths. Let b c c b ( b c) k 6 b c 8.(B propert of equl rtio) b + c k, c + k, + b k, + b + c 8 k 7k, b 6k, c 5k b c cos A bc 6k 5k 9k (6k)(5k) k 6k 5 cos A 5. A n n (n + ) (n ) n or n But n cnnot be negtive. n The sides of the re, 5, 6.. E A O r 7 r D C In ODC, OD OC r, DOC A(ODC) r.r. sin 7 r sin 7 B n + n A Are of pentgon 5 r sin 7 B n + C Let AC n, AB n +, BC n + Lrgest ngle is A nd smllest ngle is B. A B Since, A + B + C 8 B + C 8 C 8 B sin C sin(8 B) sin B sin A sin B sin C n n n sin B sin B sinb n n n sinbcosb sin B sinbsin B n n n cosb n n sin B n cos B n, sin B n n n ( cos B) n n n + n n n n n + n n n n + n + n + n + n A Are of circle r A A r 5 r sin7 5cos8 sec 8 sec Let k, b 5k, c 6k Now, s b c k 5k 6k 5k s(s )(sb)(s c) 5k 5k 5k 5k k 5k 6k 5k 7k 5k k 5 7 k B sine Rule, sin A R sin A R bcsina bc R bc R R bc k.5k.6k 8 5 7k 7 k Also rs, where r Rdius of incircle of ABC
8 Chpter : Trigonometric Functions 5 7 k r 7 k s 5k R 8 r 7 k 7k 6 7 R 6 r 7 b c 6. cos A bc cos [ ] bcsina sin s b c rs r s ( ) b + c (b + c ) + b + c b c + b + c b + b c c b c b c b + c bc b c cos A bc A B C 5 8 bc bc bc A p Let length of ltitude p Since, A + B + C 5 A A 8 8 Are of p bc sin A p bc sin p bc bc p B sine rule, sin b sin 8 c 5 sin 8.(i) sin b 8 sin 8 5 sin c 8 sin 5 8 From (i), 5 sin. sin p 8 8 P 5 sin sin sin sin cos cos cos cos 5
9 Std. XII : Triumph Mths 9. tn A nd tn B re the roots of the qudrtic eqution tn A + tn B 5 6, tn A. tn B 6 A B 5 tn A tn tn 6 A B tn tn 6 tn A B 6 A B A + B C ABC is right ngled tringle. csin B. r s ( b c) r c bc [ sin B sin 9 ] c cb c b cb c( c b) c( c b) ( c) b c cb c b Dimeter + c b. A 55, B 5, C sin 55 b sin5.[ + c b ] c sin k k sin 55, b k sin 5, c k sin c k sin k sin 55 k (sin + sin 55) (sin sin 55) k sin cos sin cos k sin 65 sin 55 k sin 5 sin 55 (k sin 55) (k sin 5) b. A, B, C re in A.P. A + C B Also, A + B + C 8 B 6 sin A sin B sin C k b c sin A k, sin B bk, sin C ck c sin C + c sin A c ( sin C cos C) + c (sin AcosA) c ( ck cos C) + c (k cos A) k cos C + kc cos A k( cos C + c cos A) kb.[ b cos C + c cos A] sin B.[ B 6]. cot tn tn + tn tn tn 9 tn 6 8 tn cot cot tn tn tn tn tn tn tn tn 7
10 Chpter : Trigonometric Functions. Let cos b cos b cos b tn cos b + tn cos b tn + tn tn tn tn tn tn tn tn tn tn tn cos b tn b 5. cos cos cos Given, cos cos cos cos cos cos Squring on both sides, we get ( ) cos cos + + cos cos + + cos cos + cos sin 6. sin + sin sin sin sin sin sin cos (sin ) cos sin (sin ) cos (sin ). (i) Let sin sin cos cos (sin ).(ii) From (i) nd (ii), we get 5 5 (squring both sides) (From the given reltion it cn be seen tht is positive) 7. L.H.S. sin sin 7 + cos cos 7 + tn tn cot cot 8 sin sin cos cos 7 + tn tn 8 + cot cot 8 sin sin cos cos tn tn 8 + cot cot [ cos () cos ]
11 Std. XII : Triumph Mths 7 b, b 7 + b sin sin + 6 sin 65 sin sin 6 65 sin sin 65 8 sin sin 65 sin sin 65 cos 6 + sin cos sin >.[.7] tn ( ) > tn.[ tn is n incresing function] tn ( ) > A >.(i) sin sin sin sin ( sin sin ) Put sin sin sin sin sin 7 sin 7 sin (.85).7.866,.85 <.866 sin (.85) < sin (.866).[ sin is lso n incresing function] sin < sin sin <...(ii) sin 5 sin (.6) < sin sin 5 <.(iii) From (ii) nd (iii), we get B sin + sin 5 < + B <.(iv) From (i) nd (iv), A > B. cot + cot + cot z tn + tn + tn z tn + tn + tn z tn (tn + tn + tn z) tn Let A tn, B tn, C tn z tn A Btn C tn (A + B + C) tn(ab)tnc tn A + tn B tn C tn A tn B tn A tn B tnc tna tnb tn A tn Btn C tn A tn Btn C tn A tn B tn B tn C tn C tn A
12 Chpter : Trigonometric Functions tn (A + B + C) tn A + tn B + tn C tn A tn B tn C tn (tn ) + tn(tn ) + tn(tn z) tn(tn ) tn(tn ) tn(tn z) + + z z. cos 9 9 cos sin cos 9 9 cos cos sin sin cos 9 cos cos 58 cos cos cos cos cos cos 7 cos nd 7 7 Principl vlue is 7. (6 + ) (8 + 6) ( 7 6) ( ) ( + ),, But >,. cot + sin 5 tn + 5 tn 5. sin tn tn tn tn + tn. tn + tn + tn.[ > ] + tn () tn tn + tn + tn. tn + tn tn tn tn 6 8 9
13 Trget Publictions Pvt. Ltd. Pir of Stright Lines Chpter : Pir of Stright Lines. L : + h + b Eqution of n line pssing through origin nd perpendiculr to L is given b b h +.(interchnging coefficients of nd nd chnge of sign for term) The required eqution of pir of lines is i.e h Here, mm b...(i) nd mm b (m m ) (m + m ) m m h b b h h.[ b h (given)] b h b h mm b...(ii) On solving (i) nd (ii), we get h h m nd m b b m : m :. The lines re prllel, if f bg f 9g f g Let g nd f bc + fgh f bg ch (9) (c) + () () (6) () 9() c (6) c is n number.. Given eqution is., b, c, f, g, h This eqution represents pir of stright lines, if bc + fgh f bg ch The given eqution of pir of lines is +, b, h Now, + b + () The lines re perpendiculr 6. The joint eqution of the lines through the point (, ) nd t right ngles to the lines + h + b is b( ) h( )( ) + ( ) joint eqution of pir of lines drwn through (, ) nd perpendiculr to the pir of lines 7 + is ( ) + 7( )( ) + ( ) 7. The given equtions re nd + 6 The joint eqution is given b ( ) ( + 6) Let the eqution of one of the ngle bisector of the co-ordinte es be + m Given eqution of pir of lines is + h + A, H h, B Now, m m b m Also m + m h b h h 5 9. The given eqution of pir of lines is + + 5, b, c, f 5, g, h Now bc + fgh f bg ch 5 75
14 Std. XII : Triumph Mths 5 5 ( 5)( + 5) 5 5 or. Let m be the common line nd let m nd m be the other lines given b + + nd + b respectivel. Then, m + m, mm, nd m + m b, mm (mm ) (mm ) m (m m ) 9 m 9.[ m m (given)] m When m, mm nd mm m nd m m + m nd m + m b 5 nd b When m, mm nd mm m nd m m + m nd m + m b 5 nd b. Given eqution of pir of lines is 8 +, h, b tn tn 57 6 tn ( ) 6
15 5 Vectors Chpter 5: Vectors. Since, b nd b c re colliner with c nd respectivel b tc (i) b c s (ii) From (i) nd (ii), we get c tcs (s) c( t) But nd c re non-colliner + s, + t s, t Substituting vlue of t in (i) nd vlue of s in (ii), we get b c nd b c Hence, bc.. Given, r r r r b c ( ) ( )b ( )c,, 7,, +. Since, the given vectors re coplnr c c c b Appling C C C, c c b ( b) + c (c) c b Hence, c is the geometric men of nd b.. ˆ ˆ, bˆb ˆ, cˆc ˆ, ˆ ˆ ˆ bbcˆcˆ ˆ ˆ ˆ ˆbˆ ˆcˆ bc bˆ ˆ bˆbˆ bˆcˆ cˆ ˆ cˆbˆ cˆcˆ 5. Since, bc cubic units b c Appling R R R nd R R R, we get b c (b)(c) ()(c) ()(b) Dividing b ( )( b)( c), we get b c Consider, b c.(i).[from (i)] 6. Volume of the prllelopiped formed b vectors is i.e., V +
16 Std. XII : Triumph Mths dv d + dv, 6 d For m. or min. of V, dv d dv 6 > for d V is minimum for 7. Given,.b b.c c. The sclr triple product of three vectors is [bc] ( b).c.b b ngle between nd b is 9 Similrl, [ bc] b n.c ˆ where ˆn is norml vector. ˆn nd c re prllel to ech other [bc] b n. c ˆ 8. Given, r b c b r c b r c is prllel to b r c b for some sclr r c b r. c. + b c. + b b c..(i). r(given).c.b Substituting the vlue of in (i), we get.c r c b.b.c r.b c.b (b.b).b ( ) r.b 9 9. Let ci ˆj ˆ kˆ cc b cb c bc b c Let b c b c 9. 9 b (i ˆj ˆ k) ˆ b. 7i ˆj ˆk ˆ ( 6 ) Now,. Given, mb nc b mc n c m nb l l l. mb nc n b mc m nb c l l l l m n n l m bc m n l l m n n l m... bc m n l l + m + n lmn (l + m + n) (l + m + n lm mn nl) l + m + n B P M D O A H Let point O be the circumcentre of ABC. Let, b, c, p, d, h, m be the position vectors of the respective points. Since, h + b + c.(stndrd formul) C
17 m p h p b c DM m d p b c b c DM PA p p p p.[ O is circumcentre, OA OP i.e., p] DM is perpendiculr to PA. 7. Chpter 5: Vectors m n m n mz nz D,, mn mn mn ( 9) (5) (6) () ( ) (),, ,, ,, ,, A(,, z ) (l,, ) (,, n) 5. Let position vector of Q be r Since, p divides PQ in the rtio : 6. r (p q) p 7 p r+ p+ q 5 p q r r 5p q B distnce formul, AB (5 ) ( ) ( ) 9 A(,, ) B(5,, ) D C ( 9, 6, ) B(,, z ) (, m, ) C(,, z ) + l, +, + On solving we get l, l, l +, + m, + On solving we get m, m, m z + z, z + z, z + z n On solving we get z n, z n, z n A(l, m, n), B(l, m, n), C(l, m, n) B distnce formul, AB (l l) + (m m) +(n + n) m + n BC (l + l) + (m m) +(n n) l + n CA (l + l) + (m m) +(n n) l + m AB BC CA l m n m n l n l m l m n l m n 8 8 l m n 8. A(,, ) AC ( 9) ( 6) ( ) Point D divides seg BC in the rtio of : B section formul, B(, 7, ) D C(, 5, ) Let D be the foot of perpendiculr nd let it divide BC in the rtio : internll
18 Std. XII : Triumph Mths 57 D,, AD d 5 7 ˆ i ˆ j kˆ ˆi kˆ 5 7 ˆ i ˆ j kˆ i ˆ 5j ˆ k ˆ i ˆ 7 ˆ j k ˆ BC ˆij ˆ kˆ Since, AD BC. AD. BC ( ) 5 7 ( ) () D,, ,, ,,
19 6 Chpter 6: Three Dimensionl Geometr Three Dimensionl Geometr., Since, cos + cos + cos Since, AD is equll inclined to the es p 5 r p 7, r cos + cos + cos cos + cos cos + cos 6 7 cos () 8 If is cute, then cos is positive. cos 7 8. The d.r.s of AB re,, 6 5 i.e.,, Let, b, c,, d.r.s. of BC re, 5, 5 i.e.,,, Let, b, c,, + b b + c c () + ()() + () + + AB nd BC re perpendiculr. mabc 9. cos l l + m m + n n sin cos. cos l m n l m n (l l + m m + n n ) ll lmlnl mmmmn +ln mn nn ll mm nn ll mmmmnnnn ll l m ll mm l m mn mmnn mn ln ll nn l n (l m l m ) + (m n m n ) + (n l n l ). Given, A(,, 7), B(,, ), C(p, 5, r) Let D be the midpoint of BC. p 5 r D,, p r,, d.r.s. of AD re p r,, 7 i.e., p 5 r,, 5. The given equtions re 6mn nl + 5lm, nd l + m + 5n.(i) m l 5n.(ii) Substituting vlue of m in eqution (i), we get 6(l 5n)n nl + 5l( l 5n) 8ln n nl 5l 5nl 5l + 5ln + n l + ln + n (l + n)(l + n) l n or l n If l n, then m n l n nd m n l m n d.r.s. of the st line re,,. If l n, then m n l n nd m n
20 Std. XII : Triumph Mths l m n d.r.s. of the nd line re,,. cos cos 6 ( ) ( ) ( ) ( ) cos l m n cos 6. Since, (l m) l lm + m l + m lm.(i) Similrl, m + n mn.(ii) nd n + l nl.(iii) Adding (i), (ii) nd (iii), we get (l + m + n ) (lm + mn + nl) lm + mn + nl The mimum vlue of lm + mn + nl is. 7. Let A (,, ), B (, b, 7) nd C (,, 5) d.r.s of AB re, b, d.r.s of BC re 6, b, Since the points re colliner b 6 b, b 8. Let the d.r.s of the line perpendiculr to both the lines be, b, c. d.r.s of lines is,, nd,, b.(i) b + c.(ii) On solving (i) nd (ii), we get b c d.r.s of the line re,, the required d.c.s re,, 9. Since cos + cos + cos cos + cos + cos.[ ] cos
21 Trget Publictions Pvt. Ltd. 7 Line Chpter 7: Line z 7. Let r 5 r, 5r +, z r + 7 Co-ordintes of n point on the line re (r, 5r +, r + 7). This point lies on the curve 5 + z ( r ) 5(5r + ) + (r + 7) r + r + 5r 6r 7 + r + 8r + 9 r 55r 66 r + 5r + 6 (r + )(r + ) r or r If r, then the point is (,, ) nd if r, then the point is (,, ) option (A) is correct.. The given eqution of line is + 5, z 6. It cn be written s 5 z 6 r, s co-ordintes of the n point on the line re (r + 5, r, r 6). This point is t distnce of 6 from the point (5,, 6) (r + 5 5) + (r ) + (r 6 + 6) 6 6r + r + 9r 6r r 9 r If r, then the point is ( + 5,, 6) (7,, ). Let the components of the line vector be, b, c. + b + c (6).(i) Also, b c k, s 6 k, b k, c 6k Substituting vlue of, b nd c in eqution (i), we get 9k + k + 6k 6 9k 6 6 k k 9 Since, the line mkes obtuse ngle with X-is component long X-is is negtive. k 9 The components of the line vector re k, k, 6k i.e., 7, 8, 5. Let M be the foot of the perpendiculr drwn from the point P(,, ) to the given line. z Let, +, z + M (, +, + ) d.r.s. of PM re, +, 8 Since, PM is perpendiculr to the given line ( )() + ( + )() + ( 8)() M (, 5, 7) length of perpendiculr (PM) ( ) ( 5) ( 7) When squre is folded co-ordintes will be D(,, ), C(,, ), A(,, ), B(,, ). X A Y D B Y z Eqution AB is, z nd eqution of DC is C X
22 Std. XII : Triumph Mths shortest distnce ( ) ( ) ( ) ( ) ( ) 6. Given eqution of motion of rocket is t, t, z t z i.e., the eqution of the pth is z i.e., Thus, the pth of the rocket represents stright line pssing through the origin. For t sec. we hve,,, z Let M(,, ) OM z km Rocket will be t 6 km from the strting point O(,, ) in seconds. 7. d.r.s. of L re,, nd d.r.s. of L re,, ˆi ˆj kˆ vector perpendiculr to L nd L ˆ i() ˆ j(9 ) k(6 ˆ ) ˆi7j ˆ 5kˆ ˆi7j ˆ5kˆ ˆi7j ˆ5kˆ unit vector Let S be the foot of perpendiculr drwn from P(,, ) to the join of points A(, 7, ) nd B(, 5, ) P (,, ) Let S divide AB in the rtio : 57 S,,.(i) Now, d.r.s. of PS re, 5 7, i.e., 7, i.e., +, 5 + 7, Also, d.r.s. of AB re,, Since, PS AB ( + )() + (5 + 7)() + ()() 7 Substituting the vlue of in (i), we get S,, 9. Eqution of the line pssing through the points (5,, ) nd (, b, ) is b z 5 b.(i) 7 The line psses through the point,, 7 b b.[from (i)] nd + b 7 b 5b b 6, b A(,7,) S B(,5,)
23 Trget Publictions Pvt. Ltd. 8 Plne Chpter 8: Plne. Given plnes re c bz.(i) c + z.(ii) b + z.(iii) Eqution of plne pssing through the line of intersection of plnes (i) nd (ii) is c bz + k(c + z) ( + ck) (c + k) (b k)z.(iv) Now, plnes (iii) nd (iv) re sme for some vlue of k, ck c k (b k) b ck c k b + ck bc bk k(b + c) ( + bc) bc k b c c k Also, b k bc c bc b c b b c bcc bc b + bc + + bc c + b + bc + b + c + bc. Let, b, c be the intercepts form b the plne on co-ordinte es. Since, b c b c The point (,, ) stisfies the eqution of the z plne. b c the required point is (,, ).. Given eution of line nd plne re ˆiˆj i ˆˆj kˆ, nd r r. ˆi j ˆkˆ b i ˆˆj kˆ nd n ˆij ˆ kˆ Consider b n i ˆ ˆ jk ˆ ˆ i j ˆ k ˆ + the line lies in the plne.. The eqution of the given line is + t, + t, z t z The given line psses through the point,, nd it s d. r.s re,, The eqution of the given plne is + + 6z d.r.s of the norml to the plne re,, 6 b cz d p b c () () , 5 5(9) 5
24 Std. XII : Triumph Mths 5. Let be the vector long the line of intersection of the plnes 7 5z nd 8 + z. the d.r.s of the normls to the plnes re, 7, 5 nd 8,,. ˆi ˆj kˆ ˆ i( 55) ˆ j(6 ) k( ˆ 56) 69i ˆ 6ˆj kˆ Similrl, let b the vector long the line of intersection of the plnes 5 + z + nd 8 + z the d.r.s of the normls to the plnes re 5,, nd 8,, ˆi ˆj kˆ b 5 8 ˆ i( 6 ) ˆ j( ) k( ˆ 55 ) 7i ˆj ˆ 9kˆ Consider, 69i ˆ 6j ˆ k ˆ. 7i ˆ j ˆ 9k ˆ.b (6) ndbre perpendiculr 9 sin sin 9 6. The eqution of the given plne is ( + ) + z + z ( ) ( z ) 7. ( ) ( z) The plne psses through the point of intersection of the plnes nd z A(,, ) M B z 9 Let A (,, ), AM be to the given plne nd let B (,, z) be the imge of A in the Plne. the d.r.s. of the norml to the plne re,, The eqution of the line AM is z k, s k +, k, z k + Let M (k +, k, k + ) eqution of plne becomes (k + ) (k ) ( k + ) 9 k 7 6 M,, ,, Since, M is the mid point of AB. 7, z, , Imge of A is 5, z B,, Since, nd b re coplnr, b is vector perpendiculr to the plne contining nd b. Similrl, c d is vector perpendiculr to the plne contining c nd d. The two plnes will be prllel, if their normls b nd c d re prllel. bcd 9. Eqution of the plne contining the given lines is z 5 ( ) (5 6) ( ) ( ) + (z ) (8 9) ( ) () ( ) () + (z ) () + + z + + z + z.(i)
25 Chpter 8: Plne Given eqution of plne is A + z d.(ii) The plnes given b eqution (i) nd (ii) re prllel. A distnce between the plnes (D) is. D d d 6 6 d 6 Q d 6 Since, direction cosines of PQ re equl nd positive the d.r.s. of PQ re,, The eqution of the line PQ is z + z k, s Co-ordinte of the point Q re (k +, k, k + ) The point Q lies on the plne + + z 9 (k + ) + k + k + 9 k k Q (,, ) PQ. Let A (,, ), B (, b, ), C (,, c) b c G (,, z),,, b, c z, b, c z P(,, ) + + z 9.(i) The eqution of the plne is z b c Since, this plne is t distnce of unit from the origin, b c b c.[from (i)] 9 9 9z z k 9 9. Let the eqution of the plne OAB be + b + cz d This plne psses through the points A(,, ) nd B(,, ) + b + c, (i) nd + b + c (ii) on solving (i) nd (ii), we get b c 5 Similrl, let the eqution of the plne ABC be ( + ) + b( ) + c(z ) Substituting the co-ordintes of A nd B, we get + b c, nd + c b c 5 If is the ngle between two plnes, then it is the ngle between their normls. 5 ( ) ( 5) ( ) ( ) cos cos 9 5
26 Std. XII : Triumph Mths. The eqution of the given plne cn be written z s 5 Let the plne intersects the, nd z es in the points A(,, ), B(, 5, ), C(,, ) i,b ˆ 5j ˆ, nd c kˆ Volume of tetrhedron b c Given lines re coplnr. 5 k k ( + k) ( + k ) + ( k) k k + k k k k(k + ) k or k
27 9 Liner Progrmming Chpter 9: Liner Progrmming. Let no. of model M nd no. of model M, Constrints re + 8 +, Mimize z + The corners of fesible region re O(, ), A(, ), B(.5, 5), C(, 6) At A (, ), z () + 6 At B (.5,5), z (.5) + (5) 7.5 At C (, 6), z + (6) 8 z is mimum t B(.5, 5).. Objective function P + The corner points of fesible region re B(, ), C(,), D(, ), E(, ), F(8, ) At B P B () + () 6 At C P C () + () 5 At D P D () + () 9 At E P E () + () 7 At F P F (8) + () 7 P is mimum t F(8, ).. For (, ), >, for (5, ), 5 + >, nd for (, ), + > Similrl, other inequlities stisfies the given points. Option (D) is the correct nswer. 5. Y X C(, 6) O X Y Y O (,) Y (, ) Y B(,) C(,) B(.5, 5) A(, ) F(8,) E(,) D(,) (9,) + (, ) + X X (,5) (,) A(,6) B(8,6) C(,5) 6 X O Y (,) X D(5,) + + 5
28 Std. XII : Triumph Mths OABCD is the fesible region O(, ), A(, 6), B(8, 6), C(, 5), D(5, ) z + At point C nd D, z is mimum. M z 5 Infinite optiml solutions eist long CD. 6. Consider option (C) + () () + () () + 5() All the bove three in-equlities hold for point (, ). Option (C) is the correct nswer. 7. Let the mnufcturer produce nd bottles of medicines A nd B. He must hve + 66, + 5,,,,,. the number of constrints is Let the compn produce telephones of A tpe nd telephones of B tpe. Constrints re + 8 +, + Mimize z + Y (, ) (, ) + (, ) X O (,) Y + the fesible region of the LPP is bounded. X 9. Given tht + 8, + 5 the fesible region lies on origin side of + 8 nd + 5. Also,, the fesible region lies in first qudrnt. option (C) is correct. X. Objective function z + The corner points of fesible region re O(, ), A(, ), B(, ), C, 7 nd D(, ) At B(, ) nd C, 7, z is mimum. M z Infinite number of solutions eists long BC. X + D(,) O C, 7 A(,) X B(, ) X +
29 Chpter 9: Liner Progrmming. Objective function z + The corner points of fesible region re 5 A,, 5 B, 6 6, C(, ), D(, ), E(, ), 5 7 F, 5 At A z A.5 5 At B z B At C z C () + () At D z D () + () 9 At E z E () + () At F z F.5 Mimum vlue of z t (,) is 5. X O Y Y 5 (,6) F(5/, 7/) E(,) A(/, 5/) B(/6,5/6) D(,) C(,) + (6,) X + 6
30 Trget Publictions Pvt. Ltd. Continuit Chpter : Continuit cos(cos ). f() lim sin sin lim sin sin sin lim sin sin lim 8. f is continuous t. log( ) log( ) f () lim sec cos lim cos cos log( ) log( ) cos log log lim sin log log cos lim sin (cos ). For f() to be continuous t, we must hve f() limf( ) lim lim lim lim f() lim sin 5 ( ) 7 ( ) lim sin 5 7 lim sin / / 5 (log ) log 7 It is discontinuous t nd it is removble. lim lim sin log tn e 5 sin log( ) tn 5 e 5 5
31 Std. XII : Triumph Mths (). () () () For f to be continuous t, f() lim ( - lim e 7. Given function is continuous t (, 6). t nd, function is continuous. If the function f() is continuous t, then limf( ) limf( ) + sin + b. Given, f() [] [ ] < <, f() (), f() < <, f(), f(), f( ), f( ), f( ), f( ), f( ), f ( ) 5, f( ) 5, f( ) 5 Hence, the given function is discontinuous t ll integers ecept. + b...(i) If the function is continuous t, then lim f( ) lim f( ) + b 6 tn + b 6...(ii) From (i) nd (ii),, b 8. Since, nd re continuous for ll. + is continuous for (, ). 9. For f() to be continuous t, we must hve lim f() f() lim f() lim f() f() lim tn /tn lim e tn tn lim e e f() b e lim f() lim ( sin ) f() lim b e / sin lim sin sin e f() e e e
32 Differentition Chpter : Differentition Now, log( + ) log( ). 5 log log( + ) log( ) log log 8 log d 8 8. (cos + i sin ) (cos + i sin ).(cos(n ) + i sin(n )) i Since, cos + i sin e e i e i e i5 i(n ). e i[ (n )] e in e d in in e d d in ine n. f 5 d f d 5 d d f f tn 5 6 () cos + sin Since, d d d cos cos d sin (cos ) + d sin d (sin ) d cos sin ( sin ) + cos sin cos When, cos cos, cos nd sin sin, sin d +
33 Std. XII : Triumph Mths n 5.. d. n +. n n When, + + Ecept st term ll terms re. ( ) ( ) ( ). ( n) d ( ) ( ) n (n )!, 6. f (), Lf () lim f( ) f() lim Rf () lim f() is differentible t nd f (). 7. f() sin(log ) f () cos(log ) f d f d d coslog. 66 coslog 9 cos log 8. d tn blog d tn + b log d log tn, b b 9. f() cos cos cos cos 8 cos 6 6 ( sin cos cos cos sin cos 8 cos 6) 6 (sin cos cos cos 8 sin cos 6) 8 (sin cos cos 8 sin cos 6) (sin 8 cos 8 cos 6) sin sin 6 cos 6 sin sin sin f () sin cossincos sin f
34 Chpter : Differentition ( + ) ( + + ) ( + ) d d d d ( + ) + b, b. Let , d 5 d 5 5 ( ) 5 d ( d ) + d d d Dividing both sides b, we get d ( d ) d k 5. + d d 5 tn e Diff. w.r.t., we get d e tn..(i) d () 5 d d d. e + d d d d Diff. w.r.t., we get d d + + d d d d + d + d d d d ( ) d d d.(ii) tn + d d From (i), when, e From (ii), when, d d d e d d e d f g h. f() f g h f g h f g h f () f g h + f g h. f g h f g h f g h + d d f g h f g h f g h + +.[ f, g, h re polnomils of nd degree, f g h ] cos sin cos sin cos 5 sin 6 cos 7 sin 8 cos.[ C C ]
35 Std. XII : Triumph Mths 5. sin cos {sin(cos )} sin cos sin sin sin[cos (cos(sin )] sin(sin ) d d 6. 8 f() + 6f + 5.(i) Replcing b, we get 8f 5 6f() + 8f 5.(ii) (i) 8 (ii) 6 gives 6 f() 6 f() f() 8 6 Given, 6 f() (8 6 + ) d 8 ( 6 + ) ( 6 ) d f( ) 5 Diff. w.r.t., we get f ( ). 5 f ( ) 5 f (7) f ( ) 5 () 5 8. Since, g() is the inverse of f(). f[g()] f g( ) g( ) f g() g () g() f (g()).(i) f() + e / f() f () g().[ g() f ()(given)] From (i), we get g() f() Now, f() + e / f () + e/ f () g() / 9. f( ) d f ( ). tn( ) z g( 5 ) dz d g (5 ).5 5 sec( 5 ) d tn 5 dz dz 5 sec tn 5 sec d. Put sin nd sin 6 6 ( ) 5 sin sin (sin sin ) cos + cos (sin sin ) cos cos.sin cos cot cot sin sin constnt Diff. w.r.t., we get 6 6 d d 6 6
36 Chpter : Differentition. Let f() p + q + r f() f() p + q + r p q + r q. f() p + r f () p f () p, f (b) bp nd f (c) cp Since,, b, c re in A.P. p, bp, cp re in A.P. f (), f (b), f (c) re in A.P. d sec tn + sin d n n nd n sec.sectn n cos.( sin ) d n n n sec tn n cos sin n n d n sec tn n cos sin d d sectn sin d Dividing N r nd D r b tn, we get d seccos n n n(sec cos ) n n n (sec cos ) d (seccos ) (seccos ) sec.cos n n [(sec n cos ) n sec n cos ] n( ) ( + ) d. f() f () + n ( + ) sin cos tn sin 5 sin cos tn sin 5 cos cos sec cos 5 + sin sin tn sin 5 f( ) sin cos tn sin 5 cos cos + sec cos 5 + sin sin tn sin 5 f( ) lim Since, g is the inverse of f. f[g()] Diff. w.r.t., we get f (g()) g() g() + [g()] 5 f(g( )) sin sin sin sin sin sin sin sin nsin(n ) sin( ) sin( ) sin((n ) n )... sin sin sin sin sin nsin(n ) sin cos cos sin sin cos sin sin sin sin sin sin cos sin sin(n ) cos n cos(n ) sin n... sin sin sin nsin (n ) sin nsin (n ) cot cot + cot cot +. + cot n cot(n+ ) cot cot(n + ) d cosec [ cosec (n + )] (n + ) (n + ) cosec (n + ) cosec 6. If r <, + r + r +. + r sin + sin + sin 6 sin +. sin sin cos tn e tn d tn e. tn sec tn e tn sec 5
37 Std. XII : Triumph Mths 7. tn + tn + tn +. to n terms 57 tn ( ) + tn ( + )( + ) + tn +. to n terms ( + )( + ) tn ( ) ( ) + ( ) ( + ) tn ( )( + ) + tn ( ) ( ) +. to n terms ( )( + ) tn ( + ) tn + tn ( + ) tn ( + ) + tn ( + ) tn ( + ) +. + tn ( + n) tn ( + (n )) tn ( + n) tn d ( n) d n n n n n 8. sin(b + c) cos(b + c).b b sin b c b sin(b + c).b b sin( + b + c) b cos(b + c).b b sin b c b ( sin(b + c).b) b sin( + b + c) b sin b c In generl, n b n sin n b c f()! f ()! f ()! n C n() f() f()! n n n C n n(n )()! n(n )(n )()! + f ()! n(n )! n f ()! n C n(n )(n )! +.+() n n f () n! n C n C + n C n C +. + () n n C n. p cos + b sin dp d. cos ( sin ) + b. sin cos (b ) sin dp d (b ) cos (b ) (cos sin ) dp p + d cos + b sin + (b ) (cos sin ) cos ( + b ) + sin (b b + ) cos ( + b ) + sin ( + b ) ( + b ) (cos + sin ) + b ( + b ) c.[ + b c (given)] 9. f() n f () n n f () n(n ) n f ( ) n(n ) (n ) n f() n n C 6
38 Applictions of Derivtives Chpter : Applictions of Derivtives. Let f() + b + c + d f() nd f(). + b. + c. + d b + 9c + d (7 + 9b + c + d) f() f() f() is polnomil function, it is continuous nd differentible. Now, f () + b + c + d B Rolle s theorem, there eist t lest root of the eqution f () in between nd.. The eqution of the curve is + b + c. d.(i) Since, the curve touches the line t (,). [ + b] (, ) () + b b Substituting the vlue of b in eqution (i), we get d Since, grdient is negtive. d < < <. The eqution of the prbol is 8. d d 8 d 8 m Slope of given line, m m m Since, tn m m tn or 8 Putting in the eqution of the curve, we get the point of contct is,.. f() tn log f () ( ) ( ) Now, f () f() tn log..785 Since, we re finding mim on n intervl,. We hve to find the vlue of f() t nd f tn + log log 6. log f ( ) tn log log the gretest vlue of f() is + log. 6
39 Std. XII : Triumph Mths 5. + cos cos sin Let cos cos cos sin sin cos. cos d Now, d cos d d Also, sin < d is mimum when it is mimum t 6. Let P(, ) be the point on the curve t which tngent is drwn. The eqution of the curve is c. d d d (, ) The eqution of the tngent is ( ) + + The tngent meets the X-is in the point A(, ) nd the Y-is in the point B(, ) P is the mid point of AB The rtio is : b 7. Let f() c d f () + b + c Now, f() + b b 6c 6d + c + d 6 f() 6d d.[ + b + 6c ] 6 Also, f() d f() f() f() is polnomil function, it is continuous nd differentible. There eists t lest one vlue of in (, ) t which f () + b + c one root of the eqution + b + c hs vlue between nd. 8. f() sin ( + cos ) sin + sin cos f() sin + sin f () cos + cos cos cos f () cos or cos or or f () sin sin <, onl when The mimum vlue of function is t f 9. f() sin + cos (sin + cos ) sin cos f() sin f () ( sin cos ) f () sin cos Now, f () sin or cos or Since, f () sin cos f () sin f() cos For, f() < For f() > At, f() is minimum Minimum vlue of f() ()
40 Chpter : Applictions of Derivtives. ( ) 7 is minimum when 7 is minimum. Since, ( ) ( 9 + 7) 9 7, for ll Minimum vlue of ( ) + 7 is. Minimum vlue of ( ) 7. f() cos 6 + b cos 6 + b.[ cos ( ) cos ] f () sin 6 The function f() is incresing for ll R. f () > sin 6 > 6 < sin < sin <. Let f() sec + b cosec f (). sec sec tn + b. cosec ( cosec cot ) sec tn b cosec cot Now, f () sec tn b cosec cot. cos sin cos b sin cos sin sin cos b tn b tn b nd cot b Also, f () sec.sec tn.sec sec tn cosec ( cosec ) b cot.cosec ( cosec cot ) sec + sec tn b cosec cosec cot f () > for ll. f() is minimum when tn b Minimum vlue of f() ( + tn ) + b ( + cot ) b + b b b b b b ( + b) + b( + b) ( + b) b b. ( )( ) 5 d ( 5) (b)(5) ( 5) For etreme (i.e., mimum or minimum) d ( 5 + ) ( + b) ( 5) Since, hs n etreme t P(, ) stisfies bove eqution ( + ) ( + b) () + + b b, stisfies the eqution of the curve () b, b. Let f() tn f () sec + tn f () > for, f() is incresing in the intervl, Since, < < < f() < f() tn < tn < tn tn
41 Std. XII : Triumph Mths 5. The point of intersection of the given curves is (, ). Now, log d d (,) log m (s) Also, 5 5 log5 d log 5 m (s) d (,) m m log log5 tn m m log log5 6. Let f() + b + c f () + b since, nd re roots of the eqution + b + c f() f() f() being polnomil function in, it is continuous nd differentible. There eists k in (, ) such tht f (k) k + b, k b But k [, ] < k < < b < 7. f() tn (sin + cos ) f () (cos sin ) (sin cos ) cos (sin cos ) For f() to be incresing, f () > cos > cos > < + < < < f() is n incresing function in,. 8. f() + 6 Diff. w.r.t., we get f () () + 6 () + 6 Now, f () ( ) ( 6) or 6 Also, f () 6 [f ()] < [f ()] 6 6 > Mim t p nd minim t q 6 p q.(given) (6) The functions e, sin, cos re continuous nd differentible in their respective domins. f() is continuous nd differentible Also f f 5 Now, f () e (sin cos ) + e (cos + sin ) e ( sin + cos + cos + sin ) e cos Also, f () cos 5,..(i) Diff. w.r.t., we get d d d d slope of the norml Since, the norml to the given curve mkes equl intercepts with the is. Substituting in (i) nd solving, we get 8 the point, 9 7.
42 Integrtion Chpter : Integrtion. Let I 5 6 d 5 5 Put t. d 5. d 5() d dt d I t dt 5 dt 5 / t. + c 5 / 5 75 / + c. Multipling N r nd D r b sin, we get cos5 cos d cos sincos5sincos d sin sin cos sin cos5 cos d sinsin 6 9 sin cos cos cos d 9 cos sin cos cos d cos cos d sin sin + c. Let I sin d Put tn t d tn t sec t dt tn t I sin tn t sec t dt tn t sin (sin t) tn t sec t dt ttntsec tdt d ttntsec tdt (t) tntsec tdtdt dt tn t tn t t.. dt ttn t (sec t)dt ttn t tntt c, where t tn tn tn + c. Let I cosec d sin d sin d sin sin sin d sin sin cos d sin sin Put sin t cos d dt I dt t t dt t t
43 Std. XII : Triumph Mths t log t t t c, where t sin dt log sin + sin sin + c 5. Let I tn d Put tn t sec d tdt t d dt t t I t. dt t t dt t t t dt t t t dt + dt t t I + I (s).(i) t I dt t t dt t t dt t t t, where t t tn tn t t t tn t t I dt t t dt t t dt t t t dm, where t + m t m log m t m log t t t log t t t t From (i), I t tn + t log t t t t + c tn tn tn tn tn + log + c tn tn / 5/ 6. Let I / d Put t 5 d / 5.( 5/ ) /. / d 5/ dt, / d 5 dt I (t ).t. dt 5 t 5/ t / t / 5 dt 7/ 5/ / t t t c, where t 5/ / / 5/ 7/ 5/ 5/ / + c
44 tn 7. Let I tn tn d tn sec tn d sin cos d sin cos cos sin cos sincos d sin d sin sin sin d sin sin d sin d I (s).(i) I sin d Put tn t sec d dt d t tn sin tn t t I dt t t t dt t t dt t t dt t t tn + c dt From (i), tn tn + c I tn tn + c A A 8. Let I log d Put log t I d dt A 9. Let I d dt t. dt t c Chpter : Integrtion log + c d d ( ) Put + tn d sec d sec I d (tn ) sec d sec + cos d ( cos ) d sin c ( + sin cos ) + c tn ( ) c tn ( ) + c
45 Std. XII : Triumph Mths. Let I d 6 6 cos sin Since, + b ( + b) b( + b) cos 6 + sin 6 sin cos.[ + b cos + sin ] I sin cos d d sin sin d cosec d cosec cosec d (cot ) ( cosec ) d cot Put cot t cosec d dt I dt t tn (t) + c tn ( cot ) + c tn cos sin + c sincos tn (cot tn ) + c tn (tn cot ) + c. f( )sincosd log[f ( )] + c (b ) d log f ( ) c d (b ) f() sin cos f () f() sin cos (b ) f ( ) f( ) (b ) sin cos [f ( )] Integrting on both sides, we get f( ) d (b ) sincosd f( ) f( ) (b ) sincosd b sincosd sincosd b ( cos ) (sin ) f( ) b cos sin f() sin b cos sin. Let I e log(sin ) cosec cosd Put sin t cos d dt t I e logt dt t t e logt dt t t t t e logt c t. d. log t dt t t t sin e log(sin ) c sin sin e log(sin ) cosec c cos sin tn log log cos sin tn Since, log tn secd log tn d log tn sec.(i) d Integrting the given epression b prts, we get sin I logtn sin secd.[from (i)] sin logtn tn d sin logtn log(sec ) c. Let t ( ) () t ( ) () t
46 Chpter : Integrtion 6 t 8 t t t + t t + t6t6 t t t Given, f + t f(t) t t 5 t t t t 8 (t ) f() 8 ( ) f( )d 5. Let I log log ()d 8 d ( ) 8 log + c d log( ) d log( ). d log dd d d log( ) + d log( ) + I.(i) Now, I Put t, d t dt d I t t t.t dt dt t t dt t t dt t tdt t t log( t) t + c log( ) + c From (i), I log( ). log ( ) + c c 6. P() d, Q() d P() + Q() d d d + I.(i) I ( ) d A Put ( ) C + A B ( ) C( ).(ii) Putting in (ii), C Putting in (ii), A Putting in (ii), B I ( ) log log log + 5
47 Std. XII : Triumph Mths From (i), P() + Q() + log log + + c (P + Q) () P() + Q() + log log + + c 5 5 log + c. 5 (PQ)() c log P() + Q() + log log + + log P() + Q() + log log + + log + log 8 sin bsin 7. Let I d (bcos ) ( bcos ) sin d (bcos ) Put b + cos t sin d dt sin d dt t b b I t dt btb dt t ( b )t bt dt b b + c t t b b + + c t t 8. Let I ( ) d Put t, d t I dt t t t dt dt t t t dt t5t dt 5 t t 5 5 dt 5 t t dt 5 t 5 5 t log t t + c log c 5 5 ( ) 5( ) 5 9. Let I 5 5 5( ) log cos sin e d sin e ( cos ) sin sin e e d Put e sin t [e sin cos + e sin ()] d dt e sin ( + cos ) d dt I dt dt t( t ) t( t)( t) + c Put A B + t( t)( t) t t + C t A( t) ( + t) + Bt( + t) + Ct( t).(i) Putting t in (i), we get A Putting t in (i), we get B 6
48 Chpter : Integrtion I Putting t in (i), we get C / / dt t t t log t log t log + t + c t e log c log t e sin sin tn(sin )d + c. Let I tn tn d d Put t, d dt, d dt + t t + t t d (t ).t (t ). dt (t ) t t d dt (t ) t t I dt t (t) t t dt t(t ) t t Put A B + t(t ) t t + C (t ) t t + A(t ) + Bt(t ) + Ct Putting t in (i), we get A Putting t in (i), we get.(i) I dt t dt t + c + c t 5/ 7/. Let I sec cosec d 5/ 7/ cos sin d 5 Now 7 5 Multipling nd dividing b cos, we get 5/ 7/ I cos cos sin sec d 7/ tn ( + tn )sec d Put tn t, sec d dt 7/ I t (+ t )dt 7/ / t +t dt / / t t + c / / (tn ) (tn ) + c. Let I Put + d t t C Putting t in (i), we get A + B + C B B I. dt t (t) (t) log t log(t ). t + c log t log(t ) t + c, where t + nd t + P, Q, R. Let I ( ) Put t, d dt t I t dt t t d 7
49 Std. XII : Triumph Mths tdt t t Put t m t dt m dm, t dt m dm mdm m m I m dm m tn c t tn c tn c tn + c cot + c tn + c tn. Let I d Dividing N r nd D r b 5, we get 5 I d + c Put t d dt 5 I dt t c t c log 5. d ( ) log.( ) d log.. d log + d ( ) log + n 6. I n sin d n sin.sin d sin n sin d d log + log log + + c d n sin sin d d d sin n ( cos ) n (n )sin cos ( cos )d sin n n cos + (n ) sin cos d sin n n cos + (n ) sin sin d sin n n n cos + (n ) sin sin d sin n n cos + (n ) sin d n (n ) sin d I n sin n cos + (n ) I n (n ) I n I n + (n )I n (n )I n sin n cos ni n (n ) I n sin n cos 7. u f () sin + f () cos du f () sin f () cos d + f () cos f () sin f () sin f () sin v f () cos + f () sin dv f () sin + f () cos d + f () cos + f () sin f () cos + f () cos du d + dv [ f () sin f () sin ] d + [f () cos + f () cos ] 8
50 Chpter : Integrtion [f ()] sin + f () f () sin + [f ()] sin + [f ()] cos + f () f () cos + [f ()] cos [f ()] + f () f () + [f ()] [f () + f ()] /.[ sin + cos ] du dv d d d f ( ) f ( ) d f () + f() + c 8. Let I ( ) d ( ) d ( ) d d sin cos sin cos sin cos d sin sin cos + cos sin cos (sin + cos ) d Put sin cos t (cos + sin )d dt I t dt sin (t) c sin (sin cos ) + c Put + t d t dt t I dt (t ) t dt t tn t + c tn + c d sin cos d cos sin sin + cos sin cos d 9. Let I tn cot (sincos ) d sin cos sin cos sincos d 9
51 Trget Publictions Pvt. Ltd. Definite Integrls Chpter : Definite Integrls log( ). Let I d Put tn t d sec t dt When, t nd when, t I I log( tn t log( tn t) dt tn t) sec t dt log tn t dt tnt log dt tnt log dt tnt [log log( tn t)]dt (log )dt I I logt / log I 8 log. 5 f( )d + f( )d + f( )d + + f( )d f( )d + 5 d d d d 5 f( )d ( ) + ( ) + 9( ) + 6(5 ) Let I I d. (i) f( ) d f( ) d f( ) f( ) f( ). f( )d f( )d.[ f() + f( ) (given)] d. (ii) Adding (i) nd (ii), we get I I f( ) d + f( ) f( ) f( ) d f( ) log. Let I d ( ) d d log log d d ( ) ( ) I + I (S).(i) log I d ( ) Put d When, nd when,
52 Std. XII : Triumph Mths I log d log ( ) log ( ) log d ( ) I I From (i), I I + I 5. n [ ]d. log log n [ ]d + [ ]d + [ ]d + + [ ]d 6. I n n d + d + d + + n (n ) n n (n )d ( ) + ( ) +. + (n )(n n + ) + () +. + (n )() (n ) (n )n n(n ) I I / sin d sin / sin d sin / / / sin d sin (sin sin ) sin (sin cos ) sin d / cos d d / (9 sin 6sin )d I +I I I, I, I re in A.P. 7. Let I d ( )( ) Put sin t + cos t d (. sin t cos t +. cos t ( sin t))dt ( ) sin t cos t dt When, sin t + ( sin t) + ( ) sin t sint, t When, ( cos t) + cos t + ( )cos t cos t, t ( ) ( ) ( sin t + cos t ) ( sin t cos t) [ cos t ( sin )] [( cos t) sin t] ( ) cos t ( ) sin t Since, > ( )( ) ( ) sin t cost I ( )sintcost dt ( )sintcost ( )dt dt t / 8. Let h() f() e e h() () e e e e e e h() h() h() is n even function.
53 Chpter : Definite Integrls tf(t)dt h(t)dt h(t)dt 9. f(m, n) t f(t)dt f( )d. f( )d m n (log ) d m n d m n d (log ) d (log ) dd n m m n (log ) m(log ) d n n m m n (log ) d n.[ log ] m f(m, n) n. () 7 6 (sin t cos t)dt () sin + cos If 7, 6, then is in the third qudrnt. sin nd cos re both negtive. () sin + cos < 7 () is decresing on the intervl, 6 7 Minimum (lest) vlue of () on, 6 / is (sin t cos t)dt 7 /6 cost sint / 7 /6 7 7 cos cos sin sin Let I b f( )d Put (b )t + d (b )dt When, t nd when b, t I f (b)t (b)dt (b ) f (b )t dt (b ) f (b ) d b. If <, then <, [ ] If <, then <, [ ] If.5, then.5, [ ].5.5 d d + d + d d + d d + (.5 ) +. f f().(given) f() f sec sec Let I f( )d f d I cos cos Put t, d dt When cos, t sec nd when sec, t cos cos sec I + I I I sec f(t)dt f(t)dt cos sec f( )d I cos
54 Std. XII : Triumph Mths. 5. n n lim n n n n n n n... n n(n) lim... n (n ) n n n n (n) lim n n r d r n ( ) () lim n n r r r n n n lim n r n r r n n n n lim n r n r r n n d Put + t. d dt d dt When, t nd when, t I dt t t 5 6. f( ) f( ) f( ) f( ) Integrting on both sides, we get logf ( ) logc f ( ) ce f() c c f() e Now, f() + g() g() e f( )g( )d 7. Let I I e( e)d e e d e e e e e e ( sin cos )d ( sin cos )d ( sin cos )d sin cos is periodic... function with period (sin cos ) d sin d+ cos d [I + I ] (S).(i) Where I sin d ( cos )( sin ) d Put cos t, sin d dt When, t cos nd when, t cos
55 Chpter : Definite Integrls I ( t )dt ( t )dt t t I 8. I cos d cos d sin d I From (i), I 8 sin cos d sincos cos sin d sincos... f( )d f d sin cos d I sincos I I I cos cos 6 6 d d.[ cos 6 is periodic f n with period ] 6 6 (cos + cos ( ))d.. f( )d [f( ) f( )]d cos 6 d I I I sin d log d log d log d.[ sin is n odd function]. log d f( )df( )d I I I I I I I, but I 9. Let I n sin n sin cos n I sin n d ( )sin ( ) n n sin ( ) cos ( ) n sin d I n n sin cos n sin n n sin cos n sin cos n n sin d n n sin cos n d d n is periodicf with period 5 f( )d f( )d., if f ( ) f ( )
56 Std. XII : Triumph Mths. 6 bsin sin cd cos i.e., I + I + I I sin d sin d sin d ( sin )dsin d cos cos / / I bsin d cos blog cos / /. cos cos c I c d c I + I + I becomes + c.[ I ] The given eqution is reltion between nd c. log. Let I cose I e d Put e t e d dt When, t e When log, t log / e cos tdt sin t / sin sin sin. f() f( + ) f() + f() + f() + 6 sin tdt + 6 sin tdt 6 sin (u 6 sin u du 6 sin tdt f( + ) f() + f(). Let f() + b + c f () + b f () f() c f () b 7 f () 8 f() sin tdt sin tdt )du, where t u + f() + f() ( 7 )d f( )d A f( )d A Asin B d A A cos B A B A B
57 Chpter : Definite Integrls Now, f() A sin B f () A cos. f A. 5. f() 6. A A sin sin sin sin sin sin sin sin sin sin sin sin sin (C C C C ) sin sin ( sin ) sin sin sin f( )d sin d cos / cos cos cost cos t sin t cos t dt / sint sintcostsint ( ) () ( ) ( ) + + from the given condition, + + ( + 5) ( ) 5 The positive integer vlues of stisfing the bove inequlit re,,,. There re such vlues. 7. Since, sin sin 5 6 [sin ]d [sin ]d [sin ]d [sin ]d [sin ]d 7 6 ()d ()d ( )d ( )d Appling R Rsec R, we get sec cot cosec cos f ( ) cos cos cosec cos cos (sec + cot cosec cos ) (cos cos ) (sec + cot cosec cos ) ( cos sin ) sin cos + cos sin sin cos ( sin ) 5 sin cos 5 f( )d (sin cos )d
58 Std. XII : Triumph Mths 9. d < /. + + < + 6 < < < < But cnnot be negtive nd ccording to the problem, < < < <. Let I Put I sin e d t d dt 6 sin t e t 6 sin e 6 [f ( )] dt d f(6) f() k 6 sin e d sin d e. [f ( )] d 8
59 5 Chpter 5: Applictions of Definite Integrl Applictions of Definite Integrl. Y. Y + 5 X O X (, ) (, ). X Required re sin d Y O sin d sin d cos cos sin d sin d cos cos() (cos cos) () ( ) + () sq. units Y Y sin X X Required re (, ) O (, ) (, ) X Y 5 d ( ) d 5 5 sin 5 ( )d + 5 sin 5 5 sin 5 sin sin Y Required re d sin / cos ( ) sq.units + 5 sin sin 5 sin sin sin cos 5 5. sin cos 5 5 sq.unit
60 Std. XII : Triumph Mths. Y B(,) X (, ) O A(,) X + (, ) + Y Required re (re of OAB) d d sq. units 5/ + 5/ ( ) sin sin sin ( ) sq.unit 6. The point of intersection of the curve nd the line re (, ) nd (, ). 5/ 5. The given eqution cn be written s Y ( ) + ( ) This is circle with centre t (, ) nd rdius. X O (, ) (, ) X Y X Required re O Y (, ) 5/ (, ) 5 5 d ( ) d () + () X Y Required re [( ) ( )]d ( )d 9 sq. unit (, )
61 Chpter 5: Applictions of Definite Integrl 7. Y ( + ) X O, (, ) Y or cos, X 9. + () sq.unit + Y Required Are cos d cos d (, ).[ cos is n even f n ] sin (sin ) sin X O Y X 8. X O Y cos sin 5 X Required re ( )d Required re cossin d Y. Y sq. unit (cos sin )d+ (sin cos )d 5 X O X + (cos sin )d 5 / 5 / sin cos cos sin / 5 / + / sin cos Y Putting in the given eqution, we get or
62 Std. XII : Triumph Mths Required Are d ( ) 8 Required re d + d / sq. units /. Y (, ) sq.units ( ). + + X B A C Y O D(, ) X. Required re + X O Y (, ) (, ) (6 ) 6 sq. units O Y Y (, ) (, ) (5, ) + (, ) X X + + d d + () + + d (,) The eqution of the tngent t the point (, ) is ( ) i.e.,. It psses through origin. Required re re of the region OABCO + re of the region OCDO d ( )d ( )d ( )d ( )d ( )d Y sq. unit 6
63 Chpter 5: Applictions of Definite Integrl. The eqution + is of ellipse with centre t origin nd the eqution is of prbol with verte t origin. Solving the equtions, we get + ( + )( ) But is not possible, since both points of intersection lie on the right hnd side of Y-is. nd ± The points of intersection re A, nd X B,. Required re + d d 8 O Y Y B, sin ( ).[ the function is even] A, X 8 5. X sin sq. unit Y O Y Slope of tngent d d + ( )d + + c The curve psses through the point (, ). + + c c The eqution of the curve is +, which is prbol s shown in the figure. Required re ( )d 5 sq. unit 6 6. Drw AP to X-is. A A(OAP) A Are bounded the curve OA nd the lines OP nd AP d d Required re A A sq. unit 6 + X 5
64 Std. XII : Triumph Mths X 6, C X Y Required re re of the rectngle OABC re of the region OBCO O Y sin sq. units + Q (, ) Y The eqution of the prbol is ( ) Diff. w.r.t., we get ( ) d d d ( ) d ( ) (,) B, A, O Y sin (, ) / cos Eqution of tngent is ( ) 6 + It cuts the X-is t the point Q (, ) nd the prbol cuts the X-is t the point R(5, ). X R (5, ) ( ) X required re d ( ) () 6 9 d sq. units 9. Required re sin sin d cos cos sin sin. cos cos cos sin cos sin cos sin cos sin cos sin cos sin d cos sin cos sin d tn tn d tn tn tn tn tn d d tn tn Put tn t sec d dt required re tn 8 t t t t ( t ) t dt dt. tn 8
65 6 Differentil Equtions Chpter 6: Differentil Equtions. The given eqution is ( ) Put sin, sin The eqution becomes cos + cos (sin sin ) cos cos sin cos cot cot sin sin cot Differentiting w.r.t., we get d d d d Degree nd order re both.. Since, the given differentil eqution cnnot be epressed s polnomil in differentil coefficients, so its degree is not defined.. The eqution of tngent t n point P(, ) is Y d (X ) d d This meets the X-is t A,. d Similrl, it meets the Y-is t B,. d According to the given condition, P is the mid-point of AB. d nd d d + d nd + d d Both of these equtions reduce to d Integrting both sides, we get log + log log c log () log c c, which is the eqution of rectngulr hperbol.. A Put tn, tn The eqution becomes sec + sec A (tn sec tn sec ) sin sin A cos cos cos cos cos cos cos cos sin sin A cos cos cos cos cos + cos A (sin sin ) cos cos cot A cot A tn tn cot A Differentiting w.r.t., we get d d A. sin cos Degree nd order of the differentil eqution re both.
66 Std. XII : Triumph Mths 5. f d f Put v d v + dv d The given eqution becomes, v + dv d v + f(v) f(v) d f(v) dv f(v) Integrting on both sides, we get log log f(v) + log K f(v)k Kf f K c, where c K 6. The given eqution is d f( ) f( )f( ) d f( )d f( ) I.F. e e the required solution is.e f () f( ) e.f( )f ( )d t e.tdt, where f() t t t t.e e.dt te t e t + c.e f () f() e f () e f () + c f () f() + ce 7. The given eqution is ( + ) f () ( e + ) f() If f(), the eqution is e, which is liner eqution d ( ) d I.F. e e the required solution is.e d + c c ( ) When, 5 c 6.e f() e 8. d ( + ) d + d d ( + ) d Dividing b, we get d d d d Integrting both sides, we get c + c When,, c the required solution is i.e.,, which is the eqution of hperbol. d 9. d + + (d + ) + d d( ) d tn Integrting both sides, we get c ( ) tn + + tn c tn c tn c tn c c tn
67 Chpter 6: Differentil Equtions. d d tn ( ). d d +. tn ( ) d d ( ) tn ( ) dz d tn z, where z d cot zdz Integrting both sides, we get log (sin z) + c log(sin ) + c When,, z log + c, c the required solution is log (sin ) + log (sin ) sin ( ) e. d + tn e sec Dividing b sec, we get tn e sec d sec cos d d + ( sin ). e Put sin t, cos d d dt d the eqution becomes, dt e t, which is liner eqution d d log log I.F. e e e the required solution is t e. d t e e + c sin. e e + c When, c sin. e e sin ( ) e.. We hve, d d tn sec d d tn sec d d tn sec Put t, dt d d The eqution becomes, dt (tn ) t d sec, which is liner eqution. tn d I.F. e log (sec ) e sec the required solution is t sec sec d c sec tn + c sec (c + tn ). ( ) d d d Dividing b, we get d d Put t d dt The eqution becomes dt t, which is liner eqution d I.F. e e log the required solution is t d + c t log + c log + c (log + c) The curve psses through the point (, ). ( + c), c the required solution is (log ).
68 Std. XII : Triumph Mths. d e ( e ) e d e ( e ) e d e e.e e d + ee e Put e dt t, e d d The given eqution becomes dt e.t e, d which is liner eqution. e d e I.F. e e the required solution is e t.e e e.e d e t.e z e.dz e z + c e e c e e e.e e c, where e z 5. The eqution of the tngent to the curve f() t P (, ) is Y d (X ) d d This meets the X-is t,. d According to the given condition, d d d d d, which is homogeneous d.e. Put v d v + dv d the eqution becomes, v + dv d v v v v dv d v v v v v v v v dv d v Integrting both sides, we get v dv d v + c log v log + c v log log + c 6. log + log log + c log c This curve psses through (, ). c log + log log e e e e.e d d d + c ( + c) ( + c) + Rdius is fied, which is nd the centre is (c, ) which is vrible centre on the X-is.
69 Chpter 6: Differentil Equtions 7. (A) t t f(t, t) t t t t f(, ) Homogeneous of degree. 8. t (B) f(t, t) (t ) (t ) tn (C) t (t) tn t f(, ) Homogeneous of degree. f(t, t) t log t t log t t t tlog t e t t log log e t f(, ) Homogeneous of degree. (D) + t e f(t, t) t t t log log(tt ) t t t + t tn t t + tlog t tn ( ) Non-Homogeneous. sin d tn d tn sin d sin tn sin, which is liner eqution cosec d log(tn ) log (tn ) I.F. e e e log cot e cot t t the required solution is tn cot cot c sin sin d c tn cos sin cos sec tn + c cot tn c The curve psses through,. + c, c the eqution of the curve is tn 9. The eqution of hperbol is m d (slope of tngent to the hperbol) m d slope of tngent to the required d fmil of curves. The curves re intersecting orthogonll, m m d d Integrting both sides, we get + c, 6 which is the eqution of required fmil of curves.. The given eqution is d ( ) ( ) d ( ) d ( ) d ( ) (+ ) d, which is liner d ( ) eqution d I.F. e e log 5
Trigonometric Functions
 Trget Publictions Pvt. Ltd. Chpter 0: Trigonometric Functions 0 Trigonometric Functions. ( ) cos cos cos cos (cos + cos ) Given, cos cos + 0 cos (cos + cos ) + ( ) 0 cos cos cos + 0 + cos + (cos cos +
Trget Publictions Pvt. Ltd. Chpter 0: Trigonometric Functions 0 Trigonometric Functions. ( ) cos cos cos cos (cos + cos ) Given, cos cos + 0 cos (cos + cos ) + ( ) 0 cos cos cos + 0 + cos + (cos cos +
CET MATHEMATICS 2013
 CET MATHEMATICS VERSION CODE: C. If sin is the cute ngle between the curves + nd + 8 t (, ), then () () () Ans: () Slope of first curve m ; slope of second curve m - therefore ngle is o A sin o (). The
CET MATHEMATICS VERSION CODE: C. If sin is the cute ngle between the curves + nd + 8 t (, ), then () () () Ans: () Slope of first curve m ; slope of second curve m - therefore ngle is o A sin o (). The
1. If * is the operation defined by a*b = a b for a, b N, then (2 * 3) * 2 is equal to (A) 81 (B) 512 (C) 216 (D) 64 (E) 243 ANSWER : D
 . If * is the opertion defined by *b = b for, b N, then ( * ) * is equl to (A) 8 (B) 5 (C) 6 (D) 64 (E) 4. The domin of the function ( 9)/( ),if f( ) = is 6, if = (A) (0, ) (B) (-, ) (C) (-, ) (D) (, )
. If * is the opertion defined by *b = b for, b N, then ( * ) * is equl to (A) 8 (B) 5 (C) 6 (D) 64 (E) 4. The domin of the function ( 9)/( ),if f( ) = is 6, if = (A) (0, ) (B) (-, ) (C) (-, ) (D) (, )
Board Answer Paper: October 2014
 Trget Pulictions Pvt. Ltd. Bord Answer Pper: Octoer 4 Mthemtics nd Sttistics SECTION I Q.. (A) Select nd write the correct nswer from the given lterntives in ech of the following su-questions: i. (D) ii..p
Trget Pulictions Pvt. Ltd. Bord Answer Pper: Octoer 4 Mthemtics nd Sttistics SECTION I Q.. (A) Select nd write the correct nswer from the given lterntives in ech of the following su-questions: i. (D) ii..p
IMPORTANT QUESTIONS FOR INTERMEDIATE PUBLIC EXAMINATIONS IN MATHS-IB
 ` K UKATP ALLY CE NTRE IMPORTANT QUESTIONS FOR INTERMEDIATE PUBLIC EXAMINATIONS IN MATHS-IB 7-8 FIITJEE KUKATPALLY CENTRE: # -97, Plot No, Opp Ptel Kunt Hud Prk, Vijngr Colon, Hderbd - 5 7 Ph: -66 Regd
` K UKATP ALLY CE NTRE IMPORTANT QUESTIONS FOR INTERMEDIATE PUBLIC EXAMINATIONS IN MATHS-IB 7-8 FIITJEE KUKATPALLY CENTRE: # -97, Plot No, Opp Ptel Kunt Hud Prk, Vijngr Colon, Hderbd - 5 7 Ph: -66 Regd
π = tanc 1 + tan x ...(i)
 Solutions to RSPL/ π. Let, I log ( tn ) d Using f () d f ( ) d π π I log( tnc d m log( cot ) d...(ii) On dding (i) nd (ii), we get +,. Given f() + ), For continuit t lim " lim f () " ( ) \ Continuous t.
Solutions to RSPL/ π. Let, I log ( tn ) d Using f () d f ( ) d π π I log( tnc d m log( cot ) d...(ii) On dding (i) nd (ii), we get +,. Given f() + ), For continuit t lim " lim f () " ( ) \ Continuous t.
MATHEMATICS PART A. 1. ABC is a triangle, right angled at A. The resultant of the forces acting along AB, AC
 FIITJEE Solutions to AIEEE MATHEMATICS PART A. ABC is tringle, right ngled t A. The resultnt of the forces cting long AB, AC with mgnitudes AB nd respectively is the force long AD, where D is the AC foot
FIITJEE Solutions to AIEEE MATHEMATICS PART A. ABC is tringle, right ngled t A. The resultnt of the forces cting long AB, AC with mgnitudes AB nd respectively is the force long AD, where D is the AC foot
Lesson-5 ELLIPSE 2 1 = 0
 Lesson-5 ELLIPSE. An ellipse is the locus of point which moves in plne such tht its distnce from fied point (known s the focus) is e (< ), times its distnce from fied stright line (known s the directri).
Lesson-5 ELLIPSE. An ellipse is the locus of point which moves in plne such tht its distnce from fied point (known s the focus) is e (< ), times its distnce from fied stright line (known s the directri).
 JEE Advnced Mths Assignment Onl One Correct Answer Tpe. The locus of the orthocenter of the tringle formed the lines (+P) P + P(+P) = 0, (+q) q+q(+q) = 0 nd = 0, where p q, is () hperol prol n ellipse
JEE Advnced Mths Assignment Onl One Correct Answer Tpe. The locus of the orthocenter of the tringle formed the lines (+P) P + P(+P) = 0, (+q) q+q(+q) = 0 nd = 0, where p q, is () hperol prol n ellipse
, MATHS H.O.D.: SUHAG R.KARIYA, BHOPAL, CONIC SECTION PART 8 OF
 DOWNLOAD FREE FROM www.tekoclsses.com, PH.: 0 903 903 7779, 98930 5888 Some questions (Assertion Reson tpe) re given elow. Ech question contins Sttement (Assertion) nd Sttement (Reson). Ech question hs
DOWNLOAD FREE FROM www.tekoclsses.com, PH.: 0 903 903 7779, 98930 5888 Some questions (Assertion Reson tpe) re given elow. Ech question contins Sttement (Assertion) nd Sttement (Reson). Ech question hs
R(3, 8) P( 3, 0) Q( 2, 2) S(5, 3) Q(2, 32) P(0, 8) Higher Mathematics Objective Test Practice Book. 1 The diagram shows a sketch of part of
 Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
15 - TRIGONOMETRY Page 1 ( Answers at the end of all questions )
 - TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
- TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
JEE(MAIN) 2015 TEST PAPER WITH SOLUTION (HELD ON SATURDAY 04 th APRIL, 2015) PART B MATHEMATICS
 JEE(MAIN) 05 TEST PAPER WITH SOLUTION (HELD ON SATURDAY 0 th APRIL, 05) PART B MATHEMATICS CODE-D. Let, b nd c be three non-zero vectors such tht no two of them re colliner nd, b c b c. If is the ngle
JEE(MAIN) 05 TEST PAPER WITH SOLUTION (HELD ON SATURDAY 0 th APRIL, 05) PART B MATHEMATICS CODE-D. Let, b nd c be three non-zero vectors such tht no two of them re colliner nd, b c b c. If is the ngle
( β ) touches the x-axis if = 1
 Generl Certificte of Eduction (dv. Level) Emintion, ugust Comined Mthemtics I - Prt B Model nswers. () Let f k k, where k is rel constnt. i. Epress f in the form( ) Find the turning point of f without
Generl Certificte of Eduction (dv. Level) Emintion, ugust Comined Mthemtics I - Prt B Model nswers. () Let f k k, where k is rel constnt. i. Epress f in the form( ) Find the turning point of f without
SUBJECT: MATHEMATICS ANSWERS: COMMON ENTRANCE TEST 2012
 MOCK TEST 0 SUBJECT: MATHEMATICS ANSWERS: COMMON ENTRANCE TEST 0 ANSWERS. () π π Tke cos - (- ) then sin [ cos - (- )]sin [ ]/. () Since sin - + sin - y + sin - z π, -; y -, z - 50 + y 50 + z 50 - + +
MOCK TEST 0 SUBJECT: MATHEMATICS ANSWERS: COMMON ENTRANCE TEST 0 ANSWERS. () π π Tke cos - (- ) then sin [ cos - (- )]sin [ ]/. () Since sin - + sin - y + sin - z π, -; y -, z - 50 + y 50 + z 50 - + +
PART - III : MATHEMATICS
 JEE(Advnced) 4 Finl Em/Pper-/Code-8 PART - III : SECTION : (One or More Thn One Options Correct Type) This section contins multiple choice questions. Ech question hs four choices (A), (B), (C) nd (D) out
JEE(Advnced) 4 Finl Em/Pper-/Code-8 PART - III : SECTION : (One or More Thn One Options Correct Type) This section contins multiple choice questions. Ech question hs four choices (A), (B), (C) nd (D) out
CBSE-XII-2015 EXAMINATION. Section A. 1. Find the sum of the order and the degree of the following differential equation : = 0
 CBSE-XII- EXMINTION MTHEMTICS Pper & Solution Time : Hrs. M. Mrks : Generl Instruction : (i) ll questions re compulsory. There re questions in ll. (ii) This question pper hs three sections : Section, Section
CBSE-XII- EXMINTION MTHEMTICS Pper & Solution Time : Hrs. M. Mrks : Generl Instruction : (i) ll questions re compulsory. There re questions in ll. (ii) This question pper hs three sections : Section, Section
KEY CONCEPTS. satisfies the differential equation da. = 0. Note : If F (x) is any integral of f (x) then, x a
 KEY CONCEPTS THINGS TO REMEMBER :. The re ounded y the curve y = f(), the -is nd the ordintes t = & = is given y, A = f () d = y d.. If the re is elow the is then A is negtive. The convention is to consider
KEY CONCEPTS THINGS TO REMEMBER :. The re ounded y the curve y = f(), the -is nd the ordintes t = & = is given y, A = f () d = y d.. If the re is elow the is then A is negtive. The convention is to consider
/ 3, then (A) 3(a 2 m 2 + b 2 ) = 4c 2 (B) 3(a 2 + b 2 m 2 ) = 4c 2 (C) a 2 m 2 + b 2 = 4c 2 (D) a 2 + b 2 m 2 = 4c 2
 SET I. If the locus of the point of intersection of perpendiculr tngents to the ellipse x circle with centre t (0, 0), then the rdius of the circle would e + / ( ) is. There re exctl two points on the
SET I. If the locus of the point of intersection of perpendiculr tngents to the ellipse x circle with centre t (0, 0), then the rdius of the circle would e + / ( ) is. There re exctl two points on the
Eigen Values and Eigen Vectors of a given matrix
 Engineering Mthemtics 0 SUBJECT NAME SUBJECT CODE MATERIAL NAME MATERIAL CODE : Engineering Mthemtics I : 80/MA : Prolem Mteril : JM08AM00 (Scn the ove QR code for the direct downlod of this mteril) Nme
Engineering Mthemtics 0 SUBJECT NAME SUBJECT CODE MATERIAL NAME MATERIAL CODE : Engineering Mthemtics I : 80/MA : Prolem Mteril : JM08AM00 (Scn the ove QR code for the direct downlod of this mteril) Nme
SCIENCE ENTRANCE ACADEMY PREPARATORY EXAMINATION-3 (II P.U.C) SCHEME 0F EVALUATION Marks:150 Date: duration:4hours MATHEMATICS-35
 JNANASUDHA SCIENCE ENTRANCE ACADEMY PREPARATORY EXAMINATION- (II P.U.C) SCHEME F EVALUATION Mrks:5 Dte:5-9-8 durtion:4hours MATHEMATICS-5 Q.NO Answer Description Mrk(s)!6 Zero mtri. + sin 4det A, 4 R 4
JNANASUDHA SCIENCE ENTRANCE ACADEMY PREPARATORY EXAMINATION- (II P.U.C) SCHEME F EVALUATION Mrks:5 Dte:5-9-8 durtion:4hours MATHEMATICS-5 Q.NO Answer Description Mrk(s)!6 Zero mtri. + sin 4det A, 4 R 4
Time : 3 hours 03 - Mathematics - March 2007 Marks : 100 Pg - 1 S E CT I O N - A
 Time : hours 0 - Mthemtics - Mrch 007 Mrks : 100 Pg - 1 Instructions : 1. Answer ll questions.. Write your nswers ccording to the instructions given below with the questions.. Begin ech section on new
Time : hours 0 - Mthemtics - Mrch 007 Mrks : 100 Pg - 1 Instructions : 1. Answer ll questions.. Write your nswers ccording to the instructions given below with the questions.. Begin ech section on new
Thomas Whitham Sixth Form
 Thoms Whithm Sith Form Pure Mthemtics Unit C Alger Trigonometry Geometry Clculus Vectors Trigonometry Compound ngle formule sin sin cos cos Pge A B sin Acos B cos Asin B A B sin Acos B cos Asin B A B cos
Thoms Whithm Sith Form Pure Mthemtics Unit C Alger Trigonometry Geometry Clculus Vectors Trigonometry Compound ngle formule sin sin cos cos Pge A B sin Acos B cos Asin B A B sin Acos B cos Asin B A B cos
MATHEMATICS PAPER IIB COORDINATE GEOMETRY AND CALCULUS. Note: This question paper consists of three sections A,B and C. SECTION A
 MATHEMATICS PAPER IIB COORDINATE GEOMETRY AND CALCULUS. TIME : 3hrs M. Mrks.75 Note: This question pper consists of three sections A,B nd C. SECTION A VERY SHORT ANSWER TYPE QUESTIONS. X = ) Find the eqution
MATHEMATICS PAPER IIB COORDINATE GEOMETRY AND CALCULUS. TIME : 3hrs M. Mrks.75 Note: This question pper consists of three sections A,B nd C. SECTION A VERY SHORT ANSWER TYPE QUESTIONS. X = ) Find the eqution
Linear Inequalities: Each of the following carries five marks each: 1. Solve the system of equations graphically.
 Liner Inequlities: Ech of the following crries five mrks ech:. Solve the system of equtions grphiclly. x + 2y 8, 2x + y 8, x 0, y 0 Solution: Considerx + 2y 8.. () Drw the grph for x + 2y = 8 by line.it
Liner Inequlities: Ech of the following crries five mrks ech:. Solve the system of equtions grphiclly. x + 2y 8, 2x + y 8, x 0, y 0 Solution: Considerx + 2y 8.. () Drw the grph for x + 2y = 8 by line.it
CBSE 2013 ALL INDIA EXAMINATION [Set 1 With Solutions]
![CBSE 2013 ALL INDIA EXAMINATION [Set 1 With Solutions] CBSE 2013 ALL INDIA EXAMINATION [Set 1 With Solutions]](/thumbs/74/69942416.jpg) M Mrks : Q Write the principl vlue of CBSE ALL INDIA EXAMINATION [Set With Solutions] SECTION A tn ( ) cot ( ) Time Allowed : Hours Sol tn ( ) cot ( ) tn tn cot cot cot cot [Rnge of tn :,, cot : ], [ 5
M Mrks : Q Write the principl vlue of CBSE ALL INDIA EXAMINATION [Set With Solutions] SECTION A tn ( ) cot ( ) Time Allowed : Hours Sol tn ( ) cot ( ) tn tn cot cot cot cot [Rnge of tn :,, cot : ], [ 5
MH CET 2018 (QUESTION WITH ANSWER)
 ( P C M ) MH CET 8 (QUESTION WITH ANSWER). /.sec () + log () - log (3) + log () Ans. () - log MATHS () 3 c + c C C A cos + cos c + cosc + + cosa ( + cosc ) + + cosa c c ( + + ) c / / I tn - in sec - in
( P C M ) MH CET 8 (QUESTION WITH ANSWER). /.sec () + log () - log (3) + log () Ans. () - log MATHS () 3 c + c C C A cos + cos c + cosc + + cosa ( + cosc ) + + cosa c c ( + + ) c / / I tn - in sec - in
Ellipse. 1. Defini t ions. FREE Download Study Package from website: 11 of 91CONIC SECTION
 FREE Downlod Stud Pckge from wesite: www.tekoclsses.com. Defini t ions Ellipse It is locus of point which moves in such w tht the rtio of its distnce from fied point nd fied line (not psses through fied
FREE Downlod Stud Pckge from wesite: www.tekoclsses.com. Defini t ions Ellipse It is locus of point which moves in such w tht the rtio of its distnce from fied point nd fied line (not psses through fied
P 1 (x 1, y 1 ) is given by,.
 MA00 Clculus nd Bsic Liner Alger I Chpter Coordinte Geometr nd Conic Sections Review In the rectngulr/crtesin coordintes sstem, we descrie the loction of points using coordintes. P (, ) P(, ) O The distnce
MA00 Clculus nd Bsic Liner Alger I Chpter Coordinte Geometr nd Conic Sections Review In the rectngulr/crtesin coordintes sstem, we descrie the loction of points using coordintes. P (, ) P(, ) O The distnce
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
SOLUTION OF TRIANGLES
 SOLUTION OF TIANGLES DPP by VK Sir B.TEH., IIT DELHI VK lsses, -9-40, Indr Vihr, Kot. Mob. No. 989060 . If cos A + cosb + cos = then the sides of the AB re in A.P. G.P H.P. none. If in tringle sin A :
SOLUTION OF TIANGLES DPP by VK Sir B.TEH., IIT DELHI VK lsses, -9-40, Indr Vihr, Kot. Mob. No. 989060 . If cos A + cosb + cos = then the sides of the AB re in A.P. G.P H.P. none. If in tringle sin A :
PARABOLA EXERCISE 3(B)
 PARABOLA EXERCISE (B). Find eqution of the tngent nd norml to the prbol y = 6x t the positive end of the ltus rectum. Eqution of prbol y = 6x 4 = 6 = / Positive end of the Ltus rectum is(, ) =, Eqution
PARABOLA EXERCISE (B). Find eqution of the tngent nd norml to the prbol y = 6x t the positive end of the ltus rectum. Eqution of prbol y = 6x 4 = 6 = / Positive end of the Ltus rectum is(, ) =, Eqution
CONIC SECTIONS. Chapter 11
 CONIC SECTIONS Chpter. Overview.. Sections of cone Let l e fied verticl line nd m e nother line intersecting it t fied point V nd inclined to it t n ngle α (Fig..). Fig.. Suppose we rotte the line m round
CONIC SECTIONS Chpter. Overview.. Sections of cone Let l e fied verticl line nd m e nother line intersecting it t fied point V nd inclined to it t n ngle α (Fig..). Fig.. Suppose we rotte the line m round
Mathematics Extension 1
 04 Bored of Studies Tril Emintions Mthemtics Etension Written by Crrotsticks & Trebl. Generl Instructions Totl Mrks 70 Reding time 5 minutes. Working time hours. Write using blck or blue pen. Blck pen
04 Bored of Studies Tril Emintions Mthemtics Etension Written by Crrotsticks & Trebl. Generl Instructions Totl Mrks 70 Reding time 5 minutes. Working time hours. Write using blck or blue pen. Blck pen
A LEVEL TOPIC REVIEW. factor and remainder theorems
 A LEVEL TOPIC REVIEW unit C fctor nd reminder theorems. Use the Fctor Theorem to show tht: ) ( ) is fctor of +. ( mrks) ( + ) is fctor of ( ) is fctor of + 7+. ( mrks) +. ( mrks). Use lgebric division
A LEVEL TOPIC REVIEW unit C fctor nd reminder theorems. Use the Fctor Theorem to show tht: ) ( ) is fctor of +. ( mrks) ( + ) is fctor of ( ) is fctor of + 7+. ( mrks) +. ( mrks). Use lgebric division
NORMALS. a y a y. Therefore, the slope of the normal is. a y1. b x1. b x. a b. x y a b. x y
 LOCUS 50 Section - 4 NORMALS Consider n ellipse. We need to find the eqution of the norml to this ellipse t given point P on it. In generl, we lso need to find wht condition must e stisfied if m c is to
LOCUS 50 Section - 4 NORMALS Consider n ellipse. We need to find the eqution of the norml to this ellipse t given point P on it. In generl, we lso need to find wht condition must e stisfied if m c is to
Higher Checklist (Unit 3) Higher Checklist (Unit 3) Vectors
 Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
SCORE JEE (Advanced)
 SLUTIN. ns. (D) L : x + y 0 S L : x + y 0 L : x + y 7 0 Point of intersection of L 0 & L 0 is (,9) Point of intersection of L 0 & L 0 is (0,) line perpendiculr to L nd pssing through (, 9) isx y + 0...
SLUTIN. ns. (D) L : x + y 0 S L : x + y 0 L : x + y 7 0 Point of intersection of L 0 & L 0 is (,9) Point of intersection of L 0 & L 0 is (0,) line perpendiculr to L nd pssing through (, 9) isx y + 0...
PREVIOUS EAMCET QUESTIONS
 CENTRE OF MASS PREVIOUS EAMCET QUESTIONS ENGINEERING Two prticles A nd B initilly t rest, move towrds ech other, under mutul force of ttrction At n instnce when the speed of A is v nd speed of B is v,
CENTRE OF MASS PREVIOUS EAMCET QUESTIONS ENGINEERING Two prticles A nd B initilly t rest, move towrds ech other, under mutul force of ttrction At n instnce when the speed of A is v nd speed of B is v,
Higher Maths. Self Check Booklet. visit for a wealth of free online maths resources at all levels from S1 to S6
 Higher Mths Self Check Booklet visit www.ntionl5mths.co.uk for welth of free online mths resources t ll levels from S to S6 How To Use This Booklet You could use this booklet on your own, but it my be
Higher Mths Self Check Booklet visit www.ntionl5mths.co.uk for welth of free online mths resources t ll levels from S to S6 How To Use This Booklet You could use this booklet on your own, but it my be
First Semester Review Calculus BC
 First Semester Review lculus. Wht is the coordinte of the point of inflection on the grph of Multiple hoice: No lcultor y 3 3 5 4? 5 0 0 3 5 0. The grph of piecewise-liner function f, for 4, is shown below.
First Semester Review lculus. Wht is the coordinte of the point of inflection on the grph of Multiple hoice: No lcultor y 3 3 5 4? 5 0 0 3 5 0. The grph of piecewise-liner function f, for 4, is shown below.
Optimization Lecture 1 Review of Differential Calculus for Functions of Single Variable.
 Optimiztion Lecture 1 Review of Differentil Clculus for Functions of Single Vrible http://users.encs.concordi.c/~luisrod, Jnury 14 Outline Optimiztion Problems Rel Numbers nd Rel Vectors Open, Closed nd
Optimiztion Lecture 1 Review of Differentil Clculus for Functions of Single Vrible http://users.encs.concordi.c/~luisrod, Jnury 14 Outline Optimiztion Problems Rel Numbers nd Rel Vectors Open, Closed nd
Mathematics Extension 2
 00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mthemtics Etension Generl Instructions Reding time 5 minutes Working time hours Write using blck or blue pen Bord-pproved clcultors my be used A tble of stndrd
00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mthemtics Etension Generl Instructions Reding time 5 minutes Working time hours Write using blck or blue pen Bord-pproved clcultors my be used A tble of stndrd
Drill Exercise Find the coordinates of the vertices, foci, eccentricity and the equations of the directrix of the hyperbola 4x 2 25y 2 = 100.
 Drill Exercise - 1 1 Find the coordintes of the vertices, foci, eccentricit nd the equtions of the directrix of the hperol 4x 5 = 100 Find the eccentricit of the hperol whose ltus-rectum is 8 nd conjugte
Drill Exercise - 1 1 Find the coordintes of the vertices, foci, eccentricit nd the equtions of the directrix of the hperol 4x 5 = 100 Find the eccentricit of the hperol whose ltus-rectum is 8 nd conjugte
Prerequisite Knowledge Required from O Level Add Math. d n a = c and b = d
 Prerequisite Knowledge Required from O Level Add Mth ) Surds, Indices & Logrithms Rules for Surds. b= b =. 3. 4. b = b = ( ) = = = 5. + b n = c+ d n = c nd b = d Cution: + +, - Rtionlising the Denomintor
Prerequisite Knowledge Required from O Level Add Mth ) Surds, Indices & Logrithms Rules for Surds. b= b =. 3. 4. b = b = ( ) = = = 5. + b n = c+ d n = c nd b = d Cution: + +, - Rtionlising the Denomintor
GEOMETRICAL PROPERTIES OF ANGLES AND CIRCLES, ANGLES PROPERTIES OF TRIANGLES, QUADRILATERALS AND POLYGONS:
 GEOMETRICL PROPERTIES OF NGLES ND CIRCLES, NGLES PROPERTIES OF TRINGLES, QUDRILTERLS ND POLYGONS: 1.1 TYPES OF NGLES: CUTE NGLE RIGHT NGLE OTUSE NGLE STRIGHT NGLE REFLEX NGLE 40 0 4 0 90 0 156 0 180 0
GEOMETRICL PROPERTIES OF NGLES ND CIRCLES, NGLES PROPERTIES OF TRINGLES, QUDRILTERLS ND POLYGONS: 1.1 TYPES OF NGLES: CUTE NGLE RIGHT NGLE OTUSE NGLE STRIGHT NGLE REFLEX NGLE 40 0 4 0 90 0 156 0 180 0
Partial Derivatives. Limits. For a single variable function f (x), the limit lim
 Limits Prtil Derivtives For single vrible function f (x), the limit lim x f (x) exists only if the right-hnd side limit equls to the left-hnd side limit, i.e., lim f (x) = lim f (x). x x + For two vribles
Limits Prtil Derivtives For single vrible function f (x), the limit lim x f (x) exists only if the right-hnd side limit equls to the left-hnd side limit, i.e., lim f (x) = lim f (x). x x + For two vribles
Einstein Classes, Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road New Delhi , Ph. : ,
 MT TRIGONOMETRIC FUNCTIONS AND TRIGONOMETRIC EQUATIONS C Trigonometric Functions : Bsic Trigonometric Identities : + cos = ; ; cos R sec tn = ; sec R (n ),n cosec cot = ; cosec R {n, n I} Circulr Definition
MT TRIGONOMETRIC FUNCTIONS AND TRIGONOMETRIC EQUATIONS C Trigonometric Functions : Bsic Trigonometric Identities : + cos = ; ; cos R sec tn = ; sec R (n ),n cosec cot = ; cosec R {n, n I} Circulr Definition
SOLUTION OF TRIANGLE GENERAL NOTATION : 1. In a triangle ABC angles at vertices are usually denoted by A, B, C
 GENERL NOTTION : SOLUTION OF TRINGLE In tringle BC ngles t vertices re usully denoted by, B, C PGE # sides opposite to these vertices re denoted by, b, c respectively Circumrdius is denoted by R 3 Inrdius
GENERL NOTTION : SOLUTION OF TRINGLE In tringle BC ngles t vertices re usully denoted by, B, C PGE # sides opposite to these vertices re denoted by, b, c respectively Circumrdius is denoted by R 3 Inrdius
HYPERBOLA. AIEEE Syllabus. Total No. of questions in Ellipse are: Solved examples Level # Level # Level # 3..
 HYPERBOLA AIEEE Sllus. Stndrd eqution nd definitions. Conjugte Hperol. Prmetric eqution of te Hperol. Position of point P(, ) wit respect to Hperol 5. Line nd Hperol 6. Eqution of te Tngent Totl No. of
HYPERBOLA AIEEE Sllus. Stndrd eqution nd definitions. Conjugte Hperol. Prmetric eqution of te Hperol. Position of point P(, ) wit respect to Hperol 5. Line nd Hperol 6. Eqution of te Tngent Totl No. of
1. If y 2 2x 2y + 5 = 0 is (A) a circle with centre (1, 1) (B) a parabola with vertex (1, 2) 9 (A) 0, (B) 4, (C) (4, 4) (D) a (C) c = am m.
 SET I. If y x y + 5 = 0 is (A) circle with centre (, ) (B) prbol with vertex (, ) (C) prbol with directrix x = 3. The focus of the prbol x 8x + y + 7 = 0 is (D) prbol with directrix x = 9 9 (A) 0, (B)
SET I. If y x y + 5 = 0 is (A) circle with centre (, ) (B) prbol with vertex (, ) (C) prbol with directrix x = 3. The focus of the prbol x 8x + y + 7 = 0 is (D) prbol with directrix x = 9 9 (A) 0, (B)
03 Qudrtic Functions Completing the squre: Generl Form f ( x) x + x + c f ( x) ( x + p) + q where,, nd c re constnts nd 0. (i) (ii) (iii) (iv) *Note t
 A-PDF Wtermrk DEMO: Purchse from www.a-pdf.com to remove the wtermrk Add Mths Formule List: Form 4 (Updte 8/9/08) 0 Functions Asolute Vlue Function Inverse Function If f ( x ), if f ( x ) 0 f ( x) y f
A-PDF Wtermrk DEMO: Purchse from www.a-pdf.com to remove the wtermrk Add Mths Formule List: Form 4 (Updte 8/9/08) 0 Functions Asolute Vlue Function Inverse Function If f ( x ), if f ( x ) 0 f ( x) y f
x 2 1 dx x 3 dx = ln(x) + 2e u du = 2e u + C = 2e x + C 2x dx = arcsin x + 1 x 1 x du = 2 u + C (t + 2) 50 dt x 2 4 dx
 . Compute the following indefinite integrls: ) sin(5 + )d b) c) d e d d) + d Solutions: ) After substituting u 5 +, we get: sin(5 + )d sin(u)du cos(u) + C cos(5 + ) + C b) We hve: d d ln() + + C c) Substitute
. Compute the following indefinite integrls: ) sin(5 + )d b) c) d e d d) + d Solutions: ) After substituting u 5 +, we get: sin(5 + )d sin(u)du cos(u) + C cos(5 + ) + C b) We hve: d d ln() + + C c) Substitute
Calculus AB Section I Part A A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAMINATION
 lculus Section I Prt LULTOR MY NOT US ON THIS PRT OF TH XMINTION In this test: Unless otherwise specified, the domin of function f is ssumed to e the set of ll rel numers for which f () is rel numer..
lculus Section I Prt LULTOR MY NOT US ON THIS PRT OF TH XMINTION In this test: Unless otherwise specified, the domin of function f is ssumed to e the set of ll rel numers for which f () is rel numer..
Set 1 Paper 2. 1 Pearson Education Asia Limited 2017
 . A. A. C. B. C 6. A 7. A 8. B 9. C. D. A. B. A. B. C 6. D 7. C 8. B 9. C. D. C. A. B. A. A 6. A 7. A 8. D 9. B. C. B. D. D. D. D 6. D 7. B 8. C 9. C. D. B. B. A. D. C Section A. A (68 ) [ ( ) n ( n 6n
. A. A. C. B. C 6. A 7. A 8. B 9. C. D. A. B. A. B. C 6. D 7. C 8. B 9. C. D. C. A. B. A. A 6. A 7. A 8. D 9. B. C. B. D. D. D. D 6. D 7. B 8. C 9. C. D. B. B. A. D. C Section A. A (68 ) [ ( ) n ( n 6n
Chapter 8: Methods of Integration
 Chpter 8: Methods of Integrtion Bsic Integrls 8. Note: We hve the following list of Bsic Integrls p p+ + c, for p sec tn + c p + ln + c sec tn sec + c e e + c tn ln sec + c ln + c sec ln sec + tn + c ln
Chpter 8: Methods of Integrtion Bsic Integrls 8. Note: We hve the following list of Bsic Integrls p p+ + c, for p sec tn + c p + ln + c sec tn sec + c e e + c tn ln sec + c ln + c sec ln sec + tn + c ln
FORM FIVE ADDITIONAL MATHEMATIC NOTE. ar 3 = (1) ar 5 = = (2) (2) (1) a = T 8 = 81
 FORM FIVE ADDITIONAL MATHEMATIC NOTE CHAPTER : PROGRESSION Arithmetic Progression T n = + (n ) d S n = n [ + (n )d] = n [ + Tn ] S = T = T = S S Emple : The th term of n A.P. is 86 nd the sum of the first
FORM FIVE ADDITIONAL MATHEMATIC NOTE CHAPTER : PROGRESSION Arithmetic Progression T n = + (n ) d S n = n [ + (n )d] = n [ + Tn ] S = T = T = S S Emple : The th term of n A.P. is 86 nd the sum of the first
Year 12 Trial Examination Mathematics Extension 1. Question One 12 marks (Start on a new page) Marks
 THGS Mthemtics etension Tril 00 Yer Tril Emintion Mthemtics Etension Question One mrks (Strt on new pge) Mrks ) If P is the point (-, 5) nd Q is the point (, -), find the co-ordintes of the point R which
THGS Mthemtics etension Tril 00 Yer Tril Emintion Mthemtics Etension Question One mrks (Strt on new pge) Mrks ) If P is the point (-, 5) nd Q is the point (, -), find the co-ordintes of the point R which
Year 12 Mathematics Extension 2 HSC Trial Examination 2014
 Yer Mthemtics Etension HSC Tril Emintion 04 Generl Instructions. Reding time 5 minutes Working time hours Write using blck or blue pen. Blck pen is preferred. Bord-pproved clcultors my be used A tble of
Yer Mthemtics Etension HSC Tril Emintion 04 Generl Instructions. Reding time 5 minutes Working time hours Write using blck or blue pen. Blck pen is preferred. Bord-pproved clcultors my be used A tble of
MORE FUNCTION GRAPHING; OPTIMIZATION. (Last edited October 28, 2013 at 11:09pm.)
 MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
Prerna Tower, Road No 2, Contractors Area, Bistupur, Jamshedpur , Tel (0657) ,
 R rern Tower, Rod No, Contrctors Are, Bistupur, Jmshedpur 800, Tel 065789, www.prernclsses.com IIT JEE 0 Mthemtics per I ART III SECTION I Single Correct Answer Type This section contins 0 multiple choice
R rern Tower, Rod No, Contrctors Are, Bistupur, Jmshedpur 800, Tel 065789, www.prernclsses.com IIT JEE 0 Mthemtics per I ART III SECTION I Single Correct Answer Type This section contins 0 multiple choice
ELLIPSE. Standard equation of an ellipse referred to its principal axes along the co-ordinate axes is. ( a,0) A'
 J-Mthemtics LLIPS. STANDARD QUATION & DFINITION : Stndrd eqution of n ellipse referred to its principl es long the co-ordinte es is > & = ( e ) = e. Y + =. where where e = eccentricit (0 < e < ). FOCI
J-Mthemtics LLIPS. STANDARD QUATION & DFINITION : Stndrd eqution of n ellipse referred to its principl es long the co-ordinte es is > & = ( e ) = e. Y + =. where where e = eccentricit (0 < e < ). FOCI
SULIT /2 3472/2 Matematik Tambahan Kertas 2 2 ½ jam 2009 SEKOLAH-SEKOLAH MENENGAH ZON A KUCHING
 SULIT 1 347/ 347/ Mtemtik Tmbhn Kerts ½ jm 009 SEKOLAH-SEKOLAH MENENGAH ZON A KUCHING PEPERIKSAAN PERCUBAAN SIJIL PELAJARAN MALAYSIA 009 MATEMATIK TAMBAHAN Kerts Du jm tig puluh minit JANGAN BUKA KERTAS
SULIT 1 347/ 347/ Mtemtik Tmbhn Kerts ½ jm 009 SEKOLAH-SEKOLAH MENENGAH ZON A KUCHING PEPERIKSAAN PERCUBAAN SIJIL PELAJARAN MALAYSIA 009 MATEMATIK TAMBAHAN Kerts Du jm tig puluh minit JANGAN BUKA KERTAS
( ) Same as above but m = f x = f x - symmetric to y-axis. find where f ( x) Relative: Find where f ( x) x a + lim exists ( lim f exists.
 AP Clculus Finl Review Sheet solutions When you see the words This is wht you think of doing Find the zeros Set function =, fctor or use qudrtic eqution if qudrtic, grph to find zeros on clcultor Find
AP Clculus Finl Review Sheet solutions When you see the words This is wht you think of doing Find the zeros Set function =, fctor or use qudrtic eqution if qudrtic, grph to find zeros on clcultor Find
Integration Techniques
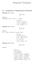 Integrtion Techniques. Integrtion of Trigonometric Functions Exmple. Evlute cos x. Recll tht cos x = cos x. Hence, cos x Exmple. Evlute = ( + cos x) = (x + sin x) + C = x + 4 sin x + C. cos 3 x. Let u
Integrtion Techniques. Integrtion of Trigonometric Functions Exmple. Evlute cos x. Recll tht cos x = cos x. Hence, cos x Exmple. Evlute = ( + cos x) = (x + sin x) + C = x + 4 sin x + C. cos 3 x. Let u
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 2014
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
Loudoun Valley High School Calculus Summertime Fun Packet
 Loudoun Vlley High School Clculus Summertime Fun Pcket We HIGHLY recommend tht you go through this pcket nd mke sure tht you know how to do everything in it. Prctice the problems tht you do NOT remember!
Loudoun Vlley High School Clculus Summertime Fun Pcket We HIGHLY recommend tht you go through this pcket nd mke sure tht you know how to do everything in it. Prctice the problems tht you do NOT remember!
Topics Covered AP Calculus AB
 Topics Covered AP Clculus AB ) Elementry Functions ) Properties of Functions i) A function f is defined s set of ll ordered pirs (, y), such tht for ech element, there corresponds ectly one element y.
Topics Covered AP Clculus AB ) Elementry Functions ) Properties of Functions i) A function f is defined s set of ll ordered pirs (, y), such tht for ech element, there corresponds ectly one element y.
MATHEMATICS (Part II) (Fresh / New Course)
 Sig. of Supdt... MRD-XII-(A) MATHEMATICS Roll No... Time Allowed : Hrs. MATHEMATICS Totl Mrks: 00 NOTE : There re THREE sections in this pper i.e. Section A, B nd C. Time : 0 Mins. Section A Mrks: 0 NOTE
Sig. of Supdt... MRD-XII-(A) MATHEMATICS Roll No... Time Allowed : Hrs. MATHEMATICS Totl Mrks: 00 NOTE : There re THREE sections in this pper i.e. Section A, B nd C. Time : 0 Mins. Section A Mrks: 0 NOTE
Set 6 Paper 2. Set 6 Paper 2. 1 Pearson Education Asia Limited 2017
 Set 6 Pper Set 6 Pper. C. C. A. D. B 6. D 7. D 8. A 9. D 0. A. B. B. A. B. B 6. B 7. D 8. C 9. D 0. D. A. A. B. B. C 6. C 7. A 8. B 9. A 0. A. C. D. B. B. B 6. A 7. D 8. A 9. C 0. C. C. D. C. C. D Section
Set 6 Pper Set 6 Pper. C. C. A. D. B 6. D 7. D 8. A 9. D 0. A. B. B. A. B. B 6. B 7. D 8. C 9. D 0. D. A. A. B. B. C 6. C 7. A 8. B 9. A 0. A. C. D. B. B. B 6. A 7. D 8. A 9. C 0. C. C. D. C. C. D Section
MTH 4-16a Trigonometry
 MTH 4-16 Trigonometry Level 4 [UNIT 5 REVISION SECTION ] I cn identify the opposite, djcent nd hypotenuse sides on right-ngled tringle. Identify the opposite, djcent nd hypotenuse in the following right-ngled
MTH 4-16 Trigonometry Level 4 [UNIT 5 REVISION SECTION ] I cn identify the opposite, djcent nd hypotenuse sides on right-ngled tringle. Identify the opposite, djcent nd hypotenuse in the following right-ngled
Alg. Sheet (1) Department : Math Form : 3 rd prep. Sheet
 Ciro Governorte Nozh Directorte of Eduction Nozh Lnguge Schools Ismili Rod Deprtment : Mth Form : rd prep. Sheet Alg. Sheet () [] Find the vlues of nd in ech of the following if : ) (, ) ( -5, 9 ) ) (,
Ciro Governorte Nozh Directorte of Eduction Nozh Lnguge Schools Ismili Rod Deprtment : Mth Form : rd prep. Sheet Alg. Sheet () [] Find the vlues of nd in ech of the following if : ) (, ) ( -5, 9 ) ) (,
DE51/DC51 ENGINEERING MATHEMATICS I DEC 2013
 DE5/DC5 ENGINEERING MATHEMATICS I DEC π π Q.. Prove tht cos α + cos α + + cos α + L.H.S. π π cos α + cos α + + cos α + + α + cos α + cos ( α ) + cos ( ) cos α + cos ( 9 + α + ) + cos(8 + α + 6 ) cos α
DE5/DC5 ENGINEERING MATHEMATICS I DEC π π Q.. Prove tht cos α + cos α + + cos α + L.H.S. π π cos α + cos α + + cos α + + α + cos α + cos ( α ) + cos ( ) cos α + cos ( 9 + α + ) + cos(8 + α + 6 ) cos α
Log1 Contest Round 3 Theta Individual. 4 points each 1 What is the sum of the first 5 Fibonacci numbers if the first two are 1, 1?
 008 009 Log1 Contest Round Thet Individul Nme: points ech 1 Wht is the sum of the first Fiboncci numbers if the first two re 1, 1? If two crds re drwn from stndrd crd deck, wht is the probbility of drwing
008 009 Log1 Contest Round Thet Individul Nme: points ech 1 Wht is the sum of the first Fiboncci numbers if the first two re 1, 1? If two crds re drwn from stndrd crd deck, wht is the probbility of drwing
Chapter 6 Techniques of Integration
 MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
RAM RAJYA MORE, SIWAN. XI th, XII th, TARGET IIT-JEE (MAIN + ADVANCE) & COMPATETIVE EXAM FOR XII (PQRS) INDEFINITE INTERATION & Their Properties
 M.Sc. (Mths), B.Ed, M.Phil (Mths) MATHEMATICS Mob. : 947084408 9546359990 M.Sc. (Mths), B.Ed, M.Phil (Mths) RAM RAJYA MORE, SIWAN XI th, XII th, TARGET IIT-JEE (MAIN + ADVANCE) & COMPATETIVE EXAM FOR XII
M.Sc. (Mths), B.Ed, M.Phil (Mths) MATHEMATICS Mob. : 947084408 9546359990 M.Sc. (Mths), B.Ed, M.Phil (Mths) RAM RAJYA MORE, SIWAN XI th, XII th, TARGET IIT-JEE (MAIN + ADVANCE) & COMPATETIVE EXAM FOR XII
INDEFINITE INTEGR ATION
 J-Mthemtics INDFINIT INTGR ATION If f & F re function of such tht F' () f() then the function F is clled PRIMITIV OR ANTIDRIVATIV OR INTGRAL of f() w.r.t. nd is written symboliclly s d f() F() c {F() c}
J-Mthemtics INDFINIT INTGR ATION If f & F re function of such tht F' () f() then the function F is clled PRIMITIV OR ANTIDRIVATIV OR INTGRAL of f() w.r.t. nd is written symboliclly s d f() F() c {F() c}
6.2 CONCEPTS FOR ADVANCED MATHEMATICS, C2 (4752) AS
 6. CONCEPTS FOR ADVANCED MATHEMATICS, C (475) AS Objectives To introduce students to number of topics which re fundmentl to the dvnced study of mthemtics. Assessment Emintion (7 mrks) 1 hour 30 minutes.
6. CONCEPTS FOR ADVANCED MATHEMATICS, C (475) AS Objectives To introduce students to number of topics which re fundmentl to the dvnced study of mthemtics. Assessment Emintion (7 mrks) 1 hour 30 minutes.
PROPERTIES OF AREAS In general, and for an irregular shape, the definition of the centroid at position ( x, y) is given by
 PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
Section 4.7 Inverse Trigonometric Functions
 Section 7 Inverse Trigonometric Functions 89 9 Domin: 0, q Rnge: -q, q Zeros t n, n nonnegtive integer 9 Domin: -q, 0 0, q Rnge: -q, q Zeros t, n non-zero integer Note: te gr lso suggests n te end-bevior
Section 7 Inverse Trigonometric Functions 89 9 Domin: 0, q Rnge: -q, q Zeros t n, n nonnegtive integer 9 Domin: -q, 0 0, q Rnge: -q, q Zeros t, n non-zero integer Note: te gr lso suggests n te end-bevior
Mathematics Extension 2
 00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mthemtics Extension Generl Instructions Reding time 5 minutes Working time hours Write using blck or blue pen Bord-pproved clcultors m be used A tble of stndrd
00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mthemtics Extension Generl Instructions Reding time 5 minutes Working time hours Write using blck or blue pen Bord-pproved clcultors m be used A tble of stndrd
Form 5 HKCEE 1990 Mathematics II (a 2n ) 3 = A. f(1) B. f(n) A. a 6n B. a 8n C. D. E. 2 D. 1 E. n. 1 in. If 2 = 10 p, 3 = 10 q, express log 6
 Form HK 9 Mthemtics II.. ( n ) =. 6n. 8n. n 6n 8n... +. 6.. f(). f(n). n n If = 0 p, = 0 q, epress log 6 in terms of p nd q.. p q. pq. p q pq p + q Let > b > 0. If nd b re respectivel the st nd nd terms
Form HK 9 Mthemtics II.. ( n ) =. 6n. 8n. n 6n 8n... +. 6.. f(). f(n). n n If = 0 p, = 0 q, epress log 6 in terms of p nd q.. p q. pq. p q pq p + q Let > b > 0. If nd b re respectivel the st nd nd terms
DEEPAWALI ASSIGNMENT
 DEEPWLI SSIGNMENT CLSS & DOPPE FO TGET IIT JEE Get Solution & Video Tutorils online www.mthsbysuhg.com Downlod FEE Study Pckges, Test Series from w ww.tekoclsses.com Bhopl : Phone : (0755) 00 000 Wishing
DEEPWLI SSIGNMENT CLSS & DOPPE FO TGET IIT JEE Get Solution & Video Tutorils online www.mthsbysuhg.com Downlod FEE Study Pckges, Test Series from w ww.tekoclsses.com Bhopl : Phone : (0755) 00 000 Wishing
Indefinite Integral. Chapter Integration - reverse of differentiation
 Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
AB Calculus Review Sheet
 AB Clculus Review Sheet Legend: A Preclculus, B Limits, C Differentil Clculus, D Applictions of Differentil Clculus, E Integrl Clculus, F Applictions of Integrl Clculus, G Prticle Motion nd Rtes This is
AB Clculus Review Sheet Legend: A Preclculus, B Limits, C Differentil Clculus, D Applictions of Differentil Clculus, E Integrl Clculus, F Applictions of Integrl Clculus, G Prticle Motion nd Rtes This is
Edexcel GCE Core Mathematics (C2) Required Knowledge Information Sheet. Daniel Hammocks
 Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
Math 190 Chapter 5 Lecture Notes. Professor Miguel Ornelas
 Mth 19 Chpter 5 Lecture Notes Professor Miguel Ornels 1 M. Ornels Mth 19 Lecture Notes Section 5.1 Section 5.1 Ares nd Distnce Definition The re A of the region S tht lies under the grph of the continuous
Mth 19 Chpter 5 Lecture Notes Professor Miguel Ornels 1 M. Ornels Mth 19 Lecture Notes Section 5.1 Section 5.1 Ares nd Distnce Definition The re A of the region S tht lies under the grph of the continuous
5.3 The Fundamental Theorem of Calculus, Part I
 59 C HAPTER 5 THE INTEGRAL θ b 87. Suppose tht f nd g re continuous functions such tht, for ll, Z Z f./d g./d Give n intuitive rgument showing tht f./ g./.eplin our ide with grph. Let R f./d R g./d.considerwhthppenss
59 C HAPTER 5 THE INTEGRAL θ b 87. Suppose tht f nd g re continuous functions such tht, for ll, Z Z f./d g./d Give n intuitive rgument showing tht f./ g./.eplin our ide with grph. Let R f./d R g./d.considerwhthppenss
Math 1102: Calculus I (Math/Sci majors) MWF 3pm, Fulton Hall 230 Homework 2 solutions
 Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
( ) as a fraction. Determine location of the highest
 AB Clculus Exm Review Sheet - Solutions A. Preclculus Type prolems A1 A2 A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f ( x). Set function equl to 0. Fctor or use qudrtic eqution if
AB Clculus Exm Review Sheet - Solutions A. Preclculus Type prolems A1 A2 A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f ( x). Set function equl to 0. Fctor or use qudrtic eqution if
( ) where f ( x ) is a. AB Calculus Exam Review Sheet. A. Precalculus Type problems. Find the zeros of f ( x).
 AB Clculus Exm Review Sheet A. Preclculus Type prolems A1 Find the zeros of f ( x). This is wht you think of doing A2 A3 Find the intersection of f ( x) nd g( x). Show tht f ( x) is even. A4 Show tht f
AB Clculus Exm Review Sheet A. Preclculus Type prolems A1 Find the zeros of f ( x). This is wht you think of doing A2 A3 Find the intersection of f ( x) nd g( x). Show tht f ( x) is even. A4 Show tht f
USA Mathematical Talent Search Round 1 Solutions Year 21 Academic Year
 1/1/21. Fill in the circles in the picture t right with the digits 1-8, one digit in ech circle with no digit repeted, so tht no two circles tht re connected by line segment contin consecutive digits.
1/1/21. Fill in the circles in the picture t right with the digits 1-8, one digit in ech circle with no digit repeted, so tht no two circles tht re connected by line segment contin consecutive digits.
US01CMTH02 UNIT Curvature
 Stu mteril of BSc(Semester - I) US1CMTH (Rdius of Curvture nd Rectifiction) Prepred by Nilesh Y Ptel Hed,Mthemtics Deprtment,VPnd RPTPScience College US1CMTH UNIT- 1 Curvture Let f : I R be sufficiently
Stu mteril of BSc(Semester - I) US1CMTH (Rdius of Curvture nd Rectifiction) Prepred by Nilesh Y Ptel Hed,Mthemtics Deprtment,VPnd RPTPScience College US1CMTH UNIT- 1 Curvture Let f : I R be sufficiently
Chapter 2. Vectors. 2.1 Vectors Scalars and Vectors
 Chpter 2 Vectors 2.1 Vectors 2.1.1 Sclrs nd Vectors A vector is quntity hving both mgnitude nd direction. Emples of vector quntities re velocity, force nd position. One cn represent vector in n-dimensionl
Chpter 2 Vectors 2.1 Vectors 2.1.1 Sclrs nd Vectors A vector is quntity hving both mgnitude nd direction. Emples of vector quntities re velocity, force nd position. One cn represent vector in n-dimensionl
BRIEF NOTES ADDITIONAL MATHEMATICS FORM
 BRIEF NOTES ADDITIONAL MATHEMATICS FORM CHAPTER : FUNCTION. : + is the object, + is the imge : + cn be written s () = +. To ind the imge or mens () = + = Imge or is. Find the object or 8 mens () = 8 wht
BRIEF NOTES ADDITIONAL MATHEMATICS FORM CHAPTER : FUNCTION. : + is the object, + is the imge : + cn be written s () = +. To ind the imge or mens () = + = Imge or is. Find the object or 8 mens () = 8 wht
FP3 past questions - conics
 Hperolic functions cosh sinh = sinh = sinh cosh cosh = cosh + sinh rcosh = ln{ + } ( ) rsinh = ln{ + + } + rtnh = ln ( < ) FP3 pst questions - conics Conics Ellipse Prol Hperol Rectngulr Hperol Stndrd
Hperolic functions cosh sinh = sinh = sinh cosh cosh = cosh + sinh rcosh = ln{ + } ( ) rsinh = ln{ + + } + rtnh = ln ( < ) FP3 pst questions - conics Conics Ellipse Prol Hperol Rectngulr Hperol Stndrd
CHAPTER 6 APPLICATIONS OF DEFINITE INTEGRALS
 CHAPTER 6 APPLICATIONS OF DEFINITE INTEGRALS 6. VOLUMES USING CROSS-SECTIONS. A() ;, ; (digonl) ˆ Ȉ È V A() d d c d 6 (dimeter) c d c d c ˆ 6. A() ;, ; V A() d d. A() (edge) È Š È Š È ;, ; V A() d d 8
CHAPTER 6 APPLICATIONS OF DEFINITE INTEGRALS 6. VOLUMES USING CROSS-SECTIONS. A() ;, ; (digonl) ˆ Ȉ È V A() d d c d 6 (dimeter) c d c d c ˆ 6. A() ;, ; V A() d d. A() (edge) È Š È Š È ;, ; V A() d d 8
First midterm topics Second midterm topics End of quarter topics. Math 3B Review. Steve. 18 March 2009
 Mth 3B Review Steve 18 Mrch 2009 About the finl Fridy Mrch 20, 3pm-6pm, Lkretz 110 No notes, no book, no clcultor Ten questions Five review questions (Chpters 6,7,8) Five new questions (Chpters 9,10) No
Mth 3B Review Steve 18 Mrch 2009 About the finl Fridy Mrch 20, 3pm-6pm, Lkretz 110 No notes, no book, no clcultor Ten questions Five review questions (Chpters 6,7,8) Five new questions (Chpters 9,10) No
x ) dx dx x sec x over the interval (, ).
 Curve on 6 For -, () Evlute the integrl, n (b) check your nswer by ifferentiting. ( ). ( ). ( ).. 6. sin cos 7. sec csccot 8. sec (sec tn ) 9. sin csc. Evlute the integrl sin by multiplying the numertor
Curve on 6 For -, () Evlute the integrl, n (b) check your nswer by ifferentiting. ( ). ( ). ( ).. 6. sin cos 7. sec csccot 8. sec (sec tn ) 9. sin csc. Evlute the integrl sin by multiplying the numertor
Math 113 Exam 2 Practice
 Mth Em Prctice Februry, 8 Em will cover sections 6.5, 7.-7.5 nd 7.8. This sheet hs three sections. The first section will remind you bout techniques nd formuls tht you should know. The second gives number
Mth Em Prctice Februry, 8 Em will cover sections 6.5, 7.-7.5 nd 7.8. This sheet hs three sections. The first section will remind you bout techniques nd formuls tht you should know. The second gives number
