CHAPTER 6 APPLICATIONS OF DEFINITE INTEGRALS
|
|
|
- Nelson Higgins
- 6 years ago
- Views:
Transcription
1 CHAPTER 6 APPLICATIONS OF DEFINITE INTEGRALS 6. VOLUMES USING CROSS-SECTIONS. A() ;, ; (digonl) ˆ Ȉ È V A() d d c d 6 (dimeter) c d c d c ˆ 6. A() ;, ; V A() d d. A() (edge) È Š È Š È ;, ; V A() d d 8 ˆ c 6 (digonl) Š Š c ˆ 8. A() ;, ; V A() d d. () STEP ) A() (side) (side) ˆ sin Š Èsin Š Èsin ˆ sin È sin STEP ), STEP ) V A() d È sin d È cos È( ) È () STEP ) A() (side) Š Èsin Š Èsin sin STEP ), STEP ) V A() d sin d c cos d 8 (dimeter) 6. () STEP ) A() (sec tn ) sec tn sec tn sin sec sec STEP ) cos, Î ˆ sin ˆ Î cos cos Î STEP ) V A() d sec d tn c Î È È Š Š Š Š È ˆ ˆ () STEP ) A() (edge) (sec tn ) ˆ sin sec cos STEP ), Î STEP ) V A() d ˆ sec d Š È È cî sin cos 7. () STEP ) A() length height 6 6 STEP ), STEP ) V A() d 6 d c 6 d 6 6 Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
2 8 Chpter 6 Applictions of Definite Integrls 6 () STEP ) A() length height 6 Š STEP ), STEP ) V A() d 6 9 d c d () STEP ) A() se height ˆ È 6 6È STEP ), STEP ) V A() d ˆ Î 6 d Î 8 È Î 8 Î () STEP ) A() ˆ dimeter Š ˆ STEP ), STEP ) V A() d ˆ Î d Î ˆ A() (dimeter) Š È ; c, d ; V A() d d d c ˆ Š 8 d ˆ 8 c c. A() (leg)(leg) È ˆ È ˆ È ; c, d ; V A() d d. The slices perpendiculr to the edge leled re tringles, nd similr tringles we hve h Ê h. The eqution of the line through, nd, is, thus the length of the se nd the height ˆ 6.Thus A se height ˆ ˆ ˆ nd V A d 6 d 6. The slices prllel to the se re squres. The cross section of the prmid is tringle, nd similr tringles we hve d 9 9 h c Ê h. Thus A se ˆ Ê V A d d. () It follows from Cvlieris Principle tht the volume of column is the sme s the volume of right prism with squre se of side length s nd ltitude h. Thus, STEP ) A() (side length) s ; STEP ), h; STEP ) V A() d s d s h h () From Cvlieris Principle we conclude tht the volume of the column is the sme s the volume of the prism descried ove, regrdless of the numer of turns Ê V s h Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
3 Section 6. Volumes Using Cross-Sections 9. ) The solid nd the cone hve the sme ltitude of. ) The cross sections of the solid re disks of dimeter ˆ. If we plce the verte of the cone t the origin of the coordinte sstem nd mke its is of smmetr coincide with the -is then the cones cross sections will e circulr disks of dimeter ˆ (see ccompning figure). ) The solid nd the cone hve equl ltitudes nd identicl prllel cross sections. From Cvlieris Principle we conclude tht the solid nd the cone hve the sme volume.. R() Ê V [R()] d ˆ d Š d 8 ˆ 9 6. R() Ê V [R()] d ˆ d d R() tn ˆ ; u Ê du d Ê du d; Ê u, Ê u ; Î Î Î ˆ V [R()] d tn d tn u du sec u du [ u tn u] ˆ 8. R() sin cos ; R() Ê nd re the limits of integrtion; V [R()] d Î Î (sin ) (sin cos ) d d; du d u Ê du d Ê ; Ê u, 8 u ˆ Ê u Ä V sin u du sin u d 9. R() Ê V [R()] d d Î. R() Ê V [R()] d d d ( Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
![R() È9 Ê V [R()] d 9 d c c 9 7 9() 8 6.](/docs-images/76/73831164/images/4-1.jpg "R() Ê V [R()] d d d ˆ (6) Î Î È.")
![R() cos Ê V [R()] d cos d csin d Î ( ).](/docs-images/76/73831164/images/4-2.jpg "R() sec Ê V [R()] d sec d Î Î Î cî cî c")
![tn d Î [ ( )] Î.](/docs-images/76/73831164/images/4-3.jpg "R() È sec tn Ê V [R()] d Î Š È sec tn d")
4 Chpter 6 Applictions of Definite Integrls. R() È9 Ê V [R()] d 9 d c c 9 7 9() 8 6. R() Ê V [R()] d d d ˆ (6) Î Î È. R() cos Ê V [R()] d cos d csin d Î ( ). R() sec Ê V [R()] d sec d Î Î Î cî cî c tn d Î [ ( )] Î. R() È sec tn Ê V [R()] d Î Š È sec tn d Î Š sec tn sec tn d È Î Î Î Œ d È sec tn d (tn ) sec d Î Œ[] È Î tn [sec ] Î ˆ È È Š Š È Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
![Î 6. R() sin ( sin ) Ê V [R()] d Î Î Î ( sin )](/docs-images/76/73831164/images/5-1.jpg "d sin sin d ( cos ) sin d ˆ cos sin Î sin cos Î")
![R() È sin Ê V [R()] d Î sin d ccos d Î Î [ ( )]](/docs-images/76/73831164/images/5-5.jpg "c. R() Écos Ê V [R()] d cos ˆ d sin c [ ( )].")
5 Î 6. R() sin ( sin ) Ê V [R()] d Î Î Î ( sin ) d sin sin d ( cos ) sin d ˆ cos sin Î sin cos Î ˆ () (8) È c c 7. R() Ê V [R()] d d c d [ ( )] Section 6. Volumes Using Cross-Sections Î 8. R() Ê V [R()] d d 9. R() È sin Ê V [R()] d Î sin d ccos d Î Î [ ( )] c. R() Écos Ê V [R()] d cos ˆ d sin c [ ( )]. R() Ê V [R()] d d Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
![Chpter 6 Applictions of Definite Integrls È. R() Ê V [R()] d d; cu Ê du d; Ê u, Ê u d Ä V u du ( ) u.](/docs-images/76/73831164/images/6-0.jpg "For the sketch given,, ; R(), r() È cos ; V [R()] [r()] d Î Î ( cos ) d ( cos ) d [ sin ] ˆ cî Î d.")
![For the sketch given, c, d ; R(), r() tn ; V [R()] [r()] d c Î Î Î tn d sec d [ tn ] ˆ. r() nd R() Ê V [R()] [r()] d ˆ d 6.](/docs-images/76/73831164/images/6-1.jpg "r() È nd R() Ê V [R()] [r()] d ( ) d ˆ 7.")
6 Chpter 6 Applictions of Definite Integrls È. R() Ê V [R()] d d; cu Ê du d; Ê u, Ê u d Ä V u du ( ) u. For the sketch given,, ; R(), r() È cos ; V [R()] [r()] d Î Î ( cos ) d ( cos ) d [ sin ] ˆ cî Î d. For the sketch given, c, d ; R(), r() tn ; V [R()] [r()] d c Î Î Î tn d sec d [ tn ] ˆ. r() nd R() Ê V [R()] [r()] d ˆ d 6. r() È nd R() Ê V [R()] [r()] d ( ) d ˆ 7. r() nd R() c Ê V [R()] [r()] d c ( ) d c c 69 d d c 68 d 6 8 ˆ 6 ˆ 8 ˆ 8 8 ˆ Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
![Section 6. Volumes Using Cross-Sections 8. r() nd R() c Ê V [R()] [r()] d c ( ) d c c 6 8 d d c 9 d 8 ˆ 8 ˆ ˆ 9. r() sec nd R() È Î Ê V [R()] [r()] d c Î Î c Î Î ˆ ˆ ( ) Î sec d [ tn ].](/docs-images/76/73831164/images/7-4.jpg "R() sec nd r() tn Ê V [R()] [r()] d sec tn d d []. r() nd R() Ê V [R()] [r()] d c( ) dd d d ˆ. R() nd r() Ê V [R()] [r()] d d ˆ c ( ) d d c d d Copright Person Eduction, Inc.")
7 Section 6. Volumes Using Cross-Sections 8. r() nd R() c Ê V [R()] [r()] d c ( ) d c c 6 8 d d c 9 d 8 ˆ 8 ˆ ˆ 9. r() sec nd R() È Î Ê V [R()] [r()] d c Î Î c Î Î ˆ ˆ ( ) Î sec d [ tn ]. R() sec nd r() tn Ê V [R()] [r()] d sec tn d d []. r() nd R() Ê V [R()] [r()] d c( ) dd d d ˆ. R() nd r() Ê V [R()] [r()] d d ˆ c ( ) d d c d d Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
8 Chpter 6 Applictions of Definite Integrls. R() nd r() È Ê V [R()] [r()] d ( ) d (6 8) 8. R() È nd r() È È Ê V [R()] [r()] d È È c d d d È È. R() nd r() È Ê V [R()] [r()] d ˆ d È ˆ È d ˆ È d Î ˆ ˆ Î 6. R() nd r() Ê V [R()] [r()] d ˆ d Î ˆ Î Î d ˆ Î Î d Î Î ˆ 7. () r() È nd R() Ê V [R()] [r()] d ( ) d (6 8) 8 () r() nd R() Ê V [R()] [r()] d d Î (c) r() nd R() È Ê V [R()] [r()] d ˆ È d ˆ È d ˆ 6 Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
![() r() nd R() Ê V [R()] [r()] d ˆ Š 8 d d ˆ () r() nd R() Ê V [R()] [r()] d ˆ d Š d 8 8 Š](/docs-images/76/73831164/images/9-1.jpg "d ˆ 6 ˆ 9.")
![() r() nd R() c c c Ê V [R()] [r()] d d d ˆ ˆ c c d d c c ( ) Ê c c d d c c ( ) () r() nd](/docs-images/76/73831164/images/9-2.jpg "R() Ê V [R()] [r()] d d ˆ (c) r() nd R() V [R()] [r()] d d ˆ.")
9 Section 6. Volumes Using Cross-Sections (d) r() nd R() Ê V [R()] [r()] d 6 d d 8 d ˆ 8. () r() nd R() Ê V [R()] [r()] d ˆ Š 8 d d ˆ () r() nd R() Ê V [R()] [r()] d ˆ d Š d 8 8 Š d ˆ 6 ˆ 9. () r() nd R() c c c Ê V [R()] [r()] d d d ˆ ˆ c c d d c c ( ) Ê c c d d c c ( ) () r() nd R() Ê V [R()] [r()] d d ˆ (c) r() nd R() V [R()] [r()] d d ˆ. () r() nd R() h Ê V [R()] [r()] d h ˆ h h d Š h d h h ˆ h ˆ h h ˆ h h h h Š ˆ h h h h h h h h () r() nd R() Ê V [R()] [r()] d d d h h Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
10 6 Chpter 6 Applictions of Definite Integrls. R() È nd r() È c Ê V [R()] [r()] d c ˆ È ˆ È d È d È d c re of semicircle of rdius c. () A cross section hs rdius r È nd re r. The volume is d c d. dv dv dv dh dh dh dv dh dt dh dt dt dt Ah dt () Vh Ahdh, so Ah. Therefore Ah, so. dh units units For h, the re is ), so. dt ) sec ) sec hc hc c c. () R() È Ê V d h (h ) Š h h ( h) h h h h Š h h h dv dh h ( h) h h () Given dt. m /sec nd m, find dt. From prt (), V(h) h Ê dv h h Ê dv dv dh h( h) dh Ê dh. dh dt dh dt dt dt h ( ) ( )(6) m/sec.. Suppose the solid is produced revolving out the -is. Cst shdow of the solid on plne prllel to the -plne. Use n pproimtion such s the Trpezoid Rule, to estimte c R d d Œ. n k d k^. The cross section of solid right circulr clinder with cone removed is disk with rdius R from which disk of rdius h hs een removed. Thus its re is A R h R h. The cross section of the hemisphere is disk of rdius ÈR h. Therefore its re is A Š ÈR h R h. We cn see tht A A. The ltitudes of oth solids re R. Appling Cvlieris Principle we find Volume of Hemisphere (Volume of Clinder) (Volume of Cone) R R R R R R() È6 Ê V [R()] d 6 d 6 d Š ˆ ˆ ˆ ˆ 6 6 cm. The plum o will weigh out W (8.) 9 gm, to the nerest grm. 7. R() È6 Ê V [R()] d 6 d 6 c7 c7 c6 c (6)( 7) Š (6)( 6) Š 6(6 7) cm 8 cm ( Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
11 Section 6. Volume Using Clindricl Shells 7 ˆ cos c c sin d ˆ cos c c sin d ˆ sin ˆ ˆ dv dc ˆ ˆ 8 ˆ ˆ. (See lso the ccompning grph.) 8. () R() kc sin k, so V [R()] d (c sin ) d c c sin sin d c c cos c c ( c ) ˆ c c. Let V(c) c c. We find the etreme vlues of V(c): (c ) Ê c is criticl point, nd V ; Evlute V t the endpoints: V() nd V() ( ). Now we see tht the functions solute minimum vlue is, tken on t the criticl point c () From the discussion in prt () we conclude tht the functions solute mimum vlue is the endpoint c. (c) The grph of the solids volume s function of c for Ÿ c Ÿ is given t the right. As c moves w from [ß ] the volume of the solid increses without ound. If we pproimte the solid s set of solid disks, we cn see tht the rdius of tpicl disk increses without ounds s c moves w from [ß ]., tken on t 9. Volume of the solid generted rotting the region ounded the -is nd f from to out the -is is V [f()] d, nd the volume of the solid generted rotting the sme region out the line f() d f() d is V [f() ] d 8. Thus [f() ] d [f()] d 8 Ê [f()] f() [f()] d Ê f() d Ê f() d d Ê Ê 6. Volume of the solid generted rotting the region ounded the -is nd f from to out the -is is V [f()] d 6, nd the volume of the solid generted rotting the sme region out the line is V [f() ] d. Thus [f() ] d [f()] d 6 Ê [f()] f() [f()] d Ê f() d Ê f() d d Ê f() d Ê f() d 6. VOLUME USING CYLINDRICAL SHELLS. For the sketch given,, ; V ˆ Š d Š d Š d ˆ 6 rdius height For the sketch given,, ; V ˆ Š d Š d Š d ( ) 6 rdius height 6. For the sketch given, c, d È ; d È È È V ˆ d Š d d c rdius height Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
12 8 Chpter 6 Applictions of Definite Integrls. For the sketch given, c, d È ; d È È È V ˆ d Š c d d d c rdius height. For the sketch given,, È ; È V ˆ Š d Š È d; rdius height u Ê du d; Ê u, È Ê u Î Ä V u du Î u ˆ Î ˆ (8 ) 6. For the sketch given,, ; V ˆ 9 Š d Š d; rdius height È 9 cu 9 Ê du d Ê du 9 d; Ê u 9, Ê u 6d 6 Ä V Î u du 6 Î u Š È6 È9 6 9 * 9 7., ; V ˆ Š d ˆ d rdius height d d c d 8 8., ; V ˆ d ˆ Š d rdius height Š d d c d 9., ; V ˆ d Š c( ) dd rdius height d 6 ˆ ˆ., ; V ˆ d Š c d d rdius height d d ˆ Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
13 ., ; V ˆ Š d È ( ) d rdius height ˆ Î d Î ˆ ˆ 7 Section 6. Volume Using Clindricl Shells 9., ; V ˆ d ˆ Î Š d rdius height Î Î Î d ˆ (8), Ÿ sin, Ÿ. () f() Ê f() ; since sin we hve,, sin, Ÿ f() Ê f() sin, Ÿ Ÿ sin, () V ˆ Š d f() d nd f() sin, Ÿ Ÿ prt () sin rdius height Ê V sin d [ cos ] ( cos cos ) tn, Ÿ tn, Ÿ /. () g() Ê g() ; since tn we hve,, g() tn, Ÿ / Ê g() tn, Ÿ Ÿ / tn, Î () V ˆ Š d g() d nd g() tn, Ÿ Ÿ / prt (). c, d ; rdius height Î Î Î Ê V tn d sec d [tn ] ˆ V ˆ Š d È ( ) d d c rdius height È È Î ˆ Î d Š È 8 8 Š 6Š Š È 6 Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
![c, d ; d V ˆ Š d [ ( )]d c rdius height d c d. c, d ; V ˆ d ˆ Š d c rdius height d 8 d c d.](/docs-images/76/73831164/images/14-5.jpg "c, d ; d V ˆ d Š c( ) dd c rdius height d ˆ (88) 8 6 6 6 Copright Person Eduction, Inc.")
14 Chpter 6 Applictions of Definite Integrls 6. c, d ; d V ˆ d Š c ( ) dd c rdius height ˆ 6 d 6ˆ 6 7. c, d ; d V ˆ d Š d c rdius height ˆ 8 d ˆ c, d ; d V ˆ d Š d c rdius height 6 d d ˆ 9. c, d ; d V ˆ Š d [ ( )]d c rdius height d c d. c, d ; V ˆ d ˆ Š d c rdius height d 8 d c d. c, d ; d V ˆ d Š c( ) dd c rdius height d ˆ (88) Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
15 Section 6. Volume Using Clindricl Shells. c, d ; d V ˆ d Š c( ) d d c rdius height d 6 6 ˆ (). () V ˆ Š d d 6 d c d 6 rdius height rdius height () V ˆ d d 6 d 6 Š 6ˆ 8 8 rdius height (c) V ˆ d d 6 d 6 Š 6ˆ 8 8 d c rdius height 9 (d) V ˆ d ˆ d ˆ d Š 6 d c rdius height 6 9 (e) V ˆ d 7 ˆ d ˆ d Š d c rdius height 9 (f) V ˆ d ˆ d ˆ d Š 8 96 rdius height. () V ˆ d 8 d 8 d Š ˆ 6 () V ˆ Š d 8 d 8 d rdius height ˆ 6 ˆ Š rdius height ˆ 6 d 8 8 ˆ Î Î 6 Š 7Î c rdius height (c) V d 8 d 6 8 d (d) V d d d 8 d c rdius height d 8 8 ˆ Î ˆ Î Î Š 7Î Î 8 c rdius height (e) V ˆ Î d 8 d ˆ Î Î Š 8 d Î 7Î 6 ˆ 96 (f) V d d d ˆ rdius height c c 8 8 ˆ 7 ˆ Š rdius height c c 6 ˆ 7 d ˆ Š ˆ È ˆ È ˆ È c rdius height Î d 8 ˆ Î d Î Î ˆ ˆ. () V ˆ d d d Š. () V d d d (c) V d d d Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
16 Chpter 6 Applictions of Definite Integrls d (d) V ˆ Š d ˆ È ˆ È d ˆ È d c rdius height ˆ È Î ˆ Î È 8 Î Î Î 8 Î ˆ 8 ˆ ˆ 8 8 d 6 8 d () V ˆ Š d d d rdius height c c 6 ˆ ˆ d ˆ Š ˆ È ˆ È É Š É c rdius height () V d d d Î d È d cu Ê u Ê du d; Ê u, Ê u d È Î uèu du 9 ˆ Èu u Î du 9 u Î u Î È È È È Š 8È È d 7. () V ˆ Š d d d c rdius height 6 d ˆ Š c d c rdius height d ˆ ˆ d ˆ ˆ 8 ˆ 8 c rdius height ˆ 8 8 ˆ 8 6 d ˆ ˆ Š c d ˆ c rdius height ˆ () V d ( ) d ( ) d (c) V Š d c dd d d ( 9 ) (d) V d d d ˆ d ˆ d ˆ (8 9 ) 6 d 8. () V ˆ Š d Š d Š d Š d c rdius height Š ˆ ˆ ˆ 8 6 d ˆ Š Š Š c rdius height Š ˆ d ˆ Š Š Š c rdius height Š ˆ d ˆ ˆ Š Š ˆ Š c rdius height 8 8 Š ˆ () V d ( ) d ( ) d d (c) V d ( ) d ( ) d d 8 (d) V d d d d Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
17 Section 6. Volume Using Clindricl Shells rdius height 9. () Aout -is: V cd ˆ Š d ˆ È d ˆ Î d ˆ Î rdius height Aout -is: V ˆ Š d ˆ d d () Aout -is: R nd r V R r Ê d c dd ˆ Aout -is: R È nd r V R r Ê d c dd ˆ. () V R r d ˆ d ˆ d () V ˆ d ˆ Š d rdius height ˆ d Š d d c ˆ ˆ ˆ ˆ rdius height ˆ ˆ Š ˆ d ) ) ( ) (c) V Š d d d Š ) d ) (d) V R r d ) d d. () V ˆ Š d ( ) d d c rdius height d ˆ 8 ˆ ˆ () 7 () V ˆ Š d ( ) d d rdius height 8 8 ˆ ˆ ˆ 6 Š rdius height 8 ˆ 8 ˆ 8 ˆ d ˆ () Š c rdius height ˆ ˆ ˆ ˆ ˆ (c) V d ( ) d d (d) V d ( )( ) d ( ) Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
18 Chpter 6 Applictions of Definite Integrls. () V ˆ Š d d d c rdius height d Š 8 rdius height () V ˆ Š d ˆ È d ˆ Î d Š 6 Î 6 Š È rdius height ˆ 6 (8 6) (c) V ˆ d ( ) ˆ d ˆ Î Î 8 d 8 ˆ 6 ( 9) () 8 Î Î 6 6 d ˆ Š c rdius height (d) V d ( ) d d ˆ (). () V ˆ Š d d d c rdius height d ˆ rdius height () V cd ˆ Š d () d d ˆ () 7 6 rdius height. () V cd ˆ Š d c dd d ˆ ( 6) () Use the wsher method: d c ( V cr () r () dd d d ˆ ( ) (c) Use the wsher method: d c ( d 7 7 (7 ) d ˆ Š c d c rdius height d d ˆ 6 ( ) V cr () r () dd c d d d ˆ (d) V d ( ) d ( ) d Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
19 . () V ˆ Š d ˆ È 8 d d c rdius height Š È Î d È Î È Š È Š 8 8 ˆ (8) Section 6. Volume Using Clindricl Shells () V ˆ Š d Š È Î Î d Š d rdius height Š Š ) ( ( ) * rdius height 6. () V ˆ Š d c d d 6 d d ˆ () V ˆ Š d ( ) c dd ( ) d rdius height ˆ 6 d (68) 7. () V cr () r () dd ˆ Î d Î6 Î ( ) ˆ Î 6 ˆ rdius height 6 ˆ d 6 ˆ ˆ ˆ 8 8 (8 ) 9 6 () V ˆ Š d Š d 8. () V cr () r () dd Š d d c 6 ˆ ˆ ( 6 6 ) 8 8 ˆ Š Š rdius height Î È ˆ Î Î d Î Î ˆ ˆ ˆ ( ) 8 () V d d 9. () H=: V V V V [R ()] d nd V [R ()] with R () É nd R () È,, ;, Ê two integrls re required Copright Person Eduction, Inc. Pulishing s Addison-Wesle.
APPLICATIONS OF DEFINITE INTEGRALS
Chpter 6 APPICATIONS OF DEFINITE INTEGRAS OVERVIEW In Chpter 5 we discovered the connection etween Riemnn sums ssocited with prtition P of the finite closed intervl [, ] nd the process of integrtion. We
R(3, 8) P( 3, 0) Q( 2, 2) S(5, 3) Q(2, 32) P(0, 8) Higher Mathematics Objective Test Practice Book. 1 The diagram shows a sketch of part of
Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
7.1 Integral as Net Change and 7.2 Areas in the Plane Calculus
7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
Mathematics. Area under Curve.
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
660 Chapter 10 Conic Sections and Polar Coordinates
Chpter Conic Sections nd Polr Coordintes 8. ( (b (c (d (e r r Ê r ; therefore cos Ê Ê ( ß is point of intersection ˆ ˆ Ê Ê Ê ß ß ˆ ß 9. ( r cos Ê cos ; r cos Ê r Š Ê r r Ê (r (b r Ê cos Ê cos Ê, Ê ß or
x 2 1 dx x 3 dx = ln(x) + 2e u du = 2e u + C = 2e x + C 2x dx = arcsin x + 1 x 1 x du = 2 u + C (t + 2) 50 dt x 2 4 dx
. Compute the following indefinite integrls: ) sin(5 + )d b) c) d e d d) + d Solutions: ) After substituting u 5 +, we get: sin(5 + )d sin(u)du cos(u) + C cos(5 + ) + C b) We hve: d d ln() + + C c) Substitute
APPM 1360 Exam 2 Spring 2016
APPM 6 Em Spring 6. 8 pts, 7 pts ech For ech of the following prts, let f + nd g 4. For prts, b, nd c, set up, but do not evlute, the integrl needed to find the requested informtion. The volume of the
Chapter 7: Applications of Integrals
Chpter 7: Applictions of Integrls 78 Chpter 7 Overview: Applictions of Integrls Clculus, like most mthemticl fields, egn with tring to solve everd prolems. The theor nd opertions were formlized lter. As
[ ( ) ( )] Section 6.1 Area of Regions between two Curves. Goals: 1. To find the area between two curves
![[ ( ) ( )] Section 6.1 Area of Regions between two Curves. Goals: 1. To find the area between two curves](/thumbs/74/70299306.jpg "[ ( ) ( )] Section 6.1 Area of Regions between two Curves. Goals: 1. To find the area between two curves")
Gols: 1. To find the re etween two curves Section 6.1 Are of Regions etween two Curves I. Are of Region Between Two Curves A. Grphicl Represention = _ B. Integrl Represention [ ( ) ( )] f x g x dx = C.
Review Exercises for Chapter 4
_R.qd // : PM Pge CHAPTER Integrtion Review Eercises for Chpter In Eercises nd, use the grph of to sketch grph of f. To print n enlrged cop of the grph, go to the wesite www.mthgrphs.com... In Eercises
(b) Let S 1 : f(x, y, z) = (x a) 2 + (y b) 2 + (z c) 2 = 1, this is a level set in 3D, hence
Problem ( points) Find the vector eqution of the line tht joins points on the two lines L : r ( + t) i t j ( + t) k L : r t i + (t ) j ( + t) k nd is perpendiculr to both those lines. Find the set of ll
7.1 Integral as Net Change Calculus. What is the total distance traveled? What is the total displacement?
7.1 Integrl s Net Chnge Clculus 7.1 INTEGRAL AS NET CHANGE Distnce versus Displcement We hve lredy seen how the position of n oject cn e found y finding the integrl of the velocity function. The chnge
APPLICATIONS OF THE DEFINITE INTEGRAL IN GEOMETRY, SCIENCE, AND ENGINEERING
6 Courtes NASA APPLICATIONS OF THE DEFINITE INTEGRAL IN GEOMETRY, SCIENCE, AND ENGINEERING Clculus is essentil for the computtions required to lnd n stronut on the Moon. In the lst chpter we introduced
Chapter 9 Definite Integrals
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
x = a To determine the volume of the solid, we use a definite integral to sum the volumes of the slices as we let!x " 0 :
Clculus II MAT 146 Integrtion Applictions: Volumes of 3D Solids Our gol is to determine volumes of vrious shpes. Some of the shpes re the result of rotting curve out n xis nd other shpes re simply given
5.2 Volumes: Disks and Washers
4 pplictions of definite integrls 5. Volumes: Disks nd Wshers In the previous section, we computed volumes of solids for which we could determine the re of cross-section or slice. In this section, we restrict
Multiple Integrals. Review of Single Integrals. Planar Area. Volume of Solid of Revolution
Multiple Integrls eview of Single Integrls eding Trim 7.1 eview Appliction of Integrls: Are 7. eview Appliction of Integrls: Volumes 7.3 eview Appliction of Integrls: Lengths of Curves Assignment web pge
APPLICATIONS OF THE DEFINITE INTEGRAL
APPLICATIONS OF THE DEFINITE INTEGRAL. Volume: Slicing, disks nd wshers.. Volumes by Slicing. Suppose solid object hs boundries extending from x =, to x = b, nd tht its cross-section in plne pssing through
First Semester Review Calculus BC
First Semester Review lculus. Wht is the coordinte of the point of inflection on the grph of Multiple hoice: No lcultor y 3 3 5 4? 5 0 0 3 5 0. The grph of piecewise-liner function f, for 4, is shown below.
Multiple Integrals. Review of Single Integrals. Planar Area. Volume of Solid of Revolution
Multiple Integrls eview of Single Integrls eding Trim 7.1 eview Appliction of Integrls: Are 7. eview Appliction of Integrls: olumes 7.3 eview Appliction of Integrls: Lengths of Curves Assignment web pge
50. Use symmetry to evaluate xx D is the region bounded by the square with vertices 5, Prove Property 11. y y CAS
68 CHAPTE MULTIPLE INTEGALS 46. e da, 49. Evlute tn 3 4 da, where,. [Hint: Eploit the fct tht is the disk with center the origin nd rdius is smmetric with respect to both es.] 5. Use smmetr to evlute 3
10.5. ; 43. The points of intersection of the cardioid r 1 sin and. ; Graph the curve and find its length. CONIC SECTIONS
654 CHAPTER 1 PARAETRIC EQUATIONS AND POLAR COORDINATES ; 43. The points of intersection of the crdioid r 1 sin nd the spirl loop r,, cn t be found ectl. Use grphing device to find the pproimte vlues of
The Trapezoidal Rule
_.qd // : PM Pge 9 SECTION. Numericl Integrtion 9 f Section. The re of the region cn e pproimted using four trpezoids. Figure. = f( ) f( ) n The re of the first trpezoid is f f n. Figure. = Numericl Integrtion
( x )( x) dx. Year 12 Extension 2 Term Question 1 (15 Marks) (a) Sketch the curve (x + 1)(y 2) = 1 2
Yer Etension Term 7 Question (5 Mrks) Mrks () Sketch the curve ( + )(y ) (b) Write the function in prt () in the form y f(). Hence, or otherwise, sketch the curve (i) y f( ) (ii) y f () (c) Evlute (i)
Total Score Maximum
Lst Nme: Mth 8: Honours Clculus II Dr. J. Bowmn 9: : April 5, 7 Finl Em First Nme: Student ID: Question 4 5 6 7 Totl Score Mimum 6 4 8 9 4 No clcultors or formul sheets. Check tht you hve 6 pges.. Find
Topics Covered AP Calculus AB
Topics Covered AP Clculus AB ) Elementry Functions ) Properties of Functions i) A function f is defined s set of ll ordered pirs (, y), such tht for ech element, there corresponds ectly one element y.
Further applications of integration UNCORRECTED PAGE PROOFS
. Kick off with CAS. Integrtion recognition. Solids of revolution. Volumes Further pplictions of integrtion. Arc length, numericl integrtion nd grphs of ntiderivtives.6 Wter flow.7 Review . Kick off with
Form 5 HKCEE 1990 Mathematics II (a 2n ) 3 = A. f(1) B. f(n) A. a 6n B. a 8n C. D. E. 2 D. 1 E. n. 1 in. If 2 = 10 p, 3 = 10 q, express log 6
Form HK 9 Mthemtics II.. ( n ) =. 6n. 8n. n 6n 8n... +. 6.. f(). f(n). n n If = 0 p, = 0 q, epress log 6 in terms of p nd q.. p q. pq. p q pq p + q Let > b > 0. If nd b re respectivel the st nd nd terms
Paul s Notes. Chapter Planning Guide
Applictions of Integrtion. Are of Region Between Two Curves. Volume: The Disk nd Wsher Methods. Volume: The Shell Method. Arc Length nd Surfces of Revolution Roof Are (Eercise, p. ) Sturn (Section Project,
Area of a Region Between Two Curves
6 CHAPTER 7 Applictions of Integrtion Section 7 Are of Region Between Two Curves Find the re of region etween two curves using integrtion Find the re of region etween intersecting curves using integrtion
AB Calculus Review Sheet
AB Clculus Review Sheet Legend: A Preclculus, B Limits, C Differentil Clculus, D Applictions of Differentil Clculus, E Integrl Clculus, F Applictions of Integrl Clculus, G Prticle Motion nd Rtes This is
CONIC SECTIONS. Chapter 11
CONIC SECTIONS Chpter. Overview.. Sections of cone Let l e fied verticl line nd m e nother line intersecting it t fied point V nd inclined to it t n ngle α (Fig..). Fig.. Suppose we rotte the line m round
( ) as a fraction. Determine location of the highest
AB Clculus Exm Review Sheet - Solutions A. Preclculus Type prolems A1 A2 A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f ( x). Set function equl to 0. Fctor or use qudrtic eqution if
FINALTERM EXAMINATION 9 (Session - ) Clculus & Anlyticl Geometry-I Question No: ( Mrs: ) - Plese choose one f ( x) x According to Power-Rule of differentition, if d [ x n ] n x n n x n n x + ( n ) x n+
7Applications of. Integration
7Applictions of Integrtion The Atomium, locted in Belgium, represents n iron crstl molecule mgnified 65 illion times. The structure contins nine spheres connected with clindricl tues. The centrl sphere
( ) where f ( x ) is a. AB Calculus Exam Review Sheet. A. Precalculus Type problems. Find the zeros of f ( x).
AB Clculus Exm Review Sheet A. Preclculus Type prolems A1 Find the zeros of f ( x). This is wht you think of doing A2 A3 Find the intersection of f ( x) nd g( x). Show tht f ( x) is even. A4 Show tht f
2 b. , a. area is S= 2π xds. Again, understand where these formulas came from (pages ).
AP Clculus BC Review Chpter 8 Prt nd Chpter 9 Things to Know nd Be Ale to Do Know everything from the first prt of Chpter 8 Given n integrnd figure out how to ntidifferentite it using ny of the following
Mathematics Extension 2
00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mthemtics Etension Generl Instructions Reding time 5 minutes Working time hours Write using blck or blue pen Bord-pproved clcultors my be used A tble of stndrd
Ch AP Problems
Ch. 7.-7. AP Prolems. Willy nd his friends decided to rce ech other one fternoon. Willy volunteered to rce first. His position is descried y the function f(t). Joe, his friend from school, rced ginst him,
Chapter 9. Arc Length and Surface Area
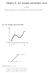Chpter 9. Arc Length nd Surfce Are In which We ppl integrtion to stud the lengths of curves nd the re of surfces. 9. Arc Length (Tet 547 553) P n P 2 P P 2 n b P i ( i, f( i )) P i ( i, f( i )) distnce
Eigen Values and Eigen Vectors of a given matrix
Engineering Mthemtics 0 SUBJECT NAME SUBJECT CODE MATERIAL NAME MATERIAL CODE : Engineering Mthemtics I : 80/MA : Prolem Mteril : JM08AM00 (Scn the ove QR code for the direct downlod of this mteril) Nme
PROPERTIES OF AREAS In general, and for an irregular shape, the definition of the centroid at position ( x, y) is given by
PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
( β ) touches the x-axis if = 1
Generl Certificte of Eduction (dv. Level) Emintion, ugust Comined Mthemtics I - Prt B Model nswers. () Let f k k, where k is rel constnt. i. Epress f in the form( ) Find the turning point of f without
Thomas Whitham Sixth Form
Thoms Whithm Sith Form Pure Mthemtics Unit C Alger Trigonometry Geometry Clculus Vectors Trigonometry Compound ngle formule sin sin cos cos Pge A B sin Acos B cos Asin B A B sin Acos B cos Asin B A B cos
Calculus AB. For a function f(x), the derivative would be f '(
lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
KEY CONCEPTS. satisfies the differential equation da. = 0. Note : If F (x) is any integral of f (x) then, x a
KEY CONCEPTS THINGS TO REMEMBER :. The re ounded y the curve y = f(), the -is nd the ordintes t = & = is given y, A = f () d = y d.. If the re is elow the is then A is negtive. The convention is to consider
4.6 Numerical Integration
.6 Numericl Integrtion 5.6 Numericl Integrtion Approimte definite integrl using the Trpezoidl Rule. Approimte definite integrl using Simpson s Rule. Anlze the pproimte errors in the Trpezoidl Rule nd Simpson
P 1 (x 1, y 1 ) is given by,.
MA00 Clculus nd Bsic Liner Alger I Chpter Coordinte Geometr nd Conic Sections Review In the rectngulr/crtesin coordintes sstem, we descrie the loction of points using coordintes. P (, ) P(, ) O The distnce
CHAPTER 11 PARAMETRIC EQUATIONS AND POLAR COORDINATES
CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
The problems that follow illustrate the methods covered in class. They are typical of the types of problems that will be on the tests.
ADVANCED CALCULUS PRACTICE PROBLEMS JAMES KEESLING The problems tht follow illustrte the methods covered in clss. They re typicl of the types of problems tht will be on the tests. 1. Riemnn Integrtion
Applications of Definite Integral
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
LINEAR ALGEBRA APPLIED
5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
A LEVEL TOPIC REVIEW. factor and remainder theorems
A LEVEL TOPIC REVIEW unit C fctor nd reminder theorems. Use the Fctor Theorem to show tht: ) ( ) is fctor of +. ( mrks) ( + ) is fctor of ( ) is fctor of + 7+. ( mrks) +. ( mrks). Use lgebric division
1. If * is the operation defined by a*b = a b for a, b N, then (2 * 3) * 2 is equal to (A) 81 (B) 512 (C) 216 (D) 64 (E) 243 ANSWER : D
. If * is the opertion defined by *b = b for, b N, then ( * ) * is equl to (A) 8 (B) 5 (C) 6 (D) 64 (E) 4. The domin of the function ( 9)/( ),if f( ) = is 6, if = (A) (0, ) (B) (-, ) (C) (-, ) (D) (, )
y = f(x) This means that there must be a point, c, where the Figure 1
Clculus Investigtion A Men Slope TEACHER S Prt 1: Understnding the Men Vlue Theorem The Men Vlue Theorem for differentition sttes tht if f() is defined nd continuous over the intervl [, ], nd differentile
ES.182A Topic 32 Notes Jeremy Orloff
ES.8A Topic 3 Notes Jerem Orloff 3 Polr coordintes nd double integrls 3. Polr Coordintes (, ) = (r cos(θ), r sin(θ)) r θ Stndrd,, r, θ tringle Polr coordintes re just stndrd trigonometric reltions. In
Applications of Definite Integral
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
8.6 The Hyperbola. and F 2. is a constant. P F 2. P =k The two fixed points, F 1. , are called the foci of the hyperbola. The line segments F 1
8. The Hperol Some ships nvigte using rdio nvigtion sstem clled LORAN, which is n cronm for LOng RAnge Nvigtion. A ship receives rdio signls from pirs of trnsmitting sttions tht send signls t the sme time.
Solutions to Problems Integration in IR 2 and IR 3
Solutions to Problems Integrtion in I nd I. For ec of te following, evlute te given double integrl witout using itertion. Insted, interpret te integrl s, for emple, n re or n verge vlue. ) dd were is te
PREVIOUS EAMCET QUESTIONS
CENTRE OF MASS PREVIOUS EAMCET QUESTIONS ENGINEERING Two prticles A nd B initilly t rest, move towrds ech other, under mutul force of ttrction At n instnce when the speed of A is v nd speed of B is v,
4.4 Areas, Integrals and Antiderivatives
. res, integrls nd ntiderivtives 333. Ares, Integrls nd Antiderivtives This section explores properties of functions defined s res nd exmines some connections mong res, integrls nd ntiderivtives. In order
The Trapezoidal Rule
SECTION. Numericl Integrtion 9 f Section. The re of the region cn e pproimted using four trpezoids. Figure. = f( ) f( ) n The re of the first trpezoid is f f n. Figure. = Numericl Integrtion Approimte
MAC 1105 Final Exam Review
1. Find the distnce between the pir of points. Give n ect, simplest form nswer nd deciml pproimtion to three plces., nd, MAC 110 Finl Em Review, nd,0. The points (, -) nd (, ) re endpoints of the dimeter
Math 1102: Calculus I (Math/Sci majors) MWF 3pm, Fulton Hall 230 Homework 2 solutions
Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Calculus AB Bible. (2nd most important book in the world) (Written and compiled by Doug Graham)
PG. Clculus AB Bile (nd most importnt ook in the world) (Written nd compiled y Doug Grhm) Topic Limits Continuity 6 Derivtive y Definition 7 8 Derivtive Formuls Relted Rtes Properties of Derivtives Applictions
x ) dx dx x sec x over the interval (, ).
Curve on 6 For -, () Evlute the integrl, n (b) check your nswer by ifferentiting. ( ). ( ). ( ).. 6. sin cos 7. sec csccot 8. sec (sec tn ) 9. sin csc. Evlute the integrl sin by multiplying the numertor
Definite integral. Mathematics FRDIS MENDELU
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Math 113 Exam 2 Practice
Mth Em Prctice Februry, 8 Em will cover sections 6.5, 7.-7.5 nd 7.8. This sheet hs three sections. The first section will remind you bout techniques nd formuls tht you should know. The second gives number
Thammasat University Department of Common and Graduate Studies
Sirindhorn Interntionl Institute of Technology Thmmst University Deprtment of Common nd Grdute Studies Semester: 3/2008 Instructors: Dr. Prpun Suksompong MAS 6: Lecture Notes 7 6 Applictions of the Definite
6.2 Volumes. V Ah 430 CHAPTER 6 APPLICATIONS OF INTEGRATION. h h w l (c) Rectangular box V=lwh. (a) Cylinder V=Ah. (b) Circular cylinder
43 CHAPTER 6 APPLICATIONS OF INTEGRATION 6. Volumes In tring to find the volume of solid we fce the sme tpe of problem s in finding res. We hve n intuitive ide of wht volume mens, but we must mke this
Math 113 Exam 1-Review
Mth 113 Exm 1-Review September 26, 2016 Exm 1 covers 6.1-7.3 in the textbook. It is dvisble to lso review the mteril from 5.3 nd 5.5 s this will be helpful in solving some of the problems. 6.1 Are Between
AP Calculus BC Review Applications of Integration (Chapter 6) noting that one common instance of a force is weight
AP Clculus BC Review Applictions of Integrtion (Chpter Things to Know n Be Able to Do Fin the re between two curves by integrting with respect to x or y Fin volumes by pproximtions with cross sections:
Definite integral. Mathematics FRDIS MENDELU. Simona Fišnarová (Mendel University) Definite integral MENDELU 1 / 30
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Trigonometric Functions
Trget Publictions Pvt. Ltd. Chpter 0: Trigonometric Functions 0 Trigonometric Functions. ( ) cos cos cos cos (cos + cos ) Given, cos cos + 0 cos (cos + cos ) + ( ) 0 cos cos cos + 0 + cos + (cos cos +
Year 12 Mathematics Extension 2 HSC Trial Examination 2014
Yer Mthemtics Etension HSC Tril Emintion 04 Generl Instructions. Reding time 5 minutes Working time hours Write using blck or blue pen. Blck pen is preferred. Bord-pproved clcultors my be used A tble of
Space Curves. Recall the parametric equations of a curve in xy-plane and compare them with parametric equations of a curve in space.
Clculus 3 Li Vs Spce Curves Recll the prmetric equtions of curve in xy-plne nd compre them with prmetric equtions of curve in spce. Prmetric curve in plne x = x(t) y = y(t) Prmetric curve in spce x = x(t)
Exercise Qu. 12. a2 y 2 da = Qu. 18 The domain of integration: from y = x to y = x 1 3 from x = 0 to x = 1. = 1 y4 da.
MAH MAH Eercise. Eercise. Qu. 7 B smmetr ( + 5)dA + + + 5 (re of disk with rdius ) 5. he first two terms of the integrl equl to becuse is odd function in nd is odd function in. (see lso pge 5) Qu. b da
Shape and measurement
C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
Not for reproduction
AREA OF A SURFACE OF REVOLUTION cut h FIGURE FIGURE πr r r l h FIGURE A surfce of revolution is formed when curve is rotted bout line. Such surfce is the lterl boundry of solid of revolution of the type
k ) and directrix x = h p is A focal chord is a line segment which passes through the focus of a parabola and has endpoints on the parabola.
Stndrd Eqution of Prol with vertex ( h, k ) nd directrix y = k p is ( x h) p ( y k ) = 4. Verticl xis of symmetry Stndrd Eqution of Prol with vertex ( h, k ) nd directrix x = h p is ( y k ) p( x h) = 4.
JUST THE MATHS UNIT NUMBER INTEGRATION APPLICATIONS 8 (First moments of a volume) A.J.Hobson
JUST THE MATHS UNIT NUMBER 3.8 INTEGRATIN APPLICATINS 8 (First moments of volume) b A.J.Hobson 3.8. Introduction 3.8. First moment of volume of revolution bout plne through the origin, perpendiculr to
Polynomials and Division Theory
Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Math 0230 Calculus 2 Lectures
Mth Clculus Lectures Chpter 7 Applictions of Integrtion Numertion of sections corresponds to the text Jmes Stewrt, Essentil Clculus, Erly Trnscendentls, Second edition. Section 7. Ares Between Curves Two
CHAPTER : INTEGRATION Content pge Concept Mp 4. Integrtion of Algeric Functions 4 Eercise A 5 4. The Eqution of Curve from Functions of Grdients. 6 Ee
ADDITIONAL MATHEMATICS FORM 5 MODULE 4 INTEGRATION CHAPTER : INTEGRATION Content pge Concept Mp 4. Integrtion of Algeric Functions 4 Eercise A 5 4. The Eqution of Curve from Functions of Grdients. 6 Eercise
Chapter 8.2: The Integral
Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
Mathematics Extension 2
00 HIGHER SCHOOL CERTIFICATE EXAMINATION Mthemtics Extension Generl Instructions Reding time 5 minutes Working time hours Write using blck or blue pen Bord-pproved clcultors m be used A tble of stndrd
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
10.2 The Ellipse and the Hyperbola
CHAPTER 0 Conic Sections Solve. 97. Two surveors need to find the distnce cross lke. The plce reference pole t point A in the digrm. Point B is meters est nd meter north of the reference point A. Point
15 - TRIGONOMETRY Page 1 ( Answers at the end of all questions )
- TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
Log1 Contest Round 3 Theta Individual. 4 points each 1 What is the sum of the first 5 Fibonacci numbers if the first two are 1, 1?
008 009 Log1 Contest Round Thet Individul Nme: points ech 1 Wht is the sum of the first Fiboncci numbers if the first two re 1, 1? If two crds re drwn from stndrd crd deck, wht is the probbility of drwing
Time : 3 hours 03 - Mathematics - March 2007 Marks : 100 Pg - 1 S E CT I O N - A
Time : hours 0 - Mthemtics - Mrch 007 Mrks : 100 Pg - 1 Instructions : 1. Answer ll questions.. Write your nswers ccording to the instructions given below with the questions.. Begin ech section on new
IMPORTANT QUESTIONS FOR INTERMEDIATE PUBLIC EXAMINATIONS IN MATHS-IB
` K UKATP ALLY CE NTRE IMPORTANT QUESTIONS FOR INTERMEDIATE PUBLIC EXAMINATIONS IN MATHS-IB 7-8 FIITJEE KUKATPALLY CENTRE: # -97, Plot No, Opp Ptel Kunt Hud Prk, Vijngr Colon, Hderbd - 5 7 Ph: -66 Regd
Section 6: Area, Volume, and Average Value
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
( ) Same as above but m = f x = f x - symmetric to y-axis. find where f ( x) Relative: Find where f ( x) x a + lim exists ( lim f exists.
AP Clculus Finl Review Sheet solutions When you see the words This is wht you think of doing Find the zeros Set function =, fctor or use qudrtic eqution if qudrtic, grph to find zeros on clcultor Find
Unit 5. Integration techniques
18.01 EXERCISES Unit 5. Integrtion techniques 5A. Inverse trigonometric functions; Hyperbolic functions 5A-1 Evlute ) tn 1 3 b) sin 1 ( 3/) c) If θ = tn 1 5, then evlute sin θ, cos θ, cot θ, csc θ, nd
Chapter 5 1. = on [ 1, 2] 1. Let gx ( ) e x. . The derivative of g is g ( x) e 1
![Chapter 5 1. = on [ 1, 2] 1. Let gx ( ) e x. . The derivative of g is g ( x) e 1](/thumbs/77/75232020.jpg "Chapter 5 1. = on [ 1, 2] 1. Let gx ( ) e x. . The derivative of g is g ( x) e 1")
Chpter 5. Let g ( e. on [, ]. The derivtive of g is g ( e ( Write the slope intercept form of the eqution of the tngent line to the grph of g t. (b Determine the -coordinte of ech criticl vlue of g. Show
Final Exam - Review MATH Spring 2017
Finl Exm - Review MATH 5 - Spring 7 Chpter, 3, nd Sections 5.-5.5, 5.7 Finl Exm: Tuesdy 5/9, :3-7:pm The following is list of importnt concepts from the sections which were not covered by Midterm Exm or.
Distributed Forces: Centroids and Centers of Gravity
Distriuted Forces: Centroids nd Centers of Grvit Introduction Center of Grvit of D Bod Centroids nd First Moments of Ares nd Lines Centroids of Common Shpes of Ares Centroids of Common Shpes of Lines Composite
We divide the interval [a, b] into subintervals of equal length x = b a n
![We divide the interval [a, b] into subintervals of equal length x = b a n](/thumbs/80/80533932.jpg "We divide the interval [a, b] into subintervals of equal length x = b a n")
Arc Length Given curve C defined by function f(x), we wnt to find the length of this curve between nd b. We do this by using process similr to wht we did in defining the Riemnn Sum of definite integrl:
Physics 3323, Fall 2016 Problem Set 7 due Oct 14, 2016
Physics 333, Fll 16 Problem Set 7 due Oct 14, 16 Reding: Griffiths 4.1 through 4.4.1 1. Electric dipole An electric dipole with p = p ẑ is locted t the origin nd is sitting in n otherwise uniform electric