EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES
|
|
|
- Britton Walton
- 5 years ago
- Views:
Transcription
1 EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES C A CHURCH Uiversity of North Carolia, Greesboro, North Carolia ad MARJORIE BICKNELL A. C. Wilco High Schl, Sata Clara, Califoria 1. INTRODUCTION Geeratig fuctios provide a startig poit for a appretice Fiboacci ethusiast who would like to do some research. I the Fiboacci Primer: P a r t VI, Hoggatt ad Lid [l] discuss ordiary geeratig fuctios for idetities relatig Fiboacci ad Lucas umbers. Also, Gould [2] has worked with geeralized geeratig fuctios. Here, we use epoetial geeratig fuctios to establish some Fiboacci ad Lucas idetities. 2. THE EXPONENTIAL FUNCTION AND EXPONENTIAL GENERATING FUNCTIONS The epoetial fuctio e appears i studyig radioactive decay, bacterial growth, compoud iterest, ad probability theory. The trascedetal costat e = is the base for atural logarithms. However, the particular property of e that iterests us is M\ i j., \A v3,, J. V^ The e - l + j? + - g j - + ~ ^ j J ad algebra shows that (2) e ^ - e ^ = ( l - l ) + ^ ^ + i 2 4 ^ + ^ - ^ To relate (2) to Fiboacci umbers, if F is the Fiboacci umber defied by Fi = F 2 = 1, F 1 = F + F f ad if a = (1 + Vl>)/2, p = (1 - N/"5)/2, the it is well 1 c +1-1 kow that (3) F = (<* - p )/(a - j3). Thus, dividig Eq. (2) by (a - p) gives at fit F ^ F 2 t 2 F 8 1? F 4 t^ * a - P 1! 2! 3! 4! 1! ~J! =l 275
2 276 EXPONENTIAL GENEBATING FUNCTIONS FOR FIBONACCI IDENTITIES [Oct. t sice F 0 = 0, we ca add the term F 0 -^ ad write the followig epoetial geeratig fuctio for Fiboacci umbers: (4) v at i3t, e - j = y F L. a - /3 Z-*! A elemetary compaio to the Fiboacci epoetial geeratig fuctio geerates Lucas umber coefficiets* The Lucas umbers are defied by Li = 1, L 2 = 3, L + L - J l * -1 = L -, ad have the property that (5) L = a + /3. If the power series for e ad e are calculated ad the added term-by-term, the result is (6) e + e r = > L -7. Z t! For a ovel use for these elemetary geeratig fuctios, the reader is directed to [3] for a prf that the determiat of eq is e, where Q = ( - 0 J. 3. PROPERTIES OF INFINITE SERIES We list without prf some properties of ifiite series ecessary to our developmet of epoetial geeratig fuctios. Give it follows that (7) ^ t ^ t A(t) = > a i,. ad B(t) = > b ^, L^J! ' Z i! A(t) B(t) = E ( EuKVklT ' \ X ' I A(t)B(-t)=E(L(-l) - k ( kkus \ ^ ' / Thus, if B(t) = e, the b = 1 for all, ad / A(t) e f ^ '-E s(jk)s \ X ' /
3 1973] EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES 277 To help the reader with the double summatio otatio, let The / A(t)B(t) = ~ A ( t T-^ t \ - ^ t > = E If «* B^ = E If \ k = 0 X ' / -(j>&*((!)-(i>)&*((!)-(0-(;>)i + - t 4t 2,. 2t v ^ t(2t) V * 2 t + 1 = 0 + ir + "2r + ' e ' +te = E -V- = E -sr V ( + D 2 t La ( + 1)! (a^v ^! where 1, I is the biomial coefficiet, ( " ) (A =! 1 k I k!( - k)f 4. EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES Geeratig fuctio (4) ad algebraic properties of a ad /3, the rts of = 0, give us a easy way to geerate Fiboacci idetities. Useful algebraic properties of a = (1 + is/t>)/2 ad 0 = (1 - \l"5)/2 iclude:. o?/3 = - 1 a 2 = a + 1 F = (a - /3 )/(a - /3) a - j3 = ^5 a m = a F + F L = a + ^ r j_ o -, HI m - 1 a + p = 1 Take B(t) = e t ad A(t) = (e a t - e^)/(a - 0). (See Eqs. (1) ad (4).) The their series product A(t) ad B(t) gives
4 278 EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES [Oct. (8) t e(a+i)t _ e(p+l)t Qah _ J$h ^ l i L r l k / ' k F, /! \ k = 0 X 7 a - p or - 0 t J zlr F 2! O the left, we used series property (7). O the right, we multiplied A(t) B(t) ad used algebraic properties of a ad p 9 ad the combied our kowledge of Eqs. (1) through (4). Lastly, equatig coefficiets of t /! gives us the idetity X ' If we follow the same steps with B(t) = e~ ad A(t) = (e^ - <s )/{a - p), the \ w / (9) -/3t -at ^, S^T/5 2 ^ (" 1} F T ' The idetity resultig from (9) is 2 <Wi) X ' F. = ( - l ) + 1 F k The techique, the, is this: Take B(t) ad A(t) as simple fuctios i terms of powers of e. Follow algebra as outlied i Eqs. (1) through (7), ad equate coefficiets of - t cp't j3^t t /! The reader is ivited to use B(t) = e" ad A(t) = (e - e H )/(a - p) to derive F O 1 2k = F For a idetity relatig Fiboacci ad Lucas umbers, let A(t) = (e at - e Pt )/(a - p), B(t) = e * + e Pt
5 1973] EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES 279 Sice B(t) is the geeratig fuctio for Lucas umber coefficiets (see Eq. (6)), computig the series product A(t) B(t) gives 00 / \ / / \ \, 2at 281 j i <"> 2 ( 2 ( 0 r * L» - t h - '-^r-- E **. r \ / yieldig. = 2 F. k Similarly, let A(t) = B(t) = (e at - ep t )/if - /3), leadig to / \ / V ' e2at + e2^t _ 2 e t } (11) = ^ l ( 2 L - 2 ) L, E ( k ) F k F - k = l ( 2 \ - 2 > ' at Bt The reader should use A(t) = B(t) = e + e K to derive i, i, To geeralize, try combiatios usig e ad e, such as Aft) = (e a fc - e^ *)/(«- /3), B(t) = e* t + e P l, which geeralize Eq. (10) as follows: o / \ _ m, 0 0m, E l X^fA \t _ e 2a t - e 2 / 3 t _ V t I Z - r l k J F m k L 2 m - m k ) T STTjg ^ F m T \ / By takig Aft) = B(t) = (e - e P )/(a - 0), Eq. (11) becomes
6 280 EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES [Oct. 00 / \ / r HiA 2 V[y/\ F F V - h a *_«f ' Z-/1 Z-* I k / mk m-mk I! 1 a - p \ X ' / \ - m, 0 0m, / m 1/a iiiv, ( l ) = i C e 2 0 t + e 2^ t - 2 e ( a ^ >*) = y ; i ( 2 L - 2 L ) ^. A / 5 m m! m, fim The geeralizatio of (12) foud by A(t) = B(t) = e^ + e^ is 00 / \ 2 / / \ \, m, 0m, * \ 0 m, o/3 m^. / m L O m u (12-) = e 2 " * + e 2^ * + 2e ( } t " ^ = y > ^ < L m + 2 L ) ^ m! The reader should ow eperimet with other simple fuctios ivolvig powers of e. A suggestio is to use some combiatios which lead to hyperbolic sies or cosies, which are defied i terms of e. 5. GENERATING FUNCTIONS FOR MORE GENERALIZED IDENTITIES To get idetities of the type F k+r = F 2+r Hi ote that the r derivative with respect to t of A(t) is Z f +r! so that if A(t) = (e at + e pt )/(a - p) t B(t) = e t, _ ^ / JL^ / \ \ t t r / e <*t _ /3t \ ar e (a+l)t ^ ( p + D t 2-/ ( Z ) ( k ) F k+r I ET = e D t ( 6 a - J ) = 2 ^ I i3 G X \ / ' (13) r " 2 t RT Ph A = a e - P e = V* F L a _ j3 Z-f 2+r!
7 1973] EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES 281 all of which suggests a whole family of idetities; e. g., for 4m, /D^m,, A(t) = (e a l - e P l )/(a - 0), B(t) = e l, \ k = 0, 4rm (a 4 m +l)t 04rm (/3 4m +l)t F I - = a - ]3 e ^ 4mk+r I! a - j3 A 2m, 2 m, 0 2 m u. 2m, 2 m I / D 2 m u 4rm a (a -f/3 )t p4rm a (a +/3 )t e (14) = 2 2 a "- Pp» J 2m 2m+4mr! From the other directio oe ca get idetities of the type (15) <*> m, Dm, (af +F )t (j3f +F )t v, a t t m m - 1 ' ^ m m - 1 ' E ^ t e - e r _ e - e m! ~ a - j3 a - j3,, <*F t j3f t \ /. \ Takig the r derivative of Eq. (15) leads to / \ ( 1 6 ) JLJ F m+rm itt = 2 ^ I 2 - M k I F m - 1 F m F k+rm J f = 0 \ k = 0 / Replace rm by s i Eq. (16) ad compare with Viso's result [4, p. 38], See also H. Leoard [5]. REFERENCES 1. V. E. Hoggatt, J r., ad D. A. Lid, A P r i m e r for the Fiboacci Numbers: P a r t V I, " Fiboacci Quarterly, 5 (1967), pp H. W. Gould, "Geeratig Fuctios for Products of Powers of Fiboacci Numbers," Fiboacci Quarterly, 1 (1963), No. 2, pp Joh L. Brow, solutio of Problem H-20 (proposed by V e r e r E. Hoggatt, J r., ad Charles H. Kig), Fiboacci Quarterly 2 (1964), pp Joh Viso, The Relatio of the Period Modulo to the Rak of Apparitio of m i the Fiboacci Sequece," Fiboacci Quarterly, 1(1963), pp Harold T. Leoard, J r., "Fiboacci ad Lucas Idetities ad Geeratig Fuctios," Master 1 s Thesis, Sa Jose State College, July 1969.
CERTAIN GENERAL BINOMIAL-FIBONACCI SUMS
 CERTAIN GENERAL BINOMIAL-FIBONACCI SUMS J. W. LAYMAN Virgiia Polytechic Istitute State Uiversity, Blacksburg, Virgiia Numerous writers appear to have bee fasciated by the may iterestig summatio idetitites
CERTAIN GENERAL BINOMIAL-FIBONACCI SUMS J. W. LAYMAN Virgiia Polytechic Istitute State Uiversity, Blacksburg, Virgiia Numerous writers appear to have bee fasciated by the may iterestig summatio idetitites
ADVANCED PROBLEMS AND SOLUTIONS
 ADVANCED PROBLEMS AND SOLUTIONS EDITED BY VERNER E, HOGGATT 9 JR 0, SAN JOSE STATE COLLEGE Sed all commuicatios cocerig Advaced P r o b l e m s ad Solutios to Verer E. Hoggatt, J r., Mathematics Departmet,
ADVANCED PROBLEMS AND SOLUTIONS EDITED BY VERNER E, HOGGATT 9 JR 0, SAN JOSE STATE COLLEGE Sed all commuicatios cocerig Advaced P r o b l e m s ad Solutios to Verer E. Hoggatt, J r., Mathematics Departmet,
GENERATING IDENTITIES FOR FIBONACCI AND LUCAS TRIPLES
 GENERATING IDENTITIES FOR FIBONACCI AND UCAS TRIPES RODNEY T. HANSEN Motaa State Uiversity, Bozema, Motaa Usig the geeratig fuctios of {F A f ad { x f, + m + m where F ^ _ deotes the ( + m) Fiboacci umber
GENERATING IDENTITIES FOR FIBONACCI AND UCAS TRIPES RODNEY T. HANSEN Motaa State Uiversity, Bozema, Motaa Usig the geeratig fuctios of {F A f ad { x f, + m + m where F ^ _ deotes the ( + m) Fiboacci umber
Send all communications regarding Elementary P r o b l e m s and Solutions to P r o f e s s o r A. P. Hillman, Mathematics Department,
 ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A.P. HILLMAN Uiversity of Sata Clara, Sata Clara, Califoria Sed all commuicatios regardig Elemetary P r o b l e m s ad Solutios to P r o f e s s o r A. P. Hillma,
ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A.P. HILLMAN Uiversity of Sata Clara, Sata Clara, Califoria Sed all commuicatios regardig Elemetary P r o b l e m s ad Solutios to P r o f e s s o r A. P. Hillma,
Hoggatt and King [lo] defined a complete sequence of natural numbers
![Hoggatt and King [lo] defined a complete sequence of natural numbers Hoggatt and King [lo] defined a complete sequence of natural numbers](/thumbs/96/128001016.jpg) REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
SOME FIBONACCI AND LUCAS IDENTITIES. L. CARLITZ Dyke University, Durham, North Carolina and H. H. FERNS Victoria, B. C, Canada
 SOME FIBONACCI AND LUCAS IDENTITIES L. CARLITZ Dyke Uiversity, Durham, North Carolia ad H. H. FERNS Victoria, B. C, Caada 1. I the usual otatio, put (1.1) F _
SOME FIBONACCI AND LUCAS IDENTITIES L. CARLITZ Dyke Uiversity, Durham, North Carolia ad H. H. FERNS Victoria, B. C, Caada 1. I the usual otatio, put (1.1) F _
DIVISIBILITY PROPERTIES OF GENERALIZED FIBONACCI POLYNOMIALS
 DIVISIBILITY PROPERTIES OF GENERALIZED FIBONACCI POLYNOMIALS VERNER E. HOGGATT, JR. Sa Jose State Uiversity, Sa Jose, Califoria 95192 ad CALVIN T. LONG Washigto State Uiversity, Pullma, Washigto 99163
DIVISIBILITY PROPERTIES OF GENERALIZED FIBONACCI POLYNOMIALS VERNER E. HOGGATT, JR. Sa Jose State Uiversity, Sa Jose, Califoria 95192 ad CALVIN T. LONG Washigto State Uiversity, Pullma, Washigto 99163
ADVANCED PROBLEMS AND SOLUTIONS
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E. WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all couicatios cocerig Advaced Probles ad Solutios to Rayod E. Whitey, Matheatics Departet,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E. WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all couicatios cocerig Advaced Probles ad Solutios to Rayod E. Whitey, Matheatics Departet,
ANOTHER GENERALIZED FIBONACCI SEQUENCE 1. INTRODUCTION
 ANOTHER GENERALIZED FIBONACCI SEQUENCE MARCELLUS E. WADDILL A N D LOUIS SACKS Wake Forest College, Wisto Salem, N. C., ad Uiversity of ittsburgh, ittsburgh, a. 1. INTRODUCTION Recet issues of umerous periodicals
ANOTHER GENERALIZED FIBONACCI SEQUENCE MARCELLUS E. WADDILL A N D LOUIS SACKS Wake Forest College, Wisto Salem, N. C., ad Uiversity of ittsburgh, ittsburgh, a. 1. INTRODUCTION Recet issues of umerous periodicals
Worksheet on Generating Functions
 Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A. P. H1LLMAN Uiversity of New Mexico, Albuquerque, New Mex. Sed all commuicatios regardig Elemetary Problems ad Solutios to Professor A* P. Hillma, Departmet
ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A. P. H1LLMAN Uiversity of New Mexico, Albuquerque, New Mex. Sed all commuicatios regardig Elemetary Problems ad Solutios to Professor A* P. Hillma, Departmet
~W I F
 A FIBONACCI PROPERTY OF WYTHOFF PAIRS ROBERT SILBER North Carolia State Uiversity, Raleigh, North Carolia 27607 I this paper we poit out aother of those fasciatig "coicideces" which are so characteristically
A FIBONACCI PROPERTY OF WYTHOFF PAIRS ROBERT SILBER North Carolia State Uiversity, Raleigh, North Carolia 27607 I this paper we poit out aother of those fasciatig "coicideces" which are so characteristically
LINEAR RECURSION RELATIONS - LESSON FOUR SECOND-ORDER LINEAR RECURSION RELATIONS
 LINEAR RECURSION RELATIONS - LESSON FOUR SECOND-ORDER LINEAR RECURSION RELATIONS BROTHER ALFRED BROUSSEAU St. Mary's College, Califoria Give a secod-order liear recursio relatio (.1) T. 1 = a T + b T 1,
LINEAR RECURSION RELATIONS - LESSON FOUR SECOND-ORDER LINEAR RECURSION RELATIONS BROTHER ALFRED BROUSSEAU St. Mary's College, Califoria Give a secod-order liear recursio relatio (.1) T. 1 = a T + b T 1,
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
SOME RESULTS ON FIBONACCI QUATERNIONS MUTHULAKSHMI R. IYER Indian Statistical Institute, Calcutta, India
 SOME RESULTS ON FIBONACCI QUATERNIONS MUTHULAKSHMI R. IYER Idia Statistical Istitute, Calcutta, Idia 1. INTRODUCTION Recetly the author derived some results about geeralized Fiboacci Numbers [3J. I the
SOME RESULTS ON FIBONACCI QUATERNIONS MUTHULAKSHMI R. IYER Idia Statistical Istitute, Calcutta, Idia 1. INTRODUCTION Recetly the author derived some results about geeralized Fiboacci Numbers [3J. I the
Interesting Series Associated with Central Binomial Coefficients, Catalan Numbers and Harmonic Numbers
 3 47 6 3 Joural of Iteger Sequeces Vol. 9 06 Article 6.. Iterestig Series Associated with Cetral Biomial Coefficiets Catala Numbers ad Harmoic Numbers Hogwei Che Departmet of Mathematics Christopher Newport
3 47 6 3 Joural of Iteger Sequeces Vol. 9 06 Article 6.. Iterestig Series Associated with Cetral Biomial Coefficiets Catala Numbers ad Harmoic Numbers Hogwei Che Departmet of Mathematics Christopher Newport
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS. Mircea Merca
 Idia J Pure Appl Math 45): 75-89 February 204 c Idia Natioal Sciece Academy A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS Mircea Merca Departmet of Mathematics Uiversity
Idia J Pure Appl Math 45): 75-89 February 204 c Idia Natioal Sciece Academy A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS Mircea Merca Departmet of Mathematics Uiversity
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A. P. HILLMAN Uiversity of Sata Clara, Sata Clara, Califoria Sed a l l c o m m u i c a t i o s r e g a r d i g E l e m e t a r y P r o b l e m s a d S o l u
ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A. P. HILLMAN Uiversity of Sata Clara, Sata Clara, Califoria Sed a l l c o m m u i c a t i o s r e g a r d i g E l e m e t a r y P r o b l e m s a d S o l u
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
The r-generalized Fibonacci Numbers and Polynomial Coefficients
 It. J. Cotemp. Math. Scieces, Vol. 3, 2008, o. 24, 1157-1163 The r-geeralized Fiboacci Numbers ad Polyomial Coefficiets Matthias Schork Camillo-Sitte-Weg 25 60488 Frakfurt, Germay mschork@member.ams.org,
It. J. Cotemp. Math. Scieces, Vol. 3, 2008, o. 24, 1157-1163 The r-geeralized Fiboacci Numbers ad Polyomial Coefficiets Matthias Schork Camillo-Sitte-Weg 25 60488 Frakfurt, Germay mschork@member.ams.org,
On Infinite Series Involving Fibonacci Numbers
 Iteratioal Joural of Cotemporary Mathematical Scieces Vol. 10, 015, o. 8, 363-379 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/ijcms.015.594 O Ifiite Series Ivolvig Fiboacci Numbers Robert Frotczak
Iteratioal Joural of Cotemporary Mathematical Scieces Vol. 10, 015, o. 8, 363-379 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/ijcms.015.594 O Ifiite Series Ivolvig Fiboacci Numbers Robert Frotczak
GAMALIEL CERDA-MORALES 1. Blanco Viel 596, Valparaíso, Chile. s: /
 THE GELIN-CESÀRO IDENTITY IN SOME THIRD-ORDER JACOBSTHAL SEQUENCES arxiv:1810.08863v1 [math.co] 20 Oct 2018 GAMALIEL CERDA-MORALES 1 1 Istituto de Matemáticas Potificia Uiversidad Católica de Valparaíso
THE GELIN-CESÀRO IDENTITY IN SOME THIRD-ORDER JACOBSTHAL SEQUENCES arxiv:1810.08863v1 [math.co] 20 Oct 2018 GAMALIEL CERDA-MORALES 1 1 Istituto de Matemáticas Potificia Uiversidad Católica de Valparaíso
SOME TRIBONACCI IDENTITIES
 Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
Applied Mathematics Letters. On the properties of Lucas numbers with binomial coefficients
 Applied Mathematics Letters 3 (1 68 7 Cotets lists available at ScieceDirect Applied Mathematics Letters joural homepage: wwwelseviercom/locate/aml O the properties of Lucas umbers with biomial coefficiets
Applied Mathematics Letters 3 (1 68 7 Cotets lists available at ScieceDirect Applied Mathematics Letters joural homepage: wwwelseviercom/locate/aml O the properties of Lucas umbers with biomial coefficiets
Sequences, Sums, and Products
 CSCE 222 Discrete Structures for Computig Sequeces, Sums, ad Products Dr. Philip C. Ritchey Sequeces A sequece is a fuctio from a subset of the itegers to a set S. A discrete structure used to represet
CSCE 222 Discrete Structures for Computig Sequeces, Sums, ad Products Dr. Philip C. Ritchey Sequeces A sequece is a fuctio from a subset of the itegers to a set S. A discrete structure used to represet
Lecture 2.5: Sequences
 Lecture.5: Sequeces CS 50, Discrete Structures, Fall 015 Nitesh Saxea Adopted from previous lectures by Zeph Gruschlag Course Admi HW posted Covers Chapter Due Oct 0 (Tue) Mid Term 1: Oct 15 (Thursday)
Lecture.5: Sequeces CS 50, Discrete Structures, Fall 015 Nitesh Saxea Adopted from previous lectures by Zeph Gruschlag Course Admi HW posted Covers Chapter Due Oct 0 (Tue) Mid Term 1: Oct 15 (Thursday)
SOME DOUBLE BINOMIAL SUMS RELATED WITH THE FIBONACCI, PELL AND GENERALIZED ORDER-k FIBONACCI NUMBERS
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 43 Number 3 013 SOME DOUBLE BINOMIAL SUMS RELATED WITH THE FIBONACCI PELL AND GENERALIZED ORDER-k FIBONACCI NUMBERS EMRAH KILIÇ AND HELMUT PRODINGER ABSTRACT
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 43 Number 3 013 SOME DOUBLE BINOMIAL SUMS RELATED WITH THE FIBONACCI PELL AND GENERALIZED ORDER-k FIBONACCI NUMBERS EMRAH KILIÇ AND HELMUT PRODINGER ABSTRACT
GENERALIZATIONS OF ZECKENDORFS THEOREM. TilVIOTHY J. KELLER Student, Harvey Mudd College, Claremont, California
 GENERALIZATIONS OF ZECKENDORFS THEOREM TilVIOTHY J. KELLER Studet, Harvey Mudd College, Claremot, Califoria 91711 The Fiboacci umbers F are defied by the recurrece relatio Fi = F 2 = 1, F = F - + F 0 (
GENERALIZATIONS OF ZECKENDORFS THEOREM TilVIOTHY J. KELLER Studet, Harvey Mudd College, Claremot, Califoria 91711 The Fiboacci umbers F are defied by the recurrece relatio Fi = F 2 = 1, F = F - + F 0 (
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A. P. H1LLMASM Uiversity of Mew Mexico, Albuquerque, New Mexico Sed all commuicatios regardig Elemetary Problems ad Solutios to Professor A. P. Hillma, Departmet
ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A. P. H1LLMASM Uiversity of Mew Mexico, Albuquerque, New Mexico Sed all commuicatios regardig Elemetary Problems ad Solutios to Professor A. P. Hillma, Departmet
ADVANCED PROBLEMS AND SOLUTIONS
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYIVIOWDE. WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Eaymod E D Whitey, Mathematics Departmet,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYIVIOWDE. WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Eaymod E D Whitey, Mathematics Departmet,
Precalculus MATH Sections 3.1, 3.2, 3.3. Exponential, Logistic and Logarithmic Functions
 Precalculus MATH 2412 Sectios 3.1, 3.2, 3.3 Epoetial, Logistic ad Logarithmic Fuctios Epoetial fuctios are used i umerous applicatios coverig may fields of study. They are probably the most importat group
Precalculus MATH 2412 Sectios 3.1, 3.2, 3.3 Epoetial, Logistic ad Logarithmic Fuctios Epoetial fuctios are used i umerous applicatios coverig may fields of study. They are probably the most importat group
SOLUTIONS TO EXAM 3. Solution: Note that this defines two convergent geometric series with respective radii r 1 = 2/5 < 1 and r 2 = 1/5 < 1.
 SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
Matrix representations of Fibonacci-like sequences
 NTMSCI 6, No. 4, 03-0 08 03 New Treds i Mathematical Scieces http://dx.doi.org/0.085/tmsci.09.33 Matrix represetatios of Fiboacci-like sequeces Yasemi Tasyurdu Departmet of Mathematics, Faculty of Sciece
NTMSCI 6, No. 4, 03-0 08 03 New Treds i Mathematical Scieces http://dx.doi.org/0.085/tmsci.09.33 Matrix represetatios of Fiboacci-like sequeces Yasemi Tasyurdu Departmet of Mathematics, Faculty of Sciece
Section 1 of Unit 03 (Pure Mathematics 3) Algebra
 Sectio 1 of Uit 0 (Pure Mathematics ) Algebra Recommeded Prior Kowledge Studets should have studied the algebraic techiques i Pure Mathematics 1. Cotet This Sectio should be studied early i the course
Sectio 1 of Uit 0 (Pure Mathematics ) Algebra Recommeded Prior Kowledge Studets should have studied the algebraic techiques i Pure Mathematics 1. Cotet This Sectio should be studied early i the course
THE DYING RABBIT PROBLEM. V. E. HOGGATT, JR., and D. A. LIIMD San Jose State College, San Jose, Calif., and University of Cambridge, England
 THE DYING RABBIT PROBLEM V. E. HOGGATT, JR., ad D. A. LIIMD Sa Jose State College, Sa Jose, Calif., ad Uiversity of Cambridge, Eglad 1. INTRODUCTION Fiboacci umbers origially arose i the aswer to the followig
THE DYING RABBIT PROBLEM V. E. HOGGATT, JR., ad D. A. LIIMD Sa Jose State College, Sa Jose, Calif., ad Uiversity of Cambridge, Eglad 1. INTRODUCTION Fiboacci umbers origially arose i the aswer to the followig
On the Inverse of a Certain Matrix Involving Binomial Coefficients
 It. J. Cotemp. Math. Scieces, Vol. 3, 008, o. 3, 5-56 O the Iverse of a Certai Matrix Ivolvig Biomial Coefficiets Yoshiari Iaba Kitakuwada Seior High School Keihokushimoyuge, Ukyo-ku, Kyoto, 60-0534, Japa
It. J. Cotemp. Math. Scieces, Vol. 3, 008, o. 3, 5-56 O the Iverse of a Certai Matrix Ivolvig Biomial Coefficiets Yoshiari Iaba Kitakuwada Seior High School Keihokushimoyuge, Ukyo-ku, Kyoto, 60-0534, Japa
... and realizing that as n goes to infinity the two integrals should be equal. This yields the Wallis result-
 INFINITE PRODUTS Oe defies a ifiite product as- F F F... F x [ F ] Takig the atural logarithm of each side oe has- l[ F x] l F l F l F l F... So that the iitial ifiite product will coverge oly if the sum
INFINITE PRODUTS Oe defies a ifiite product as- F F F... F x [ F ] Takig the atural logarithm of each side oe has- l[ F x] l F l F l F l F... So that the iitial ifiite product will coverge oly if the sum
ECE-S352 Introduction to Digital Signal Processing Lecture 3A Direct Solution of Difference Equations
 ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
BESSEL EQUATION and BESSEL FUNCTIONS
 BESSEL EQUATION ad BESSEL FUNCTIONS Bessel s Equatio Summary of Bessel Fuctios d y dy y d + d + =. If is a iteger, the two idepedet solutios of Bessel s Equatio are J J, Bessel fuctio of the first kid,
BESSEL EQUATION ad BESSEL FUNCTIONS Bessel s Equatio Summary of Bessel Fuctios d y dy y d + d + =. If is a iteger, the two idepedet solutios of Bessel s Equatio are J J, Bessel fuctio of the first kid,
On the Jacobsthal-Lucas Numbers by Matrix Method 1
 It J Cotemp Math Scieces, Vol 3, 2008, o 33, 1629-1633 O the Jacobsthal-Lucas Numbers by Matrix Method 1 Fikri Köke ad Durmuş Bozkurt Selçuk Uiversity, Faculty of Art ad Sciece Departmet of Mathematics,
It J Cotemp Math Scieces, Vol 3, 2008, o 33, 1629-1633 O the Jacobsthal-Lucas Numbers by Matrix Method 1 Fikri Köke ad Durmuş Bozkurt Selçuk Uiversity, Faculty of Art ad Sciece Departmet of Mathematics,
Some Hankel determinants with nice evaluations. Johann Cigler Talk at the occasion of Peter Paule s 60 th birthday
 Some Hakel determiats with ice evaluatios Joha Cigler Talk at the occasio of Peter Paule s 6 th birthday Itroductio For each we cosider the Hakel determiat H ( a ) + = det. i j i, j= We are iterested i
Some Hakel determiats with ice evaluatios Joha Cigler Talk at the occasio of Peter Paule s 6 th birthday Itroductio For each we cosider the Hakel determiat H ( a ) + = det. i j i, j= We are iterested i
(6), (7) and (8) we have easily, if the C's are cancellable elements of S,
 VIOL. 23, 1937 MA THEMA TICS: H. S. VANDIVER 555 where the a's belog to S'. The R is said to be a repetitive set i S, with respect to S', ad with multiplier M. If S cotais a idetity E, the if we set a,
VIOL. 23, 1937 MA THEMA TICS: H. S. VANDIVER 555 where the a's belog to S'. The R is said to be a repetitive set i S, with respect to S', ad with multiplier M. If S cotais a idetity E, the if we set a,
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Mathematics review for CSCI 303 Spring Department of Computer Science College of William & Mary Robert Michael Lewis
 Mathematics review for CSCI 303 Sprig 019 Departmet of Computer Sciece College of William & Mary Robert Michael Lewis Copyright 018 019 Robert Michael Lewis Versio geerated: 13 : 00 Jauary 17, 019 Cotets
Mathematics review for CSCI 303 Sprig 019 Departmet of Computer Sciece College of William & Mary Robert Michael Lewis Copyright 018 019 Robert Michael Lewis Versio geerated: 13 : 00 Jauary 17, 019 Cotets
FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES. 1. Introduction In some recent papers [1, 2, 4, 5, 6], one finds product identities such as.
![FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES. 1. Introduction In some recent papers [1, 2, 4, 5, 6], one finds product identities such as. FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES. 1. Introduction In some recent papers [1, 2, 4, 5, 6], one finds product identities such as.](/thumbs/89/100525310.jpg) FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES MARC CHAMBERLAND Abstract Several product ad sum idetities are established with special cases ivolvig Fiboacci ad Lucas umbers These idetities are derived
FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES MARC CHAMBERLAND Abstract Several product ad sum idetities are established with special cases ivolvig Fiboacci ad Lucas umbers These idetities are derived
FLOOR AND ROOF FUNCTION ANALOGS OF THE BELL NUMBERS. H. W. Gould Department of Mathematics, West Virginia University, Morgantown, WV 26506, USA
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 7 (2007), #A58 FLOOR AND ROOF FUNCTION ANALOGS OF THE BELL NUMBERS H. W. Gould Departmet of Mathematics, West Virgiia Uiversity, Morgatow, WV
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 7 (2007), #A58 FLOOR AND ROOF FUNCTION ANALOGS OF THE BELL NUMBERS H. W. Gould Departmet of Mathematics, West Virgiia Uiversity, Morgatow, WV
A FIBONACCI MATRIX AND THE PERMANENT FUNCTION
 A FIBONACCI MATRIX AND THE PERMANENT FUNCTION BRUCE W. KING Burt Hiils-Ballsto Lake High School, Ballsto Lake, New York ad FRANCIS D. PARKER The St. Lawrece Uiversity, Cato, New York The permaet of a -square
A FIBONACCI MATRIX AND THE PERMANENT FUNCTION BRUCE W. KING Burt Hiils-Ballsto Lake High School, Ballsto Lake, New York ad FRANCIS D. PARKER The St. Lawrece Uiversity, Cato, New York The permaet of a -square
MATH 6101 Fall 2008 Newton and Differential Equations
 MATH 611 Fall 8 Newto ad Differetial Equatios A Differetial Equatio What is a differetial equatio? A differetial equatio is a equatio relatig the quatities x, y ad y' ad possibly higher derivatives of
MATH 611 Fall 8 Newto ad Differetial Equatios A Differetial Equatio What is a differetial equatio? A differetial equatio is a equatio relatig the quatities x, y ad y' ad possibly higher derivatives of
In algebra one spends much time finding common denominators and thus simplifying rational expressions. For example:
 74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
A.1 Algebra Review: Polynomials/Rationals. Definitions:
 MATH 040 Notes: Uit 0 Page 1 A.1 Algera Review: Polyomials/Ratioals Defiitios: A polyomial is a sum of polyomial terms. Polyomial terms are epressios formed y products of costats ad variales with whole
MATH 040 Notes: Uit 0 Page 1 A.1 Algera Review: Polyomials/Ratioals Defiitios: A polyomial is a sum of polyomial terms. Polyomial terms are epressios formed y products of costats ad variales with whole
<aj + ck) m (bj + dk) n. E E (-D m+n - j - k h)(i) j=0 k=0 \ / \ /
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND j=. WHITNEY Loc Have State College Loc Have # Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Raymod E. Whitey, Mathematics Departmet,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND j=. WHITNEY Loc Have State College Loc Have # Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Raymod E. Whitey, Mathematics Departmet,
Chapter 6. Advanced Counting Techniques
 Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
FORMULA DEVELOPMENT THROUGH FINITE DIFFERENCES
 FORMULA DEVELOPMENT THROUGH FINITE DIFFERENCES BROTHER ALFRED BROUSSEAU St. Mary's College, Califoria FINITE DIFFERENCE CONCEPT Give a fuctio f() the first differece of the fuctio is defied Af() = f( +
FORMULA DEVELOPMENT THROUGH FINITE DIFFERENCES BROTHER ALFRED BROUSSEAU St. Mary's College, Califoria FINITE DIFFERENCE CONCEPT Give a fuctio f() the first differece of the fuctio is defied Af() = f( +
k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c 1. Introduction
 Acta Math. Uiv. Comeiaae Vol. LXXXVI, 2 (2017), pp. 279 286 279 k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c N. IRMAK ad M. ALP Abstract. The k-geeralized Fiboacci sequece { F (k)
Acta Math. Uiv. Comeiaae Vol. LXXXVI, 2 (2017), pp. 279 286 279 k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c N. IRMAK ad M. ALP Abstract. The k-geeralized Fiboacci sequece { F (k)
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
On Some Identities and Generating Functions for Mersenne Numbers and Polynomials
 Turish Joural of Aalysis ad Number Theory, 8, Vol 6, No, 9-97 Available olie at htt://ubsscieubcom/tjat/6//5 Sciece ad Educatio Publishig DOI:69/tjat-6--5 O Some Idetities ad Geeratig Fuctios for Mersee
Turish Joural of Aalysis ad Number Theory, 8, Vol 6, No, 9-97 Available olie at htt://ubsscieubcom/tjat/6//5 Sciece ad Educatio Publishig DOI:69/tjat-6--5 O Some Idetities ad Geeratig Fuctios for Mersee
Introductions to HarmonicNumber2
 Itroductios to HarmoicNumber2 Itroductio to the differetiated gamma fuctios Geeral Almost simultaeously with the developmet of the mathematical theory of factorials, biomials, ad gamma fuctios i the 8th
Itroductios to HarmoicNumber2 Itroductio to the differetiated gamma fuctios Geeral Almost simultaeously with the developmet of the mathematical theory of factorials, biomials, ad gamma fuctios i the 8th
Series with Central Binomial Coefficients, Catalan Numbers, and Harmonic Numbers
 3 47 6 3 Joural of Iteger Sequeces, Vol. 5 (0), Article..7 Series with Cetral Biomial Coefficiets, Catala Numbers, ad Harmoic Numbers Khristo N. Boyadzhiev Departmet of Mathematics ad Statistics Ohio Norther
3 47 6 3 Joural of Iteger Sequeces, Vol. 5 (0), Article..7 Series with Cetral Biomial Coefficiets, Catala Numbers, ad Harmoic Numbers Khristo N. Boyadzhiev Departmet of Mathematics ad Statistics Ohio Norther
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
BASIC PROPERTIES OF A CERTAIN GENERALIZED SEQUENCE OF NUMBERS 1. INTRODUCTION. d = (p - 4q) ' p. a= (p +d)/2, P= (p - d)/2
 BASIC PROPERTIES OF A CERTAIN GENERALIZED SEQUENCE OF NUMBERS A. F. HORADAM The Uiversity of North Carolia, Chapel H i l l, N. C. Let a, (3 be the roots of 1. INTRODUCTION (1.1) 2 - p + q = 0 where p,
BASIC PROPERTIES OF A CERTAIN GENERALIZED SEQUENCE OF NUMBERS A. F. HORADAM The Uiversity of North Carolia, Chapel H i l l, N. C. Let a, (3 be the roots of 1. INTRODUCTION (1.1) 2 - p + q = 0 where p,
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Infinite Series and Improper Integrals
 8 Special Fuctios Ifiite Series ad Improper Itegrals Ifiite series are importat i almost all areas of mathematics ad egieerig I additio to umerous other uses, they are used to defie certai fuctios ad to
8 Special Fuctios Ifiite Series ad Improper Itegrals Ifiite series are importat i almost all areas of mathematics ad egieerig I additio to umerous other uses, they are used to defie certai fuctios ad to
Exact Horadam Numbers with a Chebyshevish Accent by Clifford A. Reiter
 Exact Horadam Numbers with a Chebyshevish Accet by Clifford A. Reiter (reiterc@lafayette.edu) A recet paper by Joseph De Kerf illustrated the use of Biet type formulas for computig Horadam umbers [1].
Exact Horadam Numbers with a Chebyshevish Accet by Clifford A. Reiter (reiterc@lafayette.edu) A recet paper by Joseph De Kerf illustrated the use of Biet type formulas for computig Horadam umbers [1].
On Divisibility concerning Binomial Coefficients
 A talk give at the Natioal Chiao Tug Uiversity (Hsichu, Taiwa; August 5, 2010 O Divisibility cocerig Biomial Coefficiets Zhi-Wei Su Najig Uiversity Najig 210093, P. R. Chia zwsu@ju.edu.c http://math.ju.edu.c/
A talk give at the Natioal Chiao Tug Uiversity (Hsichu, Taiwa; August 5, 2010 O Divisibility cocerig Biomial Coefficiets Zhi-Wei Su Najig Uiversity Najig 210093, P. R. Chia zwsu@ju.edu.c http://math.ju.edu.c/
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
ELEMENTARY PROBLEMS AND SOLUTIONS
 ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A.P. HfLLIVSAgy Uiversity of New Mexico, Albuquerque, l\9ew Mexico 87131 Sed ail commuicatios regardig Elemetary Problems to Professor A.P. Hillma; 709 Solao
ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A.P. HfLLIVSAgy Uiversity of New Mexico, Albuquerque, l\9ew Mexico 87131 Sed ail commuicatios regardig Elemetary Problems to Professor A.P. Hillma; 709 Solao
ON THE HADAMARD PRODUCT OF BALANCING Q n B AND BALANCING Q n
 TWMS J App Eg Math V5, N, 015, pp 01-07 ON THE HADAMARD PRODUCT OF ALANCING Q AND ALANCING Q MATRIX MATRIX PRASANTA KUMAR RAY 1, SUJATA SWAIN, Abstract I this paper, the matrix Q Q which is the Hadamard
TWMS J App Eg Math V5, N, 015, pp 01-07 ON THE HADAMARD PRODUCT OF ALANCING Q AND ALANCING Q MATRIX MATRIX PRASANTA KUMAR RAY 1, SUJATA SWAIN, Abstract I this paper, the matrix Q Q which is the Hadamard
Problem Cosider the curve give parametrically as x = si t ad y = + cos t for» t» ß: (a) Describe the path this traverses: Where does it start (whe t =
 Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
arxiv: v1 [math.fa] 3 Apr 2016
![arxiv: v1 [math.fa] 3 Apr 2016 arxiv: v1 [math.fa] 3 Apr 2016](/thumbs/75/72845465.jpg) Aticommutator Norm Formula for Proectio Operators arxiv:164.699v1 math.fa] 3 Apr 16 Sam Walters Uiversity of Norther British Columbia ABSTRACT. We prove that for ay two proectio operators f, g o Hilbert
Aticommutator Norm Formula for Proectio Operators arxiv:164.699v1 math.fa] 3 Apr 16 Sam Walters Uiversity of Norther British Columbia ABSTRACT. We prove that for ay two proectio operators f, g o Hilbert
1. INTRODUCTION. P r e s e n t e d h e r e is a generalization of Fibonacci numbers which is intimately connected with the arithmetic triangle.
 A GENERALIZATION OF FIBONACCI NUMBERS V.C. HARRIS ad CAROLYN C. STYLES Sa Diego State College ad Sa Diego Mesa College, Sa Diego, Califoria 1. INTRODUCTION P r e s e t e d h e r e is a geeralizatio of
A GENERALIZATION OF FIBONACCI NUMBERS V.C. HARRIS ad CAROLYN C. STYLES Sa Diego State College ad Sa Diego Mesa College, Sa Diego, Califoria 1. INTRODUCTION P r e s e t e d h e r e is a geeralizatio of
SEQUENCES AND SERIES
 Sequeces ad 6 Sequeces Ad SEQUENCES AND SERIES Successio of umbers of which oe umber is desigated as the first, other as the secod, aother as the third ad so o gives rise to what is called a sequece. Sequeces
Sequeces ad 6 Sequeces Ad SEQUENCES AND SERIES Successio of umbers of which oe umber is desigated as the first, other as the secod, aother as the third ad so o gives rise to what is called a sequece. Sequeces
The Z-Transform. (t-t 0 ) Figure 1: Simplified graph of an impulse function. For an impulse, it can be shown that (1)
 The Z-Trasform Sampled Data The geeralied fuctio (t) (also kow as the impulse fuctio) is useful i the defiitio ad aalysis of sampled-data sigals. Figure below shows a simplified graph of a impulse. (t-t
The Z-Trasform Sampled Data The geeralied fuctio (t) (also kow as the impulse fuctio) is useful i the defiitio ad aalysis of sampled-data sigals. Figure below shows a simplified graph of a impulse. (t-t
( ) ( ) ( ) ( ) ( + ) ( )
 LSM Nov. 00 Cotet List Mathematics (AH). Algebra... kow ad use the otatio!, C r ad r.. kow the results = r r + + = r r r..3 kow Pascal's triagle. Pascal's triagle should be eteded up to = 7...4 kow ad
LSM Nov. 00 Cotet List Mathematics (AH). Algebra... kow ad use the otatio!, C r ad r.. kow the results = r r + + = r r r..3 kow Pascal's triagle. Pascal's triagle should be eteded up to = 7...4 kow ad
ELEMENTARY PROBLEMS AND SOLUTIONS. Edited by Stanley Rabinowitz
 Edited by Staley Rabiowitz Please submit all ew problem proposals ad correspodig solutios to the Problems Editor, DR. RUSS EULER, Departmet of Mathematics ad Statistics, Missouri State Uiversity, 800 Uiversity
Edited by Staley Rabiowitz Please submit all ew problem proposals ad correspodig solutios to the Problems Editor, DR. RUSS EULER, Departmet of Mathematics ad Statistics, Missouri State Uiversity, 800 Uiversity
NAME: ALGEBRA 350 BLOCK 7. Simplifying Radicals Packet PART 1: ROOTS
 NAME: ALGEBRA 50 BLOCK 7 DATE: Simplifyig Radicals Packet PART 1: ROOTS READ: A square root of a umber b is a solutio of the equatio x = b. Every positive umber b has two square roots, deoted b ad b or
NAME: ALGEBRA 50 BLOCK 7 DATE: Simplifyig Radicals Packet PART 1: ROOTS READ: A square root of a umber b is a solutio of the equatio x = b. Every positive umber b has two square roots, deoted b ad b or
The Binet formula, sums and representations of generalized Fibonacci p-numbers
 Europea Joural of Combiatorics 9 (008) 70 7 wwwelseviercom/locate/ec The Biet formula, sums ad represetatios of geeralized Fiboacci p-umbers Emrah Kilic TOBB ETU Uiversity of Ecoomics ad Techology, Mathematics
Europea Joural of Combiatorics 9 (008) 70 7 wwwelseviercom/locate/ec The Biet formula, sums ad represetatios of geeralized Fiboacci p-umbers Emrah Kilic TOBB ETU Uiversity of Ecoomics ad Techology, Mathematics
Frequency Domain Filtering
 Frequecy Domai Filterig Raga Rodrigo October 19, 2010 Outlie Cotets 1 Itroductio 1 2 Fourier Represetatio of Fiite-Duratio Sequeces: The Discrete Fourier Trasform 1 3 The 2-D Discrete Fourier Trasform
Frequecy Domai Filterig Raga Rodrigo October 19, 2010 Outlie Cotets 1 Itroductio 1 2 Fourier Represetatio of Fiite-Duratio Sequeces: The Discrete Fourier Trasform 1 3 The 2-D Discrete Fourier Trasform
CALCULATING FIBONACCI VECTORS
 THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A.P. HILLMAN University of Santa Clara, Santa Clara, California
 ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A.P. HILLMAN Uiversity of Sata Clara, Sata Clara, Califoria ' Sed all commuicatios regardig E l e m e t a r y P r o b l e m s ad Solutios to Professor A. P.
ELEMENTARY PROBLEMS AND SOLUTIONS Edited by A.P. HILLMAN Uiversity of Sata Clara, Sata Clara, Califoria ' Sed all commuicatios regardig E l e m e t a r y P r o b l e m s ad Solutios to Professor A. P.
ON THE PARTITION OF HORADAM'S GENERALIZED SEQUENCES INTO GENERALIZED FIBONACCI AND GENERALIZED LUCAS SEQUENCES
 ON THE PARTITION OF HORADAM'S GENERALIZED SEQUENCES INTO GENERALIZED FIBONACCI AND GENERALIZED LUCAS SEQUENCES A. J. W.HILTON The Uiversity of Readig, Readig, Eglad 1. INTRODUCTION If p,q are itegers,
ON THE PARTITION OF HORADAM'S GENERALIZED SEQUENCES INTO GENERALIZED FIBONACCI AND GENERALIZED LUCAS SEQUENCES A. J. W.HILTON The Uiversity of Readig, Readig, Eglad 1. INTRODUCTION If p,q are itegers,
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES
 SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
1/(1 -x n ) = \YJ k=0
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E.WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Eaymod E. Whitey, Mathematics Departmet,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E.WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Eaymod E. Whitey, Mathematics Departmet,
, 4 is the second term U 2
 Balliteer Istitute 995-00 wwwleavigcertsolutioscom Leavig Cert Higher Maths Sequeces ad Series A sequece is a array of elemets seperated by commas E,,7,0,, The elemets are called the terms of the sequece
Balliteer Istitute 995-00 wwwleavigcertsolutioscom Leavig Cert Higher Maths Sequeces ad Series A sequece is a array of elemets seperated by commas E,,7,0,, The elemets are called the terms of the sequece
CONVERGENCE OF THE COEFRCIENTS IN A RECURRING POWER SERIES JOSEPH ARK IN Nanuet, New York 1. INTRODUCTION. In this paper we use the following notation
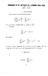 CONVERGENCE OF THE COEFRCIENTS IN A RECURRING POWER SERIES JOSEPH ARK IN Nauet, Ne York 1. INTRODUCTION I this paper e use the folloig otatio oo \ k oo 1 \ ^ (k) 1 _ X c x Ev* -E k = / = (For coveiece,
CONVERGENCE OF THE COEFRCIENTS IN A RECURRING POWER SERIES JOSEPH ARK IN Nauet, Ne York 1. INTRODUCTION I this paper e use the folloig otatio oo \ k oo 1 \ ^ (k) 1 _ X c x Ev* -E k = / = (For coveiece,
and each factor on the right is clearly greater than 1. which is a contradiction, so n must be prime.
 MATH 324 Summer 200 Elemetary Number Theory Solutios to Assigmet 2 Due: Wedesday July 2, 200 Questio [p 74 #6] Show that o iteger of the form 3 + is a prime, other tha 2 = 3 + Solutio: If 3 + is a prime,
MATH 324 Summer 200 Elemetary Number Theory Solutios to Assigmet 2 Due: Wedesday July 2, 200 Questio [p 74 #6] Show that o iteger of the form 3 + is a prime, other tha 2 = 3 + Solutio: If 3 + is a prime,
Problem. Consider the sequence a j for j N defined by the recurrence a j+1 = 2a j + j for j > 0
 GENERATING FUNCTIONS Give a ifiite sequece a 0,a,a,, its ordiary geeratig fuctio is A : a Geeratig fuctios are ofte useful for fidig a closed forula for the eleets of a sequece, fidig a recurrece forula,
GENERATING FUNCTIONS Give a ifiite sequece a 0,a,a,, its ordiary geeratig fuctio is A : a Geeratig fuctios are ofte useful for fidig a closed forula for the eleets of a sequece, fidig a recurrece forula,
A Mean Paradox. John Konvalina, Jack Heidel, and Jim Rogers. Department of Mathematics University of Nebraska at Omaha Omaha, NE USA
 A Mea Paradox by Joh Kovalia, Jac Heidel, ad Jim Rogers Departmet of Mathematics Uiversity of Nebrasa at Omaha Omaha, NE 6882-243 USA Phoe: (42) 554-2836 Fax: (42) 554-2975 E-mail: joho@uomaha.edu A Mea
A Mea Paradox by Joh Kovalia, Jac Heidel, ad Jim Rogers Departmet of Mathematics Uiversity of Nebrasa at Omaha Omaha, NE 6882-243 USA Phoe: (42) 554-2836 Fax: (42) 554-2975 E-mail: joho@uomaha.edu A Mea
arxiv: v1 [math.nt] 5 Jan 2017 IBRAHIM M. ALABDULMOHSIN
![arxiv: v1 [math.nt] 5 Jan 2017 IBRAHIM M. ALABDULMOHSIN arxiv: v1 [math.nt] 5 Jan 2017 IBRAHIM M. ALABDULMOHSIN](/thumbs/89/98516099.jpg) FRACTIONAL PARTS AND THEIR RELATIONS TO THE VALUES OF THE RIEMANN ZETA FUNCTION arxiv:70.04883v [math.nt 5 Ja 07 IBRAHIM M. ALABDULMOHSIN Kig Abdullah Uiversity of Sciece ad Techology (KAUST, Computer,
FRACTIONAL PARTS AND THEIR RELATIONS TO THE VALUES OF THE RIEMANN ZETA FUNCTION arxiv:70.04883v [math.nt 5 Ja 07 IBRAHIM M. ALABDULMOHSIN Kig Abdullah Uiversity of Sciece ad Techology (KAUST, Computer,
FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES. In some recent papers [1], [2], [4], [5], [6], one finds product identities such as. 2cos.
![FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES. In some recent papers [1], [2], [4], [5], [6], one finds product identities such as. 2cos. FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES. In some recent papers [1], [2], [4], [5], [6], one finds product identities such as. 2cos.](/thumbs/82/85697284.jpg) FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES MARC CHAMBERLAND Abstract. Several product ad sum idetities are established with special cases ivolvig Fiboacci ad Lucas umbers. These idetities are derived
FINITE TRIGONOMETRIC PRODUCT AND SUM IDENTITIES MARC CHAMBERLAND Abstract. Several product ad sum idetities are established with special cases ivolvig Fiboacci ad Lucas umbers. These idetities are derived
2.4 - Sequences and Series
 2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
arxiv: v1 [math.lo] 2 Jun 2015
![arxiv: v1 [math.lo] 2 Jun 2015 arxiv: v1 [math.lo] 2 Jun 2015](/thumbs/92/108241802.jpg) Mathematical Structures defied by Idetities III Costati M. Petridi cpetridi@math.uoa.gr cpetridi@hotmail.com arxiv:1506.00798v1 [math.lo] 2 Ju 2015 1 Itroductio Abstract.We exted the theory (formal part
Mathematical Structures defied by Idetities III Costati M. Petridi cpetridi@math.uoa.gr cpetridi@hotmail.com arxiv:1506.00798v1 [math.lo] 2 Ju 2015 1 Itroductio Abstract.We exted the theory (formal part
Subject: Differential Equations & Mathematical Modeling-III
 Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
NICK DUFRESNE. 1 1 p(x). To determine some formulas for the generating function of the Schröder numbers, r(x) = a(x) =
 AN INTRODUCTION TO SCHRÖDER AND UNKNOWN NUMBERS NICK DUFRESNE Abstract. I this article we will itroduce two types of lattice paths, Schröder paths ad Ukow paths. We will examie differet properties of each,
AN INTRODUCTION TO SCHRÖDER AND UNKNOWN NUMBERS NICK DUFRESNE Abstract. I this article we will itroduce two types of lattice paths, Schröder paths ad Ukow paths. We will examie differet properties of each,
Mathematical Series (You Should Know)
 Mathematical Series You Should Kow Mathematical series represetatios are very useful tools for describig images or for solvig/approimatig the solutios to imagig problems. The may be used to epad a fuctio
Mathematical Series You Should Kow Mathematical series represetatios are very useful tools for describig images or for solvig/approimatig the solutios to imagig problems. The may be used to epad a fuctio
COMPUTING SUMS AND THE AVERAGE VALUE OF THE DIVISOR FUNCTION (x 1) + x = n = n.
 COMPUTING SUMS AND THE AVERAGE VALUE OF THE DIVISOR FUNCTION Abstract. We itroduce a method for computig sums of the form f( where f( is ice. We apply this method to study the average value of d(, where
COMPUTING SUMS AND THE AVERAGE VALUE OF THE DIVISOR FUNCTION Abstract. We itroduce a method for computig sums of the form f( where f( is ice. We apply this method to study the average value of d(, where
September 2012 C1 Note. C1 Notes (Edexcel) Copyright - For AS, A2 notes and IGCSE / GCSE worksheets 1
 September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
Most text will write ordinary derivatives using either Leibniz notation 2 3. y + 5y= e and y y. xx tt t
 Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
