Solutions for Math 348 Assignment #4 1
|
|
|
- Edward Dennis
- 5 years ago
- Views:
Transcription
1 Solutions for Math 348 Assignment #4 1 (1) Do the following: (a) Show that the intersection of two spheres S 1 = {(x, y, z) : (x x 1 ) 2 + (y y 1 ) 2 + (z z 1 ) 2 = r 2 1} S 2 = {(x, y, z) : (x x 2 ) 2 + (y y 2 ) 2 + (z z 2 ) 2 = r 2 2} in R 3 is a curve with constant positive curvature and zero torsion, assuming that S 1 and S 2 meet at more than one point and S 1 S 2. (b) Show that a smooth curve γ : I R 3 has constant positive curvature and zero torsion if and only if γ(i) is contained in a circle. Proof. For (a), note that S 1 S 2 = {(x, y, z) :(x x 1 ) 2 + (y y 1 ) 2 + (z z 1 ) 2 = r 2 1, 2(x 2 x 1 )x + 2(y 2 y 1 )y + 2(z 2 z 1 )z = (r 2 1 r 2 2) (x y z 2 1) + (x y z 2 2)} is contained in a plane. So it has torsion 0. Since the curvature of a curve is invariant under isometry, we may use a translation to move (x 1, y 1, z 1 ) to the origin. That is, we assume that x 1 = y 1 = z 1 = 0. Let u = (x 2 x 1, y 2 y 1, z 2 z 1 ). Using Gram-Schmidt, we may expand {u/ u } to an orthonormal basis of R 3. That is, we have an orthogonal matrix A whose first column is u/ u. Let f : R 3 R 3 be the orthogonal transformation given by f(v) = A 1 v. So f(u) = ( u, 0, 0) and f(s 1 S 2 ) is { x 2 + y 2 + z 2 = r 2 1 (x u ) 2 + y 2 + z 2 = r 2 2 x = r2 1 r u 2 2 u = a y 2 + z 2 = ((r 1 + r 2 ) 2 u 2 )( u 2 (r 1 r 2 ) 2 ) = b 2 4 u 2 x = a y = b cos t z = b sin t 1 xichen/math34815f/hw4sol.pdf 1
2 2 which has constant curvature 1/b. For (b), it is obvious that a circle in R 3 has constant nonzero curvature and zero torsion. On the other hand, let γ be a curve parameterized by its arc length with constant curvature k > 0 and torsion zero. Note that the curve α : I R given by ( cos(ks) α(s) = k, sin(ks), 0 k has curvature k and torsion 0. By the Fundamental Theorem of the Local Theory of Curves, there exists an isometry f : R 3 R 3 such that γ = f α. Therefore, γ(i) is contained in a circle. (2) Find the curvature and torsion of the curve γ : R R 3 given by γ(t) = (t, t 2, t 3 ) and write down the Frenet equations associated to γ. Solution. The curvature and torsion of γ are κ = γ γ γ 3 = t 2 + 9t 4 (1 + 4t 2 + 9t 4 ) 3/2 τ = det [ γ γ γ ] γ γ 2 ) = (1, 2t, 3t2 ) (0, 2, 6t) (1, 2t, 3t 2 ) 3 3 = 1 + 9t 2 + 9t 4 respectively. So the Frenet-Serret equations associated to γ are d T N = γ T N dt B B t 2 +9t t 2 +9t 4 = 2 1+9t 2 +9t t 2 +9t 4 1+4t 2 +9t 4 1+9t 2 +9t T N t 2 +9t 4 0 B 1+9t 2 +9t 4 (3) (MPDC p. 25 Ex. 13) Let α : I R 3 be a regular smooth curve parameterized by its arc length satisfying that κ(s) 0, τ(s) 0 and κ (s) 0. Show that α(i) lies on a sphere if and only if R 2 + (R ) 2 T 2 c
3 for some constant c R, where R = 1/κ, T = 1/τ and R is the derivative of R with respect to s. Proof. Let e 1, e 2, e 3 be the unit tangent, normal and binormal vectors of α, respectively. Note that α(i) lies on a sphere if and only if there exists p R 3 such that α(s) p 2 const d ( ) α(s) p 2 0 ds (α(s) p).α (s) 0 (α(s) p).e 1 (s) 0 α(s) p f(s)e 2 (s) + g(s)e 3 (s) α (s) (f(s)e 2 (s) + g(s)e 3 (s)) e 1 (s) (f(s)e 2 (s) + g(s)e 3 (s)) for some smooth functions f and g on I. So α(i) lies on a sphere if and only if e 1 = f e 2 + g e 3 + fe 2 + ge 3 on I for some smooth functions f, g : I R. By Frenet-Serret equations, e 1 e 2 = 0 κ 0 κ 0 τ e 1 e 2 0 τ 0 we have e 3 e 1 = f e 2 + g e 3 + fe 2 + ge 3 e 1 = f e 2 + g e 3 + ( fκe 1 fτe 3 ) + gτe 2 e 3 3 on I. e 1 = fκe 1 + (f + gτ)e 2 + (g fτ)e 3 1 = fκ 1 = fκ 0 = f ( ) + gτ f 0 = g = fτ = g fτ τ 1 ( ( ) ) 1 1 κ τ = R = T (T R ) τ κ RR = T R (T R ) (R 2 ) = ((T R ) 2 ) R 2 + (R ) 2 T 2 const
4 4 (4) (MPDC p. 25 Ex. 14) Let α : I R 2 be a regular smooth curve and p be a fixed point in R 2. Suppose that α(t) p achieves a local maximum at a point t 0 I. Show that κ(t 0 ) 1 α(t 0 ) p. Proof. Suppose that α is parameterized by its arc length. Let f(t) = α(t) p 2. Since f(t) has a local maximum at t 0, f (t 0 ) = 0 and f (t 0 ) 0. Therefore, f (t 0 ) = 0 2(α(t 0 ) p).α (t 0 ) = 0 (α(t 0 ) p).α (t 0 ) = 0 f (t 0 ) 0 α (t 0 ).α (t 0 ) + (α(t 0 ) p).α (t 0 ) (α(t 0 ) p).α (t 0 ) 0. Since both α (t 0 ) and α(t 0 ) p are orthogonal to α (t 0 ), they are linearly dependent. So (α(t 0 ) p).α (t 0 ) = ± α(t 0 ) p α (t 0 ). And since (α(t 0 ) p).α (t 0 ) 1 < 0, we must have and (α(t 0 ) p).α (t 0 ) = α(t 0 ) p α (t 0 ) 1 + (α(t 0 ) p).α (t 0 ) 0 1 α(t 0 ) p α (t 0 ) 0 κ(t 0 ) = α 1 (t 0 ) α(t 0 ) p. (5) Let α : I R 3 and β : I R 3 be two regular smooth curves with nowhere vanishing curvatures and satisfying α(t) β(t) for all t I. Show that the osculating planes of α and β agree for all t I if and only if both α(i) and β(i) lie in the same plane. Proof. Clearly, if α(i) and β(i) lie in the same plane Λ, Λ is the osculating plane of α and β for all t I and hence they have the same osculating planes for all t I. Suppose that α and β have the same osculating planes for all t I. At t 0 I, the osculating planes of α and β are
5 5 parameterized by x y = α(t 0 ) + s 1 α (t 0 ) + s 2 α (t 0 ) and z x y = β(t 0 ) + s 1 β (t 0 ) + s 2 β (t 0 ) z respectively. So they agree if and only if α(t 0 ) β(t 0 ), α (t 0 ), α (t 0 ) Span{β (t 0 ), β (t 0 )}. Therefore, α and β have the same osculating planes for all t if and only if α = β + f 12 β + f 13 β α = + f 22 β + f 23 β α = + f 32 β + f 33 β on I for some smooth functions f ij. It follows that α = (β + f 12 β + f 13 β ) = f 22 β + f 23 β α = (f 22 β + f 23 β ) = f 32 β + f 33 β and hence (1 + f 12 f 22 )β + (f 12 + f 13 f 23 )β + f 13 β = 0 (f 22 f 32 )β + (f 22 + f 23 f 33 )β + f 23 β = 0. We want to show that β (t), β (t), β (t) are linearly dependent for all t I, i.e., det [ β (t) β (t) β (t) ] = 0 for all t I. Let S be the subset of I defined by { S = t I : 1 + f 12(t) f 22 (t) = f 22(t) f 32 (t) = f 12 (t) + f 13(t) f 23 (t) = f 22 (t) + f 23(t) f 33 (t) = } f 13 (t) = f 23 (t) = 0. If t 0 S, β (t 0 ), β (t 0 ), β (t 0 ) are linearly dependent. Suppose that t 0 S. If f 13(t 0 ) 0, then there exists r > 0 such that f 13 (t) 0 for t (t 0 r, t 0 + r) and t t 0 and hence t S for t (t 0, t 0 + r) det [ β (t) β (t) β (t) ] = 0 for t (t 0, t 0 + r). Then by the continuity of det [ β (t) β (t) β (t) ], we conclude that det [ β (t 0 ) β (t 0 ) β (t 0 ) ] = 0.
6 6 Suppose that f 13(t 0 ) = 0. Then } t 0 S f 12 (t 0 ) + f 13(t 0 ) f 23 (t 0 ) = f 13 (t 0 ) = f 23 (t 0 ) = 0 f 12 (t 0 ) = f 13 (t 0 ) = 0 α(t 0 ) = β(t 0 ) f 13(t 0 ) = 0 Contradiction. This proves that β (t), β (t), β (t) are linearly dependent for all t I. So β(i) is contained in some plane Λ β R 3. Since { α = f 22β + f 23β α = f 32 β + f 33 β α = f 22 β + f 23 β α = f 32 β + f 33 β α = f 32β + (f 32 + f 33)β + f 33 β α (t), α (t), α (t) Span{β (t), β (t), β (t)}, α (t), α (t), α (t) are also linearly dependent for all t I. So α(i) is contained in some plane Λ α R 3. Finally, since Λ α and Λ β are the osculating planes of α and β, respectively, we must have Λ α = Λ β.
Geometry of Cylindrical Curves over Plane Curves
 Applied Mathematical Sciences, Vol 9, 015, no 113, 5637-5649 HIKARI Ltd, wwwm-hikaricom http://dxdoiorg/101988/ams01556456 Geometry of Cylindrical Curves over Plane Curves Georgi Hristov Georgiev, Radostina
Applied Mathematical Sciences, Vol 9, 015, no 113, 5637-5649 HIKARI Ltd, wwwm-hikaricom http://dxdoiorg/101988/ams01556456 Geometry of Cylindrical Curves over Plane Curves Georgi Hristov Georgiev, Radostina
THE FUNDAMENTAL THEOREM OF SPACE CURVES
 THE FUNDAMENTAL THEOREM OF SPACE CURVES JOSHUA CRUZ Abstract. In this paper, we show that curves in R 3 can be uniquely generated by their curvature and torsion. By finding conditions that guarantee the
THE FUNDAMENTAL THEOREM OF SPACE CURVES JOSHUA CRUZ Abstract. In this paper, we show that curves in R 3 can be uniquely generated by their curvature and torsion. By finding conditions that guarantee the
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 2013
 SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
Arbitrary-Speed Curves
 Arbitrary-Speed Curves (Com S 477/577 Notes) Yan-Bin Jia Oct 12, 2017 The Frenet formulas are valid only for unit-speed curves; they tell the rate of change of the orthonormal vectors T, N, B with respect
Arbitrary-Speed Curves (Com S 477/577 Notes) Yan-Bin Jia Oct 12, 2017 The Frenet formulas are valid only for unit-speed curves; they tell the rate of change of the orthonormal vectors T, N, B with respect
Section Arclength and Curvature. (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes.
 Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
e 2 = e 1 = e 3 = v 1 (v 2 v 3 ) = det(v 1, v 2, v 3 ).
 3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
HOMEWORK 2 SOLUTIONS
 HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
SPLIT QUATERNIONS and CANAL SURFACES. in MINKOWSKI 3-SPACE
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 5 (016, No., 51-61 SPLIT QUATERNIONS and CANAL SURFACES in MINKOWSKI 3-SPACE SELAHATTIN ASLAN and YUSUF YAYLI Abstract. A canal surface is the envelope of a one-parameter
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 5 (016, No., 51-61 SPLIT QUATERNIONS and CANAL SURFACES in MINKOWSKI 3-SPACE SELAHATTIN ASLAN and YUSUF YAYLI Abstract. A canal surface is the envelope of a one-parameter
Week 3: Differential Geometry of Curves
 Week 3: Differential Geometry of Curves Introduction We now know how to differentiate and integrate along curves. This week we explore some of the geometrical properties of curves that can be addressed
Week 3: Differential Geometry of Curves Introduction We now know how to differentiate and integrate along curves. This week we explore some of the geometrical properties of curves that can be addressed
Contents. 1. Introduction
 FUNDAMENTAL THEOREM OF THE LOCAL THEORY OF CURVES KAIXIN WANG Abstract. In this expository paper, we present the fundamental theorem of the local theory of curves along with a detailed proof. We first
FUNDAMENTAL THEOREM OF THE LOCAL THEORY OF CURVES KAIXIN WANG Abstract. In this expository paper, we present the fundamental theorem of the local theory of curves along with a detailed proof. We first
OHSx XM521 Multivariable Differential Calculus: Homework Solutions 14.1
 OHSx XM5 Multivariable Differential Calculus: Homework Solutions 4. (8) Describe the graph of the equation. r = i + tj + (t )k. Solution: Let y(t) = t, so that z(t) = t = y. In the yz-plane, this is just
OHSx XM5 Multivariable Differential Calculus: Homework Solutions 4. (8) Describe the graph of the equation. r = i + tj + (t )k. Solution: Let y(t) = t, so that z(t) = t = y. In the yz-plane, this is just
MATH 332: Vector Analysis Summer 2005 Homework
 MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
Final Exam Topic Outline
 Math 442 - Differential Geometry of Curves and Surfaces Final Exam Topic Outline 30th November 2010 David Dumas Note: There is no guarantee that this outline is exhaustive, though I have tried to include
Math 442 - Differential Geometry of Curves and Surfaces Final Exam Topic Outline 30th November 2010 David Dumas Note: There is no guarantee that this outline is exhaustive, though I have tried to include
Good Problems. Math 641
 Math 641 Good Problems Questions get two ratings: A number which is relevance to the course material, a measure of how much I expect you to be prepared to do such a problem on the exam. 3 means of course
Math 641 Good Problems Questions get two ratings: A number which is relevance to the course material, a measure of how much I expect you to be prepared to do such a problem on the exam. 3 means of course
There is a function, the arc length function s(t) defined by s(t) = It follows that r(t) = p ( s(t) )
 MATH 20550 Acceleration, Curvature and Related Topics Fall 2016 The goal of these notes is to show how to compute curvature and torsion from a more or less arbitrary parametrization of a curve. We will
MATH 20550 Acceleration, Curvature and Related Topics Fall 2016 The goal of these notes is to show how to compute curvature and torsion from a more or less arbitrary parametrization of a curve. We will
An Introduction to Gaussian Geometry
 Lecture Notes in Mathematics An Introduction to Gaussian Geometry Sigmundur Gudmundsson (Lund University) (version 2.068-16th of November 2017) The latest version of this document can be found at http://www.matematik.lu.se/matematiklu/personal/sigma/
Lecture Notes in Mathematics An Introduction to Gaussian Geometry Sigmundur Gudmundsson (Lund University) (version 2.068-16th of November 2017) The latest version of this document can be found at http://www.matematik.lu.se/matematiklu/personal/sigma/
Linear Ordinary Differential Equations
 MTH.B402; Sect. 1 20180703) 2 Linear Ordinary Differential Equations Preliminaries: Matrix Norms. Denote by M n R) the set of n n matrix with real components, which can be identified the vector space R
MTH.B402; Sect. 1 20180703) 2 Linear Ordinary Differential Equations Preliminaries: Matrix Norms. Denote by M n R) the set of n n matrix with real components, which can be identified the vector space R
The Frenet Serret formulas
 The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
Smarandache Curves and Spherical Indicatrices in the Galilean. 3-Space
 arxiv:50.05245v [math.dg 2 Jan 205, 5 pages. DOI:0.528/zenodo.835456 Smarandache Curves and Spherical Indicatrices in the Galilean 3-Space H.S.Abdel-Aziz and M.Khalifa Saad Dept. of Math., Faculty of Science,
arxiv:50.05245v [math.dg 2 Jan 205, 5 pages. DOI:0.528/zenodo.835456 Smarandache Curves and Spherical Indicatrices in the Galilean 3-Space H.S.Abdel-Aziz and M.Khalifa Saad Dept. of Math., Faculty of Science,
Parallel Transport Frame in 4 dimensional Euclidean Space E 4
 Caspian Journal of Mathematical Sciences (CJMS) University of Mazandaran, Iran http://cjms.journals.umz.ac.ir ISSN: 1735-0611 CJMS. 3(1)(2014), 91-103 Parallel Transport Frame in 4 dimensional Euclidean
Caspian Journal of Mathematical Sciences (CJMS) University of Mazandaran, Iran http://cjms.journals.umz.ac.ir ISSN: 1735-0611 CJMS. 3(1)(2014), 91-103 Parallel Transport Frame in 4 dimensional Euclidean
Math 426H (Differential Geometry) Final Exam April 24, 2006.
 Math 426H Differential Geometry Final Exam April 24, 6. 8 8 8 6 1. Let M be a surface and let : [0, 1] M be a smooth loop. Let φ be a 1-form on M. a Suppose φ is exact i.e. φ = df for some f : M R. Show
Math 426H Differential Geometry Final Exam April 24, 6. 8 8 8 6 1. Let M be a surface and let : [0, 1] M be a smooth loop. Let φ be a 1-form on M. a Suppose φ is exact i.e. φ = df for some f : M R. Show
( sin(t), cos(t), 1) dt =
 Differential Geometry MT451 Problems/Homework Recommended Reading: Morgan F. Riemannian geometry, a beginner s guide Klingenberg W. A Course in Differential Geometry do Carmo M.P. Differential geometry
Differential Geometry MT451 Problems/Homework Recommended Reading: Morgan F. Riemannian geometry, a beginner s guide Klingenberg W. A Course in Differential Geometry do Carmo M.P. Differential geometry
CHAPTER 3. Gauss map. In this chapter we will study the Gauss map of surfaces in R 3.
 CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
What is a Space Curve?
 What is a Space Curve? A space curve is a smooth map γ : I R R 3. In our analysis of defining the curvature for space curves we will be able to take the inclusion (γ, 0) and have that the curvature of
What is a Space Curve? A space curve is a smooth map γ : I R R 3. In our analysis of defining the curvature for space curves we will be able to take the inclusion (γ, 0) and have that the curvature of
Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017
 Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017 This week we want to talk about curvature and osculating circles. You might notice that these notes contain a lot of the same theory or proofs
Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017 This week we want to talk about curvature and osculating circles. You might notice that these notes contain a lot of the same theory or proofs
im Γ (i) Prove (s) = { x R 3 x γ(s), T(s) = 0 }. (ii) Consider x R 3 and suppose the function s x γ(s) attains a minimum at s 0 J.
 Exercise 0.1 (Formulae of Serret Frenet and tubular neighborhood of curve). Let J R be an open interval in R and let γ : J R 3 be a C curve in R 3. For any s J, denote by (s) the plane in R 3 that contains
Exercise 0.1 (Formulae of Serret Frenet and tubular neighborhood of curve). Let J R be an open interval in R and let γ : J R 3 be a C curve in R 3. For any s J, denote by (s) the plane in R 3 that contains
DIFFERENTIAL GEOMETRY HW 4. Show that a catenoid and helicoid are locally isometric.
 DIFFERENTIAL GEOMETRY HW 4 CLAY SHONKWILER Show that a catenoid and helicoid are locally isometric. 3 Proof. Let X(u, v) = (a cosh v cos u, a cosh v sin u, av) be the parametrization of the catenoid and
DIFFERENTIAL GEOMETRY HW 4 CLAY SHONKWILER Show that a catenoid and helicoid are locally isometric. 3 Proof. Let X(u, v) = (a cosh v cos u, a cosh v sin u, av) be the parametrization of the catenoid and
On bounded and unbounded curves in Euclidean space
 On bounded and unbounded curves in Euclidean space Oleg Zubelevich Abstract. We provide sufficient conditions for curves in R 3 to be unbounded in terms of its curvature and torsion. We present as well
On bounded and unbounded curves in Euclidean space Oleg Zubelevich Abstract. We provide sufficient conditions for curves in R 3 to be unbounded in terms of its curvature and torsion. We present as well
Arc Length and Curvature
 Arc Length and Curvature. Last time, we saw that r(t) = cos t, sin t, t parameteried the pictured curve. (a) Find the arc length of the curve between (, 0, 0) and (, 0, π). (b) Find the unit tangent vector
Arc Length and Curvature. Last time, we saw that r(t) = cos t, sin t, t parameteried the pictured curve. (a) Find the arc length of the curve between (, 0, 0) and (, 0, π). (b) Find the unit tangent vector
BERTRAND CURVES IN GALILEAN SPACE AND THEIR CHARACTERIZATIONS. and Mahmut ERGÜT
 139 Kragujevac J. Math. 32 (2009) 139 147. BERTRAND CURVES IN GALILEAN SPACE AND THEIR CHARACTERIZATIONS Alper Osman ÖĞRENMİŞ, Handan ÖZTEKİN and Mahmut ERGÜT Fırat University, Faculty of Arts and Science,
139 Kragujevac J. Math. 32 (2009) 139 147. BERTRAND CURVES IN GALILEAN SPACE AND THEIR CHARACTERIZATIONS Alper Osman ÖĞRENMİŞ, Handan ÖZTEKİN and Mahmut ERGÜT Fırat University, Faculty of Arts and Science,
ON BOUNDEDNESS OF THE CURVE GIVEN BY ITS CURVATURE AND TORSION
 ON BOUNDEDNESS OF THE CURVE GIVEN BY ITS CURVATURE AND TORSION OLEG ZUBELEVICH DEPT. OF THEORETICAL MECHANICS, MECHANICS AND MATHEMATICS FACULTY, M. V. LOMONOSOV MOSCOW STATE UNIVERSITY RUSSIA, 9899, MOSCOW,
ON BOUNDEDNESS OF THE CURVE GIVEN BY ITS CURVATURE AND TORSION OLEG ZUBELEVICH DEPT. OF THEORETICAL MECHANICS, MECHANICS AND MATHEMATICS FACULTY, M. V. LOMONOSOV MOSCOW STATE UNIVERSITY RUSSIA, 9899, MOSCOW,
Space curves, vector fields and strange surfaces. Simon Salamon
 Space curves, vector fields and strange surfaces Simon Salamon Lezione Lagrangiana, 26 May 2016 Curves in space 1 A curve is the path of a particle moving continuously in space. Its position at time t
Space curves, vector fields and strange surfaces Simon Salamon Lezione Lagrangiana, 26 May 2016 Curves in space 1 A curve is the path of a particle moving continuously in space. Its position at time t
Homwework JWR. Jan Problem numbers refer to the do Carmo text.
 Homwework JWR Jan 30 014 Problem numbers refer to the do Carmo text. 1. 1.-1 The curve αs) cos s), sin s)) coss), sins)) parameterizes the circle x +y 1 in the clockwise orientation.. 1.-Thedistanceformthepointαt)
Homwework JWR Jan 30 014 Problem numbers refer to the do Carmo text. 1. 1.-1 The curve αs) cos s), sin s)) coss), sins)) parameterizes the circle x +y 1 in the clockwise orientation.. 1.-Thedistanceformthepointαt)
A METHOD OF THE DETERMINATION OF A GEODESIC CURVE ON RULED SURFACE WITH TIME-LIKE RULINGS
 Novi Sad J. Math. Vol., No. 2, 200, 10-110 A METHOD OF THE DETERMINATION OF A GEODESIC CURVE ON RULED SURFACE WITH TIME-LIKE RULINGS Emin Kasap 1 Abstract. A non-linear differential equation is analyzed
Novi Sad J. Math. Vol., No. 2, 200, 10-110 A METHOD OF THE DETERMINATION OF A GEODESIC CURVE ON RULED SURFACE WITH TIME-LIKE RULINGS Emin Kasap 1 Abstract. A non-linear differential equation is analyzed
8. THE FARY-MILNOR THEOREM
 Math 501 - Differential Geometry Herman Gluck Tuesday April 17, 2012 8. THE FARY-MILNOR THEOREM The curvature of a smooth curve in 3-space is 0 by definition, and its integral w.r.t. arc length, (s) ds,
Math 501 - Differential Geometry Herman Gluck Tuesday April 17, 2012 8. THE FARY-MILNOR THEOREM The curvature of a smooth curve in 3-space is 0 by definition, and its integral w.r.t. arc length, (s) ds,
Theorema Egregium, Intrinsic Curvature
 Theorema Egregium, Intrinsic Curvature Cartan s second structural equation dω 12 = K θ 1 θ 2, (1) is, as we have seen, a powerful tool for computing curvature. But it also has far reaching theoretical
Theorema Egregium, Intrinsic Curvature Cartan s second structural equation dω 12 = K θ 1 θ 2, (1) is, as we have seen, a powerful tool for computing curvature. But it also has far reaching theoretical
DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES IN LORENTZ-MINKOWSKI SPACE
 International Electronic Journal of Geometry Volume 7 No. 1 pp. 44-107 (014) c IEJG DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES IN LORENTZ-MINKOWSKI SPACE RAFAEL LÓPEZ Dedicated to memory of Proffessor
International Electronic Journal of Geometry Volume 7 No. 1 pp. 44-107 (014) c IEJG DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES IN LORENTZ-MINKOWSKI SPACE RAFAEL LÓPEZ Dedicated to memory of Proffessor
SOME RELATIONS BETWEEN NORMAL AND RECTIFYING CURVES IN MINKOWSKI SPACE-TIME
 International Electronic Journal of Geometry Volume 7 No. 1 pp. 26-35 (2014) c IEJG SOME RELATIONS BETWEEN NORMAL AND RECTIFYING CURVES IN MINKOWSKI SPACE-TIME KAZIM İLARSLAN AND EMILIJA NEŠOVIĆ Dedicated
International Electronic Journal of Geometry Volume 7 No. 1 pp. 26-35 (2014) c IEJG SOME RELATIONS BETWEEN NORMAL AND RECTIFYING CURVES IN MINKOWSKI SPACE-TIME KAZIM İLARSLAN AND EMILIJA NEŠOVIĆ Dedicated
Spherical Images and Characterizations of Time-like Curve According to New Version of the Bishop Frame in Minkowski 3-Space
 Prespacetime Journal January 016 Volume 7 Issue 1 pp. 163 176 163 Article Spherical Images and Characterizations of Time-like Curve According to New Version of the Umit Z. Savcı 1 Celal Bayar University,
Prespacetime Journal January 016 Volume 7 Issue 1 pp. 163 176 163 Article Spherical Images and Characterizations of Time-like Curve According to New Version of the Umit Z. Savcı 1 Celal Bayar University,
9.1 Mean and Gaussian Curvatures of Surfaces
 Chapter 9 Gauss Map II 9.1 Mean and Gaussian Curvatures of Surfaces in R 3 We ll assume that the curves are in R 3 unless otherwise noted. We start off by quoting the following useful theorem about self
Chapter 9 Gauss Map II 9.1 Mean and Gaussian Curvatures of Surfaces in R 3 We ll assume that the curves are in R 3 unless otherwise noted. We start off by quoting the following useful theorem about self
Natural Lifts and Curvatures, Arc-Lengths of the Spherical Indicatries of the Evolute Curve in E 3
 International Mathematical Forum, Vol. 9, 214, no. 18, 857-869 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/imf.214.448 Natural Lifts and Curvatures, Arc-Lengths of the Spherical Indicatries
International Mathematical Forum, Vol. 9, 214, no. 18, 857-869 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/imf.214.448 Natural Lifts and Curvatures, Arc-Lengths of the Spherical Indicatries
1 The Differential Geometry of Surfaces
 1 The Differential Geometry of Surfaces Three-dimensional objects are bounded by surfaces. This section reviews some of the basic definitions and concepts relating to the geometry of smooth surfaces. 1.1
1 The Differential Geometry of Surfaces Three-dimensional objects are bounded by surfaces. This section reviews some of the basic definitions and concepts relating to the geometry of smooth surfaces. 1.1
, where s is the arclength parameter. Prove that. κ = w = 1 κ (θ) + 1. k (θ + π). dγ dθ. = 1 κ T. = N dn dθ. = T, N T = 0, N = T =1 T (θ + π) = T (θ)
 Here is a collection of old exam problems: 1. Let β (t) :I R 3 be a regular curve with speed = dβ, where s is the arclength parameter. Prove that κ = d β d β d s. Let β (t) :I R 3 be a regular curve such
Here is a collection of old exam problems: 1. Let β (t) :I R 3 be a regular curve with speed = dβ, where s is the arclength parameter. Prove that κ = d β d β d s. Let β (t) :I R 3 be a regular curve such
Geometry of Curves and Surfaces
 Geometry of Curves and Surfaces Weiyi Zhang Mathematics Institute, University of Warwick September 18, 2014 2 Contents 1 Curves 5 1.1 Course description........................ 5 1.1.1 A bit preparation:
Geometry of Curves and Surfaces Weiyi Zhang Mathematics Institute, University of Warwick September 18, 2014 2 Contents 1 Curves 5 1.1 Course description........................ 5 1.1.1 A bit preparation:
Tangent and Normal Vectors
 Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
ON BOUNDED AND UNBOUNDED CURVES DETERMINED BY THEIR CURVATURE AND TORSION
 ON BOUNDED AND UNBOUNDED CURVES DETERMINED BY THEIR CURVATURE AND TORSION OLEG ZUBELEVICH DEPT. OF THEORETICAL MECHANICS, MECHANICS AND MATHEMATICS FACULTY, M. V. LOMONOSOV MOSCOW STATE UNIVERSITY RUSSIA,
ON BOUNDED AND UNBOUNDED CURVES DETERMINED BY THEIR CURVATURE AND TORSION OLEG ZUBELEVICH DEPT. OF THEORETICAL MECHANICS, MECHANICS AND MATHEMATICS FACULTY, M. V. LOMONOSOV MOSCOW STATE UNIVERSITY RUSSIA,
ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE. 1. Introduction
 International Electronic Journal of Geometry Volume 6 No.2 pp. 110 117 (2013) c IEJG ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE ŞEYDA KILIÇOĞLU, H. HILMI HACISALIHOĞLU
International Electronic Journal of Geometry Volume 6 No.2 pp. 110 117 (2013) c IEJG ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE ŞEYDA KILIÇOĞLU, H. HILMI HACISALIHOĞLU
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algo
 Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Unit Speed Curves. Recall that a curve Α is said to be a unit speed curve if
 Unit Speed Curves Recall that a curve Α is said to be a unit speed curve if The reason that we like unit speed curves that the parameter t is equal to arc length; i.e. the value of t tells us how far along
Unit Speed Curves Recall that a curve Α is said to be a unit speed curve if The reason that we like unit speed curves that the parameter t is equal to arc length; i.e. the value of t tells us how far along
Non-null weakened Mannheim curves in Minkowski 3-space
 An. Ştiinţ. Univ. Al. I. Cuza Iaşi. Mat. (N.S.) Tomul LXIII, 2017, f. 2 Non-null weakened Mannheim curves in Minkowski 3-space Yilmaz Tunçer Murat Kemal Karacan Dae Won Yoon Received: 23.IX.2013 / Revised:
An. Ştiinţ. Univ. Al. I. Cuza Iaşi. Mat. (N.S.) Tomul LXIII, 2017, f. 2 Non-null weakened Mannheim curves in Minkowski 3-space Yilmaz Tunçer Murat Kemal Karacan Dae Won Yoon Received: 23.IX.2013 / Revised:
HOMEWORK 2 - RIEMANNIAN GEOMETRY. 1. Problems In what follows (M, g) will always denote a Riemannian manifold with a Levi-Civita connection.
 HOMEWORK 2 - RIEMANNIAN GEOMETRY ANDRÉ NEVES 1. Problems In what follows (M, g will always denote a Riemannian manifold with a Levi-Civita connection. 1 Let X, Y, Z be vector fields on M so that X(p Z(p
HOMEWORK 2 - RIEMANNIAN GEOMETRY ANDRÉ NEVES 1. Problems In what follows (M, g will always denote a Riemannian manifold with a Levi-Civita connection. 1 Let X, Y, Z be vector fields on M so that X(p Z(p
II. Unit Speed Curves
 The Geometry of Curves, Part I Rob Donnelly From Murray State University s Calculus III, Fall 2001 note: This material supplements Sections 13.3 and 13.4 of the text Calculus with Early Transcendentals,
The Geometry of Curves, Part I Rob Donnelly From Murray State University s Calculus III, Fall 2001 note: This material supplements Sections 13.3 and 13.4 of the text Calculus with Early Transcendentals,
t f(u)g (u) g(u)f (u) du,
 Chapter 2 Notation. Recall that F(R 3 ) denotes the set of all differentiable real-valued functions f : R 3 R and V(R 3 ) denotes the set of all differentiable vector fields on R 3. 2.1 7. The problem
Chapter 2 Notation. Recall that F(R 3 ) denotes the set of all differentiable real-valued functions f : R 3 R and V(R 3 ) denotes the set of all differentiable vector fields on R 3. 2.1 7. The problem
Math 114, Section 003 Fall 2011 Practice Exam 1 with Solutions
 Math 11, Section 003 Fall 2011 Practice Exam 1 with Solutions Contents 1 Problems 2 2 Solution key 8 3 Solutions 9 1 1 Problems Question 1: Let L be the line tangent to the curve r (t) t 2 + 3t + 2, e
Math 11, Section 003 Fall 2011 Practice Exam 1 with Solutions Contents 1 Problems 2 2 Solution key 8 3 Solutions 9 1 1 Problems Question 1: Let L be the line tangent to the curve r (t) t 2 + 3t + 2, e
Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana
 University of Groningen Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish
University of Groningen Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish
Tangent spaces, normals and extrema
 Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
Tangent and Normal Vector - (11.5)
 Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out bythe vector-valued function r!!t # f!t, g!t, h!t $. The vector T!!t r! % r! %!t!t is the unit tangent vector
Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out bythe vector-valued function r!!t # f!t, g!t, h!t $. The vector T!!t r! % r! %!t!t is the unit tangent vector
Lecture D4 - Intrinsic Coordinates
 J. Peraire 16.07 Dynamics Fall 2004 Version 1.1 Lecture D4 - Intrinsic Coordinates In lecture D2 we introduced the position, velocity and acceleration vectors and referred them to a fixed cartesian coordinate
J. Peraire 16.07 Dynamics Fall 2004 Version 1.1 Lecture D4 - Intrinsic Coordinates In lecture D2 we introduced the position, velocity and acceleration vectors and referred them to a fixed cartesian coordinate
3 = arccos. A a and b are parallel, B a and b are perpendicular, C a and b are normalized, or D this is always true.
 Math 210-101 Test #1 Sept. 16 th, 2016 Name: Answer Key Be sure to show your work! 1. (20 points) Vector Basics: Let v = 1, 2,, w = 1, 2, 2, and u = 2, 1, 1. (a) Find the area of a parallelogram spanned
Math 210-101 Test #1 Sept. 16 th, 2016 Name: Answer Key Be sure to show your work! 1. (20 points) Vector Basics: Let v = 1, 2,, w = 1, 2, 2, and u = 2, 1, 1. (a) Find the area of a parallelogram spanned
The existence of light-like homogeneous geodesics in homogeneous Lorentzian manifolds. Sao Paulo, 2013
 The existence of light-like homogeneous geodesics in homogeneous Lorentzian manifolds Zdeněk Dušek Sao Paulo, 2013 Motivation In a previous project, it was proved that any homogeneous affine manifold (and
The existence of light-like homogeneous geodesics in homogeneous Lorentzian manifolds Zdeněk Dušek Sao Paulo, 2013 Motivation In a previous project, it was proved that any homogeneous affine manifold (and
M435: INTRODUCTION TO DIFFERENTIAL GEOMETRY
 M435: INTRODUCTION TO DIFFERENTIAL GEOMETRY MARK POWELL Contents 1. Introduction 1 2. Geometry of Curves 2 2.1. Tangent vectors and arc length 3 2.2. Curvature of plane curves 5 2.3. Curvature of curves
M435: INTRODUCTION TO DIFFERENTIAL GEOMETRY MARK POWELL Contents 1. Introduction 1 2. Geometry of Curves 2 2.1. Tangent vectors and arc length 3 2.2. Curvature of plane curves 5 2.3. Curvature of curves
Curves from the inside
 MATH 2401 - Harrell Curves from the inside Lecture 5 Copyright 2008 by Evans M. Harrell II. Who in the cast of characters might show up on the test? Curves r(t), velocity v(t). Tangent and normal lines.
MATH 2401 - Harrell Curves from the inside Lecture 5 Copyright 2008 by Evans M. Harrell II. Who in the cast of characters might show up on the test? Curves r(t), velocity v(t). Tangent and normal lines.
Euler Characteristic of Two-Dimensional Manifolds
 Euler Characteristic of Two-Dimensional Manifolds M. Hafiz Khusyairi August 2008 In this work we will discuss an important notion from topology, namely Euler Characteristic and we will discuss several
Euler Characteristic of Two-Dimensional Manifolds M. Hafiz Khusyairi August 2008 In this work we will discuss an important notion from topology, namely Euler Characteristic and we will discuss several
ON OSCULATING, NORMAL AND RECTIFYING BI-NULL CURVES IN R 5 2
 Novi Sad J. Math. Vol. 48, No. 1, 2018, 9-20 https://doi.org/10.30755/nsjom.05268 ON OSCULATING, NORMAL AND RECTIFYING BI-NULL CURVES IN R 5 2 Kazım İlarslan 1, Makoto Sakaki 2 and Ali Uçum 34 Abstract.
Novi Sad J. Math. Vol. 48, No. 1, 2018, 9-20 https://doi.org/10.30755/nsjom.05268 ON OSCULATING, NORMAL AND RECTIFYING BI-NULL CURVES IN R 5 2 Kazım İlarslan 1, Makoto Sakaki 2 and Ali Uçum 34 Abstract.
Killing Magnetic Curves in Three Dimensional Isotropic Space
 Prespacetime Journal December l 2016 Volume 7 Issue 15 pp. 2015 2022 2015 Killing Magnetic Curves in Three Dimensional Isotropic Space Alper O. Öğrenmiş1 Department of Mathematics, Faculty of Science,
Prespacetime Journal December l 2016 Volume 7 Issue 15 pp. 2015 2022 2015 Killing Magnetic Curves in Three Dimensional Isotropic Space Alper O. Öğrenmiş1 Department of Mathematics, Faculty of Science,
PSEUDO-SPHERICAL EVOLUTES OF CURVES ON A TIMELIKE SURFACE IN THREE DIMENSIONAL LORENTZ-MINKOWSKI SPACE
 PSEUDO-SPHERICAL EVOLUTES OF CURVES ON A TIMELIKE SURFACE IN THREE DIMENSIONAL LORENTZ-MINKOWSKI SPACE S. IZUMIYA, A. C. NABARRO AND A. J. SACRAMENTO Abstract. In this paper we introduce the notion of
PSEUDO-SPHERICAL EVOLUTES OF CURVES ON A TIMELIKE SURFACE IN THREE DIMENSIONAL LORENTZ-MINKOWSKI SPACE S. IZUMIYA, A. C. NABARRO AND A. J. SACRAMENTO Abstract. In this paper we introduce the notion of
How much does a curve curve?
 2 How much does a curve curve? In this chapter, we associate two scalar functions, its curvature and torsion, to any curve in R 3. The curvature measures the extent to which a curve is not contained in
2 How much does a curve curve? In this chapter, we associate two scalar functions, its curvature and torsion, to any curve in R 3. The curvature measures the extent to which a curve is not contained in
BÄCKLUND TRANSFORMATIONS ACCORDING TO BISHOP FRAME IN EUCLIDEAN 3-SPACE
 iauliai Math. Semin., 7 15), 2012, 4149 BÄCKLUND TRANSFORMATIONS ACCORDING TO BISHOP FRAME IN EUCLIDEAN 3-SPACE Murat Kemal KARACAN, Yilmaz TUNÇER Department of Mathematics, Usak University, 64200 Usak,
iauliai Math. Semin., 7 15), 2012, 4149 BÄCKLUND TRANSFORMATIONS ACCORDING TO BISHOP FRAME IN EUCLIDEAN 3-SPACE Murat Kemal KARACAN, Yilmaz TUNÇER Department of Mathematics, Usak University, 64200 Usak,
Lectures in Discrete Differential Geometry 2 Surfaces
 Lectures in Discrete Differential Geometry 2 Surfaces Etienne Vouga February 4, 24 Smooth Surfaces in R 3 In this section we will review some properties of smooth surfaces R 3. We will assume that is parameterized
Lectures in Discrete Differential Geometry 2 Surfaces Etienne Vouga February 4, 24 Smooth Surfaces in R 3 In this section we will review some properties of smooth surfaces R 3. We will assume that is parameterized
Homework for Math , Spring 2008
 Homework for Math 4530 1, Spring 2008 Andrejs Treibergs, Instructor April 18, 2008 Please read the relevant sections in the text Elementary Differential Geometry by Andrew Pressley, Springer, 2001. You
Homework for Math 4530 1, Spring 2008 Andrejs Treibergs, Instructor April 18, 2008 Please read the relevant sections in the text Elementary Differential Geometry by Andrew Pressley, Springer, 2001. You
Tangent and Normal Vector - (11.5)
 Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out by the vector-valued function rt vector T t r r t t is the unit tangent vector to the curve C. Now define N
Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out by the vector-valued function rt vector T t r r t t is the unit tangent vector to the curve C. Now define N
Cubic Helices in Minkowski Space
 Cubic Helices in Minkowski Space Jiří Kosinka and Bert Jüttler Johannes Kepler University, Institute of Applied Geometry, Altenberger Str. 69, A 4040 Linz, Austria Abstract We discuss space like and light
Cubic Helices in Minkowski Space Jiří Kosinka and Bert Jüttler Johannes Kepler University, Institute of Applied Geometry, Altenberger Str. 69, A 4040 Linz, Austria Abstract We discuss space like and light
A New Model for Ribbons in R 3
 A New Model for Ribbons in R 3 Tom Farmer Miami University Oxford, OH 45056 farmerta@muohio.edu Let s start with a hands-on demonstration. We take a long, rectangular strip of adhesive tape (or postage
A New Model for Ribbons in R 3 Tom Farmer Miami University Oxford, OH 45056 farmerta@muohio.edu Let s start with a hands-on demonstration. We take a long, rectangular strip of adhesive tape (or postage
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). Math 4140/5530: Differential Geometry
 Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt ( ds dt )2 Surface x(u, v)
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt ( ds dt )2 Surface x(u, v)
UNIVERSITY OF DUBLIN
 UNIVERSITY OF DUBLIN TRINITY COLLEGE JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Faculty of Engineering, Mathematics and Science school of mathematics Trinity Term 2015 Module MA3429
UNIVERSITY OF DUBLIN TRINITY COLLEGE JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Faculty of Engineering, Mathematics and Science school of mathematics Trinity Term 2015 Module MA3429
BOUNDED RIEMANNIAN SUBMERSIONS
 BOUNDED RIEMANNIAN SUBMERSIONS KRISTOPHER TAPP Abstract. In this paper, we establish global metric properties of a Riemannian submersion π : M n+k B n for which the fundamental tensors are bounded in norm:
BOUNDED RIEMANNIAN SUBMERSIONS KRISTOPHER TAPP Abstract. In this paper, we establish global metric properties of a Riemannian submersion π : M n+k B n for which the fundamental tensors are bounded in norm:
The General Solutions of Frenet s System in the Equiform Geometry of the Galilean, Pseudo-Galilean, Simple Isotropic and Double Isotropic Space 1
 International Mathematical Forum, Vol. 6, 2011, no. 17, 837-856 The General Solutions of Frenet s System in the Equiform Geometry of the Galilean, Pseudo-Galilean, Simple Isotropic and Double Isotropic
International Mathematical Forum, Vol. 6, 2011, no. 17, 837-856 The General Solutions of Frenet s System in the Equiform Geometry of the Galilean, Pseudo-Galilean, Simple Isotropic and Double Isotropic
Faculty of Engineering, Mathematics and Science School of Mathematics
 Faculty of Engineering, Mathematics and Science School of Mathematics GROUPS Trinity Term 06 MA3: Advanced Calculus SAMPLE EXAM, Solutions DAY PLACE TIME Prof. Larry Rolen Instructions to Candidates: Attempt
Faculty of Engineering, Mathematics and Science School of Mathematics GROUPS Trinity Term 06 MA3: Advanced Calculus SAMPLE EXAM, Solutions DAY PLACE TIME Prof. Larry Rolen Instructions to Candidates: Attempt
Lecture 13 The Fundamental Forms of a Surface
 Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
MA304 Differential Geometry
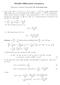 MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
CHARACTERIZATIONS OF SPACE CURVES WITH 1-TYPE DARBOUX INSTANTANEOUS ROTATION VECTOR
 Commun. Korean Math. Soc. 31 016), No., pp. 379 388 http://dx.doi.org/10.4134/ckms.016.31..379 CHARACTERIZATIONS OF SPACE CURVES WITH 1-TYPE DARBOUX INSTANTANEOUS ROTATION VECTOR Kadri Arslan, Hüseyin
Commun. Korean Math. Soc. 31 016), No., pp. 379 388 http://dx.doi.org/10.4134/ckms.016.31..379 CHARACTERIZATIONS OF SPACE CURVES WITH 1-TYPE DARBOUX INSTANTANEOUS ROTATION VECTOR Kadri Arslan, Hüseyin
CHARACTERIZATION OF SLANT HELIX İN GALILEAN AND PSEUDO-GALILEAN SPACES
 SAÜ Fen Edebiyat Dergisi (00-I) CHARACTERIZATION OF SLANT HELIX İN ALILEAN AND PSEUDO-ALILEAN SPACES Murat Kemal KARACAN * and Yılmaz TUNÇER ** *Usak University, Faculty of Sciences and Arts,Department
SAÜ Fen Edebiyat Dergisi (00-I) CHARACTERIZATION OF SLANT HELIX İN ALILEAN AND PSEUDO-ALILEAN SPACES Murat Kemal KARACAN * and Yılmaz TUNÇER ** *Usak University, Faculty of Sciences and Arts,Department
Differential Geometry of Curves and Surfaces, 1st Edition
 Thomas Banchoff, Shiing-Shen Chern, and William Pohl Differential Geometry of Curves and Surfaces, 1st Edition SPIN C346 Differential Geometry Banchoff/Chern/Pohl Monograph Mathematics January 29, 2003
Thomas Banchoff, Shiing-Shen Chern, and William Pohl Differential Geometry of Curves and Surfaces, 1st Edition SPIN C346 Differential Geometry Banchoff/Chern/Pohl Monograph Mathematics January 29, 2003
Differential Geometry Exercises
 Differential Geometry Exercises Isaac Chavel Spring 2006 Jordan curve theorem We think of a regular C 2 simply closed path in the plane as a C 2 imbedding of the circle ω : S 1 R 2. Theorem. Given the
Differential Geometry Exercises Isaac Chavel Spring 2006 Jordan curve theorem We think of a regular C 2 simply closed path in the plane as a C 2 imbedding of the circle ω : S 1 R 2. Theorem. Given the
1 Vectors and 3-Dimensional Geometry
 Calculus III (part ): Vectors and 3-Dimensional Geometry (by Evan Dummit, 07, v..55) Contents Vectors and 3-Dimensional Geometry. Functions of Several Variables and 3-Space..................................
Calculus III (part ): Vectors and 3-Dimensional Geometry (by Evan Dummit, 07, v..55) Contents Vectors and 3-Dimensional Geometry. Functions of Several Variables and 3-Space..................................
The Ruled Surfaces According to Type-2 Bishop Frame in E 3
 International Mathematical Forum, Vol. 1, 017, no. 3, 133-143 HIKARI Ltd, www.m-hikari.com https://doi.org/10.1988/imf.017.610131 The Ruled Surfaces According to Type- Bishop Frame in E 3 Esra Damar Department
International Mathematical Forum, Vol. 1, 017, no. 3, 133-143 HIKARI Ltd, www.m-hikari.com https://doi.org/10.1988/imf.017.610131 The Ruled Surfaces According to Type- Bishop Frame in E 3 Esra Damar Department
5.3 Surface Theory with Differential Forms
 5.3 Surface Theory with Differential Forms 1 Differential forms on R n, Click here to see more details Differential forms provide an approach to multivariable calculus (Click here to see more detailes)
5.3 Surface Theory with Differential Forms 1 Differential forms on R n, Click here to see more details Differential forms provide an approach to multivariable calculus (Click here to see more detailes)
3.1 Classic Differential Geometry
 Spring 2015 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry Hao Li http://cs599.hao-li.com 1 Spring 2014 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry
Spring 2015 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry Hao Li http://cs599.hao-li.com 1 Spring 2014 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry
THE FOUR VERTEX THEOREM AND ITS CONVERSE in honor of Björn Dahlberg
 Writhe - Four Vertex Theorem.14 June, 2006 THE FOUR VERTEX THEOREM AND ITS CONVERSE in honor of Björn Dahlberg The Four Vertex Theorem says that a simple closed curve in the plane, other than a circle,
Writhe - Four Vertex Theorem.14 June, 2006 THE FOUR VERTEX THEOREM AND ITS CONVERSE in honor of Björn Dahlberg The Four Vertex Theorem says that a simple closed curve in the plane, other than a circle,
Analytical Mechanics
 Analytical Mechanics R. J. Fries, 1,2 1 Cyclotron Institute, Texas A&M University, College Station TX, USA 2 Department of Physics and Astronomy, Texas A&M University, College Station TX, USA February
Analytical Mechanics R. J. Fries, 1,2 1 Cyclotron Institute, Texas A&M University, College Station TX, USA 2 Department of Physics and Astronomy, Texas A&M University, College Station TX, USA February
SOLUTIONS TO SECOND PRACTICE EXAM Math 21a, Spring 2003
 SOLUTIONS TO SECOND PRACTICE EXAM Math a, Spring 3 Problem ) ( points) Circle for each of the questions the correct letter. No justifications are needed. Your score will be C W where C is the number of
SOLUTIONS TO SECOND PRACTICE EXAM Math a, Spring 3 Problem ) ( points) Circle for each of the questions the correct letter. No justifications are needed. Your score will be C W where C is the number of
Differential Geometry
 Appendix A Differential Geometry Differential geometry is the study of geometry using the principles of calculus. In general, a curve r(q) is defined as a vector-valued function in R n space. The parameter
Appendix A Differential Geometry Differential geometry is the study of geometry using the principles of calculus. In general, a curve r(q) is defined as a vector-valued function in R n space. The parameter
FOCAL SET OF CURVES IN THE MINKOWSKI SPACE
 FOCAL SET OF CURVES IN THE MINKOWSKI SPACE A. C. NABARRO AND A. J. SACRAMENTO Abstract. We study the geometry of curves in the Minkowski space and in the de Sitter space, specially at points where the
FOCAL SET OF CURVES IN THE MINKOWSKI SPACE A. C. NABARRO AND A. J. SACRAMENTO Abstract. We study the geometry of curves in the Minkowski space and in the de Sitter space, specially at points where the
CS Tutorial 5 - Differential Geometry I - Surfaces
 236861 Numerical Geometry of Images Tutorial 5 Differential Geometry II Surfaces c 2009 Parameterized surfaces A parameterized surface X : U R 2 R 3 a differentiable map 1 X from an open set U R 2 to R
236861 Numerical Geometry of Images Tutorial 5 Differential Geometry II Surfaces c 2009 Parameterized surfaces A parameterized surface X : U R 2 R 3 a differentiable map 1 X from an open set U R 2 to R
2.3. VECTOR SPACES 25
 2.3. VECTOR SPACES 25 2.3 Vector Spaces MATH 294 FALL 982 PRELIM # 3a 2.3. Let C[, ] denote the space of continuous functions defined on the interval [,] (i.e. f(x) is a member of C[, ] if f(x) is continuous
2.3. VECTOR SPACES 25 2.3 Vector Spaces MATH 294 FALL 982 PRELIM # 3a 2.3. Let C[, ] denote the space of continuous functions defined on the interval [,] (i.e. f(x) is a member of C[, ] if f(x) is continuous
Two And Three Dimensional Regions From Homothetic Motions
 Applied Mathematics E-Notes, 1(1), 86-93 c ISSN 167-51 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Two And Three Dimensional Regions From Homothetic Motions Mustafa Düldül Received
Applied Mathematics E-Notes, 1(1), 86-93 c ISSN 167-51 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Two And Three Dimensional Regions From Homothetic Motions Mustafa Düldül Received
Figure 10: Tangent vectors approximating a path.
 3 Curvature 3.1 Curvature Now that we re parametrizing curves, it makes sense to wonder how we might measure the extent to which a curve actually curves. That is, how much does our path deviate from being
3 Curvature 3.1 Curvature Now that we re parametrizing curves, it makes sense to wonder how we might measure the extent to which a curve actually curves. That is, how much does our path deviate from being
The Natural Lift of the Fixed Centrode of a Non-null Curve in Minkowski 3-Space
 Malaya J Mat 4(3(016 338 348 The Natural Lift of the Fixed entrode of a Non-null urve in Minkowski 3-Space Mustafa Çalışkan a and Evren Ergün b a Faculty of Sciences epartment of Mathematics Gazi University
Malaya J Mat 4(3(016 338 348 The Natural Lift of the Fixed entrode of a Non-null urve in Minkowski 3-Space Mustafa Çalışkan a and Evren Ergün b a Faculty of Sciences epartment of Mathematics Gazi University
Inelastic Admissible Curves in the Pseudo Galilean Space G 3
 Int. J. Open Problems Compt. Math., Vol. 4, No. 3, September 2011 ISSN 1998-6262; Copyright ICSRS Publication, 2011 www.i-csrs.org Inelastic Admissible Curves in the Pseudo Galilean Space G 3 1 Alper Osman
Int. J. Open Problems Compt. Math., Vol. 4, No. 3, September 2011 ISSN 1998-6262; Copyright ICSRS Publication, 2011 www.i-csrs.org Inelastic Admissible Curves in the Pseudo Galilean Space G 3 1 Alper Osman
On Rectifying Dual Space Curves
 On Rectifying Dual Space Curves Ahmet YÜCESAN, NihatAYYILDIZ, anda.ceylançöken Süleyman Demirel University Department of Mathematics 32260 Isparta Turkey yucesan@fef.sdu.edu.tr ayyildiz@fef.sdu.edu.tr
On Rectifying Dual Space Curves Ahmet YÜCESAN, NihatAYYILDIZ, anda.ceylançöken Süleyman Demirel University Department of Mathematics 32260 Isparta Turkey yucesan@fef.sdu.edu.tr ayyildiz@fef.sdu.edu.tr
