A hint of renormalization
|
|
|
- Lucinda Patrick
- 6 years ago
- Views:
Transcription
1 A hint of enomalization Betand Delamotte a) Laboatoie de Phyique Théoique et Haute Enegie, Univeité Pai VI, Piee et Maie Cuie, Pai VII, Deni Dideot, 2 Place Juieu, Pai Cedex 05, Fance Received 28 Januay 2003; accepted 15 Septembe 2003 An elementay intoduction to petubative enomalization and enomalization goup i peented. No pio knowledge of field theoy i neceay becaue we do not efe to a paticula phyical theoy. We ae thu able to dientangle what i pecific to field theoy and what i intinic to enomalization. We link the geneal agument and eult to eal phenomena encounteed in paticle phyic and tatitical mechanic Ameican Aociation of Phyic Teache. DOI: / I. INTRODUCTION Han Bethe in a eminal 1947 pape wa the fit to calculate the enegy gap, known a the Lamb hift, between the 2 and 2p level of the hydogen atom. 1 Thee level wee found to be degeneate even in Diac theoy, which include elativitic coection. Seveal autho had uggeted that the oigin of the hift could be the inteaction of the electon with it own adiation field and not only with the Coulomb field. Howeve, to quote Bethe, Thi hift come out infinite in all exiting theoie and ha theefoe alway been ignoed. Bethe calculation wa the fit to lead to a finite, accuate eult. Renomalization in it moden petubative ene wa bon. 2 Since then it ha developed into a geneal algoithm to get id of infinitie that appea at each ode of petubation theoy in almot all quantum field theoie QFT. 3 7 In the meantime, the phyical oigin of thee divegence ha alo been explained ee Ref. 8 fo many inteeting contibution on the hitoy and philoophy of enomalization and enomalization goup. In QFT, a in odinay quantum mechanic, the petubative calculation of any phyical poce involve, at each ode, a ummation ove vitual intemediate tate. Howeve, if the theoy i Loentz invaiant, an infinite numbe of upplementay tate exit compaed with the Galilean cae and thei ummation, being geneically divegent, poduce infinitie. The oigin of thee new tate i deeply ooted in quantum mechanic and pecial elativity. When thee two theoie ae combined, a new length cale appea, built out of the ma m of the paticle: the Compton wavelength /mc. It vanihe in both fomal limit 0 and c, coeponding, epectively, to claical and Galilean theoie. Becaue of Heienbeg inequalitie, pobing ditance malle than thi length cale equie enegie highe than mc 2 and thu imply the ceation of paticle. Thi poibility to ceate and annihilate paticle fobid the localization of the oiginal paticle bette than the Compton wavelength becaue the paticle that have jut been ceated ae tictly identical to the oiginal one. Quantum mechanically, thee multi-paticle tate play a ole even when the enegy involved in the poce unde tudy i lowe than mc 2, becaue they ae ummed ove a vitual tate in petubation theoy. Thu, the divegence of petubation theoy in QFT ae diectly linked to it hot ditance tuctue, which i highly nontivial becaue it deciption involve the infinity of multi-paticle tate. Removing thee divegence ha been the nightmae and the delight of many phyicit woking in paticle phyic. It eemed hopele to the non-pecialit to undetand enomalization becaue it equied pio knowledge of quantum mechanic, elativity, electodynamic, etc. Thi tate of affai contibuted to the nobility of the ubject: tudying the ultimate contituent of matte and being incompehenible fit well togethe. Howeve, tangely at leat at fit ight the theoetical beakthough in the undetanding of enomalization beyond it algoithmic apect came fom Wilon wok on continuou phae tanition. 9 The phenomena that take place at thee tanition ae neithe quantum mechanical 10 no elativitic and ae non-tivial becaue of thei coopeative behavio, that i, thei popetie at lage ditance. 11 Thu neithe no c ae neceay fo enomalization. Something ele i at wok that doe not equie quantum mechanic, elativity, ummation ove vitual tate, Compton wavelength, etc., even if in the context of paticle phyic they ae the ingedient that make enomalization neceay. In fact, even divegence that eemed to be the majo poblem of QFT ae now conideed only a bypoduct of the way we have intepeted quantum field theoie. We know now that the inviible hand that ceate divegence in ome theoie i actually the exitence in thee theoie of a no man land in the enegy o length cale fo which coopeative phenomena can take place, moe peciely, fo which fluctuation can add up coheently. 12 In ome cae, they can detabilize the phyical pictue we wee elying on and thi manifet itelf a divegence. Renomalization, and even moe enomalization goup, i the ight way to deal with thee fluctuation. One of the aim of thi aticle i to dientangle what i pecific to field theoy and what i intinic to the enomalization poce. Theefoe, we hall not look fo a phyical model that how divegence, but we hall athe how the geneal mechanim of petubative enomalization and the enomalization goup without pecifying a phyical model. II. A TOY MODEL FOR RENORMALIZATION In the following, we conide an unpecified theoy that involve, by hypothei, only one fee paamete g 0 in tem of which a function F(x), epeenting a phyical quantity, i calculated petubatively, that i, a a powe eie. An example in QFT would be quantum electodynamic QED, which decibe the inteaction of chaged paticle uch a electon with the electomagnetic field. Fo high enegy pocee, the ma of the electon i negligible and the only paamete of thi theoy in thi enegy egime i it chage, 170 Am. J. Phy. 72 2, Febuay Ameican Aociation of Phyic Teache 170
2 which i theefoe the analog of g 0. F can then epeent the co ection of a catteing poce a, fo intance, the catteing of an electon on a heavy nucleu in which cae x i the enegy momentum fou-vecto of the electon. The coupling contant g 0 i defined by the Hamiltonian of the ytem, and F i calculated petubatively uing the uual à la Feynman appoach. Anothe impotant example i continuou phae tanition. Fo fluid, F could epeent a denity denity coelation function and fo magnetim a pin pin coelation function. 18 Yet anothe example i the olution of a diffeential equation that can aie in ome phyical context and that can how divegence ee the following. It i convenient fo what follow to aume that F(x) ha the fom: F x g 0 g 0 2 F 1 x g 0 3 F 2 x. Up to a edefinition of F, thi fom i geneal and coepond to what i eally encounteed in field theoy. Let u now aume that the petubation expanion of F(x) i illdefined and that the F i (x) ae function involving divegent quantitie. An example of uch a function i F 1 x 0 dt t x, which i logaithmically divegent at the uppe limit. Thi example ha been choen becaue it hae many common featue with divegent integal encounteed in QFT: the integal coepond to the ummation ove vitual tate and (t x) 1 epeent the pobability amplitude aociated with each of thee tate. 19 A imple although cucial obevation i that becaue thee i only one fee paamete in the theoy by hypothei, only one meauement of F(x), ay at the point x, i neceay to fully pecify the theoy we ae tudying. Such a meauement i ued to fix the value of g 0 o a to epoduce the expeimental value of F( ). Fo QED fo intance, thi pocedue would mean that: i ii iii 1 2 We tat by witing a geneal Hamiltonian compatible with baic aumption, fo example, elativity, cauality, locality, and gauge invaiance. We calculate phyical pocee at a given ode of petubation theoy. We fix the fee paamete of the initial Hamiltonian to epoduce at thi ode the expeimental data. Thi lat tep equie a much data a thee ae fee paamete. Once the paamete ae fixed, the theoy i completely detemined and thu pedictive. One could then think that it doe not matte whethe we paametize the theoy in tem of g 0, which i only ueful in intemediate calculation, o with a phyical, that i, a meaued quantity F( ), becaue g 0 will be eplaced by thi quantity anyway. Having thi feedom i indeed the geneic ituation in phyic, but the ubtlety hee i that the petubation expanion of F(x) i ingula, and, thu, o i the elationhip between g 0 and F( ). Thu, it eem cucial to epaametize F in tem of F( ) when the expanion i ill-defined. The enomalizability hypothei i that the epaametization of the theoy in tem of a phyical quantity, intead of g 0, i enough to tun the petubation expanion into a welldefined expanion. The hypothei i theefoe that the poblem doe not come fom the petubation expanion itelf, that i, fom the function F i (x), but fom the choice of paamete ued to pefom it. Thi hypothei mean that the phyical quantity, F(x), initially epeented by it illdefined expanion Eq. 1, hould have a well-defined petubation expanion once it i calculated in tem of the phyical paamete F( ). Thi i the implet hypothei we can make, becaue it amount to peeving the x-dependence of the function F i (x) and only modifying the coupling contant g 0. Thu, we aume that F(x) i known at one point, and we define g R by F g R. In the following, and by analogy with QFT, we call g R the enomalized coupling contant and Eq. 3 a enomalization peciption, a babaian name fo uch a tivial opeation. We ae now in a poition to dicu the enomalization pogam. It conit of epaametizing the petubation expanion of F o that it obey the peciption of Eq. 3. The point hee i that we cannot ue Eq. 3 togethe with Eq. 1 becaue Eq. 1 i ill-defined. We fit need to give a welldefined meaning to the petubation expanion. Thi i the egulaization pocedue which i the fit tep of any enomalization. 20,21 The idea i to define the petubation expanion of F by a limit uch that i the F i (x) ae welldefined befoe the limit i taken, and ii afte the enomalization ha been pefomed, the oiginal fomal expanion i ecoveed when the limit i taken. We thu intoduce a new et of egulaized function F and F i,, involving a new paamete, which we call the egulato, and uch that fo finite all thee function ae finite. We thu define F x F x,g 0, g 0 g 2 0 F 1, x g 3 0 F 2, x. 4 Thee ae infinitely many way of egulaizing the F i and fo the example given in Eq. 2, it can conit fo intance in intoducing a cut-off in the following integal: dt F 1, x 0 t x. 5 Diffeent egulaization cheme can lead to vey diffeent intemediate calculation, but mut all lead to identical eult. 22 Fo intance, dimenional egulaization i widely ued in QFT becaue it peeve Loentz and gauge ymmetie ,23 We do not need hee to pecify a egulaization fo the function F, becaue ou agument will be geneal and the few calculation elementay. Once a egulaization cheme ha been choen, it i poible to ue the enomalization peciption, Eq. 3, togethe with the egulaized expanion, Eq. 4, to obtain a well-defined petubation eie fo F in tem of the phyical coupling g R. If thi expanion make ene thi i the enomalizability hypothei it mut be finite even in the limit, becaue it expee a finite phyical quantity F(x) in tem of a phyical quantity g R. Thu, the enomalization pogam conit fit in changing F(x,g 0 ) to F (x,g 0, ), then in ewiting F in tem of g R and, F x,g 0, F x,g R,, Am. J. Phy., Vol. 72, No. 2, Febuay 2004 Betand Delamotte 171
3 and only then taking the limit at fixed g R and. If thi limit exit, F (x) i by hypothei the function F(x): F x F x,g R, F x,g R,. 7 Of coue, the divegence mut till be omewhee, and we hall ee that they uvive in the elationhip between g 0 and g R ; at fixed g R, g 0 divege when. In the taditional intepetation of enomalization, thi divegence i uppoed to be hamle becaue g 0 i uppoed to be a nonphyical quantity. We hall come back to thi point late. The enomalization pogam i pefomed ecuively, and we now implement it ode by ode to ee how it wok and the containt on the petubation expanion that it implie. Let u emphaize that the eie expanion we hall ue in intemediate calculation ae highly fomal becaue they ae ill-defined in the limit. They ae jutified only by the eult we finally obtain: a good petubation expanion in tem of g R. 24 Renomalization at ode g 0. At thi ode F(x) i contant and given by F x g 0 O g Thu the ue of Eq. 3 lead to g 0 g R O g 2 R. 9 Renomalization at ode g 2 0. Ou only feedom to eliminate the divegence of F (x) i to edefine g 0. Becaue we ae woking petubatively, we expand g 0 a a powe eie in g R. Thu, we et g 0 g R 2 g 3 g, 10 whee n g O(g n R ). At ode g 2 R we obtain F x g R 2 g g R 2 F 1, x O g R 3, 11 whee we have ued g 0 2 g R 2 O(g R 3 ). If we impoe Eq. 3 at thi ode, we obtain 2 g g 2 R F 1,, 12 which divege when. In ou example, Eq. 5, we find dt 2 g g R 2 0 t g R 2 log. 13 If we ubtitute Eq. 12 into Eq. 11, we obtain F to thi ode: F x g R g 2 R F 1, x F 1, O g 3 R. 14 It i clea that thi expeion fo F (x) i finite fo all x at thi ode if and only if the divegent pat of F 1, (x) the pat that become divegent when ) i exactly canceled by that of F 1, ( ), that i, if and only if F 1, x F 1, i egula in x and fo. 15 Thi condition of coue mean that the divegent pat of F 1, (x) mut be a contant, that i, i x-independent. If thi i o, then we define the function F(x) now called enomalized a the limit of F (x) when. The condition 15 i fulfilled fo the example of Eq. 2, and we tivially find that F(x) ead: dt F x g R x g R 2 0 t x t O g R 3, 16 which i obviouly well defined and uch that the peciption of Eq. 3 i veified. We ay that we have enomalized the theoy to thi ode. Befoe going to the next ode of petubation theoy, let u note two impotant fact. Fit, the enomalization pocedue conit of adding a divegent tem 2 g to F to emove it divegence. The cancellation take place between the econd tem of it expanion and the fit one of ode g 0. Both lead to a tem of ode g R 2, the one coming fom the expanion of g 0 in tem of g R being tuned o a to cancel the divegence of the othe. Thi mechanim of cancellation i a geneal phenomenon: a divegence coming fom the nth tem of the petubation expanion i canceled by the expanion in powe of g R of the n 1 peceding tem. Second, thi cancellation i poible fo all x only if the divegence of F 1, (x) i a numbe, that i, i x-independent. If it i not o, then F 1, (x) F 1, ( ) would till be divegent x. Thi divegence would equie the impoition of at leat one moe enomalization peciption to be emoved and thi econd peciption would define a econd, independent, coupling contant ee Appendix A fo two function, one enomalizable and one that i not. The neceity fo a econd meauement of F(x) would contadict ou aumption that thee i only one fee paamete in the theoy. Thu we conclude that thi aumption datically contain the x-dependence of the divegence at ode g 0 2. We actually how in the following that thi containt popagate to any ode of petubation theoy in a nontivial way. We alo will how that togethe with dimenional analyi and fo a vey wide and impotant cla of theoie, thee containt ae ufficient to detemine the analytical fom of the divegence. Renomalization at ode g 0 3. We uppoe that F can be enomalized at ode g R 2, that i, condition 15 i fulfilled. To undetand the tuctue of the enomalization pocedue, it i neceay to go one tep futhe. At ode g R 3 we obtain F x g R 2 g 3 g g R 2 2g R 2 g F 1, x g R 3 F 2, x O g R 4, 17 whee we have ued g 0 3 g R 3 O(g R 4 ) and g 0 2 g R 2 2g R 2 g O(g R 4 ). We again impoe the peciption Eq. 3 and obtain 3 g 2g R 3 F 1, 2 g R 3 F 2,. If we ubtitute Eq. 18 in Eq. 17, we obtain F x g R g R 2 F 1, x F 1, g R 3 F 2, x F 2, 2F 1, F 1, x F 1, O g R Once again, we equie that the divegence ha been ubtacted fo all x which impoe on the x-dependence of the divegent pat of F 2, (x): F 2, x F 2, 2F 1, F 1, x F 1, i egula in x and a Am. J. Phy., Vol. 72, No. 2, Febuay 2004 Betand Delamotte 172
4 Note that thi containt involve not only F 2,, but alo F 1,. It i convenient to ewite F 1, (x) and F 2, (x) a the um of a egula and of ingula when ) pat: F i, x F i, x F i, x. 21 Becaue anything finite, thi decompoition i not unique: the F i, (x) ae defined up to a egula pat. It i convenient to chooe F 1, (x) uch that F 1, x F 1, 0, 22 which, of coue, implie condition 15. We how in Appendix B that, ecipocally, thi choice i alway poible if 15 i fulfilled. A aleady tated, Eq. 22 mean that the divegent pat of F 1, i x-independent. We can actually impoe a moe tingent condition on F 1, becaue, by again tuning the egula pat of F 1,, we can chooe F 1, to be completely independent of x, fo any. We thu define F 1, x f In ou example, Eq. 5, we can chooe f 1 log, F 1, x log x x. 24 We now ubtitute Eq. 23 into Eq. 20 and, uing the ame kind of agument a in Appendix B, we obtain a containt on the ingula pat of F 2, (x) imila to the one on F 1, (x), Eq. 22 : F 2, x F 2, 2 f 1 F 1, x F 1, 0. Equation 25 can be ewitten a F 2, x 2 f 1 F 1, x F 2, 25 2 f 1 F 1, Equation 26 ha the ame tuctue a Eq. 22 up to the eplacement: F 1, F 2, 2 f 1 ( )F 1, and theefoe ha the ame kind of olution a Eq. 23 : F 2, x 2 f 1 F 1, x f 2, 27 whee f 2 ( ) i any function of and i independent of x. We ee in Eq. 27 that unlike F 1, (x), the divegent pat of F 2, (x) depend on x. Howeve, thi dependence i entiely detemined by the fit ode of the petubation expanion. The 2 g tem, neceay to emove the O(g 2 0 ) divegence, ha poduced at ode g 3 R an x-dependent divegent tem: 2g R 2 gf 1, (x). Thi kind of x-dependence i alo a geneal phenomenon of enomalization: the counte- tem that emove divegence at a given ode poduce divegence at highe ode. If the theoy i enomalizable, thee divegence contibute to the cancellation of divegence peent in the petubation expanion at highe ode. Thu, petubative enomalizability, that i, the poibility of eliminating ode by ode all divegence by the edefinition of the coupling, implie a pecie tuctue of the divegent pat of the ucceive tem of the petubation eie. At ode n, the ingula pat of F n, involve x-dependent tem entiely detemined by the peceding ode plu one new tem that i x-independent. In ou example of Eq. 2 and 24 we find F 2, x 2 2 log log x x f By expanding log log(x )/ x in powe of 1 and by again edefining the egula pat of F 2,, we obtain a imple fom fo F 2, (x): F 2, x 2 2 log log x f Thi elation will be impotant in the following when we hall dicu the enomalization goup. Let u daw ou fit concluion. Infinitie occu in the petubation expanion of the theoy becaue we have aumed that it wa not egulaized. Actually, thee divegence have foced u to egulaize the expanion and thu to intoduce a new cale. Once egulaization ha been pefomed, enomalization can be achieved by eliminating g 0. The limit can then be taken. The poce i ecuive and can be pefomed only if the divegence poe, ode by ode, a vey pecie tuctue. Thi tuctue ultimately expee that thee i only one coupling contant to be enomalized. Thi mean that impoing only one peciption at x i enough to ubtact the divegence fo all x. In geneal, a theoy i aid to be enomalizable if all divegence can be ecuively ubtacted by impoing a many peciption a thee ae independent paamete in the theoy. In QFT, thee ae mae, coupling contant, and the nomalization of the field. An impotant and non-tivial topic i thu to know which paamete ae independent, becaue ymmetie of the theoy like gauge ymmetie can elate diffeent paamete and Geen function. Let u once again ecall that enomalization i nothing but a epaametization in tem of the phyical quantity g R. 25 The pice to pay fo enomalizing F i that g 0 become infinite in the limit, ee Eq. 12. We again emphaize that if g 0 i believed to be no moe than a non-meauable paamete, ueful only in intemediate calculation, it i indeed of no conequence that thi quantity i infinite in the limit. That g 0 wa a divegent non-phyical quantity ha been common belief fo decade in QFT. The phyical eult given by the enomalized quantitie wee thought to be calculable only in tem of unphyical quantitie like g 0 called bae quantitie that the enomalization algoithm could only eliminate aftewad. It wa a if we had to make two mitake that compenated fo each othe: fit intoduce bae quantitie in tem of which eveything wa infinite, and then eliminate them by adding othe divegent quantitie. Undoubtly, the pocedue woked, but, to ay the leat, the intepetation eemed athe obcue. Befoe tudying the enomalization goup, let u now pecialize to a paticula cla of enomalizable theoie. III. RENORMALIZABLE THEORIES WITH DIMENSIONLESS COUPLINGS A vey impotant cla of field theoie coepond to the ituation whee g 0 i dimenionle, and x, which in QFT epeent coodinate o momenta, ha dimenion o moe geneally when g 0 and x have independent dimenion. In fou-dimenional pace time, quantum electodynamic i in thi cla, becaue the fine tuctue contant i dimenionle; quantum chomodynamic and the Weinbeg Salam 173 Am. J. Phy., Vol. 72, No. 2, Febuay 2004 Betand Delamotte 173
5 model of electo-weak inteaction ae alo in thi cla. In fou pace dimenion, the 4 model elevant fo the Ginzbug Landau Wilon appoach to citical phenomena i in thi cla too. Thi paticula cla of enomalizable theoie i the conetone of enomalization in field theoie. Ou main goal in thi ection i to how that, independently of the undelying phyical model, dimenional analyi togethe with the enomalizability containt detemine almot entiely the tuctue of the divegence. Thi undelying implicity of the natue of the divegence explain that thee i no combinatoial miacle of Feynman diagam in QFT a it might eem at fit glance. Let u now ee in detail how it wok. Becaue F (x) ha the ame dimenion a g 0, it alo i dimenionle and o ae the F i, (x). The only poibility fo a dimenionle quantity like F to be a function of a dimenional vaiable like x i that thee exit anothe dimenional vaiable uch that F depend on x only though the atio of thee two vaiable. Apat fom x, the only othe quantity on which F depend i, which mut theefoe have the ame dimenion a x. Thi i indeed the cae in ou example, Eq. 5. Thu, the function F i, (x) depend on the atio x/ only. 26 Let u how that thi i enough to pove that the F i, (x) ae um of powe of logaithm with, fo mot of them, pecibed pefacto. Let u tat with F 1, (x). On one hand, we have een that by edefining the egula pat of F 1, (x), we could take it ingula pat F 1, (x) independent of x, Eq. 23. Onthe othe hand, we know that F 1, (x) i a function of x/. Thu, by edefining F 1, (x), it mut be poible to extact an x-dependent egula pat, (x), of thi function o a to build the x/ dependence of F 1, (x): F 1, x f x f 1 x. 30 Hence, F 1, i epaable into function of x only and of only which um up to a function of x/. We how in Appendix C the well-known fact that only the logaithm obey thi popety. We obtain ee Eq. C3 and C4 F 1, x f 1 x f 1 f 1 x log x. 31 Theefoe, fo enomalizable theoie and fo dimenionle function uch a F, only logaithmic divegence ae allowed at ode g 2 0 in QFT, thi i the o-called one-loop tem. Thi i the eaon why logaithm ae encounteed eveywhee in QFT. Note that becaue of dimenional analyi, the finite pat of F 1, (x) i nothing but (x), up to an additive contant, at leat fo. Thi can be checked fo the example given in Eq. 5. Thu, by dimenional analyi, the tuctue of the divegence detemine that of the finite pat up to a contant. Notice that thing would not be that imple if F (x) depended on anothe dimenional paamete, which i the cae of maive field theoie whee mae and momenta have the ame dimenion. In thi cae, the finite pat i only patially detemined by the ingula one. Let u now how that the tuctue of F 2, alo i entiely detemined fo enomalizable theoie with dimenionle coupling both by the enomalizability hypothei and by dimenional analyi. We have aleady patially tudied thi cae with the example given in Eq. 5 whee F 1, (x) i logaithmically divegent, a chaacteitic featue of thee enomalizable theoie. In paticula, we have hown that in thi cae, enomalizability impoe at ode g 3 0 that F 2, i of the fom given in Eq. 29. Let u now ue dimenional analyi that once again impoe that F 2, depend only on x/. The only feedom we have to econtuct a function of x/ fom the fom of F 2, given in Eq. 29 i to add a egula function to it. It i not difficult to find how to poceed becaue the only admiible tem including log log x i log 2 /x: log 2 x log2 2 log log x log 2 x. 32 Thu, to obtain the dimenionally coect extenion of the tem 2 2 log log x in Eq. 29, we extact 2 log 2 fom f 2 ( ) and add the egula tem 2 log 2 x: 2 2 log log x f log log x 2 log 2 f 2 2 log log log x 2 log 2 2 log 2 x f 2 2 log 2 2 log 2 x f 2 2 log 2. Thu, we obtain fo the new function F 2, (x): F 2, x 2 log 2 x f 2 2 log Now, fo f 2 ( ) 2 log 2, we can epeat the ame agument a the one ued peviouly fo F 1, (x) which i equal to f 1 ( ), Eq. 23 : it i a function of that mut become a function of x/ only by adding a function of x. It i thu alo a logaithm, ee Eq. 30 and 31 and Appendix C. Theefoe, we add a log x tem to F 2, (x) and obtain the final eult: F 2, x 2 log 2 x log x, 35 whee i a pue numbe. We emphaize that although it i x-independent, the tem 2 log 2 involved in F 2, (x) aie fom the log log x tem thank to dimenional analyi. It i thu entiely detemined by the tem of ode g 2 0 of petubation theoy. Only the ub-leading logaithm log /x i new. It i not difficult now to gue the tuctue of the next ode of petubation: it involve a log 3 /x with a pefacto 3,a log 2 /x tem with a pefacto which i a function of and and a log /x with a pefacto independent of and. A pecie calculation how that 174 Am. J. Phy., Vol. 72, No. 2, Febuay 2004 Betand Delamotte 174
6 F x g 0 2 log x 2 g 0 3 log 2 x 3 g 0 4 log 3 x By ubtituting thi expeion in Eq. 36 and 39, we obtain at O(g R 4 ): g 0 3 log x 5 2 g 0 4 log 2 x F x g R g R 2 log x 2 g R 3 log 2 x 3 g R 4 log 3 x g 0 4 log x. 36 g R 3 log x 5 2 g R 4 log 2 x We have witten the eie o a to exhibit it tiangula natue: the fit line coepond to the leading logaithm, the econd to the ub-leading, etc., and the nth column to the (n 1)th ode of petubation. The leading logaithm ae entiely contolled by the g 2 0 tem, the ub-leading logaithm by both the g 2 0 and g 3 0 tem, etc. It i clea that ode by ode fo the divegent tem, only the log tem i new, all the log 2, log 3, etc., tem ae detemined by the peceding ode. Thi tuctue tongly ugget that we can, at leat patially, eum the petubation eie. We notice that although the leading logaithm fom a imple geometic eie, thi i no longe tue fo the ub-leading logaithm whee, fo intance, the facto 5 /2 of Eq. 36 i non-tivial. Thank to the enomalization goup, thee exit a ytematic way to pefom thee eummation 27 ee the following. We again emphaize that fo ou imple toy model the divegence togethe with dimenional analyi detemine almot entiely the entie function F(x) in the limit of lage. To how thi explicitly, we ewite F a F x,g 0, g 0 F x,g 0, F x,g 0, 37 with F (x,g 0, ) given by Eq. 36 at O(g 4 0 ) and F (x,g 0, ) O(g 2 0 ). Fom dimenional analyi, F (x,g 0, ) i alo a function of x/ only which, by definition, i finite when. Thu, fo lage, F x,g 0, F x,g 0 F 0,g F (x) i theefoe almot x-independent fo lage : itia (g 0 -dependent numbe in thi limit. Fo the ake of implicity, let u conide the cae whee it i vanihing: F x,g 0, g 0 F x,g 0, 39 with F (x,g 0, ) a function of x/ only. By uing the enomalization peciption, Eq. 3, we can calculate g R a a function of g 0 and / and by fomally inveting the eie, we obtain at O(g R 4 ): g 0 g R g R 2 log g 3 2 log 2 log g R 4 log 5 2 log2 3 log Fig. 1. An illutation of the enomalization goup: the two equivalent way to compoe change of paametization. g 4 R log x. 41 Thu, we find that the enomalization poce leave unchanged the functional fom of F, Eq. 36, and jut conit in eplacing (g 0, ) by (g R, ). Thi vey impotant fact i elated to a elf-imilaity popety that we tudy in detail fom the enomalization goup viewpoint. Notice that of coue any explicit dependence on and g 0 ha been eliminated in Eq. 41 and that the limit can now be afely taken, if deied. Note that we have obtained logaithmic divegence becaue we have tudied the enomalization of a dimenionle coupling contant. If g 0 wa dimenional, we would have obtained powe law divegence. Thi i fo intance what happen in QFT fo the ma tem ee alo in the following the expanion in Eq. 45. IV. RENORMALIZATION GROUP Although the enomalization goup will allow u to patially eum the petubation expanion, we hall not intoduce it in thi way. Rathe, we want to examine the intenal conitency of the enomalization pocedue. We have choen a enomalization peciption at the point x whee g R i defined. Obviouly, thi point i not pecial, and we could have choen any othe point o to paametize the theoy. Becaue thee i only one independent coupling contant, the diffeent coupling contant g R g R ( ), g R g R ( ), g R g R ( ) hould all be elated in uch a way that F(x) F(x,,g R ) F(x,,g R ) F(x,,g R ), etc. Thi mean that thee hould exit an equivalence cla of paametization of the ame theoy and that it hould not matte in pactice which element in the cla i choen. Thi independence of the phyical quantity with epect to the choice of peciption point alo mean that the change of paametization hould be a enomalization goup law: going fom the paametization given by (,g R ) to that given by (,g R ) and then to that given by (,g R ) o going diectly fom the fit paametization (,g R ) to the lat one (,g R ) hould make no diffeence, ee Fig. 1. Put thi way, thi tatement eem to be void. Actually, it i. Moe peciely, it would be o if we wee pefoming exact calculation: we would gain no new phyical infomation by implementing the enomalization goup law. Thi i becaue thi goup law doe not eflect a ymmety of the phyic, but only of the paametization of ou olution. Thi ituation i completely analogou to what happen fo the olution of a diffeential equation: we can paametize it at time t in tem of the initial condition at time t 0 fo intance, o we can ue the equation itelf to calculate the olution at an intemediate time and then ue thi olution 175 Am. J. Phy., Vol. 72, No. 2, Febuay 2004 Betand Delamotte 175
7 a a new initial condition to paametize the olution at time t. The change of initial condition that peeve the final olution can be compoed thank to a goup law. Let u conide, fo example, the following tivial, but illuminating, example: ẏ t y t, y t 0 0, 42 the olution of which i y t f 0,t t 0 0 e (t t 0 ). 43 The goup law can be witten a 28 f 0,t t 0 f f 0, t 0,t, 44 which you can veify uing the exact olution, Eq. 43. The non-tivial point with thee goup law i that, in geneal, they ae violated at any finite ode of the petubation expanion. In ou peviou example, we obtain to ode, y t f 1 0,t t t t 0, 45 and f 1 f 1 0, t 0,t 0 1 t t t t The goup law i veified to ode becaue the petubation expanion i exact at thi ode. Howeve, it i violated by a tem of ode 2 that can be abitaily lage even fo mall, povided t t 0 i lage enough. The inteet of the goup law, Eq. 44, i that it i poible to enfoce it and then to impove the petubation eult. Actually, when enomalization i neceay, the goup law let u patially eum the petubation eie of divegent tem. Let u now ee how thi impovement of the petubation eie wok fo the example of the diffeential equation 42. In thi cae, the divegence occu fo t 0. Thu, t 0 play the ole of the cut-off, t t 0 of log /, and t of log /. Once t 0 i finite, no divegence emain, but the elic of the divegence occuing fo t 0 ae the lage violation of the goup law becaue both the divegence and thee violation oiginate in the fact that the petubation expanion i pefomed in powe of (t t 0 ) and not of. To futhe tudy the elevance of the goup law, it i inteeting to foget the highe ode tem of the petubation expanion fo a while and to look fo an impoved appoximation that coincide at ode with the petubation eult and that obey the goup law at ode 2 : f imp 1 0,t t t t 0 2 G t t By impoing the goup law, Eq. 44, to ode 2, we obtain a functional equation fo G: G t t 0 G t 0 G t t 0 t. 48 If we diffeentiate Eq. 48 with epect to t 0 and take t 0, we obtain, etting x t, G x x G Becaue G(0) 0, Eq. 49 implie that G x x2 ax, 50 2 whee a i abitay. Fo a 0, thi eult i actually the petubation eult to ode 2 becaue y t 0 1 t t t t 0 2 O Thu, the fit ode in the petubation expanion, togethe with the goup law, detemine entiely the tem of highet degee in t t 0 at the next ode. Of coue, to veify exactly the goup law, we hould puue the expanion in to all ode. It i eay to how that to ode n, the tem of highet degee in t t 0 i completely detemined by both the fitode eult and the goup law and coincide with the petubation eult: n (t t 0 ) n /n!. Thu, the only infomation given by the petubation expanion i that all ubdominant tem, n (t t 0 ) p with p n, vanih in thi example. We could now how how the implementation of the goup law let u eum the petubation expanion. Unfotunately, thi example i too imple and ome impotant featue of the enomalization goup ae mied in thi cae. See Appendix E fo a complete dicuion of the implementation of the enomalization goup on thi example. We theefoe go back to ou toy model fo which we pecialize to enomalizable theoie with dimenionle coupling. Renomalization goup fo enomalizable theoie with dimenionle coupling. We now econide ou toy model, Eq. 4, 36, and 37, fom the point of view of the enomalization goup. Fo the ake of implicity, we keep only the dominant tem at each ode, that i, apat fom g 0, the divegent one in Eq. 39. Fit, notice that in the ame way g R i clealy aociated with the cale, Eq. 3, oig 0 with the cale becaue fom Eq. 36, wefind 29 F x g Let u define a thid coupling contant aociated with the cale, F g R, 53 and tudy the elationhip between thee diffeent coupling contant at ode g 2 0. Fom F x,g 0, g 0 g 0 2 log x O g 0 3, we obtain g R g 0 g 0 2 log O g 0 3, g R g 0 g 0 2 log O g 0 3. By eliminating g 0 between thee two equation, we find g R g R g R 2 log O g R 3, and thu, a expected, the goup law contolling the change of peciption point i veified petubatively. We note that the eential ingedient fo thi compoition law i that Eq. 57 i independent of. Thi i what enue that the ame fom can be ued to change (g 0, ) into (g R, ) and then (g R, ) into (g R, ). Thi independence, in tun, i nothing but the ignatue of petubative enomalizability which let u completely eliminate at each ode (g 0, ) fo (g R, ). Petubatively, eveything look fine. Howeve, the peviou calculation elie on a fomal tep that i not mathematically 176 Am. J. Phy., Vol. 72, No. 2, Febuay 2004 Betand Delamotte 176
8 coect, at leat fo lage. Indeed, to go fom Eq. 56 to Eq. 57, the eie g R g R (g 0 ) mut be inveted to find g 0 g 0 (g R ) while, fo, the eie g R g R (g 0 ) i clealy not convegent and thu not invetible. Thu, the neglected tem of ode g 3 R in Eq. 57 involve a tem popotional to log / log / analogou to the tem (t )( t 0 ) of Eq. 46 and 48 which i neglected becaue it i of ode g 3 R, but which i vey lage fo lage ee Appendix D. Fom a pactical point of view, the exitence at any ode of thee lage tem of highe ode poil the goup law o that the independence of the phyical eult with epect to the choice of peciption point i not veified. A in the cae of the diffeential equation 47, wecan look fo an impoved function: F imp, F imp x,g 0, g 0 g 2 0 log x g 3 0 G x O g 4 0, 58 fo which the goup law at ode g 0 3 i obeyed. It i hown in Appendix D that thi containt implie that G x 2 log 2 x log x, whee i abitay. Thu, F imp x,g 0, g 0 g 0 2 log x 2 g 0 3 log 2 x g 0 3 log x O g Once again, we find that the goup law togethe with the ode g 0 2 eult detemine the leading behavio at the next ode, hee the log 2 ( /x) tem. Moeove, we find that the goup law impoe the exitence of the ame log 2 tem a the one found fom the enomalizability containt, Eq. 35 and 36, and allow the exitence of a ub-leading logaithm. Although nontivial, thi hould not be too upiing becaue the enomalizability containt mean that once F i well defined at x, it alo i eveywhee and in paticula at x. The enomalizability containt i theefoe cetainly neceay fo the implementation of the goup law. A in the example of the diffeential equation, Eq. 42, we hould puue the expanion to all ode to obtain an exactly veified goup law. It i clea that by doing o, we would find the ame expanion a the one obtained fom the enomalizability containt. Thu, if we ue petubation theoy to calculate the coefficient in font of the fit leading logaithm of ode g 0 2 ) and impoe the goup law, we hould be able to eum all the leading logaithm. To do the eummation of the ub-leading and ub-ub-leading logaithm, a knowledge of, epectively, the ode g 0 3 and g 0 4 tem i equied. Clealy, we need to undetand how to ytematically contuct the function f giving g R in tem of g R and /, 27 g R f g R,, 61 uch that it expanion at ode n i given by the nth ode of petubation theoy, the goup law i exactly veified: f g R, f f g R,,. 62 The function f i then aid to be the elf-imila appoximation at ode n of the exact elationhip between g R and g R. 30 Fit notice one cucial thing. Ou fit aim wa to tudy the petubation expanion of a function F in a powe eie of a coupling contant g 0. Then we have dicoveed that the logaithmic divegence at ode g 2 0 popagate to all ode o that the expanion i actually pefomed in g 0 log / intead of g 0. Becaue i the egulato, it i uppoed to be vey lage compaed with, o that the lage logaithmic tem invalidate the ue of the petubation expanion. Recipocally, it i clea that petubation theoy i pefectly valid if it i pefomed between two cale 1 and 2 which ae vey cloe. Thu, intead of uing petubation theoy to make a big jump between two vey ditinct cale, ay and, we hould ue it to pefom a eie of vey little tep fo which it i valid at each of them. In geometical tem, the fact that the petubative appoach i valid only between two vey cloe cale mean that we hould not ue petubation theoy to appoximate the equation of the cuve given by the function f, Eq. 61, that join the point (,g R ) and (,g R ), but we hould ue it to calculate the field of tangent vecto to thi cuve, that i, it envelope. The cuve itelf hould then be econtucted by integation, ee Appendix E. By doing o, the goup law will be automatically veified becaue, by contuction, the integation peciely conit in compoing infiniteimal change of epaametization infinitely many time. Let u conide again Eq. 55. We want to calculate the evolution of g R ( ) with fo a given model pecified by (,g 0 ). Thu we define g R g R, 63 g 0, which give the infiniteimal evolution of the coupling contant with the cale fo the model coeponding to (g 0, ). We tivially find to thi ode fom Eq. 55, g R g 2 0 O g 3 0, 64 and thu, by tivially inveting the eie of Eq. 55, we obtain g R g 2 R O g 3 R. 65 Now, if we integate Eq. 63 togethe with Eq. 65, we obtain g R g R 1 g R log. 66 Thi elation ha eveal inteeting popetie. i When expanded to ode g R 2, the petubation eult to thi ode i ecoveed, Eq. 57. Thi i quite nomal becaue (g R ) ha been calculated to thi ode. ii When expanded to all ode, the whole eie of leading logaithm i ecoveed. Thi i moe inteeting becaue (g R ) ha been calculated only to ode g 2, but imply mean that all the leading logaithm ae detemined by the fit one. iii The goup law 62 i obeyed exactly. We have thu found the function f of Eq. 61 to thi ode. It i vey 177 Am. J. Phy., Vol. 72, No. 2, Febuay 2004 Betand Delamotte 177
9 intuctive to check the goup law diectly fom Eq. 66 and to veify that the function found in Eq. 65 i not modified if we add the leading logaithmic tem of ode g 0 3 to elation 55 : g R g 0 g 0 2 log 2 g 0 3 log 2 O g The independence of the function with epect to the addition of the ucceive leading logaithmic tem mean that thi function i indeed the ight object to build elfimila appoximation out of the petubation expanion. Let u now etun to the function itelf. Fit, we have calculated the logaithmic deivative g R / intead of the odinay deivative with epect to becaue we wanted to have a dimenionle function. Second, even the dimenionle quantity, (g R ), could have depended on /. Howeve, the evolution of g R ( ) between and d cannot depend in petubation theoy on becaue the theoy i petubatively enomalizable: the petubative elation between g R ( ) and g R ( ) depend only on and and not on. Thu, being dimenionle, the function cannot depend on alone and i thu only a function of g R. Thi popety i geneal fo any enomalizable theoy: in the pace of coupling contant, the function i alway a local function. Thid, the function i the function to be expanded in petubation theoy becaue it i given by a tue eie in g R and not in g R log /. Thi i clea fo ou example, Eq. 65, whee thee i no logaithm, and can be poven fomally by the following agument. If we ue Eq. 61 and 63, we find that g R f y g R,y y 1. If f i a double eie in g and in log( / ), f g R, n,p n,p g R n log p, it i clea fom Eq. 68 that only tem with p 1 contibute to (g), with the logaithm eplaced by 1. Thu we immediately deduce fom thi agument and fom Eq. 36 that g R g 2 R g 3 R g 4 R O g 5 R. 70 It i eay to check that the fit two coefficient, and, ae univeal in the ene that fo two diffeent theoie, paametized by (g R, ) and (g R, ), the two function have the ame fit two coefficient in thei expanion. Thi method of computing the function alo let u bypa the tange way to calculate it that we have ued in Eq. 64 and 65, whee we have fit expeed g R in tem of g 0 to calculate (g R ) a a function of g 0 and then, by inveion of the eie, e-obtained a function of g R. Thee two tep ae a pioi dangeou becaue they both involve lage logaithm. Actually, they alway cancel each othe. Thi can be een diectly fo the example of Eq. 67 and the eaon fo thi cancellation come fom Eq. 68 and 69, which how that no inveion of eie i needed to calculate (g R ). Thee i no miacle hee, becaue only the behavio at y / 1, which of coue doe not involve, matte. Finally, we mention that the integation of the function at O(g 3 R ) analogou to a two-loop eult in QFT lead to an implicit equation fo g R that genealize Eq. 66 : 1 g R 1 g R log g R g R g R g R log. 71 Thee i no imple olution of thi tancendental equation. It i howeve poible to obtain an iteative olution that i valid if the O(g R 3 ) tem i mall compaed with the O(g R 2 ) one, that i, if g R / 1. It i obtained by eplacing g R in the thid tem of Eq. 71 by it expeion obtained to ode g R 2, Eq. 66 : g R g R 1 g R log g R log 1 g R log. 72 It i eay to check that Eq. 72 eum exactly all the leading and ub-leading logaithm of the petubation expanion Eq. 41. Note that contay to the one-loop eult, Eq. 66, which eum only the leading logaithm, the exact expeion in Eq. 71 contibute alo to the ub-ub-leading logaithm a well a the ub-ub-ub-leading one and o on and o foth. V. SUMMARY 1 The long way of enomalization tat with a theoy depending on only one paamete g 0, which i the mall paamete in which petubation eie ae expanded. In paticle phyic, thi paamete i in geneal a coupling contant like an electic chage involved in a Hamiltonian moe peciely the fine tuctue contant fo electodynamic. Thi paamete i alo the fit ode contibution of a phyical quantity F. In paticle/tatitical phyic, F i a Geen/ coelation function. The fit ode of petubation theoy neglect fluctuation quantum o tatitical and thu coepond to the claical/mean field appoximation. The paamete g 0 alo i to thi ode a meauable quantity becaue it i given by a Geen function. Thu, it i natual to intepet it a the unique and phyical coupling contant of the poblem. If, a we uppoe in the following, g 0 i dimenionle, o i F. Moeove, if x i dimenional it epeent momenta in QFT it i natual that F doe not depend on it a i found in the claical theoy, that i, at fit ode of the petubation expanion. 2 If F doe depend on x, a we uppoe it doe at econd ode of petubation theoy, it mut depend on anothe dimenional paamete,, though the atio of x and. Ifwe have not included thi paamete fom the beginning in the model, the x-dependent tem ae eithe vanihing, which i what happen at fit ode, o infinite a they ae at econd and highe ode. Thi i the vey oigin of divegence fom the technical point of view. 3 Thee divegence equie that we egulaize F. Thi equiement, in tun, equie the intoduction of the cale that wa miing. In the context of field theoy, the divegence occu in Feynman diagam fo high momenta, that i, at hot ditance. The cut-off uppee the fluctuation at hot ditance compaed with 1. In tatitical phyic, thi cale, although intoduced fo fomal eaon, ha a natual intepetation becaue the theoie ae alway effective theoie built at a given micocopic cale. It coepond in geneal to the ange of inteaction of the contituent of the model, fo example, a lattice pacing fo pin, the aveage intemolecula ditance fo fluid. In paticle 178 Am. J. Phy., Vol. 72, No. 2, Febuay 2004 Betand Delamotte 178
10 phyic, thing ae le imple. At leat pychologically. It wa indeed natual in the ealy day of quantum electodynamic to think that thi theoy wa fundamental, that i, not deived fom a moe fundamental theoy. Moe peciely, it wa believed that QED had to be mathematically intenally conitent, even if in the eal wold new phyic had to occu at highe enegie. Thu, the egulato cale wa intoduced only a a tick to pefom intemediate calculation. The limit wa uppoed to be the ight way to eliminate thi unwanted cale, which anyway eemed to have no intepetation. We hall ee in the following that the community now intepet the enomalization poce diffeently. 4 Once the theoy i egulaized, F can be a nontivial function of x. The pice i that diffeent value of x now coepond to diffeent value of the coupling contant defined a the value of F fo thee x). Actually, it no longe make ene to peak of a coupling contant in itelf. The only meaningful concept i the pai (,g R ( )) of coupling contant at a given cale. The elevant quetion now i, What ae the phyical eaon in paticle/tatitical phyic that make the coupling contant depend on the cale while they ae contant in the claical/mean field appoximation? A mentioned, fo paticle phyic, the anwe i the exitence of new quantum fluctuation coeponding to the poibility of ceating and annihilating paticle at enegie highe than mc 2. What wa cale independent in the claical theoy become cale dependent in the quantum theoy becaue, a the available enegy inceae, moe and moe paticle can be ceated. The pai of vitual paticle uounding an electon ae polaized by it peence and thu ceen it chage. A a conequence, the chage of an electon depend on the ditance o equivalently the enegy at which it i pobed, at leat fo ditance malle than the Compton wavelength. Note that the enegy cale mc 2 hould not be confued with the cut-off cale. mc 2 i the enegy cale above which quantum fluctuation tat to play a ignificant ole while i the cale whee they ae cut-off. Thu, although the Compton wavelength i a hot ditance cale fo the claical theoy, it i a long ditance cale fo QFT, the hot one being 1. Thee ae thu thee domain of length cale in QFT: above the Compton wavelength whee the theoy behave claically up to mall quantum coection coming fom high enegy vitual pocee, between the Compton wavelength and the cut-off cale 1 whee the elativitic and quantum fluctuation play a geat ole, and below 1 whee a new, moe fundamental theoy ha to be invoked. 12 In tatitical phyic, the analog of the Compton wavelength i the coelation length which i a meaue of the ditance at which two micocopic contituent of the ytem ae able to influence each othe though themal fluctuation. 31 Fo the Iing model, fo intance, the coelation length away fom the citical point i the ode of the lattice pacing and the coection to the mean-field appoximation due to fluctuation ae mall. Unlike paticle phyic whee the mae and theefoe the Compton wavelength ae fixed, the coelation length in tatitical mechanic can be tuned by vaying the tempeatue. Nea the citical tempeatue whee the phae tanition take place, the coelation length become extemely lage and fluctuation on all length cale between the micocopic cale of ode 1, a lattice pacing, and the coelation length add up to modify the mean-field behavio ee Ref. 32, 33 and alo Ref. 34 fo a bibliogaphy on thi ubject. We ee hee a key to the elevance of enomalization: two vey diffeent cale mut exit between which a nontivial dynamic quantum o tatitical in ou example can develop. Thi ituation i a pioi athe unnatual a can be een fo phae tanition, whee a fine tuning of tempeatue mut be implemented to obtain coelation length much lage than the micocopic cale. Mot of the time, phyical ytem have an intinic cale of time, enegy, length, etc. and all the othe elevant cale of the poblem ae of the ame ode. All phenomena occuing at vey diffeent cale ae thu almot completely uppeed. The exitence of a unique elevant cale i one of the eaon why enomalization i not neceay in mot phyical theoie. In QFT it i mandatoy becaue the mae of the known paticle ae much malle than a hypothetical cut-off cale, till to be dicoveed, whee new phyic hould take place. Thi i a athe unnatual ituation, becaue, contay to phae tanition, thee i no analog of a tempeatue that could be finetuned to ceate a lage plitting of enegy, that i, ma, cale. The quetion of natualne of the model we have at peent in paticle phyic i till lagely open, although thee ha been much effot in thi diection uing upeymmety. 5 The claical theoy i valid down to the Compton/ coelation length, but cannot be continued naively beyond thi cale; othewie, when mixed with the quantum fomalim, it poduce divegence. Actually, it i known in QFT that the field hould be conideed a ditibution and not a odinay function. The need fo conideing ditibution come fom the nontivial tuctue of the theoy at vey hot length cale whee fluctuation ae vey impotant. At hot ditance, function ae not ufficient to decibe the field tate, which i not mooth but ough, and ditibution ae neceay. Renomalizing the theoy conit actually in building, ode by ode, the coect ditibutional continuation of the claical theoy. The fluctuation ae then coectly taken into account and depend on the cale at which the theoy i pobed: thi nontivial cale dependence can only be taken into account theoetically though the dependence of the analog of the function F with x and thu of the coupling with the cale. 6 If the theoy i petubatively enomalizable, the pai (,g( )) fom an equivalence cla of paametization of the theoy. The change of paametization fom (,g( )) to (,g( )), called a enomalization goup tanfomation, i then pefomed by a law which i elf-imila, that i, uch that it can be iteated eveal time while being fom-invaiant. 27,30 Thi law i obtained by the integation of g R g R. 73 g 0, Thi function ha a tue petubation expanion in tem of g R unlike the petubative elation between g R ( ) and g R ( ) which involve logaithm of / that can be lage. The integation of Eq. 73 patially eum the petubation eie and i thu emi-nonpetubative even if (g R ) ha been calculated petubatively. The elf-imila natue of the goup law i encoded in the fact that (g R ) i independent of. 5 In paticle phyic, the function give the evolution of the tength of the inteaction a the enegy at which it i pobed vaie and the integation of the function eum patially the petubation expanion. Fit, a the enegy inceae, the coupling contant can deceae and eventually 179 Am. J. Phy., Vol. 72, No. 2, Febuay 2004 Betand Delamotte 179
Chapter 19 Webassign Help Problems
 Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
Gravity. David Barwacz 7778 Thornapple Bayou SE, Grand Rapids, MI David Barwacz 12/03/2003
 avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
Solutions Practice Test PHYS 211 Exam 2
 Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
Precision Spectrophotometry
 Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
FI 2201 Electromagnetism
 FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
Inference for A One Way Factorial Experiment. By Ed Stanek and Elaine Puleo
 Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
On the undulatory theory of positive and negative electrons
 Su la théoie ondulatoie de électon poitif and negatif J. Phy. et le Rad. 7 (1936) 347-353. On the undulatoy theoy of poitive and negative electon By AL. PROCA Intitut Heni Poincaé Pai Tanlated by D. H.
Su la théoie ondulatoie de électon poitif and negatif J. Phy. et le Rad. 7 (1936) 347-353. On the undulatoy theoy of poitive and negative electon By AL. PROCA Intitut Heni Poincaé Pai Tanlated by D. H.
γ from B D(Kπ)K and B D(KX)K, X=3π or ππ 0
 fom and X, X= o 0 Jim Libby, Andew Powell and Guy Wilkinon Univeity of Oxfod 8th Januay 007 Gamma meeting 1 Outline The AS technique to meaue Uing o 0 : intoducing the coheence facto Meauing the coheence
fom and X, X= o 0 Jim Libby, Andew Powell and Guy Wilkinon Univeity of Oxfod 8th Januay 007 Gamma meeting 1 Outline The AS technique to meaue Uing o 0 : intoducing the coheence facto Meauing the coheence
Simulation of Spatially Correlated Large-Scale Parameters and Obtaining Model Parameters from Measurements
 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model Paamete fom PER ZETTERBERG Stockholm Septembe 8 TRITA EE 8:49 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model
Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model Paamete fom PER ZETTERBERG Stockholm Septembe 8 TRITA EE 8:49 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model
Then the number of elements of S of weight n is exactly the number of compositions of n into k parts.
 Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx.
![( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx. ( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx.](/thumbs/90/103689049.jpg) 9. LAGRANGIAN OF THE ELECTROMAGNETIC FIELD In the pevious section the Lagangian and Hamiltonian of an ensemble of point paticles was developed. This appoach is based on a qt. This discete fomulation can
9. LAGRANGIAN OF THE ELECTROMAGNETIC FIELD In the pevious section the Lagangian and Hamiltonian of an ensemble of point paticles was developed. This appoach is based on a qt. This discete fomulation can
The Substring Search Problem
 The Substing Seach Poblem One algoithm which is used in a vaiety of applications is the family of substing seach algoithms. These algoithms allow a use to detemine if, given two chaacte stings, one is
The Substing Seach Poblem One algoithm which is used in a vaiety of applications is the family of substing seach algoithms. These algoithms allow a use to detemine if, given two chaacte stings, one is
EM Boundary Value Problems
 EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
Theorem 2: Proof: Note 1: Proof: Note 2:
 A New 3-Dimenional Polynomial Intepolation Method: An Algoithmic Appoach Amitava Chattejee* and Rupak Bhattachayya** A new 3-dimenional intepolation method i intoduced in thi pape. Coeponding to the method
A New 3-Dimenional Polynomial Intepolation Method: An Algoithmic Appoach Amitava Chattejee* and Rupak Bhattachayya** A new 3-dimenional intepolation method i intoduced in thi pape. Coeponding to the method
ASTR 3740 Relativity & Cosmology Spring Answers to Problem Set 4.
 ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
Two-Body Problem with Varying Mass in Case. of Isotropic Mass Loss
 Adv Theo Appl Mech Vol no 69-8 Two-Body Poblem with Vaying Ma in Cae of Iotopic Ma o W A Rahoma M K Ahmed and I A El-Tohamy Caio Univeity Faculty of Science Dept of Atonomy Caio 6 Egypt FA Abd El-Salam
Adv Theo Appl Mech Vol no 69-8 Two-Body Poblem with Vaying Ma in Cae of Iotopic Ma o W A Rahoma M K Ahmed and I A El-Tohamy Caio Univeity Faculty of Science Dept of Atonomy Caio 6 Egypt FA Abd El-Salam
Shrinkage Estimation of Reliability Function for Some Lifetime Distributions
 Ameican Jounal of Computational and Applied Mathematic 4, 4(3): 9-96 DOI:.593/j.ajcam.443.4 Shinkage Etimation of eliability Function fo Some Lifetime Ditibution anjita Pandey Depatment of Statitic, niveity
Ameican Jounal of Computational and Applied Mathematic 4, 4(3): 9-96 DOI:.593/j.ajcam.443.4 Shinkage Etimation of eliability Function fo Some Lifetime Ditibution anjita Pandey Depatment of Statitic, niveity
Histogram Processing
 Hitogam Poceing Lectue 4 (Chapte 3) Hitogam Poceing The hitogam of a digital image with gay level fom to L- i a dicete function h( )=n, whee: i the th gay level n i the numbe of pixel in the image with
Hitogam Poceing Lectue 4 (Chapte 3) Hitogam Poceing The hitogam of a digital image with gay level fom to L- i a dicete function h( )=n, whee: i the th gay level n i the numbe of pixel in the image with
QUADRATIC DEPENDENCE MEASURE FOR NONLINEAR BLIND SOURCES SEPARATION
 QUADRATI DPNDN MASUR FR NNLINAR BLIND SURS SPARATIN Sophie Achad Dinh Tuan Pham Univ. of Genoble Laboatoy of Modeling and omputation IMAG.N.R.S. B.P. 5X 84 Genoble edex Fance Sophie.Achad@imag.f Dinh-Tuan.Pham@imag.f
QUADRATI DPNDN MASUR FR NNLINAR BLIND SURS SPARATIN Sophie Achad Dinh Tuan Pham Univ. of Genoble Laboatoy of Modeling and omputation IMAG.N.R.S. B.P. 5X 84 Genoble edex Fance Sophie.Achad@imag.f Dinh-Tuan.Pham@imag.f
Partition Functions. Chris Clark July 18, 2006
 Patition Functions Chis Clak July 18, 2006 1 Intoduction Patition functions ae useful because it is easy to deive expectation values of paametes of the system fom them. Below is a list of the mao examples.
Patition Functions Chis Clak July 18, 2006 1 Intoduction Patition functions ae useful because it is easy to deive expectation values of paametes of the system fom them. Below is a list of the mao examples.
Considerations Regarding the Flux Estimation in Induction Generator with Application at the Control of Unconventional Energetic Conversion Systems
 Conideation Regading the Flux Etimation in Induction Geneato with Application at the Contol of Unconventional Enegetic Conveion Sytem Ioif Szeidet, Octavian Potean, Ioan Filip, Vaa Citian Depatment of
Conideation Regading the Flux Etimation in Induction Geneato with Application at the Contol of Unconventional Enegetic Conveion Sytem Ioif Szeidet, Octavian Potean, Ioan Filip, Vaa Citian Depatment of
Bosons and fermions in social and economic systems. Sergey A. Rashkovskiy
 Boon and femion in ocial and economic ytem Segey A. Rahkovkiy Ihlinky Intitute fo Poblem in Mechanic of the Ruian Academy of Science, Venadkogo Ave., /, Mocow, 9526, Ruia Tomk State Univeity, 36 Lenina
Boon and femion in ocial and economic ytem Segey A. Rahkovkiy Ihlinky Intitute fo Poblem in Mechanic of the Ruian Academy of Science, Venadkogo Ave., /, Mocow, 9526, Ruia Tomk State Univeity, 36 Lenina
Noether Theorem, Noether Charge and All That
 Noethe Theoem, Noethe Chage and All That Ceated fo PF by Samalkhaiat 10 Tanfomation Let G be a Lie goup whoe action on Minkowki pace-time fomally ealized by coodinate tanfomation ( ) ( 1,3,η) M i Infiniteimally,
Noethe Theoem, Noethe Chage and All That Ceated fo PF by Samalkhaiat 10 Tanfomation Let G be a Lie goup whoe action on Minkowki pace-time fomally ealized by coodinate tanfomation ( ) ( 1,3,η) M i Infiniteimally,
Question 1: The dipole
 Septembe, 08 Conell Univesity, Depatment of Physics PHYS 337, Advance E&M, HW #, due: 9/5/08, :5 AM Question : The dipole Conside a system as discussed in class and shown in Fig.. in Heald & Maion.. Wite
Septembe, 08 Conell Univesity, Depatment of Physics PHYS 337, Advance E&M, HW #, due: 9/5/08, :5 AM Question : The dipole Conside a system as discussed in class and shown in Fig.. in Heald & Maion.. Wite
Scattering in Three Dimensions
 Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Introduction to Nuclear Forces
 Intoduction to Nuclea Foces One of the main poblems of nuclea physics is to find out the natue of nuclea foces. Nuclea foces diffe fom all othe known types of foces. They cannot be of electical oigin since
Intoduction to Nuclea Foces One of the main poblems of nuclea physics is to find out the natue of nuclea foces. Nuclea foces diffe fom all othe known types of foces. They cannot be of electical oigin since
Quantum Mechanics II
 Quantum Mechanics II Pof. Bois Altshule Apil 25, 2 Lectue 25 We have been dicussing the analytic popeties of the S-matix element. Remembe the adial wave function was u kl () = R kl () e ik iπl/2 S l (k)e
Quantum Mechanics II Pof. Bois Altshule Apil 25, 2 Lectue 25 We have been dicussing the analytic popeties of the S-matix element. Remembe the adial wave function was u kl () = R kl () e ik iπl/2 S l (k)e
Theory. Single Soil Layer. ProShake User s Manual
 PoShake Ue Manual Theoy PoShake ue a fequency domain appoach to olve the gound epone poblem. In imple tem, the input motion i epeented a the um of a eie of ine wave of diffeent amplitude, fequencie, and
PoShake Ue Manual Theoy PoShake ue a fequency domain appoach to olve the gound epone poblem. In imple tem, the input motion i epeented a the um of a eie of ine wave of diffeent amplitude, fequencie, and
Appendix B The Relativistic Transformation of Forces
 Appendix B The Relativistic Tansfomation of oces B. The ou-foce We intoduced the idea of foces in Chapte 3 whee we saw that the change in the fou-momentum pe unit time is given by the expession d d w x
Appendix B The Relativistic Tansfomation of oces B. The ou-foce We intoduced the idea of foces in Chapte 3 whee we saw that the change in the fou-momentum pe unit time is given by the expession d d w x
Study on Internal Mechanisms of Charge, Current, Electric Field and Magnetic Field
 Study on Intenal Mechanim of Chage, Cuent, Electic Field and Magnetic Field Wei Fan Abtact: In the hitoy of phyic, geat achievement have been made in the field of electomagnetim making u awae of the exitence
Study on Intenal Mechanim of Chage, Cuent, Electic Field and Magnetic Field Wei Fan Abtact: In the hitoy of phyic, geat achievement have been made in the field of electomagnetim making u awae of the exitence
one primary direction in which heat transfers (generally the smallest dimension) simple model good representation for solving engineering problems
 CHAPTER 3: One-Dimenional Steady-State Conduction one pimay diection in which heat tanfe (geneally the mallet dimenion) imple model good epeentation fo olving engineeing poblem 3. Plane Wall 3.. hot fluid
CHAPTER 3: One-Dimenional Steady-State Conduction one pimay diection in which heat tanfe (geneally the mallet dimenion) imple model good epeentation fo olving engineeing poblem 3. Plane Wall 3.. hot fluid
DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS
 DOING PHYIC WITH MTLB COMPUTTIONL OPTIC FOUNDTION OF CLR DIFFRCTION THEORY Ian Coope chool of Physics, Univesity of ydney ian.coope@sydney.edu.au DOWNLOD DIRECTORY FOR MTLB CRIPT View document: Numeical
DOING PHYIC WITH MTLB COMPUTTIONL OPTIC FOUNDTION OF CLR DIFFRCTION THEORY Ian Coope chool of Physics, Univesity of ydney ian.coope@sydney.edu.au DOWNLOD DIRECTORY FOR MTLB CRIPT View document: Numeical
A Neural Network for the Travelling Salesman Problem with a Well Behaved Energy Function
 A Neual Netwok fo the Tavelling Saleman Poblem with a Well Behaved Enegy Function Maco Budinich and Babaa Roaio Dipatimento di Fiica & INFN, Via Valeio, 347 Tiete, Italy E-mail: mbh@tiete.infn.it (Contibuted
A Neual Netwok fo the Tavelling Saleman Poblem with a Well Behaved Enegy Function Maco Budinich and Babaa Roaio Dipatimento di Fiica & INFN, Via Valeio, 347 Tiete, Italy E-mail: mbh@tiete.infn.it (Contibuted
Fall 2004/05 Solutions to Assignment 5: The Stationary Phase Method Provided by Mustafa Sabri Kilic. I(x) = e ixt e it5 /5 dt (1) Z J(λ) =
 8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
you of a spring. The potential energy for a spring is given by the parabola U( x)
 Small oscillations The theoy of small oscillations is an extemely impotant topic in mechanics. Conside a system that has a potential enegy diagam as below: U B C A x Thee ae thee points of stable equilibium,
Small oscillations The theoy of small oscillations is an extemely impotant topic in mechanics. Conside a system that has a potential enegy diagam as below: U B C A x Thee ae thee points of stable equilibium,
Supplemental Materials. Advanced Thermoelectrics Governed by Single Parabolic Band Model:
 Electonic Supplementay Mateial (ESI) fo Phyical Chemity Chemical Phyic. Thi jounal i The Royal Society of Chemity 04 Supplemental Mateial Advanced Themoelectic Govened by Single Paabolic and Model: Mg
Electonic Supplementay Mateial (ESI) fo Phyical Chemity Chemical Phyic. Thi jounal i The Royal Society of Chemity 04 Supplemental Mateial Advanced Themoelectic Govened by Single Paabolic and Model: Mg
Lecture 8 - Gauss s Law
 Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Impulse and Momentum
 Impule and Momentum 1. A ca poee 20,000 unit of momentum. What would be the ca' new momentum if... A. it elocity wee doubled. B. it elocity wee tipled. C. it ma wee doubled (by adding moe paenge and a
Impule and Momentum 1. A ca poee 20,000 unit of momentum. What would be the ca' new momentum if... A. it elocity wee doubled. B. it elocity wee tipled. C. it ma wee doubled (by adding moe paenge and a
Above Flux Estimation Issues in Induction Generators with Application at Energy Conversion Systems
 Acta Polytechnica Hungaica Vol. 3, No. 3, 2006 Above Flux Etimation Iue in Induction Geneato with Application at Enegy Conveion Sytem Ioif Szeidet, Octavian Potean, Ioan Filip, Vaa Citian Depatment of
Acta Polytechnica Hungaica Vol. 3, No. 3, 2006 Above Flux Etimation Iue in Induction Geneato with Application at Enegy Conveion Sytem Ioif Szeidet, Octavian Potean, Ioan Filip, Vaa Citian Depatment of
MATH 415, WEEK 3: Parameter-Dependence and Bifurcations
 MATH 415, WEEK 3: Paamete-Dependence and Bifucations 1 A Note on Paamete Dependence We should pause to make a bief note about the ole played in the study of dynamical systems by the system s paametes.
MATH 415, WEEK 3: Paamete-Dependence and Bifucations 1 A Note on Paamete Dependence We should pause to make a bief note about the ole played in the study of dynamical systems by the system s paametes.
Determining the Best Linear Unbiased Predictor of PSU Means with the Data. included with the Random Variables. Ed Stanek
 Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
Chem 453/544 Fall /08/03. Exam #1 Solutions
 Chem 453/544 Fall 3 /8/3 Exam # Solutions. ( points) Use the genealized compessibility diagam povided on the last page to estimate ove what ange of pessues A at oom tempeatue confoms to the ideal gas law
Chem 453/544 Fall 3 /8/3 Exam # Solutions. ( points) Use the genealized compessibility diagam povided on the last page to estimate ove what ange of pessues A at oom tempeatue confoms to the ideal gas law
TRAVELING WAVES. Chapter Simple Wave Motion. Waves in which the disturbance is parallel to the direction of propagation are called the
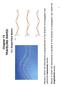 Chapte 15 RAVELING WAVES 15.1 Simple Wave Motion Wave in which the ditubance i pependicula to the diection of popagation ae called the tanvee wave. Wave in which the ditubance i paallel to the diection
Chapte 15 RAVELING WAVES 15.1 Simple Wave Motion Wave in which the ditubance i pependicula to the diection of popagation ae called the tanvee wave. Wave in which the ditubance i paallel to the diection
ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS
 ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS L. MICU Hoia Hulubei National Institute fo Physics and Nuclea Engineeing, P.O. Box MG-6, RO-0775 Buchaest-Maguele, Romania, E-mail: lmicu@theoy.nipne.o (Received
ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS L. MICU Hoia Hulubei National Institute fo Physics and Nuclea Engineeing, P.O. Box MG-6, RO-0775 Buchaest-Maguele, Romania, E-mail: lmicu@theoy.nipne.o (Received
ASTR415: Problem Set #6
 ASTR45: Poblem Set #6 Cuan D. Muhlbege Univesity of Mayland (Dated: May 7, 27) Using existing implementations of the leapfog and Runge-Kutta methods fo solving coupled odinay diffeential equations, seveal
ASTR45: Poblem Set #6 Cuan D. Muhlbege Univesity of Mayland (Dated: May 7, 27) Using existing implementations of the leapfog and Runge-Kutta methods fo solving coupled odinay diffeential equations, seveal
A new approach in classical electrodynamics to protect principle of causality
 A new appoach in classical electodynamics to potect pinciple of causality Biswaanjan Dikshit * Lase and Plasma Technology Division Bhabha Atomic Reseach Cente, Mumbai-400085 INDIA * Coesponding autho E-mail:
A new appoach in classical electodynamics to potect pinciple of causality Biswaanjan Dikshit * Lase and Plasma Technology Division Bhabha Atomic Reseach Cente, Mumbai-400085 INDIA * Coesponding autho E-mail:
Section 25 Describing Rotational Motion
 Section 25 Decibing Rotational Motion What do object do and wh do the do it? We have a ve thoough eplanation in tem of kinematic, foce, eneg and momentum. Thi include Newton thee law of motion and two
Section 25 Decibing Rotational Motion What do object do and wh do the do it? We have a ve thoough eplanation in tem of kinematic, foce, eneg and momentum. Thi include Newton thee law of motion and two
Rotational Kinetic Energy
 Add Impotant Rotational Kinetic Enegy Page: 353 NGSS Standad: N/A Rotational Kinetic Enegy MA Cuiculum Famewok (006):.1,.,.3 AP Phyic 1 Leaning Objective: N/A, but olling poblem have appeaed on peviou
Add Impotant Rotational Kinetic Enegy Page: 353 NGSS Standad: N/A Rotational Kinetic Enegy MA Cuiculum Famewok (006):.1,.,.3 AP Phyic 1 Leaning Objective: N/A, but olling poblem have appeaed on peviou
Basic propositional and. The fundamentals of deduction
 Baic ooitional and edicate logic The fundamental of deduction 1 Logic and it alication Logic i the tudy of the atten of deduction Logic lay two main ole in comutation: Modeling : logical entence ae the
Baic ooitional and edicate logic The fundamental of deduction 1 Logic and it alication Logic i the tudy of the atten of deduction Logic lay two main ole in comutation: Modeling : logical entence ae the
arxiv: v1 [math.cv] 7 Nov 2018
![arxiv: v1 [math.cv] 7 Nov 2018 arxiv: v1 [math.cv] 7 Nov 2018](/thumbs/90/101586781.jpg) INTERMEDIATE HANKEL OPERATORS ON THE FOCK SPACE OLIVIA CONSTANTIN axiv:181103137v1 [mathcv] 7 Nov 2018 Abtact We contuct a natual equence of middle Hankel opeato on the Fock pace, ie opeato which ae intemediate
INTERMEDIATE HANKEL OPERATORS ON THE FOCK SPACE OLIVIA CONSTANTIN axiv:181103137v1 [mathcv] 7 Nov 2018 Abtact We contuct a natual equence of middle Hankel opeato on the Fock pace, ie opeato which ae intemediate
Matrix regularization techniques for online multitask learning
 Matix egulaization technique fo online multitak leaning Alekh Agawal Compute Science Diviion UC Bekeley alekh@c.bekeley.edu Pete L. Batlett Compute Science Diviion Depatment of Statitic UC Bekeley batlett@c.bekeley.edu
Matix egulaization technique fo online multitak leaning Alekh Agawal Compute Science Diviion UC Bekeley alekh@c.bekeley.edu Pete L. Batlett Compute Science Diviion Depatment of Statitic UC Bekeley batlett@c.bekeley.edu
Static Electric Fields. Coulomb s Law Ε = 4πε. Gauss s Law. Electric Potential. Electrical Properties of Materials. Dielectrics. Capacitance E.
 Coulomb Law Ε Gau Law Electic Potential E Electical Popetie of Mateial Conducto J σe ielectic Capacitance Rˆ V q 4πε R ρ v 2 Static Electic Field εe E.1 Intoduction Example: Electic field due to a chage
Coulomb Law Ε Gau Law Electic Potential E Electical Popetie of Mateial Conducto J σe ielectic Capacitance Rˆ V q 4πε R ρ v 2 Static Electic Field εe E.1 Intoduction Example: Electic field due to a chage
Lecture 5 Solving Problems using Green s Theorem. 1. Show how Green s theorem can be used to solve general electrostatic problems 2.
 Lectue 5 Solving Poblems using Geen s Theoem Today s topics. Show how Geen s theoem can be used to solve geneal electostatic poblems. Dielectics A well known application of Geen s theoem. Last time we
Lectue 5 Solving Poblems using Geen s Theoem Today s topics. Show how Geen s theoem can be used to solve geneal electostatic poblems. Dielectics A well known application of Geen s theoem. Last time we
ψ - exponential type orbitals, Frictional
 ew develoment in theoy of Laguee olynomial I. I. Gueinov Deatment of Phyic, Faculty of At and Science, Onekiz Mat Univeity, Çanakkale, Tukey Abtact The new comlete othonomal et of L -Laguee tye olynomial
ew develoment in theoy of Laguee olynomial I. I. Gueinov Deatment of Phyic, Faculty of At and Science, Onekiz Mat Univeity, Çanakkale, Tukey Abtact The new comlete othonomal et of L -Laguee tye olynomial
Estimation and Confidence Intervals: Additional Topics
 Chapte 8 Etimation and Confidence Inteval: Additional Topic Thi chapte imply follow the method in Chapte 7 fo foming confidence inteval The text i a bit dioganized hee o hopefully we can implify Etimation:
Chapte 8 Etimation and Confidence Inteval: Additional Topic Thi chapte imply follow the method in Chapte 7 fo foming confidence inteval The text i a bit dioganized hee o hopefully we can implify Etimation:
Many Electron Atoms. Electrons can be put into approximate orbitals and the properties of the many electron systems can be catalogued
 Many Electon Atoms The many body poblem cannot be solved analytically. We content ouselves with developing appoximate methods that can yield quite accuate esults (but usually equie a compute). The electons
Many Electon Atoms The many body poblem cannot be solved analytically. We content ouselves with developing appoximate methods that can yield quite accuate esults (but usually equie a compute). The electons
SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS
 Appl. Comput. Math., V.10, N.2, 2011, pp.242-249 SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS A.N. GÜNDEŞ1, A.N. METE 2 Abtact. A imple finite-dimenional
Appl. Comput. Math., V.10, N.2, 2011, pp.242-249 SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS A.N. GÜNDEŞ1, A.N. METE 2 Abtact. A imple finite-dimenional
Estimates on Invariant Tori near an Elliptic Equilibrium Point of a Hamiltonian System
 jounal of diffeential equation 131, 277303 (1996) aticle no. 0165 Etimate on Invaiant Toi nea an Elliptic Equilibium Point of a Hamiltonian Sytem Amadeu Delham* Depatament de Matema tica Aplicada I, Univeitat
jounal of diffeential equation 131, 277303 (1996) aticle no. 0165 Etimate on Invaiant Toi nea an Elliptic Equilibium Point of a Hamiltonian Sytem Amadeu Delham* Depatament de Matema tica Aplicada I, Univeitat
Eddy Currents in Permanent Magnets of a Multi-pole Direct Drive Motor
 Acta Technica Jauineni Vol. 6. No. 1. 2013 Eddy Cuent in Pemanent Magnet of a Multi-pole Diect Dive Moto G. Gotovac 1, G. Lampic 1, D. Miljavec 2 Elaphe Ltd. 1, Univeity of Ljubljana, Faculty of Electical
Acta Technica Jauineni Vol. 6. No. 1. 2013 Eddy Cuent in Pemanent Magnet of a Multi-pole Diect Dive Moto G. Gotovac 1, G. Lampic 1, D. Miljavec 2 Elaphe Ltd. 1, Univeity of Ljubljana, Faculty of Electical
A Relativistic Electron in a Coulomb Potential
 A Relativistic Electon in a Coulomb Potential Alfed Whitehead Physics 518, Fall 009 The Poblem Solve the Diac Equation fo an electon in a Coulomb potential. Identify the conseved quantum numbes. Specify
A Relativistic Electon in a Coulomb Potential Alfed Whitehead Physics 518, Fall 009 The Poblem Solve the Diac Equation fo an electon in a Coulomb potential. Identify the conseved quantum numbes. Specify
Pulse Neutron Neutron (PNN) tool logging for porosity Some theoretical aspects
 Pulse Neuton Neuton (PNN) tool logging fo poosity Some theoetical aspects Intoduction Pehaps the most citicism of Pulse Neuton Neuon (PNN) logging methods has been chage that PNN is to sensitive to the
Pulse Neuton Neuton (PNN) tool logging fo poosity Some theoetical aspects Intoduction Pehaps the most citicism of Pulse Neuton Neuon (PNN) logging methods has been chage that PNN is to sensitive to the
Development of Model Reduction using Stability Equation and Cauer Continued Fraction Method
 Intenational Jounal of Electical and Compute Engineeing. ISSN 0974-90 Volume 5, Numbe (03), pp. -7 Intenational Reeach Publication Houe http://www.iphoue.com Development of Model Reduction uing Stability
Intenational Jounal of Electical and Compute Engineeing. ISSN 0974-90 Volume 5, Numbe (03), pp. -7 Intenational Reeach Publication Houe http://www.iphoue.com Development of Model Reduction uing Stability
Mathematical Modeling of Metabolic Processes in a Living Organism in Relation to Nutrition
 Mathematical Modeling of Metabolic Pocee in a Living Oganim in Relation to Nutition Dimitova N., Makov S. Depatment Biomathematic Intitute of Mathematic and Infomatic Bulgaian Academy of Science 8 Acad.
Mathematical Modeling of Metabolic Pocee in a Living Oganim in Relation to Nutition Dimitova N., Makov S. Depatment Biomathematic Intitute of Mathematic and Infomatic Bulgaian Academy of Science 8 Acad.
Physics 505 Homework No. 9 Solutions S9-1
 Physics 505 Homewok No 9 s S9-1 1 As pomised, hee is the tick fo summing the matix elements fo the Stak effect fo the gound state of the hydogen atom Recall, we need to calculate the coection to the gound
Physics 505 Homewok No 9 s S9-1 1 As pomised, hee is the tick fo summing the matix elements fo the Stak effect fo the gound state of the hydogen atom Recall, we need to calculate the coection to the gound
Solution to HW 3, Ma 1a Fall 2016
 Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
RIGID-ROTOR VLASOV EQUILIBRIUM FOR AN INTENSE CHARGED-PARTICLE BEAM PROPAGATING THROUGH A PERIODIC SOLENOIDAL MAGNETIC FIELD
 RIGID-ROTOR VLASOV EQUILIBRIUM FOR AN INTENSE CHARGED-PARTICLE BEAM PROPAGATING THROUGH A PERIODIC SOLENOIDAL MAGNETIC FIELD Chiping Chen and Renato Pakte Plama Science and Fuion Cente Maachuett Intitute
RIGID-ROTOR VLASOV EQUILIBRIUM FOR AN INTENSE CHARGED-PARTICLE BEAM PROPAGATING THROUGH A PERIODIC SOLENOIDAL MAGNETIC FIELD Chiping Chen and Renato Pakte Plama Science and Fuion Cente Maachuett Intitute
ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION. 1. Introduction. 1 r r. r k for every set E A, E \ {0},
 ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION E. J. IONASCU and A. A. STANCU Abstact. We ae inteested in constucting concete independent events in puely atomic pobability
ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION E. J. IONASCU and A. A. STANCU Abstact. We ae inteested in constucting concete independent events in puely atomic pobability
Exceptional regular singular points of second-order ODEs. 1. Solving second-order ODEs
 (May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
(May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
Math 124B February 02, 2012
 Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Honors Classical Physics I
 Hono Claical Phyic I PHY141 Lectue 9 Newton Law of Gavity Pleae et you Clicke Channel to 1 9/15/014 Lectue 9 1 Newton Law of Gavity Gavitational attaction i the foce that act between object that have a
Hono Claical Phyic I PHY141 Lectue 9 Newton Law of Gavity Pleae et you Clicke Channel to 1 9/15/014 Lectue 9 1 Newton Law of Gavity Gavitational attaction i the foce that act between object that have a
Physics 221 Lecture 41 Nonlinear Absorption and Refraction
 Physics 221 Lectue 41 Nonlinea Absoption and Refaction Refeences Meye-Aendt, pp. 97-98. Boyd, Nonlinea Optics, 1.4 Yaiv, Optical Waves in Cystals, p. 22 (Table of cystal symmeties) 1. Intoductoy Remaks.
Physics 221 Lectue 41 Nonlinea Absoption and Refaction Refeences Meye-Aendt, pp. 97-98. Boyd, Nonlinea Optics, 1.4 Yaiv, Optical Waves in Cystals, p. 22 (Table of cystal symmeties) 1. Intoductoy Remaks.
Classical Worm algorithms (WA)
 Classical Wom algoithms (WA) WA was oiginally intoduced fo quantum statistical models by Pokof ev, Svistunov and Tupitsyn (997), and late genealized to classical models by Pokof ev and Svistunov (200).
Classical Wom algoithms (WA) WA was oiginally intoduced fo quantum statistical models by Pokof ev, Svistunov and Tupitsyn (997), and late genealized to classical models by Pokof ev and Svistunov (200).
5.61 Physical Chemistry Lecture #23 page 1 MANY ELECTRON ATOMS
 5.6 Physical Chemisty Lectue #3 page MAY ELECTRO ATOMS At this point, we see that quantum mechanics allows us to undestand the helium atom, at least qualitatively. What about atoms with moe than two electons,
5.6 Physical Chemisty Lectue #3 page MAY ELECTRO ATOMS At this point, we see that quantum mechanics allows us to undestand the helium atom, at least qualitatively. What about atoms with moe than two electons,
A Bijective Approach to the Permutational Power of a Priority Queue
 A Bijective Appoach to the Pemutational Powe of a Pioity Queue Ia M. Gessel Kuang-Yeh Wang Depatment of Mathematics Bandeis Univesity Waltham, MA 02254-9110 Abstact A pioity queue tansfoms an input pemutation
A Bijective Appoach to the Pemutational Powe of a Pioity Queue Ia M. Gessel Kuang-Yeh Wang Depatment of Mathematics Bandeis Univesity Waltham, MA 02254-9110 Abstact A pioity queue tansfoms an input pemutation
On the integration of the equations of hydrodynamics
 Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Bogoliubov Transformation in Classical Mechanics
 Bogoliubov Tranformation in Claical Mechanic Canonical Tranformation Suppoe we have a et of complex canonical variable, {a j }, and would like to conider another et of variable, {b }, b b ({a j }). How
Bogoliubov Tranformation in Claical Mechanic Canonical Tranformation Suppoe we have a et of complex canonical variable, {a j }, and would like to conider another et of variable, {b }, b b ({a j }). How
Σr2=0. Σ Br. Σ br. Σ r=0. br = Σ. Σa r-s b s (1.2) s=0. Σa r-s b s-t c t (1.3) t=0. cr = Σ. dr = Σ. Σa r-s b s-t c t-u d u (1.4) u =0.
 0 Powe of Infinite Seie. Multiple Cauchy Poduct The multinomial theoem i uele fo the powe calculation of infinite eie. Thi i becaue the polynomial theoem depend on the numbe of tem, o it can not be applied
0 Powe of Infinite Seie. Multiple Cauchy Poduct The multinomial theoem i uele fo the powe calculation of infinite eie. Thi i becaue the polynomial theoem depend on the numbe of tem, o it can not be applied
The Millikan Experiment: Determining the Elementary Charge
 LAB EXERCISE 7.5.1 7.5 The Elementay Chage (p. 374) Can you think of a method that could be used to suggest that an elementay chage exists? Figue 1 Robet Millikan (1868 1953) m + q V b The Millikan Expeiment:
LAB EXERCISE 7.5.1 7.5 The Elementay Chage (p. 374) Can you think of a method that could be used to suggest that an elementay chage exists? Figue 1 Robet Millikan (1868 1953) m + q V b The Millikan Expeiment:
13. Adiabatic Invariants and Action-Angle Variables Michael Fowler
 3 Adiabatic Invaiants and Action-Angle Vaiables Michael Fowle Adiabatic Invaiants Imagine a paticle in one dimension oscillating back and foth in some potential he potential doesn t have to be hamonic,
3 Adiabatic Invaiants and Action-Angle Vaiables Michael Fowle Adiabatic Invaiants Imagine a paticle in one dimension oscillating back and foth in some potential he potential doesn t have to be hamonic,
Second Order Fuzzy S-Hausdorff Spaces
 Inten J Fuzzy Mathematical Achive Vol 1, 013, 41-48 ISSN: 30-34 (P), 30-350 (online) Publihed on 9 Febuay 013 wwweeachmathciog Intenational Jounal o Second Ode Fuzzy S-Haudo Space AKalaichelvi Depatment
Inten J Fuzzy Mathematical Achive Vol 1, 013, 41-48 ISSN: 30-34 (P), 30-350 (online) Publihed on 9 Febuay 013 wwweeachmathciog Intenational Jounal o Second Ode Fuzzy S-Haudo Space AKalaichelvi Depatment
Chapter 5 Force and Motion
 Chapte 5 Foce and Motion In chaptes 2 and 4 we have studied kinematics i.e. descibed the motion of objects using paametes such as the position vecto, velocity and acceleation without any insights as to
Chapte 5 Foce and Motion In chaptes 2 and 4 we have studied kinematics i.e. descibed the motion of objects using paametes such as the position vecto, velocity and acceleation without any insights as to
Lecture Principles of scattering and main concepts.
 Lectue 15. Light catteing and aboption by atmopheic paticuate. Pat 1: Pincipe of catteing. Main concept: eementay wave, poaization, Stoke matix, and catteing phae function. Rayeigh catteing. Objective:
Lectue 15. Light catteing and aboption by atmopheic paticuate. Pat 1: Pincipe of catteing. Main concept: eementay wave, poaization, Stoke matix, and catteing phae function. Rayeigh catteing. Objective:
THROUGHPUT OF LARGE WIRELESS NETWORKS ON SQUARE, HEXAGONAL AND TRIANGULAR GRIDS. Kezhu Hong, Yingbo Hua
 THROUGHPUT OF LARGE WIRELESS NETWORKS ON SQUARE, HEAGONAL AND TRIANGULAR GRIDS Kezhu Hong, Yingbo Hua Dept. of Electical Engineeing Univeity of Califonia Riveide, CA 9252 {khong,yhua}@ee.uc.edu ABSTRACT
THROUGHPUT OF LARGE WIRELESS NETWORKS ON SQUARE, HEAGONAL AND TRIANGULAR GRIDS Kezhu Hong, Yingbo Hua Dept. of Electical Engineeing Univeity of Califonia Riveide, CA 9252 {khong,yhua}@ee.uc.edu ABSTRACT
Nuclear and Particle Physics - Lecture 20 The shell model
 1 Intoduction Nuclea and Paticle Physics - Lectue 0 The shell model It is appaent that the semi-empiical mass fomula does a good job of descibing tends but not the non-smooth behaviou of the binding enegy.
1 Intoduction Nuclea and Paticle Physics - Lectue 0 The shell model It is appaent that the semi-empiical mass fomula does a good job of descibing tends but not the non-smooth behaviou of the binding enegy.
Perhaps the greatest success of his theory of gravity was to successfully explain the motion of the heavens planets, moons, &tc.
 AP Phyic Gavity Si Iaac Newton i cedited with the dicovey of gavity. Now, of coue we know that he didn t eally dicove the thing let face it, people knew about gavity fo a long a thee have been people.
AP Phyic Gavity Si Iaac Newton i cedited with the dicovey of gavity. Now, of coue we know that he didn t eally dicove the thing let face it, people knew about gavity fo a long a thee have been people.
2. Electrostatics. Dr. Rakhesh Singh Kshetrimayum 8/11/ Electromagnetic Field Theory by R. S. Kshetrimayum
 2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
Galilean Transformation vs E&M y. Historical Perspective. Chapter 2 Lecture 2 PHYS Special Relativity. Sep. 1, y K K O.
 PHYS-2402 Chapte 2 Lectue 2 Special Relativity 1. Basic Ideas Sep. 1, 2016 Galilean Tansfomation vs E&M y K O z z y K In 1873, Maxwell fomulated Equations of Electomagnetism. v Maxwell s equations descibe
PHYS-2402 Chapte 2 Lectue 2 Special Relativity 1. Basic Ideas Sep. 1, 2016 Galilean Tansfomation vs E&M y K O z z y K In 1873, Maxwell fomulated Equations of Electomagnetism. v Maxwell s equations descibe
New On-Line Algorithms for the Page Replication Problem. Susanne Albers y Hisashi Koga z. Abstract
 New On-Line Algoithm fo the Page Replication Poblem Suanne Albe y Hiahi Koga z Abtact We peent impoved competitive on-line algoithm fo the page eplication poblem and concentate on impotant netwok topologie
New On-Line Algoithm fo the Page Replication Poblem Suanne Albe y Hiahi Koga z Abtact We peent impoved competitive on-line algoithm fo the page eplication poblem and concentate on impotant netwok topologie
Class 2. Lesson 1 Stationary Point Charges and Their Forces. Basic Rules of Electrostatics. Basic Rules of Electrostatics
 Lesson 1 Stationay Point Chages and Thei Foces Class Today we will: lean the basic chaacteistics o the electostatic oce eview the popeties o conductos and insulatos lean what is meant by electostatic induction
Lesson 1 Stationay Point Chages and Thei Foces Class Today we will: lean the basic chaacteistics o the electostatic oce eview the popeties o conductos and insulatos lean what is meant by electostatic induction
Quantum effects in many-body gravitating systems. V. A. Golovko
 Quantum effect in many-body gavitating ytem V. A. Golovko Mocow State Evening Metallugical Intitute, Lefotovky Val 6, Mocow 5 Ruia Abtact A hieachy of equation fo equilibium educed denity matice obtained
Quantum effect in many-body gavitating ytem V. A. Golovko Mocow State Evening Metallugical Intitute, Lefotovky Val 6, Mocow 5 Ruia Abtact A hieachy of equation fo equilibium educed denity matice obtained
Conjunctive Query Answering for Description Logics with Transitive Roles
 Conjunctive Quey Anweing fo Deciption Logic with Tanitive Role Bite Glimm Ian Hoock Ulike Sattle The Univeity of Manchete, UK [glimm,hoock,attle]@c.man.ac.uk Abtact An impotant eaoning tak, in addition
Conjunctive Quey Anweing fo Deciption Logic with Tanitive Role Bite Glimm Ian Hoock Ulike Sattle The Univeity of Manchete, UK [glimm,hoock,attle]@c.man.ac.uk Abtact An impotant eaoning tak, in addition
Qualifying Examination Electricity and Magnetism Solutions January 12, 2006
 1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
Chapter 5 Force and Motion
 Chapte 5 Foce and Motion In Chaptes 2 and 4 we have studied kinematics, i.e., we descibed the motion of objects using paametes such as the position vecto, velocity, and acceleation without any insights
Chapte 5 Foce and Motion In Chaptes 2 and 4 we have studied kinematics, i.e., we descibed the motion of objects using paametes such as the position vecto, velocity, and acceleation without any insights
SENSORLESS SPEED CONTROL SYSTEMS BASED ON ADAPTIVE OBSERVERS LUENBERGER AND GOPINATH
 Annal of the Univeity of Caiova, Electical Engineeing eie, No. 32, 2008; ISSN 1842-4805 SENSORLESS SPEED CONTROL SYSTEMS BASED ON ADAPTIVE OBSERVERS LUENBERGER AND GOPINATH Maiu-Auelian PICIU, Lauenţiu
Annal of the Univeity of Caiova, Electical Engineeing eie, No. 32, 2008; ISSN 1842-4805 SENSORLESS SPEED CONTROL SYSTEMS BASED ON ADAPTIVE OBSERVERS LUENBERGER AND GOPINATH Maiu-Auelian PICIU, Lauenţiu
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II September 15, 2012 Prof. Alan Guth PROBLEM SET 2
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.07: Electomagnetism II Septembe 5, 202 Pof. Alan Guth PROBLEM SET 2 DUE DATE: Monday, Septembe 24, 202. Eithe hand it in at the lectue,
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.07: Electomagnetism II Septembe 5, 202 Pof. Alan Guth PROBLEM SET 2 DUE DATE: Monday, Septembe 24, 202. Eithe hand it in at the lectue,
New Analysis for The FGM Thick Cylinders Under Combined Pressure and Temperature Loading
 Ameican Jounal of Applied Science 5 (7): 85-859, 008 ISSN 546-939 008 Science Publication New Analyi fo The FGM Thick Cylinde Unde Combined Peue and Tempeatue Loading K. Abinia, H. Naee, F. Sadeghi and
Ameican Jounal of Applied Science 5 (7): 85-859, 008 ISSN 546-939 008 Science Publication New Analyi fo The FGM Thick Cylinde Unde Combined Peue and Tempeatue Loading K. Abinia, H. Naee, F. Sadeghi and
c n ψ n (r)e ient/ h (2) where E n = 1 mc 2 α 2 Z 2 ψ(r) = c n ψ n (r) = c n = ψn(r)ψ(r)d 3 x e 2r/a0 1 πa e 3r/a0 r 2 dr c 1 2 = 2 9 /3 6 = 0.
 Poblem {a} Fo t : Ψ(, t ψ(e iet/ h ( whee E mc α (α /7 ψ( e /a πa Hee we have used the gound state wavefunction fo Z. Fo t, Ψ(, t can be witten as a supeposition of Z hydogenic wavefunctions ψ n (: Ψ(,
Poblem {a} Fo t : Ψ(, t ψ(e iet/ h ( whee E mc α (α /7 ψ( e /a πa Hee we have used the gound state wavefunction fo Z. Fo t, Ψ(, t can be witten as a supeposition of Z hydogenic wavefunctions ψ n (: Ψ(,
11) A thin, uniform rod of mass M is supported by two vertical strings, as shown below.
 Fall 2007 Qualifie Pat II 12 minute questions 11) A thin, unifom od of mass M is suppoted by two vetical stings, as shown below. Find the tension in the emaining sting immediately afte one of the stings
Fall 2007 Qualifie Pat II 12 minute questions 11) A thin, unifom od of mass M is suppoted by two vetical stings, as shown below. Find the tension in the emaining sting immediately afte one of the stings
Revision of Lecture Eight
 Revision of Lectue Eight Baseband equivalent system and equiements of optimal tansmit and eceive filteing: (1) achieve zeo ISI, and () maximise the eceive SNR Thee detection schemes: Theshold detection
Revision of Lectue Eight Baseband equivalent system and equiements of optimal tansmit and eceive filteing: (1) achieve zeo ISI, and () maximise the eceive SNR Thee detection schemes: Theshold detection
Probablistically Checkable Proofs
 Lectue 12 Pobablistically Checkable Poofs May 13, 2004 Lectue: Paul Beame Notes: Chis Re 12.1 Pobablisitically Checkable Poofs Oveview We know that IP = PSPACE. This means thee is an inteactive potocol
Lectue 12 Pobablistically Checkable Poofs May 13, 2004 Lectue: Paul Beame Notes: Chis Re 12.1 Pobablisitically Checkable Poofs Oveview We know that IP = PSPACE. This means thee is an inteactive potocol
