A Lower Bound for the Length of a Partial Transversal in a Latin Square, Revised Version
|
|
|
- Janice Miller
- 6 years ago
- Views:
Transcription
1 A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo , Tehrn, Irn Deprtment of Mthemtis, Msshusetts Institute of Tehnology, Cmridge, MA 02139, USA Astrt It is proved tht every n n Ltin squre hs prtil trnsversl of length t lest n O(log 2 n). The previous ppers proving these results [inluding one y the seond uthor] not only ontined n error, ut were sloppily written nd quite diffiult to understnd. We hve orreted the error nd improved the lrity. 1 Introdution A Ltin squre of order n is n n n rry of ells eh ontining one of n distint symols suh tht in eh row nd olumn every symol ppers etly one. We define prtil trnsversl of length j s set of n ells with etly one in eh row nd olumn nd ontining etly j distint symols (this differs from the usul definition in tht n j etr ells re dded). Koksm [5] showed tht Ltin squre of order n hs prtil trnsversl of length t lest (2n + 1)/3. This ws improved y Drke [3] to 3n/4 nd then simultneously y Brouwer et l. [1] nd y Woolright [8] to n n. This ws in turn improved y Shor [7] to n 5.53 log 2 n nd then y Fu et l. [4], who optimized the prmeters in [7] to slightly improve the onstnt. One of us (P.H.) disovered ug in [7] tht lso ffets [4]. This pper fies the ug, whih ws used y the reversl of inequlity (26) in [7]. We still otin n n O(log 2 n) lower ound, leit with worse onstnt thn in [7, 4]. This is well elow Bruldi s onjeture of n 1, nd Ryser s of n for odd n [2, 6]. The proof in this pper is muh the sme s in [7] eept for the lst prt of Setion 4. The erlier prt of the pper hs een revised to improve the lrity of the presenttion. 1
2 d Squre 1 Figure 1: Squre 1: An emple of the opertor #. In this se, we reple the ells (1,1) nd (3,3) in the prtil trnsversl on the digonl with the ells (1,3) nd (3,1) to otin nother prtil trnsversl, lso of length 4. 2 The Opertion # Given prtil trnsversl T of length n k, with k 2, one n find nother prtil trnsversl of equl or greter length in the following mnner: Choose two ells in T, sy ells (i 1, j 1 ) nd (i 2, j 2 ), suh tht T {(i 1, j 1 ), (i 2, j 2 )} ontins n k distint symols. These two ells n either ontin two distint duplited symols, or two ourrenes of the sme symol, provided this symol ppers in the trnsversl t lest three times. Reple these two ells with the ells (i 1, j 2 ) nd (i 2, j 1 ). Sine we hose ells ontining duplited symols, the new prtil trnsversl hs length t lest n k, s eh of the symols in the originl trnsversl is represented in one of the unhnged ells (see Squre 1). We ll this opertion #, nottion hosen for its shpe. We now give motivting emple of the use of the opertion #, y pplying it to show tht every Ltin squre of order 6 hs prtil trnsversl of length t lest 5. Consider ounteremple. Assume for now tht the longest prtil trnsversl hs length 4. The squre must thus hve prtil trnsversl ontining multiset of symols either of the form (,,,,, d) or the form (,,,,, d). Let us nlyze the se where it ontins (,,,,, d) (See Squre 1). We ssume tht this prtil trnsversl is on the digonl, nd ll it T 0. We n pply # to the ells (1, 1) nd (3, 3) in T 0 to get new prtil trnsversl T 1. By our hypotheses, the new ells (1, 3) nd (3, 1) in T 1 must ontin symol hosen from the set {, d}. By symmetry, we only need to nlyze two ses here: either oth symols re the sme or there is one nd one d. We will nlyze the se where they re oth s. We n pply # to the ells (1, 3) nd (5, 5) in T 1 to otin new prtil trnsversl T 2 (s shown 2
3 d d y d d Squre 2 Squre 3 Figure 2: Squre 2: Another emple of the opertion #. In this, we reple the the ells (1,3) nd (5,5) in the prtil trnsversl indited in old with the ells ontining symols nd y. If this Ltin squre hd no prtil trnsversl of length greter thn 4, we must hve tht {, d} nd y {, d}. Squre 3: After two more pplitions of #, we know tht if the Ltin squre hd no prtil trnsversl of length greter thn 4, it would hve to look like this, with the symols hosen from the set {,,, d}. in Squre 2), nd we disover tht the symols in (1, 5) nd (5, 3) must e hosen from the set {,, d}. Now, strting from T 0 gin we n pply # to the ells (1, 1) nd (4, 4) to otin prtil trnsversl T 3, nd we disover tht the ells (1, 4) nd (4, 1) must oth ontin d. (See Squre 3.) We n now pply # to the ells (1, 4) nd (6, 6) in T 3 to otin T 4, nd disover tht the symols in (1, 6) nd (6, 4) must e hosen from the set {,, }. We now know tht our Ltin squre looks like Squre 3, where the s re symols from the set {,,, d}. The first row ontins five distint symols from the set {,,, d}, ontrdition y the pigeonhole priniple. The se where the longest prtil trnsversl hs length less thn 4, s well s the ses where the ell (3, 1) in Squre 1 is d insted of nd the se where the digonl is (,,,,, d), n e hndled using very similr nlysis, whih we will not present here. We define prtil Ltin squre s n n n squre with some of its ells ontining symols (the others we ll empty) suh tht no symol ppers twie in ny row or olumn. A prtil trnsversl of n n n prtil Ltin squre is set of n non-empty ells, one from eh row nd olumn. We sy this prtil trnsversl hs length j if it ontins j distint symols. An m m susqure S of n n n prtil Ltin squre S is the set of m 2 ells in some suset of m rows nd some suset of m olumns of S, where some nonempty ells in S my possily e repled y empty 3
4 ells in S. Consider Ltin squre with prtil trnsversl of mimum length n k, with k 2. By pplying # to this prtil trnsversl, we will get other prtil trnsversls, whose length must lso e n k nd whose set of symols is the sme s the first. Applying # repetedly to these prtil trnsversls, we eventully will otin set of suh prtil trnsversls losed under #. All of these prtil trnsversls ontin the sme set of n k distint symols, so y ignoring ll ells eept those in this set of prtil trnsversls, we otin prtil Ltin squre S ontining n k symols nd set T of prtil trnsversls of S losed under #. We will ll this pir (S, T ) prtil Ltin squre stisfying A k. More formlly, we hve: Definition. An n n prtil Ltin squre stisfying A k is prtil Ltin squre, together with nonempty set T of prtil trnsversls of S of length n k. Eh non-empty ell must pper in t lest one of the prtil trnsversls in T. The set T of prtil trnsversls must form onneted grph under the opertion #, nd must e losed under the opertion #. For prtil Ltin susqure (S, T ) stisfying A k of prtil Ltin squre (S, T ) stisfying A k, in ddition to the properties ontined in the ove definition, we lso require n inhertne property. Nmely, we require T to e suset of the set T restrited to S, i.e., tht T {T S : T T }. Note tht Bruldi s onjeture (tht ll Ltin squres of order n hve prtil trnsversl of length t lest n 1) does not pper to rule out the eistene of prtil Ltin squres stisfying A 2, or A k for k > 2. If S is n n n prtil Ltin squre stisfying A k, we n onstrut n (n + 1) (n + 1) prtil Ltin squre S stisfying A k, y dding n etr row nd olumn tht onsist entirely of empty ells eept for the (n + 1, n + 1) ell, whih ontins new symol. The prtil trnsversls in T re those in T ugmented y the ell (n + 1, n + 1). Together with the se nlysis on Ltin squres of size 6 skethed erlier, this oservtion implies tht ny prtil Ltin squre stisfying A 2 must hve size t lest 7. In terminology we will e defining lter in this pper, this mens tht n 2 7. (1) We use the properties of miniml Ltin squre stisfying A k to otin set of inequlities, nd then use these inequlities to derive our min result. We first prove lemm: Lemm 1 Given prtil Ltin squre (S, T ) stisfying A k suh tht no susqure stisfies A k, then no ell is ontined in ll prtil trnsversls in T. Tht is, given non-empty ell (i, j) nd prtil trnsversl ontining (i, j), y sequene of opertions #, one n otin prtil trnsversl in T not ontining (i, j). 4
5 Proof. Suppose there is ell (i, j) ontined in ll prtil trnsversls. We will ll this fied ell. Let e the symol in this ell. If ppers nywhere else in the prtil Ltin squre, there is trnsversl ontining oth s (the seond ppers in some prtil trnsversl sine every non-empty ell does, nd this prtil trnsversl must ontin the first sine ll prtil trnsversls do). We n then pply # to this prtil trnsversl to otin prtil trnsversl without the fied ell, ontrdition. We re left with the se where does not pper nywhere else in the prtil Ltin squre. Now, y deleting the row nd olumn ontining the, one finds susqure stisfying A k, ontrdition of the hypothesis. We hve just proved tht no ell in miniml squre stisfying A k is fied, so given non-empty ell in suh squre, there is prtil trnsversl in T ontining oth tht ell nd nother ell with the sme symol (otherwise, the grph of prtil trnsversls would not e onneted y #). We n hoose ny filled ell, sy (1, 1), nd hoose prtil trnsversl T 0 through it tht duplites the symol in it, sy. Now, let T T e the set of prtil trnsversls ontining t lest two s, inluding the one in ell (1, 1). Consider the onneted omponent of T whih is generted y sequene of opertions # strting with T 0. This omponent orresponds preisely to the set of prtil trnsversls generted y # strting from T 0 (1, 1) in the susqure formed y deleting the first row nd olumn. Tking this set of prtil trnsversls gives n (n 1) (n 1) prtil Ltin squre stisfying A k 1. Note tht this susqure my hve some empty ells whih were filled in the originl n n squre. Lemm 2 In n (n 1) (n 1) prtil Ltin squre stisfying A k 1 indued s desried ove from n n n prtil Ltin squre stisfying A k, the prtil trnsversls generted y # must hve fied ell, i.e., there is some ell tht ppers in ll of these prtil trnsversls. Proof. We ssume without loss of generlity tht the prtil trnsversl T 0 ontining two s disussed ove is the digonl. Suppose tht there re no fied ells in the (n 1) (n 1) prtil Ltin squre. Then there must e prtil trnsversl T 1 in this smller squre whih ontins the ell (i, i) s well s nother ell with the sme symol. The prtil trnsversl T 1 := T 1 (1, 1) must lso pper in the n n squre. Now, in T 1, either (1, 1) nd (i, i) ontin two different duplited symols, or there re t lest three s in T 1 nd (1, 1) nd (i, i) oth ontin. In either se, we n pply # to T 1, deleting the ells (1, 1) nd (i, i) nd otining the ells (1, i) nd (i, 1) (See Squre 4). Sine i ws ritrry, this gives us n filled ells in the first row nd olumn of the squre, ontrdition sine there re only n k distint symols. We now etend the nlysis of Lemm 2 to prove the following. Theorem 1 In prtil Ltin squre stisfying A k suh tht no susqure stisfies A k, there re t lest n k 1 + k filled ells in eh row nd olumn, where n k 1 is the size of the smllest susqure stisfying A k 1. 5
6 1 1 i 1 1 i j i i d d j Squre 4 Squre 5 Figure 3: Squre 4: Illustrtion for the proof of Lemm 2. By pplying # s shown, we find the first row ontins only non-empty ells, ontrdition. Squre 5: Illustrtion for the proof of Theorem 1. If n element lies in the first row ove the smll squre nd lso on the digonl elow nd to the right of the smll squre, we find non-empty ell in the first olumn, elow the smll squre, s shown. Proof. Consider prtil trnsversl T 0, whih we will ssume is long the digonl, nd ell within it, sy (1, 1), ontining duplited symol. Now, hold this ell fied, nd onsider the (n 1) (n 1) prtil Ltin squre stisfying A k 1 generted y the opertion # s ove. Let us ssume tht m ells of T 0 re not fied, nd re in rows nd olumns 2 through m + 1. Note tht this m m susqure stisfies A k 1. By the sme resoning s in the ove lemm, there is trnsversl with duplited symol in ell (i, i), for ll i, 2 i m + 1. Applying #, we find tht there is symol in ells (1, i) nd (i, 1), for 2 i m + 1. There re only m (k 1) symols in the m m susqure stisfying A k 1 ontining rows nd olumns 2 through m + 1, leving (k 1) symols in (1, i), 2 i m + 1, whih re not in the susqure stisfying A k 1 (See Squre 5). Note tht some of these symols my pper in the m m susqure in the originl prtil Ltin squre, ut they do not pper in the set T of prtil trnsversls ssoited with this susqure. Suppose one of these k 1 symols, sy, is in the (1, i) ell. There is in the originl prtil trnsversl T 0, nd sine it is not in the susqure, it must e in ell (j, j), for some j > m + 1. Moreover, there is prtil trnsversl of the smll squre with duplite letter in ell (i, i), sy. (Note this letter ould e, the sme s in ell (1, 1), in whih se there re three s in the orresponding prtil trnsversl of the n n squre). We n now pply # to remove the (1, 1) nd the (i, i) ells, nd we find tht the (1, i) nd (i, 1) ells re filled. Now, the in the (j, j) ell nd the symol in the (i, 1) re oth duplites, so y pplying # gin 6
7 P S j S k Squre 6 Figure 4: The region P in the proof of Theorem 2 we find tht the (j, 1) ell nd the (i, j) ell re filled. (Agin, if oth ells (j, j) nd (i, 1) ontin, there re three s in the prtil trnsversl.) Thus, we know tht the (j, 1) ell is filled. Sine there re t lest k 1 symols in the (1, i) ells, 2 i m + 1, whih re not in the susqure stisfying A k 1, we n pply the sme proess to otin k 1 filled ells in the first olumn in or elow the (m+2)nd row. This gives t lest m + k filled ells in the first olumn, sine the first m + 1 ells re lso filled. Now, m n k 1, euse m is the size of susqure stisfying A k 1, nd n k 1 ws the size of the miniml suh susqure. Sine (1, 1) ws n ritrry ell in our originl prtil trnsversl, this rgument shows tht t lest n k 1 + k ells re filled in eh row nd olumn. If we let n k = n e the size of the originl prtil Ltin squre stisfying A k, then this Theorem shows tht n k n k 1 + 2k, (2) sine the lrger squre hs n k k distint symols, of whih t lest n k 1 +k pper in eh row nd olumn. 3 An Inequlity Let S k e squre stisfying A k suh tht no susqure stisfies A k. It ws shown in Setion 2 tht there must e susqure stisfying A k 1, Choose S k 1 to e the smllest susqure of S k stisfying A k 1 nd, reursively, S m to e the smllest susqure of S m+1 stisfying A m, until the sequene ends t S 2. Let n j e the size of S j. Theorem 2 In S k, s defined ove, for ll j < k, (n k n j )(2n j + n k 1 2n k + 2k j) n j (n j n j 1 2j). (3) Proof. Consider Squre 6. We will ount the numer of filled ells in the retngle P in two different wys. First, there re n k n j olumns in P, nd sine 7
8 eh olumn of S k hs t lest n k 1 +k filled ells, we hve t lest n k 1 +k (n k n j ) filled ells in eh olumn of P, nd t lest (n k n j )(n k 1 + n j n k + k) filled ells in P. We will ll the symols in S j old symols nd those in S k nd not in S j new symols. There re n j j old symols nd n k k n j + j new symols. There re n j rows in P. In eh row of S j there re t lest n j 1 + j old symols. Sine there re only n j j distint old symols, this leves t most n j j (n j 1 + j) old symols in eh row of P, for totl of t most n j (n j n j 1 2j) filled ells ontining old symols in P. There re n k k n j +j new symols, nd n k n j olumns in P. Thus, there re t most (n k n j )(n k k n j + j) filled ells ontining new symols in P. Adding the numer of ells with old nd with new symols in P, we get upper ound for the numer of filled ells in P. Setting this upper ound greter thn or equl to the lower ound, nd simplifying, we otin the inequlity (3) ove. 4 The Min Result Suppose we hve Ltin squre with no prtil trnsversl of length more thn n l. By the previous setions, we hve sequene n 2 < n 3 <... < n l stisfying the Inequlities (1), (2), (3), from the previous setion. Reiterting these inequlities, we hve tht if 2 i l nd 1 j < k l, then n 2 7, (1) n i n i 1 + 2i, (2) (n k n j )(2n j + n k 1 2n k + 2k j) n j (n j n j 1 2j). (3) We will now derive the inequlity k log 2 n k from the Inequlity (3). We first prove the following lemm. Lemm 3 Either n j 4 5 n k or n j n j (n k n j 1 ). Proof. Letting d k := n k n k 1, d j := n j n j 1, (4) we hve, from (3) d j 2j n k n j n j (2n j d k n k + 2k j). (5) 8
9 The diretion of the inequlity lets us remove the lower order terms, giving Now, we ssume tht n j 4 5 n k. This gives d j n k n j n j (2n j d k n k ). (6) d k = n k n k 1 n k n j 1 5 n k, (7) n k + d k 6 5 n k, (8) n k + d k 3 2 n j. (9) Comining (6) nd (9) gives d j 1 2 (n k n j ), (10) By the definition of d j, we hve n j n j n k 1 2 n j, (11) so nd 3 2 n j 3 2 n j (n k n j 1 ). (12) n j n j (n k n j 1 ), (13) ompleting the proof. giving Now, suppose tht n k < 5 4 n j, so 1 3 (n k n j 1 ) n j n j 1, (14) n k n j 2 3 (n k n j 1 ). (15) Sine (15) holds for ll j where j < k, nd n k < 5 4 n j, y indution we get, 1 n k n k 1 ( ) k j 2 (n k n j 1), (16) 3 or k j log 3/2 (n k n j 1 ). (17) Now, suppose in ddition tht k j 1 > log 3/2 n j 4, (18) 9
10 then ontrdition. n j log 3/2 4 < k j 1 log 3/2(n k n j ), (19) n j 4 < n k n j (20) 5 4 n j < n k, (21) If k j log 3/2 n j, then sine log 3/2 n j > log 3/2 n j log 3/ , we hve tht (18) holds, implying tht n k 5 4 n j. We now let k 4 = 2, nd k i = k i 1 + log 3/2 (n ki 1 ). (22) By indution, we otin tht for l k i, ( ) i+1 5 n l, (23) 4 where the se se follows from n 2 7 > (5/4) 5. We know tht n ki 1 < n k for k i 1 < k. So from (22), if k i 1 < k, we hve k i k i 1 + log 3/2 n k. (24) We n now prove the following Lemm. We will speify the et vlue of lter. Lemm 4 For 1/2, either or 1 log 3/2 n k k 1 2, (25) log 5/4 n k > k 1 2. (26) Proof. If log 3/2 n k k 1 2, we hve (25). Otherwise suppose tht log 3/2 n k < k 1 2. (27) Then from (24), for ll k i 1 < k we hve k i < k i 1 + k 1 2. (28) Let j e the minimum integer suh tht k j k. Summing (28) over i gives k k j < k 4 + (j 4)k 1 2, (29) 10
11 whih rerrnges to j > k k (30) k1/2 This shows tht for minimum j suh tht k j k we hve Using (23) with i = j 1 nd (31) we otin j > k 2 k 1/2 + 4 > 1 k 1 2. (31) n kj 1 ( ) j 5 > 4 ( ) 1 5 k1/2. (32) 4 We know tht n k > n kj 1 (euse k > k j 1 ). Then giving (26). log 5/4 n k > 1 k 1 2, (33) We n now mke the left-hnd side of the two equtions in Lemm 4 equl y setting = log 5/ log 3. This gives 4 2 from whih follows: 1 log n k > k 1/2, (34) log 5 log Theorem 3 Every Ltin squre hs prtil trnsversl of length t lest n log 2 n. (35) Here (log 5 4 log 3 2 ) 1. No serious ttempt hs een mde to optimize this onstnt. As ws remrked in [7] the Inequlity (3) nnot imply nything etter thn n log 2 n, sine the sequene n k = 2 k stisfies (3). Let us tke the opportunity to remrk tht Inequlities (1 3) nnot in ft hieve ound etter thn n O(log 2 n). If we let κ = k 1 2 nd γ = k κ 2, then the sequene n k = β κ α 3κ γ for suffiiently lrge 1 nd β α stisfies these inequlities nd hs growth rte of n k = e O(k1/2). 11
12 5 Aknowledgments The uthors would like to thnk the referees for reful reding of this pper nd eeptionlly helpful omments. The seond uthor is indeted to Her Ryser, who introdued him to this prolem over 27 yers go. Referenes [1] A. E. Brouwer, A. J. de Vries, nd R. M. A. Wiering. A lower ound for the length of prtil trnsversls in Ltin squre. Nieuw Arh. Wisk., 24(3): , [2] R. A. Bruldi nd H. J. Ryser. Comintoril Mtri Theory. Cmridge Univ. Press, [3] D. A. Drke. Miml sets of Ltin squres nd prtil trnsverls. J. Sttist. Plnn. Inferene, 1: , [4] H. L. Fu, S. C. Lin, nd C. M. Fu. The length of prtil trnsversl in Ltin squre. J. Com. Mth. Comin. Comput., 43:57 64, [5] K. K. Koksm. A lower ound for the order of prtil trnsversl in Ltin squre. J. Comintoril Theory Ser. A, 7:94 95, [6] H. J. Ryser. Neuere Proleme der Komintorik. In Vorträge üer Komintorik, pges 69 91, Oerwolfh, Germny, July Mtemtishes Forshungsinstitute Oerwolfh. [7] P. W. Shor. A lower ound for the length of prtil trnsversl in Ltin squre. J. Comintoril Theory Ser. A, 33(1):1 8, [8] D. E. Woolright. An n n Ltin squre hs trnsversl with t lest n n distint elements. J. Comintoril Theory Ser. A, 24: ,
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
#A42 INTEGERS 11 (2011) ON THE CONDITIONED BINOMIAL COEFFICIENTS
 #A42 INTEGERS 11 (2011 ON THE CONDITIONED BINOMIAL COEFFICIENTS Liqun To Shool of Mthemtil Sienes, Luoyng Norml University, Luoyng, Chin lqto@lynuedun Reeived: 12/24/10, Revised: 5/11/11, Aepted: 5/16/11,
#A42 INTEGERS 11 (2011 ON THE CONDITIONED BINOMIAL COEFFICIENTS Liqun To Shool of Mthemtil Sienes, Luoyng Norml University, Luoyng, Chin lqto@lynuedun Reeived: 12/24/10, Revised: 5/11/11, Aepted: 5/16/11,
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Discrete Structures Lecture 11
 Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
Algorithms & Data Structures Homework 8 HS 18 Exercise Class (Room & TA): Submitted by: Peer Feedback by: Points:
 Eidgenössishe Tehnishe Hohshule Zürih Eole polytehnique fédérle de Zurih Politenio federle di Zurigo Federl Institute of Tehnology t Zurih Deprtement of Computer Siene. Novemer 0 Mrkus Püshel, Dvid Steurer
Eidgenössishe Tehnishe Hohshule Zürih Eole polytehnique fédérle de Zurih Politenio federle di Zurigo Federl Institute of Tehnology t Zurih Deprtement of Computer Siene. Novemer 0 Mrkus Püshel, Dvid Steurer
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
TOPIC: LINEAR ALGEBRA MATRICES
 Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
Necessary and sucient conditions for some two. Abstract. Further we show that the necessary conditions for the existence of an OD(44 s 1 s 2 )
 Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Lecture 3. In this lecture, we will discuss algorithms for solving systems of linear equations.
 Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
Computational Biology Lecture 18: Genome rearrangements, finding maximal matches Saad Mneimneh
 Computtionl Biology Leture 8: Genome rerrngements, finding miml mthes Sd Mneimneh We hve seen how to rerrnge genome to otin nother one sed on reversls nd the knowledge of the preserved loks or genes. Now
Computtionl Biology Leture 8: Genome rerrngements, finding miml mthes Sd Mneimneh We hve seen how to rerrnge genome to otin nother one sed on reversls nd the knowledge of the preserved loks or genes. Now
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
September 13 Homework Solutions
 College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Global alignment. Genome Rearrangements Finding preserved genes. Lecture 18
 Computt onl Biology Leture 18 Genome Rerrngements Finding preserved genes We hve seen before how to rerrnge genome to obtin nother one bsed on: Reversls Knowledge of preserved bloks (or genes) Now we re
Computt onl Biology Leture 18 Genome Rerrngements Finding preserved genes We hve seen before how to rerrnge genome to obtin nother one bsed on: Reversls Knowledge of preserved bloks (or genes) Now we re
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
The Word Problem in Quandles
 The Word Prolem in Qundles Benjmin Fish Advisor: Ren Levitt April 5, 2013 1 1 Introdution A word over n lger A is finite sequene of elements of A, prentheses, nd opertions of A defined reursively: Given
The Word Prolem in Qundles Benjmin Fish Advisor: Ren Levitt April 5, 2013 1 1 Introdution A word over n lger A is finite sequene of elements of A, prentheses, nd opertions of A defined reursively: Given
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
Can one hear the shape of a drum?
 Cn one her the shpe of drum? After M. K, C. Gordon, D. We, nd S. Wolpert Corentin Lén Università Degli Studi di Torino Diprtimento di Mtemti Giuseppe Peno UNITO Mthemtis Ph.D Seminrs Mondy 23 My 2016 Motivtion:
Cn one her the shpe of drum? After M. K, C. Gordon, D. We, nd S. Wolpert Corentin Lén Università Degli Studi di Torino Diprtimento di Mtemti Giuseppe Peno UNITO Mthemtis Ph.D Seminrs Mondy 23 My 2016 Motivtion:
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Reference : Croft & Davison, Chapter 12, Blocks 1,2. A matrix ti is a rectangular array or block of numbers usually enclosed in brackets.
 I MATRIX ALGEBRA INTRODUCTION TO MATRICES Referene : Croft & Dvison, Chpter, Blos, A mtri ti is retngulr rr or lo of numers usull enlosed in rets. A m n mtri hs m rows nd n olumns. Mtri Alger Pge If the
I MATRIX ALGEBRA INTRODUCTION TO MATRICES Referene : Croft & Dvison, Chpter, Blos, A mtri ti is retngulr rr or lo of numers usull enlosed in rets. A m n mtri hs m rows nd n olumns. Mtri Alger Pge If the
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER MACHINES AND THEIR LANGUAGES ANSWERS
 The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
Section 4: Integration ECO4112F 2011
 Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Hyers-Ulam stability of Pielou logistic difference equation
 vilble online t wwwisr-publitionsom/jns J Nonliner Si ppl, 0 (207, 35 322 Reserh rtile Journl Homepge: wwwtjnsom - wwwisr-publitionsom/jns Hyers-Ulm stbility of Pielou logisti differene eqution Soon-Mo
vilble online t wwwisr-publitionsom/jns J Nonliner Si ppl, 0 (207, 35 322 Reserh rtile Journl Homepge: wwwtjnsom - wwwisr-publitionsom/jns Hyers-Ulm stbility of Pielou logisti differene eqution Soon-Mo
Arrow s Impossibility Theorem
 Rep Voting Prdoxes Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Voting Prdoxes Properties Arrow s Theorem Leture Overview 1 Rep
Rep Voting Prdoxes Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Voting Prdoxes Properties Arrow s Theorem Leture Overview 1 Rep
Mid-Term Examination - Spring 2014 Mathematical Programming with Applications to Economics Total Score: 45; Time: 3 hours
 Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Intermediate Math Circles Wednesday, November 14, 2018 Finite Automata II. Nickolas Rollick a b b. a b 4
 Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
More Properties of the Riemann Integral
 More Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologil Sienes nd Deprtment of Mthemtil Sienes Clemson University Februry 15, 2018 Outline More Riemnn Integrl Properties The Fundmentl
More Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologil Sienes nd Deprtment of Mthemtil Sienes Clemson University Februry 15, 2018 Outline More Riemnn Integrl Properties The Fundmentl
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Algorithm Design and Analysis
 Algorithm Design nd Anlysis LECTURE 5 Supplement Greedy Algorithms Cont d Minimizing lteness Ching (NOT overed in leture) Adm Smith 9/8/10 A. Smith; sed on slides y E. Demine, C. Leiserson, S. Rskhodnikov,
Algorithm Design nd Anlysis LECTURE 5 Supplement Greedy Algorithms Cont d Minimizing lteness Ching (NOT overed in leture) Adm Smith 9/8/10 A. Smith; sed on slides y E. Demine, C. Leiserson, S. Rskhodnikov,
Arrow s Impossibility Theorem
 Rep Fun Gme Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Fun Gme Properties Arrow s Theorem Leture Overview 1 Rep 2 Fun Gme 3 Properties
Rep Fun Gme Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Fun Gme Properties Arrow s Theorem Leture Overview 1 Rep 2 Fun Gme 3 Properties
arxiv: v1 [math.gr] 11 Jan 2019
![arxiv: v1 [math.gr] 11 Jan 2019 arxiv: v1 [math.gr] 11 Jan 2019](/thumbs/88/115019513.jpg) The Generlized Dehn Property does not imply liner isoperimetri inequlity Owen Bker nd Timothy Riley rxiv:1901.03767v1 [mth.gr] 11 Jn 2019 Jnury 15, 2019 Astrt The Dehn property for omplex is tht every
The Generlized Dehn Property does not imply liner isoperimetri inequlity Owen Bker nd Timothy Riley rxiv:1901.03767v1 [mth.gr] 11 Jn 2019 Jnury 15, 2019 Astrt The Dehn property for omplex is tht every
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Part 4. Integration (with Proofs)
 Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.
![(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P. (a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.](/thumbs/72/66745617.jpg) Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
8.3 THE HYPERBOLA OBJECTIVES
 8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
MAT 403 NOTES 4. f + f =
 MAT 403 NOTES 4 1. Fundmentl Theorem o Clulus We will proo more generl version o the FTC thn the textook. But just like the textook, we strt with the ollowing proposition. Let R[, ] e the set o Riemnn
MAT 403 NOTES 4 1. Fundmentl Theorem o Clulus We will proo more generl version o the FTC thn the textook. But just like the textook, we strt with the ollowing proposition. Let R[, ] e the set o Riemnn
Math 4310 Solutions to homework 1 Due 9/1/16
 Mth 4310 Solutions to homework 1 Due 9/1/16 1. Use the Eucliden lgorithm to find the following gretest common divisors. () gcd(252, 180) = 36 (b) gcd(513, 187) = 1 (c) gcd(7684, 4148) = 68 252 = 180 1
Mth 4310 Solutions to homework 1 Due 9/1/16 1. Use the Eucliden lgorithm to find the following gretest common divisors. () gcd(252, 180) = 36 (b) gcd(513, 187) = 1 (c) gcd(7684, 4148) = 68 252 = 180 1
Technische Universität München Winter term 2009/10 I7 Prof. J. Esparza / J. Křetínský / M. Luttenberger 11. Februar Solution
 Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Lecture 3: Equivalence Relations
 Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
Symmetrical Components 1
 Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
System Validation (IN4387) November 2, 2012, 14:00-17:00
 System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
Bisimulation, Games & Hennessy Milner logic
 Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
Lecture 2 : Propositions DRAFT
 CS/Mth 240: Introduction to Discrete Mthemtics 1/20/2010 Lecture 2 : Propositions Instructor: Dieter vn Melkeeek Scrie: Dlior Zelený DRAFT Lst time we nlyzed vrious mze solving lgorithms in order to illustrte
CS/Mth 240: Introduction to Discrete Mthemtics 1/20/2010 Lecture 2 : Propositions Instructor: Dieter vn Melkeeek Scrie: Dlior Zelený DRAFT Lst time we nlyzed vrious mze solving lgorithms in order to illustrte
Counting Paths Between Vertices. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs
 Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
The Riemann-Stieltjes Integral
 Chpter 6 The Riemnn-Stieltjes Integrl 6.1. Definition nd Eistene of the Integrl Definition 6.1. Let, b R nd < b. ( A prtition P of intervl [, b] is finite set of points P = { 0, 1,..., n } suh tht = 0
Chpter 6 The Riemnn-Stieltjes Integrl 6.1. Definition nd Eistene of the Integrl Definition 6.1. Let, b R nd < b. ( A prtition P of intervl [, b] is finite set of points P = { 0, 1,..., n } suh tht = 0
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
Chapter 9 Definite Integrals
 Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Discrete Structures, Test 2 Monday, March 28, 2016 SOLUTIONS, VERSION α
 Disrete Strutures, Test 2 Mondy, Mrh 28, 2016 SOLUTIONS, VERSION α α 1. (18 pts) Short nswer. Put your nswer in the ox. No prtil redit. () Consider the reltion R on {,,, d with mtrix digrph of R.. Drw
Disrete Strutures, Test 2 Mondy, Mrh 28, 2016 SOLUTIONS, VERSION α α 1. (18 pts) Short nswer. Put your nswer in the ox. No prtil redit. () Consider the reltion R on {,,, d with mtrix digrph of R.. Drw
Solutions for HW9. Bipartite: put the red vertices in V 1 and the black in V 2. Not bipartite!
 Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
8 THREE PHASE A.C. CIRCUITS
 8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
Core 2 Logarithms and exponentials. Section 1: Introduction to logarithms
 Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Algorithm Design and Analysis
 Algorithm Design nd Anlysis LECTURE 8 Mx. lteness ont d Optiml Ching Adm Smith 9/12/2008 A. Smith; sed on slides y E. Demine, C. Leiserson, S. Rskhodnikov, K. Wyne Sheduling to Minimizing Lteness Minimizing
Algorithm Design nd Anlysis LECTURE 8 Mx. lteness ont d Optiml Ching Adm Smith 9/12/2008 A. Smith; sed on slides y E. Demine, C. Leiserson, S. Rskhodnikov, K. Wyne Sheduling to Minimizing Lteness Minimizing
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
A CLASS OF GENERAL SUPERTREE METHODS FOR NESTED TAXA
 A CLASS OF GENERAL SUPERTREE METHODS FOR NESTED TAXA PHILIP DANIEL AND CHARLES SEMPLE Astrt. Amlgmting smller evolutionry trees into single prent tree is n importnt tsk in evolutionry iology. Trditionlly,
A CLASS OF GENERAL SUPERTREE METHODS FOR NESTED TAXA PHILIP DANIEL AND CHARLES SEMPLE Astrt. Amlgmting smller evolutionry trees into single prent tree is n importnt tsk in evolutionry iology. Trditionlly,
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
For a, b, c, d positive if a b and. ac bd. Reciprocal relations for a and b positive. If a > b then a ab > b. then
 Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
CIT 596 Theory of Computation 1. Graphs and Digraphs
 CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
] dx (3) = [15x] 2 0
![] dx (3) = [15x] 2 0 ] dx (3) = [15x] 2 0](/thumbs/80/81916477.jpg) Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
= x x 2 = 25 2
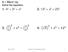 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
On Implicative and Strong Implicative Filters of Lattice Wajsberg Algebras
 Glol Journl of Mthemtil Sienes: Theory nd Prtil. ISSN 974-32 Volume 9, Numer 3 (27), pp. 387-397 Interntionl Reserh Pulition House http://www.irphouse.om On Implitive nd Strong Implitive Filters of Lttie
Glol Journl of Mthemtil Sienes: Theory nd Prtil. ISSN 974-32 Volume 9, Numer 3 (27), pp. 387-397 Interntionl Reserh Pulition House http://www.irphouse.om On Implitive nd Strong Implitive Filters of Lttie
Probability. b a b. a b 32.
 Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
 Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Figure 1. The left-handed and right-handed trefoils
 The Knot Group A knot is n emedding of the irle into R 3 (or S 3 ), k : S 1 R 3. We shll ssume our knots re tme, mening the emedding n e extended to solid torus, K : S 1 D 2 R 3. The imge is lled tuulr
The Knot Group A knot is n emedding of the irle into R 3 (or S 3 ), k : S 1 R 3. We shll ssume our knots re tme, mening the emedding n e extended to solid torus, K : S 1 D 2 R 3. The imge is lled tuulr
Graph Theory. Simple Graph G = (V, E). V={a,b,c,d,e,f,g,h,k} E={(a,b),(a,g),( a,h),(a,k),(b,c),(b,k),...,(h,k)}
 Grph Theory Simple Grph G = (V, E). V ={verties}, E={eges}. h k g f e V={,,,,e,f,g,h,k} E={(,),(,g),(,h),(,k),(,),(,k),...,(h,k)} E =16. 1 Grph or Multi-Grph We llow loops n multiple eges. G = (V, E.ψ)
Grph Theory Simple Grph G = (V, E). V ={verties}, E={eges}. h k g f e V={,,,,e,f,g,h,k} E={(,),(,g),(,h),(,k),(,),(,k),...,(h,k)} E =16. 1 Grph or Multi-Grph We llow loops n multiple eges. G = (V, E.ψ)
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Linear Inequalities. Work Sheet 1
 Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
Chapter 3. Vector Spaces. 3.1 Images and Image Arithmetic
 Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Logic Synthesis and Verification
 Logi Synthesis nd Verifition SOPs nd Inompletely Speified Funtions Jie-Hong Rolnd Jing 江介宏 Deprtment of Eletril Engineering Ntionl Tiwn University Fll 2010 Reding: Logi Synthesis in Nutshell Setion 2 most
Logi Synthesis nd Verifition SOPs nd Inompletely Speified Funtions Jie-Hong Rolnd Jing 江介宏 Deprtment of Eletril Engineering Ntionl Tiwn University Fll 2010 Reding: Logi Synthesis in Nutshell Setion 2 most
Lecture Notes No. 10
 2.6 System Identifition, Estimtion, nd Lerning Leture otes o. Mrh 3, 26 6 Model Struture of Liner ime Invrint Systems 6. Model Struture In representing dynmil system, the first step is to find n pproprite
2.6 System Identifition, Estimtion, nd Lerning Leture otes o. Mrh 3, 26 6 Model Struture of Liner ime Invrint Systems 6. Model Struture In representing dynmil system, the first step is to find n pproprite
