The Kumaraswamy GP Distribution

Transcription

1 Joural of Data Scece 11(2013), The Kumaraswamy GP Dstrbuto Saralees Nadarajah ad Sumaya Eljabr Uversty of Machester Abstract: The geeralzed Pareto (GP) dstrbuto s the most popular model for extreme values. Recetly, Papastathopoulos ad Taw Joural of Statstcal Plag ad Iferece 143 (2013), have proposed some geeralzatos of the GP dstrbuto for mproved modelg. Here, we pot that Papastathopoulos ad Taw s geeralzatos are fact ot ew ad the go o to propose a tractable geeralzato of the GP dstrbuto. For the latter geeralzato, we provde a comprehesve treatmet of mathematcal propertes, estmate parameters by the method of maxmum lkelhood ad provde the observed formato matrx. The proposed model s show to gve a better ft for the real data set used Papastathopoulos ad Taw. Key words: Beta dstrbuto, GP dstrbuto, Kumaraswamy dstrbuto, maxmum lkelhood, order statstcs. 1. Itroducto The geeralzed Pareto (GP) dstrbuto s the most wdely appled model for uvarate extreme values. Possble applcatos cover most areas of scece, egeerg ad medce. Some publshed applcatos are: lfetme data aalyss, coupo collector s problem, aalyss of rado audece data, aalyss of rafall tme seres, comparg vestmet rsk betwee Chese ad Amerca stock markets, regoal flood frequecy aalyss, drought modelg, value at rsk, aalyss of turbe steady-state, secod-order materal property closures, wd extremes, aalyss of a Spash motor lablty surace database, aalyss of fte buffer queues, rver flow modelg, measurg lqudty rsk of ope-ed fuds, modelg of extreme earthquake evets, estmato of the maxmum cluso sze clea steels, ad modelg of hgh-cocetratos short-rage atmospherc dsperso. For detals o the GP dstrbuto, ts theory ad further applcatos, we refer the readers to Leadbetter et al. (1987), Embrechts et al. (1997), Castllo et al. (2005), ad Resck (2008). Correspodg author.

2 740 Saralees Nadarajah ad Sumaya Eljabr However, the GP dstrbuto has bee msused too may areas, as ca be see from the lst gve. It does ot gve adequate fts may areas. For example, Madse ad Rosbjerg (1998) fd that the GP dstrbuto does ot gve a good ft to drought defct volumes due to may small drought evets. I a llustratve example of the SAS/ETS SEVERITY procedure, Josh (2010) fds Both plots dcate that the Exp (expoetal), Pareto, ad Gpd (geeralzed Pareto) dstrbutos are a poor ft. I ths paper, we propose a smple geeralzato of the GP dstrbuto. We provde two dfferet motvatos for ths smple geeralzato. The frst s based o the defto of the GP dstrbuto. The GP dstrbuto arses as the codtoal dstrbuto of exceedaces of a process over a large threshold (Pckads, 1975). If F ( ) deotes the cumulatve dstrbuto fucto of the process the we ca wrte ( 1 F (x) p 1 ξ x t ) 1/ξ, (1) for x > t ad some large t, where p = 1 F (t), x > t f ξ 0, t < x t /ξ f ξ < 0, < ξ < s a shape parameter ad > 0 s a scale parameter. Oe way to mprove o (1) s to take a mxture of GP cumulatve dstrbuto fuctos. That s, wrte 1 F (x) k ( ) x t 1/ξ w 1 ξ, (2) for x > t ad some large t. But mxtures of the form (2) are otorously dffcult to hadle ot just because of the complcated mathematcal form. Ifereces ad fttg of (2) are also dffcult. For example, o the subject of estmatg a mxture of Pareto dstrbutos, Bee et al. (2009) say Applcato of stadard techques to a mxture of Pareto s problematc. Ideed, applcatos of mxtures of Pareto dstrbutos have bee very lmted. A way aroud s to rewrte (2) a smple mathematcal form. There are may choces for the mathematcal form. A choce motvated by the works of Kumaraswamy (1980) ad Cordero ad de Castro (2011) s 1 F (x) = 1 G(x) a } b, (3) where G( ) deotes a GP cumulatve dstrbuto fucto ad a > 0, b > 0 are two addtoal parameters whose role s partly to troduce skewess ad to vary tal weghts. Note that the rght had sde of (3) ca be expaded as 1 G(x) a } b = c 1 G(x) b, (4) =0

3 The Kumaraswamy GP Dstrbuto 741 a mxture takg the form of (2). The coeffcets c are fuctos of a ad b. For stace, c 0 = a b. The parameter b maly dctates the tal behavors of the mxture compoets. The parameter a maly dctates the mxture coeffcets. Followg the termology used Cordero ad de Castro (2011), we shall refer to the dstrbuto gve by (3) as the KumGP dstrbuto. The probablty desty fucto correspodg to (3) s f(x) = ab g(x) G(x) a 1 1 G(x) a } b 1, (5) where g(x) = dg(x)/dx s a GP probablty desty fucto. Because g( ) ad G( ) are tractable, the KumGP dstrbuto ca be used qute effectvely eve f the data are cesored. Moreover, exstg software for the GP dstrbuto (say, to compute probablty desty fucto, cumulatve dstrbuto fucto, quatle fucto, momets, maxmum lkelhood estmates, radom umbers, etc) ca be easly adapted for the KumGP dstrbuto. Clearly, the GP dstrbuto s a specal case of the KumGP dstrbuto for a = b = 1 wth a cotuous crossover towards cases wth dfferet shapes (for example, a partcular combato of skewess ad kurtoss). The role of the two addtoal parameters, a > 0 ad b > 0, s to gover skewess ad geerate dstrbutos wth heaver/lgther tals. If a < 1 the the tals of f( ) wll be heaver tha those of g( ). Smlarly, f b < 1 the the tals of f( ) wll be heaver tha those of g( ). O the other had, f a > 1 the the tals of f( ) wll be lghter tha those of g( ). Smlarly, f b > 1 the the tals of f( ) wll be lghter tha those of g( ). Further descrpto of the role of a ad b s gve Sectos 2 ad 3. Aother physcal terpretato for the KumGP dstrbuto whe a ad b are postve tegers s as follows. Suppose a system s made of b depedet compoets ad that each compoet s made up of a depedet subcompoets. Suppose the system fals f ay of the b compoets fals ad that each compoet fals f all of the a subcompoets fal. Let X j1, X j2,, X ja deote the lfetmes of the subcompoets wth the jth compoet, j = 1, 2,, b wth a commo GP cumulatve dstrbuto fucto. Let X j deote the lfetme of the jth compoet, j = 1,, b, ad let X deote the lfetme of the etre system. So, the cumulatve dstrbuto fucto of X s Pr(X x) = 1 Pr b (X 1 > x) = 1 1 Pr (X 1 x)} b = 1 1 Pr (X 11 x, X 12 x,, X 1a x)} b = 1 1 Pr a (X 11 x)} b = 1 1 G a ξ, (x)} b, (6) where G ξ, ( ) deotes the cumulatve dstrbuto fucto of the GP dstrbuto. So, t follows that the KumGP dstrbuto gve by (3) ad (5) s precsely

4 742 Saralees Nadarajah ad Sumaya Eljabr the tme to falure dstrbuto of the etre system. The GP dstrbuto has bee wdely used to model lfetmes: see, for example, Mahmoud (2011). For the partcular case, ξ = 0, (6) s the cumulatve dstrbuto fucto of the Kumexpoetal dstrbuto. The Kumexpoetal dstrbuto has bee used to model lfetmes, see Cordero et al. (2010). There are other ways to geeralze the GP dstrbuto. The most recet geeralzatos of the GP dstrbuto were proposed by Papastathopoulos ad Taw (2013). They referred to ther geeralzatos as EGP1, EGP2 ad EGP3 dstrbutos. The EGP1 dstrbuto s specfed by the cumulatve dstrbuto fucto F (x) = 1 B (κ, 1/ ξ ) B 1 (1ξ x ξ /ξ (κ, 1/ ξ ), (7) ) for x > 0 (f ξ 0), 0 < x /ξ (f ξ < 0), > 0, κ > 0 ad < ξ <, where B x (, ) deotes the complete beta fucto defed by B x (a, b) = x 0 t a 1 (1 t) b 1 dt, ad B(, ) deotes the beta fucto defed by B(a, b) = 1 0 t a 1 (1 t) b 1 dt. The EGP2 dstrbuto s specfed by the cumulatve dstrbuto fucto F (x) = 1 κ, Γ(κ) γ 1ξ ( l 1 ξ x ), (8) for x > 0 (f ξ 0), 0 < x /ξ (f ξ < 0), > 0, κ > 0 ad < ξ <, where Γ( ) deotes the gamma fucto defed by Γ(a) = 0 t a 1 exp( t)dt, ad γ(, ) deotes the complete gamma fucto defed by γ(a, x) = x 0 t a 1 exp( t)dt. The EGP3 dstrbuto s specfed by the cumulatve dstrbuto fucto ( F (x) = 1 1 ξ x ) } 1/ξ κ, (9)

5 The Kumaraswamy GP Dstrbuto 743 for x > 0 (f ξ 0), 0 < x /ξ (f ξ < 0), > 0, κ > 0 ad < ξ <. Ufortuately, oe of the dstrbutos gve by (7)-(9) are ew. There have bee may publshed papers (possbly hudreds) proposg dstrbutos same as (7)-(9) or cotag (7)-(9) as specal cases. Besdes, the dstrbutos gve by Papastathopoulos ad Taw (2013) appear complcated: at least (7) ad (8) volve the complete beta fucto ad the complete gamma fucto, specal fuctos requrg umercal routes. We shall also see later that oe of (7)-(9) provde sgfcat mprovemets over the GP dstrbuto for the data set cosdered Papastathopoulos ad Taw (2013). We ow expla why the dstrbutos gve by (7)-(9) are ot ew. Frstly, (7) s a specal case of the class of beta-g dstrbutos troduced by Eugee et al. (2002) ad followed by Joes (2004) ad may others. The beta-g dstrbuto s specfed by the cumulatve dstrbuto fucto F (x) = 1 B(a, b) G(x) 0 t a 1 (1 t) b 1 dt, (10) for a > 0 ad b > 0. Note that (7) s a specal case of (10) for G( ) specfed by ( G(x) = 1 1 ξ x ) ξ /ξ. Ths specal case s cosdered detal by Aksete et al. (2008, Secto 2.2), Mahmoud (2011) ad may others. Secodly, (8) s a specal case of the class of gamma-g dstrbutos troduced by Zografos ad Balakrsha (2009) ad followed by Rstc ad Balakrsha (2012), Nadarajah et al. (2012) ad may others. The gamma-g dstrbuto s specfed by the cumulatve dstrbuto fucto F (x) = γ (a, log 1 G(x)), (11) Γ(a) for a > 0. Note that (8) s a specal case of (11) for G( ) a GP cumulatve dstrbuto fucto. Furthermore, the formula for the cumulatve dstrbuto fucto of the EGP2 dstrbuto gve Papastathopoulos ad Taw (2013) s ot a vald cumulatve dstrbuto fucto! Fally, (9) s detcal to the expoetated Pareto dstrbuto studed by Adeyem ad Adebaj (2004), Shawky ad Abu-Zadah (2008, 2009), Affy (2010) ad may others. I ths paper, we study the mathematcal propertes of the KumGP dstrbuto. From ow o, we wrte the cumulatve dstrbuto fucto ad the probablty desty fucto of the GP dstrbuto by G ξ, (x) = 1 u, (12)

6 744 Saralees Nadarajah ad Sumaya Eljabr ad g ξ, (x) = 1 u 1ξ, (13) respectvely, where u = 1ξ(x t)/} 1/ξ. The cumulatve dstrbuto fucto ad the probablty desty fucto of the KumGP dstrbuto ca be wrtte as ad F (x) = 1 1 (1 u) a } b, (14) f(x) = 1 abu 1ξ (1 u) a 1 1 (1 u) a } b 1, (15) respectvely. The EGP3 dstrbuto gve by (9) s a partcular case of the KumGP dstrbuto. Ulke the EGP1 ad EGP2 dstrbutos, the KumGP dstrbuto does ot volve specal fuctos. So, oe ca expect that the KumGP dstrbuto could attract wder applcablty tha the EGP1, EGP2 ad EGP3 dstrbutos. The KumGP dstrbuto gve by (15) s much more flexble tha the GP dstrbuto ad ca allow for greater flexblty of tals. Plots of the probablty desty fucto (15) ξ= 0.5 for some parameter values are gve ξ=0 Fgure 1. PDF PDF ξ= PDF PDF ξ= x x 3 4 PDF PDF x ξ=0.5 ξ= x x PDF PDF x ξ=1 ξ= x x Fgure 1: Plots of (15) for u = 0, = 1, (a, b) = (0.5, 0.5) (sold curve), (a, b) = (0.5, 1) (curve of dashes), (a, b) = (0.5, 3) (curve of dots) ad (a, b) = (3, 3) (curve of dots ad dashes)

7 The Kumaraswamy GP Dstrbuto 745 If X s a radom varable wth probablty desty fucto, (15), we wrte X KumGP(a, b,, ξ). The KumGP quatle fucto s obtaed by vertg (14): x = Q(z) = F 1 (z) = t 1 1 (1 z) 1/b} } 1/a ξ 1. (16) ξ So, oe ca geerate KumGP varates from (16) by settg X = Q(U), where U s a uform varate o the ut terval (0, 1). I the rest of ths paper, we provde a comprehesve descrpto of the mathematcal propertes of (15). We exame the shape of (15) ad ts assocated hazard rate fucto Sectos 2 ad 3, respectvely. We derve expressos for momets Secto 4. Order statstcs, ther momets ad L momets are calculated Secto 5. Asymptotc dstrbutos of the extreme values are provded Secto 6. Estmato by the method of maxmum lkelhood cludg the observed formato matrx s preseted Secto 7. A smulato study s preseted Secto 8 to assess the performace of the maxmum lkelhood estmators. A applcato of the KumGP dstrbuto to the real data set Papastathopoulos ad Taw (2013) s llustrated Secto 9. The results Sectos 4 ad 5 volve fte seres represetatos. The terms of these fte seres are elemetary, so the fte seres ca be computed by trucato usg ay stadard package, perhaps eve pocket calculators. 2. Shape of Probablty Desty Fucto The frst dervatve of logf(x)} for the KumGP dstrbuto s: d log f(x) = u1ξ 1 ξ a 1 } a(b 1)(1 u)a 1 dx u 1 u 1 (1 u) a, where u = 1 ξ(x t)/} 1/ξ. equato So, the modes of f(x) are the roots of the a(b 1)(1 u) a 1 1 (1 u) a = a 1 1 u 1 ξ u. (17) There may be more tha oe root to (17). Furthermore, the asymptotes of f(x) ad F (x) as u 0, 1 are gve by as u 0, f(x) a b b 1 u bξ, f(x) ab 1 (1 u) a 1,

8 746 Saralees Nadarajah ad Sumaya Eljabr as u 1, as u 0, ad 1 F (x) (au) b, F (x) b(1 u) a, as u 1. Note that both the upper ad lower tals of f(x) are polyomals wth respect to u. Larger values of a correspod to heaver upper tals of f. Larger values of b correspod to lghter upper tals of f. Plots of the shapes of (15) for t = 0, = 1 ad selected values of (a, b, ξ) are gve Fgure 1. Both umodal ad mootocally decreasg shapes appear possble. Umodal shapes appear whe both a ad b are large. Mootocally decreasg shapes appear whe ether a or b s small. 3. Shape of Hazard Rate Fucto The hazard rate fucto defed by h(x) = f(x)/1 F (x)} s a mportat quatty characterzg lfe pheomea of a system. For the KumGP dstrbuto, h(x) takes the form h(x) = abu1ξ (1 u) a 1 1 (1 u) a, (18) where u = 1 ξ(x t)/} 1/ξ. The frst dervatve of log h(x) s: d log h(x) dx = u1ξ 1 ξ u a 1 a(1 u)a 1 1 u 1 (1 u) a. So, the modes of h(x) are the roots of the equato a(1 u) a 1 1 (1 u) a = a 1 1 u 1 ξ u. (19) There may be more tha oe root to (19). Furthermore, the asymptotes of h(x) as u 0, 1 are gve by as u 0 ad h(x) b 1 u ξ, h(x) ab 1 (1 u) a 1,

9 The Kumaraswamy GP Dstrbuto 747 as u 1. Note that both the upper ad lower tals of h(x) are polyomals wth respect to u. Larger values of a correspod to lghter lower tals. Larger values of b correspod to heaver lower tals ad heaver upper tals of h. Fgure 2 llustrates some of the possble shapes of h(x) for t = 0, = 1 ad selected values of (a, b, ξ). Both mootocally creasg, mootocally decreasg ad bathtub shapes appear possble. Bathtub shapes appear for egatve values of ξ. Mootocally creasg shapes appear whe both a ad b are large. Mootocally decreasg shapes appear whe ether a or b s small ad ξ s ot egatve. ξ= 0.5 ξ=0 HRF HRF ξ= HRF HRF ξ= x x 3 4 HRF HRF x ξ=0.5 ξ= x x HRF HRF x ξ=1 ξ= x x Fgure 2: Plots of (18) for u = 0, = 1, (a, b) = (0.5, 0.5) (sold curve), (a, b) = (0.5, 1) (curve of dashes), (a, b) = (0.5, 3) (curve of dots) ad (a, b) = (3, 3) (curve of dots ad dashes) Bathtub shaped hazard rates are the most realstc oes practce. It s terestg to ote that the KumGP dstrbuto ca exhbt ths shape. The GP dstrbuto caot exhbt bathtub shaped hazard rates. 4. Momets Let X KumGP(a, b,, ξ). Usg the trasformato u = 1ξ(x t)/} 1/ξ, we ca wrte

10 748 Saralees Nadarajah ad Sumaya Eljabr E (X ) = ab = ab = ab = ab 0 ξ ( ) ( ξ ( )( ξ ( ) ( ξ 1 =0 =0 =0 ( ) u ξ 1 t (1 u) a 1 1 (1 u) a b 1 du ) ( t ) 1 u ξ (1 u) a 1 1 (1 u) a b 1 du ξ 0 ) ( b 1 1 )( 1) j ) ( t ξ ) ( t ξ j ) ( b 1 j 0 u ξ (1 u) aaj 1 du ) ( 1) j B (1 ξ, a aj) (20) for 1 provded that 1 ξ s ot a teger for all = 0, 1,,. The frst four momets are: ( E (X) = ab t ) ( ) b 1 ( 1) j ξ j a aj ( ) b 1 ( 1) j B (1 ξ, a aj), (21) ξ j E ( ( X 2) = ab t ) 2 ( ) b 1 ( 1) j ξ j a aj ( 2 t ) ( ) b 1 ( 1) j B (1 ξ, a aj) ξ ξ j ( ) 2 ( ) b 1 ( 1) j B (1 2ξ, a aj), (22) ξ j E ( ( X 3) = ab t ) 3 ( ) b 1 ( 1) j ξ j a aj ( 3 t ) 2 ( ) b 1 ( 1) j B (1 ξ, a aj) ξ ξ j ad ( 3 t ξ ( ξ ) ( ξ ) 3 ( b 1 ) 2 ( b 1 j j ) ( 1) j B (1 2ξ, a aj) ) ( 1) j B (1 3ξ, a aj), (23)

11 The Kumaraswamy GP Dstrbuto 749 E ( ( X 4) = ab t ) 4 ( ) b 1 ( 1) j ξ j a aj ( 4 t ) 3 ( ) b 1 ( 1) j B (1 ξ, a aj) ξ ξ j ( 6 t ξ ( 4 t ξ ( ξ ) 2 ( ) 2 ( b 1 ξ j ) ( ) 3 ( b 1 ξ j ) 4 ( b 1 j ) ( 1) j B (1 2ξ, a aj) ) ( 1) j B (1 3ξ, a aj) ) ( 1) j B (1 4ξ, a aj), (24) provded that 1 ξ, 1 2ξ, 1 3ξ ad 1 4ξ are ot tegers. The fte seres (20)-(24) all coverge. The expressos gve by (21)-(24) ca be used to compute the mea, varace, skewess ad kurtoss of X. The values of these four quattes versus ξ are plotted Fgure 3 for t = 0, = 1 ad selected values of (a, b). It s evdet each of the quattes s a creasg fucto of ξ for all choces of (a, b). Mea Mea ξ Varace Varace ξ ξ ξ Skewess Skewess ξ Kurtoss Kurtoss ξ Fgure 3: Mea, 1.0 varace, 0.6 skewess ad kurtoss 1.0 versus 0.6 ξ for t = 0.2 0, 0.0= 1, (a, b) = (0.5, 0.5) (sold curve), (a, b) = (0.5, 1) (curve of dashes), (a, b) = ξ ξ (0.5, 3) (curve of dots) ad (a, b) = (3, 3) (curve of dots ad dashes)

12 750 Saralees Nadarajah ad Sumaya Eljabr 5. Order Statstcs Order statstcs make ther appearace may areas of statstcal theory ad practce. Let X 1: < X 2: < < X : deote the order statstcs for a radom sample X 1, X 2,, X from (15). The the probablty desty fucto of the kth order statstc, say Y = X k:, ca be expressed as ab! f Y (y) = (k 1)!( k)! u1ξ (1 u) a 1 1 (1 u) a b( k1) (1 u) a b} b 1 ab! = (k 1)!( k)! ( k 1 =0! ( k 1 = (k 1)!( k)! ) ( 1) u 1ξ (1 u) a 1 1 (1 u) a b( k1) 1 =0 ) ( 1) f a,b( k1),,ξ (y), where u = 1 ξ(y t)/} 1/ξ ad f a,b,,ξ ( ) deotes the probablty desty fucto of X a,b,,ξ KumGP(a, b,, ξ). So, the probablty desty fucto of Y s a lear combato of probablty desty fuctos of KumGP(a, b,, ξ). Hece, other propertes of Y ca be easly derved. For stace, the cumulatve dstrbuto fucto of Y ca be expressed as F Y (y) =! (k 1)!( k)! ( ) k 1 ( 1) F a,b( k1),,ξ (y), =0 where F a,b,,ξ ( ) deotes the cumulatve dstrbuto fucto correspodg to f a,b,,ξ ( ). The qth momet of Y ca be expressed as E Y q =! (k 1)!( k)! ( k 1 =0 ) ( 1) E X q a,b( k1),,ξ, (25) where X a,b,,ξ KumGP(a, b,, ξ). L-momets are summary statstcs for probablty dstrbutos ad data samples (Hoskgs, 1990). They are aalogous to ordary momets but are computed from lear fuctos of the ordered data values. The rth L momet s defed by r 1 ( r 1 λ r = ( 1) r 1 j j )( r 1 j j ) β j,

13 The Kumaraswamy GP Dstrbuto 751 where β j = EXF (X) j }. I partcular, λ 1 = β 0, λ 2 = 2β 1 β 0, λ 3 = 6β 2 6β 1 β 0 ad λ 4 = 20β 3 30β 2 12β 1 β 0. I geeral, β r = (r 1) 1 E(X r1:r1 ), so t ca be computed usg (25). The L momets have several advatages over ordary momets: for example, they apply for ay dstrbuto havg fte mea; o hgher-order momets eed be fte. 6. Extreme Values Suppose X 1,, X s a radom sample from (15). If X = (X 1 X )/ deotes the sample mea, the by the usual cetral lmt theorem, (X E(X))/ Var(X) approaches the stadard ormal dstrbuto as provded that ξ < 1/2. Sometmes oe would be terested the asymptotes of the extreme order statstcs M = max(x 1,, X ) ad m = m(x 1,, X ). Frstly, suppose that G (12) belogs to the max doma of attracto of the Gumbel extreme value dstrbuto. The by Leadbetter et al. (1987, Chapter 1), there must exst a strctly postve fucto, say h(t), such that 1 G (t xh(t)) lm = exp( x), t x(g) 1 G(t) for every x (, ), where x(g) = supx : G(x) < 1}. But, usg L Hoptal s rule ad sce x(f ) = x(g), we ote that 1 F (t xh(t)) 1 G a } (t xh(t)) b lm = lm t x(f ) 1 F (t) t x(g) 1 G a (t) } 1 G (t xh(t)) b = lm = exp( bx), t x(g) 1 G(t) for every x (, ). So, t follows that F also belogs to the max doma of attracto of the Gumbel extreme value dstrbuto wth lm Pr a (M b ) x} = exp exp( bx)}, for some sutable ormg costats a > 0 ad b. Secodly, suppose that G (12) belogs to the max doma of attracto of the Fréchet extreme value dstrbuto. The by Leadbetter et al. (1987, Chapter 1), x(g) = ad there must exst a β < 0 such that 1 G(tx) lm t 1 G(t) = xβ, for every x > 0. But, usg L Hoptal s rule, we ote that 1 F (tx) 1 G a } lm t 1 F (t) = lm (tx) b 1 G(tx) t 1 G a = lm (t) t 1 G(t) = x bβ, } b

14 752 Saralees Nadarajah ad Sumaya Eljabr for every x > 0. Also x(f ) = x(g) =. So, t follows that F also belogs to the max doma of attracto of the Fréchet extreme value dstrbuto wth ( lm Pr a (M b ) x} = exp x bβ), for some sutable ormg costats a > 0 ad b. Thrdly, suppose that G (12) belogs to the max doma of attracto of the Webull extreme value dstrbuto. The by Leadbetter et al. (1987, Chapter 1), x(g) < ad there must exst a α > 0 such that 1 G (x(g) tx) lm t 0 1 G (x(g) t) = xα, for every x > 0. But, usg L Hoptal s rule ad sce x(f ) = x(g) <, we ote that 1 F (x(f ) tx) 1 G a lm t 0 1 F (x(f ) t) = lm (x(g) tx) b t 0 1 G a (x(g) t) b = x αb. = lm t 0 1 G (x(g) tx) 1 G (x(g) t) So, t follows that F also belogs to the max doma of attracto of the Webull extreme value dstrbuto wth lm Pr a (M b ) x} = exp ( x) αb}, for some sutable ormg costats a > 0 ad b. The same argumet apples to m domas of attracto. That s, F belogs to the same m doma of attracto as that of G. 7. Maxmum Lkelhood Estmato Suppose x 1, x 2,, x s a radom sample of sze from (15). Let u = 1 ξ(x t)/} 1/ξ for = 1, 2,,. The the log-lkelhood fucto for the vector of parameters (a, b,, ξ) ca be wrtte as log L(a, b,, ξ) = log(ab) log (1 ξ) log u (a 1) log (1 u ) (b 1) log 1 (1 u ) a. (26) The frst-order partal dervatves of (26) wth respect to the four parameters are:

15 The Kumaraswamy GP Dstrbuto 753 log L a log L b log L = a log (1 u ) (b 1) (1 u ) a log (1 u ) 1 (1 u ) a, (27) = b log 1 (1 u ) a, (28) = 1 ξ 2 u ξ (x t) a 1 2 u 1ξ (x t) a(b 1) 1 u 2 u 1ξ (1 u ) a 1 (x t) 1 (1 u ) a, (29) ad log L ξ a 1 ξ 2 = a(b 1) ξ 2 log u 1 ξ u 1 u log ξ 2 u (1 u ) a 1 1 (1 u ) a log 1 ξ x t log 1 ξ x t ξ (x t) 1 ξ x t ξ (x t) 1 ξ x t ξ (x t) 1 ξ x t 1 } 1 ξ x t 1 } 1 }.(30) The maxmum lkelhood estmates of (a, b,, ξ), say (â, b,, ξ), are the smultaeous solutos of the equatos log L/ a = 0, log L/ b = 0, log L/ = 0 ad log L/ ξ = 0. As, (â a, b b,, ξ ξ) approaches a multvarate ormal vector wth zero meas ad varace-covarace matrx, (EJ) 1, where 2 log L 2 log L 2 log L 2 log L a 2 a b a a ξ 2 log L 2 log L 2 log L 2 log L J = b a b 2 b b ξ 2 log L 2 log L 2 log L 2. log L a 2 log L ξ a b 2 log L ξ b 2 2 log L ξ ξ 2 log L ξ 2 The matrx, EJ, s kow as the expected formato matrx. The matrx, J, s kow as the observed formato matrx. I smulatos ad real data applcatos descrbed later o, we maxmzed the log-lkelhood fucto usg the lm fucto the R statstcal package (R Developmet Core Team, 2012). For each maxmzato, the lm fucto

16 754 Saralees Nadarajah ad Sumaya Eljabr was executed for a wde rage of tal values. Ths sometmes resulted more tha oe maxmum, but at least oe maxmum was detfed each tme. I cases of more tha oe maxmum, we took the maxmum lkelhood estmates to correspod to the largest of the maxma. I practce, s fte. The lterature (see, for example, Efro ad Hkley (1978)) suggests that t s best to approxmate the dstrbuto of (â a, b b,, ξ ξ) by a multvarate ormal dstrbuto wth zero meas ad varacecovarace matrx gve by J 1, verse of the observed formato matrx, wth (a, b,, ξ) replaced (â, b,, ξ). So, t s useful to have explct expressos for the elemets of J. They are gve Appedx A. The multvarate ormal approxmato ca be used to costruct approxmate cofdece tervals ad cofdece regos for the dvdual parameters ad for the hazard ad survval fuctos. 8. Smulato Study Here, we assess the performace of the maxmum lkelhood estmates gve by (27)-(30) wth respect to sample sze. The assessmet s based o a smulato study: 1. geerate te thousad samples of sze from (15). The verso method s used to geerate samples,.e varates of the KumGP dstrbuto are geerated usg (16). 2. compute the maxmum lkelhood estmates for the te thousad samples, say (â, b,, ξ ) for = 1, 2,, compute the bases ad mea squared errors gve by ad for h = a, b,, ξ. bas h () = MSE h () = (ĥ h), ) 2 (ĥ h, We repeat these steps for = 10, 20,, 1000 wth a = 3, b = 3, t = 0, = 1 ad ξ = 0.5, so computg bas a (), bas b (), bas (), bas ξ () ad MSE a (), MSE b (), MSE (), MSE ξ () for = 10, 20,, We kow from theory that maxmum lkelhood estmates have bases of the order O(1/) ad mea squared errors of the order O(1/). Wth ths md,

17 The Kumaraswamy GP Dstrbuto 755 we have show Fgures 4 ad 5 how tmes the four bases ad tmes the four mea squared errors vary wth respect to. The followg observatos ca be made: 1. the bases for a ad b appear geerally postve; 2. tmes the bases for a appear to level out for all greater tha 200; 3. tmes the bases for b appear to level out for all greater tha 200; 4. tmes the bases for appear to level out for all greater tha 400; 5. tmes the bases for ξ appear to level out for all greater tha 200; 6. tmes the mea squared errors for a appear to level out for all greater tha 200; 7. tmes the mea squared errors for b appear to level out for all greater tha 200; 8. tmes the mea squared errors for appear to level out for all greater tha 200; 9. tmes the mea squared errors for ξ appear to level out for all greater tha 400. We have preseted results for oly oe choce for (a, b,, ξ), amely that (a, b,, ξ) = (3, 3, 1, 0.5). But the results were smlar for other choces.. Bas of MLE. Bas (a) of MLE (a) Bas of MLE. Bas (b) of MLE (b) Bas of MLE. Bas (sgma) of MLE (sgma) Fgure 4: bas400 a () 600 (top left), 800 bas b () (top rght), bas 400 () 600(mddle 800. Bas of MLE. Bas (x) of MLE (x) rght) ad bas ξ () (bottom left) versus = 10, 20,, 1000

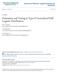
18 756 Saralees Nadarajah ad Sumaya Eljabr. MSE of MLE. MSE (a) of MLE (a) MSE of MLE. MSE (b) of MLE (b) MSE of MLE. MSE (sgma) of MLE (sgma) MSE of MLE. MSE (x) of MLE (x) Fgure 5: 200 MSE400 a () 600 (top left), 800 MSE b () (top rght), MSE () (mddle 800 rght) ad MSE ξ () (bottom left) versus = 10, 20,, 1000 I addto to computg the bases ad mea squared errors, we also computed p values to check for multvarate ormalty ad valdty of lkelhood rato tests. The p values for multvarate ormalty were based o the Shapro-Wlk test (Roysto, 1982). The p values for the valdty of lkelhood rato tests were based o the ch-square goodess of ft test. Plots of the p values versus showed that they remaed above 0.05 for all values of greater tha 200. The plots are ot show here for reasos of space. 9. A Applcato Here, we llustrate the flexblty of the KumGP dstrbuto usg a real data set aalyzed Papastathopoulos ad Taw (2013). The data set cossts of oe hudred ad ffty four exceedaces of the threshold 65m 3 s 1 by the Rver Ndd at Husgore Wer from 1934 to The data s take from NERC (1975). A mea resdual lfe plot s a tool used to select the threshold t for the GP dstrbuto. The same tool ca be used to select t for the KumGP dstrbuto because of (3) ad (4). The mea resdual lfe plot of the data s show Fgure 6. From ths plot we choose t = 65.3m 2 s 1. Ths threshold show red seems approprate.

19 The Kumaraswamy GP Dstrbuto 757 Mea Excess Threshold Fgure 6: Mea resdual lfe plot for exceedaces of the levels of Rver Ndd over the threshold 65m 3 s 1 We ftted the dstrbutos (13), (7), (8), (9) ad (15) to the data. The mddle three dstrbutos are those cosdered by Papastathopoulos ad Taw (2013). The maxmum lkelhood procedure descrbed Secto 7 was used for fttg (15). The parameter estmates, log-lkelhood values, AIC values ad BIC values are show Table 1. The umbers wth brackets are stadard errors computed by vertg the observed formato matrces. Table 1: Parameter estmates, log-lkelhood, AIC ad BIC Model Parameter estmate (s.e) log L AIC BIC (13) = (2.970), ξ = (0.134) (7) = (4.722), ξ = (0.190), κ = (0.423) (8) = (5.537), ξ = (0.139), κ = (0.508) (9) = (4.879), ξ = (0.197), κ = (0.409) (15) = (20.654), ξ = (0.264), â = (0.651), b = (0.451) Noe of the three-parameter dstrbutos (EGP1, EGP2 ad EGP3) provde sgfcat mprovemets over the GP dstrbuto. Amog these three dstrbutos, the EGP2 dstrbuto has the largest lkelhood value, the smallest AIC value ad the smallest BIC value. But the ft of the EGP2 dstrbuto s ot sgfcatly better tha that of the GP dstrbuto. The proposed four-parameter dstrbuto provdes a sgfcat mprovemet over the GP dstrbuto ad the three three-parameter dstrbutos (EGP1, EGP2 ad EGP3). It has the largest lkelhood value, the smallest AIC value ad the smallest BIC values amog all ftted dstrbutos. Furthermore, chsquare goodess of ft tests gve the p-values of , , 0.048, ad

20 758 Saralees Nadarajah ad Sumaya Eljabr for (13), (7), (8), (9) ad (15), respectvely, suggestg that (15) provdes the oly adequate ft. The cocluso based o the lkelhood values, AIC values, BIC values ad the ch-square goodess of ft tests ca be verfed by meas of probablty-probablty plots, quatle-quatle plots ad desty plots. A probablty-probablty plot cossts of plots of the observed probabltes agast probabltes predcted by the ftted model. For example, for the model gve by (13), 1 1 ξ(x (j) t)/ 1/ ξ are plotted versus (j 0.375)/( 0.25), j = 1, 2,,, as recommeded by Blom (1958) ad Chambers et al. (1983), where x (j) are the sorted values of the data ascedg order ad s the umber of observatos. A quatle-quatle plot cossts of plots of the observed quatles agast quatles predcted by the ftted model. For example, for the model gve by (13), t( / ξ)(1 (j 0.375)/(0.25)) ξ 1} are plotted versus x (j), j = 1, 2,,, as recommeded by Blom (1958) ad Chambers et al. (1983). The probablty-probablty plots ad quatle-quatle plots for the fve ftted models are show Fgures 7 ad 8. We ca see that the model gve by (15) has pots closest to the dagoal le especally the upper tal. Ths s evdet from the sum of the absolute dffereces probabltes ad quatles show Table 2. Observed GP New model Observed EGP1 New model Expected Expected Observed EGP2 New model Observed EGP3 New model Expected Expected Fgure 7: Probablty plots for the fts of (13), (7), (8), (9) ad (15) for exceedaces of the levels of Rver Ndd over the threshold t = 65.3m 3 s 1

21 The Kumaraswamy GP Dstrbuto 759 Observed GP New model Observed EGP1 New model Expected Expected Observed EGP2 New model Observed EGP3 New model Expected Expected Fgure 8: Quatle plots for the fts of (13), (7), (8), (9) ad (15) for exceedaces of the levels of Rver Ndd over the threshold t = 65.3m 3 s 1 Table 2: Sum of the absolute dffereces probabltes ad quatles Model Probabltes Quatles (13) (7) (8) (9) (15) A desty plot compares the ftted probablty desty fuctos of the models wth the emprcal hstogram of the observed data. The desty plots are show Fgure 9. Aga the ftted probablty desty fucto for (15) appears to capture the geeral patter of the emprcal hstogram best. Quattes of terest for practtoers of extreme value models are the retur levels. A T year retur level, say x T, s defed as the level that s exceeded o average every T years. For the GP model gve by (13), x T = t } (mt ) ξ 1, (31) ξ where m s the average umber of exceedaces per year. For the KumGP model gve by (15),

22 760 Saralees Nadarajah ad Sumaya Eljabr Ftted PDFs GP New model Ftted PDFs EGP1 New model Level of Rver Ndd t Level of Rver Ndd t Ftted PDFs EGP2 New model Ftted PDFs EGP3 New model Level of Rver Ndd t Level of Rver Ndd t Fgure 9: Ftted probablty desty fuctos of (13), (7), (8), (9) ad (15) for exceedaces of the levels of Rver Ndd over the threshold t = 65.3m 3 s 1 x T = t 1 1 (mt ) 1/b} } 1/a ξ 1, (32) ξ where m s aga the average umber of exceedaces per year. Plots of (31) ad (32) for T = 2, 3,, 50 alog wth 95 cofdece tervals computed by the delta method (Rao, 1973, pp ) are show Fgure 10. Retur level Retur perod, T years Fgure 10: Retur levels for exceedaces of the levels of Rver Ndd ad ther 95 percet cofdece tervals for the fts of (15) ( red) ad (13) ( black)

23 The Kumaraswamy GP Dstrbuto 761 Retur levels are mportat quattes. They are used to determe, for example, dmesos of sea walls, water dams, flood defeces, etc. Fgure 10 suggests that the retur levels gve by (31) ad (32) do ot dffer so much. The cofdece bads for (32) appear oly slghtly wder tha those for (31). Oe would expect the former to be wder because the KumGP model has more parameters tha the GP model. As a fal remark, we lke to meto that the results reported here must be treated coservatvely because of the sample sze. For = 154, some of the bases ad mea squared errors reported Fgures 4 ad 5 appear large. Furthermore, asymptotc ormalty does ot appear to have bee reached. Better estmato methods (for example, bas-corrected estmato methods or bootstrappg based methods) wll be eeded to draw more sesble results. Appedx A Here, we gve explct expressos for the elemets of J defed Secto 7: J 11 = a 2 (1 b) (1 u ) a log 2 (1 u ) (1 u ) 2a log 2 (1 u ) 1 (1 u ) a (1 b) 1 (1 u ) a 2, J 12 = J 13 = 1 2 J 14 = 1 ξ 2 (1 u ) a log (1 u ) 1 (1 u ) a, a(b 1) 2 b 1 ξ 2 u 1ξ (x t) 1 u b 1 2 u 1ξ (x t) (1 u ) a 1 a log (1 u ) 1 1 (1 u ) a u 1ξ (x t) (1 u ) 2a 1 log (1 u ) 1 (1 u ) a 2, u log 1 u u (1 u ) a 1 1 (1 u ) a log a(b 1) ξ 2 ξ (x t) a(b 1) ξ 2 1 ξ x t ξ (x t) 1 ξ x t u (1 u ) a 1 log (1 u ) 1 (1 u ) a 1 ξ x } t 1 u (1 u ) 2a 1 log (1 u ) 1 (1 u ) a 2 log 1 ξ x t ξ (x t) 1 ξ x t 1 } 1 ξ x t log 1 ξ x t 1 }

24 762 Saralees Nadarajah ad Sumaya Eljabr ξ (x t) 1 ξ x } t 1, J 22 = b 2, J 23 = a 2 J 24 = a ξ 2 u 1ξ (1 u ) a 1 (x t) 1 (1 u ) a, u (1 u ) a 1 1 (1 u ) a J 33 = 2(1 ξ) 2 3 J 34 = 1 2 a 1 ξ 2 2 a 1 ξ 2 2 a 1 4 2(a 1) 3 a2 (b 1) 4 log u ξ (x t) u 2ξ2 (x t) 2 (1 u ) 2 a(b 1)(1 ξ) 4 2a(b 1) 3 1 ξ x t ξ (x t) ξ(1 ξ) 4 (a 1)(1 ξ) 4 u ξ1 (x t) a(a 1)(b 1) 1 u 4 u 2ξ2 (1 u ) 2a 2 (x t) 2 u ξ (x t) 1 ξ a(b 1) ξ 2 2 u 1ξ (x t) 1 u u 2ξ (x t) (1 u ) 2 u 1ξ ξ(1 ξ) (x t) u 2ξ 1 (1 u ) a 2 u 2ξ (x t) 2 u 2ξ1 (1 u ) a 1 (x t) 2 1 (1 u ) a u ξ1 (1 u ) a 1 (x t) 1 (1 u ) a, 3 log log u ξ (x t) 2 1 ξ x t 1 ξ x t 1 ξ x t (x t) (1 u ) a 1 1 (1 u ) a 1 ξ x } t 1 (x t) (1 u ) a 2 1 (1 u ) a log log 1 ξ x } t 1, u 2ξ1 (x t) 2 1 u u 2ξ2 (1 u ) a 2 (x t) 2 1 (1 u ) a 1 ξ(1 ξ) (x t) ξ (x t) 1 ξ x t a(a 1)(b 1) ξ ξ x t 1 ξ x t 1 ξ x t 1 } 1 } ξ (x t) 1 ξ x } t 1

25 a2 (b 1) ξ 2 2 ad log J 44 = 1 ξ 2 2 ξ ξ 5 1 ξ 2 ξ u 2ξ 1 ξ x t The Kumaraswamy GP Dstrbuto 763 (x t) (1 u ) 2a 2 1 (1 u ) a 2 ξ (x t) 1 ξ x } t 1, log 1 ξ x t ξ (x t) 1 ξ x } t 1 log 1 ξ x t ξ (x t) 1 ξ x } t 1 2(a 1) ξ 3 a 1 ξ 4 a 1 ξ 4 a 1 ξ 2 a(b 1) ξ 4 ξ (x t) a2 (b 1) ξ 4 a(b 1) ξ 2 (x t) 2 1 ξ x t u 1 u u 1 u u 2 (1 u ) 2 log log 2 1 ξ x t ξ (x t) 1 ξ x } t 1 1 ξ x t ξ (x t) 1 ξ x } t 1 2 log 1 ξ x t ξ (x t) 1 ξ x } t 1 2 u (x t) 2 1 ξ x t 2 1 u u (1 u ) a 2 (1 au ) 1 (1 u ) a 1 ξ x } t 1 2 log 1 ξ x t u 2 (1 u ) 2a 2 1 (1 u ) a 2 log 1 ξ x t ξ (x t) 1 ξ x } t 1 2 u (1 u ) a 1 1 (1 u ) a (x t) 2 1 ξ x t 2. Explct expressos for the remag elemets of J follow by symmetry.

26 764 Saralees Nadarajah ad Sumaya Eljabr Ackowledgemets The authors would lke to thak the Edtor ad the referee for careful readg ad for commets whch greatly mproved the paper. Refereces Adeyem, S. ad Adebaj, T. (2004). The expoetated geeralzed Pareto dstrbuto. Ife Joural of Scece 6, Affy, W. M. (2010). O estmato of the expoetated Pareto dstrbuto uder dfferet sample schemes. Statstcal Methodology 7, Aksete, A., Famoye, F. ad Lee, C. (2008). Statstcs 42, The beta-pareto dstrbuto. Bee, M., Beedett, R. ad Espa, G. (2009). A ote o maxmum lkelhood estmato of a Pareto mxture. No 903, Departmet of Ecoomcs Workg Papers from Departmet of Ecoomcs, Uversty of Treto, Itala. Blom, G. (1958). Statstcal Estmates ad Trasformed Beta-Varables. Wley, New York. Castllo, E., Had, A. S., Balakrsha, N. ad Saraba, J. M. (2005). Extreme Value ad Related Models wth Applcatos Egeerg ad Scece. Wley, Hoboke, New Jersey. Chambers, J., Clevelad, W., Kleer, B. ad Tukey, P. (1983). Methods for Data Aalyss. Chapma & Hall/CRC, Lodo. Graphcal Cordero, G. M. ad de Castro, M. (2011). A ew famly of geeralzed dstrbutos. Joural of Statstcal Computato ad Smulato 81, Cordero, G. M., Ortega, E. M. M. ad Nadarajah, S. (2010). The Kumaraswamy Webull dstrbuto wth applcato to falure data. Joural of the Frakl Isttute 347, Efro, B. ad Hkley, D. V. (1978). Assessg the accuracy of maxmum lkelhood estmato: observed versus expected formato. Bometrka 65, Embrechts, P., Klüppelberg, C. ad Mkosch, T. (1997). Modellg Extremal Evets: For Isurace ad Face. Sprger, Berl.

27 The Kumaraswamy GP Dstrbuto 765 Eugee, N., Lee, C. ad Famoye, F. (2002). Beta-ormal dstrbuto ad ts applcatos. Commucatos Statstcs - Theory ad Methods 31, Hoskg, J. R. M. (1990). L-momets: aalyss ad estmato of dstrbutos usg lear combatos of order statstcs. Joural of the Royal Statstcal Socety, Seres B 52, Joes, M. C. (2004). Famles of dstrbutos arsg from dstrbutos of order statstcs (wth dscusso). Test 13, Josh, M. V. (2010). Modelg the severty of radom evets wth the SAS/ETS SEVERITY procedure. Paper SAS Isttute Ic., Cary, North Carola. Kumaraswamy, P. (1980). A geeralzed probablty desty fucto for doublebouded radom-processes. Joural of Hydrology 46, Leadbetter, M. R., Ldgre, G. ad Rootzé, H. (1987). Extremes ad Related Propertes of Radom Sequeces ad Processes. Sprger, New York. Madse, H. ad Rosbjerg, D. (1998). A regoal Bayesa method for estmato of extreme streamflow droughts. I Statstcal ad Bayesa Methods Hydrologcal Sceces (Edted by E. Paret, B. Bobeé, P. Hubert ad J. Mquel), Studes ad Reports Hydrology, UNESCO, Pars. Mahmoud, E. (2011). The beta geeralzed Pareto dstrbuto wth applcato to lfetme data. Mathematcs ad Computers Smulato 81, Nadarajah, S., Cordero, G. M. ad Ortega, E. M. M. (2012). The Zografos- Balakrsha-G famly of dstrbutos: mathematcal propertes ad applcatos. To appear Commucatos Statstcs - Theory ad Methods. NERC (1975). Flood Studes Report. Natural Evromet Research Coucl, Lodo. Papastathopoulos, I. ad Taw, J. A. (2013). Exteded geeralsed Pareto models for tal estmato. Joural of Statstcal Plag ad Iferece 143, Pckads, J. (1975). Statstcal ferece usg extreme order statstcs. Aals of Statstcs 3, R Developmet Core Team (2012). R: A Laguage ad Evromet for Statstcal Computg. R Foudato for Statstcal Computg, Vea, Austra.

28 766 Saralees Nadarajah ad Sumaya Eljabr Rao, C. R. (1973). Lear Statstcal Iferece ad Its Applcatos, 2d edto. Wley, New York. Resck, S. I. (2008). Extreme Values, Regular Varato, ad Pot Processes. Sprger, New York. Rstć, M. M. ad Balakrsha, N. (2012). The gamma expoetated expoetal dstrbuto. Joural of Statstcal Computato ad Smulato 82, Roysto, J. P. (1982). Algorthm AS 181: the W test for ormalty. Appled Statstcs 31, Shawky, A. I. ad Abu-Zadah, H. H. (2008). Characterzatos of the expoetated Pareto dstrbuto based o record values. Appled Mathematcal Sceces 2, Shawky, A. I. ad Abu-Zadah, H. H. (2009). Expoetated Pareto dstrbuto: dfferet method of estmatos. Iteratoal Joural of Cotemporary Mathematcal Sceces 4, Zografos, K. ad Balakrsha, N. (2009). O famles of beta- ad geeralzed gamma-geerated dstrbutos ad assocated ferece. Statstcal Methodology 6, Receved Jauary 10, 2013; accepted Aprl 16, Saralees Nadarajah School of Mathematcs Uversty of Machester Machester M13 9PL, UK Saralees.Nadarajah@machester.ac.uk Sumaya Eljabr School of Mathematcs Uversty of Machester Machester M13 9PL, UK