1. Determine if each of the following are valid autocorrelation matrices of WSS processes. (Correlation Matrix),R c =
|
|
|
- Magdalene Sharp
- 6 years ago
- Views:
Transcription
1 ENEE630 ADSP Part II w/ solution. Determine if each of the following are valid autocorrelation matrices of WSS processes. (Correlation Matrix) R a = 4 4 4,R b = 0 0,R c = j 0 j 0 j 0 j 0 j,r d = Recall that the properties of an autocorrelation matrix for a WSS process is that () R is Toeplitz; () R H = R; (3) R is non-negative definite. R a is NOT Hermitian; R b is NOT Toeplitz; R c is NOT Hermitian; R d is NOT non-negative definite (λ =,,3).. Consider the random process y(n) = x(n) + v(n), where x(n) = Ae j(ωn+φ) and v(n) is zero mean white Gaussian noise with a variance σv. We also assume the noise and the complex sinusoid are independent. Under the following conditions, determine if y(n) is WSS. Justify your answers. (WSS Process) (a) ω and A are constants, and φ is a uniformly distributed over the interval [0,π]. (b) ω and φ are constants, and A is a Gaussian random variable N(0,σA ). (c) φ and A are constants, and ω is a uniformly distributed over the interval [ω 0,ω 0 + ] for some fixed. (a) E[y(n)] = Ae jωn E φ [e jφ ]+E v [v(n)] = 0 E[y(n)y (n k)] = E φ [(Ae j(ωn+φ) +v(n))(a e j(ω(n k)+φ) +v (n k))] = A E φ [e jωk ]+σv δ(k) = A e jωk +σvδ(k) st and nd moments are independent of n. Thus, the process is WSS. (b) E[y(n)] = E A [A]e j(ωn+φ) +E v [v(n)] = 0 E[y(n)y (n k)] = E A [(Ae j(ωn+φ) +v(n))(a e j(ω(n k)+φ) +v (n k))] = E A [AA ]e jωk +σv δ(k) = σae jωk +σvδ(k)
2 st and nd moments are independent of n. Thus, the process is WSS. (c) E[y(n)] = E ω [x(n)]+e v [v(n)] = A E ω [e jωn ] e jφ = Aejφ jn ejωnω 0+ ω 0 E[y(n)] Aejφ 0 as n jn E[y(n)y (n k)] = E ω [(Ae j(ωn+φ) +v(n))(a e j(ω(n k)+φ) +v (n k))] = A E ω [e jωk ]+σ v δ(k) = A e jω 0k sin(k ) k +σ vδ(k) The sequence defined here is actually NOT a WSS process, but its st and nd moment statistics are approximately independent of n as n. 3. [Rec.II P(a) revisited] Determine the PSD of the WSS process y(n) = Ae j(ω 0n+φ) + v(n), where v(n) is zero mean white Gaussian noise with a variance σv, and φ is uniformly distributed over the interval [0, π]. (Power Spectral Density) In the autocorrelation function in P(a) is r y (k) = A e jωk +σ vδ(k) By taking discrete time Fourier transform on r y (k), we get P y (ω) = πa δ(ω ω 0 )+σ v 4. Assume v(n) is a white Gaussian random process with zero mean and variance. The two filters in Fig. RII.4 are G(z) = 0.4z and H(z) = 0.5z. (Auto-Regressive Process) v(n) G(z) H(z) u(n) Figure RII.4: (a) Is u(n) an AR process? If so, find the parameters. (b) Find the autocorrelation coefficients r u (0), r u (), and r u () of the process u(n). (a) U(z) = 0.9z +0.z V(z), u(n) = 0.9u(n ) 0.u(n )+v(n), a = 0.9, a = 0..
3 (b) Apply the Yule-Walker equation, ( )( ) ( ) ru (0) r u () 0.9 ru () =, r u () r u (0) 0. r u () from which we get r u () = a +a r u (0) = 3 4 r u(0) r u () = ( a +a a ) r u (0) = 9 40 r u(0) Moreover, since r u (0)+a r u ()+a r u () = 4σ v than v(n) ), we have r u (0) = +a a Note: 4σ v (+a ) a (Here, 4 because in this model it is v(n) rather = 00. Then, r u() = 50 7, and r u() = 95.. Ingeneral, for ap-orderar model, given {σ v,a,a,...,a p }, wecan find{r(0),r(),r(),...}; and vice versa. They are related by Yule-Walker Equations.. r( k) = r (k) in general (and hence matrix R is Hermitian), and r( k) = r(k) for real-valued signals. r(0) is the power of sequence u(n), and hence r(0) > 0 from physical point of view. 3. For an AR model, u(n) = p k= a ku(n k)+v(n) has NO correlation with future v(m),m = n+,n+,... (convince yourself). Simply multiply both sides by u (n) and take expectation, we get r(0) = p k= a kr( k) + E(v(n)u (n)). Note that E(v(n)u (n)) = E(v(n)( p k= a k u (n k) + v (n))) but E(v(n)u (n k)) = 0 for k. Then, r(0) = p k= a kr( k) + σv, which we have used to find the relation of r(0) (signal power) and σv (model parameter) in part (b). We could multiply u (n k) instead of u (n) and take the expectation, and this is how the Yule-Walker equations are derived. 5. Let a real-valued AR() process be described by u(n) = x(n)+a x(n )+a x(n ) where u(n) is a white noise of zero-mean and variance σ, and u(n) and past values x(n ), x(n ) are uncorrelated. (Yule-Walker Equation) (a) Determine and solve the Yule-Walker Equations for the AR process. (b) Find the variance of the process x(n). (a) Solve the Yule-Walker equation, we have r x (0) = a r x ( ) a r x ( )+σ r x () = a r x (0) a r x ( ) r x () = a r x () a r x (0) Use the relation that r x (k) = r x ( k) and solve this we get 3
4 r x (0) = a σ a +a ( a ) +a +a r x () = a r x (0) +a a r x () = ( a )r x (0) +a (b) The process is zero mean, so the variance is r x (0). 6. [Problem II.4 continued] Assume v(n) and w(n) are white Gaussian random processes with zero mean and variance. The two filters in Fig. RII.6 are G(z) = 0.4z and H(z) = 0.5z. (Wiener Filter) Figure RII.6: (a) Design a -order Wiener filter such that the desired output is u(n). What is the MSE? (b) Design a -order Wiener filter. What is the MSE? 7. The autocorrelation sequence of a given zero-mean real-valued random process u(n) is r(0) =.5, r() = r( ) = 0.5, and r(k) = 0 for any k. (Wiener Filter) (a) What model fits this process best: AR or MA? Find the corresponding parameters. (b) Design the Wiener filter when using u(n) to predict u(n+). Can we do better (in terms of MSE) if we use both u(n) and u(n ) as the input to the Wiener filter? What if using u(n) and u(n )? 8. Consider the MIMO (multi-input multi-output) wireless communications system shown in Fig. RII.8. There are two antennas at the transmitter and three antennas at the receiver. Assume the channel gain from the i-th transmit antenna to the j-th receive antenna is h ji. Take a snapshot at time slot n, the received signal is y j (n) = h j x (n) + h j x (n) + v j (n) where v j (n) are white Gaussian noise (zero mean, variance N 0 ) independent of signals. We further assume x (n) and x (n) are uncorrelated, and their power are P and P, respectively. Use y (n),y (n) and y 3 (n) as input, find the optimal Wiener filter to estimate x (n) and x (n). (Wiener Filter) 9. Given an real-valued AR(3) model with parameters Γ = 4/5, Γ = /9, Γ 3 = /8, and r(0) =. Find r(), r(), and r(3). (Levinson-Durbin Recursion) 4
5 Figure RII.8: 0. Consider the MA() process x(n) = v(n) + bv(n ) with v(n) being a zero-mean white sequence with variance. If we use Γ k to represent this system, prove that (Levinson-Durbin Recursion) Γ m+ = Γ m Γ m ( Γ m ).. Given a p-order AR random process {x(n)}, it can be equivalently represented by any of the three following sets of values: (Levinson-Durbin Recursion) {r(0),r(),...,r(p)} {a,a,...,a p } and r(0) {Γ,Γ,...,Γ p } and r(0) (a) If a new random process is defined as x (n) = cx(n) where c is a real-valued constant, what will be the new autocorrelation sequence r (k) in terms of r(k) (for k =,,...,p)? How about a k and Γ k? (b) Let a new random process be defined as x (n) = ( ) n x(n). Prove that r (k) = ( ) k r(k), a k = ( )k a k and Γ k = ( )k Γ k. (Hint: use induction when proving Γ k, since Γ k is calculated recursively.). Given a lattice predictor that simultaneously generate both forward and backward prediction errors f m (n) and b m (n) (m =,,...,M). (Lattice Structure) (a) Find E(f m (n)b i (n)) for both conditions when i m and i > m. (b) Find E(f m (n+m)fi (n+i)) for both conditions when i = m and i < m. (c) Design a joint process estimation scheme using the forward prediction errors. (d) If for some reason we can only obtain part of forward prediction error (from order 0 to order k) and part of backward prediction error (from oder k + to order M), i.e., we have 5
6 {f 0 (n),f (n),...,f k (n),b k+ (n),b k+ (n),...,b M (n)}. Describe how to use such mixed forward and backward prediction errors to perform joint process estimation. (Hint: the results from (a) and (b) will be useful for questions (c) and (d). ) 3. Consider the backward prediction error sequence b 0 (n),b (n),...,b M (n) for the observed sequence {u(n)}. (Properties of FLP and BLP Errors) (a) Define b(n) = [b 0 (n),b (n),...,b M (n)] T, and u(n) = [u(n),u(n ),...,u(n M)] T, find L in terms of the coefficients of the backward prediction-error filter where b(n) = Lu(n). (b) Let the correlation matrix for b(n) be D, and that for u(n) be R. Is D diagonal? What is relation between R and D? Show that a lower triangular matrix A exists such that R = A H A. (c) Now we are to perform joint estimation of a desired sequence {d(n)} by using either {b k (n)} or {u(n)}, and their corresponding optimal weight vectors are k and w, respectively. What is relation between k and w? 6
Parametric Signal Modeling and Linear Prediction Theory 4. The Levinson-Durbin Recursion
 Parametric Signal Modeling and Linear Prediction Theory 4. The Levinson-Durbin Recursion Electrical & Computer Engineering North Carolina State University Acknowledgment: ECE792-41 slides were adapted
Parametric Signal Modeling and Linear Prediction Theory 4. The Levinson-Durbin Recursion Electrical & Computer Engineering North Carolina State University Acknowledgment: ECE792-41 slides were adapted
Parametric Signal Modeling and Linear Prediction Theory 1. Discrete-time Stochastic Processes
 Parametric Signal Modeling and Linear Prediction Theory 1. Discrete-time Stochastic Processes Electrical & Computer Engineering North Carolina State University Acknowledgment: ECE792-41 slides were adapted
Parametric Signal Modeling and Linear Prediction Theory 1. Discrete-time Stochastic Processes Electrical & Computer Engineering North Carolina State University Acknowledgment: ECE792-41 slides were adapted
Lecture 7: Linear Prediction
 1 Lecture 7: Linear Prediction Overview Dealing with three notions: PREDICTION, PREDICTOR, PREDICTION ERROR; FORWARD versus BACKWARD: Predicting the future versus (improper terminology) predicting the
1 Lecture 7: Linear Prediction Overview Dealing with three notions: PREDICTION, PREDICTOR, PREDICTION ERROR; FORWARD versus BACKWARD: Predicting the future versus (improper terminology) predicting the
Parametric Signal Modeling and Linear Prediction Theory 1. Discrete-time Stochastic Processes (cont d)
 Parametric Signal Modeling and Linear Prediction Theory 1. Discrete-time Stochastic Processes (cont d) Electrical & Computer Engineering North Carolina State University Acknowledgment: ECE792-41 slides
Parametric Signal Modeling and Linear Prediction Theory 1. Discrete-time Stochastic Processes (cont d) Electrical & Computer Engineering North Carolina State University Acknowledgment: ECE792-41 slides
CCNY. BME I5100: Biomedical Signal Processing. Stochastic Processes. Lucas C. Parra Biomedical Engineering Department City College of New York
 BME I5100: Biomedical Signal Processing Stochastic Processes Lucas C. Parra Biomedical Engineering Department CCNY 1 Schedule Week 1: Introduction Linear, stationary, normal - the stuff biology is not
BME I5100: Biomedical Signal Processing Stochastic Processes Lucas C. Parra Biomedical Engineering Department CCNY 1 Schedule Week 1: Introduction Linear, stationary, normal - the stuff biology is not
Lesson 1. Optimal signalbehandling LTH. September Statistical Digital Signal Processing and Modeling, Hayes, M:
 Lesson 1 Optimal Signal Processing Optimal signalbehandling LTH September 2013 Statistical Digital Signal Processing and Modeling, Hayes, M: John Wiley & Sons, 1996. ISBN 0471594318 Nedelko Grbic Mtrl
Lesson 1 Optimal Signal Processing Optimal signalbehandling LTH September 2013 Statistical Digital Signal Processing and Modeling, Hayes, M: John Wiley & Sons, 1996. ISBN 0471594318 Nedelko Grbic Mtrl
EE482: Digital Signal Processing Applications
 Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu EE482: Digital Signal Processing Applications Spring 2014 TTh 14:30-15:45 CBC C222 Lecture 11 Adaptive Filtering 14/03/04 http://www.ee.unlv.edu/~b1morris/ee482/
Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu EE482: Digital Signal Processing Applications Spring 2014 TTh 14:30-15:45 CBC C222 Lecture 11 Adaptive Filtering 14/03/04 http://www.ee.unlv.edu/~b1morris/ee482/
Advanced Digital Signal Processing -Introduction
 Advanced Digital Signal Processing -Introduction LECTURE-2 1 AP9211- ADVANCED DIGITAL SIGNAL PROCESSING UNIT I DISCRETE RANDOM SIGNAL PROCESSING Discrete Random Processes- Ensemble Averages, Stationary
Advanced Digital Signal Processing -Introduction LECTURE-2 1 AP9211- ADVANCED DIGITAL SIGNAL PROCESSING UNIT I DISCRETE RANDOM SIGNAL PROCESSING Discrete Random Processes- Ensemble Averages, Stationary
Part III Spectrum Estimation
 ECE79-4 Part III Part III Spectrum Estimation 3. Parametric Methods for Spectral Estimation Electrical & Computer Engineering North Carolina State University Acnowledgment: ECE79-4 slides were adapted
ECE79-4 Part III Part III Spectrum Estimation 3. Parametric Methods for Spectral Estimation Electrical & Computer Engineering North Carolina State University Acnowledgment: ECE79-4 slides were adapted
Practical Spectral Estimation
 Digital Signal Processing/F.G. Meyer Lecture 4 Copyright 2015 François G. Meyer. All Rights Reserved. Practical Spectral Estimation 1 Introduction The goal of spectral estimation is to estimate how the
Digital Signal Processing/F.G. Meyer Lecture 4 Copyright 2015 François G. Meyer. All Rights Reserved. Practical Spectral Estimation 1 Introduction The goal of spectral estimation is to estimate how the
Probability Space. J. McNames Portland State University ECE 538/638 Stochastic Signals Ver
 Stochastic Signals Overview Definitions Second order statistics Stationarity and ergodicity Random signal variability Power spectral density Linear systems with stationary inputs Random signal memory Correlation
Stochastic Signals Overview Definitions Second order statistics Stationarity and ergodicity Random signal variability Power spectral density Linear systems with stationary inputs Random signal memory Correlation
Lecture 16: Zeros and Poles
 Lecture 16: Zeros and Poles ECE 401: Signal and Image Analysis University of Illinois 4/6/2017 1 Poles and Zeros at DC 2 Poles and Zeros with Nonzero Bandwidth 3 Poles and Zeros with Nonzero Center Frequency
Lecture 16: Zeros and Poles ECE 401: Signal and Image Analysis University of Illinois 4/6/2017 1 Poles and Zeros at DC 2 Poles and Zeros with Nonzero Bandwidth 3 Poles and Zeros with Nonzero Center Frequency
Parametric Signal Modeling and Linear Prediction Theory 1. Discrete-time Stochastic Processes
 1 Discrete-time Stochastic Processes Parametric Signal Modeling and Linear Prediction Theory 1. Discrete-time Stochastic Processes Electrical & Computer Engineering University of Maryland, College Park
1 Discrete-time Stochastic Processes Parametric Signal Modeling and Linear Prediction Theory 1. Discrete-time Stochastic Processes Electrical & Computer Engineering University of Maryland, College Park
CONTENTS NOTATIONAL CONVENTIONS GLOSSARY OF KEY SYMBOLS 1 INTRODUCTION 1
 DIGITAL SPECTRAL ANALYSIS WITH APPLICATIONS S.LAWRENCE MARPLE, JR. SUMMARY This new book provides a broad perspective of spectral estimation techniques and their implementation. It concerned with spectral
DIGITAL SPECTRAL ANALYSIS WITH APPLICATIONS S.LAWRENCE MARPLE, JR. SUMMARY This new book provides a broad perspective of spectral estimation techniques and their implementation. It concerned with spectral
EEM 409. Random Signals. Problem Set-2: (Power Spectral Density, LTI Systems with Random Inputs) Problem 1: Problem 2:
 EEM 409 Random Signals Problem Set-2: (Power Spectral Density, LTI Systems with Random Inputs) Problem 1: Consider a random process of the form = + Problem 2: X(t) = b cos(2π t + ), where b is a constant,
EEM 409 Random Signals Problem Set-2: (Power Spectral Density, LTI Systems with Random Inputs) Problem 1: Consider a random process of the form = + Problem 2: X(t) = b cos(2π t + ), where b is a constant,
Laboratory Project 2: Spectral Analysis and Optimal Filtering
 Laboratory Project 2: Spectral Analysis and Optimal Filtering Random signals analysis (MVE136) Mats Viberg and Lennart Svensson Department of Signals and Systems Chalmers University of Technology 412 96
Laboratory Project 2: Spectral Analysis and Optimal Filtering Random signals analysis (MVE136) Mats Viberg and Lennart Svensson Department of Signals and Systems Chalmers University of Technology 412 96
Multimedia Communications. Differential Coding
 Multimedia Communications Differential Coding Differential Coding In many sources, the source output does not change a great deal from one sample to the next. This means that both the dynamic range and
Multimedia Communications Differential Coding Differential Coding In many sources, the source output does not change a great deal from one sample to the next. This means that both the dynamic range and
Lecture 4 - Spectral Estimation
 Lecture 4 - Spectral Estimation The Discrete Fourier Transform The Discrete Fourier Transform (DFT) is the equivalent of the continuous Fourier Transform for signals known only at N instants separated
Lecture 4 - Spectral Estimation The Discrete Fourier Transform The Discrete Fourier Transform (DFT) is the equivalent of the continuous Fourier Transform for signals known only at N instants separated
Parametric Method Based PSD Estimation using Gaussian Window
 International Journal of Engineering Trends and Technology (IJETT) Volume 29 Number 1 - November 215 Parametric Method Based PSD Estimation using Gaussian Window Pragati Sheel 1, Dr. Rajesh Mehra 2, Preeti
International Journal of Engineering Trends and Technology (IJETT) Volume 29 Number 1 - November 215 Parametric Method Based PSD Estimation using Gaussian Window Pragati Sheel 1, Dr. Rajesh Mehra 2, Preeti
Discrete-Time Fourier Transform (DTFT)
 Discrete-Time Fourier Transform (DTFT) 1 Preliminaries Definition: The Discrete-Time Fourier Transform (DTFT) of a signal x[n] is defined to be X(e jω ) x[n]e jωn. (1) In other words, the DTFT of x[n]
Discrete-Time Fourier Transform (DTFT) 1 Preliminaries Definition: The Discrete-Time Fourier Transform (DTFT) of a signal x[n] is defined to be X(e jω ) x[n]e jωn. (1) In other words, the DTFT of x[n]
Lecture 4: FT Pairs, Random Signals and z-transform
 EE518 Digital Signal Processing University of Washington Autumn 2001 Dept. of Electrical Engineering Lecture 4: T Pairs, Rom Signals z-transform Wed., Oct. 10, 2001 Prof: J. Bilmes
EE518 Digital Signal Processing University of Washington Autumn 2001 Dept. of Electrical Engineering Lecture 4: T Pairs, Rom Signals z-transform Wed., Oct. 10, 2001 Prof: J. Bilmes
EE538 Final Exam Fall 2007 Mon, Dec 10, 8-10 am RHPH 127 Dec. 10, Cover Sheet
 EE538 Final Exam Fall 2007 Mon, Dec 10, 8-10 am RHPH 127 Dec. 10, 2007 Cover Sheet Test Duration: 120 minutes. Open Book but Closed Notes. Calculators allowed!! This test contains five problems. Each of
EE538 Final Exam Fall 2007 Mon, Dec 10, 8-10 am RHPH 127 Dec. 10, 2007 Cover Sheet Test Duration: 120 minutes. Open Book but Closed Notes. Calculators allowed!! This test contains five problems. Each of
Discrete Time Signals and Systems Time-frequency Analysis. Gloria Menegaz
 Discrete Time Signals and Systems Time-frequency Analysis Gloria Menegaz Time-frequency Analysis Fourier transform (1D and 2D) Reference textbook: Discrete time signal processing, A.W. Oppenheim and R.W.
Discrete Time Signals and Systems Time-frequency Analysis Gloria Menegaz Time-frequency Analysis Fourier transform (1D and 2D) Reference textbook: Discrete time signal processing, A.W. Oppenheim and R.W.
Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises
 Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises Random Signals Analysis (MVE136) Mats Viberg Department of Signals and Systems Chalmers University of Technology 412
Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises Random Signals Analysis (MVE136) Mats Viberg Department of Signals and Systems Chalmers University of Technology 412
Feature extraction 2
 Centre for Vision Speech & Signal Processing University of Surrey, Guildford GU2 7XH. Feature extraction 2 Dr Philip Jackson Linear prediction Perceptual linear prediction Comparison of feature methods
Centre for Vision Speech & Signal Processing University of Surrey, Guildford GU2 7XH. Feature extraction 2 Dr Philip Jackson Linear prediction Perceptual linear prediction Comparison of feature methods
6.3 Forecasting ARMA processes
 6.3. FORECASTING ARMA PROCESSES 123 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss
6.3. FORECASTING ARMA PROCESSES 123 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss
Random signals II. ÚPGM FIT VUT Brno,
 Random signals II. Jan Černocký ÚPGM FIT VUT Brno, cernocky@fit.vutbr.cz 1 Temporal estimate of autocorrelation coefficients for ergodic discrete-time random process. ˆR[k] = 1 N N 1 n=0 x[n]x[n + k],
Random signals II. Jan Černocký ÚPGM FIT VUT Brno, cernocky@fit.vutbr.cz 1 Temporal estimate of autocorrelation coefficients for ergodic discrete-time random process. ˆR[k] = 1 N N 1 n=0 x[n]x[n + k],
Generalized Sidelobe Canceller and MVDR Power Spectrum Estimation. Bhaskar D Rao University of California, San Diego
 Generalized Sidelobe Canceller and MVDR Power Spectrum Estimation Bhaskar D Rao University of California, San Diego Email: brao@ucsd.edu Reference Books 1. Optimum Array Processing, H. L. Van Trees 2.
Generalized Sidelobe Canceller and MVDR Power Spectrum Estimation Bhaskar D Rao University of California, San Diego Email: brao@ucsd.edu Reference Books 1. Optimum Array Processing, H. L. Van Trees 2.
Chapter 2 Wiener Filtering
 Chapter 2 Wiener Filtering Abstract Before moving to the actual adaptive filtering problem, we need to solve the optimum linear filtering problem (particularly, in the mean-square-error sense). We start
Chapter 2 Wiener Filtering Abstract Before moving to the actual adaptive filtering problem, we need to solve the optimum linear filtering problem (particularly, in the mean-square-error sense). We start
III.C - Linear Transformations: Optimal Filtering
 1 III.C - Linear Transformations: Optimal Filtering FIR Wiener Filter [p. 3] Mean square signal estimation principles [p. 4] Orthogonality principle [p. 7] FIR Wiener filtering concepts [p. 8] Filter coefficients
1 III.C - Linear Transformations: Optimal Filtering FIR Wiener Filter [p. 3] Mean square signal estimation principles [p. 4] Orthogonality principle [p. 7] FIR Wiener filtering concepts [p. 8] Filter coefficients
ELEG 3143 Probability & Stochastic Process Ch. 6 Stochastic Process
 Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 6 Stochastic Process Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Definition of stochastic process (random
Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 6 Stochastic Process Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Definition of stochastic process (random
Signals and Spectra - Review
 Signals and Spectra - Review SIGNALS DETERMINISTIC No uncertainty w.r.t. the value of a signal at any time Modeled by mathematical epressions RANDOM some degree of uncertainty before the signal occurs
Signals and Spectra - Review SIGNALS DETERMINISTIC No uncertainty w.r.t. the value of a signal at any time Modeled by mathematical epressions RANDOM some degree of uncertainty before the signal occurs
Statistical and Adaptive Signal Processing
 r Statistical and Adaptive Signal Processing Spectral Estimation, Signal Modeling, Adaptive Filtering and Array Processing Dimitris G. Manolakis Massachusetts Institute of Technology Lincoln Laboratory
r Statistical and Adaptive Signal Processing Spectral Estimation, Signal Modeling, Adaptive Filtering and Array Processing Dimitris G. Manolakis Massachusetts Institute of Technology Lincoln Laboratory
5 Kalman filters. 5.1 Scalar Kalman filter. Unit delay Signal model. System model
 5 Kalman filters 5.1 Scalar Kalman filter 5.1.1 Signal model System model {Y (n)} is an unobservable sequence which is described by the following state or system equation: Y (n) = h(n)y (n 1) + Z(n), n
5 Kalman filters 5.1 Scalar Kalman filter 5.1.1 Signal model System model {Y (n)} is an unobservable sequence which is described by the following state or system equation: Y (n) = h(n)y (n 1) + Z(n), n
Order Recursion Introduction Order versus Time Updates Matrix Inversion by Partitioning Lemma Levinson Algorithm Interpretations Examples
 Order Recursion Introduction Order versus Tie Updates Matrix Inversion by Partitioning Lea Levinson Algorith Interpretations Exaples Introduction Rc d There are any ways to solve the noral equations Solutions
Order Recursion Introduction Order versus Tie Updates Matrix Inversion by Partitioning Lea Levinson Algorith Interpretations Exaples Introduction Rc d There are any ways to solve the noral equations Solutions
Parameter estimation: ACVF of AR processes
 Parameter estimation: ACVF of AR processes Yule-Walker s for AR processes: a method of moments, i.e. µ = x and choose parameters so that γ(h) = ˆγ(h) (for h small ). 12 novembre 2013 1 / 8 Parameter estimation:
Parameter estimation: ACVF of AR processes Yule-Walker s for AR processes: a method of moments, i.e. µ = x and choose parameters so that γ(h) = ˆγ(h) (for h small ). 12 novembre 2013 1 / 8 Parameter estimation:
EE482: Digital Signal Processing Applications
 Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu EE482: Digital Signal Processing Applications Spring 2014 TTh 14:30-15:45 CBC C222 Lecture 11 Adaptive Filtering 14/03/04 http://www.ee.unlv.edu/~b1morris/ee482/
Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu EE482: Digital Signal Processing Applications Spring 2014 TTh 14:30-15:45 CBC C222 Lecture 11 Adaptive Filtering 14/03/04 http://www.ee.unlv.edu/~b1morris/ee482/
Linear Stochastic Models. Special Types of Random Processes: AR, MA, and ARMA. Digital Signal Processing
 Linear Stochastic Models Special Types of Random Processes: AR, MA, and ARMA Digital Signal Processing Department of Electrical and Electronic Engineering, Imperial College d.mandic@imperial.ac.uk c Danilo
Linear Stochastic Models Special Types of Random Processes: AR, MA, and ARMA Digital Signal Processing Department of Electrical and Electronic Engineering, Imperial College d.mandic@imperial.ac.uk c Danilo
Nonparametric and Parametric Defined This text distinguishes between systems and the sequences (processes) that result when a WN input is applied
 Linear Signal Models Overview Introduction Linear nonparametric vs. parametric models Equivalent representations Spectral flatness measure PZ vs. ARMA models Wold decomposition Introduction Many researchers
Linear Signal Models Overview Introduction Linear nonparametric vs. parametric models Equivalent representations Spectral flatness measure PZ vs. ARMA models Wold decomposition Introduction Many researchers
Automatic Autocorrelation and Spectral Analysis
 Piet M.T. Broersen Automatic Autocorrelation and Spectral Analysis With 104 Figures Sprin ger 1 Introduction 1 1.1 Time Series Problems 1 2 Basic Concepts 11 2.1 Random Variables 11 2.2 Normal Distribution
Piet M.T. Broersen Automatic Autocorrelation and Spectral Analysis With 104 Figures Sprin ger 1 Introduction 1 1.1 Time Series Problems 1 2 Basic Concepts 11 2.1 Random Variables 11 2.2 Normal Distribution
Frequency-Domain C/S of LTI Systems
 Frequency-Domain C/S of LTI Systems x(n) LTI y(n) LTI: Linear Time-Invariant system h(n), the impulse response of an LTI systems describes the time domain c/s. H(ω), the frequency response describes the
Frequency-Domain C/S of LTI Systems x(n) LTI y(n) LTI: Linear Time-Invariant system h(n), the impulse response of an LTI systems describes the time domain c/s. H(ω), the frequency response describes the
Least Square Es?ma?on, Filtering, and Predic?on: ECE 5/639 Sta?s?cal Signal Processing II: Linear Es?ma?on
 Least Square Es?ma?on, Filtering, and Predic?on: Sta?s?cal Signal Processing II: Linear Es?ma?on Eric Wan, Ph.D. Fall 2015 1 Mo?va?ons If the second-order sta?s?cs are known, the op?mum es?mator is given
Least Square Es?ma?on, Filtering, and Predic?on: Sta?s?cal Signal Processing II: Linear Es?ma?on Eric Wan, Ph.D. Fall 2015 1 Mo?va?ons If the second-order sta?s?cs are known, the op?mum es?mator is given
Time Series: Theory and Methods
 Peter J. Brockwell Richard A. Davis Time Series: Theory and Methods Second Edition With 124 Illustrations Springer Contents Preface to the Second Edition Preface to the First Edition vn ix CHAPTER 1 Stationary
Peter J. Brockwell Richard A. Davis Time Series: Theory and Methods Second Edition With 124 Illustrations Springer Contents Preface to the Second Edition Preface to the First Edition vn ix CHAPTER 1 Stationary
Digital Signal Processing. Midterm 1 Solution
 EE 123 University of California, Berkeley Anant Sahai February 15, 27 Digital Signal Processing Instructions Midterm 1 Solution Total time allowed for the exam is 8 minutes Some useful formulas: Discrete
EE 123 University of California, Berkeley Anant Sahai February 15, 27 Digital Signal Processing Instructions Midterm 1 Solution Total time allowed for the exam is 8 minutes Some useful formulas: Discrete
ELEG-636: Statistical Signal Processing
 ELEG-636: Statistical Signal Processing Gonzalo R. Arce Department of Electrical and Computer Engineering University of Delaware Spring 2010 Gonzalo R. Arce (ECE, Univ. of Delaware) ELEG-636: Statistical
ELEG-636: Statistical Signal Processing Gonzalo R. Arce Department of Electrical and Computer Engineering University of Delaware Spring 2010 Gonzalo R. Arce (ECE, Univ. of Delaware) ELEG-636: Statistical
Digital Signal Processing Lecture 3 - Discrete-Time Systems
 Digital Signal Processing - Discrete-Time Systems Electrical Engineering and Computer Science University of Tennessee, Knoxville August 25, 2015 Overview 1 2 3 4 5 6 7 8 Introduction Three components of
Digital Signal Processing - Discrete-Time Systems Electrical Engineering and Computer Science University of Tennessee, Knoxville August 25, 2015 Overview 1 2 3 4 5 6 7 8 Introduction Three components of
ECE534, Spring 2018: Solutions for Problem Set #5
 ECE534, Spring 08: s for Problem Set #5 Mean Value and Autocorrelation Functions Consider a random process X(t) such that (i) X(t) ± (ii) The number of zero crossings, N(t), in the interval (0, t) is described
ECE534, Spring 08: s for Problem Set #5 Mean Value and Autocorrelation Functions Consider a random process X(t) such that (i) X(t) ± (ii) The number of zero crossings, N(t), in the interval (0, t) is described
Levinson Durbin Recursions: I
 Levinson Durbin Recursions: I note: B&D and S&S say Durbin Levinson but Levinson Durbin is more commonly used (Levinson, 1947, and Durbin, 1960, are source articles sometimes just Levinson is used) recursions
Levinson Durbin Recursions: I note: B&D and S&S say Durbin Levinson but Levinson Durbin is more commonly used (Levinson, 1947, and Durbin, 1960, are source articles sometimes just Levinson is used) recursions
ELC 4351: Digital Signal Processing
 ELC 4351: Digital Signal Processing Liang Dong Electrical and Computer Engineering Baylor University liang dong@baylor.edu October 18, 2016 Liang Dong (Baylor University) Frequency-domain Analysis of LTI
ELC 4351: Digital Signal Processing Liang Dong Electrical and Computer Engineering Baylor University liang dong@baylor.edu October 18, 2016 Liang Dong (Baylor University) Frequency-domain Analysis of LTI
Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises
 Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises Random Processes With Applications (MVE 135) Mats Viberg Department of Signals and Systems Chalmers University of Technology
Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises Random Processes With Applications (MVE 135) Mats Viberg Department of Signals and Systems Chalmers University of Technology
Levinson Durbin Recursions: I
 Levinson Durbin Recursions: I note: B&D and S&S say Durbin Levinson but Levinson Durbin is more commonly used (Levinson, 1947, and Durbin, 1960, are source articles sometimes just Levinson is used) recursions
Levinson Durbin Recursions: I note: B&D and S&S say Durbin Levinson but Levinson Durbin is more commonly used (Levinson, 1947, and Durbin, 1960, are source articles sometimes just Levinson is used) recursions
Stochastic Processes. M. Sami Fadali Professor of Electrical Engineering University of Nevada, Reno
 Stochastic Processes M. Sami Fadali Professor of Electrical Engineering University of Nevada, Reno 1 Outline Stochastic (random) processes. Autocorrelation. Crosscorrelation. Spectral density function.
Stochastic Processes M. Sami Fadali Professor of Electrical Engineering University of Nevada, Reno 1 Outline Stochastic (random) processes. Autocorrelation. Crosscorrelation. Spectral density function.
Review of Fundamentals of Digital Signal Processing
 Solution Manual for Theory and Applications of Digital Speech Processing by Lawrence Rabiner and Ronald Schafer Click here to Purchase full Solution Manual at http://solutionmanuals.info Link download
Solution Manual for Theory and Applications of Digital Speech Processing by Lawrence Rabiner and Ronald Schafer Click here to Purchase full Solution Manual at http://solutionmanuals.info Link download
Autoregressive (AR) Modelling
 Autoregressive (AR) Modelling A. Uses of AR Modelling () Alications (a) Seech recognition and coding (storage) (b) System identification (c) Modelling and recognition of sonar, radar, geohysical signals
Autoregressive (AR) Modelling A. Uses of AR Modelling () Alications (a) Seech recognition and coding (storage) (b) System identification (c) Modelling and recognition of sonar, radar, geohysical signals
Adaptive Systems. Winter Term 2017/18. Instructor: Pejman Mowlaee Beikzadehmahaleh. Assistants: Christian Stetco
 Adaptive Systems Winter Term 2017/18 Instructor: Pejman Mowlaee Beikzadehmahaleh Assistants: Christian Stetco Signal Processing and Speech Communication Laboratory, Inffeldgasse 16c/EG written by Bernhard
Adaptive Systems Winter Term 2017/18 Instructor: Pejman Mowlaee Beikzadehmahaleh Assistants: Christian Stetco Signal Processing and Speech Communication Laboratory, Inffeldgasse 16c/EG written by Bernhard
2.6 The optimum filtering solution is defined by the Wiener-Hopf equation
 .6 The optimum filtering solution is defined by the Wiener-opf equation w o p for which the minimum mean-square error equals J min σ d p w o () Combine Eqs. and () into a single relation: σ d p p 1 w o
.6 The optimum filtering solution is defined by the Wiener-opf equation w o p for which the minimum mean-square error equals J min σ d p w o () Combine Eqs. and () into a single relation: σ d p p 1 w o
Discrete Time Fourier Transform (DTFT)
 Discrete Time Fourier Transform (DTFT) 1 Discrete Time Fourier Transform (DTFT) The DTFT is the Fourier transform of choice for analyzing infinite-length signals and systems Useful for conceptual, pencil-and-paper
Discrete Time Fourier Transform (DTFT) 1 Discrete Time Fourier Transform (DTFT) The DTFT is the Fourier transform of choice for analyzing infinite-length signals and systems Useful for conceptual, pencil-and-paper
Direction of Arrival Estimation: Subspace Methods. Bhaskar D Rao University of California, San Diego
 Direction of Arrival Estimation: Subspace Methods Bhaskar D Rao University of California, San Diego Email: brao@ucsdedu Reference Books and Papers 1 Optimum Array Processing, H L Van Trees 2 Stoica, P,
Direction of Arrival Estimation: Subspace Methods Bhaskar D Rao University of California, San Diego Email: brao@ucsdedu Reference Books and Papers 1 Optimum Array Processing, H L Van Trees 2 Stoica, P,
Massachusetts Institute of Technology
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.011: Introduction to Communication, Control and Signal Processing QUIZ, April 1, 010 QUESTION BOOKLET Your
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.011: Introduction to Communication, Control and Signal Processing QUIZ, April 1, 010 QUESTION BOOKLET Your
7.17. Determine the z-transform and ROC for the following time signals: Sketch the ROC, poles, and zeros in the z-plane. X(z) = x[n]z n.
![7.17. Determine the z-transform and ROC for the following time signals: Sketch the ROC, poles, and zeros in the z-plane. X(z) = x[n]z n. 7.17. Determine the z-transform and ROC for the following time signals: Sketch the ROC, poles, and zeros in the z-plane. X(z) = x[n]z n.](/thumbs/74/70037980.jpg) Solutions to Additional Problems 7.7. Determine the -transform and ROC for the following time signals: Sketch the ROC, poles, and eros in the -plane. (a) x[n] δ[n k], k > 0 X() x[n] n n k, 0 Im k multiple
Solutions to Additional Problems 7.7. Determine the -transform and ROC for the following time signals: Sketch the ROC, poles, and eros in the -plane. (a) x[n] δ[n k], k > 0 X() x[n] n n k, 0 Im k multiple
Some notes about signals, orthogonal polynomials and linear algebra
 Some notes about signals, orthogonal polynomials and linear algebra Adhemar Bultheel Report TW 180, November 1992 Revised February 1993 n Katholieke Universiteit Leuven Department of Computer Science Celestijnenlaan
Some notes about signals, orthogonal polynomials and linear algebra Adhemar Bultheel Report TW 180, November 1992 Revised February 1993 n Katholieke Universiteit Leuven Department of Computer Science Celestijnenlaan
Chap 2. Discrete-Time Signals and Systems
 Digital Signal Processing Chap 2. Discrete-Time Signals and Systems Chang-Su Kim Discrete-Time Signals CT Signal DT Signal Representation 0 4 1 1 1 2 3 Functional representation 1, n 1,3 x[ n] 4, n 2 0,
Digital Signal Processing Chap 2. Discrete-Time Signals and Systems Chang-Su Kim Discrete-Time Signals CT Signal DT Signal Representation 0 4 1 1 1 2 3 Functional representation 1, n 1,3 x[ n] 4, n 2 0,
Linear Prediction 1 / 41
 Linear Prediction 1 / 41 A map of speech signal processing Natural signals Models Artificial signals Inference Speech synthesis Hidden Markov Inference Homomorphic processing Dereverberation, Deconvolution
Linear Prediction 1 / 41 A map of speech signal processing Natural signals Models Artificial signals Inference Speech synthesis Hidden Markov Inference Homomorphic processing Dereverberation, Deconvolution
Lab 9a. Linear Predictive Coding for Speech Processing
 EE275Lab October 27, 2007 Lab 9a. Linear Predictive Coding for Speech Processing Pitch Period Impulse Train Generator Voiced/Unvoiced Speech Switch Vocal Tract Parameters Time-Varying Digital Filter H(z)
EE275Lab October 27, 2007 Lab 9a. Linear Predictive Coding for Speech Processing Pitch Period Impulse Train Generator Voiced/Unvoiced Speech Switch Vocal Tract Parameters Time-Varying Digital Filter H(z)
Spectral Analysis of Random Processes
 Spectral Analysis of Random Processes Spectral Analysis of Random Processes Generally, all properties of a random process should be defined by averaging over the ensemble of realizations. Generally, all
Spectral Analysis of Random Processes Spectral Analysis of Random Processes Generally, all properties of a random process should be defined by averaging over the ensemble of realizations. Generally, all
Probability and Statistics for Final Year Engineering Students
 Probability and Statistics for Final Year Engineering Students By Yoni Nazarathy, Last Updated: May 24, 2011. Lecture 6p: Spectral Density, Passing Random Processes through LTI Systems, Filtering Terms
Probability and Statistics for Final Year Engineering Students By Yoni Nazarathy, Last Updated: May 24, 2011. Lecture 6p: Spectral Density, Passing Random Processes through LTI Systems, Filtering Terms
6. Methods for Rational Spectra It is assumed that signals have rational spectra m k= m
 6. Methods for Rational Spectra It is assumed that signals have rational spectra m k= m φ(ω) = γ ke jωk n k= n ρ, (23) jωk ke where γ k = γ k and ρ k = ρ k. Any continuous PSD can be approximated arbitrary
6. Methods for Rational Spectra It is assumed that signals have rational spectra m k= m φ(ω) = γ ke jωk n k= n ρ, (23) jωk ke where γ k = γ k and ρ k = ρ k. Any continuous PSD can be approximated arbitrary
ADAPTIVE FILTER THEORY
 ADAPTIVE FILTER THEORY Fourth Edition Simon Haykin Communications Research Laboratory McMaster University Hamilton, Ontario, Canada Front ice Hall PRENTICE HALL Upper Saddle River, New Jersey 07458 Preface
ADAPTIVE FILTER THEORY Fourth Edition Simon Haykin Communications Research Laboratory McMaster University Hamilton, Ontario, Canada Front ice Hall PRENTICE HALL Upper Saddle River, New Jersey 07458 Preface
TUTORIAL ON UNIVARIATE AUTOREGRESSIVE SPECTRAL ANALYSIS
 Journal of Clinical Monitoring and Computing (2005) 19: 401 410 DOI: 10.1007/s10877-005-7089-x C Springer 2006 TUTORIAL ON UNIVARIATE AUTOREGRESSIVE SPECTRAL ANALYSIS Reijo Takalo, MD, PhD, 1 Heli Hytti,
Journal of Clinical Monitoring and Computing (2005) 19: 401 410 DOI: 10.1007/s10877-005-7089-x C Springer 2006 TUTORIAL ON UNIVARIATE AUTOREGRESSIVE SPECTRAL ANALYSIS Reijo Takalo, MD, PhD, 1 Heli Hytti,
Prof. Dr.-Ing. Armin Dekorsy Department of Communications Engineering. Stochastic Processes and Linear Algebra Recap Slides
 Prof. Dr.-Ing. Armin Dekorsy Department of Communications Engineering Stochastic Processes and Linear Algebra Recap Slides Stochastic processes and variables XX tt 0 = XX xx nn (tt) xx 2 (tt) XX tt XX
Prof. Dr.-Ing. Armin Dekorsy Department of Communications Engineering Stochastic Processes and Linear Algebra Recap Slides Stochastic processes and variables XX tt 0 = XX xx nn (tt) xx 2 (tt) XX tt XX
Sinusoidal Modeling. Yannis Stylianou SPCC University of Crete, Computer Science Dept., Greece,
 Sinusoidal Modeling Yannis Stylianou University of Crete, Computer Science Dept., Greece, yannis@csd.uoc.gr SPCC 2016 1 Speech Production 2 Modulators 3 Sinusoidal Modeling Sinusoidal Models Voiced Speech
Sinusoidal Modeling Yannis Stylianou University of Crete, Computer Science Dept., Greece, yannis@csd.uoc.gr SPCC 2016 1 Speech Production 2 Modulators 3 Sinusoidal Modeling Sinusoidal Models Voiced Speech
P 1.5 X 4.5 / X 2 and (iii) The smallest value of n for
 DHANALAKSHMI COLLEGE OF ENEINEERING, CHENNAI DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING MA645 PROBABILITY AND RANDOM PROCESS UNIT I : RANDOM VARIABLES PART B (6 MARKS). A random variable X
DHANALAKSHMI COLLEGE OF ENEINEERING, CHENNAI DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING MA645 PROBABILITY AND RANDOM PROCESS UNIT I : RANDOM VARIABLES PART B (6 MARKS). A random variable X
Name of the Student: Problems on Discrete & Continuous R.Vs
 Engineering Mathematics 05 SUBJECT NAME : Probability & Random Process SUBJECT CODE : MA6 MATERIAL NAME : University Questions MATERIAL CODE : JM08AM004 REGULATION : R008 UPDATED ON : Nov-Dec 04 (Scan
Engineering Mathematics 05 SUBJECT NAME : Probability & Random Process SUBJECT CODE : MA6 MATERIAL NAME : University Questions MATERIAL CODE : JM08AM004 REGULATION : R008 UPDATED ON : Nov-Dec 04 (Scan
Discrete Fourier Transform
 Discrete Fourier Transform Virtually all practical signals have finite length (e.g., sensor data, audio records, digital images, stock values, etc). Rather than considering such signals to be zero-padded
Discrete Fourier Transform Virtually all practical signals have finite length (e.g., sensor data, audio records, digital images, stock values, etc). Rather than considering such signals to be zero-padded
Applications of Linear Prediction
 SGN-4006 Audio and Speech Processing Applications of Linear Prediction Slides for this lecture are based on those created by Katariina Mahkonen for TUT course Puheenkäsittelyn menetelmät in Spring 03.
SGN-4006 Audio and Speech Processing Applications of Linear Prediction Slides for this lecture are based on those created by Katariina Mahkonen for TUT course Puheenkäsittelyn menetelmät in Spring 03.
13. Power Spectrum. For a deterministic signal x(t), the spectrum is well defined: If represents its Fourier transform, i.e., if.
 For a deterministic signal x(t), the spectrum is well defined: If represents its Fourier transform, i.e., if jt X ( ) = xte ( ) dt, (3-) then X ( ) represents its energy spectrum. his follows from Parseval
For a deterministic signal x(t), the spectrum is well defined: If represents its Fourier transform, i.e., if jt X ( ) = xte ( ) dt, (3-) then X ( ) represents its energy spectrum. his follows from Parseval
Review of Fundamentals of Digital Signal Processing
 Chapter 2 Review of Fundamentals of Digital Signal Processing 2.1 (a) This system is not linear (the constant term makes it non linear) but is shift-invariant (b) This system is linear but not shift-invariant
Chapter 2 Review of Fundamentals of Digital Signal Processing 2.1 (a) This system is not linear (the constant term makes it non linear) but is shift-invariant (b) This system is linear but not shift-invariant
Applications of Random Matrix Theory in Wireless Underwater Communication
 Applications of Random Matrix Theory in Wireless Underwater Communication Why Signal Processing and Wireless Communication Need Random Matrix Theory Atulya Yellepeddi May 13, 2013 18.338- Eigenvalues of
Applications of Random Matrix Theory in Wireless Underwater Communication Why Signal Processing and Wireless Communication Need Random Matrix Theory Atulya Yellepeddi May 13, 2013 18.338- Eigenvalues of
National Sun Yat-Sen University CSE Course: Information Theory. Maximum Entropy and Spectral Estimation
 Maximum Entropy and Spectral Estimation 1 Introduction What is the distribution of velocities in the gas at a given temperature? It is the Maxwell-Boltzmann distribution. The maximum entropy distribution
Maximum Entropy and Spectral Estimation 1 Introduction What is the distribution of velocities in the gas at a given temperature? It is the Maxwell-Boltzmann distribution. The maximum entropy distribution
7 The Waveform Channel
 7 The Waveform Channel The waveform transmitted by the digital demodulator will be corrupted by the channel before it reaches the digital demodulator in the receiver. One important part of the channel
7 The Waveform Channel The waveform transmitted by the digital demodulator will be corrupted by the channel before it reaches the digital demodulator in the receiver. One important part of the channel
6.003 Signal Processing
 6.003 Signal Processing Week 6, Lecture A: The Discrete Fourier Transform (DFT) Adam Hartz hz@mit.edu What is 6.003? What is a signal? Abstractly, a signal is a function that conveys information Signal
6.003 Signal Processing Week 6, Lecture A: The Discrete Fourier Transform (DFT) Adam Hartz hz@mit.edu What is 6.003? What is a signal? Abstractly, a signal is a function that conveys information Signal
Final Exam January 31, Solutions
 Final Exam January 31, 014 Signals & Systems (151-0575-01) Prof. R. D Andrea & P. Reist Solutions Exam Duration: Number of Problems: Total Points: Permitted aids: Important: 150 minutes 7 problems 50 points
Final Exam January 31, 014 Signals & Systems (151-0575-01) Prof. R. D Andrea & P. Reist Solutions Exam Duration: Number of Problems: Total Points: Permitted aids: Important: 150 minutes 7 problems 50 points
Digital Signal Processing. Midterm 2 Solutions
 EE 123 University of California, Berkeley Anant Sahai arch 15, 2007 Digital Signal Processing Instructions idterm 2 Solutions Total time allowed for the exam is 80 minutes Please write your name and SID
EE 123 University of California, Berkeley Anant Sahai arch 15, 2007 Digital Signal Processing Instructions idterm 2 Solutions Total time allowed for the exam is 80 minutes Please write your name and SID
A Thesis for the Degree of Master. Efficient Detection Algorithms for MMSE-SIC in MIMO Systems
 A Thesis for the Degree of Master Efficient Detection Algorithms for MMSE-SIC in MIMO Systems Junyoung Nam School of Engineering Information and Communications University 2008 Efficient Detection Algorithms
A Thesis for the Degree of Master Efficient Detection Algorithms for MMSE-SIC in MIMO Systems Junyoung Nam School of Engineering Information and Communications University 2008 Efficient Detection Algorithms
Estimation and Prediction Scenarios
 Recursive BLUE BLUP and the Kalman filter: Estimation and Prediction Scenarios Amir Khodabandeh GNSS Research Centre, Curtin University of Technology, Perth, Australia IUGG 2011, Recursive 28 June BLUE-BLUP
Recursive BLUE BLUP and the Kalman filter: Estimation and Prediction Scenarios Amir Khodabandeh GNSS Research Centre, Curtin University of Technology, Perth, Australia IUGG 2011, Recursive 28 June BLUE-BLUP
6.003 Signal Processing
 6.003 Signal Processing Week 6, Lecture A: The Discrete Fourier Transform (DFT) Adam Hartz hz@mit.edu What is 6.003? What is a signal? Abstractly, a signal is a function that conveys information Signal
6.003 Signal Processing Week 6, Lecture A: The Discrete Fourier Transform (DFT) Adam Hartz hz@mit.edu What is 6.003? What is a signal? Abstractly, a signal is a function that conveys information Signal
Adaptive Systems Homework Assignment 1
 Signal Processing and Speech Communication Lab. Graz University of Technology Adaptive Systems Homework Assignment 1 Name(s) Matr.No(s). The analytical part of your homework (your calculation sheets) as
Signal Processing and Speech Communication Lab. Graz University of Technology Adaptive Systems Homework Assignment 1 Name(s) Matr.No(s). The analytical part of your homework (your calculation sheets) as
Communication Theory Summary of Important Definitions and Results
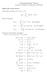 Signal and system theory Convolution of signals x(t) h(t) = y(t): Fourier Transform: Communication Theory Summary of Important Definitions and Results X(ω) = X(ω) = y(t) = X(ω) = j x(t) e jωt dt, 0 Properties
Signal and system theory Convolution of signals x(t) h(t) = y(t): Fourier Transform: Communication Theory Summary of Important Definitions and Results X(ω) = X(ω) = y(t) = X(ω) = j x(t) e jωt dt, 0 Properties
Shannon meets Wiener II: On MMSE estimation in successive decoding schemes
 Shannon meets Wiener II: On MMSE estimation in successive decoding schemes G. David Forney, Jr. MIT Cambridge, MA 0239 USA forneyd@comcast.net Abstract We continue to discuss why MMSE estimation arises
Shannon meets Wiener II: On MMSE estimation in successive decoding schemes G. David Forney, Jr. MIT Cambridge, MA 0239 USA forneyd@comcast.net Abstract We continue to discuss why MMSE estimation arises
for valid PSD. PART B (Answer all five units, 5 X 10 = 50 Marks) UNIT I
 Code: 15A04304 R15 B.Tech II Year I Semester (R15) Regular Examinations November/December 016 PROBABILITY THEY & STOCHASTIC PROCESSES (Electronics and Communication Engineering) Time: 3 hours Max. Marks:
Code: 15A04304 R15 B.Tech II Year I Semester (R15) Regular Examinations November/December 016 PROBABILITY THEY & STOCHASTIC PROCESSES (Electronics and Communication Engineering) Time: 3 hours Max. Marks:
I = i 0,
 Special Types of Matrices Certain matrices, such as the identity matrix 0 0 0 0 0 0 I = 0 0 0, 0 0 0 have a special shape, which endows the matrix with helpful properties The identity matrix is an example
Special Types of Matrices Certain matrices, such as the identity matrix 0 0 0 0 0 0 I = 0 0 0, 0 0 0 have a special shape, which endows the matrix with helpful properties The identity matrix is an example
Some Time-Series Models
 Some Time-Series Models Outline 1. Stochastic processes and their properties 2. Stationary processes 3. Some properties of the autocorrelation function 4. Some useful models Purely random processes, random
Some Time-Series Models Outline 1. Stochastic processes and their properties 2. Stationary processes 3. Some properties of the autocorrelation function 4. Some useful models Purely random processes, random
Problems on Discrete & Continuous R.Vs
 013 SUBJECT NAME SUBJECT CODE MATERIAL NAME MATERIAL CODE : Probability & Random Process : MA 61 : University Questions : SKMA1004 Name of the Student: Branch: Unit I (Random Variables) Problems on Discrete
013 SUBJECT NAME SUBJECT CODE MATERIAL NAME MATERIAL CODE : Probability & Random Process : MA 61 : University Questions : SKMA1004 Name of the Student: Branch: Unit I (Random Variables) Problems on Discrete
Discrete Time Systems
 1 Discrete Time Systems {x[0], x[1], x[2], } H {y[0], y[1], y[2], } Example: y[n] = 2x[n] + 3x[n-1] + 4x[n-2] 2 FIR and IIR Systems FIR: Finite Impulse Response -- non-recursive y[n] = 2x[n] + 3x[n-1]
1 Discrete Time Systems {x[0], x[1], x[2], } H {y[0], y[1], y[2], } Example: y[n] = 2x[n] + 3x[n-1] + 4x[n-2] 2 FIR and IIR Systems FIR: Finite Impulse Response -- non-recursive y[n] = 2x[n] + 3x[n-1]
EE 225a Digital Signal Processing Supplementary Material
 EE 225A DIGITAL SIGAL PROCESSIG SUPPLEMETARY MATERIAL EE 225a Digital Signal Processing Supplementary Material. Allpass Sequences A sequence h a ( n) ote that this is true iff which in turn is true iff
EE 225A DIGITAL SIGAL PROCESSIG SUPPLEMETARY MATERIAL EE 225a Digital Signal Processing Supplementary Material. Allpass Sequences A sequence h a ( n) ote that this is true iff which in turn is true iff
Elec4621: Advanced Digital Signal Processing Chapter 8: Wiener and Adaptive Filtering
 Elec462: Advanced Digital Signal Processing Chapter 8: Wiener and Adaptive Filtering Dr D S Taubman May 2, 2 Wiener Filtering A Wiener lter is one which provides the Minimum Mean Squared Error (MMSE) prediction,
Elec462: Advanced Digital Signal Processing Chapter 8: Wiener and Adaptive Filtering Dr D S Taubman May 2, 2 Wiener Filtering A Wiener lter is one which provides the Minimum Mean Squared Error (MMSE) prediction,
Discrete-Time Signals and Systems. Frequency Domain Analysis of LTI Systems. The Frequency Response Function. The Frequency Response Function
 Discrete-Time Signals and s Frequency Domain Analysis of LTI s Dr. Deepa Kundur University of Toronto Reference: Sections 5., 5.2-5.5 of John G. Proakis and Dimitris G. Manolakis, Digital Signal Processing:
Discrete-Time Signals and s Frequency Domain Analysis of LTI s Dr. Deepa Kundur University of Toronto Reference: Sections 5., 5.2-5.5 of John G. Proakis and Dimitris G. Manolakis, Digital Signal Processing:
x(n + 1) = Ax(n) and y(n) = Cx(n) + 2v(n) and C = x(0) = ξ 1 ξ 2 Ex(0)x(0) = I
 A-AE 567 Final Homework Spring 213 You will need Matlab and Simulink. You work must be neat and easy to read. Clearly, identify your answers in a box. You will loose points for poorly written work. You
A-AE 567 Final Homework Spring 213 You will need Matlab and Simulink. You work must be neat and easy to read. Clearly, identify your answers in a box. You will loose points for poorly written work. You
x[n] = x a (nt ) x a (t)e jωt dt while the discrete time signal x[n] has the discrete-time Fourier transform x[n]e jωn
![x[n] = x a (nt ) x a (t)e jωt dt while the discrete time signal x[n] has the discrete-time Fourier transform x[n]e jωn x[n] = x a (nt ) x a (t)e jωt dt while the discrete time signal x[n] has the discrete-time Fourier transform x[n]e jωn](/thumbs/82/86357929.jpg) Sampling Let x a (t) be a continuous time signal. The signal is sampled by taking the signal value at intervals of time T to get The signal x(t) has a Fourier transform x[n] = x a (nt ) X a (Ω) = x a (t)e
Sampling Let x a (t) be a continuous time signal. The signal is sampled by taking the signal value at intervals of time T to get The signal x(t) has a Fourier transform x[n] = x a (nt ) X a (Ω) = x a (t)e
Adaptive Modeling, Prediction, and Tracking of Wireless Fading Channels
 Adaptive Modeling, Prediction, and Tracking of Wireless Fading Channels Abdorreza Heidari and Amir K. Khandani Technical Report UW-E&CE #2007-01 Department of Electrical & Computer Engineering University
Adaptive Modeling, Prediction, and Tracking of Wireless Fading Channels Abdorreza Heidari and Amir K. Khandani Technical Report UW-E&CE #2007-01 Department of Electrical & Computer Engineering University
