REVERSE CHAIN RULE CALCULUS 7. Dr Adrian Jannetta MIMA CMath FRAS INU0115/515 (MATHS 2) Reverse Chain Rule 1/12 Adrian Jannetta
|
|
|
- Joshua Snow
- 6 years ago
- Views:
Transcription
1 REVERSE CHAIN RULE CALCULUS 7 INU05/55 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Reverse Chain Rule /2 Adrian Jannetta
2 Reversing the chain rule In differentiation the chain rule is used to get the derivative of a composite function. For example d dx (e2x )=2e 2x Integration is the reverse of differentiation. Therefore, we could reverse this statement and write: 2e 2x dx= e 2x (Ignore the constant for a moment). Dividing both sides by 2 we find e 2x dx= e2x 2 () Similarly, consider d dx [sin(3x+2)]=3cos(3x+2). Reversing this process: 3cos(3x+2)dx=sin(3x+2) Therefore: cos(3x+2)dx= sin(3x+2) 3 Can you a pattern for directly integrating the expressions given in () and (2)? Reverse Chain Rule 2/2 Adrian Jannetta (2)
3 Reversing the chain rule Here s another example of reversing the chain rule. d dx (2x 5)3 =(3)(2)(2x 5) 2 In words this process is Subtract from the power. Multiply by the old power and multiply by the derivative of the inner function. Since integration is the reverse of differentiation: (3)(2)(2x 5) 2 dx=(2x 5) 3 (Again, let s ignore the constant C for a moment). Dividing both sides by the factor(3)(2) we get (2x 5) 2 dx= (2x 5)3 (3)(2) Notice that the (3) is the power and the (2) is the derivative of the inner function(2x 5) (2x 5) 2 dx= (2x 5)3 6 The first term on the RHS is equivalent in words to Add to the power. Divide by the new power and divide by the derivative of the inner function. It is the reverse of applying the chain rule. Reverse Chain Rule 3/2 Adrian Jannetta
4 Reverse Chain Rule The examples just seen illustrate a simple procedure for integrating composite functions. It is the reverse of how we d carry out the chain rule in differentiation. In words, the general procedure doing reverse chain rule is Integrate the outer function. Divide by the derivative of the inner function Here some examples. We ll include the constant from now on! sin0x dx= cos0x + C 0 e 4x dx= e 4x 4 + C Reverse Chain Rule 4/2 Adrian Jannetta
5 Reverse chain rule Use the reverse chain rule to integrate First, write the integral in a more suitable form (3 5x) 4 dx (3 5x) 4 dx Now integrate. Use the rule for integrating powers (in this case, like x 4 ); Add to the power. Divide by the new power and divide by the derivative of the inner function. (3 5x) 4 dx= (3 5x) 3 ( 3)( 5) + C=(3 5x) 3 + C 5 It can be written without the negative power like this: (3 5x) dx= 4 5(3 5x) 3+ C Reverse Chain Rule 5/2 Adrian Jannetta
6 When can reverse chain rule be used? The reverse chain rule can only be used when the inner function is linear, which means it has the form mx + c (where m and c are constants). We cannot use the reverse chain rule when the inner function is NOT LINEAR! For example, we could not use it to find function +x 2 is not linear. Therefore (+x 2 ) 5 dx (+x2 ) 6 + C 6(2x) (+x 2 ) 5 dx because the inner (You can check this by finding the derivative of the RHS - it will not be equal to the LHS!) Reverse Chain Rule 6/2 Adrian Jannetta
7 Test yourself Which of the following can be integrated with the reverse chain rule? ( 3x) 4 dx 2e x dx x 2 dx 3x dx sinx dx cos(3x π) dx +2x dx 2x sinx dx Answers... Yes 3 No 5 No 7 Yes 2 Yes 4 Yes 6 Yes 8 No Reverse Chain Rule 7/2 Adrian Jannetta
8 Further examples Rational power Find 2x+5dx with the reverse chain rule. First rewrite without the square-root: (2x+5) 2 dx = (2x+5) 3 2 ( 3 2 )(2) + C = (2x+5) C 3 (2x+5) 3 = + C 3 You can always check the answer by differentiating it! You should end up with the original integrand. Reverse Chain Rule 8/2 Adrian Jannetta
9 A definite integral Evaluate 0 (2x+) 3 dx Using the reverse chain rule we see that (2x+) 3 dx = Looking forward... 0 = 8 = 8 (2x+) 4 (4)(2) 0 (2x+) = 8 (8 ) = 0 The reverse chain rule is a useful shortcut for simple situations. A related technique, called integration by substitution, will be demonstrated in the next lecture. Reverse Chain Rule 9/2 Adrian Jannetta 0
10 Integration of f (x)/f(x) Here is a result that we saw during our study of differentiation: d dx ln f(x) = f (x) f(x) It s a consequence of differentiating logarithm functions using the chain rule. Naturally, we can reverse this to produce an integration result: f (x) f(x) dx=ln f(x) +C (3) This is a result we should learn to recognise when it appears! Reverse Chain Rule 0/2 Adrian Jannetta
11 Integration of f (x)/f(x) 2x Find x 2 9 dx. This integral matches the form of equation (3) exactly. Therefore: Integration of f (x)/f(x) 4sin x Find +cos x dx. 2x x 2 9 dx= ln x C This integral almost fits the form of equation (3). We can rewrite it to make it the same: 4sin x sin x +cosx dx= 4 +cos x dx We took out a factor of 4 so that the numerator is now the derivative of the denominator. Therefore: 4sin x dx= 4ln +cos x +C +cosx Reverse Chain Rule /2 Adrian Jannetta
12 Test yourself Use of reverse chain rule Use the reverse chain rule to find these integrals: ( 3x) 4 dx 5 π 9 0 sin 3x dx e x dx 5+2x dx 2cos( 3 x π) dx x dx cosx sin x dx Answers... 5 ( 3x)5 + C 2 2e x + C 3 2 ln 5+2x +C 4 6sin( 3 x π)+c ln sin x + C Reverse Chain Rule 2/2 Adrian Jannetta
Introduction Derivation General formula List of series Convergence Applications Test SERIES 4 INU0114/514 (MATHS 1)
 MACLAURIN SERIES SERIES 4 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Maclaurin Series 1/ 21 Adrian Jannetta Recap: Binomial Series Recall that some functions can be rewritten as a power series
MACLAURIN SERIES SERIES 4 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Maclaurin Series 1/ 21 Adrian Jannetta Recap: Binomial Series Recall that some functions can be rewritten as a power series
Introduction Derivation General formula Example 1 List of series Convergence Applications Test SERIES 4 INU0114/514 (MATHS 1)
 MACLAURIN SERIES SERIES 4 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Maclaurin Series 1/ 19 Adrian Jannetta Background In this presentation you will be introduced to the concept of a power
MACLAURIN SERIES SERIES 4 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Maclaurin Series 1/ 19 Adrian Jannetta Background In this presentation you will be introduced to the concept of a power
PRODUCT & QUOTIENT RULES CALCULUS 2. Dr Adrian Jannetta MIMA CMath FRAS INU0115/515 (MATHS 2) Product & quotient rules 1/13 Adrian Jannetta
 PRODUCT & QUOTIENT RULES CALCULUS 2 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Proct & quotient rules 1/13 Adrian Jannetta Objectives In this presentation we ll continue learning how to differentiate
PRODUCT & QUOTIENT RULES CALCULUS 2 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Proct & quotient rules 1/13 Adrian Jannetta Objectives In this presentation we ll continue learning how to differentiate
BASIC ALGEBRA ALGEBRA 1. Dr Adrian Jannetta MIMA CMath FRAS INU0114/514 (MATHS 1) Basic algebra 1/ 17 Adrian Jannetta
 BASIC ALGEBRA ALGEBRA 1 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Basic algebra 1/ 17 Adrian Jannetta Overview In this presentation we will review some basic definitions and skills required
BASIC ALGEBRA ALGEBRA 1 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Basic algebra 1/ 17 Adrian Jannetta Overview In this presentation we will review some basic definitions and skills required
Section 3.6 The chain rule 1 Lecture. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
 Section 3.6 The chain rule 1 Lecture College of Science MATHS 101: Calculus I (University of Bahrain) Logarithmic Differentiation 1 / 1 Motivation Goal: We want to derive rules to find the derivative of
Section 3.6 The chain rule 1 Lecture College of Science MATHS 101: Calculus I (University of Bahrain) Logarithmic Differentiation 1 / 1 Motivation Goal: We want to derive rules to find the derivative of
Section 3.6 The chain rule 1 Lecture. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
 Section 3.6 The chain rule 1 Lecture College of Science MATHS 101: Calculus I (University of Bahrain) Logarithmic Differentiation 1 / 23 Motivation Goal: We want to derive rules to find the derivative
Section 3.6 The chain rule 1 Lecture College of Science MATHS 101: Calculus I (University of Bahrain) Logarithmic Differentiation 1 / 23 Motivation Goal: We want to derive rules to find the derivative
PARTIAL DIFFERENTIATION
 PARTIAL DIFFERENTIATION CALCULUS 13 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Partial Differentiation 1/ 15 Adrian Jannetta Functions of many variables The functions and derivatives which
PARTIAL DIFFERENTIATION CALCULUS 13 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Partial Differentiation 1/ 15 Adrian Jannetta Functions of many variables The functions and derivatives which
Math 106 Fall 2014 Exam 2.1 October 31, ln(x) x 3 dx = 1. 2 x 2 ln(x) + = 1 2 x 2 ln(x) + 1. = 1 2 x 2 ln(x) 1 4 x 2 + C
 Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
 Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
DETERMINANTS, MINORS AND COFACTORS ALGEBRA 6. Dr Adrian Jannetta MIMA CMath FRAS INU0114/514 (MATHS 1)
 DETERMINANTS, MINORS AND COFACTORS ALGEBRA 6 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Determinants, minors and cofactors 1/ 15 Adrian Jannetta Determinants Every square matrix has a number
DETERMINANTS, MINORS AND COFACTORS ALGEBRA 6 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Determinants, minors and cofactors 1/ 15 Adrian Jannetta Determinants Every square matrix has a number
Change of Variables: Indefinite Integrals
 Change of Variables: Indefinite Integrals Mathematics 11: Lecture 39 Dan Sloughter Furman University November 29, 2007 Dan Sloughter (Furman University) Change of Variables: Indefinite Integrals November
Change of Variables: Indefinite Integrals Mathematics 11: Lecture 39 Dan Sloughter Furman University November 29, 2007 Dan Sloughter (Furman University) Change of Variables: Indefinite Integrals November
IMPLICIT DIFFERENTIATION
 IMPLICIT DIFFERENTIATION CALCULUS 3 INU0115/515 (MATHS 2) Dr Arian Jannetta MIMA CMath FRAS Implicit Differentiation 1/ 11 Arian Jannetta Explicit an implicit functions Explicit functions An explicit function
IMPLICIT DIFFERENTIATION CALCULUS 3 INU0115/515 (MATHS 2) Dr Arian Jannetta MIMA CMath FRAS Implicit Differentiation 1/ 11 Arian Jannetta Explicit an implicit functions Explicit functions An explicit function
SMALL INCREMENTS CALCULUS 13. Dr Adrian Jannetta MIMA CMath FRAS INU0115/515 (MATHS 2) Small increments 1/15 Adrian Jannetta
 SMALL INCREMENTS CALCULUS 13 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Small increments 1/15 Adrian Jannetta Objectives In this presentation we re going to look at one of the applications
SMALL INCREMENTS CALCULUS 13 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Small increments 1/15 Adrian Jannetta Objectives In this presentation we re going to look at one of the applications
COMPLEX NUMBERS ALGEBRA 7. Dr Adrian Jannetta MIMA CMath FRAS INU0114/514 (MATHS 1) Complex Numbers 1/ 22 Adrian Jannetta
 COMPLEX NUMBERS ALGEBRA 7 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Complex Numbers 1/ 22 Adrian Jannetta Objectives This presentation will cover the following: Introduction to complex numbers.
COMPLEX NUMBERS ALGEBRA 7 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Complex Numbers 1/ 22 Adrian Jannetta Objectives This presentation will cover the following: Introduction to complex numbers.
Introduction Growthequations Decay equations Forming differential equations Case studies Shifted equations Test INU0115/515 (MATHS 2)
 GROWTH AND DECAY CALCULUS 12 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Growth and Decay 1/ 24 Adrian Jannetta Introduction Some of the simplest systems that can be modelled by differential
GROWTH AND DECAY CALCULUS 12 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Growth and Decay 1/ 24 Adrian Jannetta Introduction Some of the simplest systems that can be modelled by differential
AREA UNDER A CURVE CALCULUS 8. Dr Adrian Jannetta MIMA CMath FRAS INU0115/515 (MATHS 2) Area under a curve 1/15 Adrian Jannetta
 AREA UNDER A CURVE CALCULUS 8 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Area under a curve 1/15 Adrian Jannetta The area beneath a curve =f() The total area beneath the curve is approimatel
AREA UNDER A CURVE CALCULUS 8 INU0115/515 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Area under a curve 1/15 Adrian Jannetta The area beneath a curve =f() The total area beneath the curve is approimatel
RATIONAL FUNCTIONS AND
 RATIONAL FUNCTIONS AND GRAPHS ALGEBRA 5 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Rational functions and graphs 1/ 20 Adrian Jannetta Objectives In this lecture (and next seminar) we will
RATIONAL FUNCTIONS AND GRAPHS ALGEBRA 5 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Rational functions and graphs 1/ 20 Adrian Jannetta Objectives In this lecture (and next seminar) we will
How might we evaluate this? Suppose that, by some good luck, we knew that. x 2 5. x 2 dx 5
 8.4 1 8.4 Partial Fractions Consider the following integral. 13 2x (1) x 2 x 2 dx How might we evaluate this? Suppose that, by some good luck, we knew that 13 2x (2) x 2 x 2 = 3 x 2 5 x + 1 We could then
8.4 1 8.4 Partial Fractions Consider the following integral. 13 2x (1) x 2 x 2 dx How might we evaluate this? Suppose that, by some good luck, we knew that 13 2x (2) x 2 x 2 = 3 x 2 5 x + 1 We could then
Chapter 5: Integrals
 Chapter 5: Integrals Section 5.3 The Fundamental Theorem of Calculus Sec. 5.3: The Fundamental Theorem of Calculus Fundamental Theorem of Calculus: Sec. 5.3: The Fundamental Theorem of Calculus Fundamental
Chapter 5: Integrals Section 5.3 The Fundamental Theorem of Calculus Sec. 5.3: The Fundamental Theorem of Calculus Fundamental Theorem of Calculus: Sec. 5.3: The Fundamental Theorem of Calculus Fundamental
Practice Problems: Integration by Parts
 Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
Integration by Substitution
 November 22, 2013 Introduction 7x 2 cos(3x 3 )dx =? 2xe x2 +5 dx =? Chain rule The chain rule: d dx (f (g(x))) = f (g(x)) g (x). Use the chain rule to find f (x) and then write the corresponding anti-differentiation
November 22, 2013 Introduction 7x 2 cos(3x 3 )dx =? 2xe x2 +5 dx =? Chain rule The chain rule: d dx (f (g(x))) = f (g(x)) g (x). Use the chain rule to find f (x) and then write the corresponding anti-differentiation
Calculus I Announcements
 Slide 1 Calculus I Announcements Read sections 4.2,4.3,4.4,4.1 and 5.3 Do the homework from sections 4.2,4.3,4.4,4.1 and 5.3 Exam 3 is Thursday, November 12th See inside for a possible exam question. Slide
Slide 1 Calculus I Announcements Read sections 4.2,4.3,4.4,4.1 and 5.3 Do the homework from sections 4.2,4.3,4.4,4.1 and 5.3 Exam 3 is Thursday, November 12th See inside for a possible exam question. Slide
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Section 4.8 Anti Derivative and Indefinite Integrals 2 Lectures. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
 Section 4.8 Anti Derivative and Indefinite Integrals 2 Lectures College of Science MATHS 101: Calculus I (University of Bahrain) 1 / 28 Indefinite Integral Given a function f, if F is a function such that
Section 4.8 Anti Derivative and Indefinite Integrals 2 Lectures College of Science MATHS 101: Calculus I (University of Bahrain) 1 / 28 Indefinite Integral Given a function f, if F is a function such that
INTEGRATION: THE FUNDAMENTAL THEOREM OF CALCULUS MR. VELAZQUEZ AP CALCULUS
 INTEGRATION: THE FUNDAMENTAL THEOREM OF CALCULUS MR. VELAZQUEZ AP CALCULUS RECALL: ANTIDERIVATIVES When we last spoke of integration, we examined a physics problem where we saw that the area under the
INTEGRATION: THE FUNDAMENTAL THEOREM OF CALCULUS MR. VELAZQUEZ AP CALCULUS RECALL: ANTIDERIVATIVES When we last spoke of integration, we examined a physics problem where we saw that the area under the
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Dr. Abdulla Eid. Section 3.8 Derivative of the inverse function and logarithms 3 Lecture. Dr. Abdulla Eid. MATHS 101: Calculus I. College of Science
 Section 3.8 Derivative of the inverse function and logarithms 3 Lecture College of Science MATHS 101: Calculus I (University of Bahrain) Logarithmic Differentiation 1 / 19 Topics 1 Inverse Functions (1
Section 3.8 Derivative of the inverse function and logarithms 3 Lecture College of Science MATHS 101: Calculus I (University of Bahrain) Logarithmic Differentiation 1 / 19 Topics 1 Inverse Functions (1
Applied Calculus I. Lecture 29
 Applied Calculus I Lecture 29 Integrals of trigonometric functions We shall continue learning substitutions by considering integrals involving trigonometric functions. Integrals of trigonometric functions
Applied Calculus I Lecture 29 Integrals of trigonometric functions We shall continue learning substitutions by considering integrals involving trigonometric functions. Integrals of trigonometric functions
Section 5.6. Integration By Parts. MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10
 Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
Lecture 7 - Separable Equations
 Lecture 7 - Separable Equations Separable equations is a very special type of differential equations where you can separate the terms involving only y on one side of the equation and terms involving only
Lecture 7 - Separable Equations Separable equations is a very special type of differential equations where you can separate the terms involving only y on one side of the equation and terms involving only
Math 250 Skills Assessment Test
 Math 5 Skills Assessment Test Page Math 5 Skills Assessment Test The purpose of this test is purely diagnostic (before beginning your review, it will be helpful to assess both strengths and weaknesses).
Math 5 Skills Assessment Test Page Math 5 Skills Assessment Test The purpose of this test is purely diagnostic (before beginning your review, it will be helpful to assess both strengths and weaknesses).
Updated: January 16, 2016 Calculus II 7.4. Math 230. Calculus II. Brian Veitch Fall 2015 Northern Illinois University
 Math 30 Calculus II Brian Veitch Fall 015 Northern Illinois University Integration of Rational Functions by Partial Fractions From algebra, we learned how to find common denominators so we can do something
Math 30 Calculus II Brian Veitch Fall 015 Northern Illinois University Integration of Rational Functions by Partial Fractions From algebra, we learned how to find common denominators so we can do something
Core Mathematics 3 Differentiation
 http://kumarmaths.weebly.com/ Core Mathematics Differentiation C differentiation Page Differentiation C Specifications. By the end of this unit you should be able to : Use chain rule to find the derivative
http://kumarmaths.weebly.com/ Core Mathematics Differentiation C differentiation Page Differentiation C Specifications. By the end of this unit you should be able to : Use chain rule to find the derivative
The goal of today is to determine what u-substitution to use for trigonometric integrals. The most common substitutions are the following:
 Trigonometric Integrals The goal of today is to determine what u-substitution to use for trigonometric integrals. The most common substitutions are the following: Substitution u sinx u cosx u tanx u secx
Trigonometric Integrals The goal of today is to determine what u-substitution to use for trigonometric integrals. The most common substitutions are the following: Substitution u sinx u cosx u tanx u secx
Math 180, Final Exam, Fall 2012 Problem 1 Solution
 Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
11.5. The Chain Rule. Introduction. Prerequisites. Learning Outcomes
 The Chain Rule 11.5 Introduction In this Section we will see how to obtain the derivative of a composite function (often referred to as a function of a function ). To do this we use the chain rule. This
The Chain Rule 11.5 Introduction In this Section we will see how to obtain the derivative of a composite function (often referred to as a function of a function ). To do this we use the chain rule. This
Grade: The remainder of this page has been left blank for your workings. VERSION D. Midterm D: Page 1 of 12
 First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
Solutions to Exam 1, Math Solution. Because f(x) is one-to-one, we know the inverse function exists. Recall that (f 1 ) (a) =
 Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Integration by Substitution
 Integration by Substitution Dr. Philippe B. Laval Kennesaw State University Abstract This handout contains material on a very important integration method called integration by substitution. Substitution
Integration by Substitution Dr. Philippe B. Laval Kennesaw State University Abstract This handout contains material on a very important integration method called integration by substitution. Substitution
Differentiation by taking logarithms
 Differentiation by taking logarithms In this unit we look at how we can use logarithms to simplify certain functions before we differentiate them. In order to master the techniques explained here it is
Differentiation by taking logarithms In this unit we look at how we can use logarithms to simplify certain functions before we differentiate them. In order to master the techniques explained here it is
MATH 1231 MATHEMATICS 1B Calculus Section 4.4: Taylor & Power series.
 MATH 1231 MATHEMATICS 1B 2010. For use in Dr Chris Tisdell s lectures. Calculus Section 4.4: Taylor & Power series. 1. What is a Taylor series? 2. Convergence of Taylor series 3. Common Maclaurin series
MATH 1231 MATHEMATICS 1B 2010. For use in Dr Chris Tisdell s lectures. Calculus Section 4.4: Taylor & Power series. 1. What is a Taylor series? 2. Convergence of Taylor series 3. Common Maclaurin series
Mathematics 1 Lecture Notes Chapter 1 Algebra Review
 Mathematics 1 Lecture Notes Chapter 1 Algebra Review c Trinity College 1 A note to the students from the lecturer: This course will be moving rather quickly, and it will be in your own best interests to
Mathematics 1 Lecture Notes Chapter 1 Algebra Review c Trinity College 1 A note to the students from the lecturer: This course will be moving rather quickly, and it will be in your own best interests to
Math 230 Mock Final Exam Detailed Solution
 Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
MATH 250 TOPIC 13 INTEGRATION. 13B. Constant, Sum, and Difference Rules
 Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
Study 5.5, # 1 5, 9, 13 27, 35, 39, 49 59, 63, 69, 71, 81. Class Notes: Prof. G. Battaly, Westchester Community College, NY Homework.
 Goals: 1. Recognize an integrand that is the derivative of a composite function. 2. Generalize the Basic Integration Rules to include composite functions. 3. Use substitution to simplify the process of
Goals: 1. Recognize an integrand that is the derivative of a composite function. 2. Generalize the Basic Integration Rules to include composite functions. 3. Use substitution to simplify the process of
QUADRATIC GRAPHS ALGEBRA 2. Dr Adrian Jannetta MIMA CMath FRAS INU0114/514 (MATHS 1) Quadratic Graphs 1/ 16 Adrian Jannetta
 QUADRATIC GRAPHS ALGEBRA 2 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Quadratic Graphs 1/ 16 Adrian Jannetta Objectives Be able to sketch the graph of a quadratic function Recognise the shape
QUADRATIC GRAPHS ALGEBRA 2 INU0114/514 (MATHS 1) Dr Adrian Jannetta MIMA CMath FRAS Quadratic Graphs 1/ 16 Adrian Jannetta Objectives Be able to sketch the graph of a quadratic function Recognise the shape
1 Lecture 39: The substitution rule.
 Lecture 39: The substitution rule. Recall the chain rule and restate as the substitution rule. u-substitution, bookkeeping for integrals. Definite integrals, changing limits. Symmetry-integrating even
Lecture 39: The substitution rule. Recall the chain rule and restate as the substitution rule. u-substitution, bookkeeping for integrals. Definite integrals, changing limits. Symmetry-integrating even
Access to Science, Engineering and Agriculture: Mathematics 2 MATH00040 Chapter 4 Solutions
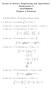 Access to Science, Engineering and Agriculture: Mathematics MATH4 Chapter 4 Solutions In all these solutions, c will represent an arbitrary constant.. (a) Since f(x) 5 is a constant, 5dx 5x] 5. (b) Since
Access to Science, Engineering and Agriculture: Mathematics MATH4 Chapter 4 Solutions In all these solutions, c will represent an arbitrary constant.. (a) Since f(x) 5 is a constant, 5dx 5x] 5. (b) Since
Exploring Substitution
 I. Introduction Exploring Substitution Math Fall 08 Lab We use the Fundamental Theorem of Calculus, Part to evaluate a definite integral. If f is continuous on [a, b] b and F is any antiderivative of f
I. Introduction Exploring Substitution Math Fall 08 Lab We use the Fundamental Theorem of Calculus, Part to evaluate a definite integral. If f is continuous on [a, b] b and F is any antiderivative of f
Math 480 The Vector Space of Differentiable Functions
 Math 480 The Vector Space of Differentiable Functions The vector space of differentiable functions. Let C (R) denote the set of all infinitely differentiable functions f : R R. Then C (R) is a vector space,
Math 480 The Vector Space of Differentiable Functions The vector space of differentiable functions. Let C (R) denote the set of all infinitely differentiable functions f : R R. Then C (R) is a vector space,
Math 226 Calculus Spring 2016 Exam 2V1
 Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Chapter 5: Integrals
 Chapter 5: Integrals Section 5.5 The Substitution Rule (u-substitution) Sec. 5.5: The Substitution Rule We know how to find the derivative of any combination of functions Sum rule Difference rule Constant
Chapter 5: Integrals Section 5.5 The Substitution Rule (u-substitution) Sec. 5.5: The Substitution Rule We know how to find the derivative of any combination of functions Sum rule Difference rule Constant
Graphs of Antiderivatives, Substitution Integrals
 Unit #10 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F (x) The guess-and-check method for anti-differentiation. The substitution
Unit #10 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F (x) The guess-and-check method for anti-differentiation. The substitution
8.3 Partial Fraction Decomposition
 8.3 partial fraction decomposition 575 8.3 Partial Fraction Decomposition Rational functions (polynomials divided by polynomials) and their integrals play important roles in mathematics and applications,
8.3 partial fraction decomposition 575 8.3 Partial Fraction Decomposition Rational functions (polynomials divided by polynomials) and their integrals play important roles in mathematics and applications,
MATH 1231 MATHEMATICS 1B Calculus Section 1: - Integration.
 MATH 1231 MATHEMATICS 1B 2007. For use in Dr Chris Tisdell s lectures: Tues 11 + Thur 10 in KBT Calculus Section 1: - Integration. 1. Motivation 2. What you should already know 3. Useful integrals 4. Integrals
MATH 1231 MATHEMATICS 1B 2007. For use in Dr Chris Tisdell s lectures: Tues 11 + Thur 10 in KBT Calculus Section 1: - Integration. 1. Motivation 2. What you should already know 3. Useful integrals 4. Integrals
The Chain Rule. The Chain Rule. dy dy du dx du dx. For y = f (u) and u = g (x)
 AP Calculus Mrs. Jo Brooks The Chain Rule To find the derivative of more complicated functions, we use something called the chain rule. It can be confusing unless you keep yourself organized as you go
AP Calculus Mrs. Jo Brooks The Chain Rule To find the derivative of more complicated functions, we use something called the chain rule. It can be confusing unless you keep yourself organized as you go
MATH 1207 R02 MIDTERM EXAM 2 SOLUTION
 MATH 7 R MIDTERM EXAM SOLUTION FALL 6 - MOON Name: Write your answer neatly and show steps. Except calculators, any electronic devices including laptops and cell phones are not allowed. () (5 pts) Find
MATH 7 R MIDTERM EXAM SOLUTION FALL 6 - MOON Name: Write your answer neatly and show steps. Except calculators, any electronic devices including laptops and cell phones are not allowed. () (5 pts) Find
Example. Evaluate. 3x 2 4 x dx.
 3x 2 4 x 3 + 4 dx. Solution: We need a new technique to integrate this function. Notice that if we let u x 3 + 4, and we compute the differential du of u, we get: du 3x 2 dx Going back to our integral,
3x 2 4 x 3 + 4 dx. Solution: We need a new technique to integrate this function. Notice that if we let u x 3 + 4, and we compute the differential du of u, we get: du 3x 2 dx Going back to our integral,
MAT 132 Midterm 1 Spring 2017
 MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
f(g(x)) g (x) dx = f(u) du.
 1. Techniques of Integration Section 8-IT 1.1. Basic integration formulas. Integration is more difficult than derivation. The derivative of every rational function or trigonometric function is another
1. Techniques of Integration Section 8-IT 1.1. Basic integration formulas. Integration is more difficult than derivation. The derivative of every rational function or trigonometric function is another
A.P. Calculus BC Test Two Section One Multiple-Choice Calculators Allowed Time 40 minutes Number of Questions 15
 A.P. Calculus BC Test Two Section One Multiple-Choice Calculators Allowed Time 40 minutes Number of Questions 15 The scoring for this section is determined by the formula [C (0.25 I)] 1.8 where C is the
A.P. Calculus BC Test Two Section One Multiple-Choice Calculators Allowed Time 40 minutes Number of Questions 15 The scoring for this section is determined by the formula [C (0.25 I)] 1.8 where C is the
The Relation between the Integral and the Derivative Graphs. Unit #10 : Graphs of Antiderivatives, Substitution Integrals
 Graphs of Antiderivatives - Unit #0 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F (x) The guess-and-check method for anti-differentiation.
Graphs of Antiderivatives - Unit #0 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F (x) The guess-and-check method for anti-differentiation.
Infinite series, improper integrals, and Taylor series
 Chapter Infinite series, improper integrals, and Taylor series. Determine which of the following sequences converge or diverge (a) {e n } (b) {2 n } (c) {ne 2n } (d) { 2 n } (e) {n } (f) {ln(n)} 2.2 Which
Chapter Infinite series, improper integrals, and Taylor series. Determine which of the following sequences converge or diverge (a) {e n } (b) {2 n } (c) {ne 2n } (d) { 2 n } (e) {n } (f) {ln(n)} 2.2 Which
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
Substitutions and by Parts, Area Between Curves. Goals: The Method of Substitution Areas Integration by Parts
 Week #7: Substitutions and by Parts, Area Between Curves Goals: The Method of Substitution Areas Integration by Parts 1 Week 7 The Indefinite Integral The Fundamental Theorem of Calculus, b a f(x) dx =
Week #7: Substitutions and by Parts, Area Between Curves Goals: The Method of Substitution Areas Integration by Parts 1 Week 7 The Indefinite Integral The Fundamental Theorem of Calculus, b a f(x) dx =
Math 261 Calculus I. Test 1 Study Guide. Name. Decide whether the limit exists. If it exists, find its value. 1) lim x 1. f(x) 2) lim x -1/2 f(x)
 Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
Grade: The remainder of this page has been left blank for your workings. VERSION E. Midterm E: Page 1 of 12
 First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm E: Page of Indefinite Integrals. 9 marks Each part is worth 3 marks. Please
First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm E: Page of Indefinite Integrals. 9 marks Each part is worth 3 marks. Please
Assignment # 8, Math 370, Fall 2018 SOLUTIONS:
 Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
Math 111 lecture for Friday, Week 10
 Math lecture for Friday, Week Finding antiderivatives mean reversing the operation of taking derivatives. Today we ll consider reversing the chain rule and the product rule. Substitution technique. Recall
Math lecture for Friday, Week Finding antiderivatives mean reversing the operation of taking derivatives. Today we ll consider reversing the chain rule and the product rule. Substitution technique. Recall
f(x) g(x) = [f (x)g(x) dx + f(x)g (x)dx
 Chapter 7 is concerned with all the integrals that can t be evaluated with simple antidifferentiation. Chart of Integrals on Page 463 7.1 Integration by Parts Like with the Chain Rule substitutions with
Chapter 7 is concerned with all the integrals that can t be evaluated with simple antidifferentiation. Chart of Integrals on Page 463 7.1 Integration by Parts Like with the Chain Rule substitutions with
Math 180, Exam 2, Practice Fall 2009 Problem 1 Solution. f(x) = arcsin(2x + 1) = sin 1 (3x + 1), lnx
 Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
OCR A2 Level Mathematics Core Mathematics Scheme of Work
 OCR A Level Mathematics Core Mathematics Scheme of Work Examination in June of Year 13 The Solomen press worksheets are an excellent resource and incorporated into the SOW NUMERICAL METHODS (6 ) (Solomen
OCR A Level Mathematics Core Mathematics Scheme of Work Examination in June of Year 13 The Solomen press worksheets are an excellent resource and incorporated into the SOW NUMERICAL METHODS (6 ) (Solomen
Methods of Integration
 Methods of Integration Professor D. Olles January 8, 04 Substitution The derivative of a composition of functions can be found using the chain rule form d dx [f (g(x))] f (g(x)) g (x) Rewriting the derivative
Methods of Integration Professor D. Olles January 8, 04 Substitution The derivative of a composition of functions can be found using the chain rule form d dx [f (g(x))] f (g(x)) g (x) Rewriting the derivative
Prelim 1 Solutions V2 Math 1120
 Feb., Prelim Solutions V Math Please show your reasoning and all your work. This is a 9 minute exam. Calculators are not needed or permitted. Good luck! Problem ) ( Points) Calculate the following: x a)
Feb., Prelim Solutions V Math Please show your reasoning and all your work. This is a 9 minute exam. Calculators are not needed or permitted. Good luck! Problem ) ( Points) Calculate the following: x a)
p324 Section 5.2: The Natural Logarithmic Function: Integration
 p324 Section 5.2: The Natural Logarithmic Function: Integration Theorem 5.5: Log Rule for Integration Let u be a differentiable function of x 1. 2. Example 1: Using the Log Rule for Integration ** Note:
p324 Section 5.2: The Natural Logarithmic Function: Integration Theorem 5.5: Log Rule for Integration Let u be a differentiable function of x 1. 2. Example 1: Using the Log Rule for Integration ** Note:
Integrated Calculus II Exam 1 Solutions 2/6/4
 Integrated Calculus II Exam Solutions /6/ Question Determine the following integrals: te t dt. We integrate by parts: u = t, du = dt, dv = e t dt, v = dv = e t dt = e t, te t dt = udv = uv vdu = te t (
Integrated Calculus II Exam Solutions /6/ Question Determine the following integrals: te t dt. We integrate by parts: u = t, du = dt, dv = e t dt, v = dv = e t dt = e t, te t dt = udv = uv vdu = te t (
Math 112 Rahman. Week Taylor Series Suppose the function f has the following power series:
 Math Rahman Week 0.8-0.0 Taylor Series Suppose the function f has the following power series: fx) c 0 + c x a) + c x a) + c 3 x a) 3 + c n x a) n. ) Can we figure out what the coefficients are? Yes, yes
Math Rahman Week 0.8-0.0 Taylor Series Suppose the function f has the following power series: fx) c 0 + c x a) + c x a) + c 3 x a) 3 + c n x a) n. ) Can we figure out what the coefficients are? Yes, yes
University Calculus I. Worksheet # 8 Mar b. sin tan e. sin 2 sin 1 5. b. tan. c. sec sin 1 ( x )) cos 1 ( x )) f. csc. c.
 MATH 6 WINTER 06 University Calculus I Worksheet # 8 Mar. 06-0 The topic covered by this worksheet is: Derivative of Inverse Functions and the Inverse Trigonometric functions. SamplesolutionstoallproblemswillbeavailableonDL,
MATH 6 WINTER 06 University Calculus I Worksheet # 8 Mar. 06-0 The topic covered by this worksheet is: Derivative of Inverse Functions and the Inverse Trigonometric functions. SamplesolutionstoallproblemswillbeavailableonDL,
DRAFT - Math 102 Lecture Note - Dr. Said Algarni
 Math02 - Term72 - Guides and Exercises - DRAFT 7 Techniques of Integration A summery for the most important integrals that we have learned so far: 7. Integration by Parts The Product Rule states that if
Math02 - Term72 - Guides and Exercises - DRAFT 7 Techniques of Integration A summery for the most important integrals that we have learned so far: 7. Integration by Parts The Product Rule states that if
Math 229 Mock Final Exam Solution
 Name: Math 229 Mock Final Exam Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and that it
Name: Math 229 Mock Final Exam Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and that it
Chapter 7: Techniques of Integration
 Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Integration 1/10. Integration. Student Guidance Centre Learning Development Service
 Integration / Integration Student Guidance Centre Learning Development Service lds@qub.ac.uk Integration / Contents Introduction. Indefinite Integration....................... Definite Integration.......................
Integration / Integration Student Guidance Centre Learning Development Service lds@qub.ac.uk Integration / Contents Introduction. Indefinite Integration....................... Definite Integration.......................
Math 181, Exam 2, Study Guide 2 Problem 1 Solution. 1 + dx. 1 + (cos x)2 dx. 1 + cos2 xdx. = π ( 1 + cos π 2
 Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
Chapter 7 Rational Expressions, Equations, and Functions
 Chapter 7 Rational Expressions, Equations, and Functions Section 7.1: Simplifying, Multiplying, and Dividing Rational Expressions and Functions Section 7.2: Adding and Subtracting Rational Expressions
Chapter 7 Rational Expressions, Equations, and Functions Section 7.1: Simplifying, Multiplying, and Dividing Rational Expressions and Functions Section 7.2: Adding and Subtracting Rational Expressions
WeBWorK, Problems 2 and 3
 WeBWorK, Problems 2 and 3 7 dx 2. Evaluate x ln(6x) This can be done using integration by parts or substitution. (Most can not). However, it is much more easily done using substitution. This can be written
WeBWorK, Problems 2 and 3 7 dx 2. Evaluate x ln(6x) This can be done using integration by parts or substitution. (Most can not). However, it is much more easily done using substitution. This can be written
To calculate the x=moment, we multiply the integrand above by x to get = )
 . ( points) The region shown below is the area between the curves y = 3x and y = x. Find the center of mass of this region. 8 6 3 We must calculate the area, x-moment, and y-moment to find the center of
. ( points) The region shown below is the area between the curves y = 3x and y = x. Find the center of mass of this region. 8 6 3 We must calculate the area, x-moment, and y-moment to find the center of
MATH 116, LECTURE 13, 14 & 15: Derivatives
 MATH 116, LECTURE 13, 14 & 15: Derivatives 1 Formal Definition of the Derivative We have seen plenty of limits so far, but very few applications. In particular, we have seen very few functions for which
MATH 116, LECTURE 13, 14 & 15: Derivatives 1 Formal Definition of the Derivative We have seen plenty of limits so far, but very few applications. In particular, we have seen very few functions for which
S56 (5.3) Further Calculus.notebook March 24, 2016
 Daily Practice 16.3.2016 Today we will be learning how to differentiate using the Chain Rule. Homework Solutions Video online - please mark 2009 P2 Polynomials HW Online due 22.3.16 We use the Chain Rule
Daily Practice 16.3.2016 Today we will be learning how to differentiate using the Chain Rule. Homework Solutions Video online - please mark 2009 P2 Polynomials HW Online due 22.3.16 We use the Chain Rule
Math Final Exam Review
 Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Final Exam Review Exercise Set A, Math 1551, Fall 2017
 Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Unit #10 : Graphs of Antiderivatives; Substitution Integrals
 Unit #10 : Graphs of Antiderivatives; Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F(x) The guess-and-check method for anti-differentiation. The substitution
Unit #10 : Graphs of Antiderivatives; Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F(x) The guess-and-check method for anti-differentiation. The substitution
8.7 MacLaurin Polynomials
 8.7 maclaurin polynomials 67 8.7 MacLaurin Polynomials In this chapter you have learned to find antiderivatives of a wide variety of elementary functions, but many more such functions fail to have an antiderivative
8.7 maclaurin polynomials 67 8.7 MacLaurin Polynomials In this chapter you have learned to find antiderivatives of a wide variety of elementary functions, but many more such functions fail to have an antiderivative
Review for the Final Exam
 Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Section 10.7 Taylor series
 Section 10.7 Taylor series 1. Common Maclaurin series 2. s and approximations with Taylor polynomials 3. Multiplication and division of power series Math 126 Enhanced 10.7 Taylor Series The University
Section 10.7 Taylor series 1. Common Maclaurin series 2. s and approximations with Taylor polynomials 3. Multiplication and division of power series Math 126 Enhanced 10.7 Taylor Series The University
( ) is called the dependent variable because its
 page 1 of 16 CLASS NOTES: 3 8 thru 4 3 and 11 7 Functions, Exponents and Polynomials 3 8: Function Notation A function is a correspondence between two sets, the domain (x) and the range (y). An example
page 1 of 16 CLASS NOTES: 3 8 thru 4 3 and 11 7 Functions, Exponents and Polynomials 3 8: Function Notation A function is a correspondence between two sets, the domain (x) and the range (y). An example
Review of Integration Techniques
 A P P E N D I X D Brief Review of Integration Techniques u-substitution The basic idea underlying u-substitution is to perform a simple substitution that converts the intergral into a recognizable form
A P P E N D I X D Brief Review of Integration Techniques u-substitution The basic idea underlying u-substitution is to perform a simple substitution that converts the intergral into a recognizable form
MATH 1A - FINAL EXAM DELUXE - SOLUTIONS. x x x x x 2. = lim = 1 =0. 2) Then ln(y) = x 2 ln(x) 3) ln(x)
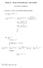 MATH A - FINAL EXAM DELUXE - SOLUTIONS PEYAM RYAN TABRIZIAN. ( points, 5 points each) Find the following limits (a) lim x x2 + x ( ) x lim x2 + x x2 + x 2 + + x x x x2 + + x x 2 + x 2 x x2 + + x x x2 +
MATH A - FINAL EXAM DELUXE - SOLUTIONS PEYAM RYAN TABRIZIAN. ( points, 5 points each) Find the following limits (a) lim x x2 + x ( ) x lim x2 + x x2 + x 2 + + x x x x2 + + x x 2 + x 2 x x2 + + x x x2 +
Calculus II/III Summer Packet
 Calculus II/III Summer Packet First of all, have a great summer! Enjoy your time away from school. Come back fired up and ready to learn. I know that I will be ready to have a great year of calculus with
Calculus II/III Summer Packet First of all, have a great summer! Enjoy your time away from school. Come back fired up and ready to learn. I know that I will be ready to have a great year of calculus with
t 2 + 2t dt = (t + 1) dt + 1 = arctan t x + 6 x(x 3)(x + 2) = A x +
 MATH 06 0 Practice Exam #. (0 points) Evaluate the following integrals: (a) (0 points). t +t+7 This is an irreducible quadratic; its denominator can thus be rephrased via completion of the square as a
MATH 06 0 Practice Exam #. (0 points) Evaluate the following integrals: (a) (0 points). t +t+7 This is an irreducible quadratic; its denominator can thus be rephrased via completion of the square as a
