A parsing technique for TRG languages
|
|
|
- Stephanie Hicks
- 6 years ago
- Views:
Transcription
1 A parsing technique for TRG languages Daniele Paolo Scarpazza Politecnico di Milano October 15th, 2004
2 Daniele Paolo Scarpazza A parsing technique for TRG grammars [1] Abstract In this presentation, we propose a parsing algorithm for TRG languages which is an extension of the Cocke-Kasami-Younger (CKY) algorithm. Our algorithm exhibits a polynomial time complexity. Agenda: a brief review of the original CKY algorithm; issues in the extension of CKY algorithm to TRGs; a formal description of the steps composing the algorithm; the derivation of time complexity; a fully-developed example illustrating the algorithm at work.
3 Daniele Paolo Scarpazza A parsing technique for TRG grammars [2] A brief review of the CKY algorithm The CKY algorithm is a bottom-up parsing technique for context-free grammars; the simplest formulation operates on grammars in the Chomsky normal form (CNF); let G = (V, Σ, P, S) be a CNF context-free grammar; let x Σ be a string and x = n its length; let x i denote the i-th symbol of x; given G and x, the algorithm decides in O(n 3 ) time whether x (G); Input : G, x; Output : x (G)?; for all r = 0 to n do V r,1 {A (A n r ) P } end for for all c = 2 to n do for all r = 1 to n c + 1 do V r,c {} for all r = 1 to n c + 1 do if (A BC) P, B V r,k, C V r+k,c k then V r,c V r,c {A} end if end for end for end for if S V 1,n then output yes else output no end if
4 Daniele Paolo Scarpazza A parsing technique for TRG grammars [3] An example illustrating the CKY algorithm Grammar: S SS S AA S b A AS A AA A a Recognition table: V r,c c : a r : 1 A A, S A, S A, S a 2 A A A b 3 S S b 4 S String: x = aabb
5 Daniele Paolo Scarpazza A parsing technique for TRG grammars [4] Preliminaries: coordinates and rectangles A rectangle, indicated as r c, is the following set of 2D integer coordinates: r c = {(1, 1), (1, 2),..., (1, c), (2, 1), (2, 2),..., (2, c),..., (r, 1), (r, 2),..., (r, c)}; example: 2 3 = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3)}. A subrectangle, indicated as r c + (a, b), is the following set of couples: r c + (a, b) = { (a, b), (a, b + 1),... (a, b + c 1), (a + 1, b), (a + 1, b + 1),... (a + 1, b + c 1), ; (a + r 1, b), (a + r 1, b + 1),... (a + r 1, b + c 1) } example: (4, 5) = {(4, 5), (4, 6), (4, 7), (5, 5), (5, 6), (5, 7)}. Note: rectangles and subrectangles are sets; usual set operators,,, =,, and are defined. Operands,, on rectangles yield sets which are not, in general, subrectangles. Example: (2 3 + (4, 5)) (2 3 + (5, 6)) = (1 2 + (5, 6)). A new notation to indicate subpictures: given p and q, we say that example: p = p[r c + (i, j)] = q iff q (i,j) p q = (r, c); a d g j m ( b e h k n d g j p[2 3 + (1, 2)] = e h k c f i l o ).
6 Daniele Paolo Scarpazza A parsing technique for TRG grammars [5] Extending the CKY algorithm to TRGs (1/3) Cells in the CKY recognition matrix represent all the possible substrings of the input string; for TRGs, we need to represent all the possible subpictures of the input picture; the extension of the recognition matrix is the tableau, where each cell represents a possible subpicture. Formally: A tableau is a matrix of variable-size matrices. A m n tableau T contains m n matrices, each denoted by T i,j, (i, j) 1 i m, 1 j n. Matrix T i,j must have size (m i + 1, n j + 1). The notation T [i j + (a, b)] indicates the (a, b) element of matrix T i,j, or (T i,j ) a,b. Example: the following figure shows a 3 6 tableau.
7 Daniele Paolo Scarpazza A parsing technique for TRG grammars [6] Extending the CKY algorithm to TRGs (2/3) In the CKY recognition matrix, a symbol A in cell V r,c indicates that substring x r...x r+c 1 is recognized as generated by non-terminal A; in TRGs, rules are isometric, and either fixed-size or variable-size; variable-size rules imply the recognition of LOC u,eq languages; as a consequence, the algorithm requires more information in a tableau cell than just A; more precisely, elements appearing in cell T [i j + (a, b)] must provide information on which rules are recognizable rule on subpicture i j + (a, b) and which tiles are missing. Example: element (R 3, {t 3,2, t 3,3, t 3,5 },...) in a tableau cell indicates that the subpicture corresponding to that tableau cell only uses tiles present in the right-part of rule R 3, and tiles t 3,2, t 3,3, are t 3,5 not used in the picture. An element (R i, {},...) indicates that the subpicture belongs to LOC u,eq of rule R i, thus can be recognized as a sentential form of rule R i.
8 Daniele Paolo Scarpazza A parsing technique for TRG grammars [7] Extending the CKY algorithm to TRGs (3/3) Due to the formal definitions of TRGs, application areas in a derivation must be disjoint, or included the latter in the former in couples. More precisely, if application areas are ordered α 1,..., α i, α i+1,..., α i+j,...: (α i α i+j = ) (α i α i+j ). During bottom-up recognition, the reversed version of the above principle must be enforced. A violation is illustrated in the following figure: To enforce the above principle, we use multipictures, i.e. pictures containing couples (symbol, area). In the above example, each B would be replaced by (B, (1, 4)). The last step would be illegal, because (4 6 + (1, 1)) (4 4 + (1, 4)), (4 6 + (1, 1)) (4 4 + (1, 4) ).
9 Daniele Paolo Scarpazza A parsing technique for TRG grammars [8] Preliminaries: Multipictures and compatibility A multipicture is a matrix m n where each cell is a set of couples (I, r) where I (Σ N), and r is a subrectangle m n; our algorithm uses one multipicture; each cell of it initially contains the pixel of the input picture; then, for every recognized application area, corresponding cells are filled with the nonterminal; Given a picture p and a multipicture M, both of size m n (and alphabet respectively I and 2 I S(m n) ), the compatibility between p and M (denoted as p :: M) is the set of pictures p, of size m n and alphabet I S(m n), such that i, k {1...m} j, l {1...n}: p i,j = (p i,j, α i,j ) M i,j and i, k {1...m} j, l {1...n}: (α i,j = α k,l p i,j = p k,l ) (α i,j α k,l = ). We say that p is compatible with M iff p :: M.
10 Daniele Paolo Scarpazza A parsing technique for TRG grammars [9] Example: pictures (p, p ) and corresponding multipictures (M, M ) in the first step of a recognition chain. Please consider the sub-multipicture M [2x2 + (1, 1)], bordered in the figure. For it, compatibilities with two tiles are reported: M [2x2 + (1, 1)] :: M [2x2 + (1, 1)] :: { } A A (A, 4 3+(1, 1)) (A, 4 3+(1, 1)) A A = (A, 4 3+(1, 1)) (A, 4 3+(1, 1)) { } x x (x, 1 1+(1, 1)) (x, 1 1+(1, 2)) = x o (x, 1 1+(2, 1)) (o, 1 1+(2, 2))
11 Daniele Paolo Scarpazza A parsing technique for TRG grammars [10] Preliminaries: Copy rules and subrectangles If G = (Σ, N, S, R) is a TRG, and A, B N, a rule in the form { } B B A B B is said to be a copy rule; it can be easily proved that for every TRG G with copy rules, G L(G) = L(G ) and G is free from copy rules; with no loss of generality, our algoritm operates on TRG grammars free from copy rules. We introduce the function Sr( ) which, given a set of coordinates, returns the smaller subrectangle containing them. Example: Sr(1 1 + (3, 4) (5, 7)) = (3, 4)
12 Daniele Paolo Scarpazza A parsing technique for TRG grammars [11] Our algorithm hypotheses Let a TRG G(Σ, N, S, R) and a picture p Σ (m,n) be given. The following algorithm determines whether p L(G) or not. let G be free from copy rules; let all rules in R be variable-size rules (the extension of the algorithm to fixed-size rules is trivial); let the rules in R be numbered as R 1, R 2,..., and their right-hand sides as ω 1, ω 2,...; let the tiles appearing in ω i be numbered as t i,1, t i,2,... ; the algorithm operates by constructing a m n tableau T, and a m n multipicture M; initially, T [r c + (i, j)] = r, c, i, j; and M i,j = {(p i,j, (i, j))}; the following steps are applied until fixed point is reached;
13 Daniele Paolo Scarpazza A parsing technique for TRG grammars [12] Our algorithm step # 1 Step 1: update each cell T [2 2 + (i, j)], adding elements: if R e = (Q ω) R, t ω, t (t :: M[2 2 + (i, j)]), then: t = ( (t1,1, α 1,1 ) (t 1,2, α 1,2 ) (t 2,1, α 2,1 ) (t 2,2, α 2,2 ) ) (R e, ω t, Sr(α 1,1 α 1,2 α 2,1 α 2,2 )) T [2 2 + (i, j)] ; Where the function Sr( ) yields the smallest subrectangle including the given elements.
14 Daniele Paolo Scarpazza A parsing technique for TRG grammars [13] Our algorithm step # 2 Step 2: update T adding elements: (r, c) 2 < r m, 2 < c n in lexicographical order: if (R e, ω 1, α 1 ) T [r (c 1)+(i, j)] (R e, ω 2, α 2 ) T [r (c 1)+(i, j + 1)] or (R e, ω 1, α 1 ) T [(r 1) c+(i, j)] (R e, ω 2, α 2 ) T [(r 1) c+(i + 1, j)] then (R e, ω 1 ω 2, Sr(α 1 α 2 )) T [r c + (i, j)] ; Comment: elements of two horizontally adjacent tableau cells m n can be merged into a corresponding m (n+1) cell. Similarly for vertically adjacent cells. Given the same rule, the set of missing tiles is the intersection of the sets of missing tiles, and the scope is the Sr( ) of the union of scopes.
15 Daniele Paolo Scarpazza A parsing technique for TRG grammars [14] Our algorithm step # 3 Step 3: update M adding elements: for each element such that (R e, {}, α) T [r c + (i, j)] α r c + (i, j), R e = (A...) add elements: (i, j) r c + (i, j) (A, (r c + (i, j)) M i,j ; Comment: whenever all the tiles of subpicture r c + (i, j) appear in the right part of rule R e, and no tile is missing (R e, {},...) and the scope α of all the recognized symbols is inside the current subpicture, then recognize the subpicture as application area of rule R e. Update multipicture, adding a couple (A, r c + (i, j)) in every cell of sub-multipicture r c + (i, j).
16 Daniele Paolo Scarpazza A parsing technique for TRG grammars [15] Our algorithm final step Final step (to be executed when fixed point is reached): if (i, j) r c (S, m n + (1, 1)) M i,j then: declare p L(G) else declare p L(G). Comment: the recognition of a rule which has the starting symbol S as the left-hand side, and the whole picture as application area (m n + (1, 1)), indicates that the picture is recognized. In short, the multipicture must contain element (S, m n) in every cell. If such area is not recognized and a fixed point is reached, the picture is not in the language.
17 Daniele Paolo Scarpazza A parsing technique for TRG grammars [16] Our algorithm informal comments The algorithm scans the tableau and the multipicture several times; at each scan, one or more disjoint application areas are recognized; each tableau cell T [r c+(i, j)] is filled with triples (R e, ω, α) where if rule R e = A ω e exists, then ω = ω e B 2,2 (M[r c + (i, j)]). When (R e,, α) T [r c + (i, j)], then exactly all the tiles in rule R e are used in subpicture M[r c + (i, j)]; moreover α is the smallest subrectangle including the activation areas of the symbols in the multipicture which comply with rule R e. If α is not smaller or equal to the subrectangle r c + (i, j) the rule is discarded, since it would violate the theorem of disjointness of application areas. Every time a rule R e = (A...) is recognized over an activation area q, a couple (A, q) is added to every cell of M[q], so that the next iteration of the algorithm can use the newly added symbol to recognize larger activation areas.
18 Daniele Paolo Scarpazza A parsing technique for TRG grammars [17] Time complexity if the input picture has dimensions m n, the input size is N = m n; time complexity is derived as a function of the size of the input N; the complexity is determined by the most complex step (number 2); this step fills a m n tableau which has m(m 1)n(n 1) 4 k 1 N 2 cells; for each cell, it compares couples of elements of exactly two other cells; elements are in the form (R e, ω, α) they can be at most R max i ω Ri S(m n), where k 2 = R max i ω Ri is fixed, while S(m n) k 1 N 2 ; therefore, the time complexity of each comparison in step 2 is (k 1 k 2 ) 2 N 4, and the overall complexity of step 2 is k 1 (k 1 k 2 ) 2 N 6. Steps 1 3 are iterated until fixed point. At every iteration, one or more application areas are detected. Thanks to the exclusion of copy rules, an application area can appear at most once in a derivation. Therefore # of iterations # application areas k 1 N 2. Therefore, the time complexity of the whole algorithm is O(N 8 ).
19 Daniele Paolo Scarpazza A parsing technique for TRG grammars [18] A full example In the next slides we fully develop an example, with the help of the above storyboard. Elements updated in each slide will be marked in black. Elements will be illustrated in this order: the input picture and the input grammar; the result of initialization on the tableau T and on the multipicture M will be shown; the effects of the first iteration; the effects of the second iteration (and conclusion). For sake of clarity, T and M at initialization, iteration 1 and 2 are represented as separate entities.
20 Daniele Paolo Scarpazza A parsing technique for TRG grammars [19] A full example: the input picture p = x x x x x x x o o o o x x o o o o x x o o o o x x x x x x x
21 Daniele Paolo Scarpazza A parsing technique for TRG grammars [20] A full example: the input grammar (1/2) G = (Σ, N, S, R) Σ = {x, o} N = {S, A, B} ( A A B B R 1 : S B 2,2 A A B B x x x R 2 : A B 2,2 x o o x o o x x x R 3 : A B 2,2 x x x o o x o o x x x x )
22 Daniele Paolo Scarpazza A parsing technique for TRG grammars [21] A full example: the input grammar (2/2) For ease of reference, we give names to the tiles in each right-hand side. R 1 : S B 2,2 ( A A B B A A B B R 2 : A B 2,2 R 3 : A B 2,2 x x x x o o x o o x x x x x x o o x o o x x x x ) = { ( A A t 1,1 = A A ( x x {t = 2,1 = x o ( x o t 2,4 = x x ( x x {t = 3,1 = o x ( o x t 3,4 = x x ) ( A B, t 1,2 = A B ) ( x x, t 2,2 = o o ) ( o o, t 2,5 = x x ) ( x x, t 3,2 = o o ) ( o o, t 3,5 = x x ) ( B B, t 1,3 = B B ) ( x o, t 2,3 = x o ) ( o o, t 2,6 = o o ) ( o x, t 3,3 = o x ) ( o o, t 3,6 = o o ), )} ), )} )}
23 Daniele Paolo Scarpazza A parsing technique for TRG grammars [22] A full example: tableau initialization At initialization time, the tableau is empty. Being the input picture dimensions equal to 6 5, also the tableau T will have 6 5 cells. The first cell, T 1,1, will be a 6 5 matrix. Cells in this matrix represent each 1 1 tile in the input picture. T 1,2, will be a 6 4 matrix, i.e. with one less column, and so on, up to T 1,6, which is a 6 1 matrix. Same considerations apply to the second and following rows. The last cell, T 5,6, is a matrix composed by a single cell, representing the whole input picture.
24 Daniele Paolo Scarpazza A parsing technique for TRG grammars [23] A full example: multipicture initialization The multipicture is initially set to the contents of the picture. The scope of each terminal symbol is set to the 1 1 cell where the symbol belong. M = (x, 1 1+(1, 1)) (x, 1 1+(1, 2)) (x, 1 1+(1, 3)) (x, 1 1+(1, 4)) (x, 1 1+(1, 5)) (x, 1 1+(1, 6)) (x, 1 1+(2, 1)) (o, 1 1+(2, 2)) (o, 1 1+(2, 3)) (o, 1 1+(2, 4)) (o, 1 1+(2, 5)) (x, 1 1+(2, 6)) (x, 1 1+(3, 1)) (o, 1 1+(3, 2)) (o, 1 1+(3, 3)) (o, 1 1+(3, 4)) (o, 1 1+(3, 5)) (x, 1 1+(3, 6)) (x, 1 1+(4, 1)) (o, 1 1+(4, 2)) (o, 1 1+(4, 3)) (o, 1 1+(4, 4)) (o, 1 1+(4, 5)) (x, 1 1+(4, 6)) (x, 1 1+(5, 1)) (x, 1 1+(5, 2)) (x, 1 1+(5, 3)) (x, 1 1+(5, 4)) (x, 1 1+(5, 5)) (x, 1 1+(5, 6))
25 Daniele Paolo Scarpazza A parsing technique for TRG grammars [24] A full example: iteration #1 All tableau cells corresponding to 1 n and n 1 cells are never used by the algorithm, and always remain empty.
26 Daniele Paolo Scarpazza A parsing technique for TRG grammars [25] A full example: iteration #1, step #1 Add elements to cells T [2 2 + (i, j)] in the tableau: informally, for each of the 2 2 tiles t in the multipicture which appear in the right-hand size of a rule, add a (R i, ω i t, (i, j)) entry. For the first cell, T [2 2 + (1, 1)]: M = (x, 1 1+(1, 1)) (x, 1 1+(1, 2))... (x, 1 1+(2, 1)) (o, 1 1+(2, 2)) T 2,2 = (R 2, {t 2,2, t 2,3, t 2,4, t 2,5, t 2,6 }, 2 2+(1, 1))
27 Daniele Paolo Scarpazza A parsing technique for TRG grammars [26] A full example: iteration #1, step #1 (continued) Same for the second cell, T [2 2 + (1, 2)]. Please note that the corresponding tile appears in the right-hand side of two rules, these two elements are added to the tableau: M = (x, 1 1+(1, 1)) (x, 1 1+(1, 2)) (x, 1 1+(1, 3))... (x, 1 1+(2, 1)) (o, 1 1+(2, 2)) (o, 1 1+(2, 3)) T 2,2 = (R 2, {t 2,2, t 2,3, t 2,4, t 2,5, t 2,6 }, 2 2+(1, 1)) (R 2, {t 2,1, t 2,3, t 2,4, t 2,5, t 2,6 }, 2 2+(1, 2))... (R 3, {t 3,1, t 3,3, t 3,4, t 3,5, t 3,6 }, 2 2+(1, 2))
28 Daniele Paolo Scarpazza A parsing technique for TRG grammars [27] A full example: iteration #1, step #2 For all the matrices in the tableau from T 2,3 to T 2,6, each cell can be filled by merging the contents of a couple of cells in the tableau matrix immediately on the } left: (R e, ω 1, α 1 ) T [r (c 1)+(i, j)] (R (R e, ω 2, α 2 ) T [r (c 1)+(i, j + 1)] e, ω 1 ω 2, Sr(α 1 α 2 )) T [r c + (i, j)] T 2,2 = (R 2, {t 2,2, t 2,3, t 2,4, t 2,5, t 2,6 }, 2 2+(1, 1)) (R 2, {t 2,1, t 2,3, t 2,4, t 2,5, t 2,6 }, 2 2+(1, 2))... (R 3, {t 3,1, t 3,3, t 3,4, t 3,5, t 3,6 }, 2 2+(1, 2)) T 2,3 = (R 2, {t 2,3, t 2,4, t 2,5, t 2,6 }, 2 3+(1, 1))
29 Daniele Paolo Scarpazza A parsing technique for TRG grammars [28] A full example: iteration #1, step #2 (continued) Also cells in matrix T 3,2 can be derived from cells in T 2,2 : } (R e, ω 1, α 1 ) T [(r 1) c+(i, j)] (R (R e, ω 2, α 2 ) T [(r 1) c+(i + 1, j)] e, ω 1 ω 2, Sr(α 1 α 2 )) T [r c + (i, j)] T 2,2 = (R 2, {t 2,2, t 2,3, t 2,4, t 2,5, t 2,6 }, 2 2+(1, 1)) (R 2, {t 2,1, t 2,3, t 2,4, t 2,5, t 2,6 }, 2 2+(1, 2))... (R 3, {t 3,1, t 3,3, t 3,4, t 3,5, t 3,6 }, 2 2+(1, 2))... (R 2, {t 2,1, t 2,2, t 2,4, t 2,5, t 2,6 }, 2 2+(2, 1)) T 2,3 = (R 2, {t 2,2, t 2,4, t 2,5, t 2,6 }, 3 2+(1, 1))
30 Daniele Paolo Scarpazza A parsing technique for TRG grammars [29] A full example: iteration #1, step #2 (continued) The contents of the remaining cells in the tableau can be derived by applying the same horizontal and vertical merging rules shown in the last two slides: (R e, ω 1, α 1 ) T [r (c 1)+(i, j)] (R e, ω 2, α 2 ) T [r (c 1)+(i, j + 1)] (R e, ω 1, α 1 ) T [(r 1) c+(i, j)] (R e, ω 2, α 2 ) T [(r 1) c+(i + 1, j)] } } (R e, ω 1 ω 2, Sr(α 1 α 2 )) T [r c + (i, j)] (R e, ω 1 ω 2, Sr(α 1 α 2 )) T [r c + (i, j)]
31 Daniele Paolo Scarpazza A parsing technique for TRG grammars [30] A full example: iteration #1, step #3 (R2,, 5 3+(1, 1)) (R2, {t 2,1, t 2,3, t 2,4, }5 3+(1, 2)) (R2, {t 2,1, t 2,3, t 2,4 }, 5 3+(1, 3)) R3,, 5 3+(1, 4)) (R3, {t 3,1, t 3,3, t 3,4 }, 5 3+(1, 2)) (R3, {t 3,1, t 3,3, t 3,4 }, 5 3+(1, 3)) Let s consider the final state of tableau cell T 5,3 : rules R2 and R 3 were recognized: an entry (A, 5 3+(1, 1)) is added to all the pixels in the 5 3+(1, 1) subpicture of the multipicture M; an entry (B, 5 3+(1, 4)) is added to all the pixels in the 5 3+(1, 4) subpicture of the multipicture M. The final state of the multipicture at the end of iteration 1 is shown in the next slide.
32 Daniele Paolo Scarpazza A parsing technique for TRG grammars [31] M = (x, 1 1+(1, 1)) (x, 1 1+(1, 2)) (x, 1 1+(1, 3)) (x, 1 1+(1, 4)) (x, 1 1+(1, 5)) (x, 1 1+(1, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 2)) (B, 5 4+(1, 3)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 1)) (B, 5 5+(1, 2)) (x, 1 1+(2, 1)) (o, 1 1+(2, 2)) (o, 1 1+(2, 3)) (o, 1 1+(2, 5)) (o, 1 1+(2, 5)) (x, 1 1+(2, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 2)) (B, 5 4+(1, 3)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 1)) (B, 5 5+(1, 2)) (x, 1 1+(3, 1)) (o, 1 1+(3, 2)) (o, 1 1+(3, 3)) (o, 1 1+(3, 4)) (o, 1 1+(3, 5)) (x, 1 1+(3, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 2)) (B, 5 4+(1, 3)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 1)) (B, 5 5+(1, 2)) (x, 1 1+(4, 1)) (o, 1 1+(4, 2)) (o, 1 1+(4, 3)) (o, 1 1+(4, 4)) (o, 1 1+(4, 5)) (x, 1 1+(4, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 2)) (B, 5 4+(1, 3)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 1)) (B, 5 5+(1, 2)) (x, 1 1+(5, 1)) (x, 1 1+(5, 2)) (x, 1 1+(5, 3)) (x, 1 1+(5, 4)) (x, 1 1+(5, 5)) (x, 1 1+(5, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 2)) (B, 5 4+(1, 3)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (B, 5 5+(1, 1)) (B, 5 5+(1, 2))
33 Daniele Paolo Scarpazza A parsing technique for TRG grammars [32]
34 Daniele Paolo Scarpazza A parsing technique for TRG grammars [33] A full example: iteration #2, step #1 Step #1 is applied on the new multipicture. Entire subrectangles of A s and B s are recognized by rule R 1. M = (A, 5 3+(1, 1)) (A, 5 3+(1, 1))... (A, 5 4+(1, 1)) (A, 5 4+(1, 1))... (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1))... (A, 5 4+(1, 1)) (A, 5 4+(1, 1))... (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) T 2,2 = (R 1, {t 1,2, t 1,3 }, 5 3+(1, 1))... (R 1, {t 1,2, t 1,3 }, 5 4+(1, 1))... (R 1, {t 1,2, t 1,3 }, 5 5+(1, 1))
35 Daniele Paolo Scarpazza A parsing technique for TRG grammars [34] A full example: iteration #2, step #2 At the end of step 2, cell T 5,6 contains the following value: T 2,2 = (R 1,, 5 6+(1, 1)). Thus, an application area for rule R 1 was recognized over the entire multipicture.
36 Daniele Paolo Scarpazza A parsing technique for TRG grammars [35] A full example: iteration #2, step #3 An element (S, 5 6+(1, 1)) is added to every cell in the multipicture belonging to the rectangle 5 6+(1, 1), which is the whole picture. The picture is therefore recognized. The final state of the multipicture is shown in the next slide.
37 Daniele Paolo Scarpazza A parsing technique for TRG grammars [36] M = (x, 1 1+(1, 1)) (x, 1 1+(1, 2)) (x, 1 1+(1, 3)) (x, 1 1+(1, 4)) (x, 1 1+(1, 5)) (x, 1 1+(1, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (B, 5 5+(1, 2)) (B, 5 4+(1, 3)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (B, 5 5+(1, 1)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (x, 1 1+(2, 1)) (o, 1 1+(2, 2)) (o, 1 1+(2, 3)) (o, 1 1+(2, 5)) (o, 1 1+(2, 5)) (x, 1 1+(2, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (B, 5 5+(1, 2)) (B, 5 4+(1, 3)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (B, 5 5+(1, 1)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (x, 1 1+(3, 1)) (o, 1 1+(3, 2)) (o, 1 1+(3, 3)) (o, 1 1+(3, 4)) (o, 1 1+(3, 5)) (x, 1 1+(3, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (B, 5 5+(1, 2)) (B, 5 4+(1, 3)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (B, 5 5+(1, 1)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (x, 1 1+(4, 1)) (o, 1 1+(4, 2)) (o, 1 1+(4, 3)) (o, 1 1+(4, 4)) (o, 1 1+(4, 5)) (x, 1 1+(4, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (B, 5 5+(1, 2)) (B, 5 4+(1, 3)) (B, 5 4+(1, 3)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (B, 5 5+(1, 1)) (B, 5 5+(1, 2)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (S, 5 6+(1, 1)) (x, 1 1+(5, 1)) (x, 1 1+(5, 2)) (x, 1 1+(5, 3)) (x, 1 1+(5, 4)) (x, 1 1+(5, 5)) (x, 1 1+(5, 6)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 3+(1, 1)) (A, 5 4+(1, 1)) (A, 5 5+(1, 1)) (B, 5 3+(1, 4))
38 Daniele Paolo Scarpazza A parsing technique for TRG grammars [37]
39 Daniele Paolo Scarpazza A parsing technique for TRG grammars [38] The end Thank you for your attention. Questions are welcome.
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
Notes on the Catalan problem
 Notes on the Catalan problem Daniele Paolo Scarpazza Politecnico di Milano March 16th, 2004 Daniele Paolo Scarpazza Notes on the Catalan problem [1] An overview of Catalan problems
Notes on the Catalan problem Daniele Paolo Scarpazza Politecnico di Milano March 16th, 2004 Daniele Paolo Scarpazza Notes on the Catalan problem [1] An overview of Catalan problems
CSCI Compiler Construction
 CSCI 742 - Compiler Construction Lecture 12 Cocke-Younger-Kasami (CYK) Algorithm Instructor: Hossein Hojjat February 20, 2017 Recap: Chomsky Normal Form (CNF) A CFG is in Chomsky Normal Form if each rule
CSCI 742 - Compiler Construction Lecture 12 Cocke-Younger-Kasami (CYK) Algorithm Instructor: Hossein Hojjat February 20, 2017 Recap: Chomsky Normal Form (CNF) A CFG is in Chomsky Normal Form if each rule
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Properties of Context-Free Languages
 Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
CYK Algorithm for Parsing General Context-Free Grammars
 CYK Algorithm for Parsing General Context-Free Grammars Why Parse General Grammars Can be difficult or impossible to make grammar unambiguous thus LL(k) and LR(k) methods cannot work, for such ambiguous
CYK Algorithm for Parsing General Context-Free Grammars Why Parse General Grammars Can be difficult or impossible to make grammar unambiguous thus LL(k) and LR(k) methods cannot work, for such ambiguous
Address for Correspondence
 Proceedings of BITCON-2015 Innovations For National Development National Conference on : Research and Development in Computer Science and Applications Research Paper SUBSTRING MATCHING IN CONTEXT FREE
Proceedings of BITCON-2015 Innovations For National Development National Conference on : Research and Development in Computer Science and Applications Research Paper SUBSTRING MATCHING IN CONTEXT FREE
Improved TBL algorithm for learning context-free grammar
 Proceedings of the International Multiconference on ISSN 1896-7094 Computer Science and Information Technology, pp. 267 274 2007 PIPS Improved TBL algorithm for learning context-free grammar Marcin Jaworski
Proceedings of the International Multiconference on ISSN 1896-7094 Computer Science and Information Technology, pp. 267 274 2007 PIPS Improved TBL algorithm for learning context-free grammar Marcin Jaworski
NPDA, CFG equivalence
 NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
Languages. Languages. An Example Grammar. Grammars. Suppose we have an alphabet V. Then we can write:
 Languages A language is a set (usually infinite) of strings, also known as sentences Each string consists of a sequence of symbols taken from some alphabet An alphabet, V, is a finite set of symbols, e.g.
Languages A language is a set (usually infinite) of strings, also known as sentences Each string consists of a sequence of symbols taken from some alphabet An alphabet, V, is a finite set of symbols, e.g.
CS481F01 Prelim 2 Solutions
 CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CS 301. Lecture 18 Decidable languages. Stephen Checkoway. April 2, 2018
 CS 301 Lecture 18 Decidable languages Stephen Checkoway April 2, 2018 1 / 26 Decidable language Recall, a language A is decidable if there is some TM M that 1 recognizes A (i.e., L(M) = A), and 2 halts
CS 301 Lecture 18 Decidable languages Stephen Checkoway April 2, 2018 1 / 26 Decidable language Recall, a language A is decidable if there is some TM M that 1 recognizes A (i.e., L(M) = A), and 2 halts
CSCI 1010 Models of Computa3on. Lecture 17 Parsing Context-Free Languages
 CSCI 1010 Models of Computa3on Lecture 17 Parsing Context-Free Languages Overview BoCom-up parsing of CFLs. BoCom-up parsing via the CKY algorithm An O(n 3 ) algorithm John E. Savage CSCI 1010 Lect 17
CSCI 1010 Models of Computa3on Lecture 17 Parsing Context-Free Languages Overview BoCom-up parsing of CFLs. BoCom-up parsing via the CKY algorithm An O(n 3 ) algorithm John E. Savage CSCI 1010 Lect 17
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION
 FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
straight segment and the symbol b representing a corner, the strings ababaab, babaaba and abaabab represent the same shape. In order to learn a model,
 The Cocke-Younger-Kasami algorithm for cyclic strings Jose Oncina Depto. de Lenguajes y Sistemas Informaticos Universidad de Alicante E-03080 Alicante (Spain) e-mail: oncina@dlsi.ua.es Abstract The chain-code
The Cocke-Younger-Kasami algorithm for cyclic strings Jose Oncina Depto. de Lenguajes y Sistemas Informaticos Universidad de Alicante E-03080 Alicante (Spain) e-mail: oncina@dlsi.ua.es Abstract The chain-code
CS5371 Theory of Computation. Lecture 7: Automata Theory V (CFG, CFL, CNF)
 CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
CSE 355 Test 2, Fall 2016
 CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
ECS 120: Theory of Computation UC Davis Phillip Rogaway February 16, Midterm Exam
 ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
Grammar formalisms Tree Adjoining Grammar: Formal Properties, Parsing. Part I. Formal Properties of TAG. Outline: Formal Properties of TAG
 Grammar formalisms Tree Adjoining Grammar: Formal Properties, Parsing Laura Kallmeyer, Timm Lichte, Wolfgang Maier Universität Tübingen Part I Formal Properties of TAG 16.05.2007 und 21.05.2007 TAG Parsing
Grammar formalisms Tree Adjoining Grammar: Formal Properties, Parsing Laura Kallmeyer, Timm Lichte, Wolfgang Maier Universität Tübingen Part I Formal Properties of TAG 16.05.2007 und 21.05.2007 TAG Parsing
ECS 120 Lesson 20 The Post Correspondence Problem
 ECS 120 Lesson 20 The Post Correspondence Problem Oliver Kreylos Wednesday, May 16th, 2001 Today we will continue yesterday s discussion of reduction techniques by looking at another common strategy, reduction
ECS 120 Lesson 20 The Post Correspondence Problem Oliver Kreylos Wednesday, May 16th, 2001 Today we will continue yesterday s discussion of reduction techniques by looking at another common strategy, reduction
Properties of context-free Languages
 Properties of context-free Languages We simplify CFL s. Greibach Normal Form Chomsky Normal Form We prove pumping lemma for CFL s. We study closure properties and decision properties. Some of them remain,
Properties of context-free Languages We simplify CFL s. Greibach Normal Form Chomsky Normal Form We prove pumping lemma for CFL s. We study closure properties and decision properties. Some of them remain,
Theory of Computation 8 Deterministic Membership Testing
 Theory of Computation 8 Deterministic Membership Testing Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Theory of Computation
Theory of Computation 8 Deterministic Membership Testing Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Theory of Computation
Parsing. Context-Free Grammars (CFG) Laura Kallmeyer. Winter 2017/18. Heinrich-Heine-Universität Düsseldorf 1 / 26
 Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
Even More on Dynamic Programming
 Algorithms & Models of Computation CS/ECE 374, Fall 2017 Even More on Dynamic Programming Lecture 15 Thursday, October 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 26 Part I Longest Common Subsequence
Algorithms & Models of Computation CS/ECE 374, Fall 2017 Even More on Dynamic Programming Lecture 15 Thursday, October 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 26 Part I Longest Common Subsequence
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form:
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form:
Context Free Grammars
 Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Parsing with CFGs L445 / L545 / B659. Dept. of Linguistics, Indiana University Spring Parsing with CFGs. Direction of processing
 L445 / L545 / B659 Dept. of Linguistics, Indiana University Spring 2016 1 / 46 : Overview Input: a string Output: a (single) parse tree A useful step in the process of obtaining meaning We can view the
L445 / L545 / B659 Dept. of Linguistics, Indiana University Spring 2016 1 / 46 : Overview Input: a string Output: a (single) parse tree A useful step in the process of obtaining meaning We can view the
Parsing with CFGs. Direction of processing. Top-down. Bottom-up. Left-corner parsing. Chart parsing CYK. Earley 1 / 46.
 : Overview L545 Dept. of Linguistics, Indiana University Spring 2013 Input: a string Output: a (single) parse tree A useful step in the process of obtaining meaning We can view the problem as searching
: Overview L545 Dept. of Linguistics, Indiana University Spring 2013 Input: a string Output: a (single) parse tree A useful step in the process of obtaining meaning We can view the problem as searching
Solutions to Problem Set 3
 V22.0453-001 Theory of Computation October 8, 2003 TA: Nelly Fazio Solutions to Problem Set 3 Problem 1 We have seen that a grammar where all productions are of the form: A ab, A c (where A, B non-terminals,
V22.0453-001 Theory of Computation October 8, 2003 TA: Nelly Fazio Solutions to Problem Set 3 Problem 1 We have seen that a grammar where all productions are of the form: A ab, A c (where A, B non-terminals,
Accepting H-Array Splicing Systems and Their Properties
 ROMANIAN JOURNAL OF INFORMATION SCIENCE AND TECHNOLOGY Volume 21 Number 3 2018 298 309 Accepting H-Array Splicing Systems and Their Properties D. K. SHEENA CHRISTY 1 V.MASILAMANI 2 D. G. THOMAS 3 Atulya
ROMANIAN JOURNAL OF INFORMATION SCIENCE AND TECHNOLOGY Volume 21 Number 3 2018 298 309 Accepting H-Array Splicing Systems and Their Properties D. K. SHEENA CHRISTY 1 V.MASILAMANI 2 D. G. THOMAS 3 Atulya
CS311 Computational Structures. NP-completeness. Lecture 18. Andrew P. Black Andrew Tolmach. Thursday, 2 December 2010
 CS311 Computational Structures NP-completeness Lecture 18 Andrew P. Black Andrew Tolmach 1 Some complexity classes P = Decidable in polynomial time on deterministic TM ( tractable ) NP = Decidable in polynomial
CS311 Computational Structures NP-completeness Lecture 18 Andrew P. Black Andrew Tolmach 1 Some complexity classes P = Decidable in polynomial time on deterministic TM ( tractable ) NP = Decidable in polynomial
Theory of Computation (IX) Yijia Chen Fudan University
 Theory of Computation (IX) Yijia Chen Fudan University Review The Definition of Algorithm Polynomials and their roots A polynomial is a sum of terms, where each term is a product of certain variables and
Theory of Computation (IX) Yijia Chen Fudan University Review The Definition of Algorithm Polynomials and their roots A polynomial is a sum of terms, where each term is a product of certain variables and
Follow sets. LL(1) Parsing Table
 Follow sets. LL(1) Parsing Table Exercise Introducing Follow Sets Compute nullable, first for this grammar: stmtlist ::= ε stmt stmtlist stmt ::= assign block assign ::= ID = ID ; block ::= beginof ID
Follow sets. LL(1) Parsing Table Exercise Introducing Follow Sets Compute nullable, first for this grammar: stmtlist ::= ε stmt stmtlist stmt ::= assign block assign ::= ID = ID ; block ::= beginof ID
This lecture covers Chapter 7 of HMU: Properties of CFLs
 This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
Chomsky Normal Form and TURING MACHINES. TUESDAY Feb 4
 Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form: A BC A a S ε B and C aren t start variables a is
Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form: A BC A a S ε B and C aren t start variables a is
Computability Theory
 CS:4330 Theory of Computation Spring 2018 Computability Theory Decidable Problems of CFLs and beyond Haniel Barbosa Readings for this lecture Chapter 4 of [Sipser 1996], 3rd edition. Section 4.1. Decidable
CS:4330 Theory of Computation Spring 2018 Computability Theory Decidable Problems of CFLs and beyond Haniel Barbosa Readings for this lecture Chapter 4 of [Sipser 1996], 3rd edition. Section 4.1. Decidable
Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules).
 Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules). 1a) G = ({R, S, T}, {0,1}, P, S) where P is: S R0R R R0R1R R1R0R T T 0T ε (S generates the first 0. R generates
Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules). 1a) G = ({R, S, T}, {0,1}, P, S) where P is: S R0R R R0R1R R1R0R T T 0T ε (S generates the first 0. R generates
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition
 Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
Statistical Machine Translation
 Statistical Machine Translation -tree-based models (cont.)- Artem Sokolov Computerlinguistik Universität Heidelberg Sommersemester 2015 material from P. Koehn, S. Riezler, D. Altshuler Bottom-Up Decoding
Statistical Machine Translation -tree-based models (cont.)- Artem Sokolov Computerlinguistik Universität Heidelberg Sommersemester 2015 material from P. Koehn, S. Riezler, D. Altshuler Bottom-Up Decoding
Notes for Comp 497 (Comp 454) Week 10 4/5/05
 Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Decidability (What, stuff is unsolvable?)
 University of Georgia Fall 2014 Outline Decidability Decidable Problems for Regular Languages Decidable Problems for Context Free Languages The Halting Problem Countable and Uncountable Sets Diagonalization
University of Georgia Fall 2014 Outline Decidability Decidable Problems for Regular Languages Decidable Problems for Context Free Languages The Halting Problem Countable and Uncountable Sets Diagonalization
Theory of Computation p.1/?? Theory of Computation p.2/?? We develop examples of languages that are decidable
 Decidable Languages We use languages to represent various computational problems because we have a terminology for dealing with languages Definition: A language is decidable if there is an algorithm (i.e.
Decidable Languages We use languages to represent various computational problems because we have a terminology for dealing with languages Definition: A language is decidable if there is an algorithm (i.e.
Non-context-Free Languages. CS215, Lecture 5 c
 Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Decision problem of substrings in Context Free Languages.
 Decision problem of substrings in Context Free Languages. Mauricio Osorio, Juan Antonio Navarro Abstract A context free grammar (CFG) is a set of symbols and productions used to define a context free language.
Decision problem of substrings in Context Free Languages. Mauricio Osorio, Juan Antonio Navarro Abstract A context free grammar (CFG) is a set of symbols and productions used to define a context free language.
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars formal properties Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2018 1 / 20 Normal forms (1) Hopcroft and Ullman (1979) A normal
Einführung in die Computerlinguistik Context-Free Grammars formal properties Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2018 1 / 20 Normal forms (1) Hopcroft and Ullman (1979) A normal
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
RNA Secondary Structure Prediction
 RNA Secondary Structure Prediction 1 RNA structure prediction methods Base-Pair Maximization Context-Free Grammar Parsing. Free Energy Methods Covariance Models 2 The Nussinov-Jacobson Algorithm q = 9
RNA Secondary Structure Prediction 1 RNA structure prediction methods Base-Pair Maximization Context-Free Grammar Parsing. Free Energy Methods Covariance Models 2 The Nussinov-Jacobson Algorithm q = 9
Grammars and Context Free Languages
 Grammars and Context Free Languages H. Geuvers and A. Kissinger Institute for Computing and Information Sciences Version: fall 2015 H. Geuvers & A. Kissinger Version: fall 2015 Talen en Automaten 1 / 23
Grammars and Context Free Languages H. Geuvers and A. Kissinger Institute for Computing and Information Sciences Version: fall 2015 H. Geuvers & A. Kissinger Version: fall 2015 Talen en Automaten 1 / 23
Decidable and undecidable languages
 The Chinese University of Hong Kong Fall 2011 CSCI 3130: Formal languages and automata theory Decidable and undecidable languages Andrej Bogdanov http://www.cse.cuhk.edu.hk/~andrejb/csc3130 Problems about
The Chinese University of Hong Kong Fall 2011 CSCI 3130: Formal languages and automata theory Decidable and undecidable languages Andrej Bogdanov http://www.cse.cuhk.edu.hk/~andrejb/csc3130 Problems about
Context-Free and Noncontext-Free Languages
 Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x where
 Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
CPS 220 Theory of Computation
 CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
In this chapter, we explore the parsing problem, which encompasses several questions, including:
 Chapter 12 Parsing Algorithms 12.1 Introduction In this chapter, we explore the parsing problem, which encompasses several questions, including: Does L(G) contain w? What is the highest-weight derivation
Chapter 12 Parsing Algorithms 12.1 Introduction In this chapter, we explore the parsing problem, which encompasses several questions, including: Does L(G) contain w? What is the highest-weight derivation
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
4.2 The Halting Problem
 172 4.2 The Halting Problem The technique of diagonalization was discovered in 1873 by Georg Cantor who was concerned with the problem of measuring the sizes of infinite sets For finite sets we can simply
172 4.2 The Halting Problem The technique of diagonalization was discovered in 1873 by Georg Cantor who was concerned with the problem of measuring the sizes of infinite sets For finite sets we can simply
Undecidable Problems and Reducibility
 University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
Chap. 7 Properties of Context-free Languages
 Chap. 7 Properties of Context-free Languages 7.1 Normal Forms for Context-free Grammars Context-free grammars A where A N, (N T). 0. Chomsky Normal Form A BC or A a except S where A, B, C N, a T. 1. Eliminating
Chap. 7 Properties of Context-free Languages 7.1 Normal Forms for Context-free Grammars Context-free grammars A where A N, (N T). 0. Chomsky Normal Form A BC or A a except S where A, B, C N, a T. 1. Eliminating
Context- Free Parsing with CKY. October 16, 2014
 Context- Free Parsing with CKY October 16, 2014 Lecture Plan Parsing as Logical DeducBon Defining the CFG recognibon problem BoHom up vs. top down Quick review of Chomsky normal form The CKY algorithm
Context- Free Parsing with CKY October 16, 2014 Lecture Plan Parsing as Logical DeducBon Defining the CFG recognibon problem BoHom up vs. top down Quick review of Chomsky normal form The CKY algorithm
Functions on languages:
 MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Ogden s Lemma for CFLs
 Ogden s Lemma for CFLs Theorem If L is a context-free language, then there exists an integer l such that for any u L with at least l positions marked, u can be written as u = vwxyz such that 1 x and at
Ogden s Lemma for CFLs Theorem If L is a context-free language, then there exists an integer l such that for any u L with at least l positions marked, u can be written as u = vwxyz such that 1 x and at
k-local Internal Contextual Grammars
 AG Automaten und Formale Sprachen Preprint AFL-2011-06 Otto-von-Guericke-Universität Magdeburg, Germany k-local Internal Contextual Grammars Radu Gramatovici (B) Florin Manea (A,B) (A) Otto-von-Guericke-Universität
AG Automaten und Formale Sprachen Preprint AFL-2011-06 Otto-von-Guericke-Universität Magdeburg, Germany k-local Internal Contextual Grammars Radu Gramatovici (B) Florin Manea (A,B) (A) Otto-von-Guericke-Universität
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Theory of Computation - Module 4
 Theory of Computation - Module 4 Syllabus Turing Machines Formal definition Language acceptability by TM TM as acceptors, Transducers - designing of TM- Two way infinite TM- Multi tape TM - Universal Turing
Theory of Computation - Module 4 Syllabus Turing Machines Formal definition Language acceptability by TM TM as acceptors, Transducers - designing of TM- Two way infinite TM- Multi tape TM - Universal Turing
Lecture 12 Simplification of Context-Free Grammars and Normal Forms
 Lecture 12 Simplification of Context-Free Grammars and Normal Forms COT 4420 Theory of Computation Chapter 6 Normal Forms for CFGs 1. Chomsky Normal Form CNF Productions of form A BC A, B, C V A a a T
Lecture 12 Simplification of Context-Free Grammars and Normal Forms COT 4420 Theory of Computation Chapter 6 Normal Forms for CFGs 1. Chomsky Normal Form CNF Productions of form A BC A, B, C V A a a T
Sorting suffixes of two-pattern strings
 Sorting suffixes of two-pattern strings Frantisek Franek W. F. Smyth Algorithms Research Group Department of Computing & Software McMaster University Hamilton, Ontario Canada L8S 4L7 April 19, 2004 Abstract
Sorting suffixes of two-pattern strings Frantisek Franek W. F. Smyth Algorithms Research Group Department of Computing & Software McMaster University Hamilton, Ontario Canada L8S 4L7 April 19, 2004 Abstract
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
NP-Completeness. A language B is NP-complete iff B NP. This property means B is NP hard
 NP-Completeness A language B is NP-complete iff B NP A NP A P B This property means B is NP hard 1 3SAT is NP-complete 2 Result Idea: B is known to be NP complete Use it to prove NP-Completeness of C IF
NP-Completeness A language B is NP-complete iff B NP A NP A P B This property means B is NP hard 1 3SAT is NP-complete 2 Result Idea: B is known to be NP complete Use it to prove NP-Completeness of C IF
Computing if a token can follow
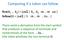 Computing if a token can follow first(b 1... B p ) = {a B 1...B p... aw } follow(x) = {a S......Xa... } There exists a derivation from the start symbol that produces a sequence of terminals and nonterminals
Computing if a token can follow first(b 1... B p ) = {a B 1...B p... aw } follow(x) = {a S......Xa... } There exists a derivation from the start symbol that produces a sequence of terminals and nonterminals
CS20a: summary (Oct 24, 2002)
 CS20a: summary (Oct 24, 2002) Context-free languages Grammars G = (V, T, P, S) Pushdown automata N-PDA = CFG D-PDA < CFG Today What languages are context-free? Pumping lemma (similar to pumping lemma for
CS20a: summary (Oct 24, 2002) Context-free languages Grammars G = (V, T, P, S) Pushdown automata N-PDA = CFG D-PDA < CFG Today What languages are context-free? Pumping lemma (similar to pumping lemma for
What Is a Language? Grammars, Languages, and Machines. Strings: the Building Blocks of Languages
 Do Homework 2. What Is a Language? Grammars, Languages, and Machines L Language Grammar Accepts Machine Strings: the Building Blocks of Languages An alphabet is a finite set of symbols: English alphabet:
Do Homework 2. What Is a Language? Grammars, Languages, and Machines L Language Grammar Accepts Machine Strings: the Building Blocks of Languages An alphabet is a finite set of symbols: English alphabet:
CS5371 Theory of Computation. Lecture 12: Computability III (Decidable Languages relating to DFA, NFA, and CFG)
 CS5371 Theory of Computation Lecture 12: Computability III (Decidable Languages relating to DFA, NFA, and CFG) Objectives Recall that decidable languages are languages that can be decided by TM (that means,
CS5371 Theory of Computation Lecture 12: Computability III (Decidable Languages relating to DFA, NFA, and CFG) Objectives Recall that decidable languages are languages that can be decided by TM (that means,
Grammars and Context Free Languages
 Grammars and Context Free Languages H. Geuvers and J. Rot Institute for Computing and Information Sciences Version: fall 2016 H. Geuvers & J. Rot Version: fall 2016 Talen en Automaten 1 / 24 Outline Grammars
Grammars and Context Free Languages H. Geuvers and J. Rot Institute for Computing and Information Sciences Version: fall 2016 H. Geuvers & J. Rot Version: fall 2016 Talen en Automaten 1 / 24 Outline Grammars
Section Summary. Relations and Functions Properties of Relations. Combining Relations
 Chapter 9 Chapter Summary Relations and Their Properties n-ary Relations and Their Applications (not currently included in overheads) Representing Relations Closures of Relations (not currently included
Chapter 9 Chapter Summary Relations and Their Properties n-ary Relations and Their Applications (not currently included in overheads) Representing Relations Closures of Relations (not currently included
Context-Free Grammar
 Context-Free Grammar CFGs are more powerful than regular expressions. They are more powerful in the sense that whatever can be expressed using regular expressions can be expressed using context-free grammars,
Context-Free Grammar CFGs are more powerful than regular expressions. They are more powerful in the sense that whatever can be expressed using regular expressions can be expressed using context-free grammars,
Formal Languages and Automata
 Formal Languages and Automata Lecture 6 2017-18 LFAC (2017-18) Lecture 6 1 / 31 Lecture 6 1 The recognition problem: the Cocke Younger Kasami algorithm 2 Pushdown Automata 3 Pushdown Automata and Context-free
Formal Languages and Automata Lecture 6 2017-18 LFAC (2017-18) Lecture 6 1 / 31 Lecture 6 1 The recognition problem: the Cocke Younger Kasami algorithm 2 Pushdown Automata 3 Pushdown Automata and Context-free
Büchi Automata and their closure properties. - Ajith S and Ankit Kumar
 Büchi Automata and their closure properties - Ajith S and Ankit Kumar Motivation Conventional programs accept input, compute, output result, then terminate Reactive program : not expected to terminate
Büchi Automata and their closure properties - Ajith S and Ankit Kumar Motivation Conventional programs accept input, compute, output result, then terminate Reactive program : not expected to terminate
Recitation 4: Converting Grammars to Chomsky Normal Form, Simulation of Context Free Languages with Push-Down Automata, Semirings
 Recitation 4: Converting Grammars to Chomsky Normal Form, Simulation of Context Free Languages with Push-Down Automata, Semirings 11-711: Algorithms for NLP October 10, 2014 Conversion to CNF Example grammar
Recitation 4: Converting Grammars to Chomsky Normal Form, Simulation of Context Free Languages with Push-Down Automata, Semirings 11-711: Algorithms for NLP October 10, 2014 Conversion to CNF Example grammar
Testing Emptiness of a CFL. Testing Finiteness of a CFL. Testing Membership in a CFL. CYK Algorithm
 Testing Emptiness of a CFL As for regular languages, we really take a representation of some language and ask whether it represents φ Can use either CFG or PDA Our choice, since there are algorithms to
Testing Emptiness of a CFL As for regular languages, we really take a representation of some language and ask whether it represents φ Can use either CFG or PDA Our choice, since there are algorithms to
Context-Free Languages (Pre Lecture)
 Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Theory of Computation Time Complexity
 Theory of Computation Time Complexity Bow-Yaw Wang Academia Sinica Spring 2012 Bow-Yaw Wang (Academia Sinica) Time Complexity Spring 2012 1 / 59 Time for Deciding a Language Let us consider A = {0 n 1
Theory of Computation Time Complexity Bow-Yaw Wang Academia Sinica Spring 2012 Bow-Yaw Wang (Academia Sinica) Time Complexity Spring 2012 1 / 59 Time for Deciding a Language Let us consider A = {0 n 1
Notes for Comp 497 (454) Week 10
 Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
Introduction to Kleene Algebras
 Introduction to Kleene Algebras Riccardo Pucella Basic Notions Seminar December 1, 2005 Introduction to Kleene Algebras p.1 Idempotent Semirings An idempotent semiring is a structure S = (S, +,, 1, 0)
Introduction to Kleene Algebras Riccardo Pucella Basic Notions Seminar December 1, 2005 Introduction to Kleene Algebras p.1 Idempotent Semirings An idempotent semiring is a structure S = (S, +,, 1, 0)
UNRESTRICTED GRAMMARS
 136 UNRESTRICTED GRAMMARS Context-free grammar allows to substitute only variables with strings In an unrestricted grammar (or a rewriting system) one may substitute any non-empty string (containing variables
136 UNRESTRICTED GRAMMARS Context-free grammar allows to substitute only variables with strings In an unrestricted grammar (or a rewriting system) one may substitute any non-empty string (containing variables
Classical Complexity and Fixed-Parameter Tractability of Simultaneous Consecutive Ones Submatrix & Editing Problems
 Classical Complexity and Fixed-Parameter Tractability of Simultaneous Consecutive Ones Submatrix & Editing Problems Rani M. R, Mohith Jagalmohanan, R. Subashini Binary matrices having simultaneous consecutive
Classical Complexity and Fixed-Parameter Tractability of Simultaneous Consecutive Ones Submatrix & Editing Problems Rani M. R, Mohith Jagalmohanan, R. Subashini Binary matrices having simultaneous consecutive
A* Search. 1 Dijkstra Shortest Path
 A* Search Consider the eight puzzle. There are eight tiles numbered 1 through 8 on a 3 by three grid with nine locations so that one location is left empty. We can move by sliding a tile adjacent to the
A* Search Consider the eight puzzle. There are eight tiles numbered 1 through 8 on a 3 by three grid with nine locations so that one location is left empty. We can move by sliding a tile adjacent to the
ACS2: Decidability Decidability
 Decidability Bernhard Nebel and Christian Becker-Asano 1 Overview An investigation into the solvable/decidable Decidable languages The halting problem (undecidable) 2 Decidable problems? Acceptance problem
Decidability Bernhard Nebel and Christian Becker-Asano 1 Overview An investigation into the solvable/decidable Decidable languages The halting problem (undecidable) 2 Decidable problems? Acceptance problem
CS5371 Theory of Computation. Lecture 14: Computability V (Prove by Reduction)
 CS5371 Theory of Computation Lecture 14: Computability V (Prove by Reduction) Objectives This lecture shows more undecidable languages Our proof is not based on diagonalization Instead, we reduce the problem
CS5371 Theory of Computation Lecture 14: Computability V (Prove by Reduction) Objectives This lecture shows more undecidable languages Our proof is not based on diagonalization Instead, we reduce the problem
acs-07: Decidability Decidability Andreas Karwath und Malte Helmert Informatik Theorie II (A) WS2009/10
 Decidability Andreas Karwath und Malte Helmert 1 Overview An investigation into the solvable/decidable Decidable languages The halting problem (undecidable) 2 Decidable problems? Acceptance problem : decide
Decidability Andreas Karwath und Malte Helmert 1 Overview An investigation into the solvable/decidable Decidable languages The halting problem (undecidable) 2 Decidable problems? Acceptance problem : decide
CPSC 421: Tutorial #1
 CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
Definition: A binary relation R from a set A to a set B is a subset R A B. Example:
 Chapter 9 1 Binary Relations Definition: A binary relation R from a set A to a set B is a subset R A B. Example: Let A = {0,1,2} and B = {a,b} {(0, a), (0, b), (1,a), (2, b)} is a relation from A to B.
Chapter 9 1 Binary Relations Definition: A binary relation R from a set A to a set B is a subset R A B. Example: Let A = {0,1,2} and B = {a,b} {(0, a), (0, b), (1,a), (2, b)} is a relation from A to B.
CDM Parsing and Decidability
 CDM Parsing and Decidability 1 Parsing Klaus Sutner Carnegie Mellon Universality 65-parsing 2017/12/15 23:17 CFGs and Decidability Pushdown Automata The Recognition Problem 3 What Could Go Wrong? 4 Problem:
CDM Parsing and Decidability 1 Parsing Klaus Sutner Carnegie Mellon Universality 65-parsing 2017/12/15 23:17 CFGs and Decidability Pushdown Automata The Recognition Problem 3 What Could Go Wrong? 4 Problem:
SCHEME FOR INTERNAL ASSESSMENT TEST 3
 SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
The Pumping Lemma for Context Free Grammars
 The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
CS 275 Automata and Formal Language Theory
 CS 275 Automata and Formal Language Theory Course Notes Part II: The Recognition Problem (II) Chapter II.4.: Properties of Regular Languages (13) Anton Setzer (Based on a book draft by J. V. Tucker and
CS 275 Automata and Formal Language Theory Course Notes Part II: The Recognition Problem (II) Chapter II.4.: Properties of Regular Languages (13) Anton Setzer (Based on a book draft by J. V. Tucker and
