11 More Regression; Newton s Method; ROC Curves
|
|
|
- Melvin Nichols
- 6 years ago
- Views:
Transcription
1 More Regression; Newton s Method; ROC Curves More Regression; Newton s Method; ROC Curves LEAST-SQUARES POLYNOMIAL REGRESSION Replace each X i with feature vector e.g. (X i ) = [X 2 i1 X i1 X i2 X 2 i2 X i1 X i2 1] > (X i ) with all terms of degree 1...p [Notice that we ve added the fictitious dimension 1 here, so we don t need to add it again to do linear or logistic regression. This basis covers all polynomials quadratic in X i1 and X i2.] Can also use non-polynomial features (e.g. edge detectors). Otherwise just like linear or logistic regression. Log. reg. + quadratic features = same logistic posteriors as QDA. Very easy to overfit! overunder.png, degree20.png, UScensusquartic.png [Here are some examples of polynomial overfitting, to show the importance of choosing the polynomial degree very carefully. At left, we have sampled points from a degree-3 curve (black) with added noise. We show best-fit polynomials of degrees 2, 4, 6, and 8 found by regression of the black points. The degree-4 curve (green) fits the true curve (black) well, whereas the degree-2 curve (red) underfits and the degree-6 and 8 curves (blue, yellow) overfit the noise and oscillate. The oscillations in the yellow degree-8 curve are a characteristic problem of polynomial interpolation.] [At upper right, a degree-20 curve shows just how insane high-degree polynomial oscillations can get. It takes a great deal of densely spaced data to tame the oscillations in a high degree curve, and there isn t nearly enough data here.] [At lower right, somebody has regressed a degree-4 curve to U.S. census population numbers. The curve doesn t oscillate, but can you nevertheless see a flaw? This shows the di culty of extrapolation outside the range of the data. As a general rule, extrapolation is much harder than interpolation. The k-nearest neighbor classifier is one of the few that does extrapolation decently without occasionally returning crazy values.]
2 60 Jonathan Richard Shewchuk WEIGHTED LEAST-SQUARES REGRESSION linear regression fn (1) + squared loss fn (A) + cost fn (c). [The idea of weighted least-squares is that some sample points might be more trusted than others, or there might be certain points you want to fit particularly well. So you assign those more trusted points a higher weight. If you suspect some points of being outliers, you can assign them a lower weight.] Assign each sample pt a weight! i ; collect them in n n diagonal matrix. Greater! i! work harder to minimize ŷ i y i recall: ŷ = Xw nx Find w that minimizes (Xw y) > (Xw y) =! i (X i w y i ) 2 [As with ordinary least-squares regression, we find the minimum by setting the gradient to zero, which leads us to the normal equations.] Solve for w in normal equations: X > Xw = X > y [Once again, you can interpret this method as a projection of y.] Note: 1/2 ŷ is the pt nearest 1/2 y on subspace spanned by columns of 1/2 X. [If you stretch the n-dimensional space by applying the linear transformation 1/2,ŷ is an orthogonal projection of y onto the stretched subspace.] i=1 NEWTON S METHOD Iterative optimization method for smooth fn J(w). Often much faster than gradient descent. [We ll use Newton s method for logistic regression.] Idea: You re at point v. Approximate J(w) near v by quadratic fn. Jump to its unique critical pt. Repeat until bored newton1.pdf, newton2.pdf, newton3.pdf [Three iterations of Newton s method in onedimensional space. We seek the minimum of the blue curve, J. Each brown curve is a local quadratic approximation to J. Each iteration, we jump to the bottom of the brown parabola.] -20
3 More Regression; Newton s Method; ROC Curves 61 newton2d.png [Steps taken by Newton s method in two-dimensional space.] Taylor series about v: rj(w) = rj(v) + (r 2 J(v)) (w v) + O( w v 2 ) where r 2 J(v) is the Hessian matrix of J at v. Find critical pt w by setting rj(w) = 0: w = v (r 2 J(v)) 1 rj(v) [This is an iterative update rule you can repeat until it converges to a solution. As usual, we don t really want to compute a matrix inverse. Instead, we solve a linear system of equations.] Newton s method: Warning: pick starting point w repeat until convergence e solution to linear system (r 2 J(w)) e = rj(w) w w + e Doesn t know di erence between minima, maxima, saddle pts. Starting pt must be close enough to desired solution. [If the objective function J is actually quadratic, Newton s method needs only one step to find the correct answer. The closer J is to quadratic, the faster Newton s method tends to converge.] [Newton s method is superior to blind gradient descent for some optimization problems for several reasons. First, it tries to find the right step length to reach the minimum, rather than just walking an arbitrary distance downhill. Second, rather than follow the direction of steepest descent, it tries to choose a better descent direction.] [Nevertheless, it has some major disadvantages. The biggest one is that computing the Hessian can be quite expensive, and it has to be recomputed every iteration. It can work well for low-dimensional weight spaces, but you would never use it for a neural net, because there are too many weights. Newton s method also doesn t work for most nonsmooth functions. It particularly fails for the perceptron risk function, whose Hessian is zero, except where the Hessian is not even defined.]
4 62 Jonathan Richard Shewchuk LOGISTIC REGRESSION (continued) [Let s use Newton s method to solve logistic regression faster.] Recall: s 0 ( ) = s( ) (1 s( )), s i = s(x i w), s = 64 2 s 1 s 2. s n 3, 75 r w J = nx (y i s i ) X i = X > (y s) i=1 [Now let s derive the Hessian too, so we can use Newton s method.] r 2 w J(w) = nx s i (1 s i ) X i X i > = X > X where = 64 i=1 2 s 1 (1 s 1 ) s 2 (1 s 2 ) s n (1 s n ) 3 75 is +ve definite 8w ) X > X is +ve semidefinite 8w ) J(w) is convex. [The logistic regression cost function is convex, so Newton s method finds a globally optimal point if it converges at all.] Newton s method: w 0 repeat until convergence e solution to normal equations (X > X) e = X > (y s) Recall:, s are fns of w w w + e [Notice that this looks a lot like weighted least squares, but the weight matrix and the right-hand-side vector y s change every iteration. So we call it... ] An example of iteratively reweighted least squares. prioritizes points with s i near 0.5; tunes out pts near 0/1. [In other words, sample points near the decision boundary have the biggest e ect on the iterations. Meanwhile, the iterations move the decision boundary; in turn, that movement may change which points have the most influence. In the end, only the points near the decision boundary make a big contribution to the logistic fit.] Idea: If n very large, save time by using a random subsample of the pts per iteration. Increase sample size as you go. [The principle is that the first iteration isn t going to take you all the way to the optimal point, so why waste time looking at all the sample points? Whereas the last iteration should be the most accurate one.]
5 More Regression; Newton s Method; ROC Curves 63 LDA vs. Logistic Regression Advantages of LDA: For well-separated classes, LDA stable; log. reg. surprisingly unstable > 2 classes easy & elegant; log. reg. needs modifying ( softmax regression ) LDA slightly more accurate when classes nearly normal, especially if n is small Advantages of log. reg.: More emphasis on decision boundary [though not as much as a hard-margin SVM] x2 x2 logregvsldauni.pdf [Logistic regression vs. LDA for a linearly separable data set with a very narrow margin. Logistic regression (center) succeeds in separating these classes, because points near the decision boundary have more influence. (Some luck is involved too; unlike a hard-margin SVM, logistic regression doesn t always separate separable points.) In this example, LDA (right) misclassifies some of the training points.] Hence less sensitive to most outliers Easy & elegant treatment of partial class membership; LDA pts are all-or-nothing More robust on some non-gaussian distributions (e.g. dists. w/large skew)
6 64 Jonathan Richard Shewchuk ROC CURVES (for test sets) ROC Curve ROC.pdf [This is a ROC curve. That stands for receiver operating characteristics, which is an awful name but we re stuck with it for historical reasons. A ROC curve is a way to evaluate your classifier after it is trained. It is made by running a classifier on the test set or validation set. It shows the rate of false positives vs. true positives for a range of settings. We assume there is a knob we can turn to trade o these two types of error. For our purposes, that knob is the posterior probability threshold for Gaussian discriminant analysis or logistic regression. However, neither axis of this plot is the probability threshold.] x-axis: false positive rate = % of ve classified as +ve y-axis: true positive rate = % of +ve classified as +ve aka sensitivity false negative rate : vertical distance from curve to top [1 sensitivity] specificity : horizontal distance from curve to right [1 false positive rate] [You generate this curve by trying every probability threshold; for each threshold, measure the false positive & true positive rates and plot a point.] upper right corner: always classify +ve (Pr 0) lower left corner: always classify ve (Pr > 1) diagonal: random classifiers [A rough measure of a classifier s e ectiveness is the area under the curve. For a classifier that is always correct, the area under the curve is one. For the random classifier, the area under the curve is 1/2, so you d better do better than that.] [IMPORTANT: In practice, the trade-o between false negatives and false positives is usually negotiated by choosing a point on this plot, based on real test data, and NOT by taking the choice of threshold that s best in theory.]
Midterm. Introduction to Machine Learning. CS 189 Spring Please do not open the exam before you are instructed to do so.
 CS 89 Spring 07 Introduction to Machine Learning Midterm Please do not open the exam before you are instructed to do so. The exam is closed book, closed notes except your one-page cheat sheet. Electronic
CS 89 Spring 07 Introduction to Machine Learning Midterm Please do not open the exam before you are instructed to do so. The exam is closed book, closed notes except your one-page cheat sheet. Electronic
12 Statistical Justifications; the Bias-Variance Decomposition
 Statistical Justifications; the Bias-Variance Decomposition 65 12 Statistical Justifications; the Bias-Variance Decomposition STATISTICAL JUSTIFICATIONS FOR REGRESSION [So far, I ve talked about regression
Statistical Justifications; the Bias-Variance Decomposition 65 12 Statistical Justifications; the Bias-Variance Decomposition STATISTICAL JUSTIFICATIONS FOR REGRESSION [So far, I ve talked about regression
Linear Discrimination Functions
 Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari November 4, 2009 Outline Linear models Gradient descent Perceptron Minimum square error approach
Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari November 4, 2009 Outline Linear models Gradient descent Perceptron Minimum square error approach
17 Neural Networks NEURAL NETWORKS. x XOR 1. x Jonathan Richard Shewchuk
 94 Jonathan Richard Shewchuk 7 Neural Networks NEURAL NETWORKS Can do both classification & regression. [They tie together several ideas from the course: perceptrons, logistic regression, ensembles of
94 Jonathan Richard Shewchuk 7 Neural Networks NEURAL NETWORKS Can do both classification & regression. [They tie together several ideas from the course: perceptrons, logistic regression, ensembles of
Statistical Methods for Data Mining
 Statistical Methods for Data Mining Kuangnan Fang Xiamen University Email: xmufkn@xmu.edu.cn Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find
Statistical Methods for Data Mining Kuangnan Fang Xiamen University Email: xmufkn@xmu.edu.cn Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find
Mark your answers ON THE EXAM ITSELF. If you are not sure of your answer you may wish to provide a brief explanation.
 CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
Midterm exam CS 189/289, Fall 2015
 Midterm exam CS 189/289, Fall 2015 You have 80 minutes for the exam. Total 100 points: 1. True/False: 36 points (18 questions, 2 points each). 2. Multiple-choice questions: 24 points (8 questions, 3 points
Midterm exam CS 189/289, Fall 2015 You have 80 minutes for the exam. Total 100 points: 1. True/False: 36 points (18 questions, 2 points each). 2. Multiple-choice questions: 24 points (8 questions, 3 points
CSC321 Lecture 7: Optimization
 CSC321 Lecture 7: Optimization Roger Grosse Roger Grosse CSC321 Lecture 7: Optimization 1 / 25 Overview We ve talked a lot about how to compute gradients. What do we actually do with them? Today s lecture:
CSC321 Lecture 7: Optimization Roger Grosse Roger Grosse CSC321 Lecture 7: Optimization 1 / 25 Overview We ve talked a lot about how to compute gradients. What do we actually do with them? Today s lecture:
CSC321 Lecture 8: Optimization
 CSC321 Lecture 8: Optimization Roger Grosse Roger Grosse CSC321 Lecture 8: Optimization 1 / 26 Overview We ve talked a lot about how to compute gradients. What do we actually do with them? Today s lecture:
CSC321 Lecture 8: Optimization Roger Grosse Roger Grosse CSC321 Lecture 8: Optimization 1 / 26 Overview We ve talked a lot about how to compute gradients. What do we actually do with them? Today s lecture:
Machine Learning Practice Page 2 of 2 10/28/13
 Machine Learning 10-701 Practice Page 2 of 2 10/28/13 1. True or False Please give an explanation for your answer, this is worth 1 pt/question. (a) (2 points) No classifier can do better than a naive Bayes
Machine Learning 10-701 Practice Page 2 of 2 10/28/13 1. True or False Please give an explanation for your answer, this is worth 1 pt/question. (a) (2 points) No classifier can do better than a naive Bayes
Linear Models for Classification
 Linear Models for Classification Oliver Schulte - CMPT 726 Bishop PRML Ch. 4 Classification: Hand-written Digit Recognition CHINE INTELLIGENCE, VOL. 24, NO. 24, APRIL 2002 x i = t i = (0, 0, 0, 1, 0, 0,
Linear Models for Classification Oliver Schulte - CMPT 726 Bishop PRML Ch. 4 Classification: Hand-written Digit Recognition CHINE INTELLIGENCE, VOL. 24, NO. 24, APRIL 2002 x i = t i = (0, 0, 0, 1, 0, 0,
CPSC 540: Machine Learning
 CPSC 540: Machine Learning First-Order Methods, L1-Regularization, Coordinate Descent Winter 2016 Some images from this lecture are taken from Google Image Search. Admin Room: We ll count final numbers
CPSC 540: Machine Learning First-Order Methods, L1-Regularization, Coordinate Descent Winter 2016 Some images from this lecture are taken from Google Image Search. Admin Room: We ll count final numbers
Last updated: Oct 22, 2012 LINEAR CLASSIFIERS. J. Elder CSE 4404/5327 Introduction to Machine Learning and Pattern Recognition
 Last updated: Oct 22, 2012 LINEAR CLASSIFIERS Problems 2 Please do Problem 8.3 in the textbook. We will discuss this in class. Classification: Problem Statement 3 In regression, we are modeling the relationship
Last updated: Oct 22, 2012 LINEAR CLASSIFIERS Problems 2 Please do Problem 8.3 in the textbook. We will discuss this in class. Classification: Problem Statement 3 In regression, we are modeling the relationship
Comments. Assignment 3 code released. Thought questions 3 due this week. Mini-project: hopefully you have started. implement classification algorithms
 Neural networks Comments Assignment 3 code released implement classification algorithms use kernels for census dataset Thought questions 3 due this week Mini-project: hopefully you have started 2 Example:
Neural networks Comments Assignment 3 code released implement classification algorithms use kernels for census dataset Thought questions 3 due this week Mini-project: hopefully you have started 2 Example:
Machine Learning Lecture 7
 Course Outline Machine Learning Lecture 7 Fundamentals (2 weeks) Bayes Decision Theory Probability Density Estimation Statistical Learning Theory 23.05.2016 Discriminative Approaches (5 weeks) Linear Discriminant
Course Outline Machine Learning Lecture 7 Fundamentals (2 weeks) Bayes Decision Theory Probability Density Estimation Statistical Learning Theory 23.05.2016 Discriminative Approaches (5 weeks) Linear Discriminant
Machine Learning 2017
 Machine Learning 2017 Volker Roth Department of Mathematics & Computer Science University of Basel 21st March 2017 Volker Roth (University of Basel) Machine Learning 2017 21st March 2017 1 / 41 Section
Machine Learning 2017 Volker Roth Department of Mathematics & Computer Science University of Basel 21st March 2017 Volker Roth (University of Basel) Machine Learning 2017 21st March 2017 1 / 41 Section
Ch 4. Linear Models for Classification
 Ch 4. Linear Models for Classification Pattern Recognition and Machine Learning, C. M. Bishop, 2006. Department of Computer Science and Engineering Pohang University of Science and echnology 77 Cheongam-ro,
Ch 4. Linear Models for Classification Pattern Recognition and Machine Learning, C. M. Bishop, 2006. Department of Computer Science and Engineering Pohang University of Science and echnology 77 Cheongam-ro,
Lecture 9: Large Margin Classifiers. Linear Support Vector Machines
 Lecture 9: Large Margin Classifiers. Linear Support Vector Machines Perceptrons Definition Perceptron learning rule Convergence Margin & max margin classifiers (Linear) support vector machines Formulation
Lecture 9: Large Margin Classifiers. Linear Support Vector Machines Perceptrons Definition Perceptron learning rule Convergence Margin & max margin classifiers (Linear) support vector machines Formulation
The classifier. Theorem. where the min is over all possible classifiers. To calculate the Bayes classifier/bayes risk, we need to know
 The Bayes classifier Theorem The classifier satisfies where the min is over all possible classifiers. To calculate the Bayes classifier/bayes risk, we need to know Alternatively, since the maximum it is
The Bayes classifier Theorem The classifier satisfies where the min is over all possible classifiers. To calculate the Bayes classifier/bayes risk, we need to know Alternatively, since the maximum it is
The classifier. Linear discriminant analysis (LDA) Example. Challenges for LDA
 The Bayes classifier Linear discriminant analysis (LDA) Theorem The classifier satisfies In linear discriminant analysis (LDA), we make the (strong) assumption that where the min is over all possible classifiers.
The Bayes classifier Linear discriminant analysis (LDA) Theorem The classifier satisfies In linear discriminant analysis (LDA), we make the (strong) assumption that where the min is over all possible classifiers.
Natural Language Processing. Classification. Features. Some Definitions. Classification. Feature Vectors. Classification I. Dan Klein UC Berkeley
 Natural Language Processing Classification Classification I Dan Klein UC Berkeley Classification Automatically make a decision about inputs Example: document category Example: image of digit digit Example:
Natural Language Processing Classification Classification I Dan Klein UC Berkeley Classification Automatically make a decision about inputs Example: document category Example: image of digit digit Example:
Machine Learning and Data Mining. Linear regression. Kalev Kask
 Machine Learning and Data Mining Linear regression Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ Parameters q Learning algorithm Program ( Learner ) Change q Improve performance
Machine Learning and Data Mining Linear regression Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ Parameters q Learning algorithm Program ( Learner ) Change q Improve performance
Machine Learning Support Vector Machines. Prof. Matteo Matteucci
 Machine Learning Support Vector Machines Prof. Matteo Matteucci Discriminative vs. Generative Approaches 2 o Generative approach: we derived the classifier from some generative hypothesis about the way
Machine Learning Support Vector Machines Prof. Matteo Matteucci Discriminative vs. Generative Approaches 2 o Generative approach: we derived the classifier from some generative hypothesis about the way
Math for Machine Learning Open Doors to Data Science and Artificial Intelligence. Richard Han
 Math for Machine Learning Open Doors to Data Science and Artificial Intelligence Richard Han Copyright 05 Richard Han All rights reserved. CONTENTS PREFACE... - INTRODUCTION... LINEAR REGRESSION... 4 LINEAR
Math for Machine Learning Open Doors to Data Science and Artificial Intelligence Richard Han Copyright 05 Richard Han All rights reserved. CONTENTS PREFACE... - INTRODUCTION... LINEAR REGRESSION... 4 LINEAR
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Neural Network Training
 Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
Physics 403. Segev BenZvi. Numerical Methods, Maximum Likelihood, and Least Squares. Department of Physics and Astronomy University of Rochester
 Physics 403 Numerical Methods, Maximum Likelihood, and Least Squares Segev BenZvi Department of Physics and Astronomy University of Rochester Table of Contents 1 Review of Last Class Quadratic Approximation
Physics 403 Numerical Methods, Maximum Likelihood, and Least Squares Segev BenZvi Department of Physics and Astronomy University of Rochester Table of Contents 1 Review of Last Class Quadratic Approximation
Classification CE-717: Machine Learning Sharif University of Technology. M. Soleymani Fall 2012
 Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Support Vector Machines
 Support Vector Machines Hypothesis Space variable size deterministic continuous parameters Learning Algorithm linear and quadratic programming eager batch SVMs combine three important ideas Apply optimization
Support Vector Machines Hypothesis Space variable size deterministic continuous parameters Learning Algorithm linear and quadratic programming eager batch SVMs combine three important ideas Apply optimization
SVAN 2016 Mini Course: Stochastic Convex Optimization Methods in Machine Learning
 SVAN 2016 Mini Course: Stochastic Convex Optimization Methods in Machine Learning Mark Schmidt University of British Columbia, May 2016 www.cs.ubc.ca/~schmidtm/svan16 Some images from this lecture are
SVAN 2016 Mini Course: Stochastic Convex Optimization Methods in Machine Learning Mark Schmidt University of British Columbia, May 2016 www.cs.ubc.ca/~schmidtm/svan16 Some images from this lecture are
20 Unsupervised Learning and Principal Components Analysis (PCA)
 116 Jonathan Richard Shewchuk 20 Unsupervised Learning and Principal Components Analysis (PCA) UNSUPERVISED LEARNING We have sample points, but no labels! No classes, no y-values, nothing to predict. Goal:
116 Jonathan Richard Shewchuk 20 Unsupervised Learning and Principal Components Analysis (PCA) UNSUPERVISED LEARNING We have sample points, but no labels! No classes, no y-values, nothing to predict. Goal:
Optimization and Gradient Descent
 Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder September 12, 2017 Prof. Michael Paul Prediction Functions Remember: a prediction function is the function
Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder September 12, 2017 Prof. Michael Paul Prediction Functions Remember: a prediction function is the function
Contents. 1 Introduction. 1.1 History of Optimization ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016
 ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016 LECTURERS: NAMAN AGARWAL AND BRIAN BULLINS SCRIBE: KIRAN VODRAHALLI Contents 1 Introduction 1 1.1 History of Optimization.....................................
ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016 LECTURERS: NAMAN AGARWAL AND BRIAN BULLINS SCRIBE: KIRAN VODRAHALLI Contents 1 Introduction 1 1.1 History of Optimization.....................................
Statistical Methods for SVM
 Statistical Methods for SVM Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find a plane that separates the classes in feature space. If we cannot,
Statistical Methods for SVM Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find a plane that separates the classes in feature space. If we cannot,
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1396 1 / 44 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1396 1 / 44 Table
Why should you care about the solution strategies?
 Optimization Why should you care about the solution strategies? Understanding the optimization approaches behind the algorithms makes you more effectively choose which algorithm to run Understanding the
Optimization Why should you care about the solution strategies? Understanding the optimization approaches behind the algorithms makes you more effectively choose which algorithm to run Understanding the
Gaussian and Linear Discriminant Analysis; Multiclass Classification
 Gaussian and Linear Discriminant Analysis; Multiclass Classification Professor Ameet Talwalkar Slide Credit: Professor Fei Sha Professor Ameet Talwalkar CS260 Machine Learning Algorithms October 13, 2015
Gaussian and Linear Discriminant Analysis; Multiclass Classification Professor Ameet Talwalkar Slide Credit: Professor Fei Sha Professor Ameet Talwalkar CS260 Machine Learning Algorithms October 13, 2015
CSC 411 Lecture 10: Neural Networks
 CSC 411 Lecture 10: Neural Networks Roger Grosse, Amir-massoud Farahmand, and Juan Carrasquilla University of Toronto UofT CSC 411: 10-Neural Networks 1 / 35 Inspiration: The Brain Our brain has 10 11
CSC 411 Lecture 10: Neural Networks Roger Grosse, Amir-massoud Farahmand, and Juan Carrasquilla University of Toronto UofT CSC 411: 10-Neural Networks 1 / 35 Inspiration: The Brain Our brain has 10 11
Neural networks and optimization
 Neural networks and optimization Nicolas Le Roux Criteo 18/05/15 Nicolas Le Roux (Criteo) Neural networks and optimization 18/05/15 1 / 85 1 Introduction 2 Deep networks 3 Optimization 4 Convolutional
Neural networks and optimization Nicolas Le Roux Criteo 18/05/15 Nicolas Le Roux (Criteo) Neural networks and optimization 18/05/15 1 / 85 1 Introduction 2 Deep networks 3 Optimization 4 Convolutional
Machine Learning Lecture 5
 Machine Learning Lecture 5 Linear Discriminant Functions 26.10.2017 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Course Outline Fundamentals Bayes Decision Theory
Machine Learning Lecture 5 Linear Discriminant Functions 26.10.2017 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Course Outline Fundamentals Bayes Decision Theory
1 What a Neural Network Computes
 Neural Networks 1 What a Neural Network Computes To begin with, we will discuss fully connected feed-forward neural networks, also known as multilayer perceptrons. A feedforward neural network consists
Neural Networks 1 What a Neural Network Computes To begin with, we will discuss fully connected feed-forward neural networks, also known as multilayer perceptrons. A feedforward neural network consists
2 Linear Classifiers and Perceptrons
 Linear lassifiers and Perceptrons 7 Linear lassifiers and Perceptrons LASSIFIERS You are given sample of n observations, each with d features. Some observations belong to class ; some do not. Eample: Observations
Linear lassifiers and Perceptrons 7 Linear lassifiers and Perceptrons LASSIFIERS You are given sample of n observations, each with d features. Some observations belong to class ; some do not. Eample: Observations
Linear Classification. CSE 6363 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington
 Linear Classification CSE 6363 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 Example of Linear Classification Red points: patterns belonging
Linear Classification CSE 6363 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 Example of Linear Classification Red points: patterns belonging
Engineering Part IIB: Module 4F10 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers
 Engineering Part IIB: Module 4F0 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers Phil Woodland: pcw@eng.cam.ac.uk Michaelmas 202 Engineering Part IIB:
Engineering Part IIB: Module 4F0 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers Phil Woodland: pcw@eng.cam.ac.uk Michaelmas 202 Engineering Part IIB:
CSC2541 Lecture 5 Natural Gradient
 CSC2541 Lecture 5 Natural Gradient Roger Grosse Roger Grosse CSC2541 Lecture 5 Natural Gradient 1 / 12 Motivation Two classes of optimization procedures used throughout ML (stochastic) gradient descent,
CSC2541 Lecture 5 Natural Gradient Roger Grosse Roger Grosse CSC2541 Lecture 5 Natural Gradient 1 / 12 Motivation Two classes of optimization procedures used throughout ML (stochastic) gradient descent,
Linear and logistic regression
 Linear and logistic regression Guillaume Obozinski Ecole des Ponts - ParisTech Master MVA Linear and logistic regression 1/22 Outline 1 Linear regression 2 Logistic regression 3 Fisher discriminant analysis
Linear and logistic regression Guillaume Obozinski Ecole des Ponts - ParisTech Master MVA Linear and logistic regression 1/22 Outline 1 Linear regression 2 Logistic regression 3 Fisher discriminant analysis
SVM optimization and Kernel methods
 Announcements SVM optimization and Kernel methods w 4 is up. Due in a week. Kaggle is up 4/13/17 1 4/13/17 2 Outline Review SVM optimization Non-linear transformations in SVM Soft-margin SVM Goal: Find
Announcements SVM optimization and Kernel methods w 4 is up. Due in a week. Kaggle is up 4/13/17 1 4/13/17 2 Outline Review SVM optimization Non-linear transformations in SVM Soft-margin SVM Goal: Find
AE = q < H(p < ) + (1 q < )H(p > ) H(p) = p lg(p) (1 p) lg(1 p)
 1 Decision Trees (13 pts) Data points are: Negative: (-1, 0) (2, 1) (2, -2) Positive: (0, 0) (1, 0) Construct a decision tree using the algorithm described in the notes for the data above. 1. Show the
1 Decision Trees (13 pts) Data points are: Negative: (-1, 0) (2, 1) (2, -2) Positive: (0, 0) (1, 0) Construct a decision tree using the algorithm described in the notes for the data above. 1. Show the
Introduction to Machine Learning HW6
 CS 189 Spring 2018 Introduction to Machine Learning HW6 Your self-grade URL is http://eecs189.org/self_grade?question_ids=1_1,1_ 2,2_1,2_2,3_1,3_2,3_3,4_1,4_2,4_3,4_4,4_5,4_6,5_1,5_2,6. This homework is
CS 189 Spring 2018 Introduction to Machine Learning HW6 Your self-grade URL is http://eecs189.org/self_grade?question_ids=1_1,1_ 2,2_1,2_2,3_1,3_2,3_3,4_1,4_2,4_3,4_4,4_5,4_6,5_1,5_2,6. This homework is
Lecture 4 Discriminant Analysis, k-nearest Neighbors
 Lecture 4 Discriminant Analysis, k-nearest Neighbors Fredrik Lindsten Division of Systems and Control Department of Information Technology Uppsala University. Email: fredrik.lindsten@it.uu.se fredrik.lindsten@it.uu.se
Lecture 4 Discriminant Analysis, k-nearest Neighbors Fredrik Lindsten Division of Systems and Control Department of Information Technology Uppsala University. Email: fredrik.lindsten@it.uu.se fredrik.lindsten@it.uu.se
Support Vector Machines
 Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find a plane that separates the classes in feature space. If we cannot, we get creative in two
Support Vector Machines Here we approach the two-class classification problem in a direct way: We try and find a plane that separates the classes in feature space. If we cannot, we get creative in two
Final Overview. Introduction to ML. Marek Petrik 4/25/2017
 Final Overview Introduction to ML Marek Petrik 4/25/2017 This Course: Introduction to Machine Learning Build a foundation for practice and research in ML Basic machine learning concepts: max likelihood,
Final Overview Introduction to ML Marek Petrik 4/25/2017 This Course: Introduction to Machine Learning Build a foundation for practice and research in ML Basic machine learning concepts: max likelihood,
Reading Group on Deep Learning Session 1
 Reading Group on Deep Learning Session 1 Stephane Lathuiliere & Pablo Mesejo 2 June 2016 1/31 Contents Introduction to Artificial Neural Networks to understand, and to be able to efficiently use, the popular
Reading Group on Deep Learning Session 1 Stephane Lathuiliere & Pablo Mesejo 2 June 2016 1/31 Contents Introduction to Artificial Neural Networks to understand, and to be able to efficiently use, the popular
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
GRADIENT DESCENT AND LOCAL MINIMA
 GRADIENT DESCENT AND LOCAL MINIMA 25 20 5 15 10 3 2 1 1 2 5 2 2 4 5 5 10 Suppose for both functions above, gradient descent is started at the point marked red. It will walk downhill as far as possible,
GRADIENT DESCENT AND LOCAL MINIMA 25 20 5 15 10 3 2 1 1 2 5 2 2 4 5 5 10 Suppose for both functions above, gradient descent is started at the point marked red. It will walk downhill as far as possible,
Regression with Numerical Optimization. Logistic
 CSG220 Machine Learning Fall 2008 Regression with Numerical Optimization. Logistic regression Regression with Numerical Optimization. Logistic regression based on a document by Andrew Ng October 3, 204
CSG220 Machine Learning Fall 2008 Regression with Numerical Optimization. Logistic regression Regression with Numerical Optimization. Logistic regression based on a document by Andrew Ng October 3, 204
Lecture 4: Types of errors. Bayesian regression models. Logistic regression
 Lecture 4: Types of errors. Bayesian regression models. Logistic regression A Bayesian interpretation of regularization Bayesian vs maximum likelihood fitting more generally COMP-652 and ECSE-68, Lecture
Lecture 4: Types of errors. Bayesian regression models. Logistic regression A Bayesian interpretation of regularization Bayesian vs maximum likelihood fitting more generally COMP-652 and ECSE-68, Lecture
CS 542G: Robustifying Newton, Constraints, Nonlinear Least Squares
 CS 542G: Robustifying Newton, Constraints, Nonlinear Least Squares Robert Bridson October 29, 2008 1 Hessian Problems in Newton Last time we fixed one of plain Newton s problems by introducing line search
CS 542G: Robustifying Newton, Constraints, Nonlinear Least Squares Robert Bridson October 29, 2008 1 Hessian Problems in Newton Last time we fixed one of plain Newton s problems by introducing line search
Lecture 7. Logistic Regression. Luigi Freda. ALCOR Lab DIAG University of Rome La Sapienza. December 11, 2016
 Lecture 7 Logistic Regression Luigi Freda ALCOR Lab DIAG University of Rome La Sapienza December 11, 2016 Luigi Freda ( La Sapienza University) Lecture 7 December 11, 2016 1 / 39 Outline 1 Intro Logistic
Lecture 7 Logistic Regression Luigi Freda ALCOR Lab DIAG University of Rome La Sapienza December 11, 2016 Luigi Freda ( La Sapienza University) Lecture 7 December 11, 2016 1 / 39 Outline 1 Intro Logistic
CSC 411: Lecture 04: Logistic Regression
 CSC 411: Lecture 04: Logistic Regression Raquel Urtasun & Rich Zemel University of Toronto Sep 23, 2015 Urtasun & Zemel (UofT) CSC 411: 04-Prob Classif Sep 23, 2015 1 / 16 Today Key Concepts: Logistic
CSC 411: Lecture 04: Logistic Regression Raquel Urtasun & Rich Zemel University of Toronto Sep 23, 2015 Urtasun & Zemel (UofT) CSC 411: 04-Prob Classif Sep 23, 2015 1 / 16 Today Key Concepts: Logistic
Linear classifiers: Overfitting and regularization
 Linear classifiers: Overfitting and regularization Emily Fox University of Washington January 25, 2017 Logistic regression recap 1 . Thus far, we focused on decision boundaries Score(x i ) = w 0 h 0 (x
Linear classifiers: Overfitting and regularization Emily Fox University of Washington January 25, 2017 Logistic regression recap 1 . Thus far, we focused on decision boundaries Score(x i ) = w 0 h 0 (x
Linear smoother. ŷ = S y. where s ij = s ij (x) e.g. s ij = diag(l i (x))
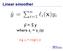 Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
SVMs: nonlinearity through kernels
 Non-separable data e-8. Support Vector Machines 8.. The Optimal Hyperplane Consider the following two datasets: SVMs: nonlinearity through kernels ER Chapter 3.4, e-8 (a) Few noisy data. (b) Nonlinearly
Non-separable data e-8. Support Vector Machines 8.. The Optimal Hyperplane Consider the following two datasets: SVMs: nonlinearity through kernels ER Chapter 3.4, e-8 (a) Few noisy data. (b) Nonlinearly
NONLINEAR CLASSIFICATION AND REGRESSION. J. Elder CSE 4404/5327 Introduction to Machine Learning and Pattern Recognition
 NONLINEAR CLASSIFICATION AND REGRESSION Nonlinear Classification and Regression: Outline 2 Multi-Layer Perceptrons The Back-Propagation Learning Algorithm Generalized Linear Models Radial Basis Function
NONLINEAR CLASSIFICATION AND REGRESSION Nonlinear Classification and Regression: Outline 2 Multi-Layer Perceptrons The Back-Propagation Learning Algorithm Generalized Linear Models Radial Basis Function
Lecture 7: Minimization or maximization of functions (Recipes Chapter 10)
 Lecture 7: Minimization or maximization of functions (Recipes Chapter 10) Actively studied subject for several reasons: Commonly encountered problem: e.g. Hamilton s and Lagrange s principles, economics
Lecture 7: Minimization or maximization of functions (Recipes Chapter 10) Actively studied subject for several reasons: Commonly encountered problem: e.g. Hamilton s and Lagrange s principles, economics
7 Gaussian Discriminant Analysis (including QDA and LDA)
 36 Jonathan Richard Shewchuk 7 Gaussian Discriminant Analysis (including QDA and LDA) GAUSSIAN DISCRIMINANT ANALYSIS Fundamental assumption: each class comes from normal distribution (Gaussian). X N(µ,
36 Jonathan Richard Shewchuk 7 Gaussian Discriminant Analysis (including QDA and LDA) GAUSSIAN DISCRIMINANT ANALYSIS Fundamental assumption: each class comes from normal distribution (Gaussian). X N(µ,
Neural networks and optimization
 Neural networks and optimization Nicolas Le Roux INRIA 8 Nov 2011 Nicolas Le Roux (INRIA) Neural networks and optimization 8 Nov 2011 1 / 80 1 Introduction 2 Linear classifier 3 Convolutional neural networks
Neural networks and optimization Nicolas Le Roux INRIA 8 Nov 2011 Nicolas Le Roux (INRIA) Neural networks and optimization 8 Nov 2011 1 / 80 1 Introduction 2 Linear classifier 3 Convolutional neural networks
Simple Techniques for Improving SGD. CS6787 Lecture 2 Fall 2017
 Simple Techniques for Improving SGD CS6787 Lecture 2 Fall 2017 Step Sizes and Convergence Where we left off Stochastic gradient descent x t+1 = x t rf(x t ; yĩt ) Much faster per iteration than gradient
Simple Techniques for Improving SGD CS6787 Lecture 2 Fall 2017 Step Sizes and Convergence Where we left off Stochastic gradient descent x t+1 = x t rf(x t ; yĩt ) Much faster per iteration than gradient
Statistical Pattern Recognition
 Statistical Pattern Recognition Support Vector Machine (SVM) Hamid R. Rabiee Hadi Asheri, Jafar Muhammadi, Nima Pourdamghani Spring 2013 http://ce.sharif.edu/courses/91-92/2/ce725-1/ Agenda Introduction
Statistical Pattern Recognition Support Vector Machine (SVM) Hamid R. Rabiee Hadi Asheri, Jafar Muhammadi, Nima Pourdamghani Spring 2013 http://ce.sharif.edu/courses/91-92/2/ce725-1/ Agenda Introduction
Overfitting, Bias / Variance Analysis
 Overfitting, Bias / Variance Analysis Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 8, 207 / 40 Outline Administration 2 Review of last lecture 3 Basic
Overfitting, Bias / Variance Analysis Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 8, 207 / 40 Outline Administration 2 Review of last lecture 3 Basic
LINEAR MODELS FOR CLASSIFICATION. J. Elder CSE 6390/PSYC 6225 Computational Modeling of Visual Perception
 LINEAR MODELS FOR CLASSIFICATION Classification: Problem Statement 2 In regression, we are modeling the relationship between a continuous input variable x and a continuous target variable t. In classification,
LINEAR MODELS FOR CLASSIFICATION Classification: Problem Statement 2 In regression, we are modeling the relationship between a continuous input variable x and a continuous target variable t. In classification,
Machine Learning and Data Mining. Linear regression. Prof. Alexander Ihler
 + Machine Learning and Data Mining Linear regression Prof. Alexander Ihler Supervised learning Notation Features x Targets y Predictions ŷ Parameters θ Learning algorithm Program ( Learner ) Change µ Improve
+ Machine Learning and Data Mining Linear regression Prof. Alexander Ihler Supervised learning Notation Features x Targets y Predictions ŷ Parameters θ Learning algorithm Program ( Learner ) Change µ Improve
April 9, Depto. de Ing. de Sistemas e Industrial Universidad Nacional de Colombia, Bogotá. Linear Classification Models. Fabio A. González Ph.D.
 Depto. de Ing. de Sistemas e Industrial Universidad Nacional de Colombia, Bogotá April 9, 2018 Content 1 2 3 4 Outline 1 2 3 4 problems { C 1, y(x) threshold predict(x) = C 2, y(x) < threshold, with threshold
Depto. de Ing. de Sistemas e Industrial Universidad Nacional de Colombia, Bogotá April 9, 2018 Content 1 2 3 4 Outline 1 2 3 4 problems { C 1, y(x) threshold predict(x) = C 2, y(x) < threshold, with threshold
Vasil Khalidov & Miles Hansard. C.M. Bishop s PRML: Chapter 5; Neural Networks
 C.M. Bishop s PRML: Chapter 5; Neural Networks Introduction The aim is, as before, to find useful decompositions of the target variable; t(x) = y(x, w) + ɛ(x) (3.7) t(x n ) and x n are the observations,
C.M. Bishop s PRML: Chapter 5; Neural Networks Introduction The aim is, as before, to find useful decompositions of the target variable; t(x) = y(x, w) + ɛ(x) (3.7) t(x n ) and x n are the observations,
Midterm Review CS 6375: Machine Learning. Vibhav Gogate The University of Texas at Dallas
 Midterm Review CS 6375: Machine Learning Vibhav Gogate The University of Texas at Dallas Machine Learning Supervised Learning Unsupervised Learning Reinforcement Learning Parametric Y Continuous Non-parametric
Midterm Review CS 6375: Machine Learning Vibhav Gogate The University of Texas at Dallas Machine Learning Supervised Learning Unsupervised Learning Reinforcement Learning Parametric Y Continuous Non-parametric
Least Mean Squares Regression. Machine Learning Fall 2018
 Least Mean Squares Regression Machine Learning Fall 2018 1 Where are we? Least Squares Method for regression Examples The LMS objective Gradient descent Incremental/stochastic gradient descent Exercises
Least Mean Squares Regression Machine Learning Fall 2018 1 Where are we? Least Squares Method for regression Examples The LMS objective Gradient descent Incremental/stochastic gradient descent Exercises
Lecture 4: Training a Classifier
 Lecture 4: Training a Classifier Roger Grosse 1 Introduction Now that we ve defined what binary classification is, let s actually train a classifier. We ll approach this problem in much the same way as
Lecture 4: Training a Classifier Roger Grosse 1 Introduction Now that we ve defined what binary classification is, let s actually train a classifier. We ll approach this problem in much the same way as
Machine Learning. Regression-Based Classification & Gaussian Discriminant Analysis. Manfred Huber
 Machine Learning Regression-Based Classification & Gaussian Discriminant Analysis Manfred Huber 2015 1 Logistic Regression Linear regression provides a nice representation and an efficient solution to
Machine Learning Regression-Based Classification & Gaussian Discriminant Analysis Manfred Huber 2015 1 Logistic Regression Linear regression provides a nice representation and an efficient solution to
Nonlinear Classification
 Nonlinear Classification INFO-4604, Applied Machine Learning University of Colorado Boulder October 5-10, 2017 Prof. Michael Paul Linear Classification Most classifiers we ve seen use linear functions
Nonlinear Classification INFO-4604, Applied Machine Learning University of Colorado Boulder October 5-10, 2017 Prof. Michael Paul Linear Classification Most classifiers we ve seen use linear functions
Machine Learning (CS 567) Lecture 5
 Machine Learning (CS 567) Lecture 5 Time: T-Th 5:00pm - 6:20pm Location: GFS 118 Instructor: Sofus A. Macskassy (macskass@usc.edu) Office: SAL 216 Office hours: by appointment Teaching assistant: Cheol
Machine Learning (CS 567) Lecture 5 Time: T-Th 5:00pm - 6:20pm Location: GFS 118 Instructor: Sofus A. Macskassy (macskass@usc.edu) Office: SAL 216 Office hours: by appointment Teaching assistant: Cheol
Day 3 Lecture 3. Optimizing deep networks
 Day 3 Lecture 3 Optimizing deep networks Convex optimization A function is convex if for all α [0,1]: f(x) Tangent line Examples Quadratics 2-norms Properties Local minimum is global minimum x Gradient
Day 3 Lecture 3 Optimizing deep networks Convex optimization A function is convex if for all α [0,1]: f(x) Tangent line Examples Quadratics 2-norms Properties Local minimum is global minimum x Gradient
CMU-Q Lecture 24:
 CMU-Q 15-381 Lecture 24: Supervised Learning 2 Teacher: Gianni A. Di Caro SUPERVISED LEARNING Hypotheses space Hypothesis function Labeled Given Errors Performance criteria Given a collection of input
CMU-Q 15-381 Lecture 24: Supervised Learning 2 Teacher: Gianni A. Di Caro SUPERVISED LEARNING Hypotheses space Hypothesis function Labeled Given Errors Performance criteria Given a collection of input
Machine Learning. Kernels. Fall (Kernels, Kernelized Perceptron and SVM) Professor Liang Huang. (Chap. 12 of CIML)
 Machine Learning Fall 2017 Kernels (Kernels, Kernelized Perceptron and SVM) Professor Liang Huang (Chap. 12 of CIML) Nonlinear Features x4: -1 x1: +1 x3: +1 x2: -1 Concatenated (combined) features XOR:
Machine Learning Fall 2017 Kernels (Kernels, Kernelized Perceptron and SVM) Professor Liang Huang (Chap. 12 of CIML) Nonlinear Features x4: -1 x1: +1 x3: +1 x2: -1 Concatenated (combined) features XOR:
DATA MINING AND MACHINE LEARNING. Lecture 4: Linear models for regression and classification Lecturer: Simone Scardapane
 DATA MINING AND MACHINE LEARNING Lecture 4: Linear models for regression and classification Lecturer: Simone Scardapane Academic Year 2016/2017 Table of contents Linear models for regression Regularized
DATA MINING AND MACHINE LEARNING Lecture 4: Linear models for regression and classification Lecturer: Simone Scardapane Academic Year 2016/2017 Table of contents Linear models for regression Regularized
18.6 Regression and Classification with Linear Models
 18.6 Regression and Classification with Linear Models 352 The hypothesis space of linear functions of continuous-valued inputs has been used for hundreds of years A univariate linear function (a straight
18.6 Regression and Classification with Linear Models 352 The hypothesis space of linear functions of continuous-valued inputs has been used for hundreds of years A univariate linear function (a straight
Stephen Scott.
 1 / 35 (Adapted from Ethem Alpaydin and Tom Mitchell) sscott@cse.unl.edu In Homework 1, you are (supposedly) 1 Choosing a data set 2 Extracting a test set of size > 30 3 Building a tree on the training
1 / 35 (Adapted from Ethem Alpaydin and Tom Mitchell) sscott@cse.unl.edu In Homework 1, you are (supposedly) 1 Choosing a data set 2 Extracting a test set of size > 30 3 Building a tree on the training
Linear models: the perceptron and closest centroid algorithms. D = {(x i,y i )} n i=1. x i 2 R d 9/3/13. Preliminaries. Chapter 1, 7.
 Preliminaries Linear models: the perceptron and closest centroid algorithms Chapter 1, 7 Definition: The Euclidean dot product beteen to vectors is the expression d T x = i x i The dot product is also
Preliminaries Linear models: the perceptron and closest centroid algorithms Chapter 1, 7 Definition: The Euclidean dot product beteen to vectors is the expression d T x = i x i The dot product is also
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
The exam is closed book, closed notes except your one-page cheat sheet.
 CS 189 Fall 2015 Introduction to Machine Learning Final Please do not turn over the page before you are instructed to do so. You have 2 hours and 50 minutes. Please write your initials on the top-right
CS 189 Fall 2015 Introduction to Machine Learning Final Please do not turn over the page before you are instructed to do so. You have 2 hours and 50 minutes. Please write your initials on the top-right
Nonparametric Bayesian Methods (Gaussian Processes)
 [70240413 Statistical Machine Learning, Spring, 2015] Nonparametric Bayesian Methods (Gaussian Processes) Jun Zhu dcszj@mail.tsinghua.edu.cn http://bigml.cs.tsinghua.edu.cn/~jun State Key Lab of Intelligent
[70240413 Statistical Machine Learning, Spring, 2015] Nonparametric Bayesian Methods (Gaussian Processes) Jun Zhu dcszj@mail.tsinghua.edu.cn http://bigml.cs.tsinghua.edu.cn/~jun State Key Lab of Intelligent
A vector from the origin to H, V could be expressed using:
 Linear Discriminant Function: the linear discriminant function: g(x) = w t x + ω 0 x is the point, w is the weight vector, and ω 0 is the bias (t is the transpose). Two Category Case: In the two category
Linear Discriminant Function: the linear discriminant function: g(x) = w t x + ω 0 x is the point, w is the weight vector, and ω 0 is the bias (t is the transpose). Two Category Case: In the two category
Topics we covered. Machine Learning. Statistics. Optimization. Systems! Basics of probability Tail bounds Density Estimation Exponential Families
 Midterm Review Topics we covered Machine Learning Optimization Basics of optimization Convexity Unconstrained: GD, SGD Constrained: Lagrange, KKT Duality Linear Methods Perceptrons Support Vector Machines
Midterm Review Topics we covered Machine Learning Optimization Basics of optimization Convexity Unconstrained: GD, SGD Constrained: Lagrange, KKT Duality Linear Methods Perceptrons Support Vector Machines
Input layer. Weight matrix [ ] Output layer
![Input layer. Weight matrix [ ] Output layer Input layer. Weight matrix [ ] Output layer](/thumbs/94/121286844.jpg) MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.034 Artificial Intelligence, Fall 2003 Recitation 10, November 4 th & 5 th 2003 Learning by perceptrons
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.034 Artificial Intelligence, Fall 2003 Recitation 10, November 4 th & 5 th 2003 Learning by perceptrons
9 Classification. 9.1 Linear Classifiers
 9 Classification This topic returns to prediction. Unlike linear regression where we were predicting a numeric value, in this case we are predicting a class: winner or loser, yes or no, rich or poor, positive
9 Classification This topic returns to prediction. Unlike linear regression where we were predicting a numeric value, in this case we are predicting a class: winner or loser, yes or no, rich or poor, positive
Support Vector Machines
 Two SVM tutorials linked in class website (please, read both): High-level presentation with applications (Hearst 1998) Detailed tutorial (Burges 1998) Support Vector Machines Machine Learning 10701/15781
Two SVM tutorials linked in class website (please, read both): High-level presentation with applications (Hearst 1998) Detailed tutorial (Burges 1998) Support Vector Machines Machine Learning 10701/15781
ECS171: Machine Learning
 ECS171: Machine Learning Lecture 4: Optimization (LFD 3.3, SGD) Cho-Jui Hsieh UC Davis Jan 22, 2018 Gradient descent Optimization Goal: find the minimizer of a function min f (w) w For now we assume f
ECS171: Machine Learning Lecture 4: Optimization (LFD 3.3, SGD) Cho-Jui Hsieh UC Davis Jan 22, 2018 Gradient descent Optimization Goal: find the minimizer of a function min f (w) w For now we assume f
Nonlinear Optimization Methods for Machine Learning
 Nonlinear Optimization Methods for Machine Learning Jorge Nocedal Northwestern University University of California, Davis, Sept 2018 1 Introduction We don t really know, do we? a) Deep neural networks
Nonlinear Optimization Methods for Machine Learning Jorge Nocedal Northwestern University University of California, Davis, Sept 2018 1 Introduction We don t really know, do we? a) Deep neural networks
Linear Regression (continued)
 Linear Regression (continued) Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 6, 2017 1 / 39 Outline 1 Administration 2 Review of last lecture 3 Linear regression
Linear Regression (continued) Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 6, 2017 1 / 39 Outline 1 Administration 2 Review of last lecture 3 Linear regression
COMS 4771 Regression. Nakul Verma
 COMS 4771 Regression Nakul Verma Last time Support Vector Machines Maximum Margin formulation Constrained Optimization Lagrange Duality Theory Convex Optimization SVM dual and Interpretation How get the
COMS 4771 Regression Nakul Verma Last time Support Vector Machines Maximum Margin formulation Constrained Optimization Lagrange Duality Theory Convex Optimization SVM dual and Interpretation How get the
