MALLA REDDY ENGINEERING COLLEGE
|
|
|
- Albert Dickerson
- 6 years ago
- Views:
Transcription
1 MODULE I MALLA REDDY ENGINEERING COLLEGE (Autonomous) I B.Tech II Semester (MR15) I- Mid Question Bank Subject: Computational Mathematics (Common for CE, ME, CSE and Min.E) 1. If f(x) is continuous in the interval [a, b] and f (a) &f (b) are of opposite signs, then the equation f(x) =0 has at least one root between [ ] a) f(a) & f(b) b) a & b c) f(a) & a d) None 2. If f(x) = x-cosx, by bisection method root may lie between [ ] a) 0 & 1 b) 1 & 2 c) 2 & 3 d) None 3. If f(x) = 4sinx-e x, by bisection method root may lie between [ ] a) 0 & 1 b) 1 & 2 c) 2 & 3 d) None 4. If f(x) = x 3 -x-1, by bisection method root may lie between [ ] a) 0 & 1 b) 1 & 2 c) 2 & 3 d) None 5. If f(x) = x 3-4x-9, by bisection method root may lie between [ ] a) 0 & 1 b) 1 & 2 c) 2 & 3 d) None 6. If f(x) = xlog 10 x-1.2, by bisection method root may lie between [ ] a) 0 & 1 b) 1 & 2 c) 2 & 3 d) None 7. Which method is Convergence is very slow [ ] a) Bisection b) Iteration c) Newton-Raphson d) The method of false position 8. If f(x) = x 3-2x-5, by method of false position root may lie between [ ] 9. If f(x) = x 3 -x-1, by method of false position root may lie between [ ] 10. Which of the following method is more accurate in finding root of equation [ ] a) Bisection b) Iteration c) Newton-Raphson d) False position Method 11. If f(x) = x 2 log e x -12, by method of false position root may lie between [ ] 12. If f(x) = x 3-5x-7, by method of false position root may lie between [ ] 13. The Regula-Falsi Method is also called as [ ] a) Bisection b) Iteration c) Newton-Raphson d) False position Method 14. If f(x) = xe x -2, by method of false position root may lie between [ ] 15. If f(x) = x 6 - x 4 - x 3-1, by method of false position root may lie between [ ] 1
2 16. If f(x) = 2x-3sinx-5, by method of false position root may lie between [ ] 17. If f(x) = x 2 - loge x -12, by method of false position root may lie between [ ] 18. The iterative formula is also called as [ ] a) Successive approximation method b) False Position Method c) Bisection method d) None 19. The iteration formula for the Regula-Falsi method is [ ] a) = b) = a) = d) None 20. If f(x) = x 2-9x+1, by interval halving method root may lie between [ ] 21. If f(x) is continuous in the interval [a, b] and f (a)< 0 & f (b)> 0 for the equation f(x) =0, then the first iteration using bisection method is [ ] a) b) c) d) None 22. The Formula for Newton-Raphson method is [ ] a) = ( ) ( ) b) = ( ) ( ) c) = ( ) ( ) d) None 23. If f(x) = e x -3x by method interval halving method root may lie between [ ] 24. If f(x) = sinx+x-1 by Newton-Raphson method root may lie between [ ] 25. If f(x) = xe x -1 by Newton-Raphson method root may lie between [ ] 26. An example of an algebraic equation is [ ] a)tanx=e x b)x=logx c)x 3-5x+3=0d)None 27. An example of a trascedental equation is [ ] a)x 2-2x+5=0 b)x 3 +x 2-3=0 c)x 3 e x =5d)None 28. In finding a real root of the equation x 3 -x-10=0 by bisection if the root lies between a=2 and b=3 then x= [ ] a)2.5 b)2.75 c)2.60 d)none 29. is used to find the iterative formula for Newton-Raphson method geometrically [ ] 2
3 a) Tangent b) Chord c) Directrix d) None 30. The approximate value of x= exact value is x=2.17 then the absolute error in the solution is [ ] a)0.014 b)0.14 c) d)none 31. Rounding number of upto 3 decimal places is [ ] a)1.683 b)1.659 c)1.658 d)none 32. The Rounded-off number of upto 2 decimal places [ ] a) b)30.06 c) d)none 33. If x is the true value and x 1 is the approximate value then absolute error E A =_[ ] a)x x 1 b)x-x 1 /x c) (x 2 -x 1 )/x d) None 34. If x is the true value and x 1 is the approximate value E A is absolute error then relative error E R = [ ] a) E A /x b)100x E A c)none 35. If E A is absolute error and E R relative error then percentage error E p = [ ] a)100x E A b)100x E R c) E A/ E R d)none 36. Geometrically the root of the equation is a point on the [ ] a)x-axis b)y-axis c)z-axis d)none 37. If α is the root of the equation then f(α)= [ ] a)0 b)1 c)2 d)none 38. If a and b are the two values between which the root of equation f(x)=0 lies then the iterative formula to find the root of the equation in bisection method [ ] a)a+b/2 b)a-b/2 c)a+2b/2 d) None 39. The order of convergence in Newton-Raphson method is [ ] a)1 b)2 c)0 d)none 40. The root of the equation x 3-3x+1=0 lies between [ ] a)1 and 2 b)2 and 3 c)3 and 4 d)none 41. In the iterative method to express x= ( ), (x) must be in the interval I containing root [ ] a) greater than 1 b)less than 1 c)not equal to 1 d)none 42. The root of the equation x 3 +x 2-1=0 lies in the interval [ ] a)(0,1) b) (1,2) c (2,3) d)none 3
4 43. is used to find the iterative formula for Regula-falsi method geometrically [ ] a) Chord b) Tangent c) Directrix d) None 44. The root of the equation 3x-cosx-1=0 lies in the interval [ ] a)(0,1) b) (1,2) c) (2,3) d)none 45. The root of the equation -3x=0 lies in the interval [ ] a) (0,1) b) (1,2) c) (2,3) d)none 46. The root of the equation xsinx=1 lies in the interval [ ] a)(0,1) b) (2,3) c) (1,2) d)none 47. If is the exact root and is the approximate root of the equation f(x)=0 then the error in the root is--- [ ] a) b) c) d)none 48. If is the root of the equation f(x)=0 then f( ) = [ ] a)1 b)0 c)2 d)none 49. Finding root of the equation + bx+c=0 by using x= ± is a method a)direct method b)iterative method c)both d)none [ ] 50. Rounding the number upto four significant figures results in [ ] a) b) c) d)none MODULE - I KEY: 1.b 2. a 3. a 4. b 5.c 6. c 7. a 8. a 9.b 10. c 11. d 12.a 13. d 14. c 15. c 16. a 17. d 18. a 19. a 20. a 21.c. 22.a 23.c 24. c 25. c 26. c 27. c 28. a 29. a 30. c 31. c 32. b 33. a 34. a 35. b 36. a 37. a 38.a 39.c 40.a 41. b 42. a 43.a 44. b 45.a 46. c 47. a 48.b 49.a 50. c 4
5 MODULE II 1. The value E -1 = [ ] a) 1+ b) 1- c) d) None 2. If f(x ) is a polynomial of degee n and the values of x are equally spaced Then the nth order difference is always [ ] a) Constant b) variable c) Non-zero value d) Zero 3. From the following which is correct [ ] a)µ = 1+ 2 b) µ 2 = 1-2 c) µ 2 = 1+ 2 d) None 4. In the Newton s forward interpolation formula p value always [ ] a) Zero b) Negative c) Positive d) None 5. If Δ is the forward difference operator then Δ 3 y 0 = [ ] a)y 3 +3y 2 +3y 1 +y 0 b) y 3-3y 2 +3y 1 -y 0 c) y 3 +3y 2-3y 1 -y 0 d)none 6. Gauss-Backward Interpolation formula is used to interpolate the values of y for [ ] a) -1<p<0 b) - <p<0 c) 0<p<1 d) 0<p<-1 7. The n th order difference of a polynomial of n th degree is [ ] a) polynomial of (n-1) th degree b)constant c)polynomial of first degree d) zero 8. The relation between E and is [ ] a) =1+E Given that b) =1+E c) =1-E d) =1-E -1 X 1 2 Y Then Δ 2 f(1) = [ ] a)4x b)2 c)4x-8 d) none 10. Δf(x)= [ ] a) f(x)- f(x-h) b) f(x)+ f(x-h) c)f(x+h)- f(x) d) None 11. f(x)= x 2 +2x+1 and h =3 then Δf(x)= [ ] a)4x b)4x+8 c)4x-8 d) none 12. Given X Y By Newton s forward interpolation formula y(2.5)= [ ] a)14.5 b)16.75 c)16.25 d) None 5
6 13. If D is the differential operator and h is the difference between equally spaced arguments then e hd [ ] a)e b) E -1 c)δ d) none 14. Consider x y To find y at x=0.8, we use [ ] a)newtons forward formula b) Newtons backward formula c) Gauss formula d) none 15. Consider x y To find y at x=16, we use [ ] a) Newtons forward formula b) Newtons backward formula c) Gauss formula d) None 16. Consider x y To find y at x=16, we use [ ] a)newtons forward formula b) Newtons backward formula c) Gauss formula d) none 17. Consider x y To find y at x=16, we use [ ] a)newtons forward formula b) Newtons backward formula c) Gauss formula d) none Δ= [ ] a) E b) E -1 C)D d )none 19. The relation between E and is [ ] a) =1+E -1 b) =1+E c) =1-E d) none δ 2 = [ ] a)μ b) μ 3 c) μ 2 d)none 21. IfΔ n f(x) is constant then Δ n+1 f(x)= [ ] a) 1 b) n c) n+1 d)0 22. If f(x) is a polynomial of degree 2016 then Δ 2020 f(x)= [ ] a) 2016 b) 2020 c) 2019 d) 0 6
7 23. Δcosx= [ ] a) sin(x+h)- sinx b)sin(x+h)+ sinx c)cos(x+h)- cosx d) none 24. Δlogf(x)= [ ] a)logf(x) b) logf(x+h) +f(x) c) logf(x+h) - f(x) d)logf(x+h)f(x) 25. IfΔ(e x ) = taking h=1 [ ] a)(e-1)(e x ) b))(e+1)(e x ) c))(e-1) 2 (e x ) d) none 26. IfΔy= 1+2x+3x 2 then which of the following is true [ ] a) y= x 3 +x 2 b)δ 3 xy=6 c) Δ 4 y =0 d) none 27. Gauss-forward Interpolation formula is used to interpolate the values of y for [ ] a) -1<p<0 b) - <p<0 c) 0<p<1 d) 0<p< The following is used for unequal interval of x values [ ] a) Lagrange s formula b) Newton s forward formula c) Gauss forward formula d) None 29. Which of the following formula is used to interpolating the values of y beginning of the table [ ] a) Newtons forward b) Newtons backward c)gauss forward d)none 30. Which of the following formula is used to interpolating the values of y ending of the table [ ] a) Newtons forward b) Newtons backward c)gauss backward d)none 31. Which of the following formula is used to interpolating the values of y center of the table [ ] a) Newtons forward b) Newton s backward c)gaussformula d)none 32. The n th order difference of a polynomial of n th degree is [ ] a) polynomial of (n-1) th degree b)constant c)polynomial of first degree d) zero 33. The relation between E and is [ ] a) =1+E -1 b) =1+E c) =1-E d) =1-E Given f(x)= x 2 +2x+1 and h =3 then Δf(x)= [ ] a) 4x b)4x+8 c)4x-8 d) none 35. Using Gauss s forward interpolation formula to find y(22) from the table p value is [ ] x f(x) a) 0.4 b)-0.6 c)0.6 d)none 36. To interporlate the y value for unequally spaced points we use formula. [ ] a)newton-forward interpolating formula b)newton-backward interpolating formula c)gauss Interpolation formula d)lagrange s interpolation formula 37. The unique polynomial p(x) of degree 2 or less such that [ ] x P(x) a)8x 2-19x+12 b) 10x 2-19x+12 c) 8x 2-25x+12 d) 15x 2-20x+12 7
8 38. The averaging operator µ is [ ] a) (y r+ + y r - ) b) (y r+ + y r - ) c) (y r+ + y r - ) d) (y r+ + y r - ) 39. The relation between and E is a) = + 1 b) = 1 c) = d) = + 2 [ ] 40. The relation between δ and E is type equation here. a) δ = + b) δ = + ) δ = - d) None 41. The relation between is [ ] a) = E b) = c) = 1 d)none 42. The relation between δ and µ is [ ] a) µ = 1+ δ b)µ = 1- δ c) µ = 1+ δ )none 43. The relation between δ and E is [ ] a) δ = + b) δ = + ) δ = - d) None 44. The relation between is [ ] a) = E b) = c) = 1 d)none 45. The relation between δ and µ is [ ] a) µ = 1+ δ b)µ = 1- δ c) µ = 1+ δ )none 46. The relation between µ and E is [ ] a) µ= ( + ) b) µ= ( - ) c) µ= ( - ) d) None 47. fk = [ ] a) f n - f 0 b ) f n - f 0 c ) f n - f 0 d)none 48. (1+ )(1- ) [ ] a)1 b)2 c)3 d)none )µ δ = [ ] a) ( + ) b) ( + ) c) ( + ) d)none 50. = [ ] a)µ - δ b) µ - δ c) µ + δ d)none MODULE - II KEY: 1.d 2. a 3.d 4. c 5.b 6. a 7. b 8. d 9.b 10. c 11. d 12.a 13. a 14. a 15. a 16. d 17. a 18. a 19. d 20. c 21.d 22.d 23.c 24. d 25.a 26. c 27. c 28. a 29. a 30. b 31. c 32. b 33. d 34. d 35. a 36. d 37. a 38.a 39. b 40. d 41. a 42. a 43.a 44.a 45.a 46. a 47. a 48. a 49.c 50. a 8
9 MODULE - III 1) If y=a+bx+c then the third normal equation by least squares method is = [ ] a) na+b x+c b) a +b + c) a x+b + d) none 2) If y=a+bx+c is fitted to the data(x,y)are(-1,2),(0,1)and(1,4)then the second normal equation is [ ] a) 2a=2 b) 2a=3 c) 2b=2 d) 2c=2 3) If y=a+bx+c then the First normal equation by least squares method is = [ ] a) na+b x+c b) a +b + c) a x+b + d) none 4) If y=a+bx+c then the Second normal equation by least squares method is = [ ] a) na+b x+c b) a +b + c) a x+b + d) none 5) If y=ax+ then the First normal equation to fit the curve is = [ ] a) na+b x b) na+b c) a + d) a + 6) If y=a+b,then the First normal equation to fit the curve is = [ ] a) na x+ b b) na+b c) na+b d) na x+b 7) If y=a+b,then the First normal equation to fit the curve is = [ ] b) a x+ b b) a + c)a + d) a x+ b 8) If y=a+bx, the First normal equation is y= [ ] a) a x+b x 3 b) a x2 + b x 4 c) na+b x d) a y i + b x 2 i y i 9) If y=a+bx, the second normal equation is xy= [ ] a) a x+b x 3 b) a x+b x2 c) na+b x d) a y i + b x 2 i y i 10) If y=a, x=36, = 204, n=8, logy=3.7393, xlogy= then the first normal equation to fit the curve is [ ] a) 8a+36logb= b) 8loga+36log(B)= c)8loga+36b= d)8a+36b= ) If y=a+bx+ cx 2 is fitted to the data(x,y)are (0,1), (1,1.8), (2,1.3), (3,2.5), (4,6.3) then the third normal equation is [ ] a) 5a+10b+30c=12.9 b) 5a+10b+29c=15 c) 5a+10b+31c=15 d) none 12) If y=a+bx+ cx 2 is fitted to the data(x,y)are (0,1), (1,1.8), (2,1.3), (3,2.5), (4,6.3) then the first normal equation is [ ] a) 5a+10b+30c=12.9 b) 5a+10b+29c=15 c) 5a+10b+31c=15 d) 5a+10b+28c= ) If y=a, then the first normal equation is logy= [ ] a) na+b x b) nloga+ b x c) a x+ b logx d) nloga+ b logx 14) If y=a+bx, x =15, y =30, xy =110, x 2 =55, then a 1 = [ ] a) 1.89 b)2.5 c)1.2 d)2 15) If y=2x+5 is the best fit for 6 pairs of values(x,y) by the method of least-squares, find x i if y i =120. [ ] a) 40 b)35 c)45 d)30 16) Curve fitting method uses= [ ] a) Least root method b) Least method c) Least square method d) all 9
10 17) If y=a+bx+c is fitted to the data(x,y)are (-1,2), (0,1) and (1,4) then the first normal equation is [ ] a) 2a+2b=6 b) 3a+3b=6 c) 2a+3b=6 d) 3a+2b=6 18) If x =15, y =30, xy =110, x 2 =55, and If y=a+bx then a= [ ] a) 2.2 b)1.52 c)1.2 d) 0 19) If z=a+bx+cy is fitted to the data(x,y,z) are (0,0,2),(1,1,4), (2,3,3), (4,2,16) and (6,8,8) then the second normal equation is [ ] a) 13a+58b+63c=122 b) 13a+57b+65c=122 c) 13a+57b+63c=122 d) none 20) If y=a then the First normal equation is log = [ ] a) na+b x b) n + x c) a x+b d) a logy+b x 21) If z=a+bx+cy is fitted to the data(x,y,z) are (0,0,2),(1,1,4), (2,3,3), (4,2,16) and (6,8,8) then the third normal equation is [ ] a)14a+63b+78c=108 b) 14a+63b+79c=109 c) 15a+63b+78c=109 d) none 22) Certain experimental values of x and y are given;(0,1),(2,5),(5,12),(7,20) if y=a+bx then the first normal equation is [ ] a) 4a+16b=36 b)5a+16b=40 c) 4a+14b=36 d) 4a+15b=36 23) If z=a+bx+cy is fitted to the data(x,y,z) are (0,0,2),(1,1,4), (2,3,3), (4,2,16) and (6,8,8) then the first normal equation is [ ] a) 5a+13b+15c=33 b) 5a+13b+14c=33 c) 6a+13b+14c=33 d) none 24) If y=a+bx+c is fitted to the data(x,y)are (-1,2), (0,1) and (1,4) then the first normal equation is [ ] a) 3a+2b=7 b) 3a+3b=7 c) 2a+3b=9 d) 3a+2b=8 25) Certain experimental values of x and y are given;(0,-1),(2,5),(5,12),(7,20) if y=a+bx then the second normal equation is [ ] a) 14a+76b=210 b)14a+78b=210 c) 15a+78b=210 d) none Key: 1.b 2. a 3.a 4.c 5.c 6.c 7.b 8.c 9.b 10.b 11.d 12.a 13.d 14.d 15.c 16.c 17.a 18.d 19.c 20.b 21.d 22.c 23.b 24.a 25.b 10
Hence a root lies between 1 and 2. Since f a is negative and f(x 0 ) is positive The root lies between a and x 0 i.e. 1 and 1.
 The Bisection method or BOLZANO s method or Interval halving method: Find the positive root of x 3 x = 1 correct to four decimal places by bisection method Let f x = x 3 x 1 Here f 0 = 1 = ve, f 1 = ve,
The Bisection method or BOLZANO s method or Interval halving method: Find the positive root of x 3 x = 1 correct to four decimal places by bisection method Let f x = x 3 x 1 Here f 0 = 1 = ve, f 1 = ve,
SOLUTION OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS BISECTION METHOD
 BISECTION METHOD If a function f(x) is continuous between a and b, and f(a) and f(b) are of opposite signs, then there exists at least one root between a and b. It is shown graphically as, Let f a be negative
BISECTION METHOD If a function f(x) is continuous between a and b, and f(a) and f(b) are of opposite signs, then there exists at least one root between a and b. It is shown graphically as, Let f a be negative
SBAME CALCULUS OF FINITE DIFFERENCES AND NUMERICAL ANLAYSIS-I Units : I-V
 SBAME CALCULUS OF FINITE DIFFERENCES AND NUMERICAL ANLAYSIS-I Units : I-V Unit I-Syllabus Solutions of Algebraic and Transcendental equations, Bisection method, Iteration Method, Regula Falsi method, Newton
SBAME CALCULUS OF FINITE DIFFERENCES AND NUMERICAL ANLAYSIS-I Units : I-V Unit I-Syllabus Solutions of Algebraic and Transcendental equations, Bisection method, Iteration Method, Regula Falsi method, Newton
Numerical and Statistical Methods
 F.Y. B.Sc.(IT) : Sem. II Numerical and Statistical Methods Time : ½ Hrs.] Prelim Question Paper Solution [Marks : 75 Q. Attempt any THREE of the following : [5] Q.(a) What is a mathematical model? With
F.Y. B.Sc.(IT) : Sem. II Numerical and Statistical Methods Time : ½ Hrs.] Prelim Question Paper Solution [Marks : 75 Q. Attempt any THREE of the following : [5] Q.(a) What is a mathematical model? With
Numerical and Statistical Methods
 F.Y. B.Sc.(IT) : Sem. II Numerical and Statistical Methods Time : ½ Hrs.] Prelim Question Paper Solution [Marks : 75 Q. Attempt any THREE of the following : [5] Q.(a) What is a mathematical model? With
F.Y. B.Sc.(IT) : Sem. II Numerical and Statistical Methods Time : ½ Hrs.] Prelim Question Paper Solution [Marks : 75 Q. Attempt any THREE of the following : [5] Q.(a) What is a mathematical model? With
Solution of Algebric & Transcendental Equations
 Page15 Solution of Algebric & Transcendental Equations Contents: o Introduction o Evaluation of Polynomials by Horner s Method o Methods of solving non linear equations o Bracketing Methods o Bisection
Page15 Solution of Algebric & Transcendental Equations Contents: o Introduction o Evaluation of Polynomials by Horner s Method o Methods of solving non linear equations o Bracketing Methods o Bisection
M.SC. PHYSICS - II YEAR
 MANONMANIAM SUNDARANAR UNIVERSITY DIRECTORATE OF DISTANCE & CONTINUING EDUCATION TIRUNELVELI 627012, TAMIL NADU M.SC. PHYSICS - II YEAR DKP26 - NUMERICAL METHODS (From the academic year 2016-17) Most Student
MANONMANIAM SUNDARANAR UNIVERSITY DIRECTORATE OF DISTANCE & CONTINUING EDUCATION TIRUNELVELI 627012, TAMIL NADU M.SC. PHYSICS - II YEAR DKP26 - NUMERICAL METHODS (From the academic year 2016-17) Most Student
Root Finding (and Optimisation)
 Root Finding (and Optimisation) M.Sc. in Mathematical Modelling & Scientific Computing, Practical Numerical Analysis Michaelmas Term 2018, Lecture 4 Root Finding The idea of root finding is simple we want
Root Finding (and Optimisation) M.Sc. in Mathematical Modelling & Scientific Computing, Practical Numerical Analysis Michaelmas Term 2018, Lecture 4 Root Finding The idea of root finding is simple we want
Mathematics, Algebra, and Geometry
 Mathematics, Algebra, and Geometry by Satya http://www.thesatya.com/ Contents 1 Algebra 1 1.1 Logarithms............................................ 1. Complex numbers........................................
Mathematics, Algebra, and Geometry by Satya http://www.thesatya.com/ Contents 1 Algebra 1 1.1 Logarithms............................................ 1. Complex numbers........................................
USHA RAMA COLLEGE OF ENGINEERING & TECHNOLOGY
 Code No: R007/R0 Set No. I B.Tech I Semester Supplementary Examinations, Feb/Mar 04 MATHEMATICAL METHODS ( Common to Civil Engineering, Electrical & Electronics Engineering, Computer Science & Engineering,
Code No: R007/R0 Set No. I B.Tech I Semester Supplementary Examinations, Feb/Mar 04 MATHEMATICAL METHODS ( Common to Civil Engineering, Electrical & Electronics Engineering, Computer Science & Engineering,
Edexcel GCE Further Pure Mathematics (FP1) Required Knowledge Information Sheet. Daniel Hammocks
 Edexcel GCE Further Pure Mathematics (FP1) Required Knowledge Information Sheet FP1 Formulae Given in Mathematical Formulae and Statistical Tables Booklet Summations o =1 2 = 1 + 12 + 1 6 o =1 3 = 1 64
Edexcel GCE Further Pure Mathematics (FP1) Required Knowledge Information Sheet FP1 Formulae Given in Mathematical Formulae and Statistical Tables Booklet Summations o =1 2 = 1 + 12 + 1 6 o =1 3 = 1 64
NUMERICAL AND STATISTICAL COMPUTING (MCA-202-CR)
 NUMERICAL AND STATISTICAL COMPUTING (MCA-202-CR) Autumn Session UNIT 1 Numerical analysis is the study of algorithms that uses, creates and implements algorithms for obtaining numerical solutions to problems
NUMERICAL AND STATISTICAL COMPUTING (MCA-202-CR) Autumn Session UNIT 1 Numerical analysis is the study of algorithms that uses, creates and implements algorithms for obtaining numerical solutions to problems
INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad
 1 P a g e INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad - 500 04 Name : Mathematics-II Code : A0006 Class : II B. Tech I Semester Branch : CIVIL Year : 016 017 FRESHMAN ENGINEERING
1 P a g e INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad - 500 04 Name : Mathematics-II Code : A0006 Class : II B. Tech I Semester Branch : CIVIL Year : 016 017 FRESHMAN ENGINEERING
Zeroes of Transcendental and Polynomial Equations. Bisection method, Regula-falsi method and Newton-Raphson method
 Zeroes of Transcendental and Polynomial Equations Bisection method, Regula-falsi method and Newton-Raphson method PRELIMINARIES Solution of equation f (x) = 0 A number (real or complex) is a root of the
Zeroes of Transcendental and Polynomial Equations Bisection method, Regula-falsi method and Newton-Raphson method PRELIMINARIES Solution of equation f (x) = 0 A number (real or complex) is a root of the
Subbalakshmi Lakshmipathy College of Science. Department of Mathematics
 ॐ Subbalakshmi Lakshmipathy College of Science Department of Mathematics As are the crests on the hoods of peacocks, As are the gems on the heads of cobras, So is Mathematics, at the top of all Sciences.
ॐ Subbalakshmi Lakshmipathy College of Science Department of Mathematics As are the crests on the hoods of peacocks, As are the gems on the heads of cobras, So is Mathematics, at the top of all Sciences.
Previous Year Questions & Detailed Solutions
 Previous Year Questions & Detailed Solutions. The rate of convergence in the Gauss-Seidal method is as fast as in Gauss Jacobi smethod ) thrice ) half-times ) twice 4) three by two times. In application
Previous Year Questions & Detailed Solutions. The rate of convergence in the Gauss-Seidal method is as fast as in Gauss Jacobi smethod ) thrice ) half-times ) twice 4) three by two times. In application
The iteration formula for to find the root of the equation
 SRI RAMAKRISHNA INSTITUTE OF TECHNOLOGY, COIMBATORE- 10 DEPARTMENT OF SCIENCE AND HUMANITIES SUBJECT: NUMERICAL METHODS & LINEAR PROGRAMMING UNIT II SOLUTIONS OF EQUATION 1. If is continuous in then under
SRI RAMAKRISHNA INSTITUTE OF TECHNOLOGY, COIMBATORE- 10 DEPARTMENT OF SCIENCE AND HUMANITIES SUBJECT: NUMERICAL METHODS & LINEAR PROGRAMMING UNIT II SOLUTIONS OF EQUATION 1. If is continuous in then under
Chapter 4. Solution of Non-linear Equation. Module No. 1. Newton s Method to Solve Transcendental Equation
 Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-713209 email: anita.buie@gmail.com 1 . Chapter 4 Solution of Non-linear
Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-713209 email: anita.buie@gmail.com 1 . Chapter 4 Solution of Non-linear
INSTITUTE OF AERONAUTICAL ENGINEERING Dundigal, Hyderabad MECHANICAL ENGINEERING TUTORIAL QUESTION BANK
 Course Name Course Code Class Branch INSTITUTE OF AERONAUTICAL ENGINEERING Dundigal, Hyderabad - 500 043 Mathematics-II A30006 II-I B. Tech Freshman Engineering Year 016 017 Course Faculty MECHANICAL ENGINEERING
Course Name Course Code Class Branch INSTITUTE OF AERONAUTICAL ENGINEERING Dundigal, Hyderabad - 500 043 Mathematics-II A30006 II-I B. Tech Freshman Engineering Year 016 017 Course Faculty MECHANICAL ENGINEERING
SRI RAMAKRISHNA INSTITUTE OF TECHNOLOGY, COIMBATORE- 10 DEPARTMENT OF SCIENCE AND HUMANITIES B.E - EEE & CIVIL UNIT I
 SRI RAMAKRISHNA INSTITUTE OF TECHNOLOGY, COIMBATORE- 10 DEPARTMENT OF SCIENCE AND HUMANITIES B.E - EEE & CIVIL SUBJECT: NUMERICAL METHODS ( SEMESTER VI ) UNIT I SOLUTIONS OF EQUATIONS AND EIGEN VALUE PROBLEMS
SRI RAMAKRISHNA INSTITUTE OF TECHNOLOGY, COIMBATORE- 10 DEPARTMENT OF SCIENCE AND HUMANITIES B.E - EEE & CIVIL SUBJECT: NUMERICAL METHODS ( SEMESTER VI ) UNIT I SOLUTIONS OF EQUATIONS AND EIGEN VALUE PROBLEMS
Maths Class 11 Chapter 5 Part -1 Quadratic equations
 1 P a g e Maths Class 11 Chapter 5 Part -1 Quadratic equations 1. Real Polynomial: Let a 0, a 1, a 2,, a n be real numbers and x is a real variable. Then, f(x) = a 0 + a 1 x + a 2 x 2 + + a n x n is called
1 P a g e Maths Class 11 Chapter 5 Part -1 Quadratic equations 1. Real Polynomial: Let a 0, a 1, a 2,, a n be real numbers and x is a real variable. Then, f(x) = a 0 + a 1 x + a 2 x 2 + + a n x n is called
, applyingl Hospital s Rule again x 0 2 cos(x) xsinx
 Lecture 3 We give a couple examples of using L Hospital s Rule: Example 3.. [ (a) Compute x 0 sin(x) x. To put this into a form for L Hospital s Rule we first put it over a common denominator [ x 0 sin(x)
Lecture 3 We give a couple examples of using L Hospital s Rule: Example 3.. [ (a) Compute x 0 sin(x) x. To put this into a form for L Hospital s Rule we first put it over a common denominator [ x 0 sin(x)
Math Numerical Analysis Mid-Term Test Solutions
 Math 400 - Numerical Analysis Mid-Term Test Solutions. Short Answers (a) A sufficient and necessary condition for the bisection method to find a root of f(x) on the interval [a,b] is f(a)f(b) < 0 or f(a)
Math 400 - Numerical Analysis Mid-Term Test Solutions. Short Answers (a) A sufficient and necessary condition for the bisection method to find a root of f(x) on the interval [a,b] is f(a)f(b) < 0 or f(a)
3.1 Introduction. Solve non-linear real equation f(x) = 0 for real root or zero x. E.g. x x 1.5 =0, tan x x =0.
 3.1 Introduction Solve non-linear real equation f(x) = 0 for real root or zero x. E.g. x 3 +1.5x 1.5 =0, tan x x =0. Practical existence test for roots: by intermediate value theorem, f C[a, b] & f(a)f(b)
3.1 Introduction Solve non-linear real equation f(x) = 0 for real root or zero x. E.g. x 3 +1.5x 1.5 =0, tan x x =0. Practical existence test for roots: by intermediate value theorem, f C[a, b] & f(a)f(b)
UNIT II SOLUTION OF NON-LINEAR AND SIMULTANEOUS LINEAR EQUATION
 UNIT II SOLUTION OF NON-LINEAR AND SIMULTANEOUS LINEAR EQUATION. If g x is continuous in a, b, then under what condition the iterative method x = g x has a unique solution in a, b? g x < in a, b. State
UNIT II SOLUTION OF NON-LINEAR AND SIMULTANEOUS LINEAR EQUATION. If g x is continuous in a, b, then under what condition the iterative method x = g x has a unique solution in a, b? g x < in a, b. State
Virtual University of Pakistan
 Virtual University of Pakistan File Version v.0.0 Prepared For: Final Term Note: Use Table Of Content to view the Topics, In PDF(Portable Document Format) format, you can check Bookmarks menu Disclaimer:
Virtual University of Pakistan File Version v.0.0 Prepared For: Final Term Note: Use Table Of Content to view the Topics, In PDF(Portable Document Format) format, you can check Bookmarks menu Disclaimer:
Two hours. To be provided by Examinations Office: Mathematical Formula Tables. THE UNIVERSITY OF MANCHESTER. 29 May :45 11:45
 Two hours MATH20602 To be provided by Examinations Office: Mathematical Formula Tables. THE UNIVERSITY OF MANCHESTER NUMERICAL ANALYSIS 1 29 May 2015 9:45 11:45 Answer THREE of the FOUR questions. If more
Two hours MATH20602 To be provided by Examinations Office: Mathematical Formula Tables. THE UNIVERSITY OF MANCHESTER NUMERICAL ANALYSIS 1 29 May 2015 9:45 11:45 Answer THREE of the FOUR questions. If more
Numerical Analysis MTH603
 Numerical Analysis Course Contents Solution of Non Linear Equations Solution of Linear System of Equations Approximation of Eigen Values Interpolation and Polynomial Approximation Numerical Differentiation
Numerical Analysis Course Contents Solution of Non Linear Equations Solution of Linear System of Equations Approximation of Eigen Values Interpolation and Polynomial Approximation Numerical Differentiation
CO-ORDINATE GEOMETRY
 CO-ORDINATE GEOMETRY 1 To change from Cartesian coordinates to polar coordinates, for X write r cos θ and for y write r sin θ. 2 To change from polar coordinates to cartesian coordinates, for r 2 write
CO-ORDINATE GEOMETRY 1 To change from Cartesian coordinates to polar coordinates, for X write r cos θ and for y write r sin θ. 2 To change from polar coordinates to cartesian coordinates, for r 2 write
Lecture 44. Better and successive approximations x2, x3,, xn to the root are obtained from
 Lecture 44 Solution of Non-Linear Equations Regula-Falsi Method Method of iteration Newton - Raphson Method Muller s Method Graeffe s Root Squaring Method Newton -Raphson Method An approximation to the
Lecture 44 Solution of Non-Linear Equations Regula-Falsi Method Method of iteration Newton - Raphson Method Muller s Method Graeffe s Root Squaring Method Newton -Raphson Method An approximation to the
BACHELOR OF COMPUTER APPLICATIONS (BCA) (Revised) Term-End Examination December, 2015 BCS-054 : COMPUTER ORIENTED NUMERICAL TECHNIQUES
 No. of Printed Pages : 5 BCS-054 BACHELOR OF COMPUTER APPLICATIONS (BCA) (Revised) Term-End Examination December, 2015 058b9 BCS-054 : COMPUTER ORIENTED NUMERICAL TECHNIQUES Time : 3 hours Maximum Marks
No. of Printed Pages : 5 BCS-054 BACHELOR OF COMPUTER APPLICATIONS (BCA) (Revised) Term-End Examination December, 2015 058b9 BCS-054 : COMPUTER ORIENTED NUMERICAL TECHNIQUES Time : 3 hours Maximum Marks
Solution of Nonlinear Equations
 Solution of Nonlinear Equations In many engineering applications, there are cases when one needs to solve nonlinear algebraic or trigonometric equations or set of equations. These are also common in Civil
Solution of Nonlinear Equations In many engineering applications, there are cases when one needs to solve nonlinear algebraic or trigonometric equations or set of equations. These are also common in Civil
Department of Mathematics, K.T.H.M. College, Nashik F.Y.B.Sc. Calculus Practical (Academic Year )
 F.Y.B.Sc. Calculus Practical (Academic Year 06-7) Practical : Graps of Elementary Functions. a) Grap of y = f(x) mirror image of Grap of y = f(x) about X axis b) Grap of y = f( x) mirror image of Grap
F.Y.B.Sc. Calculus Practical (Academic Year 06-7) Practical : Graps of Elementary Functions. a) Grap of y = f(x) mirror image of Grap of y = f(x) about X axis b) Grap of y = f( x) mirror image of Grap
Figure 1: Graph of y = x cos(x)
 Chapter The Solution of Nonlinear Equations f(x) = 0 In this chapter we will study methods for find the solutions of functions of single variables, ie values of x such that f(x) = 0 For example, f(x) =
Chapter The Solution of Nonlinear Equations f(x) = 0 In this chapter we will study methods for find the solutions of functions of single variables, ie values of x such that f(x) = 0 For example, f(x) =
MATHEMATICAL METHODS INTERPOLATION
 MATHEMATICAL METHODS INTERPOLATION I YEAR BTech By Mr Y Prabhaker Reddy Asst Professor of Mathematics Guru Nanak Engineering College Ibrahimpatnam, Hyderabad SYLLABUS OF MATHEMATICAL METHODS (as per JNTU
MATHEMATICAL METHODS INTERPOLATION I YEAR BTech By Mr Y Prabhaker Reddy Asst Professor of Mathematics Guru Nanak Engineering College Ibrahimpatnam, Hyderabad SYLLABUS OF MATHEMATICAL METHODS (as per JNTU
, B = (b) Use induction to prove that, for all positive integers n, f(n) is divisible by 4. (a) Use differentiation to find f (x).
 Edexcel FP1 FP1 Practice Practice Papers A and B Papers A and B PRACTICE PAPER A 1. A = 2 1, B = 4 3 3 1, I = 4 2 1 0. 0 1 (a) Show that AB = ci, stating the value of the constant c. (b) Hence, or otherwise,
Edexcel FP1 FP1 Practice Practice Papers A and B Papers A and B PRACTICE PAPER A 1. A = 2 1, B = 4 3 3 1, I = 4 2 1 0. 0 1 (a) Show that AB = ci, stating the value of the constant c. (b) Hence, or otherwise,
MTH603 FAQ + Short Questions Answers.
 Absolute Error : Accuracy : The absolute error is used to denote the actual value of a quantity less it s rounded value if x and x* are respectively the rounded and actual values of a quantity, then absolute
Absolute Error : Accuracy : The absolute error is used to denote the actual value of a quantity less it s rounded value if x and x* are respectively the rounded and actual values of a quantity, then absolute
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
 M 4 - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 435-436 H Q. Let A ( ) 4 and B 3 3 Compute (if possible) : AB and BA ( ) 4 AB 3 3 ( ) ( ) ++ 4+4+ 4
M 4 - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 435-436 H Q. Let A ( ) 4 and B 3 3 Compute (if possible) : AB and BA ( ) 4 AB 3 3 ( ) ( ) ++ 4+4+ 4
Root Finding: Close Methods. Bisection and False Position Dr. Marco A. Arocha Aug, 2014
 Root Finding: Close Methods Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Roots Given function f(x), we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the
Root Finding: Close Methods Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Roots Given function f(x), we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the
CHAPTER-II ROOTS OF EQUATIONS
 CHAPTER-II ROOTS OF EQUATIONS 2.1 Introduction The roots or zeros of equations can be simply defined as the values of x that makes f(x) =0. There are many ways to solve for roots of equations. For some
CHAPTER-II ROOTS OF EQUATIONS 2.1 Introduction The roots or zeros of equations can be simply defined as the values of x that makes f(x) =0. There are many ways to solve for roots of equations. For some
Regent College Maths Department. Further Pure 1 Numerical Solutions of Equations
 Regent College Maths Department Further Pure 1 Numerical Solutions of Equations Further Pure 1 Numerical Solutions of Equations You should: Be able use interval bisection, linear interpolation and the
Regent College Maths Department Further Pure 1 Numerical Solutions of Equations Further Pure 1 Numerical Solutions of Equations You should: Be able use interval bisection, linear interpolation and the
1. Method 1: bisection. The bisection methods starts from two points a 0 and b 0 such that
 Chapter 4 Nonlinear equations 4.1 Root finding Consider the problem of solving any nonlinear relation g(x) = h(x) in the real variable x. We rephrase this problem as one of finding the zero (root) of a
Chapter 4 Nonlinear equations 4.1 Root finding Consider the problem of solving any nonlinear relation g(x) = h(x) in the real variable x. We rephrase this problem as one of finding the zero (root) of a
KINGS COLLEGE OF ENGINEERING DEPARTMENT OF MATHEMATICS ACADEMIC YEAR / EVEN SEMESTER QUESTION BANK
 KINGS COLLEGE OF ENGINEERING MA5-NUMERICAL METHODS DEPARTMENT OF MATHEMATICS ACADEMIC YEAR 00-0 / EVEN SEMESTER QUESTION BANK SUBJECT NAME: NUMERICAL METHODS YEAR/SEM: II / IV UNIT - I SOLUTION OF EQUATIONS
KINGS COLLEGE OF ENGINEERING MA5-NUMERICAL METHODS DEPARTMENT OF MATHEMATICS ACADEMIC YEAR 00-0 / EVEN SEMESTER QUESTION BANK SUBJECT NAME: NUMERICAL METHODS YEAR/SEM: II / IV UNIT - I SOLUTION OF EQUATIONS
Practical Numerical Analysis: Sheet 3 Solutions
 Practical Numerical Analysis: Sheet 3 Solutions 1. We need to compute the roots of the function defined by f(x) = sin(x) + sin(x 2 ) on the interval [0, 3] using different numerical methods. First we consider
Practical Numerical Analysis: Sheet 3 Solutions 1. We need to compute the roots of the function defined by f(x) = sin(x) + sin(x 2 ) on the interval [0, 3] using different numerical methods. First we consider
Bisection and False Position Dr. Marco A. Arocha Aug, 2014
 Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Given function f, we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the function f Problem is known as root
Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Given function f, we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the function f Problem is known as root
Scilab. Prof. S. A. Katre Dept. of Mathematics, University of Pune
 Scilab Prof. S. A. Katre Dept. of Mathematics, University of Pune sakatre@math.unipune.ernet.in sakatre@gmail.com sakatre@bprim.org July 25, 2009 Page 1 of 27 1. n-th roots ->%i %i = i -->sqrt(%i) 0.7071068
Scilab Prof. S. A. Katre Dept. of Mathematics, University of Pune sakatre@math.unipune.ernet.in sakatre@gmail.com sakatre@bprim.org July 25, 2009 Page 1 of 27 1. n-th roots ->%i %i = i -->sqrt(%i) 0.7071068
Chapter 3. Vector spaces
 Chapter 3. Vector spaces Lecture notes for MA1111 P. Karageorgis pete@maths.tcd.ie 1/22 Linear combinations Suppose that v 1,v 2,...,v n and v are vectors in R m. Definition 3.1 Linear combination We say
Chapter 3. Vector spaces Lecture notes for MA1111 P. Karageorgis pete@maths.tcd.ie 1/22 Linear combinations Suppose that v 1,v 2,...,v n and v are vectors in R m. Definition 3.1 Linear combination We say
Numerical Analysis Solution of Algebraic Equation (non-linear equation) 1- Trial and Error. 2- Fixed point
 Numerical Analysis Solution of Algebraic Equation (non-linear equation) 1- Trial and Error In this method we assume initial value of x, and substitute in the equation. Then modify x and continue till we
Numerical Analysis Solution of Algebraic Equation (non-linear equation) 1- Trial and Error In this method we assume initial value of x, and substitute in the equation. Then modify x and continue till we
Functions and Equations
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario Euclid eworkshop # Functions and Equations c 006 CANADIAN
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario Euclid eworkshop # Functions and Equations c 006 CANADIAN
2013/2014 SEMESTER 1 MID-TERM TEST. 1 October :30pm to 9:30pm PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY:
 2013/2014 SEMESTER 1 MID-TERM TEST MA1505 MATHEMATICS I 1 October 2013 8:30pm to 9:30pm PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY: 1. This test paper consists of TEN (10) multiple choice questions
2013/2014 SEMESTER 1 MID-TERM TEST MA1505 MATHEMATICS I 1 October 2013 8:30pm to 9:30pm PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY: 1. This test paper consists of TEN (10) multiple choice questions
Multiplication of Polynomials
 Summary 391 Chapter 5 SUMMARY Section 5.1 A polynomial in x is defined by a finite sum of terms of the form ax n, where a is a real number and n is a whole number. a is the coefficient of the term. n is
Summary 391 Chapter 5 SUMMARY Section 5.1 A polynomial in x is defined by a finite sum of terms of the form ax n, where a is a real number and n is a whole number. a is the coefficient of the term. n is
UNIT - 2 Unit-02/Lecture-01
 UNIT - 2 Unit-02/Lecture-01 Solution of algebraic & transcendental equations by regula falsi method Unit-02/Lecture-01 [RGPV DEC(2013)] [7] Unit-02/Lecture-01 [RGPV JUNE(2014)] [7] Unit-02/Lecture-01 S.NO
UNIT - 2 Unit-02/Lecture-01 Solution of algebraic & transcendental equations by regula falsi method Unit-02/Lecture-01 [RGPV DEC(2013)] [7] Unit-02/Lecture-01 [RGPV JUNE(2014)] [7] Unit-02/Lecture-01 S.NO
Taylor Series and Numerical Approximations
 Taylor Series and Numerical Approximations Hilary Weller h.weller@reading.ac.uk August 7, 05 An introduction to the concept of a Taylor series and how these are used in numerical analysis to find numerical
Taylor Series and Numerical Approximations Hilary Weller h.weller@reading.ac.uk August 7, 05 An introduction to the concept of a Taylor series and how these are used in numerical analysis to find numerical
Roots of Equations. ITCS 4133/5133: Introduction to Numerical Methods 1 Roots of Equations
 Roots of Equations Direct Search, Bisection Methods Regula Falsi, Secant Methods Newton-Raphson Method Zeros of Polynomials (Horner s, Muller s methods) EigenValue Analysis ITCS 4133/5133: Introduction
Roots of Equations Direct Search, Bisection Methods Regula Falsi, Secant Methods Newton-Raphson Method Zeros of Polynomials (Horner s, Muller s methods) EigenValue Analysis ITCS 4133/5133: Introduction
Numerical Analysis MTH603. Virtual University of Pakistan Knowledge beyond the boundaries
 Numerical Analysis MTH6 Virtual University of Pakistan Knowledge beyond the boundaries Table of Contents Lecture # Topics Page # Lecture Introduction Lecture Errors in Computations 6 Lecture Solution of
Numerical Analysis MTH6 Virtual University of Pakistan Knowledge beyond the boundaries Table of Contents Lecture # Topics Page # Lecture Introduction Lecture Errors in Computations 6 Lecture Solution of
LECTURE NOTES ELEMENTARY NUMERICAL METHODS. Eusebius Doedel
 LECTURE NOTES on ELEMENTARY NUMERICAL METHODS Eusebius Doedel TABLE OF CONTENTS Vector and Matrix Norms 1 Banach Lemma 20 The Numerical Solution of Linear Systems 25 Gauss Elimination 25 Operation Count
LECTURE NOTES on ELEMENTARY NUMERICAL METHODS Eusebius Doedel TABLE OF CONTENTS Vector and Matrix Norms 1 Banach Lemma 20 The Numerical Solution of Linear Systems 25 Gauss Elimination 25 Operation Count
PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435
 PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435 Professor Biswa Nath Datta Department of Mathematical Sciences Northern Illinois University DeKalb, IL. 60115 USA E mail: dattab@math.niu.edu
PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435 Professor Biswa Nath Datta Department of Mathematical Sciences Northern Illinois University DeKalb, IL. 60115 USA E mail: dattab@math.niu.edu
5. Hand in the entire exam booklet and your computer score sheet.
 WINTER 2016 MATH*2130 Final Exam Last name: (PRINT) First name: Student #: Instructor: M. R. Garvie 19 April, 2016 INSTRUCTIONS: 1. This is a closed book examination, but a calculator is allowed. The test
WINTER 2016 MATH*2130 Final Exam Last name: (PRINT) First name: Student #: Instructor: M. R. Garvie 19 April, 2016 INSTRUCTIONS: 1. This is a closed book examination, but a calculator is allowed. The test
Polytechnic Institute of NYU MA 2132 Final Practice Answers Fall 2012
 Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Question Bank (I scheme )
 Question Bank (I scheme ) Name of subject: Applied Mathematics Subject code: 22206/22224/22210/22201 Course : CH/CM/CE/EJ/IF/EE/ME Semester: II UNIT-3 (CO3) Unit Test : II (APPLICATION OF INTEGRATION)
Question Bank (I scheme ) Name of subject: Applied Mathematics Subject code: 22206/22224/22210/22201 Course : CH/CM/CE/EJ/IF/EE/ME Semester: II UNIT-3 (CO3) Unit Test : II (APPLICATION OF INTEGRATION)
Practice Assessment Task SET 3
 PRACTICE ASSESSMENT TASK 3 655 Practice Assessment Task SET 3 Solve m - 5m + 6 $ 0 0 Find the locus of point P that moves so that it is equidistant from the points A^-3, h and B ^57, h 3 Write x = 4t,
PRACTICE ASSESSMENT TASK 3 655 Practice Assessment Task SET 3 Solve m - 5m + 6 $ 0 0 Find the locus of point P that moves so that it is equidistant from the points A^-3, h and B ^57, h 3 Write x = 4t,
Mathematical Focus 1 Complex numbers adhere to certain arithmetic properties for which they and their complex conjugates are defined.
 Situation: Complex Roots in Conjugate Pairs Prepared at University of Georgia Center for Proficiency in Teaching Mathematics June 30, 2013 Sarah Major Prompt: A teacher in a high school Algebra class has
Situation: Complex Roots in Conjugate Pairs Prepared at University of Georgia Center for Proficiency in Teaching Mathematics June 30, 2013 Sarah Major Prompt: A teacher in a high school Algebra class has
UNIT-I CURVE FITTING AND THEORY OF EQUATIONS
 Part-A 1. Define linear law. The relation between the variables x & y is liner. Let y = ax + b (1) If the points (x i, y i ) are plotted in the graph sheet, they should lie on a straight line. a is the
Part-A 1. Define linear law. The relation between the variables x & y is liner. Let y = ax + b (1) If the points (x i, y i ) are plotted in the graph sheet, they should lie on a straight line. a is the
ALGEBRA II WITH TRIGONOMETRY EXAM
 First Round : March 7, 00 Second Round: April, 00 at The University of Alabama ALGEBRA II WITH TRIGONOMETRY EXAM Construction of this test directed by Congxiao Liu, Alabama A&M University and Alzaki Fadl
First Round : March 7, 00 Second Round: April, 00 at The University of Alabama ALGEBRA II WITH TRIGONOMETRY EXAM Construction of this test directed by Congxiao Liu, Alabama A&M University and Alzaki Fadl
Diagnostic quiz for M337 Complex analysis
 Diagnostic quiz for M337 Complex analysis The aim of this diagnostic quiz is to help you assess how well prepared you are for M337, and to identify topics that you should revise or study before beginning
Diagnostic quiz for M337 Complex analysis The aim of this diagnostic quiz is to help you assess how well prepared you are for M337, and to identify topics that you should revise or study before beginning
Dr. Sophie Marques. MAM1020S Tutorial 8 August Divide. 1. 6x 2 + x 15 by 3x + 5. Solution: Do a long division show your work.
 Dr. Sophie Marques MAM100S Tutorial 8 August 017 1. Divide 1. 6x + x 15 by 3x + 5. 6x + x 15 = (x 3)(3x + 5) + 0. 1a 4 17a 3 + 9a + 7a 6 by 3a 1a 4 17a 3 + 9a + 7a 6 = (4a 3 3a + a + 3)(3a ) + 0 3. 1a
Dr. Sophie Marques MAM100S Tutorial 8 August 017 1. Divide 1. 6x + x 15 by 3x + 5. 6x + x 15 = (x 3)(3x + 5) + 0. 1a 4 17a 3 + 9a + 7a 6 by 3a 1a 4 17a 3 + 9a + 7a 6 = (4a 3 3a + a + 3)(3a ) + 0 3. 1a
FP1 practice papers A to G
 FP1 practice papers A to G Paper Reference(s) 6667/01 Edexcel GCE Further Pure Mathematics FP1 Advanced Subsidiary Practice Paper A Time: 1 hour 30 minutes Materials required for examination Mathematical
FP1 practice papers A to G Paper Reference(s) 6667/01 Edexcel GCE Further Pure Mathematics FP1 Advanced Subsidiary Practice Paper A Time: 1 hour 30 minutes Materials required for examination Mathematical
(0, 0), (1, ), (2, ), (3, ), (4, ), (5, ), (6, ).
 1 Interpolation: The method of constructing new data points within the range of a finite set of known data points That is if (x i, y i ), i = 1, N are known, with y i the dependent variable and x i [x
1 Interpolation: The method of constructing new data points within the range of a finite set of known data points That is if (x i, y i ), i = 1, N are known, with y i the dependent variable and x i [x
1 Arithmetic calculations (calculator is not allowed)
 1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
Engineering Mathematics through Applications
 89 80 Engineering Mathematics through Applications Finite Differences, Numerical Differentiations and Integrations 8 8 Engineering Mathematics through Applications Finite Differences, Numerical Differentiations
89 80 Engineering Mathematics through Applications Finite Differences, Numerical Differentiations and Integrations 8 8 Engineering Mathematics through Applications Finite Differences, Numerical Differentiations
Solving Non-Linear Equations (Root Finding)
 Solving Non-Linear Equations (Root Finding) Root finding Methods What are root finding methods? Methods for determining a solution of an equation. Essentially finding a root of a function, that is, a zero
Solving Non-Linear Equations (Root Finding) Root finding Methods What are root finding methods? Methods for determining a solution of an equation. Essentially finding a root of a function, that is, a zero
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
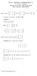 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
Formulas that must be memorized:
 Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane.
 Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 3 Lecture 3 3.1 General remarks March 4, 2018 This
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 3 Lecture 3 3.1 General remarks March 4, 2018 This
Midterm Review. Igor Yanovsky (Math 151A TA)
 Midterm Review Igor Yanovsky (Math 5A TA) Root-Finding Methods Rootfinding methods are designed to find a zero of a function f, that is, to find a value of x such that f(x) =0 Bisection Method To apply
Midterm Review Igor Yanovsky (Math 5A TA) Root-Finding Methods Rootfinding methods are designed to find a zero of a function f, that is, to find a value of x such that f(x) =0 Bisection Method To apply
CE 205 Numerical Methods. Some of the analysis methods you have used so far.. Algebra Calculus Differential Equations etc.
 CE 205 Numerical Methods Dr. Charisma Choudhury Lecture 1 March 30, 2009 Objective Some of the analysis methods you have used so far.. Algebra Calculus Differential Equations etc. Often not possible to
CE 205 Numerical Methods Dr. Charisma Choudhury Lecture 1 March 30, 2009 Objective Some of the analysis methods you have used so far.. Algebra Calculus Differential Equations etc. Often not possible to
Mathematical Methods for Numerical Analysis and Optimization
 Biyani's Think Tank Concept based notes Mathematical Methods for Numerical Analysis and Optimization (MCA) Varsha Gupta Poonam Fatehpuria M.Sc. (Maths) Lecturer Deptt. of Information Technology Biyani
Biyani's Think Tank Concept based notes Mathematical Methods for Numerical Analysis and Optimization (MCA) Varsha Gupta Poonam Fatehpuria M.Sc. (Maths) Lecturer Deptt. of Information Technology Biyani
NOTES FOR NUMERICAL METHODS MUHAMMAD USMAN HAMID
 NOTES FOR NUMERICAL METHODS MUHAMMAD USMAN HAMID PREFACE In the beginning of university life I used only those books which were recommended by my teachers, soon I realized, that books were not enough to
NOTES FOR NUMERICAL METHODS MUHAMMAD USMAN HAMID PREFACE In the beginning of university life I used only those books which were recommended by my teachers, soon I realized, that books were not enough to
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH
 UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH FACULTY OF SCIENCE AND ENGINEERING DEPARTMENT OF MATHEMATICS & STATISTICS END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA440 SEMESTER: Autumn 04 MODULE TITLE:
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH FACULTY OF SCIENCE AND ENGINEERING DEPARTMENT OF MATHEMATICS & STATISTICS END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA440 SEMESTER: Autumn 04 MODULE TITLE:
PARTIAL DIFFERENTIAL EQUATIONS
 MATHEMATICAL METHODS PARTIAL DIFFERENTIAL EQUATIONS I YEAR B.Tech By Mr. Y. Prabhaker Reddy Asst. Professor of Mathematics Guru Nanak Engineering College Ibrahimpatnam, Hyderabad. SYLLABUS OF MATHEMATICAL
MATHEMATICAL METHODS PARTIAL DIFFERENTIAL EQUATIONS I YEAR B.Tech By Mr. Y. Prabhaker Reddy Asst. Professor of Mathematics Guru Nanak Engineering College Ibrahimpatnam, Hyderabad. SYLLABUS OF MATHEMATICAL
NUMERICAL ANALYSIS SYLLABUS MATHEMATICS PAPER IV (A)
 NUMERICAL ANALYSIS SYLLABUS MATHEMATICS PAPER IV (A) Unit - 1 Errors & Their Accuracy Solutions of Algebraic and Transcendental Equations Bisection Method The method of false position The iteration method
NUMERICAL ANALYSIS SYLLABUS MATHEMATICS PAPER IV (A) Unit - 1 Errors & Their Accuracy Solutions of Algebraic and Transcendental Equations Bisection Method The method of false position The iteration method
Conic Sections Session 2: Ellipse
 Conic Sections Session 2: Ellipse Toh Pee Choon NIE Oct 2017 Toh Pee Choon (NIE) Session 2: Ellipse Oct 2017 1 / 24 Introduction Problem 2.1 Let A, F 1 and F 2 be three points that form a triangle F 2
Conic Sections Session 2: Ellipse Toh Pee Choon NIE Oct 2017 Toh Pee Choon (NIE) Session 2: Ellipse Oct 2017 1 / 24 Introduction Problem 2.1 Let A, F 1 and F 2 be three points that form a triangle F 2
Exact and Approximate Numbers:
 Eact and Approimate Numbers: The numbers that arise in technical applications are better described as eact numbers because there is not the sort of uncertainty in their values that was described above.
Eact and Approimate Numbers: The numbers that arise in technical applications are better described as eact numbers because there is not the sort of uncertainty in their values that was described above.
Section 5.8. Taylor Series
 Difference Equations to Differential Equations Section 5.8 Taylor Series In this section we will put together much of the work of Sections 5.-5.7 in the context of a discussion of Taylor series. We begin
Difference Equations to Differential Equations Section 5.8 Taylor Series In this section we will put together much of the work of Sections 5.-5.7 in the context of a discussion of Taylor series. We begin
Applied Numerical Analysis Homework #3
 Applied Numerical Analysis Homework #3 Interpolation: Splines, Multiple dimensions, Radial Bases, Least-Squares Splines Question Consider a cubic spline interpolation of a set of data points, and derivatives
Applied Numerical Analysis Homework #3 Interpolation: Splines, Multiple dimensions, Radial Bases, Least-Squares Splines Question Consider a cubic spline interpolation of a set of data points, and derivatives
NUMERICAL METHODS. x n+1 = 2x n x 2 n. In particular: which of them gives faster convergence, and why? [Work to four decimal places.
 NUMERICAL METHODS 1. Rearranging the equation x 3 =.5 gives the iterative formula x n+1 = g(x n ), where g(x) = (2x 2 ) 1. (a) Starting with x = 1, compute the x n up to n = 6, and describe what is happening.
NUMERICAL METHODS 1. Rearranging the equation x 3 =.5 gives the iterative formula x n+1 = g(x n ), where g(x) = (2x 2 ) 1. (a) Starting with x = 1, compute the x n up to n = 6, and describe what is happening.
* is a row matrix * An mxn matrix is a square matrix if and only if m=n * A= is a diagonal matrix if = 0 i
 CET MATRICES *A matrix is an order rectangular array of numbers * A matrix having m rows and n columns is called mxn matrix of order * is a column matrix * is a row matrix * An mxn matrix is a square matrix
CET MATRICES *A matrix is an order rectangular array of numbers * A matrix having m rows and n columns is called mxn matrix of order * is a column matrix * is a row matrix * An mxn matrix is a square matrix
Review. Numerical Methods Lecture 22. Prof. Jinbo Bi CSE, UConn
 Review Taylor Series and Error Analysis Roots of Equations Linear Algebraic Equations Optimization Numerical Differentiation and Integration Ordinary Differential Equations Partial Differential Equations
Review Taylor Series and Error Analysis Roots of Equations Linear Algebraic Equations Optimization Numerical Differentiation and Integration Ordinary Differential Equations Partial Differential Equations
Problems on Numerical Methods for Engineers. Pedro Fortuny Ayuso. EPIG, Gijón. Universidad de Oviedo address:
 Problems on Numerical Methods for Engineers Pedro Fortuny Ayuso EPIG, Gijón. Universidad de Oviedo E-mail address: fortunypedro@uniovi.es CC BY: Copyright c 2011 2015 Pedro Fortuny Ayuso This work is licensed
Problems on Numerical Methods for Engineers Pedro Fortuny Ayuso EPIG, Gijón. Universidad de Oviedo E-mail address: fortunypedro@uniovi.es CC BY: Copyright c 2011 2015 Pedro Fortuny Ayuso This work is licensed
Note: Final Exam is at 10:45 on Tuesday, 5/3/11 (This is the Final Exam time reserved for our labs). From Practice Test I
 MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
Numerical Methods Dr. Sanjeev Kumar Department of Mathematics Indian Institute of Technology Roorkee Lecture No 7 Regula Falsi and Secant Methods
 Numerical Methods Dr. Sanjeev Kumar Department of Mathematics Indian Institute of Technology Roorkee Lecture No 7 Regula Falsi and Secant Methods So welcome to the next lecture of the 2 nd unit of this
Numerical Methods Dr. Sanjeev Kumar Department of Mathematics Indian Institute of Technology Roorkee Lecture No 7 Regula Falsi and Secant Methods So welcome to the next lecture of the 2 nd unit of this
SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2
 SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2 Here are the solutions to the additional exercises in betsepexercises.pdf. B1. Let y and z be distinct points of L; we claim that x, y and z are not
SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2 Here are the solutions to the additional exercises in betsepexercises.pdf. B1. Let y and z be distinct points of L; we claim that x, y and z are not
5.3. Polynomials and Polynomial Functions
 5.3 Polynomials and Polynomial Functions Polynomial Vocabulary Term a number or a product of a number and variables raised to powers Coefficient numerical factor of a term Constant term which is only a
5.3 Polynomials and Polynomial Functions Polynomial Vocabulary Term a number or a product of a number and variables raised to powers Coefficient numerical factor of a term Constant term which is only a
November 20, Interpolation, Extrapolation & Polynomial Approximation
 Interpolation, Extrapolation & Polynomial Approximation November 20, 2016 Introduction In many cases we know the values of a function f (x) at a set of points x 1, x 2,..., x N, but we don t have the analytic
Interpolation, Extrapolation & Polynomial Approximation November 20, 2016 Introduction In many cases we know the values of a function f (x) at a set of points x 1, x 2,..., x N, but we don t have the analytic
Department of Applied Mathematics and Theoretical Physics. AMA 204 Numerical analysis. Exam Winter 2004
 Department of Applied Mathematics and Theoretical Physics AMA 204 Numerical analysis Exam Winter 2004 The best six answers will be credited All questions carry equal marks Answer all parts of each question
Department of Applied Mathematics and Theoretical Physics AMA 204 Numerical analysis Exam Winter 2004 The best six answers will be credited All questions carry equal marks Answer all parts of each question
11.10a Taylor and Maclaurin Series
 11.10a 1 11.10a Taylor and Maclaurin Series Let y = f(x) be a differentiable function at x = a. In first semester calculus we saw that (1) f(x) f(a)+f (a)(x a), for all x near a The right-hand side of
11.10a 1 11.10a Taylor and Maclaurin Series Let y = f(x) be a differentiable function at x = a. In first semester calculus we saw that (1) f(x) f(a)+f (a)(x a), for all x near a The right-hand side of
Determining the Roots of Non-Linear Equations Part I
 Determining the Roots of Non-Linear Equations Part I Prof. Dr. Florian Rupp German University of Technology in Oman (GUtech) Introduction to Numerical Methods for ENG & CS (Mathematics IV) Spring Term
Determining the Roots of Non-Linear Equations Part I Prof. Dr. Florian Rupp German University of Technology in Oman (GUtech) Introduction to Numerical Methods for ENG & CS (Mathematics IV) Spring Term
Program : M.A./M.Sc. (Mathematics) M.A./M.Sc. (Final) Paper Code:MT-08 Numerical Analysis Section A (Very Short Answers Questions)
 Program : M../M.Sc. (Mathematics) M../M.Sc. (Final) Paper Code:MT-08 Numerical nalysis Section (Very Short nswers Questions) 1. Write two examples of transcendental equations. (i) x 3 + sin x = 0 (ii)
Program : M../M.Sc. (Mathematics) M../M.Sc. (Final) Paper Code:MT-08 Numerical nalysis Section (Very Short nswers Questions) 1. Write two examples of transcendental equations. (i) x 3 + sin x = 0 (ii)
MTH603 - Numerical Analysis Solved final Term Papers For Final Term Exam
 MTH603 - Numerical Analysis Solved final Term Papers For Final Term Exam Exact solution of 2/3 is not exists. The Jacobi s method is A method of solving a matrix equation on a matrix that has zeros along
MTH603 - Numerical Analysis Solved final Term Papers For Final Term Exam Exact solution of 2/3 is not exists. The Jacobi s method is A method of solving a matrix equation on a matrix that has zeros along
Jim Lambers MAT 460/560 Fall Semester Practice Final Exam
 Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
