The Cross Product of Two Vectors
|
|
|
- Rachel Brooks
- 6 years ago
- Views:
Transcription
1 The Cross roduct of Two Vectors In proving some statements involving surface integrals, there will be a need to approximate areas of segments of the surface by areas of parallelograms. Therefore it is useful to introduce a method of computing areas of parallelograms in space. For the area of a parallelogram determined by two vectors, we use the "cross product" of the vectors. To define this, consider vectors = u =< u 1, u, u 3 > and = v =< v 1, v, v 3 > shown below. Form the parallelogram which has u and v as two of its sides and let A be its area. Let the angle between the two given vectors be θ. We may assume that 0 < θ < 180. From our knowledge of areas of parallelograms A = u v sin θ (1) The definition of the dot product of u and v implies that cos θ = u v u v. Since sin θ = 1 cos θ, it follows that which simplifies to A = u v sin θ = u v A = 1 ( u v ) u v u v (u v) () Since u = u 1 + u + u 3, v = v1 + v + v3 and (u v) = (u 1 v 1 + u v + u 3 v 3 ), () becomes A = (u 1 + u + u 3 ) (v 1 + v + v 3 ) (u 1v 1 + u v + u 3 v 3 ) 1
2 Expanding ( u 1 + u + u 3) ( v 1 + v + v 3) gives u v = u 1v 1 + u 1v + u 1v 3 + u v 1 + u v + u v 3 + u 3v 1 + u 3v + u 3v 3 To easily expand (u 1 v 1 + u v + u 3 v 3 ), we use the fact that (a + b + c) = a + b + c + ab + ac + bc. The result is (u v) = u 1v 1 + u v + u 3v 3 + u 1 v 1 u v + u 1 v 1 u 3 v 3 + u v u 3 v 3 Therefore u v (u v) may be written as ( u 1 v u 1 v 1 u v + u v1 ) ( + u 1 v3 u 1 v 1 u 3 v 3 + u 3v1 ) ( + u v3 u v u 3 v 3 + u 3v) (3) The expressions in parentheses can be factored! When we do so, (3) becomes (u 1 v u v 1 ) + (u 1 v 3 u 3 v 1 ) + (u v 3 u 3 v ) Now the area of the parallelogram may be written as A = (u 1 v u v 1 ) + (u 1 v 3 u 3 v 1 ) + (u v 3 u 3 v ) This is really the norm of some vector with components ± (u 1 v u v 1 ), ± (u 1 v 3 u 3 v 1 ) and ± (u v 3 u 3 v ). A convenient choice, (because, as you will soon find out, it gives a vector that is perpendicular to u and v), is (u v 3 u 3 v ) i (u 1 v 3 u 3 v 1 ) j + (u 1 v u v 1 ) k. We call it the cross product of u =< u 1, u, u 3 > and v =< v 1, v, v 3 >, and denote it by u v. We have therefore shown that the area of the parallelogram is u v. A formal definition of u v is the following: Definition 1 The cross product of two given vectors u =< u 1, u, u 3 > and v =< v 1, v, v 3 > is denoted by u v and is defined by u v = (u v 3 u 3 v ) i (u 1 v 3 u 3 v 1 ) j + (u 1 v u v 1 ) k We also refer to u v as the vector product of u and v, because, unlike u v, it is a vector. An easy way of remembering u v is to view it as the "determinant" v 1 v v 3 Examples: 1. (a) i j = k (b) j k = i (c) k i = j (d) j i = k (e) k j = i (f) i k = j (g) i i = 0 (h) j j = 0 (i) k k = 0. If u = (3, 1, ) = 3i + j k and v = ( 1, 0, 4) = i + 4k then u v = (4 0) i (1 ) j + (0 + 1) k =4i 10j + k emark The area of the parallelogram, by formula (1), is u v sin θ. Therefore u v = u v sin θ, hence u v is a vector with magnitude u v sin θ. Its direction is determined by the following right-hand rule: Imagine rotating u about the origin, towards v. Now imagine turning an ordinary screw in the same way. The direction of u v is given by the direction in which the screw moves. This is in perfect agreement with results i j = k, j i = k, etc in the above example
3 A number of useful properties of the cross product are given by the following theorem Theorem 3 Let u, v and w be given vectors and λ be a real number. Then 1. v u = u v. Thus the cross product operation is NT commutative.. u (λv) = λu v. 3. u 0 = 0. Here, 0 is the zero vector < 0, 0, 0 >. 4. u v is orthogonal to u and it is also orthogonal to v. 5. u (v + w) = u v + u w. In other words, the cross product operation is distributive with respect to addition. 6. If u =< u 1, u, u 3 >, v =< v 1, v, v 3 > and w =< w 1, w, w 3 > then u v w = v 1 v v 3 w 1 w w 3 7. u (v w) = (u v) w 8. If u v = 0 then one of the two vectors is a scalar multiple of the other. Conversely, if one of u,v is a scalar multiple of the other then u v = 0. To prove these claims, let u =< u 1, u, u 3 >, v =< v 1, v, v 3 > and w =< w 1, w, w 3 >. 1. By definition, v u = v 1 v v 3 and u v = v 1 v v 3 The first one expands as (v u 3 u v 3 ) i (v 1 u 3 u 13 v 3 ) j + (u v 1 u 1 v ) k and the second one as (u v 3 v u 3 ) i (u 13 v 3 v 1 u 3 ) j + (u 13 v u v 1 ) k. Clearly, the second one is the negative of the first one, therefore v u = u v.. Since λv = < λv 1, λv, λv 3 >, u (λv) = λv 1 λv λv 3 = (λu v 3 λv u 3 ) i (λu 1 v 3 λv 1 u 3 ) j + (λu 1 v λu v 1 ) k The right hand side may be written as λ[(u v 3 v u 3 ) i (u 1 v 3 v 1 u 3 ) j + (u 1 v u v 1 ) k] = λu v 3. u 0 = v 1 v v = 0i + 0j + 0k = 0. 3
4 4. To show that u v is orthogonal to u, it suffi ces to show that their dot product is zero. u (u v) = u 1 (u v 3 v u 3 ) u (u 1 v 3 v 1 u 3 ) + u 3 (u 1 v u v 1 ) = u 1 u v 3 u 1 v u 3 u 1 u v 3 + u v 1 u 3 + u 1 v u 3 u v 1 u 3 = 0, That u v is orthogonal to v is verified in the same way. 5. By definition, v + w =< v 1 + w 1, v + w, v 3 + w 3 >. Therefore u (v + w) = v 1 + w 1 v + w v 3 + w 3 Expanding gives [u (v 3 + w 3 ) u 3 (v + w )] i [u 1 (v 3 + w 3 ) u 3 (v 1 + w 1 )] j + [u 1 (v + w ) u (v 1 + w 1 )] k. We may rearrange this as [(u v 3 v u 3 ) i (u 1 v 3 v 1 u 3 ) j + (u 1 v u v 1 ) k] + [(u w 3 w u 3 ) i (u 1 w 3 w 1 u 3 ) j + (u 1 w u w 1 ) k] which is equal to u v + u w 6. By definition, 7. v w = (v w 3 v 3 w ) i (v 1 w 3 v 3 w 1 ) j + (v 1 w w 1 v ) k It follows that u (v w) = u 1 (v w 3 v 3 w ) u (v 1 w 3 + v 3 w 1 ) + u 3 (v 1 w w 1 v ). Expanding v 1 v v 3 w 1 w w 3 gives the same result. u (v w) = u 1 v w 3 u 1 v 3 w u v 1 w 3 + u v 3 w 1 + u 3 v 1 w u 3 w 1 v = (u v 3 u 3 v ) w 1 (u 1 v 3 u 3 v 1 ) w + (u 1 v u v 1 ) w 3 = (u v) w 8. Suppose u v = 0. We may assume that both vectors are nonzero because if one of them is zero then it is a scalar multiple of the other vector. For example, if u is zero then it is a scalar multiple of v since we may write u = 0 = 0v Let θ be the angle between the two nonzero vectors. Since u v = u v sin θ = 0, and the product u v is nonzero, it follows that sin θ = 0. This in turn implies that θ = 0 or 180, therefore u is a scalar multiple of v. Conversely, if say u is a scalar multiple of v, then u = λv where λ is a real number, and so u v =λv v =λ λv 1 λv λv 3 = 0i + 0j + 0k = 0 v 1 v v 3 4
5 Volume of a parallelepiped We will run into volumes of parallelepipeds when handling volume integrals. Here is how to construct a parallelepiped: 1. Start with a parallelogram, (an example is shown below).. Translate a copy of by a vector u = S S 5
6 3. Now join the corresponding corners of the two parallelograms to get a solid, called a parallelepiped. S To calculate its volume, simply multiply the area of the parallelogram by the vertical distance between the two parallelograms. The vertical distance from the point S to the parallelogram is equal to the dot product of S and a unit vector ( ) perpendicular ( ) to the parallelogram. (This is a result of a problem solved under dot products.) Since is a vector perpendicular to the parallelogram, the vertical distance between them, is ( ) ( ) ( ) ( ) S S ( ) ( ) = ( ) ( ) ( ) S = ( ) ( ) ( ) We ( take ) the( absolute ) value because the distance must be non-negative. But the area of the parallelogram is, therefore the volume of the parallelepiped is ( ) ( ) ( ) ( ) S ( ) ( ) ( ) ( ) = S In general, let u =, v = and w = S be vectors that are not in the same plane. 6
7 They generate a parallelepiped with volume u v w. Using a property we derived above, it follows that if u =< u 1, u, u 3 >, v =< v 1, v, v 3 > and w =< w 1, w, w 3 > then the volume of the parallelepiped determined by u, v, and w is the absolute value of v 1 v v 3 w 1 w w 3 Exercise 4 1. Compute the cross product u v given that (a) u = <, 0, 1 > and v =< 1, 0, >. u = < 4, 4, 1 > and v =< 1, 1, 3 >. u = < a,, 1 > and v =< a, 0, 3 >. u = < a, a, 1 > and v =< a, a, a >.. Use the cross product of u = 3i j + k and v = i j 4k to calculate the angle between u and v. 3. Calculate the area of the parallelogram determined by the two vectors <, 1, 4 > and < 3, 3, 5 >. 4. Calculate the area of the triangle with vertices at (1, 1, 4), (, 5, 3) and ( 1,, 4). 5. Calculate the volume of the parallelepiped generated by the vectors < 4, 5, 0 >, < 3, 7, 0 > and < 1,, 5 >. 6. True or False? If u v = u v = 0 then u = 0 or v = 0. If true, prove it. If false, give a counterexample. 7. Use appropriate properties of determinants to show that u v w = v w u = w u v 7
The Cross Product. Philippe B. Laval. Spring 2012 KSU. Philippe B. Laval (KSU) The Cross Product Spring /
 The Cross Product Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) The Cross Product Spring 2012 1 / 15 Introduction The cross product is the second multiplication operation between vectors we will
The Cross Product Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) The Cross Product Spring 2012 1 / 15 Introduction The cross product is the second multiplication operation between vectors we will
The Cross Product. In this section, we will learn about: Cross products of vectors and their applications.
 The Cross Product In this section, we will learn about: Cross products of vectors and their applications. THE CROSS PRODUCT The cross product a x b of two vectors a and b, unlike the dot product, is a
The Cross Product In this section, we will learn about: Cross products of vectors and their applications. THE CROSS PRODUCT The cross product a x b of two vectors a and b, unlike the dot product, is a
Section 13.4 The Cross Product
 Section 13.4 The Cross Product Multiplying Vectors 2 In this section we consider the more technical multiplication which can be defined on vectors in 3-space (but not vectors in 2-space). 1. Basic Definitions
Section 13.4 The Cross Product Multiplying Vectors 2 In this section we consider the more technical multiplication which can be defined on vectors in 3-space (but not vectors in 2-space). 1. Basic Definitions
Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors.
 Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
Math Linear Algebra
 Math 220 - Linear Algebra (Summer 208) Solutions to Homework #7 Exercise 6..20 (a) TRUE. u v v u = 0 is equivalent to u v = v u. The latter identity is true due to the commutative property of the inner
Math 220 - Linear Algebra (Summer 208) Solutions to Homework #7 Exercise 6..20 (a) TRUE. u v v u = 0 is equivalent to u v = v u. The latter identity is true due to the commutative property of the inner
MATH 19520/51 Class 2
 MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
MAT 1339-S14 Class 8
 MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v
 Orthogonality (I) Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v u v which brings us to the fact that θ = π/2 u v = 0. Definition (Orthogonality).
Orthogonality (I) Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v u v which brings us to the fact that θ = π/2 u v = 0. Definition (Orthogonality).
45. The Parallelogram Law states that. product of a and b is the vector a b a 2 b 3 a 3 b 2, a 3 b 1 a 1 b 3, a 1 b 2 a 2 b 1. a c. a 1. b 1.
 SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
Vectors in the Plane
 Vectors in the Plane MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Vectors vs. Scalars scalar quantity having only a magnitude (e.g. temperature, volume, length, area) and
Vectors in the Plane MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Vectors vs. Scalars scalar quantity having only a magnitude (e.g. temperature, volume, length, area) and
Chapter 2: Vector Geometry
 Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Exercise Solutions for Introduction to 3D Game Programming with DirectX 10
 Exercise Solutions for Introduction to 3D Game Programming with DirectX 10 Frank Luna, September 6, 009 Solutions to Part I Chapter 1 1. Let u = 1, and v = 3, 4. Perform the following computations and
Exercise Solutions for Introduction to 3D Game Programming with DirectX 10 Frank Luna, September 6, 009 Solutions to Part I Chapter 1 1. Let u = 1, and v = 3, 4. Perform the following computations and
Brief Review of Exam Topics
 Math 32A Discussion Session Week 3 Notes October 17 and 19, 2017 We ll use this week s discussion session to prepare for the first midterm. We ll start with a quick rundown of the relevant topics, and
Math 32A Discussion Session Week 3 Notes October 17 and 19, 2017 We ll use this week s discussion session to prepare for the first midterm. We ll start with a quick rundown of the relevant topics, and
Worksheet for Lecture 23 (due December 4) Section 6.1 Inner product, length, and orthogonality
 Worksheet for Lecture (due December 4) Name: Section 6 Inner product, length, and orthogonality u Definition Let u = u n product or dot product to be and v = v v n be vectors in R n We define their inner
Worksheet for Lecture (due December 4) Name: Section 6 Inner product, length, and orthogonality u Definition Let u = u n product or dot product to be and v = v v n be vectors in R n We define their inner
Review of Coordinate Systems
 Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Vector Geometry. Chapter 5
 Chapter 5 Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at
Chapter 5 Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at
Vectors and the Geometry of Space
 Vectors and the Geometry of Space Many quantities in geometry and physics, such as area, volume, temperature, mass, and time, can be characterized by a single real number scaled to appropriate units of
Vectors and the Geometry of Space Many quantities in geometry and physics, such as area, volume, temperature, mass, and time, can be characterized by a single real number scaled to appropriate units of
Lecture 2: Vector-Vector Operations
 Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that
![58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that 58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that](/thumbs/86/94310732.jpg) 786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
Remark 3.2. The cross product only makes sense in R 3.
 3. Cross product Definition 3.1. Let v and w be two vectors in R 3. The cross product of v and w, denoted v w, is the vector defined as follows: the length of v w is the area of the parallelogram with
3. Cross product Definition 3.1. Let v and w be two vectors in R 3. The cross product of v and w, denoted v w, is the vector defined as follows: the length of v w is the area of the parallelogram with
Objective 1. Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI FINDING THE CROSS PRODUCT OF TWO VECTORS
 Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI In this lesson you will learn how to find the cross product of two vectors how to find an orthogonal vector to a plane defined by two vectors how
Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI In this lesson you will learn how to find the cross product of two vectors how to find an orthogonal vector to a plane defined by two vectors how
Study guide for Exam 1. by William H. Meeks III October 26, 2012
 Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
4.1 Distance and Length
 Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
12.1. Cartesian Space
 12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
The Cross Product. MATH 311, Calculus III. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan The Cross Product
 The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
Linear Algebra. Alvin Lin. August December 2017
 Linear Algebra Alvin Lin August 207 - December 207 Linear Algebra The study of linear algebra is about two basic things. We study vector spaces and structure preserving maps between vector spaces. A vector
Linear Algebra Alvin Lin August 207 - December 207 Linear Algebra The study of linear algebra is about two basic things. We study vector spaces and structure preserving maps between vector spaces. A vector
v = v 1 2 +v 2 2. Two successive applications of this idea give the length of the vector v R 3 :
 Length, Angle and the Inner Product The length (or norm) of a vector v R 2 (viewed as connecting the origin to a point (v 1,v 2 )) is easily determined by the Pythagorean Theorem and is denoted v : v =
Length, Angle and the Inner Product The length (or norm) of a vector v R 2 (viewed as connecting the origin to a point (v 1,v 2 )) is easily determined by the Pythagorean Theorem and is denoted v : v =
R n : The Cross Product
 A FIRST COURSE IN LINEAR ALGEBRA An Open Text by Ken Kuttler R n : The Cross Product Lecture Notes by Karen Seyffarth Adapted by LYRYX SERVICE COURSE SOLUTION Attribution-NonCommercial-ShareAlike (CC BY-NC-SA)
A FIRST COURSE IN LINEAR ALGEBRA An Open Text by Ken Kuttler R n : The Cross Product Lecture Notes by Karen Seyffarth Adapted by LYRYX SERVICE COURSE SOLUTION Attribution-NonCommercial-ShareAlike (CC BY-NC-SA)
GEOMETRY AND VECTORS
 GEOMETRY AND VECTORS Distinguishing Between Points in Space One Approach Names: ( Fred, Steve, Alice...) Problem: distance & direction must be defined point-by-point More elegant take advantage of geometry
GEOMETRY AND VECTORS Distinguishing Between Points in Space One Approach Names: ( Fred, Steve, Alice...) Problem: distance & direction must be defined point-by-point More elegant take advantage of geometry
Electromagnetic Field Theory
 University of Babylon College of Engineering Department of Electrical Engineering Class :2 st Lectures of Electromagnetic Field Theory By ssistant lecturer : hmed Hussein Shatti l-isawi 2014-2015 References
University of Babylon College of Engineering Department of Electrical Engineering Class :2 st Lectures of Electromagnetic Field Theory By ssistant lecturer : hmed Hussein Shatti l-isawi 2014-2015 References
What you will learn today
 What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
Inner Product Spaces 6.1 Length and Dot Product in R n
 Inner Product Spaces 6.1 Length and Dot Product in R n Summer 2017 Goals We imitate the concept of length and angle between two vectors in R 2, R 3 to define the same in the n space R n. Main topics are:
Inner Product Spaces 6.1 Length and Dot Product in R n Summer 2017 Goals We imitate the concept of length and angle between two vectors in R 2, R 3 to define the same in the n space R n. Main topics are:
11.1 Vectors in the plane
 11.1 Vectors in the plane What is a vector? It is an object having direction and length. Geometric way to represent vectors It is represented by an arrow. The direction of the arrow is the direction of
11.1 Vectors in the plane What is a vector? It is an object having direction and length. Geometric way to represent vectors It is represented by an arrow. The direction of the arrow is the direction of
Part I, Number Systems CS131 Mathematics for Computer Scientists II Note 3 VECTORS
 CS131 Part I, Number Systems CS131 Mathematics for Computer Scientists II Note 3 VECTRS Vectors in two and three dimensional space are defined to be members of the sets R 2 and R 3 defined by: R 2 = {(x,
CS131 Part I, Number Systems CS131 Mathematics for Computer Scientists II Note 3 VECTRS Vectors in two and three dimensional space are defined to be members of the sets R 2 and R 3 defined by: R 2 = {(x,
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication.
 This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
MATH 12 CLASS 2 NOTES, SEP Contents. 2. Dot product: determining the angle between two vectors 2
 MATH 12 CLASS 2 NOTES, SEP 23 2011 Contents 1. Dot product: definition, basic properties 1 2. Dot product: determining the angle between two vectors 2 Quick links to definitions/theorems Dot product definition
MATH 12 CLASS 2 NOTES, SEP 23 2011 Contents 1. Dot product: definition, basic properties 1 2. Dot product: determining the angle between two vectors 2 Quick links to definitions/theorems Dot product definition
CHAPTER 10 VECTORS POINTS TO REMEMBER
 For more important questions visit : www4onocom CHAPTER 10 VECTORS POINTS TO REMEMBER A quantity that has magnitude as well as direction is called a vector It is denoted by a directed line segment Two
For more important questions visit : www4onocom CHAPTER 10 VECTORS POINTS TO REMEMBER A quantity that has magnitude as well as direction is called a vector It is denoted by a directed line segment Two
MAC Module 5 Vectors in 2-Space and 3-Space II
 MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
11.1 Three-Dimensional Coordinate System
 11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
Vectors are used to represent quantities such as force and velocity which have both. and. The magnitude of a vector corresponds to its.
 Fry Texas A&M University Math 150 Chapter 9 Fall 2014 1 Chapter 9 -- Vectors Remember that is the set of real numbers, often represented by the number line, 2 is the notation for the 2-dimensional plane.
Fry Texas A&M University Math 150 Chapter 9 Fall 2014 1 Chapter 9 -- Vectors Remember that is the set of real numbers, often represented by the number line, 2 is the notation for the 2-dimensional plane.
MTAEA Vectors in Euclidean Spaces
 School of Economics, Australian National University January 25, 2010 Vectors. Economists usually work in the vector space R n. A point in this space is called a vector, and is typically defined by its
School of Economics, Australian National University January 25, 2010 Vectors. Economists usually work in the vector space R n. A point in this space is called a vector, and is typically defined by its
Chapter 1E - Complex Numbers
 Fry Texas A&M University Math 150 Spring 2015 Unit 4 20 Chapter 1E - Complex Numbers 16 exists So far the largest (most inclusive) number set we have discussed and the one we have the most experience with
Fry Texas A&M University Math 150 Spring 2015 Unit 4 20 Chapter 1E - Complex Numbers 16 exists So far the largest (most inclusive) number set we have discussed and the one we have the most experience with
NOTES ON VECTORS, PLANES, AND LINES
 NOTES ON VECTORS, PLANES, AND LINES DAVID BEN MCREYNOLDS 1. Vectors I assume that the reader is familiar with the basic notion of a vector. The important feature of the vector is that it has a magnitude
NOTES ON VECTORS, PLANES, AND LINES DAVID BEN MCREYNOLDS 1. Vectors I assume that the reader is familiar with the basic notion of a vector. The important feature of the vector is that it has a magnitude
Calculus 1 for AE (WI1421LR) Lecture 1: 12.3 The dot product 12.4 The cross product
 Calculus 1 for AE (WI1421LR) : 12.3 The dot product 12.4 The cross product About this course Textbook James Stewart, Calculus, Early Transcendentals, 7th edition Course Coordinator Dr. Roelof Koekoek,
Calculus 1 for AE (WI1421LR) : 12.3 The dot product 12.4 The cross product About this course Textbook James Stewart, Calculus, Early Transcendentals, 7th edition Course Coordinator Dr. Roelof Koekoek,
Solution to Homework 1
 Solution to Homework 1 Olena Bormashenko September, 0 Section 1.1:, 5b)d), 7b)f), 8a)b), ; Section 1.:, 5, 7, 9, 10, b)c), 1, 15b), 3 Section 1.1. In each of the following cases, find a point that is two-thirds
Solution to Homework 1 Olena Bormashenko September, 0 Section 1.1:, 5b)d), 7b)f), 8a)b), ; Section 1.:, 5, 7, 9, 10, b)c), 1, 15b), 3 Section 1.1. In each of the following cases, find a point that is two-thirds
Distance in the Plane
 Distance in the Plane The absolute value function is defined as { x if x 0; and x = x if x < 0. If the number a is positive or zero, then a = a. If a is negative, then a is the number you d get by erasing
Distance in the Plane The absolute value function is defined as { x if x 0; and x = x if x < 0. If the number a is positive or zero, then a = a. If a is negative, then a is the number you d get by erasing
10.2,3,4. Vectors in 3D, Dot products and Cross Products
 Name: Section: 10.2,3,4. Vectors in 3D, Dot products and Cross Products 1. Sketch the plane parallel to the xy-plane through (2, 4, 2) 2. For the given vectors u and v, evaluate the following expressions.
Name: Section: 10.2,3,4. Vectors in 3D, Dot products and Cross Products 1. Sketch the plane parallel to the xy-plane through (2, 4, 2) 2. For the given vectors u and v, evaluate the following expressions.
Name: ID: Math 233 Exam 1. Page 1
 Page 1 Name: ID: This exam has 20 multiple choice questions, worth 5 points each. You are allowed to use a scientific calculator and a 3 5 inch note card. 1. Which of the following pairs of vectors are
Page 1 Name: ID: This exam has 20 multiple choice questions, worth 5 points each. You are allowed to use a scientific calculator and a 3 5 inch note card. 1. Which of the following pairs of vectors are
MATH 221: SOLUTIONS TO SELECTED HOMEWORK PROBLEMS
 MATH 221: SOLUTIONS TO SELECTED HOMEWORK PROBLEMS 1. HW 1: Due September 4 1.1.21. Suppose v, w R n and c is a scalar. Prove that Span(v + cw, w) = Span(v, w). We must prove two things: that every element
MATH 221: SOLUTIONS TO SELECTED HOMEWORK PROBLEMS 1. HW 1: Due September 4 1.1.21. Suppose v, w R n and c is a scalar. Prove that Span(v + cw, w) = Span(v, w). We must prove two things: that every element
Intro Vectors 2D implicit curves 2D parametric curves. Graphics 2011/2012, 4th quarter. Lecture 2: vectors, curves, and surfaces
 Lecture 2, curves, and surfaces Organizational remarks Tutorials: Tutorial 1 will be online later today TA sessions for questions start next week Practicals: Exams: Make sure to find a team partner very
Lecture 2, curves, and surfaces Organizational remarks Tutorials: Tutorial 1 will be online later today TA sessions for questions start next week Practicals: Exams: Make sure to find a team partner very
The Cross Product The cross product of v = (v 1,v 2,v 3 ) and w = (w 1,w 2,w 3 ) is
 The Cross Product 1-1-2018 The cross product of v = (v 1,v 2,v 3 ) and w = (w 1,w 2,w 3 ) is v w = (v 2 w 3 v 3 w 2 )î+(v 3 w 1 v 1 w 3 )ĵ+(v 1 w 2 v 2 w 1 )ˆk = v 1 v 2 v 3 w 1 w 2 w 3. Strictly speaking,
The Cross Product 1-1-2018 The cross product of v = (v 1,v 2,v 3 ) and w = (w 1,w 2,w 3 ) is v w = (v 2 w 3 v 3 w 2 )î+(v 3 w 1 v 1 w 3 )ĵ+(v 1 w 2 v 2 w 1 )ˆk = v 1 v 2 v 3 w 1 w 2 w 3. Strictly speaking,
VECTORS IN COMPONENT FORM
 VECTORS IN COMPONENT FORM In Cartesian coordinates any D vector a can be written as a = a x i + a y j + a z k a x a y a x a y a z a z where i, j and k are unit vectors in x, y and z directions. i = j =
VECTORS IN COMPONENT FORM In Cartesian coordinates any D vector a can be written as a = a x i + a y j + a z k a x a y a x a y a z a z where i, j and k are unit vectors in x, y and z directions. i = j =
Vectors and Matrices Lecture 2
 Vectors and Matrices Lecture 2 Dr Mark Kambites School of Mathematics 13/03/2014 Dr Mark Kambites (School of Mathematics) COMP11120 13/03/2014 1 / 20 How do we recover the magnitude of a vector from its
Vectors and Matrices Lecture 2 Dr Mark Kambites School of Mathematics 13/03/2014 Dr Mark Kambites (School of Mathematics) COMP11120 13/03/2014 1 / 20 How do we recover the magnitude of a vector from its
(1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3
 Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Chapter 3. The Scalar Product. 3.1 The scalar product using coördinates
 Chapter The Scalar Product The scalar product is a way of multiplying two vectors to produce a scalar (real number) Let u and v be nonzero vectors represented by AB and AC C v A θ u B We define the angle
Chapter The Scalar Product The scalar product is a way of multiplying two vectors to produce a scalar (real number) Let u and v be nonzero vectors represented by AB and AC C v A θ u B We define the angle
A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 2010
 A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 00 Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics
A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 00 Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics
Section 2.3. The Cross Product
 Section.3. The Cross Product Recall that a vector can be uniquely determined by its length and direction. De nition. The cross product of two vectors u and v, denote by u v, is a vector with length j u
Section.3. The Cross Product Recall that a vector can be uniquely determined by its length and direction. De nition. The cross product of two vectors u and v, denote by u v, is a vector with length j u
Notes on multivariable calculus
 Notes on multivariable calculus Jonathan Wise February 2, 2010 1 Review of trigonometry Trigonometry is essentially the study of the relationship between polar coordinates and Cartesian coordinates in
Notes on multivariable calculus Jonathan Wise February 2, 2010 1 Review of trigonometry Trigonometry is essentially the study of the relationship between polar coordinates and Cartesian coordinates in
Detailed objectives are given in each of the sections listed below. 1. Cartesian Space Coordinates. 2. Displacements, Forces, Velocities and Vectors
 Unit 1 Vectors In this unit, we introduce vectors, vector operations, and equations of lines and planes. Note: Unit 1 is based on Chapter 12 of the textbook, Salas and Hille s Calculus: Several Variables,
Unit 1 Vectors In this unit, we introduce vectors, vector operations, and equations of lines and planes. Note: Unit 1 is based on Chapter 12 of the textbook, Salas and Hille s Calculus: Several Variables,
NOTES ON LINEAR ALGEBRA CLASS HANDOUT
 NOTES ON LINEAR ALGEBRA CLASS HANDOUT ANTHONY S. MAIDA CONTENTS 1. Introduction 2 2. Basis Vectors 2 3. Linear Transformations 2 3.1. Example: Rotation Transformation 3 4. Matrix Multiplication and Function
NOTES ON LINEAR ALGEBRA CLASS HANDOUT ANTHONY S. MAIDA CONTENTS 1. Introduction 2 2. Basis Vectors 2 3. Linear Transformations 2 3.1. Example: Rotation Transformation 3 4. Matrix Multiplication and Function
1.1 Bound and Free Vectors. 1.2 Vector Operations
 1 Vectors Vectors are used when both the magnitude and the direction of some physical quantity are required. Examples of such quantities are velocity, acceleration, force, electric and magnetic fields.
1 Vectors Vectors are used when both the magnitude and the direction of some physical quantity are required. Examples of such quantities are velocity, acceleration, force, electric and magnetic fields.
Vectors are used to represent quantities such as force and velocity which have both. and. The magnitude of a vector corresponds to its.
 Fry Texas A&M University Fall 2016 Math 150 Notes Chapter 9 Page 248 Chapter 9 -- Vectors Remember that is the set of real numbers, often represented by the number line, 2 is the notation for the 2-dimensional
Fry Texas A&M University Fall 2016 Math 150 Notes Chapter 9 Page 248 Chapter 9 -- Vectors Remember that is the set of real numbers, often represented by the number line, 2 is the notation for the 2-dimensional
Review: Linear and Vector Algebra
 Review: Linear and Vector Algebra Points in Euclidean Space Location in space Tuple of n coordinates x, y, z, etc Cannot be added or multiplied together Vectors: Arrows in Space Vectors are point changes
Review: Linear and Vector Algebra Points in Euclidean Space Location in space Tuple of n coordinates x, y, z, etc Cannot be added or multiplied together Vectors: Arrows in Space Vectors are point changes
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Section 10.7 The Cross Product
 44 Section 10.7 The Cross Product Objective #0: Evaluating Determinants. Recall the following definition for determinants: Determinants a The determinant for matrix 1 b 1 is denoted as a 1 b 1 a b a b
44 Section 10.7 The Cross Product Objective #0: Evaluating Determinants. Recall the following definition for determinants: Determinants a The determinant for matrix 1 b 1 is denoted as a 1 b 1 a b a b
Brief Review of Vector Algebra
 APPENDIX Brief Review of Vector Algebra A.0 Introduction Vector algebra is used extensively in computational mechanics. The student must thus understand the concepts associated with this subject. The current
APPENDIX Brief Review of Vector Algebra A.0 Introduction Vector algebra is used extensively in computational mechanics. The student must thus understand the concepts associated with this subject. The current
CSCI 239 Discrete Structures of Computer Science Lab 6 Vectors and Matrices
 CSCI 239 Discrete Structures of Computer Science Lab 6 Vectors and Matrices This lab consists of exercises on real-valued vectors and matrices. Most of the exercises will required pencil and paper. Put
CSCI 239 Discrete Structures of Computer Science Lab 6 Vectors and Matrices This lab consists of exercises on real-valued vectors and matrices. Most of the exercises will required pencil and paper. Put
Linear Algebra I. Ronald van Luijk, 2015
 Linear Algebra I Ronald van Luijk, 2015 With many parts from Linear Algebra I by Michael Stoll, 2007 Contents Dependencies among sections 3 Chapter 1. Euclidean space: lines and hyperplanes 5 1.1. Definition
Linear Algebra I Ronald van Luijk, 2015 With many parts from Linear Algebra I by Michael Stoll, 2007 Contents Dependencies among sections 3 Chapter 1. Euclidean space: lines and hyperplanes 5 1.1. Definition
If the pull is downward (Fig. 1), we want C to point into the page. If the pull is upward (Fig. 2), we want C to point out of the page.
 11.5 Cross Product Contemporary Calculus 1 11.5 CROSS PRODUCT This section is the final one about the arithmetic of vectors, and it introduces a second type of vector vector multiplication called the cross
11.5 Cross Product Contemporary Calculus 1 11.5 CROSS PRODUCT This section is the final one about the arithmetic of vectors, and it introduces a second type of vector vector multiplication called the cross
Vectors for Physics. AP Physics C
 Vectors for Physics AP Physics C A Vector is a quantity that has a magnitude (size) AND a direction. can be in one-dimension, two-dimensions, or even three-dimensions can be represented using a magnitude
Vectors for Physics AP Physics C A Vector is a quantity that has a magnitude (size) AND a direction. can be in one-dimension, two-dimensions, or even three-dimensions can be represented using a magnitude
Math Vector Calculus II
 Math 255 - Vector Calculus II Review Notes Vectors We assume the reader is familiar with all the basic concepts regarding vectors and vector arithmetic, such as addition/subtraction of vectors in R n,
Math 255 - Vector Calculus II Review Notes Vectors We assume the reader is familiar with all the basic concepts regarding vectors and vector arithmetic, such as addition/subtraction of vectors in R n,
1.1 Single Variable Calculus versus Multivariable Calculus Rectangular Coordinate Systems... 4
 MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
LB 220 Homework 2 (due Tuesday, 01/22/13)
 LB 220 Homework 2 (due Tuesday, 01/22/13) Directions. Please solve the problems below. Your solutions must begin with a clear statement (or re-statement in your own words) of the problem. You solutions
LB 220 Homework 2 (due Tuesday, 01/22/13) Directions. Please solve the problems below. Your solutions must begin with a clear statement (or re-statement in your own words) of the problem. You solutions
The Cross Product -(10.4)
 The Cross Product -(10.4) Questions: What is the definition of the cross product of two vectors? Is it a scalar or vector? What can you say about vectors u and v (all possibilities) if the cross product
The Cross Product -(10.4) Questions: What is the definition of the cross product of two vectors? Is it a scalar or vector? What can you say about vectors u and v (all possibilities) if the cross product
Department of Physics, Korea University
 Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
x n -2.5 Definition A list is a list of objects, where multiplicity is allowed, and order matters. For example, as lists
 Vectors, Linear Combinations, and Matrix-Vector Mulitiplication In this section, we introduce vectors, linear combinations, and matrix-vector multiplication The rest of the class will involve vectors,
Vectors, Linear Combinations, and Matrix-Vector Mulitiplication In this section, we introduce vectors, linear combinations, and matrix-vector multiplication The rest of the class will involve vectors,
102 CHAPTER 3. VECTORS AND THE GEOMETRY OF SPACE
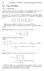 102 CHAPTER 3. VECTORS AND THE GEOMETRY OF SPACE 3.4 Cross Product 3.4.1 De nitions Unlike the dot product, the cross product is only de ned for 3-D vectors. In this section, when we use the word vector,
102 CHAPTER 3. VECTORS AND THE GEOMETRY OF SPACE 3.4 Cross Product 3.4.1 De nitions Unlike the dot product, the cross product is only de ned for 3-D vectors. In this section, when we use the word vector,
Mathematics 2203, Test 1 - Solutions
 Mathematics 220, Test 1 - Solutions F, 2010 Philippe B. Laval Name 1. Determine if each statement below is True or False. If it is true, explain why (cite theorem, rule, property). If it is false, explain
Mathematics 220, Test 1 - Solutions F, 2010 Philippe B. Laval Name 1. Determine if each statement below is True or False. If it is true, explain why (cite theorem, rule, property). If it is false, explain
Vectors. 1 Basic Definitions. Liming Pang
 Vectors Liming Pang 1 Basic Definitions Definition 1. A vector in a line/plane/space is a quantity which has both magnitude and direction. The magnitude is a nonnegative real number and the direction is
Vectors Liming Pang 1 Basic Definitions Definition 1. A vector in a line/plane/space is a quantity which has both magnitude and direction. The magnitude is a nonnegative real number and the direction is
Vectors. The standard geometric definition of vector is as something which has direction and magnitude but not position.
 Vectors The standard geometric definition of vector is as something which has direction and magnitude but not position. Since vectors have no position we may place them wherever is convenient. Vectors
Vectors The standard geometric definition of vector is as something which has direction and magnitude but not position. Since vectors have no position we may place them wherever is convenient. Vectors
Math 32A Discussion Session Week 2 Notes October 10 and 12, 2017
 Math 32A Discussion Session Week 2 Notes October 10 and 12, 2017 Since we didn t get a chance to discuss parametrized lines last week, we may spend some time discussing those before moving on to the dot
Math 32A Discussion Session Week 2 Notes October 10 and 12, 2017 Since we didn t get a chance to discuss parametrized lines last week, we may spend some time discussing those before moving on to the dot
Math 302 Test 1 Review
 Math Test Review. Given two points in R, x, y, z and x, y, z, show the point x + x, y + y, z + z is on the line between these two points and is the same distance from each of them. The line is rt x, y,
Math Test Review. Given two points in R, x, y, z and x, y, z, show the point x + x, y + y, z + z is on the line between these two points and is the same distance from each of them. The line is rt x, y,
7.1 Projections and Components
 7. Projections and Components As we have seen, the dot product of two vectors tells us the cosine of the angle between them. So far, we have only used this to find the angle between two vectors, but cosines
7. Projections and Components As we have seen, the dot product of two vectors tells us the cosine of the angle between them. So far, we have only used this to find the angle between two vectors, but cosines
a b 0 a cos u, 0 u 180 :
 Section 7.3 The Dot Product of Two Geometric Vectors In hapter 6, the concept of multiplying a vector by a scalar was discussed. In this section, we introduce the dot product of two vectors and deal specifically
Section 7.3 The Dot Product of Two Geometric Vectors In hapter 6, the concept of multiplying a vector by a scalar was discussed. In this section, we introduce the dot product of two vectors and deal specifically
CHAPTER 4 VECTORS. Before we go any further, we must talk about vectors. They are such a useful tool for
 CHAPTER 4 VECTORS Before we go any further, we must talk about vectors. They are such a useful tool for the things to come. The concept of a vector is deeply rooted in the understanding of physical mechanics
CHAPTER 4 VECTORS Before we go any further, we must talk about vectors. They are such a useful tool for the things to come. The concept of a vector is deeply rooted in the understanding of physical mechanics
A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3].
![A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3]. A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3].](/thumbs/78/77913594.jpg) Appendix : A Very Brief Linear ALgebra Review Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics Very often in this course we study the shapes
Appendix : A Very Brief Linear ALgebra Review Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics Very often in this course we study the shapes
Vectors. September 2, 2015
 Vectors September 2, 2015 Our basic notion of a vector is as a displacement, directed from one point of Euclidean space to another, and therefore having direction and magnitude. We will write vectors in
Vectors September 2, 2015 Our basic notion of a vector is as a displacement, directed from one point of Euclidean space to another, and therefore having direction and magnitude. We will write vectors in
Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems
 To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
Prepared by: M. S. KumarSwamy, TGT(Maths) Page
 Prepared by: M S KumarSwamy, TGT(Maths) Page - 119 - CHAPTER 10: VECTOR ALGEBRA QUICK REVISION (Important Concepts & Formulae) MARKS WEIGHTAGE 06 marks Vector The line l to the line segment AB, then a
Prepared by: M S KumarSwamy, TGT(Maths) Page - 119 - CHAPTER 10: VECTOR ALGEBRA QUICK REVISION (Important Concepts & Formulae) MARKS WEIGHTAGE 06 marks Vector The line l to the line segment AB, then a
Course Name : Physics I Course # PHY 107
 Course Name : Physics I Course # PHY 107 Lecture-2 : Representation of Vectors and the Product Rules Abu Mohammad Khan Department of Mathematics and Physics North South University http://abukhan.weebly.com
Course Name : Physics I Course # PHY 107 Lecture-2 : Representation of Vectors and the Product Rules Abu Mohammad Khan Department of Mathematics and Physics North South University http://abukhan.weebly.com
Distance Formula in 3-D Given any two points P 1 (x 1, y 1, z 1 ) and P 2 (x 2, y 2, z 2 ) the distance between them is ( ) ( ) ( )
 Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
LINEAR ALGEBRA - CHAPTER 1: VECTORS
 LINEAR ALGEBRA - CHAPTER 1: VECTORS A game to introduce Linear Algebra In measurement, there are many quantities whose description entirely rely on magnitude, i.e., length, area, volume, mass and temperature.
LINEAR ALGEBRA - CHAPTER 1: VECTORS A game to introduce Linear Algebra In measurement, there are many quantities whose description entirely rely on magnitude, i.e., length, area, volume, mass and temperature.
CSC 470 Introduction to Computer Graphics. Mathematical Foundations Part 2
 CSC 47 Introduction to Computer Graphics Mathematical Foundations Part 2 Vector Magnitude and Unit Vectors The magnitude (length, size) of n-vector w is written w 2 2 2 w = w + w2 + + w n Example: the
CSC 47 Introduction to Computer Graphics Mathematical Foundations Part 2 Vector Magnitude and Unit Vectors The magnitude (length, size) of n-vector w is written w 2 2 2 w = w + w2 + + w n Example: the
Intro Vectors 2D implicit curves 2D parametric curves. Graphics 2012/2013, 4th quarter. Lecture 2: vectors, curves, and surfaces
 Lecture 2, curves, and surfaces Organizational remarks Tutorials: TA sessions for tutorial 1 start today Tutorial 2 will go online after lecture 3 Practicals: Make sure to find a team partner very soon
Lecture 2, curves, and surfaces Organizational remarks Tutorials: TA sessions for tutorial 1 start today Tutorial 2 will go online after lecture 3 Practicals: Make sure to find a team partner very soon
Chapter 2. Linear Algebra. rather simple and learning them will eventually allow us to explain the strange results of
 Chapter 2 Linear Algebra In this chapter, we study the formal structure that provides the background for quantum mechanics. The basic ideas of the mathematical machinery, linear algebra, are rather simple
Chapter 2 Linear Algebra In this chapter, we study the formal structure that provides the background for quantum mechanics. The basic ideas of the mathematical machinery, linear algebra, are rather simple
Chapter 13: Vectors and the Geometry of Space
 Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space
 Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Dot Product August 2013
 Dot Product 12.3 30 August 2013 Dot product. v = v 1, v 2,..., v n, w = w 1, w 2,..., w n The dot product v w is v w = v 1 w 1 + v 2 w 2 + + v n w n n = v i w i. i=1 Example: 1, 4, 5 2, 8, 0 = 1 2 + 4
Dot Product 12.3 30 August 2013 Dot product. v = v 1, v 2,..., v n, w = w 1, w 2,..., w n The dot product v w is v w = v 1 w 1 + v 2 w 2 + + v n w n n = v i w i. i=1 Example: 1, 4, 5 2, 8, 0 = 1 2 + 4
MEP Pupil Text 13-19, Additional Material. Gradients of Perpendicular Lines
 Graphs MEP Pupil Text -9, Additional Material.B Gradients of Perpendicular Lines In this section we explore the relationship between the gradients of perpendicular lines and line segments. Worked Example
Graphs MEP Pupil Text -9, Additional Material.B Gradients of Perpendicular Lines In this section we explore the relationship between the gradients of perpendicular lines and line segments. Worked Example
Vector Basics, with Exercises
 Math 230 Spring 09 Vector Basics, with Exercises This sheet is designed to follow the GeoGebra Introduction to Vectors. It includes a summary of some of the properties of vectors, as well as homework exercises.
Math 230 Spring 09 Vector Basics, with Exercises This sheet is designed to follow the GeoGebra Introduction to Vectors. It includes a summary of some of the properties of vectors, as well as homework exercises.
