Enumeration of Sequences Constrained by the Ratio of Consecutive Parts
|
|
|
- Grant Stewart
- 6 years ago
- Views:
Transcription
1 Eumeraio of Seueces Cosraied by he Raio of Cosecuive Pars Sylvie Coreel Suyoug Lee Carla D Savage November 13, 2004; Revised March 3, 2005 Absrac Recurreces are developed o eumerae ay family of oegaive ieger seueces λ =(,,λ ) saisfyig he cosrais: λ 2 λ 1 λ 0, a 1 a 2 a 1 a for a give cosrai seuece a =a 1,,a of posiive iegers They are applied o derive ew couig formulas, o reveal ew relaioships bewee families, ad o give simple proofs of he rucaed lecure hall ad ai-lecure hall heorems Nous développos des récurreces pour éumérer des familles de suies d eiers λ =(,,λ ) saisfaisa les coraies λ 2 λ 1 λ 0, a 1 a 2 a 1 a pour ue suie d eiers posiifs doée a =a 1,,a Ces récurreces permee de dériver de ouvelles formules déuméraio, de révéler de ouvelles relaios ere ceraies familles, e de doer des preuves simples des héorèmes des pariios Lecure Hall rouées e des composiios Lecure Hall rouées 1 Iroducio We cosider he problem of eumeraig oegaive ieger seueces λ =(,,λ ) saisfyig he cosrais: λ 2 λ 1 λ 0, (1) a 1 a 2 a 1 a CNRS PRiSM, UVSQ, 45 Aveue des Eas-Uis, Versailles, Frace (syl@prismuvsfr) Compuer Sciece, Norh Carolia Sae Uiversiy, Box 8206, Raleigh, NC 27695, USA (slee7@uiycsuedu) Research suppored i par by NSF gra DMS Compuer Sciece, Norh Carolia Sae Uiversiy, Box 8206, Raleigh, NC 27695, USA (savage@csccsuedu) Research suppored i par by NSF gras DMS ad INT
2 for a give cosrai seuece a =a 1,,a of posiive iegers We refer o a seuece λ =(,,λ ) of oegaive iegers as a composiio io oegaive pars If he pars of λ are oicreasig, he λ is a pariio Pariios ad composiios are commoly defied by he se of pars allowed, he umber of occurreces of a par, or he differece bewee cosecuive pars I coras, he composiios saisfyig (1) are cosraied by he raio of cosecuive pars ad we refer o hem as raio composiios Geeraig fucios are ow for raio composiios oly for some special cosrai seueces, a, icludig: a =1, 1,,1: ordiary pariios 1; a =1, 2, 4,,2 1 : Cayley composiios 8, 2, 14, 4; a =r 1,r 2,,r,1: Hicerso pariios 13; a =, 1,,1: lecure hall pariios 5, 6, 7, 15, 16, 3; a =1, 2,,: ai-lecure hall composiios 9; a =1, 2, 1, 2,, 2 ( 1) : oe-wo composiios 11; a =, 1, + 1: rucaed lecure hall pariios 10; a = +1,,,: rucaed ai-lecure hall composiios 10 I his paper, we iroduce a commo approach for he eumeraio of raio composiios by usig as a saisic a boud o he size of he firs par This geeralizes he eumeraio of ordiary pariios via he Gaussia polyomials I Secio 2, we derive a recurrece for he geeraig fucio of ay family of raio composiios wih firs par bouded We use his o derive ew couig formulas ad heir -aalogs Amog hese, we discover a family of polyomials wih several ieresig properies which arise i he eumeraio of lecure hall pariios I addiio, we fid a fucioal relaioship bewee he geeraig fucios for he raio composiios cosraied by a seuece a 1,a 2,,a ad hose cosraied by is reverse seuece a,a 1,a 1 This reveals for he firs ime he relaioship bewee, eg, lecure hall pariios ad ai-lecure hall composiios ad bewee Hicerso pariios ad Cayley composiios I Secio 3, we derive a differe recurrece for he eumeraio of raio composiios wih firs par bouded By allowig he boud o approach ifiiy, we ge a recurrece for he geeraig fucio of ay family of raio composiios wih firs par ubouded As oe coseuece, we discover ew easy proofs of he (rucaed) lecure hall ad (rucaed) ai-lecure hall heorems I coras o earlier proofs, where derivig a recurrece was a challege, here he recurrece is geeric ad he wor is moved eirely o sadard -series maipulaio i a iducio proof 2
3 2 Eumeraio of raio composiios wih firs par bouded To build a recurrece, we firs cosider he case where he cosrai seuece a i (1) saisfies a 1,,a =s,s 1,,s 1 for a ifiie seuece of posiive iegers {s i } For 0, le S be he se of composiios λ =(,λ 2,,λ ) saisfyig s λ 2 s 1 λ 1 s 2 λ s 1 0 (2) Le S (j,i) be he se of λ S wih js + i ad le S (j,i) () = λ λ S (j,i) Theorem 1 For 0, j 0, ad0 i s, S (j,i) () = 1 if =0or j = i =0,else S (j 1,s) () if i =0,else S (j,i 1) ()+ js+i S (j, is 1/s ) 1 () oherwise Proof The heorem is clearly rue for = 0 ad for j = i =0 Le(, j, i) saisfy>0, (j, i) > (0, 0) If i = 0, he j>0adjs +i = js =(j 1)s +s, so he heorem is rue Assume, he, ha 1 i s By defiiio, λ S (j,i) if ad oly if eiher λ S (j,i 1) λ S ad = js + i Bu (js + i, λ 2,,λ ) S ifadolyif(λ 2,,λ ) S 1 ad (js + i)/λ 2 s /s 1 Tha is, λ 2 s 1 (js + i) =js 1 + i s 1 s s So, sice λ 2 is a ieger, λ 2 js 1 + i s 1 s Noe, sice 1 i s, is 1 /s s 1,so(λ 2,,λ ) S (j, is 1/s ) 1 Remar 1 For ordiary pariios, P, io oegaive pars, {s i } = {1} ad is 1 /s = i, so he recurrece of Theorem 1 reduces o he recurrece P (j,i) () =P (j,i 1) he familiar recurrece for Gaussia polyomials ()+ j+i P (j,i) 1 (), The lecure hall pariios 5, L, are hose composiios, ecessarily pariios, saisfyig λ 2 1 λ 1 2 λ 1 or 0 (3) The L = S wih {s i } = {i} i (2) Sice i( 1)/ = i 1 we ge he followig from Theorem 1 3
4 Corollary 1 For 0, j 0, ad0 i, lel (j,i) () be he geeraig fucio for he lecure hall pariios λ L wih j + i L (j,i) = 1 if =0or j = i =0,else L (j 1,) () if i =0,else L (j,i 1) ()+ j+i L (j,i 1) 1 () oherwise For fixed >0, ay 0 ca be wrie uiuely i he form = j + i, where 0 i< So, we ge a ice couig formula for lecure hall pariios wih larges par a mos Theorem 2 For 0, j 0, ad0 i, he umber of lecure hall pariios i L wih firs par bouded by j + i is L (j,i) =(j +1) i (j +2) i Proof If = 0 he i =0,so(j +1) 0 0 (j +2) 0 =1 Ifi = j = 0, he (1) 0 (2) 0 =1 Le (, j, i) saisfy>0, (j, i) > (0, 0) ad assume he heorem is rue for (,i,j ) < (, i, j) If i = 0, he j>0ad by Corollary 1, L (j,0) (j) (j +1) =(j +1) (j +2) 0 Oherwise, by Corollary 1, L (j,i) (1) = L (j 1,) (1), which, by iducio, is (1) = L (j,i 1) (1) + L (j,i 1) 1 (1) = (j +1) i+1 (j +2) i 1 +(j +1) i (j +2) i 1 = (j +1) i (j +2) i I 5, i was show ha he geeraig fucio for he lecure hall pariios, L is: 1 L () = (; 2, (4) ) where (a; ) =(1 a)(1 a) (1 a 1 ) Le D be he se of pariios io disic pars ad le O be he se of pariios io odd pars The ses D ad O have geeraig fucios D() =( ; ) ad O() =(; 2 ) 1, respecively Sice lim L = D, he Lecure Hall Theorem (4) is a fiie versio of Euler s Theorem which says ha D() = O() The polyomial L (j) () =L (j,0) () ca be viewed as a -aalog of (j +1) ha ecapsulaes a furher fiiizaio of Euler s Theorem i he followig sese Corollary 2 The lecure hall polyomials L (j) () saisfy (i) L (j) (1) = (j +1), (ii) lim L (j) () =( ; ),ad (iii) lim j L (j) () =(; 2 ) 1 4
5 Proof The firs euaio follows from Theorem 2 The secod ad hird follow from he observaios ha lim L (j) = D ad lim j L (j) = L The ai-lecure hall composiios 9, A, are hose seueces saisfyig 1 λ 2 2 λ 1 1 λ 0 (5) I was show i 9 ha A has geeraig fucio A () =(, ) /( 2 ; ) The cosrai seuece for A, i he sese of (1), is 1, 2,,, he reverse of he cosrai seuece, 1,,1 for L We iroduce some oaio o describe he relaioship bewee heir geeraig fucios Le Sa 1,a 2,,a be he se of composiios λ =(,λ 2,,λ ) saisfyig a 1 λ 2 a 2 λ 1 a 1 λ a 0, (6) wih S (j,i) a 1,a 2,,a deoig hose wih ja 1 + i ad le S (j) a 1,a 2,,a = S (j,0) a 1,a 2,,a Theorem 3 The geeraig fucios for S (j) a 1,a 2,,a ad S (j) a,a 1,,a 1 saisfy: S (j) a 1,a 2,,a () = j(a 1+a 2 + +a ) S (j) a,a 1,,a 1 (1/) Proof The resul follows if we show ha λ S (j) a,a 1,,a 1 if ad oly if µ S (j) a 1,a 2,,a, where µ is defied by µ i = js i λ +1 i So, assume λ S (j) a,a 1,,a 1, ha is, ja ad a i λ i a i+1 λ +1 i for 1 i The for 1 i, λ +1 i a i a i+1 a i+1 a i+2 a 1 a a j = a i j, so µ i = ja i λ +1 i 0 Also, µ 1 = ja 1 λ saisfies µ 1 ja 1 To show µ S (j) a 1,a 2,,a, i remais o show a i+1 µ i a i µ i+1 : a i+1 µ i = a i+1 (ja i λ +1 i )=ja i a i+1 a i+1 λ +1 i ja i a i+1 a i λ i = a i µ i+1 The coverse is similar Remar 2 The proof of Theorem 3 also shows ha for 1 i, λ S (j) a,a 1,,a 1 if ad oly if µ S (j+1) a 1,a 2,,a adµ a i Corollary 3 Lecure hall pariios, L (j), wih firs par bouded by j ad ai-lecure hall composiios, A (j) wih firs par bouded by j have he followig relaioship: A (j) () = j(+1)/2 L (j) (1/) 5
6 Proof Observe ha A (j) Theorem 3 = S (j) 1, 2,,adL (j) This gives a couig formula for ai-lecure hall composiios = S (j), 1,,1 ad apply Corollary 4 The umber of ai-lecure hall composiios i A wih firs par bouded by j is A (j) (1) = (j +1) Proof By Theorem 3, A (j) (1) = L (j) (1) By defiiio, L (j) () = L (j,0) (), ad by Corollary 2, L (j,0) (1) = (j +1) (j +2) 0 As aoher example of he applicaio of Theorems 1 ad 3, we cosider Hicerso pariios H (for r = 2) ad Cayley composiios, C H is he se of composiios io oegaive pars saisfyig λ i 2λ i+1 ad C is he se of composiios io oegaive pars saisfyig λ i λ i+1 /2 So, H = S2 1, 2 2,,1 ad C = S1, 2, 4,,2 1 Le B() be he umber of biary pariios of, ie, he umber of pariios of io powers of 2 I is easy o chec ha B(0) = B(1) = 1, B(2) =B(2 2) + B(), ad B(2) =B(2 +1) Theorem 4 For 0 i<2 1, he umber of Hicerso pariios wih firs par a mos i is H (0,i) = B(2i); wihfirsparamos2 1 + i is H (1,i) = B(2 +2i); wihfirspara mos 2 is H (2,0) = B(2 +1 ) 1 Proof Use he recurrece of Theorem 1 wih he observaio ha sice {s i } = {2 i 1 } for Hicerso pariios, is i 1 /s i = i/2 The heorem follows by iducio usig he properies of B() Cayley s Theorem 8 says ha he umber of composiios i C wih posiive pars ad wih firs par 1 is eual o he umber of pariios of io pars from he se {1, 1, 2, 4,,2 2 } If we apply Theorem 3 ad Remar 2, we ge a geeralizaio ad reformulaio of Cayley s Theorem Theorem 5 For 0 i<2 1, he umber of Cayley composiios io posiive pars wih firs par 1 ad las par a leas 2 1 i is B(2i) The umber wih firs par a mos 2 ad las par a leas 2 i is B(2 +2i) Seig i =2 1 1 i Theorem 5 gives: Corollary 5 The umber of Cayley composiios io posiive pars wih firs par 1 is B(2 2); wihfirsparamos2isb(2 +1 2) These resuls ca be geeralized o r ary Hicerso pariios ad Cayley composiios For oher families of raio composiios, we ca expec Theorem 1 o be mos useful for seueces {s i } where is 1 /s has a ice form 6
7 As ges larger, solvig for H () ges harder This is i spie of he fac ha H has he ice geeraig fucio H () = =1 (1 2 1 ) 1 13 However, we will see i he () has a ice geeraig fucio whe j = 1, here is hope ha () will also ex secio ha if S (j) lim j S (j) I he ex secio we show how o ge a recurrece for he geeraig fucio of raio composiios whe he firs par uresriced 3 Eumeraio of raio seueces wih firs par ubouded We defie wo sligh variaios of he se S (j) a 1,a 2,,a below: P (j) a 1,a 2,,a ={λ S (j) a 1,a 2,,a λ 1}; R (j) a 1,a 2,,a ={λ S (j) a 1,a 2,,a <ja 1 } I P (j), all pars mus be posiive, whereas i R (j) pars ca be oegaive, bu he boud o he firs par becomes sric Theorem 6 For j 1, P (j) a 1,a 2,,a () = (a 1+a 2 + +a ) P (1) a +1,,a ()P (j 1) a 1,,a () Proof Le λ P (j) a 1,a 2,,a adle be he maximum idex such ha λ >a The ( a 1,λ 2 a 2,,λ a ) P (j 1) a 1,,a ad(λ +1,,λ ) P (1) a +1,,a Noe ha P (1) () ca be compued usig Theorem 1 as P (1) s,,s 1 () =S (1,0) s 1,,s () S (1,0) 1 s 2,,s () Thus, aig he limi as j i Theorem 6 gives a recurrece for couig he seueces λ i P a 1,a 2,,a wihou a resricio o he size of he firs par Theorem 7 For, P a 1,a 2,,a () = (a 1+a 2 + +a ) P (1) a +1,,a ()P a 1,a 2,,a () Remar 3 Theorem 6 ad is proof are valid wih all occurreces of P replaced by R We eed oly chage he saeme le be he maximum idex such ha λ >a o le be he maximum idex such ha λ a +1 Similarly, Theorem 7 holds wih P replaced by R 7
8 Theorem 7 ca be used o fid a explici form for he geeraig fucio i families where P (1) a 1,,a (orr (1) a 1,,a ) is ow Remar 4 For ordiary pariios io posiive pars, a i =1,soP a 1,a 2,,a () = (; ) 1 ad P (1) a +1,,a () =, ad he recurrece of Theorem 7 becomes 1 =, (; ) (; ) which cous pariios io posiive pars by summig over he umber,, of pars greaer ha 1 The pariios L, = P, 1,, +1 are called rucaed lecure hall pariios wih all pars posiive The composiios A, = R +1, +2,, are called rucaed ai-lecure hall composiios wih oegaive pars These were iroduced i 10 where heir geeraig fucios were show o be L, () = (+1 2 ) A, () = ( +1 ; ) ( 2 +1 ; ), (7) ( +1 ; ) ( 2( +1) ; ) (8) We ow show how Theorem 7 ca be used o give simple proofs of he (Trucaed) Lecure Hall ad (Trucaed) Ai-lecure Hall Theorems We begi by compuig P (1), 1,, +1() forl, ad R (1) +1, +2,,() fora, Lemma 1 For 1, he geeraig fucio for rucaed lecure hall pariios io posiive pars wih firs par less ha or eual o is P (1), 1,, +1() = (+1 2 ) Proof We show P (1), 1,, +1 is he se of pariios io disic pars from {1, 2,,}, which has he geeraig fucio claimed If λ P (1), 1,, +1, 1 / λ 2 /( 1) λ /( +1) > 0, so he pars of λ are disic ad bouded by Coversely, if λ i λ i+1 +1 for 1 i 1ad, he λ i+1 i, so λ i ( i) (λ i+1 +1)( i) λ i+1 ( i)+ i λ i+1 ( i)+λ i+1 λ i+1 ( i +1), ha is, λ i /( i +1) λ i+1 /( i), so λ P (1), 1,, +1 Lemma 2 For 1, he geeraig fucio for rucaed ai-lecure hall composiios io oegaive pars wih firs par less ha +1 is R (1) +1, +2,,() = 8
9 Proof If λ R (1) +1, +2,,, he for 1 i, λ i < + i ad λ i 1 λ i ( + i 1)/( + i), so λ i 1 λ i λ i (( + i 1)/( + i) 1) = λ i /( + i) > 1 Thus, λ i 1 λ i 0adλis a pariio io a mos pars of size a mos Coversely, ay such pariio is i R (1) +1, +2,, Corollary 6 ( ) L (j), =(j) = A (j), Proof By iducio I is obviously rue for j = 0 The for j>0, by Theorem 6 ad Lemma 2, ( )( ) L (j), (1) = (j 1) We use he classical ideiy ( ( )( ) = )( ) ad he biomial heorem ad ge he resul By Theorem 3, L (j), (1) = A(j), (1) Lemma 3 The geeraig fucio for rucaed lecure hall pariios saisfies for 1 ad L,0 () =1 L, () = (+1 2 ) ( ) L, (), Proof Sice L, = P, 1,, + 1, apply Theorem 7 wih Lemma 1 o ge ad simplify L, () = +( 1)+ +( +1) ( +1 2 ) This gives he Trucaed Lecure Hall Theorem: L, () Theorem 8 10 L, () = (+1 2 ) ( +1 ; ) ( 2 +1 ; ) Proof Le L, () = L, () (+1 2 ) 9
10 We show L, () = ( +1 ; ) ( 2 +1 (9) ; ) Subsiuig for L, () adl, () i he recurrece of Lemma 3 ad simplifyig gives L,1 = 1 ad for >1, as L, () = ( )+(+1 2 ) = L, (), (10) We mae use of (a rasformaio of) oe of he -Chu Vadermode ideiies 152 from 12: ( a; ) = a (+1 2 ) ( (c/a) +1 ; ) (c; ) (c +1 ; ) We do he subsiuio a = ad c = 2 ad ge ( +1 ; ) ( 2 +1 ; ) = ( )+(+1 2 ) ( +1 ; ) ( 2 +1 ; ), which shows ha L, () as give by (9) is he soluio o he recurrece (10) From his we also ge he Lecure Hall Theorem: Theorem 9 5 L () = ( ; ) ( +1 ; ) = 1 (; 2 ) Proof Seig = i Theorem 8 gives L,, which is he se of pariios i L wih all pars posiive So, L, () = (+1 2 ) L () The approach for rucaed ai-lecure hall composiios is similar Lemma 4 For, wih A (0), () =1 A, () = ( )+(+1 2 ) A +, () Proof Sice A, = R +1, +2,,, apply Theorem 7, usig Remar 3, he Lemma 2 ad simplify Now we ge a easy proof of he Trucaed Ai-lecure Hall Theorem 10
11 Theorem A, () = ( +1 ; ) ( 2( +1) ; ) Proof Le The usig Lemma 4, we ge ha as A, () = A, () = A, () ( )+(+1 2 ) + = A +, (), (11) We mae use of aoher rasformaio of he -Chu Vadermode ideiy 152 from 12: ( c/a; ) = (c/a) ( 2) ( a; ) (c; ) (c; ) Se c = 2( +1) ad a = +1 ad ge ( +1 ; ) ( 2( +1) ; ) = ( )+(+1 2 ) ( +1 ; ) ( 2( +1) ; ), showig A, () = ( +1 ;) saisfies he recurrece ( 2( +1) ;) Seig = i Theorem 10 gives he Ai-Lecure Hall Theorem Theorem 11 9 A () = ( ; ) ( 2 ; ) 4 Cocludig Remars The recurreces of Theorems 1 ad 7 provide simple compuaioal ools o ivesigae ay family of raio composiios More imporaly, hey supply he foudaio for a iducive proof of ay cojecured eumeraio resul Our experimes sugges ha couig formulas ad geeraig fucios will be possible for may oher families of raio composiios Oe paricular uesio of ieres is o characerize he subfamily of pariios io odd pars i {1, 3,,2 1} ha is coued by he polyomial L (j) () 11
12 Refereces 1 George E Adrews The heory of pariios Addiso-Wesley Publishig Co, Readig, Mass- Lodo-Amserdam, 1976 Ecyclopedia of Mahemaics ad is Applicaios, Vol 2 2 George E Adrews The Rogers-Ramauja reciprocal ad Mic s pariio fucio Pacific J Mah, 95(2): , George E Adrews MacMaho s pariio aalysis I The lecure hall pariio heorem I Mahemaical essays i hoor of Gia-Carlo Roa (Cambridge, MA, 1996), volume 161 of Progr Mah, pages 1 22 Birhäuser Boso, Boso, MA, George E Adrews, Peer Paule, Axel Riese, ad Voler Srehl MacMaho s pariio aalysis V Bijecios, recursios, ad magic suares I Algebraic combiaorics ad applicaios (Gößweisei, 1999), pages 1 39 Spriger, Berli, Mireille Bousue-Mélou ad Kimmo Erisso Lecure hall pariios Ramauja J, 1(1): , Mireille Bousue-Mélou ad Kimmo Erisso Lecure hall pariios II Ramauja J, 1(2): , Mireille Bousue-Mélou ad Kimmo Erisso A refieme of he lecure hall heorem J Combi Theory Ser A, 86(1):63 84, Arhur Cayley O a problem i he pariio of umbers Philosophical Magazie, 13: , 1857 repried i: The Colleced Mahemaical Papers of A Cayley, Vol III, Cambridge Uiversiy Press, Cambridge, 1890, ) 9 Sylvie Coreel ad Carla D Savage Ai-lecure hall composiios Discree Mah, 263(1-3): , Sylvie Coreel ad Carla D Savage Lecure hall heorems, -series ad rucaed objecs J Combi Theory Ser A, 108(2): , Sylvie Coreel ad Carla D Savage Pariios ad composiios defied by ieualiies Ramauja J, 8(3): , George Gasper ad Miza Rahma Basic hypergeomeric series, volume 35 of Ecyclopedia of Mahemaics ad is Applicaios Cambridge Uiversiy Press, Cambridge, 1990 Wih a foreword by Richard Asey 13 Dea R Hicerso A pariio ideiy of he Euler ype Amer Mah Mohly, 81: , Hery Mic A problem i pariios: Eumeraio of elemes of a give degree i he free commuaive eropic cyclic groupoid Proc Ediburgh Mah Soc (2), 11: , 1958/ Ae Ja Yee O he combiaorics of lecure hall pariios Ramauja J, 5(3): , Ae Ja Yee O he refied lecure hall heorem Discree Mah, 248(1-3): ,
Extremal graph theory II: K t and K t,t
 Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
CLOSED FORM EVALUATION OF RESTRICTED SUMS CONTAINING SQUARES OF FIBONOMIAL COEFFICIENTS
 PB Sci Bull, Series A, Vol 78, Iss 4, 2016 ISSN 1223-7027 CLOSED FORM EVALATION OF RESTRICTED SMS CONTAINING SQARES OF FIBONOMIAL COEFFICIENTS Emrah Kılıc 1, Helmu Prodiger 2 We give a sysemaic approach
PB Sci Bull, Series A, Vol 78, Iss 4, 2016 ISSN 1223-7027 CLOSED FORM EVALATION OF RESTRICTED SMS CONTAINING SQARES OF FIBONOMIAL COEFFICIENTS Emrah Kılıc 1, Helmu Prodiger 2 We give a sysemaic approach
N! AND THE GAMMA FUNCTION
 N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
An interesting result about subset sums. Nitu Kitchloo. Lior Pachter. November 27, Abstract
 A ieresig resul abou subse sums Niu Kichloo Lior Pacher November 27, 1993 Absrac We cosider he problem of deermiig he umber of subses B f1; 2; : : :; g such ha P b2b b k mod, where k is a residue class
A ieresig resul abou subse sums Niu Kichloo Lior Pacher November 27, 1993 Absrac We cosider he problem of deermiig he umber of subses B f1; 2; : : :; g such ha P b2b b k mod, where k is a residue class
Extended Laguerre Polynomials
 I J Coemp Mah Scieces, Vol 7, 1, o, 189 194 Exeded Laguerre Polyomials Ada Kha Naioal College of Busiess Admiisraio ad Ecoomics Gulberg-III, Lahore, Pakisa adakhaariq@gmailcom G M Habibullah Naioal College
I J Coemp Mah Scieces, Vol 7, 1, o, 189 194 Exeded Laguerre Polyomials Ada Kha Naioal College of Busiess Admiisraio ad Ecoomics Gulberg-III, Lahore, Pakisa adakhaariq@gmailcom G M Habibullah Naioal College
FIXED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE
 Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
L-functions and Class Numbers
 L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
Research Article On a Class of q-bernoulli, q-euler, and q-genocchi Polynomials
 Absrac ad Applied Aalysis Volume 04, Aricle ID 696454, 0 pages hp://dx.doi.org/0.55/04/696454 Research Aricle O a Class of -Beroulli, -Euler, ad -Geocchi Polyomials N. I. Mahmudov ad M. Momezadeh Easer
Absrac ad Applied Aalysis Volume 04, Aricle ID 696454, 0 pages hp://dx.doi.org/0.55/04/696454 Research Aricle O a Class of -Beroulli, -Euler, ad -Geocchi Polyomials N. I. Mahmudov ad M. Momezadeh Easer
Using Linnik's Identity to Approximate the Prime Counting Function with the Logarithmic Integral
 Usig Lii's Ideiy o Approimae he Prime Couig Fucio wih he Logarihmic Iegral Naha McKezie /26/2 aha@icecreambreafas.com Summary:This paper will show ha summig Lii's ideiy from 2 o ad arragig erms i a cerai
Usig Lii's Ideiy o Approimae he Prime Couig Fucio wih he Logarihmic Iegral Naha McKezie /26/2 aha@icecreambreafas.com Summary:This paper will show ha summig Lii's ideiy from 2 o ad arragig erms i a cerai
Fermat Numbers in Multinomial Coefficients
 1 3 47 6 3 11 Joural of Ieger Sequeces, Vol. 17 (014, Aricle 14.3. Ferma Numbers i Muliomial Coefficies Shae Cher Deparme of Mahemaics Zhejiag Uiversiy Hagzhou, 31007 Chia chexiaohag9@gmail.com Absrac
1 3 47 6 3 11 Joural of Ieger Sequeces, Vol. 17 (014, Aricle 14.3. Ferma Numbers i Muliomial Coefficies Shae Cher Deparme of Mahemaics Zhejiag Uiversiy Hagzhou, 31007 Chia chexiaohag9@gmail.com Absrac
A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY
 U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
Big O Notation for Time Complexity of Algorithms
 BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
Lecture 9: Polynomial Approximations
 CS 70: Complexiy Theory /6/009 Lecure 9: Polyomial Approximaios Isrucor: Dieer va Melkebeek Scribe: Phil Rydzewski & Piramaayagam Arumuga Naiar Las ime, we proved ha o cosa deph circui ca evaluae he pariy
CS 70: Complexiy Theory /6/009 Lecure 9: Polyomial Approximaios Isrucor: Dieer va Melkebeek Scribe: Phil Rydzewski & Piramaayagam Arumuga Naiar Las ime, we proved ha o cosa deph circui ca evaluae he pariy
A NEW q-analogue FOR BERNOULLI NUMBERS
 A NEW -ANALOGUE FOR BERNOULLI NUMBERS O-YEAT CHAN AND DANTE MANNA Absrac Ispired by, we defie a ew seuece of -aalogues for he Beroulli umbers uder he framewor of Srod operaors We show ha hey o oly saisfy
A NEW -ANALOGUE FOR BERNOULLI NUMBERS O-YEAT CHAN AND DANTE MANNA Absrac Ispired by, we defie a ew seuece of -aalogues for he Beroulli umbers uder he framewor of Srod operaors We show ha hey o oly saisfy
Calculus Limits. Limit of a function.. 1. One-Sided Limits...1. Infinite limits 2. Vertical Asymptotes...3. Calculating Limits Using the Limit Laws.
 Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
A Note on Random k-sat for Moderately Growing k
 A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
STK4080/9080 Survival and event history analysis
 STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
Comparison between Fourier and Corrected Fourier Series Methods
 Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Moment Generating Function
 1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
Lecture 15 First Properties of the Brownian Motion
 Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
Supplement for SADAGRAD: Strongly Adaptive Stochastic Gradient Methods"
 Suppleme for SADAGRAD: Srogly Adapive Sochasic Gradie Mehods" Zaiyi Che * 1 Yi Xu * Ehog Che 1 iabao Yag 1. Proof of Proposiio 1 Proposiio 1. Le ɛ > 0 be fixed, H 0 γi, γ g, EF (w 1 ) F (w ) ɛ 0 ad ieraio
Suppleme for SADAGRAD: Srogly Adapive Sochasic Gradie Mehods" Zaiyi Che * 1 Yi Xu * Ehog Che 1 iabao Yag 1. Proof of Proposiio 1 Proposiio 1. Le ɛ > 0 be fixed, H 0 γi, γ g, EF (w 1 ) F (w ) ɛ 0 ad ieraio
LIMITS OF FUNCTIONS (I)
 LIMITS OF FUNCTIO (I ELEMENTARY FUNCTIO: (Elemeary fucios are NOT piecewise fucios Cosa Fucios: f(x k, where k R Polyomials: f(x a + a x + a x + a x + + a x, where a, a,..., a R Raioal Fucios: f(x P (x,
LIMITS OF FUNCTIO (I ELEMENTARY FUNCTIO: (Elemeary fucios are NOT piecewise fucios Cosa Fucios: f(x k, where k R Polyomials: f(x a + a x + a x + a x + + a x, where a, a,..., a R Raioal Fucios: f(x P (x,
Online Supplement to Reactive Tabu Search in a Team-Learning Problem
 Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
On The Eneström-Kakeya Theorem
 Applied Mahemaics,, 3, 555-56 doi:436/am673 Published Olie December (hp://wwwscirporg/oural/am) O The Eesröm-Kakeya Theorem Absrac Gulsha Sigh, Wali Mohammad Shah Bharahiar Uiversiy, Coimbaore, Idia Deparme
Applied Mahemaics,, 3, 555-56 doi:436/am673 Published Olie December (hp://wwwscirporg/oural/am) O The Eesröm-Kakeya Theorem Absrac Gulsha Sigh, Wali Mohammad Shah Bharahiar Uiversiy, Coimbaore, Idia Deparme
Approximately Quasi Inner Generalized Dynamics on Modules. { } t t R
 Joural of Scieces, Islamic epublic of Ira 23(3): 245-25 (22) Uiversiy of Tehra, ISSN 6-4 hp://jscieces.u.ac.ir Approximaely Quasi Ier Geeralized Dyamics o Modules M. Mosadeq, M. Hassai, ad A. Nikam Deparme
Joural of Scieces, Islamic epublic of Ira 23(3): 245-25 (22) Uiversiy of Tehra, ISSN 6-4 hp://jscieces.u.ac.ir Approximaely Quasi Ier Geeralized Dyamics o Modules M. Mosadeq, M. Hassai, ad A. Nikam Deparme
S n. = n. Sum of first n terms of an A. P is
 PROGREION I his secio we discuss hree impora series amely ) Arihmeic Progressio (A.P), ) Geomeric Progressio (G.P), ad 3) Harmoic Progressio (H.P) Which are very widely used i biological scieces ad humaiies.
PROGREION I his secio we discuss hree impora series amely ) Arihmeic Progressio (A.P), ) Geomeric Progressio (G.P), ad 3) Harmoic Progressio (H.P) Which are very widely used i biological scieces ad humaiies.
The Connection between the Basel Problem and a Special Integral
 Applied Mahemaics 4 5 57-584 Published Olie Sepember 4 i SciRes hp://wwwscirporg/joural/am hp://ddoiorg/436/am45646 The Coecio bewee he Basel Problem ad a Special Iegral Haifeg Xu Jiuru Zhou School of
Applied Mahemaics 4 5 57-584 Published Olie Sepember 4 i SciRes hp://wwwscirporg/joural/am hp://ddoiorg/436/am45646 The Coecio bewee he Basel Problem ad a Special Iegral Haifeg Xu Jiuru Zhou School of
Some Properties of Semi-E-Convex Function and Semi-E-Convex Programming*
 The Eighh Ieraioal Symposium o Operaios esearch ad Is Applicaios (ISOA 9) Zhagjiajie Chia Sepember 2 22 29 Copyrigh 29 OSC & APOC pp 33 39 Some Properies of Semi-E-Covex Fucio ad Semi-E-Covex Programmig*
The Eighh Ieraioal Symposium o Operaios esearch ad Is Applicaios (ISOA 9) Zhagjiajie Chia Sepember 2 22 29 Copyrigh 29 OSC & APOC pp 33 39 Some Properies of Semi-E-Covex Fucio ad Semi-E-Covex Programmig*
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS
 BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
The analysis of the method on the one variable function s limit Ke Wu
 Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
BIBECHANA A Multidisciplinary Journal of Science, Technology and Mathematics
 Biod Prasad Dhaal / BIBCHANA 9 (3 5-58 : BMHSS,.5 (Olie Publicaio: Nov., BIBCHANA A Mulidisciliary Joural of Sciece, Techology ad Mahemaics ISSN 9-76 (olie Joural homeage: h://ejol.ifo/idex.h/bibchana
Biod Prasad Dhaal / BIBCHANA 9 (3 5-58 : BMHSS,.5 (Olie Publicaio: Nov., BIBCHANA A Mulidisciliary Joural of Sciece, Techology ad Mahemaics ISSN 9-76 (olie Joural homeage: h://ejol.ifo/idex.h/bibchana
ON THE n-th ELEMENT OF A SET OF POSITIVE INTEGERS
 Aales Uiv. Sci. Budapes., Sec. Comp. 44 05) 53 64 ON THE -TH ELEMENT OF A SET OF POSITIVE INTEGERS Jea-Marie De Koick ad Vice Ouelle Québec, Caada) Commuicaed by Imre Káai Received July 8, 05; acceped
Aales Uiv. Sci. Budapes., Sec. Comp. 44 05) 53 64 ON THE -TH ELEMENT OF A SET OF POSITIVE INTEGERS Jea-Marie De Koick ad Vice Ouelle Québec, Caada) Commuicaed by Imre Káai Received July 8, 05; acceped
Math 6710, Fall 2016 Final Exam Solutions
 Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
Ideal Amplifier/Attenuator. Memoryless. where k is some real constant. Integrator. System with memory
 Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
AN EXTENSION OF LUCAS THEOREM. Hong Hu and Zhi-Wei Sun. (Communicated by David E. Rohrlich)
 Proc. Amer. Mah. Soc. 19(001, o. 1, 3471 3478. AN EXTENSION OF LUCAS THEOREM Hog Hu ad Zhi-Wei Su (Commuicaed by David E. Rohrlich Absrac. Le p be a prime. A famous heorem of Lucas saes ha p+s p+ ( s (mod
Proc. Amer. Mah. Soc. 19(001, o. 1, 3471 3478. AN EXTENSION OF LUCAS THEOREM Hog Hu ad Zhi-Wei Su (Commuicaed by David E. Rohrlich Absrac. Le p be a prime. A famous heorem of Lucas saes ha p+s p+ ( s (mod
FORBIDDING HAMILTON CYCLES IN UNIFORM HYPERGRAPHS
 FORBIDDING HAMILTON CYCLES IN UNIFORM HYPERGRAPHS JIE HAN AND YI ZHAO Absrac For d l
FORBIDDING HAMILTON CYCLES IN UNIFORM HYPERGRAPHS JIE HAN AND YI ZHAO Absrac For d l
K3 p K2 p Kp 0 p 2 p 3 p
 Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)
![th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x) th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)](/thumbs/80/81319353.jpg) 1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
Dynamic h-index: the Hirsch index in function of time
 Dyamic h-idex: he Hirsch idex i fucio of ime by L. Egghe Uiversiei Hassel (UHassel), Campus Diepebeek, Agoralaa, B-3590 Diepebeek, Belgium ad Uiversiei Awerpe (UA), Campus Drie Eike, Uiversieisplei, B-260
Dyamic h-idex: he Hirsch idex i fucio of ime by L. Egghe Uiversiei Hassel (UHassel), Campus Diepebeek, Agoralaa, B-3590 Diepebeek, Belgium ad Uiversiei Awerpe (UA), Campus Drie Eike, Uiversieisplei, B-260
Zhi-Wei Sun and Hao Pan (Nanjing)
 Aca Arih. 5(006, o., 39. IDENTITIES CONCERNING BERNOULLI AND EULER POLYNOMIALS Zhi-Wei Su ad Hao Pa (Najig Absrac. We esabish wo geera ideiies for Beroui ad Euer poyomias, which are of a ew ype ad have
Aca Arih. 5(006, o., 39. IDENTITIES CONCERNING BERNOULLI AND EULER POLYNOMIALS Zhi-Wei Su ad Hao Pa (Najig Absrac. We esabish wo geera ideiies for Beroui ad Euer poyomias, which are of a ew ype ad have
A Generalization of Hermite Polynomials
 Ieraioal Mahemaical Forum, Vol. 8, 213, o. 15, 71-76 HIKARI Ld, www.m-hikari.com A Geeralizaio of Hermie Polyomials G. M. Habibullah Naioal College of Busiess Admiisraio & Ecoomics Gulberg-III, Lahore,
Ieraioal Mahemaical Forum, Vol. 8, 213, o. 15, 71-76 HIKARI Ld, www.m-hikari.com A Geeralizaio of Hermie Polyomials G. M. Habibullah Naioal College of Busiess Admiisraio & Ecoomics Gulberg-III, Lahore,
Research Article A Generalized Nonlinear Sum-Difference Inequality of Product Form
 Joural of Applied Mahemaics Volume 03, Aricle ID 47585, 7 pages hp://dx.doi.org/0.55/03/47585 Research Aricle A Geeralized Noliear Sum-Differece Iequaliy of Produc Form YogZhou Qi ad Wu-Sheg Wag School
Joural of Applied Mahemaics Volume 03, Aricle ID 47585, 7 pages hp://dx.doi.org/0.55/03/47585 Research Aricle A Geeralized Noliear Sum-Differece Iequaliy of Produc Form YogZhou Qi ad Wu-Sheg Wag School
Review Exercises for Chapter 9
 0_090R.qd //0 : PM Page 88 88 CHAPTER 9 Ifiie Series I Eercises ad, wrie a epressio for he h erm of he sequece..,., 5, 0,,,, 0,... 7,... I Eercises, mach he sequece wih is graph. [The graphs are labeled
0_090R.qd //0 : PM Page 88 88 CHAPTER 9 Ifiie Series I Eercises ad, wrie a epressio for he h erm of he sequece..,., 5, 0,,,, 0,... 7,... I Eercises, mach he sequece wih is graph. [The graphs are labeled
1. Solve by the method of undetermined coefficients and by the method of variation of parameters. (4)
 7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
Some identities related to reciprocal functions
 Discree Mahemaics 265 2003 323 335 www.elsevier.com/locae/disc Some ideiies relaed o reciprocal fucios Xiqiag Zhao a;b;, Tiamig Wag c a Deparme of Aerodyamics, College of Aerospace Egieerig, Najig Uiversiy
Discree Mahemaics 265 2003 323 335 www.elsevier.com/locae/disc Some ideiies relaed o reciprocal fucios Xiqiag Zhao a;b;, Tiamig Wag c a Deparme of Aerodyamics, College of Aerospace Egieerig, Najig Uiversiy
λiv Av = 0 or ( λi Av ) = 0. In order for a vector v to be an eigenvector, it must be in the kernel of λi
 Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
The Central Limit Theorem
 The Ceral Limi Theorem The ceral i heorem is oe of he mos impora heorems i probabiliy heory. While here a variey of forms of he ceral i heorem, he mos geeral form saes ha give a sufficiely large umber,
The Ceral Limi Theorem The ceral i heorem is oe of he mos impora heorems i probabiliy heory. While here a variey of forms of he ceral i heorem, he mos geeral form saes ha give a sufficiely large umber,
Review Answers for E&CE 700T02
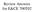 Review Aswers for E&CE 700T0 . Deermie he curre soluio, all possible direcios, ad sepsizes wheher improvig or o for he simple able below: 4 b ma c 0 0 0-4 6 0 - B N B N ^0 0 0 curre sol =, = Ch for - -
Review Aswers for E&CE 700T0 . Deermie he curre soluio, all possible direcios, ad sepsizes wheher improvig or o for he simple able below: 4 b ma c 0 0 0-4 6 0 - B N B N ^0 0 0 curre sol =, = Ch for - -
TAKA KUSANO. laculty of Science Hrosh tlnlersty 1982) (n-l) + + Pn(t)x 0, (n-l) + + Pn(t)Y f(t,y), XR R are continuous functions.
 Iera. J. Mah. & Mah. Si. Vol. 6 No. 3 (1983) 559-566 559 ASYMPTOTIC RELATIOHIPS BETWEEN TWO HIGHER ORDER ORDINARY DIFFERENTIAL EQUATIONS TAKA KUSANO laculy of Sciece Hrosh llersy 1982) ABSTRACT. Some asympoic
Iera. J. Mah. & Mah. Si. Vol. 6 No. 3 (1983) 559-566 559 ASYMPTOTIC RELATIOHIPS BETWEEN TWO HIGHER ORDER ORDINARY DIFFERENTIAL EQUATIONS TAKA KUSANO laculy of Sciece Hrosh llersy 1982) ABSTRACT. Some asympoic
SUMMATION OF INFINITE SERIES REVISITED
 SUMMATION OF INFINITE SERIES REVISITED I several aricles over he las decade o his web page we have show how o sum cerai iiie series icludig he geomeric series. We wa here o eed his discussio o he geeral
SUMMATION OF INFINITE SERIES REVISITED I several aricles over he las decade o his web page we have show how o sum cerai iiie series icludig he geomeric series. We wa here o eed his discussio o he geeral
1 Notes on Little s Law (l = λw)
 Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
ECE-314 Fall 2012 Review Questions
 ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
Hadamard matrices from the Multiplication Table of the Finite Fields
 adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
arxiv: v1 [math.co] 30 May 2017
![arxiv: v1 [math.co] 30 May 2017 arxiv: v1 [math.co] 30 May 2017](/thumbs/95/123919244.jpg) Tue Polyomials of Symmeric Hyperplae Arragemes Hery Radriamaro May 31, 017 arxiv:170510753v1 [mahco] 30 May 017 Absrac Origially i 1954 he Tue polyomial was a bivariae polyomial associaed o a graph i order
Tue Polyomials of Symmeric Hyperplae Arragemes Hery Radriamaro May 31, 017 arxiv:170510753v1 [mahco] 30 May 017 Absrac Origially i 1954 he Tue polyomial was a bivariae polyomial associaed o a graph i order
DETERMINATION OF PARTICULAR SOLUTIONS OF NONHOMOGENEOUS LINEAR DIFFERENTIAL EQUATIONS BY DISCRETE DECONVOLUTION
 U.P.B. ci. Bull. eries A Vol. 69 No. 7 IN 3-77 DETERMINATION OF PARTIULAR OLUTION OF NONHOMOGENEOU LINEAR DIFFERENTIAL EQUATION BY DIRETE DEONVOLUTION M. I. ÎRNU e preziă o ouă meoă e eermiare a soluţiilor
U.P.B. ci. Bull. eries A Vol. 69 No. 7 IN 3-77 DETERMINATION OF PARTIULAR OLUTION OF NONHOMOGENEOU LINEAR DIFFERENTIAL EQUATION BY DIRETE DEONVOLUTION M. I. ÎRNU e preziă o ouă meoă e eermiare a soluţiilor
Solutions to Problems 3, Level 4
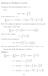 Soluios o Problems 3, Level 4 23 Improve he resul of Quesio 3 whe l. i Use log log o prove ha for real >, log ( {}log + 2 d log+ P ( + P ( d 2. Here P ( is defied i Quesio, ad parial iegraio has bee used.
Soluios o Problems 3, Level 4 23 Improve he resul of Quesio 3 whe l. i Use log log o prove ha for real >, log ( {}log + 2 d log+ P ( + P ( d 2. Here P ( is defied i Quesio, ad parial iegraio has bee used.
Notes 03 largely plagiarized by %khc
 1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
The Eigen Function of Linear Systems
 1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
ODEs II, Supplement to Lectures 6 & 7: The Jordan Normal Form: Solving Autonomous, Homogeneous Linear Systems. April 2, 2003
 ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
On The Generalized Type and Generalized Lower Type of Entire Function in Several Complex Variables With Index Pair (p, q)
 O he eeralized ye ad eeralized Lower ye of Eire Fucio i Several Comlex Variables Wih Idex Pair, Aima Abdali Jaffar*, Mushaq Shakir A Hussei Dearme of Mahemaics, College of sciece, Al-Musasiriyah Uiversiy,
O he eeralized ye ad eeralized Lower ye of Eire Fucio i Several Comlex Variables Wih Idex Pair, Aima Abdali Jaffar*, Mushaq Shakir A Hussei Dearme of Mahemaics, College of sciece, Al-Musasiriyah Uiversiy,
Available online at J. Math. Comput. Sci. 4 (2014), No. 4, ISSN:
 Available olie a hp://sci.org J. Mah. Compu. Sci. 4 (2014), No. 4, 716-727 ISSN: 1927-5307 ON ITERATIVE TECHNIQUES FOR NUMERICAL SOLUTIONS OF LINEAR AND NONLINEAR DIFFERENTIAL EQUATIONS S.O. EDEKI *, A.A.
Available olie a hp://sci.org J. Mah. Compu. Sci. 4 (2014), No. 4, 716-727 ISSN: 1927-5307 ON ITERATIVE TECHNIQUES FOR NUMERICAL SOLUTIONS OF LINEAR AND NONLINEAR DIFFERENTIAL EQUATIONS S.O. EDEKI *, A.A.
Some Newton s Type Inequalities for Geometrically Relative Convex Functions ABSTRACT. 1. Introduction
 Malaysia Joural of Mahemaical Scieces 9(): 49-5 (5) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/joural Some Newo s Type Ieualiies for Geomerically Relaive Covex Fucios
Malaysia Joural of Mahemaical Scieces 9(): 49-5 (5) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/joural Some Newo s Type Ieualiies for Geomerically Relaive Covex Fucios
A note on deviation inequalities on {0, 1} n. by Julio Bernués*
 A oe o deviaio iequaliies o {0, 1}. by Julio Berués* Deparameo de Maemáicas. Faculad de Ciecias Uiversidad de Zaragoza 50009-Zaragoza (Spai) I. Iroducio. Le f: (Ω, Σ, ) IR be a radom variable. Roughly
A oe o deviaio iequaliies o {0, 1}. by Julio Berués* Deparameo de Maemáicas. Faculad de Ciecias Uiversidad de Zaragoza 50009-Zaragoza (Spai) I. Iroducio. Le f: (Ω, Σ, ) IR be a radom variable. Roughly
10.3 Autocorrelation Function of Ergodic RP 10.4 Power Spectral Density of Ergodic RP 10.5 Normal RP (Gaussian RP)
 ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
Fresnel Dragging Explained
 Fresel Draggig Explaied 07/05/008 Decla Traill Decla@espace.e.au The Fresel Draggig Coefficie required o explai he resul of he Fizeau experime ca be easily explaied by usig he priciples of Eergy Field
Fresel Draggig Explaied 07/05/008 Decla Traill Decla@espace.e.au The Fresel Draggig Coefficie required o explai he resul of he Fizeau experime ca be easily explaied by usig he priciples of Eergy Field
Descents of Permutations in a Ferrers Board
 Desces of Permuaios i a Ferrers Board Chuwei Sog School of Mahemaical Scieces, LMAM, Pekig Uiversiy, Beijig 0087, P. R. Chia Caherie Ya Deparme of Mahemaics, Texas A&M Uiversiy, College Saio, TX 77843-3368
Desces of Permuaios i a Ferrers Board Chuwei Sog School of Mahemaical Scieces, LMAM, Pekig Uiversiy, Beijig 0087, P. R. Chia Caherie Ya Deparme of Mahemaics, Texas A&M Uiversiy, College Saio, TX 77843-3368
A Note on Prediction with Misspecified Models
 ITB J. Sci., Vol. 44 A, No. 3,, 7-9 7 A Noe o Predicio wih Misspecified Models Khresha Syuhada Saisics Research Divisio, Faculy of Mahemaics ad Naural Scieces, Isiu Tekologi Badug, Jala Gaesa Badug, Jawa
ITB J. Sci., Vol. 44 A, No. 3,, 7-9 7 A Noe o Predicio wih Misspecified Models Khresha Syuhada Saisics Research Divisio, Faculy of Mahemaics ad Naural Scieces, Isiu Tekologi Badug, Jala Gaesa Badug, Jawa
Common Fixed Point Theorem in Intuitionistic Fuzzy Metric Space via Compatible Mappings of Type (K)
 Ieraioal Joural of ahemaics Treds ad Techology (IJTT) Volume 35 umber 4- July 016 Commo Fixed Poi Theorem i Iuiioisic Fuzzy eric Sace via Comaible aigs of Tye (K) Dr. Ramaa Reddy Assisa Professor De. of
Ieraioal Joural of ahemaics Treds ad Techology (IJTT) Volume 35 umber 4- July 016 Commo Fixed Poi Theorem i Iuiioisic Fuzzy eric Sace via Comaible aigs of Tye (K) Dr. Ramaa Reddy Assisa Professor De. of
Outline. simplest HMM (1) simple HMMs? simplest HMM (2) Parameter estimation for discrete hidden Markov models
 Oulie Parameer esimaio for discree idde Markov models Juko Murakami () ad Tomas Taylor (2). Vicoria Uiversiy of Welligo 2. Arizoa Sae Uiversiy Descripio of simple idde Markov models Maximum likeliood esimae
Oulie Parameer esimaio for discree idde Markov models Juko Murakami () ad Tomas Taylor (2). Vicoria Uiversiy of Welligo 2. Arizoa Sae Uiversiy Descripio of simple idde Markov models Maximum likeliood esimae
David Randall. ( )e ikx. k = u x,t. u( x,t)e ikx dx L. x L /2. Recall that the proof of (1) and (2) involves use of the orthogonality condition.
 ! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
arxiv:math/ v1 [math.fa] 1 Feb 1994
![arxiv:math/ v1 [math.fa] 1 Feb 1994 arxiv:math/ v1 [math.fa] 1 Feb 1994](/thumbs/93/114291597.jpg) arxiv:mah/944v [mah.fa] Feb 994 ON THE EMBEDDING OF -CONCAVE ORLICZ SPACES INTO L Care Schü Abrac. I [K S ] i wa how ha Ave ( i a π(i) ) π i equivale o a Orlicz orm whoe Orlicz fucio i -cocave. Here we
arxiv:mah/944v [mah.fa] Feb 994 ON THE EMBEDDING OF -CONCAVE ORLICZ SPACES INTO L Care Schü Abrac. I [K S ] i wa how ha Ave ( i a π(i) ) π i equivale o a Orlicz orm whoe Orlicz fucio i -cocave. Here we
Discrete Mathematics. Independence polynomials of circulants with an application to music
 Discree Mahemaics 309 (2009 2292 2304 Coes liss available a ScieceDirec Discree Mahemaics joural homepage: wwwelseviercom/locae/disc Idepedece polyomials of circulas wih a applicaio o music Jaso Brow,
Discree Mahemaics 309 (2009 2292 2304 Coes liss available a ScieceDirec Discree Mahemaics joural homepage: wwwelseviercom/locae/disc Idepedece polyomials of circulas wih a applicaio o music Jaso Brow,
Simple proofs of Bressoud s and Schur s polynomial versions of the. Rogers-Ramanujan identities. Johann Cigler
 Simple proofs of Bressoud s ad Schur s polyomial versios of the Rogers-Ramaua idetities Joha Cigler Faultät für Mathemati Uiversität Wie A-090 Wie, Nordbergstraße 5 Joha Cigler@uivieacat Abstract We give
Simple proofs of Bressoud s ad Schur s polyomial versios of the Rogers-Ramaua idetities Joha Cigler Faultät für Mathemati Uiversität Wie A-090 Wie, Nordbergstraße 5 Joha Cigler@uivieacat Abstract We give
Conditional Probability and Conditional Expectation
 Hadou #8 for B902308 prig 2002 lecure dae: 3/06/2002 Codiioal Probabiliy ad Codiioal Epecaio uppose X ad Y are wo radom variables The codiioal probabiliy of Y y give X is } { }, { } { X P X y Y P X y Y
Hadou #8 for B902308 prig 2002 lecure dae: 3/06/2002 Codiioal Probabiliy ad Codiioal Epecaio uppose X ad Y are wo radom variables The codiioal probabiliy of Y y give X is } { }, { } { X P X y Y P X y Y
6.01: Introduction to EECS I Lecture 3 February 15, 2011
 6.01: Iroducio o EECS I Lecure 3 February 15, 2011 6.01: Iroducio o EECS I Sigals ad Sysems Module 1 Summary: Sofware Egieerig Focused o absracio ad modulariy i sofware egieerig. Topics: procedures, daa
6.01: Iroducio o EECS I Lecure 3 February 15, 2011 6.01: Iroducio o EECS I Sigals ad Sysems Module 1 Summary: Sofware Egieerig Focused o absracio ad modulariy i sofware egieerig. Topics: procedures, daa
OLS bias for econometric models with errors-in-variables. The Lucas-critique Supplementary note to Lecture 17
 OLS bias for ecoomeric models wih errors-i-variables. The Lucas-criique Supplemeary oe o Lecure 7 RNy May 6, 03 Properies of OLS i RE models I Lecure 7 we discussed he followig example of a raioal expecaios
OLS bias for ecoomeric models wih errors-i-variables. The Lucas-criique Supplemeary oe o Lecure 7 RNy May 6, 03 Properies of OLS i RE models I Lecure 7 we discussed he followig example of a raioal expecaios
Fuzzy Dynamic Equations on Time Scales under Generalized Delta Derivative via Contractive-like Mapping Principles
 Idia Joural of Sciece ad echology Vol 9(5) DOI: 7485/ijs/6/v9i5/8533 July 6 ISSN (Pri) : 974-6846 ISSN (Olie) : 974-5645 Fuzzy Dyamic Euaios o ime Scales uder Geeralized Dela Derivaive via Coracive-lie
Idia Joural of Sciece ad echology Vol 9(5) DOI: 7485/ijs/6/v9i5/8533 July 6 ISSN (Pri) : 974-6846 ISSN (Olie) : 974-5645 Fuzzy Dyamic Euaios o ime Scales uder Geeralized Dela Derivaive via Coracive-lie
ANTI-LECTURE HALL COMPOSITIONS AND ANDREWS GENERALIZATION OF THE WATSON-WHIPPLE TRANSFORMATION
 ANTI-LECTURE HALL COMPOSITIONS AND ANDREWS GENERALIZATION OF THE WATSON-WHIPPLE TRANSFORMATION SYLVIE CORTEEL, JEREMY LOVEJOY AND CARLA SAVAGE Abstract. For fixed ad k, we fid a three-variable geeratig
ANTI-LECTURE HALL COMPOSITIONS AND ANDREWS GENERALIZATION OF THE WATSON-WHIPPLE TRANSFORMATION SYLVIE CORTEEL, JEREMY LOVEJOY AND CARLA SAVAGE Abstract. For fixed ad k, we fid a three-variable geeratig
MATH 507a ASSIGNMENT 4 SOLUTIONS FALL 2018 Prof. Alexander. g (x) dx = g(b) g(0) = g(b),
 MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
King Fahd University of Petroleum & Minerals Computer Engineering g Dept
 Kig Fahd Uiversiy of Peroleum & Mierals Compuer Egieerig g Dep COE 4 Daa ad Compuer Commuicaios erm Dr. shraf S. Hasa Mahmoud Rm -4 Ex. 74 Email: ashraf@kfupm.edu.sa 9/8/ Dr. shraf S. Hasa Mahmoud Lecure
Kig Fahd Uiversiy of Peroleum & Mierals Compuer Egieerig g Dep COE 4 Daa ad Compuer Commuicaios erm Dr. shraf S. Hasa Mahmoud Rm -4 Ex. 74 Email: ashraf@kfupm.edu.sa 9/8/ Dr. shraf S. Hasa Mahmoud Lecure
Mean Square Convergent Finite Difference Scheme for Stochastic Parabolic PDEs
 America Joural of Compuaioal Mahemaics, 04, 4, 80-88 Published Olie Sepember 04 i SciRes. hp://www.scirp.org/joural/ajcm hp://dx.doi.org/0.436/ajcm.04.4404 Mea Square Coverge Fiie Differece Scheme for
America Joural of Compuaioal Mahemaics, 04, 4, 80-88 Published Olie Sepember 04 i SciRes. hp://www.scirp.org/joural/ajcm hp://dx.doi.org/0.436/ajcm.04.4404 Mea Square Coverge Fiie Differece Scheme for
METHOD OF THE EQUIVALENT BOUNDARY CONDITIONS IN THE UNSTEADY PROBLEM FOR ELASTIC DIFFUSION LAYER
 Maerials Physics ad Mechaics 3 (5) 36-4 Received: March 7 5 METHOD OF THE EQUIVAENT BOUNDARY CONDITIONS IN THE UNSTEADY PROBEM FOR EASTIC DIFFUSION AYER A.V. Zemsov * D.V. Tarlaovsiy Moscow Aviaio Isiue
Maerials Physics ad Mechaics 3 (5) 36-4 Received: March 7 5 METHOD OF THE EQUIVAENT BOUNDARY CONDITIONS IN THE UNSTEADY PROBEM FOR EASTIC DIFFUSION AYER A.V. Zemsov * D.V. Tarlaovsiy Moscow Aviaio Isiue
On Another Type of Transform Called Rangaig Transform
 Ieraioal Joural of Parial Differeial Equaios ad Applicaios, 7, Vol 5, No, 4-48 Available olie a hp://pubssciepubcom/ijpdea/5//6 Sciece ad Educaio Publishig DOI:69/ijpdea-5--6 O Aoher Type of Trasform Called
Ieraioal Joural of Parial Differeial Equaios ad Applicaios, 7, Vol 5, No, 4-48 Available olie a hp://pubssciepubcom/ijpdea/5//6 Sciece ad Educaio Publishig DOI:69/ijpdea-5--6 O Aoher Type of Trasform Called
RENEWAL THEORY FOR EMBEDDED REGENERATIVE SETS. BY JEAN BERTOIN Universite Pierre et Marie Curie
 The Aals of Probabiliy 999, Vol 27, No 3, 523535 RENEWAL TEORY FOR EMBEDDED REGENERATIVE SETS BY JEAN BERTOIN Uiversie Pierre e Marie Curie We cosider he age processes A A associaed o a moooe sequece R
The Aals of Probabiliy 999, Vol 27, No 3, 523535 RENEWAL TEORY FOR EMBEDDED REGENERATIVE SETS BY JEAN BERTOIN Uiversie Pierre e Marie Curie We cosider he age processes A A associaed o a moooe sequece R
INTEGER INTERVAL VALUE OF NEWTON DIVIDED DIFFERENCE AND FORWARD AND BACKWARD INTERPOLATION FORMULA
 Volume 8 No. 8, 45-54 ISSN: 34-3395 (o-lie versio) url: hp://www.ijpam.eu ijpam.eu INTEGER INTERVAL VALUE OF NEWTON DIVIDED DIFFERENCE AND FORWARD AND BACKWARD INTERPOLATION FORMULA A.Arul dass M.Dhaapal
Volume 8 No. 8, 45-54 ISSN: 34-3395 (o-lie versio) url: hp://www.ijpam.eu ijpam.eu INTEGER INTERVAL VALUE OF NEWTON DIVIDED DIFFERENCE AND FORWARD AND BACKWARD INTERPOLATION FORMULA A.Arul dass M.Dhaapal
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 4 9/16/2013. Applications of the large deviation technique
 MASSACHUSETTS ISTITUTE OF TECHOLOGY 6.265/5.070J Fall 203 Lecure 4 9/6/203 Applicaios of he large deviaio echique Coe.. Isurace problem 2. Queueig problem 3. Buffer overflow probabiliy Safey capial for
MASSACHUSETTS ISTITUTE OF TECHOLOGY 6.265/5.070J Fall 203 Lecure 4 9/6/203 Applicaios of he large deviaio echique Coe.. Isurace problem 2. Queueig problem 3. Buffer overflow probabiliy Safey capial for
Additional Tables of Simulation Results
 Saisica Siica: Suppleme REGULARIZING LASSO: A CONSISTENT VARIABLE SELECTION METHOD Quefeg Li ad Ju Shao Uiversiy of Wiscosi, Madiso, Eas Chia Normal Uiversiy ad Uiversiy of Wiscosi, Madiso Supplemeary
Saisica Siica: Suppleme REGULARIZING LASSO: A CONSISTENT VARIABLE SELECTION METHOD Quefeg Li ad Ju Shao Uiversiy of Wiscosi, Madiso, Eas Chia Normal Uiversiy ad Uiversiy of Wiscosi, Madiso Supplemeary
Pure Math 30: Explained!
 ure Mah : Explaied! www.puremah.com 6 Logarihms Lesso ar Basic Expoeial Applicaios Expoeial Growh & Decay: Siuaios followig his ype of chage ca be modeled usig he formula: (b) A = Fuure Amou A o = iial
ure Mah : Explaied! www.puremah.com 6 Logarihms Lesso ar Basic Expoeial Applicaios Expoeial Growh & Decay: Siuaios followig his ype of chage ca be modeled usig he formula: (b) A = Fuure Amou A o = iial
Sampling Example. ( ) δ ( f 1) (1/2)cos(12πt), T 0 = 1
 Samplig Example Le x = cos( 4π)cos( π). The fudameal frequecy of cos 4π fudameal frequecy of cos π is Hz. The ( f ) = ( / ) δ ( f 7) + δ ( f + 7) / δ ( f ) + δ ( f + ). ( f ) = ( / 4) δ ( f 8) + δ ( f
Samplig Example Le x = cos( 4π)cos( π). The fudameal frequecy of cos 4π fudameal frequecy of cos π is Hz. The ( f ) = ( / ) δ ( f 7) + δ ( f + 7) / δ ( f ) + δ ( f + ). ( f ) = ( / 4) δ ( f 8) + δ ( f
Academic Forum Cauchy Confers with Weierstrass. Lloyd Edgar S. Moyo, Ph.D. Associate Professor of Mathematics
 Academic Forum - Cauchy Cofers wih Weiersrass Lloyd Edgar S Moyo PhD Associae Professor of Mahemaics Absrac We poi ou wo limiaios of usig he Cauchy Residue Theorem o evaluae a defiie iegral of a real raioal
Academic Forum - Cauchy Cofers wih Weiersrass Lloyd Edgar S Moyo PhD Associae Professor of Mahemaics Absrac We poi ou wo limiaios of usig he Cauchy Residue Theorem o evaluae a defiie iegral of a real raioal
COS 522: Complexity Theory : Boaz Barak Handout 10: Parallel Repetition Lemma
 COS 522: Complexiy Theory : Boaz Barak Hadou 0: Parallel Repeiio Lemma Readig: () A Parallel Repeiio Theorem / Ra Raz (available o his websie) (2) Parallel Repeiio: Simplificaios ad he No-Sigallig Case
COS 522: Complexiy Theory : Boaz Barak Hadou 0: Parallel Repeiio Lemma Readig: () A Parallel Repeiio Theorem / Ra Raz (available o his websie) (2) Parallel Repeiio: Simplificaios ad he No-Sigallig Case
Stochastic Processes Adopted From p Chapter 9 Probability, Random Variables and Stochastic Processes, 4th Edition A. Papoulis and S.
 Sochasic Processes Adoped From p Chaper 9 Probabiliy, adom Variables ad Sochasic Processes, 4h Ediio A. Papoulis ad S. Pillai 9. Sochasic Processes Iroducio Le deoe he radom oucome of a experime. To every
Sochasic Processes Adoped From p Chaper 9 Probabiliy, adom Variables ad Sochasic Processes, 4h Ediio A. Papoulis ad S. Pillai 9. Sochasic Processes Iroducio Le deoe he radom oucome of a experime. To every
Some inequalities for q-polygamma function and ζ q -Riemann zeta functions
 Aales Mahemaicae e Iformaicae 37 (1). 95 1 h://ami.ekf.hu Some iequaliies for q-olygamma fucio ad ζ q -Riema zea fucios Valmir Krasiqi a, Toufik Masour b Armed Sh. Shabai a a Dearme of Mahemaics, Uiversiy
Aales Mahemaicae e Iformaicae 37 (1). 95 1 h://ami.ekf.hu Some iequaliies for q-olygamma fucio ad ζ q -Riema zea fucios Valmir Krasiqi a, Toufik Masour b Armed Sh. Shabai a a Dearme of Mahemaics, Uiversiy
14.02 Principles of Macroeconomics Fall 2005
 14.02 Priciples of Macroecoomics Fall 2005 Quiz 2 Tuesday, November 8, 2005 7:30 PM 9 PM Please, aswer he followig quesios. Wrie your aswers direcly o he quiz. You ca achieve a oal of 100 pois. There are
14.02 Priciples of Macroecoomics Fall 2005 Quiz 2 Tuesday, November 8, 2005 7:30 PM 9 PM Please, aswer he followig quesios. Wrie your aswers direcly o he quiz. You ca achieve a oal of 100 pois. There are
EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D. S. Palimkar
 Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
The Inverse of Power Series and the Partial Bell Polynomials
 1 2 3 47 6 23 11 Joural of Ieger Sequece Vol 15 2012 Aricle 1237 The Ivere of Power Serie ad he Parial Bell Polyomial Miloud Mihoubi 1 ad Rachida Mahdid 1 Faculy of Mahemaic Uiveriy of Sciece ad Techology
1 2 3 47 6 23 11 Joural of Ieger Sequece Vol 15 2012 Aricle 1237 The Ivere of Power Serie ad he Parial Bell Polyomial Miloud Mihoubi 1 ad Rachida Mahdid 1 Faculy of Mahemaic Uiveriy of Sciece ad Techology
Research Article A MOLP Method for Solving Fully Fuzzy Linear Programming with LR Fuzzy Parameters
 Mahemaical Problems i Egieerig Aricle ID 782376 10 pages hp://dx.doi.org/10.1155/2014/782376 Research Aricle A MOLP Mehod for Solvig Fully Fuzzy Liear Programmig wih Fuzzy Parameers Xiao-Peg Yag 12 Xue-Gag
Mahemaical Problems i Egieerig Aricle ID 782376 10 pages hp://dx.doi.org/10.1155/2014/782376 Research Aricle A MOLP Mehod for Solvig Fully Fuzzy Liear Programmig wih Fuzzy Parameers Xiao-Peg Yag 12 Xue-Gag
SUPER LINEAR ALGEBRA
 Super Liear - Cover:Layou 7/7/2008 2:32 PM Page SUPER LINEAR ALGEBRA W. B. Vasaha Kadasamy e-mail: vasahakadasamy@gmail.com web: hp://ma.iim.ac.i/~wbv www.vasaha.e Florei Smaradache e-mail: smarad@um.edu
Super Liear - Cover:Layou 7/7/2008 2:32 PM Page SUPER LINEAR ALGEBRA W. B. Vasaha Kadasamy e-mail: vasahakadasamy@gmail.com web: hp://ma.iim.ac.i/~wbv www.vasaha.e Florei Smaradache e-mail: smarad@um.edu
A Study On (H, 1)(E, q) Product Summability Of Fourier Series And Its Conjugate Series
 Mahemaical Theory ad Modelig ISSN 4-584 (Paper) ISSN 5-5 (Olie) Vol.7, No.5, 7 A Sudy O (H, )(E, q) Produc Summabiliy Of Fourier Series Ad Is Cojugae Series Sheela Verma, Kalpaa Saxea * Research Scholar
Mahemaical Theory ad Modelig ISSN 4-584 (Paper) ISSN 5-5 (Olie) Vol.7, No.5, 7 A Sudy O (H, )(E, q) Produc Summabiliy Of Fourier Series Ad Is Cojugae Series Sheela Verma, Kalpaa Saxea * Research Scholar
LIMITS OF SEQUENCES AND FUNCTIONS
 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» VV Koev LIMITS OF SEQUENCES AND FUNCTIONS TeBook
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» VV Koev LIMITS OF SEQUENCES AND FUNCTIONS TeBook
