Math Review: parameter estimation. Emma
|
|
|
- Brice Davis
- 6 years ago
- Views:
Transcription
1 Math Review: parameter estimation Emma
2 Fitting lines to dots: We will cover how Slides provided by HyunSoo Park
3 1809, Carl Friedrich Gauss
4 What about fitting line on a curved surface?
5 Least squares methods -fitting a line - Data: (x 1, y 1 ),, (x n, y n ) y=mx+b Line equation: y i = m x i + b Find (m, b) to minimize (x i, y i ) E n i 1 ( y i m x i b ) 2 Silvio Savarese
6 0 2 2 Y X XB X db de T T 2 2 n 1 n 1 n 1 i 2 i i XB Y b m 1 x 1 x y y b m 1 x y E Normal equation n i i i b m x y E 1 2 ) ( Y X XB X T T Least squares methods -fitting a line - Y X X X B T T 1 (XB ) (XB ) Y 2(XB ) Y Y XB ) (Y XB ) (Y T T T T Silvio Savarese
7 Least squares methods -fitting a line - Ax b More equations than unknowns Look for solution which minimizes Ax-b = (Ax-b) T (Ax-b) T Solve ( Ax b) ( Ax b) 0 x i LS solution x ( A T A ) 1 A T b Silvio Savarese
8 Least squares methods What if (A t A) not invertible? -fitting a line - Solving x ( A t A ) 1 A t b A t 1 ( A A ) A t = pseudo-inverse of A A U t V = SVD decomposition of A A V 1 1 U A V U 1 with equal to for all nonzero singular values and zero otherwise Silvio Savarese
9 Singular Value Decomposition A = U D V T m x n m x n n x n n x n Column orthogonal matrix U T U =I m m V T V =I n n spans column space of A spans row space of A
10 Singular Value Decomposition A = U D V T m x n m x n n x n n x n Column orthogonal matrix U T U =I m m V T V =I n n Singular value matrix D diag{,,, } where = 1 2 n 1 2 n 0
11 Example I A = [u,d,v] = svd(a) u = d = v =
12 Example I A = u*d*v' ans = Reconstruction
13 SVD of this?
14 [u,d,v] = svd(i); semilogy(diag(d(1:20,1:20)),'x-') Im2 = u(:,1:20)*d(1:20,1:20)*v(:,1:20)';
15 U(:,1:4) D(1:4,1:4) V(:,1:4)
16
17
18 Images as Vectors n = m n*m
19 Vector Mean n = = m I1 + I2 = mean image n*m n*m
20 Average face
21 Eigenfaces Eigenfaces look somewhat like generic faces.
22 Eigen-images of Berlin
23 Eigen-images Average of 16 induviduals trasformed via biometrical data of different ethnics
24 Average of 16 induviduals trasformed via biometrical data of different ages
25 Example II (Rotation) Z 1 e= i j k R= X 3 >> [u,d,v] = svd(r) u = v = d = Note that singular values are always one for a rotation matrix
26 Rank A = U D V T m x n m x n n x n n x n rank(a) = r min(m,n) D r Rank is the same as the number of nonzero singular values.
27 Nullspace A = U D V T m x n m x n n x n n x n null(a) = V r:n A V r:n =0
28 Example III (Fundamental Matrix) F = 1.0e+003 * [u,d,v] = svd(f) u = d = 1.0e+004 * v = Rank(F) = 2 d(1,1) ans = e+004 d(2,2) ans = d(3,3) ans = e-016
29 Matrix Inversion with SVD A = U D V T m x n m x n n x n n x n A = V D 1 U T AA=I 1 D = 1, 2,, n diag{1/ 1/ 1/ } if 0, otherwise zero. i
30 Linear Inhomogeneous Equations 1) rank(a) = r < n : infinite number of solutions = A x b 1 T x=vd Ub+ r+1 V r nvn Particular solution Homogeneous solution A=UDV T V= V1 V n where and. m x n n x 1 m x 1
31 Linear Inhomogeneous Equations = A x b m x n n x 1 m x 1 1) 2) rank(a) = r < n : infinite number of solutions 1 T x=vd Ub+ r+1 V r nvn Particular solution Homogeneous solution A=UDV T where and. rank(a) = n : exact solution x=a 1 b V= V1 V n
32 Linear Inhomogeneous Equations = A x b m x n n x 1 m x 1 1) 2) 3) rank(a) = r < n : infinite number of solutions 1 T x=vd Ub+ r+1 V r nvn Particular solution Homogeneous solution A=UDV T where and. rank(a) = n : exact solution x=a 1 b V= V1 V n n m : no exact solution in general (needs least squares) min Ax - b 2 x or x=a\b -1 T T x= A A A b in MATLAB.
33 Digression (but will become relevant) Power method algorithm, for computing eigenvalues, eigenvectors. Bob Collins
34 Two types of Least Square Problem: (i) Unconstrained affine Linear Least Squares min kax xr bk2 with kbk 6= 0 n (ii) Norm-constrained homogeneous Linear Least Squares min xr n kaxk2 s.t. kxk =1
35 Linear Homogeneous Equations Linear least square solve produces a trivial solution: T T x= A A A b An additional constraint on x=0 x to avoid the trivial solution: x =1 A x = 0 m x n n x 1 m x 1
36 Let E(x) =kaxk 2 be the cost function Let C(x) =1 kxk 2 be the constraint The lagrangian is L(x) =E(x)+C(x), with alagrangemultiplier We must have: L x = 0 and L =0
37 We get: L x =2AT Ax 2x From which: and L =1 kxk2 = C(x) A T Ax = x and C(x) =0 is an eigenvalue of A T A and x an (normalized) eigenvector is a squared singular value of A and x asingularvector Let an SVD (Singular Value Decomposition) of matrix A be: A svd UV T We have x = v i with i {1,...,n}
38 Plug x = v i back in the cost function E(x) =kaxk 2 : E(v i )=kav i k 2 = kuv T v i k 2 Since V is an orthonormal matrix, V T v i = e i (e i is a zero vector with one at the i-th entry): E(v i )=kue i k 2 = ku i e i k 2 Let U =(u 1 u n ), we get: E(v i )=k i u i k 2 = 2 i ku i k 2 Given that U is orthonormal: E(v i )= 2 i We therefore choose for x the singular vector associated to the smallest singular value, which concludes the proof.
39 Linear Homogeneous Equations Linear least square solve produces a trivial solution: T T x= A A A b An additional constraint on x=0 x to avoid the trivial solution: x =1 A x = 0 1) rank(a) = r < n-1 : infinite number of solutions n where 2 r+1 r+1 n n i i=r+1 x= V + + V 1 m x n n x 1 m x 1
40 Linear Homogeneous Equations Linear least square solve produces a trivial solution: T T x= A A A b An additional constraint on x=0 x to avoid the trivial solution: x =1 A x = 0 1) rank(a) = r < n-1 : infinite number of solutions x= V + + V r+1 r+1 n n where n 2 i i=r+1 1 m x n n x 1 m x 1 2) rank(a) = n -1 x=v n : one exact solution
41 Linear Homogeneous Equations Linear least square solve produces a trivial solution: T T x= A A A b An additional constraint on x=0 x to avoid the trivial solution: x =1 A x = 0 1) rank(a) = r < n-1 : infinite number of solutions x= V + + V r+1 r+1 n n where n 2 i i=r+1 1 m x n n x 1 m x 1 2) 3) rank(a) = n -1 x=v n : one exact solution n m : no exact solution in general (needs least squares) min Ax 2 x subject to x =1 x=v n
42 Least squares methods -fitting a line - E n i 1 ( y i m x i b ) 2 y=mx+b B T 1 T X X X Y m B b (x i, y i ) Limitations Not rotation-invariant Fails completely for vertical lines
43 Least squares methods -fitting a line - Distance between point (x n, y n ) and line ax+by=d ax+by=d Find (a, b, d) to minimize the sum of squared perpendicular distances E n i 1 ( a x i b y i d ) 2 (x i, y i ) ( U T U ) N 0 data model parameters
44 Least squares methods -fitting a line - A h = 0 Minimize A h subject to h 1 A UDV T h last column of V
45 (i) Unconstrained affine Linear Least Squares min kax xr bk2 with kbk 6= 0 n Solution with the pseudo-inverse x = A b Closed-form expression (for well-posed problems) A = A T A 1 A T Regularized expression (for all cases) A = V U T with A = UV T an SVD contains the reciprocal singular values = 1 if >², 0otherwise (ii) Norm-constrained homogeneous Linear Least Squares min xr kaxk2 s.t. kxk =1 n x is given by the last column of V
46 Homography Linear Estimation H h h h h h h h h h x =Hx 2 1 x u2 v x u1 v 1 1 1
47 Homography Linear Estimation x =Hx 2 1 x2 Hx1 0 u2 h1 v2h3x1 h2x1 v2 h2 x1 hx 1 1 u2h3x1 0 1 h u h x v hx T T T 0 13 x1 v 2x1 h1 T T T x u 2x1h20 T T T v2x1 u2x h3 3 x 9 because x 2 rank( ) = 2 is a rank 2 matrix. x u1 v Therefore, 4 point correspondences are required to estimate a homography.
48 Fundamental Matrix Estimation x u2 v T xfx x u1 v 1 1 1
49 Fundamental Matrix Estimation T xfx T u2 f11 f12 f13u1 v2 f21 f22 f23 v1 0 1 f f f uuf 2 111uvf 2 112uf 2 13vuf 2 121vvf 2 122vf 2 23uf 131vf 132f330 f11 f12 9 f 13 uu 2 1 uv 2 1 u2 vu 2 1 vv 2 1 v2 u1 v1 1 f21 f22 0 f23 f 31 f32 f33 Therefore, 8 point correspondences are required to estimate a fundamental matrix.
50 Point Triangulation X ( X,Y,Z ) Given camera poses, reconstruct 3D points. x X x X =P 1 1 P x P 1 X 0 1 x rank( P) = At least 2 views are required to reconstruct a 3D point.
51 Least squares: Robustness to noise outlier! Problem: squared error heavily penalizes outliers Silvio Savarese
52 Fitting Goal: Choose a parametric model to fit a certain quantity from data Techniques: Least square methods RANSAC Hough transform Silvio Savarese
53 Basic philosophy (voting scheme) Data elements are used to vote for one (or multiple) models Robust to outliers and missing data Assumption1: Noise features will not vote consistently for any single model ( few outliers) Assumption2: there are enough features to agree on a good model ( few missing data) Silvio Savarese
54 RANSAC (RANdom SAmple Consensus) : Learning technique to estimate parameters of a model by random sampling of observed data Fischler & Bolles in 81. f : I P, such that: ( P, ) O min O f ( P, ) Model parameters T 1 T P P P Silvio Savarese
55 RANSAC Sample set = set of points in 2D Algorithm: 1. Select random sample of minimum required size to fit model 2. Compute a putative model from sample set 3. Compute the set of inliers to this model from whole data set Repeat 1-3 until model with the most inliers over all samples is found Silvio Savarese
56 RANSAC Sample set = set of points in 2D Algorithm: 1. Select random sample of minimum required size to fit model [?] =[2] 2. Compute a putative model from sample set 3. Compute the set of inliers to this model from whole data set Repeat 1-3 until model with the most inliers over all samples is found Silvio Savarese
57 RANSAC Sample set = set of points in 2D Algorithm: 1. Select random sample of minimum required size to fit model [?] =[2] 2. Compute a putative model from sample set 3. Compute the set of inliers to this model from whole data set Repeat 1-3 until model with the most inliers over all samples is found Silvio Savarese
58 RANSAC Sample set = set of points in 2D Algorithm: O = Select random sample of minimum required size to fit model [?] =[2] 2. Compute a putative model from sample set 3. Compute the set of inliers to this model from whole data set Repeat 1-3 until model with the most inliers over all samples is found Silvio Savarese
59 RANSAC (RANdom SAmple Consensus) : Fischler & Bolles in 81. Algorithm: O = 6 1. Select random sample of minimum required size to fit model [?] 2. Compute a putative model from sample set 3. Compute the set of inliers to this model from whole data set Repeat 1-3 until model with the most inliers over all samples is found Silvio Savarese
60 How many samples? Number of samples N Choose N so that, with probability p, at least one random sample is free from outliers (e.g. p=0.99) (outlier ratio: e ) Initial number of points s Typically minimum number needed to fit the model Distance threshold Choose so probability for inlier is p (e.g. 0.95) Zero-mean Gaussian noise with std. dev. : t 2 = N log 1 p/ log1 1 e s proportion of outliers e s 5% 10% 20% 25% 30% 40% 50% Source: M. Pollefeys
61 Estimating H by RANSAC Silvio Savarese H 8 DOF Need 4 correspondences Sample set = set of matches between 2 images Algorithm: 1. Select a random sample of minimum required size [?] 2. Compute a putative model from these 3. Compute the set of inliers to this model from whole sample space Repeat 1-3 until model with the most inliers over all samples is found
62 Estimating F by RANSAC Silvio Savarese Outlier matches F 7 DOF Need 7 (8) correspondences Sample set = set of matches between 2 images Algorithm: 1. Select a random sample of minimum required size [?] 2. Compute a putative model from these 3. Compute the set of inliers to this model from whole sample space Repeat 1-3 until model with the most inliers over all samples is found
63 RANSAC - conclusions Good: Simple and easily implementable Successful in different contexts Bad: Many parameters to tune Trade-off accuracy-vs-time Cannot be use if ratio inliers/outliers is too small Silvio Savarese
64
1809, Carl Friedrich Gauss
 1809, Carl Friedrich Gauss Singular Value Decomposition A = U D V T m x n m x n n x n n x n Singular Value Decomposition A = U D V T m x n m x n n x n n x n Column orthogonal matrix U i T U i U j T T =
1809, Carl Friedrich Gauss Singular Value Decomposition A = U D V T m x n m x n n x n n x n Singular Value Decomposition A = U D V T m x n m x n n x n n x n Column orthogonal matrix U i T U i U j T T =
Lecture 4.3 Estimating homographies from feature correspondences. Thomas Opsahl
 Lecture 4.3 Estimating homographies from feature correspondences Thomas Opsahl Homographies induced by central projection 1 H 2 1 H 2 u uu 2 3 1 Homography Hu = u H = h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h
Lecture 4.3 Estimating homographies from feature correspondences Thomas Opsahl Homographies induced by central projection 1 H 2 1 H 2 u uu 2 3 1 Homography Hu = u H = h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h
Singular Value Decomposition (SVD)
 School of Computing National University of Singapore CS CS524 Theoretical Foundations of Multimedia More Linear Algebra Singular Value Decomposition (SVD) The highpoint of linear algebra Gilbert Strang
School of Computing National University of Singapore CS CS524 Theoretical Foundations of Multimedia More Linear Algebra Singular Value Decomposition (SVD) The highpoint of linear algebra Gilbert Strang
Linear Algebra Review. Vectors
 Linear Algebra Review 9/4/7 Linear Algebra Review By Tim K. Marks UCSD Borrows heavily from: Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Virginia de Sa (UCSD) Cogsci 8F Linear Algebra review Vectors
Linear Algebra Review 9/4/7 Linear Algebra Review By Tim K. Marks UCSD Borrows heavily from: Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Virginia de Sa (UCSD) Cogsci 8F Linear Algebra review Vectors
3D Computer Vision - WT 2004
 3D Computer Vision - WT 2004 Singular Value Decomposition Darko Zikic CAMP - Chair for Computer Aided Medical Procedures November 4, 2004 1 2 3 4 5 Properties For any given matrix A R m n there exists
3D Computer Vision - WT 2004 Singular Value Decomposition Darko Zikic CAMP - Chair for Computer Aided Medical Procedures November 4, 2004 1 2 3 4 5 Properties For any given matrix A R m n there exists
(a) If A is a 3 by 4 matrix, what does this tell us about its nullspace? Solution: dim N(A) 1, since rank(a) 3. Ax =
 . (5 points) (a) If A is a 3 by 4 matrix, what does this tell us about its nullspace? dim N(A), since rank(a) 3. (b) If we also know that Ax = has no solution, what do we know about the rank of A? C(A)
. (5 points) (a) If A is a 3 by 4 matrix, what does this tell us about its nullspace? dim N(A), since rank(a) 3. (b) If we also know that Ax = has no solution, what do we know about the rank of A? C(A)
Math 2174: Practice Midterm 1
 Math 74: Practice Midterm Show your work and explain your reasoning as appropriate. No calculators. One page of handwritten notes is allowed for the exam, as well as one blank page of scratch paper.. Consider
Math 74: Practice Midterm Show your work and explain your reasoning as appropriate. No calculators. One page of handwritten notes is allowed for the exam, as well as one blank page of scratch paper.. Consider
linearly indepedent eigenvectors as the multiplicity of the root, but in general there may be no more than one. For further discussion, assume matrice
 3. Eigenvalues and Eigenvectors, Spectral Representation 3.. Eigenvalues and Eigenvectors A vector ' is eigenvector of a matrix K, if K' is parallel to ' and ' 6, i.e., K' k' k is the eigenvalue. If is
3. Eigenvalues and Eigenvectors, Spectral Representation 3.. Eigenvalues and Eigenvectors A vector ' is eigenvector of a matrix K, if K' is parallel to ' and ' 6, i.e., K' k' k is the eigenvalue. If is
MATH 2331 Linear Algebra. Section 2.1 Matrix Operations. Definition: A : m n, B : n p. Example: Compute AB, if possible.
 MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
Linear Systems. Carlo Tomasi. June 12, r = rank(a) b range(a) n r solutions
 Linear Systems Carlo Tomasi June, 08 Section characterizes the existence and multiplicity of the solutions of a linear system in terms of the four fundamental spaces associated with the system s matrix
Linear Systems Carlo Tomasi June, 08 Section characterizes the existence and multiplicity of the solutions of a linear system in terms of the four fundamental spaces associated with the system s matrix
Linear Algebra - Part II
 Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
[3] (b) Find a reduced row-echelon matrix row-equivalent to ,1 2 2
![[3] (b) Find a reduced row-echelon matrix row-equivalent to ,1 2 2 [3] (b) Find a reduced row-echelon matrix row-equivalent to ,1 2 2](/thumbs/91/107233302.jpg) MATH Key for sample nal exam, August 998 []. (a) Dene the term \reduced row-echelon matrix". A matrix is reduced row-echelon if the following conditions are satised. every zero row lies below every nonzero
MATH Key for sample nal exam, August 998 []. (a) Dene the term \reduced row-echelon matrix". A matrix is reduced row-echelon if the following conditions are satised. every zero row lies below every nonzero
Linear Systems. Carlo Tomasi
 Linear Systems Carlo Tomasi Section 1 characterizes the existence and multiplicity of the solutions of a linear system in terms of the four fundamental spaces associated with the system s matrix and of
Linear Systems Carlo Tomasi Section 1 characterizes the existence and multiplicity of the solutions of a linear system in terms of the four fundamental spaces associated with the system s matrix and of
Notes on singular value decomposition for Math 54. Recall that if A is a symmetric n n matrix, then A has real eigenvalues A = P DP 1 A = P DP T.
 Notes on singular value decomposition for Math 54 Recall that if A is a symmetric n n matrix, then A has real eigenvalues λ 1,, λ n (possibly repeated), and R n has an orthonormal basis v 1,, v n, where
Notes on singular value decomposition for Math 54 Recall that if A is a symmetric n n matrix, then A has real eigenvalues λ 1,, λ n (possibly repeated), and R n has an orthonormal basis v 1,, v n, where
YORK UNIVERSITY. Faculty of Science Department of Mathematics and Statistics MATH M Test #1. July 11, 2013 Solutions
 YORK UNIVERSITY Faculty of Science Department of Mathematics and Statistics MATH 222 3. M Test # July, 23 Solutions. For each statement indicate whether it is always TRUE or sometimes FALSE. Note: For
YORK UNIVERSITY Faculty of Science Department of Mathematics and Statistics MATH 222 3. M Test # July, 23 Solutions. For each statement indicate whether it is always TRUE or sometimes FALSE. Note: For
Lecture 5. Epipolar Geometry. Professor Silvio Savarese Computational Vision and Geometry Lab. 21-Jan-15. Lecture 5 - Silvio Savarese
 Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
2. Every linear system with the same number of equations as unknowns has a unique solution.
 1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
σ 11 σ 22 σ pp 0 with p = min(n, m) The σ ii s are the singular values. Notation change σ ii A 1 σ 2
 HE SINGULAR VALUE DECOMPOSIION he SVD existence - properties. Pseudo-inverses and the SVD Use of SVD for least-squares problems Applications of the SVD he Singular Value Decomposition (SVD) heorem For
HE SINGULAR VALUE DECOMPOSIION he SVD existence - properties. Pseudo-inverses and the SVD Use of SVD for least-squares problems Applications of the SVD he Singular Value Decomposition (SVD) heorem For
Singular value decomposition
 Singular value decomposition The eigenvalue decomposition (EVD) for a square matrix A gives AU = UD. Let A be rectangular (m n, m > n). A singular value σ and corresponding pair of singular vectors u (m
Singular value decomposition The eigenvalue decomposition (EVD) for a square matrix A gives AU = UD. Let A be rectangular (m n, m > n). A singular value σ and corresponding pair of singular vectors u (m
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s =
 Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
Introduction to Machine Learning. PCA and Spectral Clustering. Introduction to Machine Learning, Slides: Eran Halperin
 1 Introduction to Machine Learning PCA and Spectral Clustering Introduction to Machine Learning, 2013-14 Slides: Eran Halperin Singular Value Decomposition (SVD) The singular value decomposition (SVD)
1 Introduction to Machine Learning PCA and Spectral Clustering Introduction to Machine Learning, 2013-14 Slides: Eran Halperin Singular Value Decomposition (SVD) The singular value decomposition (SVD)
Computational math: Assignment 1
 Computational math: Assignment 1 Thanks Ting Gao for her Latex file 11 Let B be a 4 4 matrix to which we apply the following operations: 1double column 1, halve row 3, 3add row 3 to row 1, 4interchange
Computational math: Assignment 1 Thanks Ting Gao for her Latex file 11 Let B be a 4 4 matrix to which we apply the following operations: 1double column 1, halve row 3, 3add row 3 to row 1, 4interchange
Linear Algebra for Machine Learning. Sargur N. Srihari
 Linear Algebra for Machine Learning Sargur N. srihari@cedar.buffalo.edu 1 Overview Linear Algebra is based on continuous math rather than discrete math Computer scientists have little experience with it
Linear Algebra for Machine Learning Sargur N. srihari@cedar.buffalo.edu 1 Overview Linear Algebra is based on continuous math rather than discrete math Computer scientists have little experience with it
2. LINEAR ALGEBRA. 1. Definitions. 2. Linear least squares problem. 3. QR factorization. 4. Singular value decomposition (SVD) 5.
 2. LINEAR ALGEBRA Outline 1. Definitions 2. Linear least squares problem 3. QR factorization 4. Singular value decomposition (SVD) 5. Pseudo-inverse 6. Eigenvalue decomposition (EVD) 1 Definitions Vector
2. LINEAR ALGEBRA Outline 1. Definitions 2. Linear least squares problem 3. QR factorization 4. Singular value decomposition (SVD) 5. Pseudo-inverse 6. Eigenvalue decomposition (EVD) 1 Definitions Vector
Mobile Robotics 1. A Compact Course on Linear Algebra. Giorgio Grisetti
 Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
Find the solution set of 2x 3y = 5. Answer: We solve for x = (5 + 3y)/2. Hence the solution space consists of all vectors of the form
 Math 2 Homework #7 March 4, 2 7.3.3. Find the solution set of 2x 3y = 5. Answer: We solve for x = (5 + 3y/2. Hence the solution space consists of all vectors of the form ( ( ( ( x (5 + 3y/2 5/2 3/2 x =
Math 2 Homework #7 March 4, 2 7.3.3. Find the solution set of 2x 3y = 5. Answer: We solve for x = (5 + 3y/2. Hence the solution space consists of all vectors of the form ( ( ( ( x (5 + 3y/2 5/2 3/2 x =
Conceptual Questions for Review
 Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Outline. Linear Algebra for Computer Vision
 Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Math 4A Notes. Written by Victoria Kala Last updated June 11, 2017
 Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Singular Value Decomposition
 Singular Value Decomposition (Com S 477/577 Notes Yan-Bin Jia Sep, 7 Introduction Now comes a highlight of linear algebra. Any real m n matrix can be factored as A = UΣV T where U is an m m orthogonal
Singular Value Decomposition (Com S 477/577 Notes Yan-Bin Jia Sep, 7 Introduction Now comes a highlight of linear algebra. Any real m n matrix can be factored as A = UΣV T where U is an m m orthogonal
Math 3191 Applied Linear Algebra
 Math 191 Applied Linear Algebra Lecture 1: Inner Products, Length, Orthogonality Stephen Billups University of Colorado at Denver Math 191Applied Linear Algebra p.1/ Motivation Not all linear systems have
Math 191 Applied Linear Algebra Lecture 1: Inner Products, Length, Orthogonality Stephen Billups University of Colorado at Denver Math 191Applied Linear Algebra p.1/ Motivation Not all linear systems have
MATH 1120 (LINEAR ALGEBRA 1), FINAL EXAM FALL 2011 SOLUTIONS TO PRACTICE VERSION
 MATH (LINEAR ALGEBRA ) FINAL EXAM FALL SOLUTIONS TO PRACTICE VERSION Problem (a) For each matrix below (i) find a basis for its column space (ii) find a basis for its row space (iii) determine whether
MATH (LINEAR ALGEBRA ) FINAL EXAM FALL SOLUTIONS TO PRACTICE VERSION Problem (a) For each matrix below (i) find a basis for its column space (ii) find a basis for its row space (iii) determine whether
COMP 558 lecture 18 Nov. 15, 2010
 Least squares We have seen several least squares problems thus far, and we will see more in the upcoming lectures. For this reason it is good to have a more general picture of these problems and how to
Least squares We have seen several least squares problems thus far, and we will see more in the upcoming lectures. For this reason it is good to have a more general picture of these problems and how to
Lecture 2: Linear Algebra Review
 EE 227A: Convex Optimization and Applications January 19 Lecture 2: Linear Algebra Review Lecturer: Mert Pilanci Reading assignment: Appendix C of BV. Sections 2-6 of the web textbook 1 2.1 Vectors 2.1.1
EE 227A: Convex Optimization and Applications January 19 Lecture 2: Linear Algebra Review Lecturer: Mert Pilanci Reading assignment: Appendix C of BV. Sections 2-6 of the web textbook 1 2.1 Vectors 2.1.1
Compressive Sensing, Low Rank models, and Low Rank Submatrix
 Compressive Sensing,, and Low Rank Submatrix NICTA Short Course 2012 yi.li@nicta.com.au http://users.cecs.anu.edu.au/~yili Sep 12, 2012 ver. 1.8 http://tinyurl.com/brl89pk Outline Introduction 1 Introduction
Compressive Sensing,, and Low Rank Submatrix NICTA Short Course 2012 yi.li@nicta.com.au http://users.cecs.anu.edu.au/~yili Sep 12, 2012 ver. 1.8 http://tinyurl.com/brl89pk Outline Introduction 1 Introduction
Math 18, Linear Algebra, Lecture C00, Spring 2017 Review and Practice Problems for Final Exam
 Math 8, Linear Algebra, Lecture C, Spring 7 Review and Practice Problems for Final Exam. The augmentedmatrix of a linear system has been transformed by row operations into 5 4 8. Determine if the system
Math 8, Linear Algebra, Lecture C, Spring 7 Review and Practice Problems for Final Exam. The augmentedmatrix of a linear system has been transformed by row operations into 5 4 8. Determine if the system
Maths for Signals and Systems Linear Algebra in Engineering
 Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
Maths for Signals and Systems Linear Algebra in Engineering Lectures 13 15, Tuesday 8 th and Friday 11 th November 016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE
Glossary of Linear Algebra Terms. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
Large Scale Data Analysis Using Deep Learning
 Large Scale Data Analysis Using Deep Learning Linear Algebra U Kang Seoul National University U Kang 1 In This Lecture Overview of linear algebra (but, not a comprehensive survey) Focused on the subset
Large Scale Data Analysis Using Deep Learning Linear Algebra U Kang Seoul National University U Kang 1 In This Lecture Overview of linear algebra (but, not a comprehensive survey) Focused on the subset
The Singular Value Decomposition
 The Singular Value Decomposition An Important topic in NLA Radu Tiberiu Trîmbiţaş Babeş-Bolyai University February 23, 2009 Radu Tiberiu Trîmbiţaş ( Babeş-Bolyai University)The Singular Value Decomposition
The Singular Value Decomposition An Important topic in NLA Radu Tiberiu Trîmbiţaş Babeş-Bolyai University February 23, 2009 Radu Tiberiu Trîmbiţaş ( Babeş-Bolyai University)The Singular Value Decomposition
Review of Some Concepts from Linear Algebra: Part 2
 Review of Some Concepts from Linear Algebra: Part 2 Department of Mathematics Boise State University January 16, 2019 Math 566 Linear Algebra Review: Part 2 January 16, 2019 1 / 22 Vector spaces A set
Review of Some Concepts from Linear Algebra: Part 2 Department of Mathematics Boise State University January 16, 2019 Math 566 Linear Algebra Review: Part 2 January 16, 2019 1 / 22 Vector spaces A set
Review of Linear Algebra
 Review of Linear Algebra Dr Gerhard Roth COMP 40A Winter 05 Version Linear algebra Is an important area of mathematics It is the basis of computer vision Is very widely taught, and there are many resources
Review of Linear Algebra Dr Gerhard Roth COMP 40A Winter 05 Version Linear algebra Is an important area of mathematics It is the basis of computer vision Is very widely taught, and there are many resources
Singular value decomposition. If only the first p singular values are nonzero we write. U T o U p =0
 Singular value decomposition If only the first p singular values are nonzero we write G =[U p U o ] " Sp 0 0 0 # [V p V o ] T U p represents the first p columns of U U o represents the last N-p columns
Singular value decomposition If only the first p singular values are nonzero we write G =[U p U o ] " Sp 0 0 0 # [V p V o ] T U p represents the first p columns of U U o represents the last N-p columns
The Singular Value Decomposition
 The Singular Value Decomposition Philippe B. Laval KSU Fall 2015 Philippe B. Laval (KSU) SVD Fall 2015 1 / 13 Review of Key Concepts We review some key definitions and results about matrices that will
The Singular Value Decomposition Philippe B. Laval KSU Fall 2015 Philippe B. Laval (KSU) SVD Fall 2015 1 / 13 Review of Key Concepts We review some key definitions and results about matrices that will
Lecture 6 Positive Definite Matrices
 Linear Algebra Lecture 6 Positive Definite Matrices Prof. Chun-Hung Liu Dept. of Electrical and Computer Engineering National Chiao Tung University Spring 2017 2017/6/8 Lecture 6: Positive Definite Matrices
Linear Algebra Lecture 6 Positive Definite Matrices Prof. Chun-Hung Liu Dept. of Electrical and Computer Engineering National Chiao Tung University Spring 2017 2017/6/8 Lecture 6: Positive Definite Matrices
EECS 275 Matrix Computation
 EECS 275 Matrix Computation Ming-Hsuan Yang Electrical Engineering and Computer Science University of California at Merced Merced, CA 95344 http://faculty.ucmerced.edu/mhyang Lecture 6 1 / 22 Overview
EECS 275 Matrix Computation Ming-Hsuan Yang Electrical Engineering and Computer Science University of California at Merced Merced, CA 95344 http://faculty.ucmerced.edu/mhyang Lecture 6 1 / 22 Overview
Vector and Matrix Norms. Vector and Matrix Norms
 Vector and Matrix Norms Vector Space Algebra Matrix Algebra: We let x x and A A, where, if x is an element of an abstract vector space n, and A = A: n m, then x is a complex column vector of length n whose
Vector and Matrix Norms Vector Space Algebra Matrix Algebra: We let x x and A A, where, if x is an element of an abstract vector space n, and A = A: n m, then x is a complex column vector of length n whose
Chapter 2. General Vector Spaces. 2.1 Real Vector Spaces
 Chapter 2 General Vector Spaces Outline : Real vector spaces Subspaces Linear independence Basis and dimension Row Space, Column Space, and Nullspace 2 Real Vector Spaces 2 Example () Let u and v be vectors
Chapter 2 General Vector Spaces Outline : Real vector spaces Subspaces Linear independence Basis and dimension Row Space, Column Space, and Nullspace 2 Real Vector Spaces 2 Example () Let u and v be vectors
Linear Least Squares. Using SVD Decomposition.
 Linear Least Squares. Using SVD Decomposition. Dmitriy Leykekhman Spring 2011 Goals SVD-decomposition. Solving LLS with SVD-decomposition. D. Leykekhman Linear Least Squares 1 SVD Decomposition. For any
Linear Least Squares. Using SVD Decomposition. Dmitriy Leykekhman Spring 2011 Goals SVD-decomposition. Solving LLS with SVD-decomposition. D. Leykekhman Linear Least Squares 1 SVD Decomposition. For any
The Singular Value Decomposition
 The Singular Value Decomposition We are interested in more than just sym+def matrices. But the eigenvalue decompositions discussed in the last section of notes will play a major role in solving general
The Singular Value Decomposition We are interested in more than just sym+def matrices. But the eigenvalue decompositions discussed in the last section of notes will play a major role in solving general
Review of some mathematical tools
 MATHEMATICAL FOUNDATIONS OF SIGNAL PROCESSING Fall 2016 Benjamín Béjar Haro, Mihailo Kolundžija, Reza Parhizkar, Adam Scholefield Teaching assistants: Golnoosh Elhami, Hanjie Pan Review of some mathematical
MATHEMATICAL FOUNDATIONS OF SIGNAL PROCESSING Fall 2016 Benjamín Béjar Haro, Mihailo Kolundžija, Reza Parhizkar, Adam Scholefield Teaching assistants: Golnoosh Elhami, Hanjie Pan Review of some mathematical
The Singular Value Decomposition and Least Squares Problems
 The Singular Value Decomposition and Least Squares Problems Tom Lyche Centre of Mathematics for Applications, Department of Informatics, University of Oslo September 27, 2009 Applications of SVD solving
The Singular Value Decomposition and Least Squares Problems Tom Lyche Centre of Mathematics for Applications, Department of Informatics, University of Oslo September 27, 2009 Applications of SVD solving
Latent Semantic Models. Reference: Introduction to Information Retrieval by C. Manning, P. Raghavan, H. Schutze
 Latent Semantic Models Reference: Introduction to Information Retrieval by C. Manning, P. Raghavan, H. Schutze 1 Vector Space Model: Pros Automatic selection of index terms Partial matching of queries
Latent Semantic Models Reference: Introduction to Information Retrieval by C. Manning, P. Raghavan, H. Schutze 1 Vector Space Model: Pros Automatic selection of index terms Partial matching of queries
x 3y 2z = 6 1.2) 2x 4y 3z = 8 3x + 6y + 8z = 5 x + 3y 2z + 5t = 4 1.5) 2x + 8y z + 9t = 9 3x + 5y 12z + 17t = 7
 Linear Algebra and its Applications-Lab 1 1) Use Gaussian elimination to solve the following systems x 1 + x 2 2x 3 + 4x 4 = 5 1.1) 2x 1 + 2x 2 3x 3 + x 4 = 3 3x 1 + 3x 2 4x 3 2x 4 = 1 x + y + 2z = 4 1.4)
Linear Algebra and its Applications-Lab 1 1) Use Gaussian elimination to solve the following systems x 1 + x 2 2x 3 + 4x 4 = 5 1.1) 2x 1 + 2x 2 3x 3 + x 4 = 3 3x 1 + 3x 2 4x 3 2x 4 = 1 x + y + 2z = 4 1.4)
The Singular Value Decomposition (SVD) and Principal Component Analysis (PCA)
 Chapter 5 The Singular Value Decomposition (SVD) and Principal Component Analysis (PCA) 5.1 Basics of SVD 5.1.1 Review of Key Concepts We review some key definitions and results about matrices that will
Chapter 5 The Singular Value Decomposition (SVD) and Principal Component Analysis (PCA) 5.1 Basics of SVD 5.1.1 Review of Key Concepts We review some key definitions and results about matrices that will
1. What is the determinant of the following matrix? a 1 a 2 4a 3 2a 2 b 1 b 2 4b 3 2b c 1. = 4, then det
 What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
Principal Component Analysis and Singular Value Decomposition. Volker Tresp, Clemens Otte Summer 2014
 Principal Component Analysis and Singular Value Decomposition Volker Tresp, Clemens Otte Summer 2014 1 Motivation So far we always argued for a high-dimensional feature space Still, in some cases it makes
Principal Component Analysis and Singular Value Decomposition Volker Tresp, Clemens Otte Summer 2014 1 Motivation So far we always argued for a high-dimensional feature space Still, in some cases it makes
The Singular Value Decomposition
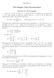 CHAPTER 6 The Singular Value Decomposition Exercise 67: SVD examples (a) For A =[, 4] T we find a matrixa T A =5,whichhastheeigenvalue =5 Thisprovidesuswiththesingularvalue =+ p =5forA Hence the matrix
CHAPTER 6 The Singular Value Decomposition Exercise 67: SVD examples (a) For A =[, 4] T we find a matrixa T A =5,whichhastheeigenvalue =5 Thisprovidesuswiththesingularvalue =+ p =5forA Hence the matrix
Linear Algebra. Session 12
 Linear Algebra. Session 12 Dr. Marco A Roque Sol 08/01/2017 Example 12.1 Find the constant function that is the least squares fit to the following data x 0 1 2 3 f(x) 1 0 1 2 Solution c = 1 c = 0 f (x)
Linear Algebra. Session 12 Dr. Marco A Roque Sol 08/01/2017 Example 12.1 Find the constant function that is the least squares fit to the following data x 0 1 2 3 f(x) 1 0 1 2 Solution c = 1 c = 0 f (x)
Problem set 5: SVD, Orthogonal projections, etc.
 Problem set 5: SVD, Orthogonal projections, etc. February 21, 2017 1 SVD 1. Work out again the SVD theorem done in the class: If A is a real m n matrix then here exist orthogonal matrices such that where
Problem set 5: SVD, Orthogonal projections, etc. February 21, 2017 1 SVD 1. Work out again the SVD theorem done in the class: If A is a real m n matrix then here exist orthogonal matrices such that where
Problem # Max points possible Actual score Total 120
 FINAL EXAMINATION - MATH 2121, FALL 2017. Name: ID#: Email: Lecture & Tutorial: Problem # Max points possible Actual score 1 15 2 15 3 10 4 15 5 15 6 15 7 10 8 10 9 15 Total 120 You have 180 minutes to
FINAL EXAMINATION - MATH 2121, FALL 2017. Name: ID#: Email: Lecture & Tutorial: Problem # Max points possible Actual score 1 15 2 15 3 10 4 15 5 15 6 15 7 10 8 10 9 15 Total 120 You have 180 minutes to
Matrices and Vectors. Definition of Matrix. An MxN matrix A is a two-dimensional array of numbers A =
 30 MATHEMATICS REVIEW G A.1.1 Matrices and Vectors Definition of Matrix. An MxN matrix A is a two-dimensional array of numbers A = a 11 a 12... a 1N a 21 a 22... a 2N...... a M1 a M2... a MN A matrix can
30 MATHEMATICS REVIEW G A.1.1 Matrices and Vectors Definition of Matrix. An MxN matrix A is a two-dimensional array of numbers A = a 11 a 12... a 1N a 21 a 22... a 2N...... a M1 a M2... a MN A matrix can
1 Linearity and Linear Systems
 Mathematical Tools for Neuroscience (NEU 34) Princeton University, Spring 26 Jonathan Pillow Lecture 7-8 notes: Linear systems & SVD Linearity and Linear Systems Linear system is a kind of mapping f( x)
Mathematical Tools for Neuroscience (NEU 34) Princeton University, Spring 26 Jonathan Pillow Lecture 7-8 notes: Linear systems & SVD Linearity and Linear Systems Linear system is a kind of mapping f( x)
Augmented Reality VU Camera Registration. Prof. Vincent Lepetit
 Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
UNIT 6: The singular value decomposition.
 UNIT 6: The singular value decomposition. María Barbero Liñán Universidad Carlos III de Madrid Bachelor in Statistics and Business Mathematical methods II 2011-2012 A square matrix is symmetric if A T
UNIT 6: The singular value decomposition. María Barbero Liñán Universidad Carlos III de Madrid Bachelor in Statistics and Business Mathematical methods II 2011-2012 A square matrix is symmetric if A T
Background Mathematics (2/2) 1. David Barber
 Background Mathematics (2/2) 1 David Barber University College London Modified by Samson Cheung (sccheung@ieee.org) 1 These slides accompany the book Bayesian Reasoning and Machine Learning. The book and
Background Mathematics (2/2) 1 David Barber University College London Modified by Samson Cheung (sccheung@ieee.org) 1 These slides accompany the book Bayesian Reasoning and Machine Learning. The book and
Math 224, Fall 2007 Exam 3 Thursday, December 6, 2007
 Math 224, Fall 2007 Exam 3 Thursday, December 6, 2007 You have 1 hour and 20 minutes. No notes, books, or other references. You are permitted to use Maple during this exam, but you must start with a blank
Math 224, Fall 2007 Exam 3 Thursday, December 6, 2007 You have 1 hour and 20 minutes. No notes, books, or other references. You are permitted to use Maple during this exam, but you must start with a blank
Econ Slides from Lecture 7
 Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
Designing Information Devices and Systems II
 EECS 16B Fall 2016 Designing Information Devices and Systems II Linear Algebra Notes Introduction In this set of notes, we will derive the linear least squares equation, study the properties symmetric
EECS 16B Fall 2016 Designing Information Devices and Systems II Linear Algebra Notes Introduction In this set of notes, we will derive the linear least squares equation, study the properties symmetric
Math 369 Exam #2 Practice Problem Solutions
 Math 369 Exam #2 Practice Problem Solutions 2 5. Is { 2, 3, 8 } a basis for R 3? Answer: No, it is not. To show that it is not a basis, it suffices to show that this is not a linearly independent set.
Math 369 Exam #2 Practice Problem Solutions 2 5. Is { 2, 3, 8 } a basis for R 3? Answer: No, it is not. To show that it is not a basis, it suffices to show that this is not a linearly independent set.
Linear Algebra- Final Exam Review
 Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
MATH 304 Linear Algebra Lecture 34: Review for Test 2.
 MATH 304 Linear Algebra Lecture 34: Review for Test 2. Topics for Test 2 Linear transformations (Leon 4.1 4.3) Matrix transformations Matrix of a linear mapping Similar matrices Orthogonality (Leon 5.1
MATH 304 Linear Algebra Lecture 34: Review for Test 2. Topics for Test 2 Linear transformations (Leon 4.1 4.3) Matrix transformations Matrix of a linear mapping Similar matrices Orthogonality (Leon 5.1
MATH 240 Spring, Chapter 1: Linear Equations and Matrices
 MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
Orthonormal Transformations and Least Squares
 Orthonormal Transformations and Least Squares Tom Lyche Centre of Mathematics for Applications, Department of Informatics, University of Oslo October 30, 2009 Applications of Qx with Q T Q = I 1. solving
Orthonormal Transformations and Least Squares Tom Lyche Centre of Mathematics for Applications, Department of Informatics, University of Oslo October 30, 2009 Applications of Qx with Q T Q = I 1. solving
Least Squares Optimization
 Least Squares Optimization The following is a brief review of least squares optimization and constrained optimization techniques. Broadly, these techniques can be used in data analysis and visualization
Least Squares Optimization The following is a brief review of least squares optimization and constrained optimization techniques. Broadly, these techniques can be used in data analysis and visualization
CS168: The Modern Algorithmic Toolbox Lecture #10: Tensors, and Low-Rank Tensor Recovery
 CS168: The Modern Algorithmic Toolbox Lecture #10: Tensors, and Low-Rank Tensor Recovery Tim Roughgarden & Gregory Valiant May 3, 2017 Last lecture discussed singular value decomposition (SVD), and we
CS168: The Modern Algorithmic Toolbox Lecture #10: Tensors, and Low-Rank Tensor Recovery Tim Roughgarden & Gregory Valiant May 3, 2017 Last lecture discussed singular value decomposition (SVD), and we
Chapter 3: Theory Review: Solutions Math 308 F Spring 2015
 Chapter : Theory Review: Solutions Math 08 F Spring 05. What two properties must a function T : R m R n satisfy to be a linear transformation? (a) For all vectors u and v in R m, T (u + v) T (u) + T (v)
Chapter : Theory Review: Solutions Math 08 F Spring 05. What two properties must a function T : R m R n satisfy to be a linear transformation? (a) For all vectors u and v in R m, T (u + v) T (u) + T (v)
Least Squares Optimization
 Least Squares Optimization The following is a brief review of least squares optimization and constrained optimization techniques. I assume the reader is familiar with basic linear algebra, including the
Least Squares Optimization The following is a brief review of least squares optimization and constrained optimization techniques. I assume the reader is familiar with basic linear algebra, including the
IV. Matrix Approximation using Least-Squares
 IV. Matrix Approximation using Least-Squares The SVD and Matrix Approximation We begin with the following fundamental question. Let A be an M N matrix with rank R. What is the closest matrix to A that
IV. Matrix Approximation using Least-Squares The SVD and Matrix Approximation We begin with the following fundamental question. Let A be an M N matrix with rank R. What is the closest matrix to A that
CS6964: Notes On Linear Systems
 CS6964: Notes On Linear Systems 1 Linear Systems Systems of equations that are linear in the unknowns are said to be linear systems For instance ax 1 + bx 2 dx 1 + ex 2 = c = f gives 2 equations and 2
CS6964: Notes On Linear Systems 1 Linear Systems Systems of equations that are linear in the unknowns are said to be linear systems For instance ax 1 + bx 2 dx 1 + ex 2 = c = f gives 2 equations and 2
Linear Algebra (Review) Volker Tresp 2017
 Linear Algebra (Review) Volker Tresp 2017 1 Vectors k is a scalar (a number) c is a column vector. Thus in two dimensions, c = ( c1 c 2 ) (Advanced: More precisely, a vector is defined in a vector space.
Linear Algebra (Review) Volker Tresp 2017 1 Vectors k is a scalar (a number) c is a column vector. Thus in two dimensions, c = ( c1 c 2 ) (Advanced: More precisely, a vector is defined in a vector space.
Applied Mathematics 205. Unit II: Numerical Linear Algebra. Lecturer: Dr. David Knezevic
 Applied Mathematics 205 Unit II: Numerical Linear Algebra Lecturer: Dr. David Knezevic Unit II: Numerical Linear Algebra Chapter II.3: QR Factorization, SVD 2 / 66 QR Factorization 3 / 66 QR Factorization
Applied Mathematics 205 Unit II: Numerical Linear Algebra Lecturer: Dr. David Knezevic Unit II: Numerical Linear Algebra Chapter II.3: QR Factorization, SVD 2 / 66 QR Factorization 3 / 66 QR Factorization
EIGENVALUES AND SINGULAR VALUE DECOMPOSITION
 APPENDIX B EIGENVALUES AND SINGULAR VALUE DECOMPOSITION B.1 LINEAR EQUATIONS AND INVERSES Problems of linear estimation can be written in terms of a linear matrix equation whose solution provides the required
APPENDIX B EIGENVALUES AND SINGULAR VALUE DECOMPOSITION B.1 LINEAR EQUATIONS AND INVERSES Problems of linear estimation can be written in terms of a linear matrix equation whose solution provides the required
Linear Algebra Review. Fei-Fei Li
 Linear Algebra Review Fei-Fei Li 1 / 51 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
Linear Algebra Review Fei-Fei Li 1 / 51 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
Cheat Sheet for MATH461
 Cheat Sheet for MATH46 Here is the stuff you really need to remember for the exams Linear systems Ax = b Problem: We consider a linear system of m equations for n unknowns x,,x n : For a given matrix A
Cheat Sheet for MATH46 Here is the stuff you really need to remember for the exams Linear systems Ax = b Problem: We consider a linear system of m equations for n unknowns x,,x n : For a given matrix A
ft-uiowa-math2550 Assignment OptionalFinalExamReviewMultChoiceMEDIUMlengthForm due 12/31/2014 at 10:36pm CST
 me me ft-uiowa-math255 Assignment OptionalFinalExamReviewMultChoiceMEDIUMlengthForm due 2/3/2 at :3pm CST. ( pt) Library/TCNJ/TCNJ LinearSystems/problem3.pg Give a geometric description of the following
me me ft-uiowa-math255 Assignment OptionalFinalExamReviewMultChoiceMEDIUMlengthForm due 2/3/2 at :3pm CST. ( pt) Library/TCNJ/TCNJ LinearSystems/problem3.pg Give a geometric description of the following
Applied Linear Algebra in Geoscience Using MATLAB
 Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Basic Math for
 Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
Chapters 5 & 6: Theory Review: Solutions Math 308 F Spring 2015
 Chapters 5 & 6: Theory Review: Solutions Math 308 F Spring 205. If A is a 3 3 triangular matrix, explain why det(a) is equal to the product of entries on the diagonal. If A is a lower triangular or diagonal
Chapters 5 & 6: Theory Review: Solutions Math 308 F Spring 205. If A is a 3 3 triangular matrix, explain why det(a) is equal to the product of entries on the diagonal. If A is a lower triangular or diagonal
2. Linear algebra. matrices and vectors. linear equations. range and nullspace of matrices. function of vectors, gradient and Hessian
 FE661 - Statistical Methods for Financial Engineering 2. Linear algebra Jitkomut Songsiri matrices and vectors linear equations range and nullspace of matrices function of vectors, gradient and Hessian
FE661 - Statistical Methods for Financial Engineering 2. Linear algebra Jitkomut Songsiri matrices and vectors linear equations range and nullspace of matrices function of vectors, gradient and Hessian
ORTHOGONALITY AND LEAST-SQUARES [CHAP. 6]
![ORTHOGONALITY AND LEAST-SQUARES [CHAP. 6] ORTHOGONALITY AND LEAST-SQUARES [CHAP. 6]](/thumbs/87/96810285.jpg) ORTHOGONALITY AND LEAST-SQUARES [CHAP. 6] Inner products and Norms Inner product or dot product of 2 vectors u and v in R n : u.v = u 1 v 1 + u 2 v 2 + + u n v n Calculate u.v when u = 1 2 2 0 v = 1 0
ORTHOGONALITY AND LEAST-SQUARES [CHAP. 6] Inner products and Norms Inner product or dot product of 2 vectors u and v in R n : u.v = u 1 v 1 + u 2 v 2 + + u n v n Calculate u.v when u = 1 2 2 0 v = 1 0
MATH36001 Generalized Inverses and the SVD 2015
 MATH36001 Generalized Inverses and the SVD 201 1 Generalized Inverses of Matrices A matrix has an inverse only if it is square and nonsingular. However there are theoretical and practical applications
MATH36001 Generalized Inverses and the SVD 201 1 Generalized Inverses of Matrices A matrix has an inverse only if it is square and nonsingular. However there are theoretical and practical applications
MATH 4211/6211 Optimization Constrained Optimization
 MATH 4211/6211 Optimization Constrained Optimization Xiaojing Ye Department of Mathematics & Statistics Georgia State University Xiaojing Ye, Math & Stat, Georgia State University 0 Constrained optimization
MATH 4211/6211 Optimization Constrained Optimization Xiaojing Ye Department of Mathematics & Statistics Georgia State University Xiaojing Ye, Math & Stat, Georgia State University 0 Constrained optimization
Expectation Maximization
 Expectation Maximization Machine Learning CSE546 Carlos Guestrin University of Washington November 13, 2014 1 E.M.: The General Case E.M. widely used beyond mixtures of Gaussians The recipe is the same
Expectation Maximization Machine Learning CSE546 Carlos Guestrin University of Washington November 13, 2014 1 E.M.: The General Case E.M. widely used beyond mixtures of Gaussians The recipe is the same
EE731 Lecture Notes: Matrix Computations for Signal Processing
 EE731 Lecture Notes: Matrix Computations for Signal Processing James P. Reilly c Department of Electrical and Computer Engineering McMaster University October 17, 005 Lecture 3 3 he Singular Value Decomposition
EE731 Lecture Notes: Matrix Computations for Signal Processing James P. Reilly c Department of Electrical and Computer Engineering McMaster University October 17, 005 Lecture 3 3 he Singular Value Decomposition
Dimension and Structure
 96 Chapter 7 Dimension and Structure 7.1 Basis and Dimensions Bases for Subspaces Definition 7.1.1. A set of vectors in a subspace V of R n is said to be a basis for V if it is linearly independent and
96 Chapter 7 Dimension and Structure 7.1 Basis and Dimensions Bases for Subspaces Definition 7.1.1. A set of vectors in a subspace V of R n is said to be a basis for V if it is linearly independent and
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Basic Information Instructor: Professor Ron Sahoo Office: NS 218 Tel: (502) 852-2731 Fax: (502)
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Basic Information Instructor: Professor Ron Sahoo Office: NS 218 Tel: (502) 852-2731 Fax: (502)
j=1 u 1jv 1j. 1/ 2 Lemma 1. An orthogonal set of vectors must be linearly independent.
 Lecture Notes: Orthogonal and Symmetric Matrices Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk Orthogonal Matrix Definition. Let u = [u
Lecture Notes: Orthogonal and Symmetric Matrices Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk Orthogonal Matrix Definition. Let u = [u
Chapter 7: Symmetric Matrices and Quadratic Forms
 Chapter 7: Symmetric Matrices and Quadratic Forms (Last Updated: December, 06) These notes are derived primarily from Linear Algebra and its applications by David Lay (4ed). A few theorems have been moved
Chapter 7: Symmetric Matrices and Quadratic Forms (Last Updated: December, 06) These notes are derived primarily from Linear Algebra and its applications by David Lay (4ed). A few theorems have been moved
Image Registration Lecture 2: Vectors and Matrices
 Image Registration Lecture 2: Vectors and Matrices Prof. Charlene Tsai Lecture Overview Vectors Matrices Basics Orthogonal matrices Singular Value Decomposition (SVD) 2 1 Preliminary Comments Some of this
Image Registration Lecture 2: Vectors and Matrices Prof. Charlene Tsai Lecture Overview Vectors Matrices Basics Orthogonal matrices Singular Value Decomposition (SVD) 2 1 Preliminary Comments Some of this
