OPTIMUM FILTERS (5) DISCRETE KALMAN FILTER. Appendix 7B. Derivation of matrix differentiation formulas
|
|
|
- Meghan Merritt
- 6 years ago
- Views:
Transcription
1 OPTIMUM FILTERS (5) DISCRETE KALMAN FILTER Klm filter: Klm filterig roblem Klm reitio roblem Summry of the imlemettio of isrete Klm filter Stey stte roerties of Klm filters Aeix 7B Deritio of mtrix ifferetitio formuls 50
2 DISCRETE KALMAN FILTER Klm filters re otimum filters tht re ifferet from Wieer filters he the folloig istitie fetures: (i) the roblems re formulte i terms of stte-se moel (or stte-se form); (ii) the solutio of the roblems is omute reursiely; (iii) they be use to tret sttiory rom roesses, s ell s o-sttiory roesses As e lert from the reious letures, otimum Wieer filter is esige usig the Wieer-of equtios i hih the utoorreltio r x () of the oise obsertio (tht otis the esire sigl ( ith r () ) the ross-orreltio r x () re use Use of r (), r x () r x () iites tht ( re ie-sese sttiory s ell s joitly ie-sese sttiory rom roesses Wheres, for o-sttiory rom roess, its sttistil roerties re ot sttiory; i other or, they re time ryig For exmle, etermiisti siusoil sigl ( Asi( ω + ϕ) iterfere ith oise ( is o-sttiory rom roess, x ( ( + (, beuse the me of, m x ( Asi( ω + ϕ ), x ee o time, the utoorreltio, r ( +, r ( ) + ( A ) os( ω) os ω( + ) + ϕ, ee ot oly o time lg but lso o time The ross-orreltio ( +, ( A ) os( ω) os ω( + ) + ϕ lso ee o time r x Therefore, i the otimum sese Wieer filter oly be use to tret sttiory rom roesses As e ill see belo, Wieer filterig roblems re just seil se, the stey-stte se, of Klm filterig roblems Klm filter: Klm filterig roblem Klm filterig resses the geerl roblem of tryig to get the best estimte of the stte of roess goere by the stte equtio (lier stohsti ifferee equtio x ( A( + ( (17) from mesuremets gie by the obsertio equtio y ( + ( (18) Fig 19 The igrm for ostrutig Klm filter Seifilly, he the mesuremets (mesuremet etor) re iut to the Klm filter h(, the filter oututs, hih is the best lier estimte etor of the stte etor of legth bse o the obsertios y (l) for 0 l (Fig 19) The best estimte of,, from the Klm filter is relize by miimizig the me-squre error 51
3 0 { } E e( ) ξ ( tr (19) here P ( E e( e ( (0) is lle estimtio error orie mtrix ( estimte error, gie by e( e (, e(,, e( ) mtrix), e ( ( etor of legth ) is the T [,,, ) ) T tr { A} mes the tre of mtrix A, hih is efie s the sum of the terms log the igol of A, (1) tr A () mm m 1 0 Thus, tr{ ( } E e( ) P Aother error orie mtrix tht e ee i eriig the Klm filter is reitio error orie mtrix, efie s ( E{ ( e e ( } P (3) here e ( (4) is the oe-ste reitio error ( etor of legth ), i hih is the reitio etor of the stte etor of legth, bse o the obsertios y (l) for 0 l To erie the Klm filter e shll rry out reursie roeure of to stes: reitio usig reious mesuremets, estimtio usig e mesuremet (refer to Fig 0) I the first ste, the stte is reite usig the reious obsertios l) u to time l 1 so s to obti I the seo ste, the e iformtio ε ( yˆ( (the iotio roess of ) from e mesuremet is e to the estimte so s to get the best estimte of, Iitiliztio ˆx (0 0) E{0)} Ste 1: reitig 1) from ˆx (0 0) > 1 0) A(0)ˆ(0 x 0) ; Ste : estimtig 1) by ig e ifo ε (1) > 1 1) 1 0) 1) ε (1) Reet 1: reitig ) from ˆx (1 1) > 1) A(1)ˆ(1 1 x ) ; Reet : estimtig ) by ig e ifo ε () > ) 0) ) ε () Reet 1: reitig > A( ˆ( x ; Reet : estimtig by ig e ifo ε ( > ε( Fig 0 The to-ste reursie roeure of eriig Klm filter Suose tht gie rom roess hs iitil stte 0) ith gie estimte ˆx (0 0) E{0)} The iitil estimtio error orie mtrix (Eq (0)) for this estimte is (0 0) E{ e(0 0) e (0 0) } With the gie estimte P ˆx (0 0) E{0)}, e first reit 1) usig the reltio ˆx (1 0) A(0) ˆx (0 0) 5
4 fi ŷ (1 0) 1) ˆx (1 0) s ell Seoly, e me otiml use of the ilble mesuremet 1) by ig to ˆx (1 0) the e iformtio ε ( 1) 1) yˆ(1 0) (the iotio roess of 1)), fi the best estimte of stte 1), ˆx (1 1) Otiml use of ε (1) is me by eightig ftor 1) tht miimizes the me-squre error ( 0 ξ t time 1, (1) tr{ 1 1) } E e( 1 1 ) ξ Reetig the boe to stes for the ext time istt, e use ˆx (1 1) to reit ) usig the reltio 1) A(1)ˆ(1 1) x fi y ˆ( 1) )ˆ( x 1) The e ute ˆx ( 1) by ig e iformtio ε ( ) ) yˆ( 1) from the ext ilble mesuremet ), fi the best estimte of ), ˆx ( ), by otimizig ), the eight o () 0 ε, tht miimizes () tr{ ) } E e( ) ξ We rry o this util time, the e formulte reursie roeure for time ; tht is for eh >0, gie P (, e reit obti ), the e me otiml use of the e iformtio ε ( yˆ( from e ilble mesuremet to fi the best estimte of the stte by fiig otiml tht miimizes the me-squre error 0 { } E e( ) ξ ( tr The Klm filter is estblishe bse o the boe reursie roeure, s follos I the first ste, is rojete he (reite) i the stte trsitio mtrix i the folloig mer A( ˆ( x (5) hih is obtie by igorig the otributio of ( i the stte equtio (Eq (17)) beuse ( is hite oise roess ith zero me is ot orrelte ith its reious lues, (l) for l< The reitio error i this se is e ( A ( + ( A( ˆ( x A ( ) e( + ( (6) Sie e ( is uorrelte ith ( (ue to the ft tht ( is hite oise thus uorrelte ith (l) for l ) so tht E{ e ( ( } 0, the reitio error orie mtrix beomes { e( e ( } A( A ( Q ( ) P ( ) E + (7) This omletes the first ste of eriig the Klm filter I the seo ste, the otimum estimtio of is oute by ig the e mesuremet to the estimte i terms of the iotio roess of, ε ( yˆ( (8) hih is the error betee its reitio y ˆ ( reresets the e iformtio tht ot be reite by y ˆ ( The reit y ˆ ( is gie by y ˆ ( ˆ( x (9) hih is erie by igorig otributio of ( i the obsertio equtio (Eq (18)) beuse ( is ssume to be zero-me hite oise is ot orrelte ith its reious lues, (l) for l< Therefore, the otimum estimte of turs out to be [ yˆ( ) (30) i hih the iotios roess is sle by otimum gi tht is etermie by miimizig mesqure error ξ ( Isertig Eq (9) i Eq (30), e he 53
5 [ ˆ( x ) () A feture i this equtio is tht the estimte is relte ith, the reit of usig reious lues of l) u to time istt l 1 Alyig Eq (5) to Eq () yiel A( ˆ( x A( ˆ( x (3) hih is the reursie reltio betee the estimte the reious estimte The gi is o s the Klm gi The reursie reltio i Eq (3) orreso to the isrete Klm filter, hih is reursie filter illustrte i Fig 1 Fig 1 The isrete Klm filter As e ill see belo, the reursie otimum estimtio of results from the otimiztio of Klm gi ξ ( tr, lie e i for otimum Wieer filters It is beuse the by miimizig MSE Klm gi is otimum tht the Klm filter is otimum filter! I geerl, A( 1), re time ryig, thus the Klm filters re lible to o-sttiory rom roesses s ell The estimte error (see Eq (1)) is e( x ( + ( ˆ( x e( 1) e( ( I K C e K (37) [ ( ( ( ( ( i hih Eqs () (18) re use Sie ( ( re uorrelte, the e( 1) both re uorrelte ith ( Thus, the reitio error orie mtrix beomes P ( E{ e( e ( } [ I [ I Q ( K ( (38) With Eq (38), e miimize the me squre error ( tr{ } ξ to get the otimum Klm gi To o so e ee to use the folloig mtrix ifferetitio formuls, tr { KC} C K (39) tr { KCK } KC K (40) here the eritie ith reset to the mtrix K mes 1 ; (41) K 1 54
6 The eritios of Eqs (39) (40) re gie i Aeix 7B With the hel of Eqs (39) (40) settig ξ ( 0, e he ξ ( tr { } [ I C ( Q ( Solig Eq (4) for e get the otimum Klm gi, 0 (4) [ C ( + Q ( ) 1 K ( C ( (43) It is iterestig to loo ito ho is te to mesuremet oise Whe Q ( ) 0 (mely, (0) the ( ) 1 K C ( so tht C (, tht is, the estimte is ietil to the stte Whe Q (, the 0 I this se, Eq (3) beomes A( ˆ( x, hih shos tht the mesuremets beome omletely urelible re ot use i the estimtio Lie e h miimum me squre error for otimum Wieer filter ue to the orthogolity riile, e fi the miimum me squre error for the otimum Klm filter by usig Eq (4) Re-rrgig the error orie mtrix P ( i Eq (38) i the folloig mer, P ( [ I + [ I C ( Q ( K ( (44) ) it follos from Eq (4) tht the seo term i the bres {} i Eq (44) is zero Thus, e obti the miimize error orie mtrix P ( I (45) ) Sie the Klm gi the error orie mtrix P ( re ieeet of the t, they be omute off-lie It shoul be oite out tht oe of the ery elig fetures of the Klm filter is the reursie ture (sho i Fig 0), hih mes rtil imlemettios muh more fesible th imlemettio of Wieer filter hih is esige to oerte o ll of the t iretly for eh estimte The Klm filter iste reursiely oitios the urret estimte o ll of the st mesuremet Klm reitio roblem A (lier) reitio of sigl is oere ith the estimtio (reitio of +m) for m>0 usig the mesuremets l) u to time l It be oe-ste or multile-ste reitio A Oe-ste Klm reitio For oe-ste reitio roblem, e erform oe-ste forr time shift o Eq (5), ie, rele ith +1, the e he + 1 A( ˆ( x (46) Isertig Eq () ito Eq (46), e obti the oe-ste isrete Klm filter + 1 A( ˆ( x + A( ˆ( x (47) hih is the reursie reltio betee the reit + 1 the reious reit For the reursie reitio reltio, e itroue Klm reitio gi K ( ) K ( A( A ( C ( [ C ( + Q ( 1 (48) With Klm reitio gi K ( ), Eq (47) beomes + 1 A( ˆ( x + K ( ˆ( x (49) 55
7 I reltio to the reursie reitio, it is iterestig to stuy the reitio error orie mtrix, P ( + 1 E e( + 1 e ( + 1 (50) Sie e ( ) + 1 A ( + ( + 1) A( ˆ( x K ( [ + ( ˆ( x A ( e( ) + ( + 1) K ( [ e( + ( [ A( K ( e( + ( + 1) K ( ( (51) (+1) e( 1) both re uorrelte ith (, the + 1 A( ) A ( + Q ( K ( A ( Usig Eq (48) i the boe equtio, e my he P ( + 1 A( A ( + Q ( A( C ( [ C ( + Q ( A ( (5) hih is o s Riti equtio tht gies the reursie reltio betee P ( + 1 P ( The best oe-ste reitio of is esily obtie from Eq (9) y ˆ( )ˆ( x + 1 (53) here + 1 is gie i Eq (47) or Eq (49) B m-ste Klm reitio A m-ste reitio of sigl, eote by + m for m>0, mes tht e reit the sigl l) t l+m usig the lues of mesuremet u to time, it be obtie by exteig the reltio i Eq (5) otig tht oly the lues of u to time re use, i the folloig y + m A( + m )ˆ( x + m (54) Performig the reursie omuttio o Eq (54), + m A( + m )ˆ( x + m A( + m ) A( + m )ˆ( x + m (55) e get the m-ste reitio of m 1 + m A( + ) (56) 0 hih is etermie by the estimte Similrly, by exteig the reltio i Eq (9) otig tht oly the sigl lues u to time re use, e fi the best m-ste reitio of m 1 ˆ y ( + m + m)ˆ( x + m A( + ) (57) 0 Summry of the imlemettio of isrete Klm filter Stte equtio: x ( A( + ( Obsertio (or mesuremet) equtio: y ( + ( Iitil lue: xˆ (0 0) E{ 0)}, 1 etor (ue to () for 1,,, ) 56
8 P (0 0) E{ 0) x (0)}, iitil error orie mtrix Reursie omuttio: For 1,, P ( ) A( A ( + Q ( (7) [ C ( + Q ( ) 1 K ( C ( (43) [ I 1) P ( (45) A( ˆ( x (5) [ ˆ( x ) () ltertiely, Eq () ith Eq (5) iserte i, A( ˆ( x A( ˆ( x (3) The oe-ste reitio of is + 1 A( ˆ( x + A( ˆ( x (47) The best m-ste reitio of is m 1 + m A( + ) (56) 0 The best m-ste reitio of is m 1 ˆ y ( + m + m)ˆ( x + m A( + ) (57) 0 Riti equtio is P ( + 1 A ( ) A ( + Q ( A( C ( [ C ( + Q ( A ( P ( P ( re error orie mtries is r mtrix For sigle obsertio, is 1 etor The roess hite oise rie mtrix Q ( E{ ( ( } B B ( σ is mtrix ( The mesuremet oise rie mtrix Q ( E{ ( ( } is r r mtrix For sigle obsertio, ( ) Q σ is slr Exmle 14 Klm filter for estimtig uo DC oltge Suose tht the mesuremet of uo DC oltge is orrute by oise ( tht is hrterize by zero-me hite oise roess ith rie σ Fi the Klm filter of the form A( ˆ( x A( ˆ( x for the estimtio of the uo DC oltge Solutio Sie is DC oltge, the the stte equtio be exresse s 1) The mesuremet equtio is + ( From the stte se form (the boe equtios), e my fi tht A( 1, 1, Q ( ) 0, ( ) Q σ Sie is slr, the e my he P ( 57
9 [ + 1 σ P σ σ ( [ 1 1 ( 1) P + σ ( 1) ( 1 1) P + σ P + σ P σ ( σ + σ Writig reursiely s follos 0 0) σ 1 1) 0 0) + σ 1 1) σ ) 1 1) + σ ) σ 3 3) ) + σ 0 0) σ 0 0) + σ 0 0) σ 30 0) + σ e my ifer geerl exressio for s follos 0 0) σ 0 0) + σ Sie 0 0) σ 0 0) +σ the the Klm filter for estimtig the uo DC oltge beomes 0) xˆ ( + [ 0) + σ Note tht 0 s, the, hih mes tht rohes stey stte lue If σ (hih imlies tht the mesuremets re omletely urelible), the 0, the estimte is I this se, the mesuremets re igore ˆx (0 0), the iitil estimte, hih hs error rie 0 0) If ˆx (0 0) 0 0 0) (hih orreso to the se of o riori iformtio bout ), the 1/, the estimte beomes 1 1 ˆ( + + x ) hih is simly reursie imlemettio of the smle me 1 xˆ ( ) 1 Exmle 15 Klm filter for estimtig AR(1) roess Cosier tht AR(1) roess 08 1) + ( 58
10 (here ( is hite oise ith rie σ 036) is mesure i oisy eiromet, s follos + ( here ( is the mesuremet oise, hite oise roess ith zero me uit rie, is uorrelte ith ( Fi Klm filter tht gies best estimte of i the folloig mer, A( ˆ( x A( ˆ( x Solutio To fi the Klm filter, e shll etermie the Klm gi Form the gie equtios, it follos tht A( 1) 08, B( 1 1, Q BB σ σ 036 Sie the stte etor is slr, the the estimtio equtio beomes [ 08 ) 08 e lso he P ( [ ) [ 1 1) K ( P ( Isertig K ( [ ito ( [ 1 P ( 1 ( ) ( 1) 1 P P P yiel Thus, Notig tht is zero-me roess ith x Q σ 1, r ( ) 0 8, ssumig tht ˆx (0 0) E{0)}0 P (0 0) E{ 0) } (0) 1, the reursie lultios of the Klm gi r x the error ories 1) for the first fe lues re sho i the folloig tble The Klm gi error ories ) From the tble e see tht fter fe itertios, 1) roh their stey-stte lues Thus, the Klm filter te to its stey-stte solutio Re-ritig the boe equtio i the folloig y, ˆ( x , or xˆ ( ( q ) 1 05q omrig it ith the IIR usl Wieer filter i Exmle 5, e see tht both ( q ) 's re ietil P ito 1 Substitutig ( K ( K ( K ( + 1, e he here is use Sie rohes ostt s, the e my ssume tht lim lim K, hih is lle stey-stte solutio The boe equtio beomes, 064K K, or K + 115K K
11 Solig the boe equtio for K, e my he K 0375 (other solutio, K 15, is uresoble thus, isre); lim 08 K Beuse the stey-stte solutio of for sttiory roess is ostt, the it is ieeet of iitil lue 0 0) (0)) I other or, the iitil lue 0 0) oes ot ffet the stey-stte solutio Exmle 15 shos tht i the se of stey stte ( ) the error orie mtries P ( P ( re ifferet, tht is, lim ) lim Therefore, if e ssume lim P ( P, the e shoul ssume lim P ( P', beuse P P' i most ses Stey stte roerties of Klm filters As e he see i Exmle 15, the stey stte solutio of the Klm filter is ietil to the Wieer filter I other or, the Wieer filter is seil se of the Klm filter i the stey stte se ere e re goig to el ith the stey stte roerties of Klm filters For WSS roess, eg, ARMA roess ( of the form ( ( q ) (, the stte-se form is of the form x ( A + B( (58) y ( Cx ( + ( (58b) here A, B, C re ll ostt mtries, ( ( he the ries of σ σ ith orresoig rie mtries Q E{ ( ( } BB Q σ σ, resetiely A Stey-stte Klm gi, estimtio error, reitio error I this se,, P ( P ( ) roh their stey stte lues for, mely, e my he lim K ( K, lim P ( lim P, lim P ( lim P ( ) P' I geerl, lim P ( lim ) For gie A, B, C, Q Q, the stey-stte reitio error lim P ( + 1 lim P ( P' be etermie usig the Riti equtio i the folloig mer, AP' A Q AP ' C [ CP' C + Q CP' A P' + (59) Whe AI, Eq (59) is of simler form 1 P ' C CP ' C Q CP Q 0 (59') ' + + Whe the reitio error P' is fou, the stey-stte Klm gi lim K ( K be etermie by [ CP' C + Q 1 K P' C (60) the stey-stte estimtio error lim P ( lim P be obtie ith [ I KC P' P (61) B Stey-stte system futio for estimtio ie, From Eq (3), it follos tht A + K CA A KCA + K, ) 60
12 [ I KC A K + The q-trsformig of the boe equtio yiel I I KC Aq K, { } ) the system futio for estimtio is, thus, etermie i the folloig y here { I [ I KC Aq } K ( q ), (6) ) { I [ I KC A } K ( q q (63) C Stey-stte system futio for reitio of Oe ste forr shiftig A yiel + 1 A, from Eqs (3) (63), e my he the oe-ste reitio of s follos + 1 A A( q ) (64) A I I KC Aq K ( q ) here { } ) 1 ( ) A( q ) A{ I [ I KC Aq } K Altertiely, sie ˆ( + 1 A + AK[ C 1 q (65) x e he + 1 A AKC + AK, ie, [ KC AK + 1 A I The q-trsform of the boe equtio is I A I KC q + 1 AK { } ) the system futio beomes here { I A[ I KC q } AK ( q ), + 1, (66) 1 ) { I A[ I KC } AK 1 ( q q (67) The best m-ste reitio of is m 1 + m A (68) 0 The best m-ste reitio of is m 1 y ˆ( + m C + m C A (69) 0 Exmle 16 A usl Wieer reitio filter - stey-stte solutio of Klm reitio filter Cosier rom roess of the form, x ( + ( here ( is zero-me hite oise ith rie σ 1 < 1, ssume y ( + ( to be oisy mesuremet of here ( is zero-me hite oise ith uit rie uorrelte ith ( 61
13 () Fi the stey-stte Klm filter gi K, ie, K lim, i terms of ; (b) Sho tht the usl IIR Wieer filter for oe-ste reitio stisfies the stey-stte solutio of the Klm filter s follos K Note tht y ˆ( ) + 1 Solutio () From gie stte-se form, it follos tht A, C1, The Riti equtio P ' AP' A + Q AP' C beomes of the slr form, P' P ' P' + 1 P' + 1 P ' P' 0 [ CP' C + Q CP' A Solig the boe equtio for P' osierig P ' The stey-stte Klm gi be fou by [ CP' C + Q 1 Q σ σ 1, Q 1 P' 0, e te the ositie soltio s follos P' K P' C ; > K P' (b) Isertig x ( + ( ito y ( + ( tig the q-trsform, e he ( y ( + ( 1 q The oer setrum of is z z P z y ( ) z 1 z 1 z 1 z ( )( ) Setrlly ftorig P y (z) yiel P y here ( 1 z )( 1 z) ( 1 z )( 1 z) ( z) σ ε 4 ( ) ( )( ) (tig ito out <1), σ ε + Thus, e my rite 1 q ε ( 1 q From Eq (166) i Otimum Filters (4) (or Exmle 6 i Otimum Filters ()) e fi the oe-ste reitio of, + yˆ( q From Eq (69), it follos tht y ˆ( + 1 C Thus, the boe equtio be exresse s
14 Sie xˆ ( + 1 ( ) [ ) ( ) the e he K ( )( ) ( ) K Exmle 17 Stey-stte solutio of Klm filter Cosier rom roess of the form, x ( + ( here ( is zero-me hite oise ith rie σ 1 < 1, ssume y ( + ( to be oisy mesuremet of here ( is zero-me hite oise ith uit rie Assumig tht the stey-stte Klm gi lim K is o ostt, () fi the stey-stte system futio ( q ) of the Klm filter for the otiml to-ste reitio, +, of (b) Sho tht the stey-stte Klm gi K stisfies 0 K < 1 the Klm filter ( q ) i () is stble Solutio () From gie stte-se form, it follos tht A, C1, B1, σ Q BB σ 1, Q 1 Sie the stey-stte Klm gi lim K is o is slr, the oe-ste reitio [ ( C ) + 1 A + AK y i this se beomes K The q-trsform of the boe equtio gies K xˆ ( K q ( ) Oe-ste forr shiftig of A( ˆ( x yiel + 1 A( ˆ( x Moreoer, m 1 sie the m-ste reitio of is + m A, e he the to-ste reitio of 0 + AA A + 1 here ( q ) K 1 ( 1 K ) q 1 (b) Sie K P' C [ CP' C + Q P' ( P' + 1) K ( ) ( 1 K ) q q is the esire system futio for the otiml to-ste reitio he (1 K) < 1 so tht the ole q ( 1 K) P' > 0, the 0 K < 1 As < 1 0 K < 1 is isie the uit irle, thus ( q ) is stble, e 63
15 Aeix 7B Deritio of mtrix ifferetitio formuls I this eix e ill erie the mtrix ifferetitio formuls i Eqs (39) (40) ere e osier the rel lue mtries so tht { KC} K tr T T C { KCK } K tr KC For the omlex-lue mtries e my rele the trsose ith the ojugte trsose 1 Assumig 3x lue mtrix 1 13 K 1, x3 mtrix C, the e he KC +, tr KC s The eritie of KC ith reset to K is 1 1 { KC} K tr K 1 1 T T C > tr { KC} C K Assumig 3x mtrix 1 T 1 K 1 x mtrix C, K, the e he KCK T K 1 T + + { T tr KCK } s T Thus { KCK } K tr K KC
Section 2.2. Matrix Multiplication
 Mtri Alger Mtri Multiplitio Setio.. Mtri Multiplitio Mtri multiplitio is little more omplite th mtri itio or slr multiplitio. If A is the prout A of A is the ompute s follow: m mtri, the is k mtri, 9 m
Mtri Alger Mtri Multiplitio Setio.. Mtri Multiplitio Mtri multiplitio is little more omplite th mtri itio or slr multiplitio. If A is the prout A of A is the ompute s follow: m mtri, the is k mtri, 9 m
First assignment of MP-206
 irt igmet of MP- er to quetio - 7- Norml tre log { : MP Priipl tree: I MP II MP III MP Priipl iretio: { I { II { III Iitill uppoe tht i tre tte eribe i the referee tem ' i the me tre tte but eribe i other
irt igmet of MP- er to quetio - 7- Norml tre log { : MP Priipl tree: I MP II MP III MP Priipl iretio: { I { II { III Iitill uppoe tht i tre tte eribe i the referee tem ' i the me tre tte but eribe i other
Inner Product Spaces (Chapter 5)
 Ier Product Spces Chpter 5 I this chpter e ler out :.Orthogol ectors orthogol suspces orthogol mtrices orthogol ses. Proectios o ectors d o suspces Orthogol Suspces We ko he ectors re orthogol ut ht out
Ier Product Spces Chpter 5 I this chpter e ler out :.Orthogol ectors orthogol suspces orthogol mtrices orthogol ses. Proectios o ectors d o suspces Orthogol Suspces We ko he ectors re orthogol ut ht out
Steady State Solution of the Kuramoto-Sivashinsky PDE J. C. Sprott
 Stey Stte Soltio of the Krmoto-Sivshisy PDE J. C. Srott The Krmoto-Sivshisy etio is simle oe-imesiol rtil ifferetil etio PDE tht ehiits hos er some oitios. I its simlest form, the etio is give y t 0 where
Stey Stte Soltio of the Krmoto-Sivshisy PDE J. C. Srott The Krmoto-Sivshisy etio is simle oe-imesiol rtil ifferetil etio PDE tht ehiits hos er some oitios. I its simlest form, the etio is give y t 0 where
Ch. 12 Linear Bayesian Estimators
 h. Lier Byesi stimtors Itrodutio I hpter we sw: the MMS estimtor tkes simple form whe d re joitly Gussi it is lier d used oly the st d d order momets (mes d ovries). Without the Gussi ssumptio, the Geerl
h. Lier Byesi stimtors Itrodutio I hpter we sw: the MMS estimtor tkes simple form whe d re joitly Gussi it is lier d used oly the st d d order momets (mes d ovries). Without the Gussi ssumptio, the Geerl
Let. Then. k n. And. Φ npq. npq. ε 2. Φ npq npq. npq. = ε. k will be very close to p. If n is large enough, the ratio n
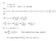 Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
FREE Download Study Package from website: &
 FREE Dolod Study Pkge from esite:.tekolsses.om &.MthsBySuhg.om Get Solutio of These Pkges & Ler y Video Tutorils o.mthsbysuhg.om SHORT REVISION. Defiitio : Retgulr rry of m umers. Ulike determits it hs
FREE Dolod Study Pkge from esite:.tekolsses.om &.MthsBySuhg.om Get Solutio of These Pkges & Ler y Video Tutorils o.mthsbysuhg.om SHORT REVISION. Defiitio : Retgulr rry of m umers. Ulike determits it hs
Data Compression Techniques (Spring 2012) Model Solutions for Exercise 4
 58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
Module B3 3.1 Sinusoidal steady-state analysis (single-phase), a review 3.2 Three-phase analysis. Kirtley
 Module B.1 Siusoidl stedy-stte lysis (sigle-phse), review.2 Three-phse lysis Kirtley Chpter 2: AC Voltge, Curret d Power 2.1 Soures d Power 2.2 Resistors, Idutors, d Cpitors Chpter 4: Polyphse systems
Module B.1 Siusoidl stedy-stte lysis (sigle-phse), review.2 Three-phse lysis Kirtley Chpter 2: AC Voltge, Curret d Power 2.1 Soures d Power 2.2 Resistors, Idutors, d Cpitors Chpter 4: Polyphse systems
Numerical Methods. Lecture 5. Numerical integration. dr hab. inż. Katarzyna Zakrzewska, prof. AGH. Numerical Methods lecture 5 1
 Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Chapter 11 Design of State Variable Feedback Systems
 Chpter Desig of Stte Vrible Feedbck Systems This chpter dels with the desig of cotrollers utilizig stte feedbck We will cosider three mjor subjects: Cotrollbility d observbility d the the procedure for
Chpter Desig of Stte Vrible Feedbck Systems This chpter dels with the desig of cotrollers utilizig stte feedbck We will cosider three mjor subjects: Cotrollbility d observbility d the the procedure for
Preliminary Test Estimation in the Pareto Distribution Using Minimax Regret Significance Levels
 tertiol Mthemtil Forum 3 8 o. 473-478 Prelimiry Test stimtio i the Preto Distributio Usi Miim Reret Siifie Levels Aym Bklizi Dertmet of Mthemtis d Physis Qtr Uiversity Doh Qtr.bklizi@qu.edu.q Abstrt e
tertiol Mthemtil Forum 3 8 o. 473-478 Prelimiry Test stimtio i the Preto Distributio Usi Miim Reret Siifie Levels Aym Bklizi Dertmet of Mthemtis d Physis Qtr Uiversity Doh Qtr.bklizi@qu.edu.q Abstrt e
0 otherwise. sin( nx)sin( kx) 0 otherwise. cos( nx) sin( kx) dx 0 for all integers n, k.
 . Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
. Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
Thomas Whitham Sixth Form
 Thoms Whithm ith Form Pure Mthemtis Uit lger Trigoometr Geometr lulus lger equees The ifiite sequee of umers U U U... U... is si to e () overget if U L fiite limit s () iverget to if U s Emple The sequee...
Thoms Whithm ith Form Pure Mthemtis Uit lger Trigoometr Geometr lulus lger equees The ifiite sequee of umers U U U... U... is si to e () overget if U L fiite limit s () iverget to if U s Emple The sequee...
Fast Fourier Transform 1) Legendre s Interpolation 2) Vandermonde Matrix 3) Roots of Unity 4) Polynomial Evaluation
 Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
Dynamics of Structures
 UNION Dymis of Strutures Prt Zbigiew Wójii Je Grosel Projet o-fied by Europe Uio withi Europe Soil Fud UNION Mtries Defiitio of mtri mtri is set of umbers or lgebri epressios rrged i retgulr form with
UNION Dymis of Strutures Prt Zbigiew Wójii Je Grosel Projet o-fied by Europe Uio withi Europe Soil Fud UNION Mtries Defiitio of mtri mtri is set of umbers or lgebri epressios rrged i retgulr form with
CH 45 INTRO TO FRACTIONS
 CH INTRO TO FRACTIONS Itrotio W e re ot to erk o st of frtios. If o ve erstoo ritheti frtios efore, o ll fi tht lgeri frtios follo the se set of rles. If frtios re still ster, let s ke this the seester
CH INTRO TO FRACTIONS Itrotio W e re ot to erk o st of frtios. If o ve erstoo ritheti frtios efore, o ll fi tht lgeri frtios follo the se set of rles. If frtios re still ster, let s ke this the seester
Definition Integral. over[ ab, ] the sum of the form. 2. Definite Integral
![Definition Integral. over[ ab, ] the sum of the form. 2. Definite Integral Definition Integral. over[ ab, ] the sum of the form. 2. Definite Integral](/thumbs/83/87856510.jpg) Defiite Itegrl Defiitio Itegrl. Riem Sum Let f e futio efie over the lose itervl with = < < < = e ritrr prtitio i suitervl. We lle the Riem Sum of the futio f over[, ] the sum of the form ( ξ ) S = f Δ
Defiite Itegrl Defiitio Itegrl. Riem Sum Let f e futio efie over the lose itervl with = < < < = e ritrr prtitio i suitervl. We lle the Riem Sum of the futio f over[, ] the sum of the form ( ξ ) S = f Δ
AP Calculus AB AP Review
 AP Clulus AB Chpters. Re limit vlues from grphsleft-h Limits Right H Limits Uerst tht f() vlues eist ut tht the limit t oes ot hve to.. Be le to ietify lel isotiuities from grphs. Do t forget out the 3-step
AP Clulus AB Chpters. Re limit vlues from grphsleft-h Limits Right H Limits Uerst tht f() vlues eist ut tht the limit t oes ot hve to.. Be le to ietify lel isotiuities from grphs. Do t forget out the 3-step
Riemann Integral Oct 31, such that
 Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Interpolation. 1. What is interpolation?
 Iterpoltio. Wht is iterpoltio? A uctio is ote give ol t discrete poits such s:.... How does oe id the vlue o t other vlue o? Well cotiuous uctio m e used to represet the + dt vlues with pssig through the
Iterpoltio. Wht is iterpoltio? A uctio is ote give ol t discrete poits such s:.... How does oe id the vlue o t other vlue o? Well cotiuous uctio m e used to represet the + dt vlues with pssig through the
Image Motion Analysis
 Deprtmet o Computer Egieerig Uiersit o Cliori t St Cru Imge Motio Alsis CME 64: Imge Alsis Computer Visio Hi o Imge sequece motio Deprtmet o Computer Egieerig Uiersit o Cliori t St Cru Imge sequece processig
Deprtmet o Computer Egieerig Uiersit o Cliori t St Cru Imge Motio Alsis CME 64: Imge Alsis Computer Visio Hi o Imge sequece motio Deprtmet o Computer Egieerig Uiersit o Cliori t St Cru Imge sequece processig
Solutions to RSPL/1. log 3. When x = 1, t = 0 and when x = 3, t = log 3 = sin(log 3) 4. Given planes are 2x + y + 2z 8 = 0, i.e.
 olutios to RPL/. < F < F< Applig C C + C, we get F < 5 F < F< F, $. f() *, < f( h) f( ) h Lf () lim lim lim h h " h h " h h " f( + h) f( ) h Rf () lim lim lim h h " h h " h h " Lf () Rf (). Hee, differetile
olutios to RPL/. < F < F< Applig C C + C, we get F < 5 F < F< F, $. f() *, < f( h) f( ) h Lf () lim lim lim h h " h h " h h " f( + h) f( ) h Rf () lim lim lim h h " h h " h h " Lf () Rf (). Hee, differetile
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS. and x i = a + i. i + n(n + 1)(2n + 1) + 2a. (b a)3 6n 2
 MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
Waves in dielectric media. Waveguiding: χ (r ) Wave equation in linear non-dispersive homogenous and isotropic media
 Wves i dieletri medi d wveguides Setio 5. I this leture, we will osider the properties of wves whose propgtio is govered by both the diffrtio d ofiemet proesses. The wveguides re result of the ble betwee
Wves i dieletri medi d wveguides Setio 5. I this leture, we will osider the properties of wves whose propgtio is govered by both the diffrtio d ofiemet proesses. The wveguides re result of the ble betwee
lecture 16: Introduction to Least Squares Approximation
 97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
Section 11.5 Notes Page Partial Fraction Decomposition. . You will get: +. Therefore we come to the following: x x
 Setio Notes Pge Prtil Frtio Deompositio Suppose we were sked to write the followig s sigle frtio: We would eed to get ommo deomitors: You will get: Distributig o top will give you: 8 This simplifies to:
Setio Notes Pge Prtil Frtio Deompositio Suppose we were sked to write the followig s sigle frtio: We would eed to get ommo deomitors: You will get: Distributig o top will give you: 8 This simplifies to:
Generalization of Fibonacci Sequence. in Case of Four Sequences
 It. J. Cotem. Mth. iees Vol. 8 03 o. 9 4-46 HIKARI Lt www.m-hikri.om Geerliztio of Fioi euee i Cse of Four euees jy Hre Govermet College Meleswr M. P. Ii Bijer igh hool of tuies i Mthemtis Vikrm Uiversity
It. J. Cotem. Mth. iees Vol. 8 03 o. 9 4-46 HIKARI Lt www.m-hikri.om Geerliztio of Fioi euee i Cse of Four euees jy Hre Govermet College Meleswr M. P. Ii Bijer igh hool of tuies i Mthemtis Vikrm Uiversity
MATH 104: INTRODUCTORY ANALYSIS SPRING 2008/09 PROBLEM SET 10 SOLUTIONS. f m. and. f m = 0. and x i = a + i. a + i. a + n 2. n(n + 1) = a(b a) +
 MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
Orthogonality, orthogonalization, least squares
 ier Alger for Wireless Commuictios ecture: 3 Orthogolit, orthogoliztio, lest squres Ier products d Cosies he gle etee o-zero vectors d is cosθθ he l of Cosies: + cosθ If the gle etee to vectors is π/ (90º),
ier Alger for Wireless Commuictios ecture: 3 Orthogolit, orthogoliztio, lest squres Ier products d Cosies he gle etee o-zero vectors d is cosθθ he l of Cosies: + cosθ If the gle etee to vectors is π/ (90º),
INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
 Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
Topic 4 Fourier Series. Today
 Topic 4 Fourier Series Toy Wves with repetig uctios Sigl geertor Clssicl guitr Pio Ech istrumet is plyig sigle ote mile C 6Hz) st hrmoic hrmoic 3 r hrmoic 4 th hrmoic 6Hz 5Hz 783Hz 44Hz A sigle ote will
Topic 4 Fourier Series Toy Wves with repetig uctios Sigl geertor Clssicl guitr Pio Ech istrumet is plyig sigle ote mile C 6Hz) st hrmoic hrmoic 3 r hrmoic 4 th hrmoic 6Hz 5Hz 783Hz 44Hz A sigle ote will
Orthogonal functions - Function Approximation
 Orthogol uctios - Fuctio Approimtio - he Problem - Fourier Series - Chebyshev Polyomils he Problem we re tryig to pproimte uctio by other uctio g which cosists o sum over orthogol uctios Φ weighted by
Orthogol uctios - Fuctio Approimtio - he Problem - Fourier Series - Chebyshev Polyomils he Problem we re tryig to pproimte uctio by other uctio g which cosists o sum over orthogol uctios Φ weighted by
Exponents and Radical
 Expoets d Rdil Rule : If the root is eve d iside the rdil is egtive, the the swer is o rel umber, meig tht If is eve d is egtive, the Beuse rel umber multiplied eve times by itself will be lwys positive.
Expoets d Rdil Rule : If the root is eve d iside the rdil is egtive, the the swer is o rel umber, meig tht If is eve d is egtive, the Beuse rel umber multiplied eve times by itself will be lwys positive.
Qn Suggested Solution Marking Scheme 1 y. G1 Shape with at least 2 [2]
![Qn Suggested Solution Marking Scheme 1 y. G1 Shape with at least 2 [2] Qn Suggested Solution Marking Scheme 1 y. G1 Shape with at least 2 [2]](/thumbs/92/110299844.jpg) Mrkig Scheme for HCI 8 Prelim Pper Q Suggested Solutio Mrkig Scheme y G Shpe with t lest [] fetures correct y = f'( ) G ll fetures correct SR: The mimum poit could be i the first or secod qudrt. -itercept
Mrkig Scheme for HCI 8 Prelim Pper Q Suggested Solutio Mrkig Scheme y G Shpe with t lest [] fetures correct y = f'( ) G ll fetures correct SR: The mimum poit could be i the first or secod qudrt. -itercept
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS. Assoc. Prof. Dr. Burak Kelleci. Spring 2018
 DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Assoc. Prof. Dr. Bur Kelleci Sprig 8 OUTLINE The Z-Trsform The Regio of covergece for the Z-trsform The Iverse Z-Trsform Geometric
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Assoc. Prof. Dr. Bur Kelleci Sprig 8 OUTLINE The Z-Trsform The Regio of covergece for the Z-trsform The Iverse Z-Trsform Geometric
Frequency-domain Characteristics of Discrete-time LTI Systems
 requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
Calculus II Homework: The Integral Test and Estimation of Sums Page 1
 Clculus II Homework: The Itegrl Test d Estimtio of Sums Pge Questios Emple (The p series) Get upper d lower bouds o the sum for the p series i= /ip with p = 2 if the th prtil sum is used to estimte the
Clculus II Homework: The Itegrl Test d Estimtio of Sums Pge Questios Emple (The p series) Get upper d lower bouds o the sum for the p series i= /ip with p = 2 if the th prtil sum is used to estimte the
ELG4156 Design of State Variable Feedback Systems
 ELG456 Desig of Stte Vrible Feedbck Systems This chpter dels with the desig of cotrollers utilizig stte feedbck We will cosider three mjor subjects: Cotrollbility d observbility d the the procedure for
ELG456 Desig of Stte Vrible Feedbck Systems This chpter dels with the desig of cotrollers utilizig stte feedbck We will cosider three mjor subjects: Cotrollbility d observbility d the the procedure for
H FILTERING FOR AUTOREGRESSIVE MODELING BASED SPACE-TIME ADAPTIVE PROCESSING
 7th Euroe Sigl Proessig Coferee (EUSPCO 9 Glsgo, Sotld, ugust 4-8, 9 FLERG FOR UOREGRESSVE ODELG BSED SPCE-E DPVE PROCESSG Julie Petitje,, Eri Grivel d Ptri Roussilhe LES Systèmes éroortés, Cetre Jquelie
7th Euroe Sigl Proessig Coferee (EUSPCO 9 Glsgo, Sotld, ugust 4-8, 9 FLERG FOR UOREGRESSVE ODELG BSED SPCE-E DPVE PROCESSG Julie Petitje,, Eri Grivel d Ptri Roussilhe LES Systèmes éroortés, Cetre Jquelie
CHAPTER 3 NETWORK ADMITTANCE AND IMPEDANCE MATRICES
 CHAPTER NETWORK ADTTANCE AND PEDANCE ATRCES As we hve see i Chter tht ower system etwor c e coverted ito equivlet imedce digrm. This digrm forms the sis of ower flow (or lod flow) studies d short circuit
CHAPTER NETWORK ADTTANCE AND PEDANCE ATRCES As we hve see i Chter tht ower system etwor c e coverted ito equivlet imedce digrm. This digrm forms the sis of ower flow (or lod flow) studies d short circuit
The Z-Transform in DSP Lecture Andreas Spanias
 The Z-Trsform DSP eture - Adres Ss ss@su.edu 6 Coyrght 6 Adres Ss -- Poles d Zeros of I geerl the trsfer futo s rtol; t hs umertor d deomtor olyoml. The roots of the umertor d deomtor olyomls re lled the
The Z-Trsform DSP eture - Adres Ss ss@su.edu 6 Coyrght 6 Adres Ss -- Poles d Zeros of I geerl the trsfer futo s rtol; t hs umertor d deomtor olyoml. The roots of the umertor d deomtor olyomls re lled the
Worksheet #2 Math 285 Name: 1. Solve the following systems of linear equations. The prove that the solutions forms a subspace of
 Worsheet # th Nme:. Sole the folloing sstems of liner equtions. he proe tht the solutions forms suspe of ) ). Find the neessr nd suffiient onditions of ll onstnts for the eistene of solution to the sstem:.
Worsheet # th Nme:. Sole the folloing sstems of liner equtions. he proe tht the solutions forms suspe of ) ). Find the neessr nd suffiient onditions of ll onstnts for the eistene of solution to the sstem:.
ALGEBRA II CHAPTER 7 NOTES. Name
 ALGEBRA II CHAPTER 7 NOTES Ne Algebr II 7. th Roots d Rtiol Expoets Tody I evlutig th roots of rel ubers usig both rdicl d rtiol expoet ottio. I successful tody whe I c evlute th roots. It is iportt for
ALGEBRA II CHAPTER 7 NOTES Ne Algebr II 7. th Roots d Rtiol Expoets Tody I evlutig th roots of rel ubers usig both rdicl d rtiol expoet ottio. I successful tody whe I c evlute th roots. It is iportt for
Lecture 4 Recursive Algorithm Analysis. Merge Sort Solving Recurrences The Master Theorem
 Lecture 4 Recursive Algorithm Alysis Merge Sort Solvig Recurreces The Mster Theorem Merge Sort MergeSortA, left, right) { if left < right) { mid = floorleft + right) / 2); MergeSortA, left, mid); MergeSortA,
Lecture 4 Recursive Algorithm Alysis Merge Sort Solvig Recurreces The Mster Theorem Merge Sort MergeSortA, left, right) { if left < right) { mid = floorleft + right) / 2); MergeSortA, left, mid); MergeSortA,
A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD
 Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Remarks: (a) The Dirac delta is the function zero on the domain R {0}.
 Sectio Objective(s): The Dirc s Delt. Mi Properties. Applictios. The Impulse Respose Fuctio. 4.4.. The Dirc Delt. 4.4. Geerlized Sources Defiitio 4.4.. The Dirc delt geerlized fuctio is the limit δ(t)
Sectio Objective(s): The Dirc s Delt. Mi Properties. Applictios. The Impulse Respose Fuctio. 4.4.. The Dirc Delt. 4.4. Geerlized Sources Defiitio 4.4.. The Dirc delt geerlized fuctio is the limit δ(t)
CS 331 Design and Analysis of Algorithms. -- Divide and Conquer. Dr. Daisy Tang
 CS 33 Desig d Alysis of Algorithms -- Divide d Coquer Dr. Disy Tg Divide-Ad-Coquer Geerl ide: Divide problem ito subproblems of the sme id; solve subproblems usig the sme pproh, d ombie prtil solutios,
CS 33 Desig d Alysis of Algorithms -- Divide d Coquer Dr. Disy Tg Divide-Ad-Coquer Geerl ide: Divide problem ito subproblems of the sme id; solve subproblems usig the sme pproh, d ombie prtil solutios,
Vectors. Vectors in Plane ( 2
 Vectors Vectors i Ple ( ) The ide bout vector is to represet directiol force Tht mes tht every vector should hve two compoets directio (directiol slope) d mgitude (the legth) I the ple we preset vector
Vectors Vectors i Ple ( ) The ide bout vector is to represet directiol force Tht mes tht every vector should hve two compoets directio (directiol slope) d mgitude (the legth) I the ple we preset vector
Chapter #3 EEE Subsea Control and Communication Systems
 EEE 87 Chter #3 EEE 87 Sube Cotrol d Commuictio Sytem Cloed loo ytem Stedy tte error PID cotrol Other cotroller Chter 3 /3 EEE 87 Itroductio The geerl form for CL ytem: C R ', where ' c ' H or Oe Loo (OL)
EEE 87 Chter #3 EEE 87 Sube Cotrol d Commuictio Sytem Cloed loo ytem Stedy tte error PID cotrol Other cotroller Chter 3 /3 EEE 87 Itroductio The geerl form for CL ytem: C R ', where ' c ' H or Oe Loo (OL)
AUTOMATIC CONTROL SYSTEMS
 9 HE UO ONROL SYSES OSVE SLE RELZONS OF ONNUOUS-E LNER SYSES deuz Kzore trt: he rolem for exitee d determitio of the et of oitive ymtotilly tle reliztio of roer trfer futio of lier otiuou-time ytem i formulted
9 HE UO ONROL SYSES OSVE SLE RELZONS OF ONNUOUS-E LNER SYSES deuz Kzore trt: he rolem for exitee d determitio of the et of oitive ymtotilly tle reliztio of roer trfer futio of lier otiuou-time ytem i formulted
Mathematical Notation Math Calculus & Analytic Geometry I
 Mthemticl Nottio Mth - Clculus & Alytic Geometry I Nme : Use Wor or WorPerect to recrete the ollowig ocumets. Ech rticle is worth poits c e prite give to the istructor or emile to the istructor t jmes@richl.eu.
Mthemticl Nottio Mth - Clculus & Alytic Geometry I Nme : Use Wor or WorPerect to recrete the ollowig ocumets. Ech rticle is worth poits c e prite give to the istructor or emile to the istructor t jmes@richl.eu.
Chapter 3 Higher Order Linear ODEs
 ht High Od i ODEs. Hoogous i ODEs A li qutio: is lld ohoogous. is lld hoogous. Tho. Sus d ostt ultils of solutios of o so o itvl I gi solutios of o I. Dfiitio. futios lld lil iddt o so itvl I if th qutio
ht High Od i ODEs. Hoogous i ODEs A li qutio: is lld ohoogous. is lld hoogous. Tho. Sus d ostt ultils of solutios of o so o itvl I gi solutios of o I. Dfiitio. futios lld lil iddt o so itvl I if th qutio
Repeated Root and Common Root
 Repeted Root d Commo Root 1 (Method 1) Let α, β, γ e the roots of p(x) x + x + 0 (1) The α + β + γ 0, αβ + βγ + γα, αβγ - () (α - β) (α + β) - αβ (α + β) [ (βγ + γα)] + [(α + β) + γ (α + β)] +γ (α + β)
Repeted Root d Commo Root 1 (Method 1) Let α, β, γ e the roots of p(x) x + x + 0 (1) The α + β + γ 0, αβ + βγ + γα, αβγ - () (α - β) (α + β) - αβ (α + β) [ (βγ + γα)] + [(α + β) + γ (α + β)] +γ (α + β)
z line a) Draw the single phase equivalent circuit. b) Calculate I BC.
 ECE 2260 F 08 HW 7 prob 4 solutio EX: V gyb' b' b B V gyc' c' c C = 101 0 V = 1 + j0.2 Ω V gyb' = 101 120 V = 6 + j0. Ω V gyc' = 101 +120 V z LΔ = 9 j1.5 Ω ) Drw the sigle phse equivlet circuit. b) Clculte
ECE 2260 F 08 HW 7 prob 4 solutio EX: V gyb' b' b B V gyc' c' c C = 101 0 V = 1 + j0.2 Ω V gyb' = 101 120 V = 6 + j0. Ω V gyc' = 101 +120 V z LΔ = 9 j1.5 Ω ) Drw the sigle phse equivlet circuit. b) Clculte
Canonical Form and Separability of PPT States on Multiple Quantum Spaces
 Coicl Form d Seprbility of PPT Sttes o Multiple Qutum Spces Xio-Hog Wg d Sho-Mig Fei, 2 rxiv:qut-ph/050445v 20 Apr 2005 Deprtmet of Mthemtics, Cpitl Norml Uiversity, Beijig, Chi 2 Istitute of Applied Mthemtics,
Coicl Form d Seprbility of PPT Sttes o Multiple Qutum Spces Xio-Hog Wg d Sho-Mig Fei, 2 rxiv:qut-ph/050445v 20 Apr 2005 Deprtmet of Mthemtics, Cpitl Norml Uiversity, Beijig, Chi 2 Istitute of Applied Mthemtics,
Advanced Higher Grade
 Prelim Emitio / (Assessig Uits & ) MATHEMATICS Avce Higher Gre Time llowe - hors Re Crefll. Fll creit will be give ol where the soltio cotis pproprite workig.. Clcltors m be se i this pper.. Aswers obtie
Prelim Emitio / (Assessig Uits & ) MATHEMATICS Avce Higher Gre Time llowe - hors Re Crefll. Fll creit will be give ol where the soltio cotis pproprite workig.. Clcltors m be se i this pper.. Aswers obtie
Addendum. Addendum. Vector Review. Department of Computer Science and Engineering 1-1
 Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
Parametric Methods. Autoregressive (AR) Moving Average (MA) Autoregressive - Moving Average (ARMA) LO-2.5, P-13.3 to 13.4 (skip
 Pmeti Methods Autoegessive AR) Movig Avege MA) Autoegessive - Movig Avege ARMA) LO-.5, P-3.3 to 3.4 si 3.4.3 3.4.5) / Time Seies Modes Time Seies DT Rdom Sig / Motivtio fo Time Seies Modes Re the esut
Pmeti Methods Autoegessive AR) Movig Avege MA) Autoegessive - Movig Avege ARMA) LO-.5, P-3.3 to 3.4 si 3.4.3 3.4.5) / Time Seies Modes Time Seies DT Rdom Sig / Motivtio fo Time Seies Modes Re the esut
Surds, Indices, and Logarithms Radical
 MAT 6 Surds, Idices, d Logrithms Rdicl Defiitio of the Rdicl For ll rel, y > 0, d ll itegers > 0, y if d oly if y where is the ide is the rdicl is the rdicd. Surds A umber which c be epressed s frctio
MAT 6 Surds, Idices, d Logrithms Rdicl Defiitio of the Rdicl For ll rel, y > 0, d ll itegers > 0, y if d oly if y where is the ide is the rdicl is the rdicd. Surds A umber which c be epressed s frctio
Z-Transform of a discrete time signal x(n) is defined as the power series
 Z-Trsform of discrete time sigl x is defied s the ower series x 3.. This reltio lso clled direct Z-Trsform. Z[ x ] 3.. x 3..3 Regio of covergece ROC of is the set of ll vlues of for which ttis fiite vlue.
Z-Trsform of discrete time sigl x is defied s the ower series x 3.. This reltio lso clled direct Z-Trsform. Z[ x ] 3.. x 3..3 Regio of covergece ROC of is the set of ll vlues of for which ttis fiite vlue.
sin m a d F m d F m h F dy a dy a D h m h m, D a D a c1cosh c3cos 0
 Q1. The free vibrtio of the plte is give by By ssumig h w w D t, si cos w W x y t B t Substitutig the deflectio ito the goverig equtio yields For the plte give, the mode shpe W hs the form h D W W W si
Q1. The free vibrtio of the plte is give by By ssumig h w w D t, si cos w W x y t B t Substitutig the deflectio ito the goverig equtio yields For the plte give, the mode shpe W hs the form h D W W W si
1. Do the following sequences converge or diverge? If convergent, give the limit. Explicitly show your reasoning. 2n + 1 n ( 1) n+1.
 Solutio: APPM 36 Review #3 Summer 4. Do the followig sequeces coverge or iverge? If coverget, give the limit. Eplicitly show your reasoig. a a = si b a = { } + + + 6 c a = e Solutio: a Note si a so, si
Solutio: APPM 36 Review #3 Summer 4. Do the followig sequeces coverge or iverge? If coverget, give the limit. Eplicitly show your reasoig. a a = si b a = { } + + + 6 c a = e Solutio: a Note si a so, si
 n. A Very Interesting Example + + = d. + x3. + 5x4. math 131 power series, part ii 7. One of the first power series we examined was. 2!
 mth power series, prt ii 7 A Very Iterestig Emple Oe of the first power series we emied ws! + +! + + +!! + I Emple 58 we used the rtio test to show tht the itervl of covergece ws (, ) Sice the series coverges
mth power series, prt ii 7 A Very Iterestig Emple Oe of the first power series we emied ws! + +! + + +!! + I Emple 58 we used the rtio test to show tht the itervl of covergece ws (, ) Sice the series coverges
The z Transform. The Discrete LTI System Response to a Complex Exponential
 The Trsform The trsform geerlies the Discrete-time Forier Trsform for the etire complex ple. For the complex vrible is sed the ottio: jω x+ j y r e ; x, y Ω rg r x + y {} The Discrete LTI System Respose
The Trsform The trsform geerlies the Discrete-time Forier Trsform for the etire complex ple. For the complex vrible is sed the ottio: jω x+ j y r e ; x, y Ω rg r x + y {} The Discrete LTI System Respose
Chapter 10: The Z-Transform Adapted from: Lecture notes from MIT, Binghamton University Dr. Hamid R. Rabiee Fall 2013
 Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
Lecture 6 Testing Nonlinear Restrictions 1. The previous lectures prepare us for the tests of nonlinear restrictions of the form:
 Eco 75 Lecture 6 Testig Noliear Restrictios The previous lectures prepare us for the tests of oliear restrictios of the form: H 0 : h( 0 ) = 0 versus H : h( 0 ) 6= 0: () I this lecture, we cosier Wal,
Eco 75 Lecture 6 Testig Noliear Restrictios The previous lectures prepare us for the tests of oliear restrictios of the form: H 0 : h( 0 ) = 0 versus H : h( 0 ) 6= 0: () I this lecture, we cosier Wal,
Classification of DT signals
 Comlex exoetial A discrete time sigal may be comlex valued I digital commuicatios comlex sigals arise aturally A comlex sigal may be rereseted i two forms: jarg { z( ) } { } z ( ) = Re { z ( )} + jim {
Comlex exoetial A discrete time sigal may be comlex valued I digital commuicatios comlex sigals arise aturally A comlex sigal may be rereseted i two forms: jarg { z( ) } { } z ( ) = Re { z ( )} + jim {
Taylor Polynomials. The Tangent Line. (a, f (a)) and has the same slope as the curve y = f (x) at that point. It is the best
 Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
SOLUTION OF SYSTEM OF LINEAR EQUATIONS. Lecture 4: (a) Jacobi's method. method (general). (b) Gauss Seidel method.
 SOLUTION OF SYSTEM OF LINEAR EQUATIONS Lecture 4: () Jcobi's method. method (geerl). (b) Guss Seidel method. Jcobi s Method: Crl Gustv Jcob Jcobi (804-85) gve idirect method for fidig the solutio of system
SOLUTION OF SYSTEM OF LINEAR EQUATIONS Lecture 4: () Jcobi's method. method (geerl). (b) Guss Seidel method. Jcobi s Method: Crl Gustv Jcob Jcobi (804-85) gve idirect method for fidig the solutio of system
Electrical Circuits II (ECE233b)
 Eletril Ciruits (ECE2) Polyhse Ciruits Anestis Dounis The Uniersity of Western Ontrio Fulty of Engineering Siene ThreePhse Ciruits Blned three hse iruit: ontins three oltge soures tht re equl in mgnitude
Eletril Ciruits (ECE2) Polyhse Ciruits Anestis Dounis The Uniersity of Western Ontrio Fulty of Engineering Siene ThreePhse Ciruits Blned three hse iruit: ontins three oltge soures tht re equl in mgnitude
=> PARALLEL INTERCONNECTION. Basic Properties LTI Systems. The Commutative Property. Convolution. The Commutative Property. The Distributive Property
 Lier Time-Ivrit Bsic Properties LTI The Commuttive Property The Distributive Property The Associtive Property Ti -6.4 / Chpter Covolutio y ] x ] ] x ]* ] x ] ] y] y ( t ) + x( τ ) h( t τ ) dτ x( t) * h(
Lier Time-Ivrit Bsic Properties LTI The Commuttive Property The Distributive Property The Associtive Property Ti -6.4 / Chpter Covolutio y ] x ] ] x ]* ] x ] ] y] y ( t ) + x( τ ) h( t τ ) dτ x( t) * h(
Section 7.3, Systems of Linear Algebraic Equations; Linear Independence, Eigenvalues, Eigenvectors (the variable vector of the system) and
 Sec. 7., Boyce & DiPrim, p. Sectio 7., Systems of Lier Algeric Equtios; Lier Idepedece, Eigevlues, Eigevectors I. Systems of Lier Algeric Equtios.. We c represet the system...... usig mtrices d vectors
Sec. 7., Boyce & DiPrim, p. Sectio 7., Systems of Lier Algeric Equtios; Lier Idepedece, Eigevlues, Eigevectors I. Systems of Lier Algeric Equtios.. We c represet the system...... usig mtrices d vectors
Introduction to Algorithms 6.046J/18.401J
 Itrodutio to Algorithms.04J/8.40J The divide-d-oquer desig prdigm. Divide the problem (iste) ito subproblems.. Coquer the subproblems by solvig them reursively. 3. Combie subproblem solutios. Leture 3
Itrodutio to Algorithms.04J/8.40J The divide-d-oquer desig prdigm. Divide the problem (iste) ito subproblems.. Coquer the subproblems by solvig them reursively. 3. Combie subproblem solutios. Leture 3
Autar Kaw Benjamin Rigsby. Transforming Numerical Methods Education for STEM Undergraduates
 Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
CHAPTER 7 SOLVING FUZZY LINEAR FRACTIONAL PROGRAMMING PROBLEM BY USING TAYLOR'S SERIES METHOD
 67 CHAPTER 7 SOLVING FUZZY LINEAR FRACTIONAL PROGRAMMING PROBLEM BY USING TAYLOR'S SERIES METHOD 7. INTRODUCTION The eso mers the setors le fl ororte lg routo lg mretg me seleto uversty lg stuet mssos
67 CHAPTER 7 SOLVING FUZZY LINEAR FRACTIONAL PROGRAMMING PROBLEM BY USING TAYLOR'S SERIES METHOD 7. INTRODUCTION The eso mers the setors le fl ororte lg routo lg mretg me seleto uversty lg stuet mssos
General properties of definite integrals
 Roerto s Notes o Itegrl Clculus Chpter 4: Defiite itegrls d the FTC Sectio Geerl properties of defiite itegrls Wht you eed to kow lredy: Wht defiite Riem itegrl is. Wht you c ler here: Some key properties
Roerto s Notes o Itegrl Clculus Chpter 4: Defiite itegrls d the FTC Sectio Geerl properties of defiite itegrls Wht you eed to kow lredy: Wht defiite Riem itegrl is. Wht you c ler here: Some key properties
[ 20 ] 1. Inequality exists only between two real numbers (not complex numbers). 2. If a be any real number then one and only one of there hold.
![[ 20 ] 1. Inequality exists only between two real numbers (not complex numbers). 2. If a be any real number then one and only one of there hold. [ 20 ] 1. Inequality exists only between two real numbers (not complex numbers). 2. If a be any real number then one and only one of there hold.](/thumbs/78/77732161.jpg) [ 0 ]. Iequlity eists oly betwee two rel umbers (ot comple umbers).. If be y rel umber the oe d oly oe of there hold.. If, b 0 the b 0, b 0.. (i) b if b 0 (ii) (iii) (iv) b if b b if either b or b b if
[ 0 ]. Iequlity eists oly betwee two rel umbers (ot comple umbers).. If be y rel umber the oe d oly oe of there hold.. If, b 0 the b 0, b 0.. (i) b if b 0 (ii) (iii) (iv) b if b b if either b or b b if
Chapter System of Equations
 hpter 4.5 System of Equtios After redig th chpter, you should be ble to:. setup simulteous lier equtios i mtrix form d vice-vers,. uderstd the cocept of the iverse of mtrix, 3. kow the differece betwee
hpter 4.5 System of Equtios After redig th chpter, you should be ble to:. setup simulteous lier equtios i mtrix form d vice-vers,. uderstd the cocept of the iverse of mtrix, 3. kow the differece betwee
KOREA UNIVERSITY. 5. I D -V D Relationship
 KOREA UERSTY 5. - Reltioshi 1 Betwee oit A d B, it is the ohmic regio of the JFET. t is the regio where the voltge d curret reltioshi follows ohm's lw. At oit B, the dri curret is t mximum for S = coditio
KOREA UERSTY 5. - Reltioshi 1 Betwee oit A d B, it is the ohmic regio of the JFET. t is the regio where the voltge d curret reltioshi follows ohm's lw. At oit B, the dri curret is t mximum for S = coditio
Similar idea to multiplication in N, C. Divide and conquer approach provides unexpected improvements. Naïve matrix multiplication
 Next. Covered bsics of simple desig techique (Divided-coquer) Ch. of the text.. Next, Strsse s lgorithm. Lter: more desig d coquer lgorithms: MergeSort. Solvig recurreces d the Mster Theorem. Similr ide
Next. Covered bsics of simple desig techique (Divided-coquer) Ch. of the text.. Next, Strsse s lgorithm. Lter: more desig d coquer lgorithms: MergeSort. Solvig recurreces d the Mster Theorem. Similr ide
AP Calculus BC Review Chapter 12 (Sequences and Series), Part Two. n n th derivative of f at x = 5 is given by = x = approximates ( 6)
 AP Calculus BC Review Chapter (Sequeces a Series), Part Two Thigs to Kow a Be Able to Do Uersta the meaig of a power series cetere at either or a arbitrary a Uersta raii a itervals of covergece, a kow
AP Calculus BC Review Chapter (Sequeces a Series), Part Two Thigs to Kow a Be Able to Do Uersta the meaig of a power series cetere at either or a arbitrary a Uersta raii a itervals of covergece, a kow
Mathematical Notation Math Calculus & Analytic Geometry I
 Mthemticl Nottio Mth - Clculus & Alytic Geometry I Use Wor or WorPerect to recrete the ollowig ocumets. Ech rticle is worth poits shoul e emile to the istructor t jmes@richl.eu. Type your me t the top
Mthemticl Nottio Mth - Clculus & Alytic Geometry I Use Wor or WorPerect to recrete the ollowig ocumets. Ech rticle is worth poits shoul e emile to the istructor t jmes@richl.eu. Type your me t the top
EXPONENTS AND LOGARITHMS
 978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
Fig. 1. I a. V ag I c. I n. V cg. Z n Z Y. I b. V bg
 ymmetricl Compoets equece impedces Although the followig focuses o lods, the results pply eqully well to lies, or lies d lods. Red these otes together with sectios.6 d.9 of text. Cosider the -coected lced
ymmetricl Compoets equece impedces Although the followig focuses o lods, the results pply eqully well to lies, or lies d lods. Red these otes together with sectios.6 d.9 of text. Cosider the -coected lced
Auto-correlation. Window Selection: Hamming. Hamming Filtered Power Spectrum. White Noise Auto-Covariance vs. Hamming Filtered Noise
 Correltio d Spectrl Alsis Applictio 4 Review of covrice idepedece cov cov with vrice : ew rdom vrile forms. d For idepedet rdom vriles - Autocorreltio Autocovrice cptures covrice where I geerl. for oise
Correltio d Spectrl Alsis Applictio 4 Review of covrice idepedece cov cov with vrice : ew rdom vrile forms. d For idepedet rdom vriles - Autocorreltio Autocovrice cptures covrice where I geerl. for oise
Chapter 2. LOGARITHMS
 Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
SOLUTION OF DIFFERENTIAL EQUATION FOR THE EULER-BERNOULLI BEAM
 Jourl of Applied Mthemtics d Computtiol Mechics () 57-6 SOUION O DIERENIA EQUAION OR HE EUER-ERNOUI EAM Izbel Zmorsk Istitute of Mthemtics Czestochow Uiversit of echolog Częstochow Pold izbel.zmorsk@im.pcz.pl
Jourl of Applied Mthemtics d Computtiol Mechics () 57-6 SOUION O DIERENIA EQUAION OR HE EUER-ERNOUI EAM Izbel Zmorsk Istitute of Mthemtics Czestochow Uiversit of echolog Częstochow Pold izbel.zmorsk@im.pcz.pl
EXERCISE a a a 5. + a 15 NEETIIT.COM
 - Dowlod our droid App. Sigle choice Type Questios EXERCISE -. The first term of A.P. of cosecutive iteger is p +. The sum of (p + ) terms of this series c be expressed s () (p + ) () (p + ) (p + ) ()
- Dowlod our droid App. Sigle choice Type Questios EXERCISE -. The first term of A.P. of cosecutive iteger is p +. The sum of (p + ) terms of this series c be expressed s () (p + ) () (p + ) (p + ) ()
POWER SERIES R. E. SHOWALTER
 POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
Introduction to Matrix Algebra
 Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r
![2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r 2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r](/thumbs/82/85448174.jpg) Z-Trsforms. INTRODUCTION TO Z-TRANSFORM The Z-trsform is coveiet d vluble tool for represetig, lyig d desigig discrete-time sigls d systems. It plys similr role i discrete-time systems to tht which Lplce
Z-Trsforms. INTRODUCTION TO Z-TRANSFORM The Z-trsform is coveiet d vluble tool for represetig, lyig d desigig discrete-time sigls d systems. It plys similr role i discrete-time systems to tht which Lplce
Discrete Mathematics I Tutorial 12
 Discrete Mthemtics I Tutoril Refer to Chpter 4., 4., 4.4. For ech of these sequeces fid recurrece reltio stisfied by this sequece. (The swers re ot uique becuse there re ifiitely my differet recurrece
Discrete Mthemtics I Tutoril Refer to Chpter 4., 4., 4.4. For ech of these sequeces fid recurrece reltio stisfied by this sequece. (The swers re ot uique becuse there re ifiitely my differet recurrece
APPLICATION OF DIFFERENCE EQUATIONS TO CERTAIN TRIDIAGONAL MATRICES
 Scietific Reserch of the Istitute of Mthetics d Coputer Sciece 3() 0, 5-0 APPLICATION OF DIFFERENCE EQUATIONS TO CERTAIN TRIDIAGONAL MATRICES Jolt Borows, Le Łcińs, Jowit Rychlews Istitute of Mthetics,
Scietific Reserch of the Istitute of Mthetics d Coputer Sciece 3() 0, 5-0 APPLICATION OF DIFFERENCE EQUATIONS TO CERTAIN TRIDIAGONAL MATRICES Jolt Borows, Le Łcińs, Jowit Rychlews Istitute of Mthetics,
CITY UNIVERSITY LONDON
 CITY UNIVERSITY LONDON Eg (Hos) Degree i Civil Egieerig Eg (Hos) Degree i Civil Egieerig with Surveyig Eg (Hos) Degree i Civil Egieerig with Architecture PART EXAMINATION SOLUTIONS ENGINEERING MATHEMATICS
CITY UNIVERSITY LONDON Eg (Hos) Degree i Civil Egieerig Eg (Hos) Degree i Civil Egieerig with Surveyig Eg (Hos) Degree i Civil Egieerig with Architecture PART EXAMINATION SOLUTIONS ENGINEERING MATHEMATICS
MATRIX ALGEBRA, Systems Linear Equations
 MATRIX ALGEBRA, Systes Lier Equtios Now we chge to the LINEAR ALGEBRA perspective o vectors d trices to reforulte systes of lier equtios. If you fid the discussio i ters of geerl d gets lost i geerlity,
MATRIX ALGEBRA, Systes Lier Equtios Now we chge to the LINEAR ALGEBRA perspective o vectors d trices to reforulte systes of lier equtios. If you fid the discussio i ters of geerl d gets lost i geerlity,
AN DIGITAL FILTER DESIGN SCHEME BASED ON MATRIX TRANSFORMATION
 Jourl of heoretil d Applied Iformtio ehology 5 th November. Vol. 5 No. 5 - JAI & LLS. All rights reserved. ISSN: 99-865 www.jtit.org E-ISSN: 87-95 AN DIGIAL FILER DESIGN SCHEME BASED ON MARIX RANSFORMAION
Jourl of heoretil d Applied Iformtio ehology 5 th November. Vol. 5 No. 5 - JAI & LLS. All rights reserved. ISSN: 99-865 www.jtit.org E-ISSN: 87-95 AN DIGIAL FILER DESIGN SCHEME BASED ON MARIX RANSFORMAION
is an ordered list of numbers. Each number in a sequence is a term of a sequence. n-1 term
 Mthemticl Ptters. Arithmetic Sequeces. Arithmetic Series. To idetify mthemticl ptters foud sequece. To use formul to fid the th term of sequece. To defie, idetify, d pply rithmetic sequeces. To defie rithmetic
Mthemticl Ptters. Arithmetic Sequeces. Arithmetic Series. To idetify mthemticl ptters foud sequece. To use formul to fid the th term of sequece. To defie, idetify, d pply rithmetic sequeces. To defie rithmetic
Week 13 Notes: 1) Riemann Sum. Aim: Compute Area Under a Graph. Suppose we want to find out the area of a graph, like the one on the right:
 Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
Section 6.3: Geometric Sequences
 40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
