Parametric Methods. Autoregressive (AR) Moving Average (MA) Autoregressive - Moving Average (ARMA) LO-2.5, P-13.3 to 13.4 (skip
|
|
|
- Cameron Singleton
- 6 years ago
- Views:
Transcription
1 Pmeti Methods Autoegessive AR) Movig Avege MA) Autoegessive - Movig Avege ARMA) LO-.5, P-3.3 to 3.4 si ) /
2 Time Seies Modes Time Seies DT Rdom Sig /
3 Motivtio fo Time Seies Modes Re the esut we hd tht eted outut PSD to iut PSD fo ie, time-ivit system: h Sig Beig Modeed Iut RP WSS w/ S ω) Outut RP LTI System WSS w/ S ω) Imuse Resose ht) Feuey Resose Hω) F{ht)} S ω) H ω) S ω) If the iut is white with owe the: S ω) H ω) The She of outut PSD is ometey set y Hω)!!! 3/
4 Time Seies Modes Pmeti Modes) Thus, ude this mode owig the LTI system s tsfe futio o feuey esose) tes eveythig out the PSD. The tsfe futio of LTI system is ometey detemied y set of metes { } d { }: H ) B ) A ) If if, if, if!!!) we ssue ouseves tht the dom oesses we e to oess e modeed s the outut of LTI system dive y white oise, the. Estimtig Pmetes Estimtig PSD ote: We Limit Disussio to Re-Vued Poesses 4/
5 5/ Pmeti PSD Modes ) j j e e S ω ω ω The most gee meti PSD mode is the: } {, } {, Mode Pmetes The outut of the LTI system gives time-domi mode fo the oess: ) Thee e thee sei ses tht e osideed fo these modes: Autoegessive AR) Movig Avege MA) Autoegessive Movig Avege ARMA)
6 6/ Autoegessive AR) PSD Modes If the LTI system s mode is ostied to hve oy oes, the: A H ) ) ) Outut deeds egessivey o itsef Ode of the mode is : ed AR) mode ) j AR e S ω ω TF hs oy Poes Poes Give Rise to PSD Sies Emes: LO Fig.. & Fig..
7 Movig Avege MA) PSD Modes If the LTI system s mode is ostied to hve oy eos, the: H ) B ), TF hs oy Zeos Ode of the mode is : ed MA) mode Outut is vege of vues iside movig widow S MA ω) e jω Zeos Give Rise to PSD us Emes: LO Fig..3 & Fig..4 7/
8 8/ Autoegessive Movig Avege ARMA) If the LTI system s mode is owed to hve Poes & Zeos, the: A B H ) ) ) Ode of the mode is, : ed ARMA,) mode Poes & Zeos Give Rise to PSD Sies & us ) ) j j e e S ω ω ω
9 9/ ACF Mode of Poess So f we ve see etioshis etwee: PSD Mode Time-Domi Mode These modes imt oesodig mode to the ACF: Let the oess oey ARMA,) mode To get ACF: mutiy oth sides of this y - & te E{}: E E E } { } { } { eed This!
10 / ACF Mode of Poess ot.) To evute this wite s outut of fite with iut : } { } { δ h h E h h E E We hve ssumed us fite fo mode: >
11 /,,, h ACF Mode of Poess ot.) Usig this esut gives the Yue-We Eutios fo ARMA: ARMA) These eutios e the ey to estimtig the mode metes!!! We ow oo t simifitios of these fo the AR & MA ses.
12 / ACF Mode fo AR Poess Yue-We Eutios AR) Seiiig to the AR se, we set d get: h ow, we see tht im ) im H h Iiti Vue Theoem fo Z-Tsfom
13 3/ ACF Mode fo AR Poess ot.) If we oo t,, fo these AR Yue-We eutios, we get simuteous eutios tht e soved fo the mode metes of { i } i,, d : If we ow the AC Mti, the we sove these eutios fo the mode metes!!! Yue-We Eutios AR)
14 4/ ACF Mode fo MA Poess,,, h Seiiig to the MA se, we set d get: But fo the MA se the system is FIR fite d we hve othewise h,,,,,,,, Yue-We Eutios MA)
15 Pmeti PSD Estimtio As metioed ove, the ide hee is to fid good estimte of the mode metes d the use those to get estimte of the PSD. The si ide hods egdess if it is ARMA, AR, o MA. Howeve, the deivtio of the mete estimtes is uite hd fo the ARMA d MA ses. So we oside oy the AR se ut eve thee we ey o ituitio to some degee. Thee hs ee HUGE mout of eseh o how to estimte the AR mode metes. EE5 disusses this to some etet; hee we simy stte few tiu methods. 5/
16 6/ Pmeti PSD Estimtio ot.) Hee is the gee AR method: Give dt {, -}. Estimte the AC Mti fom the dt:. Sove the AR Yue-We Eutios fo the AR Mode }, { }, { 3. Comute the PSD estimte fom the mode ) j AR e S ω ω
17 7/ Pmeti PSD Estimtio AR Cse ot.) i i i, Autooetio Method Estimte the ACF usig:,, j j j Covie Method Estimte usig: Sove Usig: Two ommo methods ut thee e my othes):
18 Lest Sues Method & Lie Peditio Thee is othe method tht is ofte used tht omes t the oem fom itte diffeet dietio. Re: The ove ide ws sed o the Yue-We eutios, whih e i tems of the ACF whih is uow i tie!!) Thus we eed to estimte the ACF to use this view Lest Sues ovides diffeet wy to estimte the AR metes. Re: The outut of AR mode is give y 8/
19 LS Method & Lie Peditio ot.) If we e-ge this outut eutio we get: Peditio Eo Peditio of Thee e ots of itios whee ie editio is used: Dt Comessio Tget Tig oise Cetio Et. Go: Fid set of editio oeffiiets { } suh tht the sum of sues of the editio eo is miimied Lest Sues!!! miimie V - 9/
20 / LS Method & Lie Peditio ot.) To hoose the { } to miimie V we diffeetite d set V ; ow we use: V ;
21 LS Method & Lie Peditio ot.) So to sove the LS Lie Peditio oem we eed: ; ) Defie:. Mti Γ with eemets λ. Veto λ with eemets λ 3. Veto with eemets,, whee λ ;, The ) e witte s eoitig tht ): Γ λ Γ λ /
M5. LTI Systems Described by Linear Constant Coefficient Difference Equations
 5. LTI Systes Descied y Lie Costt Coefficiet Diffeece Equtios Redig teil: p.34-4, 245-253 3/22/2 I. Discete-Tie Sigls d Systes Up til ow we itoduced the Fouie d -tsfos d thei popeties with oly ief peview
5. LTI Systes Descied y Lie Costt Coefficiet Diffeece Equtios Redig teil: p.34-4, 245-253 3/22/2 I. Discete-Tie Sigls d Systes Up til ow we itoduced the Fouie d -tsfos d thei popeties with oly ief peview
Summary: Binomial Expansion...! r. where
 Summy: Biomil Epsio 009 M Teo www.techmejcmth-sg.wes.com ) Re-cp of Additiol Mthemtics Biomil Theoem... whee )!!(! () The fomul is ville i MF so studets do ot eed to memoise it. () The fomul pplies oly
Summy: Biomil Epsio 009 M Teo www.techmejcmth-sg.wes.com ) Re-cp of Additiol Mthemtics Biomil Theoem... whee )!!(! () The fomul is ville i MF so studets do ot eed to memoise it. () The fomul pplies oly
Problem Session (3) for Chapter 4 Signal Modeling
 Pobm Sssio fo Cht Sig Modig Soutios to Pobms....5. d... Fid th Pdé oimtio of scod-od to sig tht is giv by [... ] T i.. d so o. I oth wods usig oimtio of th fom b b b H fid th cofficits b b b d. Soutio
Pobm Sssio fo Cht Sig Modig Soutios to Pobms....5. d... Fid th Pdé oimtio of scod-od to sig tht is giv by [... ] T i.. d so o. I oth wods usig oimtio of th fom b b b H fid th cofficits b b b d. Soutio
Physics 235 Final Examination December 4, 2006 Solutions
 Physics 35 Fi Emitio Decembe, 6 Soutios.. Fist coside the two u quks. They e idetic spi ½ ptices, so the tot spi c be eithe o. The Pui Picipe equies tht the ove wvefuctio be echge tisymmetic. Sice the
Physics 35 Fi Emitio Decembe, 6 Soutios.. Fist coside the two u quks. They e idetic spi ½ ptices, so the tot spi c be eithe o. The Pui Picipe equies tht the ove wvefuctio be echge tisymmetic. Sice the
For this purpose, we need the following result:
 9 Lectue Sigulities of omplex Fuctio A poit is clled sigulity of fuctio f ( z ) if f ( z ) is ot lytic t the poit. A sigulity is clled isolted sigulity of f ( z ), if f ( z ) is lytic i some puctued disk
9 Lectue Sigulities of omplex Fuctio A poit is clled sigulity of fuctio f ( z ) if f ( z ) is ot lytic t the poit. A sigulity is clled isolted sigulity of f ( z ), if f ( z ) is lytic i some puctued disk
Einstein Classes, Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road New Delhi , Ph. : ,
 MB BINOMIAL THEOREM Biomial Epessio : A algebaic epessio which cotais two dissimila tems is called biomial epessio Fo eample :,,, etc / ( ) Statemet of Biomial theoem : If, R ad N, the : ( + ) = a b +
MB BINOMIAL THEOREM Biomial Epessio : A algebaic epessio which cotais two dissimila tems is called biomial epessio Fo eample :,,, etc / ( ) Statemet of Biomial theoem : If, R ad N, the : ( + ) = a b +
Sequences and series Mixed exercise 3
 eqees seies Mixe exeise Let = fist tem = ommo tio. tem = 7 = 7 () 6th tem = 8 = 8 () Eqtio () Eqtio (): 8 7 8 7 8 7 m to te tems 0 o 0 0 60.7 60.7 79.089 Diffeee betwee 0 = 8. 79.089 =.6 ( s.f.) 0 The
eqees seies Mixe exeise Let = fist tem = ommo tio. tem = 7 = 7 () 6th tem = 8 = 8 () Eqtio () Eqtio (): 8 7 8 7 8 7 m to te tems 0 o 0 0 60.7 60.7 79.089 Diffeee betwee 0 = 8. 79.089 =.6 ( s.f.) 0 The
SOLUTIONS ( ) ( )! ( ) ( ) ( ) ( )! ( ) ( ) ( ) ( ) n r. r ( Pascal s equation ). n 1. Stepanov Dalpiaz
 STAT UIU Pctice Poblems # SOLUTIONS Stepov Dlpiz The followig e umbe of pctice poblems tht my be helpful fo completig the homewo, d will liely be vey useful fo studyig fo ems...-.-.- Pove (show) tht. (
STAT UIU Pctice Poblems # SOLUTIONS Stepov Dlpiz The followig e umbe of pctice poblems tht my be helpful fo completig the homewo, d will liely be vey useful fo studyig fo ems...-.-.- Pove (show) tht. (
PROGRESSION AND SERIES
 INTRODUCTION PROGRESSION AND SERIES A gemet of umbes {,,,,, } ccodig to some well defied ule o set of ules is clled sequece Moe pecisely, we my defie sequece s fuctio whose domi is some subset of set of
INTRODUCTION PROGRESSION AND SERIES A gemet of umbes {,,,,, } ccodig to some well defied ule o set of ules is clled sequece Moe pecisely, we my defie sequece s fuctio whose domi is some subset of set of
Chapter 5: Your Program Asks for Advice.
 Chte 5: You Pogm Asks fo Advce. Pge 63 Chte 5: You Pogm Asks fo Advce. Ths chte ntoduces new tye of ves (stng ves) nd how to get text nd numec esonses fom the use. Anothe Tye of Ve The Stng Ve: In Chte
Chte 5: You Pogm Asks fo Advce. Pge 63 Chte 5: You Pogm Asks fo Advce. Ths chte ntoduces new tye of ves (stng ves) nd how to get text nd numec esonses fom the use. Anothe Tye of Ve The Stng Ve: In Chte
Advanced Higher Maths: Formulae
 Advced Highe Mths: Fomule Advced Highe Mthemtics Gee (G): Fomule you solutely must memoise i ode to pss Advced Highe mths. Rememe you get o fomul sheet t ll i the em! Ame (A): You do t hve to memoise these
Advced Highe Mths: Fomule Advced Highe Mthemtics Gee (G): Fomule you solutely must memoise i ode to pss Advced Highe mths. Rememe you get o fomul sheet t ll i the em! Ame (A): You do t hve to memoise these
Raytracing: Intersections. Backward Tracing. Basic Ray Casting Method. Basic Ray Casting Method. Basic Ray Casting Method. Basic Ray Casting Method
 Rtig: Itesetios Bkwd Tig COC 4328/5327 ott A. Kig Bsi R Cstig iels i see hoot fom the ee though the iel. Fid losest -ojet itesetio. Get olo t itesetio Bsi R Cstig iels i see hoot fom the ee though the
Rtig: Itesetios Bkwd Tig COC 4328/5327 ott A. Kig Bsi R Cstig iels i see hoot fom the ee though the iel. Fid losest -ojet itesetio. Get olo t itesetio Bsi R Cstig iels i see hoot fom the ee though the
MA 1201 Engineering Mathematics MO/2017 Tutorial Sheet No. 2
 BIRLA INSTITUTE OF TECHNOLOGY, MESRA, RANCHI DEPARTMENT OF MATHEMATICS MA Egieeig Matheatis MO/7 Tutoia Sheet No. Modue IV:. Defie Beta futio ad Gaa futio.. Pove that,,,. Pove that, d. Pove that. & whee
BIRLA INSTITUTE OF TECHNOLOGY, MESRA, RANCHI DEPARTMENT OF MATHEMATICS MA Egieeig Matheatis MO/7 Tutoia Sheet No. Modue IV:. Defie Beta futio ad Gaa futio.. Pove that,,,. Pove that, d. Pove that. & whee
Generating Function for
 Itetiol Joul of Ltest Tehology i Egieeig, Mgemet & Applied Siee (IJLTEMAS) Volume VI, Issue VIIIS, August 207 ISSN 2278-2540 Geetig Futio fo G spt D. K. Humeddy #, K. Jkmm * # Deptmet of Memtis, Hidu College,
Itetiol Joul of Ltest Tehology i Egieeig, Mgemet & Applied Siee (IJLTEMAS) Volume VI, Issue VIIIS, August 207 ISSN 2278-2540 Geetig Futio fo G spt D. K. Humeddy #, K. Jkmm * # Deptmet of Memtis, Hidu College,
UNIT V: Z-TRANSFORMS AND DIFFERENCE EQUATIONS. Dr. V. Valliammal Department of Applied Mathematics Sri Venkateswara College of Engineering
 UNIT V: -TRANSFORMS AND DIFFERENCE EQUATIONS D. V. Vllimml Deptmet of Applied Mthemtics Si Vektesw College of Egieeig TOPICS:. -Tsfoms Elemet popeties.. Ivese -Tsfom usig ptil fctios d esidues. Covolutio
UNIT V: -TRANSFORMS AND DIFFERENCE EQUATIONS D. V. Vllimml Deptmet of Applied Mthemtics Si Vektesw College of Egieeig TOPICS:. -Tsfoms Elemet popeties.. Ivese -Tsfom usig ptil fctios d esidues. Covolutio
42. (20 pts) Use Fermat s Principle to prove the law of reflection. 0 x c
 4. (0 ts) Use Femt s Piile t ve the lw eleti. A i b 0 x While the light uld tke y th t get m A t B, Femt s Piile sys it will tke the th lest time. We theee lulte the time th s uti the eleti it, d the tke
4. (0 ts) Use Femt s Piile t ve the lw eleti. A i b 0 x While the light uld tke y th t get m A t B, Femt s Piile sys it will tke the th lest time. We theee lulte the time th s uti the eleti it, d the tke
The Area of a Triangle
 The e of Tingle tkhlid June 1, 015 1 Intodution In this tile we will e disussing the vious methods used fo detemining the e of tingle. Let [X] denote the e of X. Using se nd Height To stt off, the simplest
The e of Tingle tkhlid June 1, 015 1 Intodution In this tile we will e disussing the vious methods used fo detemining the e of tingle. Let [X] denote the e of X. Using se nd Height To stt off, the simplest
2.Decision Theory of Dependence
 .Deciio Theoy of Depedece Theoy :I et of vecto if thee i uet which i liely depedet the whole et i liely depedet too. Coolly :If the et i liely idepedet y oepty uet of it i liely idepedet. Theoy : Give
.Deciio Theoy of Depedece Theoy :I et of vecto if thee i uet which i liely depedet the whole et i liely depedet too. Coolly :If the et i liely idepedet y oepty uet of it i liely idepedet. Theoy : Give
GEOMETRY. Rectangle Circle Triangle Parallelogram Trapezoid. 1 A = lh A= h b+ Rectangular Prism Sphere Rectangular Pyramid.
 ALGEBA Popeties of Asote Ve Fo e mes :, + + Tige Ieqit Popeties of Itege Epoets is Assme tt m e positive iteges, tt e oegtive, tt eomitos e ozeo. See Appeies B D fo gps fte isssio. + ( ) m m m m m m m
ALGEBA Popeties of Asote Ve Fo e mes :, + + Tige Ieqit Popeties of Itege Epoets is Assme tt m e positive iteges, tt e oegtive, tt eomitos e ozeo. See Appeies B D fo gps fte isssio. + ( ) m m m m m m m
Mathematical Statistics
 7 75 Ode Sttistics The ode sttistics e the items o the dom smple ed o odeed i mitude om the smllest to the lest Recetl the impotce o ode sttistics hs icesed owi to the moe equet use o opmetic ieeces d
7 75 Ode Sttistics The ode sttistics e the items o the dom smple ed o odeed i mitude om the smllest to the lest Recetl the impotce o ode sttistics hs icesed owi to the moe equet use o opmetic ieeces d
BINOMIAL THEOREM SOLUTION. 1. (D) n. = (C 0 + C 1 x +C 2 x C n x n ) (1+ x+ x 2 +.)
 BINOMIAL THEOREM SOLUTION. (D) ( + + +... + ) (+ + +.) The coefficiet of + + + +... + fo. Moeove coefficiet of is + + + +... + if >. So. (B)... e!!!! The equied coefficiet coefficiet of i e -.!...!. (A),
BINOMIAL THEOREM SOLUTION. (D) ( + + +... + ) (+ + +.) The coefficiet of + + + +... + fo. Moeove coefficiet of is + + + +... + if >. So. (B)... e!!!! The equied coefficiet coefficiet of i e -.!...!. (A),
Homework 3 MAE 118C Problems 2, 5, 7, 10, 14, 15, 18, 23, 30, 31 from Chapter 5, Lamarsh & Baratta. The flux for a point source is:
 . Homewok 3 MAE 8C Poblems, 5, 7, 0, 4, 5, 8, 3, 30, 3 fom Chpte 5, msh & Btt Point souces emit nuetons/sec t points,,, n 3 fin the flux cuent hlf wy between one sie of the tingle (blck ot). The flux fo
. Homewok 3 MAE 8C Poblems, 5, 7, 0, 4, 5, 8, 3, 30, 3 fom Chpte 5, msh & Btt Point souces emit nuetons/sec t points,,, n 3 fin the flux cuent hlf wy between one sie of the tingle (blck ot). The flux fo
Advanced Higher Maths: Formulae
 : Fomule Gee (G): Fomule you bsolutely must memoise i ode to pss Advced Highe mths. Remembe you get o fomul sheet t ll i the em! Ambe (A): You do t hve to memoise these fomule, s it is possible to deive
: Fomule Gee (G): Fomule you bsolutely must memoise i ode to pss Advced Highe mths. Remembe you get o fomul sheet t ll i the em! Ambe (A): You do t hve to memoise these fomule, s it is possible to deive
12.2 The Definite Integrals (5.2)
 Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
Numerical Methods. Lecture 5. Numerical integration. dr hab. inż. Katarzyna Zakrzewska, prof. AGH. Numerical Methods lecture 5 1
 Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Week 13 Notes: 1) Riemann Sum. Aim: Compute Area Under a Graph. Suppose we want to find out the area of a graph, like the one on the right:
 Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
MATH 104: INTRODUCTORY ANALYSIS SPRING 2008/09 PROBLEM SET 10 SOLUTIONS. f m. and. f m = 0. and x i = a + i. a + i. a + n 2. n(n + 1) = a(b a) +
 MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
Introduction to Matrix Algebra
 Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Riemann Integral Oct 31, such that
 Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Limit of a function:
 - Limit of fuctio: We sy tht f ( ) eists d is equl with (rel) umer L if f( ) gets s close s we wt to L if is close eough to (This defiitio c e geerlized for L y syig tht f( ) ecomes s lrge (or s lrge egtive
- Limit of fuctio: We sy tht f ( ) eists d is equl with (rel) umer L if f( ) gets s close s we wt to L if is close eough to (This defiitio c e geerlized for L y syig tht f( ) ecomes s lrge (or s lrge egtive
2012 GCE A Level H2 Maths Solution Paper Let x,
 GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
LIPSCHITZ ESTIMATES FOR MULTILINEAR COMMUTATOR OF MARCINKIEWICZ OPERATOR
 Reseh d ouiios i heis d hei Siees Vo. Issue Pges -46 ISSN 9-699 Puished Oie o Deee 7 Joi Adei Pess h://oideiess.e IPSHITZ ESTIATES FOR UTIINEAR OUTATOR OF ARINKIEWIZ OPERATOR DAZHAO HEN Dee o Siee d Ioio
Reseh d ouiios i heis d hei Siees Vo. Issue Pges -46 ISSN 9-699 Puished Oie o Deee 7 Joi Adei Pess h://oideiess.e IPSHITZ ESTIATES FOR UTIINEAR OUTATOR OF ARINKIEWIZ OPERATOR DAZHAO HEN Dee o Siee d Ioio
ENGINEERING MATHEMATICS I QUESTION BANK. Module Using the Leibnitz theorem find the nth derivative of the following : log. e x log d.
 ENGINEERING MATHEMATICS I QUESTION BANK Modle Usig the Leibit theoem id the th deivtive o the ollowig : b si c e d e Show tht d d! Usig the Leibit theoem pove the ollowig : I si b the pove tht b I si show
ENGINEERING MATHEMATICS I QUESTION BANK Modle Usig the Leibit theoem id the th deivtive o the ollowig : b si c e d e Show tht d d! Usig the Leibit theoem pove the ollowig : I si b the pove tht b I si show
We show that every analytic function can be expanded into a power series, called the Taylor series of the function.
 10 Lectue 8 We show tht evey lytic fuctio c be expded ito powe seies, clled the Tylo seies of the fuctio. Tylo s Theoem: Let f be lytic i domi D & D. The, f(z) c be expessed s the powe seies f( z) b (
10 Lectue 8 We show tht evey lytic fuctio c be expded ito powe seies, clled the Tylo seies of the fuctio. Tylo s Theoem: Let f be lytic i domi D & D. The, f(z) c be expessed s the powe seies f( z) b (
Approximate Integration
 Study Sheet (7.7) Approimte Itegrtio I this sectio, we will ler: How to fid pproimte vlues of defiite itegrls. There re two situtios i which it is impossile to fid the ect vlue of defiite itegrl. Situtio:
Study Sheet (7.7) Approimte Itegrtio I this sectio, we will ler: How to fid pproimte vlues of defiite itegrls. There re two situtios i which it is impossile to fid the ect vlue of defiite itegrl. Situtio:
Quantum Mechanics Lecture Notes 10 April 2007 Meg Noah
 The -Patice syste: ˆ H V This is difficut to sove. y V 1 ˆ H V 1 1 1 1 ˆ = ad with 1 1 Hˆ Cete of Mass ˆ fo Patice i fee space He Reative Haitoia eative coodiate of the tota oetu Pˆ the tota oetu tota
The -Patice syste: ˆ H V This is difficut to sove. y V 1 ˆ H V 1 1 1 1 ˆ = ad with 1 1 Hˆ Cete of Mass ˆ fo Patice i fee space He Reative Haitoia eative coodiate of the tota oetu Pˆ the tota oetu tota
f(t)dt 2δ f(x) f(t)dt 0 and b f(t)dt = 0 gives F (b) = 0. Since F is increasing, this means that
 Uiversity of Illiois t Ur-Chmpig Fll 6 Mth 444 Group E3 Itegrtio : correctio of the exercises.. ( Assume tht f : [, ] R is cotiuous fuctio such tht f(x for ll x (,, d f(tdt =. Show tht f(x = for ll x [,
Uiversity of Illiois t Ur-Chmpig Fll 6 Mth 444 Group E3 Itegrtio : correctio of the exercises.. ( Assume tht f : [, ] R is cotiuous fuctio such tht f(x for ll x (,, d f(tdt =. Show tht f(x = for ll x [,
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
Auchmuty High School Mathematics Department Sequences & Series Notes Teacher Version
 equeces ad eies Auchmuty High chool Mathematics Depatmet equeces & eies Notes Teache Vesio A sequece takes the fom,,7,0,, while 7 0 is a seies. Thee ae two types of sequece/seies aithmetic ad geometic.
equeces ad eies Auchmuty High chool Mathematics Depatmet equeces & eies Notes Teache Vesio A sequece takes the fom,,7,0,, while 7 0 is a seies. Thee ae two types of sequece/seies aithmetic ad geometic.
CHAPTER 5 : SERIES. 5.2 The Sum of a Series Sum of Power of n Positive Integers Sum of Series of Partial Fraction Difference Method
 CHAPTER 5 : SERIES 5.1 Seies 5. The Sum of a Seies 5..1 Sum of Powe of Positive Iteges 5.. Sum of Seies of Patial Factio 5..3 Diffeece Method 5.3 Test of covegece 5.3.1 Divegece Test 5.3. Itegal Test 5.3.3
CHAPTER 5 : SERIES 5.1 Seies 5. The Sum of a Seies 5..1 Sum of Powe of Positive Iteges 5.. Sum of Seies of Patial Factio 5..3 Diffeece Method 5.3 Test of covegece 5.3.1 Divegece Test 5.3. Itegal Test 5.3.3
_ J.. C C A 551NED. - n R ' ' t i :. t ; . b c c : : I I .., I AS IEC. r '2 5? 9
 C C A 55NED n R 5 0 9 b c c \ { s AS EC 2 5? 9 Con 0 \ 0265 o + s ^! 4 y!! {! w Y n < R > s s = ~ C c [ + * c n j R c C / e A / = + j ) d /! Y 6 ] s v * ^ / ) v } > { ± n S = S w c s y c C { ~! > R = n
C C A 55NED n R 5 0 9 b c c \ { s AS EC 2 5? 9 Con 0 \ 0265 o + s ^! 4 y!! {! w Y n < R > s s = ~ C c [ + * c n j R c C / e A / = + j ) d /! Y 6 ] s v * ^ / ) v } > { ± n S = S w c s y c C { ~! > R = n
Taylor Polynomials. The Tangent Line. (a, f (a)) and has the same slope as the curve y = f (x) at that point. It is the best
 Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
k. s k=1 Part of the significance of the Riemann zeta-function stems from Theorem 9.2. If s > 1 then 1 p s
 9 Pimes in aithmetic ogession Definition 9 The Riemann zeta-function ζs) is the function which assigns to a eal numbe s > the convegent seies k s k Pat of the significance of the Riemann zeta-function
9 Pimes in aithmetic ogession Definition 9 The Riemann zeta-function ζs) is the function which assigns to a eal numbe s > the convegent seies k s k Pat of the significance of the Riemann zeta-function
EXERCISE - 01 CHECK YOUR GRASP
 EXERISE - 0 HEK YOUR GRASP 3. ( + Fo sum of coefficiets put ( + 4 ( + Fo sum of coefficiets put ; ( + ( 4. Give epessio c e ewitte s 7 4 7 7 3 7 7 ( 4 3( 4... 7( 4 7 7 7 3 ( 4... 7( 4 Lst tem ecomes (4
EXERISE - 0 HEK YOUR GRASP 3. ( + Fo sum of coefficiets put ( + 4 ( + Fo sum of coefficiets put ; ( + ( 4. Give epessio c e ewitte s 7 4 7 7 3 7 7 ( 4 3( 4... 7( 4 7 7 7 3 ( 4... 7( 4 Lst tem ecomes (4
BINOMIAL THEOREM & ITS SIMPLE APPLICATION
 Etei lasses, Uit No. 0, 0, Vadhma Rig Road Plaza, Vikas Pui Et., Oute Rig Road New Delhi 0 08, Ph. : 9690, 87 MB Sllabus : BINOMIAL THEOREM & ITS SIMPLE APPLIATION Biomia Theoem fo a positive itegal ide;
Etei lasses, Uit No. 0, 0, Vadhma Rig Road Plaza, Vikas Pui Et., Oute Rig Road New Delhi 0 08, Ph. : 9690, 87 MB Sllabus : BINOMIAL THEOREM & ITS SIMPLE APPLIATION Biomia Theoem fo a positive itegal ide;
Zero Level Binomial Theorem 04
 Zeo Level Biomial Theoem 0 Usig biomial theoem, epad the epasios of the Fid the th tem fom the ed i the epasio of followig : (i ( (ii, 0 Fid the th tem fom the ed i the epasio of (iii ( (iv ( a (v ( (vi,
Zeo Level Biomial Theoem 0 Usig biomial theoem, epad the epasios of the Fid the th tem fom the ed i the epasio of followig : (i ( (ii, 0 Fid the th tem fom the ed i the epasio of (iii ( (iv ( a (v ( (vi,
I PUC MATHEMATICS CHAPTER - 08 Binomial Theorem. x 1. Expand x + using binomial theorem and hence find the coefficient of
 Two Maks Questios I PU MATHEMATIS HAPTER - 08 Biomial Theoem. Epad + usig biomial theoem ad hece fid the coefficiet of y y. Epad usig biomial theoem. Hece fid the costat tem of the epasio.. Simplify +
Two Maks Questios I PU MATHEMATIS HAPTER - 08 Biomial Theoem. Epad + usig biomial theoem ad hece fid the coefficiet of y y. Epad usig biomial theoem. Hece fid the costat tem of the epasio.. Simplify +
Auto-correlation. Window Selection: Hamming. Hamming Filtered Power Spectrum. White Noise Auto-Covariance vs. Hamming Filtered Noise
 Correltio d Spectrl Alsis Applictio 4 Review of covrice idepedece cov cov with vrice : ew rdom vrile forms. d For idepedet rdom vriles - Autocorreltio Autocovrice cptures covrice where I geerl. for oise
Correltio d Spectrl Alsis Applictio 4 Review of covrice idepedece cov cov with vrice : ew rdom vrile forms. d For idepedet rdom vriles - Autocorreltio Autocovrice cptures covrice where I geerl. for oise
A Dynamical Quasi-Boolean System
 ULETNUL Uestăţ Petol Gze Ploeşt Vol LX No / - 9 Se Mtetă - otă - Fză l Qs-oole Sste Gel Mose Petole-Gs Uest o Ploest ots etet est 39 Ploest 68 o el: ose@-loesto stt Ths e oes the esto o ol theoetl oet:
ULETNUL Uestăţ Petol Gze Ploeşt Vol LX No / - 9 Se Mtetă - otă - Fză l Qs-oole Sste Gel Mose Petole-Gs Uest o Ploest ots etet est 39 Ploest 68 o el: ose@-loesto stt Ths e oes the esto o ol theoetl oet:
Quality control. Final exam: 2012/1/12 (Thur), 9:00-12:00 Q1 Q2 Q3 Q4 Q5 YOUR NAME
 Qulity contol Finl exm: // (Thu), 9:-: Q Q Q3 Q4 Q5 YOUR NAME NOTE: Plese wite down the deivtion of you nswe vey clely fo ll questions. The scoe will be educed when you only wite nswe. Also, the scoe will
Qulity contol Finl exm: // (Thu), 9:-: Q Q Q3 Q4 Q5 YOUR NAME NOTE: Plese wite down the deivtion of you nswe vey clely fo ll questions. The scoe will be educed when you only wite nswe. Also, the scoe will
MATH Midterm Solutions
 MATH 2113 - Midtem Solutios Febuay 18 1. A bag of mables cotais 4 which ae ed, 4 which ae blue ad 4 which ae gee. a How may mables must be chose fom the bag to guaatee that thee ae the same colou? We ca
MATH 2113 - Midtem Solutios Febuay 18 1. A bag of mables cotais 4 which ae ed, 4 which ae blue ad 4 which ae gee. a How may mables must be chose fom the bag to guaatee that thee ae the same colou? We ca
( ) D x ( s) if r s (3) ( ) (6) ( r) = d dr D x
 SIO 22B, Rudnick dpted fom Dvis III. Single vile sttistics The next few lectues e intended s eview of fundmentl sttistics. The gol is to hve us ll speking the sme lnguge s we move to moe dvnced topics.
SIO 22B, Rudnick dpted fom Dvis III. Single vile sttistics The next few lectues e intended s eview of fundmentl sttistics. The gol is to hve us ll speking the sme lnguge s we move to moe dvnced topics.
Technical Report: Bessel Filter Analysis
 Sasa Mahmoodi 1 Techical Repot: Bessel Filte Aalysis 1 School of Electoics ad Compute Sciece, Buildig 1, Southampto Uivesity, Southampto, S17 1BJ, UK, Email: sm3@ecs.soto.ac.uk I this techical epot, we
Sasa Mahmoodi 1 Techical Repot: Bessel Filte Aalysis 1 School of Electoics ad Compute Sciece, Buildig 1, Southampto Uivesity, Southampto, S17 1BJ, UK, Email: sm3@ecs.soto.ac.uk I this techical epot, we
SPH3UW Unit 7.5 Snell s Law Page 1 of Total Internal Reflection occurs when the incoming refraction angle is
 SPH3UW Uit 7.5 Sell s Lw Pge 1 of 7 Notes Physis Tool ox Refrtio is the hge i diretio of wve due to hge i its speed. This is most ommoly see whe wve psses from oe medium to other. Idex of refrtio lso lled
SPH3UW Uit 7.5 Sell s Lw Pge 1 of 7 Notes Physis Tool ox Refrtio is the hge i diretio of wve due to hge i its speed. This is most ommoly see whe wve psses from oe medium to other. Idex of refrtio lso lled
The formulae in this booklet have been arranged according to the unit in which they are first
 Fomule Booklet Fomule Booklet The fomule ths ooklet hve ee ge og to the ut whh the e fst toue. Thus te sttg ut m e eque to use the fomule tht wee toue peeg ut e.g. tes sttg C mght e epete to use fomule
Fomule Booklet Fomule Booklet The fomule ths ooklet hve ee ge og to the ut whh the e fst toue. Thus te sttg ut m e eque to use the fomule tht wee toue peeg ut e.g. tes sttg C mght e epete to use fomule
= 5! 3! 2! = 5! 3! (5 3)!. In general, the number of different groups of r items out of n items (when the order is ignored) is given by n!
 0 Combiatoial Aalysis Copyight by Deiz Kalı 4 Combiatios Questio 4 What is the diffeece betwee the followig questio i How may 3-lette wods ca you wite usig the lettes A, B, C, D, E ii How may 3-elemet
0 Combiatoial Aalysis Copyight by Deiz Kalı 4 Combiatios Questio 4 What is the diffeece betwee the followig questio i How may 3-lette wods ca you wite usig the lettes A, B, C, D, E ii How may 3-elemet
BINOMIAL THEOREM An expression consisting of two terms, connected by + or sign is called a
 BINOMIAL THEOREM hapte 8 8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4 5y, etc., ae all biomial epessios. 8.. Biomial theoem If
BINOMIAL THEOREM hapte 8 8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4 5y, etc., ae all biomial epessios. 8.. Biomial theoem If
By the end of this section you will be able to prove the Chinese Remainder Theorem apply this theorem to solve simultaneous linear congruences
 Chapte : Theoy of Modula Aithmetic 8 Sectio D Chiese Remaide Theoem By the ed of this sectio you will be able to pove the Chiese Remaide Theoem apply this theoem to solve simultaeous liea cogueces The
Chapte : Theoy of Modula Aithmetic 8 Sectio D Chiese Remaide Theoem By the ed of this sectio you will be able to pove the Chiese Remaide Theoem apply this theoem to solve simultaeous liea cogueces The
Lecture 24 Outline: Z Transforms. Will be 1 more HW, may be short, no late HW8s
 Lecture 4 Outie: Z Trsfors ouceets: HW 7 to e oste Friy, ue Jue Wi e ore HW, y e short, o te HW8s Lst ecture Jue 6 wi icue course review Fi ex Jue t 3:306:30 i this roo; i fterwrs ore fi ex ouceets ext
Lecture 4 Outie: Z Trsfors ouceets: HW 7 to e oste Friy, ue Jue Wi e ore HW, y e short, o te HW8s Lst ecture Jue 6 wi icue course review Fi ex Jue t 3:306:30 i this roo; i fterwrs ore fi ex ouceets ext
BINOMIAL THEOREM NCERT An expression consisting of two terms, connected by + or sign is called a
 8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4, etc., ae all biomial 5y epessios. 8.. Biomial theoem BINOMIAL THEOREM If a ad b ae
8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4, etc., ae all biomial 5y epessios. 8.. Biomial theoem BINOMIAL THEOREM If a ad b ae
APPLIED THERMODYNAMICS D201. SELF ASSESSMENT SOLUTIONS TUTORIAL 2 SELF ASSESSMENT EXERCISE No. 1
 APPIED ERMODYNAMICS D0 SEF ASSESSMEN SOUIONS UORIA SEF ASSESSMEN EXERCISE No. Show how the umeti effiiey of a ideal sigle stage eioatig ai omesso may be eeseted by the equatio ( / Whee is the leaae atio,
APPIED ERMODYNAMICS D0 SEF ASSESSMEN SOUIONS UORIA SEF ASSESSMEN EXERCISE No. Show how the umeti effiiey of a ideal sigle stage eioatig ai omesso may be eeseted by the equatio ( / Whee is the leaae atio,
Solution to HW 3, Ma 1a Fall 2016
 Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
( ) dx ; f ( x ) is height and Δx is
 Mth : 6.3 Defiite Itegrls from Riem Sums We just sw tht the exct re ouded y cotiuous fuctio f d the x xis o the itervl x, ws give s A = lim A exct RAM, where is the umer of rectgles i the Rectgulr Approximtio
Mth : 6.3 Defiite Itegrls from Riem Sums We just sw tht the exct re ouded y cotiuous fuctio f d the x xis o the itervl x, ws give s A = lim A exct RAM, where is the umer of rectgles i the Rectgulr Approximtio
Hypergeometric Functions and Lucas Numbers
 IOSR Jourl of Mthetis (IOSR-JM) ISSN: 78-78. Volue Issue (Sep-Ot. ) PP - Hypergeoetri utios d us Nuers P. Rjhow At Kur Bor Deprtet of Mthetis Guhti Uiversity Guwhti-78Idi Astrt: The i purpose of this pper
IOSR Jourl of Mthetis (IOSR-JM) ISSN: 78-78. Volue Issue (Sep-Ot. ) PP - Hypergeoetri utios d us Nuers P. Rjhow At Kur Bor Deprtet of Mthetis Guhti Uiversity Guwhti-78Idi Astrt: The i purpose of this pper
EXPONENTS AND LOGARITHMS
 978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
4. When is the particle speeding up? Why? 5. When is the particle slowing down? Why?
 AB CALCULUS: 5.3 Positio vs Distce Velocity vs. Speed Accelertio All the questios which follow refer to the grph t the right.. Whe is the prticle movig t costt speed?. Whe is the prticle movig to the right?
AB CALCULUS: 5.3 Positio vs Distce Velocity vs. Speed Accelertio All the questios which follow refer to the grph t the right.. Whe is the prticle movig t costt speed?. Whe is the prticle movig to the right?
Counting Functions and Subsets
 CHAPTER 1 Coutig Fuctios ad Subsets This chapte of the otes is based o Chapte 12 of PJE See PJE p144 Hee ad below, the efeeces to the PJEccles book ae give as PJE The goal of this shot chapte is to itoduce
CHAPTER 1 Coutig Fuctios ad Subsets This chapte of the otes is based o Chapte 12 of PJE See PJE p144 Hee ad below, the efeeces to the PJEccles book ae give as PJE The goal of this shot chapte is to itoduce
Bernoulli Numbers. n(n+1) = n(n+1)(2n+1) = n(n 1) 2
 Beroulli Numbers Beroulli umbers are amed after the great Swiss mathematiia Jaob Beroulli5-705 who used these umbers i the power-sum problem. The power-sum problem is to fid a formula for the sum of the
Beroulli Numbers Beroulli umbers are amed after the great Swiss mathematiia Jaob Beroulli5-705 who used these umbers i the power-sum problem. The power-sum problem is to fid a formula for the sum of the
Generating Function for Partitions with Parts in A.P
 Geetig Fuctio fo Ptitio wi Pt i AP Hum Reddy K # K Jkmm * # Detmet of Memtic Hidu Coege Gutu 50 AP Idi * Detmet of Memtic 8 Mi AECS Lyout B BLOCK Sigd Bgoe 5604 Idi Abtct: I i e we deive e geetig fuctio
Geetig Fuctio fo Ptitio wi Pt i AP Hum Reddy K # K Jkmm * # Detmet of Memtic Hidu Coege Gutu 50 AP Idi * Detmet of Memtic 8 Mi AECS Lyout B BLOCK Sigd Bgoe 5604 Idi Abtct: I i e we deive e geetig fuctio
A Revision Article of Oil Wells Performance Methods
 A Revisin Aticle Oil Wells emnce Methds The ductivity inde well, dented y, is mesue the ility the well t duce. It is given y: Whee: Welle ductivity inde, STB/dy/sig Avege (sttic) esevi essue, sig Welle
A Revisin Aticle Oil Wells emnce Methds The ductivity inde well, dented y, is mesue the ility the well t duce. It is given y: Whee: Welle ductivity inde, STB/dy/sig Avege (sttic) esevi essue, sig Welle
B. Examples 1. Finite Sums finite sums are an example of Riemann Sums in which each subinterval has the same length and the same x i
 Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
The Definite Riemann Integral
 These otes closely follow the presettio of the mteril give i Jmes Stewrt s textook Clculus, Cocepts d Cotexts (d editio). These otes re iteded primrily for i-clss presettio d should ot e regrded s sustitute
These otes closely follow the presettio of the mteril give i Jmes Stewrt s textook Clculus, Cocepts d Cotexts (d editio). These otes re iteded primrily for i-clss presettio d should ot e regrded s sustitute
Lecture 10. Solution of Nonlinear Equations - II
 Fied point Poblems Lectue Solution o Nonline Equtions - II Given unction g : R R, vlue such tht gis clled ied point o the unction g, since is unchnged when g is pplied to it. Whees with nonline eqution
Fied point Poblems Lectue Solution o Nonline Equtions - II Given unction g : R R, vlue such tht gis clled ied point o the unction g, since is unchnged when g is pplied to it. Whees with nonline eqution
Let. Then. k n. And. Φ npq. npq. ε 2. Φ npq npq. npq. = ε. k will be very close to p. If n is large enough, the ratio n
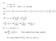 Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Neural Network Introduction. Hung-yi Lee
 Neu Neto Intoducton Hung- ee Reve: Supevsed enng Mode Hpothess Functon Set f, f : : (e) Tnng: Pc the est Functon f * Best Functon f * Testng: f Tnng Dt : functon nput : functon output, ˆ,, ˆ, Neu Neto
Neu Neto Intoducton Hung- ee Reve: Supevsed enng Mode Hpothess Functon Set f, f : : (e) Tnng: Pc the est Functon f * Best Functon f * Testng: f Tnng Dt : functon nput : functon output, ˆ,, ˆ, Neu Neto
ME 501A Seminar in Engineering Analysis Page 1
 Powe Seies Solutios Foeius Metho Septee 6, 7 Powe Seies Solutios Foeius etho L Cetto Mehil Egieeig 5AB Sei i Egieeig Alsis Otoe 6, 7 Outlie Review lst wee Powe seies solutios Geel ppoh Applitio Foeius
Powe Seies Solutios Foeius Metho Septee 6, 7 Powe Seies Solutios Foeius etho L Cetto Mehil Egieeig 5AB Sei i Egieeig Alsis Otoe 6, 7 Outlie Review lst wee Powe seies solutios Geel ppoh Applitio Foeius
Using Counting Techniques to Determine Probabilities
 Kowledge ticle: obability ad Statistics Usig outig Techiques to Detemie obabilities Tee Diagams ad the Fudametal outig iciple impotat aspect of pobability theoy is the ability to detemie the total umbe
Kowledge ticle: obability ad Statistics Usig outig Techiques to Detemie obabilities Tee Diagams ad the Fudametal outig iciple impotat aspect of pobability theoy is the ability to detemie the total umbe
Conditional Convergence of Infinite Products
 Coditioal Covegece of Ifiite Poducts William F. Tech Ameica Mathematical Mothly 106 1999), 646-651 I this aticle we evisit the classical subject of ifiite poducts. Fo stadad defiitios ad theoems o this
Coditioal Covegece of Ifiite Poducts William F. Tech Ameica Mathematical Mothly 106 1999), 646-651 I this aticle we evisit the classical subject of ifiite poducts. Fo stadad defiitios ad theoems o this
Random Signals and Noise Winter Semester 2017 Problem Set 12 Wiener Filter Continuation
 Radom Sigals ad Noise Witer Semester 7 Problem Set Wieer Filter Cotiuatio Problem (Sprig, Exam A) Give is the sigal W t, which is a Gaussia white oise with expectatio zero ad power spectral desity fuctio
Radom Sigals ad Noise Witer Semester 7 Problem Set Wieer Filter Cotiuatio Problem (Sprig, Exam A) Give is the sigal W t, which is a Gaussia white oise with expectatio zero ad power spectral desity fuctio
10. 3 The Integral and Comparison Test, Estimating Sums
 0. The Itegrl d Comriso Test, Estimtig Sums I geerl, it is hrd to fid the ect sum of series. We were le to ccomlish this for geometric series d for telescoig series sice i ech of those cses we could fid
0. The Itegrl d Comriso Test, Estimtig Sums I geerl, it is hrd to fid the ect sum of series. We were le to ccomlish this for geometric series d for telescoig series sice i ech of those cses we could fid
7.5-Determinants in Two Variables
 7.-eteminnts in Two Vibles efinition of eteminnt The deteminnt of sque mti is el numbe ssocited with the mti. Eve sque mti hs deteminnt. The deteminnt of mti is the single ent of the mti. The deteminnt
7.-eteminnts in Two Vibles efinition of eteminnt The deteminnt of sque mti is el numbe ssocited with the mti. Eve sque mti hs deteminnt. The deteminnt of mti is the single ent of the mti. The deteminnt
Week 03 Discussion. 30% are serious, and 50% are stable. Of the critical ones, 30% die; of the serious, 10% die; and of the stable, 2% die.
 STAT 400 Wee 03 Discussio Fall 07. ~.5- ~.6- At the begiig of a cetai study of a gou of esos, 5% wee classified as heavy smoes, 30% as light smoes, ad 55% as osmoes. I the five-yea study, it was detemied
STAT 400 Wee 03 Discussio Fall 07. ~.5- ~.6- At the begiig of a cetai study of a gou of esos, 5% wee classified as heavy smoes, 30% as light smoes, ad 55% as osmoes. I the five-yea study, it was detemied
SOME REMARKS ON HORIZONTAL, SLANT, PARABOLIC AND POLYNOMIAL ASYMPTOTE
 D I D A C T I C S O F A T H E A T I C S No (4) 3 SOE REARKS ON HORIZONTAL, SLANT, PARABOLIC AND POLYNOIAL ASYPTOTE Tdeusz Jszk Abstct I the techg o clculus, we cosde hozotl d slt symptote I ths ppe the
D I D A C T I C S O F A T H E A T I C S No (4) 3 SOE REARKS ON HORIZONTAL, SLANT, PARABOLIC AND POLYNOIAL ASYPTOTE Tdeusz Jszk Abstct I the techg o clculus, we cosde hozotl d slt symptote I ths ppe the
Greatest term (numerically) in the expansion of (1 + x) Method 1 Let T
 BINOMIAL THEOREM_SYNOPSIS Geatest tem (umeically) i the epasio of ( + ) Method Let T ( The th tem) be the geatest tem. Fid T, T, T fom the give epasio. Put T T T ad. Th will give a iequality fom whee value
BINOMIAL THEOREM_SYNOPSIS Geatest tem (umeically) i the epasio of ( + ) Method Let T ( The th tem) be the geatest tem. Fid T, T, T fom the give epasio. Put T T T ad. Th will give a iequality fom whee value
On a Problem of Littlewood
 Ž. JOURAL OF MATHEMATICAL AALYSIS AD APPLICATIOS 199, 403 408 1996 ARTICLE O. 0149 O a Poblem of Littlewood Host Alze Mosbache Stasse 10, 51545 Waldbol, Gemay Submitted by J. L. Bee Received May 19, 1995
Ž. JOURAL OF MATHEMATICAL AALYSIS AD APPLICATIOS 199, 403 408 1996 ARTICLE O. 0149 O a Poblem of Littlewood Host Alze Mosbache Stasse 10, 51545 Waldbol, Gemay Submitted by J. L. Bee Received May 19, 1995
Physics 604 Problem Set 1 Due Sept 16, 2010
 Physics 64 Polem et 1 Due ept 16 1 1) ) Inside good conducto the electic field is eo (electons in the conducto ecuse they e fee to move move in wy to cncel ny electic field impessed on the conducto inside
Physics 64 Polem et 1 Due ept 16 1 1) ) Inside good conducto the electic field is eo (electons in the conducto ecuse they e fee to move move in wy to cncel ny electic field impessed on the conducto inside
Lecture 24: Observability and Constructibility
 ectue 24: Obsevability ad Costuctibility 7 Obsevability ad Costuctibility Motivatio: State feedback laws deped o a kowledge of the cuet state. I some systems, xt () ca be measued diectly, e.g., positio
ectue 24: Obsevability ad Costuctibility 7 Obsevability ad Costuctibility Motivatio: State feedback laws deped o a kowledge of the cuet state. I some systems, xt () ca be measued diectly, e.g., positio
MATH /19: problems for supervision in week 08 SOLUTIONS
 MATH10101 2018/19: poblems fo supevisio i week 08 Q1. Let A be a set. SOLUTIONS (i Pove that the fuctio c: P(A P(A, defied by c(x A \ X, is bijective. (ii Let ow A be fiite, A. Use (i to show that fo each
MATH10101 2018/19: poblems fo supevisio i week 08 Q1. Let A be a set. SOLUTIONS (i Pove that the fuctio c: P(A P(A, defied by c(x A \ X, is bijective. (ii Let ow A be fiite, A. Use (i to show that fo each
Chapter 7. Kleene s Theorem. 7.1 Kleene s Theorem. The following theorem is the most important and fundamental result in the theory of FA s:
 Chpte 7 Kleene s Theoem 7.1 Kleene s Theoem The following theoem is the most impotnt nd fundmentl esult in the theoy of FA s: Theoem 6 Any lnguge tht cn e defined y eithe egul expession, o finite utomt,
Chpte 7 Kleene s Theoem 7.1 Kleene s Theoem The following theoem is the most impotnt nd fundmentl esult in the theoy of FA s: Theoem 6 Any lnguge tht cn e defined y eithe egul expession, o finite utomt,
ALGEBRA. ( ) is a point on the line ( ) + ( ) = + ( ) + + ) + ( Distance Formula The distance d between two points x, y
 ALGEBRA Popeties of Asoute Vue Fo e umes : 0, 0 + + Tige Iequity Popeties of Itege Epoets Ris Assume tt m e positive iteges, tt e oegtive, tt eomitos e ozeo. See Appeies B D fo gps fute isussio. + ( )
ALGEBRA Popeties of Asoute Vue Fo e umes : 0, 0 + + Tige Iequity Popeties of Itege Epoets Ris Assume tt m e positive iteges, tt e oegtive, tt eomitos e ozeo. See Appeies B D fo gps fute isussio. + ( )
RECIPROCAL POWER SUMS. Anthony Sofo Victoria University, Melbourne City, Australia.
 #A39 INTEGERS () RECIPROCAL POWER SUMS Athoy Sofo Victoia Uivesity, Melboue City, Austalia. athoy.sofo@vu.edu.au Received: /8/, Acceted: 6//, Published: 6/5/ Abstact I this ae we give a alteative oof ad
#A39 INTEGERS () RECIPROCAL POWER SUMS Athoy Sofo Victoia Uivesity, Melboue City, Austalia. athoy.sofo@vu.edu.au Received: /8/, Acceted: 6//, Published: 6/5/ Abstact I this ae we give a alteative oof ad
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS. and x i = a + i. i + n(n + 1)(2n + 1) + 2a. (b a)3 6n 2
 MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
2a a a 2a 4a. 3a/2 f(x) dx a/2 = 6i) Equation of plane OAB is r = λa + µb. Since C lies on the plane OAB, c can be expressed as c = λa +
 -6-5 - - - - 5 6 - - - - - - / GCE A Level H Mths Nov Pper i) z + z 6 5 + z 9 From GC, poit of itersectio ( 8, 9 6, 5 ). z + z 6 5 9 From GC, there is o solutio. So p, q, r hve o commo poits of itersectio.
-6-5 - - - - 5 6 - - - - - - / GCE A Level H Mths Nov Pper i) z + z 6 5 + z 9 From GC, poit of itersectio ( 8, 9 6, 5 ). z + z 6 5 9 From GC, there is o solutio. So p, q, r hve o commo poits of itersectio.
Dividing Algebraic Fractions
 Leig Eheme Tem Model Awe: Mlilig d Diidig Algei Fio Mlilig d Diidig Algei Fio d gide ) Yo e he me mehod o mlil lgei io o wold o mlil meil io. To id he meo o he we o mlil he meo o he io i he eio. Simill
Leig Eheme Tem Model Awe: Mlilig d Diidig Algei Fio Mlilig d Diidig Algei Fio d gide ) Yo e he me mehod o mlil lgei io o wold o mlil meil io. To id he meo o he we o mlil he meo o he io i he eio. Simill
Project 3: Using Identities to Rewrite Expressions
 MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
Generalized Fibonacci-Type Sequence and its Properties
 Geelized Fibocci-Type Sequece d is Popeies Ompsh Sihwl shw Vys Devshi Tuoil Keshv Kuj Mdsu (MP Idi Resech Schol Fculy of Sciece Pcific Acdemy of Highe Educio d Resech Uivesiy Udipu (Rj Absc: The Fibocci
Geelized Fibocci-Type Sequece d is Popeies Ompsh Sihwl shw Vys Devshi Tuoil Keshv Kuj Mdsu (MP Idi Resech Schol Fculy of Sciece Pcific Acdemy of Highe Educio d Resech Uivesiy Udipu (Rj Absc: The Fibocci
Chapter 8 Complex Numbers
 Chapte 8 Complex Numbes Motivatio: The ae used i a umbe of diffeet scietific aeas icludig: sigal aalsis, quatum mechaics, elativit, fluid damics, civil egieeig, ad chaos theo (factals. 8.1 Cocepts - Defiitio
Chapte 8 Complex Numbes Motivatio: The ae used i a umbe of diffeet scietific aeas icludig: sigal aalsis, quatum mechaics, elativit, fluid damics, civil egieeig, ad chaos theo (factals. 8.1 Cocepts - Defiitio
Multi-Electron Atoms-Helium
 Multi-lecto Atos-Heliu He - se s H but with Z He - electos. No exct solutio of.. but c use H wve fuctios d eegy levels s sttig poit ucleus sceeed d so Zeffective is < sceeig is ~se s e-e epulsio fo He,
Multi-lecto Atos-Heliu He - se s H but with Z He - electos. No exct solutio of.. but c use H wve fuctios d eegy levels s sttig poit ucleus sceeed d so Zeffective is < sceeig is ~se s e-e epulsio fo He,
Convergence rates of approximate sums of Riemann integrals
 Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsuku Tsuku Irki 5-857 Jp tski@mth.tsuku.c.jp Keywords : covergece rte; Riem sum; Riem
Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsuku Tsuku Irki 5-857 Jp tski@mth.tsuku.c.jp Keywords : covergece rte; Riem sum; Riem
Mark Scheme (Results) January 2008
 Mk Scheme (Results) Jnuy 00 GCE GCE Mthemtics (6679/0) Edecel Limited. Registeed in Englnd nd Wles No. 4496750 Registeed Office: One90 High Holbon, London WCV 7BH Jnuy 00 6679 Mechnics M Mk Scheme Question
Mk Scheme (Results) Jnuy 00 GCE GCE Mthemtics (6679/0) Edecel Limited. Registeed in Englnd nd Wles No. 4496750 Registeed Office: One90 High Holbon, London WCV 7BH Jnuy 00 6679 Mechnics M Mk Scheme Question
