Theory of Computation (VI) Yijia Chen Fudan University
|
|
|
- Sara Wilson
- 5 years ago
- Views:
Transcription
1 Theory of Computation (VI) Yijia Chen Fudan University
2 Review
3 Forced handles Definition A handle h of a valid string v = xhy is a forced handle if h is the unique handle in every valid string xhŷ where ŷ Σ.
4 Definition A deterministic context-free grammar (DCFG) is a context-free grammar such that every valid string has a forced handle. The above definition does not tell us how to decide whether a given CFG is a DCFG.
5 DK-test For any CFG we construct an associated DFA DK that can identify handles. DK accepts its input z if 1. z is the prefix of some valid string v = zy, and 2. z ends with a handle of v. Moreover, each accept state of DK indicates the associated reducing rule(s). In a general CFG, multiple reducing rules may apply, depending on which valid v extends z. But in a DCFG, each accept state corresponds to exactly one reducing rule.
6 Two provisos 1. The start variable of a CFG does not appear on the right-hand side of any rule. 2. Every variable appears in a reduction of some string in the grammar s language.
7 The plan To construct DFA DK, we will construct an equivalent NFA K and convert K to DK via the subset construction. To understand K, we introduce an NFA J which accepts every input string that ends with the right-hand side of any rule.
8 The NFA J 1. guesses a rule B u to use, 2. guesses at which point to start matching the input with u, 3. keeps track of its progress through u. We represent this progress by placing a dot in the corresponding point in the rule, yielding the following dotted rules: B.u 1u 2 u k 1 u k B u 1.u 2 u k 1 u k. B u 1u 2 u k 1.u k B u 1u 2 u k 1 u k.
9 Dotted rules 1. Each dotted rule corresponds to one state of J, i.e., for B u.v we have a state B u.v. 2. The accept states B u. correspond to the complete rules. 3. We add a separate start state with a self-loop on all symbols and an ε-move to B.u for each rule B u. Thus, J accepts if the match completes successfully at the end of the input. If a mismatch occurs or if the end of the match does not coincide with the end of the input, this branch of Js computation rejects.
10 The NFA K Like J, the states of K correspond to all dotted rules. It has a special start state that has an ε-move to S 1.u with S 1 being the start variable. for every rule Shift-moves: for a rule B uav where a can be a terminal or variable a B u.av B ua.v ε-moves: for a rule B ucv and C r ε B u.cv C.r The accept states are all B u..
11 Lemma K may enter state T u.v on reading input z if and only if z = xu and xuvy is a valid string with handle uv and reducing rule T uv, for some y Σ.
12 Proof (1) Assume K enters state T u.v on reading input z, whose path from the start state is viewed as runs of shift-moves separated by ε-moves. The shift-moves are transitions between states sharing the same rule, shifting the dot rightward over symbols read from the input. In the ith run,the rule is S i u i S i+1 v i, where S i+1 is the variable expanded in the next run. The penultimate run is for rule S l u l Tv l, and the final run has rule T uv. So the input z = u 1u 2... u l u = xu, because the strings u i and u were the shift-move symbols read from the input.
13 Proof (2) Let then xuvy is derivable in G. y = v l... v 2v 1, Fully expand all variables that appear in y until each variable derives some string of terminals, and let y be the resulting string. The string xuvy is valid because it occurs in a leftmost reduction of w L(G) of terminals obtained by expanding all variables in xuvy. uv is the handle in the reduction and its reducing rule is T uv. This proves the direction from left to right.
14 Proof (3) Assume that string xuvy is a valid string with handle uv and reducing rule T uv. We need to show that K may enter T u.v on reading input xu. 1. The parse tree is rooted at the start variable S 1 and it must contain the variable T, as T uv is the first reduce step in the reduction of xuvy. 2. Let S 2,..., S l be the variables on the path from S 1 to T. All variables in the parse tree that appear leftward of this path must be unexpanded, or else uv would not be the handle. 3. Each S i leads to S i+1 by some rule S i u i S i+1 v i : S 1 u 1S 2u k S 2 u 2S 3u 2. S l u l Tv l T uv.
15 Proof (4) On input z = xu, the path from K s start state to T u.v is: 1. K makes an ε-move to S 1.u 1S 2v Reading the symbols of u 1, it performs the corresponding shift-moves until it enters S 1 u 1.S 2v 1 at the end of u It makes an ε-move to S 2.u 2S 3v 2 and continues with shift-moves on reading u 2 until it reaches S 2 u 2.S 3v After reading u l it enters S l u l.tv l which leads by an ε-move to T.uv. 5. Finally after reading u it is in T u.v.
16 Corollary K may enter state T h. on reading input z if and only if z = xh and h is a handle of some valid string xhy with reducing rule T h.
17 From K to DK We convert NFA K to DFA DK by the subset construction. All states unreachable from the start state are removed. Thus, each of DK s states thus contains one of more dotted rules. Each accept state contains at least one completed rule.
18 146 CHAPTER 2 / CONTEXT-FREE LANGUAGES An example EXAMPLE 2.55 Here is the DFA DK showing that the grammar below is a DCFG. S T T T (T ) ε S T T T(T ) T T S T T T (T ) ( S T T T ( T ) T T (T ) T T ( T T (T ) T T (T ) ) T (T ) FIGURE 2.56 Example of a DK-test that passes Observe that all accept states satisfy the DK-test conditions.
19 The DK-test Starting with a CFG G, construct the associated DFA DK. Determine whether G is deterministic by examining DKs accept states. G passes the DK-test if every accept state contains 1. exactly one completed rule, and 2. no dotted rule in which a terminal symbol immediately follows the dot, i.e., no dotted rule of the form B u.av for a Σ.
20 Theorem G passes the DK-test if and only if G is a DCFG.
21 Proof (1) Assume that G is not deterministic and show that it fails the DK-test. Take a valid string xhy that has an unforced handle h. Some valid string xhy has a different handle ĥ h, where y is a string of terminals, i.e., y Σ. Thus xhy = ˆxĥŷ. If xh = ˆxĥ, then input xh sends DK to a state with two completed rules, failing the DK-test. If xh ˆxĥ, by symmetry, we assume that xh is a proper prefix of ˆxĥ. Then y Σ +. Let q be the state that DK enters on input xh, which must be accepting as h is a handle of xhy. A transition arrow must exit q as ˆxĥ sends DK to an accept state via q. That transition arrow is labeled with a terminal symbol since y Σ +. Hence q contains a dotted rule with a terminal symbol immediately following the dot, violating the DK-test.
22 Proof (2) Assume G fails the DK-test at some accept state q. We show that G has an unforced handle. q has a complete rule T h., for it is accepting. Let z be a string that leads DK to q. Then z = xh where some valid string xhy has handle h with reducing rule T h, for y Σ. If q has another completed rule B ĥ.. Then some valid string xhy must have a different handle ĥ with reducing rule B ĥ. Hence, h is not a forced handle.
23 Proof (3) q has a complete rule T h., for it is accepting. Let z be a string that leads DK to q. Then z = xh where some valid string xhy has handle h with reducing rule T h, for y Σ. q contains a rule B u.av with a Σ. xh takes DK to q, so xh = ˆxu, where ˆxuavŷ is valid and has a handle uav with reducing rule B uav, for some ŷ Σ. Expand all variables in v to get v Σ, and let y = av ŷ with y Σ. The following is a leftmost reduction xhy = xhav ŷ = ˆxuav ŷ ˆxuavŷ ˆxBŷ S. ˆxuavŷ is valid, and we can obtain ˆxuav ŷ from it using a rightmost derivation, so ˆxuav ŷ is also valid. The handle of ˆxuav ŷ either lies inside v (if v v ) or is uav (if u = v). In either case, the handle includes a or follows a and thus cannot be h because h fully precedes a. Hence h is not a forced handle.
24 EXAMPLE 2.53 An example failing the DK-test Here we illustrate how the DK-test fails for the following grammar. S E E E + T T T T x a a S E E E+T E T T T a T a E T T T a T a E S E E E +T + E E+ T T T a T a a T a T S E E E+T T T a T T a a T T a FIGURE 2.54
25 146 CHAPTER 2 / CONTEXT-FREE LANGUAGES An example passing the DK-test EXAMPLE 2.55 Here is the DFA DK showing that the grammar below is a DCFG. S T T T (T ) ε S T T T(T ) T T S T T T (T ) ( S T T T ( T ) T T (T ) T T ( T T (T ) T T (T ) ) T (T ) FIGURE 2.56 Example of a DK-test that passes Observe that all accept states satisfy the DK-test conditions.
26 Relationship of DPDAs and DCFGs Theorem An endmarked language is generated by a deterministic context-free grammar if and only if it is deterministic context free.
27 Endmarked languages Definition For any language A the endmarked language A is defined by { w w A }. Here is the special endmarker symbol. Theorem A is a DCFL if and only if A is a DCFL.
28 Prefix-free languages Definition A Σ is prefix-free if for every w A and every proper prefix w of w we have w / A. Lemma Every A is prefix-free. Lemma Every DCFG generates a prefix-free language.
29 Prefix-free languages (cont d) The grammar S T T T (T ) ε is DCFG, which recognizes some A A cannot be generated by DCFG, since it is not prefix-free.
30 Lemma Every DCFG has an equivalent DPDA.
31 Lemma Every DPDA that recognizes an endmarked language has an equivalent DCFG.
32 Proof (1) Let P = ( Q, Σ, Γ, δ, q 0, {q accept} ) be a DPDA. Recall the previous construction: For each pair of states p and q, the grammar has a variable A pq which generates all strings taking P from p with an empty stack to q with an empty stack. We modify P such that: 1. It has a single accept state q accept. 2. It empties its stack before accepting, which cannot be deterministic without reading the endmark. 3. Each transition either pushes a symbol onto the stack or pops one off the stack, but it does not do both at the same time.
33 Proof (2) 1. For every p, q, r, s, Q, u Γ, and a, b Σ ε, if δ(p, a, ε) = (r, u) and δ(s, b, u) = (q, ε), then add A pq aa rsb. 2. For every p, q, r Q, add A pq A pr A rq. 3. For every p Q, add A pp ε. To avoid ambiguity, we combine rules of types 1 and 2 into: 1-2. For every p, q, r, s, t Q, u Γ, and a, b Σ ε, if δ(r, a, ε) = (s, u) and δ(t, b, u) = (q, ε), add the rule A pq A pr aa stb. Let G be the resulting grammar.
34 Proof (3) In a derivation of the original grammar, for each substitution due to a type 2 rule A pq A pr A rq, we can assume that r is P s state when it is at the rightmost point where the stack becomes empty midway. Then the subsequent substitution of A rq must expand it using a type 1 rule A rq aa stb. We can combine these two substitutions into a single type 1-2 rule A pq A pr aa stb.
35 Proof (4) In a derivation using the modified grammar G, if we replace each type 1-2 rule A pq A pr aa stb by the type 2 rule A pq A pr A rq followed by the type 1 rule A rq aa stb, we get the same result.
36 Proof (5) We use DK-test to show that G is deterministic. We need to analyze how P operates on valid strings by extending its input alphabet and transition function to process variable symbols in addition to terminal symbols. Add all symbols A pq to P s input alphabet and extend its δ by defining δ(p, A pq, ε) = (q, ε). Set all other transitions involving A pq to. To preserve P deterministic behavior, if P reads A pq from the input then disallow an ε-move.
37 Proof (6) Consider the derivation: A q0,q accept = v 0 v 1 v i v k = w. Claim If P reads v i containing a variable A pq, it enters state p just prior to reading A pq. If i = 0, then v i = A q0,q accept and P starts in q 0. Assume the claim is true for some i 0. v i = xa pqy and A pq is the variable substituted in the step v i v i+1. By IH, P enters state p after reading x, prior to reading A pq. By the construction of G, the substitution rules may of two types: 1. A pq A pr aa stb or 2. A pp ε.
38 Proof (7) Thus either v i+1 = xa pr aa stby or v i+1 = xy. In the first case, when P reads A pr aa stb in v i+1, we know it starts in state p, because it has just finished reading x. As P reads A pr aa stb in v i+1, it enters the sequence of states r, s, t, and q, due to to the substitution rule s construction. Therefore, it enters state p just prior to reading A pr and it enters state s just prior to reading A st. The claim holds on variables in the y part because, after reading b, P enters state q and then it reads y. On input v i, it also enters q just before reading y, so the computations agree on the y parts of v i and v i+1. Obviously, the computations agree on the x parts. In the second case, no new variables are introduced, so we only need to observe that the computations agree on the x and y parts of v i and v i+1.
39 Proof (8) Claim G passes the DK-test. Select one of the accept states of DKfor G. It contains a completed rule R which can be 1. A pq A pr aa stb. or 2. A pp. We need to show in both cases that the state cannot contain a. another complete rule, and b. a dotted rule that has a terminal symbol immediately after the dot. In each case, we start by considering a string z on which DK goes to the above accept state.
40 Case 1a. R is a completed type 1-2 rule. For any rule in this accept state, z must end with the symbols preceding the dot in that rule because DK goes to that state on z. Hence the symbols preceding the dot must be consistent in all such rules. These symbols are A pr aa stb in R so any other type 1-2 completed rule must have exactly the same symbols on the right-hand side The variables on the left-hand side must also agree, so the rules must be the same.
41 Case 1a. (cont d) Assume that the accept state contains R and some type 3 completed ε-rule T = A ss.. From R we know that z ends with A pr aa stb. P pops its stack at the very end of z because a pop occurs at that point in R, due to G s construction. According to the way we build DK, a completed ε-rule in a state must derive from a dotted rule that resides in the same state, where the dot isn t at the very beginning and the dot immediately precedes some variable. An exception occurs at DK s start state, where this dot may occur at the beginning of the rule, but this accept state cannot be the start state because it contains a completed type 1-2 rule. In G, that means T derives from a type 1-2 dotted rule where the dot precedes the second variable. From G s construction a push occurs just before the dot. This implies that P does a push move at the very end of z, contradicting our previous statement.
Theory of Computation (IV) Yijia Chen Fudan University
 Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
October 6, Equivalence of Pushdown Automata with Context-Free Gramm
 Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
PUSHDOWN AUTOMATA (PDA)
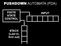 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
Theory of Computation (IX) Yijia Chen Fudan University
 Theory of Computation (IX) Yijia Chen Fudan University Review The Definition of Algorithm Polynomials and their roots A polynomial is a sum of terms, where each term is a product of certain variables and
Theory of Computation (IX) Yijia Chen Fudan University Review The Definition of Algorithm Polynomials and their roots A polynomial is a sum of terms, where each term is a product of certain variables and
Theory of Computation (II) Yijia Chen Fudan University
 Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
CPSC 421: Tutorial #1
 CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
UNIT-VI PUSHDOWN AUTOMATA
 Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Computational Models: Class 5
 Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
2.1 Solution. E T F a. E E + T T + T F + T a + T a + F a + a
 . Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
. Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
CS5371 Theory of Computation. Lecture 7: Automata Theory V (CFG, CFL, CNF)
 CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata
 Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata Salil Vadhan October 4, 2012 Reading: Sipser, 2.2. Another example of a CFG (with proof) L = {x {a, b} : x has the same # of a s and
Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata Salil Vadhan October 4, 2012 Reading: Sipser, 2.2. Another example of a CFG (with proof) L = {x {a, b} : x has the same # of a s and
September 7, Formal Definition of a Nondeterministic Finite Automaton
 Formal Definition of a Nondeterministic Finite Automaton September 7, 2014 A comment first The formal definition of an NFA is similar to that of a DFA. Both have states, an alphabet, transition function,
Formal Definition of a Nondeterministic Finite Automaton September 7, 2014 A comment first The formal definition of an NFA is similar to that of a DFA. Both have states, an alphabet, transition function,
Theory of Computation (I) Yijia Chen Fudan University
 Theory of Computation (I) Yijia Chen Fudan University Instructor Yijia Chen Homepage: http://basics.sjtu.edu.cn/~chen Email: yijiachen@fudan.edu.cn Textbook Introduction to the Theory of Computation Michael
Theory of Computation (I) Yijia Chen Fudan University Instructor Yijia Chen Homepage: http://basics.sjtu.edu.cn/~chen Email: yijiachen@fudan.edu.cn Textbook Introduction to the Theory of Computation Michael
Languages, regular languages, finite automata
 Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Pushdown Automata (2015/11/23)
 Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
Fundamentele Informatica II
 Fundamentele Informatica II Answer to selected exercises 5 John C Martin: Introduction to Languages and the Theory of Computation M.M. Bonsangue (and J. Kleijn) Fall 2011 5.1.a (q 0, ab, Z 0 ) (q 1, b,
Fundamentele Informatica II Answer to selected exercises 5 John C Martin: Introduction to Languages and the Theory of Computation M.M. Bonsangue (and J. Kleijn) Fall 2011 5.1.a (q 0, ab, Z 0 ) (q 1, b,
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Push-down Automata = FA + Stack
 Push-down Automata = FA + Stack PDA Definition A push-down automaton M is a tuple M = (Q,, Γ, δ, q0, F) where Q is a finite set of states is the input alphabet (of terminal symbols, terminals) Γ is the
Push-down Automata = FA + Stack PDA Definition A push-down automaton M is a tuple M = (Q,, Γ, δ, q0, F) where Q is a finite set of states is the input alphabet (of terminal symbols, terminals) Γ is the
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
V Honors Theory of Computation
 V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
Finite Automata and Regular languages
 Finite Automata and Regular languages Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
Finite Automata and Regular languages Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
Lecture 17: Language Recognition
 Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Theory Bridge Exam Example Questions
 Theory Bridge Exam Example Questions Annotated version with some (sometimes rather sketchy) answers and notes. This is a collection of sample theory bridge exam questions. This is just to get some idea
Theory Bridge Exam Example Questions Annotated version with some (sometimes rather sketchy) answers and notes. This is a collection of sample theory bridge exam questions. This is just to get some idea
Outline. CS21 Decidability and Tractability. Machine view of FA. Machine view of FA. Machine view of FA. Machine view of FA.
 Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
What languages are Turing-decidable? What languages are not Turing-decidable? Is there a language that isn t even Turingrecognizable?
 } We ll now take a look at Turing Machines at a high level and consider what types of problems can be solved algorithmically and what types can t: What languages are Turing-decidable? What languages are
} We ll now take a look at Turing Machines at a high level and consider what types of problems can be solved algorithmically and what types can t: What languages are Turing-decidable? What languages are
Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x where
 Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
CS500 Homework #2 Solutions
 CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules).
 Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules). 1a) G = ({R, S, T}, {0,1}, P, S) where P is: S R0R R R0R1R R1R0R T T 0T ε (S generates the first 0. R generates
Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules). 1a) G = ({R, S, T}, {0,1}, P, S) where P is: S R0R R R0R1R R1R0R T T 0T ε (S generates the first 0. R generates
Nondeterministic Finite Automata
 Nondeterministic Finite Automata Not A DFA Does not have exactly one transition from every state on every symbol: Two transitions from q 0 on a No transition from q 1 (on either a or b) Though not a DFA,
Nondeterministic Finite Automata Not A DFA Does not have exactly one transition from every state on every symbol: Two transitions from q 0 on a No transition from q 1 (on either a or b) Though not a DFA,
Please give details of your answer. A direct answer without explanation is not counted.
 Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
CSE 355 Test 2, Fall 2016
 CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
Introduction to Languages and Computation
 Introduction to Languages and Computation George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 400 George Voutsadakis (LSSU) Languages and Computation July 2014
Introduction to Languages and Computation George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 400 George Voutsadakis (LSSU) Languages and Computation July 2014
5 Context-Free Languages
 CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
Pushdown Automata: Introduction (2)
 Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Nondeterminism. September 7, Nondeterminism
 September 7, 204 Introduction is a useful concept that has a great impact on the theory of computation Introduction is a useful concept that has a great impact on the theory of computation So far in our
September 7, 204 Introduction is a useful concept that has a great impact on the theory of computation Introduction is a useful concept that has a great impact on the theory of computation So far in our
Theory of Computation
 Theory of Computation Lecture #10 Sarmad Abbasi Virtual University Sarmad Abbasi (Virtual University) Theory of Computation 1 / 43 Lecture 10: Overview Linear Bounded Automata Acceptance Problem for LBAs
Theory of Computation Lecture #10 Sarmad Abbasi Virtual University Sarmad Abbasi (Virtual University) Theory of Computation 1 / 43 Lecture 10: Overview Linear Bounded Automata Acceptance Problem for LBAs
CS481F01 Prelim 2 Solutions
 CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
Computational Models Lecture 5
 Computational Models Lecture 5 One More PDAs Example Equivalence of PDAs and CFLs Nondeterminism adds power to PDAs (not in book) Closure Properties of CFLs Algorithmic Aspects of PDAs and CFLs DFAs and
Computational Models Lecture 5 One More PDAs Example Equivalence of PDAs and CFLs Nondeterminism adds power to PDAs (not in book) Closure Properties of CFLs Algorithmic Aspects of PDAs and CFLs DFAs and
AC68 FINITE AUTOMATA & FORMULA LANGUAGES DEC 2013
 Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Accept or reject. Stack
 Pushdown Automata CS351 Just as a DFA was equivalent to a regular expression, we have a similar analogy for the context-free grammar. A pushdown automata (PDA) is equivalent in power to contextfree grammars.
Pushdown Automata CS351 Just as a DFA was equivalent to a regular expression, we have a similar analogy for the context-free grammar. A pushdown automata (PDA) is equivalent in power to contextfree grammars.
CPS 220 Theory of Computation Pushdown Automata (PDA)
 CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
ECS 120: Theory of Computation UC Davis Phillip Rogaway February 16, Midterm Exam
 ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
The Church-Turing Thesis
 The Church-Turing Thesis Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
The Church-Turing Thesis Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
Undecidable Problems and Reducibility
 University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
Chapter 6: NFA Applications
 Chapter 6: NFA Applications Implementing NFAs The problem with implementing NFAs is that, being nondeterministic, they define a more complex computational procedure for testing language membership. To
Chapter 6: NFA Applications Implementing NFAs The problem with implementing NFAs is that, being nondeterministic, they define a more complex computational procedure for testing language membership. To
CpSc 421 Final Exam December 15, 2006
 CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
Theory of Computation Turing Machine and Pushdown Automata
 Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
Instructor s Solutions Manual for Introduction to the Theory of Computation third edition Michael Sipser Mathematics Department MIT
 Instructor s Solutions Manual for Introduction to the Theory of Computation third edition Michael Sipser Mathematics Department MIT Preface This Instructor s Manual is designed to accompany the textbook,
Instructor s Solutions Manual for Introduction to the Theory of Computation third edition Michael Sipser Mathematics Department MIT Preface This Instructor s Manual is designed to accompany the textbook,
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition
 Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
CS 154, Lecture 3: DFA NFA, Regular Expressions
 CS 154, Lecture 3: DFA NFA, Regular Expressions Homework 1 is coming out Deterministic Finite Automata Computation with finite memory Non-Deterministic Finite Automata Computation with finite memory and
CS 154, Lecture 3: DFA NFA, Regular Expressions Homework 1 is coming out Deterministic Finite Automata Computation with finite memory Non-Deterministic Finite Automata Computation with finite memory and
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
SCHEME FOR INTERNAL ASSESSMENT TEST 3
 SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
CFGs and PDAs are Equivalent. We provide algorithms to convert a CFG to a PDA and vice versa.
 CFGs and PDAs are Equivalent We provide algorithms to convert a CFG to a PDA and vice versa. CFGs and PDAs are Equivalent We now prove that a language is generated by some CFG if and only if it is accepted
CFGs and PDAs are Equivalent We provide algorithms to convert a CFG to a PDA and vice versa. CFGs and PDAs are Equivalent We now prove that a language is generated by some CFG if and only if it is accepted
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
CS 530: Theory of Computation Based on Sipser (second edition): Notes on regular languages(version 1.1)
 CS 530: Theory of Computation Based on Sipser (second edition): Notes on regular languages(version 1.1) Definition 1 (Alphabet) A alphabet is a finite set of objects called symbols. Definition 2 (String)
CS 530: Theory of Computation Based on Sipser (second edition): Notes on regular languages(version 1.1) Definition 1 (Alphabet) A alphabet is a finite set of objects called symbols. Definition 2 (String)
CS Pushdown Automata
 Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION
 FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
CMSC 330: Organization of Programming Languages. Pushdown Automata Parsing
 CMSC 330: Organization of Programming Languages Pushdown Automata Parsing Chomsky Hierarchy Categorization of various languages and grammars Each is strictly more restrictive than the previous First described
CMSC 330: Organization of Programming Languages Pushdown Automata Parsing Chomsky Hierarchy Categorization of various languages and grammars Each is strictly more restrictive than the previous First described
Theory of Computation p.1/?? Theory of Computation p.2/?? Unknown: Implicitly a Boolean variable: true if a word is
 Abstraction of Problems Data: abstracted as a word in a given alphabet. Σ: alphabet, a finite, non-empty set of symbols. Σ : all the words of finite length built up using Σ: Conditions: abstracted as a
Abstraction of Problems Data: abstracted as a word in a given alphabet. Σ: alphabet, a finite, non-empty set of symbols. Σ : all the words of finite length built up using Σ: Conditions: abstracted as a
Outline 1 PCP. 2 Decision problems about CFGs. M.Mitra (ISI) Post s Correspondence Problem 1 / 10
 Outline 1 PCP 2 Decision problems about CFGs M.Mitra (ISI) Post s Correspondence Problem 1 / 10 PCP reduction Given: M, w in encoded form To construct: an instance (A, B) of MPCP such that M accepts w
Outline 1 PCP 2 Decision problems about CFGs M.Mitra (ISI) Post s Correspondence Problem 1 / 10 PCP reduction Given: M, w in encoded form To construct: an instance (A, B) of MPCP such that M accepts w
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
Part 4 out of 5 DFA NFA REX. Automata & languages. A primer on the Theory of Computation. Last week, we showed the equivalence of DFA, NFA and REX
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Great Theoretical Ideas in Computer Science. Lecture 4: Deterministic Finite Automaton (DFA), Part 2
 5-25 Great Theoretical Ideas in Computer Science Lecture 4: Deterministic Finite Automaton (DFA), Part 2 January 26th, 27 Formal definition: DFA A deterministic finite automaton (DFA) M =(Q,,,q,F) M is
5-25 Great Theoretical Ideas in Computer Science Lecture 4: Deterministic Finite Automaton (DFA), Part 2 January 26th, 27 Formal definition: DFA A deterministic finite automaton (DFA) M =(Q,,,q,F) M is
Context-Free Grammars (and Languages) Lecture 7
 Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
UNIT-VIII COMPUTABILITY THEORY
 CONTEXT SENSITIVE LANGUAGE UNIT-VIII COMPUTABILITY THEORY A Context Sensitive Grammar is a 4-tuple, G = (N, Σ P, S) where: N Set of non terminal symbols Σ Set of terminal symbols S Start symbol of the
CONTEXT SENSITIVE LANGUAGE UNIT-VIII COMPUTABILITY THEORY A Context Sensitive Grammar is a 4-tuple, G = (N, Σ P, S) where: N Set of non terminal symbols Σ Set of terminal symbols S Start symbol of the
HKN CS/ECE 374 Midterm 1 Review. Nathan Bleier and Mahir Morshed
 HKN CS/ECE 374 Midterm 1 Review Nathan Bleier and Mahir Morshed For the most part, all about strings! String induction (to some extent) Regular languages Regular expressions (regexps) Deterministic finite
HKN CS/ECE 374 Midterm 1 Review Nathan Bleier and Mahir Morshed For the most part, all about strings! String induction (to some extent) Regular languages Regular expressions (regexps) Deterministic finite
1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u,
 1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u, v, x, y, z as per the pumping theorem. 3. Prove that
1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u, v, x, y, z as per the pumping theorem. 3. Prove that
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
Chapter Five: Nondeterministic Finite Automata
 Chapter Five: Nondeterministic Finite Automata From DFA to NFA A DFA has exactly one transition from every state on every symbol in the alphabet. By relaxing this requirement we get a related but more
Chapter Five: Nondeterministic Finite Automata From DFA to NFA A DFA has exactly one transition from every state on every symbol in the alphabet. By relaxing this requirement we get a related but more
Functions on languages:
 MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
Nondeterministic Finite Automata
 Nondeterministic Finite Automata Mahesh Viswanathan Introducing Nondeterminism Consider the machine shown in Figure. Like a DFA it has finitely many states and transitions labeled by symbols from an input
Nondeterministic Finite Automata Mahesh Viswanathan Introducing Nondeterminism Consider the machine shown in Figure. Like a DFA it has finitely many states and transitions labeled by symbols from an input
Theory of Languages and Automata
 Theory of Languages and Automata Chapter 1- Regular Languages & Finite State Automaton Sharif University of Technology Finite State Automaton We begin with the simplest model of Computation, called finite
Theory of Languages and Automata Chapter 1- Regular Languages & Finite State Automaton Sharif University of Technology Finite State Automaton We begin with the simplest model of Computation, called finite
Pushdown Automata (Pre Lecture)
 Pushdown Automata (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Pushdown Automata (Pre Lecture) Fall 2017 1 / 41 Outline Pushdown Automata Pushdown
Pushdown Automata (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Pushdown Automata (Pre Lecture) Fall 2017 1 / 41 Outline Pushdown Automata Pushdown
Introduction to Bottom-Up Parsing
 Introduction to Bottom-Up Parsing Outline Review LL parsing Shift-reduce parsing The LR parsing algorithm Constructing LR parsing tables 2 Top-Down Parsing: Review Top-down parsing expands a parse tree
Introduction to Bottom-Up Parsing Outline Review LL parsing Shift-reduce parsing The LR parsing algorithm Constructing LR parsing tables 2 Top-Down Parsing: Review Top-down parsing expands a parse tree
Computational Theory
 Computational Theory Finite Automata and Regular Languages Curtis Larsen Dixie State University Computing and Design Fall 2018 Adapted from notes by Russ Ross Adapted from notes by Harry Lewis Curtis Larsen
Computational Theory Finite Automata and Regular Languages Curtis Larsen Dixie State University Computing and Design Fall 2018 Adapted from notes by Russ Ross Adapted from notes by Harry Lewis Curtis Larsen
Introduction to Bottom-Up Parsing
 Introduction to Bottom-Up Parsing Outline Review LL parsing Shift-reduce parsing The LR parsing algorithm Constructing LR parsing tables Compiler Design 1 (2011) 2 Top-Down Parsing: Review Top-down parsing
Introduction to Bottom-Up Parsing Outline Review LL parsing Shift-reduce parsing The LR parsing algorithm Constructing LR parsing tables Compiler Design 1 (2011) 2 Top-Down Parsing: Review Top-down parsing
CS311 Computational Structures More about PDAs & Context-Free Languages. Lecture 9. Andrew P. Black Andrew Tolmach
 CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
Automata & languages. A primer on the Theory of Computation. Laurent Vanbever. ETH Zürich (D-ITET) October,
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Part 3 out of 5. Automata & languages. A primer on the Theory of Computation. Last week, we learned about closure and equivalence of regular languages
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Pushdown Automata. Chapter 12
 Pushdown Automata Chapter 12 Recognizing Context-Free Languages We need a device similar to an FSM except that it needs more power. The insight: Precisely what it needs is a stack, which gives it an unlimited
Pushdown Automata Chapter 12 Recognizing Context-Free Languages We need a device similar to an FSM except that it needs more power. The insight: Precisely what it needs is a stack, which gives it an unlimited
Cliff s notes for equivalence of CFLs and L(PDAs) LisaCFL L = L(M) for some PDA M L=L(M)forsomePDAM L = L(G) for some CFG G
 What s on our plate today? Cliff s notes for equivalence of CFLs and L(PDAs) LisaCFL L = L(M) for some PDA M L=L(M)forsomePDAM L = L(G) for some CFG G Pumping Lemma (one last time) Statement of Pumping
What s on our plate today? Cliff s notes for equivalence of CFLs and L(PDAs) LisaCFL L = L(M) for some PDA M L=L(M)forsomePDAM L = L(G) for some CFG G Pumping Lemma (one last time) Statement of Pumping
