1.1 Exercises. (b) For what values of x is f x t x?
|
|
|
- Brittney Lee
- 5 years ago
- Views:
Transcription
1 CHAPTER FUNCTIONS AND MODELS. Eercises. The graph of a function f is given. (a) State the value of f. Estimate the value of f. (c) For what values of is f? (d) Estimate the values of such that f. (e) State the domain and range of f. (f) On what interval is f increasing? 5 8 Determine whether the curve is the graph of a function of. If it is, state the domain and range of the function The graphs of f and t are given. (a) State the values of f 4 and t3. For what values of is f t? (c) Estimate the solution of the equation f. (d) On what interval is f decreasing? (e) State the domain and range of f. (f) State the domain and range of t. 9. The graph shown gives the weight of a certain person as a function of age. Describe in words how this person s weight varies over time. What do ou think happened when this person was 3 ears old? f g Weight (pounds) Age (ears). The graph shown gives a salesman s distance from his home as a function of time on a certain da. Describe in words what the graph indicates about his travels on this da. 3. Figures,, and were recorded b an instrument operated b the California Department of Mines and Geolog at the Universit Hospital of the Universit of Southern California in Los Angeles. Use them to estimate the ranges of the vertical, north-south, and east-west ground acceleration functions at USC during the Northridge earthquake. 4. In this section we discussed eamples of ordinar, everda functions: Population is a function of time, postage cost is a function of weight, water temperature is a function of time. Give three other eamples of functions from everda life that are described verball. What can ou sa about the domain and range of each of our functions? If possible, sketch a rough graph of each function.. Distance from home (miles) 8 A.M. NOON 4 6 P.M. Time (hours) You put some ice cubes in a glass, fill the glass with cold water, and then let the glass sit on a table. Describe how the temperature of the water changes as time passes. Then sketch a rough graph of the temperature of the water as a function of the elapsed time.
2 SECTION. FOUR WAYS TO REPRESENT A FUNCTION 3. Sketch a rough graph of the number of hours of dalight as a function of the time of ear. 3. Sketch a rough graph of the outdoor temperature as a function of time during a tpical spring da. 4. You place a frozen pie in an oven and bake it for an hour. Then ou take it out and let it cool before eating it. Describe how the temperature of the pie changes as time passes. Then sketch a rough graph of the temperature of the pie as a function of time. 5. A homeowner mows the lawn ever Wednesda afternoon. Sketch a rough graph of the height of the grass as a function of time over the course of a four-week period. 6. An airplane flies from an airport and lands an hour later at another airport, 4 miles awa. If t represents the time in minutes since the plane has left the terminal building, let t be the horizontal distance traveled and t be the altitude of the plane. (a) Sketch a possible graph of t. Sketch a possible graph of t. (c) Sketch a possible graph of the ground speed. (d) Sketch a possible graph of the vertical velocit. 7. The number N (in thousands) of cellular phone subscribers in Malasia is shown in the table. (Midear estimates are given.) t N (a) Use the data to sketch a rough graph of N as a function of Use our graph to estimate the number of cell-phone subscribers in Malasia at midear in 994 and Temperature readings T (in F) were recorded ever two hours from midnight to : P.M. in Dallas on June,. The time t was measured in hours from midnight. t. 3 7 Find the domain of the function. 3. f 4. f Find the domain and range and sketch the graph of the function h s Find the domain and sketch the graph of the function. 3. f t t 6t t s h s 4 5 G 3 f 3 f 3 f f 3 7 if if if if if if if if if f t st s 3 t 6. tu su s4 u 9. f 5 3. F 3 Ht 4 t t F t t (a) Use the readings to sketch a rough graph of T as a function of t. Use our graph to estimate the temperature at : A.M. 9. If f 3, find f, f, f a, f a, f a, f a, f a, f a, [ f a], and f a h.. A spherical balloon with radius r inches has volume Vr 4 3 r 3. Find a function that represents the amount of air required to inflate the balloon from a radius of r inches to a radius of r inches. f h f Find f h, f h, and, h where h.. T f. f 4 46 Find an epression for the function whose graph is the given curve. 4. The line segment joining the points, and 4, 6 4. The line segment joining the points 3, and 6, The bottom half of the parabola 44. The top half of the circle
3 4 CHAPTER FUNCTIONS AND MODELS 47 5 Find a formula for the described function and state its domain. 47. A rectangle has perimeter m. Epress the area of the rectangle as a function of the length of one of its sides. 48. A rectangle has area 6 m. Epress the perimeter of the rectangle as a function of the length of one of its sides. 49. Epress the area of an equilateral triangle as a function of the length of a side. 5. Epress the surface area of a cube as a function of its volume An open rectangular bo with volume m has a square base. Epress the surface area of the bo as a function of the length of a side of the base. 5. A Norman window has the shape of a rectangle surmounted b a semicircle. If the perimeter of the window is 3 ft, epress the area A of the window as a function of the width of the window. 55. In a certain countr, income ta is assessed as follows. There is no ta on income up to $,. An income over $, is taed at a rate of %, up to an income of $,. An income over $, is taed at 5%. (a) Sketch the graph of the ta rate R as a function of the income I. How much ta is assessed on an income of $4,? On $6,? (c) Sketch the graph of the total assessed ta T as a function of the income I. 56. The functions in Eample and Eercises 54 and 55(a) are called step functions because their graphs look like stairs. Give two other eamples of step functions that arise in everda life Graphs of f and t are shown. Decide whether each function is even, odd, or neither. Eplain our reasoning g f f g 53. A bo with an open top is to be constructed from a rectangular piece of cardboard with dimensions in. b in. b cutting out equal squares of side at each corner and then folding up the sides as in the figure. Epress the volume V of the bo as a function of. 59. (a) If the point 5, 3 is on the graph of an even function, what other point must also be on the graph? If the point 5, 3 is on the graph of an odd function, what other point must also be on the graph? 6. A function f has domain 5, 5 and a portion of its graph is shown. (a) Complete the graph of f if it is known that f is even. Complete the graph of f if it is known that f is odd. 54. A tai compan charges two dollars for the first mile (or part of a mile) and cents for each succeeding tenth of a mile (or part). Epress the cost C (in dollars) of a ride as a function of the distance traveled (in miles) for, and sketch the graph of this function. _ Determine whether f is even, odd, or neither. If f is even or odd, use smmetr to sketch its graph. 6. f 6. f f f f 4 4 f 3 3
4 SECTION. MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS 35 Logarithmic Functions The logarithmic functions f log a, where the base a is a positive constant, are the inverse functions of the eponential functions. The will be studied in Section.6. Figure shows the graphs of four logarithmic functions with various bases. In each case the domain is,, the range is,, and the function increases slowl when. =log =log =log =log FIGURE Transcendental Functions These are functions that are not algebraic. The set of transcendental functions includes the trigonometric, inverse trigonometric, eponential, and logarithmic functions, but it also includes a vast number of other functions that have never been named. In Chapter we will stud transcendental functions that are defined as sums of infinite series. EXAMPLE 5 Classif the following functions as one of the tpes of functions that we have discussed. (a) f 5 t 5 (c) h (d) ut t 5t 4 s SOLUTION (a) f 5 is an eponential function. (The is the eponent.) t 5 is a power function. (The is the base.) We could also consider it to be a polnomial of degree 5. (c) h s is an algebraic function. (d) ut t 5t 4 is a polnomial of degree 4.. Eercises Classif each function as a power function, root function, polnomial (state its degree), rational function, algebraic function, trigonometric function, eponential function, or logarithmic function.. (a) f s 5 t s (c) (d) r h (e) s tan (f) t log. (a) 6 6 s (c) (d) (e) t 6 t 4 (f) cos sin
5 36 CHAPTER FUNCTIONS AND MODELS 3 4 Match each equation with its graph. Eplain our choices. (Don t use a computer or graphing calculator.) 3. (a) 5 (c) 8 g h What do the slope, the -intercept, and the -intercept of the graph represent? 9. The relationship between the Fahrenheit F and Celsius C temperature scales is given b the linear function F 9 5 C 3. (a) Sketch a graph of this function. What is the slope of the graph and what does it represent? What is the F-intercept and what does it represent? f. Jason leaves Detroit at : P.M. and drives at a constant speed west along I-96. He passes Ann Arbor, 4 mi from Detroit, at :5 P.M. (a) Epress the distance traveled in terms of the time elapsed. Draw the graph of the equation in part (a). (c) What is the slope of this line? What does it represent? 4. (a) 3 (c) 3 (d) 3 s 3 F. Biologists have noticed that the chirping rate of crickets of a certain species is related to temperature, and the relationship appears to be ver nearl linear. A cricket produces 3 chirps per minute at 7F and 73 chirps per minute at 8F. (a) Find a linear equation that models the temperature T as a function of the number of chirps per minute N. What is the slope of the graph? What does it represent? (c) If the crickets are chirping at 5 chirps per minute, estimate the temperature. f G g. The manager of a furniture factor finds that it costs $ to manufacture chairs in one da and $48 to produce 3 chairs in one da. (a) Epress the cost as a function of the number of chairs produced, assuming that it is linear. Then sketch the graph. What is the slope of the graph and what does it represent? (c) What is the -intercept of the graph and what does it represent? 5. (a) Find an equation for the famil of linear functions with slope and sketch several members of the famil. Find an equation for the famil of linear functions such that f and sketch several members of the famil. (c) Which function belongs to both families? 6. What do all members of the famil of linear functions f m 3 have in common? Sketch several members of the famil. 7. What do all members of the famil of linear functions f c have in common? Sketch several members of the famil. 8. The manager of a weekend flea market knows from past eperience that if he charges dollars for a rental space at the flea market, then the number of spaces he can rent is given b the equation 4. (a) Sketch a graph of this linear function. (Remember that the rental charge per space and the number of spaces rented can t be negative quantities.) 3. At the surface of the ocean, the water pressure is the same as the air pressure above the water, 5 lbin. Below the surface, the water pressure increases b 4.34 lbin for ever ft of descent. (a) Epress the water pressure as a function of the depth below the ocean surface. At what depth is the pressure lbin? 4. The monthl cost of driving a car depends on the number of miles driven. Lnn found that in Ma it cost her $38 to drive 48 mi and in June it cost her $46 to drive 8 mi. (a) Epress the monthl cost C as a function of the distance driven d, assuming that a linear relationship gives a suitable model. Use part (a) to predict the cost of driving 5 miles per month. (c) Draw the graph of the linear function. What does the slope represent? (d) What does the -intercept represent? (e) Wh does a linear function give a suitable model in this situation?
6 SECTION.3 NEW FUNCTIONS FROM OLD FUNCTIONS 45 t f t f t(s) s s For s to be defined we must have. For s s to be defined we must have If a b, then a b. s, that is, s, or 4. Thus, we have 4, so the domain of t f is the closed interval, 4. (c) f f f f f (s) ss s 4 The domain of f f is,. (d) t t tt t(s ) s s This epression is defined when, that is,, and s. This latter inequalit is equivalent to s, or 4, that is,. Thus,, so the domain of t t is the closed interval,. It is possible to take the composition of three or more functions. For instance, the composite function f th is found b first appling h, then t, and then f as follows: f th f th EXAMPLE 9 Find f th if f, t, and h 3. SOLUTION f th f th f t 3 f So far we have used composition to build complicated functions from simpler ones. But in calculus it is often useful to be able to decompose a complicated function into simpler ones, as in the following eample. EXAMPLE Given F cos 9, find functions f, t, and h such that F f th. SOLUTION Since F cos 9, the formula for F sas: First add 9, then take the cosine of the result, and finall square. So we let h 9 t cos f Then f th f th f t 9 f cos 9 cos 9 F.3 Eercises. Suppose the graph of f is given. Write equations for the graphs that are obtained from the graph of f as follows. (a) Shift 3 units upward. Shift 3 units downward. (c) Shift 3 units to the right. (d) Shift 3 units to the left. (e) Reflect about the -ais. (f) Reflect about the -ais. (g) Stretch verticall b a factor of 3. (h) Shrink verticall b a factor of 3.
7 46 CHAPTER FUNCTIONS AND MODELS. Eplain how the following graphs are obtained from the graph of f. (a) 5f f 5 (c) f (d) 5f (e) f 5 (f) 5f The graph of f is given. Match each equation with its graph and give reasons for our choices. (a) f 4 f 3 (c) 3 f (d) f 4 (e) f 6! 7. 5 _4 3 f # _.5 $ _6 _ The graph of f is given. Draw the graphs of the following functions. (a) f 4 f 4 (c) f (d) 5. The graph of f is given. Use it to graph the following functions. (a) f f ( ) (c) f (d) f 6 7 The graph of s3 is given. Use transformations to create a function whose graph is as shown..5 % _3 =œ 3-3 f 3 8. (a) How is the graph of sin related to the graph of sin? Use our answer and Figure 6 to sketch the graph of sin. How is the graph of s related to the graph of s? Use our answer and Figure 4(a) to sketch the graph of s. 9 4 Graph the function, not b plotting points, but b starting with the graph of one of the standard functions given in Section., and then appling the appropriate transformations cos 4. 4 sin 3 5. sin 7. s sin s tan The cit of New Orleans is located at latitude 3N. Use Figure 9 to find a function that models the number of hours of dalight at New Orleans as a function of the time of ear. Use the fact that on March 3 the Sun rises at 5:5 A.M. and sets at 6:8 P.M. in New Orleans to check the accurac of our model. 6. A variable star is one whose brightness alternatel increases and decreases. For the most visible variable star, Delta Cephei, the time between periods of maimum brightness is 5.4 das, the average brightness (or magnitude) of the star is 4., and its brightness varies b.35 magnitude. Find a function that models the brightness of Delta Cephei as a function of time.
8 SECTION.3 NEW FUNCTIONS FROM OLD FUNCTIONS (a) How is the graph of related to the graph of f? 38. f 3, t 5 3 Sketch the graph of sin. (c) Sketch the graph of s 39. f, t. 8. Use the given graph of f to sketch the graph of f. Which features of f are the most important in sketching 4. f s 3, t f? Eplain how the are used Find f th. 4. f, t, h f ( ) 4. f, t, h 43. f s, t, h f, t cos, h s Use graphical addition to sketch the graph of f t. 9. g f 3. f g 45 5 Epress the function in the form f t. 45. F 46. F sin(s) 47. G ut scos t ut 5 53 Epress the function in the form f th. tan t tan t 5. H 3 5. H s 3 s 53. H sec 4 (s) 54. Use the table to evaluate each epression. (a) f t t f (c) f f (d) tt (e) t f 3 (f) f t6 5. G f Find f t, f t, ft, and ft and state their domains. 3. f 3, t 3 3. f s, t s Use the graphs of f and t and the method of graphical addition to sketch the graph of f t. 33. f, t 34. f 3, t t Use the given graphs of f and t to evaluate each epression, or eplain wh it is undefined. (a) f t t f (c) f t (d) t f 6 (e) t t (f) f f 4 g f 35 4 Find the functions f t, t f, f f, and t t and their domains. 35. f, t f 3, t 37. f sin, t s
9 6 CHAPTER FUNCTIONS AND MODELS.5 Eercises. (a) Write an equation that defines the eponential function with base a. What is the domain of this function? (c) If a, what is the range of this function? (d) Sketch the general shape of the graph of the eponential function for each of the following cases. (i) a (ii) a (iii) a. (a) How is the number e defined? What is an approimate value for e? (c) What is the natural eponential function? ; 3 6 Graph the given functions on a common screen. How are these graphs related? 3., e, 5, 4. e, e, 8, ,,, ( 6..9,.6,.3,. 7 Make a rough sketch of the graph of the function. Do not use a calculator. Just use the graphs given in Figures 3 and 4 and, if necessar, the transformations of Section e ( 3 ) 3. Starting with the graph of e, write the equation of the graph that results from (a) shifting units downward shifting units to the right (c) reflecting about the -ais (d) reflecting about the -ais (e) reflecting about the -ais and then about the -ais 4. Starting with the graph of e, find the equation of the graph that results from (a) reflecting about the line 4 reflecting about the line Find the domain of each function. 5. (a) f e ) e 5 e f e 6. (a) tt sine t tt s t 7 8 Find the eponential function f Ca whose graph is given. 7. (, 6) (3, 4) 9. If f 5, show that f ( h) f () h. Suppose ou are offered a job that lasts one month. Which of the following methods of pament do ou prefer? I. One million dollars at the end of the month. II. One cent on the first da of the month, two cents on the second da, four cents on the third da, and, in general, n cents on the nth da.. Suppose the graphs of f and t are drawn on a coordinate grid where the unit of measurement is inch. Show that, at a distance ft to the right of the origin, the height of the graph of f is 48 ft but the height of the graph of t is about 65 mi. ;. Compare the functions f 5 and t 5 b graphing both functions in several viewing rectangles. Find all points of intersection of the graphs correct to one decimal place. Which function grows more rapidl when is large? ; 3. Compare the functions f and t e b graphing both f and t in several viewing rectangles. When does the graph of t finall surpass the graph of f? ; 4. Use a graph to estimate the values of such that e,,,. 5. Under ideal conditions a certain bacteria population is known to double ever three hours. Suppose that there are initiall bacteria. (a) What is the size of the population after 5 hours? What is the size of the population after t hours? h h, 9
10 74 CHAPTER FUNCTIONS AND MODELS EXAMPLE 4 Simplif the epression costan. SOLUTION Let tan. Then tan and. We want to find cos but, since tan is known, it is easier to find sec first: sec tan sec s since sec for FIGURE 4 œ + Thus costan cos sec s SOLUTION Instead of using trigonometric identities as in Solution, it is perhaps easier to use a diagram. If tan, then tan, and we can read from Figure 4 (which illustrates the case ) that π costan cos s _ π FIGURE 5 =tan! =arctan The inverse tangent function, tan arctan, has domain and range,. Its graph is shown in Figure 5. We know that the lines are vertical asmptotes of the graph of tan. Since the graph of tan is obtained b reflecting the graph of the restricted tangent function about the line, it follows that the lines and are horizontal asmptotes of the graph of tan. The remaining inverse trigonometric functions are not used as frequentl and are summarized here. csc sec &? &? csc sec and and,, 3,, 3 _ π π cot &? cot and, FIGURE 6 =sec The choice of intervals for in the definitions of csc and sec is not universall agreed upon. For instance, some authors use,, in the definition of sec. [You can see from the graph of the secant function in Figure 6 that both this choice and the one in () will work.].6 Eercises. (a) What is a one-to-one function? How can ou tell from the graph of a function whether it is one-to-one?. (a) Suppose f is a one-to-one function with domain A and range B. How is the inverse function f defined? What is the domain of f? What is the range of f? If ou are given a formula for f, how do ou find a formula for f? (c) If ou are given the graph of f, how do ou find the graph of f? 3 4 A function is given b a table of values, a graph, a formula, or a verbal description. Determine whether it is one-to-one f
11 SECTION.6 INVERSE FUNCTIONS AND LOGARITHMS f The formula C 5 9 F 3, where F , epresses the Celsius temperature C as a function of the Fahrenheit temperature F. Find a formula for the inverse function and interpret it. What is the domain of the inverse function?. In the theor of relativit, the mass of a particle with speed v is m m f v s v c where m is the rest mass of the particle and c is the speed of light in a vacuum. Find the inverse function of f and eplain its meaning Find a formula for the inverse of the function. 3. f s 3 4. f f e ln 3 8. e e 9. f 5. f 4 t.. t s 3. f t is the height of a football t seconds after kickoff. 4. f t is our height at age t. ; 9 3 Find an eplicit formula for f and use it to graph f, f, and the line on the same screen. To check our work, see whether the graphs of f and f are reflections about the line. 9. f, 3. f s, ; 5 6 Use a graph to decide whether f is one-to-one. 5. f 3 6. f 3 3. Use the given graph of f to sketch the graph of f. 7. If f is a one-to-one function such that f 9, what is f 9? 8. Let f 3 tan, where. (a) Find f 3. Find f f If t 3 e, find t 4.. The graph of f is given. (a) Wh is f one-to-one? State the domain and range of f. (c) Estimate the value of f. 3. Use the given graph of f to sketch the graphs of f and f. _ (a) How is the logarithmic function log a defined? What is the domain of this function? (c) What is the range of this function? (d) Sketch the general shape of the graph of the function log a if a.
12 76 CHAPTER FUNCTIONS AND MODELS 34. (a) What is the natural logarithm? What is the common logarithm? (c) Sketch the graphs of the natural logarithm function and the natural eponential function with a common set of aes Solve each inequalit for. 53. (a) e 54. (a) ln 9 ln e Find the eact value of each epression. 35. (a) log (a) log.5 log 8 log 5 log 5 3log (a) log 3 log Epress the given quantit as a single logarithm. 4. ln ln ln sin 4. Use Formula to evaluate each logarithm correct to si decimal places. (a) log log 8.4 ; Use Formula to graph the given functions on a common screen. How are these graphs related? 43. log.5, ln, log, 44. ln, log, e, ; 46. Compare the functions f. and t ln b graphing both f and t in several viewing rectangles. When does the graph of f finall surpass the graph of t? Make a rough sketch of the graph of each function. Do not use a calculator. Just use the graphs given in Figures and 3 and, if necessar, the transformations of Section (a) log (a) ln 49 5 Solve each equation for. 49. (a) ln e 5 5. (a) e 3 7 ln (a) (a) lnln e a Ce b, where a b log (a) log 8 ln e s e 3ln 39. ln4 ln 4. ln a ln b ln z log Suppose that the graph of log is drawn on a coordinate grid where the unit of measurement is an inch. How man miles to the right of the origin do we have to move before the height of the curve reaches 3 ft? ln ln ln ln CAS CAS Find (a) the domain of f and f and its domain. 55. f s3 e Graph the function f s 3 and eplain wh it is one-to-one. Then use a computer algebra sstem to find an eplicit epression for f. (Your CAS will produce three possible epressions. Eplain wh two of them are irrelevant in this contet.) 58. (a) If t 6 4,, use a computer algebra sstem to find an epression for t. Use the epression in part (a) to graph t,, and t on the same screen. 59. If a bacteria population starts with bacteria and doubles ever three hours, then the number of bacteria after t hours is n f t t3. (See Eercise 5 in Section.5.) (a) Find the inverse of this function and eplain its meaning. When will the population reach 5,? 6. When a camera flash goes off, the batteries immediatel begin to recharge the flash s capacitor, which stores electric charge given b Qt Q e ta f ln ln (The maimum charge capacit is Q and t is measured in seconds.) (a) Find the inverse of this function and eplain its meaning. How long does it take to recharge the capacitor to 9% of capacit if a? 6. Starting with the graph of ln, find the equation of the graph that results from (a) shifting 3 units upward shifting 3 units to the left (c) reflecting about the -ais (d) reflecting about the -ais (e) reflecting about the line (f) reflecting about the -ais and then about the line (g) reflecting about the -ais and then about the line (h) shifting 3 units to the left and then reflecting about the line 6. (a) If we shift a curve to the left, what happens to its reflection about the line? In view of this geometric principle, find an epression for the inverse of t f c, where f is a one-to-one function. Find an epression for the inverse of h f c, where c.
13 CHAPTER REVIEW Find the eact value of each epression. 63. (a) sin (s3) cos 64. (a) arctan csc 65. (a) tan s3 arcsin(s) 66. (a) sec s 67. (a) sinsin (a) secarctan 69. Prove that cossin s. 7 7 Simplif the epression. 7. tansin arcsin 4 tan tan 3 cos( sin ( 3)) sintan sin cos ; Graph the given functions on the same screen. How are these graphs related? 73. sin, ; sin ; 74. tan, ; tan ; 75. Find the domain and range of the function t sin 3 ; 76. (a) Graph the function f sinsin and eplain the appearance of the graph. Graph the function t sin sin. How do ou eplain the appearance of this graph? Review CONCEPT CHECK. (a) What is a function? What are its domain and range? What is the graph of a function? (c) How can ou tell whether a given curve is the graph of a function?. Discuss four was of representing a function. Illustrate our discussion with eamples. 3. (a) What is an even function? How can ou tell if a function is even b looking at its graph? What is an odd function? How can ou tell if a function is odd b looking at its graph? 4. What is an increasing function? 5. What is a mathematical model? 6. Give an eample of each tpe of function. (a) Linear function Power function (c) Eponential function (d) Quadratic function (e) Polnomial of degree 5 (f) Rational function 7. Sketch b hand, on the same aes, the graphs of the following functions. (a) f t (c) h 3 (d) j 4 8. Draw, b hand, a rough sketch of the graph of each function. (a) sin tan (c) e (d) ln (e) (f) (g) s (h) tan 9. Suppose that f has domain A and t has domain B. (a) What is the domain of f t? What is the domain of ft? (c) What is the domain of ft?. How is the composite function f t defined? What is its domain?. Suppose the graph of f is given. Write an equation for each of the graphs that are obtained from the graph of f as follows. (a) Shift units upward. Shift units downward. (c) Shift units to the right. (d) Shift units to the left. (e) Reflect about the -ais. (f) Reflect about the -ais. (g) Stretch verticall b a factor of. (h) Shrink verticall b a factor of. (i) Stretch horizontall b a factor of. (j) Shrink horizontall b a factor of.. (a) What is a one-to-one function? How can ou tell if a function is one-to-one b looking at its graph? If f is a one-to-one function, how is its inverse function f defined? How do ou obtain the graph of f from the graph of f? 3. (a) How is the inverse sine function f sin defined? What are its domain and range? How is the inverse cosine function f cos defined? What are its domain and range? (c) How is the inverse tangent function f tan defined? What are its domain and range?
14 CHAPTER LIMITS AND DERIVATIVES. Eercises. Eplain in our own words what is meant b the equation Is it possible for this statement to be true and et f 3? Eplain.. Eplain what it means to sa that f 3 l and In this situation is it possible that l f eists? Eplain. 3. Eplain the meaning of each of the following. (a) f f l3 l 4 f 5 l f 7 l (d) (e) l t (f) (g) l (h) t (i) (j) l4 t (k) t (l) _3 3 4 _ l t l4 t t l 4. For the function f whose graph is given, state the value of the given quantit, if it eists. If it does not eist, eplain wh. (a) f f l l 3 (c) f l 3 (e) f 3 4 (d) f l 3 7. For the function t whose graph is given, state the value of each quantit, if it eists. If it does not eist, eplain wh. (a) tl tt tl tt (c) tt tl (d) tl tt (e) tl tt ( f ) tt tl (g) t (h) tt tl Use the given graph of f to state the value of each quantit, if it eists. If it does not eist, eplain wh. (a) l l (c) l (d) f (e) f 5 l For the function R whose graph is shown, state the following. (a) R R l l5 (c) R (d) l3 l3 R (e) The equations of the vertical asmptotes. 4 t 4 6. For the function t whose graph is given, state the value of each quantit, if it eists. If it does not eist, eplain wh. (a) (c) t l t l t l _3 5
15 SECTION. THE LIMIT OF A FUNCTION 3 9. For the function f whose graph is shown, state the following. 5 8 Guess the value of the it (if it eists) b evaluating the (a) f f (c) f function at the given numbers (correct to si decimal places). l7 l3 l (d) f (e) f l6 l6 5.,.5,.,.5,.,.5,., (f) The equations of the vertical asmptotes. l.9,.95,.99,.995, ,,.5,.9,.95,.99, l.999,,.5,.,.,. _7 _3 6 e 7.,,.5,.,.5,. l. A patient receives a 5-mg injection of a drug ever 4 hours. The graph shows the amount f t of the drug in the bloodstream after t hours. (Later we will be able to compute the dosage and time interval to ensure that the concentration of the drug does not reach a harmful level.) Find and and eplain the significance of these one-sided its. ;. Use the graph of the function f e to state the value of each it, if it eists. If it does not eist, eplain wh. (a) f f (c). Sketch the graph of the following function and use it to determine the values of a for which l a f eists: 3 4 Sketch the graph of an eample of a function f that satisfies all of the given conditions. 3. l3 f 4, f, f, f 3 3, 4. f, f, l l l f t tl f(t) 3 5 f l3 f l 486t l f t tl if if if l f l f l f, f, f is undefined 8. ln,,.5,.,.5,.,.5,. l 9 Use a table of values to estimate the value of the it. If ou have a graphing device, use it to confirm our result graphicall. s l 6.. l 3 3 Determine the infinite it l5 6 l l 9. sec 3. l 3. Determine and 3 3 (a) b evaluating f 3 for values of that approach from the left and from the right, b reasoning as in Eample 9, and ; (c) from a graph of f. l 3. (a) Find the vertical asmptotes of the function l l tan 3 l tan l 6 l5 5 l csc ln 5 l5 ; Confirm our answer to part (a) b graphing the function. 33. (a) Estimate the value of the it l to five decimal places. Does this number look familiar? ; Illustrate part (a) b graphing the function. 34. The slope of the tangent line to the graph of the eponential function at the point, is l. Estimate the slope to three decimal places.
16 SECTION.3 CALCULATING LIMITS USING THE LIMIT LAWS EXAMPLE Show that sin. l SOLUTION First note that we cannot use l sin l l sin because l sin does not eist (see Eample 4 in Section.). However, since sin we have, as illustrated b Figure 8, sin = Watch an animation of a similar it. Resources / Module / Basics of Limits / Sound of a Limit that Eists = sin FIGURE 8 =_ We know that l and l Taking f, t sin, and h in the Squeeze Theorem, we obtain sin l.3 Eercises. Given that find the its that eist. If the it does not eist, eplain wh. (a) f 3 la f h la t la f la h 8 la (c) (e) (g) la s3 h la la f h f t (d) la f t (f) la f f (h) la h f
17 CHAPTER LIMITS AND DERIVATIVES. The graphs of f and t are given. Use them to evaluate each it, if it eists. If the it does not eist, eplain wh. (a) (c) (e) 3 9 Evaluate the it and justif each step b indicating the appropriate Limit Law(s). (d) (f) l l (a) What is wrong with the following equation? In view of part (a), eplain wh the equation is correct. 3 Evaluate the it, if it eists. 6.. l l 5. =ƒ tl3 f t l 3 f l 3 l l4s h hl h f t l t 9 t 7t 3 6 h 4 h hl h hl h 8. l l l l l 4 l = f t l f t s3 f l 6 4 t l t 3 t 3 5 su 4 3u 6 ul 5 4 l l 9 t.. tl9 3 st s l l l9s tl ts t t ; 3. (a) Estimate the value of ; 3. (a) Use a graph of to estimate the value of l f to two decimal places. Use a table of values of f to estimate the it to four decimal places. (c) Use the Limit Laws to find the eact value of the it. ; 33. Use the Squeeze Theorem to show that l cos. Illustrate b graphing the functions f, t cos, and h on the same screen. ; 34. Use the Squeeze Theorem to show that Illustrate b graphing the functions f, t, and h (in the notation of the Squeeze Theorem) on the same screen. 35. If f for all, find l f. 36. If 3 f 3 for, evaluate l f. 37. Prove that 38. Prove that. l s esin Find the it, if it eists. If the it does not eist, eplain wh. 39. ls 3 b graphing the function f (s 3 ). Make a table of values of f for close to and guess the value of the it. (c) Use the Limit Laws to prove that our guess is correct. 4 l4 f s 3 sin l 4 cos. l s3 s3 s h hl h 4 6 l tl t 3 h 3 h l h s l s 4. l4 t t 4 4
18 SECTION.3 CALCULATING LIMITS USING THE LIMIT LAWS l 45. The signum (or sign) function, denoted b sgn, is defined b (a) Sketch the graph of this function. Find each of the following its or eplain wh it does not 46. Let eist. (i) (iii) (a) Find l f and l f. Does l f eist? (c) Sketch the graph of f. 47. Let F. (a) Find (i) (ii) Does l F eist? (c) Sketch the graph of F. 48. Let l sgn l sgn l F l (a) Evaluate each of the following its, if it eists. (i) h (ii) h (iii) l (iv) h (v) h (vi) l sgn 4 f h Sketch the graph of h. 49. (a) If the smbol denotes the greatest integer function defined in Eample, evaluate (i) (ii) (iii) l l l.4 If n is an integer, evaluate (i) (ii) ln ln (c) For what values of a does l a eist? 5. Let f. (a) Sketch the graph of f. 8 (ii) sgn l (iv) l sgn F l if if if l l 3 l.5 3 l if if if if if l l h h If n is an integer, evaluate (i) f (ii) f ln ln (c) For what values of a does la f eist? 5. If f, show that l f eists but is not equal to f. 5. In the theor of relativit, the Lorentz contraction formula epresses the length L of an object as a function of its velocit v with respect to an observer, where L is the length of the object at rest and c is the speed of light. Find vlc L and interpret the result. Wh is a left-hand it necessar? 53. If p is a polnomial, show that p pa. 54. If r is a rational function, use Eercise 53 to show that r ra for ever number a in the domain of r. 55. If l a prove that l f. 56. Show b means of an eample that ma eist even though neither l a f l a f t nor l a t eists. 57. Show b means of an eample that ma eist even though neither l a f l a f t nor l a t eists. s6 58. Evaluate. ls3 59. Is there a number a such that eists? If so, find the value of a and the value of the it. 6. The figure shows a fied circle with equation and a shrinking circle C with radius r and center the origin. P is the point, r, Q is the upper point of intersection of the two circles, and R is the point of intersection of the line PQ and the -ais. What happens to R as C shrinks, that is, as rl? C f 3 a a 3 l P L L s v c Q l a if is rational if is irrational C C R
19 CHAPTER LIMITS AND DERIVATIVES a- a+ Similarl, the following is a precise version of Definition 5 in Section.. It is illustrated b Figure. a N =N FIGURE 7 Definition Let f be a function defined on some open interval that contains the number a, ecept possibl at a itself. Then means that for ever negative number N there is a positive number such that f N f la whenever a.4 Eercises. How close to do we have to take so that 5 3 is within a distance of (a). and. from 3?. How close to 5 do we have to take so that 6 is within a distance of (a).,., and (c). from 9? 3. Use the given graph of f to find a number such that whenever = Use the given graph of f to find a number such that whenever ? 4 =œ? = 4. Use the given graph of f to find a number such that?? 5. f 3.6 whenever Use the given graph of f s to find a number such that s.4 whenever 4 ; 7. Use a graph to find a number such that ; 8. Use a graph to find a number such that sin whenever 6. ; 9. For the it s4 3.5 whenever l illustrate Definition b finding values of and.. that correspond to
20 SECTION.4 THE PRECISE DEFINITION OF A LIMIT 3 ;. For the it illustrate Definition b finding values of.5 and.. ;. Use a graph to find a number such that ;. For the it illustrate Definition 6 b finding values of (a) M and M. that correspond to that correspond to 3. A machinist is required to manufacture a circular metal disk with area cm. (a) What radius produces such a disk? If the machinist is allowed an error tolerance of 5 cm in the area of the disk, how close to the ideal radius in part (a) must the machinist control the radius? (c) In terms of the, definition of l a f L, what is? What is f? What is a? What is L? What value of is given? What is the corresponding value of? ; 4. A crstal growth furnace is used in research to determine how best to manufacture crstals used in electronic components for the space shuttle. For proper growth of the crstal, the temperature must be controlled accuratel b adjusting the input power. Suppose the relationship is given b where T is the temperature in degrees Celsius and w is the power input in watts. (a) How much power is needed to maintain the temperature at C? If the temperature is allowed to var from C b up to C, what range of wattage is allowed for the input power? (c) In terms of the, definition of l a f L, what is? What is f? What is a? What is L? What value of is given? What is the corresponding value of? 5 8 Prove the statement using the, definition of it and illustrate with a diagram like Figure l 4 3 l3 e l 9 3 Prove the statement using the, definition of it. 9.. l l whenever l cot Tw.w.55w 8. ( 3) l l 4 CAS.. l a l la l 4 5 l 3 l 33. Verif that another possible choice of for showing that l3 9 in Eample 4 is 34. Verif, b a geometric argument, that the largest possible choice of for showing that l3 9 is. 35. (a) For the it l 3 3, use a graph to find a value of that corresponds to.4. B using a computer algebra sstem to solve the cubic equation 3 3, find the largest possible value of that works for an given. (c) Put.4 in our answer to part and compare with our answer to part (a). 36. Prove that. l Hint: Use s sa 38. If H is the Heaviside function defined in Eample 6 in Section., prove, using Definition, that tl Ht does not eist. [Hint: Use an indirect proof as follows. Suppose that the it is L. Take in the definition of a it and tr to arrive at a contradiction.] 39. If the function f is defined b prove that l a l Prove that s sa if a. f does not eist. 4. B comparing Definitions, 3, and 4, prove Theorem in Section How close to 3 do we have to take so that 4, 3 4. Prove, using Definition 6, that. l Prove that ln. l f min, 8. a s sa. 7 l3 3 c c la 3 l 9 l 9 s4 4 8 l3 3 8 l if is rational if is irrational s9 3
21 SECTION.5 CONTINUITY 33.5 Eercises. Write an equation that epresses the fact that a function is continuous at the number 4.. If f is continuous on,, what can ou sa about its graph? 3. (a) From the graph of f, state the numbers at which f is discontinuous and eplain wh. For each of the numbers stated in part (a), determine whether f is continuous from the right, or from the left, or neither. f (c) The altitude above sea level as a function of the distance due west from New York Cit (d) The cost of a tai ride as a function of the distance traveled (e) The current in the circuit for the lights in a room as a function of time 9. If f and t are continuous functions with f 3 5 and l3 f t 4, find t3. Use the definition of continuit and the properties of its to show that the function is continuous at the given number.. f s7,. f 3 4,. t, a a 4 a 4 _4 _ From the graph of t, state the intervals on which t is continuous. _4 _ Use the definition of continuit and the properties of its to show that the function is continuous on the given interval f,, 4. t s3, 5 Eplain wh the function is discontinuous at the given number a. Sketch the graph of the function f ln f if if a a, 3 5. Sketch the graph of a function that is continuous everwhere ecept at 3 and is continuous from the left at Sketch the graph of a function that has a jump discontinuit at and a removable discontinuit at 4, but is continuous elsewhere. 7. A parking lot charges $3 for the first hour (or part of an hour) and $ for each succeeding hour (or part), up to a dail maimum of $. (a) Sketch a graph of the cost of parking at this lot as a function of the time parked there. Discuss the discontinuities of this function and their significance to someone who parks in the lot. 8. Eplain wh each function is continuous or discontinuous. (a) The temperature at a specific location as a function of time The temperature at a specific time as a function of the distance due west from New York Cit f e if if f f 3 5 f 4 if if if if if 3 if 3 a a a 3 a 8 Eplain, using Theorems 4, 5, 7, and 9, wh the function is continuous at ever number in its domain. State the domain.. F. G s
22 34 CHAPTER LIMITS AND DERIVATIVES 3. R s f e sin 5 6. F sin 7. Gt lnt 4 8. H cos(e s ) ; 9 3 Locate the discontinuities of the function and illustrate b graphing Use continuit to evaluate the it Show that f is continuous on, Find the numbers at which f is discontinuous. At which of these numbers is f continuous from the right, from the left, or neither? Sketch the graph of f s l4s5 l e e f if s if f sin if 4 cos if 4 f f s 3 f e if if if if if 3 if 3 if if if 4. The gravitational force eerted b Earth on a unit mass at a distance r from the center of the planet is Fr GMr R 3 GM r sin sin l arctan 4 l 3 6 if r R if r R where M is the mass of Earth, R is its radius, and G is the gravitational constant. Is F a continuous function of r? 3. h sin lntan 4. For what value of the constant c is the function f continuous on,? 4. Find the constant c that makes t continuous on,. 43. Which of the following functions f has a removable discontinuit at a? If the discontinuit is removable, find a function t that agrees with f for a and is continuous on. (a) f 8, a f 7, a 7 7 (c) f 3 64, 4 (d) f 3 s, 9 f c t c c a 4 a Suppose that a function f is continuous on [, ] ecept at.5 and that f and f 3. Let N. Sketch two possible graphs of f, one showing that f might not satisf the conclusion of the Intermediate Value Theorem and one showing that f might still satisf the conclusion of the Intermediate Value Theorem (even though it doesn t satisf the hpothesis). 45. If f 3, show that there is a number c such that f c. 46. Use the Intermediate Value Theorem to prove that there is a positive number c such that c. (This proves the eistence of the number s.) 47 5 Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval ,, 48. s 3, 49. cos,, 5. ln e, 5 5 (a) Prove that the equation has at least one real root. Use our calculator to find an interval of length. that contains a root. 5. e ; (a) Prove that the equation has at least one real root. Use our graphing device to find the root correct to three decimal places if 3 if 3 if 4 if 4,, s 5 3
23 46 CHAPTER LIMITS AND DERIVATIVES Therefore, b Definition 7, l Figure 8 illustrates the proof b showing some values of and the corresponding values of N. = N= =. N=5 =. N= FIGURE 8 Finall we note that an infinite it at infinit can be defined as follows. The geometric illustration is given in Figure 9. M =M 9 Definition Let f be a function defined on some interval a,. Then f l FIGURE 9 ƒ=` ` N means that for ever positive number M there is a corresponding positive number N such that f M whenever N Similar definitions appl when the smbol is replaced b. (See Eercise 66.).6 Eercises. Eplain in our own words the meaning of each of the following. (a) f 5 l f 3 l (f) The equations of the asmptotes. (a) Can the graph of f intersect a vertical asmptote? Can it intersect a horizontal asmptote? Illustrate b sketching graphs. How man horizontal asmptotes can the graph of f have? Sketch graphs to illustrate the possibilities. 3. For the function f whose graph is given, state the following. (a) f f (c) l (d) f (e) f l l l f l 4. For the function t whose graph is given, state the following. (a) t t l l
24 SECTION.6 LIMITS AT INFINITY; HORIZONTAL ASYMPTOTES 47 (c) t l3 (e) (d) (f) The equations of the asmptotes 5 8 Sketch the graph of an eample of a function f that satisfies all of the given conditions. 5. f, f, f, f is odd f, l f l l t f, l f, l f, l ; 9. Guess the value of the it b evaluating the function f for,,, 3, 4, 5, 6, 7, 8, 9,,, 5, and. Then use a graph of f to support our guess. ;. (a) Use a graph of l t l f, l f, l f l f 3, l l f f, l f, l f 3 l to estimate the value of l f correct to two decimal places. Use a table of values of f to estimate the it to four decimal places. Evaluate the it and justif each step b indicating the appropriate properties of its. 3.. l l Find the it l l 7 7. l 8. 4u ul u u. s9 l ) l (s a s b) 6. l l s 9. ( s) 3. l l l 4 ; 35. (a) Estimate the value of b graphing the function f s. Use a table of values of f to guess the value of the it. (c) Prove that our guess is correct. ; 36. (a) Use a graph of f s3 8 6 s3 3 to estimate the value of l f to one decimal place. Use a table of values of f to estimate the it to four decimal places. (c) Find the eact value of the it. ; 37 4 Find the horizontal and vertical asmptotes of each curve. Check our work b graphing the curve and estimating the asmptotes (s ) l l 4 l tl l s9 6 l 3 cos l l s3 l etan h 4. F s t t 3 t s9 ( s ) l 3 3 l 5 l tan 4 9 s4 3
25 SECTION.7 TANGENTS, VELOCITIES, AND OTHER RATES OF CHANGE 55 Another method is to average the slopes of two secant lines. See Eample in Section.. the slope of the tangent line is BC.3 AC Therefore, the instantaneous rate of change of temperature with respect to time at noon is about.9 Ch. T A P B C FIGURE The velocit of a particle is the rate of change of displacement with respect to time. Phsicists are interested in other rates of change as well for instance, the rate of change of work with respect to time (which is called power). Chemists who stud a chemical reaction are interested in the rate of change in the concentration of a reactant with respect to time (called the rate of reaction). A steel manufacturer is interested in the rate of change of the cost of producing tons of steel per da with respect to (called the marginal cost). A biologist is interested in the rate of change of the population of a colon of bacteria with respect to time. In fact, the computation of rates of change is important in all of the natural sciences, in engineering, and even in the social sciences. Further eamples will be given in Section 3.3. All these rates of change can be interpreted as slopes of tangents. This gives added significance to the solution of the tangent problem. Whenever we solve a problem involving tangent lines, we are not just solving a problem in geometr. We are also implicitl solving a great variet of problems involving rates of change in science and engineering..7 Eercises. A curve has equation f. (a) Write an epression for the slope of the secant line through the points P3, f 3 and Q, f. Write an epression for the slope of the tangent line at P. A E. Suppose an object moves with position function s f t. (a) Write an epression for the average velocit of the object in the time interval from t a to t a h. Write an epression for the instantaneous velocit at time t a. 3. Consider the slope of the given curve at each of the five points shown. List these five slopes in decreasing order and eplain our reasoning. B ; 4. Graph the curve e in the viewing rectangles, b,,.5,.5 b.5,.5, and.,. b.9,.. What do ou notice about the curve as ou zoom in toward the point,? C D
26 56 CHAPTER LIMITS AND DERIVATIVES 5. (a) Find the slope of the tangent line to the parabola at the point 3, 3 (i) using Definition (ii) using Equation Find an equation of the tangent line in part (a). ; (c) Graph the parabola and the tangent line. As a check on our work, zoom in toward the point (3, 3) until the parabola and the tangent line are indistinguishable. 6. (a) Find the slope of the tangent line to the curve 3 at the point, (i) using Definition (ii) using Equation Find an equation of the tangent line in part (a). ; (c) Graph the curve and the tangent line in successivel smaller viewing rectangles centered at (, ) until the curve and the line appear to coincide. 7 Find an equation of the tangent line to the curve at the given point. 7. 3, 8. s, 9.., 4, 3,,, 3,. (a) Find the slope of the tangent to the curve 3 at the point where a. Find the slopes of the tangent lines at the points whose -coordinates are (i), (ii), and (iii).. (a) Find the slope of the tangent to the parabola at the point where a. Find the slopes of the tangent lines at the points whose -coordinates are (i), (ii), and (iii). ; (c) Graph the curve and the three tangents on a common screen. 3. (a) Find the slope of the tangent to the curve 3 4 at the point where a. Find equations of the tangent lines at the points, and,. ; (c) Graph the curve and both tangents on a common screen. 4. (a) Find the slope of the tangent to the curve s at the point where a. Find equations of the tangent lines at the points, and (4, ). ; (c) Graph the curve and both tangents on a common screen. 5. The graph shows the position function of a car. Use the shape of the graph to eplain our answers to the following questions. (a) What was the initial velocit of the car? Was the car going faster at B or at C? (c) Was the car slowing down or speeding up at A, B, and C? (d) What happened between D and E? s A B 6. Valerie is driving along a highwa. Sketch the graph of the position function of her car if she drives in the following manner: At time t, the car is at mile marker 5 and is traveling at a constant speed of 55 mih. She travels at this speed for eactl an hour. Then the car slows graduall over a -minute period as Valerie comes to a stop for dinner. Dinner lasts 6 min; then she restarts the car, graduall speeding up to 65 mih over a -minute period. She drives at a constant 65 mih for two hours and then over a 3-minute period graduall slows to a complete stop. 7. If a ball is thrown into the air with a velocit of 4 fts, its height (in feet) after t seconds is given b 4t 6t. Find the velocit when t. 8. If an arrow is shot upward on the moon with a velocit of 58 ms, its height (in meters) after t seconds is given b H 58t.83t. (a) Find the velocit of the arrow after one second. Find the velocit of the arrow when t a. (c) When will the arrow hit the moon? (d) With what velocit will the arrow hit the moon? 9. The displacement (in meters) of a particle moving in a straight line is given b the equation of motion s 4t 3 6t, where t is measured in seconds. Find the velocit of the particle at times t a, t, t, and t 3.. The displacement (in meters) of a particle moving in a straight line is given b s t 8t 8, where t is measured in seconds. (a) Find the average velocit over each time interval: (i) 3, 4 (ii) 3.5, 4 (iii) 4, 5 (iv) 4, 4.5 Find the instantaneous velocit when t 4. (c) Draw the graph of s as a function of t and draw the secant lines whose slopes are the average velocities in part (a) and the tangent line whose slope is the instantaneous velocit in part.. A warm can of soda is placed in a cold refrigerator. Sketch the graph of the temperature of the soda as a function of time. Is the initial rate of change of temperature greater or less than the rate of change after an hour? C D E t
CHAPTER 1 FIGURE 22 increasing decreasing FIGURE 23
 . EXERCISES. The graph o a unction is given. (a) State the value o. (b) Estimate the value o 2. (c) For what values o is 2? (d) Estimate the values o such that. (e) State the domain and range o. () On
. EXERCISES. The graph o a unction is given. (a) State the value o. (b) Estimate the value o 2. (c) For what values o is 2? (d) Estimate the values o such that. (e) State the domain and range o. () On
2.5 CONTINUITY. a x. Notice that Definition l implicitly requires three things if f is continuous at a:
 SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
(2) Find the domain of f (x) = 2x3 5 x 2 + x 6
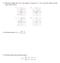 CHAPTER FUNCTIONS AND MODELS () Determine whether the curve is the graph of a function of. If it is state the domain and the range of the function. 5 8 Determine whether the curve is the graph of a function
CHAPTER FUNCTIONS AND MODELS () Determine whether the curve is the graph of a function of. If it is state the domain and the range of the function. 5 8 Determine whether the curve is the graph of a function
Infinite Limits. Let f be the function given by. f x 3 x 2.
 0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
New Functions from Old Functions
 .3 New Functions rom Old Functions In this section we start with the basic unctions we discussed in Section. and obtain new unctions b shiting, stretching, and relecting their graphs. We also show how
.3 New Functions rom Old Functions In this section we start with the basic unctions we discussed in Section. and obtain new unctions b shiting, stretching, and relecting their graphs. We also show how
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
One of the most common applications of Calculus involves determining maximum or minimum values.
 8 LESSON 5- MAX/MIN APPLICATIONS (OPTIMIZATION) One of the most common applications of Calculus involves determining maimum or minimum values. Procedure:. Choose variables and/or draw a labeled figure..
8 LESSON 5- MAX/MIN APPLICATIONS (OPTIMIZATION) One of the most common applications of Calculus involves determining maimum or minimum values. Procedure:. Choose variables and/or draw a labeled figure..
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
1.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS
 .6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
.6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
Exponential, Logistic, and Logarithmic Functions
 CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
1.5. Analyzing Graphs of Functions. The Graph of a Function. What you should learn. Why you should learn it. 54 Chapter 1 Functions and Their Graphs
 0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
5.6 RATIOnAl FUnCTIOnS. Using Arrow notation. learning ObjeCTIveS
 CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
4.3 Exercises. local maximum or minimum. The second derivative is. e 1 x 2x 1. f x x 2 e 1 x 1 x 2 e 1 x 2x x 4
 SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
v t t t t a t v t d dt t t t t t 23.61
 SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
Advanced Algebra 2 Final Review Packet KG Page 1 of Find the slope of the line passing through (3, -1) and (6, 4).
 Advanced Algebra Final Review Packet KG 0 Page of 8. Evaluate (7 ) 0 when and. 7 7. Solve the equation.. Solve the equation.. Solve the equation. 6. An awards dinner costs $ plus $ for each person making
Advanced Algebra Final Review Packet KG 0 Page of 8. Evaluate (7 ) 0 when and. 7 7. Solve the equation.. Solve the equation.. Solve the equation. 6. An awards dinner costs $ plus $ for each person making
Quick Review 4.1 (For help, go to Sections 1.2, 2.1, 3.5, and 3.6.)
 Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
(b) Find the difference quotient. Interpret your result. 3. Find the average rate of change of ƒ(x) = x 2-3x from
 6360_ch0pp00-075.qd 0/6/08 4:8 PM Page 67 CHAPTER Summar 67 69. ƒ() = 3 70. ƒ() = -5 (b) Find the difference quotient. Interpret our result. 7. ƒ() = - 7. ƒ() = 0 73. ƒ() = + 74. ƒ() = -3 + 4 75. ƒ() =
6360_ch0pp00-075.qd 0/6/08 4:8 PM Page 67 CHAPTER Summar 67 69. ƒ() = 3 70. ƒ() = -5 (b) Find the difference quotient. Interpret our result. 7. ƒ() = - 7. ƒ() = 0 73. ƒ() = + 74. ƒ() = -3 + 4 75. ƒ() =
LESSON #11 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
CHAPTER 2 Polynomial and Rational Functions
 CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
LESSON #12 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
I. Degrees and Radians minutes equal 1 degree seconds equal 1 minute. 3. Also, 3600 seconds equal 1 degree. 3.
 0//0 I. Degrees and Radians A. A degree is a unit of angular measure equal to /80 th of a straight angle. B. A degree is broken up into minutes and seconds (in the DMS degree minute second sstem) as follows:.
0//0 I. Degrees and Radians A. A degree is a unit of angular measure equal to /80 th of a straight angle. B. A degree is broken up into minutes and seconds (in the DMS degree minute second sstem) as follows:.
Answer Explanations. The SAT Subject Tests. Mathematics Level 1 & 2 TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE
 The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
Review of Essential Skills and Knowledge
 Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
Functions and Limits Peticolas / Megna, Fundamental Photographs, NYC
 Functions and Limits A ball falls faster and faster as time passes. Galileo discovered that the distance fallen is proportional to the square of the time it has been falling. Calculus then enables us to
Functions and Limits A ball falls faster and faster as time passes. Galileo discovered that the distance fallen is proportional to the square of the time it has been falling. Calculus then enables us to
LESSON #24 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
Math 121. Practice Questions Chapters 2 and 3 Fall Find the other endpoint of the line segment that has the given endpoint and midpoint.
 Math 11. Practice Questions Chapters and 3 Fall 01 1. Find the other endpoint of the line segment that has the given endpoint and midpoint. Endpoint ( 7, ), Midpoint (, ). Solution: Let (, ) denote the
Math 11. Practice Questions Chapters and 3 Fall 01 1. Find the other endpoint of the line segment that has the given endpoint and midpoint. Endpoint ( 7, ), Midpoint (, ). Solution: Let (, ) denote the
c) domain {x R, x 3}, range {y R}
 Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Summary, Review, and Test
 944 Chapter 9 Conic Sections and Analtic Geometr 45. Use the polar equation for planetar orbits, to find the polar equation of the orbit for Mercur and Earth. Mercur: e = 0.056 and a = 36.0 * 10 6 miles
944 Chapter 9 Conic Sections and Analtic Geometr 45. Use the polar equation for planetar orbits, to find the polar equation of the orbit for Mercur and Earth. Mercur: e = 0.056 and a = 36.0 * 10 6 miles
Math 123 Summary of Important Algebra & Trigonometry Concepts Chapter 1 & Appendix D, Stewart, Calculus Early Transcendentals
 Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
1.2 Functions and Their Properties PreCalculus
 1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
In everyday speech, a continuous. Limits and Continuity. Critical Thinking Exercises
 062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
Chapter 1 Prerequisites for Calculus
 Section. Chapter Prerequisites for Calculus Section. Lines (pp. ) Quick Review.. + ( ) + () +. ( +). m. m ( ) ( ). (a) ( )? 6 (b) () ( )? 6. (a) 7? ( ) + 7 + Yes (b) ( ) + 9 No Yes No Section. Eercises.
Section. Chapter Prerequisites for Calculus Section. Lines (pp. ) Quick Review.. + ( ) + () +. ( +). m. m ( ) ( ). (a) ( )? 6 (b) () ( )? 6. (a) 7? ( ) + 7 + Yes (b) ( ) + 9 No Yes No Section. Eercises.
Law of Sines, Law of Cosines, Heron s Formula:
 PreAP Math Analsis nd Semester Review Law of Sines, Law of Cosines, Heron s Formula:. Determine how man solutions the triangle has and eplain our reasoning. (FIND YOUR FLOW CHART) a. A = 4, a = 4 ards,
PreAP Math Analsis nd Semester Review Law of Sines, Law of Cosines, Heron s Formula:. Determine how man solutions the triangle has and eplain our reasoning. (FIND YOUR FLOW CHART) a. A = 4, a = 4 ards,
LESSON #28 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
( ) 2 + 2x 3! ( x x ) 2
 Review for The Final Math 195 1. Rewrite as a single simplified fraction: 1. Rewrite as a single simplified fraction:. + 1 + + 1! 3. Rewrite as a single simplified fraction:! 4! 4 + 3 3 + + 5! 3 3! 4!
Review for The Final Math 195 1. Rewrite as a single simplified fraction: 1. Rewrite as a single simplified fraction:. + 1 + + 1! 3. Rewrite as a single simplified fraction:! 4! 4 + 3 3 + + 5! 3 3! 4!
Homework Assignments Math /02 Spring 2015
 Homework Assignments Math 1-01/0 Spring 015 Assignment 1 Due date : Frida, Januar Section 5.1, Page 159: #1-, 10, 11, 1; Section 5., Page 16: Find the slope and -intercept, and then plot the line in problems:
Homework Assignments Math 1-01/0 Spring 015 Assignment 1 Due date : Frida, Januar Section 5.1, Page 159: #1-, 10, 11, 1; Section 5., Page 16: Find the slope and -intercept, and then plot the line in problems:
KEY IDEAS. Chapter 1 Function Transformations. 1.1 Horizontal and Vertical Translations Pre-Calculus 12 Student Workbook MHR 1
 Chapter Function Transformations. Horizontal and Vertical Translations A translation can move the graph of a function up or down (vertical translation) and right or left (horizontal translation). A translation
Chapter Function Transformations. Horizontal and Vertical Translations A translation can move the graph of a function up or down (vertical translation) and right or left (horizontal translation). A translation
Unit 10 - Graphing Quadratic Functions
 Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Honors Pre-Calculus. Multiple Choice 1. An expression is given. Evaluate it at the given value
 Honors Pre-Calculus Multiple Choice. An epression is given. Evaluate it at the given value, (A) (B) 9 (C) 9 (D) (E). Simplif the epression. (A) + (B) (C) (D) (E) 7. Simplif the epression. (A) (B) (C) (D)
Honors Pre-Calculus Multiple Choice. An epression is given. Evaluate it at the given value, (A) (B) 9 (C) 9 (D) (E). Simplif the epression. (A) + (B) (C) (D) (E) 7. Simplif the epression. (A) (B) (C) (D)
Name Please print your name as it appears on the class roster.
 Berkele Cit College Practice Problems Math 1 Precalculus - Final Eam Preparation Name Please print our name as it appears on the class roster. SHORT ANSWER. Write the word or phrase that best completes
Berkele Cit College Practice Problems Math 1 Precalculus - Final Eam Preparation Name Please print our name as it appears on the class roster. SHORT ANSWER. Write the word or phrase that best completes
Study Guide and Intervention
 6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
Pre-Calculus Module 4
 Pre-Calculus Module 4 4 th Nine Weeks Table of Contents Precalculus Module 4 Unit 9 Rational Functions Rational Functions with Removable Discontinuities (1 5) End Behavior of Rational Functions (6) Rational
Pre-Calculus Module 4 4 th Nine Weeks Table of Contents Precalculus Module 4 Unit 9 Rational Functions Rational Functions with Removable Discontinuities (1 5) End Behavior of Rational Functions (6) Rational
1. For each of the following, state the domain and range and whether the given relation defines a function. b)
 Eam Review Unit 0:. For each of the following, state the domain and range and whether the given relation defines a function. (,),(,),(,),(5,) a) { }. For each of the following, sketch the relation and
Eam Review Unit 0:. For each of the following, state the domain and range and whether the given relation defines a function. (,),(,),(,),(5,) a) { }. For each of the following, sketch the relation and
2.4 Library of Functions; Piecewise-defined Functions. 1 Graph the Functions Listed in the Library of Functions
 80 CHAPTER Functions and Their Graphs Problems 8 88 require the following discussion of a secant line. The slope of the secant line containing the two points, f and + h, f + h on the graph of a function
80 CHAPTER Functions and Their Graphs Problems 8 88 require the following discussion of a secant line. The slope of the secant line containing the two points, f and + h, f + h on the graph of a function
A function from a set D to a set R is a rule that assigns a unique element in R to each element in D.
 1.2 Functions and Their Properties PreCalculus 1.2 FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1.2 1. Determine whether a set of numbers or a graph is a function 2. Find the domain of a function
1.2 Functions and Their Properties PreCalculus 1.2 FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1.2 1. Determine whether a set of numbers or a graph is a function 2. Find the domain of a function
6.4 graphs OF logarithmic FUnCTIOnS
 SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
y = f(x + 4) a) Example: A repeating X by using two linear equations y = ±x. b) Example: y = f(x - 3). The translation is
 Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
6. Graph each of the following functions. What do you notice? What happens when x = 2 on the graph of b?
 Pre Calculus Worksheet 1. Da 1 1. The relation described b the set of points {(-,5,0,5,,8,,9 ) ( ) ( ) ( )} is NOT a function. Eplain wh. For questions - 4, use the graph at the right.. Eplain wh the graph
Pre Calculus Worksheet 1. Da 1 1. The relation described b the set of points {(-,5,0,5,,8,,9 ) ( ) ( ) ( )} is NOT a function. Eplain wh. For questions - 4, use the graph at the right.. Eplain wh the graph
Precalculus Notes: Functions. Skill: Solve problems using the algebra of functions.
 Skill: Solve problems using the algebra of functions. Modeling a Function: Numerical (data table) Algebraic (equation) Graphical Using Numerical Values: Look for a common difference. If the first difference
Skill: Solve problems using the algebra of functions. Modeling a Function: Numerical (data table) Algebraic (equation) Graphical Using Numerical Values: Look for a common difference. If the first difference
Polynomial and Rational Functions
 Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
3.2 LOGARITHMIC FUNCTIONS AND THEIR GRAPHS
 Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
PreCalculus Final Exam Review Revised Spring 2014
 PreCalculus Final Eam Review Revised Spring 0. f() is a function that generates the ordered pairs (0,0), (,) and (,-). a. If f () is an odd function, what are the coordinates of two other points found
PreCalculus Final Eam Review Revised Spring 0. f() is a function that generates the ordered pairs (0,0), (,) and (,-). a. If f () is an odd function, what are the coordinates of two other points found
Trigonometric Functions
 Trigonometric Functions This section reviews radian measure and the basic trigonometric functions. C ' θ r s ' ngles ngles are measured in degrees or radians. The number of radians in the central angle
Trigonometric Functions This section reviews radian measure and the basic trigonometric functions. C ' θ r s ' ngles ngles are measured in degrees or radians. The number of radians in the central angle
1.3 LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION
 . Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
. Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
P.4 Lines in the Plane
 28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
CALCULUS BASIC SUMMER REVIEW
 NAME CALCULUS BASIC SUMMER REVIEW Slope of a non vertical line: rise y y y m run Point Slope Equation: y y m( ) The slope is m and a point on your line is, ). ( y Slope-Intercept Equation: y m b slope=
NAME CALCULUS BASIC SUMMER REVIEW Slope of a non vertical line: rise y y y m run Point Slope Equation: y y m( ) The slope is m and a point on your line is, ). ( y Slope-Intercept Equation: y m b slope=
Finding Limits Graphically and Numerically. An Introduction to Limits
 8 CHAPTER Limits and Their Properties Section Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach Learn different was that a it can fail to eist Stud and use
8 CHAPTER Limits and Their Properties Section Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach Learn different was that a it can fail to eist Stud and use
4.2 Mean Value Theorem Calculus
 4. MEAN VALUE THEOREM The Mean Value Theorem is considered b some to be the most important theorem in all of calculus. It is used to prove man of the theorems in calculus that we use in this course as
4. MEAN VALUE THEOREM The Mean Value Theorem is considered b some to be the most important theorem in all of calculus. It is used to prove man of the theorems in calculus that we use in this course as
Essential Question How can you use a quadratic function to model a real-life situation?
 3. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..E A..A A..B A..C Modeling with Quadratic Functions Essential Question How can ou use a quadratic function to model a real-life situation? Work with a partner.
3. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..E A..A A..B A..C Modeling with Quadratic Functions Essential Question How can ou use a quadratic function to model a real-life situation? Work with a partner.
Properties of Limits
 33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
APPENDIXES. B Coordinate Geometry and Lines C. D Trigonometry E F. G The Logarithm Defined as an Integral H Complex Numbers I
 APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
CHAPTER P Preparation for Calculus
 CHAPTER P Preparation for Calculus Section P. Graphs and Models...................... Section P. Linear Models and Rates of Change............ Section P. Functions and Their Graphs................. Section
CHAPTER P Preparation for Calculus Section P. Graphs and Models...................... Section P. Linear Models and Rates of Change............ Section P. Functions and Their Graphs................. Section
Finding Limits Graphically and Numerically. An Introduction to Limits
 60_00.qd //0 :05 PM Page 8 8 CHAPTER Limits and Their Properties Section. Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach. Learn different was that a it can
60_00.qd //0 :05 PM Page 8 8 CHAPTER Limits and Their Properties Section. Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach. Learn different was that a it can
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
SANDY CREEK HIGH SCHOOL
 SANDY CREEK HIGH SCHOOL SUMMER REVIEW PACKET For students entering A.P. CALCULUS BC I epect everyone to check the Google classroom site and your school emails at least once every two weeks. You will also
SANDY CREEK HIGH SCHOOL SUMMER REVIEW PACKET For students entering A.P. CALCULUS BC I epect everyone to check the Google classroom site and your school emails at least once every two weeks. You will also
M122 College Algebra Review for Final Exam
 M1 College Algebra Review for Final Eam Revised Fall 017 for College Algebra - Beecher All answers should include our work (this could be a written eplanation of the result, a graph with the relevant feature
M1 College Algebra Review for Final Eam Revised Fall 017 for College Algebra - Beecher All answers should include our work (this could be a written eplanation of the result, a graph with the relevant feature
MATH 1710 College Algebra Final Exam Review
 MATH 7 College Algebra Final Eam Review MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. ) There were 80 people at a pla. The admission price was $
MATH 7 College Algebra Final Eam Review MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. ) There were 80 people at a pla. The admission price was $
CHAPTER 1 Limits and Their Properties
 CHAPTER Limits and Their Properties Section. A Preview of Calculus................... 305 Section. Finding Limits Graphically and Numerically....... 305 Section.3 Evaluating Limits Analytically...............
CHAPTER Limits and Their Properties Section. A Preview of Calculus................... 305 Section. Finding Limits Graphically and Numerically....... 305 Section.3 Evaluating Limits Analytically...............
Self- assessment 1010 (Intermediate Algebra)
 Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. 4) cot! sec! sin! 4) 6) sin! cos! sec! csc!
 Sem 1 Final Eam Review SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use basic identities to simplif the epression. 1) tan! sec! 1) 2) tan 2! csc 2!
Sem 1 Final Eam Review SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use basic identities to simplif the epression. 1) tan! sec! 1) 2) tan 2! csc 2!
Derivatives of Multivariable Functions
 Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
Rolle s Theorem and the Mean Value Theorem. Rolle s Theorem
 0_00qd //0 0:50 AM Page 7 7 CHAPTER Applications o Dierentiation Section ROLLE S THEOREM French mathematician Michel Rolle irst published the theorem that bears his name in 9 Beore this time, however,
0_00qd //0 0:50 AM Page 7 7 CHAPTER Applications o Dierentiation Section ROLLE S THEOREM French mathematician Michel Rolle irst published the theorem that bears his name in 9 Beore this time, however,
BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS & COMPUTER SCIENCE. MTH06 Review Sheet y 6 2x + 5 y.
 BRONX COMMUNITY COLLEGE of the Cit Universit of New York DEPARTMENT OF MATHEMATICS & COMPUTER SCIENCE MTH06 Review Sheet. Perform the indicated operations and simplif: n n 0 n + n ( 9 )( ) + + 6 + 9ab
BRONX COMMUNITY COLLEGE of the Cit Universit of New York DEPARTMENT OF MATHEMATICS & COMPUTER SCIENCE MTH06 Review Sheet. Perform the indicated operations and simplif: n n 0 n + n ( 9 )( ) + + 6 + 9ab
Math 111 Final Exam Review KEY
 Math 111 Final Eam Review KEY 1. Use the graph of = f in Figure 1 to answer the following. Approimate where necessar. a b Evaluate f 1. f 1 = 0 Evaluate f0. f0 = 6 c Solve f = 0. =, = 1, =, or = 3 Solution
Math 111 Final Eam Review KEY 1. Use the graph of = f in Figure 1 to answer the following. Approimate where necessar. a b Evaluate f 1. f 1 = 0 Evaluate f0. f0 = 6 c Solve f = 0. =, = 1, =, or = 3 Solution
3.2 Introduction to Functions
 8 CHAPTER Graphs and Functions Write each statement as an equation in two variables. Then graph each equation. 97. The -value is more than three times the -value. 98. The -value is - decreased b twice
8 CHAPTER Graphs and Functions Write each statement as an equation in two variables. Then graph each equation. 97. The -value is more than three times the -value. 98. The -value is - decreased b twice
Power Functions. A polynomial expression is an expression of the form a n. x n 2... a 3. ,..., a n. , a 1. A polynomial function has the form f(x) a n
 1.1 Power Functions A rock that is tossed into the water of a calm lake creates ripples that move outward in a circular pattern. The area, A, spanned b the ripples can be modelled b the function A(r) πr,
1.1 Power Functions A rock that is tossed into the water of a calm lake creates ripples that move outward in a circular pattern. The area, A, spanned b the ripples can be modelled b the function A(r) πr,
x c x c This suggests the following definition.
 110 Chapter 1 / Limits and Continuit 1.5 CONTINUITY A thrown baseball cannot vanish at some point and reappear someplace else to continue its motion. Thus, we perceive the path of the ball as an unbroken
110 Chapter 1 / Limits and Continuit 1.5 CONTINUITY A thrown baseball cannot vanish at some point and reappear someplace else to continue its motion. Thus, we perceive the path of the ball as an unbroken
(x a) (a, b, c) P. (z c) E (y b)
 ( a). FUNCTIONS OF TWO VARIABLES 67 G (,, ) ( c) (a, b, c) P E ( b) Figure.: The diagonal PGgives the distance between the points (,, ) and (a, b, c) F Using Pthagoras theorem twice gives (PG) =(PF) +(FG)
( a). FUNCTIONS OF TWO VARIABLES 67 G (,, ) ( c) (a, b, c) P E ( b) Figure.: The diagonal PGgives the distance between the points (,, ) and (a, b, c) F Using Pthagoras theorem twice gives (PG) =(PF) +(FG)
3 a = b = Period: a = b = Period: Phase Shift: V. Shift: Phase shift: V. Shift:
 Name: Semester One Eam Review Pre-Calculus I. Second Nine Weeks Graphing Trig Functions: sketch the graph of the function, identif the parts being asked. 1. sin. cos( ) 1 Domain: Range: Domain: Range:
Name: Semester One Eam Review Pre-Calculus I. Second Nine Weeks Graphing Trig Functions: sketch the graph of the function, identif the parts being asked. 1. sin. cos( ) 1 Domain: Range: Domain: Range:
CHAPTER 1 Functions, Graphs, and Limits
 CHAPTER Functions, Graphs, and Limits Section. The Cartesian Plane and the Distance Formula... Section. Graphs of Equations...8 Section. Lines in the Plane and Slope... Mid-Chapter Quiz Solutions... Section.
CHAPTER Functions, Graphs, and Limits Section. The Cartesian Plane and the Distance Formula... Section. Graphs of Equations...8 Section. Lines in the Plane and Slope... Mid-Chapter Quiz Solutions... Section.
AP Calculus BC Summer Assignment 2018
 AP Calculus BC Summer Assignment 018 Name: When you come back to school, I will epect you to have attempted every problem. These skills are all different tools that we will pull out of our toolbo at different
AP Calculus BC Summer Assignment 018 Name: When you come back to school, I will epect you to have attempted every problem. These skills are all different tools that we will pull out of our toolbo at different
Math 20-1 Year End Review
 M0- Year End Review.docx Name: Math 0- Year End Review hapter Sequences & Series... Pages hapter Trigonometr... Pages hapters & Quadratic Functions & Equations... Pages hapter Radicals... Pages hapter
M0- Year End Review.docx Name: Math 0- Year End Review hapter Sequences & Series... Pages hapter Trigonometr... Pages hapters & Quadratic Functions & Equations... Pages hapter Radicals... Pages hapter
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Practice for the Final Eam MAC 1 Sullivan Version 1 (2007) SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Find the distance d(p1, P2) between the points
Practice for the Final Eam MAC 1 Sullivan Version 1 (2007) SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Find the distance d(p1, P2) between the points
Set 3: Limits of functions:
 Set 3: Limits of functions: A. The intuitive approach (.): 1. Watch the video at: https://www.khanacademy.org/math/differential-calculus/it-basics-dc/formal-definition-of-its-dc/v/itintuition-review. 3.
Set 3: Limits of functions: A. The intuitive approach (.): 1. Watch the video at: https://www.khanacademy.org/math/differential-calculus/it-basics-dc/formal-definition-of-its-dc/v/itintuition-review. 3.
AP Calculus AB Summer Assignment Mrs. Berkson
 AP Calculus AB Summer Assignment Mrs. Berkson The purpose of the summer assignment is to prepare ou with the necessar Pre- Calculus skills required for AP Calculus AB. Net ear we will be starting off the
AP Calculus AB Summer Assignment Mrs. Berkson The purpose of the summer assignment is to prepare ou with the necessar Pre- Calculus skills required for AP Calculus AB. Net ear we will be starting off the
Practice A ( 1, 3 ( 0, 1. Match the function with its graph. 3 x. Explain how the graph of g can be obtained from the graph of f. 5 x.
 8. Practice A For use with pages 65 7 Match the function with its graph.. f. f.. f 5. f 6. f f Lesson 8. A. B. C. (, 6) (0, ) (, ) (0, ) ( 0, ) (, ) D. E. F. (0, ) (, 6) ( 0, ) (, ) (, ) (0, ) Eplain how
8. Practice A For use with pages 65 7 Match the function with its graph.. f. f.. f 5. f 6. f f Lesson 8. A. B. C. (, 6) (0, ) (, ) (0, ) ( 0, ) (, ) D. E. F. (0, ) (, 6) ( 0, ) (, ) (, ) (0, ) Eplain how
PREPARATION FOR CALCULUS
 PREPARATION FOR CALCULUS WORKSHEETS Second Edition DIVISION OF MATHEMATICS ALFRED UNIVERSITY Contents Real Numbers Worksheet Functions and Graphs Worksheet 5 Polynomials Worksheet. Trigonometry Worksheet
PREPARATION FOR CALCULUS WORKSHEETS Second Edition DIVISION OF MATHEMATICS ALFRED UNIVERSITY Contents Real Numbers Worksheet Functions and Graphs Worksheet 5 Polynomials Worksheet. Trigonometry Worksheet
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question
 Midterm Review 0 Precalculu Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question ) A graph of a function g is shown below. Find g(0). (-, ) (-, 0) - -
Midterm Review 0 Precalculu Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question ) A graph of a function g is shown below. Find g(0). (-, ) (-, 0) - -
Active Maths 2 Old Syllabus Strand 5
 Junior certificate HIGHER LEVEL Active Maths Old Sllabus Strand 5 πr m = - - πr Oliver Murph Contents. Functions.... Functions and Graphs...5.3 Graphs...7.4 Linear Graphs...7.5 Quadratic Graphs...9.6 Real-Life
Junior certificate HIGHER LEVEL Active Maths Old Sllabus Strand 5 πr m = - - πr Oliver Murph Contents. Functions.... Functions and Graphs...5.3 Graphs...7.4 Linear Graphs...7.5 Quadratic Graphs...9.6 Real-Life
2.2 SEPARABLE VARIABLES
 44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
McKinney High School AP Calculus Summer Packet
 McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
Summary, Review, and Test
 45 Chapter Equations and Inequalities Chapter Summar Summar, Review, and Test DEFINITIONS AND CONCEPTS EXAMPLES. Eponential Functions a. The eponential function with base b is defined b f = b, where b
45 Chapter Equations and Inequalities Chapter Summar Summar, Review, and Test DEFINITIONS AND CONCEPTS EXAMPLES. Eponential Functions a. The eponential function with base b is defined b f = b, where b
PRECALCULUS FINAL EXAM REVIEW
 PRECALCULUS FINAL EXAM REVIEW Evaluate the function at the indicated value of. Round our result to three decimal places.. f () 4(5 ); 0.8. f () e ; 0.78 Use the graph of f to describe the transformation
PRECALCULUS FINAL EXAM REVIEW Evaluate the function at the indicated value of. Round our result to three decimal places.. f () 4(5 ); 0.8. f () e ; 0.78 Use the graph of f to describe the transformation
17 Exponential Functions
 Eponential Functions Concepts: Eponential Functions Graphing Eponential Functions Eponential Growth and Eponential Deca The Irrational Number e and Continuousl Compounded Interest (Section. &.A). Sketch
Eponential Functions Concepts: Eponential Functions Graphing Eponential Functions Eponential Growth and Eponential Deca The Irrational Number e and Continuousl Compounded Interest (Section. &.A). Sketch
Lesson 4.1 Interpreting Graphs
 Lesson 4.1 Interpreting Graphs 1. Describe the pattern of the graph of each of the following situations as the graphs are read from left to right as increasing, decreasing, increasing and then decreasing,
Lesson 4.1 Interpreting Graphs 1. Describe the pattern of the graph of each of the following situations as the graphs are read from left to right as increasing, decreasing, increasing and then decreasing,
Name DIRECTIONS: PLEASE COMPLET E ON A SEPARATE SHEET OF PAPER. USE THE ANSWER KEY PROVIDED TO CORRECT YOUR WORK. THIS WILL BE COLLECTED!!!
 FINAL EXAM REVIEW 0 PRECALCULUS Name DIRECTIONS: PLEASE COMPLET E ON A SEPARATE SHEET OF PAPER. USE THE ANSWER KEY PROVIDED TO CORRECT YOUR WORK. THIS WILL BE COLLECTED!!! State the domain of the rational
FINAL EXAM REVIEW 0 PRECALCULUS Name DIRECTIONS: PLEASE COMPLET E ON A SEPARATE SHEET OF PAPER. USE THE ANSWER KEY PROVIDED TO CORRECT YOUR WORK. THIS WILL BE COLLECTED!!! State the domain of the rational
Problems to practice for FINAL. 1. Below is the graph of a function ( ) At which of the marked values ( and ) is: (a) ( ) greatest = (b) ( ) least
 Problems to practice for FINAL. Below is the graph of a function () At which of the marked values ( and ) is: (a) () greatest = (b) () least = (c) () the greatest = (d) () the least = (e) () = = (f) ()
Problems to practice for FINAL. Below is the graph of a function () At which of the marked values ( and ) is: (a) () greatest = (b) () least = (c) () the greatest = (d) () the least = (e) () = = (f) ()
LESSON #42 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART 2 COMMON CORE ALGEBRA II
 LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
FUNCTIONS AND MODELS
 1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS 1.6 Inverse Functions and Logarithms In this section, we will learn about: Inverse functions and logarithms. INVERSE FUNCTIONS The table gives data from an experiment
1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS 1.6 Inverse Functions and Logarithms In this section, we will learn about: Inverse functions and logarithms. INVERSE FUNCTIONS The table gives data from an experiment
