A Tropical Toolkit. Department of Mathematics University of Texas O monumento é bem moderno.
|
|
|
- Lynn Gilbert
- 5 years ago
- Views:
Transcription
1 A Tropical Toolkit Eric Katz arxiv:math/ v3 [math.ag] 4 Apr 2008 Abstract Department of Mathematics University of Texas eekatz@math.utexas.edu O monumento é bem moderno. Caetano Veloso [41] We give an introduction to Tropical Geometry and prove some results in Tropical Intersection Theory. The first part of this paper is an introduction to tropical geometry aimed at researchers in Algebraic Geometry from the point of view of degenerations of varieties using projective not-necessarily-normal toric varieties. The second part is a foundational account of tropical intersection theory with proofs of some new theorems relating it to classical intersection theory. Contents 1 Introduction 1 2 Conventions 3 3 Polyhedral geometry 4 4 Toric Schemes 5 5 Degenerations 14 6 Tropical Varieties 19 7 Intersection Theory Motivation: Bezout vs. Bernstein 24 8 Intersection Theory 25 9 Tropical Cycles and the Cohomology of Toric Varieties Deformations of Subschemes into Torus Orbits 35 References 36 1 Introduction Tropical Geometry is an exciting new field of mathematics arising out of computer science. In the mathematical realm, it has been studied by Mikhalkin [24], Speyer Preprint submitted to Elsevier 4 April 2008
2 [33], the Sturmfels school [30], Itenberg, Kharlamov, and Shustin [18], Gathmann and Markwig [15], and Nishinou and Siebert [27] among many others. It has found applications in the enumeration of curves [23], low-dimensional topology [40], algebraic dynamics [10], and the study of compactifications [17,39]. This paper is an introduction to tropical geometry from the point of view of degenerations of subvarieties of a toric variety. In this respect, its approach is close to that of the Sturmfels school. In the first part of the paper, we use not-necessarily-normal projective toric varieties to introduce standard notions such as degenerations, the Gröbner and fiber fans, and tropical varieties. In the second part of the paper, we give a foundational account of tropical intersection theory. We define tropical intersection numbers, and show that tropical intersection theory computes classical intersection numbers under certain hypotheses, use tropical intersection theory to get data on deformation of subvarieties, and associate a tropical cycle to subvarieties. The two parts can be read independently. We will express tropical geometry in the language of projective not-necessarily normal toric schemes over a valuation ring (see [16], Chapter 5 for such toric varieties over fields). These toric schemes give toric degenerations. There are other constructions of toric degenerations analogous to different constructions of toric varieties. Analogous to the fan construction as in [11] is the approach of Speyer [33]. See also the paper of Nishinou and Siebert [27]. In [32], Speyer introduced a construction of toric degenerations paired with a map to projective space. The construction we use here has the advantage of being very immediate at the expense of some loss of generality by mandating projectivity and the loss of computability versus more constructive methods. We have chosen in this paper to approach the material from the point of view of algebraic geometry and had to neglect the very beautiful combinatorial nature of this theory. We would like to suggest that the reader takes a look at [30] for a more down-to-earth introduction to tropical geometry. We also point out a number of references that are more combinatorial in nature and which relate to our approach. There is the wonderful book of Gelfand, Kapranov, and Zelevinsky [16] which gives a combinatorial description of the secondary polytope among many other beautiful results, the paper of Billera and Sturmfels on fiber polytopes [4] (see also the lovely book of Ziegler [42]), the book of Sturmfels on Convex Polytopes and Gröbner Bases [36] as well as the papers [20,35]. We should mention that since this paper first appeared in preprint form, there has emerged a synthetic approach to tropical intersection theory. The intersection theory of tropical fans was established by Gathmann, Kerber, and Markwig in [14] and was extended to general tropical varieties in R n by Allermann and Rau in [1]. Many of the results from the first part of this paper are rephrased from Speyer s dissertation [33] and the general outlook is implicit in the work of Tevelev [39] which introduced the interplay between toric degenerations and tropical compactifications. 2
3 Please see [8] for an explanation of the relationship between such work. We hope this piece will be helpful to other researchers. We would like to thank Bernd Sturmfels for suggesting the connection between tropical cycles and Minkowski weights and Hannah Markwig, David Speyer, Frédéric Bihan, and Sam Payne for helpful comments and corrections. 2 Conventions Let R be a ring with a valuation contained in a subgroup G of (R, +), v : R \ {0} G R. Let K denote the field of fractions of R, m the maximal ideal v 1 ((0, )), and k = R/m. There are two examples that will be most important: (1) K = C{{t}} = M C((t 1 M )), the field of formal Puiseux series, v : K Q, the order map and k = C. (2) K = C((t 1 M )), the field of formal Laurent series in t 1 M, v : K Z 1, and k = C. M Note that the first choice of R has the disadvantage of not being Noetherian. This is not much of a hindrance because any variety defined over K in the first case can be defined over K in the second case for some M. This will be enough in practice. In either case, given x K, we may speak of the leading term of x. This is the non-zero complex coefficient of the lowest power of t occurring in the power-series expansion of x. In either of these cases we have an inclusion k R such that the composition is the identity. k R R/m = k Also, for every u G, we have an element t u R so that v(t u ) = u. These elements have the property that t u 1 t u 2 = t u 1+u 2. The choice of a map u t u as a section of v is perhaps unnatural. In [29], Payne introduced a formalism of tilted rings which avoids the need for a section. For an n-tuple, w = (w 1,...,w n ) G n, we may write t w for (t w 1,...,t wn ) (K ) n. Similarly, we may write v : (K ) n G n for the product of valuations. For g = (g 1,...,g n ) (K ) n, χ = (χ 1,...,χ n ) Z n, we write g χ for g χ g χn n K. 3
4 3 Polyhedral geometry Here we review some notions from polyhedral geometry. Please see [42] for more details. Let A R n be a set of points. Let P = Conv(A) be their convex hull. For v (R n ), the face P v of P is the set of points x P that minimize the function x, v. Let Γ v = A P v. The cone C Γv = w (Rn ) χ i, w = χ j, w for χ i, χ j Γ v χ, w < χ, w for χ Γ v, χ / Γ v is the normal cone to the face P v. Observe that v is in the relative interior of C Γv. The correspondence between P v and C Γv is inclusion reversing. The C Γ s form a fan, N(P), called the (inward) normal fan of P. Two polytopes are said to be normally equivalent if they have the same normal fan. A polyhedron in R n is said to be integral with respect to a full-rank lattice Λ (R n ) if it is the intersection of half-spaces defined by equations of the form {x x, w > a} for w Λ, a R. We will usually not note the lattice when it is understood. Definition 3.1. A polyhedral complex in R n is a finite collection C of polyhedra in R n that contains the faces of any one of its members, and such that any non-empty intersection of two of its members is a common face. A polyhedral complex is said to be integral if all of its members are integral polyhedra. The support C of a polyhedral complex C is the set-wise union of its polyhedra. We say that a polyhedral complex C is supported on a polyhedral complex D if C D. Definition 3.2. Given two integral polyhedral complexes, C,D in R n, we say C is a refinement of D if every polyhedron in D is a union of polyhedra in C. It is well-know that for convex polytopes P and Q with normal fans N(P), N(Q), N(P) is a refinement of N(Q) if and only λq is a Minkowski summand of P for some λ R >0. See Proposition 1.2 of [3]. Given a polyhedron P in a complex C, we may construct a fan F called the star of P. Pick a point w in the relative interior of P Let D be the set of all polyhedra in C containing P as a face. For every Q D, let C Q be the cone C Q = {v R n w + ǫv Q for some ǫ > 0}. These C Q s give a fan F. If P is a maximal polyhedron in C, then its star is its affine span. Please note that this usage of star is non-standard. Definition 3.3. Given n polytopes, P 1,...,P n R n, their mixed volume is the coefficient of λ 1 λ 2...λ n of Vol(λ 1 P 1 + +λ n P n ) which is a homogeneous polynomial of degree n in λ 1,..., λ n. 4
5 4 Toric Schemes Toric Schemes over Spec R We take the point of view of [31] and use the language of toric schemes over Spec R. We use the not necessarily normal projective toric varieties of [16]. For T = (K ) n a K-torus, let T = Hom(T, K ) be the character lattice and T = Hom(K, T) be the one-parameter subgroup lattice. Let T R = R T, T R = R T, and T G = G T. A homomorphism of tori T U induces homomorphisms T U and U T. Definition 4.1. Let T = (K ) n (K ) N+1 /(K ) PGl N+1 (K) be a composition of homomorphisms of groups where (K ) N+1 /(K ) denotes the quotient by the diagonal subgroup and the last homomorphism is the diagonal inclusion. For y P N K, let T y denote the stabilizer of y in T. The toric variety associated to (T, y) is the closure Y = (T/T y )y. Y lies in the fiber over the generic point in P N R Spec R. Let the toric scheme Y be the closure of Y in P N R, and let Y 0 = Y Spec R Spec k be the special fiber. Definition 4.2. If y P n k P n K for k K then the toric scheme is said to be defined over k. Alternatively, it s obtained by base-change from a toric variety defined over k by the map Spec K Spec k induced by the inclusion. Example 4.3. Let T = (K ) 2 (K ) 4 /(K ) be the inclusion given by If y = [1 : 1 : 1 : 1] P 3 K then (x 1, x 2 ) (1, x 1, x 2, x 1 x 2 ). T y = {[1 : x 1 : x 2 : x 1 x 2 ] x 1, x 2 K }. The closure of the above is P 1 P 1 under the Segre embedding. This is defined over k. Definition 4.4. There is a natural map from (K ) n to Y given by (K ) n Y g g y The image of the map is called the big open torus. If the map is an open immersion, we say our toric variety is immersive. Now, we explain a method of defining toric schemes. Let A = {χ 1,...,χ N+1 } T = Z n be a finite set. Let a : A G be a function called a height function. Let y = (y 1,...,y N+1 ) (K ) N+1 be an element satisfying v(y i ) = a(χ i ). 5
6 The choice of A induces a homomorphism of groups T = (K ) n (K ) N+1 g = (g 1,...,g n ) (g χ 1,...,g χ N+1 ). We may consider the map as a homomorphism T (K ) N+1 /(K ) where the quotient is by the diagonal subgroup. Therefore, if y (K ) N+1, g y = (g χ 1 y 1,...,g χ N+1 y N+1 ). One may ask how the toric variety depends on the choice of y. Let y,y (K ) N+1 satisfy v(y i ) = v(y i) = a(χ i ). Then y,y are related by multiplication by an element g (K ) N+1 with v(g) = 0. This element lifts to an element of (G m ) N+1 R. Therefore, the two choices of Y A,a are related by an action of the diagonal torus in P N R. As a consequence, the special fibers are related by an action of the diagonal torus in P N k. Let Y A,a be the toric scheme associated to T and y. Note that if the integral affine span of A is Z n then Y A,a is immersive. It is a theorem that the normalization of Y is the toric variety associated to the normal fan of the polytope Conv(A). See [7] for details. Definition 4.5. The induced subdivision of Conv(A) is given as follows. Let the upper hull of a be UH = Conv({(χ, b) χ A, b a(χ)}). The faces of UH project down to give a subdivision of Conv(A). Conv(A) is called the weight polytope of Y while the induced subdivision is called the weight subdivision of Y. Example 4.6. Let A = {(0, 0), (1, 0), (0, 1), (1, 1)} be the vertices of a lattice square. Let a be given by a(0, 0) = 0, a(1, 0) = 0, a(0, 1) = 0, a(1, 1) = 1. Choose y = (1, 1, 1, t 1 ). This induces the inclusion T (K ) 4 /(K ) given by (x 1, x 2 ) (x 0 1 x0 2, x1 1 x0 2, x0 1 x1 2, x1 1 x1 1 ) = (1, x 1, x 2, x 1 x 2 ) as in Example 4.3. Therefore Y is the closure of the image of (x 1, x 2 ) [1 : x 1 : x 2 : tx 1 x 2 ]. The fiber over Spec K is isomorphic to the closure of (x 1, x 2 ) [1 : x 1 : x 2 : x 1 x 2 ], 6
7 0 1 w 1 (0,0) 0 w (-1,-1) w 1 + w Fig. 1. The subdivision and its dual complex which is P 1 K P 1 K under the Segre embedding. The special fiber can be seen as follows: taking the limit of (x 1, x 2 ) as t 0, we get [1 : x 1 : x 2 : 0] which is P 2 ; taking the limit of (t 1 x 1, t 1 x 2 ) as t 0, we get [0 : x 1 : x 2 : x 1 x 2 ] which is another P 2. One sees that the special fiber is two copies of P 2 joined along P 1. We will show that this case is indicative of a general phenomenon in Lemma Recovering the Weight Subdivision There is a way of working backwards from (T, y) to A and a subdivision of Conv(A). Definition 4.7. Let V be a K-vector space. A k-weight decomposition is a vector space isomorphism defined over k K where H acts on V χ with character χ. V = χ Z n V χ Lemma 4.8. Any K-vector space V on which H acts linearly has a k-weight decomposition. Proof. See [6], Propositions 8.4 and Lift y P N K to y KN+1 Write y = χ y χ. Let A = {χ Z n y χ 0}. Then Conv(A) is called the weight polytope of Y. If dim V χ = 1, set a χ = v(v χ ). Otherwise, write v χ = v v n where v i are vectors in a one-dimensional subspace on which H acts, and set a χ = min(v(v i )). Take the subdivision of Conv(A) induced by a χ which is independent of the lift y. Dual Complex Consider the pairing T R T R R 7
8 and the piecewise-linear function F : T R R defined by F(w) = min ( χ, w + a χ). χ A The domains of linearity of F give a polyhedral complex structure on TR. For Γ A, let C Γ = w (Rn ) χ i, w + a χi = χ j, w + a χj for χ i, χ j Γ χ, w + a χ < χ, w + a χ for χ Γ, χ / Γ If C Γ is not empty, then Γ are points of A in a face of the weight subdivision. The C Γ s fit together to form an integral polyhedral complex, the dual complex which is dual to the weight subdivision. Note that if a χ = 0 for χ A, the weight subdivision becomes the weight polytope and the dual subdivision becomes the normal fan. Example 4.9. Figure 1 shows the weight subdivision and dual complex for Example 4.6. Here, F(w) = min χ A ( χ, w + a χ ) = min(0, w 1, w 2, w 1 + w 2 + 1). The values of F on the dual complex are noted in the figure. One-parameter Families of Points Let us review the notion of specialization. For y P N K, we may take y P N R, considered as a scheme over Spec R. The specialization of y is ŷ = y Spec R Spec k P N k. We can compute the specialization by hand. Lift y to y K N+1 \ {0} such that min(v(y i )) = 0. If y i 0, write y i = c 1 t b i +... where the ellipsis denotes higher order terms. Let S = {i b i = 0} Then ŷ satisfies c i if i S ŷ i = 0 else. Definition Let Y be a toric scheme over R. Let y be a point in Y. Given g (K ) n, the family associated to (g, y) is the scheme over Spec R given by the closure of g y. 8
9 Definition The limit of (g, y) is the point in Y 0 given by g y Spec R Spec k Now, observe that v((g y) i ) =< χ i, v(g) > +a χi where v(y i ) = a χi. Therefore, when we base-change to Spec k, the only components of g y i that stay non-zero are the ones on which < χ i, v(g) > +a χi is minimized. Consequently, if v(g) C Γ for a cell Γ of the weight subdivision, and ŷ is the limit of (g, y), then ŷ i 0 if and only if χ i Γ. One-parameter Families of Subschemes We will also consider degenerations of subschemes X of Y. Definition Let w G n and g = t w. Consider the subscheme of Y given by g X, the closure of g X. Define the initial degeneration of X to be the subscheme of Y 0 given by in w (X) = g X Spec R Spec k Example This definition specializes to the usual definition of the initial form of a polynomial. Let f = x 2 1x 2 + 7x 1 x 2 x 3 + 4x 3 3 K[x 1, x 2, x 3 ], and let w = (3, 4). Let X = V (f) Y = P 2 K. Then t w V (f), a subvariety of P 2 K is V (h) for Therefore, is cut out by h = (t 3 x 1 ) 2 (t 4 x 2 ) + 7(t 3 x 1 )(t 4 x 2 )(x 3 ) + 4(x 3 ) 3 = t 10 x 2 1 x 2 + 7t 7 x 1 x 2 x 3 + 4x 3 3 = t 10 (x 2 1x 2 + 7t 3 x 1 x 2 x 3 + 4t 10 x 3 3). in w (V (f)) = t w V (f) Spec R Spec k in w (f) = x 2 1x 2. Now that if X = x is a point then, in w (X) = t w x Spec R Spec k. Every point of in w (X) occurs as a limit of the form g x Spec R Spec k for x X. This is the content of the tropical lifting lemma. This lemma was first announced without proof in [37]. A proposed proof was given in [34] but has been found to be incomplete. A proof using affinoid algebras was given by Draisma in [9]. Jensen, Markwig, and Markwig provided an algorithm that finds a tropical lift in [19]. This algorithm uses some ideas from our proof and their paper is recommended as an exposition of our proof in terms of commutative algebra. In [29], by applying a projection argument to reduce to the hypersurface case, Payne gave a stronger version of tropical lifting that works over more general fields. 9
10 We first review the concept of relative dimension from Chapter 20 of [12]. Definition Let p : Z S be a scheme over a regular base scheme S. For V, a closed integral subscheme of Z, let T = p(v ). The relative dimension of V is rdimv = tr. deg.(r(v )/R(T)) codim(t, S). We will apply this definition for T = Spec C[[t 1 M ]]. Note that a point in the special fiber is of relative dimension 1. Lemma 4.15 (Tropical Lifting Lemma). Let K = C{{t}}. If x in w (X) then there exists x X with in w (x) t w x Spec R Spec k = x. Proof. We treat X as a subscheme of P N K. If dim X = 0, then the support of tw X is a union of closed K-points. One such point specializes to x. The corresponding component has initial deformation supported on x and gives the desired point in X. Therefore, we may suppose dim X = n > 0. Pick M sufficiently large so that X is defined over F = C((t 1/M )). Let Q = C[[t 1/M ]]. By replacing X by t w X we may suppose w = 0. Let X be the closure of X in Y. Note that X is flat over Spec Q. Let W 0 be a codimension n subvariety of Y 0 P N k such that W 0 intersects X 0 = X Spec Q Spec k in a 0-dimensional subscheme containing x. Extend W 0 to a flat integral scheme W Spec Q so that W Spec Q Spec k = W 0 (for example, we may set W = W 0 Spec k Spec Q). Then, X Y W is a scheme, all of whose components have nonnegative relative dimension over Spec Q. The following equality holds for underlying sets (X Y W) Spec Q Spec k = X 0 Y0 W 0. Since the scheme on the right is 0-dimensional, there are no components of X Y W contained in the special fiber. Therefore, the induced reduced structure on X Y W is flat, has relative dimension 0 and has a component of its limit supported on x. Let W = W Spec Q Spec F. By uniqueness of flat limits, the closure of the induced reduced structure on X Y W in Y is the induced reduced structure on X Y W. Therefore, we may apply the 0-dimensional case to the induced reduced structure on X Y W. We will find the following corollary useful. Corollary Under the hypotheses of the previous lemma and the equality of underlying sets X = X (K ) n, we may suppose x X (K ) n. Proof. Produce x X as above. If x X (K ) n then we are done. Otherwise, there is a morphism f : Spec K[[s]] X 10
11 so that the generic point is sent to X (K ) n while the closed point is sent to x. This morphism is defined over some C((t 1 M )) and can be given as a base-change from f : Spec C[[t 1 M ]][[s]] X where we view X as defined over C[[t 1 M ]]. Therefore, we may extend the morphism to f : Spec C[[t 1 M ]][[s 1 M ]] X. Consider the diagonal morphism i : Spec C[[u 1 M ]] Spec C[[t 1 M ]][[s 1 M ]] induced by t M u M, s M u M. By restricting the composition f i to the generic point, Spec C((u 1 M )), we find the desired K-point. Structure of Y A,a Y A,a has well-understood fibers over the generic and special point. Definition For Γ, a face of the weight polytope, let Y 0 (Γ) Y be the set of all points y Y P N K so that their lifts y (K)N+1 \ {0} satisfy y i 0 if and only if χ i Γ Definition For Γ, a cell of the weight subdivision, let Y 0 0 (Γ) Y 0 P N k be the set of all points y Y 0 P N k so that their lifts y (k)n+1 \ {0} satisfy y i 0 if and only if χ i Γ. Proposition (1) Y = Y A,a Spec R Spec K is the toric variety associated to A. The non-empty faces of the weight polytope are in inclusion-preserving bijective correspondence with its torus orbits given by Γ Y 0 (Γ). (2) The scheme Y 0 = Y A,a Spec R Spec k is supported on the union of toric varieties associated to the top-dimensional cells of the weight subdivision such that the non-empty cells of the weight subdivision are in inclusion-preserving bijective correspondence with its torus orbits given by Γ Y0 0 (Γ). Proof. (1) is Proposition 1.9 of Chapter 5 of [16]. We give the proof of (2) which is directly analogous. Elements of Y A,a Spec R Spec k are of the form g y Spec R Spec k by Lemma If v(g) C Γ, the cell of the dual complex corresponding to Γ, then the limit g y Spec R Spec k is in the orbit Y0 0 (Γ). Similarly if w C Γ, by varying g with v(g) = w, we may make g y Spec R Spec k be any point of Y0 0 (Γ). 11
12 Part (2) of the above lemma is simply not true at the level of scheme structure. As a counterexample, take A = {0, 1, 2}, a(0) = 0, a(1) = 1, a(2) = 0. Then Y 0 is a double-line in P 2. The corresponding subdivision is the single cell [0, 2] whose toric variety is the reduced-induced structure on Y 0. The construction of toric degenerations by fans as in [33] is better behaved in this respect. In the case of Example 4.6, we see that Y 0 consists of two P 2 s, five P 1 s and four fixed-points. It is instructive to phrase the above theorem in the language of the dual complex. Given two elements g, g (K ) n with v(g) = v(g ), the limits of (g, y) and (g, y ) are related by the action of an element of (k ) n and so lie in the same open torus orbit. Therefore, we may define an equivalence relation on G n. Two elements w, w T G are equivalent, written w y w if for g, g G satisfying w = v(g) and w = v(g ), the limits of (g, y) and (g, y) lie in the same open torus orbit. Proposition w y w if and only if w and w lie in the same cell in the dual complex associated to the toric scheme Y A,a. Invariant Limits The open orbits Y 0 (Γ) and Y0 0 (Γ) are fixed point-wise by sub-tori in T. Lemma Let Γ be a face of the weight polytope (resp. cell of the weight subdivision). Let w C Γ and H T be the sub-torus with HR = Span(C Γ w). Let z Y 0 (Γ) (resp. Y0 0 (Γ)). Then the maximal sub-torus fixing z is H. Proof. We give the proof for Y 0 0 (Γ). The proof for Y 0(Γ) is similar. Let z Y 0 0 (Γ). Lift z to z k N+1 \ {0}. Every g H satisfies g χ i = g χ j for χ i, χ j Γ. Let g = g χ k for χ Γ. Since z i 0 if and only if χ i Γ, which is another lift of z, g z = g z If u T \ H, there exists χ i, χ j Γ such that χ i, u χ j, u. it follows is that z is not fixed by the one-parameter subgroup corresponding to u. We may rephrase the above lemma. Lemma Suppose g T satisfies v(g) C Γ. Then the limit of (g, y) in Y 0 is invariant under the torus H given by H R = Span(C Γ w). Proof. The limit of (g, y) lies in Y 0 0 (Γ). 12
13 Suppose v(g) lies in C Γ, the cell of the dual complex dual to a cell Γ in the weight subdivision. We may make use of the map Spec R Spec k to base-change the limit g y Spec R Spec k to ŷ = (g y Spec R Spec k) Spec k Spec R. This just means that we should consider a limit point s coordinates as points in K rather than in k and take its closure. Lemma The weight polytope of the toric scheme Ŷ = (K ) n ŷ is Conv(Γ). Proof. Lift ŷ to ŷ K N+1 \ {0}. The weights with which T acts on ŷ are χ Γ. Therefore the weight polytope in Conv(Γ). The dual complex of Ŷ is the normal fan of Conv(Γ). One may also that the normal fan of Ŷ is the star of C Γ, the cell of the dual complex dual to Γ. Lemma Let ŷ = in w (X). For u T G, for sufficiently small ǫ > 0. in u (ŷ) = in w+ǫu (y) Proof. Let w C Γ for Γ, a cell of the weight subdivision. Then the weight polytope of ŷ is Conv(Γ). Therefore, u is in a cone of the normal fan of Γ dual to some face Γ Γ. It follows that the coordinates of in u (ŷ) in P N are non-zero only for χ i Γ and in that case are equal to the leading terms of the coordinate of t w y. Now, C Γ is a face of C Γ and we may pick small ǫ > 0 such that w + ǫu C Γ. Therefore, in w+ǫu (y) = in u (ŷ). Naturality of Dual Complexes Lemma Given a proper surjective (K ) n -equivariant morphism of n-dimensional toric schemes, f : X Y then the dual complex of X is a refinement of that of Y. The normal fan to the weight polytope of X is a refinement of that of Y. Proof. Let x P N K so that X = T x and Y = T f(x) for (possibly different) diagonal actions of T on P N K, PN K. Now let C Γ be a k-dimensional cell in the dual complex of X. We must show that f (C Γ ) is in the relative interior of a cell in the dual complex of Y of dimension at least k. If g T satisfies v(g) C Γ, then the limit, ˆx of (g, x) is invariant under the k-dimensional torus H with HR = Span(C Γ v(g)). Since f is equivariant, f(ˆx) is the limit of (g, f(x)). Furthermore if v(g) C Γ, a cell in the dual complex of Y then f(ˆx) is invariant under an l-dimensional torus H with H R = Span(C Γ v(g)). Since f(ˆx) is also invariant under H, then l > k. 13
14 To prove the statement for the weight polytope, we may set X = X Spec K[[s]], Y = Y Spec K[[s]] where s is an algebraic indeterminate. Consider the valuation v : K[[s]] Z given by v(s) = 1, v(k ) = 0. Then the weight subdivision of X and Y are exactly the weight polytopes of X and Y and the same argument applies. Equivariant Inclusions In this section we consider a projection of integral polytopes p : P Q where P = Conv(A). Definition Given a finite set A Z n and a function a : A R, a projection p : Z n Z m, let B = p(a) and define the image height function by b : B R b(ψ) = min({a(χ) χ p 1 (ψ)}). The associated subdivision is the image subdivision. Note that the image subdivision is dependent on the height function not just on the original subdivision. Weight polytopes and weight subdivisions are contravariant. Lemma Let i : T U be an injective homomorphism of tori, so T v U v P n is a chain of equivariant inclusions. Then the induced projection i : U T takes the weight polytope and the weight subdivision of U v to those of T v. Proof. The proof is straightforward. 5 Degenerations Moduli Spaces Tropical geometry is, in a certain sense, a method of parameterizing degenerations of subvarieties of a toric variety. There are two useful moduli spaces for parameterizing degenerations, the Chow variety and the Hilbert scheme. Points in these moduli spaces correspond to cycles or to subschemes. This is useful because limits of points 14
15 in the moduli space correspond to limits of cycles and subschemes. This allows us to apply the machinery developed in the previous section to limits of subvarieties. Let Y P N be a projective toric variety whose torus action extends to one on P N. Recall that k-dimensional algebraic cycles of Y are finite formal sums of k- dimensional subvarieties of Y with integer coefficients. Consider a subvariety X Y, with degree d in Y and Hilbert polynomial P. There are two moduli spaces that one can construct, Chow d (Y ) and Hilb P (Y ) that each have a point corresponding to X. Points in Chow d (Y ) correspond to cycles in Y of degree d. We denote the point (called the Chow form) in Chow d (Y ) corresponding to X by R X. Chow d (Y ) is constructed as a closed subscheme of Chow d (P N ) which is a projective scheme. Points in Hilb P (Y ) correspond to closed subschemes of Y with Hilbert polynomial P. The point [X] in Hilb P (Y ) corresponding to X is called the Hilbert point. Similarly, Hilb P (Y ) is a closed subscheme of Hilb P (P N ) which is projective. See [22] for an in-depth construction of both varieties. See also [16] for a discussion of the Chow variety. We will break from the usage in [22] and use Chow to denote the un-normalized Chow variety which is there called Chow. Note that the Hilbert scheme can be constructed over an arbitrary Noetherian scheme S while there are restrictions on the base-scheme of the Chow variety. Let us review some useful properties of the Chow varieties and Hilbert schemes. Property 5.1. The torus action on Y induces a group action on Chow d and Hilb P which extends to an action on the ambient projective space. Because the torus T acts on Y, for g T, g X is a subvariety of Y of degree d and Hilbert polynomial P. Therefore, R g X Chow d (Y ) and [g X] Hilb P (Y ). This induces T-actions on Chow d (Y ) and Hilb P (Y ) given by T Chow d (Y ) Chow d (Y ), T Hilb P (Y ) Hilb P (Y ) (g, R X ) R g X, (g, [X]) [g X] Property 5.2. There is a natural equivariant morphism FC : Hilb P Chow d (see 5.4 of [26]) called the fundamental class map that takes a scheme to its underlying cycle. A subscheme X of Y has an underlying cycle. Therefore, one may define a map FC : Hilb P Chow d [X] R X. This map is equivariant with respect to the above T-actions. Property 5.3. The Hilbert scheme possesses a universal flat family Univ P Hilb P. This universal family Univ P is a subscheme of Y Hilb P (Y ). The fiber over the Hilbert point [X] is the subscheme X. In particular, if Spec K Hilb P (Y ) is the K-point [X] then Univ P HilbP (Y ) Spec K = X. The Chow variety does not usually have a universal flat family. 15
16 Property 5.4. The Hilbert scheme is natural under base-change. If Y S is projective then Hilb P (Y/S) parameterizes S-subschemes of Y with Hilbert polynomial P. If Z S is a morphism then Hilb P (Y S Z/Z) = Hilb P (Y/S) S Z. The Chow variety does not have this property. The Hilbert scheme with its universal flat family and naturality properties is a much better behaved moduli space. This makes it more useful for our purposes. However, there are very beautiful combinatorial structures associated with the Chow variety. See [16] for details. Now, we may use the Hilbert scheme to relate deformations of subschemes to limits of the form (g, y). Let X be a subscheme of a toric variety Y. Let g T and w = v(g). By uniqueness of flat limits, the Spec R-point g [X] is the Hilbert point of g X in Hilb P (Y). Therefore, the specialization of g [X], g [X] Spec R Spec k Hilb P (Y) Spec R Spec k = Hilb P (Y 0 ) is the Hilbert point, [g X Spec R Spec k]. We may pull back the universal family by Spec R Hilb P (Y) to get a scheme U over Spec R. Its special fiber is g X Spec R Spec k. If g = t w, then the special fiber is the initial degeneration in w (X). Associated Toric Schemes Let Y be a toric scheme in P N K with a torus T. Let X be a subvariety of Y. We may take the Hilbert point [X] Hilb P (Y ) or the Chow form R X Chow d (Y ) and consider the two toric schemes, called the Hilbert and Chow images, respectively HI = T/T X [X] Hilb P (Y ), CI = T/T X R X Chow d (Y ) where T X denotes the stabilizer of [X] or R X. Definition 5.5. The subdivisions (in (T/T X ) T ) associated to the Hilbert and Chow images are called the state subdivision and the secondary subdivision, respectively. The dual polyhedral complexes (in (T/T X ) ) are called the Gröbner complex and the Chow complex. In the case where X and Y are defined over k, these notions become the state polytope, fiber polytope, the Gröbner fan, and the fiber fan, respectively. In the case where X is also a toric subvariety in Y, the name fiber polytope is standard. Otherwise our usage is somewhat non-standard. Now we may apply Proposition 4.20 to the Gröbner complex. Proposition 5.6. Two points w, w lie in the same cell in the Gröbner complex if and only if in w (X) and in w(x) are related by a T k -action. 16
17 In the case where X is defined over k, this proposition is close to the usual definition of the Gröbner fan. The usual definition, however, is a refinement of our definition. This is because the initial ideals in the standard definition are sensitive to embedded primes associated to the irrelevant ideal. Our definition is not. The definition we give is based on that of [2]. We may also apply Lemma 4.22 to the Gröbner complex. Lemma 5.7. If w G n is in the relative interior of a k-dimensional cell of the Gröbner complex of X then the closed subscheme in w (X) is invariant under a k- dimensional torus. Proof. By Lemma 4.22 the Hilbert point of in w (X) is invariant under a k-dimensional torus. Therefore, the closed subscheme in w (X) is invariant under the same torus. Lemma 5.8. For u T G, for ǫ > 0 sufficiently small. in u (in w (X)) = in w+ǫu (X) Proof. This is Lemma 4.24 applied to the Hilbert point [X]. There is a natural projection p : TR (T/T X) R. We may abuse notation and use the term Gröbner or Chow complex to also denote the appropriate complex s inverse image under p. Example 5.9. Let Y be a toric variety defined over k given by a set of exponents A Z n. Let X be a hypersurface defined in Y by f(x) ω A a ω x ω = 0 where a ω K and x ω are coordinates on Y P A 1. We may treat [a ω ] as coordinates on a projective space (P A 1 ). The torus T acts on (P A 1 ) by T (P A 1 ) (P A 1 ) (g, [a ω ]) [g ω a ω ]. Then the equation a ω x ω = 0 ω A cuts out a universal hypersurface U Y (P A 1 ) over (P A 1 ). This universal family is flat and therefore defines a T-equivariant morphism (P A 1 ) Hilb P (Y ). The image of this morphism contains the Hilbert point of X. Therefore, the Hilbert image, T [X] is isomorphic to Y but with the opposite torus action. Therefore, the state polytope, which is the weight polytope of the Hilbert image is Conv(A). The Gröbner fan is the normal fan N( Conv(A)). For a down-to-earth exposition of this example, see Proposition 2.8 of [36]. 17
18 Example Suppose that Y is a toric variety defined over k. Let X be a reduced K-point contained in an open torus orbit Y 0 (Γ). The Hilbert scheme parameterizes reduced points in Y. Therefore, the Hilbert image is Y (Γ), the closure of Y 0 (Γ). The weights on the Hilbert point of X are χ Γ while the height function is a(χ) = χ, v(x). It follows that the piecewise-linear function F whose domains of linearity are the cells of the dual complex is F(w) = min χ, w + v(x). χ Γ In particular if x lies in the big open torus of Y then the Gröbner complex is just the normal fan of Conv(Γ) translated by v(x). Let us examine initial deformations if X is a point in the big open torus in a toric variety Y. If w = v(x) then t w X has valuation 0 and so in w (X) is a point in the big open torus of Y 0. Otherwise, in w (X) lies in some torus orbit. In fact, if w + v(x) C Γ for a face Γ of Y s polytope then in w (X) is a point in Y 0 (Γ). This is in agreement with the proof of Proposition Example Let Y be a toric variety defined over k. Let X be the schemetheoretic image of a map Spec k[ǫ]/ǫ 2 Y. We visualize X as a point in Y with a tangent vector anchored at it. Suppose the image lies in the big open torus and that the vector is chosen generically. Let us find the weight polytope of HI. By Proposition 4.19, it suffices to find the vertices which correspond to the torus-fixed points in HI. The torus-fixed points in HI are schemes S consisting of a fixed point p of Y together with a projectivized tangent vector pointing along a 1-dimensional orbit E containing p. By the genericity condition, all choice of (p, E) with p E are possible. We must find the weights corresponding to these fixed points. Let us first work out the case where Y = P n. If HI P N and y k N+1 \ {0} is a vector corresponding to a torus fixed point Q, then the vertex of the weight polytope of HI corresponds to the character of the action of T = (k ) n on y. Because the embedding of HI is given by the composition of the embedding of the Hilbert scheme into a Grassmannian with the Plücker embedding into P N, the action of T on y is the same as the action of T on top (Γ(O Q (l))) where l is a sufficiently large positive integer. Now, a torus fixed-point of HI consists of a pair (p, E). Suppose p is given by the point X i = δ ir in homogeneous coordinates. Let x j = X i X r be inhomogeneous coordinates on X r 0. Then the fixed point Q is given as the image of an affine morphism A n Spec k[ǫ]/ǫ 2 k[x 1,..., ˆx r,...,x n+1 ] k[ǫ]/ǫ 2 x i cδ is ǫ where c k is some constant. In other words, the tangent vector points along the x s -axis. The vector space O Q (l) is spanned by two monomials, Xr l and Xl 1 r X s. They have characters le r and (l 1)e r + e s, respectively where e i are the standard unit basis vectors of T. Therefore, top (Γ(O Q (l))) has character (2l 2)e r + (e r + e s ). 18
19 Let n 1 be the unit simplex in T and Γ the convex hull of the mid-points of 2. Then the state polytope of X which is the weight polytope of HI is (2l 2) + Γ. For a general toric variety Y P n, we note that the Hilbert scheme Hilb P (Y ) is constructed as a subscheme of Hilb P (P n ). Let U be the torus of P n, T the torus of Y, i : T U the homomorphism of tori, and i : U T the induced projection. If Q is a T-fixed point of Hilb P (Y ), then Q is a U-fixed point and the character of the corresponding vertex in U pulls back by i to the appropriate character in T. Therefore, if Γ = Conv(A) is the polytope corresponding to Y and the convex hull of the mid-points of the edges of 2Γ, the state polytope of X is (2l 2)Γ + by Lemma See [28] for a computation of the related case of the Gröbner fan of generic point configurations in affine space. The Chow image in this case is isomorphic to Y as its points correspond to points of Y with multiplicity 2. The fiber polytope is Γ. Because the fiber polytope, P is a Minkowski summand of the state polytope (2l 2)Γ +, the Gröbner fan is a refinement of the fiber fan. This is an example of a general fact. Proposition The Gröbner complex is a refinement of the fiber complex. Proof. The fundamental class map FC : HI CI satisfies the hypotheses of Lemma For a combinatorial commutative algebra proof of the above, see [35]. 6 Tropical Varieties Intersection of Sub-tori Before we give the definition of tropical varieties, we must digress to consider the intersection two sub-tori in (k ) n. Let H 1 = (k ) m 1, H 2 = (k ) m2 T = (k ) n be two injective homomorphisms with m 1 + m 2 = n such that images under the induced maps Hi T are transversal. Let y 1, y 2 (k ) n. Let V i = H i y i. We compute the intersection of V 1 and V 2. The inclusions H 1, H 2 (k ) n correspond to surjections T H i. Let M i be the kernel of the surjections. We may also write M i as H i. Proposition 6.1. The number of intersection points, V 1 V 2 is equal to [T : M 1 + M 2 ], the lattice index of M 1 + M 2 in T. Proof. The following argument is adapted from [37, pp.32-33]. Pick bases for M 1 and M 2. V i is cut out by the equations x a = y a 1, x b = y b 2 19
20 for x (k ) n where a ranges over the basis for M 1 and b ranges over a basis for M 2. We write the basis vectors as row vectors and concatenate them to form an n n-matrix. A = A 1 Put this matrix in Hermitian normal form UA = R where U SL n (Z), and R is an upper triangular invertible matrix. Therefore, the entries of R are A 2 r 11 r r 1n 0 r R = r 2n r nn Finding intersection points of V 1 and V 2 amounts to solving the system x r i1 1 x r i2 2...x r in n = c i for certain c i k. There are r 11 r 22...r nn = det(a) = [T : M 1 +M 2 ] solutions. The definition of tropical intersection numbers in [24] requires that the above lattice index be equal to [Z n : M1 +M 2 ] where M i is the perpendicular lattice to M i. For the sake of completeness, we include a proof with simplifications by Frédéric Bihan that the lattice indexes are equal. Lemma 6.2. Let L and M be saturated lattices in Z n of complementary rank so that L + M has rank n. Then [Z n : L + M] = [Z n : L + M ] where L = ker((z n ) L ), M = ker((z n ) M ). Proof. Let k = rank(l). Let Q = {q 1,...,q k } be a basis for M and R = {r 1,...,r k } be a basis for L. We first claim that [Z n : L + M] = det ([q i (r j )] i,j=1,...,k ). Since M is saturated, we may pick a basis E = {e 1,...,e n } for Z n so that {e k+1,...,e n } is a basis for M. Let F = {f 1,...,f k } be a basis for L, and form the n n-matrix A whose column vectors are the coordinates of f 1,...,f k, e k+1,...,e n with respect to the basis E. [Z n : L + M] = det(a). The matrix A is block lower-triangular with 20
21 respect to blocks of size k k and (n k) (n k) centered at the diagonal. The lower right (n k) (n k) block is the identity matrix. Therefore, det(a) = det ([a ij ] i,j=1,...k ) = det ([e i (f j)] i,j=1,...,k ). The determinant on the right is invariant under change of basis for L and M. The claim is proven. Similarly, [Z n : L + M ] is the absolute value of the determinant of the k k- matrix formed by letting a basis of (L ) act on a basis of M. Since L is saturated, (L ) = L, so R is a basis of (L ). Therefore, [Z n : L + M ] = det ([r i (q j )] i,j=1,...,k ). It follows that the lattice indexes, [Z n : L + M],[Z n : L + M ] are equal to the absolute values of determinants of transposed matrices. Therefore, they are equal. Definition of Trop Let Y be an immersive toric scheme defined over k so Y = Y 0 Spec k Spec R. Let X be some subvariety of Y that intersects the big open torus. Let HI be the Hilbert image of X. Its complex is the Gröbner complex. Definition 6.3. The tropical variety of X, Trop(X) G n is given by all w G n so that in w (X) intersects the big open torus, (k ) n Y 0. By Proposition 5.6, if w and w are in the same cell of the Gröbner complex, then in w (X) is related to in w (X) by an action of (k ) n. So, if in w (X) intersects the big open torus, so does in w(x). Therefore, the tropical variety is a union of cells of the Gröbner complex. We may put a integral polyhedral complex structure on Trop(Y ) to make it a subcomplex of the Gröbner complex. The tropical variety is usually given by the image under the valuation map. We show that these definitions are equivalent. Consider the isomorphism between the big open torus of Y and (K ) n given by g g y. This allows us to define a valuation map v : X (K ) n G n Lemma 6.4. Trop(X) is equal to the image v(x). Proof. v(x) Trop(X): Let g X (K ) n. It suffices to show that the degeneration g 1 X Spec R Spec k intersects the big open torus in Y 0. But, 1 = (g 1 g) Spec R Spec k g 1 X Spec R Spec k is a point in the big open torus. Trop(X) v(x): If w Trop(X), then t w X Spec R Spec k (k ) n 21
22 is non-empty. Let x be a closed point of the above. Then Lemma 4.15 produces a point x X with in w (x) = x. It follows that v(x) = w. Example 6.5. Let H T be a sub-torus and x T. Let X = H x. Then Trop(X) is H G v(x). Example 6.6. Let us revisit Example 5.9. The Hilbert image is the toric variety associated to A. We have the morphism (P A 1 ) HI. The hypersurface in Y corresponding to [a ω ] HI, a ω x ω = 0 ω A is disjoint from the big open torus if and only exactly one a ω is not zero. Such points correspond to the torus fixed points of HI or alternatively, the top-dimensional cones of the Gröbner fan. Therefore the tropical variety of the hypersurface V (f) is the union of the positive codimension cones of N( Conv(A)). Let us relate the tropical variety of in w (X) to that of X. Lemma 6.7. Let w be a point in a cell τ of the tropical variety, Trop(X). Then Trop(in w (X)) is the star of τ in Trop(X). Proof. Recall that by Lemma 5.8, in u (in w (X)) = in w+ǫu (X) for sufficiently small ǫ. Therefore, in u (in w (X)) intersects the open torus if and only w + ǫu Trop(X). The dimension of X and the dimension of Trop(X) are related. We give a proof adapted from [37]. We begin with the case where Trop(X) is zero-dimensional. Lemma 6.8. If X (K ) n is a variety with dim(trop(x)) = 0 then X is zerodimensional. Proof. Suppose X is positive dimensional. Choose a coordinate projection p : (K ) n K so that p(x) is an infinite set. By Chevalley s theorem [25], p(x) is a finite union of locally closed sets and, since it is infinite, it must be an open set. Therefore, Trop(X) is bigger than a point. We can reduce the general case to the above lemma. Proposition 6.9. If X (K ) n is purely d-dimensional, so is Trop(X). Proof. Suppose dim Trop(X) = k. Let w be an element of the relative interior of a top-dimensional cell of Trop(X). Then w is in the relative interior of a k-dimensional cell C Γ of the Gröbner complex. Then, by Lemma 4.22, in w (X) is invariant under a k- dimensional torus, U. The initial degeneration in w (X) intersects the open torus so if x in w (X) (k ) n, the k-dimensional variety U x is a subset of in w (X). Since in w (X) is a flat deformation of X, it is also d-dimensional. Therefore k d. By Lemma 6.7, the tropical variety of in w (X) is the k-dimensional subspace Span(C Γ w). Now, we show d = k. Let W be a variety of the form H z where H (k ) n is an (n k)-dimensional torus with H is transverse to Trop(in w (X)). Now, by the Kleiman-Bertini theorem [21], there is a choice of z so that in w (X) W is empty or of dimension d k. By Proposition 6.1, U x and W must intersect, so in w (X) W 22
23 is non-empty. But, Trop(in w (X) W) Trop(in w (X)) Trop(W) which is a point. Therefore, in w (X) W is a d k dimensional scheme whose tropicalization is a point. By the above lemma d = k. Multiplicities Let X be an m-dimensional subvariety of a toric variety Y. If w is in the relative interior of an m-dimensional cell C Γ of Trop(X), then in w (X) (k ) n is a subscheme invariant under an m-dimensional torus H with H R = Span(C Γ w). Therefore, in w (X) (k ) n is supported on i(h p i ) where p i are points in (k ) n. This allows us to define multiplicities on Trop(X). Definition Given a top-dimensional cell σ of Trop(X), let w be a point in the relative interior of σ. Decompose the underlying cycle of in w (X) (k ) n as [in w (X) (k ) n ] = m i [H p i ] for H = (k ) m T k, p i (k ) n. The multiplicity m σ is m σ = i m i. This multiplicities are also called weights. Trop(X) obeys the following balancing condition first given in Theorem of [33]. Definition An integrally weighted m-dimensional integral polyhedral complex is said to be balanced if the following holds: Let τ be an (m 1)-dimensional cell of Trop(X) and σ 1,...,σ l be the m-dimensional cells adjacent to τ. Let w τ, V = Span(τ w), and λ the projection λ : T T /V. Let p j = λ(σ j w). Note that p j is an interval adjacent to 0, and let v j T /V be the primitive integer vector along Span + (p j ). Then l m σj v j = 0. j=1 We will give a proof that the balancing condition is satisfied in Theorem The following relates the multiplicities on Trop(in w (X)) to those on Trop(X). Lemma Let w τ be a point in the relative interior of a cell of Trop(X). Let σ 1,...,σ l be the top-dimensional cells in Trop(X) containing τ. Then the multiplicities of the cones σ 1,...,σ l in Trop(in w (X)) corresponding to σ 1,...,σ k are m σ1,...,m σl. Proof. Let u σ i. Then in u (in w (X)) = in w+ǫu (X) by Lemma By shrinking ǫ further if necessary, we may suppose w + ǫu σ i. Therefore, the degeneration in u (in w (X)) used to compute m σi is the same as the degeneration in w+ǫu (X) used to compute m σi. 23
24 7 Intersection Theory Motivation: Bezout vs. Bernstein Let us consider two curves in (C ) 2 cut out by polynomials f(x, y) and g(x, y). Suppose they have no component in common and we would like to bound the number of intersection points in (C ) 2 counted with multiplicity. The Bernstein bound will motivate tropical intersection theory. Bezout Bound We first consider the Bezout bound. We compactify (C ) 2 to the projective plane P 2. The intersection number is given by topology and is equal to deg(f) deg(g). This intersection bound is rigid in that it is invariant under deformations of f and g. Unfortunately, the bound is not the best because we introduced new intersections on the coordinate hyperplanes by compactifying. Let us make this concrete by picking polynomials (all borrowed from [37]). Let f(x, y)=a 1 + a 2 x + a 3 xy + a 4 y g(x, y)=b 1 + b 2 x 2 y + b 3 xy 2. To consider these polynomials on P 2, we must homogenize them to F(X, Y, Z)=a 1 Z 2 + a 2 XZ + a 3 XY + a 4 Y Z G(X, Y, Z)=b 1 Z 3 + b 2 X 2 Y + b 3 XY 2. Then the Bezout bound is 2 3 = 6. Notice that both curves contain the points [1 : 0 : 0] and [0 : 1 : 0]. This leads Bezout s theorem to over-count the number of intersections by 2. It is impossible to remove these additional intersection points by an action of (C ) 2 since these points are fixed under the torus action. Bernstein Bound Another approach is offered by Bernstein s theorem: Theorem 7.1. Given Laurent polynomials f 1,...,f n C[x ±1 1,...,x±1 n ] with finitely many common zeroes in (C ) n, let i be the Newton polytopes of f i. The number of common zeroes is bounded by the mixed volume of the i s. Bernstein s theorem can be conceptualized in the above case as follows. One can compactify (C ) 2 to a nonsingular toric variety so that the closure of the curves cut out by f = 0 and by g = 0 does not intersect any torus fixed points. For instance, one may take the toric variety whose fan is the normal fan to the Minkowski sum 24
25 of the Newton polygons of f and g. One may apply a (C ) 2 -action to {f = 0} to ensure that there are no intersections outside of (C ) 2. By refining the fan further, we may suppose that the toric variety is smooth. Then one can bound the number of intersection points by the topological intersection number of the two curves. This reproduces the Bernstein bound. 8 Intersection Theory Henceforth, we will be using tropical varieties Y ( ) defined by a fan as in [11]. Intersection Theory over Discrete Valuation Rings Let us first review some notions of Intersection Theory from [12]. Let Y be a scheme. A k-cycle on Y is a finite formal sum, n i [V i ] where the V i s are k-dimensional subvarieties of Y and the the n i s are integers. k-cycles form a group under formal addition. There is a notion of rational equivalence on cycles, and the Chow group, A k (Y ) is the group of cycles defined up to rational equivalence. This group is analogous to homology. If Y is complete, there is a natural degree map deg : A 0 (Y ) Z given by mi [p i ] m i. For any proper morphism f : X Y, there is an induced push-forward homomorphism f : A k (X) A k (Y ). This push-forward homorphism commutes with degree. If X is a disjoint union X = X i, then we have A k (X) = A k (X i ). If Y is a smooth n-dimensional variety, there is an intersection product A k (Y ) A l (Y ) A k+l n (Y ). If V and W are varieties in Y of dimension k and l respectively, then the intersection product factors through a refined intersection product A k (Y ) A l (Y ) A k+l n (V W) i A k+l n (Y ) where i : V W Y. There is also Chow cohomology A k (Y ) which is defined operationally. Intersection theory can also be defined over discrete valuation rings. The reference is Chapter 20 of [12]. We will state the results for R = C[[t 1 M ]], but they are true for more general choices of R. In practice, however, given varieties defined over C{{t}}, we may find a sufficiently large M so that they are defined over C((t 1 M )) and apply the results for the corresponding choice of R. Let p : Y Spec R be a scheme over Spec R. Let Y = Y Spec R Spec K, Y 0 = Y Spec R Spec k. 25
LIFTING TROPICAL INTERSECTIONS
 LIFTING TROPICAL INTERSECTIONS BRIAN OSSERMAN AND SAM PAYNE Abstract. We show that points in the intersection of the tropicalizations of subvarieties of a torus lift to algebraic intersection points with
LIFTING TROPICAL INTERSECTIONS BRIAN OSSERMAN AND SAM PAYNE Abstract. We show that points in the intersection of the tropicalizations of subvarieties of a torus lift to algebraic intersection points with
Tropical Varieties. Jan Verschelde
 Tropical Varieties Jan Verschelde University of Illinois at Chicago Department of Mathematics, Statistics, and Computer Science http://www.math.uic.edu/ jan jan@math.uic.edu Graduate Computational Algebraic
Tropical Varieties Jan Verschelde University of Illinois at Chicago Department of Mathematics, Statistics, and Computer Science http://www.math.uic.edu/ jan jan@math.uic.edu Graduate Computational Algebraic
12. Hilbert Polynomials and Bézout s Theorem
 12. Hilbert Polynomials and Bézout s Theorem 95 12. Hilbert Polynomials and Bézout s Theorem After our study of smooth cubic surfaces in the last chapter, let us now come back to the general theory of
12. Hilbert Polynomials and Bézout s Theorem 95 12. Hilbert Polynomials and Bézout s Theorem After our study of smooth cubic surfaces in the last chapter, let us now come back to the general theory of
AN INTRODUCTION TO TROPICAL GEOMETRY
 AN INTRODUCTION TO TROPICAL GEOMETRY JAN DRAISMA Date: July 2011. 1 2 JAN DRAISMA Tropical numbers. 1. Tropical numbers and valuations R := R { } tropical numbers, equipped with two operations: tropical
AN INTRODUCTION TO TROPICAL GEOMETRY JAN DRAISMA Date: July 2011. 1 2 JAN DRAISMA Tropical numbers. 1. Tropical numbers and valuations R := R { } tropical numbers, equipped with two operations: tropical
SPACES OF RATIONAL CURVES ON COMPLETE INTERSECTIONS
 SPACES OF RATIONAL CURVES ON COMPLETE INTERSECTIONS ROYA BEHESHTI AND N. MOHAN KUMAR Abstract. We prove that the space of smooth rational curves of degree e on a general complete intersection of multidegree
SPACES OF RATIONAL CURVES ON COMPLETE INTERSECTIONS ROYA BEHESHTI AND N. MOHAN KUMAR Abstract. We prove that the space of smooth rational curves of degree e on a general complete intersection of multidegree
MATH 8253 ALGEBRAIC GEOMETRY WEEK 12
 MATH 8253 ALGEBRAIC GEOMETRY WEEK 2 CİHAN BAHRAN 3.2.. Let Y be a Noetherian scheme. Show that any Y -scheme X of finite type is Noetherian. Moreover, if Y is of finite dimension, then so is X. Write f
MATH 8253 ALGEBRAIC GEOMETRY WEEK 2 CİHAN BAHRAN 3.2.. Let Y be a Noetherian scheme. Show that any Y -scheme X of finite type is Noetherian. Moreover, if Y is of finite dimension, then so is X. Write f
SPACES OF RATIONAL CURVES IN COMPLETE INTERSECTIONS
 SPACES OF RATIONAL CURVES IN COMPLETE INTERSECTIONS ROYA BEHESHTI AND N. MOHAN KUMAR Abstract. We prove that the space of smooth rational curves of degree e in a general complete intersection of multidegree
SPACES OF RATIONAL CURVES IN COMPLETE INTERSECTIONS ROYA BEHESHTI AND N. MOHAN KUMAR Abstract. We prove that the space of smooth rational curves of degree e in a general complete intersection of multidegree
where m is the maximal ideal of O X,p. Note that m/m 2 is a vector space. Suppose that we are given a morphism
 8. Smoothness and the Zariski tangent space We want to give an algebraic notion of the tangent space. In differential geometry, tangent vectors are equivalence classes of maps of intervals in R into the
8. Smoothness and the Zariski tangent space We want to give an algebraic notion of the tangent space. In differential geometry, tangent vectors are equivalence classes of maps of intervals in R into the
Homogeneous Coordinate Ring
 Students: Kaiserslautern University Algebraic Group June 14, 2013 Outline Quotients in Algebraic Geometry 1 Quotients in Algebraic Geometry 2 3 4 Outline Quotients in Algebraic Geometry 1 Quotients in
Students: Kaiserslautern University Algebraic Group June 14, 2013 Outline Quotients in Algebraic Geometry 1 Quotients in Algebraic Geometry 2 3 4 Outline Quotients in Algebraic Geometry 1 Quotients in
Tropical Elliptic Curves and their j-invariant
 and their j-invariant (joint work with Eric Katz and Hannah Markwig) Elliptic Tropical Thomas Markwig Technische Universität Kaiserslautern 15th February, 2008 Elliptic Tropical The tropical j-invariant
and their j-invariant (joint work with Eric Katz and Hannah Markwig) Elliptic Tropical Thomas Markwig Technische Universität Kaiserslautern 15th February, 2008 Elliptic Tropical The tropical j-invariant
ON THE RANK OF A TROPICAL MATRIX
 ON THE RANK OF A TROPICAL MATRIX MIKE DEVELIN, FRANCISCO SANTOS, AND BERND STURMFELS Abstract. This is a foundational paper in tropical linear algebra, which is linear algebra over the min-plus semiring.
ON THE RANK OF A TROPICAL MATRIX MIKE DEVELIN, FRANCISCO SANTOS, AND BERND STURMFELS Abstract. This is a foundational paper in tropical linear algebra, which is linear algebra over the min-plus semiring.
AN INTRODUCTION TO TORIC SURFACES
 AN INTRODUCTION TO TORIC SURFACES JESSICA SIDMAN 1. An introduction to affine varieties To motivate what is to come we revisit a familiar example from high school algebra from a point of view that allows
AN INTRODUCTION TO TORIC SURFACES JESSICA SIDMAN 1. An introduction to affine varieties To motivate what is to come we revisit a familiar example from high school algebra from a point of view that allows
(1) is an invertible sheaf on X, which is generated by the global sections
 7. Linear systems First a word about the base scheme. We would lie to wor in enough generality to cover the general case. On the other hand, it taes some wor to state properly the general results if one
7. Linear systems First a word about the base scheme. We would lie to wor in enough generality to cover the general case. On the other hand, it taes some wor to state properly the general results if one
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra
 Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
Lecture 1. Toric Varieties: Basics
 Lecture 1. Toric Varieties: Basics Taras Panov Lomonosov Moscow State University Summer School Current Developments in Geometry Novosibirsk, 27 August1 September 2018 Taras Panov (Moscow University) Lecture
Lecture 1. Toric Varieties: Basics Taras Panov Lomonosov Moscow State University Summer School Current Developments in Geometry Novosibirsk, 27 August1 September 2018 Taras Panov (Moscow University) Lecture
Affine Geometry and Discrete Legendre Transform
 Affine Geometry and Discrete Legendre Transform Andrey Novoseltsev April 24, 2008 Abstract The combinatorial duality used in Gross-Siebert approach to mirror symmetry is the discrete Legendre transform
Affine Geometry and Discrete Legendre Transform Andrey Novoseltsev April 24, 2008 Abstract The combinatorial duality used in Gross-Siebert approach to mirror symmetry is the discrete Legendre transform
INTRODUCTION TO TROPICAL ALGEBRAIC GEOMETRY
 INTRODUCTION TO TROPICAL ALGEBRAIC GEOMETRY DIANE MACLAGAN These notes are the lecture notes from my lectures on tropical geometry at the ELGA 2011 school on Algebraic Geometry and Applications in Buenos
INTRODUCTION TO TROPICAL ALGEBRAIC GEOMETRY DIANE MACLAGAN These notes are the lecture notes from my lectures on tropical geometry at the ELGA 2011 school on Algebraic Geometry and Applications in Buenos
Vector bundles in Algebraic Geometry Enrique Arrondo. 1. The notion of vector bundle
 Vector bundles in Algebraic Geometry Enrique Arrondo Notes(* prepared for the First Summer School on Complex Geometry (Villarrica, Chile 7-9 December 2010 1 The notion of vector bundle In affine geometry,
Vector bundles in Algebraic Geometry Enrique Arrondo Notes(* prepared for the First Summer School on Complex Geometry (Villarrica, Chile 7-9 December 2010 1 The notion of vector bundle In affine geometry,
Tropical and nonarchimedean analytic geometry of curves
 Tropical and nonarchimedean analytic geometry of curves Sam Payne August 11, 2011 Joint work with Matt Baker Joe Rabinoff Tropicalization K is a valued field, with valuation ν : K R. X is a subvariety
Tropical and nonarchimedean analytic geometry of curves Sam Payne August 11, 2011 Joint work with Matt Baker Joe Rabinoff Tropicalization K is a valued field, with valuation ν : K R. X is a subvariety
Tropical Constructions and Lifts
 Tropical Constructions and Lifts Hunter Ash August 27, 2014 1 The Algebraic Torus and M Let K denote a field of characteristic zero and K denote the associated multiplicative group. A character on (K )
Tropical Constructions and Lifts Hunter Ash August 27, 2014 1 The Algebraic Torus and M Let K denote a field of characteristic zero and K denote the associated multiplicative group. A character on (K )
EKT of Some Wonderful Compactifications
 EKT of Some Wonderful Compactifications and recent results on Complete Quadrics. (Based on joint works with Soumya Banerjee and Michael Joyce) Mahir Bilen Can April 16, 2016 Mahir Bilen Can EKT of Some
EKT of Some Wonderful Compactifications and recent results on Complete Quadrics. (Based on joint works with Soumya Banerjee and Michael Joyce) Mahir Bilen Can April 16, 2016 Mahir Bilen Can EKT of Some
DEFORMATIONS VIA DIMENSION THEORY
 DEFORMATIONS VIA DIMENSION THEORY BRIAN OSSERMAN Abstract. We show that standard arguments for deformations based on dimension counts can also be applied over a (not necessarily Noetherian) valuation ring
DEFORMATIONS VIA DIMENSION THEORY BRIAN OSSERMAN Abstract. We show that standard arguments for deformations based on dimension counts can also be applied over a (not necessarily Noetherian) valuation ring
Algebraic Varieties. Notes by Mateusz Micha lek for the lecture on April 17, 2018, in the IMPRS Ringvorlesung Introduction to Nonlinear Algebra
 Algebraic Varieties Notes by Mateusz Micha lek for the lecture on April 17, 2018, in the IMPRS Ringvorlesung Introduction to Nonlinear Algebra Algebraic varieties represent solutions of a system of polynomial
Algebraic Varieties Notes by Mateusz Micha lek for the lecture on April 17, 2018, in the IMPRS Ringvorlesung Introduction to Nonlinear Algebra Algebraic varieties represent solutions of a system of polynomial
Tropical Algebraic Geometry 3
 Tropical Algebraic Geometry 3 1 Monomial Maps solutions of binomial systems an illustrative example 2 The Balancing Condition balancing a polyhedral fan the structure theorem 3 The Fundamental Theorem
Tropical Algebraic Geometry 3 1 Monomial Maps solutions of binomial systems an illustrative example 2 The Balancing Condition balancing a polyhedral fan the structure theorem 3 The Fundamental Theorem
Algebraic Geometry. Andreas Gathmann. Class Notes TU Kaiserslautern 2014
 Algebraic Geometry Andreas Gathmann Class Notes TU Kaiserslautern 2014 Contents 0. Introduction......................... 3 1. Affine Varieties........................ 9 2. The Zariski Topology......................
Algebraic Geometry Andreas Gathmann Class Notes TU Kaiserslautern 2014 Contents 0. Introduction......................... 3 1. Affine Varieties........................ 9 2. The Zariski Topology......................
9. Birational Maps and Blowing Up
 72 Andreas Gathmann 9. Birational Maps and Blowing Up In the course of this class we have already seen many examples of varieties that are almost the same in the sense that they contain isomorphic dense
72 Andreas Gathmann 9. Birational Maps and Blowing Up In the course of this class we have already seen many examples of varieties that are almost the same in the sense that they contain isomorphic dense
arxiv:math/ v3 [math.ag] 21 Aug 2005
![arxiv:math/ v3 [math.ag] 21 Aug 2005 arxiv:math/ v3 [math.ag] 21 Aug 2005](/thumbs/93/111591254.jpg) arxiv:math/0412329v3 [math.ag] 21 Aug 2005 COMPACTIFICATIONS OF SUBVARIETIES OF TORI JENIA TEVELEV Abstract. We study compactifications of subvarieties of algebraic tori defined by imposing a sufficiently
arxiv:math/0412329v3 [math.ag] 21 Aug 2005 COMPACTIFICATIONS OF SUBVARIETIES OF TORI JENIA TEVELEV Abstract. We study compactifications of subvarieties of algebraic tori defined by imposing a sufficiently
ELEMENTARY SUBALGEBRAS OF RESTRICTED LIE ALGEBRAS
 ELEMENTARY SUBALGEBRAS OF RESTRICTED LIE ALGEBRAS J. WARNER SUMMARY OF A PAPER BY J. CARLSON, E. FRIEDLANDER, AND J. PEVTSOVA, AND FURTHER OBSERVATIONS 1. The Nullcone and Restricted Nullcone We will need
ELEMENTARY SUBALGEBRAS OF RESTRICTED LIE ALGEBRAS J. WARNER SUMMARY OF A PAPER BY J. CARLSON, E. FRIEDLANDER, AND J. PEVTSOVA, AND FURTHER OBSERVATIONS 1. The Nullcone and Restricted Nullcone We will need
Sections of tropicalization maps (joint work with Walter Gubler and Joe Rabinoff)
 Sections of tropicalization maps (joint work with Walter Gubler and Joe Rabinoff) Annette Werner Goethe Universität Frankfurt am Main AMS Summer Institute in Algebraic Geometry 2015 1 / 32 Sections of
Sections of tropicalization maps (joint work with Walter Gubler and Joe Rabinoff) Annette Werner Goethe Universität Frankfurt am Main AMS Summer Institute in Algebraic Geometry 2015 1 / 32 Sections of
Lifting Tropical Intersections
 Documenta Math. 121 Lifting Tropical Intersections Brian Osserman and Sam Payne Received: August 23, 2011 Revised: December 5, 2012 Communicated by Gavril Farkas Abstract. We show that points in the intersection
Documenta Math. 121 Lifting Tropical Intersections Brian Osserman and Sam Payne Received: August 23, 2011 Revised: December 5, 2012 Communicated by Gavril Farkas Abstract. We show that points in the intersection
M ath. Res. Lett. 15 (2008), no. 3, c International Press 2008 ELIMINATION THEORY FOR TROPICAL VARIETIES. Bernd Sturmfels and Jenia Tevelev
 M ath. Res. Lett. 15 (2008), no. 3, 543 562 c International Press 2008 ELIMINATION THEORY FOR TROPICAL VARIETIES Bernd Sturmfels and Jenia Tevelev Abstract. Tropical algebraic geometry offers new tools
M ath. Res. Lett. 15 (2008), no. 3, 543 562 c International Press 2008 ELIMINATION THEORY FOR TROPICAL VARIETIES Bernd Sturmfels and Jenia Tevelev Abstract. Tropical algebraic geometry offers new tools
COMPLEX VARIETIES AND THE ANALYTIC TOPOLOGY
 COMPLEX VARIETIES AND THE ANALYTIC TOPOLOGY BRIAN OSSERMAN Classical algebraic geometers studied algebraic varieties over the complex numbers. In this setting, they didn t have to worry about the Zariski
COMPLEX VARIETIES AND THE ANALYTIC TOPOLOGY BRIAN OSSERMAN Classical algebraic geometers studied algebraic varieties over the complex numbers. In this setting, they didn t have to worry about the Zariski
A finite universal SAGBI basis for the kernel of a derivation. Osaka Journal of Mathematics. 41(4) P.759-P.792
 Title Author(s) A finite universal SAGBI basis for the kernel of a derivation Kuroda, Shigeru Citation Osaka Journal of Mathematics. 4(4) P.759-P.792 Issue Date 2004-2 Text Version publisher URL https://doi.org/0.890/838
Title Author(s) A finite universal SAGBI basis for the kernel of a derivation Kuroda, Shigeru Citation Osaka Journal of Mathematics. 4(4) P.759-P.792 Issue Date 2004-2 Text Version publisher URL https://doi.org/0.890/838
Discriminants, resultants, and their tropicalization
 Discriminants, resultants, and their tropicalization Course by Bernd Sturmfels - Notes by Silvia Adduci 2006 Contents 1 Introduction 3 2 Newton polytopes and tropical varieties 3 2.1 Polytopes.................................
Discriminants, resultants, and their tropicalization Course by Bernd Sturmfels - Notes by Silvia Adduci 2006 Contents 1 Introduction 3 2 Newton polytopes and tropical varieties 3 2.1 Polytopes.................................
Gröbner Complexes and Tropical Bases
 Gröbner Complexes and Tropical Bases Jan Verschelde University of Illinois at Chicago Department of Mathematics, Statistics, and Computer Science http://www.math.uic.edu/ jan jan@math.uic.edu Graduate
Gröbner Complexes and Tropical Bases Jan Verschelde University of Illinois at Chicago Department of Mathematics, Statistics, and Computer Science http://www.math.uic.edu/ jan jan@math.uic.edu Graduate
GALE DUALITY FOR COMPLETE INTERSECTIONS
 GALE DUALITY FOR COMPLETE INTERSECTIONS Abstract. We show that every complete intersection defined by Laurent polynomials in an algebraic torus is isomorphic to a complete intersection defined by master
GALE DUALITY FOR COMPLETE INTERSECTIONS Abstract. We show that every complete intersection defined by Laurent polynomials in an algebraic torus is isomorphic to a complete intersection defined by master
STEENROD OPERATIONS IN ALGEBRAIC GEOMETRY
 STEENROD OPERATIONS IN ALGEBRAIC GEOMETRY ALEXANDER MERKURJEV 1. Introduction Let p be a prime integer. For a pair of topological spaces A X we write H i (X, A; Z/pZ) for the i-th singular cohomology group
STEENROD OPERATIONS IN ALGEBRAIC GEOMETRY ALEXANDER MERKURJEV 1. Introduction Let p be a prime integer. For a pair of topological spaces A X we write H i (X, A; Z/pZ) for the i-th singular cohomology group
Algorithmic Aspects of Gröbner Fans and Tropical Varieties
 Algorithmic Aspects of Gröbner Fans and Tropical Varieties Anders Nedergaard Jensen Ph.D. Dissertation July 2007 Department of Mathematical Sciences Faculty of Science, University of Aarhus 2 Abstract
Algorithmic Aspects of Gröbner Fans and Tropical Varieties Anders Nedergaard Jensen Ph.D. Dissertation July 2007 Department of Mathematical Sciences Faculty of Science, University of Aarhus 2 Abstract
Introduction to Arithmetic Geometry Fall 2013 Lecture #18 11/07/2013
 18.782 Introduction to Arithmetic Geometry Fall 2013 Lecture #18 11/07/2013 As usual, all the rings we consider are commutative rings with an identity element. 18.1 Regular local rings Consider a local
18.782 Introduction to Arithmetic Geometry Fall 2013 Lecture #18 11/07/2013 As usual, all the rings we consider are commutative rings with an identity element. 18.1 Regular local rings Consider a local
On the Tropicalization of the Hilbert Scheme
 Collect. Math. vv, n (yyyy), 23 c yyyy Universitat de Barcelona DOI.344/collectanea.theDOIsuffix On the Tropicalization of the Hilbert Scheme Daniele Alessandrini Institut de Recherche Mathématique Avancée,
Collect. Math. vv, n (yyyy), 23 c yyyy Universitat de Barcelona DOI.344/collectanea.theDOIsuffix On the Tropicalization of the Hilbert Scheme Daniele Alessandrini Institut de Recherche Mathématique Avancée,
Representations and Linear Actions
 Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
BEZOUT S THEOREM CHRISTIAN KLEVDAL
 BEZOUT S THEOREM CHRISTIAN KLEVDAL A weaker version of Bézout s theorem states that if C, D are projective plane curves of degrees c and d that intersect transversally, then C D = cd. The goal of this
BEZOUT S THEOREM CHRISTIAN KLEVDAL A weaker version of Bézout s theorem states that if C, D are projective plane curves of degrees c and d that intersect transversally, then C D = cd. The goal of this
Logarithmic functional and reciprocity laws
 Contemporary Mathematics Volume 00, 1997 Logarithmic functional and reciprocity laws Askold Khovanskii Abstract. In this paper, we give a short survey of results related to the reciprocity laws over the
Contemporary Mathematics Volume 00, 1997 Logarithmic functional and reciprocity laws Askold Khovanskii Abstract. In this paper, we give a short survey of results related to the reciprocity laws over the
Affine Geometry and the Discrete Legendre Transfrom
 Affine Geometry and the Discrete Legendre Transfrom Andrey Novoseltsev Department of Mathematics University of Washington April 25, 2008 Andrey Novoseltsev (UW) Affine Geometry April 25, 2008 1 / 24 Outline
Affine Geometry and the Discrete Legendre Transfrom Andrey Novoseltsev Department of Mathematics University of Washington April 25, 2008 Andrey Novoseltsev (UW) Affine Geometry April 25, 2008 1 / 24 Outline
Math 418 Algebraic Geometry Notes
 Math 418 Algebraic Geometry Notes 1 Affine Schemes Let R be a commutative ring with 1. Definition 1.1. The prime spectrum of R, denoted Spec(R), is the set of prime ideals of the ring R. Spec(R) = {P R
Math 418 Algebraic Geometry Notes 1 Affine Schemes Let R be a commutative ring with 1. Definition 1.1. The prime spectrum of R, denoted Spec(R), is the set of prime ideals of the ring R. Spec(R) = {P R
Polytopes and Algebraic Geometry. Jesús A. De Loera University of California, Davis
 Polytopes and Algebraic Geometry Jesús A. De Loera University of California, Davis Outline of the talk 1. Four classic results relating polytopes and algebraic geometry: (A) Toric Geometry (B) Viro s Theorem
Polytopes and Algebraic Geometry Jesús A. De Loera University of California, Davis Outline of the talk 1. Four classic results relating polytopes and algebraic geometry: (A) Toric Geometry (B) Viro s Theorem
Math 530 Lecture Notes. Xi Chen
 Math 530 Lecture Notes Xi Chen 632 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca 1991 Mathematics Subject Classification. Primary
Math 530 Lecture Notes Xi Chen 632 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca 1991 Mathematics Subject Classification. Primary
Math 210B. Artin Rees and completions
 Math 210B. Artin Rees and completions 1. Definitions and an example Let A be a ring, I an ideal, and M an A-module. In class we defined the I-adic completion of M to be M = lim M/I n M. We will soon show
Math 210B. Artin Rees and completions 1. Definitions and an example Let A be a ring, I an ideal, and M an A-module. In class we defined the I-adic completion of M to be M = lim M/I n M. We will soon show
ADVANCED TOPICS IN ALGEBRAIC GEOMETRY
 ADVANCED TOPICS IN ALGEBRAIC GEOMETRY DAVID WHITE Outline of talk: My goal is to introduce a few more advanced topics in algebraic geometry but not to go into too much detail. This will be a survey of
ADVANCED TOPICS IN ALGEBRAIC GEOMETRY DAVID WHITE Outline of talk: My goal is to introduce a few more advanced topics in algebraic geometry but not to go into too much detail. This will be a survey of
THE CAPORASO-HARRIS FORMULA AND PLANE RELATIVE GROMOV-WITTEN INVARIANTS IN TROPICAL GEOMETRY
 THE CAPORASO-HARRIS FORMULA AND PLANE RELATIVE GROMOV-WITTEN INVARIANTS IN TROPICAL GEOMETRY ANDREAS GATHMANN AND HANNAH MARKWIG Abstract. Some years ago Caporaso and Harris have found a nice way to compute
THE CAPORASO-HARRIS FORMULA AND PLANE RELATIVE GROMOV-WITTEN INVARIANTS IN TROPICAL GEOMETRY ANDREAS GATHMANN AND HANNAH MARKWIG Abstract. Some years ago Caporaso and Harris have found a nice way to compute
Projective Varieties. Chapter Projective Space and Algebraic Sets
 Chapter 1 Projective Varieties 1.1 Projective Space and Algebraic Sets 1.1.1 Definition. Consider A n+1 = A n+1 (k). The set of all lines in A n+1 passing through the origin 0 = (0,..., 0) is called the
Chapter 1 Projective Varieties 1.1 Projective Space and Algebraic Sets 1.1.1 Definition. Consider A n+1 = A n+1 (k). The set of all lines in A n+1 passing through the origin 0 = (0,..., 0) is called the
Summer Algebraic Geometry Seminar
 Summer Algebraic Geometry Seminar Lectures by Bart Snapp About This Document These lectures are based on Chapters 1 and 2 of An Invitation to Algebraic Geometry by Karen Smith et al. 1 Affine Varieties
Summer Algebraic Geometry Seminar Lectures by Bart Snapp About This Document These lectures are based on Chapters 1 and 2 of An Invitation to Algebraic Geometry by Karen Smith et al. 1 Affine Varieties
Rings and groups. Ya. Sysak
 Rings and groups. Ya. Sysak 1 Noetherian rings Let R be a ring. A (right) R -module M is called noetherian if it satisfies the maximum condition for its submodules. In other words, if M 1... M i M i+1...
Rings and groups. Ya. Sysak 1 Noetherian rings Let R be a ring. A (right) R -module M is called noetherian if it satisfies the maximum condition for its submodules. In other words, if M 1... M i M i+1...
div(f ) = D and deg(d) = deg(f ) = d i deg(f i ) (compare this with the definitions for smooth curves). Let:
 Algebraic Curves/Fall 015 Aaron Bertram 4. Projective Plane Curves are hypersurfaces in the plane CP. When nonsingular, they are Riemann surfaces, but we will also consider plane curves with singularities.
Algebraic Curves/Fall 015 Aaron Bertram 4. Projective Plane Curves are hypersurfaces in the plane CP. When nonsingular, they are Riemann surfaces, but we will also consider plane curves with singularities.
Definition 1.1. We call X a tropical compactification if Ψ is faithfully flat and X is proper. A term tropical is explained in Section 2.
 COMPACTIFICATIONS OF SUBVARIETIES OF TORI By JENIA TEVELEV Abstract. We study compactifications of subvarieties of algebraic tori defined by imposing a sufficiently fine polyhedral structure on their non-archimedean
COMPACTIFICATIONS OF SUBVARIETIES OF TORI By JENIA TEVELEV Abstract. We study compactifications of subvarieties of algebraic tori defined by imposing a sufficiently fine polyhedral structure on their non-archimedean
10. Smooth Varieties. 82 Andreas Gathmann
 82 Andreas Gathmann 10. Smooth Varieties Let a be a point on a variety X. In the last chapter we have introduced the tangent cone C a X as a way to study X locally around a (see Construction 9.20). It
82 Andreas Gathmann 10. Smooth Varieties Let a be a point on a variety X. In the last chapter we have introduced the tangent cone C a X as a way to study X locally around a (see Construction 9.20). It
Combinatorics for algebraic geometers
 Combinatorics for algebraic geometers Calculations in enumerative geometry Maria Monks March 17, 214 Motivation Enumerative geometry In the late 18 s, Hermann Schubert investigated problems in what is
Combinatorics for algebraic geometers Calculations in enumerative geometry Maria Monks March 17, 214 Motivation Enumerative geometry In the late 18 s, Hermann Schubert investigated problems in what is
Algebraic Geometry Spring 2009
 MIT OpenCourseWare http://ocw.mit.edu 18.726 Algebraic Geometry Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.726: Algebraic Geometry
MIT OpenCourseWare http://ocw.mit.edu 18.726 Algebraic Geometry Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.726: Algebraic Geometry
CHAPTER 0 PRELIMINARY MATERIAL. Paul Vojta. University of California, Berkeley. 18 February 1998
 CHAPTER 0 PRELIMINARY MATERIAL Paul Vojta University of California, Berkeley 18 February 1998 This chapter gives some preliminary material on number theory and algebraic geometry. Section 1 gives basic
CHAPTER 0 PRELIMINARY MATERIAL Paul Vojta University of California, Berkeley 18 February 1998 This chapter gives some preliminary material on number theory and algebraic geometry. Section 1 gives basic
10. Noether Normalization and Hilbert s Nullstellensatz
 10. Noether Normalization and Hilbert s Nullstellensatz 91 10. Noether Normalization and Hilbert s Nullstellensatz In the last chapter we have gained much understanding for integral and finite ring extensions.
10. Noether Normalization and Hilbert s Nullstellensatz 91 10. Noether Normalization and Hilbert s Nullstellensatz In the last chapter we have gained much understanding for integral and finite ring extensions.
APPENDIX 3: AN OVERVIEW OF CHOW GROUPS
 APPENDIX 3: AN OVERVIEW OF CHOW GROUPS We review in this appendix some basic definitions and results that we need about Chow groups. For details and proofs we refer to [Ful98]. In particular, we discuss
APPENDIX 3: AN OVERVIEW OF CHOW GROUPS We review in this appendix some basic definitions and results that we need about Chow groups. For details and proofs we refer to [Ful98]. In particular, we discuss
ABSTRACT NONSINGULAR CURVES
 ABSTRACT NONSINGULAR CURVES Affine Varieties Notation. Let k be a field, such as the rational numbers Q or the complex numbers C. We call affine n-space the collection A n k of points P = a 1, a,..., a
ABSTRACT NONSINGULAR CURVES Affine Varieties Notation. Let k be a field, such as the rational numbers Q or the complex numbers C. We call affine n-space the collection A n k of points P = a 1, a,..., a
Math 249B. Nilpotence of connected solvable groups
 Math 249B. Nilpotence of connected solvable groups 1. Motivation and examples In abstract group theory, the descending central series {C i (G)} of a group G is defined recursively by C 0 (G) = G and C
Math 249B. Nilpotence of connected solvable groups 1. Motivation and examples In abstract group theory, the descending central series {C i (G)} of a group G is defined recursively by C 0 (G) = G and C
Toroidal Embeddings and Desingularization
 California State University, San Bernardino CSUSB ScholarWorks Electronic Theses, Projects, and Dissertations Office of Graduate Studies 6-2018 Toroidal Embeddings and Desingularization LEON NGUYEN 003663425@coyote.csusb.edu
California State University, San Bernardino CSUSB ScholarWorks Electronic Theses, Projects, and Dissertations Office of Graduate Studies 6-2018 Toroidal Embeddings and Desingularization LEON NGUYEN 003663425@coyote.csusb.edu
Chapter 1. Preliminaries
 Introduction This dissertation is a reading of chapter 4 in part I of the book : Integer and Combinatorial Optimization by George L. Nemhauser & Laurence A. Wolsey. The chapter elaborates links between
Introduction This dissertation is a reading of chapter 4 in part I of the book : Integer and Combinatorial Optimization by George L. Nemhauser & Laurence A. Wolsey. The chapter elaborates links between
Spherical Tropicalization
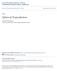 University of Massachusetts - Amherst ScholarWorks@UMass Amherst Doctoral Dissertations May 2014 - current Dissertations and Theses 2016 Spherical Tropicalization Anastasios Vogiannou University of Massachusetts
University of Massachusetts - Amherst ScholarWorks@UMass Amherst Doctoral Dissertations May 2014 - current Dissertations and Theses 2016 Spherical Tropicalization Anastasios Vogiannou University of Massachusetts
Combinatorics and geometry of E 7
 Combinatorics and geometry of E 7 Steven Sam University of California, Berkeley September 19, 2012 1/24 Outline Macdonald representations Vinberg representations Root system Weyl group 7 points in P 2
Combinatorics and geometry of E 7 Steven Sam University of California, Berkeley September 19, 2012 1/24 Outline Macdonald representations Vinberg representations Root system Weyl group 7 points in P 2
Dissimilarity maps on trees and the representation theory of GL n (C)
 Dissimilarity maps on trees and the representation theory of GL n (C) Christopher Manon Department of Mathematics University of California, Berkeley Berkeley, California, U.S.A. chris.manon@math.berkeley.edu
Dissimilarity maps on trees and the representation theory of GL n (C) Christopher Manon Department of Mathematics University of California, Berkeley Berkeley, California, U.S.A. chris.manon@math.berkeley.edu
Lecture I: Introduction to Tropical Geometry David Speyer
 Lecture I: Introduction to Tropical Geometry David Speyer The field of Puiseux series C[[t]] is the ring of formal power series a 0 + a 1 t + and C((t)) is the field of formal Laurent series: a N t N +
Lecture I: Introduction to Tropical Geometry David Speyer The field of Puiseux series C[[t]] is the ring of formal power series a 0 + a 1 t + and C((t)) is the field of formal Laurent series: a N t N +
FILTERED RINGS AND MODULES. GRADINGS AND COMPLETIONS.
 FILTERED RINGS AND MODULES. GRADINGS AND COMPLETIONS. Let A be a ring, for simplicity assumed commutative. A filtering, or filtration, of an A module M means a descending sequence of submodules M = M 0
FILTERED RINGS AND MODULES. GRADINGS AND COMPLETIONS. Let A be a ring, for simplicity assumed commutative. A filtering, or filtration, of an A module M means a descending sequence of submodules M = M 0
1 Notations and Statement of the Main Results
 An introduction to algebraic fundamental groups 1 Notations and Statement of the Main Results Throughout the talk, all schemes are locally Noetherian. All maps are of locally finite type. There two main
An introduction to algebraic fundamental groups 1 Notations and Statement of the Main Results Throughout the talk, all schemes are locally Noetherian. All maps are of locally finite type. There two main
H(G(Q p )//G(Z p )) = C c (SL n (Z p )\ SL n (Q p )/ SL n (Z p )).
 92 19. Perverse sheaves on the affine Grassmannian 19.1. Spherical Hecke algebra. The Hecke algebra H(G(Q p )//G(Z p )) resp. H(G(F q ((T ))//G(F q [[T ]])) etc. of locally constant compactly supported
92 19. Perverse sheaves on the affine Grassmannian 19.1. Spherical Hecke algebra. The Hecke algebra H(G(Q p )//G(Z p )) resp. H(G(F q ((T ))//G(F q [[T ]])) etc. of locally constant compactly supported
Math 249B. Geometric Bruhat decomposition
 Math 249B. Geometric Bruhat decomposition 1. Introduction Let (G, T ) be a split connected reductive group over a field k, and Φ = Φ(G, T ). Fix a positive system of roots Φ Φ, and let B be the unique
Math 249B. Geometric Bruhat decomposition 1. Introduction Let (G, T ) be a split connected reductive group over a field k, and Φ = Φ(G, T ). Fix a positive system of roots Φ Φ, and let B be the unique
Noetherian property of infinite EI categories
 Noetherian property of infinite EI categories Wee Liang Gan and Liping Li Abstract. It is known that finitely generated FI-modules over a field of characteristic 0 are Noetherian. We generalize this result
Noetherian property of infinite EI categories Wee Liang Gan and Liping Li Abstract. It is known that finitely generated FI-modules over a field of characteristic 0 are Noetherian. We generalize this result
David Eklund. May 12, 2017
 KTH Stockholm May 12, 2017 1 / 44 Isolated roots of polynomial systems Let f 1,..., f n C[x 0,..., x n ] be homogeneous and consider the subscheme X P n defined by the ideal (f 1,..., f n ). 2 / 44 Isolated
KTH Stockholm May 12, 2017 1 / 44 Isolated roots of polynomial systems Let f 1,..., f n C[x 0,..., x n ] be homogeneous and consider the subscheme X P n defined by the ideal (f 1,..., f n ). 2 / 44 Isolated
MODULI SPACES OF CURVES
 MODULI SPACES OF CURVES SCOTT NOLLET Abstract. My goal is to introduce vocabulary and present examples that will help graduate students to better follow lectures at TAGS 2018. Assuming some background
MODULI SPACES OF CURVES SCOTT NOLLET Abstract. My goal is to introduce vocabulary and present examples that will help graduate students to better follow lectures at TAGS 2018. Assuming some background
A tropical approach to secant dimensions
 A tropical approach to secant dimensions Jan Draisma Madrid, 30 March 2007 1/16 Typical example: polynomial interpolation in two variables Set up: d N p 1,..., p k general points in C 2 codim{f C[x, y]
A tropical approach to secant dimensions Jan Draisma Madrid, 30 March 2007 1/16 Typical example: polynomial interpolation in two variables Set up: d N p 1,..., p k general points in C 2 codim{f C[x, y]
We can choose generators of this k-algebra: s i H 0 (X, L r i. H 0 (X, L mr )
 MODULI PROBLEMS AND GEOMETRIC INVARIANT THEORY 43 5.3. Linearisations. An abstract projective scheme X does not come with a pre-specified embedding in a projective space. However, an ample line bundle
MODULI PROBLEMS AND GEOMETRIC INVARIANT THEORY 43 5.3. Linearisations. An abstract projective scheme X does not come with a pre-specified embedding in a projective space. However, an ample line bundle
GEOMETRIC STRUCTURES OF SEMISIMPLE LIE ALGEBRAS
 GEOMETRIC STRUCTURES OF SEMISIMPLE LIE ALGEBRAS ANA BALIBANU DISCUSSED WITH PROFESSOR VICTOR GINZBURG 1. Introduction The aim of this paper is to explore the geometry of a Lie algebra g through the action
GEOMETRIC STRUCTURES OF SEMISIMPLE LIE ALGEBRAS ANA BALIBANU DISCUSSED WITH PROFESSOR VICTOR GINZBURG 1. Introduction The aim of this paper is to explore the geometry of a Lie algebra g through the action
TORIC WEAK FANO VARIETIES ASSOCIATED TO BUILDING SETS
 TORIC WEAK FANO VARIETIES ASSOCIATED TO BUILDING SETS YUSUKE SUYAMA Abstract. We give a necessary and sufficient condition for the nonsingular projective toric variety associated to a building set to be
TORIC WEAK FANO VARIETIES ASSOCIATED TO BUILDING SETS YUSUKE SUYAMA Abstract. We give a necessary and sufficient condition for the nonsingular projective toric variety associated to a building set to be
Introduction to toric geometry
 Introduction to toric geometry Ugo Bruzzo Scuola Internazionale Superiore di Studi Avanzati and Istituto Nazionale di Fisica Nucleare Trieste ii Instructions for the reader These are work-in-progress notes
Introduction to toric geometry Ugo Bruzzo Scuola Internazionale Superiore di Studi Avanzati and Istituto Nazionale di Fisica Nucleare Trieste ii Instructions for the reader These are work-in-progress notes
On the Parameters of r-dimensional Toric Codes
 On the Parameters of r-dimensional Toric Codes Diego Ruano Abstract From a rational convex polytope of dimension r 2 J.P. Hansen constructed an error correcting code of length n = (q 1) r over the finite
On the Parameters of r-dimensional Toric Codes Diego Ruano Abstract From a rational convex polytope of dimension r 2 J.P. Hansen constructed an error correcting code of length n = (q 1) r over the finite
NONSINGULAR CURVES BRIAN OSSERMAN
 NONSINGULAR CURVES BRIAN OSSERMAN The primary goal of this note is to prove that every abstract nonsingular curve can be realized as an open subset of a (unique) nonsingular projective curve. Note that
NONSINGULAR CURVES BRIAN OSSERMAN The primary goal of this note is to prove that every abstract nonsingular curve can be realized as an open subset of a (unique) nonsingular projective curve. Note that
Algebraic Geometry (Math 6130)
 Algebraic Geometry (Math 6130) Utah/Fall 2016. 2. Projective Varieties. Classically, projective space was obtained by adding points at infinity to n. Here we start with projective space and remove a hyperplane,
Algebraic Geometry (Math 6130) Utah/Fall 2016. 2. Projective Varieties. Classically, projective space was obtained by adding points at infinity to n. Here we start with projective space and remove a hyperplane,
Infinite-Dimensional Triangularization
 Infinite-Dimensional Triangularization Zachary Mesyan March 11, 2018 Abstract The goal of this paper is to generalize the theory of triangularizing matrices to linear transformations of an arbitrary vector
Infinite-Dimensional Triangularization Zachary Mesyan March 11, 2018 Abstract The goal of this paper is to generalize the theory of triangularizing matrices to linear transformations of an arbitrary vector
11. Dimension. 96 Andreas Gathmann
 96 Andreas Gathmann 11. Dimension We have already met several situations in this course in which it seemed to be desirable to have a notion of dimension (of a variety, or more generally of a ring): for
96 Andreas Gathmann 11. Dimension We have already met several situations in this course in which it seemed to be desirable to have a notion of dimension (of a variety, or more generally of a ring): for
Combinatorial Aspects of Tropical Geometry and its interactions with phylogenetics
 Combinatorial Aspects of Tropical Geometry and its interactions with phylogenetics María Angélica Cueto Department of Mathematics Columbia University Rabadan Lab Metting Columbia University College of
Combinatorial Aspects of Tropical Geometry and its interactions with phylogenetics María Angélica Cueto Department of Mathematics Columbia University Rabadan Lab Metting Columbia University College of
Parameterizing orbits in flag varieties
 Parameterizing orbits in flag varieties W. Ethan Duckworth April 2008 Abstract In this document we parameterize the orbits of certain groups acting on partial flag varieties with finitely many orbits.
Parameterizing orbits in flag varieties W. Ethan Duckworth April 2008 Abstract In this document we parameterize the orbits of certain groups acting on partial flag varieties with finitely many orbits.
Hodge theory for combinatorial geometries
 Hodge theory for combinatorial geometries June Huh with Karim Adiprasito and Eric Katz June Huh 1 / 48 Three fundamental ideas: June Huh 2 / 48 Three fundamental ideas: The idea of Bernd Sturmfels that
Hodge theory for combinatorial geometries June Huh with Karim Adiprasito and Eric Katz June Huh 1 / 48 Three fundamental ideas: June Huh 2 / 48 Three fundamental ideas: The idea of Bernd Sturmfels that
4. Images of Varieties Given a morphism f : X Y of quasi-projective varieties, a basic question might be to ask what is the image of a closed subset
 4. Images of Varieties Given a morphism f : X Y of quasi-projective varieties, a basic question might be to ask what is the image of a closed subset Z X. Replacing X by Z we might as well assume that Z
4. Images of Varieties Given a morphism f : X Y of quasi-projective varieties, a basic question might be to ask what is the image of a closed subset Z X. Replacing X by Z we might as well assume that Z
Toric Varieties. Madeline Brandt. April 26, 2017
 Toric Varieties Madeline Brandt April 26, 2017 Last week we saw that we can define normal toric varieties from the data of a fan in a lattice. Today I will review this idea, and also explain how they can
Toric Varieties Madeline Brandt April 26, 2017 Last week we saw that we can define normal toric varieties from the data of a fan in a lattice. Today I will review this idea, and also explain how they can
(iv) Whitney s condition B. Suppose S β S α. If two sequences (a k ) S α and (b k ) S β both converge to the same x S β then lim.
 0.1. Stratified spaces. References are [7], [6], [3]. Singular spaces are naturally associated to many important mathematical objects (for example in representation theory). We are essentially interested
0.1. Stratified spaces. References are [7], [6], [3]. Singular spaces are naturally associated to many important mathematical objects (for example in representation theory). We are essentially interested
B 1 = {B(x, r) x = (x 1, x 2 ) H, 0 < r < x 2 }. (a) Show that B = B 1 B 2 is a basis for a topology on X.
 Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
9. Integral Ring Extensions
 80 Andreas Gathmann 9. Integral ing Extensions In this chapter we want to discuss a concept in commutative algebra that has its original motivation in algebra, but turns out to have surprisingly many applications
80 Andreas Gathmann 9. Integral ing Extensions In this chapter we want to discuss a concept in commutative algebra that has its original motivation in algebra, but turns out to have surprisingly many applications
MATH32062 Notes. 1 Affine algebraic varieties. 1.1 Definition of affine algebraic varieties
 MATH32062 Notes 1 Affine algebraic varieties 1.1 Definition of affine algebraic varieties We want to define an algebraic variety as the solution set of a collection of polynomial equations, or equivalently,
MATH32062 Notes 1 Affine algebraic varieties 1.1 Definition of affine algebraic varieties We want to define an algebraic variety as the solution set of a collection of polynomial equations, or equivalently,
PROJECTIVIZED RANK TWO TORIC VECTOR BUNDLES ARE MORI DREAM SPACES
 PROJECTIVIZED RANK TWO TORIC VECTOR BUNDLES ARE MORI DREAM SPACES JOSÉ LUIS GONZÁLEZ Abstract. We prove that the Cox ring of the projectivization PE of a rank two toric vector bundle E, over a toric variety
PROJECTIVIZED RANK TWO TORIC VECTOR BUNDLES ARE MORI DREAM SPACES JOSÉ LUIS GONZÁLEZ Abstract. We prove that the Cox ring of the projectivization PE of a rank two toric vector bundle E, over a toric variety
Formal power series rings, inverse limits, and I-adic completions of rings
 Formal power series rings, inverse limits, and I-adic completions of rings Formal semigroup rings and formal power series rings We next want to explore the notion of a (formal) power series ring in finitely
Formal power series rings, inverse limits, and I-adic completions of rings Formal semigroup rings and formal power series rings We next want to explore the notion of a (formal) power series ring in finitely
Toric Geometry. An introduction to toric varieties with an outlook towards toric singularity theory
 Toric Geometry An introduction to toric varieties with an outlook towards toric singularity theory Thesis project for the research track of the Master Mathematics Academic year 2014/2015 Author: Geert
Toric Geometry An introduction to toric varieties with an outlook towards toric singularity theory Thesis project for the research track of the Master Mathematics Academic year 2014/2015 Author: Geert
Math 121 Homework 4: Notes on Selected Problems
 Math 121 Homework 4: Notes on Selected Problems 11.2.9. If W is a subspace of the vector space V stable under the linear transformation (i.e., (W ) W ), show that induces linear transformations W on W
Math 121 Homework 4: Notes on Selected Problems 11.2.9. If W is a subspace of the vector space V stable under the linear transformation (i.e., (W ) W ), show that induces linear transformations W on W
STABLE BASE LOCUS DECOMPOSITIONS OF KONTSEVICH MODULI SPACES
 STABLE BASE LOCUS DECOMPOSITIONS OF KONTSEVICH MODULI SPACES DAWEI CHEN AND IZZET COSKUN Contents 1. Introduction 1 2. Preliminary definitions and background 3 3. Degree two maps to Grassmannians 4 4.
STABLE BASE LOCUS DECOMPOSITIONS OF KONTSEVICH MODULI SPACES DAWEI CHEN AND IZZET COSKUN Contents 1. Introduction 1 2. Preliminary definitions and background 3 3. Degree two maps to Grassmannians 4 4.
