K-QUASICONVEXITY REDUCES TO QUASICONVEXITY
|
|
|
- Candace York
- 5 years ago
- Views:
Transcription
1 K-UASICONVEXITY REDUCES TO UASICONVEXITY F. CAGNETTI Abstact. The elaton between quasconvexty and -quasconvexty,, s nvestgated. It s shown that evey smooth stctly -quasconvex ntegand wth p-gowth at nfnty, p > 1, s the estcton to -th ode symmetc tensos of a quasconvex functon wth the same gowth. When the smoothness condton s dopped, t s possble to pove an appoxmaton esult. As a consequence, lowe semcontnuty esults fo -th ode vaatonal poblems ae deduced as coollaes of well-nown fst ode theoems. Ths genealzes a pevous wo by Dal Maso, Fonseca, Leon and Mon, n whch the case = was teated. Keywods: quasconvexty, hghe ode vaatonal poblems. 1. Intoducton We consde hghe ode vaatonal poblems, n whch the enegy functonal has the expesson u fx, u, u,..., u)dx, 1.1) Ω whee Ω R N s open and bounded, N, ae ntege, and f s a scala functon satsfyng sutable gowth condtons. Although ou teatment can be extended to the vectoal case, to eep the fomulaton as smple as possble we wll teat the case of scala functons u : Ω R. Functonals of ths type appea n the study of elastc mateals of gade see 3), n the theoy of second ode stuctued defomatons see 1), n the Blae-Zsseman model fo mage segmentaton n compute vson see 5), n gadent theoes of phase tanstons wthn elastcty egmes see 7, 15, 0), and n the descpton of equlba of mcomagnetc mateals see 9, 6, 0, ). In ode to study lowe semcontnuty of functonals of ths type, Meyes ntoduced n 18 the noton of -quasconvexty see also 3 and 13), extendng the defnton of quasconvexty gven by Moey n 19. tmes {}}{ Let E R N... R N = R N be the set of -th ode tensos of R N that ae symmetc wth espect to all pemutatons of ndces. In patcula, E concdes wth the set of the symmetc N N matces. A functon f L 1 loc E ) s sad to be -quasconvex f fa + φ) fa) dx 0 fo evey A E and evey φ Cc ), whee = 0, 1) N s the open unt cube n R N, and Cc ) s the set of functons of class C wth compact suppot n. We ecall that a functon F L 1 loc RN ) s sad to be 1-quasconvex o smply quasconvex) f FA + ϕ) FA) dx 0 fo evey A R N and evey ϕ C 1 c; R N 1 ). In 18, the autho poved that -quasconvexty s a necessay and suffcent condton fo sequental lowe semcontnuty of 1.1) wth espect to wea convegence n the Sobolev space W,p Ω), unde appopate p-gowth and contnuty condtons on the ntegand f. Ths esult has been late extended to the case whee f s a Caathéodoy ntegand by Fusco see 13) and by Gudoz and Poggoln see 1), fo p = 1 and p > 1 espectvely. 1
2 F. CAGNETTI The am of ths pape s to nvestgate the elaton between -quasconvexty and quasconvexty. When = ths poblem has been studed by Dal Maso, Fonseca, Leon and Mon. In 8, they pove that evey stctly -quasconvex functon see condton a) below) of class C 1, whose gadent s locally Lpschtz contnuous, s the estcton to symmetc matces of a 1-quasconvex functon. We extend hee ths esult to the case >. Theoem 1.1. Let N,. Let f C 1 E ), and let 1 < p <, µ 0, L > 0, ν > 0. Assume that a) stct -quasconvexty) fa + φ) fa) dx ν fo evey A E and evey φ C c ); b) Lpschtz condton fo gadents) fo evey A, B E. µ + A + p φ ) φ dx fa + B) fa) L µ + A p + B ) B 1.) Then thee exsts a 1 quasconvex functon F : R N R such that fo a sutable constant c f dependng on f. FA) = fa) A E, 1.3) FA) c f 1 + A p ) A R N, 1.) Notce that the above condtons a) and b) togethe mply L ν see Poposton.8). When p, we also gve an explct expesson fo the functon F see fomula 3.9)). The poof of Theoem 1.1 see Secton 3) s obtaned by teatng 1 tmes a efned veson of 8, Theoem 1 see Lemma 3.1 fo the case 1 < p < and Lemma 3. fo the case p ). It s not clea whethe Theoem 1.1 stll holds tue by weaenng condton 1.). Howeve, f we substtute 1.) wth the mlde see Poposton.9) condton 1.5), we obtan an appoxmaton esult fo the functon f. Moe pecsely, we show that a stctly -quasconvex functon wth p-gowth at nfnty can be obtaned as pontwse lmt of a sequence of 1-quasconvex functons wth the same gowth see 8, Theoem fo the case = ). Theoem 1.. Let N,. Let 1 < p <, µ 0, ν > 0, M > 0, and let f : E R be a measuable functon such that a) stct -quasconvexty) fa + φ) fa) dx ν fo evey A E and evey φ C c ); b) p-gowth condton) fo evey A E. µ + A + p φ ) φ dx fa) M1 + A p ) 1.5) Then thee exsts an nceasng sequence {F } N of 1 quasconvex functons F : R N R, such that lm F A) = fa) A E, 1.6) + F A) M 1 + A p ) A R N, N, 1.7) whee {M } N s a sequence of postve constants dependng only on and on the constants p, µ, ν, M, but not on the specfc functon f.
3 K-UASICONVEXITY REDUCES TO UASICONVEXITY 3 To show ths, we use the popety that evey -quasconvex functon wth p-gowth s locally Lpschtz. We gve hee a poof of ths fact see Poposton.7), that was aleady nown n the cases = 1 see 17) and = see 1). Thans to Theoem 1., the study of lowe semcontnuty of 1.1) educes to a fst ode poblem. Thus, when f s a -quasconvex nomal ntegand see assumpton a) below) we can pove the followng esult see 8, Theoem 3 fo the case = ). Hee we use the notaton and E 1 := R N, E 1 := R E 1... E 1, SBH ) Ω) := {u W 1,1 Ω) : 1 u SBV Ω; E 1 )}. Theoem 1.3. Let N,. Let Ω R N be a bounded open set and let f : Ω E 1 E 0, + ) be a measuable functon such that: a) fx,, ) s lowe semcontnuous on E 1 E fo L N -a.e. x Ω; b) fx,v, ) s -quasconvex on E fo L N -a.e. x Ω and evey v E 1 ; c) thee exst a locally bounded functon a : Ω E 1 0, + ) and a constant p > 1 such that 0 fx,v, A) ax,v)1 + A p ) fo L N -a.e. x Ω and evey v, A) E 1 E. Then fx, u, u,..., u)dx lmnf fx, u j, u j,..., u j )dx Ω j + Ω fo evey u SBH ) Ω) and any sequence {u j } SBH ) Ω) convegng to u n W 1,1 Ω) and such that sup u j L p Ω) + θ 1 u j )dh N 1) < +, j S 1 u j) whee θ : 0, + ) 0, + ) s a concave, nondeceasng functon such that θt) lm = +, t 0 + t u s the densty of the absolutely contnuous pat of D 1 u ) wth espect to the N-dmensonal Lebesgue measue, and 1 u j denotes the jump of 1 u j on the jump set S 1 u j ). Ths extends to the -th ode settng a lowe semcontnuty popety of 1-quasconvex functons n SBV Ω; R d ) due to Amboso see ) and late genealzed by Kstensen see 16), and a lowe semcontnuty theoem fo -quasconvex ntegands n SBHΩ; R d ) poven by Dal Maso, Fonseca, Leon and Mon see 8). As a coollay, we ecove 1, Theoem 7.1. Coollay 1.. Let Ω, f, and p be as n Theoem 1.3. Then fx, u, u,..., u)dx lmnf fx, u j, u j,..., u j )dx j Ω fo evey u W,p Ω) and any sequence {u j } W,p Ω) wealy convegng to u n W,p Ω). We ema that n 1 Gudoz and Poggoln eque the functon f to be locally Lpschtz contnuous wth espect to the last vaable. As aleady mentoned, we do not need ths hypothess, snce we pove hee that ths s a dect consequence of -quasconvexty and p-gowth. Fnally, we menton that t emans stll an open poblem to pove the analogue of Theoem 1.3 fo the case p = 1, even when =, unless vey specal functons f ae consdeed see 11). Ths wll pobably eque new and ognal deas. Indeed, we thn that fo p = 1 the fundamental Kon-type nequaltes see Lemma.13 and Lemma.1) used n the poofs of Theoem 1.1 and Theoem 1. fal, although we do not have any explct counteexample. The plan of the pape s as follows. In Secton we gve the settng of the poblem. Secton 3 contans the poof of Theoem 1.1, whle Theoem 1. and Theoem 1.3 ae poved n Secton Ω
4 F. CAGNETTI. Fnally, some auxlay esults that ae extensvely used n the pape can be found n the Appendx.. Settng Thoughout the pape N and ae fxed ntege numbes, wth N,. Fo ths eason, we wll often omt to ndcate the explct dependence on N and. Also, Ω R N s an open bounded set, and = 0, 1) N denotes the open unt cube of R N. Snce N and ae fxed, Defnton.1. Let A R N. We say that A s a -th ode tenso n R N. The components of a tenso A R N wll be denoted wth the symbols A ,..., = 1,...,N. Moeove, the scala poduct of two tensos A, B R N s gven by A B := N 1,..., =1 A 1... B Accodngly, the nom of a -th ode tenso A R N s A := N A ,..., =1 Let now s {1,..., 1} be fxed. Fo any ζ C s ; R N s ), we can egad the s-th ode gadent s ζ of ζ as a -th ode tenso n R N, by settng s s ζ 1... ζ) 1... := s x s+1... x 1. 1,..., = 1...,N. Notce also that s ζ s symmetc wth espect to evey pemutaton of the last s ndces. To tae account of ths popety, we ntoduce some addtonal notaton. Defnton.. Let A R N be a -th ode tenso n R N, and let j, {1,..., }. The j, )-tanspose of A s the element A T j of R N such that assumng, fo nstance, j ) We then set A T j )1... = A 1... j 1 j j ,..., = 1,...,N. E N s := {A R N : A = A T j fo evey, j = s + 1,...,}. In patcula, we wll mae the dentfcaton E N 1 = R N. In ths way, fo evey ζ C s ; R N s ) we have s ζ E N s. To nclude the case s =, we defne E 1 := {A RN : A = A T j fo evey, j = 1,...,}. Vey often we wll smply wte E nstead of E 1. Hence, we have that φ E fo evey φ C ), usng the notaton φ φ) 1... := x 1... x 1,..., = 1...,N. We ae now gong to defne the symmetc pat of an element of E N s.
5 K-UASICONVEXITY REDUCES TO UASICONVEXITY 5 Defnton.3. The symmetzaton opeato S s+1 : E N s S s+1 A := 1 s + 1 = s A T s = s A + AT s A T s s + 1 We wll say that S s+1 A s the symmetc pat of A. E N s 1 s defned by fo evey A E N s. The subscpt s+1 denotes the fact that the tenso S s+1 A s symmetc n the last s+1 entes. Defnton.. Accodngly, we defne the antsymmetc pat of a tenso A E N s tenso A s+1 A E N s gven by We wll use the notaton A s+1 A := A S s+1 A = s sa AT s A T s s + 1 ). as the A s+1 E N s := {A s+1 A : A E N s } E N s. Next poposton genealzes the well-nown fact that symmetc and antsymmetc matces defne othogonal spaces. Fo the convenence of the eade, the poof s n the Appendx. Poposton.5. Thee holds A B = 0 fo evey A E N s 1 We gve now the defnton of hghe ode) quasconvexty. and fo evey B A s+1 E N s. Defnton.6. Let j {1,...,}. A functon f L 1 loc EN j ) s sad to be j-quasconvex f fa + j φ) fa) dx 0 fo evey A E N j and fo evey φ C j c ; RN j ). It s vey well-nown that evey convex functon s locally Lpschtz. Ths popety stll holds tue fo j-quasconvex functons wth p-gowth. We gve hee a poof of ths fact, that s n geneal explctly stated only fo the case j = see 1). Poposton.7. Let j {,..., }, and let f L 1 loc EN j ) be j-quasconvex. Assume, n addton, that fa) M1 + A p ) fo evey A E N j,.1) fo some M > 0 and 1 < p <. Then, thee exsts a constant L = LN, M,, j, p) > 0 such that fa + B) fa) L 1 + A p 1 + B p 1) B Poof. Let us set fo evey A, B E N j. j tmes {}}{ X := {b w... w : b R N j, w S N 1 } E N j, m = mn,, j) := dme N j. Hee, fo evey b R N j and w S N 1 the symbol b w... w denotes the element of R N such that b w... w) 1..., = b 1... j w j+1... w, 1,..., = 1...,N. It can be poven that the othogonal complement of X n E N j s zeo, so that span X = E N j.
6 6 F. CAGNETTI Let now {ω 1,..., ω m } X be a not necessaly othonomal) bass fo E N j, wth ω = 1 fo = 1,...,m, and let c 1,..., c m R be such that B = m =1 c ω. We have m ) m ) m 1 ) fa + B) fa) = f A + c ω fa) f A + c ω f A + c ω m 1 + f A + =1 c ω ) f =1 =1 m ) A + c ω + + fa + c1 ω 1 ) fa). =1 It wll be enough to pove that thee exsts C = CN, M,, j, p) such that fo evey l = 1,..., m f c l ω l + A + l 1 =0 ) c ω f =1 l 1 ) A + c ω C 1 + A p 1 + B p 1) B,.) =0 whee we set c 0 := 0 and ω 0 := 0. Then, the concluson wll follow by defnng L := mc. Thans to 1, Poposton 3. and Example 3.10 d), fo evey R E N j and evey ω X the functon t ft ω + R) s convex n R. Hence, defnng Gt) := f t c l ω l +A+ ) l 1 =0 c ω and usng.1), fo evey t 1 we have l 1 ) l 1 ) Gt) G0) f c l ω l + A + c ω f A + c ω = G1) G0) =0 =0 f t c l ω l + A + ) l 1 =0 c ω f A + ) l 1 =0 c ω = t M l 1 p A l 1 p) + t c l ω l + A + c ω + + c ω t M t M t =0 =0 + p 1 t p c l p + p 1 l 1 p) + 1) A + c ω + p 1 t p B p + p 1 p 1 + 1) A p + p 1 p 1 + 1)m p B p ), =0 t whee we set Let us now choose Notcng that t = m B := t p 1 B p = A p 1 + B p 1 ) B, =0 c ) 1. A p 1 + B p 1) 1 p 1 B A p t 1. A p 1 B, and usng the fact that and ae equvalent noms, we obtan.). B p t B p, Next poposton shows that condtons a) and b) of Theoem 1.1 necessaly mply L ν. Poposton.8. Let f C 1 E ) satsfy condtons a) and b) of Theoem 1.1 fo some constants µ 0, L, ν > 0 and 1 < p <. Then L ν. Poof. Let A E, φ Cc ), and let x. By the Mean Value Theoem, fa + φx)) fa) = fa + t φx)) fa) φx) + fa) φx),
7 K-UASICONVEXITY REDUCES TO UASICONVEXITY 7 fo some t 0, 1. Integatng last equalty, snce φ Cc ), we get fa + φx)) fa) dx = fa + t φx)) fa) φx)dx. Hence, usng popety b) fa + φx)) fa) dx L L µ + A + t p φx) ) t φx) dx µ + A + p φx) ) φx) dx, snce the functon t µ + A + t φ ) p t φ s nceasng. Compang last elaton and condton a) we conclude that L ν. We pove now that condton 1.) s stonge than 1.5). Poposton.9. Let j {,...,}, let L > 0, µ 0, 1 < p <, and let f C 1 E N j ) be such that fa + B) fa) L µ + A p + B ) B.3) fo evey A, B E N j. Then, thee exsts a postve constant c f, dependng on f, such that fa) c f 1 + A p ) A E N j. Poof. Let C E N j \ {0} be fxed. Then, by the Mean Value Theoem fo evey A E N j have fa) = fc) + fc + ta C)) fc) A C) + fc) A C), fo some t 0, 1. Thans to.3) fa) fc) + L µ + C + t p A C ) t A C + fc) A C fc) + L µ + C + A C ) p A C + fc) A C,.) snce the functon t µ + C + t A C ) p t A C s nceasng. Concenng the last tem, usng Young s nequalty we have fc) A C fc) p p + A C p p fc) p p + p 1 p we A p + C p ),.5) whee p = p p 1. Snce the functon µ + C + ) p s nceasng n R, usng nequalty we have whee Thus, snce A C A + C, µ + C p + A C ) A C µ + 3 C p + A ) A + C ) max{1, C } µ + 3 C p + A ) 1 + A ) K p max{1, C } 1 + A ) p, K = { mn{µ + 3 C, } f 1 < p <, max{µ + 3 C, } f p. 1 + A ) p C p 1 + A p ), fo some postve constant C p dependng only on p, we have L µ + C + A C ) p A C L C p K p max{1, C } 1 + A p )..6) Combnng.),.5) and.6) the concluson follows.
8 8 F. CAGNETTI We now state some mpotant esults concenng peodc functons. Defnton.10. A functon w : R N R N s s sad to be -peodc f wx + e ) = wx) fo a.e. x R N and evey = 1,...,N, whee {e 1,..., e N } s the canoncal bass of R N. Let d, N. We wll denote wth C per N ; R d ) the space of -peodc functons of C R N ; R d ). Moeove, we wll use the notaton C c ; Rd ) fo the space of functons of class C fom to R d wth compact suppot n. Next lemma wll be extensvely used n the pape. Lemma.11 Helmholtz Decomposton). Fo evey ϕ C pe; R N s ) thee exst two functons φ C pe; R N s 1 ) and ψ C pe; R N s ) such that wth ϕ 1... s = φ) 1... s + ψ 1... s, N b =1 fo 1,..., s = 1,...,N, ψ 1... b 1 b b+1... s x b = 0 fo evey b {1,..., s}..7) Poof. By applyng the usual Helmholtz Decomposton Lemma see 8, Lemma 1) to each component ϕ 1... s of the functon ϕ, the lemma follows. Befoe statng next lemma, we need the followng defnton. Defnton.1. The s-dvegence s the opeato s-dv : C s ; R N ) C; R N s ) defned by s-dvξ) 1... s := N s+1,..., =1 s ξ 1... x s+1... x 1,..., s = 1,...,N, fo evey ξ C s ; R N ). The defnton s analogous when ξ s a Sobolev functon. We ae now eady to state a fundamental Kon-type estmate. Lemma.13. Fo evey p > 1 thee exsts a constant γ = γn, p, s) 1 such that s ψ p dx γ A s+1 s ψ p dx fo evey -peodc functon ψ : R N R N s of class C satsfyng condton.7). Poof. Notce that, fo evey = s + 1,...,, we have N N s ψ) T s s ψ 1... = s 1 x 1... x =1 x s+1... x 1 x s x x =1 s N ψ 1... = s 1 = 0. x s+1... x 1 x s x x x Thus, s + 1) s-dva s+1 s ψ) 1... s N s ) = s s ψ s ψ) T s s s ψ) T s x s+1... x 1... = s = s s+1,..., =1 N s+1,..., =1 N s+1,..., =1 s x s+1... x s ψ) 1... =1 s s ψ 1... s = s s ψ 1... x s+1... x x s+1... x s,
9 K-UASICONVEXITY REDUCES TO UASICONVEXITY 9 whee wth s we denoted the s-th powe of the Laplace opeato. Hence, s ψ 1... s = s + 1 s-dv A s+1 s ψ) s 1... s 1,..., s = 1,...,N. The concluson follows applyng 1, Theoem 10.5 and followng ema. We wll also need the followng genealzaton of Lemma.13. Lemma.1. Fo evey p > 1 thee exsts a constant τ = τn, p, s) 1 such that µ + s ψ ) p s ψ dx τ µ + A s+1 s ψ ) p A s+1 s ψ dx fo evey constant µ 0 and evey -peodc functon ψ : R N R N s of class C satsfyng condton.7). Poof. The poof smply follows by adaptng the poof of 8, Lemma 11 and usng Lemma.13. We conclude ths secton gvng some defntons of hghe ode BV spaces. We set BH ) Ω) : = {u W 1,1 Ω) : D u s a fnte Radon measue } = {u W 1,1 Ω) : 1 u BV Ω; E 1 )}, whee D u stands fo the -th ode dstbutonal gadent of u, and SBH ) Ω) : = {u BH ) Ω) : 1 u SBV Ω; E 1 )} = {u W 1,1 Ω) : 1 u SBV Ω; E 1 )} BH ) Ω). 3. Poof of Theoem 1.1 To pove Theoem 1.1 we wll fst show that, fo evey j =,...,, evey stctly j-quasconvex functon of class C 1 can be extended to a stctly j 1)-quasconvex functon, povded we eque the gadent to be Lpschtz contnuous. In the case 1 < p <, that we pesent below, we actually have to consde a petubed stct j-quasconvexty. Lemma 3.1. Let j {,...,}, 1 < p <, µ 0, and let M j), ν j), and ε be postve constants. Let f j) C 1 E N j ) satsfy the followng condtons: a) stct j-quasconvexty up to a petubaton) f j) A + j φ) f j) A) dx εh j) A) + ν j) µ + A + j p φ ) j φ dx fo evey A E N j and evey φ Cc j; ), whee h j) : E RN j N j 0, + ); b) Lpschtz condton fo gadents) f j) A + B) f j) A) M j) µ + A p + B ) B fo evey A, B E N j. Then thee exsts a functon F j) C 1 E N j+1 ), and a postve constant L j) = L j) p, µ, M j), ν j), j), such that a ) stct j 1)-quasconvexty up to a petubaton) F j) A + j 1 ϕ) F j) A) dx νj) ε µ + A + j 1 ϕ ) p j 1 ϕ dx µ + A j A ) p A j A ε h j) S j A) fo evey A E N j+1 and evey ϕ C j 1 c ; R N j+1 );
10 10 F. CAGNETTI b ) Lpschtz condton fo gadents) F j) A + B) F j) A) L j) µ + A p + B ) B fo evey A, B E N j+1 ; c) F j) extends f j) ) F j) A) = f j) A) A E N j. Poof. Let β > 0 be a constant to be chosen at the end of the poof and defne F j) : E N j+1 R as F j) A) := f j) S j A) + β µ + A j A ) p µ p = f j) S j A) + β ga j A) µ p, whee g s gven by elaton 5.) wth X = E N j+1. Relaton c) s clealy satsfed. Let us show that condton a ) holds tue fo a good choce of β. Let ϕ C pe ; RN j+1 ). By Lemma.11 we can wte ϕ = φ + ψ, whee ψ C pe; R N j+1 ) satsfes condton.7) wth s = j 1, and φ C pe; R N j ). By dffeentatng j 1 tmes the pevous elaton we get j 1 ϕ = j φ + j 1 ψ, wth j 1 ϕ, j 1 ψ Cpe ; EN j+1 ), and j φ Cpe ; EN j ). We have F j) A + j 1 ϕ) F j) A) dx = f j) S j A + j φ + S j j 1 ψ) f j) S j A + j φ) dx + f j) S j A + j φ) f j) S j A) dx + β ga j A + A j j 1 ψ) ga j A)dx =: I 1 + I + I 3. Notce that f j) S j A) E N j. Then, thans to Poposton.5 and usng the fact that ψ s -peodc f j) S j A) S j j 1 ψ dx = f j) S j A) j 1 ψ dx = 0. Hence I 1 = f j) S j A + j φ + S j j 1 ψ) f j) S j A + j φ) f j) S j A) S j j 1 ψ dx. Applyng Lemma 5.6 wth ε = ν j) / thee exsts a postve constant c 1 = c 1 ν j), p, M j) ) > 0 such that I 1 µ νj) + S j A + j φ ) p j φ dx c 1 µ + S j j 1 ψ ) p S j j 1 ψ dx νj) τ c 1 µ + S j A + j φ ) p j φ dx µ + A j j 1 ψ ) p A j j 1 ψ dx,
11 K-UASICONVEXITY REDUCES TO UASICONVEXITY 11 whee τ = τn, p, j 1) s gven by Lemma.1. The petubed stct j-quasconvexty of f j) gves I ν µ j) + S j A + j φ ) p j φ dx εh j) S j A), so that I 1 + I νj) τ c 1 µ + S j A + j φ ) p j φ dx εh j) S j A) µ + A j j 1 ψ ) p A j j 1 ψ dx. We apply now Lemma 5.3 to the fst ntegal of the last expesson wth µ = µ + S j A, x = j φ, and y = j 1 ψ. Recallng that j φ + j 1 ψ = j 1 ϕ we get I 1 + I νj) νj) τ c 1 Usng the fact that 1 < p < and Lemma.1 νj) µ + S j A + j 1 ϕ ) p j 1 ϕ dx εh j) S j A) µ + S j A + j 1 ψ ) p j 1 ψ dx µ + A j j 1 ψ ) p A j j 1 ψ dx. 3.1) µ + S j A + j 1 ψ ) p j 1 ψ dx νj) τ νj) Hence, collectng 3.1) and 3.) I 1 + I νj) νj) µ + j 1 ψ ) p j 1 ψ dx µ + A j j 1 ψ ) p A j j 1 ψ dx. 3.) µ + S j A + j 1 ϕ ) p j 1 ϕ dx εh j) S j A) ) τ c 1 + νj) µ + A j j 1 ψ ) p A j j 1 ψ dx µ + A + j 1 ϕ ) p j 1 ϕ dx εh j) S j A) ) τ c 1 + νj) µ + A j j 1 ψ ) p A j j 1 ψ dx, whee we used once agan the fact that 1 < p <. Snce ga j A) A j E N j+1 -peodc, ga j A) A j j 1 ψ dx = ga j A) j 1 ψ dx = 0, so that I 3 = β gaj A + A j j 1 ψ) ga j A) ga j A) A j j 1 ψ dx. and ψ s
12 1 F. CAGNETTI Let 0 < δ < 1 to be chosen at the end of the poof. Thans to Lemma 5.1 I 3 βθ p µ + A j A + A j j 1 ψ ) p A j j 1 ψ dx βθ p δ p βθ p δ µ + A j j 1 ψ ) p A j j 1 ψ dx µ + A j A ) p A j A, whee n the second nequalty we used Lemma 5.3 wth X = E N j+1, µ = µ, x = A j A and y = A j j 1 ψ. Choosng β = β j) > 0 and δ = δ j) 0, 1) such that we obtan β j) θ p δ j) ) p τ I 1 + I + I 3 νj) c 1 + νj) ), β j) θ p δ j) ε, µ + A + j 1 ϕ ) p j 1 ϕ dx εh j) S j A) ε µ + A j A ) p A j A, so that a ) holds. To chec condton b ), we obseve that the functon g satsfes the hypotheses of Lemma 5.5. Then, fo evey A, B E N j+1 ga + B) ga) C p µ + A + B ) p B, whee C p s a postve constant dependng only on p. Usng last elaton, b), and the fact that β j) depends on ν j), τ and c 1, we conclude that b ) holds fo some postve constant L j) = L j) p, µ, M j), ν j), j). We pass now to the case p. Lemma 3.. Let j {,...,}, p, µ 0, M j) > 0, ν j) > 0, and let θ p and Θ p be gven by Lemma 5.1. Let f j) C 1 E N j ) satsfy the followng condtons: a) stct j-quasconvexty) f j) A + j φ) f j) A) dx ν j) µ + A + j p φ ) j φ dx fo evey A E N j and evey φ C j c; R N j ); b) Lpschtz condton fo gadents) f j) A + B) f j) A) M j) µ + A p + B ) B fo evey A, B E N j. Then thee exsts a functon F j) C 1 E N j+1 ), and a postve constant L j) = L j) p, µ, M j), ν j), j), such that a ) stct j 1)-quasconvexty) F j) A + j 1 ϕ) F j) A) dx ν j) θ p Θ p µ + A + j 1 ϕ ) p j 1 ϕ dx fo evey A E N j+1 and evey ϕ C j 1 c ; R N j+1 );
13 K-UASICONVEXITY REDUCES TO UASICONVEXITY 13 b ) Lpschtz condton fo gadents) F j) A + B) F j) A) L j) µ + A p + B ) B fo evey A, B E N j+1 ; c) F j) extends f j) ) F j) A) = f j) A) A E N j. Poof. Let λ 0, ν j) /Θ p and β > 0 be two constants to be detemned at the end of the poof. We defne F j) : E N j+1 R as F j) A) := f j) S j A) λ µ + S j A ) p + λ µ + S j A + β A j A ) p Let g and g β be defned by 5.) and 5.3) espectvely, wth X = E N j Settng fo evey B E N j we have f j) λ B) := fj) B) λgb), F j) A) = f j) λ S ja) + λg β S j A, A j A).. and Y = A j E N j+1. Condton c) s clea fom the defnton of F j). In ode to chec a ), let ϕ C pe ; RN j+1 ). By epeatng the agument of the pevous poof, we can wte j 1 ϕ = j φ + j 1 ψ, wth j 1 ϕ, j 1 ψ Cpe ; EN j+1 ), and j φ Cpe ; EN j ), whee ψ Cpe ; ) RN j+1 satsfes condton.7) wth s = j 1. Hence, F j) A + j 1 ϕ) F j) A) dx = f j) λ S ja + S j j 1 ϕ) f j) λ S ja + S j j 1 ϕ S j j 1 ψ) dx + f j) λ S ja + j φ) f j) λ S ja) dx + λ gβ S j A + S j j 1 ϕ, A j A + A j j 1 ϕ) g β S j A, A j A) dx =: I 1 + I + I 3. Concenng the second ntegal, snce by peodcty gs j A) j φdx = 0, usng condton a) and Lemma 5.1 we have I = fsj A + j φ) fs j A) dx λ = fsj A + j φ) fs j A) dx λ ν j) λθ p ) gsj A + j φ) gs j A) dx gsj A + j φ) gs j A) + gs j A) j φ dx µ + S j A + j p φ ) j φ dx ) Let us pass to the fst ntegal. Notcng that f j) λ S ja) E N j, thans to Poposton.5 and usng the fact that ψ s -peodc, f j) λ S ja) S j j 1 ψ dx = f j) λ S ja) j 1 ψ dx = 0.
14 1 F. CAGNETTI Hence, I 1 = f j) λ S ja + S j j 1 ϕ S j j 1 ψ) f j) λ S ja + S j j 1 ϕ) f j) λ S ja) S j j 1 ψ dx. As obseved n the pevous poof the functon g satsfes condton 5.6), and so by Lemma 5.5 condton b) stll holds fo the functon f λ fo a sutable constant M = Mp, M j), λ) n place of M j). Thus, applyng Lemma 5.6 wth ε = λθ p /, thee exsts a postve constant σ = σp, M j), λ) such that I 1 λθ p σ µ + S j A + S j j 1 ϕ ) p S j j 1 ϕ dx µ + S j A ) p Thans to Lemma.13 and usng 3.3) we get I 1 + I λθ p σ γn,, j 1) S j j 1 ψ dx σ S j j 1 ψ p dx. µ + S j A + S j j 1 ϕ ) p S j j 1 ϕ dx 3.) µ + S j A ) p A j j 1 ψ dx σ γn, p, j 1) A j j 1 ψ p dx. Snce ϕ s -peodc, 0 = g β S j A, A j A) j 1 ϕdx = x g β S j A, A j A) S j j 1 ϕ + y g β S j A, A j A) A j j 1 ϕ dx, so that I 3 = λ gβ S j A + S j j 1 ϕ, A j A + A j j 1 ϕ) g β S j A, A j A) x g β S j A, A j A) S j j 1 ϕ y g β S j A, A j A) A j j 1 ϕ dx. 3.5) We ae now gong to splt I 3 nto two tems. We wll use the fst tem to compensate the sum I 1 + I, and the emanng one to get the stct j 1)-quasconvexty. Relaton 5.5) of Lemma 5. gves I 3 λθ p + λθ pβ µ + S j A + S j j 1 ϕ ) p S j j 1 ϕ dx µ + S j A ) p If we choose β = β j) > 0 so lage that A j j 1 ψ dx + λθ pβ p A j j 1 ψ p dx. 3.6) λθ p β j) ) σγn,, j 1) and λθ p β j) ) p σγn, p, j 1), usng elatons 3.) and 3.6), we have I 1 + I + I 3 I 3.
15 K-UASICONVEXITY REDUCES TO UASICONVEXITY 15 Let us estmate the last tem. Wthout any loss of genealty we can assume β j) 1. Then, ecallng 3.5) and usng nequalty 5.) of Lemma 5. F j) A + j 1 ϕ) F j) A) dx = I 1 + I + I 3 λθ p λθ p = ν j) θ p Θ p whee we chose µ + S j A + S j j 1 ϕ + β j) ) A j A + β j) ) A j j 1 ϕ ) p µ + A + j 1 ϕ ) p j 1 ϕ dx µ + A + j 1 ϕ ) p j 1 ϕ dx, λ = νj) Θ p. S j j 1 ϕ + β j) ) A j j 1 ϕ ) dx One can show that F j) satsfes condton b ) as t was done n the poof of Lemma 3.1. We can now pass to the poof of Theoem 1.1. Poof of Theoem 1.1. Step 1. Case 1 < p <. To smplfy the notaton, fo evey B R N we set PB) := µ + B ) p B, GB) := µ + B ) p µ p. Let ε > 0 be fxed. We stat the poof by applyng Lemma 3.1 wth j =, ν ) = ν, h ) 0 and f ) A) = fa), fo evey A E. Then, we apply agan tmes Lemma 3.1 wth j = 1,,..., espectvely, wth ν j) = ν j, and f j) A) = F j+1) A), fo evey A E N j, whle the functons h j) : E N j 0, + ) wll be chosen as h 1) A) = PA A), h j) A) = PA j+1 A) + =j+ PA S 1... S j+1 A) j =,...,. In ths way afte the last step, coespondng to j =, we obtan a functon F ) : R N R gven by F ) A) := fs S 1... S ) + β ) GA A) + β ) GA S 1... S A). 3.7) Hee, fo evey j =,...,, the constant β j) s gven by the poof of Lemma 3.1 wth the coespondent ndex j. F ) has the followng popetes: a ) stct 1-quasconvexty up to a petubaton) =3 F ) A + ϕ) F ) A) dx εpa A) εh ) S A) + ν 1 µ + A + ϕ ) p ϕ dx
16 16 F. CAGNETTI fo evey A R N and evey ϕ C 1 c ; R N 1 ); b ) Lpschtz condton fo the gadent) F ) A + B) F ) A) L µ + A p + B ) B, fo evey A, B R N, wth L = Lp, µ, M, ν); c) F ) extends f) Now, let us defne F ) A) = fa) A E. { } FA) := nf F ) A + ϕx))dx : ϕ Cpe; R N 1 ) fo evey A R N. Popety a ) mples that fo evey A R N F ) A) εpa A) εh ) S A) FA) F ) A). 3.8) Snce fo evey A E PA A) = h ) S A) = 0, fom popety c) and elaton 3.8) equalty 1.3) follows. Let us chec 1.). Thans to Poposton.9, fom condton b ) we nfe that thee exsts a postve constant c, dependng on the functon F ) and n tun on f, such that F ) A) c 1 + A p ) A R N. Recallng the defntons of the functons P and h ), last elaton and 3.8) gve 1.). Step. Case p. Repeatng the stategy used fo the case 1 < p <, we fst apply Lemma 3. wth j =, ν ) = ν and f ) A) = fa), fo evey A E. Then, we apply agan tmes Lemma 3. wth j = 1,,..., espectvely, wth ) j+1 ν j) θp = ν, Θ p and f j) A) = F j+1) A), fo evey A E N j. Fnally, when j = we obtan a functon F ) : R N R gven by F ) A) = fs... S A) + L ) S A, A A) + whee we set L ) S S 1... S A, A S 1... S A), 3.9) =3 L ) A, B) := ν) µ + A ) p + ν) µ + A + β ) ) B ) p, =,...,, Θ p Θ p and fo evey j =,...,, the constant β j) s gven by the poof of Lemma 3. wth the coespondent ndex j. The functon F ) just defned s such that a ) stct 1-quasconvexty) F ) A + ϕ) F ) A) dx ν ) θp Θ p fo evey A R N and evey ϕ C 1 c ; R N 1 ); µ + A + ϕ ) p ϕ dx
17 K-UASICONVEXITY REDUCES TO UASICONVEXITY 17 b ) Lpschtz condton fo the gadent) F ) A + B) F ) A) L µ + A p + B ) B, fo evey A, B R N, wth L = Lp, µ, M, ν); c) F ) extends f) F ) A) = fa) A E. We clam that the poof s concluded by settng F := F ). Indeed, condton c) gves 1.3), whle 1.) follows by applyng Poposton.9 to F ).. Poof of Theoem 1. To pove the theoem, we fst need two pelmnay lemmas. Lemma.1. Let j {,..., }, 1 < p <, µ 0, ν j) > 0, and let {M j) } N be a sequence of postve constants. Let {f j) } N be a sequence of functons f j) : E N j R satsfyng the followng condtons: a) stct j-quasconvexty up to a petubaton) f j) A + j φ) f j) A) + ν j) dx h j) A) µ + A + j p φ ) j φ dx fo evey A E N j, fo evey φ Cc j; ), and fo evey N, whee {h j) RN j } N s a sequence of functons h j) : E N j 0, + ); b) p-gowth condton) f j) A) M j) 1 + A p ) A E N j, N. : E N j+1 Then thee exsts an nceasng sequence {F j) } N of functons F j) sequences {L j) } N and {λ j) } N of postve numbes, dependng on ν j), M j) a ) stct j 1)-quasconvexty up to a petubaton) F j) A + j 1 ϕ) F j) A) dx νj) R, and two, j, p, µ, such that µ + A + j 1 ϕ ) p j 1 ϕ dx 1 1 S ja p λ j) A j A p h j) S j A) fo evey A E N j+1, fo evey ϕ Cc j 1 ; R N j+1 ), and fo evey N; b ) p-gowth condton) c) F j) extends f j) ) F j) A) L j) 1 + A p ) A E N j+1, N; F j) A) = f j) A) A E N j, N. Poof. Fst we obseve that, thans to Poposton.7, thee exsts a postve constant L =, j, p) we do not stess hee the dependence on N and ), such that LM j) fo evey A, B E N j A E N j+1, we defne f j) A + B) f j) A) L 1 + A p 1 + B p 1) B.1). Let β > 0 be a constant to be chosen at the end of the poof. Fo evey F j) A) := f j) S j A) + β A j A p..)
18 18 F. CAGNETTI Condton c) s clealy satsfed. In ode to show a ), let us consde a functon ϕ C pe; R N j+1 ). We can wte j 1 ϕ = j φ + j 1 ψ, wth j 1 ϕ, j 1 ψ Cpe; E N j+1 ), and j φ Cpe; E N j ), whee ψ Cpe; R N j+1 ) satsfes condton.7) wth s = j 1. Hence, F j) = A + j 1 ϕ) F j) A) f j) dx S j A + j φ + S j j 1 ψ) f j) S j A + j φ) dx + f j) S j A + j φ) f j) S j A) dx Aj + β A + A j j 1 ψ p A j A p dx =: I 1 + I + I 3. By.1) and Young s nequalty, fo evey δ > 0 thee exsts a constant C = CM j), j, p, δ) such that I 1 L 1 + Sj A + j φ p 1 + S j j 1 ψ p 1) S j j 1 ψ dx δ δ S j A p δ j φ p dx C S j j 1 ψ p dx. Usng Lemma.13 I 1 δ δ S j A p δ Thans to Lemma 5., fo evey 0 < ε < 1 I 1 δ1 + εµ p ) δ1 + ε) S j A p C γ 8 δ ε p p j φ p dx C γ A j j 1 ψ p dx..3) A j j 1 ψ p dx µ + S j A + j φ ) p j φ dx. Then, applyng Lemma 5.3 wth µ = 0, x = A j A, and y = A j j 1 ψ, I 1 δ1 + εµ p ) δ1 + ε) S j A p C γ ε p Aj A p C γ ε p A j A + A j j 1 ψ ) p A j j 1 ψ dx 8 δ ε p p µ + S j A + j φ ) p j φ dx. Thus, thee exsts a sequence of postve numbes {λ j) } N, such that fo evey N I 1 µ νj) + S j A + j φ ) p j φ dx λ j) A j A + A j j 1 ψ ) p A j j 1 ψ dx 1 1 S ja p λ j) A j A p. Hee, fo evey fxed N, λ j) = λ j) ν j), M j), j, p, µ). By condton a) I ν j) µ + S j A + j p φ ) j φ dx h j) S j A),
19 K-UASICONVEXITY REDUCES TO UASICONVEXITY 19 so that I 1 + I νj) λ j) µ + S j A + j φ ) p j φ dx A j A + A j j 1 ψ ) p A j j 1 ψ dx 1 1 S ja p λ j) A j A p h j) S j A),.) We focus now on the fst tem of last expesson. Applyng Lemma 5.3 wth µ = µ + A, x = j φ, and y = j 1 ψ, and ecallng that j φ + j 1 ψ = j 1 ϕ we get ν j) µ + S j A + j φ ) p j φ dx µ νj) + A + j φ ) p j φ dx νj) νj) µ + A + j 1 ϕ ) p j 1 ϕ dx µ + A + j 1 ψ ) p j 1 ψ dx, whee n the fst lne we used the fact that 1 < p <. By Lemma.1 last nequalty becomes ν j) µ + S j A + j φ ) p j φ dx µ νj) + A + j 1 ϕ ) p j 1 ϕ dx µ νj) τ + A + A j j 1 ψ ) p A j j 1 ψ dx νj) νj) τ µ + A + j 1 ϕ ) p j 1 ϕ dx A j A + A j j 1 ψ ) p A j j 1 ψ dx,.5) agan explotng that 1 < p <. Collectng.) and.5) we have I 1 + I µ νj) + A + j 1 ϕ ) p j 1 ϕ dx λ j) + νj) τ ) A j A + A j j 1 ψ ) p A j j 1 ψ dx 1 1 S ja p λ j) A j A p h j) S j A)..6) Concenng I 3, usng the peodcty of ψ and thans to Lemma 5.1 wth µ = 0 Aj I 3 = β A + A j j 1 ψ p A j A p p A j A p A j A A j j 1 ψ dx Choosng β = β j) β θ p > 0 such that A j A + A j j 1 ψ ) p A j j 1 ψ dx..7) β j) θ p λ j) + νj) τ,
20 0 F. CAGNETTI fom.6) and.7) we obtan I 1 + I + I 3 νj) µ + A + j 1 ϕ ) p j 1 ϕ dx 1 1 S ja p λ j) so that a ) holds. Fom.) condton b ) follows. A j A p h j) S j A), The second lemma addesses the case p. Lemma.. Let j {,...,}, p, µ 0, ν j) > 0, and let {M j) } N be a sequence of postve constants. Let moeove θ p and Θ p be gven by Lemma 5.1, and let {f j) } N be a sequence of functons f j) : E N j R satsfyng the followng condtons: a) stct j-quasconvexty up to a petubaton) f j) A + j φ) f j) A) + ν j) dx h j) A) µ + A + j p φ ) j φ dx fo evey A E N j, fo evey φ Cc j; RN j ), and fo evey N, whee {h j) } N s a sequence of functons h j) : E N j 0, + ); b) p-gowth condton) f j) A) M j) 1 + A p ) A E N j, N. Then thee exsts an nceasng sequence {F j) } N of functons F j) : E N j+1 sequence {L j) } N of postve numbes, dependng on ν j), M j), j, p, µ, such that a ) stct j 1)-quasconvexty up to a petubaton) F j) A + j 1 ϕ) F j) A) + ν j) θ p Θ p dx h j) S j A) 1 1 S ja p µ + A + j 1 ϕ ) p j 1 ϕ dx fo evey A E N j+1, fo evey ϕ Cc j 1 ; R N j+1 ), and fo evey N; b ) p-gowth condton) c) F j) F j) extends f j) ) F j) A) L j) 1 + A p ) A E N j+1, N; F j) A) = f j) A) A E N j, N. A) := f j) S j A) α R, and a Poof. Let α 0, ν j) /Θ p and β > 0 to be detemned at the end of the poof. We defne µ + S j A ) p µ + S j A + β A j A ) p Condton c) s clealy satsfed. Let now ϕ C pe; R N j+1 ). As usual, we can wte + α j 1 ϕ = j φ + j 1 ψ,..8) wth j 1 ϕ, j 1 ψ Cpe; E N j+1 ), and j φ Cpe; E N j ), whee ψ Cpe; R N j+1 ) satsfes condton.7) wth s = j 1. Settng f j) ) α B) := f j) B) α µ + B ) p
21 K-UASICONVEXITY REDUCES TO UASICONVEXITY 1 fo evey B E N j, we have F j) A + j 1 ϕ) F j) A) dx = f j) ) α S j A + j φ + S j j 1 ψ) f j) ) α S j A + j φ) dx + f j) ) α S j A + j φ) f j) ) α S j A) dx + α gβ S j A + S j j 1 ϕ, A j A + A j j 1 ϕ) g β S j A, A j A) dx =: I 1 + I + I 3, wth g β defned by 5.3), wth X = E N j and Y = A j E N j+1. By epeatng the chan of nequaltes 3.3), one can show f j) ) α s j-quasconvex. In addton, applyng Lemma 5.5 and Poposton.9 to the functon B α µ + B ) p, we have that f j) j) ) α satsfes condton b), fo some postve constant M = place of M j). Thus, by applyng Poposton.7, we can stll conclude that elaton.1) holds M j) α, µ, M j) ) n ) α, fo a sutable constant L = LN, M j),, j, p, α). By epeatng the tue fo the functon f j) same agument of the pevous poof, we get that fo evey δ > 0 thee exsts a postve constant c = cm j), j, p, α, µ, δ) such that I 1 δ δ S j A p δ δ δ S j A p δ c γ A j j 1 ψ p dx. j φ p dx c γ A j j 1 ψ p dx µ + S j A + j φ ) p j φ dx Hence, we can fnd a sequence of postve numbes {λ j) } N such that fo evey N Hee λ j) 3.3) we get = λ j) ) I 1 ν j) α Θ p µ + S j A + j φ ) p j φ dx λ j) A j j 1 ψ p dx 1 1 S ja p. M j), j, p, α, µ) fo evey fxed N,. Adaptng to the pesent stuaton nequalty I = + f j) ) α S j A + j φ) f j) ) α S j A) dx h j) S j A) ) ν j) α Θ p µ + S j A + j p φ ) j φ dx.
22 F. CAGNETTI Moeove, assumng wthout any loss of genealty that β 1, I 3 α θ p µ + A + j 1 ϕ ) p j 1 ϕ dx + αθ p µ + S j A + S j j 1 ϕ ) p S j j 1 ϕ dx + αθ pβ α θ p Let us now choose and β = β j) we obtan µ + S j A ) p > 0 such that A j j 1 ψ dx + αθ pβ p µ + A + j 1 ϕ ) p j 1 ϕ dx + αθ pβ p F j) α = α j) = νj) Θ p, α j) θ p β j) ) p λ j), A + j 1 ϕ) F j) A) dx = I 1 + I + I 3 ν j) θ p Θ p A j j 1 ψ p dx µ + A + j 1 ϕ ) p j 1 ϕ dx h j) S j A) 1 1 S ja p, so that a ) holds. Fnally, condton b ) follows by.8). We ae now eady to pove Theoem 1.. Poof of Theoem 1.. A j j 1 ψ p dx. Step 1. Case 1 < p <. We stat by applyng Lemma.1 wth j =, ν ) = ν and f ) A) = fa), h ) A) = 0 fo evey A E, N. Then, we apply agan tmes Theoem.1 wth j = 1,,..., espectvely, wth ν j) = ν j, and, fo evey A E N j and N, Accodngly, the functons h j) and, fo j =,...,, h j) A) = j f j) wll be chosen as A) = F j+1) A). h 1) A) = S A p + λ ) A A p, =j+ =j+1 S S 1... S j+1 A p + λ j+1) A j+1 A p λ ) A S 1... S j+1 A p,
23 K-UASICONVEXITY REDUCES TO UASICONVEXITY 3 whee the sequences {λ j) } N ae gven by Lemma.1. In ths way afte the last step, coespondng to j =, we obtan a sequence {F ) } N of functons F ) : R N R gven by F ) A) = fs... S A) + β ) A A p + =3 β ) A S 1... S A p. Hee fo =,...,, the sequence {β ) } N s that one gven n the poof of Lemma.1. The functons F ) just defned have the followng popetes: a ) stct 1-quasconvexty up to a petubaton) F ) A + ϕ) F ) A) dx h ) S A) 1 1 S A p + ν 1 µ + A + ϕ ) p h ) S A) 1 1 S A p λ ) A A p ϕ dx λ ) A A p fo evey A R N, fo evey ϕ C 1 c ; RN 1 ), and fo evey N; b ) gowth condton) F ) A) L ) 1 + A p ) A R N, N, wth L ) = L ) ν, M, p, µ) fo evey fxed N; c) F ) extends f) F ) A) = fa) A E, N. Now, fo evey A R N and N, we set { } F A) := nf F ) A + ϕx))dx : ϕ Cpe; R N 1 ). Fom popety a ) t follows that fo evey A R N and fo evey N F ) A) h ) S A) 1 1 S A p λ ) A A p F A) F ) A)..9) Notcng that fo evey A E lm + h) S A) = lm S... S A p = 0, fom popety c) and.9) we have 1.6). Fnally, 1.7) follows fom b ) and.9). =3 Step. Case p. We fst apply Lemma. wth j =, ν ) = ν and f ) A) = fa), h ) A) = 0 fo evey A E, N. At ths pont, we apply agan tmes Lemma. wth j = 1,,..., espectvely, wth ) j+1 ν j) θp = ν, Θ p
24 F. CAGNETTI and, fo evey A E N j and N, f j) A) = F j+1) A), h j) A) = j + 1 S S 1... S j+1 A p. =j+1 Fnally, when j =, we obtan a sequence {F ) } N of functons F ) : R N R gven by whee we set F ) A) = fs... S A) + =3 L ) A, B) := ν) µ + A ) p + ν) Θ p Θ p L ) S S 1... S A, A S 1... S A) + L ) S A, A A),.10) µ + A + β ) The functons F ) just defned have the followng popetes: a ) stct 1-quasconvexty up to a petubaton) ) B ) p, =,...,. F ) A + ϕ) F ) A) dx h ) S A) 1 1 S A p + ν ) θp Θ p h ) S A) 1 1 S A p µ + A + ϕ ) p ϕ dx fo evey A R N, fo evey ϕ C 1 c ; R N 1 ), and fo evey N; b ) gowth condton) c) F ) extends f) F ) A) L ) 1 + A p ) A R N, N; F ) A) = fa) A E, N. Fo evey N, we defne now F as the quasconvexfcaton of the functon F ) { } F A) := nf F ) A + ϕx))dx : ϕ Cpe; R N 1 ) fo evey A R N. Fom popety a ) and by the defnton of F, we have F ) A) h ) S A) 1 1 S A p F A) F ) A), A R N..11) : Notcng that lm + h) S A) = 0 fo all A R N, fom popety c) and.11) we have 1.6). Fnally, 1.7) follows fom b ) and.11)..1. Poof of Theoem 1.3. To conclude the secton, we gve the poof of Theoem 1.3. Poof of Theoem 1.3. It s enough to adapt the poof of 8, Theoem 3 and to use Theoem 1.3.
25 K-UASICONVEXITY REDUCES TO UASICONVEXITY 5 5. Appendx Ths secton contans some auxlay esults used n the est of the pape. Fst, we gve the poof of Poposton.5. Poof of Poposton.5. Snce A E N s 1 and B A s+1 E N s, we can wte A = S s+1 A and B = A s+1 C, fo some C E N s. As a fst step, let us pove that fo evey, l { s+1,..., } wth l we have A T s C T s l = A C T s To fx the deas, let us assume < l. By defnton of tanspose opeatos A T s 1... C T s l = A T s C. 5.1) 1... = A 1... s 1 s s C 1... s 1 l s+1... l 1 s l+1..., fo evey 1,,..., = 1,...,N. In the last expesson, snce A E N s 1 and, l > s, we can exchange the ndces n -th and l-th poston n the fst facto, obtanng A T s 1... C T s l 1... = A 1... s 1 s l l 1 s l+1... C 1... s 1 l s+1... l 1 s l Summng last elaton wth espect to 1,..., and enumeatng the ndces A T s C T s l = = 1,N A T s 1... C T s l , 1,N 1..., A 1... s 1 s l l 1 s l+1... C 1... s 1 l s+1... l 1 s l ,N = A 1... C 1... s 1 s s = A 1... C T 1... = A C T s 1..., 1..., In the same way one can pove the second equalty n 5.1). Let us now pove the poposton. We have s + 1) A B = s + 1) S s+1 A A s+1 C) = A + A T ) s s A T s s C C T s s C T s ) = sa C + s = s+1 = s+1 A T s A T s C C T s = s+1 l= s+1 l = s+1 1,N A C T s A T s C T s l Snce the sum of the fst two tems s zeo, usng elaton 5.1) we get s + 1) A B = s 1) = s 1) = s+1 = s+1 A C T s A C T s s 1) l= s+1 l = s+1 = s+1 A C T s s A C T s = 0. In the emanng pat of the secton we state some lemmas that ae poved n 8. Lemma 5.1. Let X be a Hlbet space, and let g : X R be gven by gx) := µ + x ) p. 5.).
26 6 F. CAGNETTI Fo evey p > 1, thee exst two constants θ p > 0 and Θ p > 0 such that fo evey µ 0 the functon g defned n 5.) satsfes the followng nequaltes fo evey x, y X. θ p µ + x + y ) p y gx + y) gx) gx) y Θ p µ + x + y ) p y Lemma 5.. Let X, Y be Hlbet spaces and let p > 1, µ 0, β 0. Let g β : X Y R be gven by g β x, y) := µ + x + β y ) p. 5.3) Then g β x + ξ, y + η) g β x, y) x g β x, y) ξ y g β x, y) η 5.) θ p µ + x + ξ + β y + β η ) p ξ + β η ) fo evey x, ξ X, y, η Y, whee θ p s the fst constant n Lemma 5.1. Theefoe, f p, we have g β x + ξ, y + η) g β x, y) x g β x, y) ξ y g β x, y) η 5.5) θ p µ + x + ξ ) p ξ + θ pβ µ + x ) p η + θ pβ p η p fo evey x, ξ X, y, η Y. Lemma 5.3. Let X be a Hlbet space and let 1 < p. Then fo evey µ 0 and evey 0 < δ < 1 we have µ + x + y ) p x + y µ + x ) p x + µ + y ) p y, δ p fo evey x, y X. µ + y ) p y Lemma 5.. Let 1 < p. Then fo evey a 0, b 0, µ 0, and 0 < ε < 1. µ + x + y ) p y + δ b p 8ε p p µ + a + b ) p b + εa p + εµ p µ + x ) p Lemma 5.5. Let X be a Hlbet space, and let f C 1 X) C X \ {0}). Assume that thee exst p > 1, C > 0, and µ 0 such that fo evey x X \ {0}. Then x fx) C µ + x ) p 5.6) fx + y) fx) K p C fo evey x, y X, whee K p 1 s a constant dependng only on p. µ + x + y ) p y 5.7) Lemma 5.6. Let X be a Hlbet space and let f C 1 X). Assume that thee exst p > 1 and µ 0 such that fx + y) fx) µ + x + y ) p y fo evey x, y X. If 1 < p, then fo evey ε > 0 thee exsts a constant c 1 = c 1 ε, p) > 0, dependng only on ε and p, such that fx + y + z) fx + y) fx) z ε µ + x + y ) p y + c 1 µ + z ) p z
27 K-UASICONVEXITY REDUCES TO UASICONVEXITY 7 fo evey x, y, z X. If p, then fo evey ε > 0 thee exsts a constant c = c ε, p) > 0, dependng only on ε and p, such that fx + y + z) fx + y) fx) z ε µ + x + y ) p y + c µ + x ) p z + c z p fo evey x, y, z X. 6. Acnowledgments The autho gatefully acnowledges vey useful convesatons wth Iene Fonseca and Govann Leon on the subject of the pape. He also thans the Cente fo Nonlnea Analyss NSF Gants No. DMS and DMS ) fo ts suppot dung the pepaaton of ths pape. Refeences 1 Agmon S., Dougls A., Nenbeg L.: Estmates nea the bounday fo solutons of ellptc patal dffeental equatons satsfyng geneal bounday condtons II. Comm. Pue Appl. Math., ), Amboso L., Fusco N., Pallaa D.: Functons of bounded vaaton and fee dscontnuty poblems. Oxfod Unvesty Pess, New Yo, Ball J.M., Cue J.C., Olve P.: Null Lagangans, wea contnuty, and vaatonal poblems of abtay ode. J. Funct. Anal ), No., Ball J.M., Kchhem B., Kstensen J.: Regulaty of quasconvex envelopes. Calc. Va. Patal Dffeental Equatons, 11/ 000), Caeo M., Leac A., Tomaell F.: Stong mnmzes of Blae & Zsseman functonal. Ann. Scuola Nom. Sup. Psa Cl. Sc ), No. 1-, Chos R., Kohn R.V., Otto F.: Doman banchng n unaxal feomagnets: a scalng law fo the mnmum enegy. Comm. Math. Phys ), No. 1, Cont S., Fonseca I., Leon G.: A Γ-convegence esult fo the two-gadent theoy of phase tanstons. Comm. Pue Appl. Math ), No. 7, Dal Maso G., Fonseca I., Leon G., Mon M.: Hghe-ode quasconvexty educes to quasconvexty. Ach. Raton. Mech. Anal., ), DeSmone A.: Enegy mnmzes fo lage feomagnetc bodes. Ach. Raton. Mech. Anal., ), Fonseca I., Leon G.: Moden methods n the calculus of vaatons: L p spaces. Spnge, New Yo, Fonseca I., Leon G.: A note on Meyes theoem n w,1. Tans. Ame. Math. Soc., 35 00), Fonseca I., Mülle S.: A-quasconvexty, lowe semcontnuty, and Young measues. SIAM J. Math. Anal ), Fusco N.: uasconvexty and semcontnuty fo hghe-ode multple ntegals Italan). Rceche Mat ), No., Gudoz M., Poggoln L.: Lowe semcontnuty fo quasconvex ntegals of hghe ode. NoDEA Nonlnea Dffeental Equatons Appl ), No., Kohn R.V., Mülle S.: Suface enegy and mcostuctue n coheent phase tanstons. Comm. Pue Appl. Math ), No., Kstensen J.: Lowe semcontnuty n spaces of wealy dffeentable functons. Math. Ann ), No., Macelln P.: Appoxmaton of quasconvex functons and lowe semcontnuty of multple ntegals. Manuscpta Math., ), Meyes N.G.: uas-convexty and lowe sem-contnuty of multple vaatonal ntegals of any ode. Tans. Ame. Math. Soc., ), Moey, C.B.: uas-convexty and the lowe semcontnuty of multple ntegals. Pacfc J. Math., 195), Mülle S.: Vaatonal models fo mcostuctues and phase tanstons. Lectue Notes, MPI Lepzg, Owen D.R., Paon R.: Second-ode stuctued defomatons. Ach. Raton. Mech. Anal., ), No 3, Rvèe T., Sefaty S.: Lmtng doman wall enegy fo a poblem elated to mcomagnetcs. Comm. Pue Appl. Math ), No. 3, Toupn, R.A.: Theoes of elastcty wth couple-stess. Ach. Raton. Mech. Anal., ),
28 8 F. CAGNETTI Depatment of Mathematcal Scences, Canege Mellon Unvesty, Pttsbugh, PA 1513, USA E-mal addess, Flppo Cagnett:
8 Baire Category Theorem and Uniform Boundedness
 8 Bae Categoy Theoem and Unfom Boundedness Pncple 8.1 Bae s Categoy Theoem Valdty of many esults n analyss depends on the completeness popety. Ths popety addesses the nadequacy of the system of atonal
8 Bae Categoy Theoem and Unfom Boundedness Pncple 8.1 Bae s Categoy Theoem Valdty of many esults n analyss depends on the completeness popety. Ths popety addesses the nadequacy of the system of atonal
Set of square-integrable function 2 L : function space F
 Set of squae-ntegable functon L : functon space F Motvaton: In ou pevous dscussons we have seen that fo fee patcles wave equatons (Helmholt o Schödnge) can be expessed n tems of egenvalue equatons. H E,
Set of squae-ntegable functon L : functon space F Motvaton: In ou pevous dscussons we have seen that fo fee patcles wave equatons (Helmholt o Schödnge) can be expessed n tems of egenvalue equatons. H E,
APPLICATIONS OF SEMIGENERALIZED -CLOSED SETS
 Intenatonal Jounal of Mathematcal Engneeng Scence ISSN : 22776982 Volume Issue 4 (Apl 202) http://www.mes.com/ https://stes.google.com/ste/mesounal/ APPLICATIONS OF SEMIGENERALIZED CLOSED SETS G.SHANMUGAM,
Intenatonal Jounal of Mathematcal Engneeng Scence ISSN : 22776982 Volume Issue 4 (Apl 202) http://www.mes.com/ https://stes.google.com/ste/mesounal/ APPLICATIONS OF SEMIGENERALIZED CLOSED SETS G.SHANMUGAM,
Generating Functions, Weighted and Non-Weighted Sums for Powers of Second-Order Recurrence Sequences
 Geneatng Functons, Weghted and Non-Weghted Sums fo Powes of Second-Ode Recuence Sequences Pantelmon Stăncă Aubun Unvesty Montgomey, Depatment of Mathematcs Montgomey, AL 3614-403, USA e-mal: stanca@studel.aum.edu
Geneatng Functons, Weghted and Non-Weghted Sums fo Powes of Second-Ode Recuence Sequences Pantelmon Stăncă Aubun Unvesty Montgomey, Depatment of Mathematcs Montgomey, AL 3614-403, USA e-mal: stanca@studel.aum.edu
If there are k binding constraints at x then re-label these constraints so that they are the first k constraints.
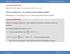 Mathematcal Foundatons -1- Constaned Optmzaton Constaned Optmzaton Ma{ f ( ) X} whee X {, h ( ), 1,, m} Necessay condtons fo to be a soluton to ths mamzaton poblem Mathematcally, f ag Ma{ f ( ) X}, then
Mathematcal Foundatons -1- Constaned Optmzaton Constaned Optmzaton Ma{ f ( ) X} whee X {, h ( ), 1,, m} Necessay condtons fo to be a soluton to ths mamzaton poblem Mathematcally, f ag Ma{ f ( ) X}, then
Energy in Closed Systems
 Enegy n Closed Systems Anamta Palt palt.anamta@gmal.com Abstact The wtng ndcates a beakdown of the classcal laws. We consde consevaton of enegy wth a many body system n elaton to the nvese squae law and
Enegy n Closed Systems Anamta Palt palt.anamta@gmal.com Abstact The wtng ndcates a beakdown of the classcal laws. We consde consevaton of enegy wth a many body system n elaton to the nvese squae law and
PHYS 705: Classical Mechanics. Derivation of Lagrange Equations from D Alembert s Principle
 1 PHYS 705: Classcal Mechancs Devaton of Lagange Equatons fom D Alembet s Pncple 2 D Alembet s Pncple Followng a smla agument fo the vtual dsplacement to be consstent wth constants,.e, (no vtual wok fo
1 PHYS 705: Classcal Mechancs Devaton of Lagange Equatons fom D Alembet s Pncple 2 D Alembet s Pncple Followng a smla agument fo the vtual dsplacement to be consstent wth constants,.e, (no vtual wok fo
Integral Vector Operations and Related Theorems Applications in Mechanics and E&M
 Dola Bagayoko (0) Integal Vecto Opeatons and elated Theoems Applcatons n Mechancs and E&M Ι Basc Defnton Please efe to you calculus evewed below. Ι, ΙΙ, andιιι notes and textbooks fo detals on the concepts
Dola Bagayoko (0) Integal Vecto Opeatons and elated Theoems Applcatons n Mechancs and E&M Ι Basc Defnton Please efe to you calculus evewed below. Ι, ΙΙ, andιιι notes and textbooks fo detals on the concepts
GENERALIZATION OF AN IDENTITY INVOLVING THE GENERALIZED FIBONACCI NUMBERS AND ITS APPLICATIONS
 #A39 INTEGERS 9 (009), 497-513 GENERALIZATION OF AN IDENTITY INVOLVING THE GENERALIZED FIBONACCI NUMBERS AND ITS APPLICATIONS Mohaad Faokh D. G. Depatent of Matheatcs, Fedows Unvesty of Mashhad, Mashhad,
#A39 INTEGERS 9 (009), 497-513 GENERALIZATION OF AN IDENTITY INVOLVING THE GENERALIZED FIBONACCI NUMBERS AND ITS APPLICATIONS Mohaad Faokh D. G. Depatent of Matheatcs, Fedows Unvesty of Mashhad, Mashhad,
Distinct 8-QAM+ Perfect Arrays Fanxin Zeng 1, a, Zhenyu Zhang 2,1, b, Linjie Qian 1, c
 nd Intenatonal Confeence on Electcal Compute Engneeng and Electoncs (ICECEE 15) Dstnct 8-QAM+ Pefect Aays Fanxn Zeng 1 a Zhenyu Zhang 1 b Lnje Qan 1 c 1 Chongqng Key Laboatoy of Emegency Communcaton Chongqng
nd Intenatonal Confeence on Electcal Compute Engneeng and Electoncs (ICECEE 15) Dstnct 8-QAM+ Pefect Aays Fanxn Zeng 1 a Zhenyu Zhang 1 b Lnje Qan 1 c 1 Chongqng Key Laboatoy of Emegency Communcaton Chongqng
Chapter Fifiteen. Surfaces Revisited
 Chapte Ffteen ufaces Revsted 15.1 Vecto Descpton of ufaces We look now at the vey specal case of functons : D R 3, whee D R s a nce subset of the plane. We suppose s a nce functon. As the pont ( s, t)
Chapte Ffteen ufaces Revsted 15.1 Vecto Descpton of ufaces We look now at the vey specal case of functons : D R 3, whee D R s a nce subset of the plane. We suppose s a nce functon. As the pont ( s, t)
ON THE FRESNEL SINE INTEGRAL AND THE CONVOLUTION
 IJMMS 3:37, 37 333 PII. S16117131151 http://jmms.hndaw.com Hndaw Publshng Cop. ON THE FRESNEL SINE INTEGRAL AND THE CONVOLUTION ADEM KILIÇMAN Receved 19 Novembe and n evsed fom 7 Mach 3 The Fesnel sne
IJMMS 3:37, 37 333 PII. S16117131151 http://jmms.hndaw.com Hndaw Publshng Cop. ON THE FRESNEL SINE INTEGRAL AND THE CONVOLUTION ADEM KILIÇMAN Receved 19 Novembe and n evsed fom 7 Mach 3 The Fesnel sne
UNIT10 PLANE OF REGRESSION
 UIT0 PLAE OF REGRESSIO Plane of Regesson Stuctue 0. Intoducton Ojectves 0. Yule s otaton 0. Plane of Regesson fo thee Vaales 0.4 Popetes of Resduals 0.5 Vaance of the Resduals 0.6 Summay 0.7 Solutons /
UIT0 PLAE OF REGRESSIO Plane of Regesson Stuctue 0. Intoducton Ojectves 0. Yule s otaton 0. Plane of Regesson fo thee Vaales 0.4 Popetes of Resduals 0.5 Vaance of the Resduals 0.6 Summay 0.7 Solutons /
Links in edge-colored graphs
 Lnks n edge-coloed gaphs J.M. Becu, M. Dah, Y. Manoussaks, G. Mendy LRI, Bât. 490, Unvesté Pas-Sud 11, 91405 Osay Cedex, Fance Astact A gaph s k-lnked (k-edge-lnked), k 1, f fo each k pas of vetces x 1,
Lnks n edge-coloed gaphs J.M. Becu, M. Dah, Y. Manoussaks, G. Mendy LRI, Bât. 490, Unvesté Pas-Sud 11, 91405 Osay Cedex, Fance Astact A gaph s k-lnked (k-edge-lnked), k 1, f fo each k pas of vetces x 1,
Groupoid and Topological Quotient Group
 lobal Jounal of Pue and Appled Mathematcs SSN 0973-768 Volume 3 Numbe 7 07 pp 373-39 Reseach nda Publcatons http://wwwpublcatoncom oupod and Topolocal Quotent oup Mohammad Qasm Manna Depatment of Mathematcs
lobal Jounal of Pue and Appled Mathematcs SSN 0973-768 Volume 3 Numbe 7 07 pp 373-39 Reseach nda Publcatons http://wwwpublcatoncom oupod and Topolocal Quotent oup Mohammad Qasm Manna Depatment of Mathematcs
Hamiltonian multivector fields and Poisson forms in multisymplectic field theory
 JOURNAL OF MATHEMATICAL PHYSICS 46, 12005 Hamltonan multvecto felds and Posson foms n multsymplectc feld theoy Mchael Foge a Depatamento de Matemátca Aplcada, Insttuto de Matemátca e Estatístca, Unvesdade
JOURNAL OF MATHEMATICAL PHYSICS 46, 12005 Hamltonan multvecto felds and Posson foms n multsymplectc feld theoy Mchael Foge a Depatamento de Matemátca Aplcada, Insttuto de Matemátca e Estatístca, Unvesdade
V. Principles of Irreversible Thermodynamics. s = S - S 0 (7.3) s = = - g i, k. "Flux": = da i. "Force": = -Â g a ik k = X i. Â J i X i (7.
 Themodynamcs and Knetcs of Solds 71 V. Pncples of Ievesble Themodynamcs 5. Onsage s Teatment s = S - S 0 = s( a 1, a 2,...) a n = A g - A n (7.6) Equlbum themodynamcs detemnes the paametes of an equlbum
Themodynamcs and Knetcs of Solds 71 V. Pncples of Ievesble Themodynamcs 5. Onsage s Teatment s = S - S 0 = s( a 1, a 2,...) a n = A g - A n (7.6) Equlbum themodynamcs detemnes the paametes of an equlbum
Chapter 23: Electric Potential
 Chapte 23: Electc Potental Electc Potental Enegy It tuns out (won t show ths) that the tostatc foce, qq 1 2 F ˆ = k, s consevatve. 2 Recall, fo any consevatve foce, t s always possble to wte the wok done
Chapte 23: Electc Potental Electc Potental Enegy It tuns out (won t show ths) that the tostatc foce, qq 1 2 F ˆ = k, s consevatve. 2 Recall, fo any consevatve foce, t s always possble to wte the wok done
Multistage Median Ranked Set Sampling for Estimating the Population Median
 Jounal of Mathematcs and Statstcs 3 (: 58-64 007 ISSN 549-3644 007 Scence Publcatons Multstage Medan Ranked Set Samplng fo Estmatng the Populaton Medan Abdul Azz Jeman Ame Al-Oma and Kamaulzaman Ibahm
Jounal of Mathematcs and Statstcs 3 (: 58-64 007 ISSN 549-3644 007 Scence Publcatons Multstage Medan Ranked Set Samplng fo Estmatng the Populaton Medan Abdul Azz Jeman Ame Al-Oma and Kamaulzaman Ibahm
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
P 365. r r r )...(1 365
 SCIENCE WORLD JOURNAL VOL (NO4) 008 www.scecncewoldounal.og ISSN 597-64 SHORT COMMUNICATION ANALYSING THE APPROXIMATION MODEL TO BIRTHDAY PROBLEM *CHOJI, D.N. & DEME, A.C. Depatment of Mathematcs Unvesty
SCIENCE WORLD JOURNAL VOL (NO4) 008 www.scecncewoldounal.og ISSN 597-64 SHORT COMMUNICATION ANALYSING THE APPROXIMATION MODEL TO BIRTHDAY PROBLEM *CHOJI, D.N. & DEME, A.C. Depatment of Mathematcs Unvesty
4.4 Continuum Thermomechanics
 4.4 Contnuum Themomechancs The classcal themodynamcs s now extended to the themomechancs of a contnuum. The state aables ae allowed to ay thoughout a mateal and pocesses ae allowed to be eesble and moe
4.4 Contnuum Themomechancs The classcal themodynamcs s now extended to the themomechancs of a contnuum. The state aables ae allowed to ay thoughout a mateal and pocesses ae allowed to be eesble and moe
Appendix B. Criterion of Riemann-Stieltjes Integrability
 Appendx B. Crteron of Remann-Steltes Integrablty Ths note s complementary to [R, Ch. 6] and [T, Sec. 3.5]. The man result of ths note s Theorem B.3, whch provdes the necessary and suffcent condtons for
Appendx B. Crteron of Remann-Steltes Integrablty Ths note s complementary to [R, Ch. 6] and [T, Sec. 3.5]. The man result of ths note s Theorem B.3, whch provdes the necessary and suffcent condtons for
A. Thicknesses and Densities
 10 Lab0 The Eath s Shells A. Thcknesses and Denstes Any theoy of the nteo of the Eath must be consstent wth the fact that ts aggegate densty s 5.5 g/cm (ecall we calculated ths densty last tme). In othe
10 Lab0 The Eath s Shells A. Thcknesses and Denstes Any theoy of the nteo of the Eath must be consstent wth the fact that ts aggegate densty s 5.5 g/cm (ecall we calculated ths densty last tme). In othe
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
COMPLEMENTARY ENERGY METHOD FOR CURVED COMPOSITE BEAMS
 ultscence - XXX. mcocd Intenatonal ultdscplnay Scentfc Confeence Unvesty of skolc Hungay - pl 06 ISBN 978-963-358-3- COPLEENTRY ENERGY ETHOD FOR CURVED COPOSITE BES Ákos József Lengyel István Ecsed ssstant
ultscence - XXX. mcocd Intenatonal ultdscplnay Scentfc Confeence Unvesty of skolc Hungay - pl 06 ISBN 978-963-358-3- COPLEENTRY ENERGY ETHOD FOR CURVED COPOSITE BES Ákos József Lengyel István Ecsed ssstant
Multipole Radiation. March 17, 2014
 Multpole Radaton Mach 7, 04 Zones We wll see that the poblem of hamonc adaton dvdes nto thee appoxmate egons, dependng on the elatve magntudes of the dstance of the obsevaton pont,, and the wavelength,
Multpole Radaton Mach 7, 04 Zones We wll see that the poblem of hamonc adaton dvdes nto thee appoxmate egons, dependng on the elatve magntudes of the dstance of the obsevaton pont,, and the wavelength,
Test 1 phy What mass of a material with density ρ is required to make a hollow spherical shell having inner radius r i and outer radius r o?
 Test 1 phy 0 1. a) What s the pupose of measuement? b) Wte all fou condtons, whch must be satsfed by a scala poduct. (Use dffeent symbols to dstngush opeatons on ectos fom opeatons on numbes.) c) What
Test 1 phy 0 1. a) What s the pupose of measuement? b) Wte all fou condtons, whch must be satsfed by a scala poduct. (Use dffeent symbols to dstngush opeatons on ectos fom opeatons on numbes.) c) What
4 SingularValue Decomposition (SVD)
 /6/00 Z:\ jeh\self\boo Kannan\Jan-5-00\4 SVD 4 SngulaValue Decomposton (SVD) Chapte 4 Pat SVD he sngula value decomposton of a matx s the factozaton of nto the poduct of thee matces = UDV whee the columns
/6/00 Z:\ jeh\self\boo Kannan\Jan-5-00\4 SVD 4 SngulaValue Decomposton (SVD) Chapte 4 Pat SVD he sngula value decomposton of a matx s the factozaton of nto the poduct of thee matces = UDV whee the columns
A. Proofs for learning guarantees
 Leanng Theoy and Algoths fo Revenue Optzaton n Second-Pce Auctons wth Reseve A. Poofs fo leanng guaantees A.. Revenue foula The sple expesson of the expected evenue (2) can be obtaned as follows: E b Revenue(,
Leanng Theoy and Algoths fo Revenue Optzaton n Second-Pce Auctons wth Reseve A. Poofs fo leanng guaantees A.. Revenue foula The sple expesson of the expected evenue (2) can be obtaned as follows: E b Revenue(,
THE WEIGHTED WEAK TYPE INEQUALITY FOR THE STRONG MAXIMAL FUNCTION
 THE WEIGHTED WEAK TYPE INEQUALITY FO THE STONG MAXIMAL FUNCTION THEMIS MITSIS Abstract. We prove the natural Fefferman-Sten weak type nequalty for the strong maxmal functon n the plane, under the assumpton
THE WEIGHTED WEAK TYPE INEQUALITY FO THE STONG MAXIMAL FUNCTION THEMIS MITSIS Abstract. We prove the natural Fefferman-Sten weak type nequalty for the strong maxmal functon n the plane, under the assumpton
Dilations and Commutant Lifting for Jointly Isometric OperatorsA Geometric Approach
 jounal of functonal analyss 140, 300311 (1996) atcle no. 0109 Dlatons and Commutant Lftng fo Jontly Isometc OpeatosA Geometc Appoach K. R. M. Attele and A. R. Lubn Depatment of Mathematcs, Illnos Insttute
jounal of functonal analyss 140, 300311 (1996) atcle no. 0109 Dlatons and Commutant Lftng fo Jontly Isometc OpeatosA Geometc Appoach K. R. M. Attele and A. R. Lubn Depatment of Mathematcs, Illnos Insttute
Machine Learning 4771
 Machne Leanng 4771 Instucto: Tony Jebaa Topc 6 Revew: Suppot Vecto Machnes Pmal & Dual Soluton Non-sepaable SVMs Kenels SVM Demo Revew: SVM Suppot vecto machnes ae (n the smplest case) lnea classfes that
Machne Leanng 4771 Instucto: Tony Jebaa Topc 6 Revew: Suppot Vecto Machnes Pmal & Dual Soluton Non-sepaable SVMs Kenels SVM Demo Revew: SVM Suppot vecto machnes ae (n the smplest case) lnea classfes that
Rigid Bodies: Equivalent Systems of Forces
 Engneeng Statcs, ENGR 2301 Chapte 3 Rgd Bodes: Equvalent Sstems of oces Intoducton Teatment of a bod as a sngle patcle s not alwas possble. In geneal, the se of the bod and the specfc ponts of applcaton
Engneeng Statcs, ENGR 2301 Chapte 3 Rgd Bodes: Equvalent Sstems of oces Intoducton Teatment of a bod as a sngle patcle s not alwas possble. In geneal, the se of the bod and the specfc ponts of applcaton
THE ISOMORPHISM PROBLEM FOR CAYLEY GRAPHS ON THE GENERALIZED DICYCLIC GROUP
 IJAMM 4:1 (016) 19-30 Mach 016 ISSN: 394-58 Avalale at http://scentfcadvances.co.n DOI: http://dx.do.og/10.1864/amml_710011617 THE ISOMORPHISM PROBEM FOR CAYEY RAPHS ON THE ENERAIZED DICYCIC ROUP Pedo
IJAMM 4:1 (016) 19-30 Mach 016 ISSN: 394-58 Avalale at http://scentfcadvances.co.n DOI: http://dx.do.og/10.1864/amml_710011617 THE ISOMORPHISM PROBEM FOR CAYEY RAPHS ON THE ENERAIZED DICYCIC ROUP Pedo
A Brief Guide to Recognizing and Coping With Failures of the Classical Regression Assumptions
 A Bef Gude to Recognzng and Copng Wth Falues of the Classcal Regesson Assumptons Model: Y 1 k X 1 X fxed n epeated samples IID 0, I. Specfcaton Poblems A. Unnecessay explanatoy vaables 1. OLS s no longe
A Bef Gude to Recognzng and Copng Wth Falues of the Classcal Regesson Assumptons Model: Y 1 k X 1 X fxed n epeated samples IID 0, I. Specfcaton Poblems A. Unnecessay explanatoy vaables 1. OLS s no longe
19 The Born-Oppenheimer Approximation
 9 The Bon-Oppenheme Appoxmaton The full nonelatvstc Hamltonan fo a molecule s gven by (n a.u.) Ĥ = A M A A A, Z A + A + >j j (883) Lets ewte the Hamltonan to emphasze the goal as Ĥ = + A A A, >j j M A
9 The Bon-Oppenheme Appoxmaton The full nonelatvstc Hamltonan fo a molecule s gven by (n a.u.) Ĥ = A M A A A, Z A + A + >j j (883) Lets ewte the Hamltonan to emphasze the goal as Ĥ = + A A A, >j j M A
24-2: Electric Potential Energy. 24-1: What is physics
 D. Iyad SAADEDDIN Chapte 4: Electc Potental Electc potental Enegy and Electc potental Calculatng the E-potental fom E-feld fo dffeent chage dstbutons Calculatng the E-feld fom E-potental Potental of a
D. Iyad SAADEDDIN Chapte 4: Electc Potental Electc potental Enegy and Electc potental Calculatng the E-potental fom E-feld fo dffeent chage dstbutons Calculatng the E-feld fom E-potental Potental of a
REAL ANALYSIS I HOMEWORK 1
 REAL ANALYSIS I HOMEWORK CİHAN BAHRAN The questons are from Tao s text. Exercse 0.0.. If (x α ) α A s a collecton of numbers x α [0, + ] such that x α
REAL ANALYSIS I HOMEWORK CİHAN BAHRAN The questons are from Tao s text. Exercse 0.0.. If (x α ) α A s a collecton of numbers x α [0, + ] such that x α
Scalars and Vectors Scalar
 Scalas and ectos Scala A phscal quantt that s completel chaacteed b a eal numbe (o b ts numecal value) s called a scala. In othe wods a scala possesses onl a magntude. Mass denst volume tempeatue tme eneg
Scalas and ectos Scala A phscal quantt that s completel chaacteed b a eal numbe (o b ts numecal value) s called a scala. In othe wods a scala possesses onl a magntude. Mass denst volume tempeatue tme eneg
The Greatest Deviation Correlation Coefficient and its Geometrical Interpretation
 By Rudy A. Gdeon The Unvesty of Montana The Geatest Devaton Coelaton Coeffcent and ts Geometcal Intepetaton The Geatest Devaton Coelaton Coeffcent (GDCC) was ntoduced by Gdeon and Hollste (987). The GDCC
By Rudy A. Gdeon The Unvesty of Montana The Geatest Devaton Coelaton Coeffcent and ts Geometcal Intepetaton The Geatest Devaton Coelaton Coeffcent (GDCC) was ntoduced by Gdeon and Hollste (987). The GDCC
Uniqueness of Weak Solutions to the 3D Ginzburg- Landau Model for Superconductivity
 Int. Journal of Math. Analyss, Vol. 6, 212, no. 22, 195-114 Unqueness of Weak Solutons to the 3D Gnzburg- Landau Model for Superconductvty Jshan Fan Department of Appled Mathematcs Nanjng Forestry Unversty
Int. Journal of Math. Analyss, Vol. 6, 212, no. 22, 195-114 Unqueness of Weak Solutons to the 3D Gnzburg- Landau Model for Superconductvty Jshan Fan Department of Appled Mathematcs Nanjng Forestry Unversty
Khintchine-Type Inequalities and Their Applications in Optimization
 Khntchne-Type Inequaltes and The Applcatons n Optmzaton Anthony Man-Cho So Depatment of Systems Engneeng & Engneeng Management The Chnese Unvesty of Hong Kong ISDS-Kolloquum Unvestaet Wen 29 June 2009
Khntchne-Type Inequaltes and The Applcatons n Optmzaton Anthony Man-Cho So Depatment of Systems Engneeng & Engneeng Management The Chnese Unvesty of Hong Kong ISDS-Kolloquum Unvestaet Wen 29 June 2009
CSJM University Class: B.Sc.-II Sub:Physics Paper-II Title: Electromagnetics Unit-1: Electrostatics Lecture: 1 to 4
 CSJM Unvesty Class: B.Sc.-II Sub:Physcs Pape-II Ttle: Electomagnetcs Unt-: Electostatcs Lectue: to 4 Electostatcs: It deals the study of behavo of statc o statonay Chages. Electc Chage: It s popety by
CSJM Unvesty Class: B.Sc.-II Sub:Physcs Pape-II Ttle: Electomagnetcs Unt-: Electostatcs Lectue: to 4 Electostatcs: It deals the study of behavo of statc o statonay Chages. Electc Chage: It s popety by
Mechanics Physics 151
 Mechancs Physcs 151 Lectue 18 Hamltonan Equatons of Moton (Chapte 8) What s Ahead We ae statng Hamltonan fomalsm Hamltonan equaton Today and 11/6 Canoncal tansfomaton 1/3, 1/5, 1/10 Close lnk to non-elatvstc
Mechancs Physcs 151 Lectue 18 Hamltonan Equatons of Moton (Chapte 8) What s Ahead We ae statng Hamltonan fomalsm Hamltonan equaton Today and 11/6 Canoncal tansfomaton 1/3, 1/5, 1/10 Close lnk to non-elatvstc
Engineering Mechanics. Force resultants, Torques, Scalar Products, Equivalent Force systems
 Engneeng echancs oce esultants, Toques, Scala oducts, Equvalent oce sstems Tata cgaw-hll Companes, 008 Resultant of Two oces foce: acton of one bod on anothe; chaacteed b ts pont of applcaton, magntude,
Engneeng echancs oce esultants, Toques, Scala oducts, Equvalent oce sstems Tata cgaw-hll Companes, 008 Resultant of Two oces foce: acton of one bod on anothe; chaacteed b ts pont of applcaton, magntude,
Density Functional Theory I
 Densty Functonal Theoy I cholas M. Hason Depatment of Chemsty Impeal College Lonon & Computatonal Mateals Scence Daesbuy Laboatoy ncholas.hason@c.ac.uk Densty Functonal Theoy I The Many Electon Schönge
Densty Functonal Theoy I cholas M. Hason Depatment of Chemsty Impeal College Lonon & Computatonal Mateals Scence Daesbuy Laboatoy ncholas.hason@c.ac.uk Densty Functonal Theoy I The Many Electon Schönge
Exercise Solutions to Real Analysis
 xercse Solutons to Real Analyss Note: References refer to H. L. Royden, Real Analyss xersze 1. Gven any set A any ɛ > 0, there s an open set O such that A O m O m A + ɛ. Soluton 1. If m A =, then there
xercse Solutons to Real Analyss Note: References refer to H. L. Royden, Real Analyss xersze 1. Gven any set A any ɛ > 0, there s an open set O such that A O m O m A + ɛ. Soluton 1. If m A =, then there
Physics 11b Lecture #2. Electric Field Electric Flux Gauss s Law
 Physcs 11b Lectue # Electc Feld Electc Flux Gauss s Law What We Dd Last Tme Electc chage = How object esponds to electc foce Comes n postve and negatve flavos Conseved Electc foce Coulomb s Law F Same
Physcs 11b Lectue # Electc Feld Electc Flux Gauss s Law What We Dd Last Tme Electc chage = How object esponds to electc foce Comes n postve and negatve flavos Conseved Electc foce Coulomb s Law F Same
On the integration of the equations of hydrodynamics
 Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Machine Learning. Spectral Clustering. Lecture 23, April 14, Reading: Eric Xing 1
 Machne Leanng -7/5 7/5-78, 78, Spng 8 Spectal Clusteng Ec Xng Lectue 3, pl 4, 8 Readng: Ec Xng Data Clusteng wo dffeent ctea Compactness, e.g., k-means, mxtue models Connectvty, e.g., spectal clusteng
Machne Leanng -7/5 7/5-78, 78, Spng 8 Spectal Clusteng Ec Xng Lectue 3, pl 4, 8 Readng: Ec Xng Data Clusteng wo dffeent ctea Compactness, e.g., k-means, mxtue models Connectvty, e.g., spectal clusteng
CHARACTERIZATION OF GRADIENT YOUNG MEASURES GENERATED BY HOMEOMORPHISMS IN THE PLANE
 ESAIM: COCV 22 (206) 267 288 DOI: 0.05/cocv/205003 ESAIM: Contol, Optmsaton and Calculus of Vaatons www.esam-cocv.og CHARACTERIZATION OF GRADIENT YOUNG MEASURES GENERATED BY HOMEOMORPHISMS IN THE PLANE
ESAIM: COCV 22 (206) 267 288 DOI: 0.05/cocv/205003 ESAIM: Contol, Optmsaton and Calculus of Vaatons www.esam-cocv.og CHARACTERIZATION OF GRADIENT YOUNG MEASURES GENERATED BY HOMEOMORPHISMS IN THE PLANE
SOME SOLVABILITY THEOREMS FOR NONLINEAR EQUATIONS
 Fixed Point Theoy, Volume 5, No. 1, 2004, 71-80 http://www.math.ubbcluj.o/ nodeacj/sfptcj.htm SOME SOLVABILITY THEOREMS FOR NONLINEAR EQUATIONS G. ISAC 1 AND C. AVRAMESCU 2 1 Depatment of Mathematics Royal
Fixed Point Theoy, Volume 5, No. 1, 2004, 71-80 http://www.math.ubbcluj.o/ nodeacj/sfptcj.htm SOME SOLVABILITY THEOREMS FOR NONLINEAR EQUATIONS G. ISAC 1 AND C. AVRAMESCU 2 1 Depatment of Mathematics Royal
Chapter I Matrices, Vectors, & Vector Calculus 1-1, 1-9, 1-10, 1-11, 1-17, 1-18, 1-25, 1-27, 1-36, 1-37, 1-41.
 Chapte I Matces, Vectos, & Vecto Calculus -, -9, -0, -, -7, -8, -5, -7, -36, -37, -4. . Concept of a Scala Consde the aa of patcles shown n the fgue. he mass of the patcle at (,) can be epessed as. M (,
Chapte I Matces, Vectos, & Vecto Calculus -, -9, -0, -, -7, -8, -5, -7, -36, -37, -4. . Concept of a Scala Consde the aa of patcles shown n the fgue. he mass of the patcle at (,) can be epessed as. M (,
SOME NEW SELF-DUAL [96, 48, 16] CODES WITH AN AUTOMORPHISM OF ORDER 15. KEYWORDS: automorphisms, construction, self-dual codes
![SOME NEW SELF-DUAL [96, 48, 16] CODES WITH AN AUTOMORPHISM OF ORDER 15. KEYWORDS: automorphisms, construction, self-dual codes SOME NEW SELF-DUAL [96, 48, 16] CODES WITH AN AUTOMORPHISM OF ORDER 15. KEYWORDS: automorphisms, construction, self-dual codes](/thumbs/75/72719313.jpg) Факултет по математика и информатика, том ХVІ С, 014 SOME NEW SELF-DUAL [96, 48, 16] CODES WITH AN AUTOMORPHISM OF ORDER 15 NIKOLAY I. YANKOV ABSTRACT: A new method fo constuctng bnay self-dual codes wth
Факултет по математика и информатика, том ХVІ С, 014 SOME NEW SELF-DUAL [96, 48, 16] CODES WITH AN AUTOMORPHISM OF ORDER 15 NIKOLAY I. YANKOV ABSTRACT: A new method fo constuctng bnay self-dual codes wth
Review of Vector Algebra and Vector Calculus Operations
 Revew of Vecto Algeba and Vecto Calculus Opeatons Tpes of vaables n Flud Mechancs Repesentaton of vectos Dffeent coodnate sstems Base vecto elatons Scala and vecto poducts Stess Newton s law of vscost
Revew of Vecto Algeba and Vecto Calculus Opeatons Tpes of vaables n Flud Mechancs Repesentaton of vectos Dffeent coodnate sstems Base vecto elatons Scala and vecto poducts Stess Newton s law of vscost
princeton univ. F 17 cos 521: Advanced Algorithm Design Lecture 7: LP Duality Lecturer: Matt Weinberg
 prnceton unv. F 17 cos 521: Advanced Algorthm Desgn Lecture 7: LP Dualty Lecturer: Matt Wenberg Scrbe: LP Dualty s an extremely useful tool for analyzng structural propertes of lnear programs. Whle there
prnceton unv. F 17 cos 521: Advanced Algorthm Desgn Lecture 7: LP Dualty Lecturer: Matt Wenberg Scrbe: LP Dualty s an extremely useful tool for analyzng structural propertes of lnear programs. Whle there
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Mean Curvature and Shape Operator of Slant Immersions in a Sasakian Space Form
 Mean Cuvatue and Shape Opeato of Slant Immesions in a Sasakian Space Fom Muck Main Tipathi, Jean-Sic Kim and Son-Be Kim Abstact Fo submanifolds, in a Sasakian space fom, which ae tangential to the stuctue
Mean Cuvatue and Shape Opeato of Slant Immesions in a Sasakian Space Fom Muck Main Tipathi, Jean-Sic Kim and Son-Be Kim Abstact Fo submanifolds, in a Sasakian space fom, which ae tangential to the stuctue
MATH 241B FUNCTIONAL ANALYSIS - NOTES EXAMPLES OF C ALGEBRAS
 MATH 241B FUNCTIONAL ANALYSIS - NOTES EXAMPLES OF C ALGEBRAS These are nformal notes whch cover some of the materal whch s not n the course book. The man purpose s to gve a number of nontrval examples
MATH 241B FUNCTIONAL ANALYSIS - NOTES EXAMPLES OF C ALGEBRAS These are nformal notes whch cover some of the materal whch s not n the course book. The man purpose s to gve a number of nontrval examples
ON THE EXTENDED HAAGERUP TENSOR PRODUCT IN OPERATOR SPACES. 1. Introduction
 ON THE EXTENDED HAAGERUP TENSOR PRODUCT IN OPERATOR SPACES TAKASHI ITOH AND MASARU NAGISA Abstract We descrbe the Haagerup tensor product l h l and the extended Haagerup tensor product l eh l n terms of
ON THE EXTENDED HAAGERUP TENSOR PRODUCT IN OPERATOR SPACES TAKASHI ITOH AND MASARU NAGISA Abstract We descrbe the Haagerup tensor product l h l and the extended Haagerup tensor product l eh l n terms of
Thermodynamics of solids 4. Statistical thermodynamics and the 3 rd law. Kwangheon Park Kyung Hee University Department of Nuclear Engineering
 Themodynamcs of solds 4. Statstcal themodynamcs and the 3 d law Kwangheon Pak Kyung Hee Unvesty Depatment of Nuclea Engneeng 4.1. Intoducton to statstcal themodynamcs Classcal themodynamcs Statstcal themodynamcs
Themodynamcs of solds 4. Statstcal themodynamcs and the 3 d law Kwangheon Pak Kyung Hee Unvesty Depatment of Nuclea Engneeng 4.1. Intoducton to statstcal themodynamcs Classcal themodynamcs Statstcal themodynamcs
Physics 2A Chapter 11 - Universal Gravitation Fall 2017
 Physcs A Chapte - Unvesal Gavtaton Fall 07 hese notes ae ve pages. A quck summay: he text boxes n the notes contan the esults that wll compse the toolbox o Chapte. hee ae thee sectons: the law o gavtaton,
Physcs A Chapte - Unvesal Gavtaton Fall 07 hese notes ae ve pages. A quck summay: he text boxes n the notes contan the esults that wll compse the toolbox o Chapte. hee ae thee sectons: the law o gavtaton,
A NOTE ON VERY WEAK SOLUTIONS FOR A CLASS OF NONLINEAR ELLIPTIC EQUATIONS
 SARAJEVO JOURNAL OF MATHEMATICS Vol3 15 2007, 41 45 A NOTE ON VERY WEAK SOLUTIONS FOR A CLASS OF NONLINEAR ELLIPTIC EQUATIONS LI JULING AND GAO HONGYA Abstact We pove a new a pioi estimate fo vey weak
SARAJEVO JOURNAL OF MATHEMATICS Vol3 15 2007, 41 45 A NOTE ON VERY WEAK SOLUTIONS FOR A CLASS OF NONLINEAR ELLIPTIC EQUATIONS LI JULING AND GAO HONGYA Abstact We pove a new a pioi estimate fo vey weak
Tian Zheng Department of Statistics Columbia University
 Haplotype Tansmsson Assocaton (HTA) An "Impotance" Measue fo Selectng Genetc Makes Tan Zheng Depatment of Statstcs Columba Unvesty Ths s a jont wok wth Pofesso Shaw-Hwa Lo n the Depatment of Statstcs at
Haplotype Tansmsson Assocaton (HTA) An "Impotance" Measue fo Selectng Genetc Makes Tan Zheng Depatment of Statstcs Columba Unvesty Ths s a jont wok wth Pofesso Shaw-Hwa Lo n the Depatment of Statstcs at
CENTRAL INDEX BASED SOME COMPARATIVE GROWTH ANALYSIS OF COMPOSITE ENTIRE FUNCTIONS FROM THE VIEW POINT OF L -ORDER. Tanmay Biswas
 J Koean Soc Math Educ Se B: Pue Appl Math ISSNPint 16-0657 https://doiog/107468/jksmeb01853193 ISSNOnline 87-6081 Volume 5, Numbe 3 August 018, Pages 193 01 CENTRAL INDEX BASED SOME COMPARATIVE GROWTH
J Koean Soc Math Educ Se B: Pue Appl Math ISSNPint 16-0657 https://doiog/107468/jksmeb01853193 ISSNOnline 87-6081 Volume 5, Numbe 3 August 018, Pages 193 01 CENTRAL INDEX BASED SOME COMPARATIVE GROWTH
Lecture 28: Convergence of Random Variables and Related Theorems
 EE50: Pobability Foundations fo Electical Enginees July-Novembe 205 Lectue 28: Convegence of Random Vaiables and Related Theoems Lectue:. Kishna Jagannathan Scibe: Gopal, Sudhasan, Ajay, Swamy, Kolla An
EE50: Pobability Foundations fo Electical Enginees July-Novembe 205 Lectue 28: Convegence of Random Vaiables and Related Theoems Lectue:. Kishna Jagannathan Scibe: Gopal, Sudhasan, Ajay, Swamy, Kolla An
Summer Workshop on the Reaction Theory Exercise sheet 8. Classwork
 Joned Physcs Analyss Cente Summe Wokshop on the Reacton Theoy Execse sheet 8 Vncent Matheu Contact: http://www.ndana.edu/~sst/ndex.html June June To be dscussed on Tuesday of Week-II. Classwok. Deve all
Joned Physcs Analyss Cente Summe Wokshop on the Reacton Theoy Execse sheet 8 Vncent Matheu Contact: http://www.ndana.edu/~sst/ndex.html June June To be dscussed on Tuesday of Week-II. Classwok. Deve all
Asymptotically Lacunary Statistical Equivalent Sequence Spaces Defined by Ideal Convergence and an Orlicz Function
 "Science Stays Tue Hee" Jounal of Mathematics and Statistical Science, 335-35 Science Signpost Publishing Asymptotically Lacunay Statistical Equivalent Sequence Spaces Defined by Ideal Convegence and an
"Science Stays Tue Hee" Jounal of Mathematics and Statistical Science, 335-35 Science Signpost Publishing Asymptotically Lacunay Statistical Equivalent Sequence Spaces Defined by Ideal Convegence and an
CSU ATS601 Fall Other reading: Vallis 2.1, 2.2; Marshall and Plumb Ch. 6; Holton Ch. 2; Schubert Ch r or v i = v r + r (3.
 3 Eath s Rotaton 3.1 Rotatng Famewok Othe eadng: Valls 2.1, 2.2; Mashall and Plumb Ch. 6; Holton Ch. 2; Schubet Ch. 3 Consde the poston vecto (the same as C n the fgue above) otatng at angula velocty.
3 Eath s Rotaton 3.1 Rotatng Famewok Othe eadng: Valls 2.1, 2.2; Mashall and Plumb Ch. 6; Holton Ch. 2; Schubet Ch. 3 Consde the poston vecto (the same as C n the fgue above) otatng at angula velocty.
A Study of C-Reducible Finsler Space. With Special Cases
 Matheatcs Today Vol.27(June-2011)( Poc. of Maths Meet 2011) 47-54 ISSN 0976-3228 A Study of C-Reducble Fnsle Space Wth Specal Cases D. Pooja S. Saxena, D. Puneet Swaoop, E. Swat Swaoop Abstact The noton
Matheatcs Today Vol.27(June-2011)( Poc. of Maths Meet 2011) 47-54 ISSN 0976-3228 A Study of C-Reducble Fnsle Space Wth Specal Cases D. Pooja S. Saxena, D. Puneet Swaoop, E. Swat Swaoop Abstact The noton
General viscosity iterative method for a sequence of quasi-nonexpansive mappings
 Avalable onlne at www.tjnsa.com J. Nonlnear Sc. Appl. 9 (2016), 5672 5682 Research Artcle General vscosty teratve method for a sequence of quas-nonexpansve mappngs Cuje Zhang, Ynan Wang College of Scence,
Avalable onlne at www.tjnsa.com J. Nonlnear Sc. Appl. 9 (2016), 5672 5682 Research Artcle General vscosty teratve method for a sequence of quas-nonexpansve mappngs Cuje Zhang, Ynan Wang College of Scence,
BOUNDEDNESS OF THE RIESZ TRANSFORM WITH MATRIX A 2 WEIGHTS
 BOUNDEDNESS OF THE IESZ TANSFOM WITH MATIX A WEIGHTS Introducton Let L = L ( n, be the functon space wth norm (ˆ f L = f(x C dx d < For a d d matrx valued functon W : wth W (x postve sem-defnte for all
BOUNDEDNESS OF THE IESZ TANSFOM WITH MATIX A WEIGHTS Introducton Let L = L ( n, be the functon space wth norm (ˆ f L = f(x C dx d < For a d d matrx valued functon W : wth W (x postve sem-defnte for all
The Order Relation and Trace Inequalities for. Hermitian Operators
 Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
KOEBE DOMAINS FOR THE CLASSES OF FUNCTIONS WITH RANGES INCLUDED IN GIVEN SETS
 Jounal of Applied Analysis Vol. 14, No. 1 2008), pp. 43 52 KOEBE DOMAINS FOR THE CLASSES OF FUNCTIONS WITH RANGES INCLUDED IN GIVEN SETS L. KOCZAN and P. ZAPRAWA Received Mach 12, 2007 and, in evised fom,
Jounal of Applied Analysis Vol. 14, No. 1 2008), pp. 43 52 KOEBE DOMAINS FOR THE CLASSES OF FUNCTIONS WITH RANGES INCLUDED IN GIVEN SETS L. KOCZAN and P. ZAPRAWA Received Mach 12, 2007 and, in evised fom,
The transonic shock in a nozzle, 2-D and 3-D complete Euler systems
 J. Dffeental Equatons 45 8 4 85 www.elseve.com/locate/jde The tansonc shock n a nozzle, -D and 3-D complete Eule systems Zhoupng Xn a,, Hucheng Yn b,c,, a Depatment of Mathematcs and IMS, CUHK, Shatn,
J. Dffeental Equatons 45 8 4 85 www.elseve.com/locate/jde The tansonc shock n a nozzle, -D and 3-D complete Eule systems Zhoupng Xn a,, Hucheng Yn b,c,, a Depatment of Mathematcs and IMS, CUHK, Shatn,
The Unique Solution of Stochastic Differential Equations With. Independent Coefficients. Dietrich Ryter.
 The Unque Soluton of Stochastc Dffeental Equatons Wth Independent Coeffcents Detch Ryte RyteDM@gawnet.ch Mdatweg 3 CH-4500 Solothun Swtzeland Phone +4132 621 13 07 SDE s must be solved n the ant-itô sense
The Unque Soluton of Stochastc Dffeental Equatons Wth Independent Coeffcents Detch Ryte RyteDM@gawnet.ch Mdatweg 3 CH-4500 Solothun Swtzeland Phone +4132 621 13 07 SDE s must be solved n the ant-itô sense
Some Approximate Analytical Steady-State Solutions for Cylindrical Fin
 Some Appoxmate Analytcal Steady-State Solutons fo Cylndcal Fn ANITA BRUVERE ANDRIS BUIIS Insttute of Mathematcs and Compute Scence Unvesty of Latva Rana ulv 9 Rga LV459 LATVIA Astact: - In ths pape we
Some Appoxmate Analytcal Steady-State Solutons fo Cylndcal Fn ANITA BRUVERE ANDRIS BUIIS Insttute of Mathematcs and Compute Scence Unvesty of Latva Rana ulv 9 Rga LV459 LATVIA Astact: - In ths pape we
Learning the structure of Bayesian belief networks
 Lectue 17 Leanng the stuctue of Bayesan belef netwoks Mlos Hauskecht mlos@cs.ptt.edu 5329 Sennott Squae Leanng of BBN Leanng. Leanng of paametes of condtonal pobabltes Leanng of the netwok stuctue Vaables:
Lectue 17 Leanng the stuctue of Bayesan belef netwoks Mlos Hauskecht mlos@cs.ptt.edu 5329 Sennott Squae Leanng of BBN Leanng. Leanng of paametes of condtonal pobabltes Leanng of the netwok stuctue Vaables:
Dynamics of Rigid Bodies
 Dynamcs of Rgd Bodes A gd body s one n whch the dstances between consttuent patcles s constant thoughout the moton of the body,.e. t keeps ts shape. Thee ae two knds of gd body moton: 1. Tanslatonal Rectlnea
Dynamcs of Rgd Bodes A gd body s one n whch the dstances between consttuent patcles s constant thoughout the moton of the body,.e. t keeps ts shape. Thee ae two knds of gd body moton: 1. Tanslatonal Rectlnea
Stellar Astrophysics. dt dr. GM r. The current model for treating convection in stellar interiors is called mixing length theory:
 Stella Astophyscs Ovevew of last lectue: We connected the mean molecula weght to the mass factons X, Y and Z: 1 1 1 = X + Y + μ 1 4 n 1 (1 + 1) = X μ 1 1 A n Z (1 + ) + Y + 4 1+ z A Z We ntoduced the pessue
Stella Astophyscs Ovevew of last lectue: We connected the mean molecula weght to the mass factons X, Y and Z: 1 1 1 = X + Y + μ 1 4 n 1 (1 + 1) = X μ 1 1 A n Z (1 + ) + Y + 4 1+ z A Z We ntoduced the pessue
Chapter 13 - Universal Gravitation
 Chapte 3 - Unesal Gataton In Chapte 5 we studed Newton s thee laws of moton. In addton to these laws, Newton fomulated the law of unesal gataton. Ths law states that two masses ae attacted by a foce gen
Chapte 3 - Unesal Gataton In Chapte 5 we studed Newton s thee laws of moton. In addton to these laws, Newton fomulated the law of unesal gataton. Ths law states that two masses ae attacted by a foce gen
STEINHAUS PROPERTY IN BANACH LATTICES
 DEPARTMENT OF MATHEMATICS TECHNICAL REPORT STEINHAUS PROPERTY IN BANACH LATTICES DAMIAN KUBIAK AND DAVID TIDWELL SPRING 2015 No. 2015-1 TENNESSEE TECHNOLOGICAL UNIVERSITY Cookevlle, TN 38505 STEINHAUS
DEPARTMENT OF MATHEMATICS TECHNICAL REPORT STEINHAUS PROPERTY IN BANACH LATTICES DAMIAN KUBIAK AND DAVID TIDWELL SPRING 2015 No. 2015-1 TENNESSEE TECHNOLOGICAL UNIVERSITY Cookevlle, TN 38505 STEINHAUS
Measure Estimates of Nodal Sets of Polyharmonic Functions
 Chin. Ann. Math. Se. B 39(5), 08, 97 93 DOI: 0.007/s40-08-004-6 Chinese Annals of Mathematics, Seies B c The Editoial Office of CAM and Spinge-Velag Belin Heidelbeg 08 Measue Estimates of Nodal Sets of
Chin. Ann. Math. Se. B 39(5), 08, 97 93 DOI: 0.007/s40-08-004-6 Chinese Annals of Mathematics, Seies B c The Editoial Office of CAM and Spinge-Velag Belin Heidelbeg 08 Measue Estimates of Nodal Sets of
Physics 1501 Lecture 19
 Physcs 1501 ectue 19 Physcs 1501: ectue 19 Today s Agenda Announceents HW#7: due Oct. 1 Mdte 1: aveage 45 % Topcs otatonal Kneatcs otatonal Enegy Moents of Ineta Physcs 1501: ectue 19, Pg 1 Suay (wth copason
Physcs 1501 ectue 19 Physcs 1501: ectue 19 Today s Agenda Announceents HW#7: due Oct. 1 Mdte 1: aveage 45 % Topcs otatonal Kneatcs otatonal Enegy Moents of Ineta Physcs 1501: ectue 19, Pg 1 Suay (wth copason
SOME GENERAL NUMERICAL RADIUS INEQUALITIES FOR THE OFF-DIAGONAL PARTS OF 2 2 OPERATOR MATRICES
 italian jounal of pue and applied mathematics n. 35 015 (433 44) 433 SOME GENERAL NUMERICAL RADIUS INEQUALITIES FOR THE OFF-DIAGONAL PARTS OF OPERATOR MATRICES Watheq Bani-Domi Depatment of Mathematics
italian jounal of pue and applied mathematics n. 35 015 (433 44) 433 SOME GENERAL NUMERICAL RADIUS INEQUALITIES FOR THE OFF-DIAGONAL PARTS OF OPERATOR MATRICES Watheq Bani-Domi Depatment of Mathematics
COLLAPSING WALLS THEOREM
 COLLAPSING WALLS THEOREM IGOR PAK AND ROM PINCHASI Abstact. Let P R 3 be a pyamid with the base a convex polygon Q. We show that when othe faces ae collapsed (otated aound the edges onto the plane spanned
COLLAPSING WALLS THEOREM IGOR PAK AND ROM PINCHASI Abstact. Let P R 3 be a pyamid with the base a convex polygon Q. We show that when othe faces ae collapsed (otated aound the edges onto the plane spanned
Remember: When an object falls due to gravity its potential energy decreases.
 Chapte 5: lectc Potental As mentoned seveal tmes dung the uate Newton s law o gavty and Coulomb s law ae dentcal n the mathematcal om. So, most thngs that ae tue o gavty ae also tue o electostatcs! Hee
Chapte 5: lectc Potental As mentoned seveal tmes dung the uate Newton s law o gavty and Coulomb s law ae dentcal n the mathematcal om. So, most thngs that ae tue o gavty ae also tue o electostatcs! Hee
INTRODUCTION. consider the statements : I there exists x X. f x, such that. II there exists y Y. such that g y
 INRODUCION hs dssetaton s the eadng of efeences [1], [] and [3]. Faas lemma s one of the theoems of the altenatve. hese theoems chaacteze the optmalt condtons of seveal mnmzaton poblems. It s nown that
INRODUCION hs dssetaton s the eadng of efeences [1], [] and [3]. Faas lemma s one of the theoems of the altenatve. hese theoems chaacteze the optmalt condtons of seveal mnmzaton poblems. It s nown that
Optimization Methods: Linear Programming- Revised Simplex Method. Module 3 Lecture Notes 5. Revised Simplex Method, Duality and Sensitivity analysis
 Optmzaton Meods: Lnea Pogammng- Revsed Smple Meod Module Lectue Notes Revsed Smple Meod, Dualty and Senstvty analyss Intoducton In e pevous class, e smple meod was dscussed whee e smple tableau at each
Optmzaton Meods: Lnea Pogammng- Revsed Smple Meod Module Lectue Notes Revsed Smple Meod, Dualty and Senstvty analyss Intoducton In e pevous class, e smple meod was dscussed whee e smple tableau at each
A NOTE ON ELASTICITY ESTIMATION OF CENSORED DEMAND
 Octobe 003 B 003-09 A NOT ON ASTICITY STIATION OF CNSOD DAND Dansheng Dong an Hay. Kase Conell nvesty Depatment of Apple conomcs an anagement College of Agcultue an fe Scences Conell nvesty Ithaca New
Octobe 003 B 003-09 A NOT ON ASTICITY STIATION OF CNSOD DAND Dansheng Dong an Hay. Kase Conell nvesty Depatment of Apple conomcs an anagement College of Agcultue an fe Scences Conell nvesty Ithaca New
COMPUTATIONAL METHODS AND ALGORITHMS Vol. I - Methods of Potential Theory - V.I. Agoshkov, P.B. Dubovski
 METHODS OF POTENTIAL THEORY.I. Agoshkov and P.B. Dubovsk Insttute of Numecal Mathematcs, Russan Academy of Scences, Moscow, Russa Keywods: Potental, volume potental, Newton s potental, smple laye potental,
METHODS OF POTENTIAL THEORY.I. Agoshkov and P.B. Dubovsk Insttute of Numecal Mathematcs, Russan Academy of Scences, Moscow, Russa Keywods: Potental, volume potental, Newton s potental, smple laye potental,
New problems in universal algebraic geometry illustrated by boolean equations
 New poblems in univesal algebaic geomety illustated by boolean equations axiv:1611.00152v2 [math.ra] 25 Nov 2016 Atem N. Shevlyakov Novembe 28, 2016 Abstact We discuss new poblems in univesal algebaic
New poblems in univesal algebaic geomety illustated by boolean equations axiv:1611.00152v2 [math.ra] 25 Nov 2016 Atem N. Shevlyakov Novembe 28, 2016 Abstact We discuss new poblems in univesal algebaic
Solutions HW #2. minimize. Ax = b. Give the dual problem, and make the implicit equality constraints explicit. Solution.
 Solutons HW #2 Dual of general LP. Fnd the dual functon of the LP mnmze subject to c T x Gx h Ax = b. Gve the dual problem, and make the mplct equalty constrants explct. Soluton. 1. The Lagrangan s L(x,
Solutons HW #2 Dual of general LP. Fnd the dual functon of the LP mnmze subject to c T x Gx h Ax = b. Gve the dual problem, and make the mplct equalty constrants explct. Soluton. 1. The Lagrangan s L(x,
Lecture 10 Support Vector Machines II
 Lecture 10 Support Vector Machnes II 22 February 2016 Taylor B. Arnold Yale Statstcs STAT 365/665 1/28 Notes: Problem 3 s posted and due ths upcomng Frday There was an early bug n the fake-test data; fxed
Lecture 10 Support Vector Machnes II 22 February 2016 Taylor B. Arnold Yale Statstcs STAT 365/665 1/28 Notes: Problem 3 s posted and due ths upcomng Frday There was an early bug n the fake-test data; fxed
Math 217 Fall 2013 Homework 2 Solutions
 Math 17 Fall 013 Homework Solutons Due Thursday Sept. 6, 013 5pm Ths homework conssts of 6 problems of 5 ponts each. The total s 30. You need to fully justfy your answer prove that your functon ndeed has
Math 17 Fall 013 Homework Solutons Due Thursday Sept. 6, 013 5pm Ths homework conssts of 6 problems of 5 ponts each. The total s 30. You need to fully justfy your answer prove that your functon ndeed has
A note on almost sure behavior of randomly weighted sums of φ-mixing random variables with φ-mixing weights
 ACTA ET COMMENTATIONES UNIVERSITATIS TARTUENSIS DE MATHEMATICA Volume 7, Number 2, December 203 Avalable onlne at http://acutm.math.ut.ee A note on almost sure behavor of randomly weghted sums of φ-mxng
ACTA ET COMMENTATIONES UNIVERSITATIS TARTUENSIS DE MATHEMATICA Volume 7, Number 2, December 203 Avalable onlne at http://acutm.math.ut.ee A note on almost sure behavor of randomly weghted sums of φ-mxng
10-801: Advanced Optimization and Randomized Methods Lecture 2: Convex functions (Jan 15, 2014)
 0-80: Advanced Optmzaton and Randomzed Methods Lecture : Convex functons (Jan 5, 04) Lecturer: Suvrt Sra Addr: Carnege Mellon Unversty, Sprng 04 Scrbes: Avnava Dubey, Ahmed Hefny Dsclamer: These notes
0-80: Advanced Optmzaton and Randomzed Methods Lecture : Convex functons (Jan 5, 04) Lecturer: Suvrt Sra Addr: Carnege Mellon Unversty, Sprng 04 Scrbes: Avnava Dubey, Ahmed Hefny Dsclamer: These notes
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
q-bernstein polynomials and Bézier curves
 Jounal of Computatonal and Appled Mathematcs 151 (2003) 1-12 q-bensten polynomals and Béze cuves Hall Ouç a, and Geoge M. Phllps b a Depatment of Mathematcs, Dokuz Eylül Unvesty Fen Edebyat Fakültes, Tınaztepe
Jounal of Computatonal and Appled Mathematcs 151 (2003) 1-12 q-bensten polynomals and Béze cuves Hall Ouç a, and Geoge M. Phllps b a Depatment of Mathematcs, Dokuz Eylül Unvesty Fen Edebyat Fakültes, Tınaztepe
